A carbonate-rich lake solution to the phosphate problem of the origin of life

Significance

Phosphate is crucial for the origin of life because it is ubiquitous in key biomolecules. A major issue is that prebiotic syntheses use concentrated phosphate to incorporate phosphate into biomolecules, whereas natural waters are generally phosphate-poor because phosphate reacts with calcium to form low-solubility apatite minerals. Here we show that carbonate-rich lakes can concentrate phosphate to >1 molal levels by locking up calcium in carbonate minerals, which prevents phosphate removal by apatite precipitation. Phosphate-rich lakes may have preferentially formed on the prebiotic Earth because of carbonic acid weathering under CO₂-rich atmospheres and the absence of microbial phosphate consumption. This specifically points to an origin of life in carbonate-rich lakes, and so defines aqueous conditions that prebiotic chemists should consider.

Abstract

Phosphate is central to the origin of life because it is a key component of nucleotides in genetic molecules, phospholipid cell membranes, and energy transfer molecules such as adenosine triphosphate. To incorporate phosphate into biomolecules, prebiotic experiments commonly use molar phosphate concentrations to overcome phosphate’s poor reactivity with organics in water. However, phosphate is generally limited to micromolar levels in the environment because it precipitates with calcium as low-solubility apatite minerals. This disparity between laboratory conditions and environmental constraints is an enigma known as “the phosphate problem.” Here we show that carbonate-rich lakes are a marked exception to phosphate-poor natural waters. In principle, modern carbonate-rich lakes could accumulate up to ∼0.1 molal phosphate under steady-state conditions of evaporation and stream inflow because calcium is sequestered into carbonate minerals. This prevents the loss of dissolved phosphate to apatite precipitation. Even higher phosphate concentrations (>1 molal) can form during evaporation in the absence of inflows. On the prebiotic Earth, carbonate-rich lakes were likely abundant and phosphate-rich relative to the present day because of the lack of microbial phosphate sinks and enhanced chemical weathering of phosphate minerals under relatively CO₂-rich atmospheres. Furthermore, the prevailing CO₂ conditions would have buffered phosphate-rich brines to moderate pH (pH 6.5 to 9). The accumulation of phosphate and other prebiotic reagents at concentration and pH levels relevant to experimental prebiotic syntheses of key biomolecules is a compelling reason to consider carbonate-rich lakes as plausible settings for the origin of life.

Phosphate is central to the origin of life (1–4) because it is a key component of nucleotides, phospholipids, and metabolites such as adenosine triphosphate used in cellular replication, compartmentalization, and energy transfer, respectively (5). A major issue for prebiotic chemistry is that phosphate combines with Ca²⁺ down to micromolar levels to form apatite-group minerals [e.g., Ca₅(PO₄)₃(OH,F,Cl)] or with Fe³⁺ and Al³⁺ in acidic solutions to form Fe/Al phosphates (6). However, laboratory experiments seeking to understand prebiotic phosphorylation (i.e., adding a phosphoryl group to an organic molecule) commonly use ∼1 molal phosphate to overcome phosphate’s poor reactivity with organics in water (2–4, 7, 8). Concentrated phosphate also catalyzes acid/base and nucleophilic reactions and acts as a pH and chemical buffer (8). The geochemical difficulty of forming concentrated phosphate, combined with its central role in prebiotic syntheses, is a long-standing enigma known as “the phosphate problem” (1, 4).

Difficulties with using aqueous phosphate have motivated research on more reactive phosphorylating agents such as struvite (MgNH₄PO₄·6H₂O), polyphosphates, and amidophosphates (9–11), and alternative solvents such as formamide and urea (12, 13). These approaches are generally problematic because the proposed reagents would have been scarce in plausible early Earth environments (10, 14, 15). Reduced phosphorus compounds, such as phosphite $\left({\text{PO}}_3^{3-}\right)$, may also form when water reacts with meteoritic material, and are more reactive and soluble than orthophosphate (1, 16); however, phosphorylation with phosphite primarily yields phosphonates, that is, compounds with P–C bonds vs. P–O–C bonds in organophosphates. These issues have motivated recent proposals for an origin of life in extremely acidic hot spring environments (17), which can accumulate aqueous phosphate as ${\text{H}}_3{\text{PO}}_4^0$ species, but measured phosphate concentrations in acid hot springs are limited to <1 mM (18).

Here we to show that carbonate-rich lakes are an exception to the rule of low phosphate concentrations found in most natural waters. Using environmental data, laboratory experiments, and geochemical models, we find that >1 molal phosphate concentrations could have occurred on the early Earth in carbonate-rich lake environments. This provides a plausible geochemical source of concentrated, soluble phosphate needed in prebiotic syntheses, and points to a specific environment for the origin of life in carbonate-rich lakes.

High Phosphate Concentrations in Present-Day, Carbonate-Rich Lakes

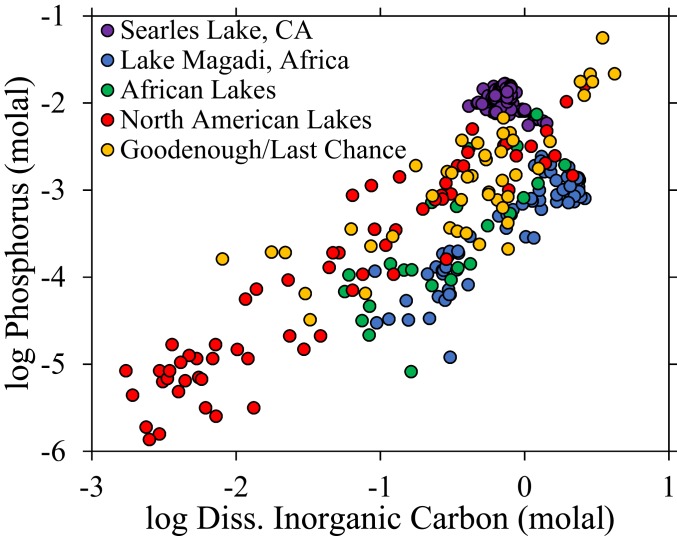
Phosphate concentrations are remarkably high in closed-basin, carbonate-rich lakes and generally increase with increasing carbonate alkalinity (Fig. 1) (see SI Appendix, Appendix A for other dissolved species). Searles Lake, located within the Mojave Desert in California, is an economically important carbonate-, boron-, and sulfate-rich groundwater brine within a dry lake basin that contains 5 to 17 mM phosphate (19). Even higher total phosphorus concentrations are found in Goodenough and Last Chance Lakes in British Columbia, which can exceed 50 mM during periods of desiccation in the summer and autumn (20, 21). Other carbonate-rich lakes, such as Lake Magadi in Africa (22, 23) and Mono Lake in California (24), contain ∼1 mM phosphate.

Fig. 1.

Phosphorus concentrations in carbonate-rich lakes, including Searles Lake (19, 69), Lake Magadi (22, 23), Goodenough and Last Chance Lakes (20, 36), various other North American lakes (36, 69–71), and various other African lakes (72–75). Inorganic phosphate was determined in most analyses; however, the Goodenough and Last Chance Lake analyses are for total phosphorus (inorganic + organic).

Closed-basin lakes accumulate high salt concentrations, including phosphates, from chemical weathering within their hydrologic basins, followed by the inflow of weathering products via streams to evaporating lake brines (25). Carbonate-rich lakes, in particular, develop when atmospheric or volcanogenic CO₂ gas dissolves in water to form carbonic acid $\left({\text{H}}_2{\text{CO}}_3^0\right)$, which chemically weathers rocks to form dissolved cations (Na⁺, K⁺, Ca²⁺, and Mg²⁺) and carbonate alkalinity (${\text{CO}}_3^{2-}$ and ${\text{HCO}}_3^{-}$). Upon evaporation of these fluids, Ca²⁺ and Mg²⁺ ions precipitate as carbonates and silicates, and the residual carbonate alkalinity concentrates as Na–HCO₃–CO₃-rich brine (26).

Phosphate is thought to accumulate in carbonate-rich lakes because the carbonate alkalinity strongly precipitates Ca²⁺ from solution as low-solubility Ca²⁺ carbonates, which allows phosphate to reach much higher concentrations before saturating with respect to apatite (27, 28). However, the specific minerals that control Ca²⁺ and phosphate concentrations, and the maximum phosphate concentrations possible, are unknown because apatites and carbonates form poorly defined and/or metastable phases in carbonate-rich brines. Na⁺, Mg²⁺, ${\text{CO}}_3^{2-}$, ${\text{SO}}_4^{2-}$, and F⁻ ions typically found at high concentrations in carbonate-rich lakes extensively substitute in apatites (26, 29, 30), which greatly influences their solubility, nucleation, and crystallization rate (30). Furthermore, even low phosphate concentrations inhibit the nucleation and growth of both calcite (CaCO₃) and aragonite (a low-temperature CaCO₃ polymorph), so other carbonate phases likely control Ca²⁺ concentrations in carbonate-rich lakes (31). A final issue is that biology cycles organic and inorganic phosphorus in carbonate-rich lakes, which makes it difficult to separate biotic vs. abiotic influences on phosphate concentrations.

Experiments on Phosphate Accumulation in Carbonate-Rich Brines

The preceding considerations motivated a series of experiments to determine how much phosphate can accumulate by abiotic processes in carbonate-rich lakes. We start by noting that carbonate-rich lakes can only accumulate phosphate if Ca²⁺ precipitates in carbonates instead of apatites; otherwise, phosphate will be removed from solution by much higher Ca²⁺ influxes to lake basins. Consequently, how much phosphate can accumulate in carbonate-rich lakes is determined by what phases Ca²⁺ preferentially precipitates in. If Ca²⁺ precipitates as apatite, it will limit phosphate concentrations in the brine. On the other hand, if Ca²⁺ carbonates form, then phosphate can accumulate at higher concentrations.

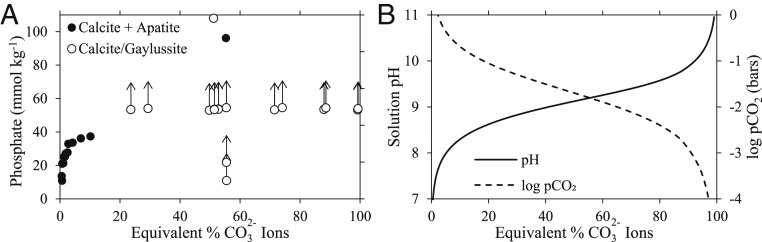
To investigate Ca²⁺ precipitation in phosphate- and carbonate-rich brines, we slowly added Ca²⁺ using gypsum (CaSO₄·2H₂O) and phosphate using Na₂HPO₄ to various saturated Na₂CO₃/NaHCO₃ brines in the laboratory at room temperature (∼23 °C). We then analyzed the salts that precipitated for mineralogy and chemistry (Methods). Results indicate that the formation of apatite and Ca²⁺ carbonate salts depends primarily on the relative concentrations of carbonate $\left({\text{CO}}_3^{2-}\right)$ vs. bicarbonate $\left({\text{HCO}}_3^{-}\right)$ ions in solution (Fig. 2A). High ${\text{CO}}_3^{2-}$ ion concentrations strongly precipitate Ca²⁺ from solution as gaylussite (Na₂CO₃·CaCO₃·5H₂O) and/or calcite (open circles in Fig. 2A), which allows phosphate to accumulate up to ∼100 mmol⋅kg⁻¹. Gaylussite is commonly found in carbonate-rich lakes, such as in Searles Lake and nearby Mono Lake (32); however, the formation of calcite is surprising because even trace phosphate levels inhibit calcite nucleation and growth (31). We infer that calcite probably formed indirectly through incongruent dissolution of primary gaylussite based on the slow conversion of gaylussite to calcite we observed over 4 wk (SI Appendix, Appendix B, Fig. S4), which is supported by observations of gaylussite converting into CaCO₃ in Mono Lake (33, 34).

Fig. 2.

Results from experiments on phosphate- and carbonate-rich brines. (A) The concentration of phosphate in saturated Na–HCO₃–CO₃ brines after 2 wk of equilibration with 50 to 100 mmol⋅kg⁻¹ Ca²⁺ in the form of gypsum (CaSO₄·2H₂O) and initial phosphate concentrations from 10 to 100 mmol⋅kg⁻¹. Solid circles indicate solutions saturated with respect to both apatite and calcite (determined via XRD; see Methods). Open circles indicate solutions that are saturated with respect to calcite and/or gaylussite (Na₂CO₃·CaCO₃·5H₂O); hence, phosphate must be more concentrated than these points for apatite to precipitate (indicated by the upwards arrows). The x axis gives the equivalent percentage of ${\text{CO}}_3^{2-}$ ions relative to the total carbonate alkalinity, that is, $100\times {2\text{CO}}_3^{2-}/\left({2\text{CO}}_3^{2-}+{\text{HCO}}_3^{-}\right)$. (B) The modeled pCO₂ and pH of the experimental saturated Na–HCO₃–CO₃ brines at 25 °C, which correspond to the solutions in A.

At low ${\text{CO}}_3^{2-}$ ion concentrations, Na-rich carbonated apatites and calcite phases occur together, and phosphate concentrations in equilibrium with these minerals decrease with decreasing ${\text{CO}}_3^{2-}$ (black circles near the left of the vertical axis in Fig. 2A). These results are consistent with Ca²⁺ from carbonate salts controlling the solubility of apatite. A decrease in ${\text{CO}}_3^{2-}$ ion concentration increases the solubility of calcite/gaylussite, which increases the concentration of Ca²⁺ in solution and causes phosphate to precipitate as apatite.

The relative proportion of ${\text{CO}}_3^{2-}$ vs. ${\text{HCO}}_3^{-}$ ions in solution also controls the pCO₂ and pH, which we model for the experimental saturated Na–HCO₃–CO₃ brines in Fig. 2B (SI Appendix, Appendix B, Table S1 and Methods). By comparing modeled pCO₂ values to recent estimates ranging from 0.01 to 1 bar CO₂ on the early Earth (35), we find that corresponding phosphate concentrations in our experiments are between 20 and 100 mmol⋅kg⁻¹, respectively. Furthermore, the pH ranges from circumneutral at 1 bar pCO₂ to pH 9 at 0.01 bar pCO₂ in saturated Na–HCO₃–CO₃ brines because the relatively high pCO₂ acidifies the solutions. This suggests that elevated phosphate concentrations could have occurred in CO₂-rich atmospheres on the early Earth.

Evaporative Concentration of Phosphate-Rich Brines

Our experiments indicate that when Ca²⁺ is added to phosphate- and carbonate-rich brines, apatite minerals only precipitate above 10 to 100 mmol⋅kg⁻¹ phosphate. Applied to a closed-basin lake setting, this means that phosphate delivered via streams can accumulate up to ∼100 mmol⋅kg⁻¹; however, at higher phosphate concentrations, Ca²⁺ delivered by stream inflows will precipitate phosphate from solution as apatite. Given that streams have much more Ca²⁺ than phosphate (36), closed-basin lakes in hydrologic balance (i.e., stream inflows balance water loss via evaporation) are constrained to <100 mmol⋅kg⁻¹ phosphate. However, once a phosphate-rich lake forms, the brine contains much more phosphate than Ca²⁺ because Ca²⁺ is sequestered into carbonate minerals (see SI Appendix, Appendix A for lake data). Consequently, in the absence of stream inflows, evaporating lake brines can reach much higher phosphate concentrations. Such evaporation may occur seasonally because of wet and dry cycles. Alternatively, lake brines may desiccate in shoreline environments by evaporation on rocks wetted by wave action or evaporation in local pools.

During lake evaporation (in the absence of Ca-rich stream inflows), phosphate will accumulate in the residual brine until it precipitates with a more concentrated cation as a salt. This phosphate-limiting salt cannot be a Ca²⁺ or Mg²⁺ phase because these ions are minor in carbonate-rich brines. We can also exclude K⁺ because it is minor relative to Na⁺ in carbonate-rich lakes and only precipitates phosphate salts at extremely high concentrations (37). The remaining major cation is Na⁺, which implies that phosphate concentrations will increase in evaporating lake brines until the brine reaches saturation with respect to sodium phosphate salts. In addition, high phosphate concentrations would only form after sodium carbonate/bicarbonate and chloride salts had precipitated because phosphate is minor relative to both carbonate alkalinity and chloride.

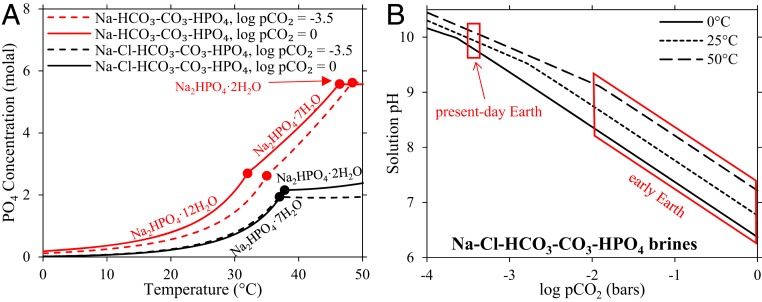
To determine the maximum phosphate concentrations possible in such brines, we model solutions saturated with respect to sodium phosphate, carbonate, and chloride salts at variable temperature (0 to 50 °C) and CO₂ gas pressure (log pCO₂ −3.5 to 0 bars). We find that up to 3 molal phosphate occurs in equilibrium with either Na₂HPO₄·7H₂O or Na₂HPO₄·2H₂O salts (Fig. 3A). Relative to pure sodium phosphate solutions (Fig. 3A, red lines), phosphate concentrations in saturated mixed brines (Fig. 3A, black lines) decrease by about one-third because the additional Na⁺ associated with chlorides and carbonates forces Na₂HPO₄ to precipitate from solution. The carbonate alkalinity precipitates as either nahcolite (NaHCO₃), natron (Na₂CO₃·10H₂O), or trona (Na₂CO₃·NaHCO₃·2H₂O) depending on the pCO₂, and chloride ions precipitate as halite (NaCl).

Fig. 3.

Phosphate concentrations and pH modeled in saturated, carbonate-rich lake brines. (A) The concentration of phosphate in solutions saturated with respect to sodium phosphate. The red lines indicate the solubility of pure Na₂HPO₄·XH₂O, where XH₂O refers to the hydration state (X = 2, 7, and 12). The black lines indicate the solubility of sodium phosphate in solutions saturated with respect to sodium phosphate, chloride, and carbonate salts. Solid lines are for 1 bar atmospheric pCO₂, and dashed lines are for log pCO₂ = −3.5 bar (the pCO₂ of present-day Earth). (B) The pH of solutions saturated with respect to sodium phosphate, chloride, and carbonate salts at variable temperature and pCO₂. The range of pH and temperature of these solutions encompasses that of the black lines in A.

The modeled pH of saturated phosphate brines depends on the temperature and atmospheric pCO₂ (Fig. 3B). At present-day pCO₂ levels, solutions are highly alkaline (pH ∼ 10), consistent with high pHs measured in modern soda lakes (38); however, in CO₂-rich atmospheres on the early Earth (log pCO₂ = −2 to 0) brines range from moderately alkaline (pH 9) to slightly acidic (pH 6.5) because of acidification by CO₂. These are maximum pH values because the solutions are saturated with respect to carbonate alkalinity; hence, for undersaturated solutions the pH will be lower. Temperature also affects the pH because CO₂ is more soluble in solutions at lower temperatures. These results provide a plausible environmental scenario for molar phosphate concentrations at moderate pH levels used in prebiotic syntheses (8).

Carbonate-Rich Lakes on the Early Earth

Carbonate-rich lakes may have been relatively common on early Earth due to strong chemical weathering of abundant, fresh volcanic rocks (39) under early Earth’s CO₂-rich atmosphere (40). Weathering would release phosphate from apatites and carbonate alkalinity from other minerals, which would accumulate in closed basins (41, 42). A potential analog for such carbonate-rich lakes on the early Earth is Lonar Lake in central India, a NaHCO₃-rich lake formed from an impact crater in basalt host rock (43). Lonar Lake also precipitates gaylussite and calcite salts (44), but phosphate concentrations are relatively low (∼5 μM) because algal blooms consume the phosphate (45).

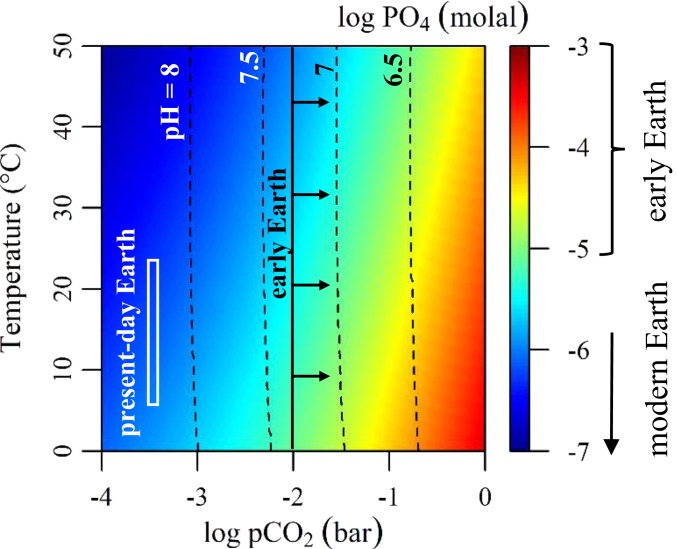
A consequence of early Earth’s CO₂-rich atmosphere is that it would have enhanced the weathering of hydroxyl- and fluorapatites in mafic rocks by lowering the pH of surface waters (46, 47). Apatites are more soluble at lower pH and weather more rapidly in CO₂-acidified stream and rainwater, resulting in potentially high phosphate fluxes to carbonate-rich lakes on the early Earth. By modeling the equilibrium solubility of fluorapatite and hydroxyapatite in the presence of calcite buffer as a function of temperature and CO₂ pressure (Fig. 4 and Methods), we find that relatively low CO₂ pressures on present-day Earth (log pCO₂ = −3.5) limit phosphate to ≤1 μM, which is consistent with phosphate concentrations found in most present-day rivers and surface waters. However, in CO₂-rich atmospheres relevant to the early Earth (pCO₂ = 0.01 to 1 bar) (35, 40), modeled phosphate concentrations are 10 to 100 times higher, which implies a much higher phosphate weathering flux on the early Earth from streams into lakes.

Fig. 4.

Modeled phosphate concentrations (log PO₄) in equilibrium with fluorapatite, hydroxylapatite, and calcite at variable pCO₂ and temperature relevant to the release of phosphate into streams that supply lakes. The pH is given by dashed contours at 0.5-pH intervals.

Phosphate concentrations were likely higher in prebiotic, carbonate-rich lakes because microbial phosphate sinks were absent. Modern carbonate-rich lake environments are some of the most productive ecosystems on Earth in terms of biomass turnover because of high nutrient levels (38). As a result, phosphate measured in modern carbonate-rich lakes is probably a minimum because microbes consume the phosphate and eventually deposit it in organic matter. This may explain why Lake Magadi in Africa, a surface lake with high biomass turnover, has over 10 times lower phosphate concentrations than Searles Lake (which cannot support photosynthetic microbes because it is a groundwater brine), despite the much higher carbonate alkalinity found in Lake Magadi (Fig. 1). Consequently, in the absence of microbial consumption, carbonate-rich lakes on the prebiotic Earth may have hosted higher phosphate concentrations than typically occur today.

A potential sink for soluble phosphate on the early Earth is reduced soluble iron (Fe²⁺), which precipitates with phosphate as the low-solubility mineral vivianite [Fe₃(PO₄)₂·8H₂O]. However, Fe²⁺ also precipitates as siderite (FeCO₃) in carbonate-rich brines, which limits Fe²⁺ to low levels and increases the solubility of phosphate from vivianite, similar to solubility relations in the CaCO₃–apatite system shown in Fig. 2. Furthermore, siderite is less soluble than calcite, and unlike calcite, the nucleation and growth of siderite is not inhibited by phosphate. Although siderite crystallizes relatively slowly from solution at low temperatures (48), near-equilibrium conditions occur on a timescale of hours to days, which is fast relative to inflow and evaporation processes in closed-basin lakes. This implies that Fe²⁺ concentrations in anoxic, phosphate- and carbonate-rich brines will be lower than Ca²⁺, which suggests that Ca²⁺, not Fe²⁺, would have controlled phosphate concentrations in carbonate-rich lakes on the early Earth.

Implications for Prebiotic Chemistry

Our experiments and model results show that carbonate-rich lakes on the early Earth would have accumulated phosphate at concentration and pH levels relevant to laboratory prebiotic syntheses. Molar phosphate concentrations can occur during evaporation in lake marginal pools, on rocks wetted by wave action, and in shore sediments. Drying promotes condensation reactions such as phosphorylation by removing water (49), as well as more generally facilitating polymerization reactions (50). Condensation reactions may also have been promoted by deliquescence of highly soluble evaporites (51). Furthermore, carbonate-rich lakes are rich in clay, zeolite, and silica mineral assemblages that catalyze phosphorylation reactions because of their high reactive surface areas (52). Once phosphate reacts, changing lake levels or wave action could reintroduce the reaction products to the lake, or reaction products could undergo successive wet–dry cycles.

More broadly, closed-basin lakes are ideal sites for “one-pot” organic syntheses because they accumulate and concentrate reagents via evaporation across hydrologic basins (41, 49, 53). As a result, closed-basin lakes may have accumulated organic precursors for phosphorylation, as well as condensation agents that promote phosphorylation by forming reactive intermediate ${\text{PO}}_3^{-}$ species (54) and polyphosphates (14). Boron also accumulates at high concentrations in closed-basin lakes (e.g., Searles Lake contains ∼0.5 molal boron; SI Appendix, Appendix A), which promotes the regioselective phosphorylation of ribose and stabilizes the furanose form needed to synthesize nucleic acids (55).

A difficulty for an origin of life in saline lakes is that high salt concentrations tend to destabilize lipid vesicles (56) and inhibit RNA oligimerization (57), but these issues are potentially resolvable. For example, lipid vesicles can stabilize in high-salt environments by binding to nucleotides and/or amino acids (58, 59). Given that concentrated prebiotic reagents and wet/dry cycles often used in the laboratory imply saline environments, more research is needed on prebiotic chemistry in salty solutions.

Recent attempts at “one-pot” syntheses have proposed closed-basin lakes as sites for the formation of amino acids, nucleotides, and lipid precursors in reaction networks involving ultraviolet light, phosphate, sulfur, and cyanide (53, 60). Our results indicate that high phosphate concentrations used in these reaction networks (8) plausibly occurred in carbonate-rich lake environments. Furthermore, the key cyanide component needed for this chemistry also preferentially accumulates in carbonate-rich lakes to make sodium ferrocyanide evaporites, which thermally decompose to sodium cyanide above 700 °C (possibly via magmatic activity or flash heating from asteroid impacts) (42, 53, 61). Concentrated sulfur needed for prebiotic syntheses may also have accumulated as sulfite ions (62). Consequently, carbonate-rich lakes accumulate a number of key reagents at high concentrations relevant to experimental prebiotic syntheses.

Conclusions

The results presented here show that carbonate-rich lakes accumulate phosphate because Ca²⁺ preferentially precipitates in gaylussite and/or calcite, which increases the solubility of apatites. In carbonate-rich lakes influenced by stream inflows, phosphate levels are limited to <0.1 molal because excess Ca²⁺ in stream water precipitates apatite above this phosphate concentration threshold. However, in the absence of stream inflows, phosphate can enrich to >1 molal levels during evaporation because phosphate concentrations exceed Ca²⁺ in carbonate-rich lakes. Such evaporation could occur continuously along lake margins, or during dry seasons.

Carbonate-rich lake environments were likely common on the early Earth due to chemical weathering of mafic rocks in early Earth’s CO₂-rich atmosphere, and would have been relatively phosphate-rich compared to the present day because of efficient weathering of apatite minerals and the lack of microbial phosphate sinks. Furthermore, phosphate-rich brines on the early Earth would have had slightly acidic to moderately basic pH (pH 6.5 to 9) because of elevated atmospheric CO₂ levels. Thus, carbonate-rich lakes are highly plausible environments for accumulating phosphate at concentration and pH levels relevant to laboratory syntheses of prebiotic organophosphate compounds. Given the central importance of phosphate in cellular processes, and that phosphate occurs at micromolar concentrations elsewhere, our results specifically point to carbonate-rich lakes as sites for prebiotic chemistry and the origin of life.

Methods

Experimental Ca²⁺ and Phosphate Precipitation in Carbonate-Rich Brines.

The goal of these experiments was to determine which salt phases precipitate Ca²⁺ and phosphate ions in phosphate- and carbonate-rich brines. To achieve this, we added gypsum (CaSO₄·2H₂O) to phosphate- and carbonate-rich brines prepared in the laboratory, and allowed the mixtures to react over 1 to 4 wk. The rationale behind this methodology is that the gypsum will slowly dissolve because it is sparingly soluble, gradually adding Ca²⁺ to solution, which approximates the slow addition of Ca²⁺ via inflow waters to closed-basin lakes. A potential complication to using gypsum as the Ca²⁺ source is that gypsum will also add ${\text{SO}}_4^{2-}$ ions to solution; however, the added ${\text{SO}}_4^{2-}$ is <0.1 molal does not precipitate as a solid phase, and is not expected to interfere with the precipitation of carbonate or phosphate salts. After equilibration of the solution, we analyzed the resulting solid phases using inductively coupled optical emission spectroscopy (ICP-OES) and X-ray diffraction (XRD). The detailed results of these experiments are given in SI Appendix, Appendix B.

To prepare phosphate- and carbonate-rich brines, we gravimetrically added NaHCO₃, Na₂CO₃, Na₂HPO₄, and NaF reagents to 150 mL of deionized water in 250-mL polyethylene bottles. We added the NaHCO₃ and Na₂CO₃ reagents in varying proportions ranging from pure NaHCO₃ to pure Na₂CO₃ to make nearly saturated solutions (i.e., the concentration just below the point at which salt precipitates). We determined the saturation point for each Na–HCO₃–CO₃ mixture at 25 °C using the THEREDA Pitzer model described in Geochemical Models. We added the Na₂HPO₄ reagent at concentrations ranging from 10 to 500 mmol⋅kg⁻¹, and the NaF reagent at 0 and 10 mmol⋅kg⁻¹. Finally, we added Ca²⁺ in the form of gypsum, capped the solutions, and agitated them with an orbital shaker for 1 to 4 wk.

We performed 4 series of experiments using the brine mixtures described above:

• 1)We varied the initial NaHCO₃:Na₂CO₃ ratio at constant equilibration time (2 wk) and initial phosphate concentration (50 mmol⋅kg⁻¹, the highest concentration measured in carbonate-rich lakes).
• 2)We varied the equilibration time at constant initial NaHCO₃:Na₂CO₃ ratio (0.6:0.4) and initial phosphate concentration (50 mmol⋅kg⁻¹).
• 3)We varied the initial phosphate concentration at constant equilibration time (2 wk) and initial NaHCO₃:Na₂CO₃ ratio (0.6:0.4).
• 4)We repeated experiments 1 and 3 described above with the addition of 10 mmol⋅kg⁻¹ F⁻. These experiments are motivated by relatively high F⁻ concentration commonly found in carbonate-rich lakes (SI Appendix, Appendix B), and because F⁻ strongly precipitates with Ca²⁺ and phosphate in natural systems to form fluorapatites.

Analysis of Solids after Equilibration.

After the brine/salt mixtures equilibrated, we removed the solid phases by filtering. We then removed excess brine from the filtered solids by rinsing with ethanol and dried them in air for ∼10 min. We then powdered the solid samples and analyzed them using a Bruker D8 Discover XRD from 10 to 60° 2θ. Furthermore, we analyzed the solids for Na, Ca, S, and P using ICP-OES. To prepare the solid samples for ICP-OES analysis, we first dried the samples in a vacuum oven at 60 °C overnight, and then acidified weighed aliquots of the dried samples (∼50 mg) with 1 mL of ∼2 M nitric acid (which completely dissolved the solid). The acid-dissolved samples were then diluted as needed for ICP-OES analysis.

We calculated the ${\text{CO}}_3^{2-}$ content of the equilibrated solid phases (on a dry weight basis) by assuming molar charge balance via the equation

$$\left[{\text{CO}}_3^{2-}\right]=\left[{\text{Ca}}^{2+}\right]+\frac{\left[{\text{Na}}^{+}\right]}{2}-\frac{3}{2}\left[{\text{PO}}_4^{3-}\right]-\left[{\text{SO}}_4^{2-}\right].$$ [1]

The total calculated weight percent of Ca²⁺, Na⁺, ${\text{PO}}_4^{3-}$, ${\text{SO}}_4^{2-}$, and ${\text{CO}}_3^{2-}$ components on a dry basis is typically within several percentage of 100% (SI Appendix, Appendix B, Table S2).

Calculation of Aqueous Species after Equilibration.

To calculate ion concentrations in the solutions after equilibration, we assumed that all of the Ca²⁺ had completely precipitated as solid phases; consequently, the total concentration of all other ions precipitated from solution may be determined relative to Ca²⁺. We also tested this assumption on a representative suite of samples and found that ∼99.9% of the Ca²⁺ remained in solid phases over the course of the experiments (see discussion in SI Appendix, Appendix B). For any given ion X, the concentration in solution after equilibration is given by

$${\left[\text{X}\right]}_{\text{final}\hspace{0.17em}\text{solution}}={\left[\text{X}\right]}_{\text{initial}\hspace{0.17em}\text{solution}}-{\left[{\text{Ca}}^{2+}\right]}_{\text{total}}{\left(\frac{\left[\text{X}\right]}{\left[{\text{Ca}}^{2+}\right]}\right)}_{\text{solid}},$$ [2]

where subscripts indicate concentrations in the equilibrated solid, the initial, and the final solutions. We neglect F⁻ concentrations because this ion is minor in the experimental solutions. Finally, to determine the pH, pCO₂, and inorganic carbon speciation of the equilibrated solutions, we modeled the solution composition determined above in equilibrium with 100 mL of headspace gas, which is the headspace volume in our experiments, using the THEREDA Pitzer model at 25 °C (described in Geochemical Models).

Geochemical Models.

We use two approaches to model phosphate solubility at variable temperature and composition. To model solution chemistry at relatively low concentrations in Fig. 4, we use the phreeqc.dat database in the geochemical program PHREEQC (63). We supplemented phreeqc.dat with temperature-dependent equilibrium constants for fluorapatite [Ca₅(PO₄)₃F] (64) and hydroxylapatite [Ca₅(PO₄)₃OH] (65). To model concentrated solutions in the Na–Cl–P–CO₂–H–OH system from 0 to 60 °C in Fig. 3, we developed a Pitzer model in PHREEQC using parameters from several existing models. The resulting PHREEQC database file, as well as a detailed description of the Pitzer model equations and the model fits to literature data, are given in SI Appendix, Appendix C.

For Pitzer parameters involving NaCl, NaHCO₃, and Na₂CO₃ salts, we use Pitzer parameters and solubility products from CHEMCHAU (66), which is parameterized from 0 to 100 °C. We include NaCl, Na₂CO₃·7H₂O, Na₂CO₃·H₂O, NaHCO₃, Na₂CO₃·10H₂O, NaHCO₃·Na₂CO₃·2H₂O, and CO₂ gas phases from CHEMCHAU. For phosphate Pitzer parameters, we use parameters from the THEREDA R-12 Pitzer database (37, 67, 68), and assume that Pitzer parameters involving phosphate are temperature-invariant. To model the temperature-dependent solubility of Na₂HPO₄·12H₂O, Na₂HPO₄·7H₂O, Na₂HPO₄·2H₂O, Na₂HPO₄, NaH₂PO₄·2H₂O, NaH₂PO₄·H₂O, and NaH₂PO₄ solid phases, we fit literature data on the solubility of these salts to the temperature-dependent expression for equilibrium constants in PHREEQC, using the THEREDA solubility product at 25 °C as a basis. Finally, to model the dissociation constants of phosphoric acid (H₃PO₄) to ${\text{H}}_2{\text{PO}}_4^{-}$, ${\text{HPO}}_4^{2-}$, and ${\text{PO}}_4^{3-}$, we use the temperature-dependent dissociation constants in the phreeqc.dat database.

Data Availability.

Experimental data from this study are available in SI Appendix, Appendix B, Tables S1 and S2. The PHREEQC database file used to make Fig. 3 is given in SI Appendix, Appendix C.