OptFill: A Tool for Infeasible Cycle-Free Gapfilling of Stoichiometric Metabolic Models

Summary

Stoichiometric metabolic modeling, particularly genome-scale models (GSMs), is now an indispensable tool for systems biology. The model reconstruction process typically involves collecting information from public databases; however, incomplete systems knowledge leaves gaps in any reconstruction. Current tools for addressing gaps use databases of biochemical functionalities to address gaps on a per-metabolite basis and can provide multiple solutions but cannot avoid thermodynamically infeasible cycles (TICs), invariably requiring lengthy manual curation. To address these limitations, this work introduces an optimization-based multi-step method named OptFill, which performs TIC-avoiding whole-model gapfilling. We applied OptFill to three fictional prokaryotic models of increasing sizes and to a published GSM of Escherichia coli, iJR904. This application resulted in holistic and infeasible cycle-free gapfilling solutions. In addition, OptFill can be adapted to automate inherent TICs identification in any GSM. Overall, OptFill can address critical issues in automated development of high-quality GSMs.

Graphical Abstract

Highlights

• •This work presents an alternative to state-of-the-art methods for gapfilling
• •Unlike current methods, this method is holistic and infeasible cycle free
• •This method is applied to three tests and one published model
• •This method might also be used to address infeasible cycling

Metabolic Engineering; Bioinformatics; Systems Biology; Metabolic Flux Analysis

Introduction

The use of systems biology in uni- and multi-cellular organisms (e.g. plants and animals) to engineer or enhance desirable phenotypes and study system-wide metabolic processes is well-established and capable of affecting the lives of millions of individuals, such as in the case of artemisinin production in yeast or enhancing the nutritional value of agricultural products (Beyer et al., 2002, Hall et al., 2008). As opposed to traditional qualitative approaches, computational approaches based on stoichiometric genome-scale models (GSMs) of metabolism can be used to predict non-intuitive genetic interventions (Srinivasan et al., 2015) by accounting for gene-protein-reaction (GPR) links. GSMs may also lead to increased understanding of how a change in environment, organism nutrition, or a gene knockout can affect the entire metabolic system of an organism through tools such as flux balance analysis (FBA) (Orth et al., 2010), OptKnock (Burgard et al., 2003), and OptForce (Ranganathan et al., 2010). GSMs have been developed for many prokaryotic (Magnúsdóttir et al., 2016, Shoaie et al., 2013), animal (Brunk et al., 2018), plant (Gomes de Oliveira Dal'Molin et al., 2015, Saha et al., 2011), and fungal (Andersen et al., 2008, Liu et al., 2013) systems, enhancing mechanistic understanding and exploration of system-wide metabolism in such organisms as E. coli (Ranganathan et al., 2010), cyanobacteria (Saha et al., 2016), yeast (Ng et al., 2012), and other species (Gudmundsson et al., 2017, Islam et al., 2018, Saha et al., 2011, Shoaie et al., 2013). GSMs are typically reconstructed by gleaning information on gene annotations, enzyme functions, associated reactions, and reaction directionality from major public databases such as KEGG (Kanehisa et al., 2017), ModelSEED (Overbeek et al., 2005), the NCBI (Limviphuvadh et al., 2018), MetaCyc (Caspi, 2006), K-Base (Arkin et al., 2018), and BIGG (King et al., 2016). At present, there is no complete knowledge of any genome. For instance, the annotated genome of one of the most prolifically studied organisms, Escherichia coli strain K-12 substrain MG1655, contains about 6.8% putative proteins and 16.1% uncharacterized proteins (UniProtKB, 2018). Furthermore, approximately 61% of proteins lack an enzyme commission (EC) number, which is important for the identification of GPR links in any GSM reconstruction (UniProtKB, 2018). Inevitably, incomplete gene annotation and system knowledge (including reaction direction) leaves metabolic gaps, imbalances, or thermodynamically infeasible cycles (TICs) in any initial GSM reconstructions, leaving the model incomplete. Particularly problematic are TICs, sets of reactions that can carry flux in the absence of nutrition provided to the model because their net stoichiometry is zero, also known as futile cycles or type III reactions (Thiele and Palsson, 2010). These cycles can negate metabolic costs (Thiele and Palsson, 2010), report infeasibly large reaction rates, be difficult to identify (De Martino et al., 2013, Schellenberger et al., 2011), and inhibit the proper function of optimization-based tools that rely on duality to optimize multiple objectives such as OptKnock (Burgard et al., 2003) and OptForce (Ranganathan et al., 2010).

A significant challenge to reconstruct GSMs is the amount of time and manual labor required to curate these incomplete reconstructed models, addressing various issues such as element and charge balances, reaction directionality, metabolic gaps, TICs, and other inconsistencies. Hence, it often requires months to years of manpower before a predictive model is generated (Thiele and Palsson, 2010), which is a prerequisite for conducting research on phenotypic enhancement or study metabolism. Two of the most challenging aspects of model development are the identification and elimination of TICs, as well as the resolving of metabolic gaps.

The existing methods/tools that have been developed to address the identification and resolution of TICs can be broadly categorized into four groups: (1) methods that can identify existing TICs in a model (De Martino et al., 2013), (2) methods that can force no-flux through existing TICs in a model (Schellenberger et al., 2011, Nigam and Liang, 2007, Chan et al., 2018), (3) a combination of the previous two (Chan et al., 2018), and (4) methods eliminating TICs by manipulating the metabolic network. Although developing these is a significant step toward building a better and more predictive GSM, there remain challenges that need to be addressed. For the first approach, Monte Carlo sampling-based method (De Martino et al., 2013) cannot guarantee the identification of all TICs as it is a stochastic approach. The second approach is the avoidance of TICs by the application of Kirchhoff's loop law in methods such as Loopless COBRA (Schellenberger et al., 2011). This approach does successfully avoid TICs but does not address the root cause in the model that can make some models problematic for tools such as OptForce that require no TICs (Ranganathan et al., 2010). Another approach is the addition of thermodynamic constraints to the model using known thermodynamic quantities (Nigam and Liang, 2007), which works well for well-studied organisms for which these in vivo parameters are known but is more difficult to implement for non-model organisms. The third approach that combines these two approaches, such as the one demonstrated by Chan et al. (2018), has shown promise and computational tractability. However, this has generally been employed as a set of loopless constraints, rather than as a method to avoid the inclusion of TICs in gapfilling. The fourth method has been used to address TICs in energy metabolism, which can allow the model to produce unlimited energy severely hampering model accuracy, by applying a variation of optimization-based tool globalfit (Fritzemeier et al., 2017). globalfit has been used by Fritzemeier et al. (2017) to identify the minimal network changes to address erroneous energy cycling in metabolic network models. These changes could take the form of removal of reactions and/or correcting of reaction direction and address root causes of TICs without using loopless constraints when applying in silico analysis tools.

It should be noted that not all the cycles in biological systems are infeasible cycles. Some cycles, such as the Calvin cycle or the citric acid cycle are well-known biological cycles. These differ from infeasible cycles in that these cycles has some net effect. In the case of the Calvin cycle this net effect of each revolution is to fix carbon dioxide to a sugar by expending cellular energy. In contrast, thermodynamically infeasible cycles result in no net production or consumption per each revolution. It should also be noted that some reactions do proceed in both directions at the same time in the same subcellular compartment in a cell, with their relative rates limited by thermodynamic considerations. Although some models do include in vivo thermodynamic information, the precise value, or more often range of values, for the Gibbs free energy and other important thermodynamic properties of a reaction are often unknown aside from being able to specify reaction direction (Thiele and Palsson, 2010). Therefore, for all but the best-studied organisms, imposing thermodynamics-based limitations on reaction rates to preclude thermodynamic cycling is very difficult if not impossible.

To address and resolve metabolic network reconstruction gaps, GapFind and GapFill (Satish Kumar et al., 2007) are some of the most common tools used (Pitkänen et al., 2014, Henry et al., 2010, Kim et al., 2012). GapFind and GapFill are optimization-based Mixed Integer Linear Programming (MILP) problems and have been successfully implemented in the reconstruction of metabolic models, prokaryotic, and eukaryotic biological systems such as cyanobacteria (Synechocystis sp. PCC 6803 and Cyanothece sp ATCC 51142) (Saha et al., 2012), corn (Zea mays) (Simons et al., 2014), yeast (Saccharomyces cerevisiae), and Chinese hamster ovary cells (Chowdhury et al., 2015). Other methods of automated gapfilling that build on the capabilities of GapFill include GenDev (Latendresse and Karp, 2018), FastDev (Latendresse and Karp, 2018), likelihood-based gapfilling (Karp et al., 2018), and phenotype-based gapfilling (Cuevas et al., 2019). All these tools are constructed with the aim of increasing the accuracy of the GapFilling method, through comparison to some level of data such as phylogenetic, phenotypic, or genetic. In this work, a problematic aspect of all these tools is considered, which these other tools were not built to address. Despite their success, the tools for gapfilling have significant limitations including the following: (1) gaps are addressed on a per-metabolite basis (as opposed to a whole-model holistic approach), (2) thermodynamic feasibility is often not considered, and (3) reaction direction is not considered in gapfilling, rather all reactions are added reversibly. From the first and second limitations, several problems arise including (1) inability to guarantee that the minimum number of reactions are added to fix metabolic gaps on a whole-model (holistic) basis; (2) inability to identify and avoid unfavorable interactions between multiple gap fixes (often, TICs); and (3) differences in the resultant model dependent of the individual curator.

To address current TIC-finding and gapfilling method limitations, this work introduces a multi-step optimization-based MILP method. The first step is to solve an iterative optimization-based TIC-Finding problem (TFP), which identifies potential TICs, which may be caused by adding reactions from a database in a given direction (see Figure 1). This method uses optimization and binary variables as opposed to null space matrices used by other methods that identify reactions participating in TICs (Saa and Nielsen, 2016) or TICs (Chan et al., 2018) and thus can provide a greater level of detail for each inherent or potential TIC. This problem is unique as it considers the direction and relative flux rate of reactions participating in TICs and can be easily adapted for the purposes of model curation sans database for the resolution of inherent TICs. The second step involves the solving of three optimization-based problems, the connecting problems (CPs), which are highly similar but have different objectives. The first connecting problem (CP1) is the maximization of model metabolites successfully connected to metabolic network, e.g. maximizing the number of metabolites that the connected model can now produce, while avoiding the addition of TICs. The second connecting problem (CP2) is the minimization of the number of reactions required to achieve the objective of CP1. The third connecting problem (CP3) is the maximization of the number of reactions to be added reversibly from the database to achieve the objectives of CP1 and CP2 subject to avoiding TICs. The connecting problems are unique in that, unlike other gapfilling algorithms, CP solutions provide whole model gapfilling solutions guaranteeing the minimum number of reactions being added for the maximum number of fixed metabolites. As proof of concept, the OptFill approach is applied to three test stoichiometric models of increasing sizes (models of 28–210 reactions, databases of 17–77 reactions) with designed metabolic gaps and one smaller (1074 reactions) GSM of Escherichia coli with acknowledged metabolic gaps (Reed et al., 2003) using another GSM of E. coli as the basis for a database (Feist et al., 2007). With the computational resources at hand, the full OptFill method is limited to relatively smaller stoichiometric models and databases but should be applicable to larger models and databases given access to greater computational power.

Figure 1.

Visualization of OptFill Results with Respect to the First Test Model and Database

This figure shows that the model and database which are inputs to OptFill are separate but are both used in the workflow to prepare for OptFill and in OptFill itself.

Then, the model and database are combined to show how they might appear and how this combination is used in the TIC-finding problem to identify potential TICs that might occur between the model and the database. Selected identified potential TICs are shown here as illustrative examples. Potential TICs #1 and #2 illustrate how TICs occurring in different directions are identified as separate TICs, how identified TICs might only occur between database reactions, and the two of the smallest identified TICs. Potential TICs #9 illustrates a larger TIC that makes use of an irreversible reaction (NGAM), and therefore has no opposite-direction TIC, making the direction of the other reactions important. Potential TICs #10 and #31 illustrate infeasible cycling involving an energy molecule (ADP/ATP), in addition to potential TIC #31 being the largest identified TIC.

Finally, this figure shows the application of the connecting problems (CPs), which make use of the database, model, and TIC-Finding Problem solutions. Shown here are the first (most optimal) and last (least optimal) solutions of the CPs. These solutions differ in the number of model metabolites that could not be connected (red boxes); the number of metabolites introduced to the model (yellow boxes); the number and reversibility of database reactions added (orange arrows); and the resultant model growth rate.

Results

Development of OptFill

OptFill was conceived and developed to address the limitations of the current state-of-the-art GapFind/GapFill (Satish Kumar et al., 2007) tool. The initial stages of the design-build-test (DBT) cycle contained the first test model (TM1) and the first test database (TDb1) and involved only a single connecting problem. TM1 was constructed as a small stoichiometric model involving starch and glycolysis metabolism to produce ethanol but with metabolic gaps preventing growth (see Figure 1). TDb1 was designed to have the capacity to fill these gaps, at the expense of potentially producing TICs. In the DBT cycle, it was soon realized that the TFP was necessary to define the potential TICs that might occur. The TFP was built to solve for the smallest TICs (i.e., the TICs with the smallest number of participant reactions) first and then solve for larger TICs to prevent multiple TICs masquerading as a single TIC solution. The workflow representing the TFP is shown in Figure 2. The CPs were developed to ensure consistency in the number, order, and identity of the CP solutions while avoiding the addition of the whole set of TICs identified as potentially occurring between the model and database. See Figure 3 for the conceptual formulation of each type of problem. All problems that are part of the OptFill tool are mixed integer linear programming (MILP) problems that ensure global optimality of each solution in each iteration.

Figure 2.

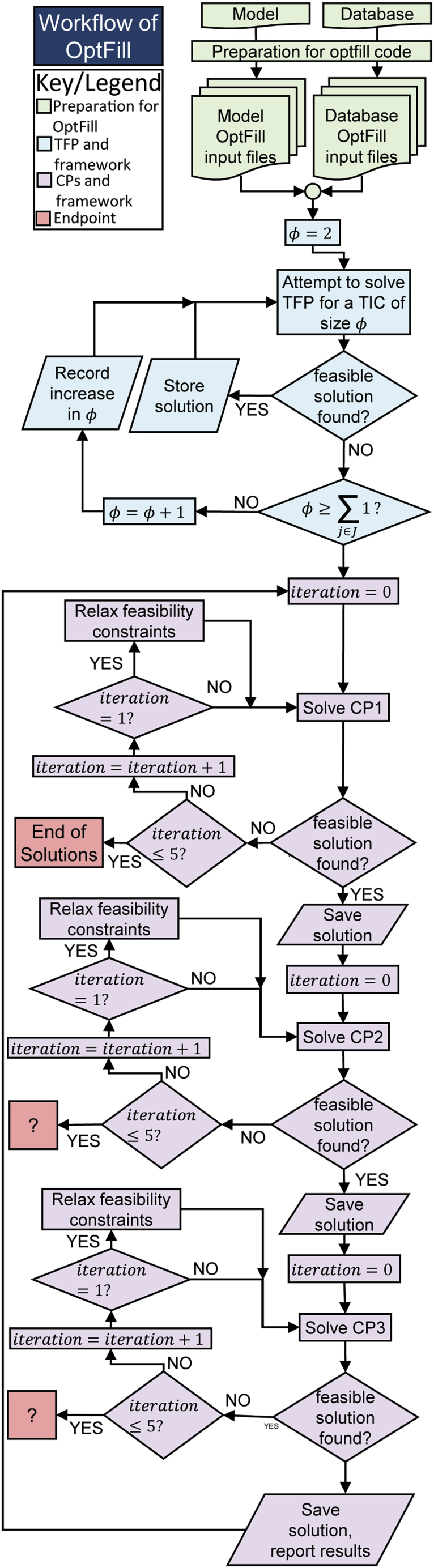
Workflow of OptFill

This is a workflow diagram of the OptFill tool. Green nodes represent the preparatory workflow, blue the workflow of the TIC-finding problem (TFP), purple the workflow of the connecting problems (CPs) including the error-handling workflow imbedded in the CPs workflow, and red the endpoints of the workflow. It should be noted that only one endpoint truly exists, when a solution to CP1 is not found, because the other problems, CP2 and CP3, will have solutions if CP1 has a solution, hence the workflow exit points being represented by a question mark at these points.

Figure 3.

Conceptual Formulation of Each Problem in OptFill

This figure gives a conceptual formulation of the TIC-finding problem, TFP, in part (A) and the connecting problems, CP1, CP2, and CP3, in part (B). In part (B), as three connecting problems are solved, each conceptual constraint has indicated CPs to which it is applied. Conceptual constraints may require multiple mathematical constraints to be realized, see Transparent Methods for mathematical formulation.

On occasion, the feasibility constraints used might be too strict to return a feasible solution to the CP problems, which could result in execution errors prematurely ending OptFill before completion. Therefore, an error handling framework was built around each CP problem allowing a one-time relaxation of feasibility constraints. These frameworks are shown in Figure 2. OptFill is ended when CP1 no longer has a feasible solution even when feasibility constraints are relaxed (which occurs because previous solutions are prevented from being re-identified) because at that point none of the CP2 and CP3 will have a feasible solution. Further, all OptFill runs described used non-standard CPLEX solver options, which effectively eliminated most types of cuts. This caused some level of reduction to the solution space, particularly those that could result in non-optimal solutions being reported as optimal. These included flow, zero-half, and Gomory fractional cuts, among others. This was done because the order of solutions is important in the OptFill method, and the order of solutions also has bearing on the number of solutions returned. See Transparent Methods for further detail.

Application of OptFill to Test Models

After finalizing the formulation (see Figure 3 and Transparent Methods) and workflow (Figure 2) of OptFill, a detailed analysis of OptFill results with respect to TM1 and TDb1 was undertaken. Some qualitative results of the application of the OptFill workflow to TM1/TDb1 are shown in Figure 1, which include the initial model and database (Figure 1), the combination of the model and database (Figure 1), selected identified potential TICs (Figure 1), and selected identified CPs' solutions (Figure 1). As is shown in Figure 1, TM1 is too disconnected to produce biomass but in combination with TDb1 can potentially produce biomass. When the TFP is applied (Figure 1), 31 potential TICs consisting of 3–12 reactions (hereafter, sizes 3–12) were identified. The average solution time (when a solution was found) was 0.175 s (σ = 0.0727 s, min = 0.0870 s, max = 0.378 s). It should be noted that all solve times reported here are not constant, even if using same resources. Figure 1 highlights five potential TICs that were identified. The first two TICs identified, TIC #1 and #2, show that the TFP can identify TICs occurring only in the database; that TICs consisting of the same metabolites and reactions are identified separately if reaction directions are different; and that two of the smallest TICs are identified. Potential TIC #9 shows a TIC of moderate size (for TM1/TDb1), which contains an irreversible model reaction related to non-growth-associated maintenance (NGAM) and, therefore, will not have a companion potential TIC of opposite direction, unlike potential TIC #1 and TIC #2 (in the opposite direction). Further, this highlights the potential for infeasible cycling, which effectively negates the cost of NGAM of the model. If added in its entirety, NGAM would be irrelevant to the model at any value and would significantly reduce model accuracy. This TIC might not be manually identified because NGAM is usually a fixed quantity. Potential TIC #10 highlights another type of infeasible cycling involving ADP/ATP, but this cycling essentially negates the cost of phosphorylation/dephosphorylation of glucose-6-phosphate isomers. Finally, potential TIC #31 is included to highlight a non-intuitive TIC, in addition to be the largest TIC identified. This TIC involves the separate cycling of sugars and 3-carbon molecules linked and is made possible by ADP/ATP cycling (sugar cycling consumes ATP and 3-carbon cycling produces ATP). These examples illustrate that many, but not all, potential TICs involve the infeasible cycling of energy molecules, which should be particularly avoided in the reconstruction of models of metabolism, as this can result in negated costs for various biological activities with which a cost should be associated. This negated cost can often result in increased model growth rate and reaction fluxes, reducing the model's accuracy.

The model, database, and TFP solutions form the input for the CPs. Before solving the CPs, a modified version of CP1 was run, which prohibited the addition of database reactions. This modified CP1 reported that the raw TM3 model was capable of producing no metabolites. The CPs, when applied to TM1 and TDb1, identified 24 potential solutions that connected between 31 and 33 metabolites with the additions of 6–10 reactions, of which 0 to 6 could be reversible without TICs. The average time to solve all three CPs for each solution was 0.639 s (σ = 0.147 s, min = 0.433 s, max = 0.950 s) (see Figure 4). From the FBA performed on each connecting problem solution with the objective of maximization of biomass, the mean maximum biomass production rate of the set of connected models was 2.43 h⁻¹ (σ = 0.394 hr⁻¹, min = 1.44 hr⁻¹, max = 2.90 hr⁻¹). Solution times for the FBA code were not recorded, as FBA solution time is generally low. Two connecting problem solutions, the first and the last, are shown in Figure 1. These solutions are notably different in terms of the number of model metabolites connected by the CPs' solution (green boxes in the metabolic sketch), the number of intermediate metabolites introduced by these solutions (yellow boxes), the number of database reactions introduced (orange arrows), and even the use of energy molecules. For instance, CPs' solution 1 introduces only two additional metabolites and six reactions reversibly from the database, which are part of the CPs' solution and connects all but two model metabolites. The first is acetate, which is a dead-end metabolite. The second is the extracellular proton, which suggests that the model is small enough that all protons produced are also consumed. This solution has the slowest growth rate of all connecting problem solutions. On the other hand, CPs' solution 24 connects two fewer metabolites than CPs' solution 1, requires two more reactions, introduces two more intermediate metabolites, and has a higher growth rate. It is hypothesized that this is due to the more efficient production of ATP allowed by reaction R01512[c] (enzyme ATP:3-phospho-D-glycerate 1-phosphotransferace in the cytosol), which is present in many other high-biomass solutions. This reaction allows two dephosphorylation events to produce ATP, as opposed to only one (the other event occurring by hydrolysis).

Figure 4.

Visualization of OptFill Solution Time and Results

This figure show the trends in solution time, (A) through (C), of the TIC-finding problem (TFP, blue) and the connecting problems (CPs, brown) with trend lines with the highest Pearson's correlation coefficient of linear, exponential, power, and logarithmic fits. These trends are considered with respect to the number of reactions in the model (A), database (B), and total reactions (C). Parts (D) through (F) highlight the trends of solutions. Part (D) highlights the number of solutions found by the TFP and CPs; part (E) highlights the range in size of the identified potential TICs by the TFP. Parts (F), (G), (H), and (I) highlight the variety of CPs' solutions. In these figures, the pie chart indicates the number of metabolites connected by the CP1 solution, and the radar chart is used to indicate the CP2 solution (number of reactions added) and the CP3 solution (number of those reactions that are added reversibly).

Two larger test models were built next to study the increase in number of solutions and time required to reach those solutions by OptFill and, ultimately, to investigate its scale-up potential. Each test model was built from an OptFill solution of a previous solution to highlight the ability of this tool to be applied in sequence. In the application of OptFill to the existing models of organisms, careful attention must be paid in selection of a CPs' solution to accept, including considerations of energy metabolism, predicted growth rates, and remaining unconnected metabolites. Here, CPs' solution 1 was selected and combined with TM1 as the base of the second test model (TM2). Reactions and metabolites from the fatty acid biosynthesis and the pentose phosphate pathway were added to this base, in which gaps were manually created. Reactions that could address these gaps formed the second test database (TDb2). Redundant metabolic functions were added to TDb2 to allow for potential TICs. Similarly, the third test model (TM3) was built from the first CPs' solution of TM2 and TDb2. Additionally, a bank of reactions from the amino acid synthesis pathways, including redundant functionalities, was created. This bank was automatically (randomly) sorted between those reactions that would be added to complete TM3 (∼80% of bank reactions) and those that would constitute the third test database (TDb3, ∼20% of bank reactions). As random sorting was used, a modified version of the TIC-finding problem (modified TIC-finding problem, mTFP), was used to identify inherent TICs in TM3 and TDb3, which resulted from the random assortment of the bank reactions. The reactions most commonly participating in identified inherent TM3 TICs were moved to the TDb3 until no inherent TICs remained (five reactions in total).

For OptFilling of TM2/TDb2, 51 TICs consisting of 3–26 reactions were identified by the TFP, with a mean solution time of 0.131 s (σ = 0.0405 s, min = 0.0850 s, max = 0.308 s). The largest TIC, potential TIC #51 consisting of 26 reactions, would have largely been very difficult to be identified by a non-automated method, as it spans six KEGG pathways including glycolysis, the pentose phosphate pathway, purine metabolism, nicotinate and nicotinamide metabolism, starch and sucrose metabolism, and riboflavin metabolism. TIC #51 involves the cycling of 3-, 4-, 5-, and 6-carbon molecules, energy molecules (ATP, NADH, and NADPH), and energy molecule hydrolysis. This TIC can be found in GitHub and Mendeley Data repositories accompanying this work.

Before solving the CPs, the modified CP1 was run and reported that the raw TM2 model was capable of producing no metabolites. Fifteen potential CPs' solutions were identified, which each connected 90 to 94 metabolites with the addition of 17–23 reactions, of which 0 to 19 could be reversible without TICs. The average time to solve all three CPs for each solution was 1.40 s (σ = 0.639 s, min = 0.404 s, max = 2.65 s) (see Figure 4). From the FBA performed, the biomass production rate of most CPs' solutions applied to TM2 was 1.31 h⁻¹, for 10 solutions, and 1.36 h⁻¹ for the remaining five. In the CPs' solutions, those with the highest biomass have fewer metabolites that could be connected (all solutions with higher biomass production were generated after lower biomass production solutions). Those with the higher biomass production rates generally have one fewer reaction that requires ATP hydrolysis and therefore has slightly more energy in the system to spend on the production of biomass than their lower biomass counterparts.

Similarly, OptFill applied to TM3/TDb3 resulted in the identification of 60 TICs consisting of 3–31 reactions by the TFP and 177 potential CPs' solutions, which each connected 202 to 214 metabolites with 12–17 reactions, of which 1 to 12 could be reversible without TICs. As earlier, the modified CP1 was used to identify 54 metabolites that the raw TM3 was capable of producing. The mean TFP solution time was 0.240 s (σ = 0.0756 s, min = 0.141 s, max = 0.541 s), whereas the mean CPs' solution time was 0.985 s (σ = 0.249 s, min = 0.573 s, max = 1.86 s). From the FBA performed, the mean biomass production rate of the connected model was 3.29 h⁻¹ (σ = 0.179 h⁻¹, min = 3.11 h⁻¹, max = 3.47 h⁻¹). Runtime and solution metrics for all solutions are shown in Figure 4. Unlike TM1 and TM2 OptFilling results, there was no solution where all database reactions to be added by the CPs' solution could be added reversibly. This indicates that, for all solutions, the direction in which database reactions are added is important to avoid TICs to produce a model without the disadvantages of TICs described previously. Furthermore, the biomass production rate does not appear as dependent on either the number of metabolites connected or reactions added as in previous CPs' solution sets. Instead, the biomass production rate seems to most depend on the method of sulfate assimilation.

Application of OptFill to iJR904

In order to show how the OptFill workflow might scale up to a GSM, the iJR904 model of Eschericia coli consisting of 761 metabolites, 1,074 reactions, and 904 genes (Reed et al., 2003) was selected as the base model to fix. The iAF1260 model, a model extending onto iJR904, consisting of 1,598 metabolites; 2,381 reactions; and 1,260 genes (Feist et al., 2007) was selected to serve as the set of reactions from which to build the database. iJR904 contains 70 dead-end metabolites (Reed et al., 2003) that need fixing. Before applying OptFill, some minor formatting changes were made (described in Transparent Methods and in the related GitHub and Mendeley Data repositories accompanying this work), and it was decided that carbon-limited aerobic growth using acetate would be the condition for which iJR904 model would be fixed. Metabolite exchange rates were taken from Reed et al. (2003) to describe this growth condition.

In order to create the database that would be applied to iJR904, all iAF1260 exchange reactions and reactions with names identical to those in iJR904 (which were assumed to be the same reaction as the former was built from the latter) were removed from iAF1260 to form the initial database that consisted of 1,441 reactions. This proved too computationally intensive for the resources, and therefore this database was further simplified in a manner that it is suggested others with limited computational resources might also use. First, the iAF1260-based database and iJR904 were combined in single model file, and flux variability analysis (FVA) (Gudmundsson and Thiele, 2010) was performed (see Table S1. iJR904, Related to Figure 4). Those iAF1260 reactions capable of holding flux as determined by FVA (715 reactions) were defined as the database of functionalities to be used with OptFill.

OptFill was performed on iJR904 using this database. This still resulted in a slow OptFill process; therefore, solutions that were reported (i.e., 4 identified) in the allotted solve time of 24 h were collected. All iAF1260 reactions that participated in at least one solution (a total of 182 reactions) were selected as the basis of the third iAF1260-based database. This resulted in significantly lower computational requirements for the application of OptFill. This database was found, upon application of OptFill, to be without TICs. For the purposes of demonstration and showing how the increase of TFP solution time changes with model and database size, it was arbitrarily decided to add six reactions manually from the previous database, which could participate in potential TICs between the model and database but which did not create TICs only within the database. Further, the mTFP was applied to the iJR904 model. From the mTFP results, it was noticed that in iJR904, some reactions were included in the model twice, both as reversible and irreversible, causing inherent TICs in the iJR904 model involving these duplicate reactions. It was decided to move the irreversible reactions of each duplicate pair to the database (nine reactions in total) so that all iJR904 models were still present in the OptFill in some capacity. The final iAF1260-based database for the OptFilling of iJR904 totals 188 reactions. Initial, final, and intermediate iAF1260-based databases used can be found in Table S1. iJR904, related to Figure 4 iJR904 and in the GitHub and Mendeley Data repositories accompanying this work.

Demonstrated here is a procedure by which the database applied to a model can be significantly decreased in size to reduce computational cost of the OptFill method, while still effectively addressing metabolic gaps. This can be summarized as follows: (1) eliminate all duplicate reactions; (2) perform FVA on a pseudomodel that is a combination of the database and model and use the results to eliminate reactions that cannot carry flux; and (3) perform OptFill using databases with larger solution time, collect a few sample solutions, and use the set of reactions participating in sampled solutions as the database. Applications of steps (1) and (2) as well as iterative applications of (3) might be used by modelers to shrink the database used in OptFilling to a size that is possible to solve in a modest period of time given the computational resources available.

This final iAF1260-based database was used to OptFill iJR904 model. In this final iteration, there were 25 TICs of size two to eight reactions identified. The associated mean TFP solution time was 0.410 s (σ = 0.0978 s, min = 0.330 s, max = 0.687 s). The TICs identified were generally simple, as they stem from reactions manually added to the database, which cause TICs. Eleven TICs occur between just two reactions, and a further four involving only a single database reaction. Each of these effectively precluded a single database reaction from being added in a certain direction. When the CPs were applied to iJR904, it was found that the CPs' solution time had increased considerably from that of other models, to a mean of 236 s (σ = 329 s, min = 15.3 s, max = 1010 s). The solution time of this model was significantly increased due to disabling of many types of cuts that a solver might use to decrease solution time but that lead to non-optimal solutions being reported as optimal. These are particularly relevant because minor cuts, such as those that accept a 0.5% reduction in the optimal solution value, can change the number of metabolites connected by the CPs by two or more for GSMs. As the order of solutions is important, even these minor relaxations were deemed problematic and were therefore mostly disabled, leading to increased solution time. If these cuts were allowed, CPs' solution time would have been approximately an order of magnitude less than reported here. The modified CP1 problem reported that the iJR904 model was capable of producing 358 metabolites under the given aerobic growth on acetate conditions, and all CPs' solutions connected 418 metabolites with the addition of 86 reactions. All CPs' solutions produced biomass at a rate of 0.108 h⁻¹. This is likely a result of the database reduction steps taken. The variation on the CPs' solution occurred in the number of connecting reactions that could be added reversibly, ranging from 5 to 86. The full set of solutions can be found in the GitHub and Mendeley Data repositories accompanying this work. It can be seen in Figure 4I that efforts to prevent non-optimal solutions from being reported as optimal were not entirely successful. There exists one CPs' solution, solution #72, where the optimal (maximum) CP3 solution value is 5, whereas the optimal (maximum) CP3 solution value was 11 from solutions #71 and #73. This occurred when all solutions were subject to approximately the same constraints (save the integer cuts necessary to prevent repeated solutions). It is noted earlier that many types of cuts were disabled, but not all, and one type of cut or other solver setting allowed this non-optimal solution to be reported as optimal; however, eliminating all such cuts and settings proved prohibitively time-consuming. Therefore, the settings, which can be found in the GitHub and Mendeley Data repositories accompanying this work, were selected as those that, for this work, best balanced solution order and solution time.

In the OptFilling solutions of iJR904, several trends can be noticed that were not present in the smaller test models. First, when performing FBA, with the objective of maximizing biomass, on the resultant OptFilled iJR904 model, not all reactions from the database held flux when biomass was maximized. This is because these reactions make it possible for the model to produce metabolites that are not required for the production of biomass or provide an alternative pathway for the production of biomass that might be less efficient. This does not mean that these connected metabolites are unimportant under other, equally valid, objective functions, for instance the connected metabolites may be bioproduction targets. Further, some TICs exist between iJR904 model reactions in the OptFill solutions and notably one database reaction. For most model reactions, these TICs occur because forward and reverse reactions are written separately. The TIC involving the database reaction resulted from the proton uptake exchange reaction being allowed a very high reaction flux in the iJR904 model. The TFP was performed with all exchange reactions fixed to a flux of zero; therefore, the TFP did not identify this TIC, which involved an exchange reaction. When the exchange reactions were allowed to carry flux again in the CPs, the high proton uptake rate (here, 1000 mmol/gDW·h) allowed the cycling of reactions. These resulting TICs highlight two important considerations in using OptFill. First, the mTFP should be used in combination with manual editing of the model to ensure that the model does not contain inherent TICs, as the usual OptFill workflow will not address inherent TICs. Second, reasonable bounds should be applied to all exchange reactions (such as the proton uptake reaction) and forward and reverse reaction pairs to prevent TICs in the OptFilled model.

OptFill Solution Times

With the caveats of the available resources (see Transparent Methods for information on the software and hardware tools available for this work), the TFP seems to have a per-TIC average solution time with linear dependence (R² ≥ 0.89) on size of model and/or database used (see Figures 4A through 4C). The same procedure was applied to the aggregated CPs' solution time but with significantly different results. Exponential trend lines were able to fit with a high correlation coefficient (R² ≥ 0.96) between model, database, total system size, and CPs aggregated solution time. This is indicative of a strong correlation between CPs aggregate solution time, number of reactions in the total system, and that increasing total system reactions greatly increases CPs aggregate solution time.

Discussion

Introduced here is an optimization-based tool, OptFill, which can be used to increase the automation of the curation of GSMs. This tool can either be used to automate the filling of metabolic gaps in a reconstructed model or to automate the identification of TICs for manual resolution (via mTFP). In this work, the OptFill was applied in sequence to three test models of increasing size as well as to a GSM of E. coli, iJR904. These applications combined with some solutions for holistically gapfilling metabolic models, the computational expense of the tool, and a method for reducing that expense highlighted the utility of OptFill.

This method has considerable potential to be adapted to other metabolic systems (both eukaryotic and prokaryotic) and is not specific to any identifier system such as KEGG or ModelSeed. For instance, although all test models as well as iJR904/iAF1260 have been prokaryotic systems, there is no reason why this approach would not similarly work in a eukaryotic organism. Further, the framework is flexible enough that any system of reaction and metabolite identifiers, such as KEGG (Kanehisa et al., 2017), MetaCyc (Caspi et al., 2014), BIGG (King et al., 2016), K-Base (Arkin et al., 2018), or custom identifiers, may be used for metabolites and/or reactions, making this tool applicable to a wide variety of existing GSM-building methods. This was demonstrated in this work as KEGG identifiers were used in the test models, whereas BIGG identifiers were used by the iJR904 and iAF1260 models (Reed et al., 2003, Feist et al., 2007).

From the observation of TFP solution times, it is evident that the TFP and mTFP could scale-up to genome-scale models of metabolism, as a linear trend line (R²$\ge$0.89) strongly describes the per-TIC solution time given the computational resources at hand. So long as the number of TICs in the system remains reasonable, this portion of OptFill is transferrable to large-scale GSM systems or to situations where computational resources are limited. The transferability of the OptFill method is likely limited by the computational resources available to the end-user, as the aggregate solution time of the three CPs is well described by an exponential trend line (R²$\ge$0.97). This suggests that those without access to powerful computational resources may have difficulty implementing OptFill in a reasonable time frame, unless, for instance the end-user makes trade-offs between the solution order (e.g. each subsequent solution is truly globally optimal) and solution time. These trade-off issues, such as shown in a minor way with the OptFilling of iJR904, may likely be fixed by more advanced MILP solvers that are currently available or by advances in optimization that may be made in future.

When implementing OptFill in other systems, a high-quality model and database should be used in order to limit both the number of solutions and the time the OptFill method takes to complete. This is primarily due to the number of feasible and unique combinations possible. For instance, if a multi-step reaction is included in a database in addition to its component reaction steps, this can potentially double the number of solutions found by both the TFP and CPs. To explain, if the multi-step reaction participates in n TICs, then its component step reactions would participate in n TICs. This results in 2n TICs, where only n TICs need be identified. The same argument applies for CPs' solutions. This error in model reconstruction could then double (or more) the number of TICs and CPs' solutions as well as the total OptFill runtime in a stroke. In larger models, such issues can result in a significant expenditure of time (potentially days) and computational resources that need not be expended should the model and database used to be of high quality. Such an issue is elsewhere referred as a combinatorial explosion (Burgard et al., 2003). This was shown in this work in the failure to achieve a reasonable number of solutions or reasonable solution times in the OptFilling of iJR904 with a poorly curated database based on iAF1260; however, when the database was better curated, reasonable numbers of solutions and solution times were achieved. Therefore, it is important to address as many inherent TICs that occur both in the model and in the database as feasible using the mTFP on both the model and the database to identify and address these TICs.

Although throughout this text reaction cycling in the absence of nutrition (i.e., thermodynamically infeasible cycling) is described as a phenomenon that is to be avoided in GSMs, this is not always the case. In many biological systems, cycling of some type does occur and the absence of that cycling in the models might affect their accuracy. However, cycles included in a GSM should be carefully considered with respect to their biological relevance, magnitude, and effect, particularly when they occur in the absence of nutrition provided to the model. In essence, this work can be used to remove and/or avoid all cycling that can occur in the absence of nutrition provided to the model or to ensure that cycles retained are deliberate and have biological relevance if included. If cycles occur in a GSM model in the absence of nutrition provided to the model and are biologically relevant, best practice should be to use other literature data available to limit the scope of the cycling to feasible number. This trade-off must be considered when applying the OptFill algorithm or when choosing to use some type of algorithm that employs the loopless constraints.

This is the essential difference between what is proposed here as the OptFill tool and other algorithms such as the algorithm employed by Chan et al. (2018) to identify all TICs in a model and avoid them. The TIC finding portions of the algorithm are largely equivalent, although Chan et al. (2018) may identify TICs faster. OptFill then precludes these TICs from being added as part of a gapfilling solution so that the resultant reconstructed metabolic model contains no inherent TICs. However, Chan et al. (2018) accepts these TICs in the reconstructed network and seeks to limit flux through these TICs so that the resulting model fluxes are feasible. The OptFill approach presents an alternative to the need to use loopless algorithms on the gapfilled model and allows use of algorithms that are sensitive to the presence of TICs, such as OptForce (Burgard et al., 2003, Chan et al., 2018) without modifying these algorithms for the use of various loopless algorithms that may be computationally expensive.

In future, this work will be used as a gapfilling and curation strategy for the development of GSMs of any prokaryotic and eukaryotic systems. In concert with advances in optimization solvers and available computational resources, these methods (i.e., the TFP, CPs, and their modified versions) will provide an alternative holistic method of model curation. At present, those model-building tools with high computational power at their disposal, such as ModelSeed (Overbeek et al., 2005) and K-Base (Arkin et al., 2018), may well be able to implement OptFill and its components for large GSMs to improve their automated curation capabilities. In addition, with the available computational resources and some adjustments (as explained earlier), Optfill is being implemented to improve the connectivity and predictive capability of the GSM of a non-model purple non-sulphur bacterium (Alsiyabi et al., 2019) and to develop the GSM of a melanized fungal strain.

Limitations of the Study

As already discussed in this work, this study does have multiple limitations. These limitations include solution speed, both of the CPs and as an overall result of combinatorial explosion; the need for powerful computational resources to efficiently use this tool; and that this tool might miss cycles that do occur in biological systems but require thermodynamic data or constraints to prevent infeasible cycling.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: January 24, 2020

Data and Code Availability

The published article does not include all datasets and code generated or analyzed during this study. The datasets and code generated during this study are available at GitHub in the ssbio/OptFill repository [https://doi.org/10.5281/zenodo.3560302] and Mendeley Data OptFill repository [https://doi.org/10.17632/npdwbmb7d7.1].

Supplemental Information

Table S1. iJR904, Related to Figure 4

This supplemental file is built from the supplemental file provided by Reed et al. (2003) with the addition of columns defining metabolite IDs used by Reed et al. (2003) with KEGG identifiers. This substitution was done in this study.

Table S2. Result Summaries, Graphs and Biomass Calculations, Related to Figure 4

Microsoft Excel workbook that was used to calculate biomass composition for the test models as well as generate graphs used in Figure 4.