The human central nervous system transmits common synaptic inputs to distinct motor neuron pools during non‐synergistic digit actions

Abstract

Key points

• Neural connectivity between distinct motor neuronal modules in the spinal cord is classically studied through electrical stimulation or multi‐muscle EMG recordings.

• We quantified the strength of correlation in the activity of two distinct populations of motor neurons innervating the thenar and first dorsal interosseous muscles during tasks that required the two hand muscles to exert matched or un‐matched forces in different directions.

• We show that when the two hand muscles are concurrently activated, synaptic input to the two motor neuron pools is shared across all frequency bandwidths (representing cortical and spinal input) associated with force control.

• The observed connectivity indicates that motor neuron pools receive common input even when digit actions do not belong to a common behavioural repertoire.

Abstract

Neural connectivity between distinct motor neuronal modules in the spinal cord is classically studied through electrical stimulation or multi‐muscle EMG recordings. Here we quantify the strength of correlation in the activity of two distinct populations of motor neurons innervating the thenar and first dorsal interosseous muscles in humans during voluntary contractions. To remove confounds associated with previous studies, we used a task that required the two hand muscles to exert matched or un‐matched forces in different directions. Despite the force production task consisting of uncommon digit force coordination patterns, we found that synaptic input to motor neurons is shared across all frequency bands, reflecting cortical and spinal inputs associated with force control. The coherence between discharge timings of the two pools of motor neurons was significant at the delta (0–5 Hz), alpha (5–15 Hz) and beta (15–35 Hz) bands (P < 0.05). These results suggest that correlated input to motor neurons of two hand muscles can occur even during tasks not belonging to a common behavioural repertoire and despite lack of common innervation. Moreover, we show that the extraction of activity from motor neurons during voluntary force control removes cross‐talk associated with global EMG recordings, thus allowing direct in vivo interrogation of spinal motor neuron activity.

Key points

• Neural connectivity between distinct motor neuronal modules in the spinal cord is classically studied through electrical stimulation or multi‐muscle EMG recordings.

• We quantified the strength of correlation in the activity of two distinct populations of motor neurons innervating the thenar and first dorsal interosseous muscles during tasks that required the two hand muscles to exert matched or un‐matched forces in different directions.

• We show that when the two hand muscles are concurrently activated, synaptic input to the two motor neuron pools is shared across all frequency bandwidths (representing cortical and spinal input) associated with force control.

• The observed connectivity indicates that motor neuron pools receive common input even when digit actions do not belong to a common behavioural repertoire.

Introduction

The CNS generates voluntary movements by sending neural commands to muscles. It has been argued that muscle coordination is the result of neural activation of motor modules in the spinal cord (Bizzi & Cheung, 2013). This hypothesis is based on extensive evidence from animal studies. For example, in the frog (Bizzi et al. 1991), cat (Lemay, 2003) and rat (Tresch & Bizzi, 1999), electrical stimulation of spinal interneurons generates complex functional movement patterns that depend on the position of the stimulation site. These experiments led to the hypothesis that groups of muscles may be activated by shared inputs to their motor neuron pools and that the CNS coordinates movements by sending inputs to multiple motor modules, reducing the dimensionality and therefore the complexity of control. The sets of relative weights of activation of individual muscles in each module have been referred to as muscle synergies (d'Avella & Lacquaniti, 2013).

Despite experimental evidence from animal experiments, evidence for muscle synergies in humans during natural tasks is mainly indirect. The regularities of limb kinematics that have been found during a vast repertoire of movements, such as gait (Ivanenko et al. 2003) and grasping (Santello et al. 1998; for a review see Santello et al. 2013), have been associated with low dimensionality in multi‐muscle EMG recordings (Weiss & Flanders, 2004; Lacquaniti et al. 2012). Performance of a complex task could then be explained by a number of ‘commands’ (motor primitives) that is smaller than the number of active muscles (Ivanenko et al. 2004; Dominici et al. 2011). Moreover, it has been hypothesized that correlated muscle activity should be associated with correlated spiking activity of the respective motor neuron pools (De Luca & Erim, 2002; Winges & Santello, 2004; Hockensmith et al. 2005; Winges et al. 2008; Bizzi & Cheung, 2013; Laine et al. 2015). However, previous studies have assessed the amount of neural connectivity across synergistic muscles (Winges & Santello, 2004; Winges et al. 2006; Laine & Valero‐Cuevas, 2017). A remaining question is whether and the extent to which correlated activity in intramuscular or surface EMG signals might be a byproduct of biomechanical constraints. One such constraint might be the need for neural activity of multiple muscles to be temporally coordinated to contribute to the performance of a given task; for example, correlated activity across compartments of finger flexors or extensors would contribute to coordinating digit forces to prevent object slip during object hold or digit release (De Luca & Erim, 1994; Santello & Fuglevand, 2004; Hockensmith et al. 2005; Winges et al. 2006; McIsaac & Fuglevand, 2008; Keen et al. 2012). Critically, it is currently unknown if motor nuclei of different muscles share common inputs when these neurons perform a task that is not part of the common repertoire of movements encountered in activities of daily living, such as grasping or manipulation.

Lastly, we note that previous studies have estimated neural connectivity mainly using interference surface EMG signals. These studies have reported relatively high values of intermuscular coherence when using global EMG during concurrent activation of hand muscles in human and non‐human primates (Baker et al. 1999; Farmer et al. 2007; Laine & Valero‐Cuevas, 2017). A potential issue with these findings is that global EMG may bias coherence estimation due to cross‐talk between EMG signals.

Our study was designed to address the above gaps by (1) investigating the behaviour of populations of single motor neurons innervating the first dorsal interosseous (FDI) and thenar muscles while performing non‐synergistic digit actions, and (2) estimating the amount of cross‐talk between their EMG signals by quantifying the contribution of motor unit action potentials in one muscle to the EMG of the other muscle. Although the FDI and the thenar muscles have a common origin on the first metacarpal, their control is not biomechanically constrained by connective tissue as occurs, for example, for compartments of finger flexor or extensor finger muscles (reviewed by Schieber and Santello, 2004), nor is constrained by a common insertion point on the mechanical degree of freedom (Laine et al. 2015). Therefore, when FDI and thenar muscles are activated concurrently to abduct the index finger and flex the thumb, respectively, this task could theoretically be performed by independent activation of the two motor neuron pools even when digit forces are unequal. Furthermore, our task was designed to avoid alignment of thumb flexion and index finger abduction force vector directions as occurs during functional tasks (e.g. a key grip). Therefore, neural connectivity between the two pools of motor neurons is not functionally needed to assist force production by each digit for task execution, nor neurally constrained by common innervation. If, however, there are neural constraints limiting independent digit force control, one would expect partly correlated spiking activity of the motor neuron pools. We hypothesized that the CNS reduces the redundancies of motor control by projecting common synaptic input to distinct motor modules in a default way, as observed during synergistic actions. This hypothesis was based on the fact that the two populations of motoneurons may receive common input from both supraspinal and afferent pathways and this strategy is needed to reduce the available number of motor dimensions (Lacquaniti et al. 2012; Boonstra et al. 2016; Santello et al. 2016; Kerkman et al. 2018). Indeed, when the CNS is performing a new motor act, the reduction in the number of available dimensions simplifies the size of search space and thus motor solutions. We also hypothesized a significant bias on coherence when inferring neural connectivity using global EMG.

Materials and methods

Participants

Eleven subjects (28 ± 2 years, 69.18 ± 6.29 kg, eight men) participated in the study. All subjects were right‐handed, had normal or corrected‐to‐normal vision and reported no previous history of neuromuscular diseases. The procedures were in accordance with the Declaration of Helsinki and were approved by the Imperial College ethical committee and registered in a database (N 18IC4685). The subjects signed an informed consent before participating in the study.

Experimental protocol

Participants were comfortably seated on a chair with both arms resting on a table. A custom‐made apparatus firmly secured to a table supported the right hand in a vertical position (half‐way between pronation and supination) and immobilized the forearm and wrist. The index finger was aligned with the forearm and the thumb was kept in a resting position at the same height as the index finger (Fig. 1 B).The visual feedback of force was displayed on an LCD monitor positioned at ∼60 cm in front of the subject. Visual gain was kept constant at 66 pixels per % maximal voluntary contraction (MVC) force for each muscle (axis). Force exerted by each digit was measured with a three‐axis force transducer (Nano25, ATI Industrial Automation, Apex, NC, USA), digitized at 2048 Hz (USB‐6225, National Instruments, Austin, TX, USA), and low‐pass filtered with a 15‐Hz cutoff frequency.

Figure 1. Experimental set‐up and data analysis.

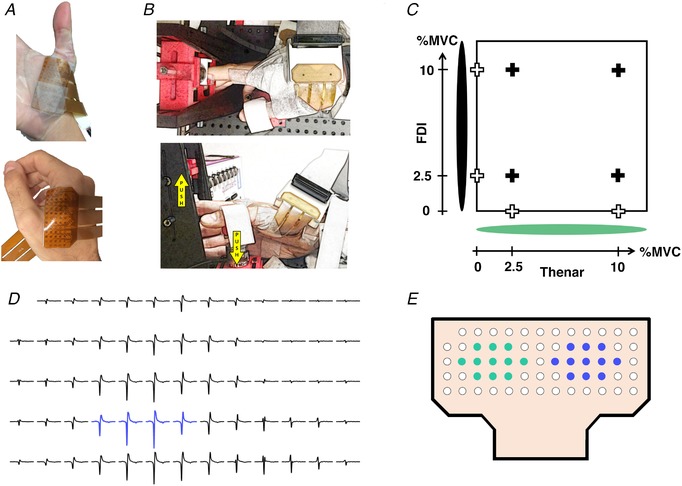
A, two high‐density surface EMG grids of 64 electrodes, each placed on the thenar and first dorsal interosseous (FDI) muscles (top and bottom row, respectively). B, the experimental apparatus that was used for the index finger abduction and thumb flexion isometric contractions (top and bottom row, respectively). The yellow arrows indicate the force directions for the hand digits. C, visual feedback shown as a cursor in which the x‐axis corresponded to the force of the thumb flexion and the y‐axis to the force of the index finger abduction. The eight contraction conditions are marked with crosses (individual contractions for the index finger and thumb: white crosses; simultaneous contractions: black crosses). Two LEDs were used to indicate the onset of contraction and the finger active (green light). MVC, maximal voluntary contraction. D, selection of four consecutive electrodes with the greatest amplitude to estimate motor unit action potentials through monopolar electrode derivation. E, two groups of 11 electrodes used to estimate the bipolar derivation. [Color figure can be viewed at http://wileyonlinelibrary.com]

High‐density surface EMG signals were recorded with a multichannel amplifier (OTBioelettronica Quattrocento, Turin, Italy; bandwidth: 10–500 Hz; resolution: 16 bits) at a sampling rate of 2048 Hz. Two 13 × 5 flexible grids of high‐density surface EMG electrodes (4‐mm interelectrode distance) were placed on the FDI (Fig. 1 A, top row) and thenar muscles (Fig. 1 A, bottom row). The high‐density grids on the thenar muscles targeted the activity of the flexor pollicis brevis and abductor pollicis brevis.

The force‐matching tasks consisted of steady isometric index finger abduction and thumb flexion of the interphalangeal joint either individually or simultaneously at 2.5% and 10% MVC force. The thumb was securely fixed approximately on the medial side of the palm directing the force across the palm. Subjects performed eight tasks. In four tasks, subjects performed only index finger abduction or thumb flexion (contractions at 2.5% and 10% MVC for each digit), whereas in the other four tasks subjects performed both contractions simultaneously (index abduction and thumb flexion at 2.5% and 10% MVC, in all combinations; Fig. 1 C). Visual feedback was provided as a moving dot cursor in which the x‐axis and y‐axis corresponded to the forces of the thumb and index finger, respectively (Fig. 1 C), and the centre of a red cross marked the target. Subjects were required to maintain the force signal within the target area with a maximum tolerance of 10% of the target level. During the simultaneous contractions, the force visual feedback corresponded to the outputs of the two force sensors. In contrast, during the individual digit contractions, the force of the other digit was recorded but not shown on the monitor in order not to influence the motor strategy used by the subject to execute the task. Subjects were guided on which movement to perform by showing a green light that was placed on the respective axis of the active feedback cursor, and a cross indicated the targets (Fig. 1 C).

The experiments started with the performance of MVC that lasted 10 s for each digit. The MVC force for each digit was defined as the maximum value of two attempts. After MVC for each digit was recorded, visual feedback of the target force was shown for 60 s to the subjects in order to get acquainted with the task. Subsequently, subjects were asked to perform two trials of 15 s for each force target for the tasks with two active muscles. In addition, one trial of thumb flexion or index abduction were performed for each force level. By the end of this familiarization session, all subjects were able to reach the target in less than 10 s and maintain force at the target level. The last part of the experiment consisted of steady contractions of 60 s duration for each of the eight target forces. Each of the eight contractions was performed twice. The order of trial presentation was randomized, and subjects were given 30 s of rest between trials.

As noted in the Introduction, we designed our task to determine the extent to which distinct motor neuron pools would receive common inputs using contexts that are far removed from habitual patterns of muscle activation associated with daily activities (e.g. grasping or manipulation). Therefore, our ‘non‐synergistic’ task was, by design, artificial because (1) the two digits were required to exert un‐matched forces, and (2) the digit force vectors were not aligned or in the same plane. The fact that it took subjects ∼10 min to become acquainted with the task confirms the artificial nature of our force production task. Therefore, using such a non‐synergistic task, together with analysis of activity of two muscles that do not share the same mechanical action or innervation, should provide a rigorous test of the task‐dependency of shared neural inputs to motor neuron pools.

Data analysis

Signals were processed offline in MATLAB (The MathWorks, Natick, MA, USA).

Digit force

The force signal was low‐pass filtered (fourth‐order Butterworth digital filter, 15 Hz cut‐off frequency) and detrended. The initial 9.5 s and last 0.5 s of the recordings were discarded from the force, EMG and motor unit analyses. Therefore, all the reported metrics were computed in an interval of 50 s. The coefficient of variation of force (CoV) was computed to quantify force steadiness (Feeney et al. 2018). The similarity between the force signals generated by the two digits was quantified as Pearson's correlation coefficient (rho).

Global EMG

EMG signals were averaged across all channels (64 per muscle), low‐pass filtered at 250 Hz (fourth‐order Butterworth), full‐wave rectified and normalized to unit variance (Z‐score) (Laine & Valero‐Cuevas, 2017). The similarity between FDI and thenar normalized EMGs was assessed by pooled coherence analysis (Amjad et al. 1997). In each contraction condition, normalized EMGs from all subjects and trials were used to concatenate the EMG trials. Coherence was then estimated by Welch's averaged periodogram with non‐overlapping Hanning window of 1 s duration. Similarity in the time domain was assessed by the analysis of Pearson's correlation coefficient (rho) between FDI and thenar detrended EMG envelopes, estimated after low‐pass filtering (cut‐off at 1 Hz, second‐order Butterworth) the normalized EMGs.

Motor unit decomposition

High‐density EMG signals were decomposed into motor unit spike trains using a blind source separation algorithm (Holobar & Zazula, 2007). The pulse to noise ratio (PnR) that estimated the accuracy in discharge identification was set to 30 dB (Holobar et al. 2014). After automatic decomposition, the motor unit spike trains were visually inspected (Del Vecchio et al. 2019b). From the motor unit spike trains, we estimated the neural drive to the muscle as the cumulative spike train (CST) of the identified motor units (Del Vecchio et al. 2019b). This estimate was smoothed with a Hanning window of 400 ms duration (sCST).

Time‐ and frequency‐domain correlation analyses

Correlations between the neural drive to the FDI and thenar muscles were evaluated in the time and frequency domains. The time domain correlation was computed as the Pearson's correlation coefficient (rho) between detrended sCSTs. Cohen's effect size was used to determine the strength of the association: correlation coefficients of 0.1, 0.3 and 0.5 represent a small, moderate and large association, respectively. In the frequency domain, we estimated the pooled coherence between the CST from the FDI and thenar motor units (Amjad et al. 1997). CST was treated as a point process and respects the time order assumption (Amjad et al. 1997). In each trial, coherence analysis was performed on the pooled CSTs consisting of permutations of all possible combinations of groups of three motor units, or until completing 100 permutations. Coherence was estimated with Welch's averaged periodogram with non‐overlapping Hanning window of 1 s duration. Pooled coherence was then transformed to a standard Z‐score using the equation: $Z=\sqrt{2L}\mathrm{atanh}(\sqrt{(c)})-bias$, where c is coherence, L is the number of time segments used in each coherence analysis and $bias$ was calculated empirically as the mean coherence Z‐value between 250 and 500 Hz (Baker, 2002). Standard Z‐scores were transformed back to coherence using the maximum and most frequent number of time segments used in the pooled coherence analysis, L _max of 5000 (100 permutations of trials of 50 s duration). The peak values of the coherence in the delta (0–5 Hz), alpha (5–15 Hz) and beta (15–35 Hz) bands were identified for each simultaneous contraction condition for all valid trials (trials with more than three decomposed motor units). For a given contraction condition, the overall coherence across subjects was computed by combining values from N valid trials to produce a composite coherence according to: $\epsilon =\frac{1}{\sqrt{N}}{\sum }_{i=1}^N{Z}_i$, where $Z_i$ is the transformed Z‐score in each trial (Kilner et al. 1999). The level for significant coherence was set to $COF=1-(1-0.95)\wedge (1/(L_{max}-1))$ (Rosenberg et al. 1989). The coherence function was also computed from random contraction conditions for the motor unit data.

Global EMG cross‐talk analysis

We used the motor unit spike trains identified in the thenar and FDI muscles to estimate the amount of cross‐talk between global EMG signals. The discharge timings for individual motor units identified by decomposition (Fig. 1 D) were used to trigger the multi‐channel global EMG to determine the waveforms of the motor unit action potentials (MUAPs) recorded by the grids over both muscles. MUAPs with the lowest amplitude between the two muscles were defined as cross MUAPs.

Peak‐to‐peak amplitude was computed for the MUAPs recorded from the muscle generating the motor unit activity and from the other muscle (cross‐talk). Both MUAP amplitudes were compared against the amplitude of the spike‐triggered average performed with random triggers (equivalent baseline noise and with the same number of MUAPs). The MUAPs corresponding to random triggers was defined as random MUAPs. Cross‐talk for each MUAP was quantified as the ratio $(crossMUAP/MUAP)\times 100\%)$ (Fig. 2).

Figure 2. Coherence from EMG signals: influence of cross‐talk.

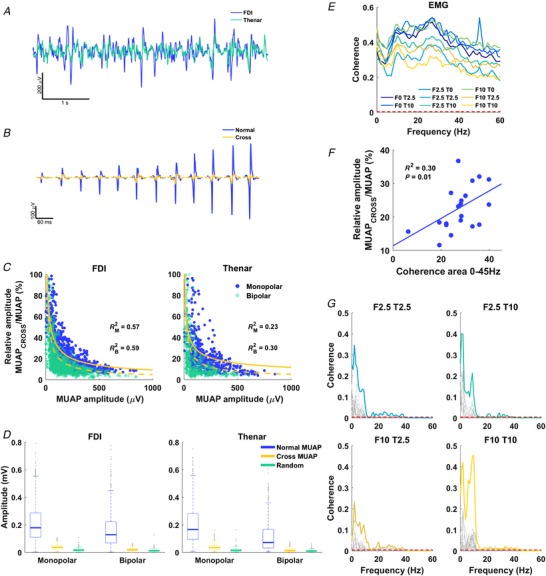
A, global EMG signals for first dorsal interosseous (FDI) and thenar muscles (blue and green curves, respectively). B, FDI motor unit action potentials (MUAPs) extracted by spike‐triggered averaging the FDI EMG (blue) and the thenar EMG (cross MUAP, orange). C, ratio between the amplitude of the MUAP in one muscle triggered by the MUAP in the other muscle (cross MUAP) normalized by the amplitude of the trigger MUAP with monopolar and bipolar derivations. D, box plot of the amplitude of the regular, cross and random MUAP for FDI and thenar with monopolar (left) and bipolar (right) EMG signals (median, 25th and 75th percentiles are given). E, mean coherence between FDI and thenar EMG of all subjects at frequencies up to 60 Hz for all contraction conditions; contraction conditions are indicated by the intensity of contraction (0, 2.5 or 10% MVC) of FDI (F) and thenar (T). Dashed red lines denote 95% confidence level for statistical significance. F, relationship between relative amplitude of cross and normal MUAP to coherence area of the spectrum up to 45 Hz for each contraction condition (circles). G, coherence between cumulative spike trains for FDI and thenar for simultaneous contraction conditions. Each spectrum in grey represents a trial, and colour lines the pooled coherence for all trials (see Methods). Data in C–G are from all subjects. [Color figure can be viewed at http://wileyonlinelibrary.com]

Cross‐talk analysis was performed for both monopolar and bipolar derivations reflecting commonly used EMG recording systems. For the monopolar derivation, the resulting MUAPs were identified as the average of the estimated waveforms from four consecutive neighbouring electrodes with the greatest amplitude (Fig. 1 D). For the bipolar derivation, the MUAP waveforms were estimated as recorded by the difference between two sets of 11 neighbouring electrodes that corresponded to the centroid of the high‐density EMG grids (Fig. 1 E).

Statistical analysis

We examined the influence of contraction condition (simultaneous versus individual digit actions) on force output, motor unit behaviour and neural connectivity. Moreover, we tested the amount of surface EMG cross‐talk during the different voluntary force contractions.

Statistical analysis was performed using SPSS (IBM, version 21). Before group comparisons, assumptions for normality and sphericity were accessed by a Shapiro–Wilk test and Mauchly's test of sphericity, respectively. A Friedeman's test accessed differences in MUAP amplitude between discriminated MUAP (normal) as well as cross and random MUAP (see previous section). Post hoc analysis with Wilcoxon's signed‐rank test was conducted with a Bonferroni correction. A three‐way analysis of variance with repeated measures (three‐way RM‐ANOVA, N = 11 subjects) estimated the effect of three factors on mean force, force CoV and MU discharge rate: Muscle (FDI and Thenar), Contraction intensity (2.5% and 10% MVC) and Contraction condition (contraction intensity of the other muscle: 0%, 2.5% and 10% MVC). For all correlations analysis (between force time series, EMG envelopes and sCSTs) a two‐way RM‐ANOVA (N = 11) was performed to compare the absolute correlation coefficient (rho) between simultaneous contraction conditions (factors: Muscle and Contraction intensity).

Analysis of peak coherence was performed only for trials with a minimum of three motor units in each muscle, which resulted in missing cases of trials and subjects for statistical analysis. Therefore, a one‐way ANOVA (simultaneous contraction conditions) on valid trials only was used to compare peak coherence profiles between contraction conditions. Multiple comparisons were corrected with Bonferroni's post hoc test, and a 95% significance level was adopted. Data are reported as mean values ± 95% confidence interval.

Results

Motor unit analysis

In total, 1635 motor units (FDI: 1163; thenar: 472) were decomposed, with an average number of 8.55 ± 1.00 and 3.64 ± 0.58 for FDI and thenar muscles per contraction, condition and subject. In some cases, we observed few motor units active in the muscle that was required to be inactive during the independent force control task. In these cases, the total number of identified motor units was 88 and 6 for FDI and thenar, respectively. One subject, however, contributed the most to these active motor units, with 37.5% of the decomposed motor units for FDI. On average, 2 motor units were decomposed for the FDI during individual thenar contractions, and only 0.1 for thenar muscles during FDI contractions, in agreement with the observed negligible forces generated (<1% MVC). These cases were excluded from further analysis because the number of motor units was small and the force exerted was negligible.

The motor unit discharge rate did not differ between muscles (F _1,7 = 0.009, P = 0.926) nor between simultaneous or individual control of both muscles (F _2,14 = 2.622, P = 0.108). However, as expected, there was a significant increase in the discharge rate of the identified motor units with increasing force (F _1,7 = 35.943, P = 0.001).

Coherence computed on global EMG signals is contamined by cross‐talk

Figure 1 A and B shows an example of positioning of the two high‐intensity EMG grids and the experimental apparatus that recorded the force signals from the hand digits. We first aimed to assess the correlation between the EMG signals of the thenar and FDI muscles during the hand digit tasks. Average EMG signals from the FDI and thenar muscles were highly correlated (Fig. 2 A) during the voluntary isometric contractions. This correlation could be explained either by a large proportion of shared synaptic inputs or from cross‐talk myoelectrical activity arising from the motor unit discharges from the other muscle. To test this hypothesis, we decoded the motor unit action potentials from both muscles and used the discharge times of each motor unit to identify concurrent motor unit action potential in both muscles. Figure 2 B shows an example of action potentials that were represented in both muscles due to cross‐talk.

Cross‐talk analysis showed that motor units of low amplitude, which are probably deeper in the muscle, generated relatively greater cross‐talk (see example in Fig. 2 B). Indeed, the ratio between the amplitude of the MUAP in one muscle triggered by the MUAP in the other muscle (cross MUAP) normalized by the amplitude of the trigger MUAP decreased monotonically with the trigger MUAP size (Fig. 2 C), regardless of the EMG derivation (monopolar or bipolar). We found a significant difference between amplitude for the MUAP (normal MUAP), the cross MUAP and the MUAP identified by random triggers (random MUAP) for the FDI and thenar muscles, both for monopolar and for bipolar derivations (P < 0.001) (Fig. 2 D). The random MUAPs were consistently lower in amplitude than the cross MUAPs for the FDI using monopolar and bipolar derivations (Z = −28.722 and −22.982, respectively; both P < 0.001) and for the thenar muscles using monopolar and bipolar derivations (Z = −17.436 and −10.157, respectively; both P < 0.001). This clearly shows that the global interference EMG signal from the thenar and FDI muscles is largely influenced by the activity of the neighbouring muscles. Indeed, on average, 28.38 ± 1.97% and 25.75 ± 2.32% of the motor units active in the FDI and thenar muscles, respectively, were identified in the neighbouring muscle (Fig. 2 C).

The above results indicate that the significant coherence values between global EMGs for the FDI and thenar muscles found at most frequencies and digit force combinations (Fig. 2 E) was probably contaminated by the high cross‐talk between global EMG signals. This was confirmed by linear regression analysis showing that the absolute amount of cross‐talk explained the variance in EMG coherence across subjects (Fig. 2 F), indicating that cross‐talk was one of the main determinants of the observed EMG coherence. This analysis indicates that the surface EMG signal from hand muscles is strongly biased by cross‐talk, and that neural connectivity analysis in these conditions cannot be performed by using interference EMG, but rather requires the identification of motor unit spike trains. Conversely, when the coherence was obtained from the spiking motor units (binary signal), it was possible to observe clear peaks in the frequency bands associated with the common synaptic inputs to the motor neurons (Fig. 2 G), without any influence of EMG cross‐talk. Because of cross‐talk, it was possible to identify the same motor units in the two muscles by the blind source separation decomposition technique, thus leading to an inflated correlation between spike trains (∼1). The motor units identified in both muscles were removed from the muscle where they exhibited the lowest peak‐to‐peak value.

Digit forces

For the individual action of one digit, the other digit was required to exert no force (Fig. 1 C). To verify that subjects complied with this requirement, we analysed the forces of the non‐instructed digit. We confirmed that the non‐instructed digit exerted negligible force, i.e. < 1% MVC (0.56 ± 0.13% and 0.26 ± 0.07% MVC for index finger and thumb, respectively). The average digit force at each target force did not change when the FDI and thenar muscles were contracting simultaneously or individually (no significant Muscle × Contraction condition interaction, F _2,18 = 2.156, P = 0.145). Figure 3 A shows the changes in force variability across the experimental conditions. The CoV of force was greater during index abduction when compared to thumb flexion (F _1,9 = 17.504, P = 0.002, Fig. 3 A) and at lower (2.5% MVC) than at higher forces (10% MVC) for both muscles, independently of simultaneous or individual digit control (F _2,18 = 129.616, P < 0.001). However, variability in force at 2.5% MVC increased from individual contraction to simultaneous activation of both muscles (significant interaction between Contraction intensity and Contraction condition, F _2,18 = 30.993, P < 0.001, Fig. 3 A). Indeed, Fig. 3 A shows that when one digit exerted 2.5% MVC force, the variability in force systematically increased with the contraction force of the other digit. The decrease in steadiness was further exacerbated when one digit exerted force at 2.5% MVC and the other at 10% MVC, independently of the muscle. This is probably the result of neural constraints, i.e. the common drive to both muscles as outlined below.

Figure 3. Neuromechanical connectivity between hand digits.

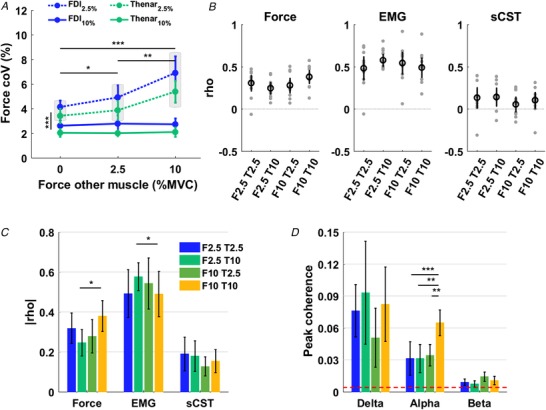
A, influence of force exerted by one digit on force variability (CoV) of the first dorsal interosseous (FDI) and thenar muscles (blue and green curves, respectively) when contracting at 2.5% and 10% maximal voluntary contraction (MVC) (dashed and dotted curves, respectively). Shaded blocks indicate groups with significant difference. B, Pearson's correlation between forces (left), EMG (middle) and smoothed cumulative spike trains (sCST; right) for FDI and thenar for simultaneous contraction conditions. Subjects are represented as grey circles and the average in black. Contraction conditions are indicated by the intensity of contraction (0, 2.5 or 10% MVC) of FDI (F) and thenar (T). C, absolute Pearson's correlation for force, EMG and sCST for simultaneous contractions. D, peak coherence for the cumulative spike trains of FDI and thenar muscles in the delta (0–5 Hz) alpha (5–15 Hz) and beta (15–35 Hz) bands for simultaneous contraction conditions. Dashed red lines denote 95% confidence level for statistical significance. Asterisks indicate a significant difference between contraction conditions (^*0.01 < P < 0.05, ^**0.001 < P < 0.01, ^*** P < 0.001) and the mean and confidence interval are shown. [Color figure can be viewed at http://wileyonlinelibrary.com]

The abduction and flexion forces exerted by the index finger and thumb, respectively, were significantly correlated for all simultaneous contraction conditions (Fig. 3 B, left panel, P < 0.05 for each attempt). The strength of correlation was moderate (0.3 < |rho| < 0.5) for contractions in which the digits exerted the same force (0.38 ± 0.09 and 0.32 ± 0.09 at 2.5% and 10% MVC, respectively), and small (0.1 < |rho| < 0.3) when the digit exerted different forces (0.25 ± 0.07 and 0.28 ± 0.09, for FDI 2.5% and thenar 10% MVC, and FDI 10% and thenar 2.5%, respectively) (Fig. 3 C, left panel). A significant interaction between digit forces was observed (F _1,10 = 10.050, P = 0.01), but no main effects of FDI force (F _1,10 = 2.353, P = 0.156) and thenar force (F _1,10 = 0.181, P = 0.680) were found. Pairwise comparisons showed that correlation increased significantly when thenar muscles exerted 10% MVC force and the FDI increased force from 2.5% to 10% MVC (P = 0.010) (Fig. 3 C, left panel).

Motor neuron pools of FDI and thenar muscles received common inputs across multiple frequency bands

Time and frequency domain analyses revealed significant correlations in the neural drive to the two muscles. However, the amount of synchrony in the FDI and thenar EMG was significantly greater than the coupling between motor neuron discharges (Fig. 3 B, middle and right panel, respectively) because of the large cross‐talk in the former type of data (see above).

Figure 3 B (middle panel) shows Pearson's correlation coefficient for EMG envelopes for each subject. A significant interaction between FDI and thenar contraction intensity was found (F _1,10 = 24.348, P = 0.001), and pairwise comparisons showed that correlation for FDI and thenar at 10% MVC was significantly smaller than for the condition FDI 2.5% and thenar 10% MVC (Fig. 3 C, middle panel).

Unlike correlation between EMG envelopes, correlation between the two time series of sCSTs exhibited a weaker but significant correlation than global EMG envelopes (0.18 ± 0.03; P < 0.05 for all cases), whereas no significant differences were found between contraction conditions (P > 0.238 for all factors) (Fig. 3 C, right panel). Analysis of coherence of the two cumulative motor neuron discharge timings showed significant peaks at the delta, alpha and beta bands (Fig. 3 D). Peak coherence was greatest at the delta band and weakest at the beta band, with an intermediate strength at the alpha band. Peak coherence was significantly modulated as a function of contraction condition in the alpha band (P < 0.001), but not in the delta and beta bands (P = 0.489 and P = 0.0889, respectively). In the alpha band, when both digits were contracting at 10% MVC, peak coherence was twice the magnitude than other force conditions (0.06 ± 0.01 and 0.03 ± 0.02, respectively; P < 0.001, P = 0.001 and P = 0.004 for all pairwise comparisons; Fig. 3 D). The average peak coherence in the delta and beta bands was 0.08 ± 0.02 and 0.01 ± 0.00, respectively (Fig. 3 D). When the coherence function was calculated for random contraction conditions within the same participant, the coherence values were very low (delta: 0.025 ± 0.024; alpha: 0.008 ± 0.004; beta: 0.005 ± 0.003).

Discussion

We report evidence of neural connections between two populations of motor neurons innervating the thenar and first dorsal interosseous muscle during a non‐synergistic task that involved production of un‐matched or matched digit forces at different directions. Importantly, common inputs were found at frequency bands associated with spinal and cortical mechanisms. Moreover, common input was modulated as a function of voluntary force in the alpha band. These results reveal the underlying neural strategies of muscle control being characterized by shared spinal and supraspinal inputs to motor neurons during simultaneous digit force control. They suggest that correlated input to motor neurons of two hand muscles can occur even during tasks not belonging to a common behavioural repertoire and despite lack of common innervation. Finally, we show that intermuscular coherence estimated from global EMG signals, as used in previous work, is strongly influenced by cross‐talk and therefore is an unreliable measure of neural connectivity.

Muscle synergies

The seamless control of multi‐joint movements is commonly described as muscle coordination. The classic concept of motor synergies posits that multiple degrees of freedom are controlled in a lower‐dimensional space than the available number of dimensions (D'Avella et al. 2003; Ivanenko et al. 2004; Santello et al. 2016). This definition has been adopted by many studies, particularly when accounting for synergistic muscle activation during locomotion and control of the hand during grasping (Ivanenko et al. 2004; Dominici et al. 2011; Santello et al. 2016). Most previous work has assessed neural connectivity during synergistic tasks. However, the potential existence of neural coupling at the motor neuronal level during a ‘non‐synergistic’ task has not been systematically explored. We also note that the analysis was previously limited to global EMG analysis, which is strongly influenced by volume conduction. In this study, we tested the hypothesis of the presence of neural coupling during the control of two hand muscles that could have been, theoretically, independently activated during an uncommon force production task (i.e. a digit was required to exert forces of different magnitudes relative to the other digit and at divergent force directions). We confirmed this hypothesis by detecting significant neural coupling in the activity of two motor neuron pools. The fact that the observed neural coupling was present across a wide frequency bandwidth indicates the existence of common input to the two hand muscles from several sources (Farmer et al. 1993; De Luca & Erim, 1994; Baker et al. 1997; Farina et al. 2014; Negro et al. 2016).

Moreover, we report that cross‐talk between myoelectrical activity of two hand muscles significantly biases coherence estimation. Previous research has focused on the extraction of intermuscular coordination by coherence analysis of the global EMG activity (Baker et al. 1999; Farmer et al. 2007; Laine & Valero‐Cuevas, 2017). These studies report a significant level of coherence at cortical frequencies. In the present study, we show that the strength of coherence between global EMG signals from hand muscles is largely determined by the action potentials being represented at the surface of both muscles due to volume conduction (i.e. cross‐talk). Therefore, we conclude that it is not possible to infer the amount of neural connectivity between populations of motor neurons by coherence analysis of global EMG. This conclusion also points to the need of re‐evaluating previous work that has applied coherence analysis to global EMG signals.

Synaptic input to pools of motor neurons

Motor neurons innervating an individual muscle receive common synaptic inputs for the control of muscle force (Nordstrom et al. 1992; Farmer et al. 1993; Laine et al. 2015). Classic muscle synergy studies have focused on neural connectivity between pools of motor neurons during tasks that impose common spatio‐temporal activations (e.g, grasping, walking and pointing). Our study focused on two pools of motor neurons innervating hand muscles that can be activated independently based on different force vector directions and magnitudes, and because they lack mechanical coupling by connective tissue. We also note that the two muscles do not share the same innervation: the FDI is innervated by the ulnar nerve, whereas the thenar muscles – the superficial head of flexor pollicis brevis and abductor pollicis brevis – are innervated by the median nerve. Therefore, the thenar and FDI muscles could have theoretically been controlled independently. It follows that if coherence between spike trains of their motor neuron pools is still found, it would imply that neural connectivity may not play a functional role to attain a specific task goal (Boonstra et al. 2016). Despite all of these factors and our non‐synergistic task, significant neural coupling among motor neurons still occurred. This finding, together with the result that neural coupling was sensitive to the exerted force in the alpha band, suggests a combination of ‘default’ synergistic distribution of neural inputs that nevertheless maintains some degree of task dependency. Indeed, this may be an efficient solution obtained by the CNS to reduce the redundancies of motor control, as occurs during synergistic tasks (Dominici et al. 2011; d'Avella & Lacquaniti, 2013; Boonstra et al. 2016). Moreover, the evidence from this study supports the theoretical and experimental observations found in muscle synergy studies (D'Avella et al. 2003; Ivanenko et al. 2004; Lacquaniti et al. 2012), showing that motor neurons may be grouped in a way that reflects a distinct set of motor primitives (commands) that are shared across different motor nuclei. Indeed, our task was not part of a common behavioral repertoire. Bernstein (1967) proposed that, during learning of a new motor skill, the CNS may reduce the number of motor solutions to simplify coordination. Therefore, common synaptic input to distinct motor modules may be a default strategy of the CNS when controlling a motor task, regardless of whether the motor action is novel and requires training (our task) or belongs to the repertoire of daily activities. The co‐activation of FDI and thenars may be suppressed with skill learning, but this would require time. Finally, it cannot be disregarded that at the central pattern generator level, the task employed in this study may recall a more common task and thus the neural code shows a fixed correlated activity that is needed in many daily tasks, such as in preventing object slipping. However, these hypotheses should be examined explicitly.

Interestingly, neural coupling was found at all the frequency bands of the motor neuron output (Fig. 3 D). Moreover, this neural coupling occurred only when the two hand digits were contracting simultaneously. Although the FDI does interact mechanically with the muscles of the thenar eminence, their shared inputs are not an obligatory consequence of such mechanical interaction. This is demonstrated by the rare occurrence of the motor unit of FDI or thenar muscles being recruited only when one of the muscles is required to exert force. If the mechanical interaction were engaged by default, one would expect co‐activation even when only one muscle is required to be active. Indeed, only in rare cases (with one subject contributing to most of the variance) did we find active motor units in the muscle that was required to be inactive.

Coherence in the delta, alpha and beta band has been linked to both spinal (Vallbo & Wessberg, 1993; Baker, 2002; Williams & Baker, 2009; Farina et al. 2014) and supraspinal inputs (Farmer et al. 1993; Baker et al. 1997; Salenius et al. 1997; Watanabe & Kohn, 2015). The commonality in the output of the FDI and thenar muscle motor neurons in the beta band could represent distributed neural drive to both pools of motor neurons from supraspinal circuitries that are sensitive to task requirements (Farmer et al. 1993; Baker et al. 1997; Salenius et al. 1997). However, correlation analysis revealed even stronger common input in the alpha band, which suggests a contribution from muscle afferents and other spinal circuitries (Conway et al. 1995; Williams & Baker, 2009). It is likely that afferent inputs had common projections into the two motor neuron pools investigated here (Farmer et al. 1993; Vallbo & Wessberg, 1993). Indeed, we found an increase in the alpha band when both fingers were contracting at 10% of maximal voluntary force, which would have elicited greater somatosensory and tactile afferent inputs (Fig. 3 D).

Coherent oscillations produced by motor neurons are tuned by recurrent inhibition/excitation (Cullheim et al. 1977, 1984; Williams & Baker, 2009). Although intrinsic hand muscles lack recurrent inhibition by Renshaw cells (Katz et al. 1993; Illert & Kümmel, 1999; Williams & Baker, 2009), motor neuron to motor neuron monosynaptic connections (Cullheim et al. 1977, 1984) and interneuronal connections (Machacek & Hochman, 2006) can generate recurrent excitatory/inhibitory periodic inputs to motor neurons at the tremor frequency (∼10 Hz). These mechanisms may account for the significantly correlated motor neuronal activity in the alpha and delta bands. The primary motor cortex generates activity at frequencies of ∼10 and ∼20 Hz, as revealed by corticomuscular coherence (Conway et al. 1995; Baker et al. 1997; Salenius et al. 1997). Therefore, these inputs could contribute to common oscillations in motor neuronal activity by modulating interneuronal inputs to motor neurons, and/or by the non‐linear conversion of these inputs to coherent motor neuron output at both the delta and the beta frequency (Watanabe & Kohn, 2015). Synchronized motor neuronal discharges, coupled with coherent suppressions of tremor frequencies by spinal loops, may be advantageous for performing accurate, precise force tasks because force variability is reduced with decreased variability in the common synaptic input to motor neurons (Feeney et al. 2018), as discussed below.

Low‐frequency component of the neural drive to the muscle

We show that the low frequency bandwidth of the neural drive to the muscle (<5 Hz), which is partly responsible for the muscular force oscillations around a fixed target, was modulated in both fingers in a coherent way and in all contraction conditions, supporting the hypothesis that both pools of motor neurons receive shared synaptic inputs. The mechanisms responsible for the low‐frequency component of the neural drive to the muscle are currently unknown, but simulation studies suggest that an increase in motor neuron beta coherence causes an increase in the power of motor neuron output in the delta band and therefore in muscle force (Watanabe & Kohn, 2015). We did not observe a significant increase in beta band coherence with force, although a significant increase with voluntary output was seen for the alpha band (Fig. 3). This result, however, could be due to the relatively small number of identified motor units for the thenar muscles. Estimates of beta band coherence are indeed more dependent on the number of motor units used for the estimate than lower frequencies, due to the intrinsically greater sampling rate needed to estimate higher frequency components as input to motor neurons (Negro et al. 2016).

The neural coupling in the delta band of motor neuron output could be partly anticipated from the force recordings because force is directly determined by the low‐frequency components of the neural drive to the muscle (Negro et al. 2009; Del Vecchio et al. 2018). The low‐pass filtering (<5 Hz) of the discharge timings from populations of motor neurons accurately predicts the force output of a muscle in a wide range of voluntary contractions (Del Vecchio et al. 2018). The increase of the CoV of force generated by the thumb and index finger when producing two distinct force levels (e.g. 2.5% for the FDI and 10% for the thenar muscles; Fig. 2 A) indirectly indicates a neural link (i.e. the action of one digit significantly influences the action of the other). Indeed, force steadiness exhibited by most daily tasks may require similar relative cortical inputs to different pools of motor neurons. For example, during grasping or pinching, the net relative cortical drive to the muscle may be the same for the index finger and thumb (e.g. pinching), as indirectly indicated by the in‐phase fingertip force relationships during static object hold (Santello & Soechting, 2000). Indeed, the strength of these in‐phase relationships of force exerted by two muscles increases when both motor unit pools discharge synchronously (Santello & Fuglevand, 2004). We would speculate that during synergistic tasks (e.g. pinching) the common input to motor neurons may show a higher degree of synchrony (Santello et al. 1998; Winges & Santello, 2004; McIsaac & Fuglevand, 2008; Winges et al. 2008). However, this needs to be examined explicitly.

Conclusions

By analysing the behaviour of single motor units, we demonstrate for the first time that distinct populations of motor neurons innervating two intrinsic hand muscles receive common synaptic inputs in all frequency bands responsible for force control when generating forces at different force directions and magnitudes. The neurophysiological mechanisms underlying this synchronous activity appear to be widely spread across multiple central and spinal nuclei responsible for force modulation. Indeed, the significant coherence found within three frequency bands suggests that motor cortex and spinal modules send common inputs to multiple motor neurons even when digit actions do not need to be coordinated to attain a task goal or belong to a common behavioural repertoire. These results have important implications for the study of muscle synergies as they provide an experimental basis for identifying common neural projections to distinct pools of motor neurons.

Additional information

Competing interests and funding

This study was partly funded by the Proof‐of‐Concept Project Interspine (737570). C.M.G. is a recipient of a PhD scholarship from CAPES. She also received a Visiting Student Grant from PDSE/CAPES (CAPES Foundation, Ministry of Education of Brazil, proc. no. 88881.134842/2016‐01). L.A.E. is currently funded by CNPq (Brazilian NSF, proc. no. 312442/2017‐3) and FAPESP (The Sao Paulo Research Foundation, proc. no. 2017/22191‐3). The authors declare no competing financial interests. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (project NaturalBionicS; grant agreement No 810346).

Author contributions

All authors contributed to the conception and design of the work. A.D.V. and C.M.G. acquired and analysed the data. A.D.V. and C.M.G. drafted the manuscript and plotted the figures. All authors contributed to the interpretation of the results and in the revision of the manuscript. All authors have approved the final version of the submitted manuscript for publication and are accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Biographies

Alessandro Del Vecchio is a research associate at the Department of Bioengineering, Imperial College London. He received a BSc, MSc and PhD in Human Movement Sciences. He is interested in the organization and adaptation of the neuromuscular system in healthy and pathological conditions. His current work is based on recordings of brain and spinal motor neuron activity during voluntary force contractions.

Carina M. Germer received a BS and MS in Electrical Engineering from the University of Campinas (UNICAMP). Recently, she obtained her PhD at the Neural Engineering Research Laboratory, UNICAMP. Her research focuses on motor control, sensorimotor integration and motor unit physiology. She is interested in the neurophysiology of human movement under healthy and pathological conditions.