Computational fluid dynamics modeling, a novel, and effective approach for developing scalable cell therapy manufacturing processes

Abstract

Induced pluripotent stem cells (iPSCs) hold great potential to generate novel, curative cell therapy products. However, current methods to generate these novel therapies lack scalability, are labor‐intensive, require a large footprint, and are not suited to meet clinical and commercial demands. Therefore, it is necessary to develop scalable manufacturing processes to accommodate the generation of high‐quality iPSC derivatives under controlled conditions. The current scale‐up methods used in cell therapy processes are based on empirical, geometry‐dependent methods that do not accurately represent the hydrodynamics of 3D bioreactors. These methods require multiple iterations of scale‐up studies, resulting in increased development cost and time. Here we show a novel approach using computational fluid dynamics modeling to effectively scale‐up cell therapy manufacturing processes in 3D bioreactors. Using a GMP‐compatible iPSC line, we translated and scaled‐up a small‐scale cardiomyocyte differentiation process to a 3‐L computer‐controlled bioreactor in an efficient manner, showing comparability in both systems.

Induced pluripotent stem cells (iPSCs) hold great potential to generate novel, curative cell therapy products. However, current methods to generate these novel therapies lack scalability, are labor‐intensive, require a large footprint, and are not suited to meet clinical and commercial demands. Therefore, it is necessary to develop scalable manufacturing processes to accommodate the generation of high‐quality iPSC derivatives under controlled conditions.

1. INTRODUCTION

The generation of human‐induced pluripotent stem cells (iPSCs) from somatic cells was a major leap forward in the field of regenerative medicine. Yamanaka and colleagues showed that viral induction of four key transcription factors (Oct4, Sox2, Klf4, and c‐Myc) in somatic cells was enough to force cells back to an “embryonic‐like” state (Takahashi et al., 2007). These cells demonstrated similar proliferative potential and differentiation propensities to embryonic stem cells (ESCs) but had none of the ethical issues surrounding ESCs. In addition, because Yamanaka's methods for generating iPSCs using viruses, the field has advanced to using nonintegrating and nonviral methods, resulting in increased safety of using these cells and their derivatives for clinical indications (Haake, Ackermann, & Lachmann, 2018).

Currently, the development and production of cell‐replacement therapies from iPSCs is performed in a small‐scale culture that is not suitable for the generation of a large number of cells required for most therapies. For instance, it is estimated that 10⁹ cells would be required per patient in heart failure (Mummery et al., 2012), and with the market for heart failure potentially requiring thousands of doses a year, 10¹¹–10¹⁴ cells may be required annually. The development of scalable platforms is required to accommodate future demand for these therapies. However, there are a number of challenges with industrializing the manufacture of iPSCs and their derivatives including (a) access to acceptable starting material (including iPSCs) generated under current good manufacturing practices (cGMP), (b) development of appropriate optimized and qualified analytical methods for assessing cellular characteristics and function and, (c) development of scalable bioprocessing platforms.

The use of cGMP‐acceptable starting material is required for manufacturing a clinical product. This includes reagents, consumables, and media used in the process and also the starting cell population. We have recently reported manufacturing of iPSC master cell banks under cGMP and their directed differentiation potential to three germ layers (Baghbaderani et al., 2016, 2015; Shafa, Yang, Fellner, Rao, & Baghbaderani, 2018). The use of these cGMP‐compliant iPSC banks allows for starting clinical development with GMP‐sourced material thereby facilitating a smoother transfer to cGMP manufacturing.

Using appropriate methods to properly characterize the cell therapy manufacturing process is extremely important. iPSCs differentiation to clinically‐relevant cells usually involves passing through a number of different stages and it may be necessary to understand the extent of differentiation through each stage. As an example, for differentiating iPSCs to cardiomyocytes, the cells go from pluripotency to mesoderm to cardiac progenitors and finally mature cardiomyocytes. The commitment of the cells to mesoderm is a critical step in this process and measurement of this commitment is crucial, as incomplete commitment can result in high variation or no cardiomyocyte maturation/production.

The development of a scalable system is necessary to facilitate the large‐scale manufacture of iPSCs and their derivatives. The most commonly employed format for scale‐up are stirred tank bioreactors due to their ability to accommodate a large range in volume (i.e., up to 2,000 L) and the existence of relatively simple numerical calculations to estimate hydrodynamics between different size vessels and approximate scale‐up. However, the equations typically used rely heavily on the geometry of the bioreactors, impeller design, and can be quite inaccurate when geometries are not similar between small and large‐scale vessels. The hydrodynamics also have an impact on the phenotype and differentiation of iPSCs, and the inaccuracy present in these equations impedes the ability to properly scale from lower to higher volumes. To address this, computational fluid dynamics (CFD) modeling have been developed to accurately calculate different hydrodynamic properties in fluids and can be used to scale‐up bioreactors cultures (Borys, Roberts, Le, & Kallos, 2018).

In the current study, we show that CFD modeling can be used as an innovative and reliable methodology for scaling up iPSC cultures in 3D bioreactors. As an example, we have utilized a spinner‐flask scale protocol for differentiating iPSCs to cardiomyocytes and translated it to using a cGMP‐derived hiPSC line for scale‐up in a 3 L computer‐controlled bioreactor.

2. MATERIALS AND METHODS

2.1. Cell culture

The human iPSC line LiPSC‐18R was generated as described previously (Baghbaderani et al., 2015) under cGMP‐compliant environment and were continuously maintained in feeder‐independent conditions using L7™ hPSCs Medium on defined L7 hPSC Matrix (Lonza, FP‐5020). The L7 hPSC medium included L7 hPSC medium supplement (Lonza, FP‐5207) and L7 hPSC basal medium (Lonza, FP‐5107). The cells were cultured in a humidified incubator operating at 37°C and 5% CO₂ and passaged when the cells reached 80–90% confluence with L7 hPSC Passaging Solution (Lonza, FP‐5013). Importantly, as the cells were expanded from a six‐well plate to a 10‐layer Cellstack (Corning) the iPSCs exhibited low levels of spontaneous differentiation before the start of CM induction (<5%). To prepare the spinner flask and bioreactor cell inoculum, the iPSCs were dissociated into single cells using TrypLE solution (ThermoFisherScientific) for 8 min at 37°C followed by dilution in L7 medium supplemented with 10 µM Y‐27632 (Abcam, 120129). Viable cell counts were analyzed using the NucleoCounter NC‐200 (Chemometec, Denmark).

2.2. Spinner flask and BioBLU 3c setup and iPSC expansion

BioBLU 3c stirred tank bioreactors (Eppendorf) and 125 ml spinner flasks (Corning) were used in this study. The BioBlu 3c was equipped with dissolved oxygen (DO) probe (Mettler Toledo) and a pH probe (Mettler Toledo). The pH probe was calibrated using a two‐point calibration method with standard pH solutions. For the DO probe calibration, vessels were filled with RPMI‐1640 medium (1500 ml) and aerated with air and 5% CO₂ by headspace gassing under the process conditions (i.e., 68 rpm agitation, 37°C) for at least 6 hr. After stable DO values were observed, a slope calibration was performed. The basal RPMI‐1640 medium was removed after DO calibration, and iPSCs were inoculated at 1.0 × 10⁶ cells/ml in 1500 ml of L7 medium supplemented with 10 μM Y‐27632 (referred to as Day 3). The BioBLU 3c was agitated at 68 rpm from Day 3 to 0. Also from Day 2 to 0 the medium was exchanged every day in the bioreactor by removing 50% of the supernatant and adding in the same amount of fresh L7 medium into the bioreactor.

The spinner flask was inoculated at 1.0 × 10⁶ cells/ml in 100 ml of L7 medium supplemented with 10 μM Y‐27632. The spinner flask was placed on a magnetic stir plate agitated at 70 rpm in a humidified incubator operating at 37°C and 5% CO₂. From Day 2 to 0, 50% of the spinner flask supernatant was removed every day and replaced with 100 ml of fresh L7 medium.

2.3. Differentiation of iPSCs into cardiomyocytes in spinner flask and BioBLU 3c

iPSCs cardiomyocyte induction was based on the protocol described by Chen et al. (2015) with some modifications (Figure 1). Following iPSC expansion, iPSCs aggregates were collected and reinoculated into a spinner flask and the BioBLU 3c at a density of 1.0 × 10⁶ cells/ml in RPMI‐1640 media supplemented with B27 (minus insulin, ThermoFisher) and 12 μM CHIR99021 (TOCRIS Bioscience). After 24 hr, the entire medium was exchanged with RPMI‐1640 with B27. On Day 2, the entire medium was exchanged with RPMI‐1640 with B27 supplemented with 4 μM Wnt‐C59 (Tocris Bioscience). On Day 4 (and every other day), 80% of the medium was exchanged in both the spinner flasks and BioBLU 3c with RPMI‐1640 supplemented with B27 (with insulin) until Day 14. From the entire cardiomyocyte differentiation process, the BioBLU 3c was agitated at 60 rpm and the spinner flask at 55 rpm.

Figure 1.

LiPSC‐18R cardiomyocyte differentiation process flow diagram [Color figure can be viewed at wileyonlinelibrary.com]

2.4. Sampling and aggregate size analysis

From the BioBLU 3c, a 7.0–8.0 ml sample was taken every day for metabolite/nutrient analysis and viable cell counts. Sampling was also performed on the spinner flask but a lower volume of 3.0 ml was withdrawn. Metabolites, nutrients and pH data were acquired using the BioProfile® FLEX2^™ (Nova Biomedical). Sampled aggregates were placed in a six‐well culture plate (ThermoFisherScientific) and two independent light microscopic images were captured from each sample at 4× and 10× magnification using a Nikon Eclipse Ti inverted microscope using NIS Elements software. Aggregates size was analyzed by fitting the sampled aggregates, from each timepoint, within the elliptical selection in ImageJ. Sizing was done for at least 40 aggregates; however, 100 aggregates were measured for the majority of timepoints. The elliptical selection provided the diameter for the major and minor axis of each aggregate. Average individual aggregates size is represented as the average of the major and minor aggregate diameter.

2.5. Harvest and cryopreservation of iPSC‐derived cardiomyocytes

iPSC‐derived cardiomyocytes were collected from the bioreactor on Day 14, washed with phosphate buffered saline (PBS)^−/− (ThermoFisherScientific) once and resuspended in Liberase solution (50 μg/ml; Roche) and incubated at 37°C for 30 min. The aggregates were triturated every 15 min using 10 ml serological pipettes (Corning). Following dissociation, an equal volume of growth medium (RPMI‐1640 + B27 with insulin) was added to the cell suspension to dilute the Liberase. The cells were centrifuged at 200g for 3 min at room temperature. Following centrifugation, the supernatant was removed and discarded. TrypLE solution was added to the cells and incubated for 7–8 min at 37°C. The enzyme was subsequently diluted by adding equal volume of growth medium. Viable cell counts were performed with the NC‐200 and the cells centrifuged at 200g for 3 min at 4°C. The supernatant was removed, discarded and the cell pellet was resuspended in CryoStor CS10 (BioLife Solutions) supplemented with 10 μM Y‐27632 at 5 × 10⁶ cells/ml. Cryovials (ThermoFisherScientific) were filled at 1.0 ml and cryopreserved using a Controlled Rate Freezer (ThermoFisherScientific).

2.6. Thawing and expansion of hiPSC‐CM

Before thawing, six‐well plates were coated with laminin‐521 at 1 μg/cm² following the manufacturer's protocol (BioLamina, Matawan, NJ). One vial of frozen LiPSC‐derived cardiomyocytes was thawed onto three‐wells of the coated six‐well plates for each bioreactor and spinner conditions. The cells were thawed using growth media supplemented with 10 μM Y‐27632. A 100% media exchange was performed the day after thawing with growth media and every other day until fixation.

3. ANALYTICAL ASSAYS

3.1. Flow cytometry

3.1.1. Pluripotency analysis

Flow cytometry was performed on static‐expanded iPSCs passaged into the bioreactor/spinner flask on the day of inoculation. The dissociated single cells were either fixed and permeabilized for intracellular staining with 4% PFA (Electron Microscopy Sciences) and Perm/Wash buffer (Becton Dickinson), respectively, or stained directly for extracellular staining. Permeabilized cells were incubated with Alexa‐488 anti‐OCT3/4 (5177S; Cell Signaling Technology) or respective Alexa‐488 anti‐IgG isotype control (2975S; Cell Signaling Technology). Unfixed cells were stained with PE‐conjugated antigen‐specific antibodies and respective isotypes using the manufacturer's recommended concentrations of anti‐TRA‐1–60 (Becton Dickinson), anti‐TRA‐1–81 (Becton Dickinson), anti‐SSEA4 (Becton Dickinson), anti‐IgG3 isotype (Becton Dickinson), and anti‐IgM isotype (Becton Dickinson). The samples were then processed through a FACSCanto™ II flow cytometer (Becton Dickinson). Data were acquired using BD FACS Diva software and analyzed with FlowJo 7.6 software (FlowJo).

3.1.2. Mesoderm analysis

Differentiated iPSC cells were sampled on Day 3 from the spinner flask and BioBLU 3c, and dissociated into single‐cell using TrypLE solution for 10 min at 37°C. The cells were washed and stained with PE‐conjugated anti‐ROR2, PDGFR‐α, anti‐IgG2a isotype, and anti‐IgG1 isotype for 30 min (all antibodies from R&D Systems). The samples were then processed through a FACSCanto II flow cytometer (Becton Dickinson). Data were acquired using BD FACS Diva software and analyzed with FlowIo 7.6 software.

3.1.3. Cardiomyocyte analysis

iPSC‐derived cardiomyocytes were washed once with 1 × PBS^−/− and were treated first with Liberase (2.5 mg/ml or 13 units/ml) for 30 min. The solution was neutralized with the addition of cardiac differentiation media. After three to four times pipetting with a 5 ml pipette, the cells were centrifuged at 300g at room temperature for 5 min. The pellet was further treated with TrypLE solution for another 10 min at 37°C and was neutralized with the addition of cardiac differentiation media. The cells were centrifuged, resuspended in 5–7 ml of media and filtered using 100 μM cell strainer (352360; BD). The cells were fixed and permeabilized for intracellular staining with the 4% PFA and Perm/Wash buffer, respectively. Permeabilized cells were incubated with anti‐cTnT (abcam) and anti‐Nkx2.5 (Santa Cruz) and respective anti‐IgG isotype control (Abcam) and (Santa Cruz). The cells were washed and were incubated with PE goat anti‐mouse IgG antibody (ThermoFisherScientific). The samples were then processed through a FACSCanto II flow cytometer (Becton Dickinson). Data were acquired using BD FACS Diva software and analyzed with FlowJo 7.6 software.

3.1.4. Immunocytochemistry

iPSC‐derived cardiomyocytes were prepared for immunocytochemical analysis per following procedure: the culture medium was aspirated and washed twice with 1× PBS^−/−. The cells were then fixed in 1× PBS^−/−containing 4% PFA for 20 min, then permeabilized with 0.1% Triton X‐100 (Sigma‐Aldrich) in 1× PBS^−/− for 15 min followed by a 15 min incubation with 10% goat serum in 1× PBS^−/− in 0.1% Triton X‐100 at room temperature. The cells were then treated with primary antibodies in 1% BSA (A1595; Sigma) in 1× PBS^−/− overnight at 4°C. Primary antibodies against cTNT (1:100; ab8295; Abcam) and NKX2.5 (1:200; sc‐376565; Santa Cruz) were used in combination with the corresponding secondary antibodies Alexa Fluor 594 Goat anti‐mouse (1:1000; ThermoFisherScientific). All cells were incubated with secondary antibodies and 5 μg/ml 4′,6‐diamidino‐2‐phenylindole (ThermoFisherScientific) in 1% BSA in 1× PBS^−/− for 1 hr at room temperature in the dark. Cells were rinsed between the incubation of the primary and secondary antibodies three times with 1% bovine serum albumin in 1× PBS^−/−. All fluorescence detection was visualized using a Zeiss Observer.Z1 microscope equipped with ZEN software.

3.1.5. Karyotype analysis

Karyotype analyses were performed by a qualified service provider (Genetica LabCorp) using a standard G‐banding method as described elsewhere (Baghbaderani et al., 2016). Briefly, harvested single cells on Day 0 were seeded on L7 matrix‐coated T25 flask with L7 medium supplemented with 10 μM Y‐27632. The cells were expanded for 3–4 days until 40–50% confluency before shipping to the external testing lab.

3.2. CFD modeling

3.2.1. Description of bioreactors

In this study, the hydrodynamics of stirred tank cell culture vessels were investigated at two different scales 100 ml and 3 L. The 100 ml single‐use spinner flask (Corning) was used as a baseline to scale‐up the expansion and differentiation of iPSCs to the single‐use BioBLU 3c computer‐controlled bioreactor (Eppendorf). These two bioreactor platforms have a very different vessel and impeller geometries. Each system has a cylindrical vessel with a flat bottom, however, the spinner flask has a large paddle impeller driven by a cylindrical magnetic stir bar attached to the bottom of the impeller, whereas the BioBlu 3c is agitated by an overhead motor and a 45° pitch‐blade impeller. In addition, the BioBLU 3c is equipped with DO, temperature, and pH probes to facilitate control of the bioreactor environment. In addition, there are many other ports for sampling, liquid addition, harvesting, and sparging. The spinner flask and BioBLU 3c were operated at working volumes of 100 ml and 1.5 L, respectively.

3.2.2. Modeling and post‐processing for scale‐up values

A total of 10 models were run by testing the two different vessels at five different impeller speed (55, 65, 70, 75, and 85 rpm). At the completion of the simulations, postprocessing was performed to determine the volume average velocity, shear rate, and turbulent energy dissipation rate for each of impeller speeds for both the spinner flask and BioBLU 3c. The volume average energy dissipation rate, shear rate, and velocity values were then plotted as a function of impeller speed to generate equations that were then used to determine the impeller speed required in the BioBLU 3c to maintain the same values in the spinner flask.

3.2.3. Computational fluid dynamics (CFD theory)

The core of computational fluid dynamics modeling is centered around the Navier–Stokes equations. These transport equations represent the transport of mass and momentum through a viscous fluid. The following equations represent the mass and momentum transfer:

$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathit{u})=0$$

$$\frac{\partial \rho \mathit{u}}{\partial t}+\nabla (\rho \mathit{uu})=-\nabla P+\mu {\nabla }^2\mathit{u}+\rho g$$

In the above equations ρ represents density, u is a velocity vector, t is time, P is pressure, μ is viscosity, and g is the gravity vector

$$\mathit{u}=\begin{array}{c}u\\ v\\ w\end{array}$$

$$\mathit{g}=\begin{array}{c}{g}_x\\ g_y\\ g_z\end{array}$$

The velocity vector is defined where u, v, and z represent the velocity components in the x, y, and z directions. Similarly, the gravity vector is defined where g_x, g_y, and g_z represent the acceleration due to gravity in the x, y, and z direction. Here we assume incompressibility of the fluids which gives the Navier‐Stokes equations is:

$$\nabla \cdot \mathit{u}=0$$

$$\frac{\partial \mathit{u}}{\partial t}+\mathit{u}\cdot \nabla \mathbf{u}=-\frac{\nabla P}{\rho }+v{\nabla }^2\mathit{u}+g$$

We can then write these equation in Einstein notation to obtain

$$\frac{\partial u_i}{\partial x_i}=0$$

$$\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial P}{\partial x_i}+\frac{\partial }{\partial x_i}\left[\left[,v\left(\left(,\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i},\right)\right),\right]\right]+g_i$$

To account for the effect of turbulent eddies within the bioreactor, the above equations need to be modified to represent turbulence. The Reynolds Averaged Navier–Stokes (RANS) turbulence equations is one way of doing this:

$$U=\overline{u}+u\prime$$

Where U represents the instantaneous velocity vector, $\stackrel{\circledR }{u}$ represents the average or main flow, and $u^{\prime }$ represents the turbulent velocity. This turbulent velocity definition can then be substituted into the Navier‐Stokes equation to get

$${\overline{u}}_j\frac{\partial {\overline{u}}_i}{\partial x_i}=-\frac{1}{\rho }\frac{\partial \overline{P}}{\partial x_i}+\frac{\partial }{\partial x_i}\left[\left[,v\left(\left(,\frac{\partial {\overline{u}}_i}{\partial x_j}+\frac{\partial {\overline{u}}_j}{\partial x_i},\right)\right),\right]\right]+g_i-\frac{\partial }{\partial x_i}\left(\left(,\overline{{u\prime }_i{u\prime }_j},\right)\right)$$

The bulk flow in the bioreactor is represented by the $\stackrel{\circledR }{u}$ leaving the majority of the equation unchanged, with the biggest change adding on the $-\frac{\partial }{\partial x_i}\left(\left(,\overline{{u\prime }_i{u\prime }_j},\right)\right)$ term with represents the transport of momentum caused by turbulent flow.

One of the most common ways of modeling these complex systems is using the two‐equation realizable k‐epsilon model which is based on the derivation of the RANS equations. This model introduces kinetic energy (k) and the energy dissipation rate (ε) to help understand the hydrodynamics of the system.

$$k=\frac{1}{2}{u\prime }_i{u\prime }_j$$

$$\epsilon =v\overline{\frac{\partial {u\prime }_i}{\partial u_j}\frac{\partial {u\prime }_i}{\partial u_j}}$$

The realizable k‐epsilon model implements two additional transport equations, one for the kinetic energy and one for the energy dissipation rate

$$\frac{\partial k}{\partial t}+\frac{\partial (k{u}_i)}{\partial u_i}=\frac{\partial }{\partial x_i}\left[\left[,\left(\left(,v+\frac{v_t}{{\sigma }_k},\right)\right)\frac{\partial k}{\partial x_j},\right]\right]+v_t{S}^2-\epsilon$$

$$\frac{\partial \epsilon }{\partial t}+\frac{(\partial \epsilon u_i)}{\partial x_i}=\frac{\partial }{\partial x_i}\left[\left[,\left(\left(,v+\frac{v_t}{{\sigma }_{\epsilon }},\right)\right)\frac{\partial \epsilon }{\partial x_j},\right]\right]+C_{1}S\epsilon -C_2\frac{{\epsilon }^2}{k+\sqrt{v\epsilon }}$$

In the above equations, the terms ${\sigma }_k$ and ${\sigma }_{\epsilon }$ are the turbulent Prandtl numbers for k and ε, respectively, and have constant values of 1.0 and 1.2, respectively. In addition C ₂ is a constant with a value of 1.9 and C ₁ is determined by the following equation:

$$C_1=\mathrm{m}\mathrm{a}\mathrm{x}\left[0.43,\frac{S\frac{k}{\epsilon }}{S\frac{k}{\epsilon }+5}\right]$$

Where the S term represent the magnitude of the main flow strain rate tensor and is determined by

$$S=\sqrt{2{\left(\frac{{\partial u}_i}{{\partial x}_i}\right)}^2+{\left(\frac{{\partial u}_i}{{\partial u}_j}+\frac{{\partial u}_j}{{\partial u}_i}\right)}^2}$$

Finally, the term $v_t$ is the turbulent viscosity and is calculated by

$$v_t=\frac{\rho C_{\mu }{k}^2}{\epsilon }$$

In this equation, the term $C_{\mu }$ is a model‐specific expression whose definition can be found in the ANSYS Fluent Theory Guide.

3.2.4. Model set‐up

Virtual geometry models were created of the two bioreactors using the computer‐aided design (CAD) software AutoCAD. The measurements of each bioreactor were taken using hand calipers. These CAD drawings were imported into the meshing software ICEM from ANSYS and discretized using tetrahedral elements. The control volumes were then transformed into polyhedral mesh elements as they have benefits of both tetrahedral and hexahedral elements.

The CFD simulation software Fluent 16.0 was used to numerically solve the single‐phase fluid dynamic models for each of the vessels. Boundary conditions were set at different surfaces. For both vessels, the walls, impellers, and probes were treated as nonslip boundaries with standard wall functions. The liquid surface was modeled as a free‐surface (zero‐shear) boundary condition. The impeller rotation was implemented using a moving reference frame. Finally, the domain interface boundary condition was used for the interface between the rotating and stationary domains.

A semi‐implicit method for pressure linked equations (SIMPLE) algorithm for numerically solving the realizable k‐epsilon Navier–Stokes equation was used. All equations were discretized using a Second‐Order Upwind scheme. A time step for the models was chosen to ensure the Courant–Friedrich–Lewy (CFL) number remained below 1. Convergence was assumed when the residuals decreased below 10⁻³.

3.2.5. Grid dependence

A grid dependency test was conducted to determine the fewest number of elements that are needed for the most accurate results. The mesh size was selected when the maximum and average values of velocity, shear rate, and energy dissipation rate change by less than 2% from one mesh size to the next. The grid dependence was complete for both the spinner flask and the BioBLU 3c. The spinner flask was tested between 100,000 and 600,000 polyhedral elements, and the BioBLU 3c was tested between 250,000 and 1,000,000 polyhedral elements. The models were run at an agitation rate of 70 rpm until steady state was reached or a minimum of 10 s of flow time. For the spinner flask and BioBLU 3c mesh sizes of 600,000 and 1,000,000 elements respectively were used to determine the scale‐up values.

3.2.6. Other scale‐up equations

The Reynolds number, Power number, average energy dissipation rate, maximum shear stress, and tip speed were also calculated for the spinner flask to compare the scale‐up values generated by our CFD model and commonly utilized empirical equations. The Reynolds number (N_RE) was calculated with

$$N_{\mathrm{R}\mathrm{E}}=\frac{\rho \cdot N\cdot D_i^2}{\mu }$$

where, ρ is the density of the medium, N is the agitation speed, D_i is the diameter of the impeller and μ is the medium viscosity.

The Power number (N_P) was calculated using the following equations (Nagata, 1975):

$$N_P=\frac{K_1}{N_{\mathrm{R}\mathrm{E}}}+K_2{\left(\frac{{10}^3+1.2\cdot N_{\mathrm{R}\mathrm{E}}^{0.66}}{{10}^3+3.2\cdot N_{\mathrm{R}\mathrm{E}}^{0.66}}\right)}^{K_4}$$

$$K_1=14+\left(\frac{W}{D_t}\right)\cdot \left[670\cdot {\left(\frac{D_i}{D_t}-0.6\right)}^2+185\right]$$

$$K_2={10}^{K_3}$$

$$K_3=1.3-4\cdot {\left(\frac{W}{D_t}-0.5\right)}^2-11.4\cdot \left(\frac{D_i}{D_t}\right)$$

$$K_4=1.1+4\cdot \left(\left(,\frac{W}{D_t},\right)\right)-2.5\cdot {\left(\left(,\frac{D_i}{D_t}-0.5,\right)\right)}^2-7\cdot {\left(\left(,\frac{W}{D_t},\right)\right)}^4$$

where, W is the impeller width and D _t is the diameter of the vessel.

The average energy dissipation rate (ε) is given by the following equation:

$$\epsilon =\frac{P}{V\cdot \rho }$$

Where, V is the working volume of the vessel and P is the power input. The power input is calculated by using the equation

$$P=N_P\cdot N^3\cdot D_i^5\cdot \rho$$

And is used to calculate the maximum shear stress (τ _max) given by the equation

$${\mathit{\tau }}_{\mathit{max}}=5.33ċ\rho ċ{(\epsilon ċ\nu )}^{0.5}$$

where, ν is the kinematic viscosity.

Finally, the tip speed was calculated with the following equation:

$$\mathrm{T}\mathrm{i}\mathrm{p}\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{e}\mathrm{d}=N\cdot \frac{1\mathrm{m}\mathrm{i}\mathrm{n}}{60\mathrm{s}}\cdot \pi D_i$$

Each equation was used to calculate the scale‐up values and corresponding BioBlu 3c agitation rates at the two different spinner flask agitation rates: 55 and 70 rpm.

4. RESULTS

4.1. Establishment of baseline 3D cardiomyocyte differentiation process with LiPSC‐18R iPSCs in spinner flasks

Human LiPSCs‐18R were thawed and serially subcultured in L7™ hPSC culture system before initiating differentiation. Using a defined culture condition based on established and published protocols, iPSCs were expanded and differentiated into cardiomyocytes for 14 days in 3D spinner flasks (100 ml working volume). During the expansion stage (from Day 3 to 0), the undifferentiated iPSCs were adapted to suspension culture and formed small aggregates with an average diameter of 300 μm (Figure 2a). Aggregates compacted further from Day 6 until harvest (Day 14). Between Day 6 to 8, a small area within the aggregates started beating and as the cultured proceeded this beating encompassed the entire aggregate and was synchronized within each aggregate (Figure 2a and Video S1). It was also observed that cell numbers decreased slightly after inoculation, but recovered by Day 0 (Figure 2b). On Day 14 cell counts and viability (CCV) analysis showed greater than 90% viability and a viable cell density of 6.35 × 10⁵ cells/ml. Flow cytometry analysis on Day 3, 6, and 14 cells confirmed the differentiation of iPSCs through the cardiac mesoderm, cardiac progenitor and cardiomyocyte differentiation stages (Figure 2c,d). Cells analyzed on Day 3 for markers of mesoderm (i.e., ROR2 and PDGFRα) showed expression of both markers around 86.7% and differentiated well to cardiomyocytes when analyzed for the cardiac marker, cardiac Troponin T (i.e., cTnT: 55.7%; Figure 2d). This transferred process to our labs established the baseline 3D differentiation process and was used for the development of the scaled‐up process.

Figure 2.

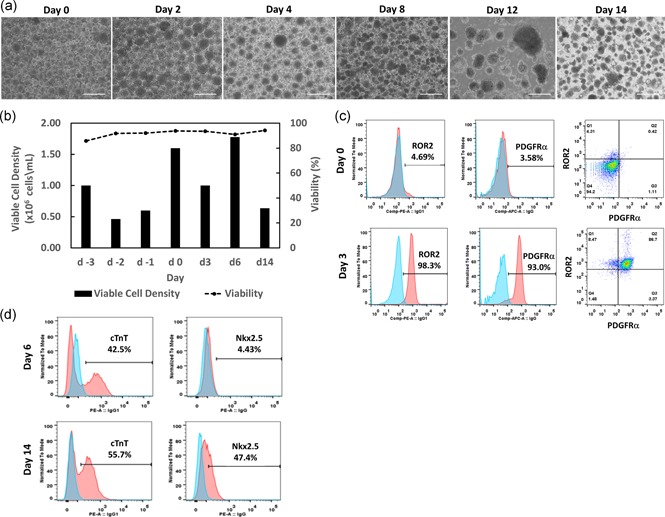
Expansion and cardiomyocyte differentiation of cGMP‐compliant iPSC line (LiPSC 18R) in 3D spinner flask. (a) Representative phase contrast aggregate images taken during LiPSC‐18R expansion and directed differentiation. LiPSC‐18R formed aggregates and expanded from Day −3 to 0 in the spinner flask. The aggregates were cultured until Day 14 as defined by the differentiation process. (b) Viable cell density and percent viability during expansion and differentiation of LiPSC‐18R. (c, d) Flow cytometry analysis of iPSCs during the induction process on Day 0, 3, 6, and 14 (pink: target, blue: isotype). Scale bars represent 200 μm. iPSC, induced pluripotent stem cells [Color figure can be viewed at wileyonlinelibrary.com]

4.2. CFD modeling and establishing scale‐up criteria

Following the establishment of the baseline 3D differentiation process in spinner flasks, we focused on generating a proof‐of‐concept CFD modeling to scale the culture up to the BioBLU 3c, computer‐controlled bioreactor to enable manufacturing of clinically relevant cell numbers. One of the main challenges with scaling from the 100 ml spinner flask to the BioBLU 3c was the difference in geometry between the vessels (Figure 3a,b). Utilizing CFD modeling, the geometry differences between small and large‐scale vessels were considered in the modeling, and the scale‐up was measured based on volume averaged hydrodynamic forces. In this study, our main focus was to evaluate the volume‐averaged energy dissipation rate (EDR) within the spinner flask and BioBLU 3c. Each vessel was modeled and simulated at agitations between 55 and 85 rpm using ANSYS Fluent. ANSYS Fluent provides comprehensive modeling capabilities of many different types of fluid flow problems, using mathematical models for transport phenomena combined with the ability to model complex geometries. The simulations of the hydrodynamic environment were run for 15 s, but reached pseudo‐steady state values after an average of 8 s for the 100 ml spinner flasks and 12 s for the BioBLU 3c.

Figure 3.

Geometry of the BioBLU 3c and spinner flask with corresponding average energy dissipation rate contour plots and values for scale‐up. (a) Geometrical dimensions of the BioBLU 3c and spinner flask were used to construct the (b) geometry in AutoCAD. (c) Ansys Fluent was used to model the bioreactor and spinner flask to produce the horizontal slice contour plots of the energy dissipation rate (d) and volume‐averaged energy dissipation rate relationship between the BioBLU 3c and spinner flask to determine an appropriate scale‐up value [Color figure can be viewed at wileyonlinelibrary.com]

Fluent solved the EDR in every elemental volume within the bioreactors and generated contour plots (Figure 3c) showing that the highest values occur at any walls in the system—that is the impeller faces and probes in the BioBLU 3c. The bulk liquid volume had a relatively low EDR at low agitation rates in both vessels. However, as the agitation rate increased, there was also an increase in the EDR in the bulk media especially within the rotating domain, with peak values occurring at the tips of the impeller. The distribution of EDR was graphed for both vessels at 55 and 70 rpm. It was observed that there are differences in the shapes of the EDR distribution curves between the two vessels at the same agitation rate. (Figure S4e). This was expected as there were significantly different contour plots between the spinner and BioBLU 3c. To utilize the computed EDRs for scaling up cell cultures from spinner flasks to BioBLU 3c, we averaged the EDRs over the entire volume and plotted against the agitation rate to compare the values at the different scales, for each vessel (Figure 3d). A trend line was fit to the EDR generated data (R ² > 0.997) and it was observed that the EDR increased exponentially as the agitation rate increased. Based on the two generated trend lines, we were able to determine the corresponding agitation rate for iPSC expansion and directed differentiation in the BioBLU 3c to maintain the same EDR as seen in the spinner flask. Based on this correlation, the expansion agitation rate of 70 rpm in the spinner flask corresponds to 67 rpm in the BioBLU 3c and the differentiation agitation rate of 55 rpm in the spinner flask corresponds to 53 rpm in the BioBLU 3c. These corresponding values were used for the expansion and differentiation steps, respectively.

4.3. 3D expansion and cardiomyocyte differentiation of LiPSC‐18R iPSCs in the BioBLU 3c bioreactor

LiPSC‐18R was thawed and expanded to a 10‐layered CellStack (CS10) to generate the necessary amount of cells for bioreactor and spinner flask inoculation. The iPSCs showed normal typical phenotype during the seed train expansion from six‐well to CS10 (Figure S1a). CS10 harvested cells were inoculated into both a spinner flask and a BioBLU 3c at a density of 1.0 × 10⁶ cells/ml with small aggregates forming in both the spinner and computer‐controlled bioreactor systems after 24 hr (Figure 4a). The aggregates size was higher in the BioBLU 3c as compared to the spinner flask on day −1, but on Day 0 were similar (107.1 ± 37.1 µm in diameter) before cardiomyocyte induction (Figure 4b). In addition, the iPSC viable cell number decreased on day −2 in both conditions, but subsequently increased by Day 0 to that of the inoculated cell number and had a viability of more than 90%. Similar cell numbers were observed in both the spinner flask and BioBLU 3c conditions (Figure 4C). The iPSCs retained pluripotency during both spinner flask and BioBLU 3c expansion as shown by expression of Oct4, SSEA‐4, Tra‐1–80, and Tra‐1–61 by flow cytometry analysis (Figure 4d). Finally, after expansion, iPSC aggregates were sampled for karyotype analysis and were shown to retain the ability to form typical colonies after dissociation and demonstrated normal G‐banding karyotype (Figure S2).

Figure 4.

Expansion of human iPSCs in the BioBLU 3c and spinner flask. (a) Representative phase‐contrast aggregate images were taken during iPSC expansion. iPSCs formed aggregates which grew from Day −3 to 0 in both the spinner flask and bioreactor. (b) The average aggregate size was shown to be similar between the BioBLU 3c and spinner flask. (c) Viable cell density and percent viability during expansion showed similar growth kinetics. (d) Flow cytometry analysis of undifferentiated iPSCs on Day 0 of the cardiomyocyte induction process showed high expression of key pluripotency markers SSEA‐4, Tra‐1–81, Tra‐1–60, and Oct4 in both spinner flask and bioreactor (pink: target, blue: isotype). Scale bars represent 200 μm. iPSC, induced pluripotent stem cells [Color figure can be viewed at wileyonlinelibrary.com]

The undifferentiated human iPSC aggregates were then directly induced to differentiate into cardiomyocytes in suspension culture. Cell aggregates on Days 1, 4, 8, and 14 of differentiation showed an average diameter of 106 ± 27, 113 ± 39, 112 ± 30, and 119 ± 36 µm within the spinner flask and 156 ± 53, 113 ± 61, 191 ± 80, and 265 ± 95 µm within the BioBLU 3c, respectively (Figure 5a,b; Figure S3). At harvest, the spinner flask and BioBLU 3c cultures had significantly different viable cell densities (2.67 × 10⁵ and 1.21 × 10⁵ cells/ml, respectively; Figure 5c). It was observed that cell loss started after cardiac induction and may be due to the differentiation protocol and independent of the scaling. The spontaneous aggregate beating was observed by Day 10 postinduction in both culture systems. In some cases, the beating cells were initially confined to a small area of aggregate but expanded gradually to the whole aggregate while beating synchronically on Day 14 (Video S2 and S3). Flow cytometry of Day 3 and 6 cells confirmed the cardiac mesoderm, cardiac progenitor and cardiomyocyte differentiation of LiPSC‐18R iPSCs in the spinner flask and BioBLU 3c (Figure 5d,e). The percent of a cell population expressing NKX2.5 increased to 76.6% and 91.8% for BioBLU 3c and spinner flask whereas the cell population expressing cTnT increased to 91.8% and 76.6% for BioBLU 3c and spinner flask on Day 14, respectively (Figure 5f). Differentiated cells in the BioBLU 3c and spinner flask successfully attached to laminin‐coated plates postthaw and expressed cardiac‐specific markers (Figure S5Aa,b)

Figure 5.

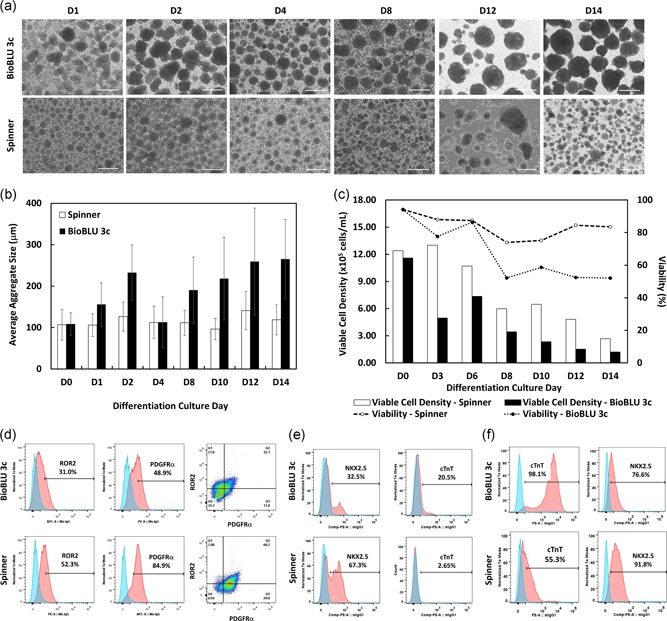
Cardiomyocyte differentiation of iPSCs in BioBLU 3c and spinner flask. (a) Representative phase‐contrast aggregate images taken during iPSC cardiomyocyte directed differentiation. iPSCs aggregates expanded and changed their morphology from Day 0–14 postcardiomyocyte‐induction in both the BioBLU 3c and spinner flask. (b) Average aggregate size in the BioBLU 3c and spinner flask during the cardiomyocyte‐induction process. (c) Viable cell density and percent viability during differentiation. (d–f) Flow cytometry analysis of differentiated iPSCs on Day 3, 6, and 14, respectively, postcardiomyocyte‐induction in both the BioBLU 3c and spinner flask (pink: target, blue: isotype). Scale bars represent 200 μm. iPSC, induced pluripotent stem cells [Color figure can be viewed at wileyonlinelibrary.com]

5. DISCUSSION

The path to industrializing cell therapies requires standardizing materials, cell handling procedures, and implementing appropriate characterization methods in the manufacture of these cell‐based therapies. For one of such cell therapies focused on human iPSC‐derived cardiomyocytes, there have been some attempts to generate them in suspension through EB formation but this method has many shortcomings such as batch‐to‐batch variability, high apoptotic cells and noncontrolled EB size (Chen et al., 2012). In addition, as these cultures are scaled‐up, to generate higher cell numbers there are challenges with matching the hydrodynamics and environment the cells experience from small to large‐scale cultures. Therefore, it is necessary to understand the important hydrodynamic parameters influencing the cells and cell‐fate decisions and establish robust methods to scale‐up cultures by matching these important hydrodynamic parameters. In addition, as experiments “at scale” can be costly and lengthy, these methods should be able to reduce “real‐life” optimization experiments by providing an in silico environment to work in. In this manuscript, we utilized a novel and effective CFD modeling approaches to adapt a published protocol for the differentiation of iPSCs to cardiomyocytes to a scalable and controlled bioprocess utilizing a GMP iPSC cell line. Focusing on critical process parameters, such as the control of aggregate size through culture hydrodynamics, we established a proof‐of‐concept up‐scaled and cGMP‐compliant expansion and directed differentiation process for aggregate‐based iPSCs in a serum‐free and carrier‐free 3 L computer‐controlled bioreactor system in a relatively efficient manner. CFD is used to conduct iterative simulations to support complex experimental designs where the key findings can then be verified by real experimentation. Traditional scale‐up methods require multiple experiments to determine the best scale‐up parameters. However, using CFD we ran multiple simulations to determine the best scale‐up parameter allowing us to verify with real experimentation using a single run, showing successful scale‐up, significantly reducing the time, and materials needed for scaling up.

Current methods of scale‐up for stirred tank bioreactors are based on empirical equations and are heavily reliant on geometry. The most commonly used scale‐up equations were proposed by Nagata (1975) and were developed specifically for nonbaffled tanks with bladed paddle impellers. These geometry dependent scale‐up methods (i.e., dependent on the geometry of vessel and impeller design) work well for bioreactors of similar geometry, however, changing impeller type, adding probes, or significantly increasing the size can lead to inaccurate scale‐up approach and eventually the need for further adjustment of cell culture parameters in multiple iterations. These equations do not accurately describe the local flow patterns within the bioreactor, which are highly dependent on geometry. Therefore, for more accurate scale‐up parameters, numerical techniques and CFD modeling are much better suited.

In this manuscript, we investigated many different scale‐up methods using both CFD modeling and empirical hand calculations derived by Nagata (1975) to determine the best method. Each of these different methods gave significantly different corresponding scaled‐up agitation rates in the BioBlu 3c (Figures 4SA–SD; Table 1). One common scale‐up method is the Power number. Scaling‐up on the power number resulted in BioBlu 3c agitation rates of 188 and 157 rpm corresponding to the small scale 70 and 55 rpm agitation rates respectively. As EDR and maximum shear stress are dependent on the Power number, the high agitation rate determined for the BioBlu 3c were also seen with the empirically calculated EDR and maximum shear stress.

Table 1.

Comparison of CFD modeling and empirical hand calculations

		Scale‐up method corresponding agitation rate (rpm)
		Average EDR	Maximum shear	Average shear	Average velocity	Maximum velocity	Reynolds number	Power number
CFD modeling	70 rpm	67	23	107	88	–	–	–
	55 rpm	53	19	81	69	–	–	–
Empirical equations	70 rpm	104	104	–	–	53	40	188
	55 rpm	81	81	–	–	42	32	157

Other parameters that have been studied in literature are the average shear rate, Reynolds number, and impeller tip speed (Borys et al., 2018). In our case, the average shear rate and tip speed scale‐up using CFD generated agitation rates of 107 and 88 rpm, respectively, for the 70 rpm; and, 81 and 69 rpm for the 50 rpm at a small scale. Based on our hands‐on experience with handling cell cultures and scaling‐up stirred tank reactors, we believed that these agitation rates were much too fast in the BioBlu 3c. Conversely, scale‐up based on the Reynolds number and impeller tip speed was much too slow to maintain the aggregates in suspension (Table 1). In addition, all four of these scale‐up methodologies did not allow for the maintenance of aggregate diameter according to recently published work (Borys et al., 2018). Therefore, we determined that they were not appropriate methods for our scale‐up work.

Two scale‐up values that have had success in literature are the average EDR and maximum shear stress (Borys et al., 2018, Johnson, Natarajan, & Antoniou, 2014). We determined these values using both CFD modeling and empirical equations. When comparing, the CFD‐determined values tended to underestimate the shear and EDR when probes are added, generating higher than expected scale‐up values. From the contour plots (Figure 2c) it is clear that there is a lot of energy that is dissipated, with corresponding increased shear, around the probes. This is not accounted for in the CFD model calculations. In contrast, the empirical equations seem to generate values much too high compared to what others have reported (Borys et al., 2018), as it is commonly reported that the agitation rate tends to decrease as the scale increases. Therefore, CFD models generate more reasonable scale‐up results.

It is assumed that the maximum shear rate would be the most important factor in the bioreactor, as high shear rates can result in decreased cell yield and negatively impact cellular phenotype. In addition, shear‐induced effects on pluripotency and differentiation have been well documented (Stolberg & McCloskey, 2009). However, Borys et al. (2018) showed that for the scale‐up of a murine embryonic stem cell bioreactor expansion process from 10 to 100 ml, the average EDR was more effective in maintaining average aggregate size and aggregate size distribution between the cultures (Borys et al., 2018). Based on this, we chose to use average EDR as our scale‐up parameter in this study. As the EDR in the vessels cannot be directly measured, we evaluated the scale‐up using an orthogonal method—the aggregate size of the iPSCs. In the Borys et al. (2018) study, as well as other studies investigating CFD for scale‐up, the focus has been with bioreactors of similar geometry. In contrast, we use the principles of stirred tank hydrodynamic scale‐up methods and CFD modeling, to determine operating parameters for a bioreactor of significantly different geometry and impeller design.

To test and verify if the CFD model and chosen scale‐up parameter supported the comparable expansion and differentiation of iPSCs we first expanded our iPSCs using GMP‐compatible reagents (i.e., the L7 system of reagents from Lonza). The expansion of pluripotent stem cells (PSCs) in small scale (100–500 ml) feeder‐free suspension culture has already been shown by several groups (Amit et al., 2010; Chen & Couture, 2015; Hookway, Butts, Lee, Tang, & McDevitt, 2016; Kehoe, Jing, Lock, & Tzanakakis, 2010; Meng, Liu, Poon, & Rancourt, 2017; Olmer et al., 2012; Wang et al., 2013; Zweigerdt, Olmer, Singh, Haverich, & Martin, 2011). Recently, iPSCs were expanded and cultured as aggregates in single‐use Mobius bioreactors (1000 ml working volume; Millipore) while maintaining their pluripotent phenotype (Kwok et al., 2018). This study also showed the ability of the cells to differentiate to cardiomyocytes as well as exhibit spontaneous germ layer differentiation. However, one caveat of this study was the use of non‐GMP materials such as, the starting material (i.e., iPSCs) and dissociation reagent. In our human iPSC expansion process, we demonstrated the generation of high density, viable, pluripotent, and karyotypically normal GMP‐produced iPSCs in 3 days. In addition, we used a GMP‐compatible expansion system to accomplish this—with a serum‐free expansion medium and a chemically‐defined passaging solution, enabling the smooth transition of this process into GMP. This suspension‐based bioprocess circumvents the labor‐intensive and costly expansion of iPSC in the traditional 2‐dimensional (2D) format and minimizes the related process scale‐up hurdles such as vessel coating, manufacturing cost, and potential contaminations. The application of a 3‐dimensional (3D) computer‐controlled bioreactor also increases batch‐to‐batch consistency, ability to monitor and control intermediate products and final product quality, shortens the processing period, and reduces the number of deviations during cGMP manufacturing (Abbot et al., 2018).

While the suspension culture of human iPSC‐derived cardiomyocytes in a small‐scale spinner and bioreactor system has previously been demonstrated by several labs (Chen et al., 2015; Kempf et al., 2014), the challenges existing with scaling‐up human iPSC differentiation processes have not been adequately explored. As mentioned previously, the hydrodynamics can influence cell‐fate decisions and thus it is important to scale‐up cultures based on a proper understanding of the cell culture environment. Scaling‐up based on matching the volume‐averaged EDR to agitation rate worked well for the expansion of the iPSC in this process. We were able to maintain very similar cell densities (1.24 × 10⁶ and 1.16 × 10⁶ cells/ml) and aggregate size (108.7 ± 27 and 107.1 ± 37.1 µm) between the spinner flask and BioBLU 3c, respectively, while maintaining pluripotency. However, during differentiation, the same method of scale‐up led to more inconsistent results. At the end of the differentiation phase, the average aggregate size in the BioBLU 3c was nearly double that of the spinner flask. In addition, even though we were able to generate cells expressing cardiomyocyte markers in both platforms, there was a higher expression of many of the cardiomyocyte markers in the spinner flask condition compared to the bioreactor condition. However, overall cell numbers and cardiomyocyte expression were found to be lower in both the spinner flask and bioreactor compared to the baseline conditions established prior in spinner flasks. Based on these results, for a complex differentiation process, there are additional factors that need to be considered during the differentiation other than solely the hydrodynamic environment. Laco et al. (2018) recently published on the inconsistencies and low reproducibility observed with cardiac differentiation. It was observed that the cell cycle profile could influence the effects of GSK3β inhibition (i.e., CIHR99021) on cardiac differentiation and cell death. The timing is critical and careful monitoring of the extent of mesoderm induction is necessary rather than having set cytokine exposure times during differentiation. In addition, for the scale‐up method used in this study, utilizing the average EDR in the bioreactor could artificially lead to a lower than optimal agitation rate. Looking at the contour heat map of EDR (Figure 2c), it can be observed that the high EDR in the BioBLU 3c is located around the impeller and a low EDR in the bulk media. A similar EDR profile can be seen for the spinner flask (i.e., with a higher EDR around the impeller), but because there is a larger impeller diameter to vessel diameter ratio, this EDR is then more efficiently transferred into the bulk media. Therefore, in the BioBLU 3c, because the aggregates spend more time in the bulk media compared to around the impeller they are exposed to much lower EDR than in the bulk media in the spinner flask, leading to an increase in aggregate size that could potentially contribute to the lower differentiation efficiency. The CFD modeling could be used to re‐design the bioreactor system to more closely match the hydrodynamic environment in the spinner. For the 3D culture systems used in this paper, this may consist of modifying the BioBlu 3c impeller to have a similar aspect ratio to the vessel as observed in the spinner; the inclusion of baffles can increase the EDR and average shear stress in the vessel; and/or the addition of a secondary impeller along the same shaft in the BioBlu to facilitate better mixing. However, it can be quite cumbersome, costly, and time‐consuming to develop a bioreactor vessel that can be utilized in the manufacturing of clinical products and the majority of researchers/companies will utilize commercially‐available, single‐use bioreactor systems in their clinical manufacturing processes. In addition, for more complex bioprocessing applications (such as directed differentiation), additional process parameters must be considered in the development and scale‐up of the process. Despite the need for additional considerations, the differentiation process in the large‐scale bioreactor successfully led to acceptable key cardiac differentiation characteristics.

Further optimization of scaling‐up this differentiation process is where CFD really outshines the common methods of scale‐up. As seen, bioreactors have complicated hydrodynamics and therefore assigning an average or maximum value may not always address the scale‐up problem at its core. With CFD modeling, it is possible to analyze the hydrodynamics (EDR, shear stress, velocity) in more detail by breaking the volume down into elemental volumes to look at the distributions, areas of high or low values, flow patterns, values in specific Cartesian coordinates, and the number of time cells spend in different areas of the bioreactor. This allows determining time‐averaged values increasing the accuracy of the scale‐up parameters. By using CFD instead of conventional methods, we are able to determine the best methods for scale‐up, making process development, and scale‐up much more efficient and cheaper as fewer experiments will be needed, bringing these processes to the clinic faster. This is particularly important because the cost of cell therapy development and speed to GMP manufacturing (and therefore clinical trial) are key in increasing the efficiency, reducing the cost of therapies, and availability of high‐quality products for a large number of patients.

To date, various cardiomyocyte differentiation methods have been reported that induce or inhibit pathways such as Wnt, SHH, TGF‐β using small molecules and proteins (Gonzalez, Lee, & Schultz, 2011; Lian et al., 2012). In the present study, we were able to take a feeder‐free, carrier‐free and chemically‐defined protocol adapted from the literature (Chen et al., 2015), transition and scale‐up the process using CFD to a 3 L computer‐controlled bioreactor. Furthermore, the current scale can be easily scaled‐up to larger bioreactors using the established methods in this paper and CFD modeling. Even though not fully optimized, we were able to directly differentiate human iPSC aggregates to CM through a step‐wise approach, with the majority of aggregates at Day 14 showing spontaneous contractility and characteristics of cardiomyocytes by expressing cardiac‐specific markers. By further incorporation of a purification step (such as lactate‐base media similar to what has been done for the static culture system; Burridge et al., 2014; Yang, Chen, Kaushal, Reece, & Yang, 2016), and by optimizing the bioprocess critical variables (including dissolve oxygen tension, small molecules concentrations/timing, and harvesting strategies), a large‐scale human iPSC‐CMs process suitable for cGMP manufacturing can be developed and validated, as it moves towards the clinic.

Taken together, we have shown that the expansion and directed differentiation of human iPSC can be scaled up from a 125 ml spinner flask to a 3 L computer‐controlled bioreactor using CFD modeling. In particular, using parameters calculated from this modeling it was possible to expand human iPSCs in large‐scale computer‐controlled bioreactors using defined L7 media while maintaining their pluripotency. Subsequently, the aggregated cells could be differentiated into cardiomyocytes through a multi‐step induction approach using a defined culture media. This newly developed CFD modeling has the potential to be used in custom development and scale‐up of manufacturing processes with less labor and cost. Although further optimization studies are required to exhibit the robustness of the scaled process, we believe this proof‐of‐concept work is a major step forward in the development of affordable and commercial ready cell therapies derived from pluripotent stem cells. Moreover, this methodology can be applicable to a wide range of cell therapy applications in 3D bioreactors, for instance, allogenic therapies using mesenchymal stem cells.

CONFLICT OF INTEREST

The authors declare that there are no conflict of interest.

AUTHOR CONTRIBUTIONS

M. S. wrote the manuscript, designed the process development studies and performed the experiments. K. M. P. wrote the manuscript and designed the process development studies. T. W. wrote the manuscript, performed the CFD modeling and helped with the experiment. T. R. designed the experiment and performed the experiment. B. A. B. wrote the manuscript and provided supervision and intellectual guidance. All authors have read and approved the final version of the manuscript.

Supporting information

Supporting information

Supporting information

Supporting information

Supporting information

Supporting information

Supporting information

Supporting information

Supporting information

Supporting information

Shafa M, Panchalingam KM, Walsh T, Richardson T, Baghbaderani BA. Computational fluid dynamics modeling, a novel, and effective approach for developing scalable cell therapy manufacturing processes. Biotechnology and Bioengineering. 2019;116:3228–3241. 10.1002/bit.27159