Measurement of Angstrom to Nanometer Molecular Distances with ¹⁹F Nuclear Spins by EPR/ENDOR Spectroscopy

Abstract

Spectroscopic and biophysical methods for structural determination at atomic resolution are fundamental in studies of biological function. Here we introduce an approach to measure molecular distances in bio‐macromolecules using ¹⁹F nuclear spins and nitroxide radicals in combination with high‐frequency (94 GHz/3.4 T) electron–nuclear double resonance (ENDOR). The small size and large gyromagnetic ratio of the ¹⁹F label enables to access distances up to about 1.5 nm with an accuracy of 0.1–1 Å. The experiment is not limited by the size of the bio‐macromolecule. Performance is illustrated on synthesized fluorinated model compounds as well as spin‐labelled RNA duplexes. The results demonstrate that our simple but strategic spin‐labelling procedure combined with state‐of‐the‐art spectroscopy accesses a distance range crucial to elucidate active sites of nucleic acids or proteins in the solution state.

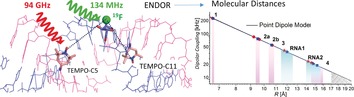
What did the NO say to the ¹⁹ F? Dipolar couplings between nitroxide spin labels and ¹⁹F nuclear spins report inter‐spin distances in the range of ≲15 Å at sub‐angstrom accuracy. These couplings are measured with sub‐nanomole spin sensitivity by high frequency (94 GHz) electron–nuclear double resonance (ENDOR) and can be employed to obtain detailed structural insights into biomolecules.

Introduction

High‐resolution structural information is fundamental for understanding the function of biological macromolecules like proteins or nucleic acids. Biophysical methods such as X‐ray crystallography,1 cryo‐electron microscopy (EM),2 or nuclear magnetic resonance (NMR)3 can provide this information under their specific sample requirements. Nevertheless, an integrative approach to structural biology which takes into account data from multiple other sources including small‐angle X‐ray scattering as well as optical and magnetic resonance spectroscopies is being increasingly appreciated.4 For instance, NMR and fluorescence energy transfer (FRET) can provide unique information in the solution state, addressing the inherent structural flexibility and dynamics of biomolecules.5 Additionally, NMR in the liquid and solid state (SSNMR) provides atomistic or residue resolution but suffers from an overall low spin sensitivity.6 Electron paramagnetic resonance (EPR) spectroscopy has the advantage of a high spin sensitivity on the order of a few picomoles due to the higher polarization of electron spins that have a much larger magnetic moment as compared to nuclear spins.7 This advantage gets even more pronounced at high magnetic fields and frequencies,8 where also spectral resolution increases.9 Moreover, EPR is not restricted by the size of the bio‐macromolecule, however, it requires the presence of at least one paramagnetic center. In the last decade, EPR‐based pulsed dipolar spectroscopy10 has emerged as an important tool for structural biology, as it allows for measuring dipolar coupling between two paramagnetic centers (typically nitroxide spin labels) separated by ≈1.5 up to approximately 8 nm, where the distance range can be extended by using either sophisticatedly shaped pulses11 or deuterated proteins.12 At such long distances, the dipolar coupling depends on the inverse cube of the inter‐spin separation. Using advances in data analysis,13 the method provides the distance distribution of the molecular ensemble and thus reports on conformational distributions from the dynamics of the labelled molecules. In principle, distances below 1.5 nm could also be measured,14 however, at such short distances it is inadequate to treat the two coupled electrons as localized, quasi‐classical point dipoles.15 Thus, distance determination is complicated by quantum effects like spin delocalization or exchange couplings.16

Here we present an approach that conveys the spin‐labelling concept from pulsed dipolar spectroscopy to electron–nuclear double resonance (ENDOR) by replacing one of the nitroxides with a nuclear ¹⁹F spin label to access molecular distances ≲1.5 nm. The value of ¹⁹F nuclear labels has been recently recognized in the NMR literature, where the large gyromagnetic ratio of ¹⁹F and its scarcity in biological samples have been exploited to selectively measure couplings between ¹H and ¹⁹F or between pairs of ¹⁹F nuclei separated by up to ≈20 Å.17 The combination of nitroxide and ¹⁹F labelling on cyanovirin‐N allowed for measuring distances of 12–24 Å using paramagnetic relaxation enhancement (PRE) experiments.18 While requiring the same labelling strategy, PRE and EPR/ENDOR are complementary to some extent. PRE allows measuring distances in liquid solution with an r ⁻⁶ distance dependence, providing access to average inter‐spin distances. ENDOR is typically performed in frozen solution and thus potentially provides access to distance distributions as well as information about the orientation of the electron‐spin center. As an advantage, EPR‐based methods are not limited by the size of the sample molecule and require a much smaller amount of sample. An early example of measuring ¹⁹F hyperfine (hf) couplings by EPR was presented by Wells and Makinen, who used cw ENDOR to measure distances from nitroxides to ¹⁹F nuclei in model compounds.19 However, their study was hampered by the low magnetic field strengths of only ≈0.35 T, which led to ¹⁹F resonances heavily overlapping with ¹H resonances. A possibility to circumvent this issue was presented by Zänker et al., who employed ³¹P nuclei instead of ¹⁹F.20 Using Mims′ ENDOR experiments,21 couplings as small as ≈33 kHz could be resolved corresponding to a distance of about 1 nm between a nitroxide and a ³¹P nucleus. The availability of high‐field/high‐frequency EPR spectrometers (ν _EPR≳94 GHz) meanwhile allows for a sufficient resolution of nuclear frequencies, as we reported in recent publications,9, 22 and for a general implementation of ¹⁹F ENDOR for structural investigations. Here we demonstrate the ability of 94 GHz (3.4 T) ¹⁹F ENDOR to detect distances up to ≈15 Å with atomic resolution in orthogonally labelled ¹⁹F/nitroxide model systems and RNA duplexes.

Results and Discussion

We synthesized four mono‐fluorinated nitroxide model compounds 1–4 by Steglich esterification23 and subsequently crystallized them by slow evaporation of saturated solutions of 1–4. As shown in Figure 1 a–d, the inter‐spin distances R _XRD from the X‐ray structures range from 6.8 Å for 1 to 14.8 Å for 4, using the midpoint of the N−O bond as a reference for the electron‐spin localization.15 Echo‐detected EPR spectra at 94 GHz of 1–4 showed a line shape typical for nitroxides, with a representative spectrum displayed in Figure 1 e. Details on the syntheses, X‐ray structures, 94 GHz EPR experimental setup and experimental parameters are given in the Supporting Information.

Figure 1.

a)–d) Structures of 1 (a), 2 (b), 3 (c), and 4 (d) as determined by crystallography. Inter‐spin distances R _XRD between the midpoint of the N−O bond and ¹⁹F are indicated. Ellipsoids at 50 % probability. Color code: gray=C, blue=N, red=O, yellow=F. e) Representative echo‐detected EPR spectrum of 1 with ENDOR observer positions A–E. f) Schematic Mims ENDOR pulse sequence denoting the time intervals τ and T. g) Orientation of the nitroxide g tensor axes and definition of the dipolar tensor (R∥T_x or 2 T) as well as the Euler angles α and β between g and the dipolar tensor.

Assuming a localized electron‐spin density, the hf coupling as a function of the distance between a nitroxide spin label and ¹⁹F can be estimated using the point‐dipole model [Eq. (1)]24

$${\displaystyle T=\frac{{\mu }_0}{4\pi h}\left(g_{\mathrm{e}}{g}_{\mathrm{n}}{\mu }_{\mathrm{B}}{\mu }_{\mathrm{N}}/R^3\right)=C/R^3}$$ (1)

where T is the principal‐axes value (T _⊥) of the dipolar part of the hf tensor, μ ₀ the vacuum permeability, h the Planck constant, and C=74.52 MHz ų is calculated from the g factors and Bohr magnetons of nitroxides (g _iso≈2.005) and ¹⁹F, respectively. For distances >5 Å, as in model systems 1–4, all expected couplings are smaller than 1 MHz. To detect such small couplings, we choose the Mims ENDOR experiment (Figure 1 f), which has notably highest sensitivity, however, it produces blind spots in the hf spectrum according to the function25

$${\displaystyle F=0.5{\sin }^2\left(2\pi \frac{{\nu }_{\mathrm{H}\mathrm{F}\mathrm{C}}}{2}\tau \right)}$$ (2)

where F represents the ENDOR efficiency, τ is the separation between the two 90° preparation pulses, and ν _HFC the expected coupling frequency. Thus, the τ values have to be optimized for each sample to detect the canonical resonances of the dipolar powder pattern (Pake pattern), with principal axes frequencies at ν _HFC=±T and ±T/2. Under consideration of the relaxation times T _m (Figure S11, Supporting Information), τ values were chosen that optimize detection of the parallel component of the dipolar tensor at ν _HFC=±T.

Figure 2 displays representative ¹⁹F‐Mims ENDOR spectra at 94 GHz for 1 and 4 in [D₆]DMSO/[D₄]MeOD (1:1.5) at 50 K. The sample volume amounted to 2 μL at concentrations of 250–300 μm. All individual ENDOR spectra report orientation selection9 due to the narrow excitation bandwidth of the microwave (mw) pulses with respect to the broad EPR line. In principle, the full Pake pattern might be reconstructed by summing over all orientations, which would correspond to measuring and summing spectra at a set of narrowly spaced resonance fields. However, this procedure is experimentally not feasible due to the long spectral averaging, and also not necessary. In order to find the principal resonance components of the Pake pattern and to optimize experimental time, spectra at only a few resonance positions A–E (Figure 1 e), including the canonical orientations of the g tensor, were recorded. A sum spectrum is reported for a qualitative comparison with a calculated, ideal Pake pattern. Summation was performed after normalizing the individual spectra (A–E) to the number of scans.

Figure 2.

94 GHz ¹⁹F Mims ENDOR spectra of 1 and 4 (black and gray lines) at EPR resonances A–E at 50 K. The top spectrum is the weighted sum of spectra A–E. Mims ENDOR simulations with (red) and without (purple) orientation selection are superimposed. The blue spectrum represents the corresponding undistorted Pake pattern. Spectra of 4 have been smoothed, unsmoothed data are shown as black dotted lines. Sum spectra contain 2693 (1) and 39 892 (4) scans. Acquisition times were about 15–20 hours per spectrum A–E for 4. Optimized τ values were 850 (1) and 2250 ns (4). RF pulses were 54 μs for 1–3 and 110 μs for 4. Further experimental parameters are given in the Supporting Information. The ENDOR effect was overall a few percent of the electron‐spin echo.

At position A, high selectivity for the parallel component of the dipolar coupling tensor is observed (for all compounds 1–4). This leads to a high sensitivity at this observer position, which is even higher than at position B, where the echo intensity is maximized. Owed to this effect, the corresponding features in the sum spectrum are also slightly over‐weighted. ENDOR spectra of 2 and 3 looked very similar to those of 1 and are reported in Figure S12. Inspection of all spectra for 1–3 reveals that peaks appear approximately at half of the frequency of the edges (grid lines) consistent with a dipolar Pake pattern.

For sample 4, the individual spectra show resonances consistent either with ±T (A) or ±T/2 (B–E). The sum spectrum, however, does not represent a fully resolved Pake pattern because the resolution no longer suffices, despite using RF pulses twice as long as for compounds 1–3 (note the factor of 10 in the frequency axis between spectra of 1 and 4). Indeed, a separation between the spectral features exceeding the ENDOR line width is a requirement to resolve such features. In the case of 4, the line width and the separation of the perpendicular and parallel components are nearly identical, which is why the corresponding spectral features are not as clearly resolved as in the spectra of 1–3 (spectral resolution is discussed further in the Supporting Information). Nevertheless, owed to the axial symmetry of the dipolar coupling tensor, peaks at ±T/2 are dominant in most of the orientation‐selected spectra. The simplest way to extract inter‐spin distances is to read off the T values from the spectra (Figure 2) and then apply Equation (1). For compounds 1–4, the respective values T _read are 243±9, 86±6, 63±6, and 21±3 kHz, respectively, where the error was estimated as three times the resolution of the frequency axes. These values correspond to distances R _read of 6.7±0.1, 9.5±0.2, 10.6±0.3, and 15.2±0.7 Å, respectively, in excellent agreement with the distances R _XRD observed in the crystal structure (Figure 1).

To examine the fidelity of a simple point‐dipole analysis, we performed spectral simulations by taking into account a conformational analysis provided by the ORCA quantum chemistry program package,26 which allowed finding stable conformers a–d for 1–4 (Figures 3 and S4).

Figure 3.

DFT‐derived stable conformers. 1: R₁=F, R₂=R₃=H, 2: R₂=F, R₁=R₃=H, 3: R₃=F, R₁=R₂=H and 4: R₁=p‐F‐Ph, R₁=R₂=H.

For all compounds, rotation of the pyrroline‐N‐oxyl moiety leads to conformation c, which comes at an energetical cost of ≈2.5–3 kJ mol⁻¹ when compared to conformation a. Conformation b is energetically equal to conformation a in the case of 2, whereas it is ≈1.8 kJ mol⁻¹ less stable than a in the case of 1. The relative weight W of the conformers was determined based on their respective energies and populations according to a Boltzmann distribution at a temperature of 180 K (Table 1). While the weighted average of the melting temperatures of DMSO and methanol amounts to ≈220 K, we chose this lower temperature to reflect that the solvent system forms a glass, leading to decreased freezing temperatures.27 From the geometry of the conformers we could extract the distances R _DFT (Table 1) between the midpoint of the NO group and the ¹⁹F nucleus as well as the Euler angles α and β between the nitroxide g tensor and the dipolar tensor (Figure 1 g and Table S6). The DFT‐predicted dipolar couplings T _DFT (Supporting Information, Section S4) for all conformers are listed in Table 1. Subsequently, all conformers with their respective weights were considered for the ENDOR simulations.

Table 1.

Summary of dipolar T and R parameters obtained for 1–4 from the different methods, that is, X‐ray, DFT, and ENDOR spectra (read‐off and simulations).

Sample[a]	W [%]	T read [kHz]	T sim [b,c] [kHz]	T DFT [c] [kHz]	R read [d] [Å]	R sim [b,c,d] [Å]	R XRD [Å]	R DFT [d] [Å]	lw [e] [kHz]
1, abc	70, 21, 9	243±9	260, 224, 290	255, 209, 283	6.7±0.1	6.6, 6.9, 6.4	6.8	6.7, 7.2, 6.5	26
2, abcd	42, 42, 8, 8	86±6	93, 83, 96, 106	95, 83, 100, 109	9.5±0.2	9.3, 9.6, 9.2, 8.9	9.4	9.4, 9.7, 9.3, 9.0	19
3, ac	85, 15	63±6	66, 73	61, 67	10.6±0.3	10.4, 10.1	10.6	10.6, 10.2	17
4, ac	82, 18	21±3	24, 25	23, 24	15.2±0.7	14.6, 14.4	14.8	14.8, 14.5	10 (16)

[a] Compound and conformers used in the simulations. [b] Errors are assumed to be identical as in the read‐off case. [c] High‐weight conformers are given in bold. [d] Calculated using Equation (1). [e] Number in parentheses is the linewidth for 4 using RF pulses of 54 μs (see Supporting Information for experimental data) as for 1–3.

Figure 2 shows Mims ENDOR simulations carried out with the software EasySpin.28 The DFT‐predicted couplings T _DFT were slightly re‐adjusted to best reproduce the Mims ENDOR spectra, whereas the Euler angles α and β were kept fixed during the simulation. From the simulated T _sim (Table 1) values, the point‐dipole distances R _sim were computed according to Equation (1). Overall, our approach provided four sets of values for the inter‐spin distances, two each from X‐ray and DFT‐optimized structures R _XRD and R _DFT, respectively, to be compared with those obtained from the ENDOR spectra, R _read and R _sim. We find that the R _sim values for the different conformers are consistent with the distances R _DFT within about 0.3 Å (Table 1). Furthermore, R _read agrees within its uncertainty with the distance from the conformer that has the highest weight. In the case of 2, where two high‐weight conformers are present, R _read is found in between the expected distances for the two conformers. Additionally, the simulation reports a line‐width parameter which contains contributions from different sources. Contributions arising from the experimental settings, such as the length of the RF pulse, or from the spin system, such as the nuclear‐ or electron‐spin relaxation times T _M or T ₁,25 are expected to be similar across the samples. Increasing the RF pulse length (that is, decreasing the RF power) consistently led to smaller line widths, however at the expense of sensitivity. For 1–3, RF pulses of ≈50 μs represented a good compromise between sensitivity and resolution (Figure S13). In the case of 4, a significant improvement of the resolution was obtained by prolonging the RF pulse up to ≈100 μs (Figure 2) with still sufficient sensitivity (see Supporting Information for spectra of 4 recorded with ≈50 μs RF pulses). For a given RF power, the line width decreases from compound 1 to 4 (Table 1), indicating that line widths are also affected by distance distributions. Indeed, line broadening owed to distance distributions is expected to be the largest for compound 1, where the distances are short. For example, a variation of ±0.1 Å around a mean distance of 6.6 Å leads to a spread in frequencies of ≈23 kHz, whereas the same variation around a mean distance of 9.6 Å (2) leads to a spread of only ≈5 kHz.

To examine the method on a bio‐macromolecule, two 16mer RNA duplexes RNA1 and RNA2 were designed and investigated (Figure 4) following a previously published protocol (see Supporting Information).29 In both duplexes, strand A carries a ¹⁹F nucleus at the 2′‐position of the ribose attached to an adenine base at position 7 (blue in Figure 4). Strand B (red in Figure 4) carries the semi‐rigid TEMPO‐based C^T label29, 30 at either position 5 (RNA1) or position 11 (RNA2). Our previous investigations had shown that the C^T label allows maintaining base‐pairing in the duplex so that an A‐RNA conformation is conserved.31 To visualize the structures of RNA1 and RNA2, the coordinates of the 16mer A‐RNA helix with a raise and a twist of 2.81 Å and 32.7°, respectively, were generated by employing the w3dna server.32 Subsequently, the C^T label was introduced in one of the most energetically stable conformations compatible with hydrogen bonding using PyMOL, as predicted by previous DFT calculations of the C^T energy surface.31 The C^T conformations were defined by two dihedral angles φ ₁ and φ ₂ (Figure 4) and values of φ ₁≈120±75 and φ ₂≈0±60 were found within the energy minimum (Figure S18), with a second, less broad minimum at φ ₁≈−60±20 and φ ₂≈0±40.31 These models allow for estimating NO–¹⁹F distances of approximately 12 Å and 14 Å in RNA1 and RNA2, respectively. Mims ENDOR spectra of RNA1 and RNA2 show clearly resolved peaks at ±T (spectrum A) or ±T/2 (spectra B–D), as shown in Figure 4 (RNA sample preparation, experimental setup, and EPR characterization are detailed in the Supporting Information). The S/N ratio is worse than in the model systems since the sample concentration is about a factor of two lower and the spectra are broader. From the individual spectra, the sum spectrum was generated as for 1–4 (Figure 4). The sum spectra do not represent a typical Pake pattern due to visible broadening, thus T _read was obtained representatively from spectrum C (Figure 4), leading to T _read=43±6 kHz and T _read=23±4 kHz for RNA1 and RNA2, respectively. Using Equation (1), these translate to average ¹⁹F–electron‐spin distances of 12.0±0.6 Å and 14.8±0.9 Å.

Figure 4.

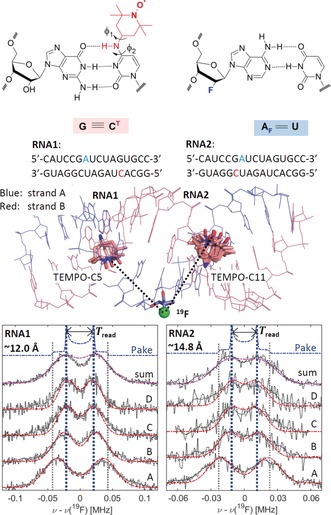
Top left: Structure of the C^T label and visualization of the base‐pairing to G in the spin‐labelled duplexes. Dihedral angles defining the label conformation are marked. Top right: Structure of the ¹⁹F‐labeled nucleotide. Center: Model of the 16mer A‐RNA duplex visualizing the spatial arrangement of the C^T labels with respect to the ¹⁹F‐labeled adenosine in conformers consistent with the ENDOR data (conformations b, n, and o for RNA1 and b, c, and k–o for RNA2, see Supporting Information). Bottom: Normalized 94 GHz ¹⁹F Mims ENDOR spectra of RNA1 and RNA2 (smoothed data in gray, unsmoothed data in black, dotted lines) with simulations using a single C^T conformer (red, conformation n for RNA1, conformation b for RNA2). T _read is inferred from spectrum C. Distances R _read are indicated. Optimized τ values were 2200 (RNA1) and 2180 ns (RNA2). RF pulses were 54 μs. The acquisition times amount to approximately 18 and 30 h per spectrum for RNA1 and RNA2, respectively. Further experimental parameters are given in the Supporting Information.

Simulations based on 12 individual conformations with different dihedral angles φ ₁ and φ ₂ within the energy minima (Figure S18) indicated that only some conformers with dihedral angles φ ₁≈80±40 and φ ₂≈15±30 allow for simulating ENDOR spectra that are consistent with the experimental data. Interestingly, the conformations which agree with the ENDOR data also produce considerably fewer short contacts (Table S8) between the label and the RNA backbone, thereby providing further evidence that the A‐RNA form is preserved after labelling with C^T. The best simulation based on a single conformer is superimposed to the data for RNA1 and RNA2 in Figure 4. We note that for RNA2, the spectrum at position A might be indicative for a splitting and thus for a second component. However, the resolution at the other excitation positions does not allow for a simple, unambiguous analysis with multiple components. For both RNA duplexes the T _sim values agree within the uncertainty with the read‐off values T _read (Table 2). Noteworthy, line‐width parameters considerably larger than for 1–4 had to be used to simulate the spectra of RNA1 and RNA2. Furthermore, the line‐width parameter turns out anisotropic and is largest at excitation positions B∥g _x, which report the 2T (T _∥) resonances. This is consistent with inhomogeneous broadening due to a conformational distribution of inter‐spin distances, since the value 2T is affected twice as much by such a distribution as the T component. The detailed analysis (Figures S19–S21) revealed that also a distribution of Euler angles in the different geometries contribute significantly to the observed ENDOR linewidths in the orientation‐selective spectra. It is plausible that the line widths observed for the RNAs reflect a conformation distribution arising from degrees of freedom of the C^T label, including a distribution of distances on the order ±0.5 Å, consistent with previous data derived from PELDOR studies.31

Table 2.

Hyperfine parameters from the ENDOR spectra of the RNA duplexes.

Sample	T read [kHz]	T sim [kHz]	R read [Å]	R sim [Å]	lw[a] [kHz]	φ 1/φ 2
RNA1	43±6	45±4	12.0±0.6	11.8±0.4	30 (44)	47/20
RNA2	23±4	26±3	14.8±0.9	14.2±0.6	20 (24)	77/13

[a] The value in parentheses is the value used for the spectrum at position A.

Figure 5 summarizes the range of measured dipolar couplings as a function of the distances. The plot permits some conclusions about the detection limit. According to the R ⁻³ distance dependence [Eq. (1)], T decreases by a factor of ≈10 if the distance increases from 6.7 to ≈15 Å and by an additional factor of approximately 2 from 1.5 to 2.0 nm. The question arises as to whether a distance of 2 nm (T≈9 kHz) would be detectable. Our data show that the resolution of the Mims ENDOR experiment with nitroxides is within the range 10–15 kHz due to the different broadening mechanisms and the spectral hole [Eq. (2)]. The loss of signal intensity due to the spectral hole cannot be compensated by longer τ values. Indeed, the optimized τ value for 4 is already almost identical to the T _M value of the nitroxide20 and spectral acquisition time amounts to about four days. Therefore, although it might be somewhat sample‐dependent, the detection limit at present appears to be ≲1.7 nm (Figure 5). In the case of short distances <6 Å, the simple point‐dipole model might break down, as electron‐spin delocalization cannot be neglected anymore. A plot of the point‐dipole model vs. a distributed dipole model (Figure 5) in which a spin‐density delocalization between N and O is considered (Supporting Information, Section S6) already shows this deviation. Additionally, isotropic HFC interactions might occur at such short distances. In this regime, the experiment is still feasible, but a distance interpretation will require quantum‐chemical modelling to take into account the detailed spin‐density distribution. For nitroxides in the distance regime studied here, only minor improvements are expected by taking into account spin‐density delocalization as compared to the simple mid‐point analysis, at the expense of considerably more modelling. However, when studying more delocalized spin centers like aromatic radicals or trityls, a detailed analysis of the spin‐density distribution will be necessary.33

Figure 5.

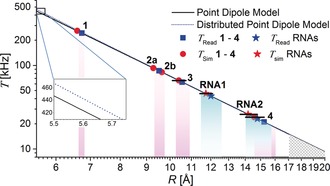
Distances calculated from the measured dipolar coupling constants T using the point‐dipole model (black, full line) or the distributed‐dipole model (blue, dotted line). Only conformer a for 1, 3, and 4; a and b for 2 is shown. Uncertainties in R reflect the estimated error in T (Tables 1 and 2). Uncertainties in R _read are indicated by purple (1–4) and cyan shading (RNAs) as well as by solid bars for R _sim. Distances above the estimated resolution limit in T are indicated by the hatched area. Inset: Deviation of the point dipole and the distributed model towards short distances.

Conclusion

In conclusion, using high‐frequency 94 GHz EPR/ENDOR combined with strategic ¹⁹F and nitroxide spin labelling we have reported inter‐spin distances up to ≈15 Å in bio‐macromolecules with accuracies of 0.1–1 Å that depend on the distances and the sample‐specific inhomogeneous broadening. The advantage of this technique as compared to the other widespread approach to measure hyperfine couplings, that is, ESEEM spectroscopy,34 is the increasing performance towards high field and frequencies, which do not rely on the excitation of forbidden transitions and on specific matching conditions. Moreover, ESEEM generally suppresses frequencies corresponding to the canonical orientations, which are crucial in this analysis and could only be indirectly obtained from ESEEM data by detailed simulation.

Compared to other methods available in structural biology, the advantages are the atomic resolution, the absence of limitations by protein size, and sensitivities in the sub‐nanomole range, which can complement, for instance, cryo‐EM in frozen‐solution studies or access macromolecules not amenable by NMR methods. Moreover, wide applicability is expected since the methods are already well‐established for introducing ¹⁹F labels into proteins and nucleic acids. Examples include fluorinated purine and pyrimidine nucleobases35 and 2′‐fluoro ribose modifications36 as well as fluorinated amino acids,17c, 37 particularly when introduced site‐specifically into recombinant proteins as artificial amino acids by amber stop‐codon suppression.38 Structural knowledge from distances at atomic resolution plays a central role, for instance, in mechanistic studies of enzymes39 and functional nucleic acids such as nucleic‐acid catalysts (ribozymes/deoxyribozymes)40 for which the method will have immediate application. In a trend similar to the establishment of long‐range distance measurements in EPR, it is expected that progress in ENDOR spectroscopy will improve resolution and that mathematical procedures will be developed to extract distance distributions.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

A. Meyer, S. Dechert, S. Dey, C. Höbartner, M. Bennati, Angew. Chem. Int. Ed. 2020, 59, 373.