Electric activities of time-delay memristive neuron disturbed by Gaussian white noise

Abstract

To study the effect of electromagnetic induction on the electric activities of neuron, memristive neuron models have been proposed by coupling membrane potential with magnetic flux. In this paper, on the basis of memristive Hindmarsh-Rose neuron model, time-delay memristive Hindmarsh-Rose neuron model is described and the responses of neuron in electrical activities are detected. The effect of time-delay on the dynamical behaviors of the neuron is discussed and the transition of electrical activities of the neuron is investigated with the change of noise intensity. It is found that, both the time-delay and the noise have effect on the electrical activities of the neuron. Especially, by selecting appropriate parameters, the noise not only can excite neuron from quiescent state to bursting state, but also can suppress the electrical activities in neuron during certain discharge period. Results mean that multiple modes and coherence resonance can be observed by changing the size of time-delay or the noise intensity, which could be associated with memory effect and self-adaption in neurons.

Introduction

Composed of a large number of neurons, neuron system is in complex environment. Therefore, electric activities of neurons are affected by a lot of interior and exterior factors, such as neuronal intracelluar and extracellular ion concentration, activities of ion channels, intrinsic and extrinsic noise, depolarizing current, and so on.

Since the pioneering work of Hodgkin and Huxley (1990) on the electric activities of squid’s axon nerve, computational neuroscience has been developed greatly. To better describe the rich electric activities of neurons, some simplified neuron models, such as FitzHugh-Nagumo model, Hindmarsh-Rose model, Morris-Lecar model and Chay model, have been established on the basis of Hodgkin-Huxley neuron model. As a simplified version of the Hodgkin-Huxley model, FitzHugh-Nagumo model (Scott 1976) is established to describe the detailed manner activation and deactivation dynamics of a spiking neuron. Hindmarsh-Rose model (Hindmarsh and Rose 1984) is used to discuss the spiking-bursting of the membrane potential observed in experiments with a single neuron. Morris-Lecar model (Morris and Lecar 1981), as a biological neuron model, is addressed to reproduce the variety of oscillatory behavior in relation to Ca++ and K+ conductance in the muscle fiber of the giant barnacle. Chay model (Chay 1985), as an electrophysiological model, is used to describe the dynamics of β–cell in pancreas.

Based on above classical neuron models, much research has been done on the electrical activities of neurons or neuron networks. Guo and Li (2012) investigated the stochastic dynamics of Hodgkin-Huxley neuron driven by stochastic excitatory. Gu et al. (2013) studied the pattern formation of a network composed of Morris-Lecar neurons induced by white noise. Han et al. (2015) addressed a modified bursting Hodgkin-Huxley neuron model and realized the synchronization of the systems with heterogeneous neurons coupled by delayed chemical synapses. Wang and Ma (2014) considered the electrical activity as well as the transition of firing patterns of Hindmarsh-Rose (HR) neuron model induced by three types of autapses. The response of neuron to the electric autapse forcing and the effect of gain in autapse on the oscillating behaviors have been depicted (Song et al. 2015; Kim 2017; Yilmaz et al. 2016; Guo et al. 2016). A four-variable biological neuron model is set up to discuss the dynamical behaviors by altering external forcing current (Gu and Pan 2015). Results in Refs. Harris et al. (2012), Torrealdea et al. (2009) suggest that the metabolism of neuron is found to be associated with the electrical activities of itself and information transition should be considered when studying the signal communication between neurons. Gafarov (2018) pointed out that electrical activity of neuron plays an important role in establishing the initial interneuronal connections. Ref. Mao (2018) focused on the dynamic behaviors of a kind of delay-coupled networks and the transitions between different behaviors. Wei et al. (2018) found that chimera states emerge when the neurons are connected through electrical synapses. Kim and Lim (2017) studied the dynamical responses of neurons in complex small-world networks to external stimuli depend on the synaptic-coupling type and depicted the effect of spike-timing-dependent plasticity on stochastic burst synchronization in a scale-free neuronal network (Kim and Lim 2018). Parastesh et al. (2019) discussed a system of two ephaptically coupled neurons with a periodically time-varying link between the two membrane potentials and derived the master stability function. Dharani et al. (2017) explored the synchronization of a class of generalized reaction–diffusion neural networks with mixed time-varying delays. The existing results may be helpful for understanding the dynamical behaviors of neuron.

Due to the complex environment in which the neuron is in, more influence factors have been considered when studying the electric activity of neuron or dynamical behaviors of neuron network. To solve the effect of magnetic radiation on the electric activities of neuron, magnetic flux was introduced into neuron model and corresponding research has been carried out. For example, Rostami et al. (2018) studied the effects of an external time-varying magnetic induction on the formation of spatiotemporal patterns in a model of excitable tissue. Lv et al. (2016), Lv and Ma (2016) designed a four-variable neuron model by introducing magnetic flow as a variable into Hindmarsh-Rose neuron model and observed multiple modes of electric activities by altering initial state. Considering physical effects, Wang and Ma et al. (2017) improved Hodgkin-Huxley neuron model with memristor to detect the dynamical response to the electromagnetic induction. Yu et al. (2017) improved Chay neuron model by imposing electromagnetic flow on it and revealed the transition of electrical activities in the proposed neuron. A new neuron model is proposed considering inner magnetic fluctuation and external electromagnetic radiation as a significant missing part participating in neural activity and some dynamical properties of the model are investigated (Panahi et al. 2018). Mostaghimi et al. (2019) developed four models on the basis of Hindmarsh-Rose (HR) model under magnetic flow effect and compared the different dynamics of the models. Wei et al. (2018) investigated the finite-time synchronization and fixed-time synchronization of inertial memristive neural networks with time-varying delays. Results in (Ma et al. 2017) suggested that synchronization degree is closely related to the intensity of external electromagnetic radiation. Inspired by the physical effect of memristor, Xu and Ma et al. (2019) detected the variety of mode selection in electrical activities under different patch temperatures, which provided insights to modulate the neural activities in appropriate temperature condition. For a single neuron or a neuron in a network, noise is inevitable. Therefore, some results have been obtained about the effect of noise on the dynamical behaviors of neuron or neuron network (Zhao et al. 2017; Wang et al. 2014). These research results may be helpful for understanding the mode selection and transition of electrical activities in neurons exposed to electromagnetic radiation. Along with the research of membrane neuron or neuron network, researcher proposed soft-threshold adaptive sparse coding algorithm named MMN-SLCA based on the memristor, neural network and sparse coding theory, which can be used in a hardware implementation framework to provide feasible solutions for hardware acceleration, real-time processing and embedded applications (Ji et al. 2019).

Factually, when signal is propagated between neurons, time-delay and noise disturbance always coexist.

According to above, in this paper, the electric activity of time-delay memristive neuron disturbed by Gaussian white noise is investigated. Other parts are given as follows. In Sect. 2, the neuron model to be discussed is described. Section 3 gives the numerical results and discussions. Some conclusions are provided in Sect. 4.

Model description

Hindmarsh-Rose (HR) neuron model, a three-variable neuron model (Hindmarsh and Rose 1984), can be described as

$$\left\{\begin{array}{c}\dot{x}=y-a{x}_{}^3+b{x}_{}^2-z+I_{\mathit{ext}}\hfill \\ \dot{y}=c-d{x}_{}^2-y\hfill \\ \begin{array}{c}\dot{z}=r\left[S\left(x+k\right)-z\right]\end{array}\hfill \end{array}\right),$$ 1

where x denotes the membrane potential, y is the recovery variable for slow current and z is the adaption current. I_ext is the external forcing current. For a = 1.0, b = 3.0, c = 1.0, d = 5.0, r = 0.006, S = 4.0, k = 1.6, system (1) can produce main dynamical properties shown in electric activities of neuron.

To investigate the effect of electromagnetic induction on the electrical activities, by introducing a new variable for magnetic flow, memristive HR neuron model

$$\left\{\begin{array}{c}\dot{x}=y-a{x}^3+b{x}^2-z+I_{\mathit{ext}}-k_1\rho \left(w\right)x\hfill \\ \dot{y}=c-d{x}^2-y\hfill \\ \dot{z}=r\left[S\left(x+k\right)-z\right]\hfill \\ \dot{w}=k_{2}x-k_{3}w\hfill \end{array}\right)$$ 2

was established and some dynamical behaviors of it have been discussed (Lv et al. 2016), where $\rho \left(w\right)=\left(\alpha +3\beta w^2\right)$ is the memory conductance of memristor and is used to describe the coupling between magnetic flux and membrane potential of neuron. The fourth variable w describes the magnetic flux across membrane. $k_1\rho \left(w\right)x$ is the induced current.$k_{2}x$ and $-k_{3}w$ are defined as the effect of electromagnetic induction and self-inductance, respectively. $k_1$ and $k_2$ are the gains dependent on the media.

In real neural system, time-delay will inevitably exist in activation between neurons, even in one neuron, which will affect the dynamics of the neuron or neuron networks (Xie et al. 2016; Yao and Ma 2018; Shafiei et al. 2019; Kachhvah 2017). To describe the dynamical behaviors of neuron for both theoretical research and practical applications, time-delay should not be neglected. Considering the existence of time-delay in the information transferring among the neurons, memristive neuron model can be further improved as

$$\left\{\begin{array}{c}\dot{x}=y-a{x}^3+b{x}^2-z\left(t-\tau \right)+I_{\mathit{ext}}-k_1\rho \left(w\right)x\hfill \\ \dot{y}=c-d{x}^2-y\hfill \\ \dot{z}=r\left[S\left(x+k\right)-z\right]\hfill \\ \dot{w}=k_{2}x-k_{3}w\hfill \end{array}\right),$$ 3

where $\tau$ is the time-delay. Compared with previous HR model, model (3) is with more bifurcation parameters and could be reliable for further investigation on the effect of electromagnetic radiation on biological tissue.

In model (3), time-delay and magnetic flux are both included. Although both of them can be used to describe the memory effect, they depict the memory from different aspects. Magnetic flux is used to describe the effect of magnetic field with memory according to the physical characteristics of magnetic field, while time-delay is used to describe the effect of memory in line with the delay of information propagation. In actual biological system, on the one hand, neurons are in a constantly changing magnetic field; on the other hand, the transmission of information between neurons or within neuron has certain time lag. Therefore, to describe the dynamical behaviors of neuron more accurately, both time-delay and magnetic flux should be considered. What’s more interesting is that time-delay can induce stochastic resonance or coherence resonance (Zhu and Mei 2014; Yu et al. 2017).

Numerical simulation results and discussions

In this section, differential equation system (3) is solved via fourth-order Runge–Kutta algorithm by selecting time-step $\mathrm{\Delta }h=0.001$. Initial values of system (3) are taken as $\left(x_0,y_0,z_0,w_0\right)=\left(0.01,0.9,0.8,0.3\right)$.

Since external forcing current and time-delay both play important role in the electric activity of neuron, it is necessary to study the dynamical behaviors with the variations of the external forcing current I_ext or the time-delay $\tau$. In these simulations, the system parameters are chosen as a = 1.0, b = 3.0, c = 1.0, d = 5.0, r = 0.006, S = 4.0, k = 1.6, $k_1$ = 0.01, $k_2$ = 1.0, $k_3$ = 6.2, α = 0.4, β = 0.01.

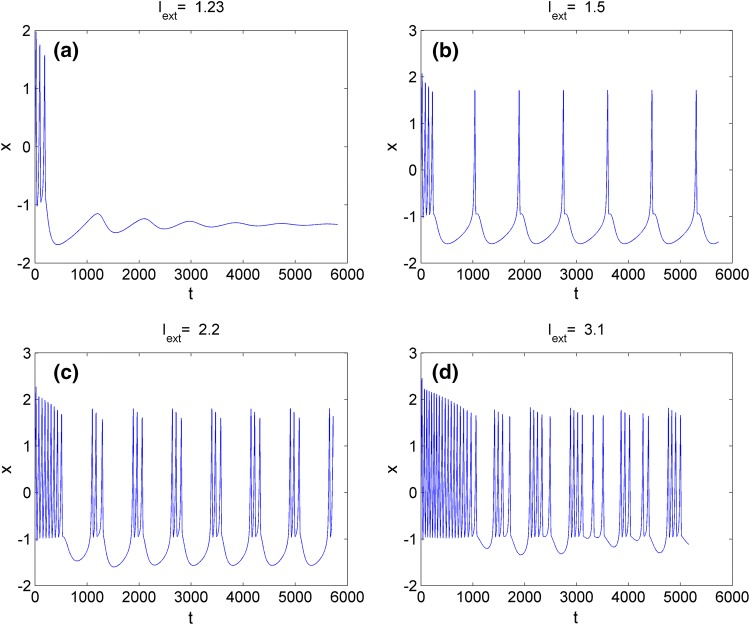
Firstly, the effect of external forcing current I_ext on electric activities of neuron system (3) is discussed. For this end, time delay is fixed as a constant, such as $\tau =1$. The external forcing current I_ext is taken as the bifurcation parameter and the bifurcation diagram of x verses I_ext is plotted in Fig. 1, which suggests that the electric activities of neuron system (3) can show multiple modes with the change of the external forcing current. To describe the electric activities of neuron system (3) in detail, the sampled time series of it are calculated and plotted in Fig. 2 by applying different external forcing currents. Figure 2 confirms that, stable state, spiking, periodic bursting and chaotic bursting could be observed by selecting appropriate external forcing current.

Fig. 1.

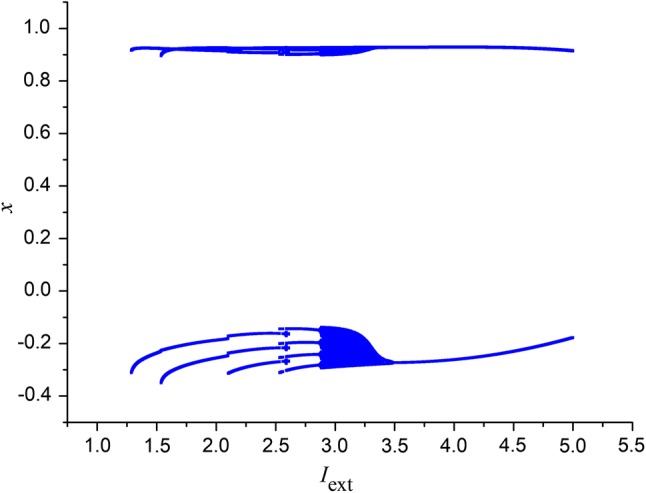
Bifurcation diagram of variable x in system (3) with the change of I_ext with $\tau =1$

Fig. 2.

Sampled time series of variable x in system (3) with $\tau =1$ for different external forcing current, aI_ext = 1.23, bI_ext = 1.5, cI_ext = 2.2, dI_ext = 3.1

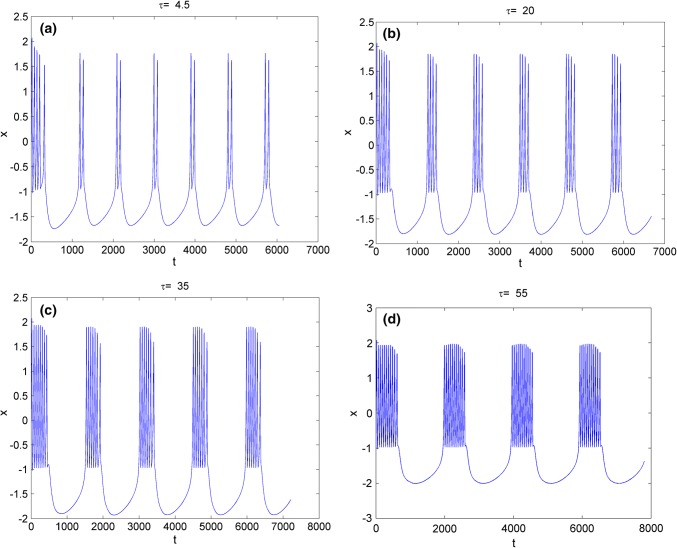
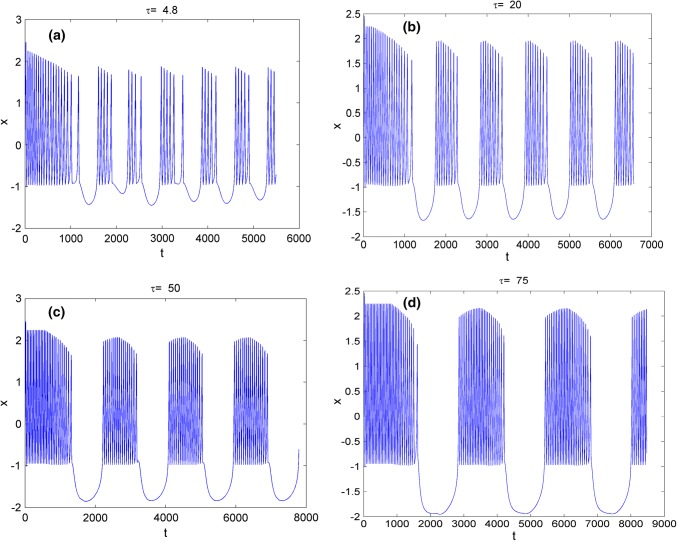
Secondly, the effect of time-delay on the dynamics of variable x in system (3) is studied. The external forcing current is fixed as constant while time-delay $\tau$ is chosen as different values. Two cases are considered including $I_{\mathit{ext}}=1.5$ and $I_{\mathit{ext}}=3.1$. When $I_{\mathit{ext}}=1.5$, the bifurcation diagram of x verses $\tau$ is plotted in Fig. 3 and the time series of variable x are depicted in Fig. 4. From Figs. 3 and 4, it is obvious to see that the electric activities of neuron system (3) can also show multiple modes with the change of time-delay $\tau$. For fixed small value of external forcing current, appropriate value of time-delay can alter the period and frequency of the electricity activity of neuron system (3). When the external forcing current is fixed as a larger value $I_{\mathit{ext}}=3.1$, time-delay τ is also taken as various values, the bifurcation diagram of x verses $\tau$ and the time series of x are calculated and drawn in Figs. 5 and 6, respectively. From Figs. 1 and 2d, it is known that system (3) is provided with chaotic bursting for $I_{\mathit{ext}}=3.1$ and $\tau =1.$ But from Figs. 5 and 6, we know that, with the increasing of time-delay $\tau ,$ electric activity of neuron system (3) shows multiple modes including periodic bursting and chaotic bursting. This phenomena indicates that time-delay play an important role in selecting the discharge mode of neuron system (3).

Fig. 3.

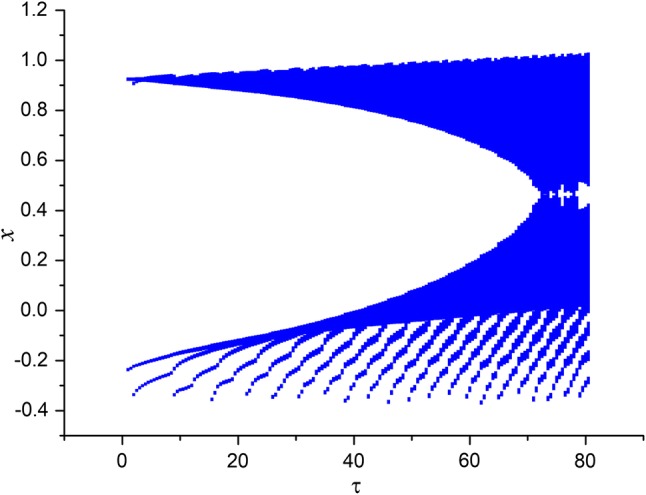
Bifurcation diagram of variable x in system (3) with the change of $\tau$ for $I_{\mathit{ext}}=1.5$

Fig. 4.

The time series of membrane potential x in neuron system (3) for I_ext = 1.5 with different values of time-delay, a $\tau =4.5$, b$\tau =20$, c$\tau =35$, d$\tau =55$

Fig. 5.

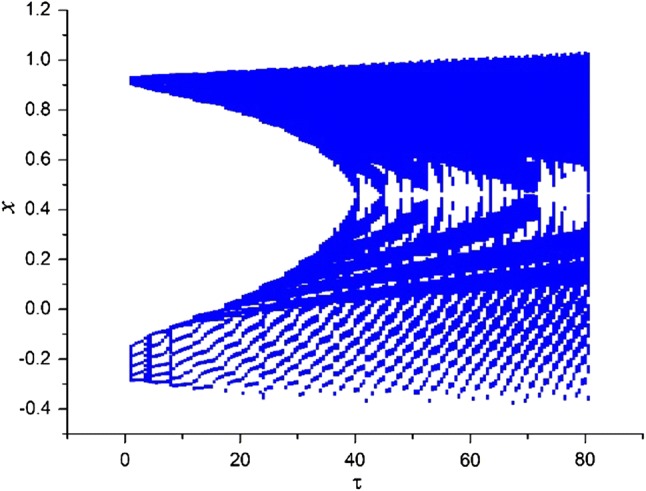
Bifurcation diagram of variable x in system (3) with the change of $\tau$ for $I_{\mathit{ext}}=3.1$

Fig. 6.

The time series of membrane potential x in neuron system (3) for fixed external forcing current I_ext = 3.1 with different values of time-delay, a$\tau =4.8$, b$\tau =20$, c$\tau =50$, d$\tau =75$

To quantitatively characterize the orderliness of the electric activities of neuron, coefficient variability (CV) of inter-spike interval (ISI) is calculated as evaluating indicator (Rajasekar et al. 2012) to discern coherence resonance degree, which can be calculated by

$$CV=\frac{\sqrt{〈T_k^2〉-{〈T_k〉}^2}}{〈T_k〉},$$ 4

where $〈T_k〉$ denotes the mean value of inter-spike interval $T_k,T_k^2$ is the mean variance of inter-spike interval $T_k$. Figure 7 gives the trend of CV with the increase of time-delay, which confirmed that, coherence resonance can occur and regularity in electrical activities can be found by selecting appropriate size of time-delay.

Fig. 7.

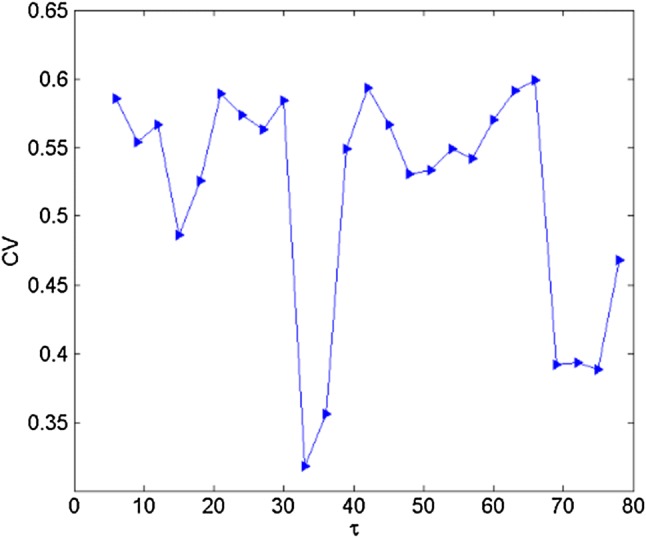
Trend of CV with the change of $\tau$ for I_ext = 1.23

Finally, the effect of noise on the dynamics of variable x in system (3) is discussed. Noise is usually regarded as a disadvantage or interference due to its always affecting the development of things. Therefore, people always try their best to eliminate noise. But in nonlinear dynamics, noise is necessary for the occurrence of some important dynamic processes and its positive role has gradually been discovered, such as stochastic resonance or coherence resonance induced by noise, especially in biological systems. To investigate the effect of noise on the electric activities of neuron, Gaussian White Noise is imposed on the Hindmarsh-Rose neuron model (3) and

$$\left\{\begin{array}{c}\dot{x}=y-a{x}^3+b{x}^2-z\left(t-\tau \right)+I_{\mathit{ext}}-k_1\rho \left(w\right)x+\xi \left(t\right)\hfill \\ \dot{y}=c-d{x}^2-y\hfill \\ \dot{z}=r\left[S\left(x+k\right)-z\right]\hfill \\ \dot{w}=k_{2}x-k_{3}w\hfill \end{array}\right)$$ 5

can be obtained, where $\xi \left(t\right)$ is the Gaussian white noise with zero average and statistical relation as $\xi \left(t\right)\xi \left(t^{\prime }\right)=2D\delta \left(t-t^{\prime }\right)$, and D is noise intensity.

For neuron system (5), two cases are considered.

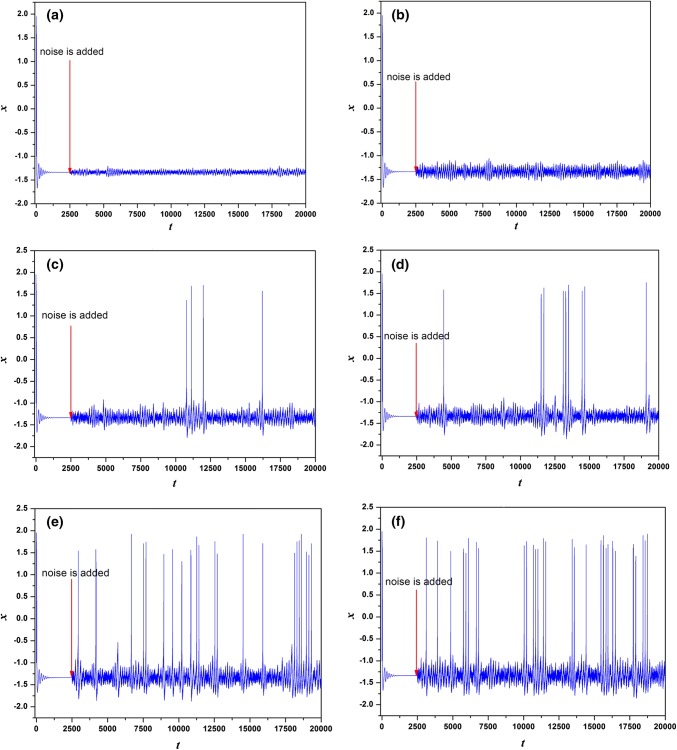
In the first case, the parameters are chosen as a = 1.0, b = 3.0, c = 1.0, d = 5.0, r = 0.006, S = 4.0, k = 1.6, $k_1$ = 0.01, $k_2$ = 6.2, $k_3$ = 1.0, α = 0.4, β = 0.01 and I_ext = 1.23. The time series of membrane potentials x under different intensities D are calculated and given in Fig. 8. In Fig. 8, to discern the effect of Gaussian White Noise on the dynamics of the neuron, the electric activities develop from the stable state without noise driving before t = 2500 time units. Results in Fig. 8 confirm that, with the increasing of noise intensity, more peaks of neuronal cell membrane are located. When the noise intensity is too small (D = 0.1 and D = 0.5), neuronal membrane potential cannot cross the threshold to trigger action potential. With the increase of noise intensity (D = 0.7, 0.9, 1.2, 1.6), neuronal membrane potential can randomly cross the threshold and produce peak discharge and the peak position is basically random distribution. This is because excessive noise obliterates the regularity of discharge sequence. It means Gaussian White Noise with appropriate intensity can excite the neuron from the quiescent state to bursting state and stronger intensity can arouse bursting with more chance. Figure 9 gives the trend of CV with the change of noise intensity. From Fig. 9, we know that coherence resonance can occur and regularity in electrical activities can be observed under appropriate noise intensity.

Fig. 8.

The transition of electric activities of neuron system (5) for I_ext = 1.23 with noise imposed on t = 2500 time units, aD = 0.1, bD = 0.5, cD = 0.7, dD = 0.9, eD = 1.2, fD = 1.6

Fig. 9.

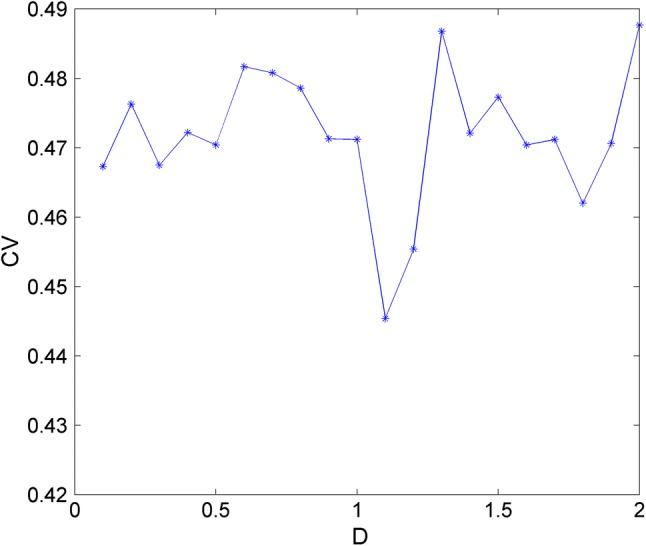
Trend of CV with the change of noise intensities D for I_ext = 1.23

In the second case, the system parameters are chosen as a = 1.0, b = 3.0, c = 1.0, d = 5.0, r = 0.006, S = 4.0, k = 1.6, $k_1$ = 1.0, $k_2$ = 0.8, $k_3$ = 0.5, α = 0.1, β = 0.02 and I_ext = 1.5, with which the membrane potential of neuron system (3) is in periodic bursting. Then Gaussian White Noise is imposed at t = 2000 time units with different intensities and the time series of membrane potentials are calculated and drawn in Fig. 10, which confirmed that Gaussian White Noise can make the electric activity transit from periodic bursting to chaotic bursting. This phenomenon means that Gaussian White Noise with suitable intensity can suppress the electric activity of neuron within certain transient period and stronger noise has greater effect on the electric activity. Simultaneously, CV of inter-spike interval are calculated and given in Fig. 11, which means that coherence resonance behavior can also be observed and regularity in electrical activities can also be detected under appropriate noise.

Fig. 10.

The transition of dynamical behaviors of neuron system (5) for I_ext = 1.5 with noise imposed on t = 2000 time units for different intensities, aD = 0.1, bD = 0.5, cD = 0.9, dD = 1.2, eD = 1.5, fD = 1.8

Fig. 11.

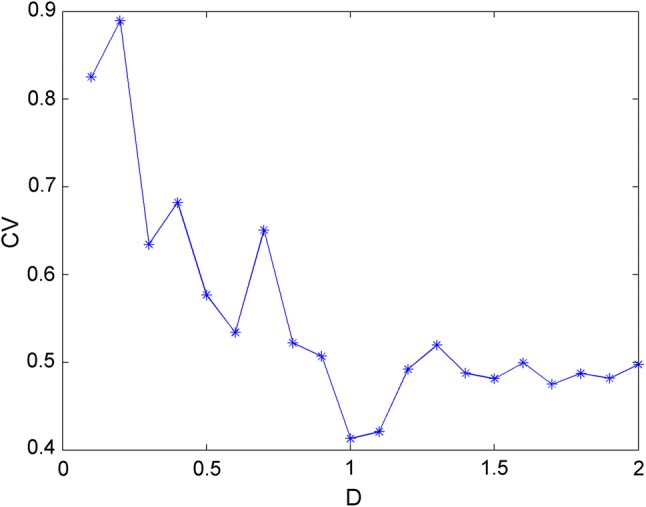
Trend of CV with the change of noise intensities D for I_ext = 1.5

Conclusions

Considering the physical effect on the neuron activity, memristive Hindmarsh-Rose neuron model is improved by introducing time-delay. The dynamical response to the time-delay of the neuron is discussed via numerical simulations. The transition of electric activities of the neuron is investigated when the noise is imposed on the neuron. Results suggest that, when noise is not imposed on the neuron, the electric activities just tend to sole mode under external forcing. But the dynamical behaviors of the neuron become more complex and interesting when noise is imposed on the neuron. Multiple modes in electric activities can be observed by changing the noise intensity. The noise with suitable intensity not only can inspire the spiking of the neuron and make the dynamical behaviors of membrane potential develops from stable state to busting state, but also can suppress the electric activities within certain transient period and make the neuron show multiple electric activities. Calculation about coefficient variability (CV) of inter-spike interval (ISI) confirmed that time-delay and Gaussian White Noise both can induce coherent resonance in neuron by selecting appropriate value.

For this guidance, in addition to some traditional variables, some other appropriate terms consistent with physical units should be considered in the neuron model.