Discrete time forecasting of epidemics

Abstract

Forecasting in the domain of infectious diseases aims at estimating the number of cases ahead of time during an epidemic, hence fundamentally requires understanding its dynamics. In fact, estimates about the dynamics help to predict the number of cases in an epidemic, which will depend on determining a few of defining factors such as its starting point, the turning point, growth factor, and the size of the epidemic in total number of cases. In this work a phenomenological model deals with a practical aspect often disregarded in such studies, namely that health surveillance produces counts in batches when aggregated over discrete time, such as days, weeks, months, or other time units. This model enables derivation of equations that permit both estimating key dynamics parameters and forecasting. Results using both severe acute respiratory illness data and synthetic data show that the forecasting follows very well over time the dynamics and is resilient with statistical noise, but has a delay effect due to the discrete time.

1. Introduction

Patterns for infectious diseases transmission include outbreaks with varying intensities that require appropriate responses from health surveillance teams. Intervening actions to avoid or to mitigate the problems clearly depend on evaluation of the outbreak as it happens. Responses to an epidemic in timely fashion poses many challenges, among them the need to recognize the start of an epidemic or even a short-term forecasting.

Outbreaks of a specific disease in a city or state often happen with varying degrees of intensity over the years due to seasonality effects, pathogen evolution and other factors. The patterns, however, are normally non–linear, which motivated the design of mechanistic models for describing transmission of multiple diseases, such as malaria, dengue, cholera, tuberculosis and more.

Recently, data-driven approaches have also been used for both detection of start of an epidemic and also obtaining estimates of number of cases. Such approaches rely on the knowledge of temporal series of count data, such as aggregate number of cases in discrete time units (days, weeks, months).

Recent approaches (Chowell et al., 2016; Lega & Brown, 2016; Pell, Kuang, Viboud, & Chowell, 2018; Santillana et al., 2018) applied various forms of logistic growth model or a generalized Richards model, in which the growth of the epidemic is essentially described by a ramp up phase and a slow down phase. Such properties are clearly useful, but the times for these phases to start are unknown, as well as the growth intensity, and by consequence, also the total size of the epidemic.

In this work these patterns are segmented in discrete units of time since most surveillance data comes in counts per days, weeks, months or other time units. The discrete nature of aggregating data in regular time units such as days, weeks or months can constrain quick actions to intervene in the process. The data-driven approach presented here generates estimations for short-term forecasting of case numbers, using notification data of Severe Acute Respiratory Illness (SARI) in Brazil, but this discrete nature limits accurate, timely estimates, even in the case of one-week ahead forecasting. This methodology also holds in face of time series of case numbers that contain significant statistical noise.

2. Material and methods

2.1. Notification data of SARI from Paraná, Brazil

Case numbers were aggregated on a weekly basis from National System of Disease Notification (SINAN) of Severe Acute Respiratory Illnesses (SARI) in the state of Paraná from years 2011 to 2016. Epidemiological weeks were the unit of time for analysis, since daily measurements are very noisy, having spurious biased effects such as sharp decreases in weekends, and typical surveillance decisions are analyzed on weekly schedule. Cases are typically classified as Acute influenza when infected individuals are hospitalized. Paraná has a comprehensive surveillance system, and influenza not only exhibits seasonal effects but also the total number of hospitalizations varied greatly over the past recent years.

Paraná is a state in the south of Brazil with latitudes varying from $-22.5206$ to $-26.721$. There is strong evidence linking latitude effects and the seasonality of influenza in Brazil (Almeida, Codeço, & Luz, 2018). Incidence of influenza in the state is seasonal with peaks of number of cases happening in the winter season. Climate in Paraná is temperate, and for the month of June average temperature is historically at around ${12}^o$ C.

Give this seasonal structure, data from years 2011–2016 are analyzed separately per year, on units of epidemiological weeks, such that every year has $N=52$ weeks and number $c_k$, $1\le k\le N$, of cases comprise the time series for the given year.

2.2. Synthetic data

Synthetic data is generated from an SIR model with parameters β, which describe the transmission intensity and γ, which describes the recovery rate. The dynamic of a susceptible–infected–recovered model permits to construct a time series with non–linear growth with such properties exhibited in outbreaks. These models are well-known and as well as the procedures for implementing and generating such datasets (Bjornstad, 2018; Keeling & Rohani, 2011).

This model permits obtaining for every epidemiological week k the sum of cases over that week for a population of constant size N_H. Therefore, ${\lambda }_k={\int }_{k-1}^k\beta S\left(I/N_H\right)dt$, where ${\lambda }_k$ is the number of cases and $S\left(t\right)$ and $I\left(t\right)$ are number of susceptibles and infected at time t, respectively.

Since actual datasets exhibit some level of statistical noise to the case numbers due to stochasticity, different datasets are constructed with varying levels of noise. In this case, with ${\lambda }_k$ as the number of infected in week k from the SIR model, the random effect has a standard deviation proportional to the number of cases in the model. As consequence, the number of cases is $c_k={\lambda }_k+{\phi }_k$, where ${\phi }_k~Normal\left(0,\delta {\lambda }_k\right)$, and $c_k$ is rounded to integer.

Parameters for constructing datasets were $\beta =0.6$ (day⁻¹) and $\gamma =0.1$ (day⁻¹) in deterministic simulations with days as regular time units. After simulation, numbers of new cases are aggregated on weekly basis, as regular surveillance health teams approach epidemics.

2.3. Richards model

The Richards model has been applied in various contexts, which includes ecological settings and also studying the infectious disease transmission. In this case, the model is applied to the cumulative number of cases during an epidemic. The continuous equation used in this model is (Wang, Wu, & Yang, 2012), as follows.

$$G\left(t\right)=\frac{K}{{\left(1+a{e}^{-ar\left(t-t_c\right)}\right)}^{1/a}},$$ (1)

where $G\left(t\right)$ describes the cumulative number of cases in time t, and K, r, a, $t_c$ are constants. Constant K describes the total number of cases when reaching equilibrium. Parameter r describes the intensity of growth and $t_c$ describes the time at which growth rate starts decreasing (turning point). Constant a has no clear biological meaning, other than making intensity effects varying. In particular, here the case when $a=1$ is of interest, which is the case of the classical logistic growth model. This model is very well known in Population Ecology, where K is known as the carrying capacity and r as the growth rate parameter.

3. Theory/calculation

3.1. Derivation of number of cases and forecasts

An application of the model finds how parameters in the model determine the relationship between the number of cases and the cumulative number of cases. In this sense, the own definition of cumulative number of cases in the discrete time is important: $G_k={\sum }_{i=1}^k{c}_i,$ where time is divided in discrete units of time and $G_k$ describes the cumulative number of cases up to the k unit of time, and $c_i$ is the total number of cases notified in the interval $[i-1,i)$. The methodology is general such that units of time can be days, weeks, months and so on.

As a consequence, the number $c_k$ of cases at unit of time k is given by $c_k=G_k-G_{k-1}$. Therefore, for a surveillance problem the knowledge of the aggregate number of cases at each interval of time up to the k unit of time is known, which easily constructs the cumulative number $G_k$ of cases.

I apply a discrete version of the logistic model for the cumulative number of cases. Thus, using $G_k=\frac{K}{1+e^{-r\left(k-t_c\right)}}$ allows to obtain $c_k$ as follows.

$$c_k=G_k-G_{k-1}=\frac{K}{1+e^{-r\left(k-t_c\right)}}-\frac{K}{1+e^{-r\left(k-1-t_c\right)}}$$

$$=\frac{K{e}^{-r\left(k-1-t_c\right)}\left(1-e^{-r}\right)}{\left(1+e^{-r\left(k-t_c\right)}\right)\left(1+e^{-r\left(k-1-t_c\right)}\right)}$$

Hence the following relationship between $c_k$, $G_k$, and $G_{k-1}$ holds:

$$c_k=\left(1-e^{-r}\right)G_k\left(1-G_{k-1}/K\right).$$ (2)

Also, an alternative version is

$$c_k=\left(e^r-1\right)G_{k-1}\left(1-G_k/K\right).$$ (3)

Equation (2) is an important theoretical result to be used with a number of n observations during an epidemic to obtain estimates of parameters r and K using methodology from Equations (8), (9)) in the MCMC simulation.

For forecasting purposes, the ratio between successive observations is useful:

$$\frac{c_{n+1}}{c_n}=\frac{\left(1-e^{-r}\right)G_{n+1}\left(1-G_n/K\right)}{\left(1-e^{-r}\right)G_n\left(1-G_{n-1}/K\right)}$$ (4)

Since by definition $G_{n+1}=c_{n+1}+G_n$, and defining the term $l_n=\frac{1-G_n/K}{1-G_{n-1}/K}$, Equation (4) permits the derivation

$$c_{n+1}=\frac{c_n{l}_n}{1-c_n{l}_n/G_n}.$$ (5)

Equation (5) noticeably does not involve knowledge of parameter r. This recursive equation is the key to obtain estimates for $n+1,n+2,n+3,$ and so on. Together, Equations (2), (5)) are fundamental for obtaining parameter estimates of the dynamics and obtaining forecasting values, including uncertainty, respectively.

Furthermore, Equation (1) also permits to obtain the turning point $t_c$ (or transition time), once parameters r and K are estimated, as follows.

$$t_c=\frac{\text{log}\left(K/G_n-1\right)}{r}+n,$$ (6)

using the cumulative number $G_n$ at n-th time point.

The basic reproduction number $R_0$ deserves epidemiological interest since it describes the number of secondary infections after an initial primary infection. After estimating the number r, the approach described by Wallinga and Lipsitch (Wallinga & Lipsitch, 2006) permits to obtain the basic reproduction number $R_0$, upon an assumption of the distribution of the generation time interval. For instance, a relationship

$$R_0={\left(1+\mu \kappa \bar{r}\right)}^{1/\kappa },$$ (7)

describes the basic reproduction number assuming the generation time distribution as a gamma distribution with coefficient of variation κ and mean μ, where $\bar{r}$ is the mean estimate of r (Park, Champredon, Weitz, & Dushoff, 2019).

3.2. Inference and forecasting – statistical approach and algorithm

The logistic growth model in Equation (1) is instrumental to obtain in discrete times a function

$$\rho \left(k\right)=f\left(G_k,G_{k-1},\dots ,r,K\right),$$ (8)

linking the number of cases in k-th interval to the cumulative number of cases. In the current approach, $\rho \left(k\right)$ is directly linked to the number $c_k$ of cases, using the descriptor given by Equation (2). The number of cases is modeled with a Poisson distribution given the descriptor $\rho \left(k\right)$:

$$c_k~Poisson\left({\rho }_k\right).$$ (9)

Under this statistical framework, MCMC simulations permit obtaining posterior distribution of parameters r and K and also for forecasting number of new cases. Uninformative prior distributions are applied to parameters r and K, such that $r~Normal\left(\mathrm{0,10}\right)$ and $K~Gamma\left(0.001,0.001\right)$. To perform MCMC simulations several tools can be used, in this case the JAGS tool (version 4.3), with a number of 5000 warmup iterations plus 3000 more iterations (8000 total) in 4 chains to obtain posterior distribution of the parameters and predictions.

The algorithm for obtaining posterior distributions of parameters r and K, as well as estimates of the turning point and basic reproduction number is shown in Table 1.

Table 1.

Algorithm for obtaining estimates.

Step	Input	Method	Output
1.	vector $\mathbf{c}$: $c_1$, $c_2$, … $c_n$ (number of cases)	cumulative sum	vector $\mathbf{G}$: number of cumulative cases $G_1$, $G_2$, … $G_n$
2.	vectors $\mathbf{c}$, $\mathbf{G}$	MCMC simulation	posterior distribution of r and K and forecasting values $c_{n+1}$, $c_{n+2}$, …
3.	posterior distribution of parameters r, K	summary functions	Estimates of mean, median and intervals of credibility
4.	$\bar{r}$	Equation (7)	Estimate of $R_0$
5.	$\bar{r}$, $\bar{K}$, $c_n$, $G_n$	Equation (6)	Estimate $t_c$

The methodology is evaluated with data for N periods of time. Then, assuming knowledge of the aggregate number of cases only up to n-th period of time, $1<n<N$, proceeding with inference for $n+1$, $n+2$, and further. Inference of parameters up to time n will enable estimation of the next number ($c_{n+1},c_{n+2},\dots$) of cases, effectively forecasting the next number of cases in the following intervals (Equation (5) recursively).

4. Results

4.1. One-week ahead forecasting

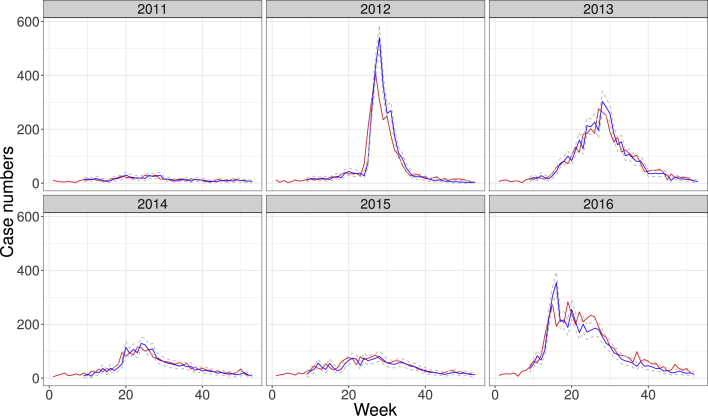
Fig. 1 shows the number of SARI Influenza cases in the state of Paraná from years 2011–2016. The incidence is typically seasonal with peaks happening in the middle of the years (winter season), when an epidemic takes place. Here, one-week forecasting algorithm using Equation (5) starts from week 8 every year. Hence, data from weeks 1 to n along with MCMC estimates using Equations (2), (5)) permits forecasting value for $n+1$ week, and the algorithm repeats this process starting from $n=8$. The forecasting in the ramp up weeks underestimates the number of cases due to the one week delay. When reaching the peak, the forecasting tends to overestimate, especially when the ramp up effect is very strong. In 2012, when the ramp up phase starts, predicted values are a week behind but the two curves will meet at approximately the peak of case numbers.

Fig. 1.

Case numbers of SARI in the state of Paraná, Brazil, in the years from 2011 to 2016. Red lines depict the actual number of cases. Blue lines indicate a one-week forecasting performed with data limited to the earlier epidemiological week. Gray dashed lines show the bounds given by credibility intervals.

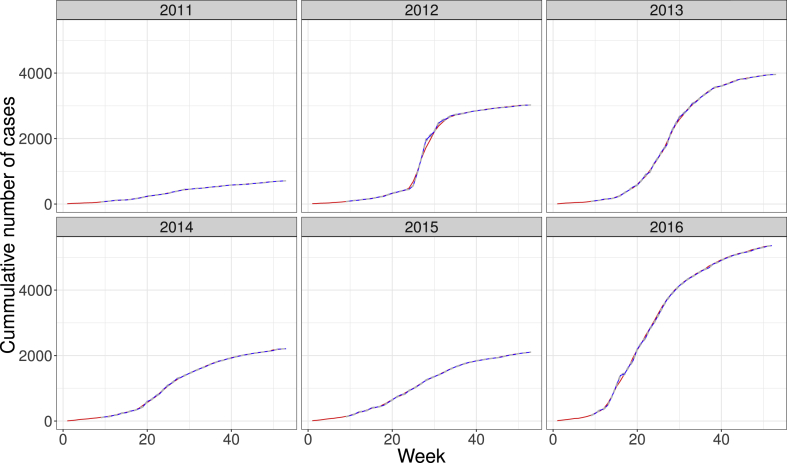
Fig. 2 shows the cumulative number of cases of acute influenza in the state of Paraná, Brazil. Top incidence years were both 2013 and 2016. The pattern of how the epidemic increases in total numbers is very similar over the years, albeit varying in intensity and total size. The estimation from one-week forecasting is quite close to the actual numbers.

Fig. 2.

Cumulative number of cases of SARI influenza in the state of Paraná, Brazil, in the years from 2011 to 2016. Red lines and blue lines show the actual number of cases and estimated from one-week forecasting.

4.2. Estimation of the total size of the epidemic

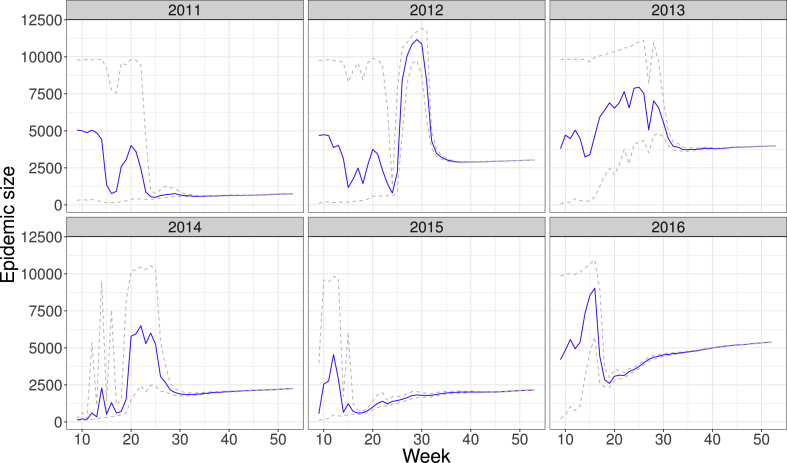
Fig. 3 shows the prediction of the total number K of cases in the season from epidemiological week 8 onwards. In the first weeks the credibility intervals are quite large but reduce over time to the actual epidemic size. This uncertainty effect is present regardless of the total size at the end of the epidemic.

Fig. 3.

Estimation of the total cumulative number K of SARI cases in the years from 2011 to 2016. Blue lines depict the mean values obtained from MCMC simulation, whereas gray, dashed lines show credibility intervals.

4.3. The effect of statistical noise

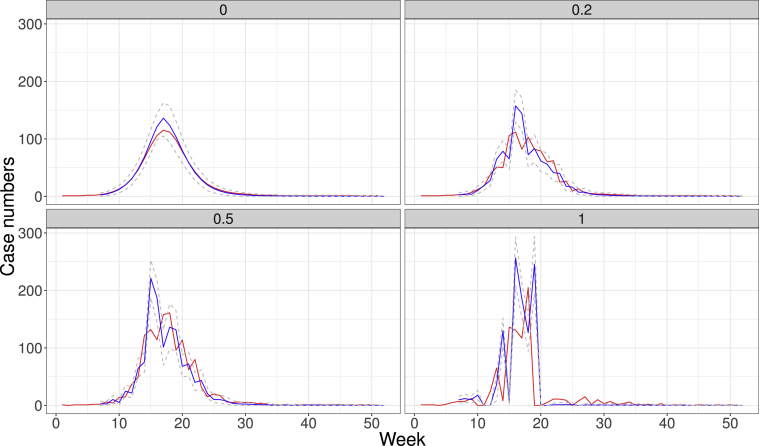
I also applied this methodology to synthetic data using the SIR model. Here, $\beta =0.6$ (day⁻¹) and $\gamma =0.1$ (day⁻¹). Fig. 4 shows the estimation of number of cases over a perfect, deterministic data obtained from SIR model to various datasets in which standard deviation of the random effects added to the data varies. An overestimation in the ramp up phase is noticeable for the dataset with no noise, where a slight overestimation of the mean number of cases appears, although the actual numbers are clearly within the credibility intervals. As expected, as noise levels increase, forecasting becomes much harder. However, the fourth plot in which standard deviation equals the number of cases, the pattern for the synthetic number of cases appears quite different to the expected pattern in most epidemics, such that the statistical noise is already excessive.

Fig. 4.

Estimates of one-week ahead number of cases using a synthetic dataset obtained from an SIR model. Red lines show the weekly number of cases, whereas blue lines show the estimates for one-week forecastings using the model. Gray, dashed lines are built with credibility intervals. The number on the top of each plot describes the standard deviation of the noise applied to each simulated dataset.

4.4. Forecasting of epidemic numbers for multiple weeks

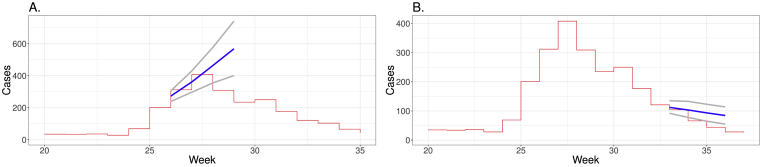
In Fig. 5, I apply the forecasting using Equation (5) on multiple iterations, i.e. for estimates over multiple weeks, for obtaining forecasting in the ramp up and the slow down phases of the 2012 epidemic of SARI. In the ramp up phase, number of cases until epidemiological week 25 are used to obtain forecasting for weeks from 26 to 29, whereas in the slow down phase data until week 32 allows obtaining estimates for weeks 33–36. Credibility intervals increase as forecasting is intended to go further ahead in time. For weeks 26 and 27 the estimates are close to the actual numbers. However, forecasting of mean values for epidemiological weeks 28 and 29 was approximately 500 cases or even greater, whereas the actual numbers were about 300 cases and below. In this time range the credibility intervals clearly do not include the actual numbers. When estimating in the decline portion of the epidemic, credibility intervals increase and fail to predict the actual numbers in 4 weeks ahead, although the estimation is closer in this phase.

Fig. 5.

Forecasting of number of cases of SARI in Paraná. Red lines show in steps the number of cases of SARI in 2012, epidemiological weeks from 20 to 35. Blue lines show the forecasting for the interval between weeks 26 and 29 (A) and between weeks 33 and 36 (B). Gray lines show the credibility intervals.

4.5. Estimation of basic reproduction number and transition time

Table 2 shows per year the estimation of the total number of cases, the transition time, the rate r, and the basic reproduction number. For estimating the reproduction number, a gamma distribution is assumed as a good approximation for the generation time distribution applying Equation (7) as shown by Park et al. (Park et al., 2019). This generation time distribution considers values with an average time of 4.8 days and standard deviation of 1.8 days obtained from previous studies (Carrat et al., 2008). Even though the outbreaks typically differ in magnitude over the years from 2011 to 2016, the basic reproduction number is very close in the range from 1.31 to 1.7.

Table 2.

Mean estimates of parameters K, total number of cases, r, the growth factor, $t_c$, the transition time, and the basic reproduction number $R_0$ using data from years 2011 to 2016, each of them separately.

Year	Total number of cases	Transition time	Rate r	$R_0$
2011	745	28	0.85	1.70
2012	3027	26	0.40	1.31
2013	3977	28	0.75	1.61
2014	2243	27	0.81	1.65
2015	2152	27	0.77	1.62
2016	5384	23	0.65	1.51

5. Discussion

Health surveillance can benefit greatly from data-driven forecasting, even though possibly suffering from delay effects. Such approach proved helpful with notification data of SARI particularly for short-term forecasting, i.e., in one or two weeks ahead. Results from a well behaved synthetic dataset show how this approach is targeted. However, noise and spurious effects might be present in the series of case numbers which make estimations harder as observed in the analysis of the SARI dataset and the synthetic datasets containing statistical noise.

The equation for the number of cases as a function of the cumulative number of cases (Equation (2)) has a structure similar to the differential equation of the continuous logistic model, but Equation (2) shows that in the discrete setting the derived function requires the cumulative sum and the previous cumulative sum, i.e., an expression that relates the number of cases in a given unit of time to the cumulative number of cases up to the week and the number from a week earlier. The result is proportional to the product between the number of cases and the complement of normalized number of cases in the week earlier or vice-versa.

The result from Equation (2) permits estimation of the parameters without making specific assumptions for initial number of cases. This is quite relevant, since the surveillance may start at any given point of time. Also, the forecast using equation (5) does not require the growth parameter r which cancels on the sources of uncertainty.

In the initial phase of the epidemic and in the ramp up phase, there is great uncertainty about the total size of the epidemic. While mean values vary greatly and credibility intervals are very large in the beginning of the time series, a much better estimation is possible after the epidemic passes its turning point.

The approach here can also be used for obtaining estimates of the transition time and the basic reproduction number $R_0$. In the latter, a previous knowledge is required on the distribution of the generation time of the disease. In the case of the transition time, estimates expectedly also carry great uncertainty in the ramp up phase.

The model for synthetic data considers that statistical noise has greater variance during peak periods, which make the problem harder to predict. Estimation is unsurprisingly more difficult as variance increases. Nevertheless, estimation using synthetic data proved quite accurate, although still suffering from the delay effect.

Surveillance teams can make more targeted efforts during an epidemic recognizing the need to analyze over short timescales, for instance in days. Such efforts might impose difficulties due to collection of data and applying responses in face of imminent or ongoing health crisis. In this sense, tools that apply these methodologies can assist in the process.

Wang et al. (Wang et al., 2012) provide a comprehensive view of the Richards model applied to infectious diseases which require more parameters to be estimated. Other works apply either a model selection or model ensemble in which they consider the Richards model, logistic–growth model or some variation (Liu, Tang, & Xiao, 2015; Sebrango-Rodriguez et al., 2017). Recent approaches (Chowell et al., 2016; Lega & Brown, 2016; Pell et al., 2018) considered various forms of the Generalized Richards Model. Lega and Brown (Lega & Brown, 2016) show that in practical terms plotting the number of cases as a function of the cumulative number of cases has a practical feature but the forecasting problem still persists since case numbers are present in the response and the data. The derivation in this work expresses the relationship to be used for estimation of parameters, effectively permitting forecasting. The approach for estimating parameters in a full Generalized Richards model requires estimation of four parameters, requiring prior distributions and eventual transformation/normalization, whereas the method described here requires initially two parameters as shown in Equations (2), (3)) and other parameters such as the turning point are also estimated in an indirect manner.

The logistic equation in discrete settings generate different outcomes depending on the choice of the parameters (Otto & Day, 2011; Petropoulou, 2010). Here, I have taken the common continuous function that describes the total number in a logistical growth model and segmented the function which effectively describes the timely observations of count data for notifications in discrete units.

The delay effect can cause an underestimation (or the opposite) quite significant. More uncertainty could be added since notifications are often delayed, i.e. when doing forecasting health surveillance teams often do not have the complete number of cases in the current week.

The use of such data-driven approach on a regular basis effectively enables short-time forecasting of number of cases of infectious diseases in a general manner. These estimates are clearly important for helping to evaluate the risk of an epidemic and forecasting itself. Surveillance must take into account such results along with treatment of delay effects and potential additional effects to be evaluated, depending on other variables such as climate data for diseases with seasonal patterns and presence of vector populations for vector–based transmission diseases such as dengue. Focused analysis during the ramp up phase could also help, for instance working with data on shorter times scales, though in situations of crisis a complete data availability might not be possible or human resources might become extremely occupied.

Declaration of competing interest

As author, I declare no conflicts of interests.

Handling editor: Dr. J Wu