Temporo-frontal activation during phonological processing predicts gains in arithmetic facts in young children

Highlights

• •Activation during phonological processing of rhymes predicts math gains.
• •Temporo-frontal activation predicts gains in fluency and multiplication skill.
• •Both storage and access to phonology are important for math gains.
• •Effects were specific to younger children showing early importance of phonology.
• •Predictive effects specific to math tasks relying on verbal retrieval.

Abstract

Behavioral studies have shown discrepant results regarding the role of phonology in predicting math gains. The objective of this study was to use fMRI to study the role of activation during a rhyming judgment task in predicting behavioral gains on math fluency, multiplication, and subtraction skill. We focused within the left middle/superior temporal gyrus and left inferior frontal gyrus, brain areas associated with the storage of phonological representations and with their access, respectively. We ran multiple regression analyses to determine whether activation predicted gains in the three math measures, separately for younger (i.e. 10 years old) and older (i.e 12 years old) children. Results showed that activation in both temporal and frontal cortex only predicted gains in fluency and multiplication skill, and only for younger children. This study suggests that both temporal and frontal cortex activation during phonological processing are important in predicting gains in math tasks that involve the retrieval of facts that are stored as phonological codes in memory. Moreover, these results were specific to younger children, suggesting that phonology is most important in the early stages of math development. When the math task involved subtractions, which relies on quantity representations, phonological processes were not important in driving gains.

1. Introduction

Acquiring proficient math skills is critical for academic success and is foundational for the science, technology and engineering disciplines. Because of the cumulative nature of math skills, successful learning of arithmetic in the early stages of education is crucial for acquiring more advanced skills. Understanding how the brain supports the successful development of arithmetic skills will allow us to understand why some children show improvement while others fall behind. Evidence has consistently shown that different arithmetic operations are solved by relying on different cognitive mechanisms (Dehaene et al., 2003). The clearest difference is probably shown between multiplications and subtractions (Lee and Kang, 2002). While multiplications are usually learned by repeatedly reciting multiplication tables, subtractions are rarely memorized and most likely rely on numerical operations. According to the Triple code model of numerical processing (Dehaene et al., 2003), solving multiplications involves retrieving phonological codes from long-term memory. Functional magnetic resonance imaging (fMRI) studies have shown that solving multiplications engages the same brain areas as phonological processing tasks: left posterior temporal cortex, including left middle and superior temporal gyri (MTG; STG), which are implicated in housing phonological representations (Booth et al., 2002, 2003, 2004; Prado et al., 2011, 2014), and left inferior frontal gyrus (IFG), involved in the cognitive control invested to access those representations (Andin et al., 2015; Bookheimer, 2002; Booth et al., 2003, 2004; Fedorenko et al., 2012; Poldrack et al., 1999; Pollack and Ashby, 2017; Prado et al., 2011, 2014; Rickard et al., 2000). While some studies have found evidence suggesting that math and phonology engage slightly different areas within the left IFG (Andin et al., 2015; Fedorenko et al., 2012) others, including Pollack & Ashby’s (2017) meta-analysis, have reported evidence of overlapping brain activation for math and phonology in this region.

Prado et al. (2011) identified areas of the brain responsible for phonological processing and numerical operations in adults using rhyming judgment and numerosity comparison localizer tasks, respectively, and found that multiplication engaged verbal areas, as compared to subtractions, and that subtractions engaged numerical operations areas, as compared to multiplications (see Prado et al. (2014) for similar findings in children). Other studies, investigating children’s differences in brain activation associated with strategy use regardless of operation have shown that retrieval use, as compared to the use of other indirect procedures, engaged verbal regions in left temporal and frontal cortices (Polspoel et al., 2017). The fact that different operations rely on different cognitive and brain mechanisms is important for understanding the role that domain-general cognitive abilities may play in math skill in typical and atypical populations. Phonological skills have been suggested as a crucial domain-general ability for math skill, explaining up to 31 % of the variance in arithmetic performance in 7-year-old children (Leather and Henry, 1994). De Smedt, Taylor, Archibald, & Ansari (2010) found that phonological awareness was uniquely related to children’s performance on problems with a higher probability of being retrieved, but not with problems typically solved with numerical operations or with an untimed test of calculation skill. Supporting evidence for the role of phonological skills in math comes from studies of individuals with dyslexia. According to Simmons and Singleton (2008), children with dyslexia may have weak phonological representations that impact those aspects of arithmetic requiring the manipulation of verbal representations of numbers, such as retrieval of arithmetic facts from memory. Consistent with this, De Smedt and Boets (2010) found that adults with dyslexia showed lower frequency and less efficient use of the retrieval strategy (Göbel and Snowling, 2010). Boets and De Smedt (2010) extended this finding by showing that children with dyslexia were less accurate and slower in solving single-digit multiplications.

Longitudinal studies have shown that phonological skills are not only concurrently associated, but also predict future math skill. Studies have found that phonological awareness assessed at 4–5 years of age was significantly associated with math skills at the beginning of 1st grade (Alloway et al., 2005) and significantly predicted arithmetic skill 1 year later (Simmons et al., 2007). However, these and other studies (e.g. Passolunghi et al., 2007; Passolunghi and Lanfranchi, 2012) did not measure math skills at T1, so they were not able to assess the role of phonological skills in predicting math gains. An exception is Fuchs et al. (2005), which investigated the effect that seven cognitive abilities had in predicting gains in several math measures, including timed math fluency and untimed calculation tests. They found that phonological skill was the only measure significantly predicting gains in math fluency and that it did not predict gains in any of the other math measures (see Fuchs et al. (2006) and Vukovic and Lesaux (2013) for similar results using a phonological decoding measure).

While Fuchs et al (2005) dissected different math outcome measures, they measured phonological skills by using a composite score including both phonological awareness and rate of access, not addressing their separate effects in predicting math gains. Lefevre et al. (2010) found that kindergarteners’ linguistic skill was related to a number naming task and with performance on a variety of math outcomes 2 years later, but linguistic skills comprised both phonological awareness and vocabulary measures. Most of the studies looking at the relationship between phonological skills and math gains have not disentangled the three subcomponents of phonological skill, that is, phonological awareness, rate of access and phonological memory (Wagner and Torgesen, 1987) and, importantly, they have not studied their unique and specific contribution to math gains after accounting for other phonological subcomponents or domain-general abilities. An exemption to this is De Smedt and Boets (2010) who investigated which phonological subcomponents better predicted performance on timed multiplication and subtraction tasks that 4th and 5th graders were asked to solve as accurately and fast as possible. They found that, after accounting for the other subcomponents, only phonological awareness predicted unique variance in multiplication fact retrieval, but not in subtraction.

Findings from adult studies inform us about arithmetic processing in a mature brain, which may not be generalizable to all ages (Ansari, 2010). Cross-sectional studies, by including children from different ages, introduce large individual variability that can lead to falsely suggesting changes over time due to cohort effects or may fail to detect real changes over time (Casey et al., 2005). For these reasons, studies examining children longitudinally are needed (Karmiloff-Smith, 2010). To the best of our knowledge, the only longitudinal study with children that disentangled the effects of the phonological subcomponents in predicting gains in math skill is the study by Hecht et al. (2001). They studied the role of phonological awareness, rate of access and phonological memory in predicting gains in math skill in 2nd to 5th graders, as measured with an untimed standardized paper-and-pencil test including different operations and difficulty levels1. They found that while the three phonological subcomponents significantly predicted gains in math skill from 2nd to 3rd grade, only phonological awareness emerged as a significant predictor of gains from 3rd grade onwards.

In contrast to the evidence suggesting a role for phonological processing in math, some correlational (Durand et al., 2005) and longitudinal (de Jong, and van der Leij, 1999; Passolunghi et al., 2007; Passolunghi and Lanfranchi, 2012) studies have found no evidence for the relationship between phonological and math skills. This can be explained by numerous sources of variability in the studies, including, but not limited to age of the participants, variability in the tests used to measure phonological skill, the study of the phonological skill overall or the unique contribution of their subcomponents, the use of general tests to measure math skill versus tests measuring more specific math outcomes, whether initial level of math skill was controlled for or not, the extent to which domain-general cognitive abilities were accounted for, and language transparency. Perhaps, fMRI can provide a complementary measure of phonological processing that can help to clarify these discrepancies in the literature. To the best of our knowledge, however, only one correlational study has used fMRI to explore this relationship in typically developing children. Berteletti et al. (2014b) studied 3rd to 7th graders and found that the higher children’s level of phonological awareness, the more they engaged verbal areas in the left temporal cortex to solve easy multiplications. They suggested that children with better phonological skills are able to form higher quality phonological representations of the multiplication facts in long-term memory, so they rely on retrieval to solve the task. However, the Berteletti et al. (2014b) study was limited because they examined the correlation between only one of the phonological skill subcomponents (i.e. phonological awareness) and their analysis was restricted to concurrent brain activation while children solved a multiplication task inside the scanner.

The objectives of this study were twofold: First, to predict gains in math by using fMRI to measure temporal and frontal cortex activation during phonological processing2, brain areas claimed to be indices of the storage of phonological representations (Booth et al., 2002, 2003, 2004, Prado et al., 2011, 2014) and access to those representations (Andin et al., 2015; Bookheimer, 2002; Booth et al., 2003, 2004; Fedorenko et al., 2012; Poldrack et al., 1999; Pollack and Ashby, 2017; Prado et al., 2011, 2014; Rickard et al., 2000), respectively. Second, to disentangle the effects that these brain measures of phonological processes have on different math outcomes, depending on whether they focused on verbal fluency or quantitative procedures. We used three math outcome measures: a timed standardized test of math fluency, an untimed standardized test of multiplication skill and an untimed standardized test of subtraction skill. The fluency measure mainly tapped into simple single-digit arithmetic, whereas skill measures tapped into a wide range of difficulty, including multi-digit arithmetic problems.

Regarding math fluency, we hypothesized that both temporal and frontal cortex activation during phonological processing would predict longitudinal gains. This is supported by Fuchs et al. (2005)’s longitudinal results showing that their measure of phonological skill, which included both phonological awareness and rate of access, predicted gains in math fluency in first graders. This hypothesis is also in line with evidence showing that phonological awareness predicted children’s performance on problems solved by retrieval (De Smedt et al., 2010), that the higher the level of phonological awareness, the more children activated temporal cortex to solve a timed multiplication task (Berteletti et al., 2014b), and that rate of access and performance on single-digit additions are correlated in 7-year-old children (Bull and Johnston, 1997). As for multiplication skill, we formulated two hypotheses: First, based on longitudinal evidence showing that phonological awareness was the only subcomponent predicting gains from 3rd to 5th grades in an untimed and relatively complex test of math skill (Hecht et al., 2001), we expected that temporal cortex activation during phonological processing would predict gains in our untimed and relatively complex multiplication test. However, given that measures of phonological awareness require the access to representations, it might be the case that frontal cortex activation would also be a significant predictor of gains. Alternatively, based on evidence showing that phonological skills predicted gains only in math fluency, but not in any of the untimed measures of math skill (Fuchs et al., 2005), it could be that the complexity of some of the items of our untimed multiplication test would prevent its association with phonological activation. Finally, based on numerous studies (e.g. De Smedt and Boets, 2010; De Smedt et al., 2010), we did not expect temporo-frontal cortex activation during phonological processing to predict gains in subtraction skill, given that this operation is considered to rely more on numerical operations in parietal cortex (Prado et al., 2011, 2014).

Considering the evidence suggesting that the association between phonology and math skill changes over time (Hecht et al., 2001) and that age variability across studies could be one of the reasons for discrepancies in the literature, we explored potential differences in the role of temporo-frontal regions during phonological processing in predicting gains in math for younger (i.e. approximately 10 years old at time 1) and older children (i.e. approximately 12 years old at time 1).

2. Materials and methods

2.1. Participants

2.1.1. Whole sample

Sixty-five children from 3rd to 8th grade were recruited from schools in the Chicago metropolitan area to participate in the study3. Data collection took place between the years 2010 and 2014. All participants were native English speakers, right-handed, were free of past and present psychiatric disorders including Attention Deficit Hyperactivity Disorder (ADHD), neurological disease or epilepsy. According to parental report, no participant had hearing impairments, uncorrected visual impairment, was born prematurely (less than 36 weeks), was taking medication affecting the central nervous system or had any contraindication for being scanned, such as having braces. Participants had no history of intellectual deficits, all of them scoring above 85 standard scores (hereinafter, SS) on the Wechsler Abbreviated Scale of Intelligence – WASI (Weschler, 1999). All participants scored above 71 SS on the math fluency subtest from the Woodcock-Johnson III Test of Achievement (WJ-III; Woodcock et al., 2001) and above 85 SS on the Word Attack test of the WJ-III. Written consent was obtained from the children and their parents or guardians to participate in the study. Parents were compensated $20 per hour for their time. The Institutional Review Board at Northwestern University approved all experimental procedures.

Data from three participants were excluded because of excessive movement in the scanner, that is, more than 10 % of the total volumes replaced or more than five consecutive volumes replaced (for more details, see the “fMRI data analysis” section). Ten participants were excluded for showing low accuracy in the rhyming judgment task solved inside the scanner (for more specific information see section “3.1.1 Rhyming judgment task”). One participant was excluded for being left-handed and another one for having missing data for the tests we used to measure gains in multiplication skill and math fluency.

The final sample consisted of 50 participants who were tested longitudinally, with sessions being approximately 2 years apart. More detailed information about the sample is given in Table 1.

Table 1.

Whole sample and age groups characteristics. Means and standard deviations (in parenthesis) for age at each time point, time between sessions, and standard scores (SS) on standardized tests of domain-general cognitive abilities for the whole sample (n = 50), the younger group (n = 25) and the older group (n = 25).

	Whole sample	Younger	Older
Age at T1 a	11.0 (1.4)	9.9 (0.6)	12.2 (0.9)
Age at T2 a	13.2 (1.4)	12.0 (0.6)	14.4 (1.0)
Time between sessions a	2.2 (0.2)	2.1 (0.2)	2.2 (0.3)
Reading skill at T1c	107.8 (11.4)	107.7 (13.4)	108 (9.4)
Verbal short term memory at T1 b, c	105.0 (16.0)	103 (15.2)	106.2 (17.0)
Verbal working memory at T1 b, c	104.2 (12.9)	101.4 (10.2)	107.1 (14.8)
Verbal intelligence quotient (IQ) at T1 c	112.9 (14.4)	114.4 (16.0)	111.4 (12.8)

^aIn years.

^bBased on n = 48 due to missing data for two participants.

^cStandard scores. T1: time 1; T2: time 2.

2.1.2. Age groups

Two groups were created based on the median-split of participant’s age at time 1: younger group and older group. Each age group comprised 25 participants. Age groups differed in age at time 1 (hereinafter, T1) (t(48) = −10.75, p < .001) and age at time 2 (hereinafter, T2) (t(48) = −10.28, p < .001), but not in time between sessions (t(48) = −1.20, p = .24), reading skill (t(48) = −.11, p = .91), verbal short-term memory (t(46) = −.66, p = .51), verbal working memory (t(46) = −1.55, p = .13), or verbal IQ (t(48) = .73, p = .47). More detailed information about the age groups is provided in Table 1.

2.2. Standard measures

2.2.1. Gains in math skills

In order to measure participants’ gains in math skills, children were administered three tests. 1) The math fluency subtest of the Woodcock-Johnson III Test of Achievement (Woodcock et al., 2001) was the timed math fluency measure. This test comprises 136 single-digit addition, subtraction and multiplication problems that have to be solved within a 3-min time limit, in paper-and-pencil format; 2) The multiplication subtest of the Comprehensive Mathematical Abilities Test (CMAT; Hresko et al., 2003) was the untimed standardized test of multiplication skill. This test includes 26 multiplication problems that are solved in paper and pencil format. The test has a wide range of problems difficulty, including single-digit multiplications, multi-digit multiplications, multiplications of decimals, and multiplication of fractions. 3) The subtraction subtest of the Comprehensive Mathematical Abilities Test (CMAT; Hresko et al., 2003) was the untimed standardized test of subtraction skill. This test includes 23 subtraction problems that are solved in paper-and-pencil format. It has a wide range of difficulty, including single-digit subtractions, multi-digit subtractions, subtraction of decimals, and subtraction of fractions. The three tests were measured both at T1 and at T2. Changes in raw scores4 over time (T2-T1) constituted the measure of gains.

2.2.2. Domain-general cognitive abilities: control variables

Reading skill was measured at T1 by the Word Identification subtest from the Woodcock-Johnson III Test of Achievement (WJ-III; Woodcock et al., 2001), which requires pronouncing words. Given the association between phonological and reading skills (Wagner and Torgesen, 1987), individuals with higher reading skill might perform better on the math skill tests, revealing a general relationship between reading and arithmetic rather than one that is specific to phonological processing. Because the rhyming judgment task we used to measure phonological processing inside the scanner required reading written words, participants’ reading standard scores (mean = 100, standard deviation = 15) at T1 was used as a control variable in the analyses.

Verbal short-term memory (STM) was measured with the Digit Recall subtest of the Automated Working Memory Assessment (AWMA; Alloway et al., 2007), in which participants heard a sequence of digits and attempted to recall each sequence in the correct order.

Verbal working memory (WM) was measured by the Listening Recall subtest of the Automated Working Memory Assessment (AWMA; Alloway et al., 2007). This subtest involves simultaneous storage and processing of verbal information. It requires children to decide whether a sentence is true or false, for example, “Bananas live in water”, and also to remember the final word of the sentence, that is “water”. The number of sentences per item increases as children proceed through the test, increasing the number of final words they have to hold in memory to later retrieve.

Verbal STM and WM have been previously used to measure the phonological memory subcomponent of phonological skills (Hecht et al., 2001). Given that the rhyming task used to measure phonological processing inside the scanner required that participants hold the first word of the pair in STM until the second word of the pair was presented, and also to judge whether words rhymed or not while holding the word pairs in memory (i.e. WM), we controlled for these two abilities in order to obtain a purer measure of phonological processing. Short-term and working memory abilities have also been suggested to play an important role in math development (De Smedt et al., 2009; Geary et al., 2007; Passolunghi et al., 2007; Passolunghi and Lanfranchi, 2012) and in the recruitment of different brain areas for multiplication problem solving (Demir et al., 2014), so it was important to control for them, so that we could determine the unique contribution of temporal and frontal cortex activation during phonological processing in predicting gains in math skill. Standard scores were used in the analyses (mean = 100, standard deviation = 15).

Verbal intelligence was measured with the Wechsler Abbreviated Scale of Intelligence – WASI (Wechsler, 1999), which includes the Vocabulary and Similarities subtests. In the Vocabulary subtest, the participant has to define words, while in the Similarities test the participants are presented with two words that represent common objects or concepts and they have to describe how they are similar. To calculate the full IQ score, the distribution of the sums of T scores was converted to a scale with a mean of 100 and SD of 15. Previous studies have suggested the importance of intelligence (Geary et al., 1999) and especially of verbal intelligence (Passolunghi et al., 2012) in predicting math performance and academic success (Deary et al., 2007), so we controlled for this measure in our analyses.

2.3. Task solved inside the scanner

Participants solved a written rhyming judgment task inside the scanner.5 Two monosyllabic English words were sequentially presented and participants had to decide whether the words rhymed or not. To ensure that participants had to rely on phonology and not orthography to solve the task, orthography and phonology were manipulated independently, leading to four conditions where the two pairs of the words had: 1) similar orthography and similar phonology (i.e. O + P+; e.g., dime–lime; 12 trials); 2) similar orthography but different phonology (i.e. O + P-; e.g., pint–mint; 10 trials); 3) different orthography but similar phonology (i.e. O-P+; e.g., jazz–has; 10 trials); 4) different orthography and different phonology (i.e. O-P-; e.g., press–list; 14 trials) (i.e. hereinafter, rhyming conditions). The O + P + and O-P- constituted the non-conflicting conditions, given that orthographic information was consistent with the right answer, whereas the O-P + and O + P- conditions constituted the conflicting conditions because orthographic information was inconsistent with the right answer.

The control conditions comprised a baseline and a perceptual condition. The baseline control condition consisted of a blue square and participants were asked to press a button as soon as it turned into red. In the perceptual control condition, two symbol strings were presented on the screen as increasing, decreasing or steady in height and participants’ task was to determine whether the two symbol strings matched or not. Symbols matched in half of the trials. Twenty-four trials of the baseline control condition and 12 trials of the perceptual control condition were presented. Fig. 1 shows an example of the six conditions included in the rhyming judgment task.

Fig. 1.

Rhyming judgment task stimuli and timing. Rhyming conditions comprising: (A) O + P+, (B) O + P-, (C) O-P + and (D) O-P- word pairs of the rhyming judgment task. Control conditions comprised (E) a baseline condition, consisting of a blue square in which participants had to press a button when the blue square turned into red and (F) a perceptual condition in which two strings of letters increasing, decreasing or showing no changes in height were presented and participants task was to judge whether they matched or not.

In order to make sure that the participant understood the task, children solved a practice version of the task before entering the fMRI room. Twelve trials of each condition, different from the ones used for the scanning session, were presented in the practice session.

2.4. Experimental protocol

Subjects participated in a practice session after informed consent was obtained and standardized tests were administered. During this session, they practiced all trial types and learned to minimize head movement in a mock fMRI scanner. The actual scanning session took place within a week of the practice session. In the fMRI scanner, participants performed one run of the rhyming judgment task, which had a duration of approximately 7 min. The timing and order of trial presentation were optimized for estimation efficiency using optseq2 (http://surfer.nmr.mgh.harvard.edu/optseq/). Behavioral responses were recorded using an MR-compatible keypad and participants responded with their right hand. Participants responded with their index finger if the two words rhymed, when the symbols from the perceptual control condition match (i.e. both increased, both decreased or both remain steady) or when the blue square from the baseline control condition turned into red. Participants used their middle finger if the two words did not rhyme or if the symbols from the perceptual control condition did not match. Stimuli were generated using E-prime software (Psychology Software Tools, Pittsburgh, PA) and projected onto a screen that was viewed by the participants through a mirror attached to the head-coil.

2.5. Stimulus timing

Each word was presented for 800 ms on a white background separated by a 200 ms interstimulus interval. Variable periods of fixation, ranging from 2200 to 3000, were added after each trial in order to help with convolution, during which the red square was presented (Fig. 1A–D). Participants could respond as soon as the second word was presented until the beginning of the next trial. As for the control conditions, the baseline condition consisted of a blue square presented for 800 ms, which was followed by a red fixation square lasting 2200−3000 ms (Fig. 1E). The perceptual condition consisted of two strings of letters presented for 800 ms each, separated by a 200 ms interstimulus interval and followed by a red fixation square lasting 2200−3000 ms (Fig. 1F). The run ended with 22 s of passive visual fixation in order to aid in de-convolution of the final trials.

2.6. fMRI data acquisition

Images were collected using a Siemens 3 T TIM Trio MRI scanner (Siemens Healthcare, Erlangen, Germany) at CAMRI, Northwestern University’s Center for Advanced MRI. The fMRI blood oxygenation level dependent (BOLD) signal was measured with a susceptibility weighted single-shot echo planar imaging (EPI) sequence. The following parameters were used: TE =20 ms, flip angle = 80 s, voxel size: 1.7 × 1.7 × 3 mm, matrix size = 128 × 120 × 37, field of view = 220 × 206.25 × 111 mm, slice thickness = 3 mm (.48 mm gap), number of slices = 32, TR =2000 ms. Before functional image acquisition, a high resolution T1 weighted 3D structural image was acquired for each subject, with the following parameters: TR =2300 ms, TE =3.36 ms, matrix size = 256 × 256, field of view = 240 mm, slice thickness = 1 mm, number of slices = 160.

2.7. fMRI data analysis

2.7.1. Preprocessing

Data analysis was performed using SPM8 (www.fil.ion.ucl.ac.uk/spm). The first six images of the run were discarded to allow for T1 equilibration effects. The remaining functional images were corrected for slice acquisition delays, realigned to the first image of the run to correct for head movements, and spatially smoothed with a Gaussian filter equal to twice the voxel size (4 × 4 × 8 mm³ full width at half maximum). Prior normalizing images with SPM8, we used ArtRepair (Mazaika et al., 2009) http://cibsr.standford.edu/tools/ArtRepair/ArtRepair.htm) to suppress residual fluctuations due to large head motion and to identify volumes with significant artifact and outliers relative to the global mean signal (4 % from the global mean). Volumes showing rapid scan-to-scan movements of greater than 1.5 mm were excluded via interpolation of the 2 nearest non-repaired volumes. All participants had less than 10 % of the total number of volumes replaced and less than 5 volumes replaced in a row. Interpolated volumes were then partially deweighted when first-level models were calculated on the repaired images (Mazaika et al., 2007). Functional volumes were co-registered with the segmented anatomical image and normalized to the standard T1 Montreal Neurological Institute (MNI) template volume (normalized voxel size, 2 × 2 × 4 mm³).

2.7.2. fMRI processing

Event-related statistical analysis was performed according to the general linear model. Activation was modeled as epochs with onsets time-locked to the presentation of the first stimulus in each trial. All epochs were convolved with a canonical hemodynamic response function. The time series data were high-pass filtered (1/128 Hz), and serial correlations were corrected using an autoregressive AR model.

2.7.3. ROIs definition and analyses

Two brain areas consistently associated with phonological processing in the literature (e.g. Bookheimer, 2002; Booth et al., 2002, 2004; Poldrack et al., 1999), the posterior left MTG/STG (posterior to Y= −25) and the left IFG, were defined using the anatomical automatic labeling (AAL) template, which is part of the Wfupickatlas tool (Maldjian et al., 2003). These anatomically defined regions constituted our masks. We then defined functional ROIs by selecting the 100 voxels showing maximal activation for the contrast “all word pairs of the rhyming judgment task vs. perceptual control condition” (hereinafter, “all word pairs vs. perceptuals”) within the anatomical masks in the left IFG and posterior left MTG/STG, individually for every participant, regardless of significance. This decision was made because having selected only significant voxels would have resulted in participants having a different number of voxels for the functional contrast, and that would have affected the power of that measure across participants. We decided to use the perceptual control (Fig. 1F) as compared to the baseline control (Fig. 1E) because it is more similar to the rhyming judgment task in terms of the cognitive processes needed to solve the task.

We decided to use individually defined functional ROIs following Fedorenko and Kanwisher (2009)’s paper, in which they claim that traditional group-based methods are bound to overestimate overlap and underestimate specificity, not being appropriate to detect functional specificity. The authors proposed that defining regions of interest functionally in individual subjects can help to provide higher sensitivity, the ability to detect an effect, and higher selectivity, the ability to distinguish between conditions (Fedorenko et al., 2010; Nieto-Castañón and Federenko, 2012).

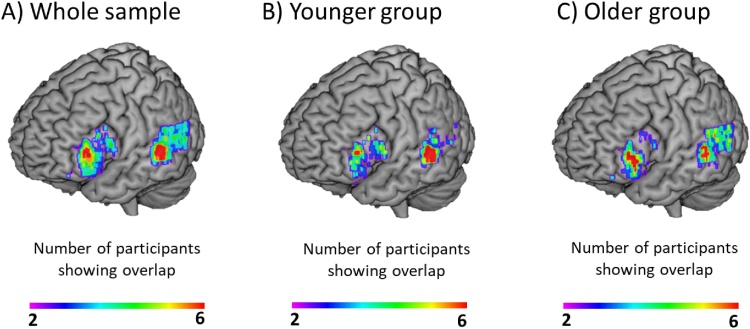
Table A1 in the Appendix shows more specific information about the functional ROIs selected for each participant, including MNI coordinates and t values of the peak activation and the percentage of voxels showing activation in left MTG vs. left STG, as well as the percentage of voxels showing activation in the three parts of the left IFG (i.e. Opercularis, Triangularis and Orbitalis). Fig. 2 shows cluster overlap among participants in these two ROIs for (A) the whole sample and separately for (B) younger and (C) older children. Parameter estimates (or β weights) were then extracted from these ROIs at the individual level using MarsBar and submitted for statistical testing in SPSS 22 (IBM, SPSS Statistics, IBM Corporation, New York, USA).

Fig. 2.

Brain activation overlap among participants in regions of interest. Voxel overlap within the left IFG and the left MTG/STG anatomical masks, after selecting the 100 voxels showing maximal activation for all word pairs vs. perceptuals for every single participant for (A) the whole sample (n = 50), (B) for the younger group (n = 25), and (C) for the older group (n = 25). For the whole sample, color bar shows the number of participants showing overlap, from 2 participants, shown in purple/blue colors to 10 participants shown in yellow/red colors. For the two age groups, the extremes of the color bar represent 2 and 6 participants.

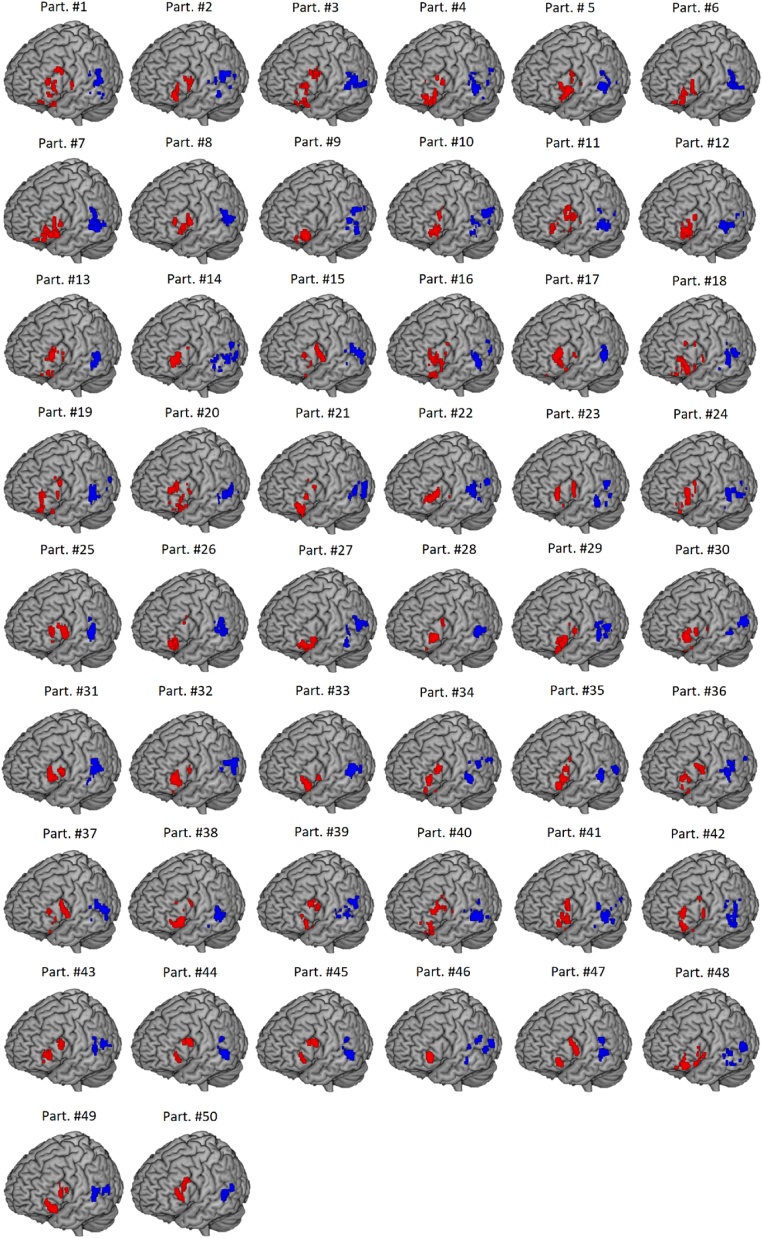
As shown in Table A1 and in Fig. 2, the majority of participants showed greater activation in left MTG than in left STG, and the majority showed greater activation in Triangularis as compared to Opercularis or Orbitalis. Fig. A1 in the Appendix shows individually selected clusters within temporal and frontal cortex for every single participant (n = 50), for visualization purposes.

Fig. A1.

One hundred voxels selection for every participant. One hundred voxels showing maximal activation for the contrast “all word pairs vs. perceptuals” within the anatomical left inferior frontal gyrus (IFG) in red, and within the anatomical posterior left middle and superior temporal gyri (MTG/STG) in blue, for every participant of the sample (n = 50).

Table A2 in the Appendix shows a correlation matrix between brain activation during phonological processing, math performance at each time point and math gains.

2.7.4. Multiple regression analyses

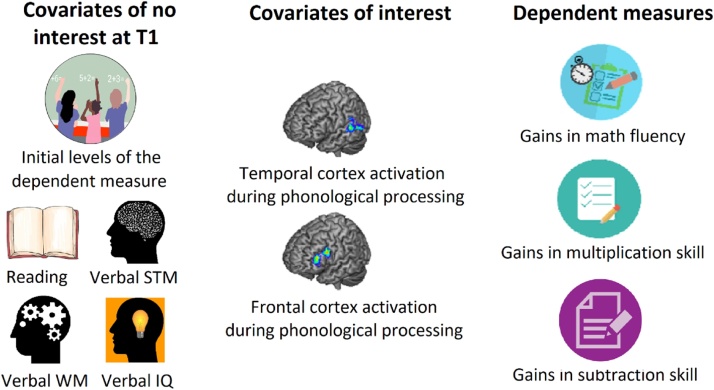
As illustrated in Fig. 3, six hierarchical regression analyses were carried out in SPSS in order to study whether it is temporal or frontal cortex activation during phonological processing that predicts longitudinal gains in math fluency, multiplication skill, and subtraction skill, separately for younger (Fig. 3A) and older children (Fig. 3B)6. In the first step of the hierarchical regression analysis we entered all the control variables, that is, reading skill, verbal short-term memory, verbal working memory, and verbal IQ at T1. Given that we aimed to study the role of temporo-frontal cortex during phonological processing in predicting gains in math regardless of the starting point, and given that younger and older children had different raw scores at T1 in all math measures, we included initial levels of the dependent measure (i.e. raw scores at T1) as another control variable7. In order to study the predictive value of our brain measures over and above these cognitive skills, temporal and frontal cortex activation during phonological processing were entered in a second step in the regressions. The same analysis was repeated three times with gains in math fluency, multiplication skill, and subtraction skills as dependent measures and separately for younger and older children.

Fig. 3.

Illustration of the six regression analyses. Illustration of the predictors of interest, predictors of no interest, and dependent variables included in the regression analyses carried out to study whether it is temporal or frontal cortex activation during phonological processing that predicts longitudinal gains in math fluency, multiplication skill, or subtraction skill. These three regression analyses were carried out separately for younger and older children.

Note. Covariates of no interest at T1: Initial levels of the dependent measure (i.e. raw scores at time 1); Reading skill in standard scores; Verbal STM: Verbal short-term memory in standard scores; Verbal WM: Verbal working memory in standard scores; Verbal IQ: verbal intelligence in standard scores; Dependent measures: difference in raw scores between time 2 and time 1 for each of the math measures.

3. Results

3.1. Behavioral results

3.1.1. Rhyming judgment task

All the participants included in the analysis had an accuracy above 50 % on the perceptual control condition and on the average of the easy/non-conflicting conditions (i.e. O + P + and O-P) of the rhyming judgment task. Four participants were excluded due to not responding to one of the conditions of the rhyming judgment task (i.e. O + P-) and six were excluded for not responding to the perceptual control condition.

Participants were more accurate solving non-conflicting trials (mean = 89.2 %, SD = 10.5) as compared to conflicting (mean = 72.1 %, SD = 16.6) ones (t(49) = 8.87, p <  .001). Participants were faster solving non-conflicting trials (mean = 1206, SD = 259) as compared to conflicting (mean = 1293, SD = 281) ones (t(49) = −4.38, p <  .001).

Participants were more accurate to solve those pairs of words that rhymed (mean = 89 %, SD = 10.3) as compared to non-rhyming (mean = 72.3 %, SD = 18.4) pairs (t(49) = 6.79, p <  .001). Participants were also faster to solve rhyming (mean = 1170, SD = 262) pairs as compared to non-rhyming (mean = 1329, SD = 283) ones (t(49) = −6.96, p <  .001).

We explored possible age differences by running an Age group x Conflict and an Age group x Rhyming repeated measures ANOVAs. There was no Age group x Conflict significant interaction either for accuracy (F(1,48) = .44, p =  .51, partial η² = .009) or for response times (F(1,48) = 1.36, p =  .25, partial η² = .03). There was no Age group x Rhyming significant interaction either for accuracy (F(1,48) = .18, p =  .67, partial η² = .004) or for response times (F(1,48) = 3.18, p =  .08, partial η² = .06). Age groups did not differ in overall accuracy (t(48) = −1.70, p =  .10) or overall response times (t(48) = 1.56, p =  .13) in the rhyming judgment task.

3.1.2. Measures of math gains by age groups

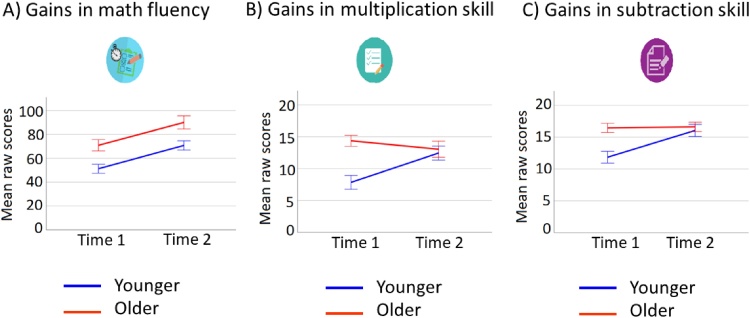
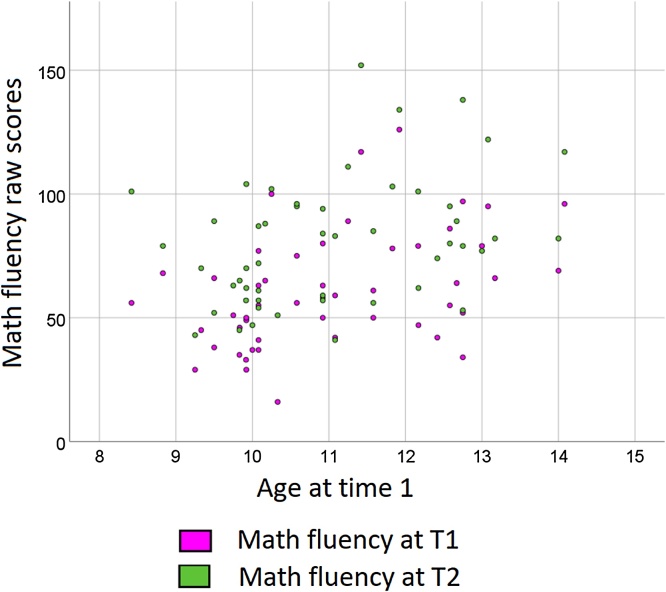
We studied the changes in math fluency over time for children depending on their age by running an Age group (younger, older) x Time (T1, T2) repeated measures ANOVA. We found a significant main effect of Time (F(1,48) = 94.25, p <  .001, partial η² = .66), showing that both younger (t(24) = 6.24, p <  .001) and older (t(24) = 7.77, p <  .001) children improved over time. Younger and older children differed at T1 (t(24) = 3.27, p =  .002) and at T2 (t(24) = 2.86, p =  .006). More detailed information about the groups’ math fluency raw scores at each time point is provided in Table 2. Fig. 4A shows the changes over time in math fluency raw scores for younger and older children.

Table 2.

Whole sample and age groups’ performance on math tests. Mean of raw scores (standard deviation in parenthesis) for the math fluency, multiplication skill and subtraction skill tests at each time point, and gains (T2-T1), for the whole sample (n = 50) and for the groups of younger (n = 25) and older (n = 25) children.

	Whole sample	Younger	Older
Math fluency raw T1	61 (2.3)	51.2 (18.5)	70.8 (23.7)*
Math fluency raw T2	80.4 (25.5)	70.8 (19.4)	90.0 (27.6)*
Gains math fluency (T2-T1)	19.4 (14.0)	19.6 (15.7)	19.2 (12.4)
Multiplication raw T1	11.1 (5.9)	7.8 (5.4)	14.4 (4.3)*
Multiplication raw T2	12.7 (5.9)	12.4 (5.8)	13.0 (6.3)
Multiplication gains (T2-T1)	1.6 (6.1)	4.6 (5.7)	−1.4 (5.1)*
Subtraction raw T1	14.1 (4.7)	11.8 (4.6)	16.4 (3.6)*
Subtraction raw T2	16.3 (4.2)	16.0 (4.7)	16.6 (3.6)
Subtraction gains (T2-T1)	2.2 (3.8)	4.2 (3.5)	0.2 (2.9)*

Note. T1: Time 1; T2: Time 2. (*) Indicate significant differences between younger and older groups at p <  .005.

Fig. 4.

Changes in math skill over time by age groups. Graph showing changes in (A) math fluency, (B) multiplication skill, and (C) subtraction skill raw scores from time 1 to time 2 for younger (n = 25; in blue) and older (n = 25; in red) children. Error bar shows standard error of the mean.

We also ran the Age group x Time repeated measures ANOVA for multiplication skill raw scores. This analysis showed a significant Age group x Time interaction (F(1,48) = 15.18, p <  .001, partial η² = .24). Follow-up tests showed that this interaction was due to younger and older children differing at T1 (t(48) = 4.11, p <  .001), but not at T2 (t(48) = .36, p =  .72), and due to younger children showing significant changes over time (t(24) = 4.07, p <  .001), while older children did not (t(24) = 1.30, p =  .78)⁸. More detailed information about the groups’ multiplication skill raw scores at each time point is provided in Table 2. Fig. 4B shows the changes over time in multiplication skill raw scores for younger and older children.

Finally, we ran the Age group x Time repeated measures ANOVA for subtraction skill raw scores. This analysis showed a significant Age group x Time interaction (F(1,48) = 19.69, p <  .001, partial η² = .29). Follow-up tests showed that this interaction was due to younger and older children differing at T1 (t(48) = 3.95, p <  .001), but not at T2 (t(48) = .47, p =  .64), and due to younger children showing significant changes over time (t(24) = 5.96, p <  .001) as compared to older children, who showed no significant change (t(24) = .28, p =  .78)8. More detailed information about the groups’ subtraction skill raw scores at each time point is provided in Table 2. Fig. 4C shows the changes over time in subtraction skill raw scores for younger and older children.

3.2. fMRI results

3.2.1. Temporal and frontal cortex activation during phonological processing predicted gains in math fluency, but only for younger children

As shown in Table 3, the regression analyses showed that, when temporal and frontal cortex activation during phonological processing were entered as predictors in the model, both of them significantly predicted gains in math fluency9. Fig. A2 in the Appendix shows the large variability in math fluency raw scores both at T1 and at T2 for participants of this age group.

Table 3.

Regression results predicting math fluency gains for younger and older children. Results of the regression analyses performed to study the role of temporal and frontal cortex activation during phonological processing (entered in step 2) in predicting gains in math fluency, over and above the cognitive skills entered in step 1.

Predicting gains in math fluency
Younger children
Step	Predictor	Stand. β	t	p	R2	ΔR2	F	ΔF	p ΔF
1	Math fluency at T1	-.369	−1.555	.137	.179	.179	.786	.786	.573
	Reading at T1	-.275	-.794	.438
	Verbal STM at T1	.259	.933	.363
	Verbal WM at T1	.009	.030	.976
	Verbal IQ at T1	.133	.350	.731
2	Math fluency at T1	-.322	−1.537	.144	.442	.263	1.811	3.771	.046
	Reading at T1	-.154	-.477	.640
	Verbal STM at T1	.438	1.688	.111
	Verbal WM at T1	.219	.824	.422
	Verbal IQ at T1	-.157	-.446	.662
	Frontal activation T1	-.692	−2.120	.050
	Temporal activation T1	.898	2.745	.014

Predicting gains in math fluency
Older children
Step	Predictor	Stand. β	t	p	R2	ΔR2	F	ΔF	ΔF
1	Math fluency at T1	.078	.373	.713	.277	.277	1.377	1.377	.279
	Reading at T1	.375	1.248	.228
	Verbal STM at T1	.222	.902	.379
	Verbal WM at T1	-.189	-.769	.452
	Verbal IQ at T1	.111	.391	.700
2	Math fluency at T1	.088	.416	.683	.380	.103	1.398	1.327	.293
	Reading at T1	.382	1.277	.220
	Verbal STM at T1	.251	1.036	.315
	Verbal WM at T1	-.254	-.927	.368
	Verbal IQ at T1	.018	.063	.951
	Frontal activation T1	-.286	-.994	.335
	Temporal activation T1	-.088	-.324	.750

Note. ΔR²: change in R². ΔF: Change in F. No multicollinearity was found in these analyses, with the VIF values ranging from 1.23 to 3.57 for the regression analysis with younger children and from 1.09 to 2.30 for the regression analysis with older children.

Fig. A2.

Distribution of math fluency scores at each time point for the whole sample. Scatterplot showing the wide distribution of raw scores in the math fluency test at time 1 (T1) and at time 2 (T2) for the whole sample (n = 50).

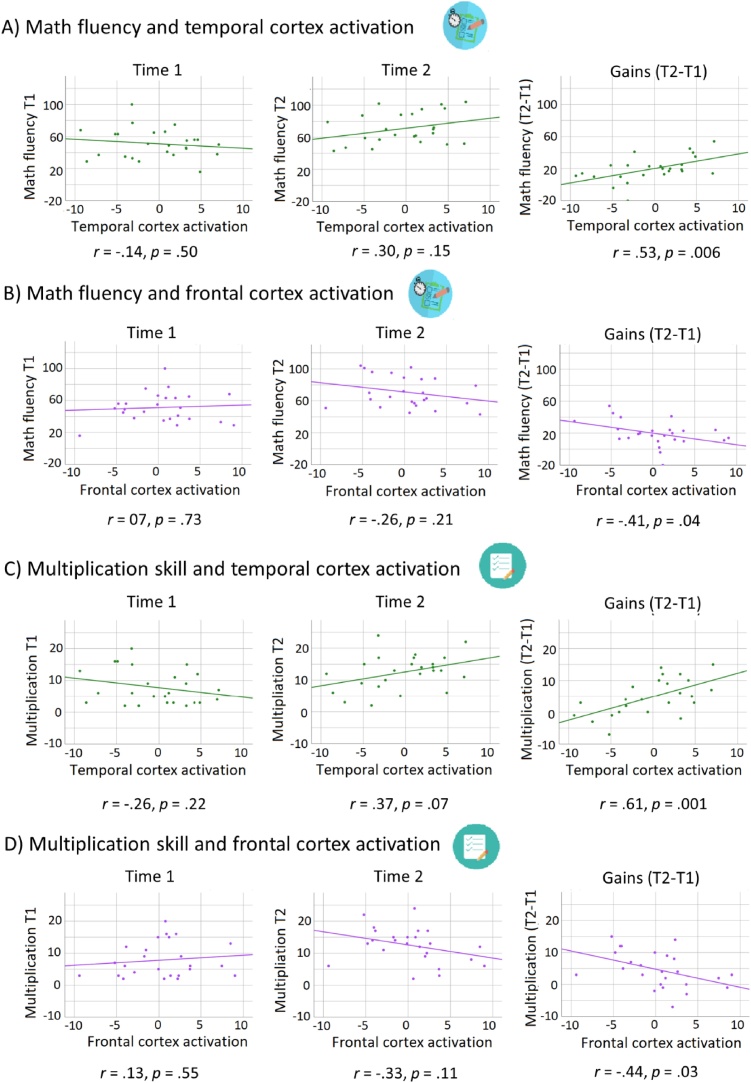
Scatterplots in Fig. 5 shows the association between math fluency at T1, at T2, and for gains (T2-T1) and brain activation during phonological processing in (A) temporal and (B) frontal cortex, for younger children. This figure shows that greater engagement of temporal cortex (Fig. 5A) and less engagement of frontal cortex (Fig. 5B) were associated with greater gains in math fluency over time. While the correlation between math fluency and temporal cortex activation was not significant either at T1 (r = −.14, p =  .50) or at T2 (r = .30, p =  .15), the two correlations were significantly different (Z = −2.56, p =  .01), suggesting that these variables became more strongly and positively associated over time. All correlation differences were based on Steiger (1980)’s Z10 obtained using Cocor online tool (Diedenhofen and Musch, 2015).

Fig. 5.

Scatterplots showing the correlations of brain activation with math fluency and multiplication skill for the younger group. Scatterplots showing the correlation between temporal cortex activation (i.e. residuals after the effect of reading skill, verbal STM, verbal WM, verbal IQ, and frontal cortex activation have been accounted for) with (A) math fluency at time 1 (T1), at time 2 (T2) and for gains (T2-T1) and with (C) multiplication skill at time 1 (T1), at time 2 (T2) and for gains (T2-T1). Scatterplot showing the correlation between frontal cortex activation (i.e. residuals after the effect of reading skill, verbal STM, verbal WM, verbal IQ, and temporal cortex activation have been accounted for) with (B) math fluency at time 1 (T1), at time 2 (T2) and for gains (T2-T1) and with (D) multiplication skill at time 1 (T1), at time 2 (T2) and for gains (T2-T1).

Similarly, while the correlation between math fluency and frontal cortex activation was not significant either at T1 (r = .07, p =  .72) or at T2 (r = −.26, p =  .21), the two correlations were significantly different (Z = −2.95, p =  .003), suggesting that these variables became more strongly and negatively associated over time.

3.2.2. Temporal and frontal cortex activation during phonological processing predicted gains in multiplication skill, but only for younger children

As shown in Table 4, the regression analyses showed that, when temporal and frontal cortex activation during phonological processing were entered as predictors in the model and after the effect of the covariates of no interest has been accounted for, both temporal and frontal cortex activation during phonological processing significantly predicted gains in multiplication skill11. This effect, however, was specific to younger children, with no significant predictive effect for older children.

Table 4.

Regression results predicting gains in multiplication skill for younger and older children. Results of the regression analyses performed to study the role of temporal and frontal cortex activation during phonological processing (entered in step 2) in predicting gains in multiplication skill, over and above the cognitive skills entered in step 1.

Predicting gains in multiplication skill
Younger children
Step	Predictor	Stand. β	t	p	R2	ΔR2	F	ΔF	p ΔF
1	Multiplication skill at T1	-.601	−2.993	.008	.458	.458	3.042	3.042	.037
	Reading at T1	.300	1.061	.303
	Verbal STM at T1	-.301	−1.273	.219
	Verbal WM at T1	-.147	-.639	.531
	Verbal IQ at T1	.424	1.359	.191
2	Multiplication skill at T1	--.466	−2.748	.014	.687	.229	5.008	5.838	.012
	Reading at T1	.445	1.838	.085
	Verbal STM at T1	-.174	-.878	.393
	Verbal WM at T1	.057	.292	.774
	Verbal IQ at T1	.106	.391	.701
	Frontal activation T1	-.653	−2.661	.017
	Temporal activation T1	.858	3.417	.004

Predicting gains in multiplication skill
Older children
Step	Predictor	Stand. β	t	p	R2	ΔR2	F	ΔF	ΔF
1	Multiplication skill at T1	-.281	−1.240	.231	.247	.247	1.182	1.182	.356
	Reading at T1	.496	1.644	.118
	Verbal STM at T1	.107	.422	.678
	Verbal WM at T1	-.214	-.858	.402
	Verbal IQ at T1	-.008	-.026	.980
2	Multiplication skill at T1	-.345	−1.407	.179	.340	.093	1.176	1.122	.350
	Reading at T1	.530	1.743	.101
	Verbal STM at T1	.118	.463	.649
	Verbal WM at T1	-.335	−1.181	.255
	Verbal IQ at T1	-.101	-.332	.744
	Frontal activation T1	-.377	−1.204	.246
	Temporal activation T1	.056	.191	.851

Note. ΔR²: change in R². ΔF: Change in F. No multicollinearity was found in these analyses, with the VIF value ranging from 1.34 to 3.74 for the regression analysis with younger children and from 1.22 to 2.37 for the regression analysis with older children.

Scatterplots in Fig. 5 shows the association between multiplication skill at T1, at T2, and for gains (T2-T1) and brain activation during phonological processing in (C) temporal and (D) frontal cortex, for younger children. This figure shows that greater engagement of temporal cortex (Fig. 5C) and less engagement of frontal cortex (Fig. 5D) were associated with greater gains in multiplication skill over time. While the correlation between multiplication skill and temporal cortex activation at T1 was not significant (r = −.26, p =  .22), the correlation at T2 was marginally significant (r = .37, p =  .07). The two correlations were significantly different (Z = 1.90, p =  .05), suggesting that these variables became more strongly and positively associated over time. All correlation differences were based on Steiger (1980)’ s Z12 obtained using Cocor online tool (Diedenhofen and Musch, 2015).

Similarly, while the correlation between multiplication skill and frontal cortex activation was not significant either at T1 (r = .13, p =  .55) or at T2 (r = −.33, p =  .11), the two correlations were significantly different (Z = 2.12, p =  .03), suggesting that these variables became more strongly and negatively associated over time.

3.2.3. Brain activation during phonological processing does not predict gains in subtraction skill, regardless of children’s age

As shown in Table 5, neither the temporal cortex nor the frontal cortex activation during phonological processing significantly predicted gains in subtraction skill, for either younger or older children.

Table 5.

Regression results predicting gains in subtraction skill for younger and older children. Results of the regression analyses performed to study the role of temporal and frontal cortex activation during phonological processing (entered in step 2) in predicting gains in subtraction skill 14, over and above the cognitive skills entered in step 1.

Predicting gains in subtractions skill
Younger children
Step	Predictor	Stand. β	t	p	R2	ΔR2	F	ΔF	p ΔF
1	Subtraction skill at T1	-.606	−2.577	.019	.34	.344	1.892	1.892	.146
	Reading at T1	.241	.783	.444
	Verbal STM at T1	-.182	-.713	.485
	Verbal WM at T1	-.072	-.288	.777
	Verbal IQ at T1	.466	1.349	.194
2	Subtraction skill at T1	-.523	−2.054	.057	.424	.079	1.681	1.101	.357
	Reading at T1	.135	.413	.685
	Verbal STM at T1	-.081	-.305	.764
	Verbal WM at T1	-.077	-.300	.768
	Verbal IQ at T1	.461	1.319	.206
	Frontal activation T1	.136	.386	.705
	Temporal activation T1	.189	. 564	.581

Predicting gains in subtractions skill
Older children
Step	Predictor	Stand. β	t	p	R2	ΔR2	F	ΔF	ΔF
1	Subtraction skill at T1	-.750	−3.018	.007	.379	.379	2.193	2.193	.100
	Reading at T1	.447	1.467	.160
	Verbal STM at T1	-.312	−1.362	.190
	Verbal WM at T1	-.135	-.582	.568
	Verbal IQ at T1	.310	1.156	.263
2	Subtraction skill at T1	-.755	−2.897	.011	.425	.047	1.692	.651	.535
	Reading at T1	.470	1.484	.157
	Verbal STM at T1	-.296	−1.261	.225
	Verbal WM at T1	-.240	-.894	.384
	Verbal IQ at T1	.233	.829	.420
	Frontal activation T1	-.293	−1.075	.298
	Temporal activation T1	.108	.411	.686

Note. ΔR²: change in R². ΔF: Change in F. No multicollinearity was found in these analyses, with the VIF value ranging from 1.52 to 3.27 for the regression analysis with younger children and from 1.52 to 2.68 for the regression analysis with older children.

4. Discussion

Given that single-digit arithmetic facts are considered to be stored in long-term memory as phonological codes (Dehaene et al., 2003), several studies have explored the role that phonological skills have in predicting longitudinal math gains. The current literature is not conclusive, however, with some longitudinal studies finding evidence supporting that phonological skills predict gains in math skill (e.g. Fuchs et al., 2005; Hecht et al., 2001), while others have not (e.g. Passolunghi et al., 2007, 2012). The objective of our study was to use fMRI to measure brain activation in temporal and frontal cortex during a phonological processing task, brain regions associated with the storage of (Booth et al., 2002, 2003, 2004; Prado et al., 2011, 2014) and access to (Andin et al., 2015; Bookheimer, 2002; Booth et al., 2003, 2004; Fedorenko et al., 2012; Poldrack et al., 1999; Pollack and Ashby, 2017; Prado et al., 2011, 2014; Rickard et al., 2000) phonological representations, respectively, and to use these brain measures to predict gains in different math tests. De Smedt et al. (2010) suggested that finding an association between phonological and arithmetic processing might depend on its time constraints and the amount of fact retrieval necessary. Therefore, we included a time-limited test of math fluency, which encouraged the use of retrieval of solutions from memory, an untimed test of multiplication skill, which is considered to tap into retrieval, and an untimed test of subtraction skill, which is considered to rely on quantity representations.

Both behavioral (Barrouillet et al., 2008; De Smedt, 2016; Jordan et al., 2003) and fMRI (e.g. De Smedt et al., 2011; Suárez-Pellicioni et al., 2018) studies have shown that there is large intersubject variability in the mastery of arithmetic facts and its fluency development in typically developing children, a variability that extends into adulthood (LeFevre et al., 1996a; Lefevre et al., 1996b). Given this variability, studying 10- to 14-year-old children provided an interesting time window to investigate the role of phonology in predicting the development of fluency with basic arithmetic facts (see Fig. A2 in the Appendix). Studying this age range also allowed us to explore the role of phonology in the acquisition of more advanced math content that differed in its demands on retrieval, as measured with untimed tests of multiplication and subtraction skill. Based on Fuchs et al. (2005)’s longitudinal study showing that their measure of phonological skill, including both phonological awareness (i.e. quality of phonological representations) and rapid naming (i.e. access to representations), predicted gains in math fluency, we hypothesized that both temporal and frontal cortex activation during phonological processing would play a significant role in predicting gains in math fluency. While Fuchs and colleagues did not disentangle whether phonological awareness or rate of access had a greater impact in predicting gains in math fluency, we studied the unique contribution of brain measures of the storage of and the access to phonological representations.

We found that greater activation of MTG/STG and reduced activation of IFG predicted greater math fluency gains. These results are interpreted as showing that greater reliance on phonological representations (i.e. greater MTG/STG) and a more automatic access to those representations (i.e. decreased IFG) are equally important in predicting gains in math fluency. This could be due to phonological representations in temporal cortex being of better quality, allowing a less effortful access to them. This goes in line with research showing that, with more years of math instruction, children show greater activation in temporal and less activation in frontal cortex when solving single-digit multiplications inside the scanner, suggesting that children built more robust representation of arithmetic facts so that the retrieval of those facts becomes more efficient over development (Prado et al., 2014). Our finding is also consistent with a recent meta-analysis showing the important role of access to phonological representations in math achievement, especially for math fluency (Koponen et al., 2017). Importantly, while both younger and older children showed behavioral improvements in math fluency, temporo-frontal activation during phonology only predicted gains in fluency for younger children13, suggesting a time-limitted role of phonology in explaining math fluency development. Our results extends to 5th graders, Fuchs et al. (2005)’s findings with 1st graders, showing the importance of phonological awareness and rate of access in predicting math fluency gains.

Our study showed that temporal and frontal cortex activation during phonological processing not only explained gains in a math fluency test, but also predicted gains in an untimed test of multiplication skill with a wide range of difficulty, including more challenging multi-digit problems. As with math fluency, we found that greater temporal cortex and reduced frontal cortex activation predicted greater gains, suggesting that more robust phonological representations enabled efficient access, allowing for greater improvement. This finding is partially consistent with Hecht et al. (2001) showing that phonological awareness was the only predictor explaining gains in an untimed test including a wide range of problem difficulty levels for 3rd to 5th graders. While Hecht found their measure of access to phonology to have a time-limited effect, predicting math gains only up to 3rd grade, our study extends the importance of this phonological processing in predicting multiplication gains in children up to 5^th grade. Our results suggests that, even when the complex nature of the test may have involved other operations beyond multiplication (e.g. solving 825 × 74 requires the addition of intermediate results), the recruitment of temporo-frontal cortex during phonological processing is an important determinant of gains, as long as the operation being solved requires the retrieval of solutions stored in long term memory. In this case, the predictive role of temporo-frontal activation during phonological processing was limited to the younger group. Although this suggests a time-limitted effect of phonology in predicting multiplication skill, like with math fluency, it might also be due to the lack of variability in multiplication skill for the older group. It is important to note that we did not find brain activation during phonological processing to be concurrently associated with math fluency or multiplication skill at time 1 or time 2, as we only showed prediction of gains over time (see Fig. 5). This could be seen as contradictory with the Berteletti et al. (2014) finding that higher phonological awareness was concurrently associated with greater activation when solving small multiplication problems in verbal areas of the left temporal cortex. These differences likely result from the nature of the phonological and math measures. Berteletti et al. (2014) found the concurrent phonology-math association using a multiplication task solved inside the scanner and a measure of phonological skill administered outside the scanner. In our study, we did the opposite, using a phonological processing task inside the scanner and a standardized test of math achievement outside the scanner. As for the math measures, Berteletti asked participants to solve multiplication problems with operands smaller or equal 5, whereas we used more demanding math tasks asking children to solve multiplication problems within a 3-minute time limit with a wide range of complexity. For the phonological measures, Berteletti used the Blending words subtest from the CTOPP, whereas we used a rhyming judgement task. In the Blending words test, different sounds are presented in an untimed auditory format to be blended into words. In the rhyming judgement task, children were presented with words visually and had to convert orthographic representations to phonological representations in order to solve the task within about 3–4 s. Future studies should use different math and phonological measures to systematically investigate brain-behavior correlations.

Given that subtraction problem solving relies on semantic representations of quantity (Dehaene et al., 2003; Arsalidou and Taylor, 2011) and engages parietal areas both in adults (Prado et al., 2011) and in children (Prado et al., 2014), we did not expect brain activation during phonological processing to predict gains in subtraction skill. Our results confirmed our predictions by showing that temporo-frontal activation during phonological processing did not predict gains in subtraction skill, regardless of children’s age. These results are consistent with previous studies showing that phonological skills did not predict performance on subtraction problems (De Smedt and Boets, 2010), on problems typically solved by numerical procedures (De Smedt et al., 2010), on a standardized and untimed measure of calculation (De Smedt et al., 2010), or on gains in several types of calculation tests (Fuchs et al., 2005). In contrast, our findings support the link between phonological skills and math tasks that require the retrieval of phonological codes from long-term memory (e.g. De Smedt et al., 2010; Simmons and Singleton, 2008).

Our findings highlight the importance of studying the role of domain-general cognitive abilities, such as phonological processing, in predicting gains in math skill. Given our experimental design, we could not effectively study the role that a brain measure of phonological memory would have in predicting math gains. Some studies have shown that phonological memory has a time-limited influence on math development, explaining math performance in children younger than the ones we studied (i.e. up to 3rd grade; Hecht et al., 2001) and others have shown that when phonological awareness and other cognitive skills are controlled for, phonological memory does not predict unique variance of gains in math skill (Fuchs et al., 2005, 2006). However, given the numerous studies suggesting that phonological memory is important for math development (e.g. De Smedt et al., 2009; Geary et al., 2007; Passolunghi et al., 2007; Passolunghi and Lanfranchi, 2012), future longitudinal fMRI studies should investigate its role in explaining gains in math skill, particularly in younger children.

As compared to the large number of studies investigating the role of domain-general cognitive abilities in reading acquisition, research on the effect of those abilities in math development is sparse. Different phonological processes seem to play a different role in predicting reading development depending on the transparency of the language. In opaque languages, such as English, with an inconsistent spelling-sound correspondence, phonological awareness (i.e. quality of representations) seems to play a more important role than rapid naming (i.e. access) in predicting reading development (Torgesen et al., 1997). In transparent languages, on the other hand, with consistency between spelling and sound, reading development is better predicted by rapid naming measures than by phonological awareness ones. This finding has been shown for transparent languages such as German (Landerl and Wimmer, 2008), Dutch (de Jong, and van der Leij, 1999), or Italian (Di Filippo et al., 2005). Researchers have suggested that it is possible that the different phonological processes may also play a different role in predicting gains in math depending on the transparency of language (De Smedt, 2018). It might be the case that we found that temporal cortex activation during phonological processing predicted gains in certain math skills because we tested native English-speaking children, but that we would have found no significant effect of temporal cortex activation during phonological processing had we studied children speaking more transparent languages.

Our longitudinal study, the first one to use fMRI brain activations during phonological processing as predictors of math fluency gains in children, provides evidence of the directionality of the effects suggesting that temporal and frontal cortex activation during phonological processing drives gains in retrieval-based math skills in younger children. Our study also provides evidence for the role of phonological processing in gains in more advanced math content that goes beyond basic arithmetic, but only for operations that require the retrieval of solutions from long-term memory and not for operations that involve quantity representations.

In terms of future research lines, it would be interesting to address the role that brain activation during phonological processing has in counting, a more basic math skill that also requires the storage of phonological codes of numbers in long-term memory (Geary, 1993). Krajewski and Schneider (2009) suggested that phonological skills are foundational for counting because they facilitate the isolation of single number words (i.e. “one”, “two”, “three”) from the speech stream (i.e. “onetwothree”). While phonological skill seems to impact counting (Koponen et al., 2007), some have argued that it does not directly affect later math skills, as subsequent differences in math skills appear to be explained by earlier differences in counting ability (Passolunghi et al., 2007; Krajewski and Schneider, 2009). Given that children with poor phonological skills are less efficient counters (Ackerman et al., 1990), they have fewer opportunities to associate problems with solutions, resulting in less efficient arithmetic fact retrieval (Jordan et al., 2010). While this explanation seems reasonable for single-digit addition problems, for which there is a clear transition from counting to retrieval, it is not likely for multiplication, as multiplication facts are learned by rote from the very beginning. Our finding on gains in math fluency, which included addition problems, could in part be explained by initial differences in counting skill, but the effect of initial counting skills on gains in multiplication skill is less likely. Because we did not measure counting skill, this interpretation remains speculative and future studies should be carried out to clarify the role of counting skill as a mediator between phonology and arithmetic skill.

Our neuroimaging results add to previous behavioral evidence showing the importance of phonological processing in predicting math gains (Hecht et al., 2001; Fuchs et al., 2005), regardless of initial performance levels and after accounting for the effect of other potential confounds. While previous evidence has claimed that math fluency is a basic building block on which more advanced math is built (e.g. Price et al., 2013), our study supports the idea that phonological processing may act as a crucial skill for math skills that require the storage and retrieval of arithmetic facts in verbal form. Overall, our findings highlight that the development of math skill depends not only on domain-specific cognitive abilities but on domain-general ones.

Declaration of Competing Interest

None.

Appendix A

Table A1.

ROI information for each participant. Peak coordinates (MNI) for the functional ROIs in the left IFG and left MTG/STG and t value of peak activation for all participants (n = 50). Corresponding age group: younger/older based on median-split. Percentage of voxels showing activation in left IFG Opercularis (OP), Triangularis (TR) and Orbitalis (OR) and in left MTG and STG.

Part	Age	Peak in IFG				% voxels in IFG			Peak in MTG/STG				% in MTG/STG
		X	Y	Z	t	Op	Tr	Or	X	Y	Z	t	STG	MTG
1	Older	−62	5	14	2.45	12	57	31	−60	−37	10	2.77	53	47
2	Young	−44	35	−6	4.89	20	50	30	−56	−39	18	2.61	73	27
3	Young	−38	27	−22	2.62	12	52	36	−44	−51	−2	2.54	14	86
4	Older	−34	33	−10	2.63	13	26	61	−66	−29	2	3.05	25	75
5	Young	−56	21	6	3.56	16	78	6	−64	−31	6	4.04	30	70
6	Young	−36	33	−14	3.39	0	67	33	−48	−43	2	3.31	31	69
7	Older	−44	31	−6	5.76	8	27	65	−68	−37	2	8.05	0	100
8	Older	−56	25	6	4.52	49	47	4	−48	−57	6	6.34	31	69
9	Older	−16	15	−22	2.99	0	16	84	−66	−45	−6	2.36	13	87
10	Older	−44	19	22	4.87	5	80	15	−64	−49	18	4.31	40	60
11	Older	−52	11	18	3.03	41	53	6	−60	−35	2	3.82	7	93
12	Younger	−46	29	−2	3.84	2	73	25	−56	−27	2	3.56	22	78
13	Younger	−52	33	14	2.97	6	76	18	−48	−43	2	2.88	0	100
14	Older	−42	37	6	5.99	1	99	0	−66	−45	2	3.66	1	99
15	Younger	−60	17	18	3.83	62	34	4	−56	−57	6	4.95	19	81
16	Older	−48	23	14	5.11	0	84	16	−48	−33	−18	2.51	14	86
17	Younger	−54	35	6	3.68	4	70	26	−64	−31	6	3.38	11	89
18	Older	−52	33	18	4.38	6	89	5	−48	−45	2	3.99	12	88
19	Younger	−54	33	−6	2.84	3	62	35	−64	−43	14	2.93	35	65
20	Older	−44	17	10	2.20	16	51	33	−60	−33	6	5.05	30	70
21	Older	−36	35	14	2.16	5	64	31	−64	−37	2	3.71	0	100
22	Older	−28	31	−14	3.34	4	23	73	−58	−65	2	3.64	5	95
23	Older	−54	27	10	2.81	0	100	0	−58	−37	6	2.50	44	56
24	Older	−46	33	10	5.48	31	68	1	−64	−41	22	3.93	34	66
25	Younger	−48	31	14	1.92	8	77	15	−50	−37	6	2.05	26	74
26	Younger	−60	15	14	5.32	50	48	2	−64	−31	6	5.18	48	52
27	Younger	−52	39	−2	3.04	1	24	75	−46	−47	6	3.01	47	53
28	Older	−54	21	−2	5.71	0	23	77	−66	−27	−10	5.46	2	98
29	Older	−50	29	2	4.40	15	84	1	−54	−43	6	4.08	1	99
30	Younger	−48	21	−2	2.60	11	29	60	−66	−27	6	3.61	50	50
31	Younger	−54	39	6	3.97	2	93	5	−60	−61	14	5.14	4	96
32	Younger	−48	11	10	3.95	46	54	0	−48	−41	2	4.44	36	64
33	Older	−54	33	14	3.61	12	84	4	−58	−61	14	2.65	24	76
34	Older	−48	27	−10	5.60	9	30	61	−62	−43	10	6.98	33	67
35	Younger	−52	39	2	3.11	28	54	18	−56	−67	22	2.20	29	71
36	Younger	−58	23	14	5.76	4	30	66	−62	−55	10	4.87	46	54
37	Older	−40	25	−10	4.41	0	58	42	−60	−61	10	4.28	10	90
38	Younger	−42	25	2	4.32	51	40	9	−64	−27	10	3.45	63	37
39	Younger	−46	21	−6	3.04	2	38	60	−46	−41	6	3.51	5	95
40	Older	−46	19	22	6.10	23	56	21	−58	−37	2	2.91	55	45
41	Younger	−22	17	−26	0.71	3	46	51	−70	−33	2	2.28	13	87
42	Older	−50	23	26	2.88	13	76	11	−70	−33	2	4.43	23	77
43	Younger	−30	35	−6	2.57	16	36	48	−70	−35	−2	2.46	26	74
44	Younger	−40	39	14	3.71	3	95	2	−58	−37	−10	2.19	16	84
45	Older	−46	13	18	2.89	43	55	2	−64	−47	18	2.99	47	53
46	Younger	−44	11	22	3.81	43	57	0	−64	−39	2	4.40	21	79
47	Older	−54	39	2	7.59	0	100	0	−62	−39	22	3.67	27	73
48	Younger	−38	17	18	4.32	17	83	0	−56	−41	6	4.01	4	96
49	Younger	−40	31	−6	6.06	47	23	30	−50	−37	2	5.55	32	68
50	Older	−56	11	2	6.64	9	18	73	−66	−51	14	6.37	20	80

Table A2.

Correlation matrix for younger and older children. Correlation matrix showing correlations between math fluency, multiplication skill, and subtraction skill raw scores at each time point and gains over time (T2-T1) as well as temporal and frontal cortex activation during phonological processing after accounting for the effect of control variables, separately for younger and older children.

Younger children
	2	3	4	5	6	7	8	9	10	11
1.Temporal activation a	-.82**	-.14	.30	.53**	-.26	.37	.60**	.08	.12	.05
2.Frontal activation b	–	.07	-.26	-.41*	.13	-.33	-.44*	-.21	-.05	.20
3.Math fluency T1	–	–	.66**	-.37	.77**	.58**	-.18	.74**	.65**	-.11
4.Math fluency T2	–	–	–	.46*	.37	.55**	.18	.59**	.61**	.05
5.Gains math fluency	–	–	–	–	−45*	-.002	.42*	-.15	-.006	.191
6.Multiplication skill T1	–	–	–	–	–	.46*	-.51**	.78**	.57**	-.26
7.Multiplication skill T2	–	–	–	–	–	–	.53**	.59**	.77**	.27
8.Gains multiplication	–	–	–	–	–	–	–	.18	.21	.51**
9.Subtraction skill T1	–	–	–	–	–	–	–	–	.71**	-.35
10.Subtraction skill T2	–	–	–	–	–	–	–	–	–	.41*
11.Gains subtraction	–	–	–	–	–	–	–	–	–	–
Older children
	2	3	4	5	6	7	8	9	10	11
1.Temporal activation a	-.63**	.15	.11	-.04	.33	.16	-.08	.16	.06	-.13
2.Frontal activation b	–	-.20	-.25	-.17	-.33	-.39	-.20	-.14	-.15	-.02
3.Math fluency T1	–	–	.90**	.09	.48*	.51**	.23	.48*	.14	-.42*
4.Math fluency T2	–	–	–	.52*	.55**	.64**	.32	.51**	.35	-.21
5.Gains math fluency	–	–	–	–	.32	.45*	.29	.22	.50*	.35
6.Multiplication skill T1	–	–	–	–	–	.60**	-.11	.53**	.53**	.009
7.Multiplication skill T2	–	–	–	–	–	–	.73**	.57**	.74**	.22
8.Gains multiplication	–	–	–	–	–	–	–	.25	.46*	.27
9.Subtraction skill T1	–	–	–	–	–	–	–	–	.68**	-.39
10.Subtraction skill T2	–	–	–	–	–	–	–	–	–	.41*
11.Gains subtraction	–	–	–	–	–	–	–	–	–	–

Note. ^(*)p ≤  .05; ^(**)p ≤ .01; ^a Brain activation after accounting for the covariates of no interest: reading skill, verbal short-term memory, verbal working memory, verbal IQ and brain activation in frontal cortex. ^b Brain activation after accounting for the covariates of no interest: reading skill, verbal short-term memory, verbal working memory, verbal IQ and brain activation in temporal cortex.