Cellular Dialogues: Cell-Cell Communication through Diffusible Molecules Yields Dynamic Spatial Patterns

Summary

Cells form spatial patterns by coordinating their gene expressions. How a group of mesoscopic numbers (hundreds to thousands) of cells, without pre-existing morphogen gradients and spatial organization, self-organizes spatial patterns remains poorly understood. Of particular importance are dynamic spatial patterns such as spiral waves that perpetually move and transmit information. We developed an open-source software for simulating a field of cells that communicate by secreting any number of molecules. With this software and a theory, we identified all possible “cellular dialogues”—ways of communicating with two diffusing molecules—that yield diverse dynamic spatial patterns. These patterns emerge despite widely varying responses of cells to the molecules, gene-expression noise, spatial arrangements, and cell movements. A three-stage, “order-fluctuate-settle” process forms dynamic spatial patterns: cells form long-lived whirlpools of wavelets that, following erratic dynamics, settle into a dynamic spatial pattern. Our work helps in identifying gene-regulatory networks that underlie dynamic pattern formations.

Graphical Abstract

Highlights

• •Communicating cells can form spatial patterns without morphogen gradients
• •Disordered field of communicating cells forms dynamic patterns (e.g., spiral waves)
• •Simulations and theory found dynamic-pattern-forming cell-communication methods
• •Dynamic patterns form via a three-stage (“order-fluctuate-settle”) process

Dang et al. developed a software and a theoretical framework to discover and classify all moving spatial patterns (e.g., waves) that cells can form by secreting two diffusible molecules that control their gene expressions. They identified all gene regulations that the molecules can have for forming moving patterns, which self-organize through a three-stage, “order-fluctuate-settle” dynamic.

Introduction

Spatial patterns can form when multiple cells, without pre-existing morphogen gradients, communicate with each other to coordinate their gene expressions (Gregor et al., 2010, Lubensky et al., 2011, Sgro et al., 2015, Idema et al., 2013, Manukyan et al., 2017, Jörg et al., 2019). Understanding how cells collectively organize spatial patterns through cell-cell communication is crucial for understanding and engineering mammalian tissues (Javaherian et al., 2013). Many synthetic and natural mammalian tissues are monolayers of genetically identical cells (e.g., epithelial sheets) whose gene expression levels are initially uncorrelated but become more correlated over time during development, leading to specialized cell types within tissues. This process often involves cell-cell communication (Menéndez et al., 2010). There has been a rising interest in developing experimental methods for spatially arranging individual cells in a monolayer and then observing how such a heterogeneous tissue—composed of cells at differing locations having different gene expression levels—develops over time (Javaherian et al., 2014). Although there are quantitative models to explain such experiments, they are often tailored to specific tissues and signaling molecules. Thus, it is challenging to use them as a general framework that one can adapt to different gene circuits, signaling molecules, and cell types (Drasdo et al., 2007). Currently unknown is a comprehensive set of generally applicable, quantitative mechanisms by which organized spatial patterns can form in heterogeneous tissues made of mesoscopic numbers (hundreds to thousands) of cells without pre-existing morphogen gradients (Figure 1A, top).

Figure 1.

Computationally Screening Cellular Dialogues to Find Ones that Enable Dynamic Patterns to Form

(A) Pattern formation by cells versus chemicals. (Top) Mechanisms by which an initially disordered field of a mesoscopic number of cells (∼hundreds to thousands) (left panel) become more ordered through cell-cell communication (right panel) remain poorly understood, as is the method to analyze this complex self-organization dynamics. (Bottom) A field of chemicals or a continuum of cells (large number of tightly packed cells) initially having no pattern (left) can form a pattern (right) without pre-existing morphogens. This is usually modeled by reaction-diffusion equations and can be understood through the Turing mechanism.

(B) Static versus dynamic patterns. (Top) Static patterns do not change over time. (Bottom) In dynamic patterns, a structure changes over time without ever stopping (e.g., shown here is a traveling wave).

(C) Schematic of cellular dialogues. Brown (molecule-1) and green (molecule-2) circles are ligands that bind to their cognate receptors on the cell membrane. Ligand-bound receptors trigger intracellular signal transductions that either positively or negatively regulate the production and secretion of molecules-1 and 2 (molecule-1 can self-promote or self-repress its own secretion while also regulating the secretion of molecule-2, and vice versa). Bottom row shows graphic representation of cellular dialogues.

(D) Elements that we varied in simulations: cellular dialogues of all possible topologies, the values of the parameters for each cellular dialogue, and spatial arrangement of cells. Our study first begins with an infinite Hill coefficient (i.e., digital response to each of the two signaling molecules) and a regular lattice. After reporting the outcomes of these simulations, we report the result of relaxing these two constraints and well as other elements not depicted.

See also Figure S1.

To explain pattern formations, one often uses reaction-diffusion equations and Turing instability in which a uniformly spread field of chemicals develops minute fluctuations in its chemical concentrations at some locations that grow over time to yield spatial patterns (Figure 1A, bottom) (Turing, 1952). Although theoretical studies of Turing instability uncovered many insights into how continuous fields of chemicals or cells form patterns, the instability does not treat gene expressions of individual cells when there are biologically realistic, mesoscopic numbers of cells (Figure 1A, top). Furthermore, while many gene networks can use Turing instability to generate spatial patterns, they are not robust as their circuit parameters need to be finely tuned (Marcon et al., 2016, Scholes et al., 2019). In light of these difficulties, a promising route for explaining multicellular patterning would be to develop multiscale models that link intracellular signaling with cell-cell communication for mesoscopic numbers of cells. While researchers have developed such models for specific systems—examples include studies of how eyes form (Lubensky et al., 2011) and neurons differentiate (Jörg et al., 2019 —we currently lack a general framework for identifying widely applicable principles of pattern formation. Motivated by this shortcoming, we sought to build a generalized framework that uncovers relationships between properties of cellular communication—the various ways in which the cells secrete and sense signaling molecules—and gene expression patterns (spatial patterns) that emerge for mesoscopic populations of cells.

Here, we developed an open-source software that simulates spatial-patterning dynamics for a system of communicating cells. One can easily modify and expand our software with more ingredients and use it for both research and educational purposes. We also developed algorithms for analyzing these simulations. With the software and analysis algorithms, we sought to quantitatively reveal mechanisms by which mesoscopic numbers of cells can form spatial patterns. We focused on dynamic patterns—patterns that constantly change over time without ever stopping such as oscillations and spiral waves (Sgro et al., 2013)—instead of static patterns that remain still after forming (Figure 1B). Our computational search discovered all the ways in which cells can communicate with just two diffusing molecules to form dynamic patterns, including those that have been experimentally observed. We found that a few ways of communicating, which we refer to as “cellular dialogues,” can generate a large palette of complex, dynamic spatial patterns such as whirlpools of wavelets and traveling waves of various shapes and orientations. We devised an analytical (pen and paper) approach that recapitulates the simulations and used it to understand why only certain cellular dialogues can sustain dynamic spatial patterns. We found that cells form dynamic spatial patterns through a three-stage, “order-fluctuate-settle” process. Starting from a configuration in which there is no spatial correlation among cells' gene expression levels, cells rapidly become more spatially correlated over time, resulting in self-organized wavelets. This is followed by a prolonged transient phase in which the wavelets constantly and erratically form and annihilate each other. Finally, as the wavelets settle down, a dynamic spatial pattern such as a traveling wave emerges. We show that self-organized dynamic patterns can still form despite widely varying gene expression noise, cellular responses to the sensed molecules, spatial arrangements of cells, and diffusive (random) motions of cells. As a theoretical study, we focused on exploring how cells can form dynamic spatial patterns, rather than explaining any specific biological system. But our computational screen still uncovered cellular dialogues that are known to generate dynamic spatial patterns in specific multicellular systems. Our paper ends by suggesting how one can expand our work, including the open-source software, to identify as-yet-unknown cellular dialogues that produce known dynamic spatial patterns in multicellular systems.

Results

Computational Search for Cellular Dialogues that Enable Self-Organized Patterns

We built a visualization software that simulates all possible ways in which cells can communicate—which we call “cellular dialogues”—by secreting, sensing, and responding to two diffusing molecules (Figure 1C). Such cells, which simultaneously secrete and sense one or more signaling molecules, are ubiquitous in nature (Hart et al., 2014, Youk and Lim, 2014a, Youk and Lim, 2014b, Chen et al., 2015, Maire and Youk, 2015b). Our simulations combine reaction-diffusion equations—describing the concentrations of the molecules—and a cellular automaton—describing the cells' gene expression levels that are set by the concentrations of the two molecules. We represent a cellular dialogue as a network diagram that consists of two nodes (one for each molecule) joined by signed arrows, which can be positive (activating) or negative (repressing). A signed arrow denotes how the sensing of one molecule, represented by the node on which the arrow begins, increases (for a positive arrow) or decreases (for a negative arrow) the sensing cell's secretion rate of a molecule that is represented by the node on which the arrow ends (Figure 1C). We assume that both molecules diffuse on a faster timescale than the cells can respond—the two molecules “rapidly” diffuse and reach steady-state concentrations to which the cells then respond—as is the case in many multicellular systems (Heemskerk et al., 2019).

We first considered cells that digitally respond to each molecule: a cell secretes “molecule-i” at either a low rate (“OFF” state for molecule-i) or a high rate (“ON” state for molecule-i). If molecule-j activates (represses) molecule-i, then a cell becomes ON (OFF) for molecule-i if and only if it senses a concentration of molecule-j that is “above” a set threshold concentration. We first considered these digital cells for two reasons. First, experimental studies have shown that signal transduction pathways such as MAPK or other phospho-relay cascades, which are triggered by ligand-bound receptors and control gene expressions downstream—as in our digital cells (Figure 1C)—can have an effective Hill coefficient with a value of 4 or more (e.g., as high as 32 [Trunnell et al., 2011]). An effective Hill coefficient characterizes the “sharpness” of the cell's response to a ligand (Ferrell and Ha, 2014a, Ferrell and Ha, 2014b, Ferrell and Ha, 2014c, Plotnikov et al., 2011, Trunnell et al., 2011). Such high numbers are due to multiple molecular parts amplifying each other's effects in combination. A digital (ON/OFF) response models such high-valued Hill coefficients. The second reason is that a digital response simplifies the mathematics that describes the response, while retaining its main qualitative features, even when the actual Hill coefficient of the system being modeled is relatively low (Alon, 2006). Finally, the digital cells also have a reporter gene for each molecule, which we call genes “1” and “2,” which are also either ON or OFF to reflect the secretion state of its corresponding molecule (Figure 1C, brown and green boxes). In our simulations, we assigned a distinct color to each of the four states, which are (ON for gene-1, ON for gene-2), (ON, OFF), (OFF, ON), and (OFF, OFF).

We began each simulation by randomly assigning the four gene expression states (i.e., four colors) to each cell so that the gene expression levels were spatially uncorrelated. Thus, the field of cells initially did not exhibit any spatial organization. We quantitatively verified this with a “spatial index” metric, which is a weighed spatial autocorrelation function that is zero when cells are completely, spatially disorganized and increases toward one as the cells become more spatially organized (see STAR Methods and Figure S1). We then observed how each cell’s state (i.e., four colors) changed over time to determine whether a spatial pattern formed and, if so, what type of a pattern formed. For each cellular dialogue, we fixed the values of all parameters (e.g., threshold concentrations and secretion rates for each molecule), and then ran large numbers of simulations with different initial conditions (see STAR Methods). We screened a wide range of parameter values for every possible cellular dialogue (STAR Methods). We first performed such a computational search with immobile digital cells that were placed on a regularly spaced lattice. We will first describe these results in the next sections before explaining how these results change when we relax the constraints—by randomly displacing cells so that they no long form a regular lattice, having each cell continuously move, allowing the Hill coefficient to be any finite value (i.e., analogue instead of digital response), and including gene expression noise (Figure 1D).

Cellular Dialogues Enable Self-Organization of Wide Array of Dynamic Patterns

The computational search revealed a wide variety of dynamic patterns from never-ending traveling waves (Figure 2A and Video S1) to complex patterns consisting of wavelets that evolved over time in an erratic, complex manner (Figure 2B). All patterns self-organized from completely disorganized fields of cells by their ON/OFF-states becoming more spatially correlated over time (Figures 2A and 2B). The time taken to self-organize widely varied and depended on the type of pattern formed. For example, if we assume that a gene expression change such as an ON-cell becoming an OFF-cell takes 1 min—this is one time-step of a simulation and every cell synchronously changes their ON/OFF states—then horizontal waves could take nearly 6 h to form (Figure 2A) whereas the constantly changing, complex whirlpool of wavelets would not show any signs of settling into any pattern that cyclically repeats itself even after a week or longer (Figure 2B). Since the simulations are deterministic for now—we will later add gene expression noise—once a simulation reproduces a spatial configuration that it had before, the cell population has formed a dynamic pattern that periodically repeats itself forever.

Figure 2.

Examples of Self-Organized Dynamic Patterns Found through Computational Screening

In all the figures shown here, a cell (drawn as a circle) can have four colors. Each color represents a distinct gene expression state, (gene 1 = ON/OFF, gene 2 = ON/OFF): black means (ON, ON), red means (ON, OFF), blue means (OFF, ON), and white means (OFF, OFF). In all the simulations, a field of cells starts with a completely spatial disordered configuration—there is no correlation between neighboring cells' gene expression states—as exemplified by the leftmost picture shown in (A).

(A) Traveling wave of horizontal bands. Snapshots of the formation process shown at different stages of a simulation. Assuming that one time step in the simulation takes one min, the clocks show time passed from noon (beginning of the simulation).

(B) Complex pool of multiple wavelets formed, starting with a spatially disorganized field of cells. Snapshots at different stages of the simulation are shown. Assuming that one time step represents 1 min, the clock and the days elapsed indicate at which time steps in the simulation the snapshots are taken.

(C–J) Each filmstrip shows three non-contiguous snapshots of a moving, dynamic pattern that formed, starting from a spatially disorganized configuration (not shown, see examples in the first snapshots in (A). Where shown, the arrows represent the direction of travel. The dynamic patterns are: (C) a single traveling horizontal band, (D) traveling vertical bands, (E) a traveling zigzag band, (F) a spiral wave, (G) traveling diagonal bands, (H) a small island of cells (enclosed in the blue hexagon) oscillating over time while all cells outside the island remain static, (I) every cell oscillates between red and blue with period 2, and (J) seemingly erratic, never-ending dynamics in which multiple wavelets form and meet and annihilate each other with the pool of wavelets constantly evolving and never repeating the same configuration throughout the simulation.

The dynamic patterns that we uncovered differed in their shape, complexity, and movements (Figures 2C–2J; Videos S1, S2, S3, and S4; and Supplemental Analysis Section S1). Among these, the most prominent were rectilinear traveling waves and spiral waves, both of which have high degrees of spatial order (Figures 2C–2F). In the case of traveling waves—which can be oriented horizontally, vertically, or diagonally (Figures 2C, 2D, and 2G) and have a straight or bent shape (Figures 2D and 2E)—a rigid shape moves across space over time. Since the simulations were deterministic and the system had periodic boundary conditions, if the simulation revisits an earlier spatial configuration, then it would periodically and forever repeat the same dynamics from then on. In the case of traveling waves, this meant that the waves perpetually propagated, disappearing at one edge of the field and then appearing at the opposite end. This behavior also applies to patterns that do not propagate over space, but rather, oscillate in time. In some cases, such oscillations were limited to a few cells that formed an island (Figure 2H) whereas in others, every cell in the field oscillated together (Figure 2I). In particular, an island of cells could oscillate in such a way that individual cells oscillated with different periods (Figure 2H), causing the entire island, as a collective entity, to display a complex oscillation with a period larger than four time steps. We call this a “complex” oscillation because the simplest oscillation would involve all cells in the island having the same gene expression state that oscillates with a period of at most 4 time steps, since a cell can have at most four distinct gene expression states (i.e., [ON/OFF, ON/OFF]). Finally, some cellular dialogues yielded temporally non-repeating, complex patterns consisting of whirlpools of wavelets that evolved over time in an erratic manner (Figure 2J), which, in many cases, transiently existed for tens of thousands of time steps before the cells formed temporally repeating, well-defined dynamic patterns such as horizontal waves.

Common Structural Elements in Cellular Dialogues that Generate Dynamic Patterns

The wide array of dynamic patterns that we observed fall into two categories (Figure 3A): (1) dynamic temporal patterns, in which cells periodically oscillate over time but do not propagate information over space (e.g., Figures 2H and 2I), and (2) dynamic spatial patterns, in which cells propagate information over space in the form of a well-defined shape (e.g., a wave front) that moves from one part of the field to another, often from one edge to the other edge of the field (e.g., Figures 2C–2F). There are 44 distinct cellular dialogues in total (see STAR Methods) that we could group into three categories: (1) those that cannot form any dynamic patterns, (2) those that can form only dynamic temporal patterns, and (3) those that can form both dynamic spatial patterns and dynamic temporal patterns. To categorize them, we developed a method to deduce, for each cellular dialogue, all possible ways that a cell's state (ON/OFF, ON/OFF) can change over time. Concretely, we constructed a directed graph for each cellular dialogue (see Supplemental Analysis Section S2), which has four nodes—one for each gene expression state—that are connected by edges with directions that represent the allowed transitions between the nodes. We deduced how some of the directed edges become inaccessible while others become accessible as we change the cellular dialogue's parameter values (Figure S2). Then, following the directed edges from node to node yields all possible ways that a cell's gene expression can change over time. By looking for graphs that contained cyclic paths, we identified cellular dialogues and ranges of their parameter values that can potentially sustain dynamic patterns if they were to form. Since self-organization of dynamic patterns can only occur for parameter values that can sustain dynamic patterns in the first place, we only had to check these values in simulations to see if they led to dynamic patterns. This method, thus, vastly reduced the range of parameter values that we had to screen. For each cellular dialogue, we generated a large set of random parameters and ran many simulations (see STAR Methods), each starting with a different and randomly generated gene expression pattern. We checked whether each of these simulations yielded a dynamic pattern using automated methods (see STAR Methods).

Figure 3.

Computational Search Revealed Tree Structures that Group Cellular Dialogues Based on Their Ability to Generate Either Static Patterns, Dynamic Temporal Patterns, or Dynamic Spatial Patterns

(A) Two classes of dynamic patterns. (Top) Dynamic temporal patterns repeat themselves over time without transmitting information across space. (Bottom) Dynamic spatial patterns involve cells that transmit information over space through a coherent structure that moves across the field.

(B–D) Tree diagrams show a full classification of all 44 unique, non-trivial cellular dialogues into three distinct classes (see STAR Methods). In each tree diagram, a cellular dialogue is a leaf (box) that is joined by branches to other cellular dialogues. As one moves from one leaf to the next, an edge is either removed or added to the cellular dialogue. (B) Tree diagram showing all cellular dialogues that cannot generate any dynamic patterns. All cellular dialogues here lack mutual interactions and self-repressions. (C) Tree diagram showing all cellular dialogues that can generate dynamic temporal patterns but not dynamic spatial patterns. These all have either a self-repression (red boxes), a mutual interaction of the same sign (blue boxes), or both (purple boxes). Cellular dialogue 14 is an exception—it has mutual interactions of different signs and no self-interactions. (D) Tree diagram showing all cellular dialogues that can generate dynamic spatial patterns, as well as dynamic temporal patterns. These are all generated by adding at least one additional self-interaction to cellular dialogue 14. Cellular dialogues in the five red boxes have at least one positive feedback loop and can generate non-oscillatory dynamic spatial patterns (e.g., traveling waves). Cellular dialogues in the blue boxes have only negative self-interactions and produce dynamic spatial patterns but always with a concurrent dynamic temporal pattern (e.g., a traveling wave where the cells oscillate simultaneously) (see Figure S3 for examples).

(E) The maximum observed simulation time is a metric that naturally separates the three classes of cellular dialogues (B–D) (see Figure S4 for other metrics). A node represents a cellular dialogue and the node's shape represents the type of cellular dialogue (one of the three B–D). A node's color indicates the longest observed simulation time among a large set of simulations that were performed with different parameters.

See also Figures S2–S4.

We discovered that cellular dialogues, when grouped into the three categories mentioned above, form distinct tree structures (Figures 3B–3D) in which a node denotes a particular cellular dialogue and an edge connects two nodes if one node (cellular dialogue) comes from the other node (another cellular dialogue) by adding or removing one regulatory interaction. The fact that tree structures emerged, which link the different cellular dialogues together if they form the same type of patterns, suggests that there may be common elements in the cellular dialogues that belong to the same tree. Indeed, we found that all ten cellular dialogues (Figure 3B) that can only generate static configurations, and no dynamic patterns at all, consist of two molecules that do not mutually regulate each other and also do not have any self-repressions. We also found that twenty-six cellular dialogues can produce dynamic temporal patterns but not dynamic spatial patterns (Figure 3C). Their common feature is that they all contain a self-repression and/or a mutual feedback of the same sign (i.e., both molecules either activate or repress each other's production). The sole exception to this rule, within this family of cellular dialogues, is cellular dialogue 14 (Figure 3C). Cellular dialogue 14 consists of an activator-inhibitor pair, whereby one molecule promotes the production of the second molecule, which in turn represses the production of the first molecule. Here, neither molecule regulates its own production. However, all eight cellular dialogues that one can obtain from cellular dialogue 14 by adding one or more self-interactions can yield dynamic spatial patterns, in addition to dynamic temporal patterns (Figure 3D). We could further divide these eight cellular dialogues into two classes: ones that contain only self-repressions (Figure 3D, blue boxes) and ones that contain at least one self-activation (Figure 3D, red boxes). The three cellular dialogues that contain only self-repressions produce dynamic spatial patterns in which the moving shape periodically changes its gene expression composition (Figure S3 and Video S3). In contrast, the five cellular dialogues that contain at least one self-activation yield dynamic spatial patterns such as traveling waves (Figures 2C–2G) in which the pattern moves across the field of cells without changing in shape or composition.

Grouping Cellular Dialogues Based on How Fast They Form Patterns Is Equivalent to Grouping Them Based on Their Shared Structural Elements

We discovered that if we analyze the typical times or the longest time that a cellular dialogue takes to form a pattern (static configuration or a dynamic pattern), and then group the cellular dialogues based on those times, then we would identify the same three categories of cellular dialogues (Figures 3E and S4). Specifically, all eight cellular dialogues that can form dynamic spatial patterns stood out as taking the longest times to form patterns compared to the other cellular dialogues, by at least about 100-fold longer durations (Figure 3E, circles). As we will later discuss, we found that these long self-organization times (∼1 week if one time step represents 1 min) are due to complex dynamics that is intrinsic to the pattern-formation process. We found that all cellular dialogues that cannot form dynamic spatial patterns but do form dynamic temporal patterns take less times to form patterns, by at least a 100-fold less, than the ones that form dynamic spatial patterns (Figure 3E, triangles). Finally, we discovered that the cellular dialogues that cannot form any dynamic patterns and thus only form static configurations—some of which are highly organized patterns—require the least amounts of time to form these configurations (Figure 3E, squares).

Analytic Framework Explains How Cells Collectively Sustain Dynamic Spatial Patterns

To explain why certain cellular dialogues enable cells to sustain the dynamic spatial patterns after having formed them, we developed a theory that does not use simulations and still correctly predicts when dynamic spatial patterns occur and explains how the cells sustain them (Figures 4A–4C). The key idea behind this analytical approach is that many dynamic spatial patterns, from the complex whirlpools of wavelets to spiral waves, share a common structure: one can build diverse dynamic spatial patterns by gluing together multiple rectilinear waves (i.e., horizontal, vertical, and bent waves). Thus, if we can understand how cells can sustain rectilinear waves, we can piece them together to understand the more complex shapes that are built out of them. Each rectilinear wave has six distinct layers of gene expression states (Figure 4A). Three of the layers—“front,” “middle,” and “back” (Figure 4A, red, black, and blue cells)—constitute the wave itself and continuously move forward while the other three layers—“exterior front,” “exterior,” and “exterior back”—consist of all the other cells. After a one-time step, each layer adopts the identity of the layer just behind it (e.g., the exterior-front layer, which is just in front of the front layer, becomes the front layer) (Figure 4C). This must occur at every time step in order for the wave to continuously propagate, meaning that the concentrations of the two molecules within each layer must coordinately change so that the layers can synchronously move forward. We developed a method to estimate the concentrations of the molecules in each layer (Figure 4B; Supplemental Analysis Section S3).

Figure 4.

Analytic Framework Predicts and Explains How Cells Can Sustain Dynamic Spatial Patterns

(A–C) Three-step overview of an analytic (pen and paper) approach to understanding the simulations (see Supplemental Analysis Section S3 for details). (A) Step 1: decompose straight (top) and bent (bottom) waves into distinct layers of cells. Cells of the same layer have the same gene expression state. (B) Step 2: estimate the total concentrations of molecules that a cell senses by exactly calculating the portions of those concentrations that are due to the cell itself and its nearest neighbors and by approximating the portions of the total concentrations that are due to further-away cells. (C) Step 3: (right) Directed graph-representation showing how a cell must transition to distinct layers shown in (A) at each time step, which is explained by six mathematical inequalities that are derived through step 2.

(D) Numerically solving the six inequalities in (C) shows that only two types of waves, shown here are possible and which cellular dialogues can produce them (cellular dialogues 15, 36, and 33 for wave type 1; cellular dialogues 19, 33, and 34 for wave type 2).

(E) Adding self-activation to cellular dialogue 14 yields, in the left column, cellular dialogues 15 and 19. Directed graph -representation showing the gene expression transitions of a cell for each cellular dialogue (see Supplemental Analysis Section S2).

(F) Parameter values that allow for sustaining of rectilinear waves, when represented as red points, form a dense region (red region) as shown in these spider charts. These parameter values satisfy the six inequalities derived by the analytic theory (C) (see Figure S6C for a direct comparison with parameter values found purely through computational search). The spider charts show the following parameters: threshold concentrations $K^{\left(ij\right)}$ for each molecular interaction and the maximum secretion rate $C_{ON}^{\left(j\right)}$ for each of the two molecules.

See also Figures S5 and S6.

Using the analytical approach, we derived six mathematical inequalities, one for each layer that must all be satisfied in order for the concentrations of the two molecules to coordinately change to enable the rectilinear wave to propagate (Figure 4C; Supplemental Analysis Section S3). The inequalities impose relationships among the different parameters of the cellular dialogues, such as the maximal secretion rates and sensing thresholds (Figure 1D). By solving these inequalities, we found that only five cellular dialogues—the exact same ones that we computationally identified—can satisfy all six inequalities and thus generate non-oscillatory dynamic spatial patterns (i.e., the ones that do not involve concurrent dynamic temporal patterns) (Figure 3D, red boxes). In accordance with the computational screening, the analytical approach revealed that only two types of rectilinear waves are possible, each differing by which gene expression state is assigned to each layer: all cellular dialogues with cellular dialogue 15 as the common motif (i.e., molecule-1 promotes its own secretion) generate one type of rectilinear wave (Figure 4D, top row) while the others, having cellular dialogue 19 as the common motif (i.e., molecule-2 promotes its own secretion), generate the other type of rectilinear wave (Figure 4D, bottom row). As an exception, cellular dialogue 33 can generate both types of traveling waves because nested in it are both cellular dialogues 15 and 19 as sub-graphs.

To understand why only these five cellular dialogues (Figure 4D) can generate dynamic spatial patterns, we considered the directed-graph representation of the cellular dynamics that we introduced earlier (Supplemental Analysis Section S2). For a wave, the directed graph must contain a cyclic path that goes through all four nodes—one node for each gene expression state—since an exterior cell must eventually become a front-layer cell, then a middle-layer cell, then a back-layer cell, and then finally an exterior cell again (Figure 4C). Cellular dialogue 14, which is the backbone of all five cellular dialogues that generate dynamic spatial patterns (Figure 3D, red boxes), can potentially produce a cyclic graph with these four nodes (Figure 4E, left panel) as long as they permit parameter values that allow each cell to cyclically traverse through the nodes. This is because starting with a gene expression state of (1, 0)—where the 1 means ON-state for molecule-1 and the 0 means OFF-state for molecule-2—may lead to (1, 1) due to molecule-1 promoting molecule-2 secretion, which then may lead to (0, 1) due to molecule-2 repressing molecule-1 secretion, which then may lead to (0, 0) due to there being not enough molecule-1 for promoting molecule-2 secretion, and finally, this may lead back to the starting state, (1, 0), due to there being not enough molecule-2 for inhibiting molecule-1 secretion. However, such a cycle through the four nodes alone is insufficient for sustaining a wave because the exterior cells must remain as exterior cells unless they are adjacent to the front or back layer (Figure 4C). But if the exterior cells have state (0, 0) and the front-layer cells have state (1, 0), then the exterior cells near the front layer (i.e., the exterior-front cells) would sense more molecule-1 than the exterior cells that are further away from the wave. Modifying cellular dialogue 14 by having molecule-1 promoting its own secretion, as in cellular dialogue 15, would create the possibility of the exterior-front cells activating molecule-1 secretion and thus transition to (1,0) at the next time step, thereby becoming a front layer whereas the exterior-layer cells remain in the (0, 0) state (Figure 4E, top right). A similar reasoning also yields an analogous result for cellular dialogue 19 (Figure 4E, bottom right).

To realize the qualitative scenario described above, a cellular dialogue must contain parameter values that satisfy all six inequalities that we derived (Figure 4C). We found that the five cellular dialogues indeed admit such parameter values and that these values—obtained through the analytical approach—nearly perfectly match those found in the computational screen (Figures S5 and S6). We can represent these parameter values as spider charts (Figure 4F), which show that each of the five cellular dialogues can realize dynamic spatial patterns with parameter values that vary over many orders of magnitude. The spider charts also geometrically reveal a common feature among the five cellular dialogues: the threshold concentration must be low for a molecule that promotes its own secretion (Figure 4F, note the inward indentations in the red spider webs along the axes that represent the threshold concentrations). This makes sense because, for all types of rectilinear waves (Figure 4D), the exterior-front cells need to turn on the secretion of a molecule that promotes its own secretion by sensing it from the other layers and having a low activation threshold for that molecule would facilitate this. Taken together, our analytical approach unveiled how cells can sustain dynamic spatial patterns.

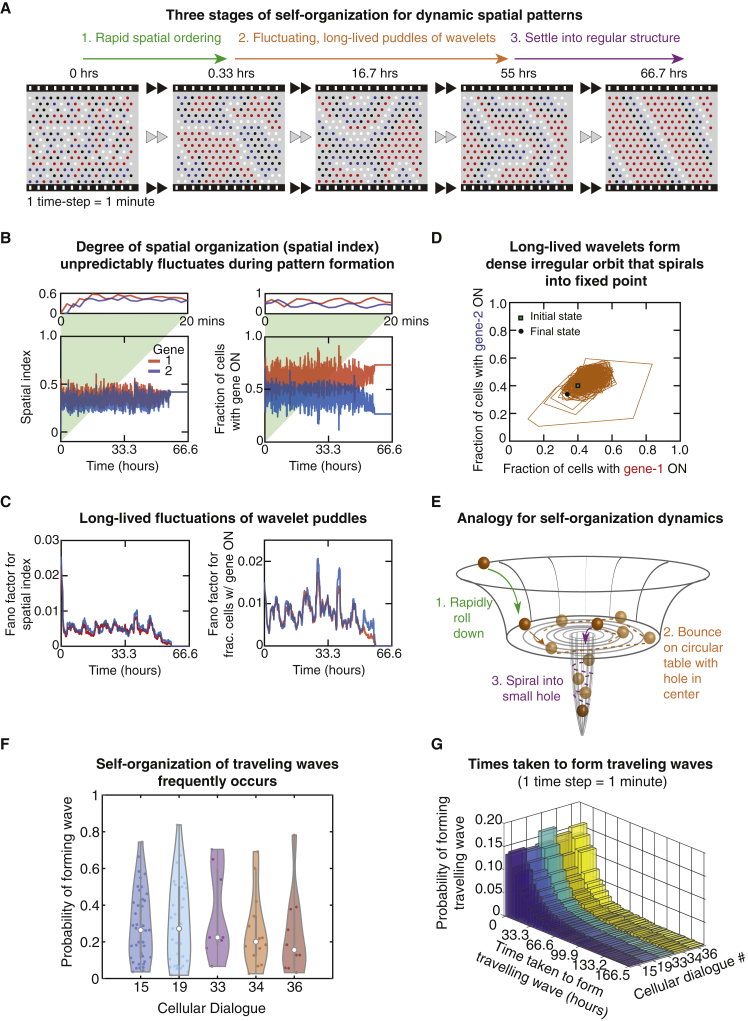
Self-Organization Occurs through a Three-Stage, “Order-Fluctuate-Settle” Process

We now turn to the self-organization process itself. Given that many of the dynamic spatial patterns are traveling waves and that more complex dynamic spatial patterns can be built from gluing together multiple rectilinear waves, we focused on traveling waves and the core features of their self-organization process. Our simulations revealed that traveling waves form in three stages (Figure 5A and Video S2). First, a field of cells whose gene expression levels form a completely disorganized spatial configuration rapidly becomes more spatially ordered, meaning that the gene expression levels of neighboring cells tend to become more correlated over time. To quantify the degree of spatial organization, we used “spatial index”—a metric from our previous work whose value is zero for a completely disorganized spatial configuration and increases toward one as the spatial configuration becomes more organized (see STAR Methods and Figure 5B, left panel's inset) (Maire and Youk, 2015a, Olimpio et al., 2018).

Figure 5.

Three-Step, “Order-Fluctuate-Settle” Process Leads to Formation of Dynamic Spatial Patterns

(A) Snapshots of a simulation showing the three stages of a traveling-wave formation—the three stages are described above the filmstrip. Assuming that one time step of a simulation represents 1 min, indicated above each snapshot is the elapsed time in hours. Color scheme for cells is the same as in Figure 2.

(B) Two macroscopic parameters—the spatial index and the fractions of cells with a particular gene ON—plotted as a function of time for the wave-forming simulation shown in (A). 1 min represents one timestep. (Left panel) the spatial index—with magnitude between zero and one—measures the degree of spatial organization (zero means complete disorder, i.e., no spatial correlation in gene expression among cells and increasing values correspond to more spatial organization). Inset shows the spatial index rapidly increasing for the first twenty time steps. Spatial index for gene 1 (red) and gene 2 (blue). (Right panel) Fractions of cells with gene 1 ON (red) and of gene 2 ON (blue) for a typical wave-formation process. Inset shows the first twenty time steps.

(C) For data in (B) and genes 1 (red) and 2 (blue), we used a moving window to compute the moving coefficient of variations in the spatial index (left panel) and in the fractions of cells with the specified gene ON (see STAR Methods).

(D) For a typical simulation that self-organizes into a traveling wave, we plot the trajectory in phase space formed by the fractions of cells with gene 1 ON and gene 2 ON. The trajectory begins at the square (first time step of the simulation) and terminates at the circle (last time step of the simulation).

(E) Analogy for the three-stage self-organization process—a billiard ball rolls down a bowl, bounces around on the flat circular bottom, and then fall through a tunnel after finding a small hole drilled into the circular bottom.

(F) Probability of forming a traveling wave for each of the five cellular dialogues (detailed results in Figure S8). Violin plots showing the non-parametric kernel density (colored distributions), together with the median (white circle), interquartile range (thick vertical line) and 1.5× interquartile range (thin vertical line). Results are obtained by running 500 simulations for each of the parameter sets for which at least one traveling wave formed in the computational screening (see STAR Methods). Individual dots represent probabilities for individual parameter sets.

(G) Distributions of the time taken to form traveling waves for each of the five cellular dialogues that enable cells to form dynamic spatial patterns (detailed results in Figure S10).

See also Figures S7–S10.

In the following discussion, we consider one time step to represent 1 min and express the time in minutes or hours. Then this rapid spatial ordering typically takes less than an hour (Figure 5A, green arrow and Figure 5B, left panel). At the end of this process, the cells have formed multiple whirlpools of wavelets (Figure 5A, frame at 0.33 h). Thus, begins the second stage of self-organization: long-lived complex dynamics—lasting for days or weeks—in which multiple wavelets travel through the field of cells, meeting and annihilating each other, all the while as the cells form new wavelets to replace the destroyed ones (Figure 5A, filmstrip from 0.33 h to 55 h). During this days-long dynamics, the spatial organization neither stably increases nor decreases—the spatial index erratically (unpredictably) fluctuates over time (Figure 5B, left panel; Figure S7; Videos S4 and S5), which we can see by plotting the Fano factor for the spatial index over time (Figure 5C, left panel; STAR Methods). The spatial index erratically fluctuating represents multiple wavelets forming and annihilating at various, seemingly random locations and wavelets unpredictably morphing over time, all despite the fact that the simulations are completely deterministic. Crucially, we verified that the same spatial configuration never repeats itself throughout the days-long dynamics which could, in fact, last for weeks or longer if we do not terminate the simulations (i.e., some fields of cells never reach a steady state and never attain a dynamic pattern within the allotted time for the simulations). Such erratic, complex dynamics is followed by the third and final stage of the self-organization process: the wavelets die down and as this occurs, a more rigid, spatially ordered structure that travels as a wave emerges (Figure 5A, last frame). During this final process, the spatial index's fluctuations rapidly decay, typically over a few hours. The system then settles into a regular dynamic pattern that repeats itself over time. This is marked by the sudden disappearance of the fluctuations in the spatial index (Figure 5B, left figure). This settling process takes a few minutes to several hours (Figures 5A, purple arrow, and 5B, left panel). Leading up to this last stage, there are no clear indications that a well-organized regular shape will emerge. This highlights the erratic, complex nature of the self-organization dynamics.

The spatial index, one for each gene, represents a macrostate variable—a single number that measures how much spatial correlation there is in the expression of a particular gene (see STAR Methods). Another macrostate variable is the fraction of cells that have the same gene expression level (i.e., fractions of cells that have gene-i in the ON-state). There are two such fractions, one for each gene. During the self-organization process, these two fractions erratically fluctuate over time—just like the spatial indices—as the wavelets constantly and erratically change their shapes while meeting and annihilating each other for days. Afterward, the two fractions' fluctuations quickly decay over time—the decay takes a few hours whereas the whole self-organization process takes days—and eventually settle at steady-state values (Figures 5B, 5C, right panel, and S7). When we view the temporal change of these two fractions as a trajectory in a plane—a phase space—defined by the two fractions, we see an irregular orbit that eventually stops at a single point (Figure 5D, black circle). Specifically, a point in the two-dimensional phase space—representing the values of the two fractions at a given time—erratically moves within a restricted region of the plane. If we follow the trajectory with a pencil, we would obtain a jagged curve that densely and nearly entirely fills the whole space within the restricted region that encloses the single point where the trajectory terminates (Video S4).

The phase-space trajectory described above suggests the following analogy for the self-organization dynamics (Figure 5E): a ball quickly rolls down a steep side of a large bowl, speeding up as it does so, until it reaches the bowl's flat bottom. This is the first stage of self-organization in which the decreasing height represents more spatial ordering (Figure 5E, green arrow). After reaching the frictionless, flat circular bottom, the ball rapidly bounces off the sidewalls, like a billiard ball, without ever losing its speed (Figure 5E, brown dashed lines). This bouncing ball, which would produce seemingly erratic yet deterministic motion—as Newton's laws of motion are deterministic—represents the second stage of self-organization in which multiple whirlpools of wavelets are unpredictably created and destroyed. Eventually, the ball finds the small hole, falls into it, and then spirals its way downward along the sidewalls of the trench through the hole until it reaches the bottom of the trench (Figure 5E, purple arrow). This would represent the third and the final stage of the self-organization. The shape of the bowl and the location of the trench would be determined by the parameters of the cellular dialogue.

In each of the five cellular dialogues that can yield dynamic spatial patterns, we found that, for parameter values that enable dynamic pattern formations, approximately 30% of the initially disorganized spatial-configurations successfully self-organized traveling waves (Figure 5F). Moreover, our simulations and the analytical approach revealed that cells can have arbitrarily high parameter values and still form traveling waves, as long as the secretion rates and threshold concentrations are appropriately tuned (Figures S6 and S8). Our analytical framework presents an optimization strategy for ensuring that cells form traveling waves for the largest possible set of parameter values (Figure S9). This strategy depends on balancing how much a cell communicates with itself by capturing back the molecules that it had just secreted (self-communication) with how much a cell communicates with the other cells by sending its secreted molecules to them (neighbor-communication). In short, we found that when the cells are sparsely packed, there is not enough neighbor communication for sustaining traveling waves. On the other hand, when the cells are densely packed, then cells cannot cycle through a set of gene expression states—a requirement for dynamic patterns such as waves - because the signaling molecules quickly reach saturating concentrations rather than undergoing the necessary cycles of decreases and increases. This leaves us with intermediate, “goldilocks” density of cells as being ideal for forming and sustaining waves and dynamic spatial patterns (Figure S9B). Furthermore, for all five cellular dialogues, we discovered that the probability of forming a traveling wave at a given time is well described by an exponential distribution (Figures 5G and S10A), with a characteristic decay time of thousands of time steps (i.e., tens of hours if one time step is 1 min). This strongly suggests that traveling wave formation is a memoryless process whereby at each time step, the probability that the next time step yields a traveling wave remains the same regardless of at which time step the simulation is. This reflects the fact that watching the simulations that yield a dynamic spatial pattern does not give the observer a sense that the cells are getting anywhere closer to forming a dynamic spatial pattern as time passes (Figures S10B–S10D).

Dynamic Patterns with More Complex Elements

We next extended our investigation by relaxing the two main constraints in the simulations—having an infinite Hill coefficient and cells on a regular lattice. We modified the simulations by separately adding four elements (Figure 6A; STAR Methods): (1) stochastic response to the signaling molecules (Figure 6A, top left), (2) a sigmoidal response function characterized by a finite Hill coefficient (i.e., cells no longer digitally respond to the signaling molecules) (Figure 6A, top right), (3) randomized locations of cells instead of each cell residing on a regular lattice (Figure 6A, bottom left), and (4) random (diffusive) motion of each cell (Figure 6A, bottom right). We tuned each element and asked two questions: (1) can the cells still form traveling waves if they start with a completely disordered spatial configuration? (Figure 6B, top)—this probes the self-organization capability—and (2) can the cells still sustain traveling waves after forming them? (Figure 6B, bottom) —this investigates whether dynamic spatial patterns can be sustained once formed. In general, we found that cells could still form a wide range of dynamic spatial patterns with the four additional elements (Figure 6C). For example, we discovered that cells under the influence of a moderate noise could form a band that travels as a wave despite a number of cells stochastically obtaining the “wrong” (incoherent) gene expression state. In this case, the wave, thus, propagates while stochastically evolving (Figure 6C, top left; Video S6). As another example, we discovered that even when we randomly arrange cells in space, instead of on a regular lattice, the cells could still form never-ending, complex wavelets (Figure 6C, bottom left; Video S7).

Figure 6.

Dynamic Spatial Patterns Still Form Even with More Complex Elements

(A) Schematic of four additional, more complex elements that we added to our computational screen.

(B) We examined two features with the elements in (A): (Top) can a disorganized field of cells still self-organize dynamic spatial patterns? (Bottom) Starting with a traveling wave, can the cells sustain it?

(C) Examples of dynamic spatial patterns formed for each of the elements shown in (A). Colored boxes that enclose the filmstrips correspond to the colors used for each element shown in (A).

(D) Fraction of simulations that form a dynamic pattern as a function of the deviation from the more idealized setting—cells placed on a regular lattice and responding digitally with an infinite Hill coefficient—in which the results for Figures 1, 2, 3, 4, and 5 were reported. Four colored boxes with each color corresponding to colored box in (A) that shows the modified element in the simulations. For each data point, we ran a large set of simulations with a fixed set of initial conditions as we varied the parameter controlling the deviation from our original model and classified their final states (see Figure S11 for details on finite Hill coefficient and noise). All results here are for cellular dialogue 15.

(E) Fraction of simulations with cellular dialogue 15 that can sustain a traveling wave for at least one full period after starting with a traveling wave. We took parameter values for which the simulations with simpler elements (i.e., infinite Hill coefficient and cells on a regular lattice) can propagate traveling waves.

See also Figures S11–S14.

By running many simulations for each of the four complex elements, we discovered that the dynamic spatial patterns that we previously observed, on a regular lattice with an infinite Hill coefficient (Figure 2), still formed as long as the amount of the deviation introduced by the four elements, relative to the regularity of the lattice and the infinite Hill coefficient, was non-negligible but not too large (Figure 6D). For instance, we found that, with a moderate noise, dynamic spatial patterns continued to form and persist (Figures 6D, 6E, top left, and S11). The probability that an initially disordered configuration morphed into a traveling wave became higher with moderate noise, compared to not having any or low noise, indicating that noise can drive the system toward more ordered states—a phenomenon also observed for static patterns in an earlier work (Olimpio et al., 2018). To account for this observation, we extended our theory, which we developed for explaining wave propagation without noise (Figures 4A–4C), to now include noisy gene expression. Using this extended theory, we calculated the probability that a wave, after forming, “survives” for a given amount of time. This probability closely matched the actual fraction of simulations in which waves survived (Figure S12 and Supplemental Analysis Section S4). The theory also let us calculate, for each of the five cellular dialogues that can form dynamic spatial patterns, how much noise there must be to prevent waves from forming (see Supplemental Analysis Section S4).

By varying the Hill coefficient over a wide range, we discovered that dynamic patterns can form for finite Hill coefficients of values ∼4 or higher (Figures 6D, top right, and S11). However, these did not typically include “pure” traveling waves that neatly decompose into the previously identified layers. Moreover, an already-formed traveling wave—as in the case of a simulation that starts with a wave—could persist for Hill coefficients of values down to ∼3 (Figure 6E, top right). These results indicate that a finite Hill coefficient is mainly detrimental to the self-organization of traveling waves whereas it is less detrimental to the cells' ability to sustain a traveling wave once it is formed. With a Monte Carlo algorithm that randomly displaces the cells and quantifies the amount of resulting “lattice disorder” (see STAR Methods), we found that dynamic spatial patterns still formed and persisted even with a high degree of spatial disorder (Figures 6D, 6E, bottom left, and S6). Even with saturating amounts of spatial disorder, we still observed self-organized wavelets that propagated, albeit with a lesser degree of regularity than in a regular lattice (Figure 6C, bottom left). When we allowed the cells to diffusively move—we tuned the cells' motility by adjusting the diffusivity of their Brownian motion (see STAR Methods)—we found that large-scale, uncoordinated motion of the cells prevented any kind of dynamic spatial patterns from stably propagating, as large variations between the local environments of individual cells tended to diminish the cells’ ability to spatially propagate information (Figure 6D, bottom right). However, we found that motile cells could still propagate waves, once formed, for an extended amount of time before the wave disintegrated even when the cells had a high degree of diffusive motion (Figure 6E, bottom right). Together, these results strongly suggest that diffusively moving cells can sustain traveling waves as long as the waves travel sufficiently rapidly (i.e., compared to the cells’ average speed).

We also studied three more complex elements. First, we considered the influence of a spatial gradient of parameter values on traveling-wave formation (see STAR Methods). Researchers have suggested that spatial gradients of parameter values can influence the orientation of Turing patterns such as stripes (Hiscock and Megason, 2015). Similarly, we observed that a spatially varying parameter, having a simple step-function profile over space, can influence the direction in which the traveling waves moved after forming: the waves tended to align perpendicularly to the gradient (Figure S11). Second, whereas until now the cells integrated the two signals with an AND-logic scheme—both molecules were required for activating or repressing gene expression—we repeated the computational search (Figure 1D) but now with an OR-logic scheme in which only one of the molecules is required for activation or repression of a gene (see STAR Methods). We found that the OR-logic scheme yields exactly the same groupings of cellular dialogues as in the AND-logic scheme in terms of the three classes of patterns that they generate—static, dynamic temporal, and dynamic spatial patterns (Figure S13 and Video S8). But we discovered that the OR-logic scheme produces a different “wave structure” (Figure 4D) than the AND-logic scheme (Figure S13). Finally, we performed simulations in which we disrupted the individual cell’s gene expression to check whether traveling waves could still form and propagate. Experimentally, one can perturb individual cells this way with optogenetics. Our main finding is that traveling waves can still form and continue to propagate as long as we disrupted sufficiently low numbers of cells (e.g., up to ∼20 cells in a field of ∼200 cells) (Figure S14).

Discussion

The dynamic-pattern-forming cellular dialogues that we identified include some that have been experimentally observed to yield patterns. They all have interlocked positive and negative feedbacks (Figure 3D). Researchers have found that, without any cell-cell communication, such interlocked feedbacks can cause gene expression levels to robustly oscillate temporally (Stricker et al., 2008, Tsai et al., 2008, Li et al., 2017). Researchers have also synthetically engineered a quorum-sensing gene circuit resembling cellular dialogue 20 (Figure 3D) and observed that the cells' gene expression levels synchronously oscillate over time and, under certain conditions, spontaneously form traveling waves (Danino et al., 2010). More generally, the activator-inhibitor structure of cellular dialogue 15 is qualitatively similar to the structure of the FitzHugh–Nagumo (FHN) model, which describes excitable systems such as cells whose biomolecule concentrations oscillate over time and/or form traveling waves (Gelens et al., 2014, Sgro et al., 2015, Hubaud et al., 2017). Cellular dialogue 15 has an activating molecule that promotes its own production and an indirect negative feedback through the second molecule. This indirect negative feedback is analogous to the slow repression in the FHN model. Similarly, the interlocked positive-negative feedback loops of the dynamic-pattern-forming cellular dialogues resemble the activator-inhibitor systems that generate Turing patterns (Kondo and Miura, 2010) and resemble the two-gene networks that can generate Turing patterns (Scholes et al., 2019). But the cells in our simulations do not generate Turing patterns such as stripes or spots of fixed sizes, likely due the large separation of timescales between molecular and gene expression dynamics in our simulations.

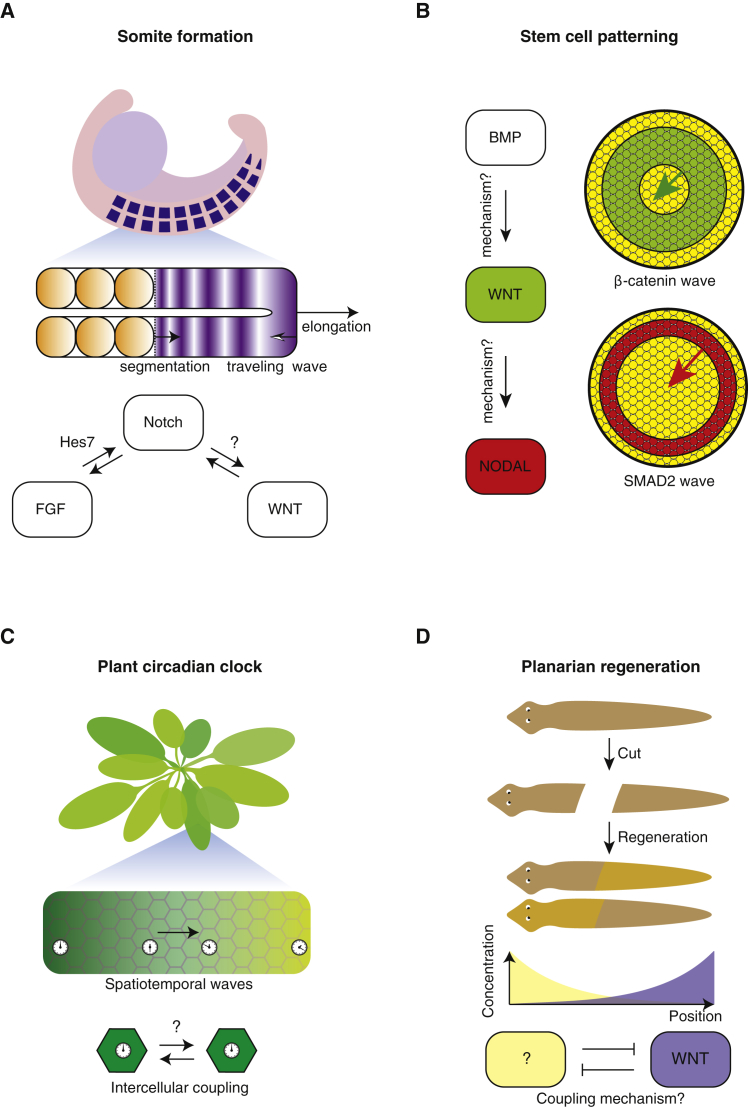
Here, we focused on cellular dialogues with two molecules and the two genes that they control. But our software can easily be modified to include multiple—more than two—extracellular molecules and genes as well as arbitrary regulations of those genes (as showcased by our inclusion of finite Hill coefficients). Such extensions would allow one to explore more complex ways that cellular dialogues can mediate dynamic-pattern formations. These extensions, our analytical method for analyzing the simulations, and our results on two-molecule cellular dialogues may provide insights on poorly understood systems in which multiple signaling molecules interact with each other. For many biological systems, the regulatory links among the various molecular players remain unknown (Figure 7). For example, researchers have found that three signaling molecules—Fgf, Notch, and Wnt—regulate one another during somite formations. But how Wnt and Notch regulate each other so that their levels coordinately oscillate over time remains unknown (Figure 7A) (Oates et al., 2012, Harima and Kageyama, 2013, Sonnen et al., 2018). One may address this question by modifying our software to include three-molecule cellular dialogues and then applying our analysis method to analyze those simulations. Doing so may also help in identifying, in stem cells, the as-yet-unknown regulatory links among Bmp, Wnt, and Nodal that lead to self-organized spatiotemporal waves (Figure 7B) (Chhabra et al., 2019). In the Arabidopsis thaliana leaves, the circadian clocks of individual cells may be synchronized through self-organized traveling waves (Wenden et al., 2012, Gould et al., 2018) (Figure 7C). While these waves are known to occur through interactions between cells on a regular lattice, the exact interaction mechanism remains unknown (Greenwood et al., 2019). Finally, in planaria—flatworms that regenerate their bodies after they are cut into pieces—a self-organized Wnt gradient specifies where the tail reforms after it is cut. Researchers believe that an as-yet-unidentified signaling molecule may interact with Wnt in a mutually antagonistic way to indicate where the head should reform after it is excised (Figure 7D) (Stückemann et al., 2017). Thus, our results on two-molecule cellular dialogues may provide insights into this system.

Figure 7.

Self-Organized Dynamic-Pattern-Forming Systems with Poorly Understood Interactions that Our Software and Analytic Framework May Help in Elucidating

(A–D) Biological systems with two or more interacting pathways that generate spatiotemporal patterns but whose exact mechanisms and cellular dialogues remain poorly understood. (A) During somitogenesis, a wave of gene expression states propagates along the anterior-posterior axis of an elongating, pre-somite mesoderm. The conventional view is that this wave is mediated by a coupling between individual oscillators—oscillations in expression levels of Wnt, Notch, and Fgf and/or by large-scale gradients in the gene expression levels for those molecules. But how Notch regulates Wnt and vice versa remains questionable while Hes7 is known to mediate the Fgf-Notch interaction (Sonnen et al., 2018). Figure partially adapted from (Oates et al., 2012). (B) Waves of β-catenin (green ring) and Smad2 (red ring) expression levels propagate in a field of stem cells. Although we know that these waves form because of BMP inducing β-catenin (part of the Wnt pathway) and SMAD2 (part of the NODAL pathway), how exactly these two inductions occur remains poorly understood (Chhabra et al., 2019). (C) The circadian clocks of each cell within the leaf of Arabidoposis thaliana are thought to be coupled to each other through an as-yet-unknown mechanism, which is suspected to involve a variety of hormones, sugars, mRNAs, and other molecules (Greenwood et al., 2019). (D) A planarian regenerates itself after being cut into two or more pieces. This is thought to rely on mutual antagonism between gradients of Wnt expression (purple) and of an as-yet-unidentified molecule (yellow) (Stückemann et al., 2017). Figure partially adapted from (Stückemann et al., 2017).

Our work revealed that complex, erratic dynamics is integral to the cellular dialogues enabling dynamic spatial patterns. Researchers have experimentally observed irregular, complex heart beats during ventricular fibrillations (Ten Tusscher and Panfilov, 2006, Qu et al., 2014) and turbulent flows of cytoskeletal fluids (Giomi, 2015) and fluids of Min proteins (MinC, MinD, and MinE) from E. coli lysates that form patterns on a petri dish (Halatek and Frey, 2018). Our work expands this repertoire to include pattern formations through cellular dialogues. Such complex spatial-patterning dynamics may be difficult to observe in experiments because genetic or developmental programs might be triggered and “take over” the pattern-forming dynamics before the cells had enough time to exhibit the kind of prolonged, erratic dynamics that we uncovered here. For example, before a pattern finalizes, some of the cells in the tissue or an embryo may turn on a different developmental program such as those that lead to cavitation in parts of the tissue or some of the cells to collectively migrate. Consequently, cells may not have the time to exhibit the prolonged complex dynamics for a sufficiently long enough time for us to experimentally distinguish it from a short-lived, transient dynamics. Moreover, another experimental challenge to observing the prolonged complex dynamics is that one must measure gene expression levels of every cell in a tissue or an embryo with sufficiently high temporal and spatial resolutions and do so continuously for a sufficiently long time. With these difficulties in mind, a plate of natural or synthetic cells that use two-molecule cellular dialogues—rather than a full embryo—may allow us to fully observe the complex dynamics using time-lapse microscopy. It may also be interesting to interpret and analyze our work in the context of complex systems theory (Bar-Yam, 2003). Doing so may link our findings to those of non-living chemical systems that self-organize patterns (Nicolis and Prigogine, 1977).

Key Changes Prompted by Reviewer Comments

In response to the reviewers’ comments, we lightly modified the main and supplementary figures to stress the main message contained in them. Although the reviewers did not ask for more work, we added six new supplemental figures to further clarify and support the message that was contained in the original figures. We also added a paragraph in the Discussion section to describe the experimental challenges that one faces in observing the prolonged, erratic self-organization dynamics. For context, the complete Transparent Peer Review Record is included within the Supplemental Information.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
MATLAB R2019a	MathWorks	https://www.mathworks.com
Algorithms for running simulations and analyzing results	This paper	https://github.com/YitengDang/Cell_Systems_2019
Software for visualizing and processing individual simulations	This paper	https://github.com/YitengDang/MultiCellSim
Deposited Data
All raw data used for the main figures	This paper	https://doi.org/10.5061/dryad.6hdr7sqw5

Lead Contact and Materials Availability

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Hyun Youk (h.youk@tudelft.nl). This study did not generate any new materials.

Method Details

Detailed Description of Our Model

In this section, we provide a detailed description of a generalized version of our model, which one can apply to an arbitrary number of diffusing molecules that cells secrete and sense. Our aim here is to concisely summarize the model. For motivations behind the assumptions of our model, please see the main text and our earlier studies (Maire and Youk, 2015a, Olimpio et al., 2018).

We consider N cells that communicate through l distinct, diffusing signaling-molecules that the cells secrete and sense. We first consider cells that are placed on a triangular lattice such that each cell has six nearest neighbors, each at a distance of $a_0$. We specify the state of the system - a "system state" - by

$\mathit{X}\left(t\right)={\left\{X_{k\left(t\right)}\right\}}_{k=1}^N$, where $X_k=\left(X_k^{\left(i\right)},\dots ,X_k^{\left(l\right)}\right)$ is the state of cell k, which we call a "cell state" for cell k. In our description below, we will distinguish between the system state $\mathit{X}$ and the cell state of cell k, $X_k$.

Suppose that cell k secretes a signaling molecule i ($1\le i\le l$) at a rate $C_k^{\left(i\right)}$, which is bounded below and above as: $C_{OFF}^{\left(i\right)}\le C_k^{\left(i\right)}\le C_{ON}^{\left(i\right)}$. Note that we allow for the possibility that the lower and upper bounds on the secretion rate can be different for each signaling molecule. The secretion rate is related to the cell state through the relation

$$C^{\left(i\right)}\left(X_k^{\left(i\right)}\right)\equiv \left(C_{ON}^{\left(i\right)}-C_{OFF}^{\left(i\right)}\right)X_k^{\left(i\right)}+C_{OFF}^{\left(i\right)}\text{.}$$

In the simplest scenario, the cells secrete signaling molecules at a rate which is either low or high. In this case, each of the $X_k^{\left(i\right)}$ takes binary values - 0 or 1 - such that $C^{\left(i\right)}\left(X_k^{\left(i\right)}=1\right)=C_{ON}^{\left(i\right)}$ and $C^{\left(i\right)}\left(X_k^{\left(i\right)}=0\right)=C_{OFF}^{\left(i\right)}$. Alternatively, the secretion rate could take continuous values within the closed interval $\left[C_{OFF}^{\left(i\right)},C_{ON}^{\left(i\right)}\right]$. If so, then the cell states are continuous variables (i.e., $X_k^{\left(i\right)}$ can take any value between 0 and 1. For convenience, we set $C_{OFF}^{\left(i\right)}=1$ for all i and measure all concentrations in units of this OFF-secretion rate (which we take to be equal for all molecules, unless we state otherwise).

The concentration of a signaling molecule, once it reaches a steady state, decays with distance from the cell that is secreting it as follows (Olimpio et al., 2018):

$$c^{\left(i\right)}\left(r\right)=C_k^{\left(i\right)}{f}^{\left(i\right)}\left(r\right)\text{,}$$

$$f^{\left(i\right)}\left(r\right)=\frac{{\lambda }^{\left(i\right)}}{r}\exp \left(\frac{R_{cell}-r}{{\lambda }^{\left(i\right)}}\right)\sinh \left(\frac{R_{cell}}{{\lambda }^{\left(i\right)}}\right)\text{.}$$

Here we assumed that the cells are spherical with radius $R_{cell}\equiv r_{cell}{a}_0$ and ${\lambda }^{\left(i\right)}$ is the diffusion length of signaling molecule i. The diffusion length measures how far the molecule can typically travel before degrading and is set by the molecule's diffusion constant and degradation rate (Olimpio et al., 2018). Here, we also introduced an “interaction function” function $f^{\left(i\right)}\left(r\right)$ to capture the distance-dependent decay. Note that $C_{ON}^{\left(i\right)}\text{and}{C}_{OFF}^{\left(i\right)}$ are effective secretion rates for ON- and OFF-cells respectively that lump together several terms which appear in the reaction-diffusion equation for molecule i. They can depend on the diffusion lengths ${\lambda }^{\left(i\right)}$. But we will consider them to be independent of the diffusion lengths by assuming that $C_{ON}^{\left(i\right)}\text{and}{C}_{OFF}^{\left(i\right)}$ remain constant as we change ${\lambda }^{\left(i\right)}$ by tuning other parameters which we do not specify here for brevity. We can reduce the number of parameters by expressing all lengths in units of lattice spacing, $a_0$. We define $l^{\left(i\right)}\equiv ({\lambda }^{\left(i\right)}/a_0)$ and rewrite the interaction function as

$$f^{\left(i\right)}\left(\rho \right)=\frac{1}{\rho }\exp \left(\frac{r_{cell}-\rho }{l^{\left(i\right)}}\right)\sinh \left(\frac{r_{cell}}{l^{\left(i\right)}}\right)$$

where we introduced $\rho \equiv (r/a_0)$. Here, $r_{cell}\equiv R_{cell}/a_0$ is the radius of a cell expressed in units of the lattice spacing $a_0$.

At any given time, the concentration that a cell senses is the sum of the concentrations due to each of the cells in the system. We express the concentration of molecule i that a cell k senses as

$$Y_k^{\left(i\right)}=\sum _{m=1}^N{f}_{km}^{\left(i\right)}{C}_m^{\left(i\right)}\text{,}$$

where $f_{km}^{\left(i\right)}$ is a distance-dependent interaction strength between cells k and m. Explicitly, we have

$$f_{km}^{\left(i\right)}\equiv \{\begin{array}{ll}{f}^{\left(i\right)}\left(r_{km}\right),\hfill & \left(k\ne m\right)\hfill \\ 1,\hfill & \left(k=m\right)\hfill \end{array}\text{,}$$

with $r_{km}$ being the distance between cells k and m and $f^{\left(i\right)}\left(r\right)$ as defined above.

For later reference, we introduce an "interaction strength" $f_N^{\left(i\right)}$ for each signaling molecule i:

$$f_N^{\left(i\right)}=\sum _{m\ne k}{f}_{km}^{\left(i\right)}\text{.}$$

Note that if all cells secrete at the same rate $C^{\left(i\right)}$, then they would all sense the following concentration

$$Y^{\left(i\right)}=\left(1+f_N^{\left(i\right)}\right)C^{\left(i\right)}\text{.}$$

Regulatory Interactions

We now consider how the sensing of one signaling molecule affects the secretion of itself and other molecules by a cell. Molecule j can affect the secretion of signaling molecule i in three distinct ways (note that i can be equal to j). First, molecule j may activate secretion of molecule i, meaning that a higher concentration of j leads to a higher secretion rate of i. Secondly, molecule j may repress secretion of molecule i, meaning that a higher concentration of j leads to a lower secretion rate of i. Finally, molecule j may not influence the secretion rate of molecule i at all. We can capture these three possibilities by an “interaction matrix” $M_{\text{int}}$, defined as

$$M_{\text{int}}^{\left(ij\right)}=f\left(x\right)=\{\begin{array}{cc}1,& \text{j}\text{activates}\text{i}\\ -1,& \text{j}\text{represses}\text{i}\\ 0,& \text{no}\text{interaction}\end{array}$$

The interaction matrix allows us to define a “cellular dialogue” as a directed (multi)graph in which each node represents one of the l signaling molecules and each directed edge represents one molecule (node) controlling the secretion rate of either itself (self-loop) or another molecule (directed edge from one node to another) as dictated by the interaction matrix.

A cell may respond in one of multiple possible ways to the sensed concentrations of all the signaling molecules. Its biochemical circuitry sets its response. Here we consider a relatively simple case in which the cell senses the extracellular signaling molecules and then uses one of two standard logic gates – AND and OR gates – to integrate the signals triggered by the sensed molecules to regulate the genes that encode each of the signaling molecules. These gates apply to cells with infinite and finite Hill coefficients (i.e., cell’s response is not necessarily binary for either logic gates). First, let us consider a cell that uses an AND-gate to integrate the intracellular signals triggered by the sensing of two signaling molecules. For two signaling molecules that activate the secretion of each other, one way to achieve an AND-gate is having two transcription factors – one for each signaling molecule – both needing to bind to the promoter of the gene that encodes the signaling molecules. One of the two transcription factors alone binding to the promoter would be insufficient for activating expression of – and thus secretion of - any of the signaling molecules. Only when both transcription factors are bound to the same promoter, their cooperative interactions would induce the expression and secretion of the signaling molecule that the gene encodes (Buchler et al., 2003). This scenario leads to a multiplicative update rule for our model. Namely, we determine the cell’s secretion rate at the next time step in the cellular automaton by multiplying several mathematical functions – one for each transcription factor – with each function describing the bound fraction of a given transcription factor. Alternatively, a cell may use an OR-gate to regulate genes that encode the two signaling molecules. Here, either of two transcription factors can induce transcription, without the need for both transcription factors to be present. In practice, this can be realized by placing strong binding sites for both molecules at a considerable distance apart, so that the two transcription factors can individually bind to the promoter and recruit RNA polymerases (Buchler et al., 2003).

Mathematically, let $g^{\left(ij\right)}\left(\mathit{X}\right)$ be the result of the regulation of the gene that encodes molecule i by molecule j, given a system state $\mathit{X}$. If $g^{\left(ij\right)}\left(\mathit{X}\right)=1$, then the gene is activated or unrepressed, whereas $g^{\left(ij\right)}\left(\mathit{X}\right)=0$ means that the gene is either un-activated or repressed. The specific mathematical form of $g^{\left(ij\right)}\left(\mathit{X}\right)$ depends on the regulatory interaction. As a general form, we can write it as

$$g^{\left(ij\right)}\left(\mathit{X}\left(t\right)\right)=\text{θ}\left(\left(Y_k^{\left(j\right)}-K^{\left(ij\right)}\right)M_{\text{int}}^{\left(ij\right)}\right)\text{,}$$

where $\theta \left(x\right)=\{\begin{array}{cc}1,& x>0\\ 0,& x<0\end{array}$ is the step function. The value of $\theta \left(0\right)$ is unspecified, but to be consistent with the case of not having a regulatory interaction ($M_{\text{int}}^{\left(ij\right)}=0$), we set $\theta \left(0\right)=1$ for the AND-logic and $\theta \left(0\right)=0$ for the OR-logic. Using the standard syntax of Boolean algebra, we can denote the AND-operation as $\wedge$ and the OR-operation as $\vee$. Then, using arithmetic representation of logic gates, we have $x\wedge y=xy$ and

$x\vee y=x+y-xy$. Hence, a cell’s response with an AND-gate takes the form

$$X_k^{\left(i\right)}\left(t+1\right)=g_k^{\left(i1\right)}\left(\mathit{X}\left(t\right)\right)\wedge g_k^{\left(i2\right)}\left(\mathit{X}\left(t\right)\right)=g_k^{\left(i1\right)}\left(\mathit{X}\left(t\right)\right)g_k^{\left(i2\right)}\left(\mathit{X}\left(t\right)\right)\text{,}$$

and a cell’s response with an OR-gate takes the form

$$X_k^{\left(i\right)}\left(t+1\right)=g_k^{\left(i1\right)}\left(\mathit{X}\left(t\right)\right)\vee g_k^{i2}\left(\mathit{X}\left(t\right)\right)=g_k^{\left(i1\right)}\left(\mathit{X}\left(t\right)\right)+g_k^{\left(i2\right)}\left(\mathit{X}\left(t\right)\right)-g_k^{\left(i1\right)}\left(\mathit{X}\left(t\right)\right)g_k^{\left(i2\right)}\left(\mathit{X}\left(t\right)\right)\text{,}$$

We can readily generalize these expressions to cells with more than two signaling molecules by using the standard rules of Boolean algebra.

Steady States of the System

For regulatory interactions with infinite Hill coefficients, each cell has one of two states for each signaling molecule – OFF (i.e., basally secreting the molecule) and ON (i.e., maximally secreting the molecule). Hence, if the system has a total of N cells, the total number of possible gene-expression states for the population is finite ($2^N$), meaning that the system (i.e., population) is bound to eventually reach one of two types of steady states in terms of the population-level gene-expression:

• 1Stationary steady-state: There is a time $t^{\ast }$ such that for all $t\ge t^{\ast }$, the system does not change any more (i.e., $\mathit{X}(t+1)=\mathit{X}\left(t\right)$). Simply put, this means that the population-level gene-expression state remains constant starting at time $t^{\ast }$.
• 2Periodic steady-state: There exists a time $t^{\ast }$ after which we have $\mathit{X}(t+\tau )=\mathit{X}\left(t\right)$ for all $t\ge t^{\ast }$. Then $\tau$ is the period of the periodic steady-state. Simply put, this means that the population-level gene-expression state undergoes a periodic oscillation with a period $\tau$.

The $t^{\ast }$ - which we will call equilibration time - is the time that the system takes to reach either one of the two types of steady states. For stationary steady-states, this is simply the first time when the system reaches a state that does not change over time any more. For periodic steady-states, we define the equilibration time when the onset of the periodicity occurs.

Enumerating Cellular Dialogues

If we have two signaling molecules, there are four possible interactions between those two molecules. Each interaction can be either activating, repressing or absent. Hence two molecules can form a total of $3^4=81$ possible cellular dialogues. However, many of these cellular dialogues are equivalent to one another because swapping the labels "1" and "2" on the two molecules (Figure 1C) conserves the topology of the graphs that represent the cellular dialogues (i.e., which molecule is labeled "1" or "2" is arbitrary). Under this label-swapping operation, the interaction matrix becomes

$$\left(\begin{array}{cc}{M}_{\text{int}}^{\left(11\right)}& M_{\text{int}}^{\left(12\right)}\\ M_{\text{int}}^{\left(21\right)}& M_{\text{int}}^{\left(22\right)}\end{array}\right)\mapsto \left(\begin{array}{cc}{M}_{\text{int}}^{\left(22\right)}& M_{\text{int}}^{\left(21\right)}\\ M_{\text{int}}^{\left(12\right)}& M_{\text{int}}^{\left(11\right)}\end{array}\right)\text{.}$$

Hence, for cellular dialogues that are invariant under the label-swapping operation, we must have $M_{\text{int}}^{\left(11\right)}=M_{\text{int}}^{\left(22\right)}$ and $M_{\text{int}}^{\left(12\right)}=M_{\text{int}}^{\left(21\right)}$, leaving us with two independent elements in the interaction matrix. Each of these two elements can have one of three possible values. Thus, the cellular dialogues that are invariant under the label-swapping operation reduce down to a set of 9 distinct cellular dialogues. We can reduce the remaining 72 cellular dialogues to a set of 36 unique cellular dialogues. Hence, we have total of 45 distinct cellular dialogues. After neglecting the trivial cellular dialogues - those in which neither of the two molecules regulates the other - we obtain the set of 44 cellular dialogues that are shown in Figure 3. Note that we also enumerate all cellular dialogues in which a molecule regulates itself but does not regulate the other molecule.

Population-Level Description

To characterize the population-level behavior without focusing on the state of every single cell, we introduce "macroscopic variables". Specifically, we define two macroscopic variables for each molecule, leading to a total of four macroscopic variables for a population. One of them is the average expression level of the gene that encodes molecule i which, in the case of the digital cells, is equal to the fraction of cells that have gene i turned on:

$$p^{\left(i\right)}=\frac{1}{N}\sum _{k=1}^N{X}_k^{\left(i\right)}\text{.}$$

The other macroscopic variable is the "spatial index" for gene i, which characterizes how spatially correlated the expression levels for gene i is among the cells. We first introduced this in earlier studies (Maire and Youk, 2015a, Olimpio et al., 2018) and we now define it for a population with multiple signaling molecules as follows:

$$I^{\left(i\right)}=\frac{1}{{\sum }_{n\ne m}{f}_{mn}^{\left(i\right)}}\frac{{\sum }_m{\sum }_{n\ne m}{f}_{mn}^{\left(i\right)}(X_m^{\left(i\right)}-⟨X^{\left(i\right)}⟩)(X_n^{\left(i\right)}-⟨X^{\left(i\right)}⟩)}{\frac{1}{N}{\sum }_{m=1}^N{\left(X_m^{\left(i\right)}-X^{\left(i\right)}\right)}^2}\text{,}$$

The spatial index for gene i, $I^{\left(i\right)}$, quantifies how spatially ordered the cells are in terms of their expression level for gene i. It can have a value between -1 and 1, with negative values indicating that neighboring cells tend to have different gene-expression levels (such as in checkerboard patterns or anti-ferromagnetism in spin models) and positive values indicating that neighboring cells that tend to have similar gene-expression levels (forming islands with the same gene expression level, similar to ferromagnetism). When $I^{\left(i\right)}=0$, the cells' expression levels of gene i are, on average, uncorrelated. In the case of spatially ordered patterns such as traveling waves, the values of $I^{\left(i\right)}$ are positive and relatively high, with exact values depending on the parameters of the system and the wave's shape.

Together, the set of macroscopic variables ${\left\{p^{\left(i\right)},I^{\left(i\right)}\right\}}_{i=1}^l$ - for l signaling molecules (we considered l = 2 here) - convey population-level information. However, this description does not contain information about correlations between different genes. For example, we may specify, for two-molecule cellular dialogues, that $p^{\left(1\right)}=p^{\left(2\right)}=0.5$ and $I^{\left(1\right)}=I^{\left(2\right)}=0.5$. This tells us that half of the genes of each type are turned on and that the cells which have a certain gene on will tend to cluster with other cells that have the same gene turned on. However, we cannot infer whether a cell that has gene 1 turned on is likely to have gene 2 turned on as well or whether its neighbors tend to have gene 2 turned on. There are different ways to consider metrics that also consider such cross-correlations. For example, we can group together cells with each of the four cell states (i.e., (gene 1=ON, gene 2=ON), (ON, OFF), (OFF, ON), (OFF, OFF)) and study the evolution of these populations. However, the disadvantage of this approach is that it does not easily generalize to continuous gene-expression states that we also consider in our work (i.e., for gene regulations with finite Hill coefficients). Alternatively, we can use established statistical metrics for correlations between two sets of values (i.e., gene-expression levels for the two different genes) such as the Hamming distance, the Jaccard index (JI) and the Sørensen-Dice coefficient. As we are mainly interested in knowing whether a spatial configuration is ordered or disordered (i.e., whether the cells have an "interesting" pattern or not), we have not studied such cross-correlations. Nevertheless, our open-source software, MultiCellSim, computes the cross-correlation along with $p^{\left(i\right)}$ and $I^{\left(i\right)}$.

Moving Averages

We calculated the Fano factor - variance divided by the mean - for each macroscopic variable in Figures 5C and S7 by using a sliding time-window of 10 timesteps (i.e., for a macroscopic variable y(t), we compute its mean and variance for values of t within the interval (t, t+10)). Specifically, we calculated a moving variance using the MATLAB function ttmovvar and the moving mean using ttmovmean. The Fano factor represents a signal-to-noise ratio within a given time-window frame.

Simulation and Analysis of the Model

In this section, we provide a concise overview of our simulations and analyses.

Fixing Initial Conditions

We started simulations by generating a randomly chosen, initial spatial-configuration that is subject to certain constraints. Unless we chose $p^{\left(i\right)}$ and $I^{\left(i\right)}$ to each have a specific value at the beginning of a simulation, we let each cell to have a 50% chance of having gene i be ON. This tends to generate spatial configurations in which half of the cells have gene i turned on. In some cases, we chose $p^{\left(i\right)}$ and $I^{\left(i\right)}$ to each have a specific value at the beginning of a simulation (Figure S6). Here, we fixed the value of $p^{\left(i\right)}$ by randomly selecting this fraction of cells, for which we turn on gene i. To fix the value of $I^{\left(i\right)}$, we used a Monte Carlo algorithm outlined below.

Algorithm for Generating Spatial Configurations with a Given Spatial Index

We devised an algorithm that generated spatial configurations, for initializing our simulations, with specified values for the spatial index $I^{\left(i\right)}$ and $p^{\left(i\right)}$. Our algorithm was motivated by a similar problem in physics - a problem on Ising spin systems - in which one needs to fix the total energy of the spins (analogous to $I^{\left(i\right)}$) without changing the average magnetization (analogous to $p^{\left(i\right)}$). Our algorithm is illustrated in Figure S1 and is as follows:

• 1Given a spatial configuration with a given value of p, start by computing the value of the I for this configuration
• 2Check whether we should increase or decrease I by comparing it to the target value $I_{\text{target}}$
• 3
  If $I<I_{\text{target}}$

  • a)
    Select the ON-cell with the minimum number of neighbors which are also ON. Turn this cell OFF.
  • b)
    Select the OFF-cell with the maximum number of neighbors which are also OFF. Turn this cell ON.
• 4
  Else if $I>I_{\text{target}}$

  • a)
    Select the ON-cell with the maximum number of neighbors which are also ON. Turn this cell OFF.
  • b)
    Select the OFF-cell with the minimum number of neighbors which are also OFF. Turn this cell ON.
• 5Compute the spatial index of the new configuration, $I_{\text{new}}$. Check whether it has increased or decreased as required.
• 6If it has changed as required, accept the change. Go to step 8.
• 7Else, reject the new configuration. Go to step 1.
• 8If $I_{\text{new}}\in \left[I_{\text{target}}-\varepsilon ,I_{\text{target}}+\varepsilon \right]$, terminate the simulation.
• 9Else, go to step 1 with the new configuration with $I=I_{\text{new}}$.

Because we switch the state of both an ON-cell and an OFF-cell, the average number of ON-cells remains constant. To increase I, we choose cells that tend to have a different state from most of their neighbors and change their state. To decrease I, we change cells whose state are similar to that of their neighbors. Note that this algorithm is not guaranteed to converge to $I_{\text{target}}$ because at each iteration of the loop outlined above, we are not guaranteed to increase or decrease I as required. In particular, if the specified value of I is outside the range of possible values for I (Olimpio et al., 2018), the algorithm cannot reach the specified value of I. Therefore, we typically set a limit on the maximum number of iterations before we terminate the algorithm. Finally, we typically set $\varepsilon =0.01$, which allowed for convergence at reasonable speeds while limiting deviations from the target value.

Terminating Simulations

As noted earlier, we terminate a simulation either when the population reaches a steady state or the simulation reaches the maximum number of time steps $t_{\text{max}}$, which we arbitrarily set to be a sufficiently large number. As an example, we chose $t_{\text{max}}={10}^5$ for populations with $N=225$ cells. At each time step, we checked for stationary steady-states by comparing the current system state with the previous timestep’s system state. To check for periodic steady-states, one might resort to manually checking the system state at every timestep to see whether the current state has been visited earlier. This becomes computationally infeasible for running many simulations. So, we devised a more efficient scheme for detecting whether the simulation has entered a periodic steady-state. Instead of checking at every timestep, at every $t_{\text{check}}$ timesteps we manually check whether the previous system state has been visited earlier (we chose $t_{\text{check}}={10}^3$). If we find periodicity in the system states, we ran a second algorithm to find the earliest time at which any state has repeated itself, which told us when the periodic steady-state began.

Batch Simulations

Many of the results presented here are from batch simulations, which means that we performed a large set of simulations and obtained statistics on various measures. In many cases, we fixed all parameter values and only varied the initial spatial configuration. By performing a large set of such simulations, we could distinguish whether an observed feature was a general feature for a particular set of parameters or was merely an artifact of a specific initial spatial-configuration. We also ran many simulations, each time varying the parameter values, to find features that were general for a large range of parameter values. Since the parameter values form a continuum, we could not simulate all possible parameter values and thus had to find a way to sample over the space of all parameter values. Specifically, we employed Latin hypercube sampling (McKay et al., 1979), in which we efficiently sampled over a multi-dimensional parameter space by taking parameter sets that were non-overlapping in any of the dimensions. We used this method to generate a large set of conditions for each of the 44 distinct cellular dialogues that we computationally screened. The results in Figures 3, S4, and S13 used this approach. Specifically, to obtain these results, we defined a region in the parameter space in which we varied the parameters $K^{\left(ij\right)}$ and $C_{ON}^{\left(j\right)}$ over a range of values – ranging from 1 to ${10}^3$ - while keeping all other parameters held fixed. We sampled parameter values within this region by using the MATLAB function lhsdesign to generate a Latin hypercube sample with 10,000 points. We used this approach for each of the 44 cellular dialogues, with both the AND-logic (Figures 3 and S4) and the OR-logic gate (Figure S13).

Identifying Traveling Waves

We devised an algorithm for automatically identifying traveling waves in large sets of simulations. Since traveling waves retain their shape while propagating through space, the values of $p^{\left(i\right)}$ and $I^{\left(i\right)}$ would remain constant over time. Due to the periodic boundary conditions that we used, having a traveling wave would mean that the system state returns to itself after n time steps, where $n=\sqrt{N}$ and N is the total number of cells. Hence, we first screened through the simulations to find the ones that had a periodic steady-state with a period that was a multiple of n – we looked for integer multiples of n since there may be more complicated waves whose shapes slightly morph as they enter the edges of the field. We next checked whether $p^{\left(i\right)}$ and $I^{\left(i\right)}$ were (sufficiently) constant over the course of one period. Using these two features, we could identify traveling waves in batch simulations without, by eye, examining the simulations explicitly one by one. We then extended the algorithm such that it also gave the orientation of the wave if the cells indeed formed a traveling wave (see Figure S11C). We did so through a two-step procedure. First, we distinguished cells that formed the “background” (exterior cells – Figure 4A) from the cells that formed the wave band (assuming that there were three states that made up a wave – see Figure 4A). Then, we traced the cells from an arbitrarily chosen layer of the wave band to see whether they percolate the system from one horizontal (vertical) edge to the other. If so, then we assigned a horizontal (vertical) orientation to the wave. Else, we assigned a diagonal orientation to the wave.

Extending the Model by Adding Complex Elements

In this section, we discuss how we extended our model by adding more complex elements (Figure 6A). In the main text and Figures 6, S11, and S12, we describe in detail how adding the four complex elements shown in Figure 6A affect the formation and propagation of dynamic spatial-patterns. Below, we dedicate one section for each of these four complex elements as well as for another complex element that is not shown in Figure 6 (i.e., spatial gradient of parameter values).

Stochastic Sensing and Response

There are various sources of stochasticity that can affect pattern formations. These include stochastic expression of the genes that encode the signaling molecules and the fact that a cell cannot determine the concentration of the signaling molecules to an arbitrary level of accuracy (i.e., the Berg-Purcell limit). We did not try to specify the exact source of noise. Instead, we modeled the cells’ noisy responses to the signaling molecules by taking a phenomenological approach in which we lumped together various possible sources of stochasticity into a single mathematical term. Specifically, based on our previous work (Olimpio et al., 2018), we let the threshold concentration for how gene I is regulated by molecule j - denoted $K^{\left(ij\right)}$ - to fluctuate from cell to cell and from time to time (Figure 5A – top left). Mathematically, we can represent this fluctuation as

$$K^{\left(ij\right)}=K_0^{\left(ij\right)}+\delta K^{\left(ij\right)}\text{.}$$

Here $K_0^{\left(ij\right)}$ is the threshold concentration for gene i being regulated by molecule j in the absence of any noise and $\delta K^{\left(ij\right)}\sim N(0,{\alpha }^{\left(ij\right)})$ is a normally distributed random variable. At each time step, we used above equation to update the threshold concentration $K^{\left(ij\right)},$ independently for each cell. In order to define a global noise-strength without introducing many variables, we have let ${\alpha }^{\left(ij\right)}=\alpha K_0^{\left(ij\right)}$. In other words, $\alpha ={\alpha }^{\left(ij\right)}/K_0^{\left(ij\right)}$ was fixed for all interactions (i.e., for all pairs (i, j)), meaning that the variation in the threshold concentration was proportional to the threshold concentration, with the same proportionality factor $\alpha$ used for every pair (i, j).

Continuous Cell-Response Function

In our model, we so far assumed that cells are binary and secrete signaling molecule I at either a low, basal rate $C_{OFF}^{\left(i\right)}$ or at a high, maximal rate $C_{ON}^{\left(i\right)}$. This is a valid assumption whenever the response function is sufficiently ultrasensitive, as discussed in the main text. However, to treat more gradual response functions, we replaced the step-response function (i.e., infinite Hill coefficient) by a continuous, Hill function with a finite Hill coefficient. The Hill coefficient quantifies the steepness of the Hill function. For simplicity, we assumed that all molecules have the same Hill coefficient n. The update rule for the cells' states is still the same as previous, but now with

$$g_k^{\left(ij\right)}\left(\mathit{X}\left(t\right)\right)=\{\begin{array}{ll}\frac{{\left({\text{Y}}_{\text{k}}^{\left(\text{j}\right)}\right)}^{\text{n}}}{{\left({\text{Y}}_{\text{k}}^{\left(\text{j}\right)}\right)}^{\text{n}}+{\left({\text{K}}^{\left(\text{ij}\right)}\right)}^{\text{n}}},\hfill & \text{j}\text{activates}\text{i}\hfill \\ \frac{{\left({\text{K}}^{\left(\text{ij}\right)}\right)}^{\text{n}}}{{\left({\text{Y}}_{\text{k}}^{\left(\text{j}\right)}\right)}^{\text{n}}+{\left({\text{K}}^{\left(\text{ij}\right)}\right)}^{\text{n}}},\hfill & \text{j}\text{represses}\text{i}\hfill \\ 1,\hfill & \text{no}\text{interaction}\hfill \end{array}$$

Note that the Hill coefficient in our model does not have a direct physical interpretation. Instead, it is a phenomenological parameter that describes the steepness of the response function. This is because, in real cells, a ligand-bound receptor typically induces gene expression through a complex signal-transduction cascade rather than through a single molecular process such as a binding of a transcription factor at a promoter. As such, the Hill coefficient does not model any one specific biomolecular process. Therefore, whereas in cooperative binding models, Hill coefficients less than one and larger than two are rare, our model allows for the Hill coefficient to be arbitrarily high or low.

Disordered Cell Positions

In the previous sections, we considered cells to be on a triangular lattice. This is a fair representation of certain multicellular systems (see Table S1 in Olimpio et al., 2018 for a list of examples). But in general, communicating cells do not need to be on a regular lattice. To extend our model to account for alternative spatial arrangements of cells, we adapted our model to allow for randomization of the cell positions through an algorithm adapted from Markov Chain Monte Carlo (MCMC) simulations of hard spheres (Krauth, 2006). The algorithm allowed us to tune the degree of randomness of the cell positions, varying from a perfect lattice to a fully disordered arrangement of cells. However, we still assumed that the cells are immobile or move at a much slower time scale than the time scale involved in molecular/gene-expression changes.

We modeled the cells as 2D hard spheres with a radius of $R_{\text{cell}}$ (identical for all cells). The cells were placed in such a way that no two cells overlapped. Initially, the cells were placed on a regular hexagonal lattice, with distance $a_0$ between the cells. We selected a random cell j with position $x_j=(x_j^{\left(1\right)},x_j^{\left(2\right)})$. We then performed a Monte Carlo step, where we attempted to move the cell by a displacement, $x_j\to x_j+\delta x_j$. Here $\delta x_j=(\delta x_j^{\left(1\right)},\delta x_j^{\left(2\right)})$, with $\delta x_j^{\left(1\right)},\delta x_j^{\left(2\right)}$ being two random variables that are independent of each other and drawn from a uniform distribution on $[-\varepsilon ,\varepsilon ]$. If the cell did not overlap with any other cell at the new position, we accepted the move. Otherwise, we rejected the move and a new move was proposed. To avoid repeated rejections, the cell radius and $\varepsilon$ were chosen to be sufficiently small. In all our simulations, we took $R_{\text{cell}}=0.2a_0$ and $\varepsilon =(a_0-2R_{\text{cell}})/4=0.15a_0$.

The number of Monte Carlo steps we performed using this algorithm is a measure for the degree of randomness in our cells' positions. As a rough indication, for a system of N = 144 cells, after 100 Monte Carlo steps, the arrangement still appears to be very similar to a minutely perturbed lattice. After 10⁴ Monte Carlo steps, we observed that the cells were clearly not on a lattice anymore and that distinct rows and columns of cells were still recognizable. After 10⁵ Monte Carlo steps, we found that the arrangement of cells looked similar to what one would obtain by randomly "dropping" cells onto a plane. We can make these statements more precise by looking at the spatial distribution of cells surrounding each cell. Quantitatively, we now have a different interaction strength $f_N^{\left(i\right)}$ for each cell in the system. As the cells become more randomly arranged, the distribution of the interaction strengths becomes broader and the mean also increases. From these calculations, one can show for example, that after ∼10⁵ Monte Carlo steps, a field of N=144 cells obtains spatial configuration that is indistinguishable from that of a field of randomly placed cells.

Cell Motility

We also extended our model to account for undirected, diffusive movements of the cells. Researchers have considered diffusive cell motility as a stochastic process and modeled it with the Langevin equation. They have applied this approach to treat fibroblasts (Dunn and Brown, 1987), endothelial cells (Stokes et al., 1991) and granulocytes (Schienbein and Gruler, 1993). More precisely, these earlier studies have proposed that the underlying process is that of an Ornstein-Uhlenbeck process, in which cells randomly drift while experiencing a restorative force - this force represents friction in a Brownian motion - which tends to bring the cells back to their original positions. A previous work showed that one can represent the discrete time process that corresponds to this process with the following equation (Dunn and Brown, 1987):

$$dx\left(t\right)=\varphi dx(t-1)+\eta \left(t\right)+\theta \eta (t-1)\text{,}$$

where $dx\left(t\right)=x\left(t\right)-x(t-1)$ is the displacement of a cell at time t, $\eta \left(t\right)$ is a discrete random noise term with mean zero, and $\varphi \text{and}\theta$ are real numbers that depend on the restorative force's strength.

For our system, we took a simpler approach to model cell motility by neglecting the temporal correlations which arise in the frictional term. Hence, we assumed that the cells drift around without one cell's motion being correlated with another cell's motion, as in a classic random-walk and Wiener process. To model cell motility then, we used the same Monte Carlo algorithm that we used for randomizing the cell positions but now move all cells at each time step instead of perturbing the initial positions for a fixed number of cells. We defined the cell motility ${\sigma }_D$ to be the width of the Gaussian term, in units of $a_0$, describing the Brownian motion process through which we update the cell positions. Explicitly, at each time step, we updated each of the N cells one by one through

$$\begin{array}{cc}{x}_j\left(t\right)\to x_j\left(t\right)+\delta x_j,& \delta x_j\sim N(0,{\sigma }_D{a}_0)\end{array}\text{.}$$

Here ${\sigma }_D$ is a parameter that quantifies the extent of a cell's motion in units of the lattice constant $a_0$ (i.e., the distance between two neighboring cells when placed on a regular lattice).

Spatial Gradient of Parameter Values

Studies of the Turing-patterning mechanism have revealed that a spatial gradient of production rates and other parameters as well as more complex, spatially anisotropic parameter values can affect in which direction stripes become aligned after forming through Turing instability (Hiscock and Megason, 2015). Motivated by this observation, we wondered whether spatial gradients of parameter values can influence the direction in which waves would travel after forming in our system. To this end, we experimented with applying spatial gradient of parameter values in various directions and for various parameters. As an example, cells at the top edge may have a higher maximal secretion rate for molecule I than the cells at the bottom edge, with the maximal secretion rate continuously changing as we traverse the field of cells row by row. Starting from a parameter set which is able to generate waves, we modified one of the parameters P of a cell k to be position dependent:

$$P\left(x_k\right)=\left(1+f\left(x_k\right)\right)P_0\text{,}$$

where $x_k=\left(x_k^{\left(1\right)},x_k^{\left(2\right)}\right)$ is the position of cell k, $f\left(x_k\right)$ is a modulation term that adjusts the parameter PP, and $P_0$ is a constant. The simplest type of a spatial gradient that we could consider was a step function defined in either a horizontal or vertical direction (Figure S11C). For example, we could take a vertical gradient by defining $f\left(x_j\right)=A_y\theta \left(x_j^{\left(2\right)}\right)$, with a step function $\theta \left(x\right)=\{\begin{array}{cc}1,& x\ge 0\\ -1,& x<0\end{array}$ (this assumes that half of the cells are at $x^{\left(2\right)}>0$). We then quantified the sharpness of the gradient by a gradient-strength parameter $A_y$, which represents the fractional change in the value of P on either side of the step. Note that with this gradient, the average value of the parameter remains unchanged from cell to cell (i.e., ${\sum }_{j}f\left(x_j\right)=0$).

Data and Code Availability

The software with graphical user interface used to visualize simulations is available in the GitHub repository: https://github.com/YitengDang/MultiCellSim. All codes that we used for simulations, analyses of results, and generating plots are available in the GitHub repository: https://github.com/YitengDang/Cell_Systems_2019. All raw data used for the main figures are available at Dryad: https://doi.org/10.5061/dryad.6hdr7sqw5

Published: January 15, 2020