Optimizing the Quality of 4D-DSA Temporal Information

Abstract

BACKGROUND AND PURPOSE:

Quantification of blood flow using a 4D-DSA would be useful in the diagnosis and treatment of cerebrovascular diseases. A protocol optimizing identification of density variations in the time-density curves of a 4D-DSA has not been defined. Our purpose was to determine the contrast injection protocol most likely to result in the optimal pulsatility signal strength.

MATERIALS AND METHODS:

Two 3D-printed patient-specific models were used and connected to a pulsatile pump and flow system, which delivered 250–260 mL/min to the model. Contrast medium (Isovue, 370 mg I/mL, 75% dilution) was injected through a 6F catheter positioned upstream from the inlet of the model. 4D-DSA acquisitions were performed for the following injection rates: 1.5, 2.0, 2.5, 3.0 and 3.5 mL/s for 8 seconds. To determine pulsatility, we analyzed the time-density curve at the inlets using the oscillation amplitude and a previously described numeric metric, the sideband ratio. Vascular geometry from 4D-DSA reconstructions was compared with ground truth and micro-CT measurements of the model. Dimensionless numbers that characterize hemodynamics, Reynolds and Craya-Curtet, were calculated for each injection rate.

RESULTS:

The strongest pulsatility signal occurred with the 2.5 mL/s injections. The largest oscillation amplitudes were found with 2.0- and 2.5-mL/s injections. Geometric accuracy was best preserved with injection rates of >1.5 mL/s.

CONCLUSIONS:

An injection rate of 2.5 mL/s provided the strongest pulsatility signal in the 4D-DSA time-density curve. Geometric accuracy was best preserved with injection rates above 1.5 mL/s. These results may be useful in future in vivo studies of blood flow quantification.

Quantification of blood flow with invasive techniques using pressure and flow-sensing guidewires and catheters is routinely performed as a part of diagnostic and therapeutic procedures involving the heart and peripheral vasculature. Measurement of velocity and flow using MRA or Doppler techniques is also widely available. None of these methods have, however, shown satisfactory utility as a part of diagnostic or interventional procedures of the CNS vasculature. After the discovery of DSA by Mistretta et al in the 1970s, almost immediately, investigators began to use the density of a contrast bolus, as it passed between 2 points, to determine the velocity of blood flow.¹ In a comprehensive review, these techniques, along with their potential benefits and limitations, were described by Shpilfoygel et al.² More recent reports have described using the combination of 2D- and 3D-DSA to quantify blood flow.^3–6

In 2013, Davis et al⁷ reported a technique for reconstructing time-resolved vascular volumes (4D-DSA) from conventional 3D-DSA acquisitions. 4D-DSA provides both the temporal and spatial information required to calculate velocity and flow.^8–10 The velocity and flow calculations depend on the following: 1) visualizing the cardiac-induced rhythmic changes in contrast bolus density occurring between systole and diastole, 2) quantifying the arrival time of the time-varying bolus between 2 points along a vessel, and 3) quantifying the vessel cross-sectional area. The method exploits a naturally occurring image signal in 4D-DSA acquired with arterial injection. During injection, a contrast bolus rapidly mixes with blood flowing downstream from the injection site. Rhythmic changes in the rate of nonopacified blood coflowing with the contrast medium result in a time-varying contrast density.

Studies documenting the feasibility of using the data from a 4D-DSA reconstruction to quantify velocity and flow were recently published by Shaughnessy et al⁸ and by Wu et al.⁹ In both reports, calculation of velocity and flow was found to be dependent on accurate identification of a pulsatility signal in the time-density curves (TDCs) of a reconstruction; this requirement was noted to be a potential limitation of both methods used for quantification. The pulsatility signal is defined as the change in bolus density between systole and diastole as seen in a TDC for a given point in the volume as a function of time. The pulsatility signal strength (ie, amplitude) is largely dependent on the ratio between nonopacified blood and the blood-contrast mixture causing x-ray attenuation changes that are clearly apparent in the TDCs of a reconstruction.

By defining an injection protocol that optimizes this signal strength, our study aimed to increase the utility of the temporal information in a 4D-DSA reconstruction. The goal was to quantitatively evaluate a variety of injection protocols using patient-specific 3D-printed vascular models. From this, an optimal protocol, which provided reconstructions preserving the dimensional accuracy of the vasculature while also optimizing the pulsatility signal strength, was defined. The capacity to quantify blood flow in the angiography suite would enhance treatment planning, evaluation of treatment results, and diagnostic accuracy for a variety of cerebrovascular diseases such as occlusive diseases, AVMs, and aneurysms. Because most patients undergoing studies in the angiography suite will already have an arterial catheter in place, acquiring 4D-DSA data will not necessitate any increase in invasiveness of the angiographic evaluation.

MATERIALS AND METHODS

Vascular Models

Two patient-specific vascular models were created using angiographic data from an institutional review board (UW-Madison School of Medicine and Public Health)–approved data base. The models were 3D-printed out of a rigid photopolymer using a stereolithographic process (Form 2; Formlabs, Somerville, Massachusetts). Details of the 3D printing protocol were recently described by Ruedinger et al.¹⁰ Both models included the ICA and M1 and A1 segments of the MCA and the anterior cerebral artery. The model had ICA inlets of sufficient length to allow full development of flow.¹¹

Flow System

The models were connected to a closed-loop flow system driven by a positive-displacement pulsatile pump (Bdc PD-1100; Bdc Laboratories, Wheat Ridge, Colorado) (Fig 1). Contrast medium was injected through a catheter (6F, Penumbra 5MAX ACE; Penumbra, Alameda, California), which was inserted through an introducer sheath positioned upstream from the ICA inlet. Contrast medium (iopamidol, Isovue 370 mg I/mL, 75% concentration; Bracco, Princeton, New Jersey) was injected with a dual-head power injector (Press Duo Kemoto Kyorindo co., Ltd Nemoto, Kyoto, Japan). A mixture of 40% glycerol and 60% de-ionized water was used as blood-mimicking fluid (density = 1111kg/m³, viscosity = 3.79 cP) to match physiologic parameters. To establish fluid flow rates that simulated physiologic flow hemodynamics, we set total flow to match a cardiac output averaging 5.5 L/min at a frequency of 60 beats per minute. Over each cardiac cycle, the flow varied between 0 and 7 L/min. A bypass loop was used to simulate the systemic circulation so that the average flow delivered to the model inlet (ICA) was between 250 and 260 mL/min. Flow rates were measured using an ultrasonic flow probe (16PXL-MS25; Transonic, Ithaca, New York).

Fig 1.

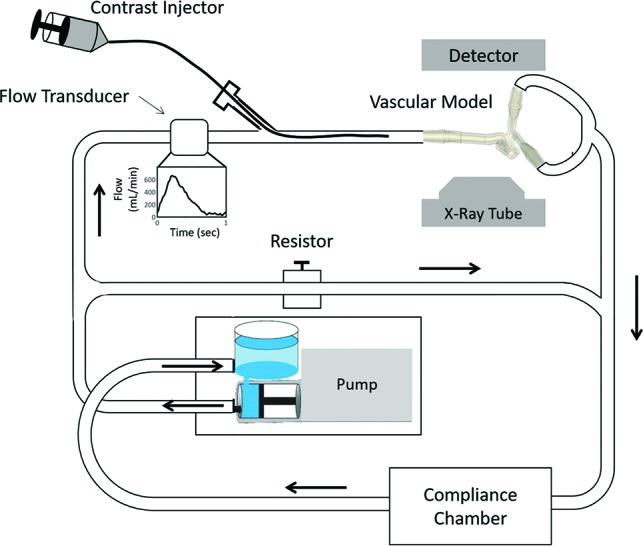
Closed-loop flow system. Setup includes a pulsatile pump, flow transducer, power injector, patient-specific vascular model, flow-diverting loop to simulate systemic vasculature, a compliance chamber, and location of the x-ray detector.

Data Acquisition

A commercially available C-arm angiographic system was used for x-ray imaging. (Artis zee; Siemens, Erlangen, Germany). Rotational angiographic data for each of the models were acquired using a vendor-approved protocol for 4D-DSA (70 kV, 0.36 μGy/frame, 260° rotation, 304 projections/rotation). Each 4D-DSA acquisition consisted of a noncontrast (“mask”) rotation followed by a contrast-enhanced (“fill”) rotation. Contrast medium was injected at rates of 1.5, 2.0, 2.5, 3.0, 3.5 mL/s for 8 seconds with no x-ray delay. Two datasets (trials) were acquired for each of the 2 models at each injection rate (n = 10). The mask runs were assessed to ensure that the interval between injections was sufficient for the contrast not to accumulate in the fluid to a degree that would reduce the pulsatility signal strength in the fill rotation. The fluid was renewed if necessary.

Image Postprocessing

Each dataset was reconstructed using a 4D-DSA prototype reconstruction, not commercially available, on a vendor-supplied research workstation (X-Workplace; Siemens). These reconstructions comprised temporal series of 512 × 512 × 384 voxel volumes with a homogeneous voxel size of 0.46 mm. The reconstructions contained temporal and spatial information as voxel-specific TDCs.

Sideband Ratio and Amplitude Calculation

The inlet of each model was manually segmented from the rest of the model vasculature, resulting in approximately 20,000 voxels and their corresponding TDCs. A previously described numeric metric, the sideband ratio (SBR), was used to determine pulsatility signal strength from a TDC.⁸ If a given TDC exhibits strong pulsatility signal strength, a large peak will be prominent in the Fourier transform; therefore, a large ratio between the peak and the nearby neighboring frequency signals (high SBR) will be present. The SBR values for the largest pulsatile signal within each TDC were used to analyze overall pulsatility signal strength within the inlet section. The median SBR value within the entire inlet section was then used as the final metric for determining pulsatility strength in the 4D-DSA reconstruction. Each of the 2 trials for both of the models was included in the SBR cohort, and the median was determined. The median estimator was chosen instead of the mean because it is less sensitive to outlier SBR values resulting from the noise and artifacts in the 4D-DSA image sets.

The amplitude of the pulsatility signals was quantified for each of the 4D-DSA reconstuctions as a secondary metric. The analysis of pulsatility signal amplitude was made within voxels defined by 2 cubes (5 × 5 × 5 voxels) placed at the proximal and distal extents of the inlet. Voxels that were positioned fully outside the vessel did not show a TDC and were not included in the analysis. The average of the median pulsatility signal was calculated for each of the 2 trials.

Hemodynamic Analysis

A change in the injection rate of contrast results in changes in the hemodynamics of the contrast bolus. To characterize this feature, 2 dimensionless numbers (Reynolds [Re] and Craya-Curtet [Ct]) were calculated for each of the injection rates. The Reynolds number describes the ratio of inertial-to-viscous forces within the fluid. It was calculated for both the blood-mimicking fluid (base fluid) and the contrast medium using Equation 1, where ρ = density, v = velocity, D = diameter, μ is the viscosity of the base fluid (f) or contrast (c).

The Ct number describes the ratio of momentums of the base fluid to the contrast. This number is an indicator of the type of flow patterns that will occur during an injection.¹¹ In turn, this determines how well mixing of contrast with the base fluid will occur.¹¹

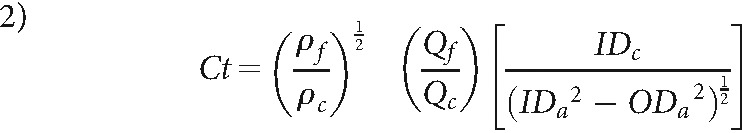ρ_b and Q_b and ρ_c and Q_c are the densities and mean flow rates of blood and contrast, respectively, ID_c and OD_c represent the inner and outer diameters of the catheter, and ID_a is the lumen diameter of the artery.

Geometry Comparison

Ground truth geometries of both vascular models were determined using results from previously acquired micro-CT scans.¹⁰ Measurement of the inlet diameters of each model was performed using a geometry-analysis tool available on a vendor-provided workstation (syngo Neuro Aneurysm Analysis; Siemens). The inlet of each model was measured 3 times, resulting in a total of 12 (2 models × 2 trials × 3 measurements) measurements for each injection rate. The mean absolute difference between the measured inlet diameter and the ground truth diameter (model 1 = 4.60 mm, model 2 = 4.96 mm) and the SD was calculated for each dataset.

RESULTS

4D-DSA Reconstructions

Except for 1 acquisition, at an injection rate of 1.5 mL/s in model 2, the TDCs showed an appropriate increase in density immediately after contrast injection with clearly defined oscillations in bolus density between systole and diastole. The outlier was due to contrast layering with slow washout with time, which created a higher-than-expected overall intensity (Fig 2, model 2).

Fig 2.

TDCs from both trials of the 5 different injection rates, 1.5, 2.0, 2.5, 3.0, 3.5 mL/s. TDCs show differences in contrast intensity from varying injection rates. Variation at the 1.5-mL/s injection rate in model 2 stems from contrast layering.

SBR and Amplitude

In model 1, the median SBR at the inlet was highest (11) with the 2.5 mL/s injection (Fig 3). The median oscillation amplitude between systole and diastole was highest in the acquisitions with 2.0- and 2.5-mL/s injection rates (Fig 3). Details of the median SBR and oscillation amplitudes for trials 1 and 2 in this model are shown in Fig 3.

Fig 3.

SBR and amplitude of oscillation within the TDC for model 1. The median SBR at different injection rates is presented for the entire inlet section for the combination of trials (lower bar graph). A higher SBR corresponds to stronger contrast pulsatility, with an injection rate of 2.5 mL/s producing the highest SBR. The amplitude of oscillation is studied in 2 cubes that transect the vessel diameter at 2 locations within the inlet of model 1. The median of the oscillation amplitude and median absolute derivation within each cube of voxels are presented for each trial (upper bar graphs). AU indicates Arbitrary Units, and the error bars show SBR variance from the voxels within the 2 cubes.

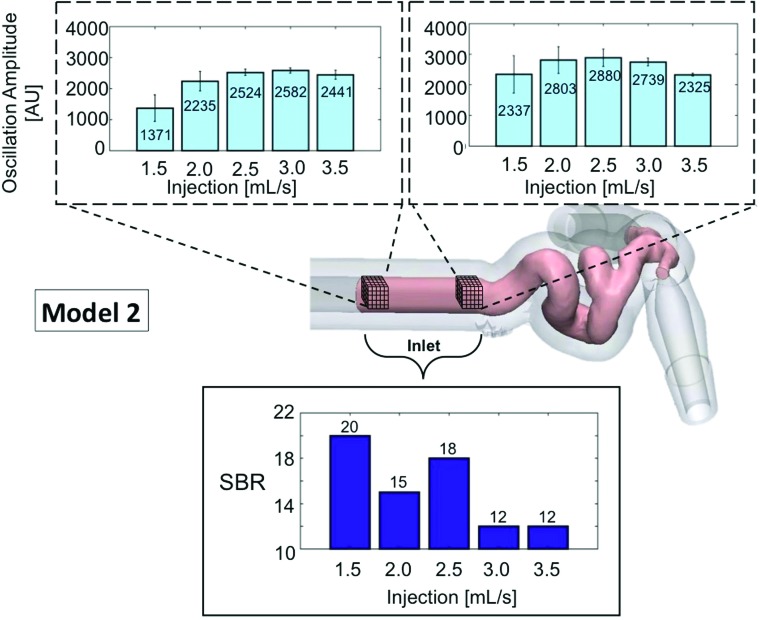
In model 2, excluding the acquisition at 1.5 mL/s in which contrast layering and stasis were observed, the 2.5-mL/s injection rate also provided the highest SBR (18) and the second highest amplitude in the proximal section and the highest in the distal section of the inlet. Details of the median SBR and oscillation amplitudes for both trials in model 2 are shown in Fig 4.

Fig 4.

SBR and amplitude of oscillation within the TDC for model 2. The median SBR at different injection rates is presented for the entire inlet section for the combination of trials (lower bar graph). A high SBR represents strong contrast pulsatility; 1.5 mL/s is abnormally high due to contrast layering causing an erroneous signal in the 4D-DSA reconstruction. The amplitude of oscillation is studied in 2 cubes that transect the vessel diameter at 2 locations within the inlet of model 2. The median of the oscillation amplitude and median absolute derivation within each cube of voxels are presented for each trial (upper bar graphs). AU indicates Arbitrary Units, and the error bars show SBR variance from the voxels within the 2 cubes.

Geometric Analysis

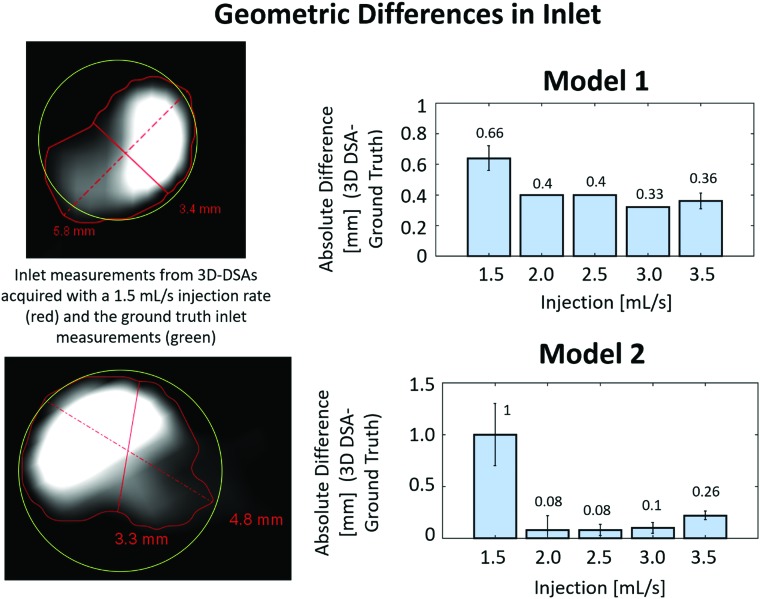
The largest absolute differences in inlet diameter measurements from the 4D-DSA reconstructions to the ground truth micro-CT measurements were 0.66 ± 0.08 mm in model 1 and 1.0 ± 0.3 mm in model 2 at the lowest injection rate, 1.5 mL/s (Fig 5). The 1.5-mL/s injection rate also had the largest SD in inlet measurements from the 4D-DSA reconstruction in both model 1 (0.08 mm) and model 2 (0.3 mm). Figure 5 also illustrates a smaller difference in geometry with injection rates at 2.0 mL/s and above.

Fig 5.

Left, effect of contrast layering on volumetric reconstruction. The absolute difference (millimeters) between the inlet diameter measurement using the workstation tool and the ground truth inlet diameter from micro-CT measurements is shown in the bar graphs (right). The greatest geometric difference in both models occurs with the 1.5-mL/s injection rate. Error bars represent variance in absolute differences based on multiple measurements.

Hemodynamic Analysis

Achieving a ratio between the contrast blood mixture and the nonopacified blood comprising an injection bolus is dependent on the type of mixing flows created at the injection site. Because the inner diameter of an injection catheter is typically much smaller than that of the artery into which contrast is injected, the velocity of the contrast medium is considerably higher than that of blood flow. The dimensionless Ct number is an indicator of the characteristics of these flows and thus of the degree to which mixing occurs during an injection. In a previous study, optimal mixing, as desired for temporal sig-nal encoding through contrast-density changes, was seen when the Ct number was in the range of 0.4–0.9.¹¹ The Table illustrates hemodynamic parameters of both the base and contrast flow and velocity, as well as the governing dimensionless numbers of Reynolds and Ct or model 1 (upper half) and model 2 (lower half). Changes in hemodynamic parameters were consistent with those expected (Table).

Hemodynamic parameters characterizing flow profiles achieved from various injection rates within the closed-loop flow setup^a

Injection Rate	Qf (mL/min)	Vf (cm/s)	Vc (cm/s)	Ref	Rec	Ct
1.5			120.30		101.6	0.69
2			160.40		135.5	0.52
2.5	252	22.27	200.50	328.72	169.3	0.41
3			240.60		203.2	0.35
3.5			280.70		237.0	0.30
1.5			120.30		101.6	0.70
2			160.40		135.5	0.52
2.5	260	22.43	200.50	335.05	169.3	0.42
3			240.60		203.2	0.35
3.5			280.70		237.0	0.30

Note:—Significant figures varied depending on the hemodynamic parameter. Q_f indicates flow rate of working fluid; V_f, velocity of working fluid; V_c, velocity contrast; Re_f = Reynolds number of working fluid; Re_c, Reynolds number of contrast.

^aUpper half refers to model 1, and bottom half refers to model 2.

DISCUSSION

Using 2 patient-specific 3D printed vascular models and a closed-loop pulsatile flow system, we demonstrated that the pulsatility signal strength in TDCs from a 4D-DSA reconstruction is sensitive to small changes in the rate of contrast medium injection. An injection protocol was found that optimized the quality of the temporal data while also maintaining the fidelity of the spatial data. These results could be helpful in clinical studies aimed at assessing the utility of 4D-DSA for measuring blood flow.

Since Tenjin’s original description of using TDC analysis for the evaluation of blood velocity, additional studies using variations on his method have been reported for the analysis of flow under a variety of conditions.^12–15 The feasibility of measuring some parameters of flow (eg, time to peak, inflow, outflow) was shown in studies of aneurysms and AVMs both before and after treatment.^13–15 In 2 of these, contrast was manually injected intra-arterially, and analysis was based on placement of an ROI on projections of the vasculature chosen to eliminate or minimize vessel overlap. The use of manual injection of contrast and the lack of information regarding the length of time for the DSA acquisitions reduce the utility of the temporal data acquired from these studies.

Another study reported the use of parametric processing of 2D-DSA to provide color-coded images of hemispheric blood flow in 18 patients with chronic ischemic disease. Contrast medium was injected into the aortic arch using a power injector. All patients also had conventional PET perfusion imaging; the mean interval between the x-ray and PET studies was 2.05 ± 1.75 days. Strong correlation was found between relative perfusion parameters measured with PET and flow parameters determined from the 2D x-ray angiographic perfusion technique. The combination of a lack of any details of the software and the inability to measure anything more than global blood flow (ie, hemispheric with a 2D technique and the long interval between the x-ray and PET studies) makes it difficult to assess the validity of the reported results. Lin et al¹⁴ evaluated the ability to measure flow velocity in the angiographic suite using data from 4D-DSAs in a study consisting of healthy control, ruptured AVM, and unruptured AVM groups. In measurements made from ROIs placed on the ICA and MCA, they reported that the amplitude of pulsatile waveforms in patients with AVMs was greater than that of the controls, with pulsatile waveforms not seen in some 20% of the control group as well as in the ruptured AVM group. Lin et al commented on the need for a better understanding of how the injection protocol may impact pulsatility waveforms; therefore, it directly relates to our study.

Blood flow, bolus volume, injection rate, downstream resistance, and artery size all influence the amplitudes of TDCs. These are intrinsically less in small vessels compared with larger ones. Downstream amplitudes are similar to ones measured upstream when resistance downstream is lower (eg, in the nidus of an AVM as in healthy controls).¹⁵ Image quality (SNR) is less when nonopacified blood enters the vessel of interest downstream from the injection site or when the contrast injection does not result in either adequate mixing of contrast with blood or causes mixing to a degree in which variations in bolus density between systole and diastole are much reduced (ie, the bolus becomes homogeneous). Of these variables, the only one controllable in clinical studies is the injection protocol.

Our study defined 1 way for evaluating how variations in injection rates may influence the amplitudes of the pulsatility waveforms. The ability to achieve optimal pulsatility strength would increase the accuracy and utility of velocity and flow measurements using a 4D-DSA reconstruction. Having this ability in the angiography suite could result in increased ability to identify those arteries that have increased or decreased velocity and flow (eg, AVMs and steno-occlusive disease), compared with those with normal velocity and flow. This, in turn, could allow a more accurate selection of target arteries for embolization in AVMs and for stent placement or thrombectomy. The ability to compare velocity and flow before and after an intervention would also likely add value to assessing the effectiveness of said intervention.

Limitations of our study include the inability to transfer the results to acquisitions with catheters and vessels of different sizes. Just as the Reynolds and Ct numbers changed dramatically with small (ie, 0.5 mL/s) changes in the injection rate, these parameters may also change considerably with small changes in the internal diameter of the injection catheter and vessel size. Our results also directly apply only to situations when blood flow is in the range of that used for our experiments. These limitations may be reduced by studies of amplitude changes performed with other commonly used catheters and a range of physiologically realistic flow rates.

CONCLUSIONS

The availability of blood flow quantification in the angiography suite would add to the ability to understand the significance of flow abnormalities that are either too slow or too fast. It would also improve the ability to measure the degree to which interventions to augment or reduce flow are effective. The reliability of blood flow quantification using the temporal information from a 4D-DSA reconstruction depends on the ability to consistently and accurately detect the cardiac-induced pulsatility in the time-density curves. The greatest pulsatility signal strength while maintaining geometric accuracy in the 4D-DSA reconstruction was provided with the contrast injection rate of 2.5 mL/s. The definition of an optimal contrast injection protocol for 1 catheter size and flow rate is 1 step in creating a tool that would provide guidance regarding a patient-specific injection protocol.

ABBREVIATIONS:

Ct

Craya-Curtet number

SBR

sideband ratio

TDC

time-density curve