Molecular dynamics simulations and linear response theories jointly describe biphasic responses of myoglobin relaxation and reveal evolutionarily conserved frequent communicators

Abstract

In this study, we provide a time-dependent mechanical model, taking advantage of molecular dynamics simulations, quasiharmonic analysis of molecular dynamics trajectories, and time-dependent linear response theories to describe vibrational energy redistribution within the protein matrix. The theoretical description explained the observed biphasic responses of specific residues in myoglobin to CO-photolysis and photoexcitation on heme. The fast responses were found to be triggered by impulsive forces and propagated mainly by principal modes <40 cm⁻¹. The predicted fast responses for individual atoms were then used to study signal propagation within the protein matrix and signals were found to propagate ~8 times faster across helices (4076 m/s) than within the helices, suggesting the importance of tertiary packing in the sensitivity of proteins to external perturbations. We further developed a method to integrate multiple intramolecular signal pathways and discover frequent “communicators”. These communicators were found to be evolutionarily conserved including those distant from the heme.

Significance.

We provide a general time-dependent linear response theory to describe molecular allostery that does and does not involve protein conformational changes (the latter is referred to as dynamic allostery), validated using biphasic Ultraviolet Resonance Raman (UVRR) data. The theory also described acoustic-wave-validated mechanical signal propagation in and across secondary structural elements, the results of which suggested the importance of tertiary packing in proteins. We further discovered frequent “communicators” via a newly devised communication matrix tallying pairwise communication in short time intervals when perturbations were initiated in every residue along 21 evenly distributed directions. The communicators were found to be evolutionarily conserved, including those distant from the heme.

Understanding the allosteric control of molecular functions through investigation of energy flows within biomolecules has been continuously arousing scientific and medical interest over the past 20 years, encouraged by ever-increasing computing power and the implementation of appropriate physical theories. Exemplary systems include the relaxation dynamics of photolyzed heme-proteins [1–8], such as the photodissociation of monoxide (CO) originally captured in carbonmonoxy myoglobin (MbCO). This can be studied by ultrafast spectroscopy, which allows the characterization of relaxation dynamics on the time scale of fem-to-to picoseconds [2,3,9,10]. The energy flows of multiple-stage relaxations, traced by ultrafast lasers, start from a photoexcited electronic state of heme, through the vibrational excitation of heme to the protein environment, and end by dissipating into the solvent [1]. Using time-resolved near-infrared absorbance spectra [1], it has been reported that the photoexcited electronic state of heme relaxes to its ground state with a time constant of 3.4±0.4 ps and the ensuing thermal relaxation characterized by the temperature cooling exponentially with a time constant of 6.2±0.5 ps [1]. In the crystalline environment, such a relaxation was reported to approach equilibrium at a faster pace through damped oscillations with a time period of 3.6 ps [11]. Furthermore, the excited heme communicates with distant sites through vibrational modes within a few picoseconds, where the delocalized “doming modes” of heme are identified around 40 cm⁻¹ using nuclear resonance vibrational spectroscopy [7]. Two in-plane heme modes ν₄ and ν₇ were referred to couple with motions along the doming coordinate (40–50 cm⁻¹) and with spatially extended modes (centered at 25 cm⁻¹) using high frequency laser pulses [8].

Recently, the advancement of ultraviolet resonance Raman (UVRR) spectroscopy has been exploited to investigate redistribution of vibrational energy in the protein matrix with the aid of its enhanced intensity of the Raman scattering [2,3,9,10]. Mizutani and colleagues used time-resolved UVRR (UV-TR3) spectroscopy to measure the time constants of relaxation dynamics for several tryptophans in two different experiments of the photodissociation of MbCO [2,3]. The band intensity of Trp7 and Trp14, situated at the A helix, changed as a function of time owing to the change of their hydrophobic environment in the photodissociation-induced relocation of E helix relocation as well as its interaction with the A helix [2]. The study also reported biphasic changes in Trp14 and Tyr146 (on H helix) with a fast decaying response in a couple of picoseconds, followed by a slower recovery response for 7 to >40 ps, involving permanent intensity changes [2]. In the study, Tyr146 was able to recover fully to its original hydrophobic environment before the CO dissociation, whereas W14 can only recover half of the original intensity. In 2014, the same group irradiated and excited heme, and vibrational relaxation of Mb, without a permanent conformational change, was monitored by UVRR spectroscopy [3]. In these studies [2,3], the biphasic decay of relaxation motions was observed, and the time constants of fast and slow responses of several residues were identified, which provides an excellent model system for our theoretical studies on the energy flow and its underlying mechanism of vibrational energy transfer within Mb.

On the other hand, many theories and algorithms have been developed to describe the vibrational energy relaxation and mechanical signal propagation [12–18]. The lifetime of CO vibrations estimated using the Landau–Teller formula were found to agree well with the time-resolved mid-infrared absorbance experiments [4]. To further understand the inherent inhomogeneity in the spatially dependent relaxation rate of the solvated protein, Langevin model has been used to estimate the inherent friction in protein motion [19–21]. Besides the propagation of heat flow, kinetic energy or vibrational energy redistribution in proteins has also been investigated with mode diffusion (or mode-coupling) [22–25], MD simulations [26–28], and linear response theory (LRT) [21,29–31].

In our previous work, we were able to use normal mode-based time-dependent LRT (NMA-td-LRT) [21] to describe the relaxation dynamics of ligand photodissociation of MbCO in the UV-TR3 experiment as solvent-damped harmonic oscillators solved using Langevin dynamics [2]. A general assumption of the normal mode-based theory is that the conformational space of protein motions is around the global minimum of the potential energy surface. However, a protein evolves across a wide range of the potential energy surface [32,33] at room temperature, and the span of the motion can be described by PC modes derived from the essential dynamics or principal component analysis (PCA). Although this entails regard for external perturbation that is no longer small, which challenges the validity of the td-LRT, we earlier proved that, for systems evolving a harmonic energy surface, the assumption of a small perturbation is no longer a requirement [21,34] (see also Supplementary Materials).

In this study, we formulated a PCA-based td-LRT (PCAtd-LRT) to investigate the signal propagation in Mb. The theoretical formulation was examined by comparing the estimated time constants of several residues for short (the “fast” response in the UVRR spectroscopy experiment) and long (the “slow” response in the UVRR spectroscopy experiment) relaxation with those observed in two UV-TR3 experiments [2,3]. A large difference in the energy-transfer speed for inter- and intra-helical signals, suggesting the importance of protein tertiary packing in mediating vibrational energy was reported. We also explored the mode dependence of the signal propagation to understand the range of modes heavily involved in transmitting fast response signals. Finally, following a recently introduced communication matrix strategy to record the counts of mechanical signals [17] launched from sites nearest to the Fe atom propagating through donor-acceptor pairs, a communication score (CS) of each residue was assigned, which quantified how frequently mechanical signals go through this residue. The sites with high CS were termed “communication centers” (CCs), which were found in this study to be evolutionarily conserved. In addition, these CCs were previously found to be able to allosterically regulate enzyme activity [17].

Methods

Summary of the theories and algorithms used in this study

Extending from our NMA-td-LRT [21], a new implementation of td-LRT was made based on MD simulations and PCA of the trajectories. The conformational changes of CO association were described by constant force (CF-) td-LRT (CF-td-LRT) (Fig. 1). Previously, UV-T3R [2], NMA-based CF-td-LRT [21], and currently the MD-based CF-td-LRT all showed a fast response of Y146 taking place within ~2 ps, as a beating component in the course of slower conformational relaxation due to the CO dissociation. This inspired our use of impulse force (IF) to formulate the td-LRT, which gave a similar result (2.4 ps; see Results). In both td-LRTs, we expressed the td covariance matrix with the PC modes, each of which was subject to Langevin damping after Chandrasekhar’s treatment [35]. We then use this IF-td-LRT to examine the speed of intra- and inter-helix communication (Fig. 2) as well as the influence of mode composition on IF-td-LRT-sampled response times (Fig. 3). Given the theoretical agreement with a number experimental results, we developed a communication map (Fig. 4), using IF-td-LRT with perturbations triggered from multiple sites in multiple directions, to discover the communication hubs in a protein. The so-called CCs were found to be evolutionarily conserved (Fig. 5), and not necessarily overlapping with mechanical hinges, folding cores, and highly correlated residue pairs (Fig. 6).

Figure 1.

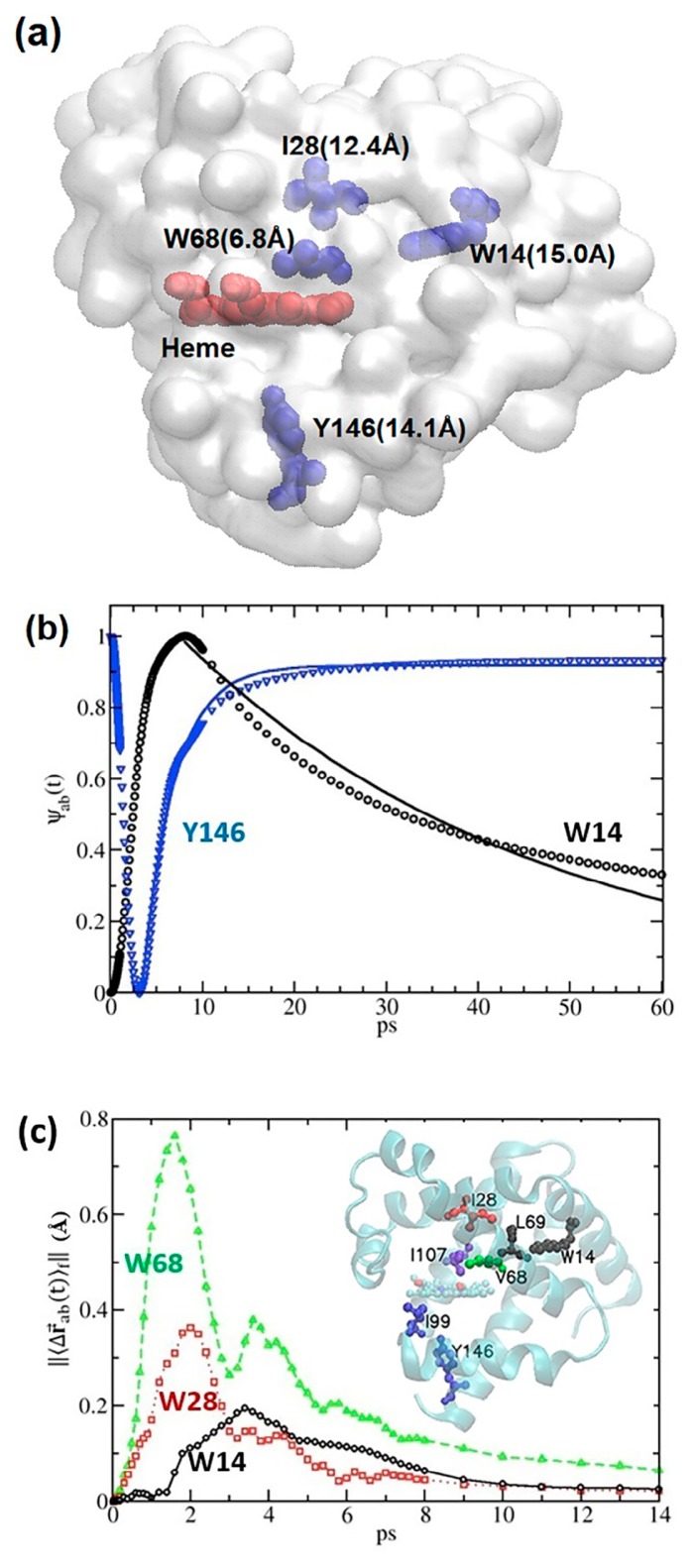
Time-dependent linear response theory using constant forces and impulse forces to explore biphasic relaxation dynamics in myoglobin. (a) The distances between the heme (in red) and the 4 Trp sensors (V68W, I28W, Y146, and W14 colored in cyan; note that Y146 was not studied in Fujii et al. [3]) are marked in parentheses; the transparent structures in the surface presentation are the deoxy-Mb (1A6N). (b) Using constant force time-dependent linear response theory (CF-td-LRT), the reaction coordinate Ψ_ab (t), a normalized distance between the geometry centers of the residue pairs (the residues of interest studied by UV-TR3 and the residues representing their hydrophobic environment) is plotted as a function of time. 350 PC modes up to ~40 cm⁻¹ (see Fig. 3) were used in the CF-td-LRT calculations. (c) The relative distance between the center of mass of the side chain, ||〈Δ⇉_ab (t)〉_f||, was investigated using impulse-force (IF) td-LRT (IF-td-LRT), where the IFs included: (1) a point force exerted at Fe atoms pointed from CO (if bound) and (2) forces along the directions of the heme vibrational mode ν₇ [8]. Here, The characteristic times of V68, I28, and W14, whose hydrophobic environment is represented by their closest contact residues I107, I107, and L69, were 1.6, 2.0, and 3.4 ps, respectively.

Figure 2.

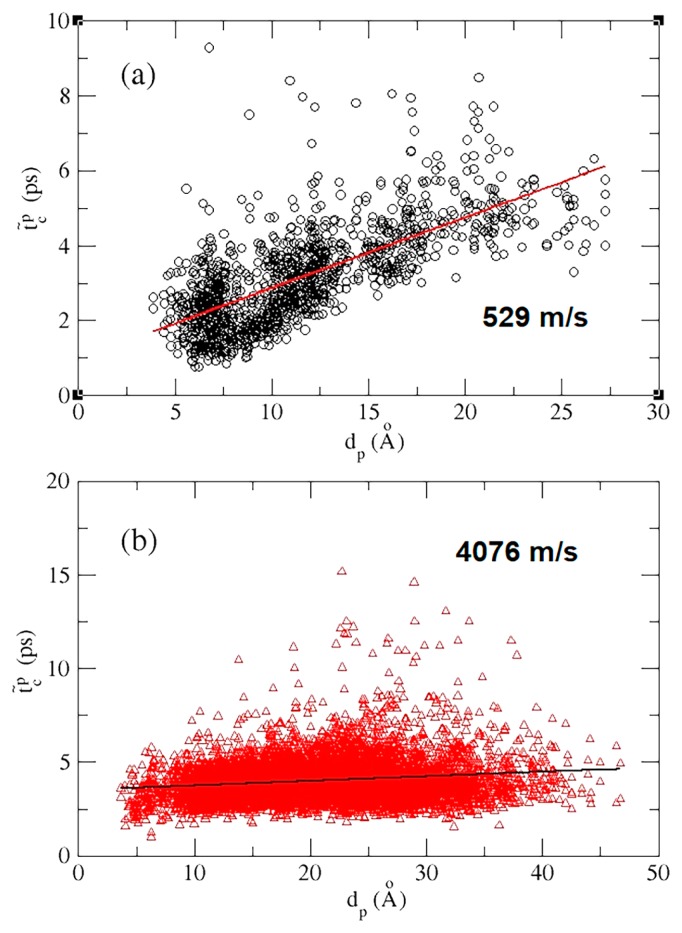
The site-to-site mean characteristic time, ${\tilde{\mathit{t}}}_{\mathit{c}}^{\mathit{P}}$, as a function of distance, d_p, between perturbed sites and sensing sites. (a) Intra-helical signal propagation, where both perturbed and sensing sites are located in the same helix. (b) Inter-helical signal propagation, where perturbed and sensing sites are located in different helices. To estimate the intra-helical and inter-helical signal propagation speed, a linear regression is taken to give a speed, which is the inverse of the slopes.

Figure 3.

The characteristic time ${\tilde{\mathit{t}}}_{\mathit{c}}^{\mathit{r}}$ as a function of the cut-off frequency ω_max in the range of 12<ω_max<1100 cm⁻¹ where ω_max indicates the upper bound of the PC modes used in building the covariance matrix. ${\tilde{\mathit{t}}}_{\mathit{c}}^{\mathit{r}}$ is the characteristic time over evenly distributed impulse forces acting on the Fe atom only, and an error bar of ${\tilde{\mathit{t}}}_{\mathit{c}}^{\mathit{r}}$ reflects the variance of characteristic times for constituent atoms in a residue. W14, I28, V68, and Y146 were the four residues studied by UVRR spectroscopy [3] (their distances from heme are shown in Fig. 1a), and our ${\tilde{\mathit{t}}}_{\mathit{c}}^{\mathit{r}}$ calculation of results for them are shown in black circles, red squares, green upward-facing triangles, and blue downward-facing triangles, respectively.

Figure 4.

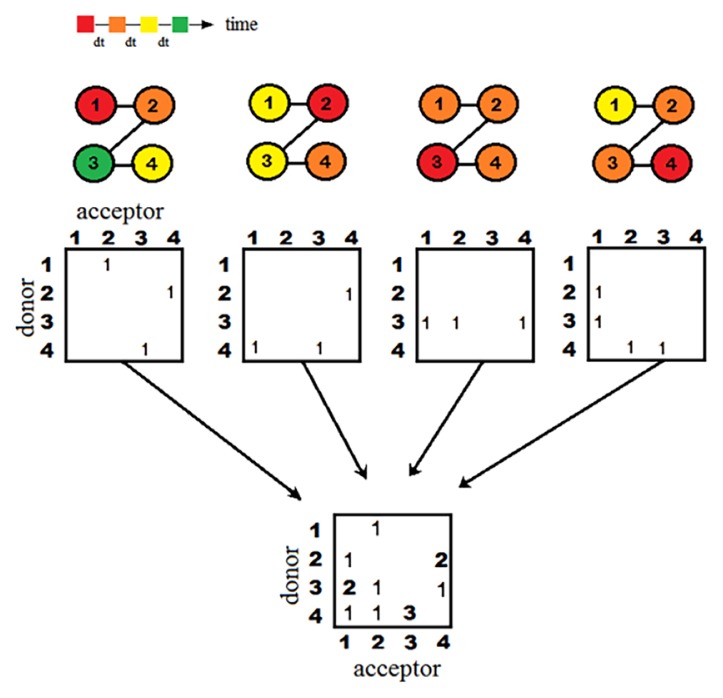
Recording the signal propagation into communication matrices. From the top, the number-labelled spheres linked by solid lines model a tetrapeptide (or four covalently bonded atoms), where the number is the residue (or atom) index. The colors indicate a time sequence of characteristic times (t_c). The signals start from the red nodes and then propagate to orange, yellow, and eventually green nodes in equal intervals. Donor–acceptor matrices are used to note the pairwise signal transmissions from a donor to an acceptor, if their t_c differs by a selected time interval, dt=0.2 ps in this study. Counts are added to a cell in the communication matrix corresponding to a given “connected” pair when perturbations are initiated from a number of nodes and in 21 different directions. Following eq. (3), after summation over all matrices with perturbation initiated at different node j (k⃗_j), toward a selected set of directions, we can have the all-atom communication matrix F(a_d, a_r) that notes the residue pairs communicating the most.

Figure 5.

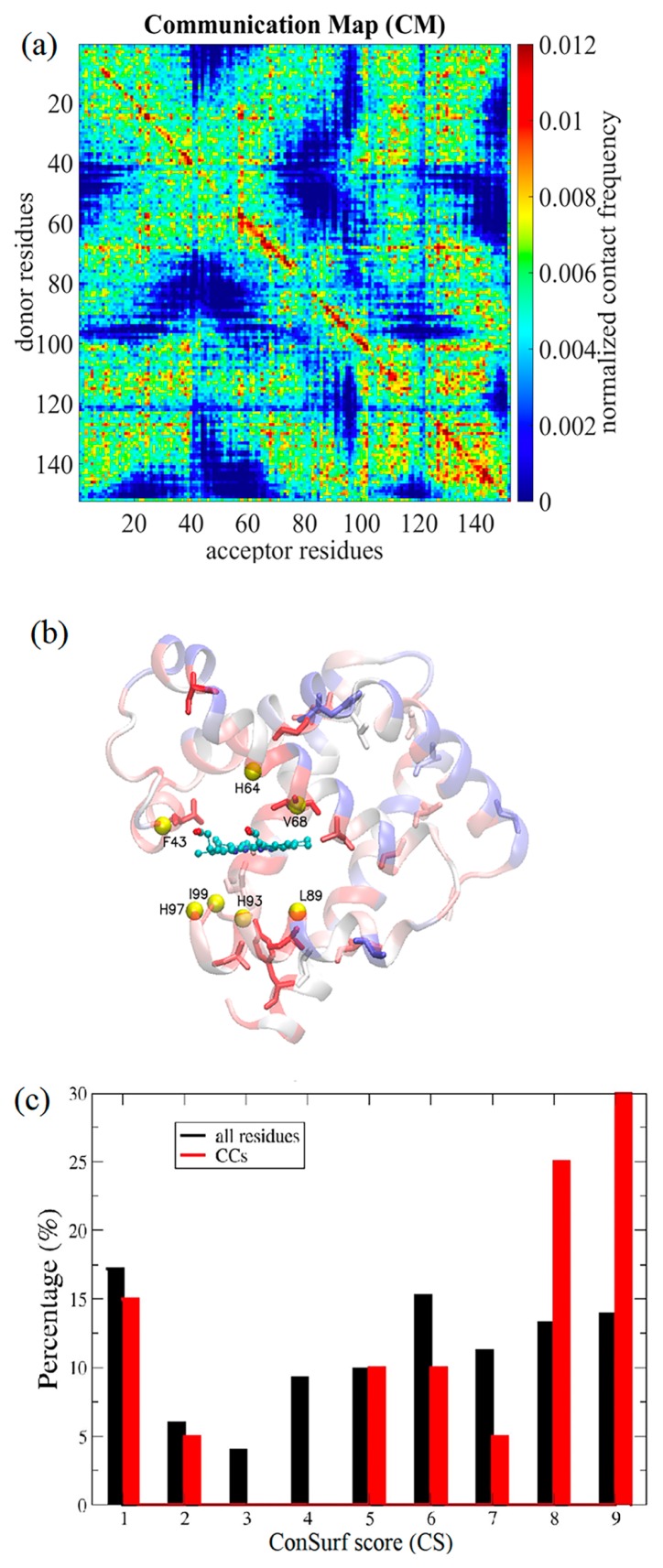
Conservation analysis of communication centers. (a) The communication maps (CMs) are shown for Mb. (b) The residues within 6 Å from Fe—F43, H64, V68, L89, H93, H97, I99, and Fe were chosen to be the perturbation sites, represented by yellow balls. In the CMs, the communication score of a residue was defined as the maximum off-diagonal elements of the column (signal receiver) and row (signal donor) that contains the residue. Residues with the highest 20 communication scores were termed the communication centers (CCs) of Mb, which were rank-ordered by their communication scores as V68, A134, A84, A130, G124, T39, G25, A71, A94, A90, A127, S58, H24, A143, G5, Y146, D141, K102, L115, and V114, presented in sticks; the colors of the ribbon diagram indicate residues’ evolutionary conservation from the least conserved (score 1, dark blue) to the most conserved (score 9, dark red), where the scores are derived from the multiple sequence alignment results provided by the Consurf server [36,37]. The normalized histograms of the ConSurf scores from 1 to 9 of all the residues and CCs are colored in black and red for Mb (c).

Figure 6.

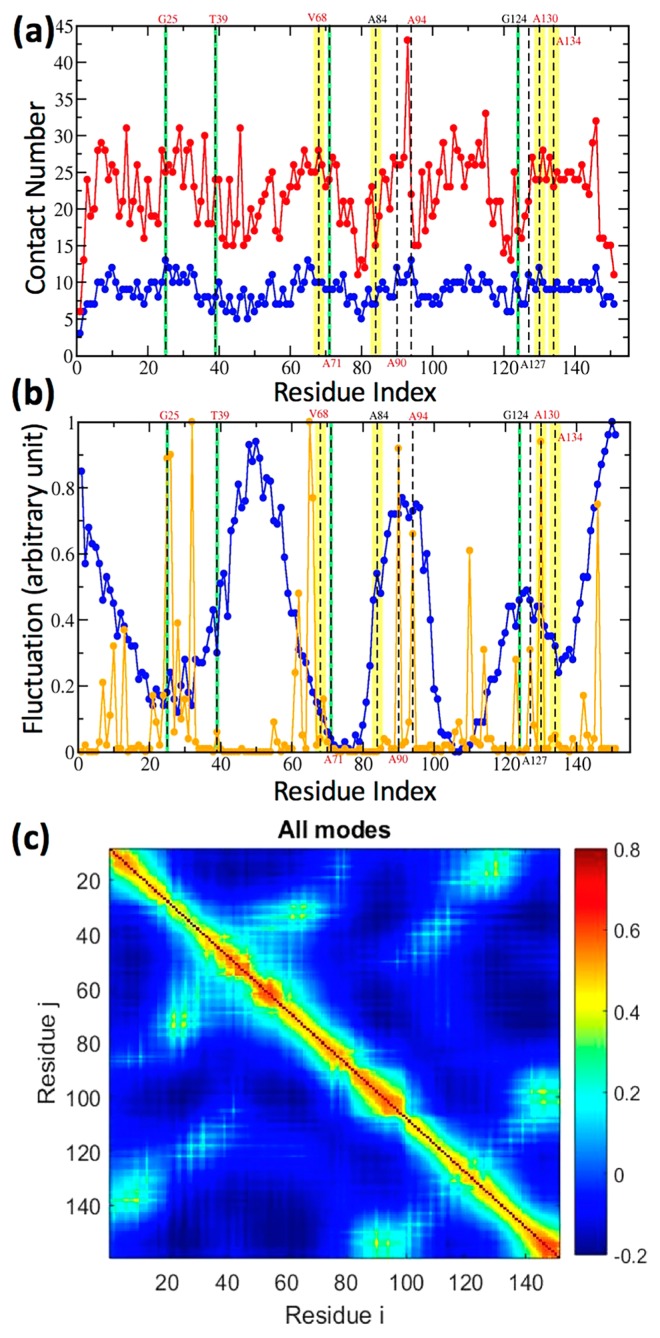
Contact number (a), fluctuation amplitude (b) and residue correlation (c) for Mb. Dashed lines on the residues that are deemed as the communication centers (CCs) derived by our IF-LRT. The top four communicators are highlighted in yellow; those that rank 5 to 8 are in green. In (a), Per residue contact numbers based on atoms (red) and on residues (blue) are plotted along the residue index of Mb. In (b), the frequency weighted fluctuation profiles comprising the slowest two modes (blue) and the fastest 10 modes (orange) are drawn. (c) Intrinsic (unperturbed) residue-residue correlation examined by GNM implemented in the DynOmics web portal [38].

MD protocols and PCA

Unligated (PDB ID: 1A6N) and CO-ligated (PDB ID: 1A6G) Mb structures [21] are used in the MD simulations using the NAMD package with the CHARMM36 forcefield [39]. Proteins were immersed in a box of size 78 Å×71 Å×71 Å containing 33276 TIP3P water molecules and neutralizing ions containing one sodium and nine chloride ions. Structures were energy-minimized, heated, and equilibrated at 300 K and 1 bar, maintained using a Langevin thermostat and barostat. Particle Mesh Ewald and SHAKE were applied in the simulations. The production run at 300 K and 1 bar took 80 ns, with snapshots saved every 100 fs. We took the non-hydrogen atoms for the last 50 ns, totaling 500,000 snapshots (frames), for the subsequent PCA [40]. The structural change with perturbations 〈Δ⇉_i〉_f (see below) was taken from the difference between averaged ligated and unligated snapshots. The time-dependent and independent covariance matrices were calculated by PCA-derived quantities using the averaged unligated structure, to which the “0” of “〈 〉₀” in the eqs. (1) and (2) refer.

We performed (atom-) mass-weighted superimposition for each snapshot [41] of the unligated Mb onto the averaged structure in an iterative fashion [40,42]. In accordance with our earlier protocols [40], the mass-weighted protein atom coordinates in an ensemble of superimposed frames were used to build the residue–residue covariance matrix for positional deviations, to which PCA was applied. PCA provided a set of principal component modes (PC modes) and their corresponding mass-weighted variance σ² (eigenvalues). In accordance with the equipartition theorem of harmonic oscillators [40], at a given temperature T, the energy of a harmonic PC mode was σ²×ω²=k_BT, where the effective frequency, ω, of the PC mode can be defined as $\sqrt{\frac{k_{B}T}{Q^2}}$.

PCA-based td-LRT

In studies of the photodissociation of MbCO [2,3], a biphasic relaxation—a fast response following by a long-time relaxation—for UV-TR3-detectable residues was observed. In the model, the slow and fast (biphasic) relaxation dynamics corresponded to the residue responses with and without conformational changes [2,3], we developed two PCA-based td-LRTs [21]—a CF-td-LRT and an IF-td-LRT. The CF-td-LRT reads as:

$${\langle \mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{i}}(\text{t})\rangle }_{\text{f}}=\frac{1}{k_{B}T}\sum _j({\langle \mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{j}}(0)\mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{i}}(0)\rangle }_0-{\langle \mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{j}}(0)\mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{i}}(\text{t})\rangle }_0){\overrightarrow{\mathbf{f}}}_{\text{j}}$$ (1)

where k_B and T are the Boltzmann constant and temperature, respectively. The td covariance matrix, 〈Δ⇉_j(0)Δ⇉_i(t)〉₀, can be expressed as the sum of solvent-damped harmonic oscillators treated using the Langevin equation (see supporting information, SI). When time goes to infinite, 〈Δ⇉_j(0)Δ⇉_i(t)〉₀ vanishes and eq. (1) retreats back to the time-independent form, ${\langle \mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{i}}(\text{t})\rangle }_{\text{f}}=\frac{1}{k_{B}T}\sum _j{\langle \mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{j}}\mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{i}}\rangle }_0{\overrightarrow{\mathbf{f}}}_{\text{j}}$ [31]. The constant forces that drive Mb to evolve from unbound to bound conformations, upon CO binding, can be derived from the time independent LRT in the form ${\overrightarrow{\mathbf{f}}}_{\text{j}}=k_{B}T{\sum }_i{\langle \mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{i}}\mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{j}}\rangle }_0^{-1}{\langle \mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{i}}\rangle }_{\text{f}}$ in kcal/mol/Å, where 〈Δ⇉_i〉_f in this study was the structural difference between bound and unbound Mb structures that were the averaged MD snapshots. The residues taking the largest forces (>200 kcal/mol/Å) were GLN26, ASP27, ILE28, PHE33, ARG45, HSP48, LYS98, SER108, ASN132, and heme, where the first 9 residues are found on average to be 8.7 Å away from the heme.

Because multiple-point constant forces were used to drive the time responses of conformational relaxation of Mb, one may question the validity of LRT with a small-perturbation assumption. However, it has been shown by Kidera’s group (a database of ligand-induced conformational changes in proteins) [43] and our group (ribosomal rolling motion triggered by PRF-driven mRNA pseudoknot) [44] that LRT with perturbations on multiple nodes still can reproduce experimentally observed structural changes. In fact, it can be analytically proved that LRT applied to systems subject to multi-site perturbations can still be valid as long as the equilibrium dynamics evolve over a harmonic energy surface (see Supplementary Methods).

To model the relaxation dynamics for UV-TR3 experiment without conformational changes, we use the IF-td-LRT [21] in the form

$${\langle \mathrm{\Delta }{\overrightarrow{\mathbf{r}}}_{\text{i}}(\text{t})\rangle }_{\text{f}}=\frac{1}{k_{B}T}\sum _j{\langle \mathrm{\Delta }{\dot{\overrightarrow{r}}}_j(0)\mathrm{\Delta }{\overrightarrow{r}}_i(t)\rangle }_0{\overrightarrow{k}}_j$$ (2)

where k⃗_j is an impulse force applied on atom j. In this study, we modeled the laser pump pulse, which deposits excess energy on heme by the force pointing from CO (if bound) to the Fe atom plus a set of forces that model the “heme breathing” (ν₇) mode [8].

In both td-LRTs, we expressed the time-dependent covariance matrix with the PC modes subjecting to the Langevin damping following Chandrasekhar’s treatment [35]; whereby the position–position (eq. 1) and position–velocity (eq. 2) time correlation functions can be expressed as superimposition of overdamped and underdamped harmonic oscillators (see Supporting Methods for details). The solvent friction β that divided the underdamped and overdamped was found to be 27 cm⁻¹ using our earlier calculation [21] based on Haywards’ method [20]. With this friction constant, PC modes of frequency higher than 13.5 cm⁻¹ were underdamped, which agreed with the observation of orientation-sensitive terahertz near-field microscopy that vibrational modes of frequency larger than 10 cm⁻¹ are overdamped in chicken egg white lysosome of 129 residues [45].

The mean characteristic time of a residue, ${\tilde{t}}_c^R$

Using the IF-td-LRT in Eq. 2, after an impulse force k⃗_j is applied on a C_α atom, atoms evolve as a function of time. After perturbations are introduced to the system at time 0, the atom i achieves its maximal displacement from the initial position at time t_i. The time when ||〈Δ⇉_i〉_f|| is at the maximum of all time is defined as the characteristic time of atom i, $t_c^i$. Our previous study [21] showed that characteristic time is a function of the directions of applied impulse forces. When a single point force is applied on one atom in the system, the $t_c^i$ does not change with the absolute magnitude of the force and remains unchanged if the force points to the opposite direction. To average out the effects of applied force directions, we defined a set of 21 IFs, with unit magnitude and pointing toward evenly distributed 21 directions in a hemisphere at spherical angles of Ω, acting on a heavy atom of an residue of interest. Consequently, a set of characteristic times $t_c^i$ were derived. We then averaged $t_c^i$ over 21 directions as well as all heavy atoms i of a residue R; the averaged characteristic time of a residue R was expressed as ${\tilde{t}}_c^R={\sum }_{i\in R}{\langle {t_c}^i\rangle }_{\mathrm{\Omega }}/{\sum }_{i\in R}$ where i was the index of heavy atoms. To estimate the signal propagation speed, t̃_c was plotted as a function of the distance, t̃_c (d), where d is the distance between the perturbed C_α atom and the C_α atom that senses the coming signal. For instance, to calculate the intra-helical communication speed, we first chose a pair of residues (C_α atoms) in the same helix that were d Å away from each other. Then, from one residue the signal was launched from 21 different directions, the other “sensed” the signal after 21 different time durations (by having 21 different $t_c^i$). t̃_c (d) was obtained by averaging these 21 different time intervals. To calculate the inter-helical communication speed, we made sure that the perturbed site and sensing site were located in different helices. By taking the linear regression for a set of t̃_c (d) as a function of d, we obtained the propagation speed as the reciprocal of the slope (see Fig. 2).

Communication matrix/map and communication score

With the aid of IF-td-LRT providing the characteristic time $t_c^i$ to characterize the dynamical signal propagation, we further developed a method that traces the signal propagation pathways and identified which residues are essential to mediate the signals when considering all the pathways. Here, we introduce the “communication map” (CM) to record the signal propagations between residues, from which we derived the “communication centers” (CCs)—the residues that are frequently used to communicate signals in most pathways. $t_c^i$ can provide causality of signal propagation. We traced the signal transmission pathways consisting of the donor-acceptor pairs illustrated in Figure 4. There were two communication criteria to determine the atom communication between a donor atom, a_d, and an acceptor atom, a_r. First, given an IF exerted on an atom in the system, the atoms with characteristic times that differed by Δt, were considered “communicating” such that $t_c^{a_r}-t_c^{a_d}=\mathrm{\Delta }t$, where fixed Δt was chosen as 0.2 ps in this study. In order to maintain the causality of signal propagation, the candidates that satisfied the first criterion were required to meet the second criterion such that the angle between the vector pointing from the perturbed atom to a_r and that pointing from the perturbed atom to a_d needed to be less than 90 degrees. It is possible that a donor atom connected multiple acceptor atoms, or multiple donors connected to a single acceptor atom. Consequently, in order to quantitatively recognize how frequently a residue participates in the signal propagation, we defined an all-atom communication matrix F(a_d, a_r), which accounted for the number of the communication that the donor, a_d, connected to the acceptor, a_r, as

$$F(a_d,a_r)={\sum }_j{\langle \delta (\mathrm{\Delta }t-[t_c^{a_r}({\mathrm{\Omega }}_j)-t_c^{a_d}({\mathrm{\Omega }}_j)])\rangle }_{\mathrm{\Omega }}$$ (3)

where j runs over all the selected C_α atoms being perturbed (when a given C_α is perturbed, whether a_d and a_r have their largest responses with a time offset of interval Δt; if yes, add on count), δ(x) is a Kronecker delta function of x. Ω_j are forces orientation angles as defined in the previous section. The lower part of Figure 4 illustrates how communication matrix F was constructed by summing all the pairwise communications when signals were initiated from different sites in the system, one at a time. With the all-atom F matrix, we further defined the residue level CM by summing the counts belonging to each residue pair, $C(R_d,R_r)={\sum }_{a_d\in R_d}{\sum }_{a_r\in R_r}\frac{F(a_d,a_r)}{N_d{N}_r}$, where R_d and R_r are donor and acceptor residues, respectively; N_d and N_r are the number of atoms in donor and acceptor residues, respectively.

To model the signals propagation process, we perturbed the residues within 6 Å from the ferrous ion (Fe): F43, H64, V68, L89, H93, H97, I99, and the Fe itself are represented in yellow spheres in Figure 5b. Consequently, 21 evenly distributed IFs were applied to each perturbation site, and all the resulting signal communications were summed in a CM, C(R_d, R_r). In the CM, the diagonal elements belong to intra-residue communication and have high C(R_d, R_r) scores, which is intuitive but less meaningful in terms of the allostery. For the off-diagonal elements satisfying |R_d−R_r|>2 Å, they provide information on the signal propagation between long-range contacts (say, within or between secondary structures). Several hot spots that have high CM scores indicate their strategic locations to frequently communicate mechanical signals in multiple pathways. Then, a unique “communication score (CS)” can be assigned to each residue, which is defined as the highest CM score between this residue and any other non-neighboring residues in the protein—in other words, residue i’s CS is the highest score in either the i-th row or the i-th column (corresponding to donors or acceptors, respectively) of the CM.

Results

Modeling the biphasic relaxation of residues of time-resolved ultrafast spectroscopy

It has been reported that the time constant of residue relaxation measured by the resonance Raman spectra of tryptophan residues are sensitive to changes in its hydrophobic environment [3,46,47]. For the four measured residues in the UV-TR3 experiments: W14 on helix A [2,3], Y146 on helix H [3], V68W on helix E [2], and I28W on helix B [2], their hydrophobic environment changes were monitored by distance fluctuations between them and their closest hydrophobic residues (herein, distances for Trp14-Leu69, Ile28-I107, Val68-I107, and Tyr146-Ile99 pairs). The residues’ spatial distributions relative to heme can be found in Figure 1a. To quantify the dynamics of corresponding residues, we defined the reaction coordinate, Ψ_ab(t)=|| 〈Δ⇉_ab(t)〉_f||/max(||〈Δ⇉_ab(t)〉_f||), where ||〈Δ⇉_ab(t)〉_f||=||〈Δ⇉_a(t)〉_f−〈Δ⇉_b(t)〉_f||−min(||〈Δ⇉_a(t)〉_f−〈Δ⇉_b(t)〉_f||), and ||〈Δ⇉_a(t)〉_f−〈Δ⇉_b(t)〉_f|| was the time-evolved distance between the side chain centers of residues a and b starting from when the force perturbations were introduced.

Considering conformational changes initiated by photodissociation of MbCO [3], we used CF-td-LRT particularly shown to be suitable for describing the conformational change [21]. The time correlation functions (interchangeably used as time-dependent covariance) in eqn (1) are composed of 350 PC modes up to ~40 cm⁻¹ (see Fig. 3). As described in the Methods, the constant forces that result from CO photodissociation can be derived from the known conformational changes and the inversion of the covariance matrix through time-independent linear response theory [21]. With the derived forces and td covariance in eqn (1), the td conformational changes of Mb can be tracked. The normalized response curves Ψ_ab(t) for the two pairs, W14-L69 and Y146-I99, can be drawn (Fig. 1b). Fitting the data corresponding to the structural-change-associated slow relaxation (after the peak for W14 and after the minimum for Y146) to the exponential function A exp(−t/τ) or B−A exp(−t/τ) (from t₀ to 60 ps where t₀ is at the end of the fast responses) revealed that the time constants τ obtained for the two pairs were 39.0 and 3.5 ps, respectively, which were closely compared with the time constants 49.0 and 7.4 ps observed in time-resolved UVRR spectroscopy experiments [3]. It is worth noting that there was a fast rise or drop in Ψ_ab(t) appearing in the first a few picoseconds before the signal partly (W14) or fully (Y146) recovered from a slower relaxation (Fig. 1b). Revealed below, these fast responses can be described by td-LRT using IFs.

In Fuji’s study, heme in the empty Mb (no CO attached to the heme) was irradiated and excited by a 405 nm pump pulse [3]. Then, the vibrational energy propagation was traced using a pump-probed technique with tryptophan as the sensor to observe anti-stoke intensity changes [3], without a permanent conformational change. Besides W14 and Y146, the relaxation time constants of another two tryptophan mutants V68W and I28W have been characterized previously by the UV-TR3 [3], where the tryptophan band of anti-stokes intensities gave time constants for V68W and I28W of 3.0±0.4 and 4.0±0.6 ps, respectively [3]. We used the IF-td-LRT in eqn (2) to model the relaxation dynamics and the IF used to mimic the laser pump pulse was a force pointing from CO (if bound) to the Fe atom perpendicular to heme plus the forces that modelled the “heme breathing” motion (ν₇ mode) [8]. Figure 1c shows the reaction coordinates, ||〈Δ⇉_ab(t)〉_f||, for residues V68, I28, and W14 whose hydrophobic environment was represented by their closest contact residues I107, I107, and L69, respectively. We defined characteristic time t_c as the time when ||〈Δ⇉_ab(t)〉_f|| reached its maximal amplitude. The t_c for ||〈Δ⇉_V68−I107(t)〉_f|| was 1.6 ps, shorter than ||〈Δ⇉_I28−I107(t)〉_f|| of 2.0 ps, which were slightly faster but still comparable to the UV-TR3-observed time constants of 3.0±0.4 and 4.0±0.6 ps, respectively [2]. W14 had a t_c of 3.4 ps according to our IF-td-LRT, whereas the signal was too weak to be detected in the UV-TR3 experiment [2].

Inter-helix signals propagate faster than intra-helix ones

The characteristic time t_c that indicates the arrival time of mechanical signals to individual atoms or residues enables us to examine how fast such signals propagate through secondary and tertiary protein structures. We quantified the signal propagation between (inter-) or within (intra-) α-helices, corresponding to perturbed sites and sensing sites located in different or the same helices, respectively.

It can be seen in Figure 2a that the intra-helical t̃_c^P(d_P) (see symbol definition in Fig. 2) increased with d_P linearly with a correlation coefficient of 0.71, where the linear regression gave a speed of 529 m/s, about two-fold slower than previously reported 10 Å/ps (=1000 m/s) [48]. In comparison to the intra-helix signals, the ${\tilde{t}}_c^R$ for signal propagation across different helices was much shorter than its intra-helical counterpart. The linear regression gave a speed of 4076 m/s, falling in between that in water (1482 m/s) [49] and in steel (5930 m/s) [50], for the inter-helical communication with a correlation coefficient of 0.16. The low linearity may suggest a more topology-dependent nature of the inter-helical signal propagation than that for the intra-helical case. These results implied that the 3D packing of secondary structures may significantly accelerate the signal propagation speed, exemplified by the rigid molecule, Mb.

The signal propagation mediated by selected modes

As a property derived from the time-correlation function used in IF-td-LRT, the characteristic time (${\tilde{t}}_c^R$) should be a function of its constituent PC modes. To understand the mode dependence of the characteristic time of residues of interest and therefore the inferred propagation, we calculated the ${\tilde{t}}_c^R$ from the time dependent covariance matrix that comprised all the PC modes that were slower than a cut-off frequency, ω_max, set to be from 12 to 1100 cm⁻¹. Figure 3 shows the ${\tilde{t}}_c^R$ of the four residues examined in UV-TR3 experiments [2,3] as a function of ω_max when the perturbation was introduced at the Fe atom of the heme from 21 evenly distributed forces. When taking all the modes ≤1100 cm⁻¹, we obtained ${\tilde{t}}_c^R$ for I28, V68, and Y146 (note: this was a signal-residue response; not the aforementioned residue-environment responses) as 3.0±0.4, 2.4±0.2, and 2.4±0.3 ps, respectively, which were compatible with the UV-TR3 results of 4.0±0.6, 3.0±0.4, and 2.0±0.8 ps [2,3], respectively. However, we should note again that the experimental data for I28 and V68 were obtained from photoexcited Mb involving no conformational changes, whereas that for Y146 was measured from CO-photolyzed Mb with accompanying conformational changes, which involved multiple force perturbations on and near the heme. It can be seen in Figure 3a that ${\tilde{t}}_c^R$ does not vary much until ω_max continues to drop below ~40 cm⁻¹ where monotonic increases of the ${\tilde{t}}_c^R$ started to become apparent in all four residues. In addition, we found that PC modes larger than 100 cm⁻¹ were barely influential to ${\tilde{t}}_c^R$. This could be because these modes were spatially localized and did not propagate the signals.

The intramolecular communication centers are evolutionarily conserved

To investigate whether the residues frequently mediating the vibrational signals have any functional or evolutional importance, we defined a set of residues as CCs (See Methods), which frequently communicated signals in multiple pathways. The CCs were functions of perturbing sites. Perturbing heme-binding residues located within 6 Å of the ferrous atom, F43, H64, V68, L89, H93, H97, I99, and Fe (yellow balls in Fig. 5b), resulted in a CM (Fig. 5a; see Methods). The CCs were assigned for the 20 residues having the highest CSs (see Methods), which were rank-ordered (from the highest to the lowest) as V68, A134, A84, A130, G124, T39, G25, A71, A94, A90, A127, S58, H24, A143, G5, Y146, D141, K102, L115, and V114. On the other hand, we calculated the evolutionarily conserved residues in Mb based on multiple sequence alignment results using the ConSurf database [36,37], where residues were grouped into nine conservation levels by their “ConSurf scores” from 1 (most diverse) to 9 (most conserved) color-coded from blue to red, respectively, in Figure 5b.

We then examined the distribution of ConSurf scores for all the residues as well as for the CCs. It was found in the normalized histograms of CS (Fig. 5c) that the average ConSurf score of CCs was 6.4, larger than the average ConSurf score for all the residues, 5.3. In addition, there were 60% CCs of the ConSurf score value greater than or equal to 7, whereas only 38% of the residues in Mb that met the same criterion. Similarly, we found previously that CCs were generally more conserved than average residues in dihydrofolate reductase (DHFR), which catalyzes the reduction of dihydrofolate in the presence of the cofactor NADPH into terahydrofolate and NADP⁺ [17,51,52]. Two-sample Kolmogorov−Smirnov tests revealed a p-value of 0.1 for the distributions of CCs and all residues in the case of Mb, and a p-value <0.03 for the case of DHFR [17]. These results suggested that CCs, bearing mechanical/communication importance, were evolutionarily conserved.

CCs are not co-localized with functional mechanical hinges, folding cores or residue pairs in highly correlated motion

We further asked whether these conserved CCs are a natural consequence of their important structural and mechanical roles in serving as folding cores [53] or being at the mechanical hinges [53,54]. Among the 20 CCs in Mb, we found that there were seven folding cores (35% of CCs) including G25, A90, A94, V114, A127, A130, and Y146, which were identified using the fastest GNM mode peaks [53], and residue A71 was identified as a mechanical hinge using the slowest GNM mode (see Fig. 6) [54–58]. On the other hand, we also examined whether these CCs belonged to one of these highly correlated residues in the unperturbed state of Mb, examined by GNM [38,54–58]. In the top 10 residues, subjected to the highest correlation with others, F43, K47, T51, M55, K145, Y146, K147, L149, G150, Y151, only Y146 is one of the CCs. However, all 12 CCs, including the top three communicators V68, A134, and A84 (highlighted in Fig. 6), are neither folding cores nor mechanical hinges, suggesting that these CCs are not properties readily derivable from proteins’ structural topology and low-frequency dynamics. Within the 12 CCs, T39, S58, V68, A134, and D141 with a ConSurf score >8, are highly conserved, whereas S58 (ConSurf score =9), A134, and D141 are not anywhere close to the heme. The results suggested that CCs cannot be alternatively derived from apparent structural and dynamics properties.

Discussion

We have developed two td-LRTs, CF-td-LRT and IFtd-LRT, to model the long-time (involving conformational changes) and short-time relaxation (without conformational changes), respectively. Although the initial stage of the electronic excitation within the heme group involved quantum effects [5], the consequent relaxation process in the protein environment seemed to be qualitatively captured by our classical approach that described the time characteristics of the energy transfer measured by UVRR spectroscopy. In this study, we also showed that the PC modes can serve as a well-defined basis set to mediate the vibrational energy using the MD-PCA-based td-LRTs. With IF-td-LRT, we were able to formulate a theory to study mechanical signal propagation between two designated sites as well as the frequent communication pathways. In the latter, CCs were identified and found to be evolutionarily conserved. These communication hubs were found not to overlap with mechanical hinges, folding cores, highly correlated residue pairs or those have large distance changes in the conformational changes.

In the description of CF-td-LRT on the conformational change of Mb upon ligand dissociation, we found qualitative and quantitative agreement with earlier X-ray free-electron laser (XFEL) results [59]. In the study of Barends et al., the authors used XFEL to resolve the ultrafast structural changes taking place in the MbCO complex upon photolysis of the Fe-CO bond, which was also studied by our CF-td-LRT. Because both our theory and the XFEL observations described the F-helix departing from the heme and the E-helix approaching the heme upon CO dissociation, it was found by td-LRT that more than 80% and 50% of the response was completed within 10 ps for Y146 and W14, respectively, whereas Barends’s data also showed (in their Fig. 3) that the first 10 ps could react with at least 50% of the overall response from 0.5 ps to 150 ps. It is worth noting that UV-TR3 [2], NMA-based CF-td-LRT [21] and PCA-based CF-td-LRT in the current study all detected a fast beating response of Y146 at 2 ps, which inspired our earlier efforts to formulate a IF-td-LRT that later reproduced the same fast response. In our PCA-based CF-td-LRT, we needed to include PC modes at least as fast as 40 cm⁻¹ to observe this fast response at ~2 ps. 40 cm⁻¹ corresponded to a vibration motion period of 0.8 ps, which agreed with the time scale of XFEL-observed heme O-His97 and Lys98 O-Lys42 N oscillation in a period of 0.5–0.8 ps [59].

In the description of IF-td-LRT on vibrational energy relaxation in heme-excited Mb, three substantial issues were carefully investigated in this study: 1. How do we model the quantum external perturbation using a classical approach? 2. What kinds (frequency range of modes) of relaxation motions of the measured residues are captured using td UVRR spectra? 3. Are there essential residues taking charge of the energy flow pathway?

In this study, the external perturbations were modeled by two kinds of classical forces: constant force induced by conformational changes, and point impulse forces at the heme. According to an earlier study by Mizutani and Kitagawa [5], the laser pulse first excited the electronic state of the Fe atoms, and then the excess heat relaxed to the vibrational state of heme before further propagating into the protein matrix. We described the process by which our IF-td-LRT using a point IF at the Fe atom along the direction perpendicular to the heme plus “effective forces” along the heme breathing (ν₇) mode, observed using visible few-cycle-duration light pulses [8], out of the aforementioned vibrational relaxation (Fig. 1c and 2). In addition, it is known that the time constant of the measured residues is attributed to the change in their hydrophobic environment [3]. In this study, we represented the hydrophobic environment of the measured residue using the displacement between the center of mass of the measured residues and their closest hydrophobic residue. From Figure 1b and 1c, these approaches were shown to estimate the time constant appropriately. It was notable that the beating components found at 3–8 ps in the IF-td-LRT-depicted responses of W68 and W28 (Fig. 1c) that can actually be found in Fuji’s time-resolved UVRR spectra from 5 to 10 ps [3] (see Supplementary Fig. S1).

On the other hand, the corresponding band in the UVRR spectrum for a measured residue may be dominated by a specific set of vibrational modes [2], and residues of interest instead of its hydrophobic environment can also be monitored (Fig. 3). In this aspect, we also measured the mean characteristic time of a residue, ${\tilde{\mathit{t}}}_{\mathit{c}}^{\mathbf{R}}$, shown in Figure 3. For the full mode case, ${\tilde{t}}_c^R$ of I28, V68, and Y146 were 3.0±0.4, 2.4±0.2, and 2.4±0.3 ps, respectively, which were compatible to the fast response results in UVRR spectra of 4.7±1.3, 3.0±0.7, and 2.0±0.8 ps [2,3], respectively. As shown in Figure 3, the deletion of fast PC modes above 40 cm⁻¹ only affected the time constants slightly, whereas the deletion of PC modes below 40 cm⁻¹ caused the time constants to fluctuate significantly. The results suggested that the medium frequency modes between 27 and 40 cm⁻¹ play an important role in propagating signals. However, this does not rule out the possible mechanism mediating vibrational energy flows such like mode resonance or modes couplings [9,24,48].

Lastly, we addressed the third issue by building a time-dependent covariance matrix in eq. 1 and eq. 2 using selected modes. Launching signals from several active site residues, we can keep track of the accumulated count on the atom pairs where the signals flow through within a short time interval. Such a tally has shown a surprising accordance with remote residues’ importance in regulating protein function and their high conservation in evolution. The new “communication” property did not seem to co-localize with the mechanical hinges defined by ENM’s slowest mode, previously shown to be functional relevant [40,56,57], folding cores or highly correlated residues (Fig. 6). The CM also did not agree with the XFEL-characterized pairwise distance changes [59]. It is worth noting that the most frequently communicating pairs are usually not primary sequence neighbors (|R_d−R_r|>10 Å), whereas most correlated residues identified by GNM are still those primary sequence neighbors (|R_d−R_r|=4 or 5 Å). A similar phenomenon was observed in DHFR [17]. The difference between CM and the covariance matrix calculated in an unperturbed state may be understood as the following. LRT describes the conformational changes under perturbation being an interplay between a covariance matrix sampled at an unperturbed state and force perturbations; As long as the perturbation is not vanishingly small or at single-point (as the case here), the perturbed covariance matrix constituted by perturbation-driven conformational changes would not be similar to the unperturbed covariance matrix. However, CM is not an alternative presentation of covariance under perturbation; nodes communicate if their maximal responses occur at a time difference of 0.2 ps, as well as the two “connecting” nodes stay on the same side of the perturbation node, which does not require the two to be correlated directionally. Furthermore, CM is the accumulated sum of multi-point perturbations in multiple directions, so doing to increase the signal to noise ratio. From the results of Figure 6, it is likely that these evolutionarily conserved communication centers play a distinct physical role in mediating vibrational energy propagation throughout the protein matrix, or dynamics allostery.

A preliminary version of this work, doi: 10.1101/682195, was deposited in the bioRxiv on July 02, 2019.