Allosteric response to ligand binding: Molecular dynamics study of the N-terminal domains in IP₃ receptor

Abstract

Inositol 1,4,5-trisphosphate (IP₃) receptor (IP₃R) is a huge tetrameric intracellular Ca²⁺ channel that mediates cytoplasmic Ca²⁺ signaling. The structural basis of the gating in IP₃R has been studied by X-ray crystallography and cryo-electron microscopy, focusing on the domain rearrangements triggered by IP₃ binding. Here, we conducted molecular dynamics (MD) simulations of the three N-terminal domains of IP₃R responsible for IP₃ binding (IBC/SD; two domains of the IP₃ binding core, IBCβ and IBCα, and suppressor domain, SD) as a model system to study the initial gating stage. The response upon removal of IP₃ from the IP₃-bound form of IBC/SD was traced in MD trajectories. The two IBC domains showed an immediate response of opening after removal of IP₃, and SD showed a simultaneous opening motion indicating a tight dynamic coupling with IBC. However, when IBC remained in a more closed form, the dynamic coupling broke and SD exhibited a more amplified closing motion independently of IBC. This amplified SD motion was caused by the break of connection between SD and IBCβ at the hinge region, but was suppressed in the native tetrameric state. The analyses using Motion Tree and the linear response theory clarified that in the open form, SD and IBCα moved collectively relative to IBCβ with a response upon IP₃ binding within the linear regime, whereas in the closed form, such collectiveness disappeared. These results suggest that the regulation of dynamics via the domain arrangement and multimerization is requisite for large-scale allosteric communication in IP₃R gating machinery.

Significance.

Allostery has long been a key concept of biomolecular physics in the context of molecular function. Here, we simulated the allosteric structural change of IBC/SD domains in IP₃R and found the response upon IP₃ binding appearing in two different modes: one with a collective motion within a linear response regime and the other with an over-amplified motion beyond the linear regime. The domain and subunit arrangement in IP₃R is designed to maintain collective and linear dynamics, which enables the large-scale allosteric communication from the IP₃ binding site to the ion channel gate in IP₃R.

Proteins consists of many heterogeneous degrees of freedom, complicating their motions, but concurrently functioning properly in the cell. Biophysics aims at understanding or modelling such complex but robust biomolecular dynamics on the basis of physics, delineating the relation between structure, dynamics, and function. The concept of the collective dynamics in proteins was first derived as an answer to this problem, from normal mode analysis and later, from the principal component analysis by Nobuhiro Go [1–3]. The collective nature of protein dynamics, occurring in a small dimensional space but spanning a large spatial range, has been the basis of functional allosteric transitions [4]. The linear response theory of protein dynamics explaining functional motions is a straightforward extension of Go’s concept of the collective dynamics [5].

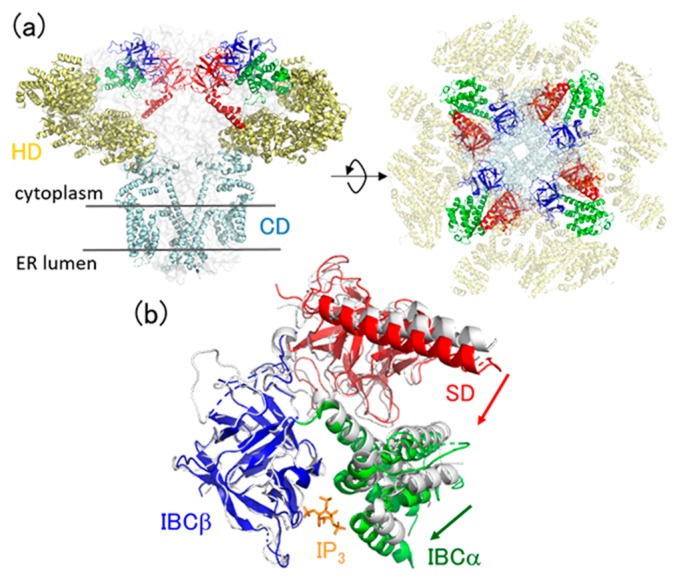
In this article, from the viewpoint of the collective dynamics, we present a computational study of allosteric dynamics of inositol 1,4,5-trisphosphate (IP₃) receptor (IP₃R), a family of tetrameric intracellular calcium ion channels expressed in the endoplasmic reticulum (Fig. 1a). IP₃R is activated by cytoplasmic Ca²⁺ and IP₃ as a second messenger to release Ca²⁺ to the cytoplasm, eliciting Ca²⁺ signaling [6–9]. The architecture of the full-length IP₃R consists of a large cytosolic domain in the cytoplasm and a channel domain (CD) that is embedded in the membrane and forms a channel for Ca²⁺ transport (Fig. 1a). Recently, the structural dynamics of the IP₃R gating process has been solved by X-ray crystallography [10–14] and cryo-electron microscopy [13,15–17]. These structural data revealed that IP₃ binding to the cytosolic domain at the IP₃-binding core (IBC) causes a closing motion of the two constituent domains (IBCα/IBCβ) [10], followed by an allosteric motion of the suppressor domain (SD) [13] (Fig. 1b). These responses upon IP₃ binding is further transmitted to the three α-helical domains (HDs), and finally to the trans-membrane CD to achieve pore opening.

Figure 1.

(a) Architecture of the full-length IP₃ receptor (PDB: 6dqj). Domains are colored by red (SD), blue (IBCβ), green (IBCα), yellow (HD), and cyan (CD). (b) Crystal structures of IP₃-bound (colored, PDB: 3uj0) and -unbound (gray, PDB: 3uj4) forms of IBC/SD. IBCβ of the two structures are superimposed. IP₃ is also shown by orange sticks. Domain motions via IP₃ binding are depicted by arrows.

In the present study, we focus on the initial stage of the whole gating process, how the three N-terminal domains, IBC/SD, respond to IP₃ binding, where IBCα/IBCβ binds IP₃ at their interface and SD also responds in an allosteric manner [13]. To see the allosteric response, we performed molecular dynamics (MD) simulations of IBC/SD initiating at the IP₃-bound structure after the removal of IP₃, in addition to the equilibrium simulations of IP₃-bound and -unbound structures. The structural dynamics thus obtained were analyzed by the use of principal component analysis [2], and by our original methods using Motion Tree [18,19] and linear response theory [5].

Methods

Simulation models

MD simulations were performed for the three N-terminal domains of IP₃R (IBC/SD) with (named herein as “holo”) and without (named herein as “apo”) IP₃ to elucidate the associated structural dynamics via IP₃ binding. The holo and apo simulation systems were constructed from the crystal structures of 3uj0 (residues 6–585 in chain B) and 3uj4 (residues 7–577 in chain A) in the protein data bank (PDB), respectively [13]. The thirteen alanine residues (15, 37, 56, 61, 206, 214, 253, 292, 326, 394, 530, 553, and 556), which were mutated from cysteine for crystallization, were replaced by cysteine, and the missing loops of the structures were modeled using MODELLER [20]. For the holo simulation, the bound IP₃ molecule, which was found to be distorted in 3uj0, and the cis peptide between K230 and D231 were remodeled using the structure in 1n4k [10]. The MD simulation for the relaxation process after removal of IP₃ was also performed starting at the holo structure (named herein as “apo-from-holo”).

For the three systems (holo, apo, and apo-from-holo), rectangular simulation boxes were constructed with a margin of 10 Å to the boundary of the simulation box and filled with TIP3P water molecules [21] and sodium ions to neutralize the simulation systems. The number of atoms in the simulation boxes were 131009, 182471, and 183624 for holo, apo, and apo-from-holo, respectively. The CHARMM 36 all-atom force field [22] was used for potential energy function. The force field parameter of IP₃ was adopted from our previous study of IP₃-bound and -unbound IBC simulations [23].

MD simulations

Simulations were performed with MARBLE [24]. Electrostatic interactions were calculated using the Particle Mesh Ewald (PME) method [25]. The Lennard-Jones potential was smoothly switched to zero over the range of 8–10 Å. The symplectic integrator for rigid bodies was used to constrain the bond lengths and angles involving hydrogen atoms [24], using a time step of up to 2.0 fs. The systems were energy minimized with 1,000 steps of the conjugate gradient method. In the subsequent equilibration phase, the systems were gradually heated to 300 K for 1 ns with lowering position-harmonic restraints for the proteins, and then equilibrated at 300 K without restraints for 2 ns. The simulations were performed for the NPT ensemble at T=300 K and P=1 atm. One hundred nanosecond production runs were iterated six times for each system, thus 100 ns×6 runs×3 systems = 1.8 μs in total.

Principal component analysis

The principal component analyses (PCAs) were performed to extract the essential dynamics of IBCα and SD relative to IBCβ. For this purpose, the coordinates of Cα-atoms in the secondary structures (94 atoms in SD, 69 atoms in IBCα and 71 atoms in IBCβ) were fitted to IBCβ of the reference coordinates, and the principal components (PCs) were calculated separately in IBCα and SD. The contributions of the PCs with the largest amplitudes were 0.64 and 0.65 for IBCα (named herein as “IBCα-PC1”) and SD (named herein as “SD-PC1”), respectively, indicating dominance in the overall motions.

Motion Tree

Collective protein dynamics can be described in such a way that the overall motion is separated into slow motions between the building blocks and fast vibrations within each building block. We developed a method to define the building blocks by hierarchical clustering of residue-residue distance fluctuation to construct a tree diagram named “Motion Tree” [18,19]. The Motion Tree illustrates in a hierarchical manner, a pair of rigid-like domains at each node that moves in-between with the amplitude of the respective tree height (named as Motion Tree score). The local motions within small segments such as a single α helix can also be detected if the associated distance fluctuations are large enough: This is the advantage over conventional methods such as PCA that determines large-amplitude collective motions.

Here, two Motion Trees were compared, one calculated from the MD trajectories of the apo form within the linear response regime, and the other from the holo form beyond the linear regime (see Results for details). The distance fluctuation, $D_{mn}={\langle \mathrm{\Delta }{d}_{mn}^2\rangle }^{1/2}$, where d_mn is the distance between the Cα atoms of residues m and n, was calculated and used as a metric for hierarchical clustering. As a reference, Motion Tree was also calculated from a pair of structures, the holo and apo crystal structures, by clustering the distance difference matrix, $D_{mn}^{pair}=\mid d_{mn,\text{holo}}-d_{mn,\text{apo}}\mid$ [18], where d_mn,holo/apo is the distance between the Cα atoms of residues m and n in the holo/apo structure.

To construct Motion Trees from the MD trajectories or multiple PDB structures, executable binaries for Linux and Mac are available at http://idp1.force.cs.is.nagoya-u.ac.jp/rk1/mtntr/forMD/.

Linear response theory

The linear response theory is a formula which relates the equilibrium fluctuation with the structural change via external perturbation such as ligand binding [5]. In the linear approximation, the displacement vector Δx after the perturbation is derived from the variance-covariance matrix C, and the eternal force f, as Δx=β Cf, where β=1/k_BT, k_B is the Boltzmann constant and T is the temperature of the system.

In the present study, the theory was used to evaluate the structural response of IBC/SD on IP₃ binding. C was calculated from the MD trajectories of the apo simulations with the condition, −30<IBCα-PC1<–10 (see Results for detail). The external force, f was taken as the force exerted on L516 at the center of IBCα directing to V262 at the center of IBCβ, mimicking the driving force for domain closure of IBC upon IP₃ binding. The magnitude of f was scaled linearly so as to be in accordance with the actual structural change. As in PCAs, Cα atoms in the secondary structures of IBC/SD were taken as the degrees of freedom and those in IBCβ were used for structural alignment.

Results and Discussion

Dynamics of the N-terminal domains in IP₃R

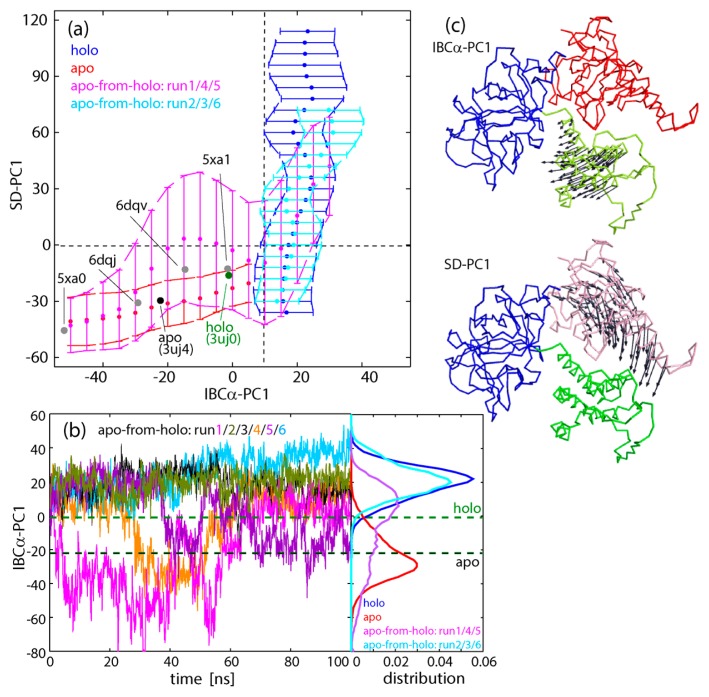
The simulation results for the three systems, holo, apo, and apo-from-holo, showed that IBC/SD predominantly underwent inter-domain motions, where each domain behaves as a rigid body except for flexible linkers: The intra-domain RMSF (root mean square fluctuation) for Cα atoms in the secondary structures was 0.77 Å for SD, 0.64 Å for IBCβ, and 0.61 Å for IBCα. Below, dynamics of IBC/SD was evaluated by IBCα-PC1, the first principal component of IBCα relative to IBCβ, and SD-PC1, the first principal component of SD relative to IBCβ (see Methods and Fig. 2c).

Figure 2.

(a) Two dimensional plots along IBCα-PC1 and SD-PC1. Apo simulation (red), holo simulation (blue), apo-from-holo: run1/4/5 (pink), and apo-from-holo: run2/3/6 (cyan). Plots are omitted for clarity with probability less than 0.01 out of the overall trajectories. The values from the crystal structures of IP₃-bound and -unbound forms are shown by green (holo) and black (apo), respectively, as well as the other four PDB structures (gray). (b) Time courses of IBCα-PC1 for six apo-from-holo simulations (starting at the holo structure after IP₃ was removed). Three runs (1: magenta, 4: orange, and 5: violet) underwent transitions to the apo structure in the IBC domain, while the other three runs (2: gray, 3: dark green, and 6: cyan) remained in the holo structure. The distributions of IBCα-PC1 were also shown in the right panel. Colors are the same as in (a). (c) The residue motions of IBCα-PC1 and SD-PC1 relative to IBCβ are shown by arrows.

The resultant structural distributions plotted on the two-dimensional space, IBCα-PC1 vs. SD-PC1, clarified that equilibrium simulations for holo and apo forms yielded completely separate distributions (Fig. 2a and Supplementary Fig. S1): In the apo form, IBCα exhibits large-scale opening/closing motions against IBCβ. At the same time, the closing motion of IBCα accompanies the closing motion of SD. It is found that the distribution entirely covers various experimental structures of both holo and apo states, such as IBC/SD (PDB: 3uj0/3uj4 [13]), IBC/SD+HD (PDB: 5xa1/5xa0 [14]), and full-length IP₃R (PDB: 6dqv/6dqj [16]) for holo/apo forms, respectively. The correlation between SD and IBCα is also consistent with the experimental structures; SD is more closed in the holo structures (3uj0, 5xa1, and 6dqv) than in the apo structures (3uj4, 5xa0, 6dqj). In contrast, the holo form shows completely different motions. A large-scale opening/closing motion of SD against IBCβ occur with IBC kept at the closed state due to IP₃ binding (actually, the IP₃ binding site is a little more closed than that of the experimental holo structures).

In the non-equilibrium apo-from-holo simulation, three runs (run 1/4/5) out of the six runs relaxed quickly to the apo distribution within the simulation time which was as short as 100 ns, while the other three runs (run 2/3/6) showed a distribution overlapping with the holo distribution even though IBC did not bind to IP₃ (Fig. 2b), indicating no direct effect of the IP₃ binding on the SD structure via such a long-range electrostatic force.

Structural basis of the biphasic inter-domain dynamics

Here, we tried to identify the structural basis of the biphasic response of IBC/SD (see Fig. 2a) in the inter-domain contacts of SD to IBCα or IBCβ. Figure 3a shows a sharp decrease in the number of atom contacts between SD and IBCβ (N_SD/IBCβ) with increasing SD-PC1 at SD-PC1~0. This indicates that the closing motion of SD tends to separate SD from IBCβ at the hinge region, and finally breaks their connection. The contact statistics of each residue, given in Supplementary Table S1 (the associated residue positions in IBCβ are depicted in Fig. 3c), also indicates dissociation between SD and IBCβ for SD-PC1>0. The stable opening/closing motion of SD against IBCβ requires the hinge contacts, which are maintained in the experimental structures (see Fig. 2a). Once it is broken, SD starts to move independently of IBCβ. These different hinge states produce the two separated responses of N_SD/IBCβ.

Figure 3.

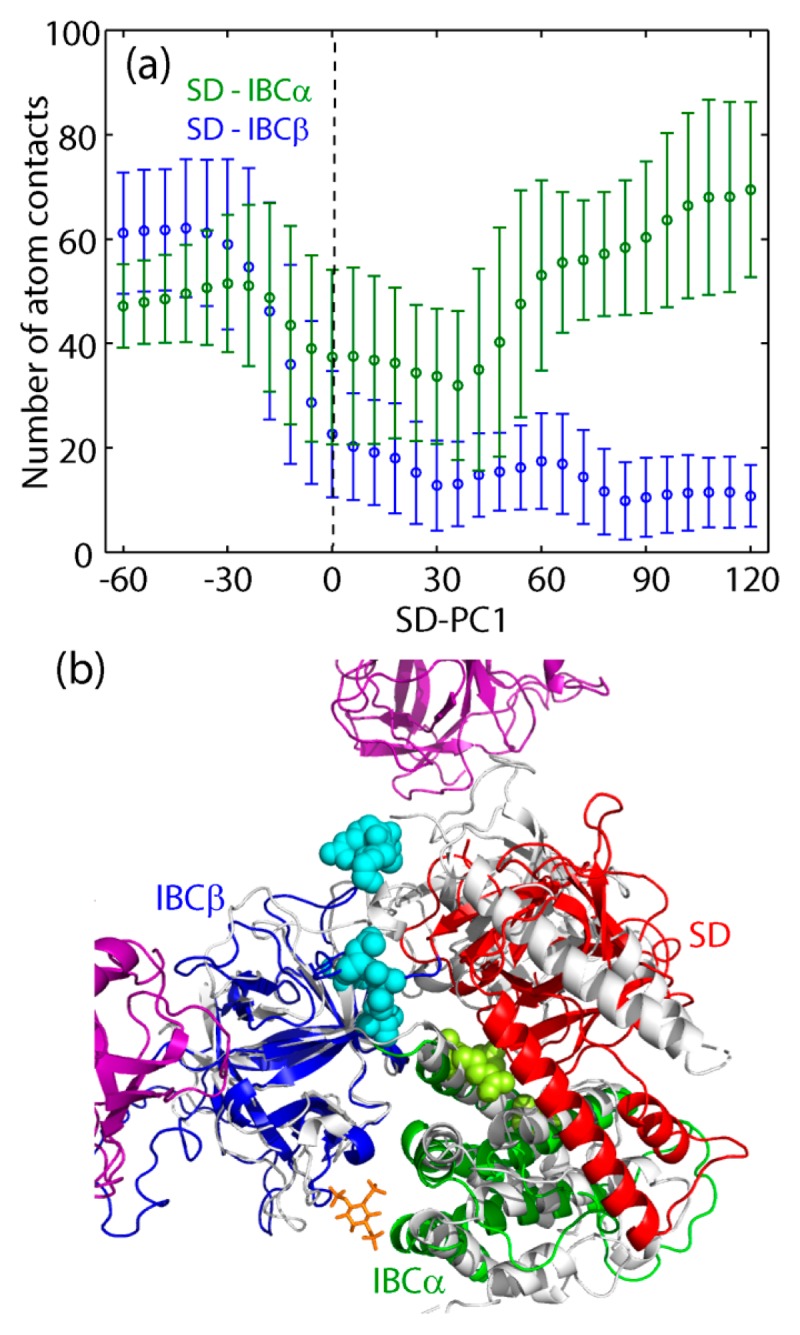
(a) Number of atom contacts between SD and IBCα (green) and between SD and IBCβ (blue) as a function of SD-PC1. (b) Representative structure of holo simulation and staying in the nonlinear region. The residues in IBCβ losing contacts with SD are shown by cyan spheres, while the residues in IBCα gaining contact with SD, by light green spheres (see Table S1 and S2). IBCβ is superimposed on that of the tetramer structure in holo form (gray, PDB: 6dqv). Colored by magenta is the neighboring monomers in IP₃R, showing the loss of atom contact with SD.

Figure 3a also shows the number of atom contacts between SD and IBCα (N_SD/IBCα). For SD-PC1<0, the number of atom contacts is maintained at the high level, indicating that significantly stable contacts between SD and IBCα make these two domains to behave as a single rigid-body, where 14 residue-residue pairs have P_contact>0.6 (Supplementary Table S2 and Fig. 3c). This is the reason for the dynamic correlation between the motions of IBCα and SD in apo form (see Fig. 2a). However, the dissociation of SD from IBCβ as a result of the closure motion of SD enhances the fluctuations of SD to diminish P_contact of the 14 residue-residue pairs listed in Supplementary Table S2, instead produces many transient contacts with small values of P_contact. Although N_SD/IBCα increases slightly for SD-PC1>0, these transient contacts reduce the dynamic correlation between ST and IBCα.

In the non-equilibrium apo-from-holo simulations, the two different responses occur, one relaxing to the apo form and the other staying in the holo region. This is because the starting structure of the simulation, the holo crystal structure (3uj0) but with IP₃ removed, is positioned close to the transition state separating the two states, one with the hinge connecting SD with IBCβ and the other with the hinge dislocated. With 50% probability, the relaxation to the apo region occurs with maintaining the hinge (runs 1/4/5), whereas the dislocation of the hinge occurs three times out of six (runs 2/3/6).

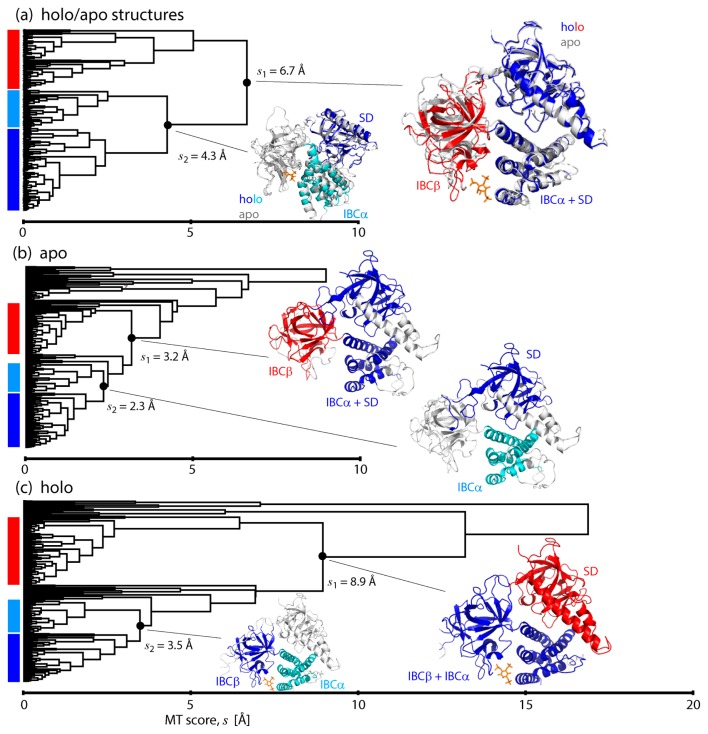
Analyses using Motion Tree and the linear response theory

To scrutinize the biphasic dynamics, we constructed and compared the Motion Trees [18,19] of IBC/SD. First, as a reference, the Motion Tree for the comparison of the two crystal structures, holo (PDB: 3uj0) and apo (PDB: 3uj4) [13], was calculated (Fig. 4a). The hierarchical description of the structural difference illustrates the overall motions occurring between IBCβ and IBCα/SD, indicating that IBCα/SD moves together as a single rigid body. Then, each part is further divided into smaller blocks, IBCβ into two subsets of β-sheets, and IBCα/SD into each domain. The apo simulation with IBCα-PC1<10 resulted in the Motion Tree of almost the same arrangement as the one comparing the crystal structures, though small segments such as loops and parts of helices in SD are not included in the domain due to large fluctuations in the simulation (Fig. 4b). Agreement of these two Motion Trees indicates that IBCα/SD moves as a rigid body relative to IBCβ in response to IP₃ binding/unbinding, resulting from the stable hinge regulating dynamics occurring between IBCβ and IBCα/SD. In contrast, in the Motion Tree calculated from the holo simulation with IBCα-PC1>10 (Fig. 4c), it is found that SD moves independently of IBC (IBCβ and IBCα are linked together by IP₃) with the largest MT score (8.9 Å), or the largest amplitude, among the three Motion Trees. This is due to the dislocated hinge between SD and IBCβ.

Figure 4.

Motion Trees constructed from (a) the two crystal structures of IP₃-bound (PDB: 3uj0; colored) and -unbound (PDB: 3uj4; gray) forms (see Fig. 1b), (b) MD trajectories of apo simulation with IBCα-PC1<10 and (c) MD trajectories of holo simulation with IBCα-PC1>10. The nodes separating small fragments, like N-/C-terminals, are omitted for clarity.

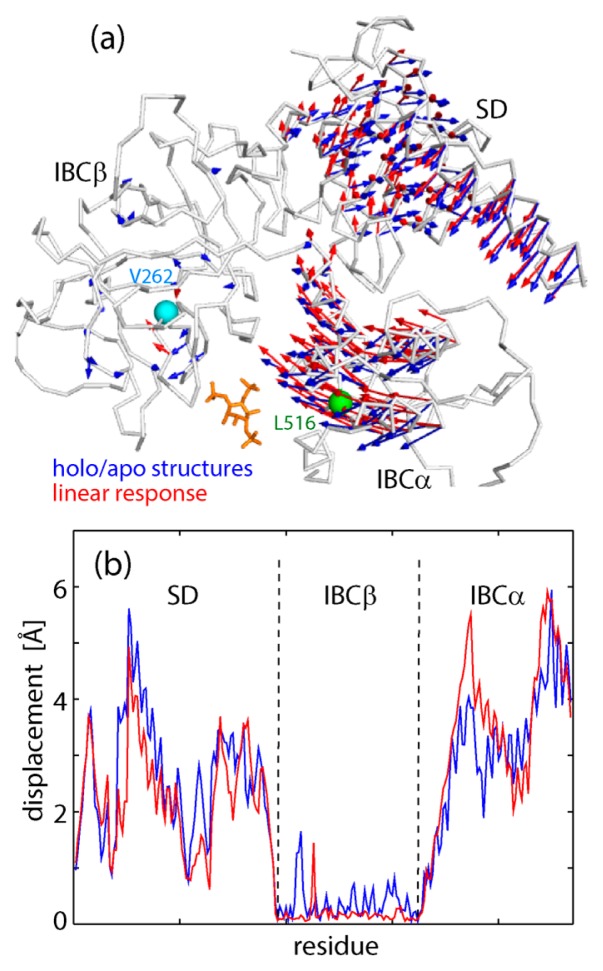
Finally, we examined the dynamics from the viewpoint of the response of IBC/SD upon IP₃ binding by utilizing the linear response theory [5]. Here, we tried to predict the structure of the holo form from the crystal structure of the apo form based on the linear response scheme, i.e., the unperturbed (apo state) dynamics represented in the form of a variance-covariance matrix and the perturbation mimicking IP₃ binding. The variance-covariance matrix for the unperturbed state was calculated from the apo trajectories near the apo crystal structures, or with −30<IBCα-PC1<–10 (see Fig. 2a). The perturbing force mimicking IP₃ binding was modeled by a force vector exerted on the center of IBCα (L516) directed to the center of IBCβ (V262). The prediction result demonstrates reasonable agreement between the experimental and predicted structural changes upon IP₃ binding; the motions of SD/IBCα relative to IBCβ are similar to each other (the correlation coefficient for the two sets of the vectors is 0.79 (Fig. 5a), and the correlation coefficient for the displacement amplitudes of Cα atoms is 0.91 (Fig. 5b). A small discrepancy may come from curvilinear (rotational) domain motions that cannot be described by the linear Cartesian coordinates [26,27]. The success of the prediction by the linear response theory suggests that the response of IBC/SD upon IP₃ binding is within the linear regime, that is, the perturbed state (the holo state) is chosen from the structural ensemble of the unperturbed state (the apo state) according to the exerted perturbation (IP₃ binding). Quick response is characteristic of the dynamics in the linear regime, where the free energy surface is rather smooth and lacking a significant barrier. Actually, in the non-equilibrium apo-from-holo simulations, it was shown that IBCβ and IBCα opened immediately after removal of IP₃ to reach the apo form (Fig. 2b).

Figure 5.

Structural changes derived from the two crystal structures of IP₃-bound and -unbound forms (blue, see Fig. 1b) and predicted by linear response theory (red). (a) Residue motions are shown by arrows. The force is exerted on L516 in the center of IBCα (green) directing to V262 in the center of IBCβ (cyan). (b) The magnitudes of residue displacement.

Regulation of dynamics in IP₃ receptor

As shown in Figure 2a, the experimental structures of both apo and holo states in the tetrameric full length of IP₃R (PDB: 6dqj/6dqv [16]) are within the apo distribution in the monomeric form. This means that the motion from the apo to the holo state occurring in the tetramer is also in the linear response regime upon IP₃ binding. In contrast, large scale structural changes of SD accompanied with dislocation of the hinge is incompatible with the inter-subunit contacts in the tetramer, as seen in Figure 3b. In other words, the response beyond the linear regime is suppressed by the tetrameric native structure of IP₃R. The importance of the inter-subunit contacts in the tetramer was confirmed by the mutation, Y167A, disrupting the interaction at the interface between SD and IBCβ in the neighboring subunit, and impairing the gating process [13,28].

We have found such regulation mechanism of IP₃R dynamics, not only through the subunit multimerization, but also from the inter-residue and inter-domain interactions. First, we noticed that the dynamics of IBC (IBCβ and IBCα) was properly regulated by the salt bridge of Arg241-Glu439 located between the two domains [23]. Without the salt bridge, IBC can scarcely form the stable IP₃-bound form and freely change the domain arrangement as the two domains are connected by a single linker [10]. Further, the multiple domain arrangement was found to reduce excessive fluctuations at the functionally important portion. The fluctuations of IBC are restrained by SD; in the MD simulations, the RMSD value from the crystal structure was significantly reduced from 4.8 Å in IBC to 2.4 Å in IBC/SD [23]. In conclusion, IP₃R dynamics is regulated via residue-residue interaction, domain arrangement and subunit multimerization to maintain the collective and linear response to the upstream stimuli.