Abstract
The combination of molecular dynamics (MD) simulations and small-angle X-ray scattering (SAXS), called the MD-SAXS method, is efficient for investigating protein dynamics. To overcome the time-scale limitation of all-atom MD simulations, coarse-grained (CG) representations are often utilized for biomolecular simulations. In this study, we propose a method to combine CG MD simulations with SAXS, termed the CG-MD-SAXS method. In the CG-MD-SAXS method, the scattering factors of CG particles for proteins and nucleic acids are evaluated using high-resolution structural data in the Protein Data Bank, and the excluded volume and the hydration shell are modeled using two adjustable parameters to incorporate solvent effects. To avoid overfitting, only the two parameters are adjusted for an entire structure ensemble. To verify the developed method, theoretical SAXS profiles for various proteins, DNA/RNA, and a protein-RNA complex are compared with both experimental profiles and theoretical profiles obtained by the all-atom representation. In the present study, we applied the CG-MD-SAXS method to the Swi5-Sfr1 complex and three types of nucleosomes to obtain reliable ensemble models consistent with the experimental SAXS data.
Keywords: MD simulation, SAXS, protein solution structure, structural ensemble, nucleosome
Significance.
Protein dynamics are important for protein functions. To investigate protein dynamics, the combination of molecular dynamics (MD) simulations and small-angle X-ray scattering (SAXS) experiments, known as the MD-SAXS method, has been shown to be useful. However, all-atom MD simulations are limited to the microsecond time scale, which is significantly shorter than the typical time scale of large-scale protein motions. To overcome the time-scale limitation in the all-atom MD simulations, we propose a combined method of coarse-grained (CG) MD simulations and SAXS, termed the CG-MD-SAXS method, which was successfully applied to flexible and large biomolecules such as nucleosomes.
Molecular dynamics (MD) are crucial to the structure and function of proteins [1]. To investigate the dynamic features of proteins, computational methods, such as MD simulations and normal mode analysis, are highly useful [1,2]. Simulation methods have also been utilized in combination with experimental data. Nuclear magnetic resonance (NMR) data are often incorporated into molecular simulations [3–6]. Small-angle X-ray scattering (SAXS) is another experimental tool for measuring macromolecular structures in solution. In contrast to NMR, SAXS has no limitation on the macromolecular size. However, the SAXS data are low in resolution, because they are an averaged quantity over rotational and conformational variants of solution structures. Therefore, a combination of simulation methods and SAXS has demonstrated successful modeling of detailed solution structures and a structure ensemble of proteins [7,8].
To compare simulation results with SAXS data, theoretical SAXS profiles are calculated from 3D structures of proteins. Several methods (e.g., CRYSOL [9], FoXS [10], AquaSAXS [11], the Zernike polynomials-based method [12], Fast-SAXS [13] and Fast-SAXS-pro [14]) have been proposed for the estimation of theoretical SAXS profiles from all-atom and CG models. In most of these methods, a theoretical SAXS profile is obtained from a single structure. For highly flexible proteins, a single structure is not sufficient to obtain theoretical SAXS profiles consistent with experimental profiles, because the experimental SAXS profile is an average of scattering from various conformations in solution. To handle a set of the structural ensemble of proteins, several methods (e.g. EOM [15], MES [16], EROS [17] and BSS-SAXS [18]) have been proposed. However, the unique determination of the structural ensemble is still difficult solely from SAXS data due to the limited information content. To overcome the difficulty originating from the flexibility of proteins, the incorporation of physicochemical methods such as MD simulations into the SAXS analysis is useful.
Water molecules contribute significantly to the SAXS profile. In the calculation of theoretical SAXS profiles, the following two major effects of water molecules should be considered: solvent-excluded volume and hydration water. In SAXS experiments, scattering from only the buffer solution is measured in addition to that from the protein solution. The experimental SAXS profile is obtained as the difference between two scattering intensities of the protein and buffer solutions. Thus, the excess electron density of proteins from the solvent molecules excluded by proteins becomes the source of the experimental SAXS profiles. Therefore, the X-ray scattering from the excluded solvent molecules should be considered while calculating theoretical SAXS profiles; this effect is referred to as the excluded-volume effect in this study. Another important effect of water on the SAXS profile is scattering from hydration water. Because the electron density of hydration water is higher than that of bulk water, the increment of scattering from hydration water significantly affects the SAXS profile. In the combination of all-atom MD simulations and SAXS [19–22] (e.g. the MD-SAXS method [19]), the MD simulation for the pure solvent is performed in addition to the simulation for the protein solution, and their theoretical scattering intensities are obtained. The theoretical SAXS profile is then calculated as the difference between the two scattering intensities, as done in actual experiments. Thus, two major solvent effects on SAXS profiles, i.e., the solvent-excluded volume of proteins and hydration water, are considered at the atomic level. In addition, since the electron density of bulk solvent depends on the ion concentration, ions in bulk significantly affect the SAXS profiles. In the all-atom MD-SAXS method, ion effects are also considered [23]. As an alternative approach of the explicit solvent model, the implicit solvent model has also been employed for the calculation of the theoretical SAXS profile [4,9]. In CRYSOL, the hydration water is modeled as the continuum hydration shell of proteins. The solvent-excluded volume is modeled as Gaussian spheres with effective radii. However, the estimation of the increment of electron density in the hydration shell and the determination of the effective radius of Gaussian spheres are difficult because they depend on the properties of protein surfaces, packing of protein interiors, and solvent compositions. Therefore, in CRYSOL, two parameters, i.e., the increment of electron density in the hydration shell and the effective radius of Gaussian spheres, are adjusted for fitting to experimental SAXS profiles.
Although the all-atom treatment in MD simulations precisely describes protein dynamics and solvent effects, sufficient sampling is computationally expensive particularly for very large and/or very flexible proteins due to the long timescale of their dynamics. For such targets, coarse-grained (CG) models are often utilized to reduce computational burden [24]. For example, the CG-MD software CafeMol [25] employs a CG model in which one amino-acid residue is represented by one CG particle, and the effect of water molecules is implicitly incorporated by a continuum dielectric model. Owing to the CG representation, CG-MD simulations can be performed in a substantially fast computation; the combination of CG-MD simulations and SAXS will thus be efficient, particularly for the sampling of large and flexible proteins. Therefore, in this study, we propose a method of combining CG-MD and SAXS, referred to as the CG-MD-SAXS method.
To develop the CG-MD-SAXS method, due to the implicit treatment of water molecules, solvent effects on SAXS profiles should be modeled in a CG manner. As in CRYSOL, two parameters, i.e., the increment of electron density in the hydration shell and the effective radius of Gaussian spheres, are adjusted in the CG-MD-SAXS method. However, if the two parameters are adjusted for every snapshot in MD trajectories, a large number of parameters are required in total with respect to one experimental SAXS profile. Owing to limited SAXS resolution, a large number of adjustable parameters should be avoided. In this study, we propose a method to overcome this problem. First, in our method, six terms comprising the CG-MD-SAXS profile are independently evaluated from MD trajectories. Second, the six terms are combined into one CG-MD-SAXS profile using the abovementioned two adjustable parameters. Therefore, only these two adjustable parameters of solvent effects are used for an entire MD trajectory. In this study, it is shown that these two parameters are sufficient for solvent modeling in the calculation of CG-MD-SAXS profiles for trajectories.
For CG-MD simulations, the software CafeMol was employed. In CafeMol, one amino acid is represented as one CG particle for proteins, as described above. For nucleic acids, the base, sugar and phosphate of nucleotides are represented as three different CG particles, respectively. First, the scattering factors of the CG particles for 20 amino acids, 5 bases, 2 sugars (ribose/deoxyribose), and 1 phosphoric acid were evaluated from atomic scattering factors by averaging structural data in the Protein Data Bank (PDB). Next, the hydration model in a CG manner was developed for the CG-MD-SAXS analysis. In the hydration model, only the two adjustable parameters were employed for an entire trajectory. The performance of the CG-MD-SAXS method was examined by comparisons with the all-atom MD-SAXS analysis and experimental data. Additionally, the position dependencies of CG particles for theoretical SAXS profiles were examined. Four positions representing an amino acid as a CG particle, i.e., the Cα, Cβ atoms, the center of electron, and the center of mass of the side-chain atoms, were compared in terms of accuracy for calculated SAXS profiles. Finally, the CG-MD-SAXS method was applied to a flexible protein, i.e., the Swi5-Sfr1 complex including disordered regions and to large/flexible complexes, i.e., three types of nucleosomes including flexible DNA, as examples for calculating theoretical profiles obtained from structural ensembles.
Methods
Scattering factor of CG particles
The excess scattering intensity of a CG-model protein in dilute solution, ICG(q), is defined by the Debye formula as
| (1) |
where q is the wave vector transfer defined as q=4π sinθ/λ (2θ is the scattering angle, and λ is the X-ray wave length), N is the number of CG particles for proteins, M is the number of grid points in the hydration shell, is a scattering factor for the i-th CG particle or grid, and rij is the distance between the i- and j-th particle or grid. The scattering factor can be expressed by
| (2) |
where is the scattering factor of CG particle i in vacuo, and is the factor of the solvent-excluded volume. The scattering factor for the hydration shell can be expressed by
| (3) |
where is the factor of the contrast of electron densities between the hydration shell and the buffer solution.
Scattering factors of CG particles in vacuo and solvent-excluded volume
The scattering factor of CG particle k representing an amino acid, base, sugar or phosphate in vacuo, , was calculated from the averaged scattering intensity of the corresponding moiety in the PDB data as follows:
| (4) |
where is an atomic scattering factor in vacuo of the i-th atom belonging to CG particle k. In this calculation, we used a set of high-resolution crystal structures including hydrogen atoms as described in the last paragraph of this section.
Next, the factors of the solvent-excluded volume of CG particles are examined. First, the treatment of the solvent-excluded volume in an all-atom model is briefly described. The modified atomic scattering factor [26], fvac_ex(q), in which the effect of the solvent-excluded volume is incorporated, is defined as
| (5) |
where the second term on the right-hand side represents the effect of the excluded volume by a Gaussian sphere, vi is the atomic volume of the i-th atom, and ρs is the electron density of the bulk solvent. Using the modified atomic scattering factor, the excess scattering intensity, Ivac_ex(q), of a protein is then calculated by
| (6) |
This formula is used in CRYSOL, and vi is scaled so that the theoretical SAXS data are fitted to the experimental SAXS data because the excluded volume depends on the packing density of the protein interior.
Yang, S., et al. extended Eq. (5) to obtain the modified CG scattering factor, including the excluded volume [13]. The modified CG scattering factor is defined by a knowledge-based formula as
| (7) |
In this approach, the parameters for excluded volumes such as vi and ρs must be determined before the evaluation of , and these parameters cannot be modified after evaluation of because the excluded-volume term is already averaged over many conformations in the PDB. Therefore, we introduced another definition of the modified CG scattering factor including the solvent-excluded volume.
In our method, to modify the parameters for the excluded volume after evaluating the atomic scattering factors in vacuo and that of the excluded volume, we defined a CG scattering factor by introducing the excluded volume of CG particles explicitly as
| (8) |
where the second term on the right-hand side represents the excluded volume of i-th CG particle, is the volume of i-th CG particle defined as the total volume of atoms in an amino acid, base, sugar or phosphate represented by a CG particle. The radius of the Gaussian sphere, αi, is determined by minimization of Si:
| (9) |
To control the amount of the excluded-volume effect sampled by CG-MD simulations, was scaled after the evaluation of .
The determination of was conducted using high-resolution crystal structures of the following 5 proteins, 2 DNA structures, and 2 RNA structures. The proteins were serine protease (PDB ID: 1GCI [27], 0.78 Å resolution), xylose isomerase (PDB ID: 1MUW, 0.86 Å resolution), trypsin (PDB ID: 1PQ7 [28], 0.8 Å resolution), P. abyssi rebredoxin (PDB ID: 2PYA [29], 0.86 Å resolution) and HEW lysozyme (PDB ID: 2VB1 [30], 0.65 Å resolution). The nucleic acids were DNA (PDB ID: 1BNA [31], 1.9 Å resolution), DNA (PDB ID: 1EN3 [32], 0.99 Å resolution), RNA (PDB ID: 1P79 [33], 1.1 Å resolution) and a CAG RNA repeat (PDB ID: 3NJ6 [34], 0.95 Å resolution). Using Eq. (4), for each CG particle corresponding to 20 types of the amino acid was determined. For nucleotides, the 3SPN.1 model [35,36] was used as the CG representation. In the model, the sugar, phosphate, and base were represented as three different CG particles, and the determination of for the CG particles was performed using guanine, adenine, cytosine, thymine, uracil, ribose, deoxyribose and phosphate in DNA/RNA. Using Eq. (9), the radius of the Gaussian sphere, αi, for each type of CG particle was determined.
Scattering from the hydration shell
Next, scattering from the hydration shell was examined. The water density of the hydration shell of proteins is higher than that of the bulk solvent. The contrast of the electron densities between the hydration shell and the bulk solvent were incorporated in the calculation of the excess scattering intensity. In our method, the effects of the hydration shell were incorporated by generating grids of the high-density region around the protein, as follows: A cubic lattice with a spacing of ΔD was generated in the vicinity of proteins. A unit cell of the lattice (ΔD3) was set such that a water molecule can be fit in a cell. Then, the grid points of the hydration shell were selected as the points that were satisfied with the range of rkj+rw<r<rkj+rs over all the CG particles. In this instance, r is the distance of the grid point from a CG particle, rkj is the radius of the CG particle, rw is the radius of a water molecule, and rs is the thickness of the hydration shell. In the present calculations, ΔD, rw and rs were set at 3 Å, 1.5 Å and 4.5 Å, respectively. For each grid point in the hydration shell, the scattering factor is assigned. The scattering factor represents the contrast of the electron densities between the hydration shell and the buffer solution as
| (10) |
where i represents the i-th grid point, w is the ratio of the electron-density increase in the hydration shell from the buffer solution, and is the scattering factor of a water molecule in an all-atom representation (one oxygen atom and two hydrogen atoms) given by
| (11) |
To incorporate the amount of the contrast of the electron-density in a CG manner, the parameter w is scaled after evaluation of .
Computational details of the scattering intensity from CG models
The excess scattering intensity of a CG model, ICG(q), including effects of the excluded volume and the hydration shell was developed by Eqs. (1)–(4), (8) and (10). In the CG-MD-SAXS method, ICG(q) is averaged over a large number of snapshot structures in CG-MD trajectories. The two parameters of and w defined in Eqs. (8) and (10) are adjustable parameters. For computational convenience, we introduced a scaling factor cvρ by replacing in Eq. (8). Taken together, Eq. (1) can be rewritten as,
| (12) |
In this equation, are:
| (13) |
Before the determinations of cvρ and w, the factors can be averaged over MD trajectories as
| (14) |
Next, cvρ and w were searched through a specified range to minimize χ2 defined by
| (15) |
| (16) |
where Nq is the number of q, Iexp(q) is the experimental scattering intensity, Icalc(q) is a trial intensity of Eq. (14) with fixed parameters in the search, and σexp(q) is the experimental error. The search ranges of cvρ and w were set at 0.9≤cvρ≤1.1, and 0.0≤w≤0.01, respectively. These ranges are similar to those used in CRYSOL; the parameter of the excluded volume is searched up to a 10% decrement/increment, and the contrast in the hydration shell is searched up to a 27% corresponding to w=0.01.
Comparison of the intensities calculated from CG-MD-SAXS, CRYSOL, and all-atom MD-SAXS
To examine the performance of the CG-MD-SAXS method, the scattering intensity of a crystal structure calculated using the CG-MD-SAXS method was compared to that calculated using CRYSOL in an all-atom manner and that calculated using the all-atom MD-SAXS for HEW lysozyme (PDB ID: 6LYZ [37]) with explicit water. The experimental profile was included in the CRYSOL package. When the CG-MD-SAXS method was applied to the crystal structure, an amino acid was represented as one CG particle placed at the center of electrons. The calculation of CRYSOL was performed using the default setting. When the all-atom MD-SAXS was applied, the excess scattering intensity of lysozyme was calculated as in the following protocol. In this report, the procedure is described only briefly. See reference [19] for details. Two all-atom MD simulations of both a protein solution and a pure solvent were carried out independently. From the trajectory of the protein solution, a spherical region including the protein and hydration shell was extracted, and the region was used in the calculation of the scattering intensities. In the present calculation, a radius of 36 Å from the center of mass was employed. Next, the scattering intensities of snapshots in the trajectory were averaged. To extract the scattering intensity of the pure solvent, a spherical region of the same size region determined in the protein solution was extracted from the trajectory of the pure-solvent MD simulation, and the scattering intensities for snapshots were averaged. The excess scattering intensity was then obtained by subtracting the two scattering intensities.
All-atom MD simulations were carried out with the MD program MARBLE [38] using the CHARMM27/CMAP force field [39,40] and the TIP3P water model [41]. The solution system was prepared by placing the crystal structure at a cubic cell and adding a 20 Å layer of water molecules. No counterions were added. A 1-ns production run was performed in the isothermal-isobaric (NPT) ensemble at 1 atm and 293 K. Before the production run, a 100 ps heating simulation from 10 K to 293 K with harmonic constraints on the heavy atoms of the solute in the NVT ensemble and a 100 ps simulation for gradually removing the constraints in the NPT ensemble were sequentially performed. In addition, the MD simulations of the pure solvent were performed under the same procedure as the protein solution.
Comparison of CG-SAXS profiles for various structures and CG models
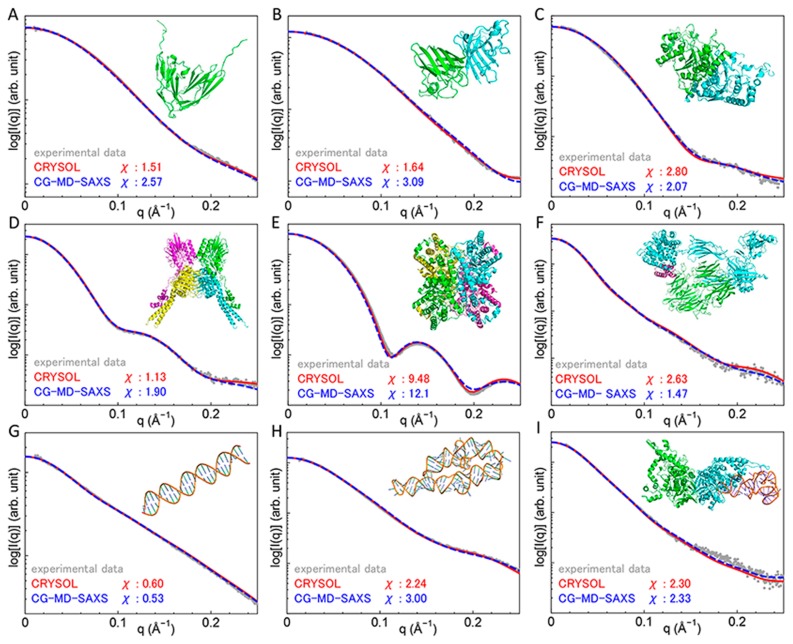
For the performance test of the CG-MD-SAXS method, the scattering intensities of various proteins, DNA/RNA, and a protein-RNA complex were calculated with their fixed structures. The intensities were compared with those calculated by CRYSOL and their experimental profiles. The experimental SAXS data were taken from BIOISIS.net (http://www.bioisis.net/). The examined proteins are Immunoglobulin-like domains 1 and 2 of the protein tyrosine phosphatase LAR3 (BIOISIS ID: LAR12P [42], PDB ID: 3PKJ), Superoxide dismutase (BIOISIS ID: APSODP [43], PDB ID: 1HL5 [44]), Ubiquitin-like modifier-activating enzyme ATG7 C-terminal domain (BIOISIS ID: ATG7CP [45], PDB ID: 3T7E [45]), DNA double-strand break repair protein MRE11 (BIOISIS ID: MRERAP [46], PDB ID: 3AV0), glucose isomerase (BIOISIS ID: GISRUP, PDB ID: 2G4J [47]), and Complement C3b+Efb-C (BIOISIS ID: C3BEFP [48]). The examined DNA/RNA and complexes are 28 base-pairs of DNA (BIOISIS ID: 28BPDD), the P4–P6 RNA ribozyme domain (BIOISIS ID: 1P4P6R [49], PDB ID: 1GID [50]), and A. aeolicus MnmG bound to tRNA (BIOISIS ID: MNMG2X [51]).
To examine the choice of CG particle placement, four CG models for proteins and two CG models for nucleic acids were compared. For proteins, a CG particle represents an amino acid, and there are four different variations in terms of the locations of the CG particle: the center of electrons (CME model), Cα position (CA model), Cβ position (CB model) and the center of the side chain of each residue (CMS model). For nucleic acids, three different CG particles represent a base, sugar and phosphate, respectively, and there are two different variations about the locations. The first is that the CG particles are located at the centers of electrons of each moiety (CME model). The other model is the 3SPN.1 model employed in CafeMol. In the 3SPN.1 model, the CG particles for the sugar and phosphate are placed at the center of mass for each moiety. The CG particle for purine bases (adenine and guanine) is located at the N1 position, and that for pyrimidine bases (cytosine and thymine) is located at the N3 position. Using various proteins, DNA/RNA, and the protein-RNA complex described above, CG-SAXS profiles for the different models were calculated and were compared to the experimental SAXS data and the all-atom SAXS profile calculated using CRYSOL.
CG-MD-SAXS analysis for a flexible Swi5-Sfr1 protein complex
The Swi5-Sfr1 protein complex was employed in the CG-MD-SAXS analysis. The crystal structure of Swi5 and the C-terminal domain of the Sfr1 complex, referred to as Swi5-Sfr1C, (PDB ID: 3VIQ [52]) was used. The mutated residues 170–180 of Sfr1 and the missing side chain of residue 299 of Sfr1 were replaced with wild-type residues using the program MODELLER [53].
All the CG-MD simulations were performed using the program CafeMol with the atomic interaction-based CG2+ (AICG2+) model [54] for the energy potential of proteins. One residue was coarse-grained as one CG particle, located at the Cα position (CA model). For disordered regions, the flexible local potential (FLP) [54] was used. The electrostatic interaction was handled by the Debye-Hückel type interactions. The ion concentration was set at 200 mM corresponding to the same conditions used in the SAXS experiments [52]. The time evolution was handled by Langevin dynamics at 300 K. Changing the range of the disordered region modulated by the FLP, a 107-step CG simulation was independently repeated 10 times in each calculation condition. Snapshots were saved at every 1,000th step in one simulation, the latter half of the simulation was used in the CG-MD-SAXS analysis (5,000 snapshots in one simulation), and the snapshots of 10 different simulations were merged (50,000 snapshots in total). Using the merged snapshots, a theoretical SAXS profile was calculated. The experimental SAXS profile from q=0.015 to 0.25 was used.
CG-MD-SAXS analysis for large and flexible nucleosomes
Three types of nucleosomes were employed: the canonical nucleosome, the CENP-A nucleosome, and the H2A.B nucleosome. The initial structures of the three nucleosomes were prepared by modeling processes, as follows. The crystal structure of the canonical nucleosome and the CENP-A nucleosome were used; their PDB IDs were 3AFA [55] and 3AN2 [56], respectively. All missing histone tails were added by MODELLER. In the canonical nucleosome, 1 base pair was added to the edge of DNA (I1, J292 in 3AFA), and then the DNA sequence was changed to that of the SAXS experiment (147 base pairs) [56] using the MMTSB tool [57]. In the crystal structure of the CENP-A nucleosome, both ends of DNA (26 base pairs in total) were short compared with the DNA used in the SAXS experiment. Because the DNA sequence used in the SAXS experiment for the CENP-A nucleosome is the same as that of the SAXS experiment for the canonical nucleosome, the missing part of DNA was transplanted from those of the modeled canonical nucleosome. The modeled canonical nucleosome was superimposed into the CENP-A nucleosome such that the root mean square deviation (RMSD) values of H2A/B and H4 were minimized, and then the superimposed coordinates of both ends of DNA of the canonical nucleosome were added to the missing part of DNA of the CENP-A nucleosome. Because no crystal structures of the H2A.B nucleosome have been reported to date, homology modeling was performed using the modeled canonical nucleosome as a reference structure: H2A in the canonical nucleosome was changed to H2A.B. Since the DNA sequence of the H2A.B nucleosome used in SAXS experiments [58] was 145 base pairs, each 1 base pair at both ends of DNA was erased from the modeled nucleosome, and the DNA sequence (145 base pairs) was changed to those used in SAXS experiments [58] using the MMTSB tool. After the modeling processes described above, all modeled structures of canonical, CENP-A, and H2A.B nucleosomes were relaxed in solution by a 2000 step minimization (steepest descent method) by MARBLE with the CHARMM27/CMAP force field and the TIP3P water model. Counterions were added to keep the system charge-neutral.
The CG-MD simulations for the nucleosomes were performed using the program CafeMol. One residue in proteins was represented as one CG particle by the CA model, and one base in DNA was represented as three CG particles by the 3SPN.1 model. The AICG2+ model was used as a potential for proteins, and the FLP was used for the CG particles in the histone tails. For the energy potential of DNA, both Gō potential and physical interactions of base pairing were used, and the interaction between DNA and proteins was handled by the Gō potential. In the simulations of the CENP-A nucleosome, the interaction between both ends of DNA and proteins was not incorporated since both ends of DNA were missing in the crystal structure and might be flexible [58]. The electrostatic interaction was handled by the Debye-Hückel type interactions. For the structural investigation, CG-MD simulations were performed by changing both the strength of the Gō potential of the interactions among proteins and DNA, and the ion strength. The strength of the Gō potential was changed by introducing the scaling coefficient, and the range of the scaling was 0.4, 0.6, 0.8, and 1.0. The range of the ion strength was 0, 0.5, 1, 2.5, 5, 10, 25, 50, 100, 200, 300, 400, 500, 600, 700, 800, 900 and 1000 (unit is mM). In each calculation condition, a 107-step simulation at 300 K was performed and was independently repeated 100 times. Snapshots were saved at every 10,000th step in one simulation, the latter half of the simulation was used in the CG-MD-SAXS analysis (500 snapshots in one simulation), and the snapshots of 100 different simulations were merged (50,000 snapshots in total). Using the merged snapshots, a theoretical SAXS profile was obtained. The experimental SAXS profile from q=0.0103 to 0.165 was used.
Results and Discussion
Determination of scattering factors for CG particles
First, the scattering factors of CG particles were determined by Eqs. (4), (8) and (9) using high-resolution crystal structures. Next, the radii of the Gaussian spheres, αi, were determined by minimization of the difference between the CG scattering factors calculated by our formulation, , and by the formulation of Yang, S., et al. [13], . The CG scattering factors for 20 types of amino acids and 5 types of nucleic acids are shown in Supplementary Figures S1A and S1B, respectively. In all the CG particles for amino acids and bases, and are in good agreement with each other, suggesting that the scattering factors of the CG particles were successfully determined. In our formulation, the term for the excluded volume can be scalable through after the determination of the atomic scattering factors. This property is advantageous over the formulation of Yang, S., et al. The scattering factor of a water molecule given by Eq. (11) was also determined (Supplementary Fig. S1C).
Comparison of intensities calculated by the all-atom model and the CG model
To examine the accuracy of our method, the theoretical scattering intensities calculated from the CG-MD-SAXS method, CRYSOL and the all-atom MD-SAXS method, as well as the experimental profile were compared for the HEW lysozyme crystal structure (PDB ID: 6LYZ), which was not used in the determination of the scattering factor of CG particles. In the CG-MD-SAXS method, each amino acid was represented as one CG particle placed at the center of electrons, and the theoretical profile was calculated from the CG model using the CG-MD-SAXS method. For comparison, the theoretical profile of the all-atom model of the crystal structure was calculated using CRYSOL. In addition, a 1-ns trajectory of the all-atom MD simulation with explicit water was prepared, and the theoretical profile was calculated from the MD trajectory using the all-atom MD-SAXS method. Four SAXS profiles are shown in Figure 1A. The theoretical scattering intensities are in good agreement with each other. In addition, the discrepancy between the theoretical and experimental curves, χ, showed a similar value in the three methods. These results indicate that the CG-MD-SAXS method is accurate and that the CG-MD-SAXS profile is largely consistent with those calculated in an all-atom manner. Because the solvent effect is explicitly incorporated in the all-atom MD-SAXS method, the agreement of the profiles between the all-atom MD-SAXS and CG-MD-SAXS methods indicates that the current CG treatment of the solvent effects is appropriate to calculate SAXS profiles.
Figure 1.
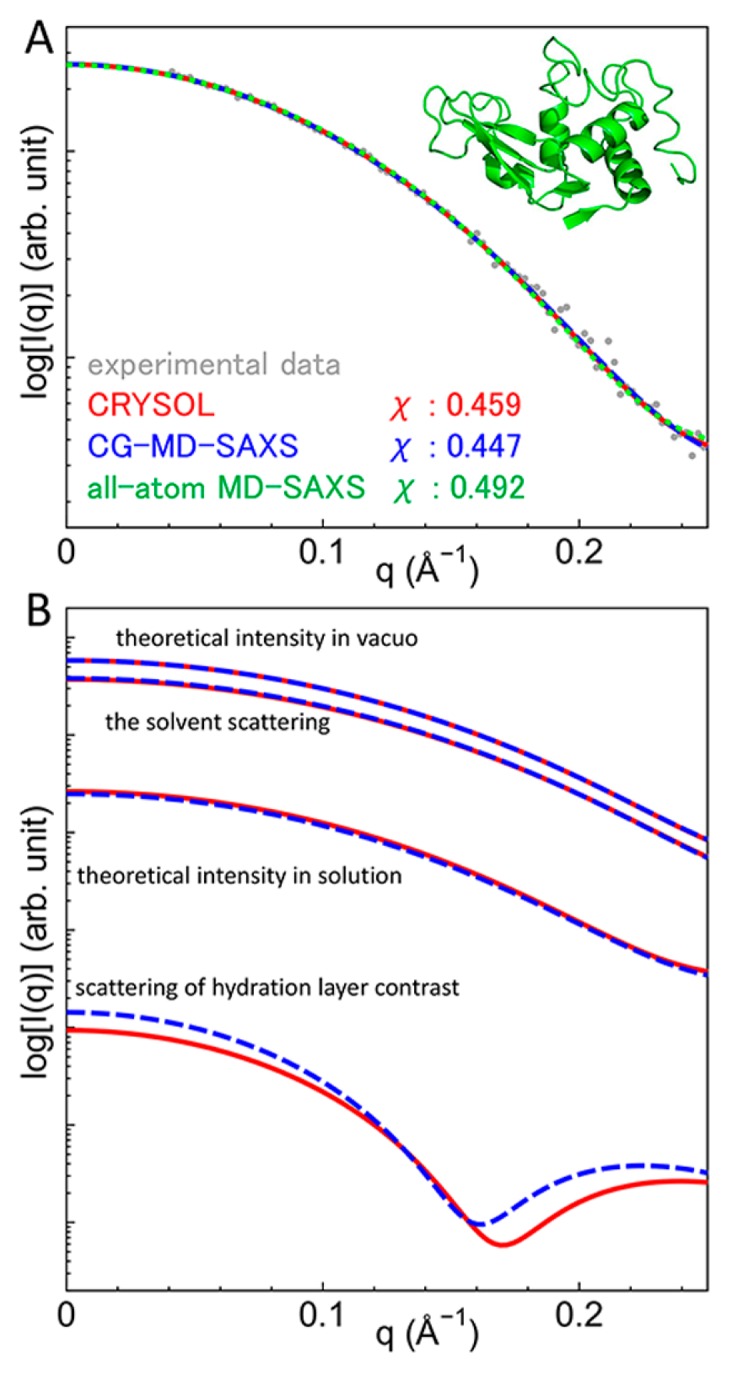
Experimental and theoretical scattering intensities of lysozyme. (A) The experimental intensity (gray) and theoretical intensities using CRYSOL (red), the CG-MD-SAXS method (blue) and the all-atom MD-SAXS method (green) are compared. (B) Components of the scattering intensity calculated using CRYSOL (red) and the CG-MD-SAXS method (blue) are compared.
Components of the scattering intensity were compared between CG and all-atom models at a fixed structure. The comparison was performed using the intensity calculated from CRYSOL since the solvent effect was implicitly incorporated in CRYSOL, as was the case in the CG-MD-SAXS method. The scattering intensities in vacuo, the solvent scattering, and the scattering of the hydration layer contrast are shown in Figure 1B. All the components calculated from the CG-MD-SAXS and CRYSOL are consistent with each other. This result also shows that all component intensities with the CG model are correctly calculated and are successfully implemented in the CG-MD-SAXS method.
The scattering intensities for various structures and CG models
To examine the dependence of CG models, theoretical profiles for various proteins, DNA/RNA, and a protein-RNA complex were calculated using the various CG models. In the CG models for proteins, the locations of the CG-particles were different: the center of electrons (CME model), Cα position (CA model), Cβ position (CB model), and the center of the side chain of each residue (CMS model). For nucleic acids, the three CG particles represent a base, sugar, and phosphate, respectively, and the CME model and the 3SPN.1 model were examined. The χ values for all the examined CG models as well as the all-atom model (the SAXS profile was calculated using CRYSOL) are compared in Supplementary Figure S2. Among the CG models, the χ values are comparable. Thus, the CA and 3SPN.1 models for proteins and nucleic acids, respectively, were used for the following analysis, because these models are usually used in CafeMol.
The theoretical SAXS profiles calculated using the CG-MD-SAXS method with the CA and 3SPN.1 models are shown in Figure 2. For comparison, SAXS profiles calculated using CRYSOL with the all-atom model are also shown. In all the examined structures, the theoretical SAXS profiles using both the CG and all-atom models are in good agreement with the experimental profiles, although the profiles using the all-atom models showed slightly better χ values for some proteins and complexes.
Figure 2.
Experimental and theoretical scattering intensities of proteins and nucleic acids calculated using CRYSOL and the CG-MD-SAXS method (A) Immunoglobulin-like domains 1 and 2 of the protein tyrosine phosphatase LAR3 (BIOISIS ID: LAR12P). (B) Superoxide dismutase (BIOISIS ID: APSOD). (C) Ubiquitin-like modifier-activating enzyme ATG7 C-terminal domain (BIOISIS ID: ATG7CP). (D) DNA double-strand break repair protein MRE11 (BIOISIS ID: MRERAP). (E) Glucose isomerase (BIOISIS ID: GISRUP). (F) Complement C3b+Efb−C (BIOISIS ID: C3BEFP). (G) 28 base pairs of DNA (BIOISIS ID: 28BPDD). (H) The P4–P6 RNA Ribozyme domain (BIOISIS ID: 1P4P6R). (I) A. aeolicus MnmG bound to tRNA (BIOISIS ID: MNMG2X).
CG-MD-SAXS analysis of the Swi5-Sfr1C complex
The Swi5-Sfr1 complex is an activator of Rad51-mediated strand exchange in homologous recombination [59,60]. The Swi5-Sfr1 complex is bound directly to the Rad51 filament and stabilizes it [60]. According to Kuwabara, N., et al. [52], a truncated Sfr1 lacking the N-terminal intrinsically disordered region forms a complex with Swi5, and the complex, known as Swi5-Sfr1C, still has the ability to stimulate strand exchange. X-ray crystallography and SAXS measurements of Swi5-Sfr1C [52] showed that the envelope of the dummy atoms calculated from the SAXS data was essentially similar to the crystal structure (PDB ID: 3VIQ [52]). However, two regions protruded from the envelope (Fig. 3A). One region is the β-sheet region of Sfr1 (250–270 residues), while the other is the helical structure of the C-terminal region of Swi5 (70–85 residues); the regions were termed βSfr1 and CSwi5, respectively. In the crystal structure, βSfr1 interacts with the other dimer (Fig. 3B). In contrast, CSwi5 interacts with its own core-domain.
Figure 3.
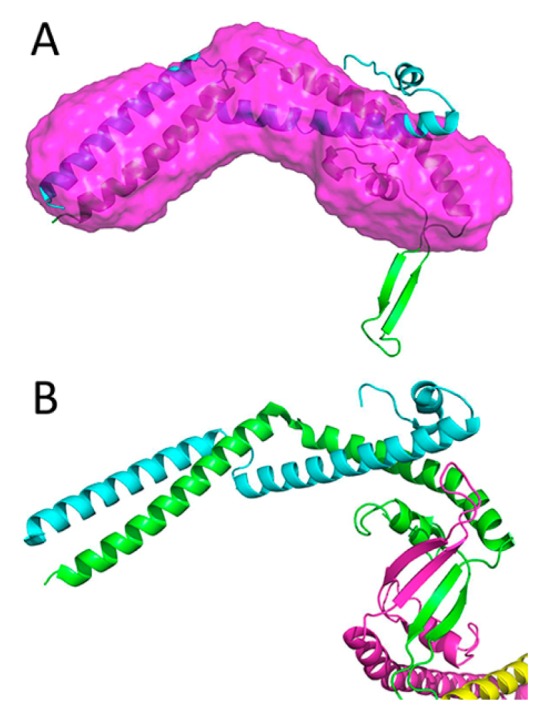
Crystal structure and the dummy residue model of the Swi5-Sfr1C complex. (A) A dummy residue model (magenta) and the crystal structure of the Swi5 (cyan) and Sfr1C (green) complex. (B) Two heterodimers (cyan-green and yellow-magenta) of the Swi5-Sfr1C complex in the asymmetric unit.
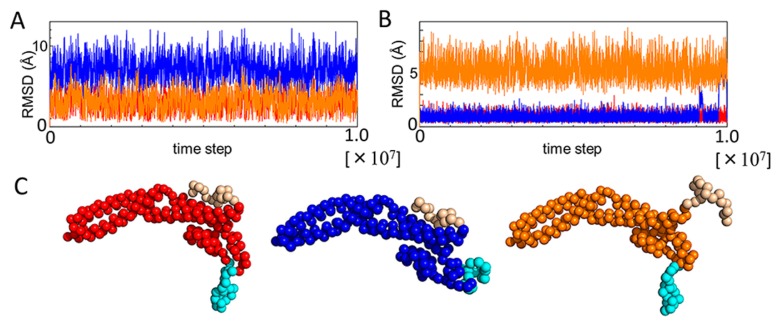
To examine how conformations of βSfr1 and CSwi5 adopt in solution, the CG-MD-SAXS analysis was performed. To simulate ordered/disordered conformations of the regions, the flexible local potential (FLP) was employed in CG-MD simulations. When the FLP is activated, the residues in the region move freely as disordered conformations. Using the FLP, three different simulations were carried out: both ordered βSfr1 and CSwi5 (βOCO), disordered βSfr1/ordered CSwi5 (βDCO) and ordered βSfr1/disordered CSwi5 (βOCD). The RMSD of βSfr1 and CSwi5 of the three simulations are illustrated in Figure 4A and 4B, respectively. The final structures in the simulations are shown in Figure 4C. The RMSD of βSfr1/CSwi5 with the FLP is larger than those without the FLP, suggesting that the difference between ordered/disordered conformations was sufficiently large. Theoretical SAXS profiles were then calculated from the ensembles using the CG-MD-SAXS method.
Figure 4.
RMSD of βSfr1 and CSwi5 in three CG-MD simulations, and final structures. (A) RMSD of βSfr1 in three simulations, βOCO (red), βDCO (blue) and βOCD (orange). (B) RMSD of CSwi5 in three simulations, βOCO (red), βDCO (blue), and βOCD (orange). (C) Final structures of three simulations, βOCO (red), βDCO (blue), and βOCD (orange).
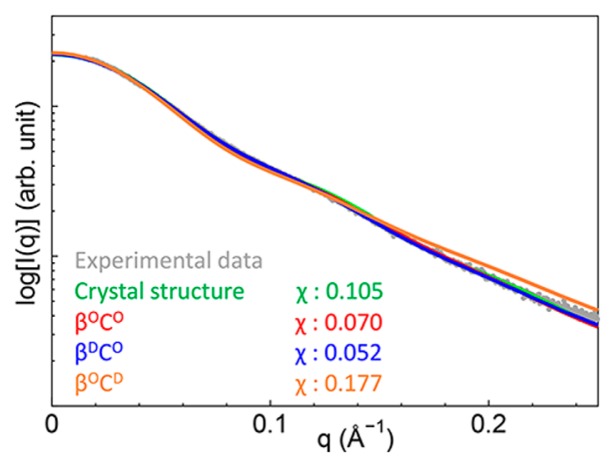
The theoretical SAXS profiles showed that the structural ensemble including disordered βSfr1 was close to that observed in the experiment (Fig. 5). The χ value of the profile of βDCO was the smallest, indicating good agreement with the experimental profile. Therefore, βSfr1 was presumably disordered in solution unlike the crystal structure. Indeed, βSfr1 interacts with other molecules in the crystal (Fig. 3B), and the β-sheet structure may be an artifact of crystal packing. Interestingly, the χ value of the theoretical CG-SAXS profile obtained from the structural ensemble was smaller than that obtained from the crystal structure by CRYSOL. This result indicates the importance of structural flexibility in solution. The CG-MD-SAXS analysis can provide an explicit view of the structural ensemble for flexible proteins including disordered regions.
Figure 5.
Experimental and theoretical scattering intensities of the Swi5-Sfr1C complex. The experimental intensity is represented by gray dots, and the theoretical intensity of the crystal structure obtained using CRYSOL is represented by a green line. Theoretical intensities obtained from βOCO, βDCO, and βOCD simulations are represented by red, blue, and orange lines, respectively.
CG-MD-SAXS analysis of three types of nucleosomes
The nucleosome is the elemental unit of chromatin in eukaryotes [55]. The nucleosome is a complex of core histones and DNA. In the canonical nucleosome, the core histones are H2A, H2B, H3, and H4, and two of the H2A-H2B dimer and the H3-H4 dimer form an octamer wrapped with DNA [55]. The nucleosome can be formed with variants of the core histones. CENP-A is a variant of H3, and several H3 histones of the nucleosome in centromeres are replaced with CENP-A [56]. H2A.B (formerly H2A.Bbd (Barr-body deficient)) is a variant of H2A and is known to be incorporated into the nucleosome in transcribed genes [58]. Hereafter, the nucleosomes with variant histones are termed CENP-A nucleosomes and H2A.B nucleosomes, respectively. SAXS measurements of the three nucleosomes have been obtained [56,58], however, explicit structures satisfying the SAXS profiles were not understood because the theoretical profiles obtained from the crystal structures of canonical and CENP-A nucleosomes were different from the experimental profiles. In addition, the crystal structure of the H2A.B nucleosome has not been reported to date; therefore, no structural information was derived from the SAXS data.
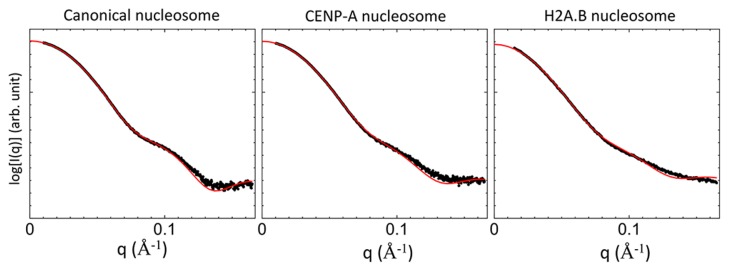
To examine structural information of the three nucleosomes in solution, CG-MD-SAXS analysis was applied. First, the missing histone tails and DNA were modeled, and a whole structure of the H2A.B nucleosome was prepared by homology modeling (Supplementary Fig. S3). Then CG-MD simulations were carried out by changing two parameters, i.e., the ion strength and the strength of the Gō potential between the histone core and DNA. The two parameters affect the flexibility of DNA in CG-MD simulations. The theoretical CG-MD-SAXS profiles were calculated under various conditions, i.e., two parameters (Supplementary Fig. S4). Next, from the χ values representing the difference between the theoretical and experimental SAXS profiles, we identified the condition corresponding to the lowest χ values (Supplementary Fig. S4). For the canonical nucleosome, the χ value was the lowest under the condition of the ion strength of 600 and the Gō strength of 0.6. For the other two nucleosomes, the χ value under the same condition (the ion strength of 600 and the Gō strength of 0.6) was also close to the minimum. Because the experimental SAXS profiles for the three nucleosomes were measured using the common solvent condition, we chose the condition (the ion strength of 600 and the Gō strength of 0.6) for the following analyses of all three nucleosomes. The theoretical SAXS profiles under the condition are shown in Figure 6. All theoretical profiles are in good agreement with the experimental profiles.
Figure 6.
Experimental and theoretical scattering intensities of the canonical, CENP-A, and H2A.B nucleosomes. The experimental and theoretical intensities are represented by black dots and red lines, respectively.
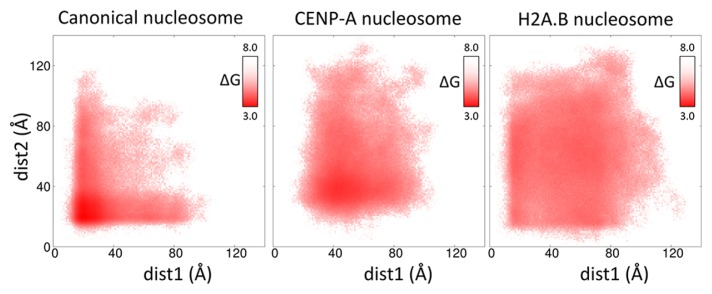
The CG-MD-SAXS analysis revealed an explicit view of the solution structures of the nucleosome satisfied with the experimental SAXS profile. In CG-MD simulations, both ends of DNA moved toward the outside of the histone core and fluctuated between the distant and close positions from the histone core. To analyze how the DNA fluctuates, the separation of DNA from the histone core was characterized by a minimum distance between the end of DNA and the histone core. The free energy representation of the DNA fluctuation against two distances is shown in Figure 7. Structures of the canonical, CENP-A, and H2A.B nucleosomes at the free energy minimum are illustrated in Figures 8A, 8C and 8D, respectively. The free-energy distributions were different from each other. In the canonical nucleosome, the structures were almost distributed around the free energy minimum (20 Å, 20 Å) and showed an L-shaped distribution. By contrast, in the CENP-A nucleosome, the free-energy distribution around the minimum (43 Å, 38 Å) was wide, and the area of the distribution was larger than that of the canonical nucleosome. In the H2A.B nucleosome, the free-energy distribution around the minimum (59 Å, 67 Å) was broader than the other nucleosomes, and the structures were almost evenly distributed.
Figure 7.
Free energy map plotted against two distances. Free energy was defined by a logarithm of the population of the structures characterized by two distances (dist1 and dist2), which are the minimum distances between the edges of DNA and the histone core. Dist1 and dist2 were measured from one and the other sides of DNA, respectively. The unit of free energy is kcal/mol.
Figure 8.
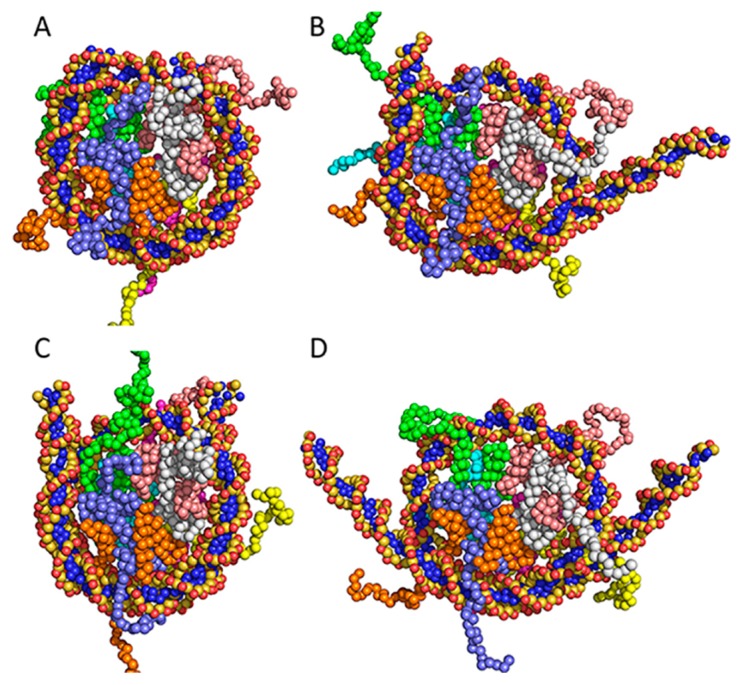
Solution structures of three nucleosomes. (A) The canonical nucleosome structure at the free-energy minimum. (B) A loose form of the canonical nucleosome corresponding to dist1=80 Å, dist2=20 Å in the free-energy map. (C) The CENP-A nucleosome structure at the free-energy minimum. (D) The H2A.B nucleosome structure at the free-energy minimum.
From the free-energy maps, solution structures in the structural ensembles can be described, as follows: The canonical nucleosome almost adopted a compact form as shown in Figure 8A and occasionally adopted a loose form with one separated-DNA (Fig. 8B). In contrast, the CENP-A and H2A.B nucleosomes adopted a loose form. In the CENP-A nucleosome, both edges of DNA were slightly separated from the histone core (Fig. 8C). However, in the H2A.B nucleosome, the lengths of the separated DNAs were long (Fig. 8D), and both edges of the DNA fluctuated widely. These structural characteristics are not obtained solely from X-ray crystallography or SAXS, demonstrating the effectiveness of the CG-MD-SAXS method for large and flexible molecules.
Conclusion
In this study, we proposed a combined method of CG MD simulations and SAXS, termed the CG-MD-SAXS method. First, the scattering factors of CG particles representing 20 amino acids, 5 bases, ribose, deoxyribose and a phosphate were obtained from a set of high-resolution crystal structures. Two important solvent effects, i.e., the excluded volume and the hydration shell, were then incorporated into the CG-MD-SAXS method. For the excluded-volume effects, the Gaussian-sphere model was employed. For the hydration shell, the hydration grids were generated around protein structures. To avoid overfitting, only two adjustable parameters were used for the entire MD trajectories. The theoretical SAXS profiles calculated using the CG-MD-SAXS method were almost identical to those from all-atom models including MD simulations with explicit solvent. Furthermore, for 9 structures of proteins, DNA and RNA, the theoretical SAXS profiles using the CG-MD-SAXS method were in good agreement with experimental profiles and theoretical profiles from the all-atom model. Finally, the CG-MD-SAXS method was applied to the flexible proteins, Swi5-Sfr1C, and nucleosomes. In the Swi5-Sfr1C analysis, the disorder of the β sheet improved the agreement with the experimental SAXS profile. In the nucleosome analysis, three types of nucleosomes, i.e., the canonical, CENP-A and H2A.B nucleosomes were compared, and the CG-MD-SAXS method clearly indicated the difference in the DNA conformations bound to three types of nucleosomes. Finally, the proposed method is not limited to the CG models used in CafeMol. Because the procedure of this method is general, it will be applicable to other coarse-graining methods such as the Martini model.
Supplementary Material
Acknowledgments
The authors are grateful to Prof. Mamoru Sato, Prof. Masaaki Sugiyama, Prof. Hitoshi Kurumizaka and Dr. Takashi Oda for generously providing the SAXS data for nucleosomes. This work was financially supported by the Innovative Drug Discovery Infrastructure through Functional Control of Biomolecular Systems, Priority Issue 1 in Post-K Supercomputer Development from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) to M. I. (Project ID: hp150269, hp160223, hp170255, hp180191 and hp190171); by the Basis for Supporting Innovative Drug Discovery and Life Science Research (BINDS) from the Japan Agency for Medical Research and Development (AMED) (19am0101109j0003) to M. I.; a Grant-in Aid for Scientific Research on Innovative Areas “Molecular Engine” (18H05426) to M. I.; and by a RIKEN Dynamic Structural Biology Project to M. I. This research used computational resources of the K computer provided by the RIKEN Center for Computational Science. Finally, we celebrate the 80th anniversary of Prof. Nobuhiro Gō. His excellent research on biomolecules has largely inspired us to computationally study biomolecular structures. We are honored to make a contribution to this anniversary issue.
Footnotes
Conflicts of Interest
None.
Author Contribution
M. I. designed the research. Y. K., T. O. and M. I. developed the theory. Y. K. performed the simulations. T. E. and Y. K analyzed the results. T. E, Y. K., T. O. and M. I. wrote the manuscript.
References
- 1.Han K, Zhang X, Yang M, editors. Protein Conformational Dynamics. Springer; 2014. [Google Scholar]
- 2.Gō N, Noguti T, Nishikawa T. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc Natl Acad Sci USA. 1983;80:3696–3700. doi: 10.1073/pnas.80.12.3696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Braun W, Bösch C, Brown LR, Gō N, Wüthrich K. Combined use of proton-proton overhauser enhancements and a distance geometry algorithm for determination of polypeptide conformations. Application to micelle-bound glucagon. Biochim Biophys Acta. 1981;667:377–396. doi: 10.1016/0005-2795(81)90205-1. [DOI] [PubMed] [Google Scholar]
- 4.Wargner G, Braun W, Havel TF, Shaumann T, Gō N, Wüthrich K. Protein structures in solution by nuclear magnetic resonance and distance geometry: The polypeptide fold of the basic pancreatic trypsin inhibitor determined using two different algorithms, DISGEO and DISMAN. J Mol Biol. 1987;196:611–639. doi: 10.1016/0022-2836(87)90037-4. [DOI] [PubMed] [Google Scholar]
- 5.Yamane T, Okamura H, Ikeguchi M, Nishimura Y, Kidera A. Water-mediated interactions between DNA and PhoB DNA-binding/transactivation domain: NMR-restrained molecular dynamics in explicit water environment. Proteins. 2008;71:1970–1983. doi: 10.1002/prot.21874. [DOI] [PubMed] [Google Scholar]
- 6.Yamane T, Okamura H, Nishimura Y, Kidera A, Ikeguchi M. Side-chain conformational changes of transcription factor PhoB upon DNA binding: a population-shift mechanism. J Am Chem Soc. 2010;132:12653–12659. doi: 10.1021/ja103218x. [DOI] [PubMed] [Google Scholar]
- 7.Ekimoto T, Ikeguchi M. Hybrid methods for modeling protein structures using molecular dynamics simulations and small-angle x-ray scattering data. In: Markley JL, Burley S, Nakamura H, Kleywegt G, editors. Integrative Structural Biology with Hybrid Methods. Springer; Nature: 2018. pp. 237–258. [DOI] [PubMed] [Google Scholar]
- 8.Anami Y, Shimizu N, Ekimoto T, Egawa D, Itoh T, Ikeguchi M, et al. Apo- and antagonist-binding structures of vitamin D receptor ligand-binding domain revealed by hybrid approach combining small-angle x-ray scattering and molecular dynamics. J Med Chem. 2016;59:7888–7900. doi: 10.1021/acs.jmedchem.6b00682. [DOI] [PubMed] [Google Scholar]
- 9.Svergun DI, Barberato C, Koch MJH. CRYSOL—a program to evaluate x-ray solution scattering of biological macromolecules from atomic coordinates. J Appl Cryst. 1995;28:768–773. [Google Scholar]
- 10.Schneidman-Duhovny D, Hammel M, Tainer JA, Sali A. Accurate SAXS profile computation and its assessment by contrast variation experiments. Biophys J. 2013;105:962–974. doi: 10.1016/j.bpj.2013.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Poitevin F, Orland H, Doniach S, Koehl P, Delarue M. AquaSAXS: a web server for computation and fitting of SAXS profiles with non-uniformally hydrated atomic models. Nucleic Acids Res. 2011;39:W184–W189. doi: 10.1093/nar/gkr430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liu H, Morris RJ, Hexemer A, Grandison S, Zwart PH. Computation of small-angle scattering profiles with three-dimensional Zernike polynomials. Acta Cryst. 2012;A68:278–285. doi: 10.1107/S010876731104788X. [DOI] [PubMed] [Google Scholar]
- 13.Yang S, Park S, Makowski L, Roux B. A rapid coarse residue-based computational method for x-ray solution scattering characterization of protein folds and multiple conformational states of large protein complexes. Biophys J. 2009;96:4449–4463. doi: 10.1016/j.bpj.2009.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ravikumar KM, Huang W, Yang S. Fast-SAXS-pro: a unified approach to computing SAXS profiles of DNA, RNA, protein, and their complexes. J Chem Phys. 2013;138:024112. doi: 10.1063/1.4774148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bernado P, Mylonas E, Petoukhov MV, Blackledge M, Svergun DI. Structural characterization of flexible proteins using small-angle x-ray scattering. J Am Chem Soc. 2007;129:5656–5664. doi: 10.1021/ja069124n. [DOI] [PubMed] [Google Scholar]
- 16.Pelikan M, Hura GL, Hammel M. Structure and flexibility within proteins as identified through small angle x-ray scattering. Gen Physiol Biophys. 2009;28:174–189. doi: 10.4149/gpb_2009_02_174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rozycki B, Kim YC, Hummer G. SAXS ensemble refinement of ESCRT-III CHMP3 conformational transitions. Structure. 2011;19:109–116. doi: 10.1016/j.str.2010.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang S, Blachowicz L, Makowski L, Roux B. Multi-domain assembled states of Hck tyrosine kinase in solution. Proc Natl Acad Sci USA. 2010;107:15757–15762. doi: 10.1073/pnas.1004569107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Oroguchi T, Hashimoto H, Shimizu T, Sato M, Ikeguchi M. Intrinsic dynamics of restriction endonuclease EcoO109I studied by molecular dynamics simulations and x-ray scattering data analysis. Biophys J. 2009;96:2808–2822. doi: 10.1016/j.bpj.2008.12.3914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Park S, Bardhan JP, Roux B, Makowski L. Simulated x-ray scattering of protein solutions using explicit-solvent models. J Chem Phys. 2009;130:134114. doi: 10.1063/1.3099611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Köfinger J, Hummer G. Atomic-resolution structural information from scattering experiments on macromolecules in solution. Phys Rev E. 2013;87:052712. doi: 10.1103/PhysRevE.87.052712. [DOI] [PubMed] [Google Scholar]
- 22.Chen P, Hub JS. Interpretation of solution x-ray scattering by explicit-solvent molecular dynamics. Biophys J. 2015;108:2573–2584. doi: 10.1016/j.bpj.2015.03.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Oroguchi T, Ikeguchi M. Effects of ionic strength on SAXS data for proteins revealed by molecular dynamics simulations. J Chem Phys. 2011;134:025102. doi: 10.1063/1.3526488. [DOI] [PubMed] [Google Scholar]
- 24.Saunders MG, Voth GA. Coarse-graining methods for computational biology. Annu Rev Biophys. 2013;42:73–93. doi: 10.1146/annurev-biophys-083012-130348. [DOI] [PubMed] [Google Scholar]
- 25.Kenzaki H, Koga N, Hori N, Kanada R, Li WF, Okazaki K, et al. CafeMol: a coarse-grained biomolecular simulator for simulating proteins at work. J Chem Theory Comput. 2011;7:1979–1989. doi: 10.1021/ct2001045. [DOI] [PubMed] [Google Scholar]
- 26.Fraser RDB, MacRae TP, Suzuki E. An improved method for calculating the contribution of solvent to the x-ray diffraction pattern of biological molecules. J Appl Cryst. 1978;11:693–694. [Google Scholar]
- 27.Kahn P, Knapp M, Soltis SM, Ganshaw G, Toene M, Bott R. The 0.78 Å structure of a serine protease: Bacillus lentus subtilisin. Biochemistry. 1998;37:13446–13452. doi: 10.1021/bi9813983. [DOI] [PubMed] [Google Scholar]
- 28.Schmidt A, Jelsch C, Ostergaard P, Rypniewski W, Lamzin VS. Trypsin revisited: crystallpography at (sub) atomic resolution and quantum chemistry revealing details of catalysis. J Biol Chem. 2003;278:43357–43362. doi: 10.1074/jbc.M306944200. [DOI] [PubMed] [Google Scholar]
- 29.Bonisch H, Schmidt CL, Bianco P, Ladenstein R. Ultrahigh-resolution study on pyrococcus abyssi rubredoxin: II. Introduction of an O-H...Sγ-Fe hydrogen bond increased the reduction potential by 65mV. J Biol Inorg Chem. 2007;12:1163–1171. doi: 10.1007/s00775-007-0289-8. [DOI] [PubMed] [Google Scholar]
- 30.Wang J, Dauter M, Alkire R, Joachimiak A, Dauter Z. Triclinic lysozyme at 0.65 Å resolution. Acta Crystallogr D. 2007;63:1254–1268. doi: 10.1107/S0907444907054224. [DOI] [PubMed] [Google Scholar]
- 31.Drew HR, Wing RM, Takano T, Broka C, Tanaka S, Itakura K, et al. Structure of a B-DNA dodecamer: conformation an dynamics. Proc Natl Acad Sci USA. 1981;78:2179–2183. doi: 10.1073/pnas.78.4.2179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chiu TK, Dickerson RE. 1 Å crystal structures of B-DNA reveal sequence-specific binding and groove-specific bending of DNA by magnesium and calcium. J Mol Biol. 2000;301:915–945. doi: 10.1006/jmbi.2000.4012. [DOI] [PubMed] [Google Scholar]
- 33.Pan B, Xiong Y, Shi K, Sundaralingam M. Crystal structure of a bulged RNA tetraplex at 1.1 Å resolution: Implications for a novel binding site in RNA tetraplex. Structure. 2003;11:1423–1430. doi: 10.1016/j.str.2003.09.017. [DOI] [PubMed] [Google Scholar]
- 34.Kiliszek A, Kierzek R, Krzyzosiak WJ, Rypniewski W. Atomic resolution structure of CAG RNA repeats: structural insights and implications for the trinucleotide repeat expansion diseases. Nucleic Acids Res. 2010;38:8370–8376. doi: 10.1093/nar/gkq700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Knotts TVIV, Rathore N, Schwartz DC, de Pablo JJ. A coarse grain model for DNA. J Chem Phys. 2007;126:084901. doi: 10.1063/1.2431804. [DOI] [PubMed] [Google Scholar]
- 36.Sambriski EJ, Schwartz DC, de Pablo JJ. A mesoscale model of DNA and its renaturation. Biophys J. 2009;96:1675–1690. doi: 10.1016/j.bpj.2008.09.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Diamond R. Real-space refinement of the structure of hen egg-white lysozyme. J Mol Biol. 1974;82:371–391. doi: 10.1016/0022-2836(74)90598-1. [DOI] [PubMed] [Google Scholar]
- 38.Ikeguchi M. Partial rigid-body dynamics in NPT, NPAT and NPγT ensembles for proteins and membranes. J Comput Chem. 2004;25:529–541. doi: 10.1002/jcc.10402. [DOI] [PubMed] [Google Scholar]
- 39.MacKell AD, Feig M, Brooks CL. Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J Comput Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 40.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 41.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926. [Google Scholar]
- 42.Biersmith BH, Hammel M, Geisbrecht ER, Bouyain S. The immunoglobulin-like domains 1 and 2 of the protein tyrosine phosphatase LAR adopt an unusual horseshoe-like conformation. J Mol Biol. 2011;408:616–627. doi: 10.1016/j.jmb.2011.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shin DS, DiDonato M, Barondeau DP, Hura GL, Hitomi C, Berglund JA, et al. Superoxide dismutase structures, stability, mechanism and insights into the human disease amyotrophic lateral sclerosis from eukaryotic thermophile alvinella pompejana. J Mol Biol. 1998;385:1534–1555. doi: 10.1016/j.jmb.2008.11.03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Strange RW, Antonyuk S, Hough MA, Doucette P, Rodriguez J, Hart PJ, et al. The structure of holo and metal-deficient wild-type human Cu, Zn superoxide dismutase and its relevance to familial amyotrophic lateral sclerosis. J Mol Biol. 2003;328:877–891. doi: 10.1016/s0022-2836(03)00355-3. [DOI] [PubMed] [Google Scholar]
- 45.Taherbhoy AM, Tait SW, Kaiser SE, Williams AH, Deng A, Nourse A, et al. Atg8 transfer from Atg7 to Atg3: a distinctive E1-E2 architecture and mechanism in the autophagy pathway. Mol Cell. 2011;44:451–461. doi: 10.1016/j.molcel.2011.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Williams GJ, Williams RS, Williams JS, Moncalian G, Arvai AS, Limbo O, et al. ABC ATPase signature helices in Rad50 link nucleotide state to Mre11 interface for DNA repair. Nat Struct Mol Biol. 2011;18:423–431. doi: 10.1038/nsmb.2038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mueller-Dieckmann C, Panjikar S, Schmidt A, Mueller S, Kuper J, Geerlof A, et al. On the routine use of soft x-rays in macromolecular crystallography. part IV. efficient determination of anomalous substructures in biomacromolecules using longer x-ray wavelengths. Acta Crystallogr D. 2007;63:366–380. doi: 10.1107/S0907444906055624. [DOI] [PubMed] [Google Scholar]
- 48.Chen H, Ricklin D, Hammel M, Garcia BL, McWhorter WJ, Sfyroera G, et al. Allosteric inhibition of complement function by a staphylococcal immune evasion protein. Proc Natl Acad Sci USA. 2010;107:17621–17626. doi: 10.1073/pnas.1003750107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rambo RP, Tainer JA. Improving small-angle x-ray scattering data for structural analyses of the RNA world. RNA. 2010;16:638–646. doi: 10.1261/rna.1946310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cate JH, Gooding AR, Podell E, Zhou K, Golden BL, Kundrot CE, et al. Crystal structure of a group I ribozyme domain: principles of RNA packing. Science. 1996;273:1678–1685. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- 51.Fislage M, Brosens E, Deyaert E, Spilotros A, Pardon E, Loris R, et al. SAXS analysis of the tRNA-modifying enzyme complex MnmE/MnmG reveals a novel interaction mode and GTP-induced oligomerization. Nucleic Acids Res. 2014;42:5978–5992. doi: 10.1093/nar/gku213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kuwabara N, Murayama Y, Hashimoto H, Kokabu Y, Ikeguchi M, Sato M, et al. Mechanistic insights into the activation of Rad51-mediated strand exchange from the structure of a recombination activator, the Swi5-Sfr1 complex. Structure. 2012;20:440–449. doi: 10.1016/j.str.2012.01.005. [DOI] [PubMed] [Google Scholar]
- 53.Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- 54.Li W, Terakawa T, Wang W, Takada S. Energy landscape and multiroute folding of topologically complex proteins adenylate kinase and 2ouf-knot. Proc Natl Acad Sci USA. 2012;109:17789–17794. doi: 10.1073/pnas.1201807109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Tachikawa H, Kagawa W, Osakabe A, Kawaguchi K, Shiga T, Hayashi-Tanaka Y, et al. Structural basis of instability of the nucleosome containing a testis-specific histone variant, human H3T. Proc Natl Acad Sci USA. 2010;107:10454–10459. doi: 10.1073/pnas.1003064107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Tachikawa H, Kagawa W, Shiga T, Osakabe A, Miya Y, Saito K, et al. Crystal structure of the human centromeric nucleosome containing CENP-A. Nature. 2011;476:232–235. doi: 10.1038/nature10258. [DOI] [PubMed] [Google Scholar]
- 57.Feig M, Karanicolas J, Brooks CL., III MMTSB tool set: enhanced sampling and multiscale modeling methods for applications in structural biology. J Mol Graph Model. 2004;22:377–395. doi: 10.1016/j.jmgm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 58.Arimura Y, Kimura H, Oda T, Sato K, Osakabe A, Tachikawa H, et al. Structural basis of a nucleosome containing histone H2A.B/H2A.Bbd that transiently associates with reorganized chromatin. Sci Rep. 2013;3:3510. doi: 10.1038/srep03510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Haruta N, Kurokawa Y, Murayama Y, Akamatsu Y, Unzai S, Tsutsui Y, et al. The Swi5-Sfr1 complex stimulates Rhp51/Rad51- and Dmc1-mediated DNA strand exchange in vitro. Nat Struct Mol Biol. 2006;13:823–830. doi: 10.1038/nsmb1136. [DOI] [PubMed] [Google Scholar]
- 60.Kurokawa Y, Murayama Y, Haruta-Takahashi N, Urabe I, Iwasaki H. Reconstitution of DNA strand exchange mediated by Rhp51 recombinase and two mediators. PLoS Biol. 2008;6:e88. doi: 10.1371/journal.pbio.0060088. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.