Snake cube puzzle and protein folding

Abstract

The snake cube puzzle made of a linear array of 27 cubes and its modified and extended versions are used as theoretical models to study the mechanism of folding of proteins into their sequence-specific native three-dimensional structures. Each of the three versions is characterized by the respective set of characteristics attributed to each of its constituent cubes and an array is characterized by its specific sequence of the cube characteristics. The aim of the puzzles is to fold the cube array into a compact 3×3×3 cubic structure. In all three versions, out of all possible sequences, only a limited fraction of sequences are found foldable into the compact cube. Even among foldable sequences, the structures folded into the compact 3×3×3 cube are found often not uniquely determined from the sequence. By comparing the results obtained for the three versions of models, we conclude that the power of the hydrophobic interactions to make the folded structure unique to the sequence is much weaker than the geometrical varieties of constituent cubes as modelled in the original snake cube puzzle. However, when this weak cube attribute is compounded to that of the original snake cube puzzle, the power is enhanced very effectively. This is a strong manifestation of the consistency principle: The sequence-specific native structure of protein is realized as a result of consistency of various types of interactions working in protein.

Significance.

Mechanism of sequence determination of protein native state three-dimensional structures is studied by new theoretical models. The result provides a quantitative evidence for the viewpoint of the consistency principle; the unique native state structure is realized by various interaction terms working together consistently. Especially, respective roles of variety of shapes of amino acid residues and hydrophobic interactions in the structure determination are discussed.

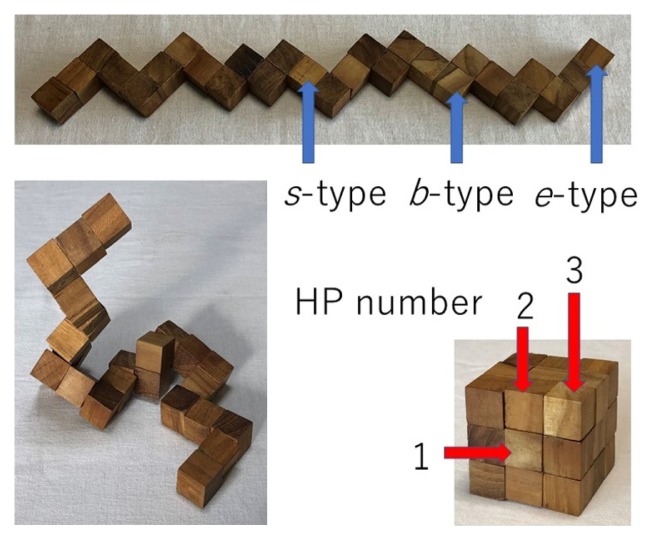
The snake cube is a puzzle of a linear array of 27 cubes connected together by a string running through their centers (Fig. 1). Every cube (except for the one at either end, e-type) has two faces with a hole in the center through which the string runs. A cube has holes either in opposite faces, so that the string runs straight through (s-type), or in adjacent faces, so that the string makes a right angled bend through the cube (b-type). An array is characterized by its specific sequence of cube types. Adjacent cubes in an array can rotate freely about the connecting string, so that the array can assume various three-dimensional conformation. The aim of the puzzle is to fold the array into a compact 3×3×3 cubic structure. A variety of puzzle problems can be produced depending on the sequence of cube types.

Figure 1.

Snake cube puzzle in extended (top), arbitrary (bottom left) and folded (bottom right) conformations. Constituent cubes can be of either e-type (at either end), s-type or b-type. Numbers of exposed surfaces of constituent cubes in the folded conformation are indicated as HP numbers, which will be used in the definition of a new puzzle, the HP puzzle, to be introduced later.

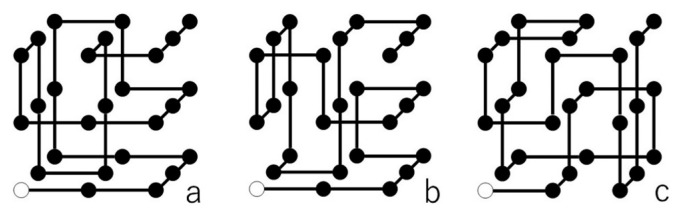
There are at least three different puzzle problems on the market with sequences of cube types given in the legends of Figures 2a, b and c. I have written a computer program to find all possible folded structures for a given type sequence. In the program, structures folded into a 3×3×3 cube are searched for in a logical tree where all possible three-dimensional conformations of the snake cube array on the simple cubic lattice are arranged. Each of the three problems with the indicated sequences was found to fold into a unique three-dimensional structure shown in Figures 2a, b and c, respectively. These folded three-dimensional structures are described in the legends by sequences of six letters R, L, B, F, U and D standing for the six directions of the string to the next cube, namely Right, Left, Back, Front, Up and Down.

Figure 2.

(a) Unique folded structure of a snake cube puzzle problem with a sequence of cube types, esb sbs bsb bbb sbs bbb sbb sbb bse. The first cube position is shown by a white sphere with remaining cube positions by black spheres. Six letter description of this folded structure is RR BB LL UU RD RF FL LU BD DR UU FR BB. The puzzle problem in Figure 1 has this sequence of cube types. (b) Unique folded structure RR BB LU RF FL UL DB UB DD FR UU BR FF of a snake cube puzzle problem with a sequence of cube types, esb sbb bbs bbb bbb bbs bbb sbb bse. (c) Unique folded structure RB UB RD LL FU BU RF LF DR UR DD BU UB of a snake cube puzzle problem with a sequence of cube types, ebb bbb bsb bbb bbb bbb bbb sbb sbe.

Thus, the sequence determines the folded structure, a situation similar to the relationship between protein amino-acid sequence and native three-dimensional structure. Here, one parenthetical remark is necessary. All of the above three types of cubes have mirror image symmetry, which is a situation different from that in protein where amino acids residues, generally in the l-type isomers, do not have mirror image symmetry. Because of this higher symmetry in the snake cube puzzle, it turns out that, when one three-dimensional conformation is possible, its mirror image is similarly possible. Because of this situation, we treat in this paper any three-dimensional conformation and its mirror image as the same one. The uniqueness of the folded structures in Figures 2a, b and c is to be understood under this treatment.

If there is a common logic or mechanism behind this similarity, we may be able to learn something from the snake cube puzzle about the protein folding mechanism. In this context we want to ask naively why the unique folded structure is determined from the sequence in the snake cube puzzle. The simplest working hypothesis would be that the possibility of a puzzle problem with an arbitrary sequence can fold into a compact 3×3×3 structure is so small that, even when it can fold into one compact structure, the possibility of being able to fold into a second compact structure is virtually vanishing. If so, the three-dimensional structure should turn out to be determined uniquely from the sequence.

A mechanism very similar to this has been mentioned by F. M. Richards, who carried out a systematic study of space packing of atoms within the interior of protein three-dimensional structures. The packing was found generally so good that he expressed the impression [1,2]; “one might consider that it is, in a major sense, through simple space-filling requirements that the amino acid sequence controls the final three-dimensional structure.” This impression is based first on an anticipation that it would be generally very difficult to fold linear chains of 20 types of amino-acid residues, having a variety of shapes, into well packed structures, and second by the finding that the actual protein interiors are so amazingly well packed. The good packing is a result of optimization of Van der Waals (VdW) interactions. Therefore, the above impression stresses the role of the combination of the variety of shapes of amino acid residues and the optimization of the VdW interactions in the mechanism of the protein specific three-dimensional structure determination.

This mechanism is very similar to our working hypothesis, where the three different cube types can be understood as a simplified expression of the variety of shapes of amino acid residues and the requirement of folding into a compact structure is an expression of the role of optimization of the VdW interactions. In this context we will call henceforth the sequence of cube types also as the sequence of the backbone geometry. The snake cube puzzle can be regarded as a theoretical model of protein folding where the role of the combination of geometrical varieties of amino acid residues and VdW interactions is emphasized. In the next section we will examine if our working hypothesis works.

Sequence control of the folded structure in the snake cube puzzle

The total number of the sequences of the backbone geometry is 2²⁵=33,554,432, because each of the 25 cubes in the array (excepting the two terminal ones) can be either s- or b-type. The validity of our working hypothesis can be verified unambiguously by running my program for all of these sequences. (One of the merits of the snake cube puzzle as a model of protein folding is that we can do exhaustive calculations so that the conclusions are unambiguous.) A logically equivalent and computationally less demanding calculation has been carried out as follows. At first I have done an exhaustive enumeration of all possible structures of a linear array of 27 units on the simple cubic lattice that are confined in a 3×3×3 cube. As has already been reported [3], a total of 103,346 different folded structures were found, where those related by mirror image symmetry are treated as the same one structure. Then, the sequence of the backbone geometry compatible with each of the folded structures is identified. Out of the 2²⁵ sequences of the backbone geometry, 22,897 sequences (0.068%) are found to fold into one of the 103,346 folded structures. The remaining (2²⁵–22,897) sequences cannot fold into any compact structures. Out of the 22,897 foldable sequences, 7,268 sequences are found to fold into a unique structure. The uniqueness ratio (UR) defined as the fraction of sequences folding into a unique structure out of all foldable sequences is thus 7,268/22,897≒0.32. Each of the remaining (22,897–7,268) sequences are found to fold into more than one compact structure. Let us name such a number the structural multiplicity number (SMN). A sequence with the SMN being unity is the one that folds into a unique structure. The average SMN of the foldable sequences is thus 103,346/22,897≒4.51.

The sequences in Figures 2a, b and c are now recognized as examples out of the 7,268 sequences folding into unique structures. Many of foldable sequences fold into more than one structure. Because our working hypothesis can be rephrased as assuming both UR and average SMN being unity, this result indicates clearly that our working hypothesis is not correct. Sequence determination of protein native structures can also be expressed as that both UR and average SMN are unity in protein. Therefore, the snake cube puzzle behaves somewhat differently from protein. The power of the combination of geometrical varieties of amino acid residues and VdW interaction as modelled in the snake cube puzzle is not strong enough to render all foldable structures unique. Understanding clearly how the snake cube puzzle differs from protein should contribute to our understanding of protein. With such a view we explore somewhat more deeply into the relationship between sequence and folded structure in the snake cube puzzle.

Unlike amino acid residues in protein, the structural units in the snake cube puzzle do not have either the difference of l- and d-residues or the directional difference of N- and C-termini. Because of the lack of the former difference we needed to treat a pair of structures related by mirror image symmetry as the same. The lack of the latter difference means that one sequence of the backbone geometry and another with chain numbering (CN) reversed are essentially the same, so that we describe such a pair CN conjugate. A sequence which is CN conjugate with itself is termed palindromic. A pair of sequences which are CN conjugate with each other, if foldable, fold into a pair of structures which are CN conjugate with each other in the three-dimensional structures.

From this point of view of classification of sequences, the 22,897 foldable sequences consist of 11,410 pairs of mutually CN conjugate sequences and 77 palindromic ones (22,897=2×11,410+77). The 7,268 sequences folding into a unique structure consist of 7,258 non-palindromic and 10 palindromic sequences. The 77 palindromic sequences fold into 764 compact structures, which consist of 351 pairs of CN conjugate structures, and 62 structures with space inversion symmetry (764=2×351+62). The 11,410 sequences which contain those with a SMN greater than unity fold into 51,291 different compact structures (103,346=2×51,291+764). When we regard a pair of CN conjugate three-dimensional structures as the same structure, the total number of different folded structures turns out to be 51,291+351+62=51,704. These results have already been obtained and reported in internet web pages, as far as I am aware, by E. Vershen (http://cantaforda.com/cfcl/eryk/puzzles/chain_cube.html, dated 2003/04/16) and later by J. Scherphuis (https://www.jaapsch.net/puzzles/snakecube.htm). The method of presenting three-dimensional folded structures by a sequence of six letters was given in the latter web page.

I will now discuss some of the interesting cases, which, as a result, would contribute to clarify how this puzzle resembles and differs from protein.

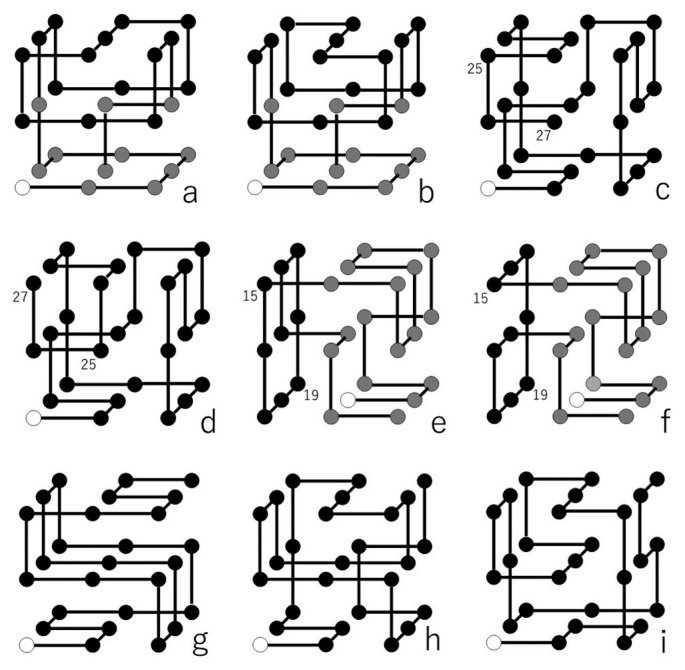
The first is shown in Figures 3a and b, and is an example out of 5,390 non-palindromic sequences which fold into two compact structures, i.e., the SMN being equal to 2. When we compare these two structures, we see that the bottom part with white or gray cubes are the same in the two structures, while the top parts with black cubes are mirror images of each other. The lack of the difference of l- and d-residues in this snake cube makes these two folded structures similarly possible.

Figure 3.

Two folded structures (a) RR BB LL FU UB DR RU LF FL DR RU BD LD and (b) RR BB LL FU UF DR RU LB BL DR RU FD LD of a snake cube puzzle problem with a sequence of cube types, esb sbs bbs bbb sbb bsb bbs bbb bbe. Four out of 142 folded structures, (c) RB LU RB UR DF UF DD BB LL UU FR FL DR, (d) RB LU RB UR DF UF DD BB LL UU FR FD LU, (e) RB LU RU LF RD FU LL DD BB UU FD RF DR, and (f) RB LU RU LF RD FU LL BB DD FF UB RF DR, possible for a snake cube puzzle problem with a sequence of cube types, ebb bbb bbb bbb bsb sbs bsb bbb bbe. Three folded structures described by sequences (g) RB LB RR UL LU FD RR DF UL LU RR BL BR, (h) RB LB UU RF FR BD LL UF DR RD BB LU RU, and (i) RB RF UU LB BL DR FF LU BD DB RR UF UB of a snake cube puzzle problem with a palindromic sequence of cube types, ebb bbs bbs bbb bsb bbb sbb sbb bbe. The structure in (g) has space inversion symmetry. The structures in (h) and (i) are CN conjugate with each other.

The second is also a case of non-palindromic sequence but with the largest value of SMN which is 142. Four out of these structures are shown in Figures 3c, d, e and f. When we compare the two structures in Figures 3c and d, we see that only the positions of cubes 25 and 27 are interchanged. When we compare the two structures in Figures 3e and f, we see that the part on the right with white or gray cubes are the same in the two structures, while the part on the left with black cubes are mirror images of each other with respect to the diagonal line going through cubes 15 and 19. The lack of the difference of l- and d-residues in the snake cube also explains these structural multiplicities. One may suspect that the rather large number of b-type cubes in this sequence, 21, explains the large value of the SMN, 142. However, the sequence of Figure 2c with the SMN being unity has even larger number of b-type cubes, i.e., 22. There are 15 non-palindromic sequences with 22 b-type cubes and the SMN being unity, including the one given in Figure 2c. We realize that sequence is important. The largest and smallest number of b-type cubes in the 22,897 foldable sequences are 23 and 14, respectively.

The third is a case of a palindromic sequence given in Figures 3g, h and i with the SMN being equal to 3. The three structures consist of a structure with space inversion symmetry and a pair of CN conjugate structures. Out of the above mentioned 77 palindromic sequences, 47 sequences have only CN conjugate pairs of folded structures. There are 15 sequences which have only folded structures with space inversion symmetry. The remaining 15 sequences, including the one in Figures 3g, h and i, have both structures with space inversion symmetry and pairs of CN conjugate structures. Among them, sequence esb bbb bbb bbb bsb bbb bbb bbb bse has as many as 4 structures with space inversion symmetry and 18 pairs of CN conjugate structures.

Most of the cases of structural multiplicities can be recognized as a result of the lack of the difference of l- and d-residues in the snake cube. Existence of CN conjugate sequences and CN conjugate three-dimensional structures and also of palindromic sequence and structures with space inversion symmetry is a result of the lack of the directional difference of N- and C-termini in the snake cube puzzle. The snake cube puzzle resembles protein in that only a very limited number of sequences fold into a compact structure. However, it differs from protein in that the constituent units possess a lower type variety and higher symmetry.

Now, similarity and dissimilarity in folding of the snake cube puzzle and protein have been elucidated to a reasonable extent. Dissimilarity is mainly attributed so far to the simplicity and higher symmetry in the cubes of the snake cube puzzle, which is, in a sense, a reasonable result. However, whether the sequence-control of the three-dimensional protein structure can be attributed sufficiently to the good packing of amino acids residues with more complex shapes is, of course, not answered by the study of the snake cube puzzle. It is clear that in real proteins various factors other than the structural varieties of amino acids and the VdW interactions also play important roles. Here I will briefly review a view as to the relative roles of various types of interactions working in protein, summarized as “the consistency principle”. After that, I will try to learn something more about protein folding by extending the snake cube puzzle.

The consistency principle

In real proteins, various types of interactions, not only VdW interactions but also electrostatic interactions, hydrophobic interactions, etc., have roles in determining their various properties. According to Anfinsen [4], the native state of a protein with the three-dimensional structure specific to its amino acid sequence is realized as the thermodynamic equilibrium state. Therefore, the sum of conformational free energy terms for various types of interactions is minimized at the native state structure. “The consistency principle” asserts that not only the sum but each individual term is also minimized at the native state structure. This is a view I arrived in 1983 [5,6] by overviewing various facts known at that time about the protein native state three-dimensional structures.

Each individual term tries to determine the stable three-dimensional structure as the structure realized at its own minimum. If the consistency principle is satisfied, various energy terms work together consistently or harmoniously to determine the same structure. If such a situation is realized, there will be a well-defined global minimum, leading to realization of the specific native state three-dimensional structure.

This is a situation which is in clear contrast to the situation met in the state of glass, where constituent energy terms are inconsistent or conflicting to each other. In such a situation the global minimum state becomes highly degenerate, making the state of glass glassy. Because inconsistent energy terms do not work harmoniously, they are sometimes described as being frustrated. When Bryngelson and Wolynes [7] studied the protein native state from the point of view of the glass state theory in 1987, they realized that the system is minimally frustrated in protein. I think that this is essentially the same finding as my consistency principle.

Various energy terms are minimized at the same conformational state. Such a situation may appear possible only as a miracle. The view of “the consistency principle” regards that amino acid sequences allowing realization of such a miracle have been selected during evolution.

It should further be commented that the consistency principle holds only at the conformational resolution where we regard the native state grossly as one state. When a conformational state is observed at higher resolutions, conformations are undergoing thermal fluctuations within the native state. The native state is a name given to describe a certain range of conformational space available under the physiological condition. The free energy surface within such a range is determined from relative roles of various energy terms, which are not necessarily consistent to each other at the higher resolution. Higher resolution conformational transitions within the native state are often important for proteins to perform their biological functions.

Even though the consistency principle is a very powerful view generally applicable to understand various aspects of protein, not only folding but even functioning mechanisms, it remains, in a sense, to have the character of a viewpoint. In this situation I want to take advantage of the snake cube puzzle (especially its character of sometimes allowing exhaustive calculations, thereby making conclusions unambiguous) to learn something more about the consistency principle by extending the puzzle so that it models not only the VdW but also other types of interactions.

Introducing a new puzzle, HP puzzle

Earlier in this paper the requirement of folding into a compact structure was interpreted as an expression of the role of optimization of the VdW interactions. To be precise hydrophobic interactions are also a big driving force for a polypeptide chain to assume compact structures. Therefore, folding into a 3×3×3 compact structure should be regarded as a result of optimization of the sum of free energies associated with square faces of constituent cubes that are in contact in the compact structure. Such a contact free energy have contributions from both VdW and hydrophobic interactions.

To proceed along this line I will now introduce a new puzzle, the HP puzzle, again made of an array of 27 cubes designed to model the hydrophobic interactions more explicitly. In this new puzzle I assume that each of the six surfaces of each constituent cube of the array is classified into either hydrophobic or polar. The number of polar surfaces of each of the constituent cubes is assumed to be specific to the cube. Such a number will be called as the HP number of the cube. The array of the cubes is then characterized by a sequence of its specific HP numbers. The aim of the new puzzle is to fold the array into a compact 3×3×3 cube in such a way that all of its exposed surfaces in the folded structure to be polar and all of its buried surfaces to be hydrophobic (the HP requirement). In this folded structure, the center of the 3×3×3 cube must be occupied by a cube with the HP number 0, centers of six 3×3 square surfaces by a cube with the HP number 1, centers of twelve edges by a cube with HP number 2 and eight corners by a cube with HP number 3 (Fig. 1). Therefore, foldable sequence of the HP numbers must have eight 3’s, twelve 2’s, six 1’s and one 0. Also, as we proceed by one step along the sequence, they must either increase or decrease always by unity. When I enumerated all sequences of the HP numbers satisfying these rules, 6,435 different sequences have been identified.

While the original snake cube puzzle has been recognized as a theoretical model of protein folding where the role of the combination of geometrical varieties of amino acid residues and VdW interactions is focused, the geometrical varieties are not modelled in this new puzzle, but instead the hydrophobic and VdW interactions are modelled in a simplified manner. This new HP puzzle is similar in spirit to the HP model of Lau and Dill [8] used in their lattice model study of protein folding. However, they simply classified all units into H (nonpolar) and P (polar) (one-bit classification), and assumed a uniform attractive free energy for each of HH nearest neighbor pairs. In contrast we classified units into four types (two-bit classification) according to their HP numbers, which can be 0, 1, 2 or 3. These two models should behave somewhat differently, at least to the extent ours is one-bit more detailed.

Now as we did for the original snake cube puzzle, we identified the sequence of the HP numbers compatible with each of the 103,346 folded structures. Out of the above mentioned 6,435 sequences, 6,291 sequences are found to fold into one of the 103,346 folded structures. Out of the 6,291 foldable sequences, 120 sequences are found to fold into a unique structure. As an example, a sequence of the HP numbers 323 232 323 212 121 232 121 012 323 is found foldable into the structure shown in Figure 2a. Another sequence 323 232 323 232 323 212 121 212 101 cannot fold into any compact structure satisfying the HP requirement. The uniqueness ratio (UR) is thus 120/6291≒0.019. The average of the structural multiplicity number (SMN) is thus 103,346/6,291≒16.43. These two values, being very far from unity, indicates that the power of the hydrophobic interaction to make the folded structure unique to the sequence is weak. At least it is much weaker than the geometrical varieties as modelled in the snake cube puzzle.

Extension of the snake cube puzzle, Compound puzzle

Now we extend the puzzle of an array of 27 cubes, so that it models both geometrical varieties of amino acid residues and VdW plus hydrophobic interactions. This extension can be attained by specifying an array of 27 cubes by the compound sequence of both of the backbone geometry and the HP numbers. So, we name it compound puzzle. An example of a compound sequence is given in the legend to Figure 4. From this compound sequence we can derive a snake cube puzzle problem with a sequence of the backbone geometry esb sbb bbb bbb bbb bbb bbb bbs bse (which happens to be palindromic), and a HP puzzle problem with a HP sequence 323 232 101 212 321 232 121 232 323.

Figure 4.

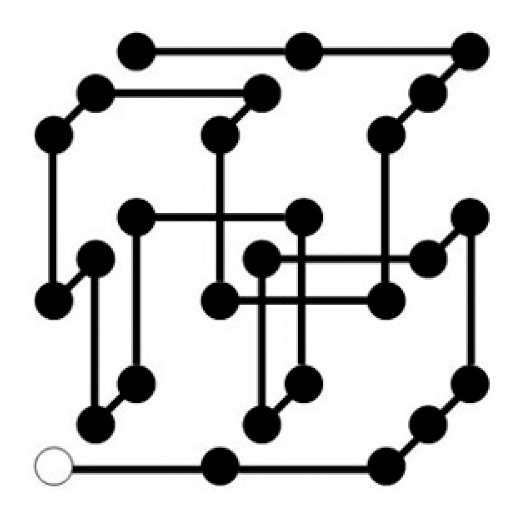
Unique folded structure RR BB UF LD BU LD FU FU BR FD RU BB LL of a compound puzzle problem with a compound sequence, (e3)(s2)(b3) (s2)(b3)(b2) (b1)(b0)(b1) (b2)(b1)(b2) (b3)(b2)(b1) (b2)(b3)(b2) (b1)(b2)(b1) (b2)(b3)(s2) (b3)(s2)(e3).

Now as we did for the original snake cube puzzle and the HP puzzle, we identified the compound sequence compatible with each of the 103,346 folded structures. Totally 43,824 compound sequences are found to fold into one of the 103,346 folded structures. Out of these foldable sequences, 18,950 compound sequences are found to fold into a unique structure. The uniqueness ratio (UR) is thus 18,950/43,824≒0.43. The average of the structural multiplicity number (SMN) is thus 103,346/43,824≒2.36. These values of UR and average SMN for the compound puzzle are to be compared with those for the snake cube puzzle and the HP puzzle. Even though the power of the hydrophobic interactions as modelled in the HP puzzle to make the folded structure unique to the sequence was found weak, compounding it to the snake cube puzzle worked very effectively to enhance the power; the UR increased from 0.32 to 0.43 and the average SMN decreased from 4.51 to 2.36.

We can see an example of the enhancement in Figure 4. This is a unique folded structure for the compound sequence given in the figure legend. The SMN of the snake cube puzzle problem derived from this compound puzzle problem is 34. The SMN of the HP puzzle problem derived from this compound puzzle problem is 22. By imposing both sequence characteristics to be satisfied at the same time, the SMN reduced from 34 and 22 to unity. This is a strong case of demonstrating that the consistency of constituent energy terms works effectively for the realization of the unique folded structure.

Discussion and Conclusion

Three different versions of puzzles made of a linear array of 27 cubes are used as theoretical tools to study the mechanism of folding of proteins into their sequence-specific native three-dimensional structures. Each version is characterized by its respective characteristics attributed to its constituent cubes that would contribute to the power of sequence determination of the folded structure. In the first version, the snake cube puzzle, cubes are characterized by an attribute which is a simplified expression of the variety of shapes of amino acid residues in protein. In the second version, the HP puzzle, cubes are characterized by a degree of the hydrophobicity. In the third version, the compound puzzle, cubes are characterized by both attributes given to the snake cube puzzle and HP puzzles.

In order to quantify the power of characteristics attributed to constituent cubes in each version to make the folded structure unique to the sequence, two quantities, uniqueness ratio (UR) and average of the structural multiplicity number (SMN), are introduced. When both of them become unity, sequence determines the folded structure uniquely, the situation realized in protein. For the snake cube puzzle, the UR and the average SMN were found to be 0.32 and 4.51, respectively, which is a result indicating a difference from protein. When some of individual cases with the SMN larger than unity were examined in detail, the difference appeared largely attributable to the smaller type variety and higher symmetry possessed by the constituent cubes of the snake cube puzzle. Instead of pursuing to improve the puzzle along the implied direction, the effect of quite a new characteristic, hydrophobicity, is examined in the second version of the puzzle, the HP puzzle. Such a choice was motivated by a view advocated by “the consistency principle” [5,6]. For this puzzle, UR and average SMN were found to be 0.019 and 16.43, respectively. These values, both far from unity, indicate that the power of the hydrophobic interaction to make the folded structure unique to the sequence is much weaker than the geometrical varieties as modelled in the snake cube puzzle. However, when this weak attribute of the HP puzzle is compounded to that of the snake cube puzzle as in the compound puzzle, UR and average SMN were improved from 0.32 and 4.51 to 0.43 and 2.36. This result indicates that, when two types of attributes work consistently, the power to make the folded structure unique to the sequence is enhanced effectively, even when one of the attributes is weak.

We see that the newly introduced theoretical models have opened the way to endow “the consistency principle” with a quantitative character.

Discussions so far have been done mainly from the point of view of the folded structures. To discuss folding phenomenon as a whole we also have to pay attention to unfolded structures. Folding-unfolding transition in protein is caused as a result of balance between free energies of entropy driven unfolded state and contact energy driven folded state. In the cases of the snake cube puzzle model and the compound puzzle model, the former free energy would be roughly proportional to the number of b-type cubes, which varies between 14 and 23 as mentioned earlier, while the latter free energy is assumed to be proportional to the number of contact surfaces in the compact structure, which is a fixed number 28. Therefore, the transition temperatures of puzzle model proteins vary very much depending on the sequences. Interestingly, difficulty of finding correct folding structures of commercially available puzzle problems in Figure 2 by manual operation increases as the number of b-type cubes in the sequence increases.

We must also comment on the assumption of the uniform value for the contact energy. This is of course a drastic simplification from the real proteins. We may further refine our model by employing non-uniform contact energies, which could be similar in spirit to those of Miyazawa and Jernigan [9], who determine a set of parameters from the analysis of native structures of proteins. The point in the present paper is that even before going into such refined study, the importance of the consistency principle can be appreciated strongly.

At the end it may be appropriate to discuss comparison of our study to that of Sali, Shakhnovich and Karplus [10,11] who also employed a lattice model of protein (SSK model in short hereinafter) where the native structure is folded compactly into a 3×3×3 cube. They assumed the following contact energy function for a polymer of self-avoiding 27 monomers on a simple cubic lattice;

$$\text{E}=\sum _{i<j}{B}_{ij}\mathrm{\Delta }(r_i,r_j),$$ (1)

where r_i are the positions of monomers i, B_ij are the contact energies for pairs of monomers i, j, and Δ(r_i,r_j) is 1, if monomers i and j are in contact and is 0 otherwise. The values of the B_ij are given from a Gaussian distribution with a mean B₀ and standard deviation σ_B. A “sequence” in this model is defined by a set of values of the B_ij contact energies. They generated and studied behavior of 200 such “sequences.” The native conformation is the one with the lowest energy among the 103,346 structures folded compactly into the 3×3×3 cube. Folding simulations of 50×10⁶ Metropolis Monte Carlo steps starting with a random-coil conformation were carried out 10 times for each sequence. Folding tendency of a given sequence is defined as the fraction of the 10 MC runs that reached the native conformation under a given set of conditions. A sequence is judged as a folding sequence if the native conformation is structurally unique and folding tendency is high (≥0.4) under conditions where the native structure is thermodynamically stable. The values of parameters B₀(−2) and σ_B(1) were determined so as to optimize the folding tendency. Each sequence is studied at a temperature where the native state has a high probability to be reasonably thermodynamically stable; the native state has a weight exp[−E/k_BT] larger than 0.2 relative to other compact structures. As a result, 30 out of the 200 sequences (15%) were found to be folding sequences and regarded to correspond to actual protein sequences.

We compare this SSK model with our snake cube model. There are two differences in the definition of the model. At first, in the snake cube model, 25 non-terminal units of “a protein with a given sequence” are fixed to either s- or b-type. A sequence of these types defines a protein sequence. Whereas in SSK model all units can assume both s- and b-conformations. At second, in the snake cube model, σ_B=0 is assumed, i.e., uniform value is assumed for all contact energies.

These two differences of the definition of models introduce big differences in their behavior. One consequence of the first difference of the definition is the “stiffness” of the model. In the SSK model the polymer chain with any sequence is assumed flexibly foldable into any of the 103,346 compact structures, but with different energies. The structure with the lowest energy is regarded as the native structure of a polymer with the given sequence. In the snake cube model, polymers only with very rare 22,897 sequences can fold into the compact structure. This is 0.068% of all possible sequences. This stiffness is a result of introducing a backbone geometrical characteristic (i.e., s- or b-type) to the constituting units. We think that this is a good expression of the impression of Richards [2], i.e., it would be generally very difficult to fold linear chains of 20 types of amino-acid residues, having a variety of shapes, into well packed structures. In this situation as already mentioned we call the sequence of cube types also as the sequence of the backbone geometry.

Mainly because the constituent units of the snake cube model have simpler shapes with higher symmetry than real amino-acid residues, foldable sequence can often fold into a multiple number (structural multiplicity number, SMN) of compact structures. Because we are assuming uniform contact energies, all compact folded structures have the same ground energy, i.e., they are degenerate. Out of the 22,897 foldable sequences, 7,268 sequences are found to fold into a unique structure. When we regard these sequences folding into unique structures as corresponding to proteins, their frequency is very low, 0.022%, which is 0.068% times (7,268/22,897). We have seen in this paper that, when other characteristic is compounded to constituent units, this number is somewhat increased, but not very much. This number is to be compared with 15% for the folding sequences in the SSK model. We have to clarify the reason for this enormous difference.

Following the logic described in the paper of SSK model [10,11], the number of 15% was obtained by optimizing various parameters, especially B₀ and σ_B, so as to optimize the folding tendency. With this logic alone, the number of 15% remains to express the success of the mathematical optimization procedure. However, the authors claim [10,11] that the values of B_ij sampled with the optimized values of B₀ and σ_B correspond to the contact energies in real proteins, such as those described by Miyazawa and Jernigan [9] in the sense that the expression of Equation (1) is for the total energy difference between the solvated extended and solvated native structure of a protein. Here we must remember that Miyazawa and Jernigan determined their values of contact energies from successfully folded native structures of proteins where atoms are very well packed. Therefore their parameters are well suited for judging compatibility of a given sequence with a given native three-dimensional structure of a protein. However, before a protein molecule finds the native structure in the process of folding, atoms in transient residue-residue interfaces would not be so well packed as in the native structures. If so, it is not appropriate to use the Miyazawa-Jernigan parameters to the studies of folding process. I think whether or not the very high number of 15% has a meaning beyond a mere result of optimization procedure should be examined seriously. If it is applicable to real proteins, it means 15% of polypeptide chains with all possible amino-acid sequences can fold into their native structures, not only thermodynamically but also kinetically. It is very precious to know this fraction for real proteins.