Different motilities of microtubules driven by kinesin-1 and kinesin-14 motors patterned on nanopillars

Nanopatterning of motors reveals that the number and spacing of kinesin-14, and not of kinesin-1, dictate microtubule velocity.

Abstract

Kinesin is a motor protein that plays important roles in a variety of cellular functions. In vivo, multiple kinesin molecules are bound to cargo and work as a team to produce larger forces or higher speeds than a single kinesin. However, the coordination of kinesins remains poorly understood because of the experimental difficulty in controlling the number and arrangement of kinesins, which are considered to affect their coordination. Here, we report that both the number and spacing significantly influence the velocity of microtubules driven by nonprocessive kinesin-14 (Ncd), whereas neither the number nor the spacing changes the velocity in the case of highly processive kinesin-1. This result was realized by the optimum nanopatterning method of kinesins that enables immobilization of a single kinesin on a nanopillar. Our proposed method enables us to study the individual effects of the number and spacing of motors on the collective dynamics of multiple motors.

INTRODUCTION

Motor proteins convert chemical energy into structural changes and produce mechanical work necessary for various cellular processes including vesicle transport (1), cell division (2), muscle contraction (3), and beating of flagella and cilia (4). In vivo, motor proteins do not work alone but as a team (5–7). In intracellular transport, approximately 10 motors coordinate to transport a cargo (8–10) and cooperate to produce a higher speed or larger force than that by a single motor. The velocity of cargo with several kinesin motors increases by three- to fourfold compared to a single kinesin motor in vitro (11, 12). Similarly, the force exerted by kinesin-14 motors increases with their number (13, 14). In cell divisions, 20 to 100 motors are involved in assembling the spindle to segregate chromosomes (15). Approximately 10⁴ axonemal dynein molecules, assembled with a defined spacing of 24 or 96 nm, collectively produce the beating motion of a cilium or a flagellum (16, 17). Evidently, to understand the physiological functions of motor proteins, it is necessary to know how the number and spacing of motor proteins influence their motility.

The effect of the number of motors on microtubule behavior has been investigated using a microtubule gliding assay because the number of motors interacting with gliding microtubules can be estimated from the length of the microtubule and motor density on the surface (i.e., the number of motor molecules per unit area). Bieling et al. (18) found that the microtubule velocity decreased with an increase in motor density when a truncated kinesin-1 was used. Roostalu et al. (19) reported that the directionality of gliding microtubules could be switched by increasing the number of kinesin-5 proteins and argued that directionality was determined by the total number of kinesin-5 proteins interacting with the microtubule. These studies suggest that the number of motors is an important factor in the collective dynamics of motors.

The spacing between motors has also been shown to affect the collective dynamics of motors. Axonemal dynein molecules are arranged along the microtubule of cilia and flagella at equally spaced intervals (16, 17). Using extract from cilia, Seetharam and Satir (20) reconstituted that the gliding of microtubules on axonemal dynein molecules is periodically arranged in vitro and found that the microtubules could slide at a high velocity (average of 196 μm/s). As this measured velocity is an order of magnitude greater than the typical gliding velocity on a dynein-coated glass surface, where the spacing of axonemal dynein molecules is variable (21), it is thought that equal spacing between dynein molecules may be necessary to realize a higher velocity.

One disadvantage of a conventional gliding assay is that it cannot distinguish the effects of direct and indirect interactions between motors on their collective dynamics. Direct interactions caused by steric hindrance between adjacent motors lead to detachment or pausing of motors, decreasing the velocity of microtubules (22). An indirect interaction occurs when one motor’s activity influences other more distant motors transporting the same microtubule (6). When a microtubule is transported by multiple kinesins, some of them generate a force that acts in a direction that is opposite to the moving direction of the microtubule because not all kinesins are synchronized. Direct interactions could be eliminated by increasing the space between the motors. Therefore, to investigate the individual effects of direct and indirect interactions, the spacing between motors could be controlled.

The mechanisms explaining how the number and spacing of motors affect their collective dynamics remain poorly understood, primarily because of the experimental difficulties in controlling these parameters in vitro. Using flat surfaces, the number and spacing of motors can be controlled by varying their concentration and the length of the microtubules. However, the estimated number of motors interacting with a microtubule is less deterministic, because motors are stochastically distributed on the surface. Although DNA origami scaffolding allowed us to precisely define the number and spacing of motors (13, 23–25), only up to 10 motors can be controlled, which is much lower than the number in vivo. It is necessary to develop a method to modulate the number and spacing of motors in vitro.

Several studies have addressed the difficulty of controlling the number of motors using micro/nanopillars. Lard et al. (26, 27) demonstrated that the number of myosin interacting with an actin filament can be controlled by immobilizing myosin molecules on a nanowire array. However, because myosin molecules were immobilized not only on the top of nanowires but also on the substrate and sides of the nanowires, actin filaments frequently glided along the sides of the nanowires down to the substrate, resulting in short observation times. In addition, their method is less deterministic because multiple motor molecules were attached on the tops of the large-diameter (150 to 170 nm) nanowires. Roos et al. (28) took an approach similar to Lard et al., selectively immobilizing kinesin molecules on the tip of micropillars made of polydimethylsiloxane. However, many kinesin molecules were attached to a single micropillar owing to its large diameter (1 to 5 μm).

Here, we propose the nanopatterning method of kinesins to accurately determine the number (10 to 100 motors per microtubule) and spacing (200 to 1000 nm) of kinesin motors. Because we used smaller nanopillars (50 nm in diameter) to immobilize only a single kinesin molecule per pillar, we can precisely define the number of motors and the spacing of the motors interacting with a microtubule. Moreover, this method enables us to perform the microtubule gliding assay at a much lower motor density (<10 molecules/μm²) than that required for the conventional gliding assay with flat surfaces (20 to 10,000 molecules/μm²) (18). This makes it possible to study the relationship between the number and velocity of motors in the range of 3 to 100 motors, similar to the number of motors working together in vivo (29). In addition, our method enables us to isolate the effects of indirect interactions between motors because the distance between them is greater than twice the length of a kinesin molecule. We found that the number and spacing of kinesin molecules separately affect the microtubule velocity in the case of nonprocessive kinesin-14, whereas the velocity is independent of both the number and spacing for processive kinesin-1. The proposed patterning method facilitates a new assay that can be used to investigate how the number and spacing of motors affect the collective dynamics of multiple motors.

In addition to enabling the study of the relationship between velocity and the number and/or spacing of motors, our method has the potential to guide microtubules along nanopillars and motivate practical usage of motor-driven bio-nano/microdevices (30). The microtubule-kinesin system can be combined with microfluidics and used as a molecular transporter, sorter, concentrator, and detector. The directional control of gliding microtubule shuttles has been a challenge that has hampered practical usage of microtubule-kinesin, as microtubules glide in random directions owing to Brownian motion of the free leading tip (31). Although a fabricated track can control the gliding direction of microtubules, the precision is still limited up to a few micrometers, and the efficiency of microtubule transport is deteriorated by frequent sidetrack of microtubules. In this study, we demonstrate that the gliding direction is defined with high precision by defining the position of each kinesin with nanometer-scale precision. Therefore, our method can also be used to control the direction of gliding microtubules and drive the practical usage of microtubule-kinesin systems.

RESULTS AND DISCUSSION

Nanofabrication of gold nanopillars and selective immobilization of kinesin molecules on self-assembled monolayer–modified surfaces

Kinesin molecules were selectively immobilized on gold nanopillars as illustrated in Fig. 1A. Gold nanopillar arrays were fabricated on a silicon dioxide substrate by electron beam lithography and lift-off processes, followed by the passivation of a silicon dioxide surface with a silane–poly(ethylene glycol) (PEG) self-assembled monolayer (SAM) (Fig. 1B and fig. S1A). To attach only one kinesin molecule to a nanopillar, we designed the diameter of the nanopillars to measure 50 nm. By optimizing the smallest spacing in the nanofabrication processes, nanopillar arrays with spacing ranging from 200 to 1000 nm were fabricated (fig. S1B). SEM observations confirmed that the diameters of the nanopillars were close to the designed value (55.7 ± 4.17 nm, mean ± SD, n = 30) (fig. S1C).

Fig. 1. Nanopatterning of kinesin molecules by selective immobilization of kinesin on gold nanopillars.

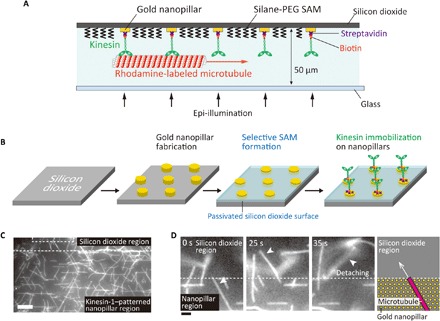
(A) Schematic illustration of nanopatterned kinesin molecules. (B) The experimental procedure of nanopatterning of kinesin molecules. (C) Fluorescence image of microtubules gliding at the boundary of the passivated silicon dioxide region and the kinesin-1–patterned region on gold nanopillars. Scale bar, 10 μm. (D) Sequential images of a microtubule at the boundary between the nanopillar region and silicon dioxide region. Scale bar, 2 μm.

Before performing a gliding assay on the pillars, we confirmed that both kinesin-1 and kinesin-14 could be selectively immobilized only on a planar gold surface and not on the passivated silicon dioxide surface. On the gold surface, where biotinylated kinesin-1 was immobilized via nonspecifically absorbed streptavidin, the microtubule velocity was recorded as 0.75 ± 0.02 μm/s (mean ± SD, n = 5). No microtubule was found on the silicon dioxide surface because of the silane-PEG SAM (32). In a control experiment using a glass substrate, where kinesin-1 was immobilized via streptavidin and biotinylated bovine serum albumin, the microtubule velocity was recorded as 0.42 ± 0.02 μm/s (mean ± SD, n = 5). When the same measurement was conducted using kinesin-14, recorded velocities were 0.123 ± 0.015 μm/s (mean ± SD, n = 5) on a gold surface and 0.091 ± 0.003 μm/s (mean ± SD, n = 5) on a glass surface. The silane-PEG SAM–modified surface also suppressed microtubule absorption in the kinesin-14 assay.

It is known that the velocity strongly depends on temperature (33), the construct (length) of kinesin (18), and the surface density of the motors (18). Therefore, measured velocities are compared to previous studies conducted under conditions similar to ours. Our recorded velocity on a kinesin-1–coated glass surface (0.42 ± 0.02 μm/s) is in agreement with the ≈0.43 μm/s obtained in a previous study (18). Experimental conditions for our study were similar to theirs: a surface density of ≈1000 molecules/μm² using a truncated kinesin-1 (Kin401, amino acids 1 to 401; 1 to 465 in this study) at 26°C (23° to 25°C in this study). Velocity on a kinesin-14–coated glass surface (0.091 ± 0.003 μm/s) is slightly lower than a previously reported value (0.135 ± 0.006 μm/s) (34). We used the same truncated kinesin-14 (amino acid 195 to 700) as Furuta et al., so the difference in velocity may have come from their use of green fluorescent protein tag or a difference in the surface density of motors, since theirs was not controlled.

Our results show that the velocities on kinesin-1– or kinesin-14–coated gold surfaces are higher than those on glass surfaces. A possible explanation is the elevation of temperature near the gold surface owing to the absorption of excitation light. According to our previous study (35), the temperature on a gold surface is elevated from 23°C to 28°C when the surface is illuminated by excitation light with an irradiance of 7.2 W/cm² (equivalent to the intensity we used in this study), resulting in an increased velocity compared to that on a glass surface. Motility functions of kinesin molecules were retained after the selective patterning on a gold surface. Therefore, we decided to immobilize kinesin molecules on gold nanopillars via nonspecifically absorbed streptavidin.

Microtubule gliding assay on kinesin-1– or kinesin-14–immobilized nanopillars

A microtubule gliding assay was performed to verify the selective immobilization of kinesin molecules on gold nanopillars. It was found that, in the gold nanopillar region where kinesin-1 motors were immobilized, many microtubules attached to the surface and glided smoothly (Fig. 1C and movie S1). On the other hand, we found no microtubule attachment within the silicon dioxide region. When the microtubules crossed the boundary from the nanopillar region and entered the silicon dioxide region, they detached from the surface (Fig. 1D and movie S2). The same behavior was observed on the kinesin-14–patterned surface (fig. S2 and movies S3 and S4). These results support the idea that kinesin molecules exist only within the gold nanopillar region.

To evaluate the number of kinesin molecules attached to the nanopillars, we observed the behavior of short microtubules on patterned kinesin-1. We used kinesin-1 because it is a highly processive motor, and a single molecule has the ability to move a microtubule. Short microtubules (1 to 5 μm) were introduced into a flow chamber where kinesin-1 was patterned by 5-μm spacing nanopillars. We observed that several microtubules exhibited pivoting motions on an anchored point (fig. S3B), which is known to be observed when a microtubule is driven by a single kinesin-1 molecule (fig. S3A) (36). In addition, the microtubules showed a gliding motion at the anchored point (fig. S3D). These results indicated that a single kinesin-1 molecule was attached to a pillar and drove the microtubules.

As kinesin-14 is not a processive motor, it frequently detaches from microtubules in the presence of adenosine triphosphate (ATP). For this reason, we evaluated the number of kinesin-14 on a pillar by the same method for kinesin-1 but in the absence of ATP (see Materials and Methods for detail). We observed pivoting motions of microtubules at an anchored point (fig. S3C), indicating that a single kinesin-14 molecule was attached to a pillar.

As the hydrodynamic radius of kinesin is approximately 10 nm (37), six kinesin molecules can be immobilized on a pillar with a diameter of 50 nm. However, this assumption is inconsistent with our finding that only a single kinesin was attached to each pillar. Here, casein may have a significant role in decreasing the number of kinesin molecules on a pillar, because it forms micelles with a hydrodynamic radius of ~12 nm and attaches to pillars (38).

Our result also indicates that there are very few, if any, pillars with more than one motor. If pillars had more than one motor, then we would have observed a smooth gliding of short microtubules. However, we did not observe this behavior; we observed only instances of pivoting motions.

To statistically examine whether all nanopillars capture a single kinesin molecule, the average spacing between kinesin motors immobilized on nanopillars can be discussed. When a short microtubule glides on a kinesin-1–coated surface, it frequently binds to a single kinesin-1 molecule and displays a pivoting motion around the motor (39). The average distance travelled by the microtubule between successive rotations depends on the length of the microtubule and the average spacing between kinesin-1 motors. Hence, the average distance between motors <d_k> was derived using the following equation (40)

$$<\mathrm{S}>=\frac{L+2<d_{\mathrm{k}}>}{L+3d_{\mathrm{k}}}\frac{{<d_{\mathrm{k}}>}^2}{L}(e^{\frac{L}{d_k}}-1-\frac{L}{<d_{\mathrm{k}}>})$$ (1)

Here, <S> is the average distance travelled between pivots, and L is the length of the microtubule. If the measured average spacing between motors is equivalent to the spacing of nanopillars (d_p), then we can assume that each nanopillar has a kinesin molecule. Previously, we demonstrated a selective immobilization of kinesin-1 on a nanopillar array via thiol-PEG-biotin SAM and measured the average spacing between motors (41). When the diameter of the pillars was 50 nm, the measured spacing was 99.2 ± 4.2 nm for pillars designed with 100-nm spacings. However, the difference between the measured and designed spacings increased when the diameter of the pillars was 100 nm (267 ± 10 nm for 300-nm spacing; 452 ± 21 nm for 500-nm spacing). These results indicate that pillars with diameters of 50 nm have only a single kinesin molecule, whereas multiple kinesin molecules can be immobilized on pillars with diameters of >100 nm. Although we immobilized kinesin molecules via a different method (nonspecific absorption of streptavidin), we are able to assume that almost all the nanopillars have a single kinesin molecule in the current study.

Our method enables us to conduct microtubule gliding assays at an extremely low motor density (1 to 10 molecules/μm²), which cannot be done in a conventional gliding assay on a flat glass surface (20 to 10,000 molecules/μm²) (18). This can be explained by the difference in the number of motors interacting with a microtubule. On a flat surface, motors are stochastically immobilized and attach to a microtubule only when the distance between the longitudinal axis of the microtubule and a motor is less than 45 nm (42). Therefore, the number of motors attached to the microtubules can be calculated as (2 × 0.045 μm) × ρ = 0.09ρ (molecules/1-μm microtubule). Here, ρ is the surface density of the motors (molecules/μm²). On a nanopillar array, a microtubule glides on aligned pillars as discussed in the following sections. When focusing on a microtubule gliding in the direction of highest pillar density (Fig. 2B, line A), the number of motors attached to the microtubule can be calculated as 1/d_p = $0.66\sqrt{\mathrm{\rho }}$ (molecules/1-μm microtubule). Here, we used the relationship between the spacing of nanopillars and the surface density of nanopillars (motors): $d_{\mathrm{p}}=\sqrt{2/\mathrm{\rho }\text{sin}60°}=1.52/\sqrt{\mathrm{\rho }}$. Therefore, when the density is set to ρ = 1.0 molecule/μm², a 10-μm microtubule can bind to only ≈1 motor on a flat surface, which easily leads to detachment of the microtubules from the surface. However, ≈7 motors can support microtubule gliding on a nanopillar array, resulting in stable gliding of microtubules. One advantage of our method is that the gliding assay can be conducted at such a low motor density (3 to 100 motors per microtubule), similar to the number of motors working together in vivo (29).

Fig. 2. Alignment of microtubules on patterned kinesin molecules.

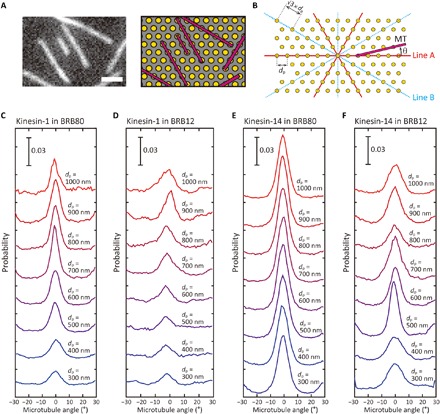
(A) Fluorescence image of aligned microtubules on patterned kinesin-1 (left) and corresponding illustration of microtubules and nanopillars (right). The spacing between the pillars, d_p, is 500 nm. Scale bar, 2 μm. The illustration is not to scale. (B) The definition of the orientation angle of microtubules. d_p indicates the designed spacing between pillars. (C to F) The distribution of angles between microtubules and line A on patterned kinesin-1 in (C) BRB80 and (D) BRB12 and on patterned kinesin-14 in (E) BRB80 and (F) BRB12.

Compared to previous studies using a micro/nanopillar array (26–28), our method allows us to more accurately count the motors and define their spacing. Even in studies with a pillar array, motors coated all surfaces, including the substrate and sidewall of the pillars (26, 27). This resulted in actin filaments gliding unpredictably across surfaces. However, in our study, the SAM coating and SiO₂ substrate prevented nonspecific binding and limited microtubule gliding to the tops of pillars. In addition, we used smaller nanopillars (50 nm in diameter) than previous studies (> 150 nm in diameter) to immobilize only a single kinesin molecule on each nanopillar. Therefore, our assay continued for enough time to study the relationship between the velocity and the number or spacing of motors. The method can be applied to kinesin-microtubules, actin-myosin, and other motors.

Alignment of microtubules on patterned kinesin molecules

We measured the orientation angle of microtubules with two kinds of kinesins (kinesin-1 or kinesin-14), two buffers with different ionic strengths (BRB12 or BRB80), and eight kinds of pillar spacings (300 to 1000 nm). Figure 2A shows the fluorescence image and the schematic illustration of microtubules on patterned kinesin molecules. The angles of the microtubules are defined with respect to the solid red lines (Fig. 2B, line A) connecting two adjacent pillars with the designed spacing, p, which ranges from −30° to +30°.

We found that there are two populations of microtubules indicated by the two peaks in the probability graph in Fig. 2 (C to F): one glides in the direction of 0° and the other glides in the direction of ±30°. The former peak corresponds to the main population of the microtubules that glide along line A. The latter corresponds to the subpopulation of the microtubules moving along line B, as shown in Fig. 2B. These two populations of microtubules are independent of the type of motors, the ionic strength of the buffer, and the spacing of the pillars (Fig. 2, C to F, and fig. S4, A to D). Fluorescence images of aligned microtubules under each condition are summarized in fig. S4 (A to D). As the persistence length of 4 to 8 mm is much larger than the pillar spacings, it is evident that most microtubules keep gliding straight once they start gliding on aligned pillars (43, 44). In addition, the microtubules are more likely to land in the directions of lines A and B, as the microtubules can bind to larger number of kinesin molecules in this region than in other directions (fig. S5, A and B). This is the reason why microtubules are settled in these two directions, and two peaks can be observed in Fig. 2 (C to F).

The degree of microtubule alignment becomes higher with an increase in the spacing of the pillars, reaching a maximum at a spacing of 700 nm in any condition (Fig. 2, C to F, and fig. S4, A to D). When the spacing between pillars is small, microtubules land not only in the direction of the two lines A and B but also in other directions because they can bind to enough kinesins to remain on the surface. For example, a microtubule with a length of 10 μm lands in other than the two directions and binds only to ~2 kinesin molecules in the case of a 700-nm pillar spacing, whereas it can bind to ~12 kinesin molecules in the case of a 300-nm spacing (fig. S5B). This is why the height of the peaks increases when the spacing of the pillars increases. In the case where spacing between pillars is equal to or more than 700 nm, we found that many microtubules changed their gliding directions by touching pillars or the silicon dioxide surface owing to tip fluctuation. Numerical simulation (see the next section for details) reveals that the tip thermally fluctuates by 37.9 nm (3× SD) at a 700-nm spacing. Therefore, when microtubules fluctuate in the z direction, their tip can easily touch the substrate as the pillar height (the chromium and gold thickness) is only 23 nm. When the leading tip touches the substrate, the tip would be pinned on the surface, while the microtubule rear end continues to move forward, resulting in rotation of the microtubule around the pinned point and a change in the gliding direction.

The ionic strength of the motility buffer also influences the degree of microtubule alignment. The population of microtubules that moves along line A or line B is larger in BRB80 buffer than in BRB12 buffer on both the kinesin-1–patterned surface (Fig. 2, C and D, and fig. S4, A and B) and the kinesin-14–patterned surface (Fig. 2, E and F, and fig. S4, C and D). This can be explained by the difference in the off-rate of kinesins from microtubules. As a run length of kinesins decreases with increasing ionic strength (34, 45), it is suggested that the off-rate increases with increasing ionic strength. In addition, the off-rate is known to increase when neck linkers of kinesin molecules are extended (42, 46). Thus, the microtubules detached more frequently from the surface in BRB80 than in BRB12 if they landed in other than the two directions. Therefore, in BRB80, it is observed that most of microtubules continue to attach to kinesin molecules in the directions of lines A and B rather than in other directions, and the degree of microtubule alignment increases.

We also found that the degree of the microtubule alignment is higher on the kinesin-14– than on kinesin-1–patterned surface: The height of peaks at 0° and ±30° are higher on kinesin-14 (Fig. 2, E and F) than kinesin-1 (Fig. 2, C and D) in both BRB80 and BRB12. This is because kinesin-14 has a smaller detachment force (i.e., stall force) than kinesin-1: <1 pN for kinesin-14 (13) and ~6 pN for kinesin-1 (47). As the load applied to kinesin heads increases with the extension of neck linkers, microtubules are detached more frequently from the kinesin-14–patterned surface than from the kinesin-1–patterned surface when the microtubules land in other than the two directions.

A run length of motors also plays a role in aligning microtubules along pillars. Kinesin-14 has a shorter run length (≈−400 nm) than kinesin-1 (≈1600 nm) (34). The shorter run length causes rapid detachment of microtubules from the surface when a microtubules lands in other than the two directions.

In summary, the microtubules were highly aligned on patterned kinesins according to the pillar arrangement. The degree of microtubule alignment increases with (i) an increase in spacing and reached a maximum at a spacing of 700 nm; (ii) an increase in the ionic strength of the buffer solution; (iii) a decrease in the stall force of the motors; and (iv) a decrease in the run length of motors.

Simulating thermal fluctuation of the free tip of a microtubule on patterned kinesins

Next, we simulated the fluctuation of the leading tips of microtubules and investigated how the microtubules aligned along the pillars (Fig. 3A). Here, the microtubule is assumed to move along line A (Fig. 2B), and the free tip is considered as a cantilever beam tethered at one end (31). The length of a free tip, L, is equal to the spacing of the pillars, d_p.

Fig. 3. Simulation of a fluctuating leading tip of microtubules.

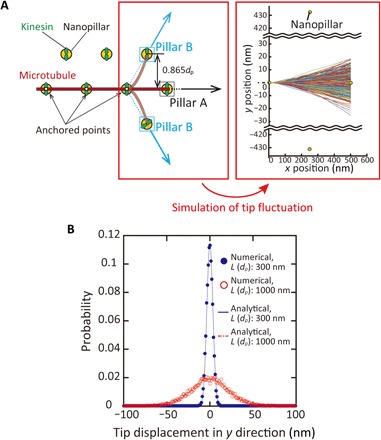
(A) Schematic illustration of a fluctuating tip of the microtubule (left) and representative traces of the simulated shape of the tip (right). Traces were obtained by 500 runs of a simulation. (B) Probability density function of the displacement of the tip in y direction. L, the length of a free tip; d_p, the spacing between pillars. n > 10,000.

Figure 3B shows the probability density functions of displacement of the tip in the y direction for the 300- and 1000-nm pillar spacings. It is obvious that microtubules glide toward pillar A because the probability is maximum at y = 0 nm, resulting in the peaks at 0° as shown in Fig. 2 (C to F). Next, we evaluated the amplitude of thermal fluctuation by comparing the SD of the displacement of the tip: SD is calculated as 3.54 nm for d_p = 300 nm and 21.2 nm for d_p = 1000 nm. The distance between pillar B and the microtubule is 0.865 d_p as shown in Fig. 3B and is calculated as ~260 nm for d_p = 300 nm and ~870 nm for d_p = 1000 nm. This indicates that the distance between pillar B and the microtubule is more than 40 times larger than the amplitude of the free tip. Therefore, the possibility that the end of a free tip moved to the position of pillar B is zero.

The amplitude of thermal fluctuation can also be analytically calculated by the effective elastic constant of the tip as K = 3κ_MT/d_p³ and the fluctuation amplitude as $\mathrm{\sigma } = \sqrt{k_{\mathrm{B}}T/K}$, where k_B is the Boltzmann constant, and T is the temperature in the experiments (298 K). With this calculation, σ = 3.51 nm for p = 300 nm and σ = 21.4 nm for p = 1000 nm, which is consistent with our simulation results and confirms the adequacy of our simulation model.

Together, the numerical simulation indicates that the microtubules move along the straight lines (Fig. 2B, line A) corresponding to the pillars when kinesin molecules are immobilized only on pillars. However, we observed that some microtubules changed their direction of gliding. To find an explanation for this contradiction, we investigated how the microtubules changed their gliding directions on patterned kinesin molecules.

Behavior of microtubules that changed their direction of gliding on patterned kinesin molecules

We carefully observed the behavior of microtubules on patterned kinesin molecules and investigated how the microtubules changed their direction of gliding. We found that events related to changes in the gliding direction can be classified into four types: (I) collision and unchanged, (II) collision and changed, (III) spontaneous, and (IV) pinning.

Figure 4 (A to D) shows the sequential images of microtubules that represent the events (I) to (IV). (I) “Collision and unchanged” is the event where the leading tip of a microtubule collides with other microtubules but does not change its gliding direction (Fig. 4A). (II) “Collision and changed” represents the event where the tip collides with other microtubules, and the microtubule changes its direction of gliding (Fig. 4B). In detail, the tip detached from the surface, glided over the other microtubules, and then exhibited Brownian motion. Last, the tip reattached to a kinesin in a different direction from the initial one and kept gliding (Fig. 4B, 16 to 20 s). (III) “Spontaneous” represents the event where the leading tip spontaneously changes its gliding direction by Brownian motion without colliding with other microtubules (Fig. 4C). (IV) “Pinning” indicates the event where the leading tip is temporally pinned on the surface, and the microtubule starts rotating around the pinned point and changes its gliding direction (Fig. 4D).

Fig. 4. Behavior of microtubules that changed travel direction on patterned kinesins.

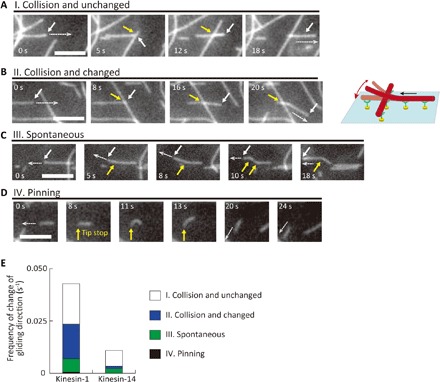
(A to D) Representative sequential images of the microtubules. Scale bars, 5 μm (A) “I. Collision and unchanged”: A microtubule did not change direction after collision; (B) “II. Collision and changed”: A microtubule changed direction after a collision. The white arrows indicate the leading tip of the microtubule. The white dashed arrows show the direction of microtubule gliding. The yellow arrows indicate the point of collision; (C) “III. Spontaneous”: A microtubule spontaneously changed its gliding direction. The yellow arrows indicate the position in which the leading tip changed its direction; (D) “IV. Pinning”: A microtubule changed direction because the leading end was pinned. (E) Frequency of the events (I) to (IV) on patterned kinesin-1 and kinesin-14.

Figure 4E shows the frequency of each event, i.e., the number of observations for each event per second, on patterned kinesin-1 and kinesin-14. The sum of the frequency of (II) to (IV) indicates how many times the microtubules changed their gliding directions per second: 0.023 s⁻¹ on kinesin-1 and 0.003 s⁻¹ on kinesin-14. Microtubules changed their gliding directions on kinesin-1 at a frequency that was seven times higher than that on kinesin-14. On kinesin-1, the change was mainly caused by Collision and changed (0.017 s⁻¹) and the effects of Spontaneous (0.006 s⁻¹), and Pinning were negligible (0.0005 s⁻¹). On kinesin-14, the frequencies of Collision and changed (0.001 s⁻¹) and Spontaneous (0.002 s⁻¹) were almost the same and that of Pinning was also negligible.

According to these results, the collision of the leading tip (II. Collision and changed; Fig. 4B) is the main reason for the change in direction observed in the experiments but not in the numerical simulation. Although the frequency of the Spontaneous event was not zero in the experiments, the low frequency can reasonably explain why no microtubule could bind to a kinesin on pillar B in the simulation.

One possible reason why we observed Spontaneous events in the experiment, but not in the numerical simulation, is the underestimation of the amplitude of the free tip of a microtubule in the simulation. We assumed that the microtubule was tightly clamped to pillars, and the tip could be considered as a cantilever rigidly fixed at the frontmost motor. However, the stalk domain of a kinesin molecule is flexible in the experiment (42), and thus, the tip of microtubule is rather loosely clamped to the pillar, causing a larger fluctuation than that seen in the simulation. To estimate the amplitude of fluctuating tip more accurately, it will be necessary to construct a simulation that considers the elasticity of kinesin molecules.

Investigating the relationship between microtubule velocity and the number or spacing of motors

Figures 5 and 6 (A and B) show the dependence of the microtubule velocity on the number and spacing of kinesin-1 and kinesin-14 motors in the BRB80 buffer. We assumed that only a single kinesin molecule is attached to a nanopillar for both the kinesin-1 and kinesin-14 cases, according to the observed pivoting motion of short microtubules on nanopillars. The velocity was found to be independent of the number of kinesin-1 motors in the range of 3 to 30 motors and spacing of the kinesin-1 motors (Fig. 5 and fig. S6). In contrast, the velocity decreased within the range of 3 to 10 kinesin-14 motors and reached a plateau of over 10 motors (Fig. 6A). On the other hand, the velocity is independent of the spacing for kinesin-14 motors (Fig. 6B).

Fig. 5. Effect of the number and spacing of kinesin-1 proteins on microtubule velocity in BRB80 buffer.

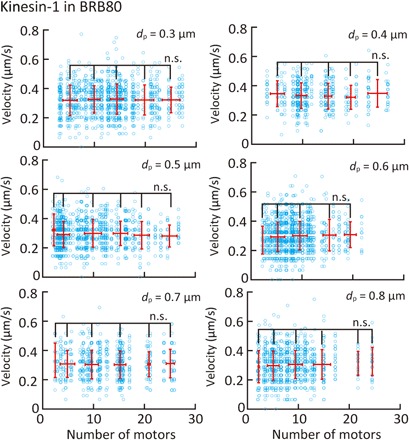
Blue open circles represent individual measurements, and red points represent the average velocity binned into five-motor intervals. Means ± SD; n.s., not significant (Steel-Dwass test).

Fig. 6. Effect of the number and spacing of kinesin-14 proteins on microtubule velocity.

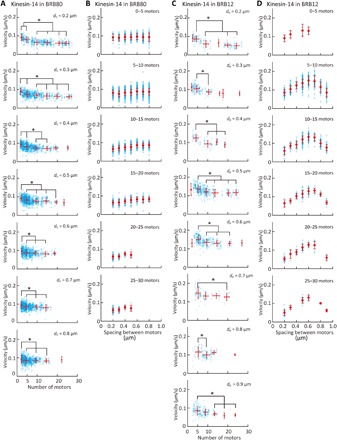
(A and B) Dependence of microtubule velocity on (A) the number of kinesin-14 proteins and (B) the spacing of kinesin-14 proteins in the BRB80 buffer. (A and B) Dependence of the microtubule velocity on (A) the number of kinesin-14 proteins and (B) the spacing of kinesin-14 proteins in the BRB12 buffer. Blue open circles represent individual measurements, and red circles represent the average velocity binned into five-motor intervals. Means ± SD; *P < 0.05 (Steel-Dwass test).

Figure 6 (C and D) shows the dependence of the microtubule velocity on the number and spacing of kinesin-14 motors in BRB12 buffer. Unlike in the BRB80 buffer, in the BRB12 buffer, both the number and spacing of kinesin-14 motors affect the microtubule velocity. In BRB12 buffer, such as in the BRB80 buffer (Fig. 6A), the velocity decreased with an increase in the number of kinesin-14 motors (Fig. 6C).On the other hand, the velocity increased with an increase in the spacing until the spacing reached 0.6 μm and decreased with an increase in the spacing of over 0.6 μm (Fig. 6D).

The relationship between the microtubule velocity and the number of kinesin-1 motors has been examined in previous studies. Bieling et al. (18) reported that, when a truncated kinesin-1 (amino acid residues 1 to 401) was used, the microtubule velocity sharply decreased with an increase in motor density in the case of high motor density (>500 molecules/μm²) and slightly decreased with an increase in motor density in the case of low motor density (<500 molecules/μm²). In our experiments, a truncated kinesin (amino acid residues 1 to 465) was used at a very low-density range owing to the patterning (2 to 58 molecules/μm²) and could not be investigated with a glass substrate. Therefore, our experiment indicates that velocity is independent of the number and spacing of motors at such a low motor density.

The relationship between the microtubule velocity and the number of kinesin-14 motors was also evaluated in a previous study. Furuta et al. (13) revealed that the velocity of kinesin-14 motors was independent of the number of motors in the range of 1 to 4 motors. Lüdecke et al. (14) examined the relationship between the velocity at which a microtubule glides on a kinesin-14–coated surface and the length of the microtubule. They found that the velocity was independent of microtubule length and thus motor number. When Lüdecke et al. performed the assay using >1-μm microtubules on a surface coated with a saturated kinesin-14 motor (i.e., the density of the motor was ≈4000 molecules/μm²) (48), their results indicated that the velocity is independent of motor number for >50 motors. Our results revealed that the velocity decreased from 3 motors to 10 motors and was constant in the range of 10 to 30 motors (Fig. 6, A and C), which fills the gap of motor number between two studies (13, 14). Together, our studies reveal that velocity is independent of motor number in the range of 1 to 3 motors, decreases in the range of 3 to 10 motors, and is again independent at >10 motors.

The dependency of velocity on the number and spacing of kinesin-14 motors also agrees with a previous study (49), which reported that the velocity decreased with increasing kinesin-14 density. Braun et al. attributed the decrease in velocity to the direct interaction (steric hindrance) between motors but not to the indirect interaction between motors bridged by a solid microtubule structure. However, in our system, motors cannot directly interact on the nanopillar array because they are separated by a distance of more than 200 nm, which is more than twice as long as the roughly 60-nm kinesin stalk (50). Therefore, the decrease in velocity with an increasing number and spacing of motors is explained by the indirect interaction between motors through microtubules.

The velocity decreased with an increase in the number of kinesin-14 motors in the range of 3 to 10 motors (Fig. 6, A and C). This can be explained by the greater diffusive motion of kinesin-14 motor domains along a microtubule (34); unlike kinesin-14, kinesin-1 is known as a processive motor. The construct of kinesin-14 that was used in this study has two microtubule binding domains (MTBDs): The first MTBD, which is referred to as the motor domain, is at the C terminus, and the second MTBD is at the N terminus. However, the kinesin-14 motors on the nanopillars could interact with a microtubule only via the first MTBD, because the N terminus was immobilized via streptavidin-biotin binding. Furuta and Toyoshima (34) generated a kinesin-14 construct without the second MTBD by truncating the N terminus and calculated the diffusion coefficient (D = 7.1 × 10⁴ nm²/s) and the mean velocity (v = −20 nm/s) in the BRB12 buffer by the quadratic fit [msd(t) = 2 Dt + v²t² + C], where t is the time and v is the mean velocity. This calculation indicates that the first MTBD of the kinesin-14 motor, compared to kinesin-1 (D = 0.48 × 10⁴ nm²/s, v = 690 nm/s), shows significant diffusive motion along a microtubule (34).

The diffusive motion of kinesin-14 motors implies that the motors hinder each other’s movement during collective transport. When multiple kinesin-14 motors transport a microtubule, a fraction of motors move toward the plus end of the microtubule owing to their diffusive motion, while most of the motors move toward the minus end. According to a previous study, kinesin-14 motors generate a drag force when they are pulled backward (13). This indicates that kinesin-14 motors that move to the plus end hinder the movement of the microtubule by transmitting the drag force through the microtubule. Such an indirect interaction via a microtubule causes the decrease in velocity observed on the nanopillar array.

We also obtained the unexpected dependence of velocity on spacing. The velocity increased with an increase in the spacing of the kinesin-14 motors and reached a maximum at a 600-nm spacing, when the ionic strength was low (Fig. 6D). This result indicates that, although kinesin-14 motors indirectly interfere with each other, the interaction was weakened with increasing spacing of kinesin-14 motors. At a spacing over 600 nm, the velocity decreased with an increase in the spacing of kinesin-14 motors (Fig. 6D). We observed that microtubules sometimes showed stop-and-go motions with the large spacings, causing lower average velocities. The thermal fluctuation of the tip increased with spacing, and the tip frequently touched the substrate. Unlike in low ionic strength buffers, we did not find any dependence of velocity on spacing in high ionic strength buffers (Fig. 6B). This was possibly because the affinity between the kinesin-14 motor heads and microtubules was weak; therefore, kinesin-14 motors did not interact via a microtubule (34).

CONCLUSION

In this study, we proposed a nanopatterning method of kinesin molecules that enables us to control the number and spacing of motors transporting a single microtubule filament. Using the patterned motor, we revealed that both the number and spacing of motors affect the velocity of the microtubule transported by multiple motors in the case of kinesin-14 but not in the case of kinesin-1. As the proposed method is applicable for various motor species such as kinesin-5 (Eg5) and kinesin-7 (CENP-E), it can be a powerful assay platform to study the coordination of motors.

MATERIALS AND METHODS

Proteins

The kinesin-1 sequence from Homo sapiens (amino acid 1 to 465) was ligated into the pET30b (Novagen) plasmid containing an N-terminal His₆ tag and a C-terminal AviTag (Avidity). The AviTag peptide is covalently linked to biotin by Escherichia coli biotin ligase (BirA) (51). The plasmid was transformed into an E. coli Rosetta (DE3) pLysS (Novagen). This construct was a gift from Y. Hiratsuka of the School of Materials Science, Japan Advanced Institute of Science and Technology. The His₆-tagged kinesin-1 was purified by nickel-nitrilotriacetic acid (Ni-NTA) affinity as previously described (52). The kinesin-14 was constructed from Drosophila melanogaster (amino acids 195 to 700) and cloned into the pBirAcm (Avidity) plasmid containing an N-terminal histidine tag and AviTag. The construct was expressed in BL21 (DE3) Star (Novagen) and purified by Ni-NTA affinity as previously described (34). Phosphocellulose (PC) tubulin was purified from porcine brains after 2 cycles of assembly-disassembly and PC chromatography (53) and stored in liquid nitrogen. Fluorophore-tagged tubulin was prepared by adding a 10-fold molar excess of carboxytetramethylrhodamine (TAMRA, C-1171, Invitrogen, Carlsbad, CA, USA) to tubulin for a labeling stoichiometry of 0.40 to 0.70 (54).

Buffers

The experiments were conducted in two types of PIPES-based buffer solutions: (i) BRB80 consisting of 80 mM PIPES, which was adjusted to pH 6.8 by using KOH, 1 mM EGTA, and 1 mM MgCl₂; and (ii) BRB12, which is identical to BRB80 except for its PIPES concentration, which was 12 mM, and MgCl₂ concentration, which was 2 mM. To adjust the kinesin concentration, we used a casein-containing solution (casein buffer) composed of BRB80, 1 mM dithiothreitol (DTT), 100 μM ATP, and casein (0.1 to 0.7 mg/ml). To optimize kinesin-driven microtubule motility, we used a motility buffer with a different composition for the experiments using kinesin-1 and kinesin-14. For kinesin-1, we used the motility buffer consisting of BRB80 or BRB12 supplemented with 3 mM MgCl₂ (4 mM final concentration), 20 mM DTT, 1% 2-mercaptoethanol, casein (0.3 mg/ml), and 1 mM ATP. For kinesin-14, the motility buffer was composed of BRB80 or BRB12, 25 mM potassium acetate, casein (0.7 mg/ml), and 3 mM ATP.

Nanofabrication

Arrays of 50-nm-diameter nanopillars, including variations in the spacing (from 0.2 to 5.0 μm) were fabricated on a silicon wafer with a 1-μm-thick thermal oxide film. The wafers were cleaned in piranha solution (H₂SO₄: H₂O₂ = 7:3) at 80°C for 10 min. Caution: Piranha solution reacts violently with most organic materials and must be handled with extreme care. The positive photoresist (ZEP520A, ZEON) was diluted with an equal volume of anisole and spin-coated onto wafers at 1800 rpm for 60 s, followed by baking at 180°C for 2 min. An organic antistatic compound (Espacer 300Z, Showa Denko) was spin-coated at 1500 rpm for 60 s and baked at 100°C for 60 s. The pattern of the nanopillar arrays was written using an electron beam writer (F7000s-KYT01, Advantest). The Espacer was removed by rinsing the wafer with deionized water. The resist was developed by placing the wafer in the ZED-N50 developer (ZEON) for 140 s. A 3-nm-thick chromium adhesion layer and a 20-nm-thick gold layer were evaporated onto the patterned resist using a thermal deposition machine (VPC-260FI, ULVAC). The resist was removed by soaking the wafer in the ZDMAC remover (ZEON) at 65°C for 10 min, followed by a 10-min sonication in acetone. To protect the nanopillars, the photoresist (S1813, Shipley) was spin-coated onto the wafers at 1500 rpm for 40 s and was baked at 90°C for 2 min. The wafer was diced into flow cell–sized (15 mm × 10 mm) substrates (DAD322, Disco). The resist was removed by soaking substrates in acetone for 10 min, followed by rinsing with isopropyl alcohol and the deionized water. The pillars were visualized by a field-emission scanning electron microscope (SU8020, Hitachi High Technologies). The diameter and spacing of the fabricated nanopillar array were measured with ImageJ software (National Institutes of Health).

Microtubule gliding assay on kinesin-1– or kinesin-14–immobilized gold nanopillars

The substrates with arrays of nanopillars were cleaned in the piranha solution (H₂SO₄: H₂O₂ = 7:3) at 80°C for 10 min, followed by extensive rinsing with deionized water and drying under N₂ flow. Within 1 hour after the cleaning, the substrates were incubated in the SAM solution for ~16 hours with nitrogen gas providing the inert atmosphere. The SAM solution is a mixture of 3 mM 2-[methoxy(polyethyleneoxy)9-12propyl]trimethoxysilane (S25236, Fluorochem) and hydrochloric acid (0.8 ml/liter) in toluene. After SAM treatment, the substrates were rinsed in toluene, ethanol, and deionized water, followed by a 2-min sonication in deionized water and drying in the N₂ flow. The substrates were baked at 120°C for an hour for annealing. The substrates were stored under a nitrogen atmosphere and used within a day.

A flow chamber (15 mm by 5 mm, 3.75-μl volume) was constructed with a coverslip (C030401, Matsunami micro cover glass, Matsunami), and a substrate with SAM-modified gold nanopillars was separated by two stripes of 50-μm-thick double-stick tape (400P50, Kyodo Giken Chemical Co.). First, a solution of streptavidin (0.2 mg/ml; 434301, Thermo Fisher Scientific) diluted in BRB80 buffer was flushed three times into a chamber and was incubated for 5 min, followed by washing with BRB80 buffer three times. The flow chamber was then incubated with biotin-conjugated kinesin (0.1 mg/ml; ≈0.85 μM) in casein buffer for 5 min, followed by washing with casein buffer. Last, microtubules in the motility buffer supplemented with 20 μM paclitaxel and O₂ scavenging system [catalase (36 μg/ml), glucose oxidase (216 μg/ml), and 25 mM d-glucose] were sequentially introduced to observe microtubule gliding. The experiments were performed at room temperature (23° to 25°C).

Evaluation of the number of kinesin molecules attached to the nanopillars

To evaluate the number of kinesin-1 molecules attached to the nanopillars, kinesin-1 molecules were immobilized on pillars with 5.0-μm spacing. Short microtubules (L = 3.55 ± 1.46 μm, n = 9) were prepared by shearing through a 30-gauge syringe needle (90030; Osaka Chemical). A gliding assay was performed in an assay buffer containing 10 μM ATP. For evaluation of the number of kinesin-14 molecules, a gliding assay was conducted in the same manner, except that the assay buffer did not contain ATP.

Microtubule gliding assay on a plane surface

The experiments were performed at room temperature (23° to 25°C). A flow cell was constructed using a plane gold substrate. The flow cell was filled with BRB80 and incubated in streptavidin (1.0 mg/ml) for 3 min. After rinsing the flow cell with BRB80, biotin-conjugated kinesin-1 or kinesin-14 (4.5 μg/ml, ≈36 nM) was introduced and incubated for 3 min before rinsing again. Last, microtubules in the motility buffer supplemented with 20 μM paclitaxel and O₂ scavenging system (see above) were sequentially introduced to observe microtubule gliding. As a control experiment, the microtubule gliding assay on a glass substrate was conducted in the same manner except that the flow cell was incubated with biotinylated bovine serum albumin (1.0 mg/ml; A8549, Sigma) for 3 min before introducing the streptavidin solution.

To evaluate the protein-repellent ability of silane-PEG SAM, the microtubule gliding assay was conducted on a SAM-modified silicon dioxide surface. A flow cell was constructed using a silane-PEG SAM–modified silicon dioxide substrate, and the gliding assay was performed as described in the “Microtubule gliding assay on kinesin-1– or kinesin-14–immobilized gold nanopillars” section.

Imaging

Images were obtained using an Olympus IX73 inverted epifluorescence microscope equipped with an Hg lamp (U-HGLGPA, Olympus), a 100× oil-immersion objective lens (UPlanSApo, numerical aperture of 1.40, Olympus), and a scientific complementary metal–oxide semiconductor camera (ORCA-Flash4.0, Hamamatsu) in conjunction with HCImage (Hamamatsu) software. Rhodamine-labeled microtubules were imaged with a U-FGW filter set (excitation, 530/50; dichroic, 570; absorption 575/infinity; Olympus). The images (1024 pixels × 1024 pixels) were acquired at 0.5-s intervals for 180 to 360 s with a 200-ms exposure time for each image.

To evaluate the number of kinesins on the nanopillars, we used an electron multiplying charge-coupled device camera (iXon Ultra, Andor) in conjunction with iQ3 (Andor) software. Images (512 pixels × 512 pixels) were acquired at 0.1-s intervals for 360 s with a 10-ms exposure time for each image.

Analysis

To measure microtubule velocities, the ends of the microtubules were tracked with the Mark2 image analysis software at 2-s intervals (four frames) for kinesin-1 and 30-s intervals (60 frames) for kinesin-14. To evaluate the number of kinesin molecules on the nanopillars, the distances between the rotation center and the end of the microtubule were measured with ImageJ.

To quantify the alignment of microtubules, we measured the orientation angle of the microtubule using the OrientationJ plugin, an ImageJ plugin. OrientationJ characterizes the orientation angle of a region of interest in an image based on an evaluation of the structure tensor in a local neighborhood (55). The angle of the microtubule with respect to line A is defined as shown in Fig. 2B. Using OrientationJ, the angles were calculated for each pixel of the fluorescence images of the microtubules. The fluorescence images of the microtubules were converted into binary images via Otsu’s thresholding algorithm using ImageJ. Using this binary image of microtubules, we acquired the orientation angle of only a region of microtubules with a custom-written MATLAB algorithm (MathWorks). The distributions of the orientation angle of the microtubules were normalized by the total area of the microtubules, which was measured from binary images of microtubules.

Simulation

The thermal fluctuation of the free tip of the microtubules was simulated using the same method used in our previous work (31). Briefly, we modeled the free tip of a microtubule as a cantilever beam tethered at one end. The flexural rigidity (κ_MT) was set to 0.3 × 10⁻²³ N m², which is the typical flexural rigidity of paclitaxel-stabilized microtubules (56). The length of the free tip (L) was assumed to be equal to the spacing between pillars and set to 0.3 and 1.0 μm. We set the x and y axes as shown in Fig. 3A. The origin of the coordinates was set at the point where the microtubule segment attached to the first pillar. The shape of the microtubule-free segment y(s) was expressed by the following equation

$$y(s)={\displaystyle \sum _{n=1}^{\infty }}\sqrt{\frac{1}{L}}{a}_n{W}_n\left(\frac{s}{L}\right)$$ (2)

Here, s is the path length from the tethered end along the microtubule. W_n(s/L) is expressed as

$$\begin{array}{cc}\hfill W_n\left(\frac{s}{L}\right)=& \frac{-\text{cosh}(q_n)-\text{cos}(q_n)}{\text{sin}(q_n)+\text{sinh}(q_n)}\left(\text{sin}\right(\frac{q_{n}s}{L})-\text{sinh}(\frac{q_{n}s}{L}\left)\right)+\hfill \\ & \text{cos}\left(\frac{q_{n}s}{L}\right)-\text{cosh}\left(\frac{q_{n}s}{L}\right)\hfill \end{array}$$ (3)

where q_n is 1.875 (n = 1), 4.695 (n = 2), 7.855 (n = 3), and (n − 0.5)π (n ≥ 4). The SD of the amplitude a_n was calculated using the following equation

$$\text{var}(a_n)=\frac{k_{B}T}{{\mathrm{\kappa }}_{\text{MT}}}{\left(\frac{L}{q_n}\right)}^4$$ (4)

where k_B is the Boltzmann constant, and T is the temperature in the experiments (298 K).

We numerically solved Eq. 2 using a custom-made algorithm in MATLAB and calculated the probability density function of displacement of the end of the tip (s = L) from the calculation results of simulation that was run 1000 times. In this study, we set n in the range of 1 ≤ n ≤ 12. The result of the numerical analysis is expressed as “Numerical” in Fig. 3.

Separately, we derived an analytical solution of the probability density function of displacement of the end of tip, R(y), from Eq. 2

$$\mathrm{R}(y)=\frac{1}{\sqrt{2\mathrm{\pi }{\displaystyle {\sum }_k^{12}}{\mathrm{\sigma }}_k^2}}\text{exp}(-\frac{y^2}{2{\displaystyle {\sum }_k^{12}}{\mathrm{\sigma }}_k^2})$$ (5)

σ_k is defined by the following equation

$${\mathrm{\sigma }}_k^2=\frac{1}{L}{W}_k\left(\frac{s}{L}\right)\frac{k_{B}T}{{\mathrm{\kappa }}_{\text{MT}}}{\left(\frac{L}{q_k}\right)}^4$$ (6)

The result of this analysis is given in “Analytical” in Fig. 3.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/4/eaax7413/DC1

Fig. S1. Fabrication of the gold nanopillars.

Fig. S2. Fluorescence images of microtubules gliding in the kinesin-14–patterned region on gold nanopillars.

Fig. S3. Pivoting motion of a microtubule driven by a single kinesin motor on a nanopillar.

Fig. S4. Fluorescence images of microtubules on patterned kinesin-1 or kinesin-14.

Fig. S5. Relationship between microtubule angle and the number of kinesin molecules attached to the microtubules.

Fig. S6. Dependence of microtubule velocity on the spacing of kinesin-1 in BRB80.

Movie S1. Microtubules gliding in the kinesin-1–patterned region on the gold nanopillars.

Movie S2. Microtubule at the boundary between the kinesin-1–patterned region on the gold nanopillars and passivated silicon dioxide region.

Movie S3. Microtubules gliding in the kinesin-14–patterned region on the gold nanopillars.

Movie S4. Microtubule at the boundary between the kinesin-14–patterned region on the gold nanopillars and passivated silicon dioxide region.

Reference (42)

View/request a protocol for this paper from Bio-protocol.