Abstract
It is well known that heart failure (HF) typically coexists with atrial fibrillation (AF). However, until now, no clear mechanism has been established that relates HF to AF. In this study, we apply a multiscale computational framework to establish a mechanistic link between atrial myocyte structural remodeling in HF and AF. Using a spatially distributed model of calcium (Ca) signaling, we show that disruption of the spatial relationship between L-type Ca channels (LCCs) and ryanodine receptors results in markedly increased Ca content of the sarcoplasmic reticulum (SR). This increase in SR load is due to changes in the balance between Ca entry via LCCs and Ca extrusion due to the sodium-calcium exchanger after an altered spatial relationship between these signaling proteins. Next, we show that the increased SR load in atrial myocytes predisposes these cells to subcellular Ca waves that occur during the action potential (AP) and are triggered by LCC openings. These waves are common in atrial cells because of the absence of a well-developed t-tubule system in most of these cells. This distinct spatial architecture allows for the presence of a large pool of orphaned ryanodine receptors, which can fire and sustain Ca waves during the AP. Finally, we incorporate our atrial cell model in two-dimensional tissue simulations and demonstrate that triggered wave generation in cells leads to electrical waves in tissue that tend to fractionate to form wavelets of excitation. This fractionation is driven by the underlying stochasticity of subcellular Ca waves, which perturbs AP repolarization and consequently induces localized conduction block in tissue. We outline the mechanism for this effect and argue that it may explain the propensity for atrial arrhythmias in HF.
Significance
In this article, we apply numerical simulations to show that structural remodeling in heart failure is proarrhythmic. Specifically, we show that a disruption in the spatial relationship between calcium signaling proteins leads to an increased sarcoplasmic reticulum load, which promotes arrhythmogenic calcium waves. We show further that in cardiac tissue, these calcium waves induce wave fractionation, which can cause wave break and reentry. Thus, this work presents a mechanistic link between structural remodeling in heart failure and the induction of atrial arrhythmias.
Introduction
Heart failure (HF) is a major health problem and is responsible for tens of thousands of deaths each year (1). The reason for this high morbidity is that HF typically coexists with cardiac arrhythmias such as atrial fibrillation (AF) (2,3). However, despite decades of work, the relationship between HF and the induction of AF is still not well understood. In particular, it is not understood how the subcellular and electrophysiological remodeling that occurs in HF promotes fibrillation on the scale of the whole heart. In the last decade, there has been growing recognition that calcium (Ca) cycling plays a fundamental role in the pathology of HF (4, 5, 6, 7). An important insight from these studies is that HF induces structural remodeling at the subcellular scale that disrupts Ca cycling and consequently cell electrophysiology. In particular, it was pointed out by Gómez et al. (8) that during HF, the ability of L-type Ca channels (LCCs) to trigger Ca sparks from ryanodine receptor (RyR) clusters is substantially reduced. They argued that this was likely due to an alteration of the spatial relationship between LCCs and RyRs, which is caused by structural remodeling. This finding highlighted the importance of the finely tuned spatial relationships between signaling proteins, which are particularly sensitive to the structural perturbations occurring in HF. Subsequent work in the field has shown that HF is indeed associated with substantial structural remodeling that alters Ca cycling and cell electrophysiology (7,9,10). However, it remains unclear how this disruption can perturb Ca cycling in such a way as to promote AF on the tissue scale.
A fundamental difficulty in establishing the link between structural remodeling in HF and the initiation of AF is that the underlying phenomena span a vast range of length and timescales. In particular, HF causes structural rearrangements of proteins at the submicron scale, and it is difficult to assess how these events translate to a tissue-scale arrhythmia. In a recent study, Song et al. (11) showed, using computer modeling, that the extent of the t-tubule (TT) system determined the onset of Ca cycling alternans in ventricular myocytes. This study suggested that spatial remodeling can disrupt the beat-to-beat dynamics of Ca cycling and therefore potentially lead to the induction of cardiac arrythmia. Using a similar approach, we have previously developed a multiscale computational model of an atrial myocyte (12). At the subcellular level, this model accounts for the stochastic dynamics of Ca signaling proteins that are distributed in a three-dimensional (3D) geometry representation of the cell. In this study, we will apply this computational model to explore how structural remodeling leads to changes in Ca cycling homeostasis and cell electrophysiology. Based on this detailed computational model of an atrial myocyte, we have also developed a phenomenological model of Ca cycling that can be implemented in tissue-scale simulations (13). This model allows us to explore the link between subcellular events to the dynamics of several thousand electrically coupled cells. Using this multiscale approach, we investigate the mechanistic link between structural remodeling in HF and the induction of AF in atrial tissue.
The main finding in this study is that structural remodeling in HF can induce distinct electrophysiological changes that are arrhythmogenic. In particular, we show that a disruption of the spatial relationship between LCCs and RyR clusters substantially alters Ca cycling homeostasis in HF cells. These homeostatic changes arise because the distance relationship between Ca signaling proteins determines the balance between Ca extrusion due to the sodium-calcium exchanger (NCX) and Ca entry due to LCCs. Consequently, we find that the relationship between structural remodeling and Ca cycling homeostasis explains several key features of the electrophysiology of HF cells (14). A crucial finding in this study is that structural remodeling induces an increase in the sarcoplasmic reticulum (SR) load, which promotes the formation of Ca waves when the cell is rapidly paced. This is because the majority of atrial cells lack a well-defined TT system. Thus, there is a large pool of RyR clusters in the cell interior that can support Ca wave propagation at elevated SR loads and during rapid pacing. Furthermore, we have applied our phenomenological model of voltage and Ca dynamics to show that when a two-dimensional (2D) sheet of HF cells is rapidly paced, then a planar excitation wavefront tends to fractionate and form multiple wavelets. This wave break arises because of the spatial heterogeneity induced by stochastic Ca waves, which promotes localized conduction block during rapid pacing. Thus, our computational model uncovers a detailed mechanism linking the remodeling of the Ca signaling architecture in HF with the initiation of atrial arrhythmias at the tissue scale.
Methods
A spatially distributed cell model
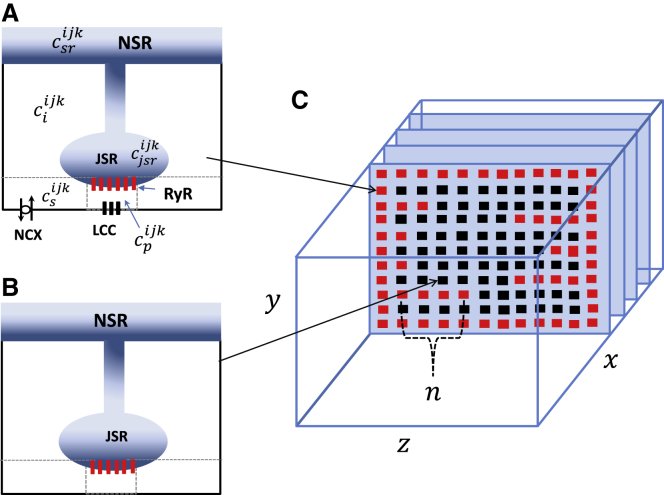
To model the spatiotemporal distribution of Ca in atrial myocytes, we have implemented an established mathematical model developed by Restrepo et al. (15,16), which has been adapted to describe atrial myocytes (12). In this model, the cell interior is divided into an array of compartments that represent distinct intracellular spaces. The Ca concentration within these compartments is treated as spatially uniform, and neighboring compartments are diffusively coupled. We refer to the space in the vicinity of an RyR cluster as a Ca release unit (CRU). Following our previous study (12), we distinguish between compartments that are close to or far from the cell membrane. Therefore, CRUs in the cell can be divided into two groups. The first are the junctional CRUs (Fig. 1 A), which are those units in which the RyR cluster is positioned close to the cell membrane and can interact with membrane-bound LCCs and the NCX. The second type are nonjunctional CRUs (Fig. 1 B), which contain RyR clusters that are located distally from the cell membrane. The RyR clusters within these nonjunctional CRUs are often referred to in the literature as orphaned RyRs. The intracellular compartments that comprise the junctional CRUs are 1) the dyadic junctional space at the CRU located at position i, j, k in our 3D lattice representation of the cell. This space has a Ca concentration and volume vp. This compartment represents the volume of the cell that is in the immediate vicinity of the local RyR cluster, which is roughly a pillbox of 10 nm height and 100 nm diameter. For intact CRUs, this space includes one to five LCCs along with a cluster of RyR channels. In this study, we have fixed the number of RyR channels per cluster to be 50; 2) the submembrane space, with a concentration and volume vs, which represents a volume of space in the vicinity of the dyadic junction. This space is larger than the dyadic junction but much smaller than the local bulk cytosol. For junctional CRUs, we follow Restrepo et al. (15) and take vs to be 5% of the cytosolic volume within a CRU. This volume includes NCX transporters that are regulated by Ca concentrations that vary much faster than the average Ca concentration in the cytosol but much more slowly than the concentration changes in the dyadic junction; 3) the cytosol, with concentration and volume vi, which characterizes the volume of space into which Ca diffuses before being pumped back into the SR via the sarcoplasmic-endoplasmic reticulum calcium ATPase transporter; 4) the junctional SR (JSR), with concentration , which is a protruding synapse-like section of the SR network in which the RyR channels are embedded; and 5) the network SR, with concentration , which represents the bulk SR network that is spatially distributed in the cell. For nonjunctional CRUs, we simply remove LCCs and NCX transporters (Fig. 1 B) because the RyR cluster is located far from the cell membrane where these channels reside. Full model parameters are given in our previous study (12).
Figure 1.
Schematic illustration of the spatial architecture of Ca signaling in an atrial myocyte. Ca signaling and release occurs within dyadic junctions distributed in the 3D volume of the cell. Junctional CRUs close to the cell membrane (A) possess LCCs and NCX channels, whereas nonjunctional CRUs (B) do not have these membrane channels. Here, the superscript ijk denotes the CRU at position i, j, k in a 3D grid representing the cell. (C) The spatial architecture of the cell interior showing TT invaginations along z-planes is displayed. All compartments in the outer boundary and along transverse TT invaginations are treated as junctional CRUs (red squares). To see this figure in color, go online.
The atrial myocyte architecture
In this study, we will apply our spatially distributed network of compartments to model Ca cycling in atrial myocytes. To determine the spatial distribution of signaling units, we rely on recent measurements of the TT distribution in dog atrial myocytes (17). This study reported that roughly 20% of atrial cells had virtually no TTs, whereas the remainder exhibited a sparse distribution of TTs that was significant but substantially less than that measured in ventricular myocytes. This result is consistent with a study of Frisk et al. (18), who found that almost 58% of rat atrial myocytes were devoid of TTs, 32% had a sparse yet significant TT system, and the remaining 10% had a fully developed TT system comparable to ventricular myocytes. This finding indicates that TTs are present in atrial myocytes in varying degrees, with the bulk of the cells dominated by Ca signaling close to, but not restricted to, the cell boundary.
To incorporate these experimental observations in the model, we will allow the cell membrane to invaginate into the cell by designating junctional CRUs along linear extensions from the cell membrane. As illustrated in Fig. 1 C, we place CRUs in 3D along three axes as shown. The transverse plane is oriented along the y-z axis and will be composed of an array of 16 × 16 regularly spaced CRUs. We then stack 40 planes along the longitudinal (x) direction to form the full atrial myocyte. To model the TT structure in these cells, we first identify CRUs that are on the outer membrane of the cell as junctional CRUs. To incorporate TTs, we first pick a coordinate on the x-y plane (lx, ly). TTs are then generated by designating n sites in the z direction as junctional CRUs (Fig. 1 C). Specifically, we insert a TT with a fixed probability ptt = 0.25 so that only a fraction of transverse sites serve as points of TT invagination. Here, we assume that the number of junctional CRUs along a TT, denoted by n, is taken from an exponential distribution P(n) = αexp(−αn) with average . Thus, we call a random number from this distribution and then take n to be the nearest integer. Also, if n > 14, then we set n = 14 so that the TT at that position extends fully into the cell. In this study, we will set for most simulations because it is known that the majority of atrial myocytes exhibit a sparse TT system. To assess the robustness of our simulations, we will also vary to analyze the sensitivity of our results to the degree of TT invagination.
A phenomenological model of Ca cycling
To model atrial tissue, we apply our recently developed phenomenological model of Ca cycling in atrial myocytes (13). In this model, we keep track only of the population of Ca sparks in the cell. To model Ca release, we denote ni(t) to be the number of nonjunctional CRUs at which Ca is being released because of a Ca spark at time t. Similarly, we tally the number of sparks at junctional CRUs denoted as nb(t). Ca sparks are formed and extinguished in their respective volumes according to the reaction scheme
| (1) |
| (2) |
where 0 denotes an “off” cluster that is shut and 1 denotes an “on” cluster at which Ca is being released because of a spark. The rate at which Ca sparks are activated at nonjunctional and junctional clusters is given by αi and αb, respectively, and with corresponding extinction rates βi and βb. The time evolution of the number of sparks at Ni nonjunctional CRUs is modeled according to
| (3) |
where
| (4) |
and
| (5) |
and where B(p, n) is a random number picked from a binomial distribution with success probability p and number of trials n. The time evolution of the number of junctional sparks nb is modeled in a similar fashion. Spark activation and extinction rates are taken to be phenomenological functions of Ca cycling variables as developed previously (13). Details of the spark rate parameters are given in the Supporting Materials and Methods.
Action potential model
To model rapid pacing, we have integrated our Ca cycling equations with the major ion currents from the Grandi et al. (19) human atrial cell model. In particular, we incorporate their ion current formulations for the fast sodium current (INa), the rapidly activating delayed rectifier K+ current (IKr), the slowly activating delayed rectifier K+ current (IKs), the ultrarapid delayed rectifier K+ current (IKur), the inward rectifier K+ current (IK1), the transient outward K+ current (Ito), the Na+/K+ exchange current (INaK), and finally, the sodium-calcium exchanger current (INaCa). All Ca cycling components used in the Grandi model have been replaced either by the spatially distributed or phenomenological model described above.
Simulations of 2D cardiac tissue
In this study, we will explore the dynamics of electrical propagation in a 2D tissue of cells described by our phenomenological model of HF. To model electrical propagation, we apply the cable equation
| (6) |
where Cm = 1 μF/cm2 is the membrane capacitance, DV = 2.5 × 10−4 cm2/ms is the effective voltage diffusion coefficient, and Iion is the total transmembrane current. The cable equation is integrated using an operator splitting approach (20), with a space step Δx = 0.015 cm and with a variable time step in the range dt = 0.01–0.1 ms.
Results
A simple model of structural remodeling in HF
In this section, we will apply our 3D spatially distributed model to understand how Ca cycling is altered in HF atrial myocytes. To guide our computational approach, we outline the features of Ca signaling that will inform the model construction. As a starting point, we first review the work of Peskoff and Langer (21), who analyzed the spread of Ca around an open LCC. In particular, they simulated the spatial distribution of Ca after a typical LCC opening of duration ∼1 ms and current ∼0.3 pA and in the absence of a local RyR flux. Using a realistic distribution of Ca buffers in the vicinity of the dyadic cleft, they found that the Ca concentration falls off rapidly as a function of distance from the LCC. In effect, within 50 nm of the LCC, the Ca concentration rises to a maximum of ∼10 μM, whereas at a distance of 200 nm, the maximal Ca concentration reached is small and close to the resting diastolic Ca ∼0.1 μM. Now, it is known that RyR open probability is sensitive to cytoplasmic Ca concentration, with a half-maximal activation constant in the range 1–5 μM and with a steep Hill coefficient between 2 and 4 (22). Therefore, the probability that an LCC opening triggers RyRs will be highly sensitive to the distance between these channels. Thus, during structural remodeling in HF, it is expected that local signaling between LCCs and RyRs will be disrupted. This observation is confirmed by a classic study by Gómez et al. (8), who demonstrated that Ca release in HF is substantially reduced because of the reduction in the coupling fidelity between LCCs and RyRs. It was argued that this effect is due to the increased distance between LCCs and RyRs, which is caused by the structural remodeling in HF. This work is consistent with a recent study by Lipsett et al. (23), who showed that the distance between LCCs and RyRs increases in a rat model of HF. In related work (9,24), several groups have shown that the density of functional LCCs in the TT system is reduced in HF, which may result from the migration of LCCs from intact dyads. Furthermore, recent evidence of RyR “dispersion” during HF (25,26), including break-up of RyR clusters, suggests an additional mechanism that may alter the signaling between LCC and RyR. Overall, there is ample evidence that in HF, the geometric relationship between LCCs and RyRs is altered in a manner that reduces Ca signaling fidelity.
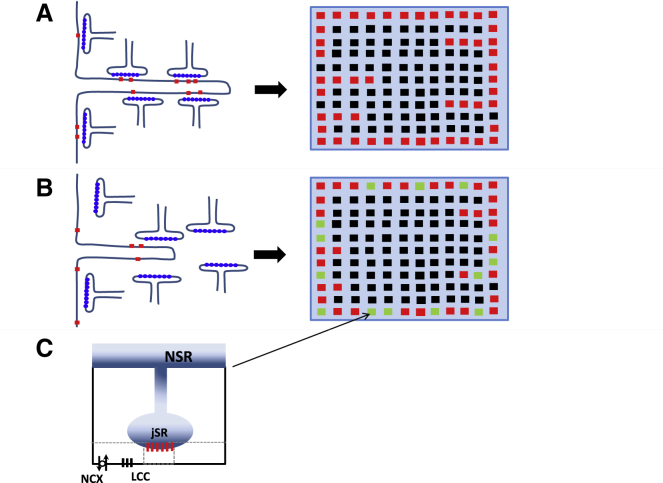
To incorporate these experimental observations, we will model HF by disrupting the spatial relationship between LCCs and RyRs. Under normal conditions, we expect that most dyadic junctions are intact, with normal signaling between LCCs and RyR clusters in the same dyadic junction (Fig. 2 A). Structural remodeling in HF (Fig. 2 B) will then lead to an increase in the average distance between these channels because the JSR is likely to be repositioned with respect to the cell membrane and/or LCCs and RyRs migrate away from each other. Finally, we also expect TTs to retract in HF so that LCCs are pried away from their RyR cluster pair. This effect is likely to be small in atrial myocytes because the TT system is sparse at baseline. However, given the pronounced heterogeneity of the TT system observed in these cells, we will explore how signaling is altered by modifications of the average TT penetration depth. To model the loss of coupling fidelity, we introduce a population of CRUs in which LCCs are moved from the dyadic space to the submembrane space. The repositioned LCCs then deliver Ca into a much larger volume so that the rise in local Ca is less effective in triggering a Ca spark at the nearest RyR cluster. To implement this repositioning of LCCs, we will divide the junctional CRUs in the cell into two distinct populations. For each junctional CRU, we will label that CRU as “intact” with probability q and “nonintact” with probability 1 − q. Intact junctional CRUs will then have their LCCs placed within the dyadic junction, whereas nonintact CRUs will have their LCCs placed within the submembrane space. This is illustrated in Fig. 2 B, in which the population of junctional CRUs can be labeled red or green depending on whether they have been designated intact or nonintact, respectively. Hereafter, we will refer to the variable q as the coupling fidelity, and it will serve as the key parameter to assess the effect of structural remodeling on Ca cycling. Finally, because structural remodeling in HF is associated with a reduction in TTs, we will also consider variations in the average penetration depth . Thus, we will decrease to simulate an HF cell with a reduced TT system.
Figure 2.
Illustration of Ca signaling proteins under normal (A) and HF (B) conditions. In HF, the close positioning of LCCs and RyR clusters is disrupted because JSR compartments are pried away from the cell membrane and LCCs migrate outside of the dyadic junction. In (A) and (B), red squares denote junctional CRUs, black squares are nonjunctional CRUs, and green denotes nonintact junctional CRUs. In nonintact CRUs, LCCs are placed in the submembrane space rather than the dyadic junction (C). To see this figure in color, go online.
Ca cycling homeostasis during rapid pacing
In this section, we investigate how Ca cycling homeostasis depends on the coupling fidelity between LCCs and RyR clusters. As a starting point, we first compute the global Ca transient as the average Ca concentration in the cytosol for all CRUs in the cell. This quantity is defined as
| (7) |
where N is the total number of CRUs in the cell and the summation is over all CRUs. To achieve steady state, the cell is paced for 50 beats at a fixed cycle length of CL = 400 ms. In this model, we will consider spatially distributed TTs with an average penetration depth = 2, so that the cell has a randomly generated sparse array of TTs. In Fig. 3, A and B, we plot the steady-state Ca transient and the voltage as a function of time for high (q = 0.9) and low (q = 0.4) coupling fidelity. Our results show that at steady state, both the diastolic Ca levels and the action potential duration (APD) increase with a reduction in coupling fidelity. This observation is consistent with the experimental work of Yeh et al. (14), who observed a similar rise in diastolic Ca, along with a prolongation of the APD, in HF dog atrial myocytes compared to normal myocytes. To proceed, we note that because the TT system is sparse in these cells, the bulk of the cell interior is accordingly composed of mostly nonjunctional CRUs. Because these junctions are crucial for the formation of cell-wide Ca wave activity, we will track the average Ca concentration at nonjunctional JSR compartments. This quantity is defined as
| (8) |
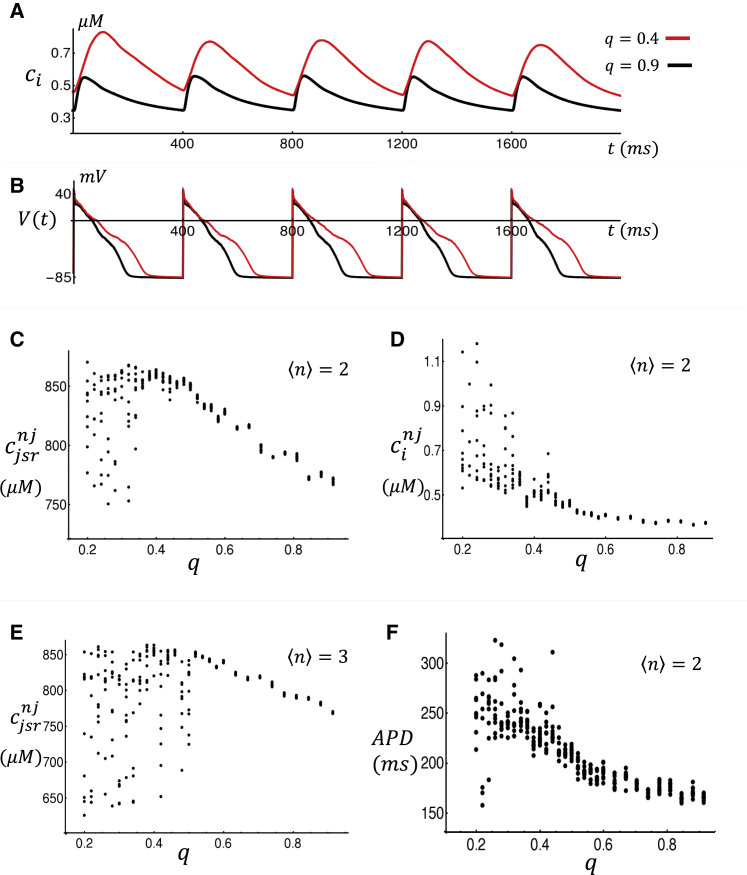
where Nnj is the number of nonjunctional JSRs and the summation is over these compartments. Similarly, we can track the average cytosolic Ca concentration at nonjunctional CRUs, which we denote here as . In Fig. 3 C, we plot at the beginning of each CL for the last 10 beats after pacing for 50 beats. This simulation is done for a range of q, and the steady-state is plotted as a function of q. Here, we find that as the coupling fidelity is reduced from q ∼ 0.9 to q ∼ 0.4, the average JSR load increases from ∼ 750 μM to ∼ 850 μM. For coupling fidelity below a critical value qc ∼ 0.4, we find that the JSR load fluctuates substantially from beat to beat in a manner that increases with decreasing coupling fidelity. Similarly, in Fig. 3 D we show the steady-state diastolic Ca at nonjunctional CRUs at the beginning of each beat. Here, we find that diastolic Ca also rises with decreasing q and then fluctuates abruptly below qc. In Fig. 3 E, we consider a cell model with more TTs by setting = 3. In this case, we find similar behavior but with the critical transition occurring at a larger value of qc ∼ 0.5. Finally, in Fig. 3 F we show the steady-state APD for the last 10 beats as a function of q, showing that APD increases with decreasing q and then exhibits aperiodic beat-to-beat fluctuations below qc.
Figure 3.
(A) Average Ca concentration ci in the cytosol for high and low coupling fidelity. The concentration ci is computed as the average diastolic Ca within all CRUs in the cell. (B) The corresponding voltage time course is shown. In these simulations, the last five beats are shown after pacing for 50 beats. (C) Average JSR load for nonjunctional CRUs as a function of coupling fidelity q is shown. Concentration is measured at the beginning of each beat. Concentrations shown are for the last 10 beats after pacing for 50 beats. (D) The average cytosolic Ca concentration at the beginning of each beat at nonjunctional CRUs is shown. (E) shows the same computation as in (C) but with a more extensive TT system, with = 3. (F) APD vs. coupling fidelity q is shown. Parameters are the same as those used in (C). To see this figure in color, go online.
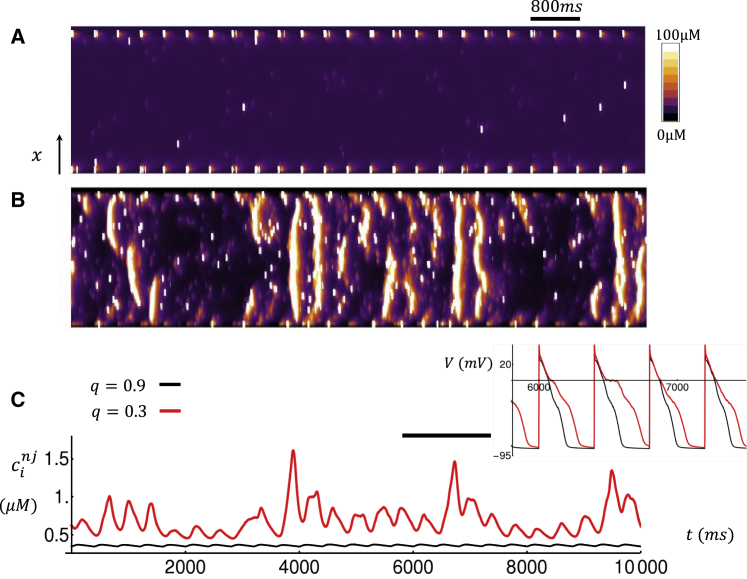
To uncover the underlying mechanism for beat-to-beat fluctuations below qc, we have plotted a linescan image for the last 25 beats after pacing to steady state for 50 beats. In Fig. 4 A, we plot the Ca concentration within the dyadic junction as a function of time along a line oriented in the longitudinal direction and passing through the cell center. In this simulation, we set q = 0.9 and observe that Ca release occurs at CRUs mostly at the cell boundary because we have simulated a relatively sparse TT density. In Fig. 4 B, we show the corresponding linescan and Ca transients for the case q = 0.3. Here, we find that at steady state, Ca release occurs in the cell interior via propagating Ca waves that occur intermittently in between paced beats. In Fig. 4 C, we also show the average cytosolic Ca concentration at nonjunctional CRUs as a function of time. Here, we observe that for q = 0.9, the average Ca concentration is small because only a few Ca sparks are recruited in the cell interior. On the other hand, for q = 0.3, we see large increases in average Ca concentration due to the propagation of Ca waves in the cell interior. Thus, for q < qc, we find that Ca waves are nucleated in the cell, and this is what causes the large fluctuations in the steady-state SR load, diastolic Ca, and APD observed in Fig. 3, C–E.
Figure 4.
Simulated linescans and Ca transients for (A) high (q = 0.9) and (B) low (q = 0.3) coupling fidelity. The linescan is taken along the longitudinal direction at the center of the cell. The cell is paced for 50 beats, and the linescans for the last 25 beats are shown. (C) The average cytosolic Ca concentration at nonjunctional CRUs is shown. Inset shows the corresponding voltage time course during the time interval indicated by the horizontal black line. To see this figure in color, go online.
Mechanism for SR loading
The main finding of our HF atrial cell model is that decreasing the fraction of intact junctional CRUs leads to a significant loading of the SR at steady state. To uncover the underlying mechanism for this SR loading, it is necessary to analyze the conditions for Ca cycling homeostasis during pacing. A basic requirement for homeostasis is that at steady state, the total Ca entry into the cell via LCCs should equal the total Ca extrusion due to NCXs. To quantify this balance of fluxes, let us define the quantity
| (9) |
where T is the cycle length and JCa is the Ca flux into the cell because of LCCs. This quantity gives the total number of Ca ions that enter the cell through LCCs at beat n. Similarly, we can define
| (10) |
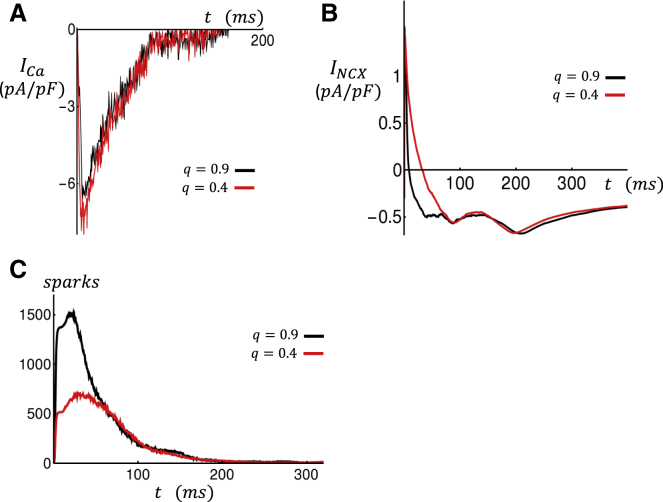
as the total amount of Ca ions extruded by the NCX Ca ion flux JNCX. At equilibrium, the average Ca entry for each beat must be equal to the average Ca extrusion because if this does not hold, then the cell will either accumulate more Ca or be further depleted. Formally, this requirement can be written as , where denotes the average over many beats at steady state. To assess how this balance of Ca fluxes is changed by structural remodeling, we will compute how the whole-cell Ca current ICa ∝ JCa and INCX ∝ JNCX are altered as a function of coupling fidelity q. In Fig. 5 A, we plot the whole-cell ICa current over one paced beat for the case q = 0.9 (black line) and q = 0.4 (red line). In this simulation, all initial Ca concentration variables are identical, and only the coupling fidelity q is changed. Here, we find that there is an increase of ∼15% of the integrated ICa current when q is reduced from 0.9 to 0.4. Similarly, in Fig. 5 B we have plotted the whole-cell INCX and find that the total Ca extrusion over one beat is reduced by ∼15%. These results indicate that, keeping all variables fixed, a reduction in the coupling fidelity leads to an increase in Ca entry into the cell and, at the same time, reduces Ca extrusion. This result indicates that for this beat, QCa(1) > QNCX(1), so there will be a net Ca entry into the cell.
Figure 5.
Time course of membrane currents measured over one paced beat. Black and red traces correspond to high (q = 0.9) and low (q = 0.4) coupling fidelity. All initial conditions are identical for both simulations. (A) Whole-cell ICa is shown. (B) Whole-cell INCX is shown. (C) The total number of Ca sparks in the cell is shown. To see this figure in color, go online.
To explain the dependence of the whole-cell LCC and NCX on the coupling fidelity q, it is necessary to measure the number of Ca sparks in the cell. In Fig. 5 C, we plot the total number of active Ca sparks in the cell as a function of time for the simulations shown in Fig. 5, A and B. In this simulation, the number of open RyRs in all junctions is computed, and a spark is counted at that unit if the number of open channels exceeds 10. Indeed, when q is reduced, the number of Ca sparks recruited is decreased substantially because the population of intact junctional CRUs is reduced. This computation indicates that the average Ca concentration seen by LCCs in the cell is reduced because of the lower number of recruited Ca sparks. Now, because LCCs are inactivated in a Ca-dependent manner, then a reduction in q leads to an increase in the total ICa. Similarly, Ca extrusion due to INCX is also reduced because Ca extrusion due to NCX transporters increases in proportion to the local Ca concentration. This result is not surprising because the average distance between a Ca spark location and the nearest NCX transporter is increased because the number of sparks in the cell is reduced. Thus, the loss of flux balance QCa(1) > QNCX(1) is caused by the reduced number of Ca sparks recruited in the cell because of the loss of coupling fidelity between LCCs and RyR clusters.
Ca cycling homeostasis in response to a reduction in coupling fidelity
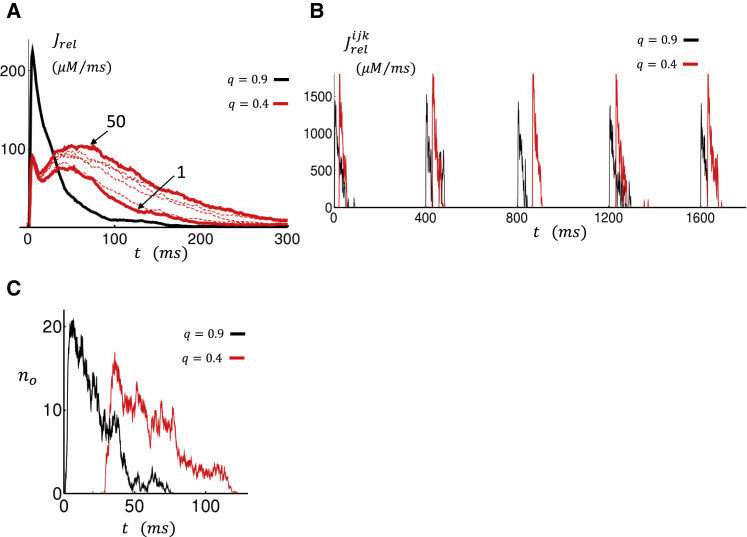
A reduction in coupling fidelity between LCCs and RyR clusters yields a larger inward ICa and less outward INCX. Therefore, the Ca content in the cell will rise until flux balance is achieved. For this to occur, the Ca released into the cell must increase to reduce ICa via Ca-induced inactivation or increase Ca extrusion by increasing the Ca at the vicinity of NCX transporters. In Fig. 6 A, we plot the total Ca flux from the SR, denoted as Jrel, for both high and low coupling fidelity. The black line shows the total current flux at steady state after 50 paced beats for the case q = 0.9. The red lines show the current flux on the first beat and at the 50th beat for the case q = 0.4. In this case, we observe that the Ca current flux from the SR gradually increases as the SR load builds in the cell. Computing the integrated flux reveals that the amount of Ca released in the cell over one beat, at steady state, is roughly double for q = 0.4 compared to q = 0.9. Thus, even though the coupling fidelity is reduced, the total amount of Ca released from the SR is larger because of the increase of SR load. Indeed, we find that the increased SR release reduces ICa due to Ca-induced inactivation and leads to an increased outward INCX so that at steady state, flux balance is achieved.
Figure 6.
(A) Total Ca flux from the SR (Jrel). Black line corresponds to flux at the 50th beat for the case q = 0.9. Solid red line denotes flux for the first and 50th beat for the case q = 0.4. Dashed lines show flux at intervals of 10 beats. (B) Local Ca flux from the SR at a specific junction is shown. Black trace corresponds to an intact junctional CRU for the case q = 0.9. Red trace corresponds to a nonintact junctional CRU for the case q = 0.4. In this CRU, LCCs are placed at the submembrane space. (C) The number of open RyRs (no) as a function of time averaged over the last 10 beats after pacing for 50 beats is shown. To see this figure in color, go online.
In Fig. 6 A, we notice that for low coupling fidelity, the steady-state SR flux peaks at roughly ∼50–80 ms, which is substantially slower than the high coupling fidelity case, in which the SR flux peaks at ∼10 ms after the action potential (AP) upstroke. To understand the underlying mechanism for this slowed release, in Fig. 6 B we plot the local Ca flux at a specific CRU in the cell. In this simulation, we plot the last five beats after pacing to steady state for 50 beats. The black line corresponds to the case q = 0.9, in which the CRU shown has LCCs in the dyadic junction. Here, we see that the local Ca release occurs immediately after the AP upstroke because LCC openings rapidly triggered RyR channel openings. The red line shows the steady-state current flux in the case in which q = 0.4 and the CRU chosen has LCCs in the submembrane space. Here, we observe that Ca sparks are still recruited, but they are delayed by ∼30–80 ms. To quantify this effect more clearly, we have computed the average number of open RyR channels at that junction as a function of time. In Fig. 6 C, we plot the number of open RyR channels averaged over 10 beats after pacing the cell for 50 beats. Here, we find that on average, the local Ca release due to RyRs is delayed. This effect can be explained by the fact LCCs are placed in the larger submembrane space, where the change of the local Ca concentration varies more slowly. Thus, at the elevated SR loads, Ca sparks can be recruited at nonintact junctions but with a delay due to the increased distance between the LCCs and RyR clusters.
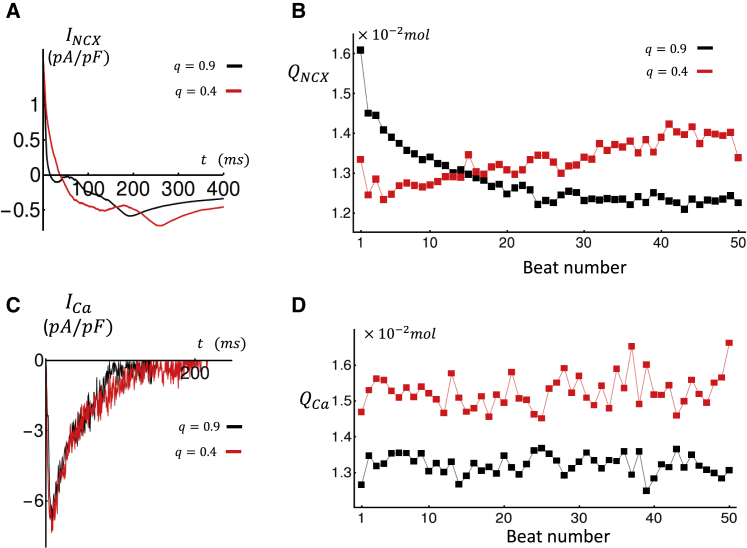
To evaluate the electrophysiological consequences of the slowed SR Ca release, in Fig. 7 A we show INCX at steady state after pacing for 50 beats. Indeed, we observe that outward INCX peaks later in the AP because the current mirrors the delayed Ca release from the SR. This change in the time course of INCX promotes APD prolongation and therefore explains the increase in APD observed in Fig. 3 B. In Fig. 7 B, we show the beat-to-beat evolution of the total Ca that is extruded during one paced beat QNCX(n) for the case q = 0.9 (black) and q = 0.4 (red). In these simulations, we observe that on the first beat, QNCX(1) is larger for high coupling fidelity. However, the Ca extrusion for q = 0.4 rises thereafter and exceeds that of the high coupling fidelity case after 15 beats. This occurs because of the gradual Ca loading and the increase number of delayed sparks recruited in the cell. In Fig. 7 C, we plot the steady-state ICa. Here, we find that the whole-cell ICa peak is essentially identical in the high and low coupling case. However, total Ca entry for q = 0.4 is larger because of the prolonged APD. In Fig. 7 D, we show the beat-to-beat evolution of QCa(n), illustrating that total Ca entry is larger for the case q = 0.4. Examination of Fig. 7 C shows that the increased Ca entry at steady state is mainly due to the larger APD.
Figure 7.
(A) Steady-state INCX measured at the 50th paced beat. (B) Beat-to-beat evolution of total Ca extrusion QNCX is shown. (C) Steady-state ICa measured at the 50th paced beat is shown. (D) Beat-to-beat evolution of total Ca entry QCa is shown. To see this figure in color, go online.
Arrhythmogenic consequences of subcellular Ca waves
Phenomenological model of HF cells
The key finding of our spatially distributed model is that a reduction in coupling fidelity necessarily leads to a marked increase in SR load. Furthermore, below a critical coupling fidelity qc, the SR load rises to a level at which Ca waves begin to propagate in the cell interior. In a previous study, we showed that these Ca waves are mostly nucleated at junctional CRUs and then proceed to spread via calcium induced calcium release at nonjunctional CRUs in the cell interior (12). To model the effect of these waves in cardiac tissue, we have previously developed a phenomenological model of Ca cycling in atrial myocytes (13). In this approach, Ca release from the SR is modeled by keeping track only of the number of Ca sparks recruited in the cell. This is achieved by developing a set of phenomenological equations that describe the dynamics of the number of junctional and nonjunctional sparks. This approach captures the main features of the Ca fluxes at the whole-cell level but lacks the detailed spatial resolution of the 3D compartment model. Full details of the model structure are given in the Supporting Materials and Methods. Here, we describe the key features of the model relevant to describing structural remodeling in HF.
Following our spatially distributed model, we note that during the AP, Ca sparks are recruited at intact junctional CRUs because of LCC openings. Therefore, the effect of structural remodeling will be to effectively reduce the number of intact CRUs at which LCC-induced sparks can occur. Also, we observe that spark recruitment is delayed because more Ca sparks occur later in the AP. To incorporate these two effects, we will make the spark recruitment rate at junctional CRUs (αb) obey a phenomenological form
| (11) |
where is the steady-state spark rate and τq is a delay time constant. The steady-state spark recruitment rate will have the form
| (12) |
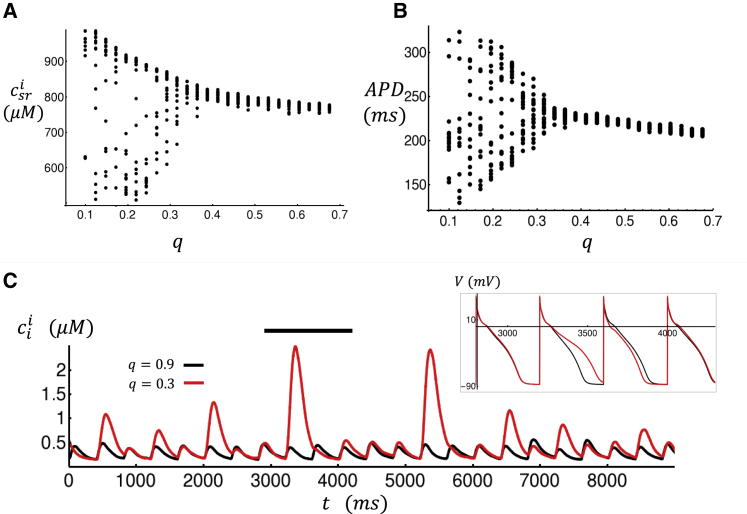
where a is a proportionality constant, q is the fraction of intact junctional CRUs, and ICa is the whole-cell L-type Ca current. Also, here csrb denotes the average Ca concentration in the SR of junctional CRUs, and Φ(csrb) gives the SR load dependence of the spark recruitment rate. The rationale for this choice is that it is well known that Ca release is graded with respect to the whole-cell ICa (27). Therefore, the recruitment rate of sparks at junctional CRUs will be approximately proportional to the magnitude of ICa. Also, because the number of intact junctional CRUs is reduced by a factor q, then we simply scale down the recruitment rate by the same factor. To model the delay time for spark activation, we use a simple phenomenological form in which τq = τ0 + (τ1 − τ0)q and where τ0 ∼ 45 ms and τ1 ∼ 5 ms, which are chosen to approximate the time course of the total RyR flux (Jrel) for different values of q. In Fig. 8 A, we plot the average SR load at nonjunctional CRUs as a function of q. In this simulation, we pace the cell for 100 beats and then plot the SR load for the last 20 beats. Indeed, we find that as q is reduced, the steady-state average SR load at nonjunctional CRUs increases. In Fig. 8 B, we plot the corresponding APD, which also increases with decreasing coupling fidelity. In Fig. 8 C, we show the Ca transient in the cell interior for the case q = 0.9 and q = 0.3. Indeed, we find that large intermittent Ca release events occur in the cell interior for the case q = 0.3, whereas Ca release is small and periodic for q = 0.9. In the phenomenological approach, these intermittent Ca release events arise from the interaction between nonlinear dynamics of Ca spark recruitment and stochasticity. To ensure that these beat-to-beat variations match the detailed model, we have computed the statistics of APD fluctuations for the case q = 0.3. In the detailed model, APD varies from beat to beat and also depends on the cellular structure. Thus, we generate a cell structure and then compute the average APD for the last 20 beats after pacing to steady state. The resulting average is the beat-to-beat average, which is denoted as . Once this average is computed for a given cell structure, we then average over different cell realizations and compute the average . The average APD over 10 cell realizations is given by = 241 ms with a standard deviation of = 73 ms. Our phenomenological model is averaged over 50 beats at steady state, and we find that = 259 ms with σ = 68 ms. Thus, the magnitude and fluctuations of the phenomenological model are comparable to those of the detailed model. To summarize, our phenomenological model reproduces the increase in SR load with decreasing coupling fidelity and the emergence of large intermittent Ca release events due to subcellular Ca waves.
Figure 8.
Phenomenological model of subcellular Ca in HF atrial myocytes. (A) Average nonjunctional Ca concentration in the SR at steady state as a function of parameter q is shown. Points shown correspond to the last 20 beats after pacing to steady state. (B) The corresponding APD is given. (C) Average Ca concentration for nonjunctional sites for the case of high and low coupling fidelity is shown. The inset shows the corresponding voltage time course for the duration indicated by the horizontal black line. To see this figure in color, go online.
Paced cardiac tissue
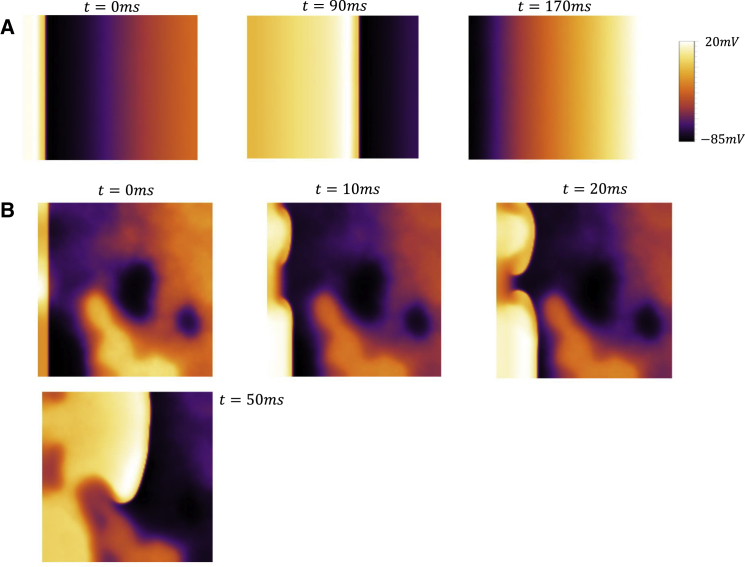
To explore the dynamics of cardiac tissue, we simulate a 2D sheet of 170 × 170 cells described by our phenomenological atrial cell model. In this simulation, we will explore the dynamics of planar wave propagation by pacing a vertical strip of size 10 × 170 on the left edge of the 2D sheet and treating all cells as identical so that cell-to-cell variations arise solely because of stochastic spark recruitment. In Fig. 9 A, we show snapshots of planar wave propagation in a homogeneous tissue of cells when q = 0.9. In this simulation, we pace our 2D tissue at CL = 300 ms for 40 beats. The images shown correspond to snapshots of the voltage distribution at three times after the 20th paced beat. In this simulation, we observe that the wavefront and waveback are spatially uniform for all beats. Thus, although the number of sparks recruited at each cell is stochastic, electrotonic coupling dampens the cell-to-cell differences, and the resulting electrical propagation is spatially homogeneous. In Fig. 9 B, we show snapshots of the membrane voltage at four time intervals after the 16th paced beat in the case in which q = 0.3. Here, we find that after several beats, the planar wavefront emanating from the left edge becomes irregular and fractionates to form a spiral wave. In this regime, we find that during rapid pacing, a planar wavefront develops conduction abnormalities that eventually lead to localized conduction block. Once this occurs, reentrant patterns are then formed in the system that coexist with the periodic pacing emanating from the left edge.
Figure 9.
Propagation of a planar wave on a tissue of 170 × 170 cells. The tissue is paced by stimulating a vertical strip of size 10 × 170 on the left edge of the square tissue. (A) Voltage snapshots at the indicated times after the 20th paced beat for cell model with q = 0.9 are shown. (B) Voltage snapshots at the indicated times after the 16th paced beat for q = 0.3 are shown. To see this figure in color, go online.
Mechanism for planar wave instability
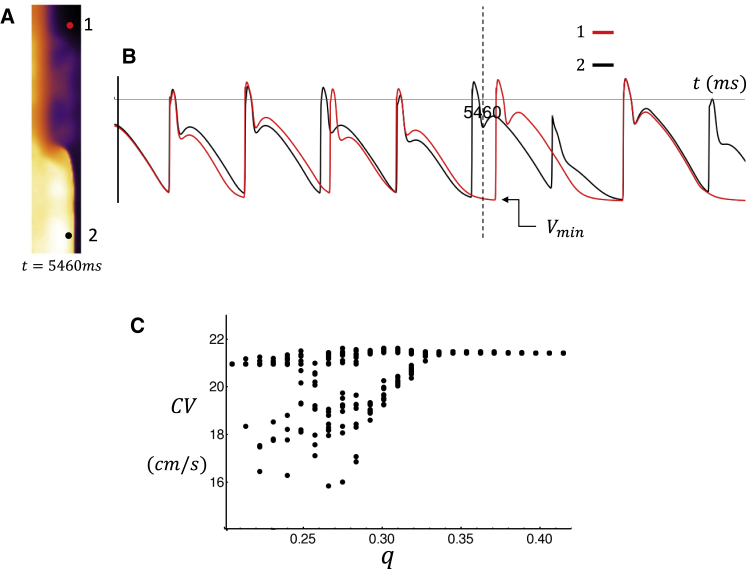
To uncover the precise mechanism for wave break, we pace a thin vertical strip of tissue (lx = 40, ly = 200) along the left edge. In Fig. 10 A, we show a snapshot of the spatial distribution of voltage after the 18th beat (t = 5460 ms) and for which we have set the coupling fidelity at q = 0.3. In this case, we observe that on this beat, wavefront propagation is spatially heterogeneous. In Fig. 10 B, we show the corresponding voltage time course for two cells at locations 1 (lx = 30, ly = 180) and 2 (lx = 30, ly = 20). Here, a horizontal dashed vertical line indicates the time at which the spatial snapshot was taken. An examination of the voltage time course at these two cells reveals that there is substantial variability in the AP repolarization dynamics. This difference is due to the fact that the timing and magnitude of triggered waves are stochastic. Therefore, regions that are far apart will exhibit independent fluctuations of the AP because of perturbations from the local population of cells. Fig. 10 B also indicates that these AP differences are sufficient to induce spatial variations in the conduction velocity (CV). This is because the time course of AP repolarization determines the maximal diastolic voltage, which we will denote as Vmin (indicated in Fig. 10 B), before the next AP upstroke. Now, it is well known that CV is highly sensitive to Vmin such that fluctuations in AP repolarization can induce substantial variations in CV. In fact, in the 2D simulations described in Fig. 9 B, these fluctuations were sufficient to induce localized conduction block, which led to the formation of spiral waves in the tissue. To assess the sensitivity of CV to coupling fidelity, we have paced a cable of 200 cells and measured the beat-to-beat fluctuations in CV. To measure CV, we compute the time to travel from the 20th cell to the 180th cell on the cable. In Fig. 10 C, we plot the CV along the cable for the last 10 paced beats after pacing our cable for 40 beats. Here, we find that indeed, as q is reduced, larger beat-to-beat variations of CV are induced on the cable. This result demonstrates that stochastic perturbations of the AP time course can induce CV variations that can drive wave break and reentry in atrial tissue.
Figure 10.
(A) Snapshot of voltage on a strip of tissue of size (lx = 40, ly = 200) paced at the left edge. The image shown is at the time indicated during the 18th beat. (B) The voltage time course at points 1 (lx = 30, ly = 180) and 2 (lx = 30, ly = 20) is shown. Vertical dashed line corresponds to the time of snapshot shown in (A). (C) CV as a function of q measured on a cable of 200 cells is shown. CV is measured for the last 15 beats after pacing for 50 beats. To see this figure in color, go online.
Discussion
Structural remodeling in HF leads to an increase in SR Ca content
A main finding in this study is that HF induces structural remodeling of critical proteins involved in excitation-contraction coupling, which causes a marked increase in SR load. Specifically, we show that if colocalization of LCCs and RyRs is lost, then the Ca content in the cell must necessarily increase. The mechanism for this effect is that the increased distances between LCCs and RyRs reduce the number of recruited Ca sparks at junctional CRUs. This reduction in spark number leads to a reduction in the average cytoplasmic Ca concentration sensed by NCX transporters, which reduces the amount of Ca extruded from the cell. Also, there is less Ca-induced inactivation, which leads to a larger amount of Ca entry via LCCs. The combination of both effects implies that a reduction in coupling fidelity must lead to a net Ca entry into the cell. Therefore, the Ca content in the cell must increase until homeostasis is achieved. For this to occur, the Ca released from the SR into the cell must rise to increase INCX and inactivate ICa such that flux balance is achieved. In our simulations, we find that homeostasis is achieved when the SR load rises to a level such that LCCs, which are further away from the RyR clusters, begin to trigger Ca sparks. In effect, the increase in SR load makes RyR clusters more sensitive, which compensates for their increased distances from LCCs. Thus, once homeostasis is achieved, INCX is increased because of the greater number of Ca sparks recruited at the elevated SR load. This result is consistent with experimental studies in dogs with HF showing that atrial SR content is substantially larger than in normal dogs (14). Also, an experimental model of HF in sheep atrial myocytes demonstrated an increase in SR load (28). However, in this study it was found that both whole-cell ICa and APD are substantially reduced in HF, in sharp contrast to the dog model. In this case, we expect that the reduced ICa is also compensated by reduced extrusion via INCX. The latter effect is likely driven by a reduction in the Ca transient, which has the effect of reducing outward INCX. Thus, it is likely that both the reduced ICa and the increased distances between signaling channels will produce an increase in the SR load. However, it is unclear which of these effects dominates in sheep atrial myocytes.
Reduced coupling fidelity leads to a prolongation of the APD
Our simulations reveal further that because LCCs in HF cells are, on average, further away from RyRs, then there is a delay for LCC openings to trigger Ca sparks. This delayed recruitment of Ca sparks leads to an increased release of Ca later in the AP, which enhances late INCX and therefore induces a prolongation of the APD. This effect is likely to contribute to the well-known observation that the APD of HF atrial cells is prolonged (14). Here, we show that this electrophysiological property of HF atrial cells is a direct consequence of reduced coupling fidelity due to the spatial positioning of LCCs, NCXs, and RyR clusters. We also stress that although the effect of HF on cell electrophysiology is multifactorial, there is an important component that arises purely from the geometrical arrangement of the signaling proteins involved. In fact, in our study we find that the resulting homeostatic changes are substantial, which suggests that subcellular architecture is likely a critical component for understanding the electrophysiological changes in HF. These findings are consistent with the work of Eisner et al. (29,30), who emphasize the importance of flux balance to determine the steady-state Ca content in the cell. In that study, they emphasize the concept of autoregulation, which referred to the gradual changes in Ca cycling homeostasis to maintain flux balance. Our study shows that the position of Ca signaling proteins with respect to each other plays an important role in this autoregulation. To our knowledge, this perspective has not been reported in the literature, and our study suggests that this is an important component of HF.
Homeostatic changes promote triggered Ca waves
A consequence of the increased SR load in HF atrial myocytes is that these cells become more prone to subcellular Ca waves. These waves occur because an increase in SR load makes RyR clusters more excitable, so a Ca spark at one cluster can diffuse and ignite a spark at neighboring clusters. At high SR loads, this domino-like effect can generate Ca waves that can propagate across the cell. In a previous work and in the simulations performed in this study, we find that in paced atrial myocytes, these Ca waves are nucleated at junctional sites where LCCs open and trigger Ca sparks (31). This is in sharp contrast to spontaneous Ca waves, which occur during a pause and are nucleated at RyR clusters where a few channels open because of stochastic fluctuations. Thus, we refer to these Ca waves as “triggered Ca waves” because these waves tend to occur during the AP when LCCs have a high open probability. In this study, we show that the increased SR load in HF promotes these triggered Ca waves, which is responsible for the aperiodic response of the Ca transient and APD observed when q < qc. As shown in our previous work, an important requirement for triggered waves is that the atrial cell has an underdeveloped TT structure (12). In these cells, we expect that there is a large pool of orphaned RyRs that can serve as a substrate for wave propagation. Therefore, when the SR load increases in these cells, then LCC channel openings at junctional CRUs can ignite a Ca wave that propagates into the cell. However, we point out here that some studies have demonstrated an extensive TT system in the atria. For example, Dibb et al. (32) have shown that most sheep atrial myocytes possess an extensive TT system. In this case, we expect triggered waves to occur in these cells only after extensive remodeling in which there is a substantial loss of TTs, which produces a pool of excitable RyR clusters that can support Ca wave propagation.
Finally, we stress that our simulation studies indicate that the increased SR loads in HF will also promote spontaneous Ca waves. However, these waves can only be observed during a pause because the coupling interval for spontaneous waves is much longer than that of triggered waves. This is because spontaneous Ca waves originate at RyR clusters, where stochastic channel openings lead to the nucleation of Ca waves. As shown in our previous study (12), these spontaneous waves occur with a greater coupling interval than triggered waves, which are excited by LCC openings during the AP. Thus, during rapid pacing conditions, the Ca waves observed during pacing are most likely to be triggered because LCCs have a higher probability of nucleating a wave compared to fluctuations of RyR. Therefore, our findings suggest that if Ca waves are indeed fundamental to the genesis of atrial arrhythmias, then these waves are very likely to be triggered rather than spontaneous.
HF in ventricular myocytes
In this study, we have focused primarily on structural remodeling in atrial myocytes. Here, we discuss the relevance of our findings to ventricular myocytes. We first note that ventricular myocytes have a substantially more developed TT system, so Ca signaling between LCC and RyRs in these cells occurs throughout the cell volume (17,33). Consequently, we do not expect triggered Ca waves in these cells because most RyR clusters are activated during the AP. However, in HF it is well established that the TT system of ventricular myocytes retracts substantially, leaving a large population of orphaned RyR clusters in the cell interior (11,34,35). As in atrial myocytes, the effect of this remodeling will be to promote triggered Ca waves because Ca sparks ignited at intact junctions can propagate into a population of orphaned RyRs. Also, the coupling fidelity between LCCs and RyRs will be reduced as these proteins are pulled away from each other during remodeling. Therefore, if we require flux balance due to Ca entry from ICa and Ca extrusion due to INCX, then Ca should accumulate in the cell because of a reduction in INCX caused by the lesser number of Ca sparks recruited. Consequently, we also expect Ca release to be delayed and more dyssynchronous because of the increased distances between LCCs and RyRs. This effect will also lead to a prolonged APD due to INCX activated by delayed Ca release events during the AP. This result is consistent with experimental studies in HF ventricular myocytes showing that in these cells, Ca release is delayed and more dyssynchronous and that the APD in these cells is prolonged (10). Thus, as in atrial myocytes, we expect that structural remodeling in ventricular myocytes to induce the same arrhythmogenic activity described in this study.
It is important to note that a crucial difference between HF in ventricular and atrial myocytes is that the SR load in ventricular myocytes is decreased and the magnitude of the Ca transient is reduced (36). However, the Ca flux balance requirement suggests that as long as ICa is not reduced in HF, then the Ca content in the cell must necessarily increase in response to the reduction in Ca signaling fidelity. This result is surprising because one would then expect an increased SR load in HF ventricular myocytes. A potential resolution to this observation is suggested by Kubalova (36), who demonstrated that RyRs in HF ventricular myocytes are phosphorylated and become leaky. They argued that it is this leak that led to a reduction in SR load and a blunted Ca transient, a result that has been corroborated by computational modeling of the relationship between HF remodeling and SR load (11,37). These authors also showed that Ca wave activity is enhanced in HF, which is again surprising because a reduction in SR load should reduce the excitability of RyR clusters. Here, we suggest that it is the rise in diastolic Ca caused by the increased Ca content in the cell, in conjunction with leaky RyRs, that increases RyR cluster excitability. This is because the increased diastolic Ca concentration will reduce the local Ca rise necessary to induce a Ca spark. Thus, RyR clusters will be closer to their activation threshold even though the SR load is reduced. Therefore, we expect that in ventricular myocytes, the diastolic Ca levels play a crucial role in the regulation of arrhythmogenic wave activity.
Role of RyR remodeling in persistent AF
HF remodeling is a multifactorial process, and we expect a wide range of structural changes. Here, we discuss in particular recent findings showing that RyR cluster organization is altered during persistent AF. In particular, Macquaide et al. (38) analyzed atrial myocytes from sheep with persistent AF, showing a more complex reorganization of RyRs. They found that average cluster sizes remained the same as that found in normal myocytes, but were more closely spaced in AF. In this case, CRUs are more densely packed with RyR clusters, which will make them more sensitive to local Ca concentration changes. The effect of this increased sensitivity is twofold. Firstly, it is clear that these cells will exhibit a higher frequency of triggered Ca waves because the threshold for Ca wave nucleation and propagation is reduced. This result suggests that triggered waves may play a role in AF maintenance by inducing AP perturbations, leading to sustained wave break and reentry. On the other hand, the increased CRU sensitivity is likely protective because it will compensate for the increased distances between LCCs and RyRs and therefore tend to counter the decrease in coupling fidelity. These results suggest that RyR reorganization likely plays a mechanistic role in the initiation and maintenance of AF. However, a detailed analysis of these competing effects and their relationship to atrial arrhythmogenesis is lacking.
Triggered Ca waves during rapid pacing induces aperiodic APD fluctuations
An important observation in our computational study is that for q < qc, the Ca transient and APD exhibited large beat-to-beat variations because of intermittent triggered waves that occurred during pacing. Here, we point out that the timing of these Ca waves is inherently random because Ca wave nucleation likely originates at a single or at small groups of dyadic junctions, where local Ca signaling is stochastic. It is this stochasticity that leads to the intermittent wave propagation events, which did not exhibit a regular pattern. Furthermore, this stochastic process is coupled with the dynamics of Ca cycling because the SR load, which regulates local Ca signaling, is changing during pacing. Thus, the nonlinear dynamics of Ca cycling is bidirectionally coupled with the stochastic dynamics of wave nucleation, and this induces the random aperiodic dynamics observed below qc. Here, we also point out that the Ca released into the cell because of a propagating wave can be substantial because the SR in the cell interior is largely intact. Thus, once a wave occurs, a large pool of Ca is then released into the cell at the several thousand orphaned RyR clusters in the cell interior. The Ca released then diffuses and is pumped out of the cell via NCXs. Here, we emphasize the observation that triggered waves during the AP can significantly perturb the time course of AP repolarization. These dynamics are in sharp contrast to that induced by spontaneous Ca waves, which typically occur during the diastolic interval and generally do not influence AP repolarization. In that case, a spontaneous Ca wave can lead to delayed afterdepolarization (DAD), which may propagate in tissue as an ectopic beat. In our rapid pacing simulations, we did not observe DADs because there was essentially no time for the SR load to recover to a level in which the rate of spontaneous Ca sparks was significant.
Planar wave instability caused by feedback between Ca waves, AP repolarization, and conduction velocity
In this study, we have shown that when triggered Ca waves occur in atrial tissue, then planar excitation waves tend to fractionate via localized conduction block. This wave fractionation is due to two critical features of HF cells in tissue. Firstly, as argued above, during rapid pacing, triggered waves occur with increasing frequency and can induce substantial APD variation from beat to beat. Thus, if a triggered wave occurs on one beat, then AP repolarization can be slowed so that the AP upstroke on the following beat will be delivered at a voltage that is ∼10–20 mV higher than the resting potential. This AP will then propagate at a reduced CV because of incomplete recovery of the sodium channel. This effect can be seen clearly when a one-dimensional cable of cells is paced rapidly in the regime of triggered waves (Fig. 10 C). In this case, we find that for q < qc, there are substantial variations in CV from beat to beat, which are driven by the fluctuations in AP repolarization. This effect is exacerbated at rapid stimulation rates at which the diastolic interval is small, so APD fluctuations can substantially perturb the voltage at which the AP is delivered.
Now, in our 2D tissue simulations, we find that this effect leads to localized conduction slowing that induces wave break. The reason for this is that two regions of tissue that are separated by a distance larger than the electrotonic length (space constant) may develop conduction slowing at different beats. This is due to the fact that triggered waves are stochastic, so distant parts of the tissue are not synchronized and can reach the onset of conduction slowing at different times. This effect induces spatial variations of CV, which destabilizes the planar wave excitations, which are spatially uniform in the absence of triggered waves.
The mechanism for wave break presented here provides a, to our knowledge, new link between HF and the induction of atrial arrhythmias. A crucial observation is that the underlying arrhythmia is most likely a conduction abnormality that is caused by stochastic Ca waves that perturb AP repolarization in a heterogeneous manner. This is in sharp contrast to triggered activity, in which it is assumed that the Ca waves summate across many myocytes to form a triggered excitation in tissue. In our study, we find that during rapid pacing conditions, triggered activity such as DADs is unlikely because these events typically require a longer pause to occur. This pause is because the nucleation rate of spontaneous waves is typically lower than that of triggered waves and synchronization of spontaneous waves requires a longer waiting time. At the subcellular level, we do observe occasional spontaneous Ca wave activity, but these waves do not synchronize sufficiently to induce a triggered excitation. Indeed, previous studies have shown that the necessary conditions for Ca wave synchronization on the tissue scale are stringent, so these events are likely to be rare (39). This is in sharp contrast to the mechanism proposed here, which occurs readily at the onset of triggered waves. Early afterdepolarizations (EADs), which are caused by a reactivation of ICa, have also been proposed as a possible mechanism for atrial arrhythmogenesis (4). However, EADs require a prolonged APD for ICa to recover from inactivation and induce AP depolarization. This typically does not occur in atrial cells because the APD is short in these cells. Consequently, EADs are generally not observed in atrial myocytes, with the exception of a few studies (40). Our study suggests the possibility that atrial arrythmias in HF are due to wave break caused by stochastic Ca cycling dynamics.
Author Contributions
Y.S., G.L.A., W.E.L., and J.A.W. designed research, performed research, contributed analytic tools, analyzed data, and wrote the article.
Acknowledgments
This work was supported by the National Heart, Lung, and Blood Institute grant RO1HL101196 (Y.S. and J.A.W.). Further support was provided by the European Union’s Horizon 2020 research and innovation program (Consolidator grant, W.E.L.) under grant agreement no. 647714 and The South-Eastern Norway Regional Health Authority (W.E.L.).
Editor: Raimond Winslow.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.12.012.
Supporting Material
References
- 1.Nattel S. New ideas about atrial fibrillation 50 years on. Nature. 2002;415:219–226. doi: 10.1038/415219a. [DOI] [PubMed] [Google Scholar]
- 2.Li D., Fareh S., Nattel S. Promotion of atrial fibrillation by heart failure in dogs: atrial remodeling of a different sort. Circulation. 1999;100:87–95. doi: 10.1161/01.cir.100.1.87. [DOI] [PubMed] [Google Scholar]
- 3.Maisel W.H., Stevenson L.W. Atrial fibrillation in heart failure: epidemiology, pathophysiology, and rationale for therapy. Am. J. Cardiol. 2003;91:2D–8D. doi: 10.1016/s0002-9149(02)03373-8. [DOI] [PubMed] [Google Scholar]
- 4.Heijman J., Voigt N., Dobrev D. Calcium handling and atrial fibrillation. Wien. Med. Wochenschr. 2012;162:287–291. doi: 10.1007/s10354-012-0109-9. [DOI] [PubMed] [Google Scholar]
- 5.Hove-Madsen L., Llach A., Cinca J. Atrial fibrillation is associated with increased spontaneous calcium release from the sarcoplasmic reticulum in human atrial myocytes. Circulation. 2004;110:1358–1363. doi: 10.1161/01.CIR.0000141296.59876.87. [DOI] [PubMed] [Google Scholar]
- 6.Dobrev D., Nattel S. Calcium handling abnormalities in atrial fibrillation as a target for innovative therapeutics. J. Cardiovasc. Pharmacol. 2008;52:293–299. doi: 10.1097/FJC.0b013e318171924d. [DOI] [PubMed] [Google Scholar]
- 7.Nattel S., Maguy A., Yeh Y.H. Arrhythmogenic ion-channel remodeling in the heart: heart failure, myocardial infarction, and atrial fibrillation. Physiol. Rev. 2007;87:425–456. doi: 10.1152/physrev.00014.2006. [DOI] [PubMed] [Google Scholar]
- 8.Gómez A.M., Valdivia H.H., Lederer W.J. Defective excitation-contraction coupling in experimental cardiac hypertrophy and heart failure. Science. 1997;276:800–806. doi: 10.1126/science.276.5313.800. [DOI] [PubMed] [Google Scholar]
- 9.Sanchez-Alonso J.L., Bhargava A., Gorelik J. Microdomain-specific modulation of L-type calcium channels leads to triggered ventricular arrhythmia in heart failure. Circ. Res. 2016;119:944–955. doi: 10.1161/CIRCRESAHA.116.308698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wagner E., Lauterbach M.A., Lehnart S.E. Stimulated emission depletion live-cell super-resolution imaging shows proliferative remodeling of T-tubule membrane structures after myocardial infarction. Circ. Res. 2012;111:402–414. doi: 10.1161/CIRCRESAHA.112.274530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Song Z., Liu M.B., Qu Z. Transverse tubular network structures in the genesis of intracellular calcium alternans and triggered activity in cardiac cells. J. Mol. Cell. Cardiol. 2018;114:288–299. doi: 10.1016/j.yjmcc.2017.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shiferaw Y., Aistrup G.L., Wasserstrom J.A. Mechanism for triggered waves in atrial myocytes. Biophys. J. 2017;113:656–670. doi: 10.1016/j.bpj.2017.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shiferaw Y., Aistrup G.L., Wasserstrom J.A. Synchronization of triggered waves in atrial tissue. Biophys. J. 2018;115:1130–1141. doi: 10.1016/j.bpj.2018.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yeh Y.H., Wakili R., Nattel S. Calcium-handling abnormalities underlying atrial arrhythmogenesis and contractile dysfunction in dogs with congestive heart failure. Circ Arrhythm Electrophysiol. 2008;1:93–102. doi: 10.1161/CIRCEP.107.754788. [DOI] [PubMed] [Google Scholar]
- 15.Restrepo J.G., Weiss J.N., Karma A. Calsequestrin-mediated mechanism for cellular calcium transient alternans. Biophys. J. 2008;95:3767–3789. doi: 10.1529/biophysj.108.130419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Restrepo J.G., Karma A. Spatiotemporal intracellular calcium dynamics during cardiac alternans. Chaos. 2009;19:037115. doi: 10.1063/1.3207835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Arora R., Aistrup G.L., Wasserstrom J.A. Regional distribution of T-tubule density in left and right atria in dogs. Heart Rhythm. 2017;14:273–281. doi: 10.1016/j.hrthm.2016.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Frisk M., Koivumäki J.T., Louch W.E. Variable t-tubule organization and Ca2+ homeostasis across the atria. Am. J. Physiol. Heart Circ. Physiol. 2014;307:H609–H620. doi: 10.1152/ajpheart.00295.2014. [DOI] [PubMed] [Google Scholar]
- 19.Grandi E., Pandit S.V., Bers D.M. Human atrial action potential and Ca2+ model: sinus rhythm and chronic atrial fibrillation. Circ. Res. 2011;109:1055–1066. doi: 10.1161/CIRCRESAHA.111.253955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Qu Z., Garfinkel A. An advanced algorithm for solving partial differential equation in cardiac conduction. IEEE Trans. Biomed. Eng. 1999;46:1166–1168. doi: 10.1109/10.784149. [DOI] [PubMed] [Google Scholar]
- 21.Peskoff A., Langer G.A. Calcium concentration and movement in the ventricular cardiac cell during an excitation-contraction cycle. Biophys. J. 1998;74:153–174. doi: 10.1016/S0006-3495(98)77776-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Laver D.R. Regulation of the RyR channel gating by Ca2+ and Mg2. Biophys. Rev. 2018;10:1087–1095. doi: 10.1007/s12551-018-0433-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lipsett D.B., Frisk M., Louch W.E. Cardiomyocyte substructure reverts to an immature phenotype during heart failure. J. Physiol. 2019;597:1833–1853. doi: 10.1113/JP277273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bryant S.M., Kong C.H., Orchard C.H. Altered distribution of ICa impairs Ca release at the t-tubules of ventricular myocytes from failing hearts. J. Mol. Cell. Cardiol. 2015;86:23–31. doi: 10.1016/j.yjmcc.2015.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shen X., van den Brink J., Louch W.E. 3D dSTORM imaging reveals disassembly of ryanodine receptor clusters in failing cardiomyocytes. Biophys. J. 2018;114:621a. [Google Scholar]
- 26.Kolstad T.R., van den Brink J., Louch W.E. Ryanodine receptor dispersion disrupts Ca2+ release in failing cardiac myocytes. eLife. 2018;7:e39427. doi: 10.7554/eLife.39427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bers D.M. Cardiac excitation-contraction coupling. Nature. 2002;415:198–205. doi: 10.1038/415198a. [DOI] [PubMed] [Google Scholar]
- 28.Clarke J.D., Caldwell J.L., Trafford A.W. Perturbed atrial calcium handling in an ovine model of heart failure: potential roles for reductions in the L-type calcium current. J. Mol. Cell. Cardiol. 2015;79:169–179. doi: 10.1016/j.yjmcc.2014.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Eisner D.A., Choi H.S., Trafford A.W. Integrative analysis of calcium cycling in cardiac muscle. Circ. Res. 2000;87:1087–1094. doi: 10.1161/01.res.87.12.1087. [DOI] [PubMed] [Google Scholar]
- 30.Eisner D., Bode E., Trafford A. Calcium flux balance in the heart. J. Mol. Cell. Cardiol. 2013;58:110–117. doi: 10.1016/j.yjmcc.2012.11.017. [DOI] [PubMed] [Google Scholar]
- 31.Aistrup G.L., Arora R., Wasserstrom J.A. Triggered intracellular calcium waves in dog and human left atrial myocytes from normal and failing hearts. Cardiovasc. Res. 2017;113:1688–1699. doi: 10.1093/cvr/cvx167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dibb K.M., Clarke J.D., Trafford A.W. Characterization of an extensive transverse tubular network in sheep atrial myocytes and its depletion in heart failure. Circ Heart Fail. 2009;2:482–489. doi: 10.1161/CIRCHEARTFAILURE.109.852228. [DOI] [PubMed] [Google Scholar]
- 33.Brette F., Orchard C. T-tubule function in mammalian cardiac myocytes. Circ. Res. 2003;92:1182–1192. doi: 10.1161/01.RES.0000074908.17214.FD. [DOI] [PubMed] [Google Scholar]
- 34.Wei S., Guo A., Song L.S. T-tubule remodeling during transition from hypertrophy to heart failure. Circ. Res. 2010;107:520–531. doi: 10.1161/CIRCRESAHA.109.212324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Song L.S., Sobie E.A., Cheng H. Orphaned ryanodine receptors in the failing heart. Proc. Natl. Acad. Sci. USA. 2006;103:4305–4310. doi: 10.1073/pnas.0509324103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kubalova Z., Terentyev D., Györke S. Abnormal intrastore calcium signaling in chronic heart failure. Proc. Natl. Acad. Sci. USA. 2005;102:14104–14109. doi: 10.1073/pnas.0504298102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nivala M., Song Z., Qu Z. T-tubule disruption promotes calcium alternans in failing ventricular myocytes: mechanistic insights from computational modeling. J. Mol. Cell. Cardiol. 2015;79:32–41. doi: 10.1016/j.yjmcc.2014.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Macquaide N., Tuan H.T., Sipido K.R. Ryanodine receptor cluster fragmentation and redistribution in persistent atrial fibrillation enhance calcium release. Cardiovasc. Res. 2015;108:387–398. doi: 10.1093/cvr/cvv231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Xie Y., Sato D., Weiss J.N. So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophys. J. 2010;99:1408–1415. doi: 10.1016/j.bpj.2010.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Burashnikov A., Antzelevitch C. Late-phase 3 EAD. A unique mechanism contributing to initiation of atrial fibrillation. Pacing Clin. Electrophysiol. 2006;29:290–295. doi: 10.1111/j.1540-8159.2006.00336.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.