Skip to main content
PMC home page
iScience logoLink to iScience
. 2020 Jan 7;23(2):100819. doi: 10.1016/j.isci.2020.100819

Critical Transitions in Plant-Pollinator Systems Induced by Positive Inbreeding-Reward-Pollinator Feedbacks

Heng Huang 1,2,∗, Paolo D'Odorico 1
PMCID: PMC6976937  PMID: 31981922

Summary

In many regions of the world pollinator populations are rapidly declining, a trend that is expected to disrupt major ecosystem functions and services. These changes in pollinator abundance may be prone to critical transitions with abrupt shifts to a state strongly depleted both in pollinator and vegetation abundance. Here we develop a process-based model to investigate the effect of a positive pollinator-vegetation feedback, whereby an initial decline in plant density increases selfing thereby reducing floral resources and negatively affecting pollinators. We show that a decline in resource availability and an increase in disturbance intensity can induce an abrupt shift in vegetation and pollinator dynamics and potentially lead to the collapse of plant-pollinator systems. Thus, endogenous feedbacks can induce strong non-linearities in plant-pollinator dynamics, making them vulnerable to critical transitions to a state depleted of both plants and pollinators in response to resource deficiency and natural or anthropogenic disturbance.

Subject Areas: Environmental Science, Ecology, Mathematical Biosciences

Graphical Abstract

graphic file with name fx1.jpg

Open in a new tab

Highlights

  • •

    Increased selfing in plants reduces nectar quality and pollinator visitation

  • •

    Bistability can emerge from endogenous positive pollinator-vegetation feedbacks

  • •

    Plant-pollinator dynamics may exhibit critical transitions under global change

Environmental Science; Ecology; Mathematical Biosciences

Introduction

Plant-pollination interactions are important in maintaining the biodiversity of terrestrial ecosystems, as many agricultural crops and wild plants rely intensively on pollinators such as bees to sustain their reproduction (Ashman et al., 2004, Klein et al., 2007, Garibaldi et al., 2011). Empirical studies are providing overwhelming evidence of a global decline of pollinator abundance, a trend that is expected to disrupt ecosystem functions and services worldwide with negative impact on food security and rural livelihoods (Klein et al., 2007, Potts et al., 2010). In particular, pollinator specialists are at a greater extinction risk because they rely on fewer plant species (Potts et al., 2010). Multiple drivers have been invoked to explain pollinator declines, including habitat loss and fragmentation, climate change, pathogen infections, pesticide applications, reduction in floral resources, and environmental pollution (Goulson et al., 2008, Potts et al., 2010, Fuentes et al., 2016).

The availability of resources such as soil water and nutrients, light, and physical space has significant impacts on vegetation dynamics in terrestrial ecosystems (Craine and Dybzinski, 2013). For example, plant growth and development strongly depend on the availability of water and nutrients, which directly regulate ecophysiological processes such as photosynthesis and transpiration that are key to the metabolism of plants (Sibly et al., 2012). Drought conditions can also affect plant population dynamics by altering plant-pollination interactions (Gallagher and Campbell, 2017, Phillips et al., 2018). Experimental studies suggest that increasing drought stress may reduce plant photosynthetic assimilation and lead to a significant decline in resource allocation to reproduction, including the capacity of plants to attract pollinators. For example, reduced water availability negatively influences floral volatiles and decreases floral abundance, pollen quantity and quality, and nectar rewards (i.e., nectar volume and sugar concentration) (Halpern et al., 2010, Burkle and Runyon, 2016), which further limits the visitation frequency of pollinators (Glenny et al., 2018).

In addition, environmental disturbances such as habitat loss, fire, herbivory, and pesticide can directly influence plant-pollinator interactions (Potts et al., 2010). Habitat loss and degradation has been considered as the most significant driver of pollinator declines (Potts et al., 2010). Furthermore, herbivory may induce plants to produce fewer and smaller flowers with less nectar rewards (Caruso, 2006), thus decreasing the floral attractiveness to pollinators (Schiller et al., 2000, Moreira et al., 2019). Indirectly, the negative effect of herbivory on pollinator visitation can reduce plant reproductive success such as seed production and plant density, which in turn further influences pollinator behavior (Morgan et al., 2005, Burkle and Runyon, 2016).

Many plant species tend to increase the probability of selfing compared with outcrossing under reduced pollinator visitation and resource-limited environmental conditions such as drought (Levin, 2010). This shift in reproduction strategy can be attributed to the decreased plant population density due to water limitation, which raises the possibility of pollinator-mediated selfing (Morgan et al., 2005). For example, environmental stress such as drought and nutrient deficiency may result in a reduction in floral abundance and nectar rewards thereby discouraging pollinator visits and outcrossing (Gallagher and Campbell, 2017). Selfing usually causes significant declines in pollen quality/quantity and seed production, and eventually decreases plant population size because of inbreeding depression (Charlesworth and Charlesworth, 1987). Therefore, a positive feedback exists between plant reproductivity and pollination, whereby a decrease in plant density increases the reliance on reproduction by selfing (instead of outcrossing), with the effect of reducing pollen quality and quantity and the consequent decline in pollinator abundance and plant density. We argue that this positive feedback may lead to the emergence of alternative stable states in pollinator-plant dynamics in the sense that the system can be stable both in a configuration with relatively high levels of plant density and pollinator abundance (“healthy” ecosystem state) and with strongly depleted plant and pollinator populations (“degraded state”). Resource limitation and disturbance intensification may trigger an abrupt shift from the stable state of healthy ecosystem conditions with full plant cover and a sufficiently abundant pollinator community to the alternative stable state characterized by low plant and pollinator densities.

Despite some recent experimental evidence indicating strong effects of changes in soil water availability on plant-pollinator interactions (Gallagher and Campbell, 2017), a theoretical framework to investigate the ecological impacts of resource dynamics and environmental disturbances on the stability of plant-pollinator dynamics is still missing. Bistability has been documented to occur in a variety of ecosystems, including arid and semiarid grasslands/shrublands, savannas/forests, arctic tundra/woodlands, and coastal environments (May, 1977, Scheffer et al., 2001, McGlathery et al., 2013, Huang et al., 2018). These ecosystems can shift non-linearly from one stable state to another when the external forcing reaches a critical threshold (often termed “tipping point”) (e.g., Ratajczak et al., 2018). This state change can be highly irreversible and result in catastrophic degradation of ecosystem functions and services (D'Odorico et al., 2013). Previous work has shown that tipping points may emerge in complex pollinator-plant systems as a result of the structure of mutualistic ecological networks (Jiang et al., 2019). However, the ability of positive plant-pollinator feedbacks (i.e., reduced pollinator abundance → inbreeding → reduced nectar quality → decline in pollinator abundance) to induce critical transitions in plant-pollinator systems has remained unexplored. Here we develop a minimalist process-based modeling framework to evaluate whether these feedbacks may lead to the emergence of alternative stable states and critical transitions in pollinator-vegetation dynamics and affect the ecological stability and resilience of plant-pollinator systems. Our goal is to capture the most fundamental biological processes that are involved in the response of plant-pollinator interactions to changes in environmental conditions.

In brief, we model the dynamics of plant population density (G) through a modified logistic growth equation with a carrying capacity KG. The intrinsic growth rate α of the logistic equation is modeled as accounting for both outcrossing and selfing, of which the latter causes a reduction in seed production due to inbreeding depression (Charlesworth and Charlesworth, 1987). The pollinator population density (P) is also modeled by a logistic growth equation with a carrying capacity KP. P determines the visitation rate of pollinators and quantitatively alters the rates of selfing and outcrossing, thereby eventually affecting plant population dynamics. In addition, environmental disturbance can lead to declines in plant and pollinator population growth here expressed by the rates of c and k, respectively. More details about the modeling framework can be found in Transparent Methods.

Results

Plant and Pollinator Dynamics under Different Conditions of Resource Availability and Disturbance

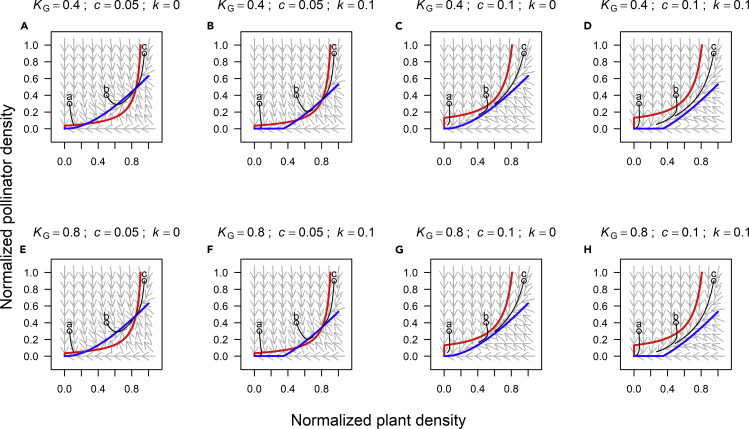
We first conducted phase-plane analyses (Holling, 1973) to study the transient behavior of the population dynamics of plant-pollinator systems by setting dG/dt = 0 and dP/dt = 0. The results show that the stability of plant-pollinator system is highly dependent on the resource availability, which is indicated by KG, and the intensity of environmental disturbance, c and k (Figure 1). For example, the system has two stable nodes and an unstable saddle point when c is relatively small (Figures 1A and 1E). However, with greater rates of environmental disturbance (without changing KG) the dynamics exhibit only one stable node at the origin (0, 0) (Figures 1D and 1H). Likewise, a decrease in KG induced by resource deficiency may turn bistable plant-pollinator interactions into dynamics with only one stable attractor with G∗ = P∗ = 0 (Figures 1C and 1G). In other words, both resource deficiency and environmental disturbance may reduce plant biomass below a critical level at which plant-pollinator feedbacks induce a critical transition to a “depleted state” with neither plant nor pollinator biomass. The trajectories in Figure 1 also suggest the existence of differences in transient plant-pollinator dynamics, depending on environmental conditions. For example, trajectory b, which starts with moderate plant and pollinator population densities, converges to the “non-depleted” stable state with relatively low rates of environmental disturbance (Figures 1A and 1E), but leads to the collapse of both plant and pollinator populations with greater values of c and k (Figures 1D and 1H).

Figure 1.

Figure 1

Open in a new tab

Phase-Plane Diagram for Plant (G) and Pollinator (P) Population Dynamics under Different Conditions of Resource Availability (Indicated by KG) and Environmental Disturbance (c and k)

Results from different combinations of KG, c and k values are shown (A–H). Red and blues are zero isolines for plant and pollinator population (i.e., dG/dt = 0 and dP/dt = 0), respectively. The arrows denote the direction of the vector field, and the black lines are trajectories with different initial plant and pollinator population densities (open circles).

Bistable States of Plant and Pollinator Dynamics through Vegetation-Pollinator Feedbacks

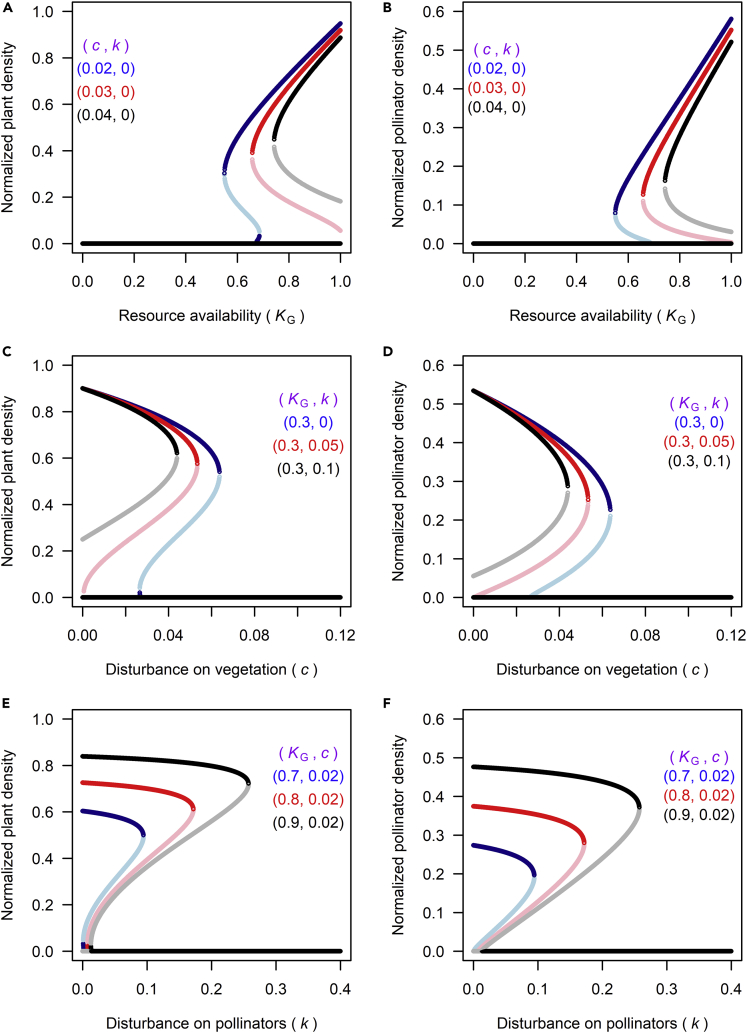
To investigate the conditions underlying the occurrence of alternative stable states in plant-pollinator dynamics, we look at how P∗ and G∗ vary in response to continuous changes in resource availability (indicated by KG) and disturbance intensity (c and k) (Figure 2). The results show that bistable dynamics may exist with moderate pressure from resource deficiency and disturbance (KG is not “too low” and c or k is not “too high”). This means that the system can be stable both in a “depleted state” (P∗ = G∗ = 0) and in a “non-depleted” state able to sustain a community of plants and pollinators. In these cases, the system is bistable and can shift from one stable state to another following a disturbance.

Figure 2.

Figure 2

Open in a new tab

Ecological Bistability of Plant-Pollinator Systems

Bistable states of plant and pollinator population dynamics can be induced by changes in resource availability (A and B) and environmental disturbance (C–F) through vegetation-pollinator feedbacks. Curves are drawn for different combinations of parameter values. Stable states are indicated by black, red, and blue lines, and unstable states are denoted by gray, pink, and light blue lines. The default values of other model parameters are summarized in the methods.

Resilience is an attribute of a stable state of the system expressing its ability to recover after a disturbance. It depends on the size of the basin of attraction, i.e., the capacity of the system to remain in the same stable state under disturbance (Holling, 1973, Scheffer et al., 2001), which can be quantified by the distance between the middle saddle point and the stable equilibrium point with P∗ and G∗ ≠ 0. The resilience of both vegetation and pollinator dynamics increases with resource availability, indicating that, as resource availability increases, progressively greater perturbations are required to drive the ecological state shift to the “depleted state” (Figures 2A and 2B). The resilience of both plant and pollinator populations in response to resource availability is also dependent on environmental disturbance because it decreases with increasing c, suggesting that disturbance increases the vulnerability of vegetation dynamics critical transitions in response to resource availability.

Figures 2C–2F show how disturbance and plant-pollinator feedbacks induce bistability in plant and pollinator dynamics. The system has two stable states within a certain range of c and k depending on resource conditions. There exists a threshold value of c and k beyond which a critical transition to a stable state with no vegetation and pollinators occurs. The response of plant and pollinator dynamics to environmental disturbance varies with resource availability in the sense that critical transitions to the degraded state P∗ = G∗ = 0 occur when c or k exceeds a critical threshold whose value increases with increasing KG. Collectively, these results highlight how positive feedbacks inherent to plant-pollinator dynamics may induce non-linear behaviors such as bifurcations, bistability, and critical transitions, suggesting that the ongoing decline in pollinator abundance in regions experiencing vegetation loss may lead to an abrupt and highly irreversible shift to a degraded state with low plant and pollinator abundance.

Discussion

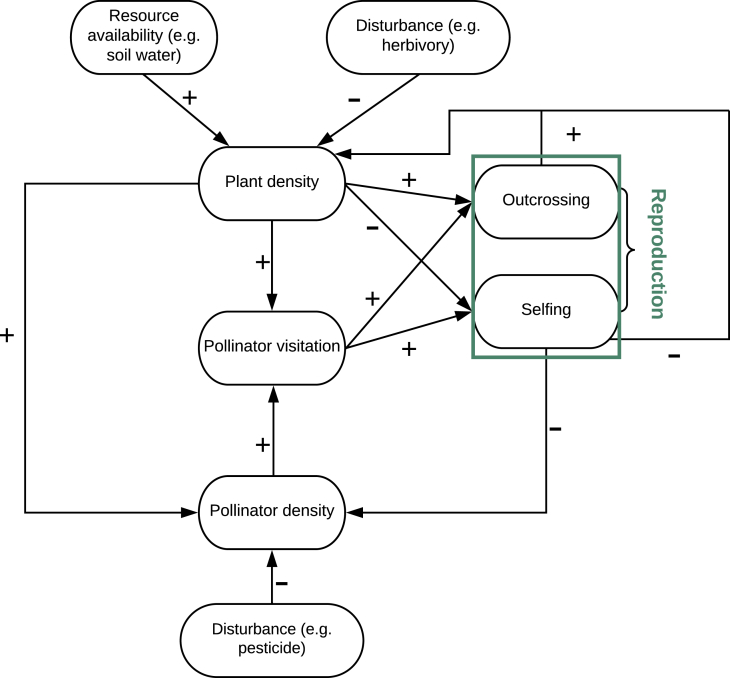
This study provides the first theoretical framework to investigate to what extent a catastrophic population collapse could emerge in plant-pollinator systems as a result of the interaction between internal feedbacks and exogenous drivers such as resource availability and natural and anthropogenic disturbances. For example, a decline in resource availability can cause the shift in plant cover from a stable vegetated state to a stable state without vegetation cover. Changes in resource (e.g., soil water and nutrients) availability underlie some of the key mechanisms through which climate change influences vegetation dynamics (e.g., Gallagher and Campbell, 2017). Variations in resource availability such as soil water content have important effects on plant-pollinator interactions through multiple pathways. Empirical studies have found that reductions in soil water content can result in a decrease in plant investments in reproduction (Gallagher and Campbell, 2017). In fact, plants in drought conditions are likely to produce fewer and smaller flowers as well as poorer nectar rewards, thereby further decreasing pollinator visits and outcrossing rates (Caruso, 2006). The consequent increasing reliance on selfing leads to inbreeding depression and further reduces pollen viability (e.g., Carr and Dudash, 1997) and the success of seed production (Charlesworth and Charlesworth, 1987). The declining success of plant reproduction eventually negatively affects plant density and in turn reduces pollinator visitation rates (Ivey and Carr, 2005, Yeamans et al., 2014), in a self-sustained positive feedback loop between vegetation and pollination (Figure 3). The positive cycles in Figure 3 qualitatively indicate that plant-pollinator systems may be prone to critical transitions under changes in external drivers, because the existence of positive cycles in a diagraph (interaction graph) can induce state changes (Soulé, 2003, Mincheva and Roussel, 2007).

Figure 3.

Figure 3

Open in a new tab

The Feedback Loop between Vegetation and Pollination Underlying the Modeling Framework

Positive and negative effects are indicated by “+” and “−” respectively.

Bistable plant-pollinator dynamics exist within a specific range of disturbance intensity (Figures 2C–2F). Empirical evidence has shown that natural and anthropogenic disturbances can influence vegetation dynamics both directly through habitat loss and degradation and indirectly by affecting floral traits, pollinator behavior, and plant reproductive strategies (Caruso, 2006, Moreira et al., 2019). Our simplified model captures this fundamental mechanism and demonstrates the non-linear response of vegetation and pollinator density to changes in disturbance. In addition, bistability is often associated with hysteresis such that the forward and backward transitions between ecological states differ. The existence of hysteresis in bistable plant-pollinator systems limits the ability to reverse them back to the original state after a transition (Ratajczak et al., 2018). For example, our modeling results reveal that the system can switch from a stable state with vegetation cover and a sizable pollinator community to the unvegetated stable state and low pollinator abundance when KG = 0.7, c = 0.03, and k = 0. However, KG needs to increase to nearly 1 to allow the system to reverse back to the original stable state. This is consistent with previous work showing that changes in external drivers may lead to irreversible transitions in ecosystems (Walker et al., 1981). Our modeling results are further supported by empirical evidence showing that in some dryland ecosystems the specialist bee fauna has declined significantly since the 1960s due to fragmentation and the consequent reduced floral resources (Cane et al., 2006). Similar responses to changes in floral resources have been observed in the Arctic (Pradal et al., 2009). Our findings suggest that the vegetation-pollinator feedbacks could play an important role in driving the catastrophic collapse of plant-pollinator networks under ongoing global change.

Changes in either resource availability and disturbance regime can significantly alter both the transient dynamics and stable equilibria of the system through complex biological processes regulating plant-pollinator interactions (Figure 1). Nearly 90% of flowering plant species rely on animals, especially insects for pollination, and decreases in either plant or pollinator population size may eventually cause the collapse of plant-pollinator systems (Biesmeijer, 2006, Fishman and Hadany, 2010) and the loss of the associated ecosystem functions and services across scales (Potts et al., 2010). Previous work has investigated the direct causes of pollinator declines, focusing on the case in whichenvironmental changes such as habitat loss and degradation are the drivers of pollinator loss (Potts et al., 2010). In this study we explored to what extent the combined effect of internal feedbacks and external drivers of disturbance may lead to critical transitions with the collapse of both plant and pollinator populations. Such a collapse can result either from a reduction in plant cover triggered by resource depletion or disturbance such as herbivory (controlled by the parameters KG and c in the model) or from a decline in pollinator density caused by disturbances such as pesticide (the parameter k) and sustained by plant-pollinator feedbacks.

Limitations of the Study

The findings of this study are based on the model output, and therefore experimental data from field or laboratory observations are needed to verify the modeling results, although the model has captured the fundamental biological processes involved in plant-pollinator interactions. As noted in the previous sections, to reduce the complexity of the system, our approach accounts neither for the diversity of plant and pollinator species nor for the nestedness of plant-pollinator networks. Nevertheless, this assumption allows us to develop a simplified framework to highlight how endogenous feedbacks can make plant-pollinator systems prone to critical transitions leading to the collapse of both plants and pollinators. For instance, these assumptions are suitable for the investigation of highly specialized plant-pollinator systems in which several bee species are found to be pollen specialists of only one shrub species, which makes pollinator dynamics extremely dependent on changes in vegetation cover, landscape fragmentation, and trends in floral production for that shrub (e.g., Minckley et al., 2000).

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Acknowledgments

This study was supported by a graduate fellowship from the University of California's Institute for the Study of Ecological and Evolutionary Climate Impacts (ISEECI), funded by a UC Presidential Research Catalyst Award. The graphical abstract was created with BioRender.com.

Author Contributions

H.H. and P.D. conceived the idea and developed the model. H.H. wrote the first draft of the manuscript, and P.D. contributed to revisions.

Declaration of Interests

The authors declare no conflict of interest.

Published: February 21, 2020

Footnotes

Supplemental Information can be found online at https://doi.org/10.1016/j.isci.2020.100819.

Supplemental Information

Document S1. Transparent Methods
mmc1.pdf (156.9KB, pdf)

References

  1. Ashman T., Knight T., Steets J., Amarasekare P., Burd M., Campbell D., Dudash M., Johnston M., Mazer S., Mitchell R. Pollen limitation of plant reproduction: ecological and evolutionary causes and consequences. Ecology. 2004;85:2408–2421. [Google Scholar]
  2. Biesmeijer J.C. Parallel declines in pollinators and insect-pollinated plants in Britain and the Netherlands. Science. 2006;313:351–354. doi: 10.1126/science.1127863. [DOI] [PubMed] [Google Scholar]
  3. Burkle L.A., Runyon J. Drought and leaf herbivory influence floral volatiles and pollinator attraction. Glob. Change Biol. 2016;22:1644–1654. doi: 10.1111/gcb.13149. [DOI] [PubMed] [Google Scholar]
  4. Cane J.H., Minckley R.L., Kervin L.J., Roulston T.H., Williams N.M. Complex responses within a desert bee guild (Hymenoptera: Apiformes) to urban habitat fragmentation. Ecol. Appl. 2006;16:632–644. doi: 10.1890/1051-0761(2006)016[0632:crwadb]2.0.co;2. [DOI] [PubMed] [Google Scholar]
  5. Carr D.E., Dudash M.R. The effects of five generations of enforced selfing on potential male and female function in Mimulus guttatus. Evolution. 1997;51:1797–1807. doi: 10.1111/j.1558-5646.1997.tb05103.x. [DOI] [PubMed] [Google Scholar]
  6. Caruso C.M. Plasticity of inflorescence traits in Lobelia siphilitica (Lobeliaceae) in response to soil water availability. Am. J. Bot. 2006;93:531–538. doi: 10.3732/ajb.93.4.531. [DOI] [PubMed] [Google Scholar]
  7. Charlesworth D., Charlesworth B. Inbreeding depression and its evolutionary consequences. Annu. Rev. Ecol. Evol. Syst. 1987;18:237–268. [Google Scholar]
  8. Craine J.M., Dybzinski R. Mechanisms of plant competition for nutrients, water and light. Funct. Ecol. 2013;27:833–840. [Google Scholar]
  9. D'Odorico P., He Y., Collins S., De Wekker S., Engel V., Fuentes J. Vegetation-microclimate feedbacks in woodland-grassland ecotones. Glob. Ecol. Biogeogr. 2013;22:364–379. [Google Scholar]
  10. Fishman M.A., Hadany L. Plant–pollinator population dynamics. Theor. Popul. Biol. 2010;78:270–277. doi: 10.1016/j.tpb.2010.08.002. [DOI] [PubMed] [Google Scholar]
  11. Fuentes J., Chamecki M., Roulston T., Chen B., Pratt K. Air pollutants degrade floral scents and increase insect foraging times. Atmos. Environ. 2016;141:361–374. [Google Scholar]
  12. Gallagher M., Campbell D. Shifts in water availability mediate plant-pollinator interactions. New Phytol. 2017;215:792–802. doi: 10.1111/nph.14602. [DOI] [PubMed] [Google Scholar]
  13. Garibaldi L.A., Steffan-Dewenter I., Kremen C., Morales J.M., Bommarco R., Cunningham S.A., Carvalheiro L.G., Chacoff N.P., Dudenhöffer J.H., Greenleaf S.S. Stability of pollination services decreases with isolation from natural areas despite honey bee visits. Ecol. Lett. 2011;14:1062–1072. doi: 10.1111/j.1461-0248.2011.01669.x. [DOI] [PubMed] [Google Scholar]
  14. Glenny W.R., Runyon J.B., Burkle L.A. Drought and increased CO2 alter floral visual and olfactory traits with context dependent effects on pollinator visitation. New Phytol. 2018;220:785–798. doi: 10.1111/nph.15081. [DOI] [PubMed] [Google Scholar]
  15. Goulson D., Lye G., Darvill B. Decline and conservation of bumble bees. Annu. Rev. Entomol. 2008;53:191–208. doi: 10.1146/annurev.ento.53.103106.093454. [DOI] [PubMed] [Google Scholar]
  16. Halpern S., Adler L., Wink M. Leaf herbivory and drought stress affect floral attractive and defensive traits in Nicotiana quadrivalvis. Oecologia. 2010;163:961–971. doi: 10.1007/s00442-010-1651-z. [DOI] [PubMed] [Google Scholar]
  17. Holling C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Evol. Syst. 1973;4:1–23. [Google Scholar]
  18. Huang H., Zinnert J., Wood L., Young D., D'Odorico P. Non-linear shift from grassland to shrubland in temperate barrier islands. Ecology. 2018;99:1671–1681. doi: 10.1002/ecy.2383. [DOI] [PubMed] [Google Scholar]
  19. Ivey C.T., Carr D.E. Effects of herbivory and inbreeding on the pollinators and mating system of Mimulus guttatus (Phrymaceae) Am. J. Bot. 2005;92:1641–1649. doi: 10.3732/ajb.92.10.1641. [DOI] [PubMed] [Google Scholar]
  20. Jiang J., Hastings A., Lai Y.-C. Harnessing tipping points in complex ecological networks. J. R. Soc. Interface. 2019;16:20190345. doi: 10.1098/rsif.2019.0345. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Klein A., Vaissière B., Cane J., Steffan-Dewenter I., Cunningham S., Kremen C., Tscharntke T. Importance of pollinators in changing landscapes for world crops. Proc. R. Soc. B. 2007;274:303–313. doi: 10.1098/rspb.2006.3721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Levin D. Environment-enhanced self-fertilization: implications for niche shifts in adjacent populations. J. Ecol. 2010;98:1276–1283. [Google Scholar]
  23. May R.M. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature. 1977;269:471–477. [Google Scholar]
  24. McGlathery K.J., Reidenbach M.A., D'Odorico P., Fagherazzi S., Pace M.L., Porter J.H. Nonlinear dynamics and alternative stable states in shallow coastal systems. Oceanography. 2013;26:220–231. [Google Scholar]
  25. Mincheva M., Roussel M.R. Graph-theoretic methods for the analysis of chemical and biochemical networks. I. Multistability and oscillations in ordinary differential equation models. J. Math. Biol. 2007;55:61–68. doi: 10.1007/s00285-007-0099-1. [DOI] [PubMed] [Google Scholar]
  26. Minckley R.L., Cane J.H., Kervin L. Origins and ecological consequences of pollen specialization among desert bees. Proc. R. Soc. B. 2000;267:265–271. doi: 10.1098/rspb.2000.0996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Moreira X., Castagneyrol B., Abdala-Roberts L., Traveset A. A meta-analysis of herbivore effects on plant attractiveness to pollinators. Ecology. 2019;100:e02707. doi: 10.1002/ecy.2707. [DOI] [PubMed] [Google Scholar]
  28. Morgan M., Wilson W., Knight T. Plant population dynamics, pollinator foraging, and the selection of self-fertilization. Am. Nat. 2005;166:169–183. doi: 10.1086/431317. [DOI] [PubMed] [Google Scholar]
  29. Phillips B., Shaw R., Holland M., Fry E., Bardgett R., Bullock J., Osborne J. Drought reduces floral resources for pollinators. Glob. Change Biol. 2018;24:3226–3235. doi: 10.1111/gcb.14130. [DOI] [PubMed] [Google Scholar]
  30. Potts S., Biesmeijer J., Kremen C., Neumann P., Schweiger O., Kunin W. Global pollinator declines: trends, impacts and drivers. Trends Ecol. Evol. 2010;25:345–353. doi: 10.1016/j.tree.2010.01.007. [DOI] [PubMed] [Google Scholar]
  31. Pradal C., Olesen J., Wiuf C. Temporal development and collapse of an arctic plant–pollinator network. BMC Ecol. 2009;9:24. doi: 10.1186/1472-6785-9-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ratajczak Z., Carpenter S.R., Ives A.R., Kucharik C.J., Ramiadantsoa T., Stegner M.A., Williams J.W., Zhang J., Turner M.G. Abrupt change in ecological systems: inference and diagnosis. Trends Ecol. Evol. 2018;33:513–526. doi: 10.1016/j.tree.2018.04.013. [DOI] [PubMed] [Google Scholar]
  33. Scheffer M., Carpenter S., Foley J., Folke C., Walker B. Catastrophic shifts in ecosystems. Nature. 2001;413:591–596. doi: 10.1038/35098000. [DOI] [PubMed] [Google Scholar]
  34. Schiller J., Zedler P., Black C. The effect of density-dependent insect visits, flowering phenology, and plant size on seed set of the endangered vernal pool plant Pogogyne abramsii (Lamiaceae) in natural compared to created vernal pools. Wetlands. 2000;20:386–396. [Google Scholar]
  35. Sibly R.M., Brown J.H., Kodric-Brown A. Wiley-Blackwell; 2012. Metabolic Ecology: A Scaling Approach. [Google Scholar]
  36. Soulé C. Graphic requirements for multistationarity. ComPlexUs. 2003;1:123–133. [Google Scholar]
  37. Walker B.H., Ludwig D., Holling C.S., Peterman R.M. Stability of semi-arid savanna grazing systems. J. Ecol. 1981;69:473–498. [Google Scholar]
  38. Yeamans R.L., Roulston T.H., Carr D.E. Pollen quality for pollinators tracks pollen quality for plants in Mimulus guttatus. Ecosphere. 2014;5:91. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Transparent Methods
mmc1.pdf (156.9KB, pdf)

Articles from iScience are provided here courtesy of Elsevier

RESOURCES