Abstract.
Hyperspectral imaging has shown great potential for optical skin analysis by providing noninvasive, pixel-by-pixel surface measurements from which, applying an optical model, information such as melanin concentration and total blood volume fraction can be mapped. Such applications have been successfully performed on small flat skin areas, but existing methods are not suited to large areas such as an organ or a face, due to the difficulty of ensuring homogeneous illumination on complex three-dimensional (3-D) objects, which leads to errors in the maps. We investigate two methods to account for these irradiance variations on a face. The first one relies on a radiometric correction of the irradiance, using 3-D information on the face’s shape acquired by combining the hyperspectral camera with a 3-D scanner; the second relies on an optimization metric used in the map computation, which is invariant to irradiance. We discuss the advantages and drawbacks of the two methods, after having presented in detail the whole acquisition setup, which has been designed to provide high-resolution images with a short acquisition time, as required for live surface measurements of complex 3-D objects such as the face.
Keywords: hyperspectral imaging, three-dimensional scanning, full face, in vivo analysis, skin chromophore
1. Introduction
Skin, described as an optical object, is characterized by its heterogeneous distribution of light absorption and scattering properties.1 These optical properties determine the spectral reflectance of skin and thus, its color, which plays an important role in the perception of a person’s health and age.2,3 Consequently, there is a growing demand for optical methods and devices dedicated to the measurement of skin in cosmetology and dermatology. In recent years, research in this area has focused on noninvasive in vivo methods, as ex vivo methods are known to alter the properties of the skin, and invasive analysis can cause patient discomfort. Optical methods that have emerged for retrieving skin data include diffuse reflectance spectroscopy,4 spatial frequency domain imaging,5 color imaging, and spectral imaging.6,7 Data retrieved from these methods have been analyzed using various models including the Monte Carlo method,8 the radiative transfer equation,9 the diffusion approximation,5 flux models,7 and independent component analysis.10
Hyperspectral imaging11 (HSI) is a noninvasive and contactless method that provides more information on a surface’s reflectance than conventional color imaging, by collecting spectral information at many wavelengths. Using this modality of imaging, the spectral reflectance distribution can be acquired over a large area. Afterward, certain skin composition properties, such as melanin concentration or blood oxygen rate, can later be estimated pixel by pixel and displayed in the form of images or maps, using an optical model combined with a skin structure model. In previous work by Séroul et al.,7 a two-flux model applied to a two-layer skin structure was shown to give satisfactory results when computing up to five skin composition maps of , from hyperspectral images captured using the SpectraCam® camera7,12 (Newtone Technologies, France). The efficacy of this device, however, is limited to planar areas of maximum dimensions and has not been designed to take into account the effect of shadows occurring on complex three-dimensional (3-D) objects. When shadows are not taken into account during image processing, the spectrum variation due to irradiance drift can be interpreted as a variation of skin properties, leading to errors in the skin analysis. The combination of HSI with 3-D scanning suggests itself as a solution to overcome the aforementioned limitations, allowing for accurate measurement of large, nonflat areas. We focus in this paper on the human face, the part of the body that presents the biggest challenge for 3-D scanning, as well as being of greatest interest to cosmetology. The method described, however, can be applied to any part of the human body.
Although 3-D spectral imaging is an active field of research, the few existing near-field 3-D spectral imaging systems are not entirely suited to broad spectral and spatial measurement on living organs. They are either multispectral systems13–15 providing spectral resolutions that are too low to be used for optical analysis, or in the case of those 3-D spectral imaging systems that do provide high spectral resolutions,16 the acquisition process is not adapted to living subjects. As the capacity of HSI to reveal fine details is directly related to the image resolution, an imaging system with high spatial and spectral resolutions is necessary. Moreover, a short acquisition time is required to reduce the risk of the subject moving during acquisition. A final consideration is the computation time needed to analyze the spectral information. As computation time increases proportionally to the number of pixels, the skin model and the optical model chosen should be as simple as possible to make the time needed for data analysis acceptable. The above constraints have led us to develop the 3-D hyperspectral measurement setup and the method of analysis presented in this paper. Our approach differs from existing methods for imaging still objects,17 by combining several elements into a unique solution in the field of skin measurement. The novelty of our acquisition method is that it allows for a short acquisition time with optimal spatial and spectral resolutions using a single camera, making it suited to wide-field in vivo measurements. For each part of the project, calibration methods, performance, and limitations are discussed. In addition, two solutions for addressing the shadowing effects are investigated: the first consists of using the 3-D information to correct shadows according to radiometric principles; the second uses a metric that is robust to shadows as part of the optical analysis optimization.
The remainder of this paper is structured as follows: the measurement setup is described in Sec. 2, hyperspectral acquisition and 3-D scanning are discussed in Secs. 3 and 4, the question of irradiance correction is addressed in Sec. 5, and optical analysis of the measured data is detailed in Sec. 6. Finally, conclusions are drawn in Sec. 7.
2. Three-Dimensional Hyperspectral Acquisition Setup
The proposed 3-D hyperspectral acquisition system is an extension of the existing hyperspectral camera, SpectraCam®7,12 (Newtone Technologies, France), incorporating the acquisition of depth map information and allowing wide field acquisition.
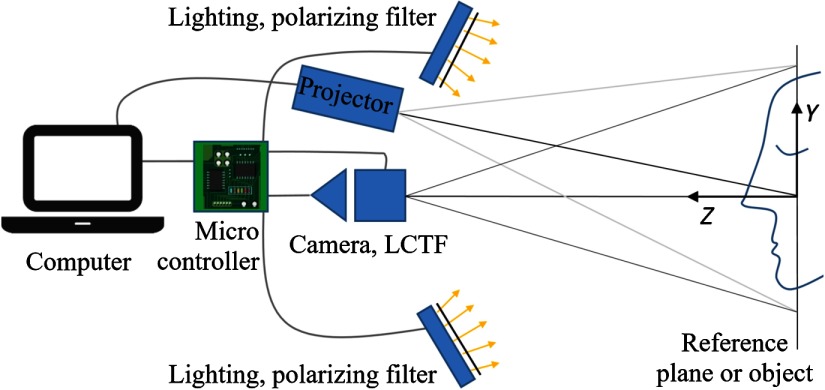
The setup, illustrated in Fig. 1, comprises two lighting systems used sequentially. The first is a portable digital LED projector (ML330, Optoma, Taiwan) used to project fringes for depth map acquisition. The angle between the camera and the projector is and allows full face acquisition while minimizing the occluded areas. The second comprises two LED lighting units, designed with blue and white LEDs, which provide sufficient irradiance on the skin over the whole visible spectrum for the hyperspectral acquisition. The sensor part is composed of a monochrome CMOS camera (acA2040-90um, Basler, Germany), a 35-mm focal length lens, and a liquid crystal tunable filter (LCTF) (VariSpec, PerkinElmer).
Fig. 1.
Schematic representation of the acquisition system.
Linear polarizing filters are added to each lighting unit. They are oriented to create a cross-polarized (CP) configuration with the LCTF polarization direction, the latter playing the role of an analyzer for the reflected light. This CP configuration is used to remove the gloss component of the reflected light: when light interacts with a diffusing medium, a portion of the flux is reflected by the air–medium interface according to the Fresnel formula, without being scattered and without any change in polarization. This specular reflection of light, related to the visual attribute called gloss, is removed by the analyzer in a CP configuration. The remaining portion of flux, constituting the diffuse reflection, is depolarized from being scattered, partially crosses the analyzer, and can reach the sensor. In the rest of this paper, the specularly reflected light will be discarded and only the unpolarized light component will be addressed. For nonsmooth surfaces such as skin, it can be noted that the diffuse reflection is the sum of surface diffusion and volume diffusion, with only the latter being of interest in our application, as it contains information about absorption and scattering properties of the material.
A panel is used for reference and calibration, defining the and axes of the Cartesian coordinate system shown in Fig. 1. The panel is perpendicular to the optical axis of the camera ( axis) and is mounted on a translation system, which allows precise translations along the axis. The camera and projector pupils are located on the same () plane.
Hyperspectral images over the visible spectrum (400 to 700 nm) and data for 3-D reconstruction are sequentially acquired in around 5 s, a duration that does not totally obviate the risk of the subject moving but remains acceptable.
3. Hyperspectral Imaging
HSI extends classical RGB imaging by replacing the three channels corresponding to three large wavebands with a significantly higher number of narrow wavebands covering the entire visible spectrum (and possibly the UV and IR domains). Hyperspectral image data are also called “hypercubes” since they are three dimensional: two dimensions corresponding to the spatial domain, one dimension corresponding to the spectral domain. The information captured in each pixel is proportional to the spectral radiance coming from one direction in the camera’s field. By dividing the spectral radiance measured from the object with the spectral radiance measured from a perfectly white diffuser illuminated identically as the object, the spectral reflectance factor of each pixel is obtained. This spectral reflectance factor is often considered equivalent to the spectral reflectance, but this is theoretically true only when the object is a Lambertian reflector.
Various HSI systems have been developed using diverse approaches, resulting in different specificities in terms of spatial resolution, spectral resolution, surface shape constraints, and acquisition time.11 The considered method is a wavelength scanning approach also called staring approach. This method relies on successively recording the full spatial information for each spectral band and requires a temporal scan of the spectral dimension. It relies either on active illumination or on adding a filtering system in front of the sensor, which can be a filtering wheel, a tunable filter, or an interferometer. Active illumination methods,18 which consist of illuminating the object using multiple light sources with discrete narrow spectral bandwidths, seem promising in terms of cost and acquisition time, given the availability of a wide range of LEDs with different emission spectra. However, it is often difficult to achieve a homogenous illumination of a complex 3-D shape like a human face, which is why we have opted for a wavelength scanning approach using an LCTF.
3.1. LCTF-Based Hyperspectral Camera
LCTF allows rapid filtering scanning within the visible spectrum while providing a sufficiently high spectral resolution for skin study. It is based on the association of several Lyot filters19 and is equivalent to high-quality interference filters with a bandwidth of 10 nm and a precision of 1 nm for the central wavelength. The data obtained with the hyperspectral camera are uncalibrated hypercubes of wavelengths covering the visible spectrum (400 to 700 nm) with an acquisition time of .
3.2. Camera Calibration
Once the hyperspectral acquisition has been performed, a radiometric calibration is necessary to retrieve the reflectance information from the measured radiance. The radiance measured on each pixel () for each wavelength depends on: the surface reflectance of the object (assuming that the object is Lambertian); the incident irradiance ; the sensor sensitivity ; the camera’s lens transmittance ; and the background noise , estimated to be similar on all the images:
| (1) |
, and are the unknown parameters that are calibrated via the acquisition of the radiances and on black and white reference Lambertian samples (4A Munsell color, references N 9.5/ for white and N 2/ for black, Munsell Color) of respective albedo and . The expression of the measured radiance [respectively, ] can be obtained by replacing with [respectively, ] in Eq. (1). The calibration, illustrated by Fig. 2, results in the object reflectance for each pixel and each wavelength after applying the formula:
| (2) |
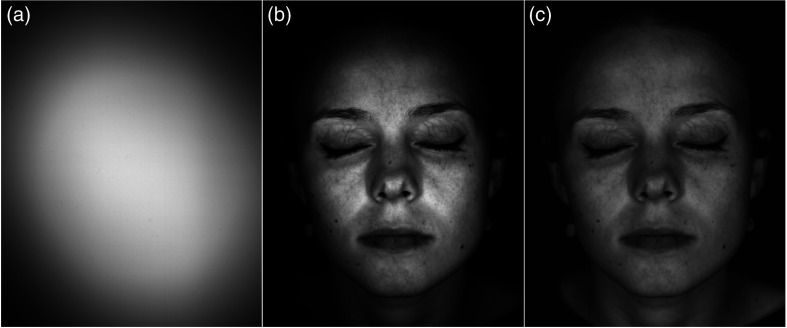
Fig. 2.
Acquired and corrected images at 590 nm: (a) nonuniform illumination on the white reference plane, (b) uncalibrated image, and (c) calibrated image.
3.3. Hypercubes and Color Images
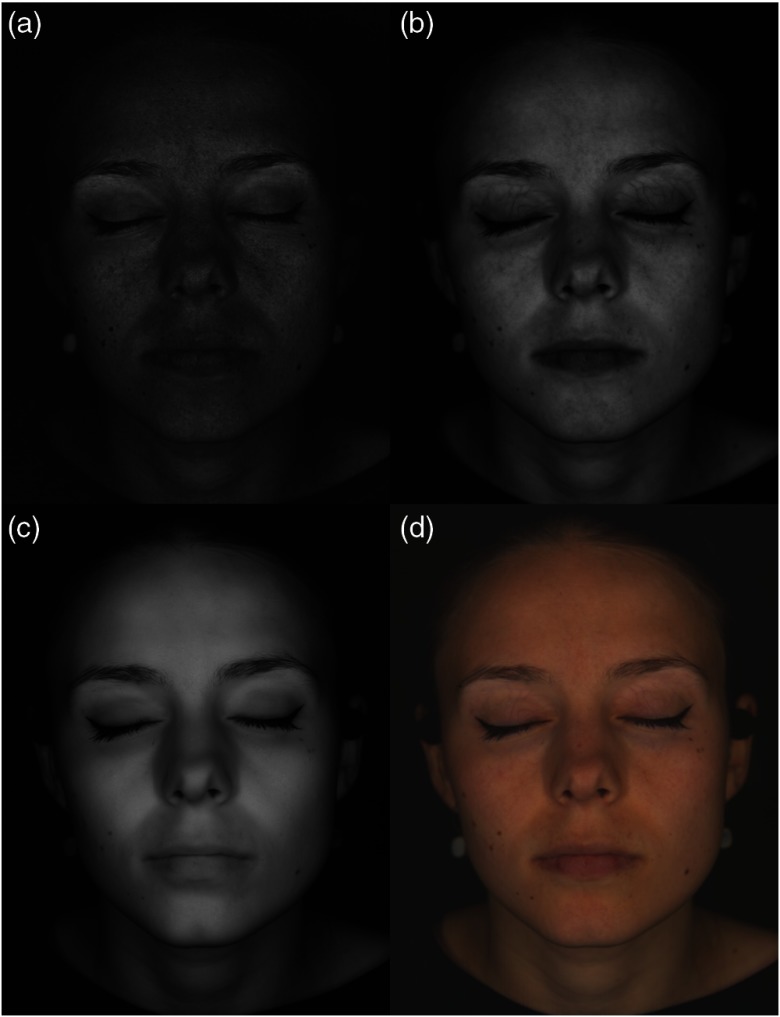
The calibrated images can be visualized at any defined wavelength [Figs. 3(a)–3(c)] or converted into a color image [Fig. 3(d)]. Each of the chosen wavelengths shown in Fig. 3 highlight a specific skin characteristic: melanin stains are visible in the lower wavelengths [Fig. 3(a)], blood vessels can be visualized with a good contrast between 560 and 600 nm [Fig. 3(b)], and finally, when seen in infrared [Fig. 3(c)], the skin appears uniform and more transparent, due to blood being transparent in this waveband and to skin scattering light less at higher wavelengths.
Fig. 3.
Example of a hyperspectral image: (a) image at 420 nm, (b) image at 590 nm, (c) image at 700 nm, and (d) color image after D65 illuminant RGB conversion.
From each hypercube, it is possible to calculate the RGB colors perceived under a given illuminant [Fig. 3(d)]. First, the spectrum in each pixel is converted into tri-stimulus values () of the CIE1931 color system using the color matching functions , and .20 Then a matrix transform is used to convert the obtained values into sRGB values.
3.4. Discussion and Performance
The implemented hyperspectral camera captures hypercubes with resolution adequate for analysis: spatial resolution is high enough for seeing fine details, and spectral resolution is sufficient for estimating concentrations of skin components (Sec. 6).
The proposed calibration method gives satisfactory results when applied to flat objects. Applied to 3-D objects, however, the incident irradiance on the reference samples differs from the incident irradiance on the measured object, which results in an error in the calibration output. For example, this is observable in Fig. 2(c), where the sides of the nose appear darker than the rest of the skin. For nonplanar objects, a “3-D irradiance calibration” (described in Sec. 5), requiring a more complex photometric calculation and knowledge of the 3-D geometry of the object, is necessary to retrieve the spectral reflectance independently from irradiance variations.
The spectral performance of the camera was investigated by measuring an A4 Munsell sheet (X-Rite) representing the color of light skin (reference CC2 of the ColorChecker®). Two areas of different sizes were analyzed, as illustrated in Fig. 4. Area 1 corresponds to the entire field of view of the camera and is larger than a human face. Area 2 is of a smaller size, comparable to that of a human face. The spectrum and the color values (obtained after a conversion using D65 illuminant as a white reference) of the acquired data were compared to values measured on the same sample using the X-Rite Color i7 spectrophotometer (X-Rite). The results are shown in Fig. 4(b) and Table 1. On average, the measured spectra of the two areas are similar. The high standard deviation observed in Area 1 can be explained by the border of the image being affected by noise. This is not the case for the measurement of Area 2, the camera can, therefore, be used for full face measurement as long as the corners of the image are not part of the area of interest. The color difference between the camera measurement and the Color i7 measurement on Area 2 is 2.41. This difference, which appears on the spectral reflectance factor graph [Fig. 4(b)] as a constant shift, is the consequence of using two different configurations for the measurements. The Color i7 spectrophotometer measurement was obtained using the “specular reflection excluded” mode of the device, which means that the light in the specular direction is excluded, whereas the light scattered everywhere else in the hemisphere is measured. The hyperspectral camera relies on a CP configuration to discard the gloss component of the reflection, which implies that all the scattered light is cut by the polarizer. In that latter configuration, more flux is discarded and the recorded reflectance factor is therefore lower. For skin analysis, this difference is not problematic, as it does not affect the shape of the spectrum that contains the “spectral signature” of the measured area.
Fig. 4.
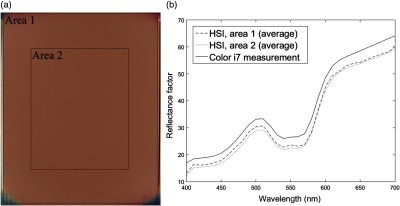
(a) Color image of an A4 light skin Munsell sheet measured using the hyperspectral camera and (b) average spectrum on three different areas (dotted lines) and comparison with the spectrum acquired using the X-Rite Color i7 spectrophotometer (solid line).
Table 1.
CIE1976 values acquired on the Munsell sheet using the Color i7 and the hyperspectral camera.
| Color i7 | HSI Area 1 | HSI Area 2 | ||
|---|---|---|---|---|
| Mean value | 64.65 | 60.86 | 62.28 | |
| 13.57 | 14.77 | 14.20 | ||
| 17.84 | 18.75 | 18.34 | ||
| REF | 3.86 | 2.41 | ||
| Standard deviation | — | 5.47 | 0.47 | |
| — | 18.77 | 0.89 | ||
| — | 27.75 | 0.78 |
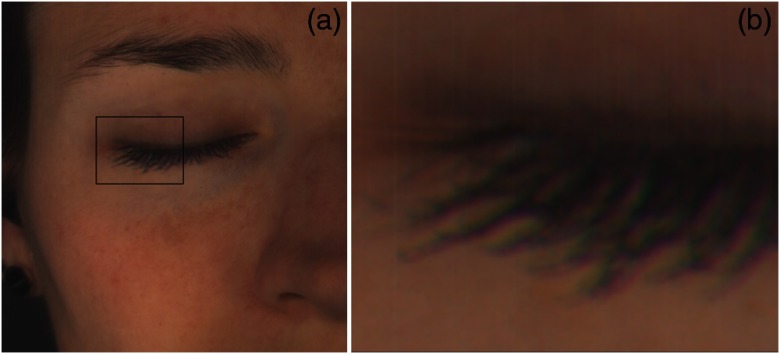
Finally, the LCTF and the camera bring chromatic distortion, resulting in spectral errors on small objects in the image, such as spots and hairs. This chromatic error, which can be described as a geometrical distortion for each spectral channel of the camera, is not visible to the eye, but can lead to errors of analysis, discussed in Sec. 6. Chromatic errors can also result from the subject moving during the acquisition process. The eyelashes are especially susceptible to involuntary micromovements during acquisition, as illustrated in Fig. 5.
Fig. 5.
Example of chromatic error on eyelashes due to small movement: (a) part of the face image and (b) zoom on the eyelashes.
4. Three-Dimensional Scanning
Various optical and imaging technologies offer noncontact methods for scanning the geometry of an object.21 Most existing methods fall into two categories: passive and active. Passive methods rely on ambient light, whereas active methods require controlled illumination. Stereovision, a typical passive method, mimics binocular vision and capture a scene from at least two points of view. The 3-D geometry is estimated using the triangulation principle, after solving a correspondence problem between the positions of a set of defined points on the images. Structured light projection is an active method based on the same triangulation problem, but contrary to stereovision, one of the cameras is replaced with a controllable illumination source that projects a pattern onto the object.22,23 This makes the correspondence problem easier to solve, especially when the texture of the object is smooth.
The scanning system we have developed is based on sinusoidal fringe projection with a phase-shift method,24 a structured light projection method offering an excellent compromise between speed, quality, and cost. Fringe projection also allows using the same camera for both hyperspectral and 3-D acquisition, which reduces the complexity of the system by having a single camera while ensuring a good pixel-to-pixel correspondence between the 3-D shape and the texture.
4.1. Triangulation Principle
Sinusoidal fringes are projected onto an object and deformed according to the object geometry. Once the phase deformation is measured, the triangulation principle22 is applied to retrieve the depth information between the object and the reference plane. The depth between the acquired object and the reference plane satisfies the following equation:
| (3) |
where is the phase recorded by a pixel of the camera on the object, is the phase recorded by the same pixel of the camera on the reference plane, is the fringe frequency on the reference plane, is the distance between the projector and the camera, and is the distance between the camera and the reference plane along the optical axis of the camera.
4.2. Acquisition and Reconstruction of the Phase
The phase shift method24 is used to obtain information about each pixel (). fringe images, defined by the following equation, are projected:
| (4) |
where is the average intensity and is the intensity modulation.
The projected images () represent identical fringes, each of which are successively shifted by . From the images () recorded by the camera, the modified phase is given by
| (5) |
The grayscale image (or measured radiance) is given by
| (6) |
The selection of the value is contingent upon the application requirements. When increases, the acquisition time also increases but noise is reduced.25 The observed noise, a consequence of the nonlinearity of the projector-to-camera gray scale function, is specific to fringe projection for 3-D acquisition: it is periodic, with a period of multiplied by the period of the projected fringes. An value around 5 or 6 is a good compromise between noise reduction (which is already much lower than with ) and acquisition time (which should be as low as possible for live surfaces, which are subject to movement).
The phase calculated according to Eq. (5) is discontinuous since its values are restricted to the interval (). The continuous phase is retrieved through a phase unwrapping algorithm. Since a temporal phase unwrapping method26 relying on multiple frequency acquisition increases acquisition time, a spatial solution using the continuity between pixels has been chosen. We have opted for Ghilia’s “2-D unweighted phase unwrapping,”27 which has shown sufficient robustness to noise for facial acquisition and adapted it for masked images (Fig. 6).
Fig. 6.
3-D acquisition intermediate results: (a) recorded fringe image, (b) wrapped phase computed from six fringe images, and (c) unwrapped phase on a selected zone of interest.
4.3. Calibration
The acquisition process comprises two calibration steps for 3-D scanning: a radiometric calibration, which has to be done prior to generating the projected fringes and a geometrical calibration, which allows the conversion of the phase into () coordinates expressed in millimeters.
4.3.1. Radiometric calibration
The projected fringes must be perfectly sinusoidal to ensure optimal 3-D reconstruction quality. In practice, however, the sinusoidal profile of the projected image is often distorted due to the radiometric nonlinearity of the projector. A radiometric calibration25 is, therefore, necessary. The method we have selected consists in measuring the projector nonlinearity and creating corrected fringes. To computationally correct the fringes, multiple gray levels are projected successively onto the reference plane. The measured gray levels are plotted against the input gray levels, then the quadratic polynomial that best matches the experimental curve is identified using a least-square algorithm. Finally, a lookup table is created to relate each targeted gray level of an 8-bit scale and the value given as an input of the projector.
This radiometric correction, however, only takes into account the effect of the projector nonlinearity and does not account for projector resolution, which also limits the fringe quality. Furthermore, as skin is a turbid medium, subsurface scattering is inevitable, deteriorating the quality of the projected fringes by blurring the projected image. This subsurface scattering can be described by a point spread function (PSF) or by a modulation transfer function (MTF) in the Fourier domain. In theory, the effects of scattering on a pattern projected onto a medium can be estimated by the convolution of the PSF of the medium with the projected pattern. This is equivalent to a multiplication in the Fourier domain of the medium MTF and the Fourier transform of the pattern. When the projected pattern is sinusoidal, its Fourier transform is a Dirac delta function. Hence, whatever the PSF of the medium, the result of the multiplication in the Fourier domain remains a Dirac delta function and the impact in the real domain is a loss of contrast. In practice, however, the implemented radiometric calibration was not able to guarantee a perfectly sinusoidal output signal, resulting in distortion caused by subsurface scattering. This subsurface scattering can be minimized by limiting the acquisition to the blue channel28 of the projector, which is the waveband, in which the skin is the most opaque (the lower the wavelength, the higher the opacity). However, as the camera in the proposed acquisition setup is more susceptible to noise in this waveband, we have chosen to perform 3-D scanning at a green wavelength (520 nm).
4.3.2. Geometrical calibration
To convert the phase information into depth information, the geometrical parameters , and must be determined. These parameters, which depend on the pixel location (), are difficult to measure accurately and require a calibration step. We have chosen to use a nonlinear calibration proposed by Jia et al.,29 which relies on the acquisition of several phase maps on planes located at several positions () along the axis to find two coefficients and in each pixel such that
| (7) |
A minimum of three acquisitions is necessary, but further measurements can be performed to obtain better estimates of and by applying a least-square algorithm.
Once the and coefficients, in , have been determined, the object depth map can be retrieved. A ruler is imaged to obtain the pixel-to-millimeter ratio, in order to compute a point cloud that represents the object surface in the real world coordinate system, which can also be described as the “2.5-D” information. The method that we have implemented is basic and assumes that the area of interest is not affected by optical distortion and that the acquired depth range is sufficiently small for the pixel-to-millimeter ratio to remain the same on the whole object.
4.4. Three-dimensional Mesh and Color Mapping
Three-dimensional scanning produces a depth map that needs to be converted into a mesh in order to be displayed as a 3-D object. The depth map is first filtered with a low-pass Butterworth filter to reduce noise [Fig. 7(b)], then converted into a vtk 3-D file using a function from the visual toolkit (VTK)30 library [see Fig. 7(c)]. During 3-D mesh conversion, a texture can be added to represent information such as reflectance for a given wavelength, or color, or to visualize chromophore maps calculated with the skin analysis algorithm described in Sec. 6. Figure 7(d) shows the results of the 3-D scanning and HSI after conversion of the spectral reflectances into RGB colors (assuming a D65 illuminant).
Fig. 7.
(a) Three-dimensional hyperspectral acquisition results: depth map before smoothing, (b) depth map after smoothing, (c) 3-D mesh without texture, and (d) 3-D mesh with color texture.
4.5. Measurement Accuracy
The precision of the acquisition system has been ascertained by measuring a tilted plane. The analysis of the 3-D results presented in Fig. 8 shows that the noise is not only white but a combination of white noise, periodic noise, and a low-frequency deformation. On an opaque plane such as the one used for the accuracy measurement, the periodic noise results from the projector–camera nonlinearity and varies depending on the fringe frequency and the number of images used in the phase-shift method. This periodic noise is not visible in Fig. 8 but appears more clearly after smoothing the white noise using a Gaussian filter. The low-frequency deformation is caused by the geometrical distortions of the camera and the projector, resulting in distance greater disparity between the best fitting plane and the acquired data on the corner of the image, as seen in Fig. 8(b). For face acquisition, the region of interest is located in the center of the image; therefore, the distortion observed in the corner of the image does not significantly affect our results.
Fig. 8.
(a) Point cloud display of the measured titled plane before smoothing and (b) difference between the measured data and the best fitting plane.
The maximum deviation between the acquired data and the best-fitting plane in the region of interest is 1.4 mm, the average deviation is 0.3 mm, and the standard deviation is 0.4 mm. These measured deviations are to be interpreted as minimum values characterizing the acquisition method on nontranslucent objects. For in vivo skin acquisition, noise can also be caused by unintentional movements during acquisition, blurred fringes resulting from the limited depth of field of the projector,25 and diffuse fringes due to the acquired object not being opaque but turbid. The acquisition setups must be optimized to minimize noise: the acquisition time must be short, the camera focus must be carefully adjusted and the red channel must be avoided (as discussed in Sec. 4.3.1). The acquisition accuracy of the current method is acceptable for full face acquisition, regarding the simplicity of the setup. However, for applications targeting finer details, such as wrinkles, higher precision would be necessary.
5. Irradiance Correction
As mentioned in Sec. 3.4, a simple radiometric correction based on a flat reference sample is inadequate to provide accurate spectral measurement of complex 3-D objects. When a hyperspectral acquisition is performed on a full face, the reconstructed color is a faithful representation of the actual spectral reflectance under the considered illuminant only on the areas perpendicular to the lighting, i.e., the forehead and the cheeks. The other areas of the face are shadowed, that is to say, the measured spectral reflectance corresponds to the actual reflectance multiplied by a factor that accounts for the difference between illumination on the surface and the illumination on the reference. To address this limitation, an irradiance correction method is considered as a preprocessing of skin optical analysis. The proposed method is an extension of the spectral calibration detailed in Sec. 3.4 to a “3-D irradiance correction.” By assuming in a first approximation that the skin is a Lambertian reflector and acquiring the 3-D geometry of the object, we can compute the irradiance of each pixel and subsequently perform an irradiance normalization.
Such a method has been implemented by Gioux et al.31 on spatially modulated imaging for a single illumination configuration, using the angle between the object surface and the optical axis of the camera. This method, however, is valid only for a punctual illumination. As we have used a complex illumination configuration to acquire the hyperspectral image, our approach must consider the full geometry of the acquisition system, using radiometric calculation. First, the quantity of light received on each point of the object from a single punctual source must be computed. The result is then extended to the full hyperspectral image.
5.1. Irradiance Normalization for Single Illumination Configurations
Let us consider the following configuration: a punctual source emits light in a cone, the object surface is Lambertian, and the area of interest is a small part of the object that corresponds to one pixel () when imaged on the camera sensor. This area receives the irradiance that can be expressed according to Bouguer’s law as a function of the source intensity in the direction of the object and the 3-D surface [i.e., the distance to the source and the angle between the normal of the surface and the lighting direction, illustrated in Fig. 9]:
| (8) |
Fig. 9.
Geometry of the object and the lighting, useful quantities for irradiance correction.
The application of Lambert’s law results in Eq. (9). For Lambertian surfaces, the radiance leaving the surface depends only on the reflectance of the object and on the received irradiance:
| (9) |
Finally, the radiance received on the pixel of the camera is given by Eq. (10) and depends on the radiance leaving the surface in the direction of the camera , the sensor response , the optics transmittance , the angular position of the pixel in the field of view of the camera , and the noise :
| (10) |
In Eq. (10), is a coefficient that depends on the properties of the camera (focal length, aperture, and pixel size). The combination of Eqs. (8)–(10) yields
| (11) |
The surface reflectance , which is the parameter to be determined, can be retrieved by performing a lighting calibration using a flat black sample and a flat white sample to provide the lighting intensity and the two quantities and related to the camera. The acquisition on the white reference plane of albedo can be described by
| (12) |
The acquisition on the black reference plane can be described by the same expression, by replacing with .
In Eq. (12), the pixel () corresponds to the area on the flat reference surface, which is illuminated under the same angle () as the area on the object imaged in the pixel (); is the distance between the light source and the pixel; is the angle between the normal of the reference plane and the illumination direction; and is the angular position of the pixel in the camera’s field of view.
In order to simplify Eq. (12), we assume that the lighting intensity of the projector is the same in the direction of the pixel () and in the direction of the pixel (). With this approximation, the reflectance of the object can be obtained independently from the sensor properties, the source intensity and the background noise, by combining Eqs. (11) and (12):
| (13) |
This formula is similar to the classical flat irradiance calibration described by Eq. (2), with an additional normalization factor that takes into account the 3-D geometry of the object.
5.2. Irradiance Normalization for Complex Illumination Configurations
In the proposed system, each lighting unit of the hyperspectral camera comprises 10 LEDs and the total incident irradiance is the sum of each LED’s irradiance. The difficulty of accurately knowing the position of each LED makes the method described above very difficult to implement for a hyperspectral image. Therefore, the method was adjusted to make it suitable for complex illumination configurations.
The 3-D scanning, performed for a single wavelength, provides the depth map and the radiance [see Eq. (6)] for a given wavelength . For this acquisition, the geometry of the lighting is simple because there is only one source, the digital projector, which emits light inside a cone. Its position can be determined by calibration. By performing an irradiance normalization using Eq. (13) on the output image of the 3-D scanning acquisition , the normalized reflectance factor for the wavelength is obtained. For this wavelength, the output of the hyperspectral acquisition is a non-normalized radiance [see Eq. (2)]. The ratio of the output of the irradiance normalization to this radiance gives a correction factor , which stands for all wavelengths. Finally, this correction factor is used on the hyperspectral image to obtain the normalized spectral reflectance factor for each wavelength:
| (14) |
where
| (15) |
5.3. Full Face Irradiance Correction Results and Performances
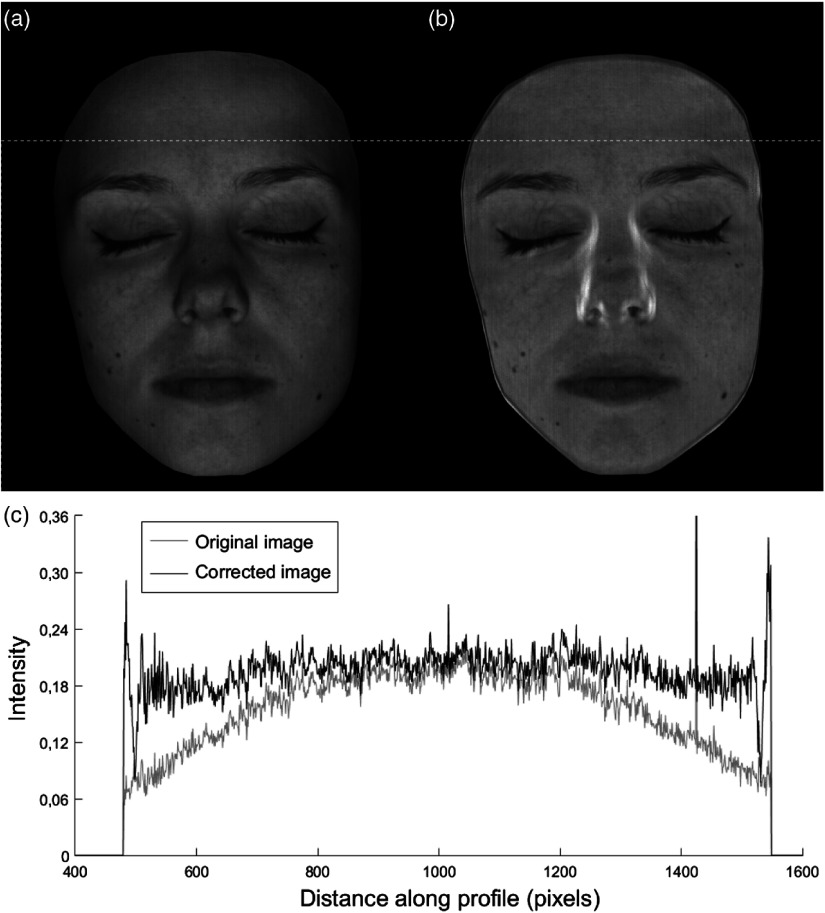
Figure 10 shows the results obtained in a simple configuration with the projector illuminating only the face, for a single wavelength (520 nm), before [Fig. 10(a)] and after [Fig. 10(b)] irradiance correction. Figure 10(c) shows the irradiance horizontal profile on the forehead before and after correction. The implemented method corrects the irradiance variation observed on the forehead. The curve observed on the gray line in Fig. 10(c) is the consequence of irradiance nonuniformities on the forehead but does not describe the skin reflectance on this zone. The black line shows that the reflectance profile is more homogeneous after applying the irradiance correction. Local variations are due to skin texture.
Fig. 10.
Image at 520 nm: (a) original image with incident irradiance nonuniformities, (b) image after correction, and (c) profile of the radiance intensity on the forehead before (gray) and after correction (black). The dotted line on images (a) and (b) indicates the location of the profile. For display purposes, the maximum gray level corresponds to a reflectance of 0.5.
Although this method yields good results for most parts of the face, there are areas for which it is not satisfactory. When , the angle between the lighting direction and the normal to the surface, is high, the cosine of the angle is close to zero. Since in Eq. (13), the original radiance is divided by , a small error on the angle yields a high error on the corrected reflectance factor. This can be seen on the sides of the nose, where the shadows are overcorrected.
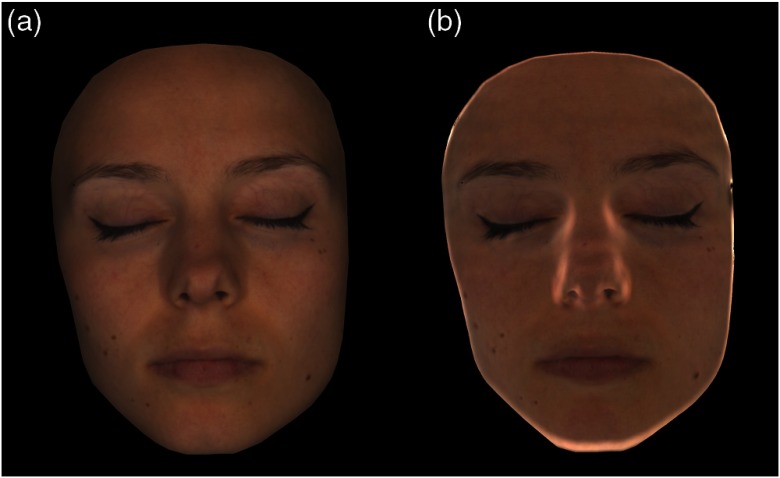
Figure 11 shows the results of the irradiance normalization method based on 3-D for the full hyperspectral image. The spectral image has been converted into a color image (D65 illuminant) for better visualization. Except for the overcorrected areas observed on the nose and border, the color result is satisfactory, which validates the irradiance correction method described by Eq. (14). However, the errors observed on areas such as the nose that seems inevitable with a depth map acquired from a single point of view, represent a limitation of this method.
Fig. 11.
(a) Original color image and (b) corrected color image.
Given this limitation, we have not implemented this irradiance correction method as a preprocessing for skin analysis. Instead, we have designed an analysis algorithm that is robust to irradiance shifts, described in the next section.
6. Optical Skin Analysis
The hyperspectral data analysis relies on two optical models: one for the skin structure that represents skin as a stack of two layers, and one for the light–skin interaction that predicts the reflectance of the skin according to the absorption and scattering properties of the two layers. These models are applied to describe a direct problem, used to solve the inverse problem by optimization and to compute chromophore concentration maps. The optimization method chosen is as robust as possible to irradiance drift in order to limit the impact of shadows on the chromophore concentration estimation.
6.1. Skin Model
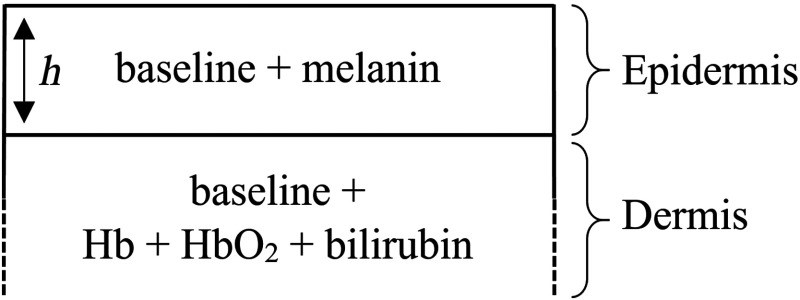
Our model considers the skin as a two-layer medium, roughly corresponding to the epidermis and the dermis, whose composition and optical properties are significantly different. The actual structure of skin is much more complex, as the epidermis and dermis can be further divided into several sublayers, each of which have their own specific cell structures and chemical compositions.1 The literature on tissue optics usually considers skin as a stack of between 1 and 22 layers. Some studies using Monte Carlo algorithms have limited their model to one layer to minimize calculation time;5 the Kubelka–Munk method is often applied using two layers;6 three layers have also been used to separate the dermis and the hypodermis;32 and Magnain showed that using the radiative transfer theory, the most accurate skin spectra were obtained using a 22-layer model.9 Our decision to use two layers is a trade-off between accurately describing the skin and a model that is sufficiently simple to allow for optimization-based model inversion: the higher the number of layers, the higher the number of parameters that must be taken into account by the algorithm—and concomitantly, the higher the risk of failing to find the minimum of the cost function during the optimization process, which can result significant errors. Our two-layer model does not separate the stratum corneum (SC) from the epidermis. The SC is the outermost layer of the epidermis composed of dead cells filled with keratin,1 especially affecting skin surface reflection, and consequently skin gloss. For our application, the CP configuration used in the imaging system discards this reflection. In addition, as the SC is a mainly scattering layer, which has little impact on the absorption properties that we are estimating, the nonseparation of the SC from the epidermis in our model has a little effect on our analysis results.
The two-layer model for skin (Fig. 12) is a simplification, in which each layer is considered as flat and homogeneous. The epidermis is composed of a baseline and melanin, and the dermis is composed of a baseline, deoxyhemoglobin (Hb), oxyhemoglobin (HbO2), and bilirubin.
Fig. 12.
Skin model used in the optical analysis of hyperspectral data.
Each layer can be characterized by absorption and scattering coefficients and . The absorption coefficient depends on the spectral absorption properties of chromophores contained in the layer and their volume fraction: according to the Beer–Lambert–Bouguer law, the spectral absorption coefficients of the epidermis and dermis can be written according to additive linear laws:
| (16) |
and
| (17) |
We refer to the work of Jacques33 for the spectral absorption coefficient values of the baseline , melanin , hemoglobin , oxyhemoglobin , and bilirubin , as well as for the spectral scattering coefficients of the epidermis and dermis . The volume fractions of melanin , hemoglobin , oxyhemoglobin , and bilirubin are unknown quantities that can be estimated through an optimization based on a two-flux model.
6.2. Two-Flux Model
The hyperspectral reflectance results are analyzed with a two-flux model described in Seroul et al.,7 where the light propagation in each layer of skin is described according to the Kubelka–Munk model.34 The advantage of the Kubelka–Munk model over other light scattering models is that it provides analytical formulae for the reflectance and transmittance of a multilayer scattering structure. The epidermis is characterized by its thickness , spectral absorption coefficient , and spectral scattering coefficient . Its reflectance and transmittance , expressed according to the Kubelka–Munk model, are (for each wavelength):
| (18) |
and
| (19) |
where
| (20) |
The dermis is assumed to be opaque, therefore, infinitely thick from an optical point of view. It is characterized by its spectral absorption coefficient and spectral scattering coefficient . Its reflectance , predicted according to the Kubelka–Munk model, is given by
| (21) |
where parameters and are functions of and , defined in the same way as in Eq. (20).
The total spectral reflectance of the skin, superposition of the dermis and epidermis, is given by Kubelka’s formula:34
| (22) |
6.3. Optimization Robust to Shadows
The direct model described above gives the skin spectral reflectance when the skin chromophore composition is known. In our case, we wish to determine the skin chromophore concentrations () from the measured spectral reflectance by solving the inverse problem. This process consists of finding for each pixel the parameters that minimize the distance between the measured spectrum and the theoretical spectrum [computed using Eq. (22)]:
| (23) |
The result of the optimization is dependent on the definition of the distance. A classical distance that can be used is the Euclidean distance, defined as
| (24) |
On complex shapes like the face, some areas receive less light and consequently the amplitude of the measured spectrum is lower. Using the Euclidian distance in the analysis algorithm, these irradiance nonuniformities can be mistaken for a change in the chromophore concentrations. In order to avoid these errors, the chosen metric must be independent from the spectrum amplitude, as is the case for the spectral angle mapper35 (SAM) (also equivalent to a normalized correlation), defined as
| (25) |
The SAM metric renders only the shape difference between the two spectra and is insensitive to irradiance variations. Owing to these properties, the use of the SAM metric yields better results for skin analysis and has been chosen to solve the problem of irradiance nonuniformities.
6.4. Skin Analysis Results
The skin analysis optimization gives the chromophore concentrations in each pixel. A map showing the residual distance of the optimization for each pixel has been created, allowing us to compare the performances of the different optimization metrics. Figure 13(a) shows the residual distance map obtained when using the SAM and Fig. 13(b) shows the residual distance map obtained when using the Euclidean distance.
Fig. 13.
Maps of the residual distance from the skin optical analysis: (a) SAM-based optimization, residual distance map and (b) euclidean distance-based optimization, residual distance map.
We can notice in Fig. 13(b) that the values of the Euclidean residual distance map are correlated with the shape of the face. As such, this metric cannot be applied on nonplanar objects unless each pixel receives the same incident irradiance. The SAM, on the other hand, is more robust to irradiance drifts: Fig. 13(a) shows that the optical analysis using SAM is good at distinguishing skin (low residual distance) from other elements such as hair, fabric, make-up, and background (high residual distance). This validates the use of the SAM rather than the Euclidean distance in the optimization. The residual distance map is not an error map, but it gives a general idea of the quality of the analysis.
The skin analysis results are displayed in the form of maps that show the concentrations of melanin, the oxygen rate, and the volume fraction of blood [Figs. 14(a)–14(c)]. Figure 14(d) shows the reconstructed color image obtained after color conversion (D65) of the simulated theoretical spectrum. This simulated spectrum is computed using the optical model [Eq. (22)] and the estimated chromophore concentrations. As the computation erases irradiance drifts, we have the impression that the face has been flattened, especially in the reconstructed color image.
Fig. 14.
Optical analysis results: (a) oxygen rate, (b) volume fraction of blood, (c) concentration of melanin, and (d) reconstructed color (D65 illuminant).
6.5. Performance and Discussion
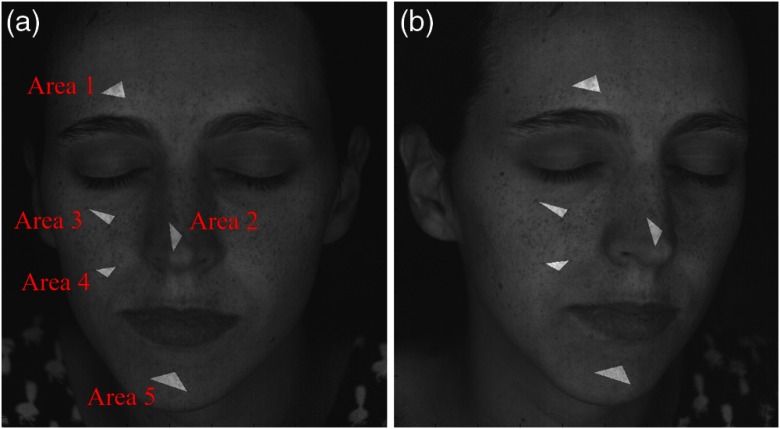
The error of this skin analysis method is difficult to assess as no ground truth chromophore concentration is available for in vivo measurements. It is also difficult to validate the method using skin phantoms as this would require samples of exactly the same structure and spectral properties as skin. The results of the SpectraCam® camera have been validated12 by showing that the estimated chromophore concentrations are consistent with those expected in terms of melanin when measuring skin with lentigos, and in terms of blood content and oxygen rate after applying local pressure to induce blood inflow. This method of validation can, however, only be applied to planar areas. On a full face, the proposed method can be validated by comparing two acquisitions of the same person at different orientations and verifying that the estimated chromophore concentrations remain similar. This comparison has been implemented by calculating the deviation between the average chromophore concentrations corresponding to the same areas on a front view and a side view. The areas used are illustrated in Fig. 15, and the results are shown in Table 2. The chromophore concentrations estimated using the analysis method are very similar on the two views of the face: for most values, the deviation is inferior to 3%, with values as low as 0%. The maximum deviation is 10.2%. Given the median deviation value of 2.3%, we consider that the results validate our method.
Fig. 15.
Areas selected for verifying the constancy of the chromophore concentration estimation independently from the orientation of the face: (a) front view and (b) side view.
Table 2.
Average chromophore concentrations for front and side view of the face, and deviation between the two measurements.
| Alpha (%) | Blood (%) | Melanin (%) | ||
|---|---|---|---|---|
| Area 1 | Front | 71.2 | 5.4 | 28.4 |
| Side | 71.6 | 5.3 | 30.6 | |
| Deviation | 0.6 | 0.8 | 7.4 | |
| Area 2 | Front | 70.8 | 9.0 | 35.4 |
| Side | 72.2 | 8.3 | 36.5 | |
| Deviation | 2.0 | 7.7 | 2.8 | |
| Area 3 | Front | 80.1 | 4.2 | 30.2 |
| Side | 80.1 | 4.6 | 33.4 | |
| Deviation | 0.0 | 7.7 | 10.2 | |
| Area 4 | Front | 82.7 | 6.0 | 28.3 |
| Side | 83.8 | 6.0 | 29.0 | |
| Deviation | 1.3 | 0.1 | 2.2 | |
| Area 5 | Front | 69.3 | 8.6 | 34.0 |
| Side | 72.1 | 8.4 | 35.9 | |
| Deviation | 4.0 | 2.3 | 5.7 |
A residual distance map, shown in Fig. 13, can also be used to see how far the spectral reflectance reconstructed in the skin analysis method deviates from the measured spectral reflectance at each point. A close examination of the fine details in Fig. 13(a) reveals that the residual distance is higher on small structures such as the eyelid blood vessels or on the border of nevi. This is caused by the chromatic aberration of the acquisition system: on small structures or on borders, the pixel spectrum is altered by chromatic aberration, affecting the pixel-by-pixel chromophore map. We can consider, however, that the number of pixels affected by this error is sufficiently low to be negligible in the final image.
Higher residual distance can also be found on regions such as the sides of the nostril and the ears, where the geometry is convex. A possible explanation for this is the occurrence of interreflections.36 Interreflections are multiple light reflections within a concave surface, which modify the reflected radiance as a nonlinear function of the spectral reflectance. These spectral modifications impact the chromophore map reconstruction and results in an error. We intend to investigate this topic in the near future.
Finally, error is also higher on the sides of the face, where the incident light is grazing. This is especially visible in Fig. 14(d) where the color on the side of the face is noticeably lighter and does not correspond to a realistic skin color as seen on the original picture. We interpret this as a limitation of the model: the optical analysis is based on the assumption that skin is Lambertian (ignoring the gloss component) and that the Kubelka–Munk model can be applied in the same way whether the observed surface is normal to the observation direction or not. However, at grazing angles, skin cannot be modeled as a Lambertian reflector. An extended model taking into account the angular dependence of the skin reflectance would be necessary to improve the accuracy of the method.
7. Conclusion
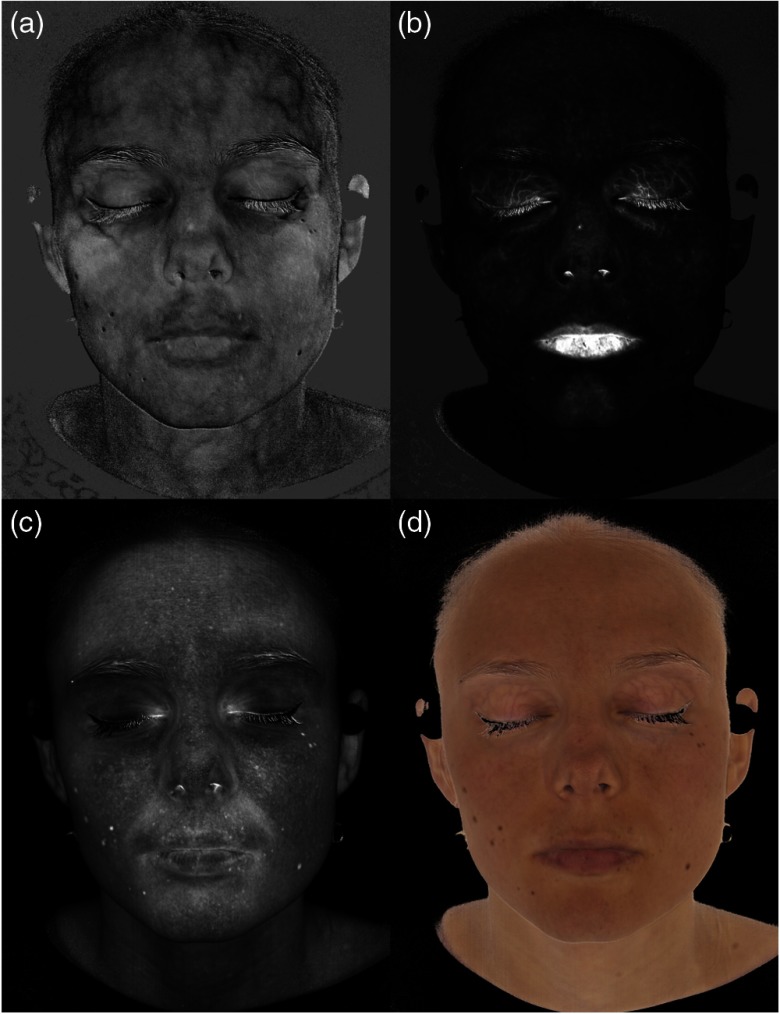
The developed system is, as far as we know, one of the first 3D-HSI systems conceived for living tissue, satisfying the requirements of large field of view, good spectral and spatial resolutions, and short acquisition time. Figure 16 shows the complete results of the 3D-HSI and skin optical analysis, with a spectral resolution of 31 wavelengths in the visible spectrum, a spatial resolution of 4 mega pixels, and an acquisition time of around 5 s. These 3-D displays are obtained by adding the color and chromophore maps as textures onto the 3-D mesh. The software used to display these images renders shadows using a virtual light source to give the impression of volume.
Fig. 16.
Three-dimensional hyperspectral acquisition results: (a) 3-D visualization of the oxygen rate, (b) 3-D visualization of volume fraction of blood, (c) 3-D visualization of the concentration of melanin, and (d) 3-D visualization of the color (D65 illuminant).
The possibility of using 3-D information for correcting irradiance nonuniformity and improving the measurement of spectral reflectance was the initial motivation for developing a 3-D scanning system. This study, however, demonstrates that although geometry-based irradiance correction is a “physics-based” method, the chosen approach is too sensitive to acquisition noise. A less “brute-force” method, which partially relies on optimization or deep learning, needs to be considered to address this issue. Nevertheless, the combination of 3-D scanning with HSI demonstrates high potential for other applications, such as investigating the bidirectional reflectance distribution function of objects without shape constraints, or providing shape information in addition to color. The visualization of the face in 3-D can be used to supplement chromophore map information, potentially aiding the study of skin properties that implicate shape.
Although the chromophore maps show very promising results, the method currently implemented for skin analysis does not take into account scattering, an important optical property of skin. Quantification of scattering could provide a better description of skin properties for applications such as inflammation or aging study. Such would require the addition of spatial frequency domain imaging to the proposed method and could be done with several minor modifications to the camera.
Acknowledgments
A preliminary version of this work was presented at IS&T Electronic Imaging Symposium, Material Appearance (Burlingame, USA, 29 January to 2 February 2018) and published in the conference proceedings.37 This work was supported by the Région Auvergne-Rhône-Alpes within the program ARC 6, and the French National Research Agency (ANR) as part of the program “Investissements d’Avenir” (ANR-11-IDEX-0007), in the framework of the LABEX MANUTECH-SISE (ANR-10-LABX-0075) of Université de Lyon.
Biography
Biographies of the authors are not available.
Disclosures
Cyprien Adnet and Pierre Séroul were full-time employees of Newtone Technology at the time of the study.
References
- 1.Igarashi T., Nishino K., Nayar S. K., “The appearance of human skin: a survey,” Found. Trends Comput. Graphics Vision 3(1), 1–95 (2007). 10.1561/0600000013 [DOI] [Google Scholar]
- 2.Matts P. J., et al. , “Color homogeneity and visual perception of age, health, and attractiveness of female facial skin,” J. Am. Acad. Dermatol. 57(6), 977–984 (2007). 10.1016/j.jaad.2007.07.040 [DOI] [PubMed] [Google Scholar]
- 3.Iglesias-Guitian J. A., et al. , “A biophysically-based model of the optical properties of skin aging,” Comput. Graphics Forum 34(2), 45–55 (2015). 10.1111/cgf.2015.34.issue-2 [DOI] [Google Scholar]
- 4.Zonios G., Bykowski J., Kollias N., “Skin melanin, hemoglobin, and light scattering properties can be quantitatively assessed in vivo using diffuse reflectance spectroscopy,” J. Invest. Dermatol. 117(6), 1452–1457 (2001). 10.1046/j.0022-202x.2001.01577.x [DOI] [PubMed] [Google Scholar]
- 5.Cuccia D. J., et al. , “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. Opt. 14(2), 024012 (2009). 10.1117/1.3088140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Doi M., et al. , “Estimation of local skin properties from spectral images and its application to appearance reproduction,” J. Imaging Sci. Technol. 60(5), 50404–1–50404–11 (2016). 10.2352/J.ImagingSci.Technol.2016.60.5.050404 [DOI] [Google Scholar]
- 7.Séroul P., et al. , “Model-based skin pigment cartography by high-resolution hyperspectral imaging,” J. Imaging Sci. Technol. 60(6), 60404-1–60404-7 (2016). 10.2352/J.ImagingSci.Technol.2016.60.6.060404 [DOI] [Google Scholar]
- 8.Nishidate I., Aizu Y., Mishina H., “Estimation of melanin and hemoglobin in skin tissue using multiple regression analysis aided by Monte Carlo simulation,” J. Biomed. Opt. 9(4), 700–710 (2004). 10.1117/1.1756918 [DOI] [PubMed] [Google Scholar]
- 9.Magnain C., Elias M., Frigerio J.-M., “Skin color modeling using the radiative transfer equation solved by the auxiliary function method,” J. Opt. Soc. Am. A 24(8), 2196–2205 (2007). 10.1364/JOSAA.24.002196 [DOI] [PubMed] [Google Scholar]
- 10.Tsumura N., Haneishi H., Miyake Y., “Independent-component analysis of skin color image,” J. Opt. Soc. Am. A 16(9), 2169–2176 (1999). 10.1364/JOSAA.16.002169 [DOI] [PubMed] [Google Scholar]
- 11.Lu G., Fei B., “Medical hyperspectral imaging: a review,” J. Biomed. Opt. 19(1), 010901 (2014). 10.1117/1.JBO.19.1.010901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nkengne A., et al. , “SpectraCam®: a new polarized hyperspectral imaging system for repeatable and reproducible in vivo skin quantification of melanin, total hemoglobin, and oxygen saturation,” Skin Res. Technol. 24(1), 99–107 (2018). 10.1111/srt.2018.24.issue-1 [DOI] [PubMed] [Google Scholar]
- 13.Paquit V. C., et al. , “3-D and multispectral imaging for subcutaneous veins detection,” Opt. Express 17(14), 11360–11365 (2009). 10.1364/OE.17.011360 [DOI] [PubMed] [Google Scholar]
- 14.Hirai K., Nakahata R., Horiuchi T., “Measuring spectral reflectance and 3-D shape using multi-primary image projector,” Lect. Notes Comput. Sci. 9680, 137–147 (2016). 10.1007/978-3-319-33618-3 [DOI] [Google Scholar]
- 15.Zhang C., et al. , “A novel 3-D multispectral vision system based on filter wheel cameras,” in IEEE Int. Conf. Imaging Syst. and Tech. (IST), IEEE, Chania, Greece, pp. 267–272 (2016). 10.1109/IST.2016.7738235 [DOI] [Google Scholar]
- 16.Kim M. H., “3-D graphics techniques for capturing and inspecting hyperspectral appearance,” in Int. Symp. Ubiquitous Virtual Reality, IEEE, Daejeon, Republic of Korea, pp. 15–18 (2013). 10.1109/ISUVR.2013.15 [DOI] [Google Scholar]
- 17.Chane C. S., et al. , “Integration of 3-D and multispectral data for cultural heritage applications: survey and perspectives,” Image Vision Comput. 31(1), 91–102 (2013). 10.1016/j.imavis.2012.10.006 [DOI] [Google Scholar]
- 18.Goel M., et al. , “HyperCam: hyperspectral imaging for ubiquitous computing applications,” in Proc. ACM Int. Joint Conf. Pervasive and Ubiquitous Comput. UbiComp, ACM Press, Osaka, Japan, pp. 145–156 (2015). [Google Scholar]
- 19.Gat N., “Imaging spectroscopy using tunable filters: a review,” Proc. SPIE 4056, 50–65 (2000). 10.1117/12.381686 [DOI] [Google Scholar]
- 20.Wyszecki G., Stiles W. S., Color Science: Concepts and Methods, Quantitative Data and Formulae, 2nd edn., Wiley, New York: (1982). [Google Scholar]
- 21.Remondino F., El-Hakim S., “Image-based 3-D modelling: a review,” Photogramm. Rec. 21(115), 269–291 (2006). 10.1111/j.1477-9730.2006.00383.x [DOI] [Google Scholar]
- 22.Lanman D., Taubin G., “Build your own 3-D scanner: 3-D photography for beginners,” in ACM SIGGRAPH Courses, ACM Press, New Orleans, Louisiana, pp. 1–94 (2009). [Google Scholar]
- 23.Gorthi S. S., Rastogi P., “Fringe projection techniques: whither we are?” Opt. Lasers Eng. 48(2), 133–140 (2010). 10.1016/j.optlaseng.2009.09.001 [DOI] [Google Scholar]
- 24.Srinivasan V., Liu H. C., Halioua M., “Automated phase-measuring profilometry of 3-D diffuse objects,” Appl. Opt. 23(18), 3105–3108 (1984). 10.1364/AO.23.003105 [DOI] [PubMed] [Google Scholar]
- 25.Li Z., Li Y., “Gamma-distorted fringe image modeling and accurate gamma correction for fast phase measuring profilometry,” Opt. Lett. 36(2), 154–156 (2011). 10.1364/OL.36.000154 [DOI] [PubMed] [Google Scholar]
- 26.Zuo C., et al. , “Temporal phase unwrapping algorithms for fringe projection profilometry: a comparative review,” Opt. Lasers Eng. 85, 84–103 (2016). 10.1016/j.optlaseng.2016.04.022 [DOI] [Google Scholar]
- 27.Ghiglia D. C., Romero L. A., “Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods,” J. Opt. Soc. Am. A 11(1), 107–117 (1994). 10.1364/JOSAA.11.000107 [DOI] [Google Scholar]
- 28.Wang Y., et al. , “3-D absolute shape measurement of live rabbit hearts with a superfast two-frequency phase-shifting technique,” Opt. Express 21(5), 5822–5832 (2013). 10.1364/OE.21.005822 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jia P., Kofman J., English C., “Comparison of linear and nonlinear calibration methods for phase-measuring profilometry,” Opt. Eng. 46(4), 043601 (2007). 10.1117/1.3116706 [DOI] [Google Scholar]
- 30.Kitware, “The visual toolkit,” https://vtk.org/ (2017).
- 31.Gioux S., et al. , “Three-dimensional surface profile intensity correction for spatially modulated imaging,” J. Biomed. Opt. 14(3), 034045 (2009). 10.1117/1.3156840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schmitt J. M., et al. , “Multilayer model of photon diffusion in skin,” J. Opt. Soc. Am. A 7(11), 2141–2153 (1990). 10.1364/JOSAA.7.002141 [DOI] [PubMed] [Google Scholar]
- 33.Jacques S. L., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37–R61 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 34.Kubelka P., “New contributions to the optics of intensely light-scattering materials part II: nonhomogeneous layers,” J. Opt. Soc. Am. 44(4), 330–335 (1954). 10.1364/JOSA.44.000330 [DOI] [PubMed] [Google Scholar]
- 35.Yuhas R., Goetz A., Boardman J., “Discrimination among semiarid landscape endmembers using the spectral angle mapper (SAM) algorithm,” in Summaries Third Annu. JPL Airborne Geosci. Workshop, I, JPL Publication, pp. 147–149 (1992). [Google Scholar]
- 36.Forsyth D., Zisserman A., “Mutual illumination,” in Proc. IEEE Comput. Soc. Conf. Comput. Vision and Pattern Recognit., IEEE, pp. 466–473 (1989). 10.1109/CVPR.1989.37889 [DOI] [Google Scholar]
- 37.Gevaux L., et al. , “Three-dimensional hyperspectral imaging: a new method for human face acquisition,” Electron. Imaging 2018(8), 152–1–152–10 (2018). 10.2352/ISSN.2470-1173.2018.8.MAAP-152 [DOI] [Google Scholar]