In silico study of the role of cell growth factors in photosynthesis using a virtual leaf tissue generator coupled to a microscale photosynthesis gas exchange model

We combined a virtual leaf tissue generator and a microscale model of gas diffusion. With this tool, we demonstrated that light-saturated photosynthesis could be improved by altering cell growth and development factors.

Abstract

Computational tools that allow in silico analysis of the role of cell growth and division on photosynthesis are scarce. We present a freely available tool that combines a virtual leaf tissue generator and a two-dimensional microscale model of gas transport during C₃ photosynthesis. A total of 270 mesophyll geometries were generated with varying degrees of growth anisotropy, growth extent, and extent of schizogenous airspace formation in the palisade mesophyll. The anatomical properties of the virtual leaf tissue and microscopic cross-sections of actual leaf tissue of tomato (Solanum lycopersicum L.) were statistically compared. Model equations for transport of CO₂ in the liquid phase of the leaf tissue were discretized over the geometries. The virtual leaf tissue generator produced a leaf anatomy of tomato that was statistically similar to real tomato leaf tissue. The response of photosynthesis to intercellular CO₂ predicted by a model that used the virtual leaf tissue geometry compared well with measured values. The results indicate that the light-saturated rate of photosynthesis was influenced by interactive effects of extent and directionality of cell growth and degree of airspace formation through the exposed surface of mesophyll per leaf area. The tool could be used further in investigations of improving photosynthesis and gas exchange in relation to cell growth and leaf anatomy.

Introduction

Leaf anatomy impacts the growth and yield of a plant through its influence on fundamental physiological processes such as water transport, CO₂ exchange, and light propagation during photosynthesis (Terashima et al., 2011; Buckley et al., 2015; Barbour et al., 2016). Improving photosynthesis efficiency for increased yield is an important research target (Zhu et al., 2010; Evans, 2013; Ort et al., 2015; Yin and Struik, 2017). Several researchers developed models at the cellular level, when experimental investigations become difficult, for improving insights into the influence of leaf anatomy on photosynthesis (Terashima et al., 2011; Ho et al., 2012, 2016; Defraeye et al., 2014b; Retta et al., 2016; Berghuijs et al., 2017; Gong et al., 2017; Wang et al., 2017), water transport (Defraeye et al., 2014a; Buckley et al., 2015), and light propagation (Terashima et al., 2011; Ho et al., 2016; Wang et al., 2017). Recently, some of these efforts have been integrated into crop growth models for assisting efforts to improve crop productivity (Xiao et al., 2017; Wu et al., 2018). Central to these studies is a geometric model of the leaf microstructure.

A representative model of the leaf anatomy is usually developed from a set of leaf anatomical parameters (Tholen and Zhu, 2011; Xiao et al., 2016; Wang et al., 2017). However, it is cumbersome to generate a large number of distinct leaf topologies, which could be desirable in simulation models to study the role of diversity in leaf anatomy in photosynthesis (Tholen et al., 2012). The geometric model may also be built from a reconstruction of images of the leaf anatomy obtained from imaging technologies (Ho et al., 2012, 2016; Retta et al., 2016; Earles et al., 2018). However, the image acquisition may involve complex procedures for sample preparation and image processing, or may require access to expensive infrastructures such as a synchrotron radiation facility (Verboven et al., 2015). Methods that allow generation of simulated microscale tissue structures exist today (Mishnaevsky, 2005; Mebatsion et al., 2006, 2008; Pieczywek and Zdunek, 2012; Rahman et al., 2018) but are essentially vectorized representations of images of the cellular architecture in 2D or 3D. The tissue geometries obtained from the aforementioned methods are not parameterized and thus difficult to use in studies on the responses of model-predicted rates of physiological processes to changes in microscopic tissue features. To circumvent these limitations, we have developed tissue generation algorithms that can produce representative parenchyma tissues in fruits in both 2D and 3D based on the biomechanics of cell growth (Abera et al., 2013, 2014). These generators have been proven useful for a systematic study of gas and water transport processes in fruits at multiple scales (Fanta et al., 2013, 2014; Aregawi et al., 2014). These were not yet extended to leaves to study the influence of leaf anatomy on photosynthesis.

The rate of photosynthesis per unit leaf area could be improved by curbing the limitation of leaf anatomy on CO₂ diffusion and light propagation through alteration of leaf anatomy (Zhu et al., 2010; Tholen et al., 2012; Lehmeier et al., 2017). Mesophyll architecture determines the tortuosity and porosity of the intercellular airspaces which could limit photosynthesis in low-porosity leaves (Parkhurst, 1994). In addition, stromal CO₂ concentration and available light to chloroplasts are influenced by the mesophyll geometry (Tholen et al., 2012), while the aspect ratio of mesophyll cells influences the uniformity of light distribution in the leaf (Terashima et al., 2001; Kume, 2017). Moreover, there are large differences in cell size distribution among various cultivars of the same species that contribute to considerable differences in the area of exposed mesophyll surface per leaf area and photosynthesis (Nobel, 2005; Verboven et al., 2015; Ouyang et al., 2017). Environmental conditions during growth also influence the size and columnarity of palisade mesophyll cells and the size and density of spongy mesophyll cells, which ultimately influence photosynthesis (Wilson and Cooper, 1970; Nobel et al., 1975; Vogelmann and Martin, 1993; Terashima et al., 2001; Tosens et al., 2012). While the limitations on C₃ photosynthesis imposed by leaf anatomy have been widely investigated, more research is needed to link cell division and growth, leaf development, and genetic and environmental cues to photosynthesis and productivity (De Vos et al., 2012; Evans, 2013; Furbank et al., 2015; Xiao et al., 2017). A detailed mechanistic mathematical model integrating such knowledge is currently sought after since it may assist in designing crops for better yield (Zhu et al., 2016; Xiao et al., 2017).

Traditionally, leaf dry mass per unit area (LMA) is used to study the influence of variations in leaf structure on photosynthesis (Niinemets and Sack, 2006; Poorter et al., 2009; Hassiotou et al., 2010). However, a strong relationship to photosynthesis may not always be obtained due to dissimilar associations of leaf density and leaf thickness, composites of LMA, with photosynthesis (Niinemets, 1999). The influence of leaf morphology on photosynthesis could be studied experimentally by a combination of cell cycle manipulation, measurement of photosynthesis using combined gas exchange and chlorophyll fluorescence, and imaging of the leaf anatomy in 3D using X-ray computed tomography (Dorca-Fornell et al., 2013; Lehmeier et al., 2017). However, experimental manipulation of leaf anatomy might result in simultaneous changes in other anatomical features and biochemical factors, thus impeding interpretation of effects of the manipulations on physiological processes (Dorca-Fornell et al., 2013). Alternatively, the role of cell division, growth, and development in physiology could be systematically studied using computer programs of virtual tissue growth coupled with models of relevant physiological phenomena (Merks et al., 2011; De Vos et al., 2012; Fanta et al., 2013, 2014; Aregawi et al., 2014; Bassel and Smith, 2016; Zhu et al., 2016). Moreover, 2D microscale gas transport models were shown to be effective in predicting the rate of photosynthesis, and they are better able than conductance-based models to investigate the CO₂ diffusion path in leaves at microscale (Ho et al., 2012; Berghuijs et al., 2017; Retta et al., 2017).

The objectives of this study were: (i) to develop a virtual leaf tissue generator algorithm and validate it using the real leaf anatomy of tomato (Solanum lycopersicum); and (ii) to quantitatively assess the influence of mesophyll topology, characterized by the aspect ratio of cells, volume of palisade mesophyll cells, and exposed length of mesophyll surface per leaf width (L_m), as determined by growth rates, degrees of growth anisotropy, and extent of airspace formation in palisade mesophyll, on light-saturated photosynthesis. The influence of leaf biochemical and biophysical factors on photosynthesis in conjunction with the diverse mesophyll architecture is also analyzed.

Materials and methods

Gas exchange measurements and leaf anatomy

Combined gas exchange and chlorophyll fluorescence measurements were carried out on tomato (S. lycopersicum L.) plants. The details of tomato plant growth conditions, gas exchange measurements, and acquisition of images of leaf anatomy were described by Berghuijs et al. (2015). In brief, tomato plants (cv. Doloress, De Ruiter Seeds, The Netherlands) were grown in a glasshouse at a day temperature of 21 °C and a night temperature of 16 °C. The photoperiod was 16 h. Combined gas exchange and chlorophyll fluorescence measurements were carried out using an infrared gas analyzer (LI 6400 XT, Lincoln, NE, USA) on 25-day-old leaves. Light microscopy images of the leaves were made (Berghuijs et al., 2015). Five replicates of images were digitized to obtain coordinates of individual cells in Matlab (The Mathworks, Natick, MA, USA) (Mebatsion et al., 2006). Three images were used to validate the model while the rest were used for calibration (see below). For convenience, these digitized leaf geometries are referred to as ‘real’, while the generated ones are referred to as ‘virtual’ from here on.

Virtual leaf tissue generator and leaf geometrical models

The virtual leaf tissue generator is based on a cell growth model explained in detail previously (Abera et al., 2013). In brief, the cell is conceptualized as an elastic thin-walled structure sustained by turgor pressure (Rudge and Haseloff, 2005). Initial cell wall network topologies are generated using a Voronoi tessellation which gives a random partitioning of a plane. Newton’s first law and Hooke’s law for springs are applied to simulate cell growth and expansion. Cell shapes are driven by net forces caused by turgor on the vertices of the network. Detailed explanation of the leaf tissue algorithm along with the full set of equations is given in Supplementary Protocol S1 at JXB online. Only those equations describing the technique used in generating topologies varying in the range of anatomical properties are given below. Definition of symbols, units, and values are given in Table 1.

Table 1.

Parameters of the cell growth and microscale CO₂ transport model

Variable	Symbol	Unit	Value	Notes and references
Net rate of photosynthesis	A	µmol m−2 s−1	–	Calculated
Net hydration of CO 2 to bicarbonate	B	µmol m−3 s−1	–	Calculated
Concentration of CO 2 at CO 2 fixation site	C c	µmol m−3	–	Calculated
Concentration of bicarbonate at the CO 2 fixation site	C HCO3 −	µmol m−3	–	Calculated
Diffusivity of CO 2 (25 °C)	D l	m2 s−1	$1.89\times {10}^{-9}$	Lide, 1999
Diffusivity of CO 2 in cell wall	C CW	m2 s−1	3.78×10–10	Assuming effective porosity of 0.20 (Evans et al., 2009)
Diffusivity of H CO3 –	D HCO3 −	m2 s−1	1.17×10–9	Geers and Gros (2000)
Average thickness of tissue	d	µm	–	Calculated from the topologies
Ratio of final and initial resting lengths of walls	F	–	1 (spongy mesophyll) 1–10 (palisade mesophyll)	See the Materials and methods
Henry’s constant for CO 2 (25 °C)	H	–	0.83	Lide (1999)
Maximum rate of electron transport	J max	μmol m−2 s−1	233.23	‘Doloress’ tomato (Berghuijs et al., 2015)
Spring constant of cells aligned along maximum growth direction	k min	MN m−1	Calculated	See the Materials and methods
Turnover rate of carbonic anhydrase	k a	s−1	3×105	Pocker and Miksch (1978)
Michaelis–Menten constant for carbonic anhydrase hydration	K CO2	mol m−3	2.8	Hatch and Burnell (1990)
Equilibrium constant of carbonic anhydrase	K eq	mol m−3	5.6×10–7	Pocker and Miksch (1978)
Michaelis–Menten constant of Rubisco for CO 2	K m,c	mbar	267a	Berghuijs et al. (2015)
Michaelis–Menten constant for carbonic anhydrase hydration	K HCO3 −	mol m−3	34	Pocker and Miksch (1978)
Michaelis–Menten constant of Rubisco for O 2	K m,0	mbar	164a	Berghuijs et al. (2015)
Conversion efficiency of light to electron transport	K 2LL	–	0.357	Berghuijs et al. (2015)
Length of mesophyll surface exposed to air per leaf width	L m	–	–	Calculated
Length to width ratio of palisade mesophyll cells	L:W	–	–	Variable
Initial resting length of cell wall	l n,0	µm	Computed	Abera et al. (2013)
Maximum resting length of cell wall	l n,max	µm	Computed	Abera et al. (2013)
Oxygen concentration in stroma	O 2	mbar	210	Assumed
CO 2 permeability of chloroplast envelope	P CO2	m s−1	3.5×10–3	Gutknecht (1977), or variable
Mitochondrial respiration	R d	µmol m−2 s−1	2.65	Berghuijs et al. (2015)
Relative CO 2 /O 2 specificity for Rubisco	S C/O	mbar µbar−1	3.260	Berghuijs et al. (2015)
Thickness of cell wall	t cw	µm	0.128	Berghuijs et al. (2015)
Thickness of cytosol	t cy	µm	0.212	Berghuijs et al. (2015)
Thickness of membrane	T mem	µm	0.02	Tholen and Zhu (2011)
Rate of triose phosphate utilization	T p	µmol m−2 s−1	13.6	Berghuijs et al. (2015)
Carboxylation capacity of Rubisco	V c,max	µmol m−2 s−1	274	Berghuijs et al. (2015)
Concentration of carbonic anhydrase	X a	mol m−3	0.27	Tholen and Zhu (2011)
Angle expressing directionality of cell wall growth	α	–	Computed	Abera et al. (2013)
Anisotropy factor	β	–	0 (spongy mesophyll)	See the Materials and methods
			0–1 (palisade mesophyll)
Polarity of cell growth	λ	–	0≤λ≤1	See the Materials and methods
Convexity factor	θ	–	0.797	Berghuijs et al. (2015)
Time constant for length to reach maximum	τ	s	200 000	Assumed
CO 2 compensation point	Γ* a	µbar	0.5O2/SC/O	Berghuijs et al. (2015)

^a These parameters were converted into µmol m⁻³ liquid by multiplying by PH/RT, where P=101 325 Pa, H=0.83, R=8.314 m³ Pa K⁻¹ mol⁻¹, and T=298 °K.

Cell growth is modeled by increasing the natural length (l_n) of the unpressurized cell wall. The change of l_n is given by (Abera et al., 2013):

$${\displaystyle \begin{array}{l}{\displaystyle \frac{\mathrm{d}{l}_{\mathrm{n}}}{\mathrm{d}t}=\frac{1}{\mathrm{\tau }}(l-l_{\mathrm{n}})(l_{\mathrm{n},\mathrm{m}\mathrm{a}\mathrm{x}}-l_{\mathrm{n}})}\end{array}}$$

where l is the actual cell wall length at a current time; l_n,max is the final resting length of the spring; and τ is the time constant. Anisotropic expansion of the cell wall is modeled by varying the spring constant of the wall k and l_n,max based on the orientation of cell walls (λ) as:

$${\displaystyle \begin{array}{l}{\displaystyle k=k_{\mathrm{m}\mathrm{i}\mathrm{n}}+k_{\mathrm{m}\mathrm{i}\mathrm{n}}(F-1)(1-\mathrm{ƛ})}\end{array}}$$

where k_min is the spring constant of the walls parallel to the maximum growth direction and F is the ratio of final and initial resting lengths (l_n,0) of the walls.

$${\displaystyle \begin{array}{l}{\displaystyle l_{\mathrm{n},\mathrm{m}\mathrm{a}\mathrm{x}}=\lambda (F-1)l_{\mathrm{n},0}+l_{\mathrm{n},0}}\end{array}}$$

Polarity of cell growth is expressed by λ which is given by:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{ƛ}=1-\beta \mathrm{c}\mathrm{o}{\mathrm{s}}^2(\mathrm{ɑ}+\frac{\mathrm{\pi }}{2})}\end{array}}$$

where β is the degree of growth anisotropy (0≤β≤1) and α is the angle between cell walls and the major axis of the cell.

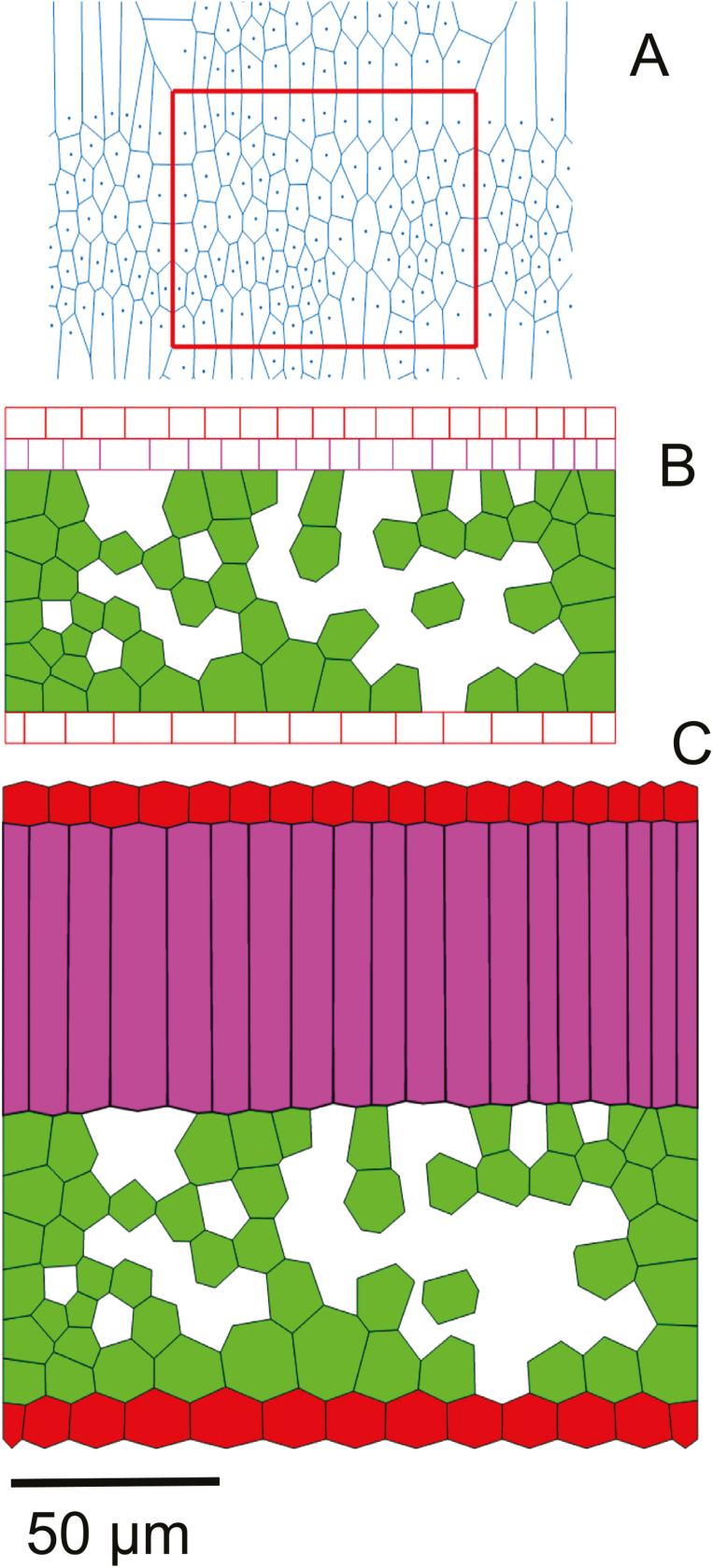
The initial topology consists of a Voronoi tessellation of the cells in the spongy mesophyll layer (Fig. 1A). Pores in the leaf tissue that result from death of cells (lysogenous origin) were simulated here using a procedure in Matlab (The Mathworks) that uses a convex envelope to select Voronoi cells that lie completely in the envelope. Some of these were then assigned to be pores to match porosity (Abera et al., 2013). Layers of rectangular cells for palisade mesophyll and epidermis were then added (Fig. 1B). Values of l_n,0 were obtained from this starting topology. k_min was calculated by dividing the assumed Young’s modulus of elasticity of the cell wall of 30 MPa (Abera et al., 2014) by the average value of l_n,0 . The value of C for all the walls of palisade mesophyll cells except those that are parallel to the major axis of each cell was set to 1. For walls of palisade mesophyll cells that are parallel to the major axis of growth, λ (Equation 4) was calculated assuming an anisotropy of 0.9. Only for the aforementioned walls, therefore, C was scaled using a fixed factor for the length to width ratio of those walls. Consequently, l_n,max is calculated using Equation 3. When a wall in a cell is perpendicular to the major axis of the cell, l_n,max=l_n,0 and growth is zero (Equation 1). The initial value of turgor pressure in the cells (Fig. 1B) was zero. Cell expansion results from turgor pressure acting on the yielding cell wall material. Velocities of vertices were then calculated from the net force due to the turgor and tension forces. The degree of growth anisotropy (Equation 8) was varied between spongy and palisade mesophyll cells to mimic their contrasting topology. Intercellular airspaces among adjacent walls were formed by loosening the zero-resting length springs, simulating the separation of cells along the middle lamella occurring during growth; this type of airspace formation is called schizogenous (Abera et al., 2013). The resulting topology is shown in Fig. 1C. At the end of growth, larger intercellular airspaces in the palisade mesophyll were created in a separate step. Depending on the extent of the airspace desired, a number of walls connecting the pores formed at the common vertex of three cells were removed, thereby connecting these pores (Abera et al., 2013). For this, a random number from a uniform distribution was chosen to determine the number of walls in the palisade mesophyll cell to separate. When all the parallel walls of palisade mesophyll are separated, maximum porosity is achieved. Formation of additional intercellular airspaces due to death of cells (lysigenous origin) was also simulated here by simple random sampling and removing some of the virtual cells. In this case, an airspace was introduced where three cells abut (Abera et al., 2013) and the extent of airspace formation within the palisade mesophyll cells, from here on, is referred to be as being ‘low’. The extent of airspace formation was further increased by selecting, from uniform distribution, the cell walls to be separated (Table 1) resulting in two extents of airspace formation, referred to as ‘medium’ and ‘high’.

Fig. 1.

Transformation of initial tessellations to leaf topology. The Voronoi tessellation (A) in the region of interest (red rectangle) combined with layers for epidermis and palisade mesophyll (B) was used in the simulation of tissue growth, resulting in the topology shown in (C). In (C), the epidermis is colored red while spongy mesophyll is light green and palisade mesophyll is magenta. Scale bar=50 µm.

The values of C and the growth anisotropy factor for palisade mesophyll cells were optimized using a separate set of light microscopy images as described above. The optimization minimized the differences in the mean area of cells and the aspect ratio between the images from light microscopy and the virtual leaf tissue generator in Matlab (The Mathworks).

The degrees of growth anisotropy of palisade mesophyll cells were varied to be 0.1 (close to isotropic growth), 0.5, and 1.0 (fully anisotropic growth in which growth in the direction of the major axis of the cells dominates) while that of spongy mesophyll cells was 0 (fully isotropic). For a given anisotropy factor, the l_n,max for palisade mesophyll cells walls that are parallel to major growth direction (λ=1) was scaled by setting the length to width ratio (L:W ratio) of palisade mesophyll cells from 1 in steps of 1–10 so that F (Equation 3) is changed (Table 1). For walls parallel to the growth direction (λ=0), F was set to 1 and thus growth (Equation 1) was zero.

The starting tessellation of Voronoi cells was varied to generate three replicate geometries for a given anisotropy factor and L:W ratio. The resulting airspaces were considered as the intercellular airspace. Consequently, a total of 270 leaf geometries (10 L:W ratio values by three anisotropy factors by three extents of airspace formation by three replicates) were generated.

Calculation of leaf anatomical parameters

The calculated leaf anatomical properties were cell shape, cell size, and the ratio of total length of mesophyll cells exposed to the intercellular airspaces to the length of the leaf (L_m). These properties have been shown to be relevant in assessing the influence of anatomy on photosynthesis of leaves (Berghuijs et al., 2015; Xiao et al., 2016). The porosity of virtual geometries was matched to that of real tissues by randomly removing some of the generated cells.

Aspect ratio is defined as the ratio of the minor diameter to the major diameter of a fitted ellipse (on the scale of 0–1). The diameters of the equivalent ellipses were calculated according to the procedure outlined by Mebatsion et al. (2006). Cells at the edge of the geometries were removed to avoid the bias in distribution as a result of cropping images. The size of cells presented as cell area (in 2D) was calculated by applying Green’s theorem to the vertices of the cells defining the boundaries of the cells (Kreyszig, 2005). L_m, for both the palisade and spongy mesophyll, was calculated as the sum of the length of walls of the cells exposed to the intercellular airspaces divided by the total length of the leaf. The geometrical properties such as mean aspect ratios, mean volume of palisade mesophyll cells (area in 2D due to azimuthal symmetry, A_p), leaf thickness, leaf width, and L_m were quantified to characterize the geometries.

The coordinates of cell vertices obtained for each geometry were exported to Comsol Multiphysics 5.0 (COMSOL AB, Stockholm) using the Matlab (v.18, The Mathworks) interface and converted into solid objects in Comsol to generate computational domains.

Microscale CO2 transport model and numerical simulations

Here we adapt the gas transport model for C₃ photosynthesis developed previously by Ho et al. (2012). The model combines kinetics of photosynthesis (Farquhar et al., 1980; Yin et al., 2004; Sharkey et al., 2007) and gas transport models to derive microscale CO₂ concentration profiles from which the photosynthesis rate is calculated. The model presented here makes the following adaptations. Since a gas transport model in 2D is unable to deal with gas diffusion in 3D intercellular space (Berghuijs et al., 2016), diffusion in the airspace was neglected. The CO₂ concentration in the intercellular airspace was, therefore, assumed to be equal to that measured experimentally, justified by the uniform CO₂ profile in the intercellular airspace in tomato leaves (Ho et al., 2016). An insulated boundary condition was used at the mesophyll–epidermis interface since CO₂ diffuses mainly through the stomata. The cell wall was explicitly modeled as in Ho et al. (2012) but here its resistance was accounted for (see below). Unlike Ho et al. (2012), we included carbonic anhydrase- (CA) catalyzed hydration of CO₂. In addition, geometrical models for the chloroplast and vacuole were not made. The absence of a vacuole layer reduced photosynthesis only slightly (Ho et al., 2012). Moreover, the light absorption gradient in the leaf was assumed to be uniform.

Input parameters of photosynthesis kinetics were adopted from Berghuijs et al. (2015) for the tomato cultivar ‘Doloress’ for which the validation of the virtual leaf geometry was done. The values of the microscale model parameters are given in Table 1.

The net rate of photosynthesis, A, is given as (Farquhar et al., 1980):

$${\displaystyle \begin{array}{l}{\displaystyle A=(1-\frac{\mathrm{\Gamma }*}{C_{\mathrm{c}}})\left(\frac{C_{\mathrm{c}}a}{C_{\mathrm{c}}+b}\right)-R_{\mathrm{d}}}\end{array}}$$

where Γ* is the CO₂ compensation point (i.e. the CO₂ concentration at which the CO₂ consumption by ribulose bisphosphate carboxylation by Rubisco equals the CO₂ production by photorespiration); C_c is the concentration of CO₂ at the fixation sites; and R_d is the rate of respiration in the light. When photosynthesis is limited by Rubisco, a=V_c,max, the maximum rate of Rubisco carboxylation, and b=K_m,c(1+O₂/K_m,0). K_m,c and K_m,0 are Michaelis–Menten constants for carboxylation and oxygenation by Rubisco, respectively. O₂ is the concentration of O₂. When photosynthesis is limited by the rate of electron transport, J, a=J/4 and b=2Γ*, assuming that the rate of linear electron transport is limited by NADPH production. J is given by:

$${\displaystyle \begin{array}{l}{\displaystyle J=\frac{k_{2\mathrm{L}\mathrm{L}}{I}_{\mathrm{i}\mathrm{n}\mathrm{c}}^{}+J_{\mathrm{m}\mathrm{a}\mathrm{x}}-\sqrt{{(k_{2\mathrm{L}\mathrm{L}}{I}_{\mathrm{i}\mathrm{n}\mathrm{c}}^{}+J_{\mathrm{m}\mathrm{a}\mathrm{x}})}^2-4\mathrm{\theta }{J}_{\mathrm{m}\mathrm{a}\mathrm{x}}{k}_{2\mathrm{L}\mathrm{L}}{I}_{\mathrm{i}\mathrm{n}\mathrm{c}}^{}}}{2\mathrm{\theta }}}\end{array}}$$

where k_2LL is the conversion efficiency of irradiance to linear electron transport under limiting light; I_inc is the incident irradiance on the leaf; J_max is the maximum rate of electron transport; and θ is the convexity factor for the response of J to I_inc (Yin et al., 2004). When the rate of triose phosphate utilization, T_p, limits photosynthesis, a=3T_p and b= –Γ*(Sharkey, 1985).

The reaction–diffusion model of CO₂ transport in the mesophyll cells is given by:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{\nabla }\cdot \left(D_{\mathrm{c}{\mathrm{o}}_2}\mathrm{\nabla }{C}_{\mathrm{c}}\right)-A/(d\times f_{\mathrm{c}})-B=0}\end{array}}$$

Where ▽ is the gradient operator; D_CO2 is the diffusion coefficient of CO₂ in the liquid phase; d is the average thickness of the tissue; f_c is the volume (area in 2D) fraction of mesophyll cells; and B is the rate of CA-catalyzed hydration of CO₂ in the stroma. B is given by (Spalding and Portis, 1985; Tholen and Zhu, 2011):

$${\displaystyle \begin{array}{l}{\displaystyle B=\frac{k_{\mathrm{a}}{X}_{\mathrm{a}}(C_{\mathrm{c}}-\frac{\left[H^{+}\right]}{K_{\mathrm{e}\mathrm{q}}})}{K_{\mathrm{C}{\mathrm{O}}_2}+\frac{K_{\mathrm{C}{\mathrm{O}}_2}}{K_{{\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}}}{C}_{{\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}}+C_{\mathrm{c}}}}\end{array}}$$

where k_a is the CA turnover rate; X_a is the concentration of CA; K_CO2 and K_HCO3^– are Michaelis–Menten constants of CA hydration and dehydration, respectively; K_eq is the equilibrium constant for CA; C_HCO3^– is the concentration of bicarbonate in the mesophyll cytosol; and [H⁺] is the concentration of H⁺ ions in the stroma.

The reaction–diffusion equation for bicarbonate in the mesophyll cytosol is given by:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{\nabla }\cdot \left(D_{{\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}}\mathrm{\nabla }{C}_{{\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}}\right)+B=0}\end{array}}$$

where D_HCO3^– is the diffusion coefficient of bicarbonate.

The boundary layer between the intercellular airspaces and the mesophyll cells was modeled as a thin diffusion barrier. The resistance for CO₂ diffusion over this barrier, r_CO2, is calculated as the sum of the resistances for CO₂ transport of the plasma membrane, the mesophyll cell wall, the chloroplast envelope, and the cytosol:

$${\displaystyle \begin{array}{l}{\displaystyle r_{\mathrm{C}{\mathrm{O}}_2}=1/P_{{\mathrm{C}\mathrm{O}}_2^{}}+t_{\mathrm{c}\mathrm{w}}/D_{\mathrm{c}\mathrm{w}}+2/P_{\mathrm{C}{\mathrm{O}}_2}+t_{\mathrm{c}\mathrm{y}}/D_{\mathrm{l}}}\end{array}}$$

where P_CO2 is the CO₂ permeability of the plasma membrane; t_cw is the thickness of the cell wall; D_cw is the effective diffusivity of CO₂ in the cell wall; t_cy is the thickness of the cytosol; and, D_l is the diffusivity of CO₂ in the cytosol. Accounting for the fact that the chloroplast envelope is a double membrane, the resistance of the chloroplast envelope was assumed to be double that of the plasma membrane (Ho et al., 2012).

The flux of CO₂ at the exposed surface of the mesophyll, J_CO2 is given by:

$${\displaystyle \begin{array}{l}{\displaystyle J_{\mathrm{C}{\mathrm{O}}_2}=-(1/r_{\mathrm{C}{\mathrm{O}}_2})\mathrm{\Delta }C}\end{array}}$$

ΔC is the difference in CO₂ concentration across a biological membrane or cell compartment.

The rate of photosynthesis was computed from the microscale model ($\overline{A}$) by integrating A (Eqution 5) in mesophyll (m) cells as:

$${\displaystyle \begin{array}{l}{\displaystyle {\displaystyle \overline{A}}=\frac{{\displaystyle \underset{m}{\int }}A\mathrm{d}v}{{\displaystyle \underset{m}{\int }}\mathrm{d}v}}\end{array}}$$

The volume of mesophyll cells was calculated by summing the product of differential elements dx, dy, and dz (dz=1 for 2D) over a mesophyll as: $\underset{m}{\overset{}{\int }}\mathrm{d}v=\underset{m}{\iiint }\mathrm{d}x\mathrm{d}y\mathrm{d}z$.

At the interface between palisade and spongy mesophyll cells and at the internal boundary of these cells, a thin diffusion barrier was assumed. The thickness of the layer was twice the thickness of the cell wall, cytosol, chloroplast envelope, and plasma membrane. Henry’s law was used to calculate the equivalent liquid phase concentration of the CO₂ at the exposed surface of mesophyll cells.

The model development for the 270 geometries of leaf structures was automated using Matlab linked with Comsol Multiphysics in such a way that coordinates of geometrical cells from Matlab were directly used in Comsol to create a computational domain. Then, the reaction–diffusion model equations (Equations 5–12) were coupled automatically along with the respective boundary conditions and resistances to diffusion due to microstructural features. The steady-state reaction–diffusion equations were discretized over the 2D geometrical models and solved. The code for generating virtual tissues is included in Supplementary Protocol S2. Supplementary Protocol S3 provides the Matlab file for solving the gas diffusion model using the virtual tissue geometries. The responses of photosynthesis to intercellular CO₂ and irradiance were computed for comparing model predictions with measurements. The rates of photosynthesis at saturating irradiance (1500 μmol m⁻² s⁻¹) and external CO₂ concentration levels of 400 µmol mol⁻¹ and 80 µmol mol⁻¹ were used to compare photosynthesis for leaf structures generated above. In addition, the effects of possible simultaneous changes of leaf biochemistry and biophysical properties of walls and membranes with mesophyll topology were examined. For this, the V_c,max, J_max, cell wall thickness of mesophyll cells (t_cw), and CO₂ permeability of the chloroplast envelope (P_CO2) (Eq. 10) were varied within biologically relevant values.

Statistical analysis

The leaf anatomical properties defined above were calculated for the real tissues in three replicates. For a comparable number of cells as the real geometries, five virtual tissue samples were generated. The mean and SDs of their anatomical properties were calculated and compared with those of the real tissues using Student’s t-test. The comparisons were done for palisade and spongy mesophyll cells.

A two-sample Kolmogorov–Smirnov test (KS test) was used to compare the distributions of the leaf anatomical properties of the real and virtual geometries. In this case, the distribution of all the replicates combined was considered for the tissue types. The null hypothesis was that both were from the same continuous distribution. The alternative hypothesis was that they were from different continuous distributions.

The effects of changes in growth factors, L:W ratio, anisotropy factor, and extent of airspace formation on anatomy and photosynthesis were analyzed using ANOVA. For equal levels in the growth factors, L:W ratios of 1, 5, and 10 were used in the analysis. Mean values of leaf anatomical parameters and the photosynthesis rate were compared using Tukey’s honestly significant difference in JMP 13 statistical software (SAS Institute, Cary, NC, USA). A 5% significance level was used for the statistical tests.

Results

The virtual leaf tissue generator produced realistic microstructures of a tomato leaf

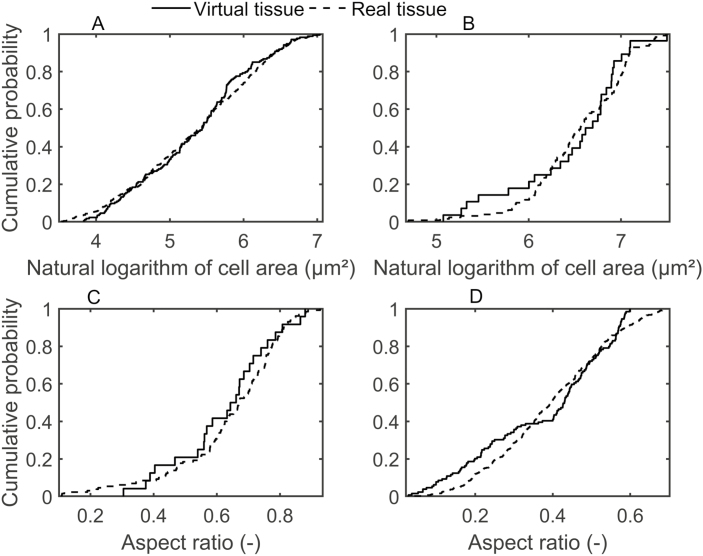
Table 2 shows that the anatomical properties of the real and virtual tissue geometries compared well. The statistical comparison revealed that the mean values of L_m, the natural logarithm of the mean cell area, and the aspect ratios of both spongy and palisade mesophyll were not significantly different. The comparison of the distribution of the anatomical properties using KS tests further demonstrated the ability of the growth model to simulate cell shapes in leaves different from those observed in real leaves. To this end, distributions of the natural logarithm of the cell area and aspect ratio were plotted in Fig. 2. The plots show that cumulative probabilities for spongy (Fig. 2A, C) and palisade (Fig. 2B, D) mesophyll were similar for the real and virtual tissue geometries. The P-values of the KS test were 41% for the spongy mesophyll cell area comparison; 70% for the spongy aspect ratio comparison; 37% for the palisade mesophyll cell area comparison; and 18% for the palisade aspect ratio comparison. In addition, the KS test results confirmed that the distributions of anatomic properties of the virtual and real tissues were not significantly different.

Table 2.

Geometrical properties of the virtual and the real leaf tissues. The values are means ±SD

Properties	Real tissue	Virtual tissue
L m (palisade mesophyll) (–)	5.59±0.716	5.34±0.771
L m (spongy mesophyll) (–)	7.06±0.169	6.84±0.283
Mean cell area (palisade mesophyll) (µm2)	761.8±372	805±264
Mean cell area (spongy mesophyll) (µm2)	276.1±230	285±293
Mean aspect ratio (palisade mesophyll) (–)	0.64±0.17	0.70±0.07
Mean aspect ratio (spongy mesophyll) (–)	0.41±0.16	0.32±0.08

For measurements of L_m, the number of geometries was three for real geometries and five for virtual geometries.

Fig. 2.

Comparison of geometrical parameter distributions of the real and the virtual leaf tissues: cumulative probability functions for spongy mesophyll cell area (A); natural logarithm of the palisade mesophyll cell area (B); natural logarithm of the spongy mesophyll aspect ratio (C); and palisade mesophyll cell aspect ratio (D). Mean properties are given in Table 2.

Generating one virtual leaf of 102 cells (Fig. 1) required 1.6 h, while the additional airspace formations required a further total of 0.5 h on a 3.40 GHz, 16 GB RAM, 64-bit operating system computer. This time is considerably shorter than that required to obtain 2D images of real images using traditional microscopic techniques (Abera et al., 2013; Verboven et al., 2015) and convert them to geometrical models ready for use in simulation models.

Leaf anatomical properties of the virtual tissues as influenced by the cell growth factors

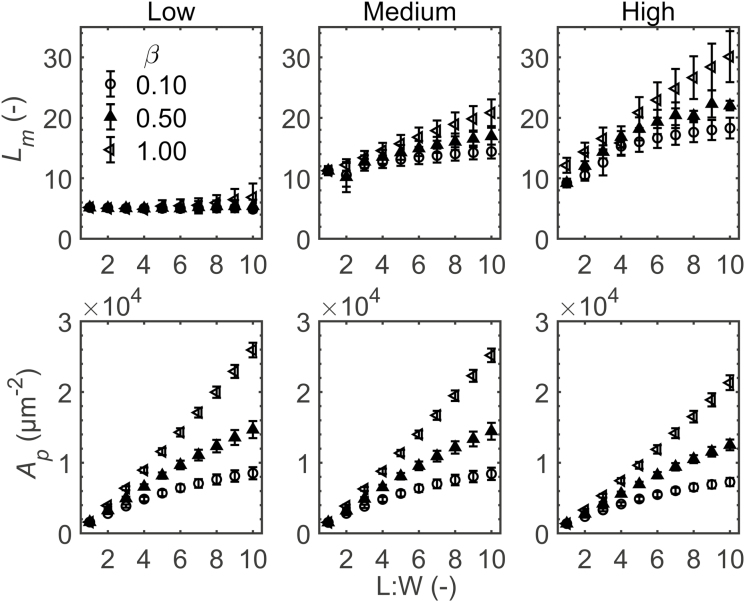
Variations of cell growth factors such as growth anisotropy factor, L:W ratio, and extent of airspace formation in the palisade parenchyma caused significant changes in the leaf anatomy. The mean cell areas of spongy parenchyma and epidermis were not significantly different for different values of the L:W ratio, anisotropy factor, and extent of airspace formation, and were not discussed further. The extents of airspace formation resulted in mean leaf porosities of 0.197±0.04 (low), 0.205±0.04 (medium), and 0.266±0.02 (high) due to porosity determined mainly by the intercellular airspaces in spongy mesophyll.

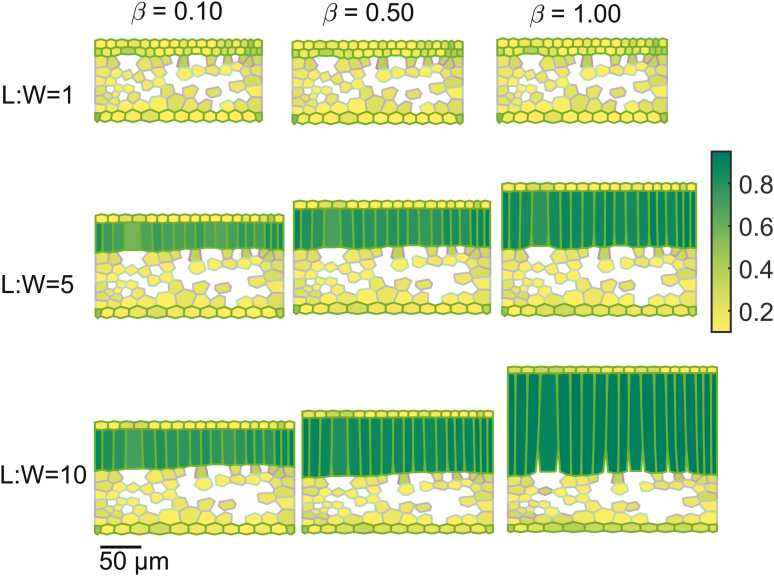
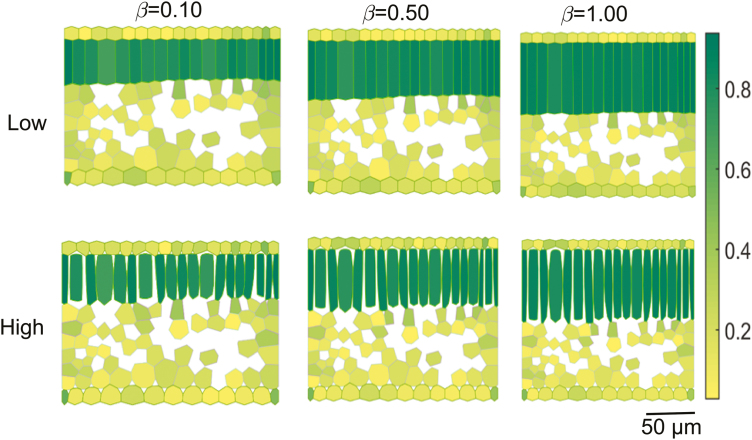
Figure 3 shows virtual leaf tissue geometries generated by setting the growth anisotropy factor to 0.10, 0.50, and 1.00 for L:W ratios of 1, 5, and 10 at a medium extent of airspace formation. Overlaid in a color map is the aspect ratio of individual cells. At an L:W ratio of 1 and an anisotropy factor of 0.10, the mesophyll was dominated by spongy mesophyll cells, while at an L:W ratio of 10 and 1.00, palisade mesophyll cells dominated. Figure 4 shows the effect of extents of airspace formation (by increasing cell wall separation) in the palisade parenchyma on the structure of cells for an L:W ratio of 5 and anisotropy factors of 0.10, 0.50, and 1.00.

Fig. 3.

Effect of growth anisotropy factor and palisade mesophyll height to width ratio on the aspect ratio of cells of virtual leaf tissue geometries. The growth anisotropies (β) were 0.10, 0.50, and 1.00, while values for palisade mesophyll height to width set during growth were 1, 5, and 10. The extent of airspace formation in the palisade mesophyll was medium. The color map shows the aspect ratio of individual cells. Scale bar=50 µm.

Fig. 4.

Effect of the extent of airspace formation on the aspect ratio of cells of the virtual leaf tissue geometries. Shown are a low (top) and high (bottom) degree of palisade mesophyll airspace formation. The growth anisotropy factor (β) was 0.10, 0.50, and 1.00, while the palisade mesophyll height to width ratio, L:W ratio, was 5. The color map shows the aspect ratio of individual cells. Scale bar=50 µm.

L _m of the geometries was not altered significantly by the growth anisotropy factor and L:W ratio at the low extent of airspace formation (Fig. 5). In contrast, leaf thickness increased for each increase in L:W ratio at all anisotropy factors (Supplementary Fig. S1). The same was true for geometries having medium and high extents of airspace formation. In addition, the palisade mesophyll area A_p increased with L:W for all anisotropy factors (Fig. 5). Both leaf thickness and palisade mesophyll area were influenced by changes in the growth anisotropy factor at a fixed L:W ratio for medium and high extents of airspace formation. For the same number of cells in a tissue, the leaf width increased (Supplementary Fig. S1) with increasing L:W ratio.

Fig. 5.

Effect of palisade mesophyll length to width (L:W) ratio on exposed length of mesophyll cells (L_m) and palisade mesophyll volume (A_p). The extent of airspace formation in palisade mesophyll was low, medium, and high. The anisotropies during growth (β) were 0.10 (open circles), 0.50 (filled triangles), and 1.00 (open triangles). Errors bars show the SD (n=3).

The effect of the interaction of growth anisotropy factor and L:W ratio on L_m was significant for medium and high extents of airspace formation (Fig. 5). At the medium extent of airspace formation, L_m of geometries with the growth anisotropy factor set to 0.50 had significantly larger L_m at an L:W ratio of 5 and 10 than at an L:W of 1. At an anisotropy factor of 1, the increase in L_m with L:W was significant. At the high extent of airspace formation, geometries with a growth anisotropy factor of 0.10 or 0.50 had a higher L_m at an L:W ratio of 5 and 10 than at an L:W ratio of 1. When the growth anisotropy factor was set to 1, each increase in L:W resulted in a larger L_m.

Comparison of the virtual and real leaf tissue geometry in the prediction of the response of photosynthesis

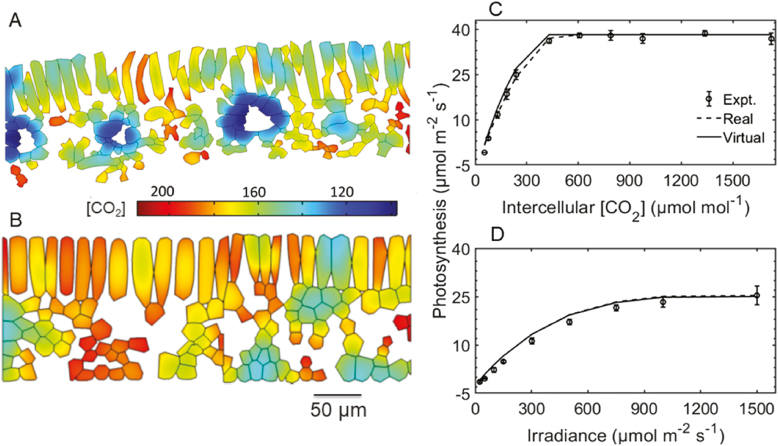
Figure 6 compares the prediction of photosynthesis and microscale CO₂ profile of a geometry created by the virtual leaf tissue generator with that obtained from a light microscopy image. For the virtual geometry, the L:W ratio was 5, the anisotropy factor was 0.9, and the extent of airspace formation was high. The L_m values were 12.3 and 13.0, while the mesophyll cell area was 0.54×10^–7 m² and 0.52×10^–7 m² for virtual and real geometries, respectively. Vascular bundles were removed from the real geometry (Fig. 6A) since they were also not accounted for in the virtual geometry. There was a good similarity in spatial CO₂ concentration profile (Fig. 6A, B). The models with real tissue or with virtual tissue geometry also predicted almost identical responses of photosynthesis to irradiance (Fig. 6D).

Fig. 6.

Comparison of CO₂ concentration profiles in real and virtual tissues and measured and predicted rates of photosynthesis. Geometry of mesophyll anatomy obtained from a light microscopy image (referred to as ‘real’) (A) and that from the virtual leaf tissue generator (referred to as ‘virtual’; L:W of 5, a high extent of airspace formation, and anisotropy factor of 0.9) (B) were used in the gas transport model. Shown in (C) and (D) are a comparison of the CO₂ response of photosynthesis predicted from the model with real and virtual geometry with that measured experimentally. CO₂ concentration was expressed as equivalent gas phase concentration (µmol mol⁻¹). The CO₂ concentration profiles were computed at a CO₂ concentration of 400 µmol mol⁻¹, stomatal conductance of 0.15 mol m⁻² s⁻¹, and irradiance of 1500 µmol m⁻² s⁻¹ at 21% O₂. The CO₂ response of photosynthesis was calculated at an irradiance of 1500 µmol m⁻² s⁻¹. Bars show the SE (n=4).

Light-saturated photosynthesis rate in relation to cell growth factors

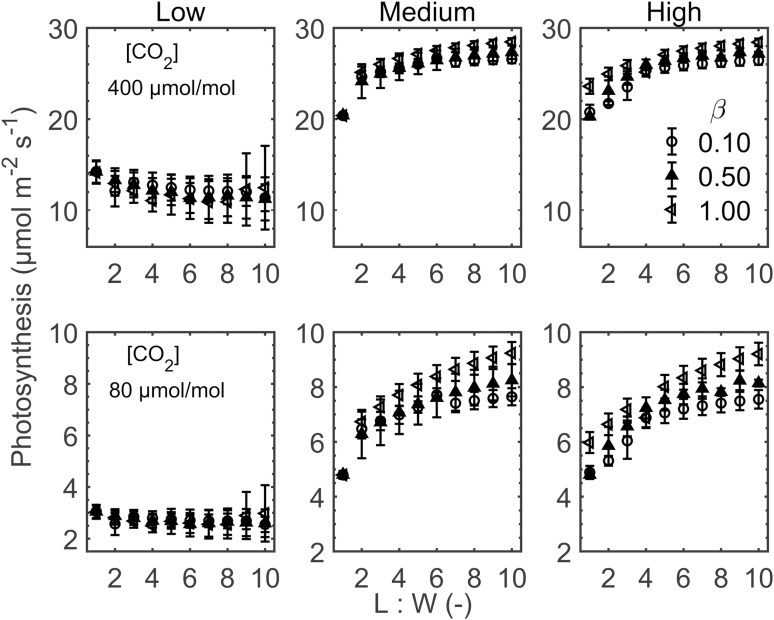
The impact of cell growth factors on photosynthesis through changes in leaf anatomy was evaluated at external CO₂ concentrations of 400 µmol mol⁻¹ and 80 µmol mol⁻¹. The irradiance was 1500 µmol m⁻² s⁻¹, and the external O₂ was 21%. The results are shown in Fig. 7. Changes in photosynthesis are presented as follows.

Fig. 7.

Response of photosynthesis to palisade mesophyll length to width ratio (L:W ratio). The top row shows photosynthesis at a CO₂ concentration ([CO₂]) of 400 µmol mol⁻¹ and a stomatal conductance of 0.15 mol m⁻² s⁻¹, while bottom rows are at [CO₂] of 80 µmol mol⁻¹ and stomatal conductance of 0.17 mol m⁻² s⁻¹. Irradiance was 1500 µmol m⁻² s⁻¹. The extents of airspace formation in palisade mesophyll were low, medium, and high. The anisotropies (β) during growth were 0.10 (open circles), 0.50 (filled triangles), and 1.00 (open triangles). Errors bars show the SD (n=3).

The photosynthesis rate for the low airspace formation was considerably lower than the rates of medium and high airspace formation, at both low and high CO₂ levels. The change of photosynthesis with L:W was more modest than for the structural parameters. For low airspace formation, we observed almost no effect of L:W, while for the higher extents, there was an increasing trend that generally leveled off at a higher L:W. With respect to the anisotropy factor, differences were minor for the high CO₂ level (Fig. 7, top panels) and more pronounced for the low CO₂ concentration (Fig. 7, bottom pannels). A higher anisotropy factor increased photosynthesis rates when the leaf palisade mesophyll was well aerated. At low aeration, the anisotropy factor did not play a role.

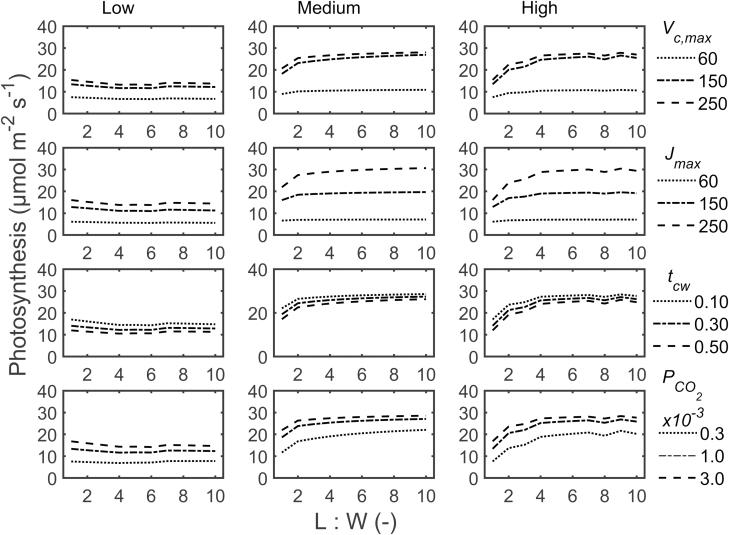
Interaction of biochemical and anatomical factors

We observed the same general trends for the effects of L:W and airspace formation as in the previous section: photosynthesis was lower and more independent of L:W at low airspace formation than at medium or high airspace formation (Fig. 8). At medium and high airspace formation, the rate increased asymptotically with L:W, with minor changes only at low values of V_c,max and J_max. Reducing V_c,max to a low value minimized photosynthesis in all cases, while differences between the two higher levels were minor. The roles of changes in J_max were similar to those of V_c,max except that the maximum photosynthesis increased considerably for each J_max. Figure 8 also shows that photosynthesis decreased slightly with increased palisade mesophyll cell wall thickness irrespective of L:W ratio and airspace formation. Increased P_CO2 increased photosynthesis asymptotically at all aeration levels.

Fig. 8.

Effect of biochemical and biophysical factors on the response of photosynthesis to palisade mesophyll length to width (L:W) ratio. The factors were V_c,max, J_max, cell wall thickness of palisade mesophyll (t_cw), and CO₂ permeability of the chloroplast envelope (P_CO2). The extents of airspace formation in palisade mesophyll were low, medium, and high. The anisotropy factor during growth was 0.50. Photosynthesis was calculated at 400 µmol mol⁻¹ CO₂, stomatal conductance of 0.15 mol m⁻² s⁻¹, and irradiance of 1500 µmol m⁻² s⁻¹.

Discussion

The anatomy of a leaf is influenced by the need for adequate mechanical strength and a surface for gas exchange, water transport, and light absorption (Nobel, 2005; Cutler et al., 2008). Comparison of anatomical properties of three tomato cultivars (S. lycopersicum L. cvs. Admiro, Doloress, and Growdena) showed that they differ in the relative size of intercellular airspaces, shape of cells, and the relative thickness of palisade mesophyll and spongy mesophyll, among others (Berghuijs et al., 2015; Verboven et al., 2015). In addition, these differences partly explain the differences in the rate of photosynthesis of the cultivars (Berghuijs et al., 2015; Ho et al., 2016). Field-grown plants exhibit considerable area per leaf (Poorter et al., 2009). At the cellular level, the directionality of microfibril arrangement could give rise to an anisotropy in cell growth (Baskin, 2005). The large diversity in cellular patterning and its close link to physiology in leaves present an interesting challenge for virtual tissue generation.

The virtual leaf tissue generator can produce leaf tissues that are similar not only in the average values but also in the distribution of anatomical properties to the real leaf tissues of tomato. Consistent with the shape of the mesophyll cells of a typical leaf, the mean aspect ratio of the palisade mesophyll cells was 0.70±0.07 whereas that of the spongy mesophyll cells was 0.32±0.08 (Verboven et al., 2015). The L_m values were similar to reports in the literature for tomato leaves (Berghuijs et al., 2015; Muir et al., 2017) and were within the range of values reported for C₃ plants (Dengler et al., 1994; von Caemmerer et al., 2007). In addition, the higher L_m value for spongy mesophyll than for palisade mesophyll is a consequence of larger intercellular airspaces in the spongy mesophyll.

Through systematic modeling of leaf cell growth, a range of distinct mesophyll topologies was generated (Figs 3, 4). Geometries with growth anisotropies of 0.50 and 1.00 along with a medium or high extent of airspace formation resemble the typical mesophyll topology having columnar palisade mesophyll cells. Those obtained with anisotropy factors of 0.10 for the medium or high extents of airspace formation mimic the mesophyll of young and/or low-light-grown leaves, which show more rounded palisade mesophyll cells (Vogelmann and Martin, 1993; Tosens et al., 2012). The calculated anatomical properties (Figs 2, 3) have similar values to those reported for leaves of C₃ plants, including tomato leaves (Dengler et al., 1994; Berghuijs et al., 2015; Verboven et al., 2015). Slight variations in the cell growth factors resulted in different anatomical properties such as leaf thickness and A_p, and anatomical features such as columnarity of palisade mesophyll cells (Fig. 3). Comparison of anatomical properties showed that significant changes in L_m depended upon the combination of the cell growth factors. This might explain why some experimental manipulations of cell growth did not cause significant changes in mesophyll surface area per leaf area (Dorca-Fornell et al., 2013; Lehmeier et al., 2017). A_p was more sensitive to increases in the L:W ratio than L_m, resulting in a decreased L_m:A_p ratio with an increased L:W ratio (Supplementary Fig. S2A). Consequently, smaller palisade mesophyll cells had a larger L_m:A_p than larger cells. Supplementary Fig. S2A in addition shows that for a given expansion of palisade mesophyll cells (L:W ratio), isotropic growth will result in more gas exchange surface per tissue volume than anisotropic growth of palisade mesophyll cells. These predictions are in line with suggestions that decreasing cell size is one strategy to increase photosynthesis per cell volume (Terashima et al., 2001; Nobel, 2005).

Combining the virtual leaf tissue generator with the microscale gas exchange model allowed us to explore the influence of mesophyll topology on photosynthesis. When the airspace in the palisade mesophyll was formed in cell corners only (low extent of airspace formation), photosynthesis did not improve (Fig. 7) no matter how the palisade mesophyll length was altered (L:W ratio and anisotropy factor). This is because the increased length of palisade mesophyll cells contributed to more contact area between cells and, thus, increased local CO₂-limited regions. Consequently, the mean CO₂ concentration in the mesophyll decreased (Supplementary Fig. S3). In reality, schizogeny results in a more exposed surface area. In this case, consistent with the effect of the extent of airspace formation on L_m (Fig. 5), photosynthesis also showed a significant increase with increased aeration (Fig. 7). In addition, the manipulation of schizogeny was more effective in improving photosynthesis when the growth of palisade mesophyll cells was fully anisotropic (Fig. 7), explained by the similar positive effects on L_m (Fig. 5). The growth anisotropy factor impacted photosynthesis only when there was a high extent of airspace formation in palisade mesophyll cells, irrespective of the expansion of palisade mesophyll cells (L:W ratio). For the same number of cells, more rounded palisade mesophyll cells had lower photosynthesis per leaf area (Fig. 7) but greater photosynthesis rate per L_m than columnar palisade mesophyll cells (Supplementary Fig. S2). These predictions are consistent with the negative correlations between mesophyll mean cell area (size) and light-saturated photosynthesis (Wilson and Cooper, 1970; Lehmeier et al., 2017) but contradicts the claimed positive correlation between cell volume and photosynthesis (Byrne et al., 1981).

Comparisons so far were made at the same biochemical capacity of the leaf and biophysical properties. However, increased cell sizes of the mesophyll may require a thicker cell wall for reasons of structural support or for continuing cell expansion (John et al., 2013). In addition, cell size may scale with biochemical capacity to make efficient use of the increased size (Terashima et al., 2001). Enhancing the gas exchange surface and volume of the mesophyll was of no use for photosynthesis when the biochemical capacity of Rubisco was low (Fig. 8). When the biochemical capacity was increased, mesophyll topologies with a moderate L:W ratio of palisade mesophyll cells (L:W ratio=5) had a higher rate of photosynthesis. Figure 8 also shows that increased thickness of palisade mesophyll cell walls would diminish the return of enhanced gas exchange surface as a result of higher L:W ratio values. In contrast, increased CO₂ permeability of the chloroplast envelope along with a higher L:W ratio boosts photosynthesis. These results are consistent with the hypothesis that a trade-off exists between leaf structure and biochemical capacity (Terashima et al., 2001; Tholen et al., 2012). To this end, the ‘cost’ to construct a leaf was assessed by LMA using leaf thickness as a proxy (Poorter et al., 2009). The high porosity leaves resulted in an increased photosynthesis rate for increased cost of the leaf but up to certain values of LMA above which the gain in photosynthesis became negligible (Supplementary Fig. S4). In addition, Supplementary Fig. S4 shows that more spherical cells enabled gaining high photosynthesis at lower cost. For leaves with a low and medium extent of airspace formation, the benefit to photosynthesis from a large increase in construction cost was only small.

The approach presented here resulted in a parameterized leaf anatomy which can be manipulated easily. The generator may need to be calibrated for a specific cultivar as a comparison of three tomato cultivars showed significant differences in palisade and spongy mesophyll (Verboven et al., 2015). Calibration of the generator requires generating many geometries in the range of expected anatomical properties through modification especially of L:W. The generator, once calibrated for a specific genotype, will avoid the dependency of modeling efforts of photosynthesis that include leaf microstructure on imaging and the subsequent image processing procedures. It is recommended to extend the 2D model to 3D to analyze the gas diffusion in the intercellular airspaces especially at low porosity, and accurately model the light propagation in leaves (Vogelmann and Martin, 1993; Ho et al., 2016; Xiao and Zhu, 2017). Although the time required to generate a virtual tissue is less than if the geometry were obtained from light microscopy, it may limit rapid analysis if coupling with an optimization algorithm is desired. However, with the advancement in computing power and technology, this problem may become obsolete.

We have developed a tool, freely available (Retta et al., 2019), that couples a virtual leaf tissue generator algorithm with a microscale model of photosynthetic gas exchange that can generate representative leaf tissue sections in 2D and simulate photosynthesis. With this tool, we demonstrated that we can simulate the role of cell division, growth, development, and schizogeny in mesophyll anatomy, CO₂ diffusion, and light-saturated photosynthesis. The tool allowed analysis of the influence of the development level of palisade mesophyll on CO₂ availability and in optimization of photosynthesis. Light-saturated photosynthesis was shown to be influenced by interactive effects of leaf growth factors through the exposed surface of mesophyll per leaf area. The combined virtual leaf tissue generator and photosynthesis gas exchange model is an important step towards development of tools that allow in silico study of the relationship between cell growth, morphology, and photosynthesis.

Supplementary data

Supplementary data are available at JXB online.

Protocol S1. Algorithm for the virtual leaf tissue generator.

Protocol S2. Matlab code for the growth algorithm.

Protocol S3. Matlab code for solving the microscale model of gas exchange during C₃ photosynthesis using virtual leaf tissue geometries.

Table S1. Parameters of the growth model.

Fig. S1. Effect of the L:W ratio on leaf width and leaf thickness.

Fig. S2. Effect of the growth anisotropy factor on L_m:A_p and A:L_m.

Fig. S3. Comparison of the CO₂ profile for extents of airspace formation.

Fig. S4. Photosynthesis in relation to leaf mass per area.

Data deposition

Matlab codes are available from the Dryad digital repository: doi:10.5061/dryad.46h5nc0.