Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Jan 9;5(2):1277–1286. doi: 10.1021/acsomega.9b03967

Theoretical Study of the Kinetics of the Gas-Phase Reaction between Phenyl and Amino Radicals

Tien V Pham †,*, Hoang T Tue Trang ‡, Trinh Le Huyen §, Tue Ngoc Nguyen †
PMCID: PMC6977206  PMID: 31984286

Abstract

graphic file with name ao9b03967_0004.jpg

The potential energy surface (PES) of the C6H5 + NH2 reaction has been investigated by using ab initio CCSD(T)//B3LYP/6-311++G(3df,2p) calculations. The conventional transition-state theory (TST) and the variable reaction coordinate-TST (VRC-TST) have been used to predict the rate constants for the channels possessing tight and barrierless transition states, respectively. The Rice–Ramsperger–Kassel–Marcus/Master equation (RRKM/ME) theory has been utilized to determine the pressure-dependent rate constants for these reactions. The PES shows that the reaction begins with an exothermic barrierless addition of NH2 to C6H5 producing the vital intermediate state, namely, aniline (C6H5NH2, IS1). Once IS1 is generated, it can further isomerize to various intermediate states, which can give rise to different products, including PR4 (4,5,6-trihydro-1-amino phenyl + H2), PR5 (3,4,5,6-tetrahydro phenyl + NH3), PR6 (2,3,5,6-tetrahydro-1-imidogen phenyl + H2), PR9 (3,4,5,6-tetrahydro-1-imidogen phenyl + H2), and PR10 (2,5,6-trihydro-1-amino phenyl + H2), of which the most stable product, PR5, was formed by the most favorable channel going through the two advantageous transition states T1/11 (−28.9 kcal/mol) and T11P5 (−21.5 kcal/mol). The calculated rate constants for the low-energy channel, 1.37 × 10–9 and 2.16 × 10–11 cm3 molecule–1 s–1 at T = 300, P = 1 Torr and T = 2000 K, P = 760 Torr, respectively, show that the title reaction is almost pressure- and temperature-dependent. The negative temperature-dependent rate coefficients can be expressed in the modified Arrhenius form of k1 = 8.54 × 1013T–7.20 exp (−7.07 kcal·mol–1/RT) and k2 = 2.42 × 1015T–7.61 exp (−7.75 kcal·mol–1/RT) at 1 and 10 Torr, respectively, and in the temperature range of 300–2000 K. The forward and reverse rate coefficients as well as the high-pressure equilibrium constants of the C6H5 + NH2 ↔ IS1 process were also predicted; their values revealed that its kinetics do not depend on pressure at low temperature but strongly depend on pressure at high temperature. Moreover, the predicted formation enthalpies of reactants and the enthalpy changes of some channels are in good agreement with the experimental results.

1. Introduction

The phenyl radical, C6H5, has been known to play a vital role in the pyrolysis and oxidation of polycyclic aromatic hydrocarbons (PAHs), as well as in soot formation in combustion chemistry for many years.1−5 In extraterrestrial environments, some species such as benzene, phenyl radical, and cyclo-C5H5 radicals have been considered to be crucial reaction intermediates in the formation of PAHs, as shown in several studies.1−3 In combustion conditions, similarly, the formation of PAHs and soot particles is usually derived from an aromatic compound like a benzene molecule or a phenyl radical.6 Because of the important function of C6H5 as mentioned above, there have been theoretical and experimental investigations into its reaction with closed- and/or open-shell species such as C2H2, C3H4, CH4, NO, O2, CH3, etc. in different environments including the circumstellar envelopes of carbon-rich stars, the interstellar medium, and the combustion processes.7−25

Glassman25 and Bittner et al.13 reported that, at high temperatures, blocks of soot particles in the combustion of hydrocarbons can be obtained via the two reactions of C6H5 with C2H2 and O2, in which, if the C6H5 + nC2H2 → PAHs reaction shows the polymerization process of phenyl radical, the C6H5 + O2 reaction shows the oxidization of C6H5. The mechanisms, rate constants, and branching ratios of these two reactions under distinct temperature and pressure conditions were also investigated sufficiently to specify the quantity of soot formed in combustion. Frenklach et al.4,5 proposed a sequential-addition mechanism of C2H2 to the phenyl radical to yield PAHs, which is the best chosen synthetic way in interstellar and combustion chemistry instead of the old-fashioned means based on the combination of C3H3 and C3H2 or C2H2 and C4Hx considered by most authors.26−30 The other reaction series involved in phenyl radical including C6H5 + H2, C6H5 + CH3, C6H5 + CH4, C6H5 + NO, and C6H5 + CO have been carried out theoretically and experimentally,30−37 which indicated that these reactions occurred quickly in combustion conditions.

As far as we are aware, the mechanism and kinetics of the reaction between the C6H5 radical and the NH2 radical, at various temperatures and pressures, have not yet been investigated both theoretically and experimentally. Due to the lack of such qualitative and quantitative data, the reaction of C6H5 with NH2 should be researched fully and carefully. Therefore, the PES characterizing the C6H5 + NH2 reaction has been theoretically figured out in the present work. This reaction was not suggested earlier as a possible source of PAH precursors, but it is an appropriate representative of the layer of reactions of aromatic molecules with species with a single electron. The PES of this reaction reveals that the energetically most favorable reaction path yields 3,4,5,6-tetrahydro phenyl and that this advantageous path is straightforward to approach with an activated intermediate generated initially, even at very low temperatures and/or pressures. This work, subsequently, has focused on the rate constants of the energetically low-lying channel proceeding over this PES by theoretical–kinetic analysis. The thermochemical parameters denoted as enthalpy, Gibbs free energy, and entropy changes of some main channels involved in the system were also measured and were compared to experimental data to determine the validity of the method used in this calculation.

2. Computational Methods

The density functional theory (DFT) with the common B3LYP38−40 and M06-2×41−43 functionals in conjunction with the 6-311++G(3df,2p)44 and aug-cc-pVTZ45−47 basis sets, respectively, was used to figure out the mechanism for the title reaction. In this work, the geometries optimized by the B3LYP/6-311++G(3df,2p) method were utilized for the establishment of the PES and the kinetic prediction. The correlative parameters, including vibrational frequencies, moments of inertia, and zero-point vibrational energies (ZPVE), were obtained using the same method. All species in the system were classified based on their vibrational analysis, of which the local minima such as reactants, intermediates, and products all have positive frequencies, while each saddle point like a transition state contains only one unreal frequency. The intrinsic reaction coordinate (IRC)48,49 predictions were employed to verify the validity of transition states. The B3LYP/6-311++G(3df,2p) relative energies of all points were then refined by the single-point energy calculations using the CCSD(T)/6-311++G(3df,2p)50 + ZPVEs level of theory. The ZPVE values were corrected by a factor of 0.97.51 The Gaussian 16 software package52 was utilized to optimize and compute single-point energies for all species in this system.

The rate coefficients for the energetically low-lying channel have been predicted by employing the Variflex code53 and the Multiwell code54 depending on the transition-state theory (TST),55 variable reaction coordinate-TST (VRC-TST),56,57 and the Rice–Ramsperger–Kassel–Marcus (RRKM) theory58 with Eckart tunneling corrections.59 The sum and density of state in the kinetic model were estimated from the input data file containing the energy barriers of the reaction path and the species’ parameters mentioned above. The master equation60 involving multistep vibrational energy transfer for the C6H5NH2 excited intermediate state was solved to obtain the pressure- and temperature-dependent rate constants using the energy-dependent microcanonical RRKM statistical rate constants, k(E).

The collisional frequency of the bath gas (Ar in the present work) and the intermediate states have been taken from references. In the present study, the values of Lennard-Jones (L-J) of Ar are ε/kB = 113.50 K and σ = 3.465 Å,61 whereas the values of the intermediates are σ = 5.923 Å and ε = 407.8 K.62 The average energy transferred per collision, ⟨ΔE⟩down = 400 cm–1, was used for the standard form of the “exponential down” model.63 A brief discussion of the rate constant prediction is presented in Supporting Information (SI).

3. Results and Discussion

3.1. Potential Energy Surface and Reaction Mechanism

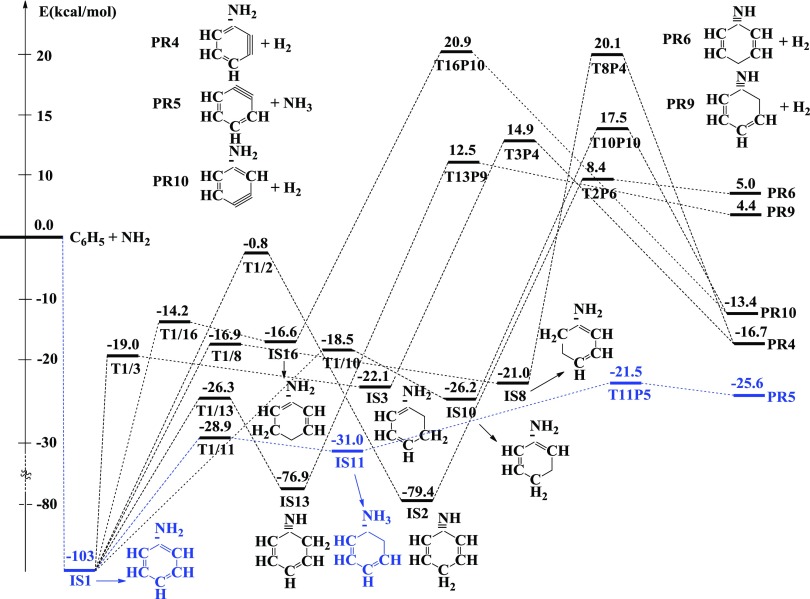
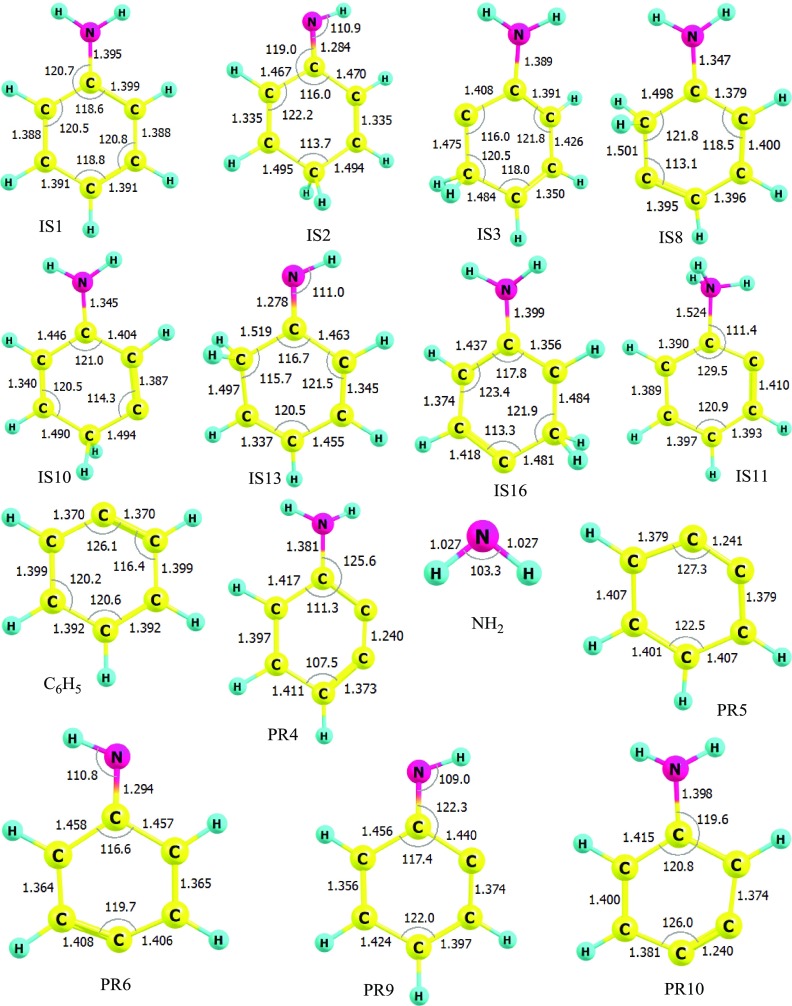
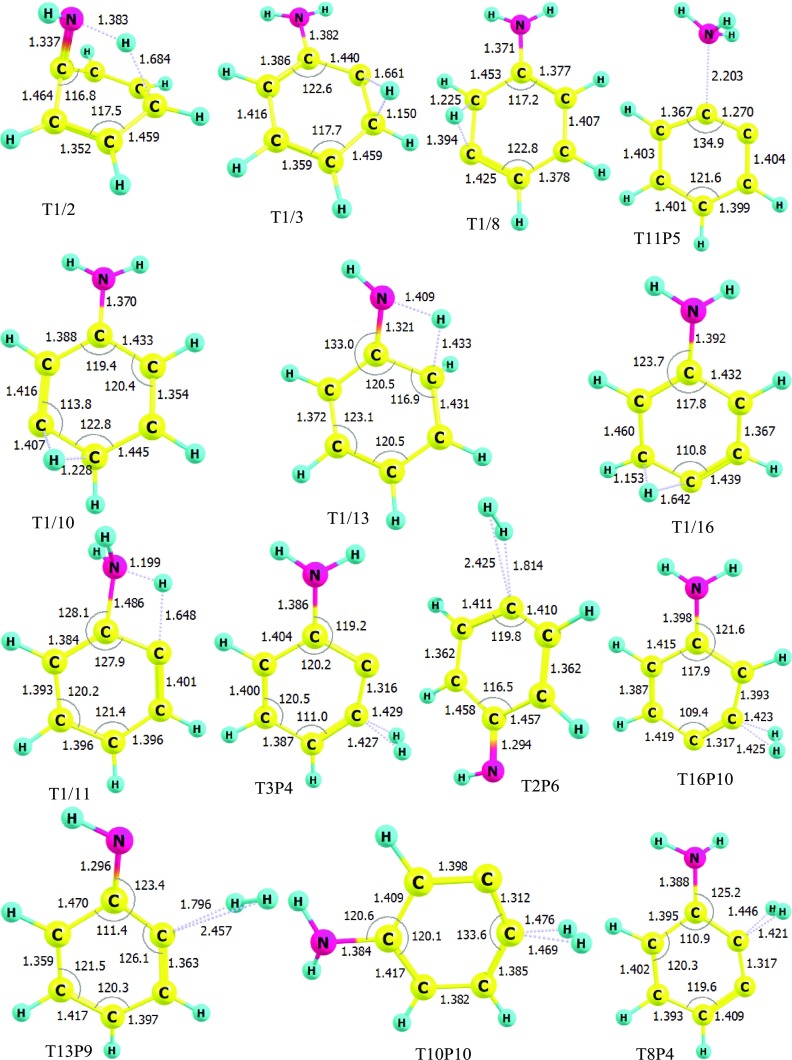
The detailed PES characterized at the (U)CCSD(T)//B3LYP/6-311++G(3df,2p) level is indicated in Figure S1 (see the SI), while the simplified PES containing the significant channels is presented in Figure 1 of this work. The geometric structures of all species for the C6H5 + NH2 reaction were optimized at the B3LYP/6-311++G(3df,2p) level and are shown in Figures 2 and 3 as well as in Figure S2 of the SI file.

Figure 1.

Figure 1

Open in a new tab

Simplified potential energy surface (PES) for the C6H5 + NH2 reaction calculated at the CCSD(T)//B3LYP/6-311++G(3df,2p) + zero-point vibrational energies (ZPVE) level of theory (energies are in kcal/mol).

Figure 2.

Figure 2

Open in a new tab

Geometries of the intermediate states, complexes, reactants, and products optimized at the B3LYP/6-311++G(3df,2p) level (bond lengths are in angstrom and bond angles are in degrees).

Figure 3.

Figure 3

Open in a new tab

Geometries of the main transition states optimized at the B3LYP/6-311++G(3df,2p) level (bond lengths are in angstrom and bond angles are in degrees).

The relative energies for all species related to Figure 1 at various levels of theory are shown in Table 1. The calculated heats of formation and heats of reaction in the C6H5 + NH2 system are compared to the experimental data and presented in Table 2. The harmonic vibrational frequencies and the Cartesian coordinates of the species involved are listed in Tables S1 and S2, respectively. The Gibbs free energies (ΔG) and entropies (ΔS) under the standard condition of all channels are presented in Table S3.

Table 1. Theoretical Prediction of the Relative Energies, ΔE (kcal/mol), for the Species Involved in Figure 1 of the C6H5 + NH2 Reaction at Two Different Levels.

  relative energies (kcal/mol)
species CCSD(T)/aug-cc-pVTZ//M06-2×/aug-cc-pVTZ CCSD(T)/6-311++G(3df,2p)//B3LYP/6-311++G(3df,2p)
C6H5 + NH2 0.0 0.0
IS1 –101.4 –103.0
IS2 –77.6 –79.4
IS3 –20.1 –22.1
IS8 –19.6 –21.0
IS10 –24.7 –26.2
IS13 –75.0 –76.9
IS16 –14.7 –16.6
IS11 –29.4 –31.0
T1/2 1.3 –0.8
T1/3 –14.4 –19.0
T1/8 –15.7 –16.9
T1/10 –17.2 –18.5
T1/13 –25.1 –26.3
T1/16 –12.0 –14.2
T1/11 –27.8 –28.9
T11P5 –20.9 –21.5
T2P6 11.3 8.4
T3P4 16.3 14.9
T8P4 21.5 20.1
T10P10 18.8 17.5
T13P9 14.5 12.5
T16P10 22.5 20.9
PR4 –14.0 –16.7
PR5 –24.3 –25.6
PR6 8.2 5.0
PR9 7.7 4.4
PR10 –10.6 –13.4
Open in a new tab

Table 2. Comparison of the Predicted Heats of Formation (ΔfH°, in kcal/mol) and Heats of Reaction (ΔrH°, in kcal/mol) at 298.15 K in This Work with Available Data.

  methods
species/paths CCSD(T)//M06-2×/aug-cc-pVTZ CCSD(T)//B3LYP/6-311++G(3df,2p) experiments
C6H5 81.82 80.47 80.54 ± 0.6065
80.62 ± 0.1466
NH2 42.43 44.05 44.5 ± 0.24a
45.567
C6H5NH2 20.29 20.26 20.8 ± 0.2468
19.6969
19.8870
19.36 ± 0.7271
20.4172
C6H5 + NH2 → IS1 (C6H5NH2) –103.96 –104.26 –104.21 ± 0.38a
C6H5 + NH2 → PR4 –14.34 –16.13  
C6H5 + NH2 → PR5 –25.23 –25.53 –25.79 ± 1.54a
C6H5 + NH2 → PR6 7.71 5.35  
C6H5 + NH2 → PR9 7.27 4.89  
C6H5 + NH2 → PR10 –10.93 –12.74  
Open in a new tab
a

Ref from NIST (webbook.nist.gov).

It can be seen from Table 2 that the predicted heats of formation of some species C6H5, NH2, and C6H5NH2 at the CCSD(T)//B3LYP/6-311++G(3df,2p) level of theory are 80.47, 44.05, and 20.26 kcal/mol, respectively, while the values at the CCSD(T)//M06-2×/aug-cc-pVTZ level are 81.82, 42.43, and 20.29 kcal/mol, respectively. These values are in reasonable agreement with the experimental results. Likewise, the heats of several reaction paths creating IS1, PR4, PR5, PR6, PR9, and PR10 at the CCSD(T)//B3LYP/6-311++G(3df,2p) level of theory are −104.26, −16.13, −25.53, 5.35, 4.89, and −12.74 kcal/mol, respectively. Those values at the CCSD(T)//M06-2×/aug-cc-pVTZ level are −103.96, −14.34, −25.23, 7.71, 7.27, and −10.93 kcal/mol, respectively. Both sets of results are in agreement with available experimental data. In addition, the bond-dissociation energy for the C6H5NH2 → C6H5 + NH2 process calculated in this work based on the heats of formation of C6H5, NH2, and C6H5NH2 is 104.26 kcal/mol at the CCSD(T)//B3LYP/6-311++G(3df,2p) level, which is in excellent agreement with the experimental value, 104.21 ± 0.38 kcal/mol (ref from NIST, webbook.nist.gov).

As shown in Figures 1 and S1, the first intermediate IS1 located at −103 kcal/mol is the result of the additional reaction between two reactants, which takes place without a well-defined transition state. From IS1, there are various different subchannels created to yield other intermediates or products (see Figure S1), of which some subchannels can be ignored because they proceed via high-energy barriers of over 18 kcal/mol. In Figure 1, hence, we only consider seven potential channels possessing low transition states. Those channels go through two tight transition states before reaching the products. The first path proceeds via transition states, T1/11 (−28.9 kcal/mol) and T11P5 (−21.5 kcal/mol), and stops at the product PR5 [C6H4 (o-benzyne) + NH3] at −25.6 kcal/mol. The T1/11 transition state connecting IS1 with IS11 (−31 kcal/mol) has only one imaginary frequency of 1288i corresponding to an H-shift from the ortho position to the −NH2 group with a distance of 1.648 and 1.199 Å, respectively, which makes the C–NH2 bond elongate from 1.395 Å in IS1 to 1.486 Å in IS11. Whereas the ∠C2C1C2 angle increases nearly 11 °C, the ∠C1C2C3 angle decreases about 8 °C, in which C2 and C3 denote the carbon atoms at ortho and meta positions, respectively. It is worth noting that the structure of T1/11 has been confirmed by IRC analysis with the B3LYP/6-311++G(3df,2p) method along the forward direction from IS1 to IS11 as well as the reverse direction from IS11 back to IS1 (see Figure S3). These results reveal that T1/11 is the accurate transition state connecting IS1 and IS11. Similarly, the T11P5 transition state connecting IS11 to the product PR5 also has only one imaginary frequency of 131.9617i relating to the dissociation of the C–NH3 bonding with a distance of 2.203 Å. It can be seen from Figure 1 that the reaction path generating PR5 is the most favorable channel in terms of energy compared to the others. Therefore, the process from the reactants to PR5 contributes mainly to the overall rate constant of the title reaction. The second path producing the product PR9 passes two transition states T1/13 and T13P9, for which the transition state T1/13 connecting IS1 with IS13 shows a transfer of a H atom from the NH2 group to the CH group at the ortho location. It may be noted that IS13 can be easily produced because T1/13 lies at a fair depth below the reactants about 26 kcal/mol; thus, an extremely enormous exothermicity from the first step (reactants to IS1) can help IS1 easily cross T1/13. Once IS13 is formed, it can be converted to product PR9 via T13P9; this process needs plenty of energy to pass over the high barrier of nearly 90 kcal/mol. In addition, the reaction path giving product PR9 is an exothermic channel with 4.4 kcal/mol. This product, hence, is guessed hardly to appear at room temperature. The product PR4 can be established from two different paths; the first path goes through two transition states such as T1/3 and T3P4, while the second path occurs via T1/8 and T8P4. Both channels effortlessly pass transition states T1/3 (−19 kcal/mol) and T1/8 (−16.9 kcal/mol) at the early stages, but it is difficult to overcome high-energy barriers T3P4 (∼15 kcal/mol) and T8P4 (∼20 kcal/mol) at the later stages. Of these, T1/3 and T1/8 show a 2,3-H-shift and a 3,2-H-shift, respectively, whereas T3P4 and T8P4 present two H2-abstractions from para and ortho positions, respectively. Therefore, PR4 is also considered to be difficult to form in normal conditions even though the formation of PR4 from these two channels is exothermic by 16.7 kcal/mol. Similarly, the product PR10 was also created by two different pathways: one passes through the transition states T1/10 and T10P10, while the other one proceeds via the transition states T1/16 and T16P10. Figure 1 shows that if T1/10 describes a H-shift between meta and para locations yielding IS10 (−26.2 kcal/mol), T1/16 shows a reverse transfer of a H atom from para to meta positions forming the intermediate state IS16 lying under the reactants by 16.6 kcal/mol. The relative energy of T16P10 in the second channel is higher than the one of T10P10 in the first channel by about 3 kcal/mol. The second channel is thus predicted to donate less consideration to the PR10 product. However, both TSs possess very high-energy barriers (see Figure 1); thus, the PR10 product is predicted to be difficult to form in the low-temperature region. The overall exothermicity of the reaction path resulting in the PR10 product is 13.4 kcal/mol. It is worth noting that the PR5 product is the most stable one compared to the others on the whole PES. Last but not least, the IS1 intermediate state formed at the first step can also isomerize to the IS2 isomer, which is located at −79.4 kcal/mol, via T1/2 with a 102 kcal/mol energy barrier. The geometry of T1/2 in Figure 3 shows a very far H-shift from the NH2 group to the para-C atom at distances of 1.383 and 1.684 Å, respectively, which makes this process lose more energy than others. The bimolecular products C6H4NH + H2 (denoted as PR6) with 5.0 kcal/mol of endothermicity can be generated by eliminating a hydrogen molecule out of the IS2 geometry when it proceeds via the T2P6 transition state lying 8.4 kcal/mol above the entry point.

Briefly, many various products can be formed through the addition channel, as shown in Figure 1, in which, the channel going via transition structures T1/11 (−28.9 kcal/mol) and T11P5 (−21.5 kcal/mol) producing PR5 is found to be dominant, while the others proceeding via T1/3 (−19 kcal/mol), T1/10 (−18.5 kcal/mol), T1/8 (−16.9 kcal/mol), T1/16 (−14.2 kcal/mol), and T1/2 (−0.8 kcal/mol) forming PR4, PR6, PR9, and PR10 are less favorable. Accordingly, the dominant reaction path yielding PR5 is expected to be kinetically advantageous.

3.2. Rate Constant Calculations

The rate constants for the title reaction have been calculated based on the main PES shown in Figure 1. Many channels of the reaction, as discussed above, can be overlooked due to their too high-energy barriers. Only one reaction path proceeding via the two transition states T1/11 and T11P5 giving rise to the product PR5 has been considered. For this reason, the rate constants of the C6H5 + NH2 reaction have been calculated relying on the channel as shown below

3.2.

The rate constants of the barrierless process, C6H5 + NH2 → IS1, have been determined by using the VRC-TST procedure with the Variflex code.53 The treatment of microvariational RRKM and the Morse functional model64 have also been utilized to estimate the minimum energy path (MEP) curve presented as follows

3.2.

where De is the dissociation energy excluding the zero-point energy; r and re are the reaction coordinate and equilibrium value of r; and β is the constant derived from the fitted equation to the estimated MEP.

The computed barrierless rate coefficients under the conditions of this study are shown in Table S4 in the SI file and are plotted in Figure 4. It is shown that the rate constants, at low temperatures (T ≤ 600 K), slightly increase and do not depend on pressures. At high temperatures (T ≥ 700, 800, 900, 1000, 1100, and 1200 K at P = 1, 10, 100, 760, 7600, and 76 000 Torr, respectively), those values sharply decrease and strongly depend on pressure.

Figure 4.

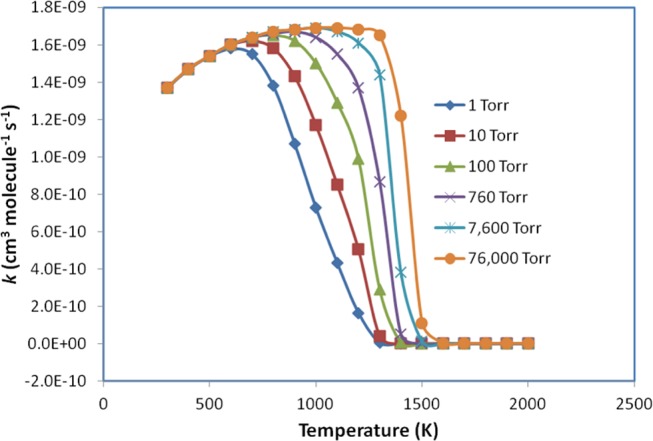
Figure 4

Open in a new tab

Plots of predicted rate constants for the C6H5 + NH2 → C6H5NH2 process in the temperature range of 300–2000 K at various pressures of 1–76 000 Torr Ar.

The rate constants for the reverse process, C6H5NH2 → C6H5 + NH2, have also been computed with the RRKM theory under varying T, P conditions. Similar to the forward process, this channel takes place without a well-defined transition state; its rate constants can thus be predicted with the VRC-TST approach based on the maximum ΔG‡ criterion. The rate constants predicted by solving the master equation using the Multiwell code54 for various Ar pressures between 1 and 76 000 Torr in the temperature range of 300–2000 K are given in Table S5 and Figure 5. As can be seen, the decomposition rate constants quickly increase in the temperature range of 300 ≤ T ≤ 1100 K and gradually decrease when temperatures surpass over 1200 K (at 1 Torr), 1300 K (at 10, 100, and 760 Torr), and 1400 K (at 7600 and 76 000 Torr). Moreover, the equilibrium constants at the high-pressure limit for the C6H5 + NH2 ↔ IS1 process have been calculated and are shown in Table S4. These values drop sharply as temperatures increase, e.g., K∞(equiv) = 1.18 × 1048 and 2.74 ×10–16 cm3 molecule–1 at 300 and 2000 K, respectively.

Figure 5.

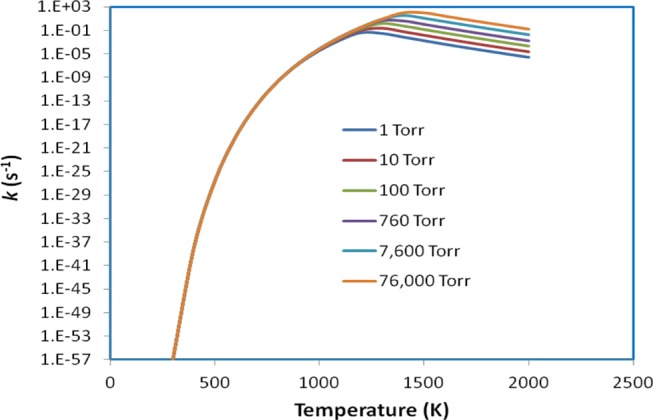
Figure 5

Open in a new tab

Plots of predicted rate constants for the decomposition process, C6H5NH2 → C6H5 + NH2, in the temperature range of 300–2000 K at various pressures of 1–76 000 Torr Ar.

The pressure- and temperature-dependent rate constants, k(T, P), for the C6H5 + NH2 → PR5 channel were determined by using the Multiwell program54 with the use of the Eckart tunneling effects59 under the same conditions as above. The calculated results are presented in Table S6 and are plotted in Figure 6. The modified Arrhenius equation with three parameters adequately describes those data in the temperature range of 300–2000 K at various pressures of Ar and can be given (in units of cm3 molecule–1 s–1) as follows

3.2.
3.2.
3.2.
3.2.
3.2.
3.2.

It is observed that the rate constants for the designated reaction channel shown in Table S6 and Figure 6 tend to gradually increase in the low-temperature regions (T ≤ 600, 700, 800, 900, 1000, and 1100 for k1, k2, k3, k4, k5, and k6, respectively). For instance, the rate constants at T = 300, P = 1 Torr and T = 600 K, P = 1 Torr are 1.37 × 10–9 and 1.58 × 10–9 cm3 molecule–1 s–1, respectively. As the temperature increases (T > 600, 700, 800, 900, 1000, and 1100 at 1, 10, 100, 760, 7600, and 76 000 Torr, respectively), the rate coefficients sharply decrease, e.g., the rate constants are 1.67 × 10–9 and 2.16 × 10–11 cm3 molecule–1 s–1 at T = 900 K, P = 760 Torr and T = 2000 K, P = 760 Torr, respectively. In addition, it is found that the effect of pressure on the rate constants is negligible at low and high temperatures (e.g., T ≤ 600 and T > 1700 K, cf. Figure 6) owing to higher-energy decomposition processes and indirect isomerization/decomposition processes. In the temperature range of 600–1700 K, the predicted rate coefficients positively depend on pressure (e.g., at the same temperature, T = 1000 K, k1 = 8.61 × 10–10 cm3 molecule–1 s–1 at P = 1 Torr, while k6 = 1.69 × 10–9 cm3 molecule–1 s–1 at P = 76 000 Torr).

Figure 6.

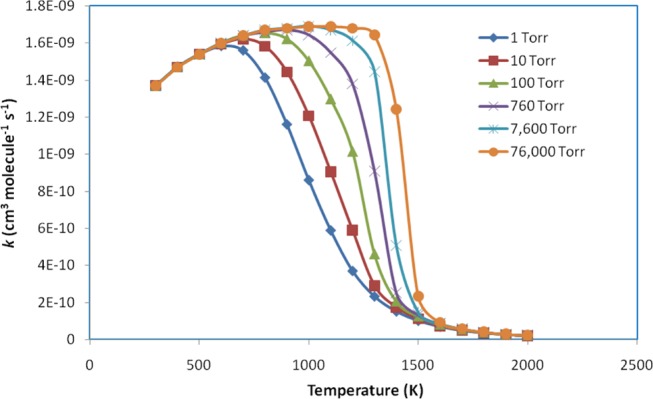
Figure 6

Open in a new tab

Plots of predicted rate constants for the C6H5 + NH2 → PR5 reaction in the temperature range of 300–2000 K at various pressures of 1–76 000 Torr Ar.

The rate coefficients at high-pressure limit, k∞(T), were also predicted and are listed in Table S6 in the temperature range of 300 ≤ T ≤ 2000 K. In this situation, likewise, the rate constants slightly increase with an increase of temperature from 300 to 1100 K and gradually decrease at temperatures above 1200 K. At low temperature (T ≤ 600 K), as discussed above, k∞(T) is equal to ki (i = 1–6) (e.g., 1.37 × 10–9 at T = 300 K or 1.60 × 10–9 cm3 molecule–1 s–1 at T = 600 K), while in the high-temperature region (T ≥ 1500 K), the high-pressure limit rate constant is much greater than the others in the range of pressure P = 1–76 000 Torr (e.g., at T = 2000 K, k1 = 2.10 × 10–11 vs k∞(T) = 1.52 × 10–9 cm3 molecule–1 s–1), as shown in Table S6.

The effects of the error margins of energy about ± 2 kcal/mol estimated by the CCSD(T)//B3LYP/6-311++G(3df,2p) method on the rate constants for the formation and dissociation of C6H5NH2 were also considered. The computed values in various conditions are presented in Figures S7–S10 in the SI file. These results show that the rate constants for the formation of C6H5NH2 remain almost unchanged at low temperatures (T ≤ 1200 K) but change quickly at high temperatures (T ≥ 1300 K). At 2000 K and 760 Torr Ar, the value associated with a −101 kcal/mol energy of C6H5NH2 is 3.01 × 10–19 cm3 molecule–1 s–1, which is 4.97 × 10–19 cm3 molecule–1 s–1 at the energy of −103 kcal/mol, while the value at −105 kcal/mol energy increases by nearly 2 orders of magnitude in going to 1.57 × 10–17 cm3 molecule–1 s–1 (see Tables S4, S7, and S9). In contrast, at low temperatures (T ≤ 1100 K), the rate constants for the decomposition of C6H5NH2 → C6H5 + NH2 decrease according to the reduction of the C6H5–NH2-binding energy (BDE). However, at high temperatures (T ≥ 1400 K), those values increase slightly when the BDE increases from 101 to 105 kcal/mol, as shown in Tables S5, S8, and S10.

4. Conclusions

The mechanism and kinetics, as well as thermodynamics of the C6H5 + NH2 reaction, have been investigated based on the quantum chemical theory. The B3LYP method in conjunction with the basic set 6-311++G(3df,2p) has been employed to optimize for the species related in this reaction, such as reactants, intermediate states, transition states, and products. The high method CCSD(T) with the same basic set above has also been utilized to calculate single-point energies for all species on the potential energy surface.

The mechanism of the title reaction at the entrance channel takes place as the additional style without a well-defined transition state to form the stable intermediate C6H5NH2 standing at 103 kcal/mol below the reactants. The most dominant channel connecting IS1 with product PR5 proceeds via two different transition states T1/11 and T11P5 lying 28.9 and 21.5 kcal/mol under the reactants, respectively.

The predicted heats of formation of several species (C6H5, NH2, C6H5NH2), as well as the heats of reaction of some reaction paths producing IS1, PR4, PR5, PR6, PR9, and PR10 at the CCSD(T)//B3LYP/6-311++G(3df,2p) and CCSD(T)//M06-2×/aug-cc-pVTZ levels of theory are in agreement with the available experimental data. Those results confirm that the methods used in this work are reliable and the calculated energies can be utilized to compute rate constants for the title reaction.

The predicted rate coefficients for the C6H5 + NH2 → PR5 channel in the pressure and temperature ranges of 1–76 000 Torr and 300–2000 K, respectively, reveal that its kinetics strongly depends on pressure and temperature, i.e., the rate constants increase at low temperature and decrease at high temperature. The association and dissociation rate constants of the barrierless processes, C6H5 + NH2 → C6H5NH2 and C6H5NH2 → C6H5 + NH2, respectively, were nearly independent of pressure at a low temperature and strongly dependent on pressure at a high temperature. Observation of the C6H5 + NH2 = C6H5NH2 process showed that there was a large negative temperature dependence of the high-pressure limit equilibrium constants. The effects of the error margins of the energy on the rate constants for the formation and dissociation of C6H5NH2 were also considered. The results show that the rate constants for the formation of C6H5NH2 remain almost unchanged at low temperatures but change quickly at high temperatures. In contrast, at low temperatures, the rate constants for the C6H5NH2 → C6H5 + NH2 decomposition decrease according to the reduction of the C6H5–NH2 binding energy but slightly increase at high temperatures.

The results in this study are very important to understand the mechanism and kinetics of the aromatic radical C6H5 with some small species such as NH2, CH3, etc. They will help researchers in working with various experiments related to this species in the future.

Acknowledgments

The authors thank The Center for Computational Science of Hanoi National University of Education in Vietnam for computational support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b03967.

  • Variational transition-state theory (VTST) applied for the C6H5 + NH2 → C6H5NH2 process; frequencies and coordinates of reactants, intermediates, transition states, and products of the C6H5 + NH2 → product reaction at the B3LYP/6-311++G(3df,2p) level of theory; Gibbs free energies (ΔG) in kcal/mol using CCSD(T)//B3LYP/6-311++G(3df,2p) and entropies (ΔS) in cal/mols·K using B3LYP/6-311++G(3df,2p); predicted rate constants (cm3 molecule–1 s–1) for the C6H5 + NH2 → C6H5NH2, C6H5NH2 → C6H5 + NH2, and C6H5 + NH2 → PR5 reactions in the temperature and pressure ranges of 300–2000 K and 1–76 000 Torr, respectively, as well as Keq (cm3 molecule–1) of the C6H5 + NH2 → C6H5NH2 process; detailed potential energy surface of the C6H5 + NH2 system; geometries of the reactants, intermediate states, transition states, and products optimized at the B3LYP/6-311++G(3df,2p) level; and the IRC profile for the transition state T1/11 calculated at the B3LYP/6-311++G(3df,2p) level of theory (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b03967_si_001.pdf (1.4MB, pdf)

References

  1. Cherchneff I.; Barker J. R. Polycyclic aromatic hydrocarbons and molecular equilibria in carbon-rich stars. Astrophys. J. 1992, 394, 703–716. 10.1086/171624. [DOI] [Google Scholar]
  2. Messenger S.; Amari S.; Gao X.; Walker R. M.; Clemett S. J.; Chillier X. D. F.; Zare R. N.; Lewis R. S. Indigenous polycyclic aromatic hydrocarbons in circumstellar graphite grains from primitive meteorites. Astrophys. J. 1998, 502, 284–295. 10.1086/305874. [DOI] [Google Scholar]
  3. Allain T.; Sedlmayr E.; Leach S. PAHs in circumstellar envelopes. I. Processes affecting PAH formation and growth. Astron. Astrophys. 1997, 323, 163–176. [Google Scholar]
  4. Frenklach M.; Clary D. W.; Gardiner W. C.; Stein S. E. Detailed kinetic modeling of soot formation in shock-tube pyrolysis of acetylene. Symp. (Int.) Combust. 1985, 20, 887–901. 10.1016/S0082-0784(85)80578-6. [DOI] [Google Scholar]
  5. Kazakov A.; Frenklach M. On the relative contribution of acetylene and aromatics to soot particle surface growth. Combust. Flame 1998, 112, 270–274. 10.1016/S0010-2180(97)81776-2. [DOI] [Google Scholar]
  6. Kern R. D.; Wu C. H.; Yong J. N.; Pamidimukkala K. M.; Singh H. J. Correlation of Benzene Production with Soot Yield Measurements As Determined from Fuel Pyrolyses. Energy Fuels 1988, 2, 454–457. 10.1021/ef00010a011. [DOI] [Google Scholar]
  7. Abramovich R. A., Ed. Reactive Intermediates; Plenum: New York, 1980. [Google Scholar]
  8. Almond M. J., Ed. Short-lived Molecules; Ellis Horwood: New York, 1990. [Google Scholar]
  9. Matthews H.; Irvine W. M. The hydrocarbon ring C3H2 is ubiquitous in the Galaxy. Astrophys. J. 1985, 298, L61–L65. 10.1086/184567. [DOI] [PubMed] [Google Scholar]
  10. Thaddeus P.; Vrtilek J. M.; Gottlieb C. A. Laboratory and astronomical identification of cyclopropenylidene, C3H2. Astrophys. J. 1985, 299, L63–L66. 10.1086/184581. [DOI] [Google Scholar]
  11. Cernicharo J.; Gottlieb C. A.; Gue′lin M.; Killian T. C.; Paubert G.; Thaddeus P.; Vrtilek J. M. Astronomical detection of H2CCC. Astrophys. J. 1991, 368, L39–L41. 10.1086/185943. [DOI] [Google Scholar]
  12. Homann K. Fullerenes and soot formation—new pathways to large particles in flames. Angew. Chem., Int. Ed. 1998, 37, 2435–2451. . [DOI] [PubMed] [Google Scholar]
  13. Bittner J. D.; Howard J. B. Mechanism of hydrocarbon decay in fuel-rich secondary reaction zones. Symp. (Int.) Combust. 1982, 19, 211–221. 10.1016/S0082-0784(82)80191-4. [DOI] [Google Scholar]
  14. Castaldi M. J.; Marinov N. M.; Melius C. F.; Huang J.; Senkan S. M.; Pitz W. J.; Westbrook C. K. Experimental and modeling investigation of aromatic and polycyclic aromatic hydrocarbon formation in a premixed ethylene flame. Symp. (Int.) Combust. 1996, 26, 693–702. 10.1016/S0082-0784(96)80277-3. [DOI] [Google Scholar]
  15. Bhargava A.; Westmoreland P. R. Measured flame structure and kinetics in a fuel-rich ethylene flame. Combust. Flame 1998, 113, 333–347. 10.1016/S0010-2180(97)00208-3. [DOI] [Google Scholar]
  16. Vereecken L.; Peeters J.; Bettinger H. F.; Kaiser R. I.; Schleyer P. V. R.; Schaefer H. F. Reaction of Phenyl Radicals with Propyne. J. Am. Chem. Soc. 2002, 124, 2781–2789. 10.1021/ja017018+. [DOI] [PubMed] [Google Scholar]
  17. Tokmakov I. V.; Kim G. S.; Kislov V. V.; Mebel A. M.; Lin M. C. The Reaction of Phenyl Radical with Molecular Oxygen: A G2M Study of the Potential Energy Surface. J. Phys. Chem. A 2005, 109, 6114–6127. 10.1021/jp051712k. [DOI] [PubMed] [Google Scholar]
  18. Yu T.; Lin M. C. Kinetics of the C6H5 + O2 reaction at low temperatures. J. Am. Chem. Soc. 1994, 116, 9571–9576. 10.1021/ja00100a022. [DOI] [Google Scholar]
  19. Carpenter B. K. Computational prediction of new mechanisms for the reactions of vinyl and phenyl radicals with molecular oxygen. J. Am. Chem. Soc. 1993, 115, 9806–9807. 10.1021/ja00074a060. [DOI] [Google Scholar]
  20. Mebel A. M.; Lin M. C. Ab initio molecular orbital calculations of C6H5O2 isomers. J. Am. Chem. Soc. 1994, 116, 9577–9584. 10.1021/ja00100a023. [DOI] [Google Scholar]
  21. Lin M. C.; Mebel A. M. Ab initio molecular orbital study of the O + C6H5O reaction. J. Phys. Org. Chem. 1995, 8, 407–420. 10.1002/poc.610080605. [DOI] [Google Scholar]
  22. Fadden M. J.; Barckholtz C.; Haddad C. M. Computational study of the unimolecular decomposition pathways of phenylperoxy radical. J. Phys. Chem. A 2000, 104, 3004–3011. 10.1021/jp993990n. [DOI] [Google Scholar]
  23. Fadden M. J.; Hadad C. M. Unimolecular decomposition of the 2-oxepinoxy radical: a key seven-membered ring intermediate in the thermal oxidation of benzene. J. Phys. Chem. A 2000, 104, 8121–8130. 10.1021/jp0017238. [DOI] [Google Scholar]
  24. Merle J. K.; Hadad C. M. Computational study of the oxygen initiated decomposition of 2-oxepinoxy radical: A key intermediate in the oxidation of benzene. J. Phys. Chem. A 2004, 108, 8419–8433. 10.1021/jp047317w. [DOI] [Google Scholar]
  25. Glassman I.Combustion, 2nd ed.; Academic Press: New York, 1986. [Google Scholar]
  26. Wu C. H.; Kern R. D. Shock-tube study of allene pyrolysis. J. Phys. Chem. A 1987, 91, 6291–6296. 10.1021/j100308a042. [DOI] [Google Scholar]
  27. Alkemade U.; Homann K. H. Formation of C6H6 isomers by recombination of propynyl in the system sodium vapour/propynylhalide. Z. Phys. Chem. 1989, 161, 19–34. 10.1524/zpch.1989.161.Part_1_2.019. [DOI] [Google Scholar]
  28. Melius C. F.; Miller J. A.; Evleth E. M. Unimolecular reaction mechanisms involving C3H4, C4H4, and C6H6 hydrocarbon species. Symp. (Int.) Combust. 1992, 24, 621–628. 10.1016/S0082-0784(06)80076-7. [DOI] [Google Scholar]
  29. Morter C.; Farhat S.; Adamson J.; Glass G.; Curl R. Rate constant measurement of the recombination reaction C3H3 + C3H3. J. Phys. Chem. A 1994, 98, 7029–7035. 10.1021/j100079a023. [DOI] [Google Scholar]
  30. Miller J. A.; Volponi J. V.; Pauwels J.-F. The effect of allene addition on the structure of a rich C2H2/O2/Ar flame. Combust. Flame 1996, 105, 451–461. 10.1016/0010-2180(95)00227-8. [DOI] [Google Scholar]
  31. Mebel A. M.; Morokuma K.; Lin M. C. Modification of the gaussian–2 theoretical model: The use of coupled-cluster energies, density-functional geometries, and frequencies. J. Chem. Phys. 1995, 103, 7414–7421. 10.1063/1.470313. [DOI] [Google Scholar]
  32. Park J.; Dyakov I. V.; Lin M. C. FTIR and Mass-Spectrometric Measurements of the Rate Constant for the C6H5 + H2 Reaction. J. Phys. Chem. A 1997, 101, 8839–8843. 10.1021/jp972162w. [DOI] [Google Scholar]
  33. Tokmakov I. V.; Park J.; Gheyas S.; Lin M. C. Experimental and Theoretical Studies of the Reaction of the Phenyl Radical with Methane. J. Phys. Chem. A 1999, 103, 3636–3645. 10.1021/jp983140s. [DOI] [Google Scholar]
  34. Tokmakov I. V.; Park J.; Gheyas S.; Lin M. C. Experimental and Theoretical Studies of the Reaction of the Phenyl Radical with Methane. J. Phys. Chem. A 1999, 103, 3636–3645. 10.1021/jp983140s. [DOI] [Google Scholar]
  35. Park J.; Gheyas S. I.; Lin M. C. Kinetics of C6H5 radical reactions with 2-methylpropane, 2,3-dimethylbutane and 2,3,4-trimethylpentane. Int. J. Chem. Kinet. 1999, 31, 645–653. . [DOI] [Google Scholar]
  36. Yu T.; Lin M. C. Kinetics of the reaction of C6H5 with HBr and DBr. Int. J. Chem. Kinet. 1994, 26, 771–778. 10.1002/kin.550260711. [DOI] [Google Scholar]
  37. Nam G. J.; Xia W.; Park J.; Lin M. C. The Reaction of C6H5 with CO: Kinetic Measurement and Theoretical Correlation with the Reverse Process. J. Phys. Chem. A 2000, 104, 1233–1239. 10.1021/jp993245a. [DOI] [Google Scholar]
  38. Becke A. D. Density functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  39. Becke A. D. Density-functional exchange-energy approximation with correct asymptotic-behavior. Phys. Rev. A 1988, 38, 3098–3010. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  40. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  41. Zhao Y.; Truhlar D. G. A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101 10.1063/1.2370993. [DOI] [PubMed] [Google Scholar]
  42. Zhao Y.; Truhlar D. G. Density Functional for Spectroscopy: No Long-Range Self-Interaction Error, Good Performance for Rydberg and Charge-Transfer States, and Better Performance on Average than B3LYP for Ground States. J. Phys. Chem. A 2006, 110, 13126–13130. 10.1021/jp066479k. [DOI] [PubMed] [Google Scholar]
  43. Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  44. Scuseria G. E.; Janssen C. L.; Schaefer H. F. III An efficient reformulation of the closed-shell coupled cluster single and double excitation (CCSD) equations. J. Chem. Phys. 1988, 89, 7382–7387. 10.1063/1.455269. [DOI] [Google Scholar]
  45. Dunning T. H. Jr Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  46. Peterson K. A. Chapter 11 Gaussian Basis Sets Exhibiting Systematic Convergence to the Complete Basis Set Limit. Annu. Rep. Comput. Chem. 2007, 3, 195–206. 10.1016/S1574-1400(07)03011-3. [DOI] [Google Scholar]
  47. Hill J. G. Gaussian Basis Sets for Molecular Applications. Int. J. Quantum Chem. 2013, 113, 21–34. 10.1002/qua.24355. [DOI] [Google Scholar]
  48. Gonzalez C.; Schlegel H. B. An improved algorithm for reaction path following. J. Chem. Phys. 1989, 90, 2154–2161. 10.1063/1.456010. [DOI] [Google Scholar]
  49. Gonzalez C.; Schlegel H. B. Reaction path following in mass-weighted internal coordinates. J. Chem. Phys. 1990, 94, 5523–5527. 10.1021/j100377a021. [DOI] [Google Scholar]
  50. Bartlett R. J.; Musial M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. 10.1103/RevModPhys.79.291. [DOI] [Google Scholar]
  51. Alecu I. M.; Zheng J.; Zhao Y.; Truhlar D. G. Computational Thermochemistry: Scale Factor Databases and Scale Factors for Vibrational Frequencies Obtained from Electronic Model Chemistries. J. Chem. Theory Comput. 2010, 6, 2872–2887. 10.1021/ct100326h. [DOI] [PubMed] [Google Scholar]
  52. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16; Gaussian, Inc.: Wallingford, CT, 2016. [Google Scholar]
  53. Klippenstein S. J.; Wagner A. F.; Dunbar R. C.; Wardlaw D. M.; Robertson S. H.. VARIFLEX, version 1.00, 1999.
  54. Barker J. R.; Nguyen T. L.; Stanton J. F.; Aieta C.; Ceotto M.; Gabas F.; Kumar T. J. D.; Li C. G.; Lohr L. L.. et al. Multiwell-2017.1 Software Suite; J.R. Barker, University of Michigan: Ann Arbor, Michigan, 2017, http://claspresearch.engin.u-mich.edu/multiwell/.
  55. Eyring H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. 10.1063/1.1749604. [DOI] [Google Scholar]
  56. Klippenstein S. J. Variational optimizations in the Rice–Ramsperger–Kassel–Marcus theory calculations for unimolecular dissociations with no reverse barrier. J. Chem. Phys. 1992, 96, 367–371. 10.1063/1.462472. [DOI] [Google Scholar]
  57. Klippenstein S. J. A bond length reaction coordinate for unimolecular reactions. II. Microcanonical and canonical implementations with application to the dissociation of NCNO. J. Chem. Phys. 1991, 94, 6469–6482. 10.1063/1.460276. [DOI] [Google Scholar]
  58. Holbrook K. A.; Pilling M. J.; Robertson S. H.. Unimolecular Reactions; J. Wiley: Chichester, UK, 1996. [Google Scholar]
  59. Eckart C. The penetration of a potential barrier by electrons. Phys. Rev. 1930, 35, 1303–1309. 10.1103/PhysRev.35.1303. [DOI] [Google Scholar]
  60. Miller J. A.; Klippenstein S. J. The recombination of propargyl radicals: Solving the master equation. J. Phys. Chem. A 2001, 105, 7254–7266. 10.1021/jp0102973. [DOI] [Google Scholar]
  61. Hippler H.; Troe J.; Wendelken H. J. Collisional deactivation of vibrationally highly excited polyatomic molecules. II. Direct observations for excited toluene. J. Chem. Phys. 1983, 78, 6709–6717. 10.1063/1.444670. [DOI] [Google Scholar]
  62. Mourits F. M.; Rummens F. H. A. A critical evaluation of Lennard–Jones and Stockmayer potential parameters and of some correlation methods. Can. J. Chem. 1977, 55, 3007–3020. 10.1139/v77-418. [DOI] [Google Scholar]
  63. Tardy D. C.; Rabinovitch B. S. Collisional Energy Transfer. Thermal Unimolecular Systems in the Low-Pressure Region. J. Chem. Phys. 1966, 45, 3720–3730. 10.1063/1.1727392. [DOI] [Google Scholar]
  64. Yu J.; Dong S. H.; Sun G. H. Series solutions of the Schrödinger equation with position-dependent mass for the Morse potential. Phys. Lett. A 2004, 322, 290–297. 10.1016/j.physleta.2004.01.039. [DOI] [Google Scholar]
  65. Alecu I. M.; Gao Y.; Hsieh P.-C.; Sand J. P.; Ors A.; McLeod A.; Marshall P. Studies of the Kinetics and Thermochemistry of the Forward and Reverse Reaction Cl + C6H6 = HCl + C6H5. J. Phys. Chem. A 2007, 111, 3970–3976. 10.1021/jp067212o. [DOI] [PubMed] [Google Scholar]
  66. Moskaleva L. V.; Lin M. C. Theoretical Study of the NH2 + C2H2 Reaction. J. Phys. Chem. A 1998, 102, 4687–4693. 10.1021/jp980823z. [DOI] [Google Scholar]
  67. Chase M. W., Jr.NIST-JANAF Thermochemical Tables, 4th ed.; American Chemical Society–American Institute of Physics for the National Institute of Standards and Technology: Washington D. C.–Woodbury, New York, 1998. [Google Scholar]
  68. Hatton W. E.; Hildenbrand D. L.; Sinke G. C.; Stull D. R. Chemical Thermodynamic Properties of Aniline. J. Chem. Eng. Data 1962, 7, 229–231. 10.1021/je60013a021. [DOI] [Google Scholar]
  69. Vriens G. N.; Hill A. G. Equilibria of several reactions of aromatic amines. Ind. Eng. Chem. 1952, 44, 2732–2735. 10.1021/ie50515a062. [DOI] [Google Scholar]
  70. Cole L. G.; Gilbert E. C. The heats of combustion of some nitrogen compounds and the apparent energy of the N-N bond. J. Am. Chem. Soc. 1951, 73, 5423–5427. 10.1021/ja01155a120. [DOI] [Google Scholar]
  71. Anderson C. M.; Gilbert E. C. The apparent energy of the N-N bond as calculated from heats of combustion. J. Am. Chem. Soc. 1942, 64, 2369–2372. 10.1021/ja01262a041. [DOI] [Google Scholar]
  72. Lemoult M. P. Recherches theoriques et experimentales sur les chaleurs de combustion et de formation des composes organiques. Ann. Chim. Phys. 1907, 12, 395–432. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b03967_si_001.pdf (1.4MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES