Evidence Synthesis for Stochastic Epidemic Models

Abstract

In recent years, the role of epidemic models in informing public health policies has progressively grown. Models have become increasingly realistic and more complex, requiring the use of multiple data sources to estimate all quantities of interest. This review summarises the different types of stochastic epidemic models that use evidence synthesis and highlights current challenges.

1. Background

Epidemic models have become increasingly central to public health decision making, providing quantitative support to the efficient planning of health-care resources, the determination of optimal control strategies and the assessment of interventions to interrupt disease transmission. All of these require knowledge on hidden aspects of epidemics, such as current disease prevalence, severity, incidence and transmission, which can only be indirectly inferred through modelling. As a consequence of this crucial role of models, the methodologies underpinning epidemic modelling have come under increasing scrutiny. This has lead to more frequent adoption of rigorous approaches to linking models to data [21], increasing realism and, therefore, model complexity, and the need to use rich data arrays to guarantee reliable estimation. The result has been a recent proliferation of models incorporating data from multiple sources (e.g., [1, 13]).

We will summarise and review some selected key examples in this literature by characterising models using a common construct. Most epidemic processes can be expressed through a state vector X_t representing unobservable characteristics of the epidemic and a vector of observable quantities Y_t, under a generalised parameter-driven state-space framework:

$$\begin{array}{l}{\mathit{\text{X}}}_t|{\mathit{\text{X}}}_{1:t-1,}{\mathit{\text{Y}}}_{1:t-1}\sim {\mathit{\text{p}}}_{\mathit{\varphi }}(\cdot |{\mathit{\text{X}}}_{t-1})\\ (\mathrm{state}\mathrm{equation}),\end{array}$$ (1.1)

$$\begin{array}{l}{\mathit{\text{Y}}}_t|{\mathit{\text{X}}}_{1:t},{\mathit{\text{Y}}}_{1:t-1}\sim p_{(\mathit{\varphi },\mathit{\text{η}})}(\cdot |{\mathit{\text{X}}}_t)\\ (\mathrm{observation}\mathrm{equation}),\end{array}$$ (1.2)

where t = 1,…, T and the p(·|·) are appropriately chosen probability density functions [10]. Equation (1.1) governs the development of the epidemic system, characterised by a vector of parameters ϕ. Equation (1.2) relates the underlying epidemic process to relevant potential data Y_t. These data are typically imperfect observations associated with X_t, constrained by the limitations of surveillance schemes and subject to (a vector of) nuisance parameters, η. State vectors consist of all latent quantities that may change over time, usually probabilistically, and ϕ governs their temporal development. In some cases, the state vector is simply a deterministic function of ϕ. More commonly, epidemic models are compartmental, partitioning a population according to, for example, infection status. The distribution of individuals in each model compartment is part of the state vector, as is any quantity describing model dynamics that evolves over time, for example, incidence of infection λ_t [6] or the transmission potential β_t, the disease transmission rate conditional on contact between an infectious and a susceptible individual [34].

The focus of the statistical analysis could be to estimate unobserved system states X_1:T either sequentially (filtering) or retrospectively (smoothing), and/or to make inference about components of θ = (ϕ, η) that have some crucial interpretation. These parameter components might measure some headline statistic for the epidemic, such as the epidemic’s reproductive number R₀, the average number of secondary infections caused by a single primary infection in a wholly susceptible population, or the effect of an intervention. This inference, ideally, would be based on direct observations Y_t on the states X_t, that is,

$${\mathit{\text{Y}}}_t={\mathit{\text{X}}}_t+{\eta }^T{\epsilon }_{Y,t},\mathrm{where}{\epsilon }_{Y,t}\sim N(\mathit{0},\mathit{\text{I}}).$$ (1.3)

However, equation (1.3) implies observation of, for instance, new infections as they occur, which, especially in large populations, is rarely feasible. More realistically, data are indirectly related to the quantities of interest and inference becomes possible only through the integration of data from multiple sources. Thus, given $\mathit{\theta },{\mathit{\text{Y}}}_t=({\mathit{\text{Y}}}_t^1,\mathrm{\dots },{\mathit{\text{Y}}}_t^N)$ is a collection of N independent data sources with observed values ${\mathit{\text{y}}}_t=({\mathit{\text{y}}}_t^1,\mathrm{\dots .},{\mathit{\text{y}}}_t^N).$

Evidence does not just come in the form of data. There are also modelling assumptions that underlie the parametric forms of p_ϕ(·) and p_(ϕ,η)(·), based on relevant literature, expert opinion and/or collateral data not included in the model. In particular, pragmatic choices might need to be made over which parameter components can realistically be estimated by the available data, and which components it is prudent to assume to be known from literature (but can be varied as part of a sensitivity analysis). Synthesis of these kinds of evidence can be formalised by adopting a Bayesian framework centered on the posterior distribution

$$\begin{array}{l}p(\mathit{\theta },{\mathit{\text{x}}}_{1:T}|{\mathit{\text{y}}}_{1:T})\\ \propto p({\mathit{\text{y}}}_{1:T}|{\mathit{\text{x}}}_{1:T},\mathit{\theta })p({\mathit{\text{x}}}_{1:T}|\mathit{\theta })p(\mathit{\theta }),\end{array}$$ (1.4)

where p(θ), the prior distribution for θ, encodes all that is known of θ from sources external to the present study. The posterior distribution represents a natural synthesis of this additional external information with y_1:T.

In this paper, we shall provide an overview of evidence syntheses in stochastic epidemic modelling where multiple types of data are explicitly used in an integrated analysis. In Section 2, we will focus on nonmechanistic statistical models for epidemic data, that is, where transmission is not explicitly modelled. Initially, these models will be static, and the aim of the analysis is to estimate the current state of an epidemic. This setup will then be extended by adding a time dimension, initially to estimate time-varying disease incidence. In Section 3, we consider how multiple sources of data are used for inference in mechanistic models for disease transmission. In Section 3.1, the dynamics governing transmission are assumed to be deterministic [i.e., var (X_t |X_t−1) = 0, ∀t], so that stochasticity is only provided by the observational component (1.2). Section 3.2 reviews evidence syntheses in epidemic models with stochastic dynamics [i.e., var (X_t |X_t−1) ≠ 0]. The paper concludes with a discussion, identifying some ongoing and future challenges in the use of multiple datasets in stochastic epidemic modelling.

2. Nonmechanistic Epidemic Modelling

2.1. Static Models

Often estimation of the state of an epidemic at a particular point in time is of interest. In such examples, static or ‘snapshot’ models are used, and the temporal evolution in equations (1.1) and (1.2) is not relevant:

$$\begin{array}{l}\mathit{\text{X}}\sim p_{\mathit{\varphi }}(\cdot ),\\ \mathit{\text{Y}}\sim p_{\mathit{\theta }}(\cdot |\mathit{\text{X}}).\end{array}$$

In many cases, X will be a deterministic function of ϕ, that is, X ≡ X(ϕ), or can be integrated out of the analysis entirely if estimation of ϕ is the focus. We shall therefore write θ = (ϕ, η, X).

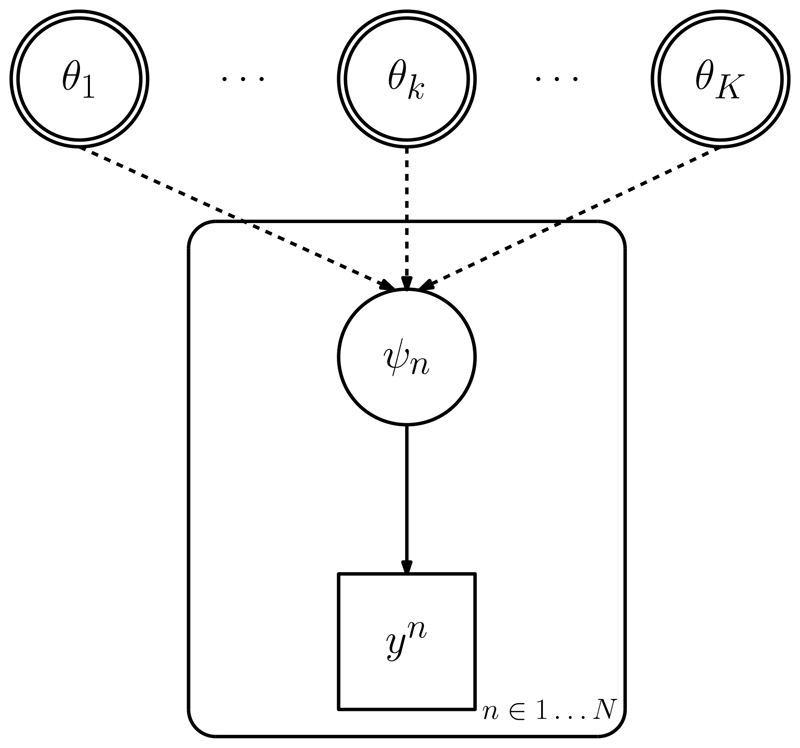
As anticipated in Section 1, data come in the form of N independent components y = (y¹,…, y^N), where each yⁿ,n ∈ 1,…, N may be multivariate. The aim of the evidence synthesis is to estimate a set of K basic parameters θ = (θ₁,…, θ_K) from the complete array of information. Each dataset yⁿ is assumed to inform a function ψ_n = ψ_n(θ) of the basic parameters, where ψ_n is denoted a functional parameter. If ψ_n(θ) ≡ θ_k, the data yⁿ are said to directly inform θ_k, whereas if the function is more complex and/or a function of multiple components of θ, yⁿ indirectly informs one or more parameters. Denote by ψ the collection of functional parameters (ψ₁,… ψ_N) informed by y. Assuming conditional independence of each dataset, the likelihood is then

$$\mathit{\text{L}}(\mathit{\theta };\mathit{\text{y}})={\displaystyle \mathit{\text{∏}}_{n=1}^N{\mathit{\text{L}}}_n({\psi }_n(\mathit{\theta });{\mathit{\text{y}}}^n),}$$

where each L_n(ψ_n(θ); yⁿ) is the contribution of yⁿ to the basic parameters. Either this likelihood is maximised, in a frequentist setting, or in the Bayesian setting we consider here, a posterior distribution is obtained [equation (1.4)], summarising all information, both direct and indirect, as well as prior, on the basic parameters.

Such an evidence synthesis model can be represented as a directed acyclic graph (DAG) that encodes the conditional independence assumptions [25]. In the example of Figure 1, each basic parameter θ_k ∈ θ, denoted by double circles, is a founder node of the DAG, that is, using family relationships to describe the relationships between nodes, it has no parents, only descendants. Functional parameters ψ_n ∈ ψ (single circles) are children of the basic parameters of which they are functions, with the dashed arrows denoting the (deterministic) functional relationship. By contrast, a solid arrow denotes a distributional (stochastic) relationship between nodes. Squares denote observed quantities yⁿ. In a more complex hierarchical model with multiple levels, consequential nodes internal to the DAG may be either deterministically or stochastically related to their ancestors or descendants. Repetition over variables is represented by ‘plates’, rounded rectangles surrounding the repeated nodes as, for example, the repetition of each yⁿ, n ∈ 1 … N informing a different functional parameter ψ_n in the figure.

Fig. 1.

Directed acyclic graph (DAG) of a model with basic parameters, functional parameters and data.

Evidence synthesis methods in the context of healthcare were introduced in a synthesis of HIV prevalence data from different groups, reviewed in [1]. These have inspired a proliferation of comprehensive evidence syntheses for static models of infectious diseases, including Hepatitis C virus (e.g., [28]), influenza severity (e.g., [35]) and campylobacter infection [2]. A key example is the estimation of HIV prevalence, undiagnosed prevalence in particular, in different European countries [11, 14, 31], including annually for the United Kingdom (UK) (https://www.gov.uk/government/statistics/hiv-in-the-united-kingdom). Estimates are produced from multiple routine HIV surveillance datasets combined with contemporaneous cross-sectional survey data.

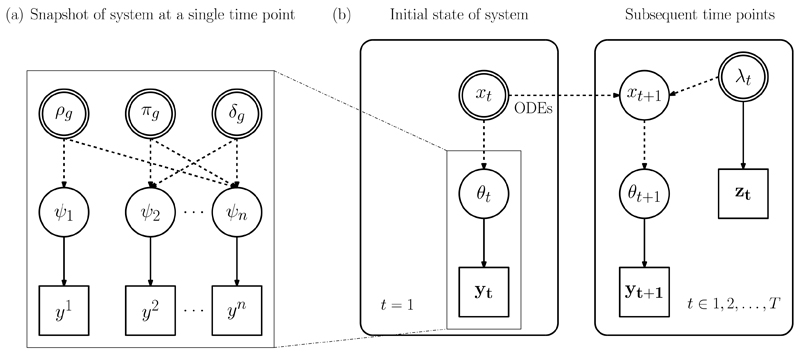
Figure 2(a) presents a DAG of this general approach, summarised in [14]. Here, the ψ are expressed as a function of basic parameters θ = {(ρ_g, π_g, δ_g) : g ∈ 1,…, G}, where ρ_g is the proportion of a population in a particular risk group g for HIV; π_g is the proportion of group g infected; and δ_g is the proportion of infections in group g that are detected (diagnosed). Example functional parameters include ψ_ng (θ) = π_g(1 − δ_g), the prevalence of undiagnosed infection and ψ_mg (θ) = Nρ_gπ_gδ_g, the number of diagnosed infections in group g. As the data are either proportions or counts, the likelihood is comprised of binomial and Poisson terms whose parameters are the functional parameters ψ. Two key challenges in building such an evidence synthesis are: sparse data leading to identifiability issues and requiring hierarchical models to borrow strength, that is, extending the DAG of Figure 2(a) vertically; and in contrast, multiple data sources informing the same parameter, with a resultant potential for these data to conflict. Such conflicts are typically due to unaccounted biases, and need to be detected, measured and resolved (see [13] and references therein).

Fig. 2.

(a) DAG of a HIV prevalence model with basic parameters θ = {(ρ_g, π_g, δ_g) : g ∈ 1,…, G}. (b) Linking a series of snap-shot HIV prevalence models at multiple time points t, to estimate HIV incidence in a ODE-driven compartmental model. Time t data $y_t=\left(y_t^1,y_t^2,\mathrm{\dots },y_t^n\right)$ are augmented by demographic and other data $Z_{t=}\left(y_t^{n+1},\mathrm{\dots },y_t^N\right),$ informing some of the transition rates λ_t, such as migration and new HIV diagnoses. The parameters from (a), both basic and functional, are now encapsulated within θ_t.

The motivation behind evidence synthesis is to frame all the available information on the state of an epidemic within a single integrated analysis to address identifiability. For a number of reasons, however, including computational efficiency, conflict assessment or uncertainty in model structure, it may be convenient to break the problem into smaller components, for example, [28] fit a model for HCV prevalence in two stages. Although this ‘modular’ approach is often reasonable and computationally convenient, merging the resulting submodels into a single analysis is nontrivial (see Section 4).

2.2. Dynamic Models

When interest is in estimating the temporal evolution of an epidemic, and the rates of infection in particular, dynamic models are necessary. There are two alternative approaches depending on the nature of the available information: linking the snapshot analyses of Section 2.1 over time; or using routine time series data on the sequelae of infection. In the first approach, at time t, the observational model is

$${\mathit{\text{Y}}}_t\sim p_{\mathit{\theta }}\left(\cdot |{\mathit{\text{X}}}_t\right),$$

and the snapshots are linked over time via some smoothing of the state variables X_t. In the case of the HIV prevalence example (Figure 2), for a generic risk group g and a series of snapshots over time, this linkage is achieved by embedding a continuous-time multi-state model in the serial snapshot evidence synthesis [27]. The population is partitioned into disease states X_t and model dynamics are described by a system of ordinary differential equations. Time-varying transition rates, including HIV incidence, are the basic parameters ϕ = λ_t, which are identifiable through the inclusion of additional demographic data z_t, contributing to the likelihood as Poisson or binomial terms. The basic parameters θ_t = (ρ_t, π_t, δ_t) of the prevalence model are now deterministic functions θ_t = f (X_t) of the disease states in the dynamic model.

Such temporally linked snapshot evidence syntheses can be used also to estimate state vectors, X_t, that represent log-incidence, as in a study of toxoplasmosis [38], where temporal smoothing of the state vector is through a random walk, for example,

$$\log \left({\mathit{\text{X}}}_t\right)\sim \log \left({\mathit{\text{X}}}_{t-1}\right)+{\mathit{\text{ϕ}}}^T{\mathit{\text{ε}}}_{X,t}.$$

In the second (dynamic) approach, when the available data are time series counts of clinical endpoints, back-calculation has been widely employed to estimate disease incidence by combining the time series with information on the time from infection to the end point (the incubation period). The basic convolution equation

$$\mu (t)={\displaystyle {\int }_0^{t}h(s)}f(t-s)ds$$ (2.1)

expresses the link between the rate of occurrence of a clinical end point, μ(t), the rate h(·) at which new infections occur and the distribution of the time from infection to the end point, f (·).

To estimate HIV incidence, equation (2.1), initially based on AIDS diagnoses, has been developed extensively to incorporate additional data, for example, to: improve identifiability of h(·) in the recent past [12], identify recent infections amongst new diagnoses (e.g., [43]) and provide a more comprehensive description of the epidemic.

In particular, various discrete-time multi-state back-calculations have been proposed, where states are defined by CD4 cell counts ([6] and references therein). Through such an approach, estimation of the number of undiagnosed infections is possible, by incorporating data on HIV diagnoses and CD4 counts taken at diagnosis. In such models, the distribution f (·) in equation (2.1) is characterised by progression rates through disease states and diagnosis probabilities, d_t. Together with incidence, h_t, these quantities are modelled by [6] using random walks and the backcalculation can be framed as a state-space model as in equations (1.1) and (1.2) [40]. Here, the state vector, X_t = (h_t, d_t, E_t), comprises the infection and diagnosis rates, as well as the state occupancies, E_t. As new infections are assumed to occur according to a Poisson process, the likelihood is tractable when marginalised over the E_t, which greatly improves the efficiency and accuracy with which inference on (h_t, d_t) can be drawn. In this case, the diagnoses are Poisson distributed and the CD4 data follow a multinomial distribution. The challenge here is to be able to incorporate additional sources of data, such as information from tests for recent infection performed on new diagnoses, whilst maintaining this tractability.

3. Evidence Synthesis in Mechanistic Transmission Models

The classic approach to tracking the spread of an epidemic is through compartmental models that partition the population into Susceptible/Infected/Removed (SIR) states [3], or one of many similar variants. In the epidemic modelling literature, these models are labelled as mechanistic transmission models. They differ from the multi-state models of Section 2 due to the explicit modelling of the transmission mechanisms, where rates of infection are a function of the prevalent number of infected and infectious individuals. The dynamics of such mechanistic models unfold according to a system of ordinary or stochastic differential equations or their discrete-time difference approximations.

3.1. Deterministic Epidemic Dynamics

Models with a deterministic state relationship, but for which states are imperfectly observed, can be expressed as

$$\begin{array}{l}{\mathit{\text{X}}}_t=f_{\mathit{\varphi }}\left({\mathit{\text{X}}}_{t-1}\right),\\ {\mathit{\text{Y}}}_t\sim p_{\mathit{\theta }}\left(\cdot |{\mathit{\text{X}}}_t\right),\end{array}$$ (3.1)

where f_ϕ (·) is a deterministic function, characterised by parameter ϕ, and X_t represents the distribution of the population in the SIR states, that is, X_t = (S_t, I_t, R_t). Typically, ϕ will include rates of transition between model states, relative rates of contact between different population strata and the transmission potential. Movements between model states will be unobserved, and as in Section 2, the use of multiple data sources becomes necessary to identify both parameters and latent quantities. A number of examples exist where traditional epidemic surveillance information is augmented by additional serological, demographic, administrative or environmental data.

Surveillance and serological data

Serological data, from testing of blood samples to detect the presence of antibodies, provide crucial information on the level of immunity in a population. The important role played by this type of data in uncovering an epidemic’s dynamics is highlighted in applications to influenza data from Israel [42] and from England [8]. Due to the presence of asymptomatic infection, the magnitude of the epidemic cannot be estimated while the epidemic is ongoing from influenza-like illness data and associated virological swabbing alone. This idea is extended in [16], where changes in the immunity profile of a population and the fluctuating transmissibility of the virus between temporally distinct waves of infection are estimated.

In the language of transmission modelling, serological data ${\mathit{\text{Y}}}_t^{\text{sero}}$ provide direct evidence on the number of people in the susceptible state. Incorporation of these data extends the observation model characterised by p_θ in equation (3.1). The additional component, at time t, is typically binomial:

$${\mathit{\text{Y}}}_t^{\text{sero}}|{\mathit{\text{X}}}_t\sim \text{Bin}\left(n_t^{\text{sero}},p_t^{\text{sero}}\right),$$

where

$$p_t^{\text{sero}}=\mathbb{P}\left(\text{seropositive}\text{at}\text{time}t\right)=1-S_t/N$$

and $n_t^{\text{sero}}$ is an assumed known sample size and N is the population size.

However, serological data can hold richer information than mere binary responses. In an application to the Dutch A/H1N1pdm influenza outbreak [37], data obtained from more sensitive micro-array assays are used to give a probabilistic interpretation of immunity. This is achieved via the specification of a mixture model for the log-titre values, classifying individuals into groups who are susceptible, recently infected or have long-held immunity. Here, the ${\mathit{\text{Y}}}_t^{\text{sero}}$ are continuous responses distributed as

$$Y_t^{\text{sero}}\sim \frac{S_t}{N}p\left(\cdot |{\mathit{\theta }}^{\text{s}}\right)+\frac{S_0-S_t}{N}p\left(\cdot |{\mathit{\theta }}^{\text{r}}\right)+\frac{N-S_0}{N}p\left(\cdot |{\mathit{\theta }}^{\text{i}}\right),$$

where the p(·|θ) for θ = (μ, σ) are normal density functions, corresponding to the distribution of log-titre values for susceptible (s), recently infected (r) and immune (i) subgroups.

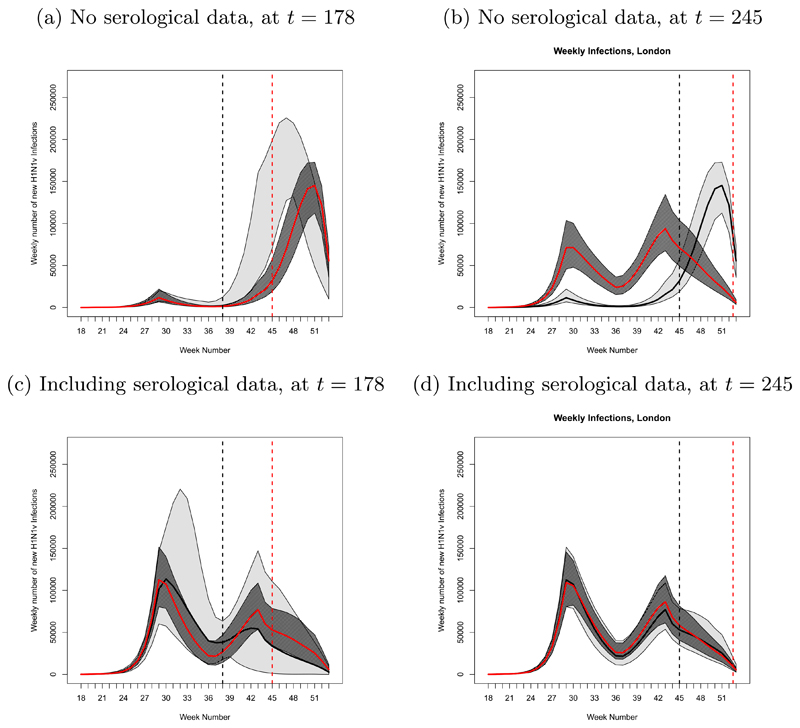
The impact of serological data can be significant. Adapting figures from [8], Figures 3(a) and (b) show estimates and predictions of the number of new A/H1N1pdm influenza infections, when only data on syndromic consultations with a doctor are used. Analyses are carried out approximately three quarters of the way through and towards the end of the epidemic, respectively, without any serological information. Figures 3(c) and (d) display the same results from analyses that additionally use the serological data. In the bottom row of Figure 3, epidemic projections appear to be nested as data accrue, with credible intervals narrowing. In the top row, a coherent picture of the epidemic is only obtained once the epidemic is almost over. In the absence of direct serological information on the number of infections, fitting a transmission model to doctor consultation data alone is of limited utility. A major epidemiological challenge, however, is to develop systems that can ensure the timely provision of these data during an ongoing pandemic.

Fig. 3.

Forecasts of the number of new A/H1N1pdm influenza infections after t = 178 and 245 days of 2009 pandemic data, in the absence [(a) and (b)] and presence [(c) and (d)] of serological data: posterior median (red central line); 95% credible interval (light grey region) for a forecast at a previous time (grey dashed vertical lines); 95% credible interval (dark grey region) for a ‘current’ forecast at t (red dashed vertical lines).

Surveillance and demographic, administrative or environmental data

An example of joint modelling of surveillance and demographic data is in [27], where the model in Figure 2(b) is extended to include a component of disease transmission utilising information z_t on aging, migration and mortality. This is a rare example where such data are directly modelled, that is, both (Y_t, Z_t) have distributions, whereas more commonly, demographic data are treated as fixed covariates, rather than a joint outcome. In the latter case, the system equation in (3.1) is replaced by

$${\mathit{\text{X}}}_t=f_{\mathit{\varphi }}\left({\mathit{\text{X}}}_{t-1},{\mathit{\text{Z}}}_t\right).$$

These explanatory data can come in many forms: [5] uses vaccination data to inform transition rates out of a susceptible state; [9] use commuting data to describe inter-region transmission; [42] relate transmission of A/H1N1pdm influenza in Israel to an index of ‘mean absolute humidity’.

3.2. Stochastic Epidemic Dynamics

The full state-space specification of equations (1.1) and (1.2) is required in two contexts. The first context arises when the numbers of infected individuals are small enough for stochastic fluctuations in transmission to significantly impact on the future epidemic trajectory (‘demographic stochasticity’). Statistical inference based on a model with deterministic dynamics can lead to poor forecasts for the timing of an epidemic peak and can preclude the possibility of epidemic extinction when R >1, no matter how small the population of infected individuals. Second, deterministic dynamics are inadequate in the presence of environmental or other external factors not captured by the transmission model. Stochasticity in the temporal evolution of parameter values (‘environmental stochasticity’) can eliminate the possibility of over-optimistic, possibly biased forecasts that may otherwise result. Models that account for demographic stochasticity, such as, for example, the chain multinomial [40], model the evolution of the epidemic in discrete time. The evolution of the SIR-type disease states X_t forms a Markov process as in equation (1.1). However, the second context of environmental stochasticity is more prevalent in the literature. Here, mechanistic transmission models are driven by a time-varying transmission potential β_t, commonly modelled as a stochastic process. In [17] and [41], β_t is cast as Wiener and Gaussian processes, respectively, whereas [34] impose a random effects model on the probability p_g of a susceptible individual in population subgroup g being infected within a chain-binomial model. The probability of a member of group g not being infected by any other infectious individual is expressed as

$${\left(1-\frac{p_g}{N_g}\right)}^{w_t{\displaystyle {\sum }_{g^{\prime }}{C}_{g^{\prime },g}{I}_{g^{\prime },t-1}}},$$

where w_t ∑_g′ C_g′,_gI_g′,t−1 is the total number of infectious contacts experienced by a member of g, with C being a contact matrix and I_g′,t−1 giving the time t − 1 number of infectious individuals in strata g′. The correlated random effects, w_t, absorb any temporal fluctuations in infectivity and rates of contact. Here, due to the stratified population, the transmission potential has to be expressed for each type of contact, ${\beta }_t^{g,g^{\prime }}=w_t\left(p_g{C}_{g^{\prime },g}/N_g\right).$ A global value is derived as the dominant eigenvalue of a matrix β_t, commonly known as the next-generation matrix, that has ${\beta }_t^{g,g^{\prime }}$ as its (g, g′)th entry.

The motivation for the use of multiple sources of data in stochastic epidemic modelling is no different to the deterministic case. However, there are fewer examples of their use.

Surveillance data

Of these few examples, [34] constitutes a rare instance of using multiple epidemiological time series: the observations y_1:T comprise both laboratory-confirmed data on ‘mild’ cases and data on (nested) admissions to hospitals and to ICUs. Both of the types of stochasticity described above are incorporated. However, the complexity inherent in this model means that its run-time on a high-performance computing cluster is measured in months. Whilst this is not an impediment to retrospective epidemic analysis, it is deeply prohibitive for real-time analysis. Computational, potentially sequential, methods that enable a more swift use of such a model would be of great utility.

Surveillance and phylogenetic data

The synthesis of genetic and epidemiological data is more common in the literature and is used to improve understanding of the transmission dynamics of a particular pathogen. Genetic sequence data (comprising the sequences themselves, together with associated sampling times) can allow reconstruction of transmission trees either by modelling the evolution of the pathogen explicitly using coalescent models to estimate the branching points of the trees (e.g., [15] and references therein) or by using the genetic distance between the observed sequences [39]. The precise method depends on the assumptions that are appropriate for the pathogen and epidemic under investigation. These assumptions cover the possible presence of: within-host pathogen genetic variation; transmission bottlenecks (where a subset of the within-host variants are transmitted); unobserved cases; and introductions into the population. Attendant epidemiological data can add precision to the reconstruction of transmission trees, for example, by providing information on infectious periods or generation intervals, or on the dates at which particular individuals were at risk of infection [15].

There is an increasing body of work linking phylogenies into mechanistic transmission models. A general framework for identifying SIR and SEIR transmission models on the basis of phylogenetic data alone is developed in [24], additionally presenting an application incorporating time series data on removals from the population. Similarly, it is noted in [29] that phylogenetic information is of particular utility in the case where the surveillance data that are typically used to inform transmission modelling are highly noisy or only weakly informative. Their work demonstrates the improved estimation of epidemiological parameters possible when the analysis of epidemiological surveillance data using a continuous-time, continuous-space stochastic epidemic model is augmented by a sample of infection lineages.

As identified by [23], the challenge remains to relax many of the assumptions listed above for phylogenetic modelling, whilst incorporating additional aspects of outbreak dynamics. Consideration of an everincreasing array of epidemiological data should make this a more achievable goal.

4. Discussion

The recent increase in the number of evidence syntheses, mostly Bayesian, to estimate latent characteristics of epidemics is testimony of the crucial role of data from multiple sources. This role has been comprehensively explored in other reviews [1, 14], but briefly, include two key aims: identifiability of a wider range of (unobservable) quantities that can inform public health efforts to control epidemics than would be achievable from a single data source; and increased precision in estimates of these quantities, due to the use of all available relevant data, both direct and indirect. Advantages of Bayesian evidence synthesis include the ability to: introduce and formally quantify expert judgement in the form of prior distributions; readily account for and estimate known biases in observational data through the introduction of bias parameters with carefully chosen priors; and minimise selection bias. However, the adoption of evidence synthesis methods, to achieve identifiability and precision, necessitates models of increasing realism and complexity, which are in turn accompanied by some general challenges that remain open questions [13], as we have highlighted through various examples in this review.

Complex models imply a need for various model building strategies, including hierarchical modelling for identifiability and modular approaches. How best to achieve identifiability from the currently available data is an active area of research. An algebraic determination, ahead of any inference, of parameter identifiability in a complex dynamic system has been explored recently in systems biology (e.g., [20]): such methods have the potential to be adapted to transmission modelling. A promising alternative is the extension of value-of-information methods to the evaluation of gains in precision in parameter estimates resulting from collecting or incorporating further evidence, proposed in application to the HIV prevalence context in [22].

Reasons for a modular approach, dividing a complex model into smaller submodels, include: understanding the influence of each evidence source on joint inference; assessing and resolving conflict during the model building process; and computational tractability. However, incorporating the results of each submodel into a second-stage joint model in a manner that retains the feedback from different data sources to common parameters is not straightforward. Recent work that allows for principled inference from a fully joint model given posterior samples from submodels has been proposed [19]. The application of this ‘Markov melding’ approach to evidence syntheses has the potential to facilitate the increasingly realistic and complex models required in the stochastic epidemic field.

The potential for conflicting evidence is a challenge, but evidence synthesis provides a framework in which, once any conflict has been detected, measured and resolved, models are internally validated: an adequate final model is consistent with every data source included. However, systematic cross-validatory conflict assessment [13] as with any modular approach, is computationally intensive: adaptation is needed to enable timely inference. Conflict resolution through, for example, bias modelling and evidence weighting methods, is a next step [13]. However, while in a frequentist framework there are well-established methods to account for selection biases in the types of observational data usually included in epidemic evidence syntheses, Bayesian equivalents are still in their infancy [36].

A recurring theme through each of the above challenges is that of computationally efficient statistical inference. In the context of epidemic modelling, timely estimation is crucial to address public health policy needs in the midst of an emerging epidemic [13]. Much progress has been made in developing and applying efficient algorithms for epidemic evidence syntheses, such as: sequential Bayesian methods [33, 7], including likelihood-free particle MCMC [29] and approximate Bayesian computation [30]. Alternatively, to achieve computational efficiency, one might approximate the complex epidemic model with a readily implementable proxy. Shaman and colleagues have extensively used an extended Kalman filter (e.g., [32]), to provide a stochastic time series approximation to the dynamics of SIR models. Another approach is Bayesian emulation [18], which seeks to characterise an epidemic model with an emulator, built from a dynamic Gaussian process prior. A similar emulation approach is adopted by [4], who use history matching to calibrate a complex, multi-output epidemic simulation model. This latter work is an attempt to tackle the next challenge, to broaden the scope of all such algorithms to handle multiple datasets, possibly diverse in nature.

4.1. Conclusions

A recent review of infectious disease modelling [26] suggests that the full potential of mechanistic models that ‘simultaneously link data from diverse, heterogeneous data sources’ has yet to be reached. This is certainly true for fully stochastic transmission models, though rare examples of such models embedded within an evidence synthesis do exist [30, 34]. Such rarity and the challenges discussed above motivate the need for further development in this area.

However, the many examples reviewed in Section 3.1, particularly for deterministic models, suggest that evidence synthesis for mechanistic models is both a well established and rapidly expanding field.