JASS: command line and web interface for the joint analysis of GWAS results

Abstract

Genome-wide association study (GWAS) has been the driving force for identifying association between genetic variants and human phenotypes. Thousands of GWAS summary statistics covering a broad range of human traits and diseases are now publicly available. These GWAS have proven their utility for a range of secondary analyses, including in particular the joint analysis of multiple phenotypes to identify new associated genetic variants. However, although several methods have been proposed, there are very few large-scale applications published so far because of challenges in implementing these methods on real data. Here, we present JASS (Joint Analysis of Summary Statistics), a polyvalent Python package that addresses this need. Our package incorporates recently developed joint tests such as the omnibus approach and various weighted sum of Z-score tests while solving all practical and computational barriers for large-scale multivariate analysis of GWAS summary statistics. This includes data cleaning and harmonization tools, an efficient algorithm for fast derivation of joint statistics, an optimized data management process and a web interface for exploration purposes. Both benchmark analyses and real data applications demonstrated the robustness and strong potential of JASS for the detection of new associated genetic variants. Our package is freely available at https://gitlab.pasteur.fr/statistical-genetics/jass.

INTRODUCTION

The human genetics community has now access to a wealth of genome-wide association study (GWAS) summary statistics for a wide spectrum of phenotypes, ranging from biometric measurements to molecular phenotypes and most common diseases. For example, as of May 2019, the NHGRI-EBI GWAS Catalog contains the results from 3989 GWAS (1). The tremendous value and practical utility of those summary data have been demonstrated for a range of secondary analyses (2–7). Indeed, working with GWAS summary data solves both practical and ethical concerns, such as the protection of the anonymity of the participants, the secure storage of millions of variants across hundreds of thousands of individuals and the harmonization of consortium data.

The joint analysis of multiple phenotypes based on GWAS summary statistics is currently a very active area of research with dozens of approaches published in the past few years (8–16). The primary goal of analyzing multiple phenotypes jointly is to increase statistical power to detect associated variants missed by univariate analyses (17–19). However, large-scale real data multivariate GWAS analyses are still rare despite recent extensive effort from the community. While published methods have shown efficiency in simulated data and real data examples composed of few GWAS, we found more demanding applications, including dozens of GWAS performed from various platforms with partial sample overlap, to be very challenging. Among most prominent issues were harmonizing and cleaning heterogeneous summary statistics data format across studies, optimizing computation time to deliver joint analysis results in few minutes for several millions of single-nucleotide polymorphisms (SNPs), and summarizing and comparing joint analysis results versus univariate results.

Moreover, an important aspect of exploring complex multivariate data—here GWAS summary statistics of multiple phenotypes—is the visualization and management of results and data. This is a common issue in human genetics, and a number of software have been published to help investigators coping with these issues. There are now many user-friendly tools allowing for the annotation of results based on existing functional database [e.g. Dalliance (20) and Toppar (21)], the secure storage and extraction of results from database (e.g. GWAS ATLAS (7)] or the plotting of results integrating specific features (e.g. LocusZoom (22) and Assocplots (23)]. Similarly, the dissemination of the methodology for the joint analysis of multiple GWAS summary statistics requires the development of robust and computationally efficient tools. With thousands of GWAS studies now publicly available, this requirement has become even more crucial.

Here, we present JASS (Joint Analysis of Summary Statistics), an integrated package for the joint analysis of multiple GWAS summary statistics, including at the same time analytical tools, visualization functions and an embedded web interface. JASS provides the following features: (i) functions for the fast and efficient computation of multiple joint statistics from dozens to hundreds of GWAS results; (ii) an interactive web server for the visualization of a selection of GWAS, along with the result of their joint analysis; (iii) the possibility to install the software locally, so that interested users might apply the analysis to their own data in the safety of their own computation facility; (iv) a command line interface for advanced users; and (v) a nextflow (24) pipeline integrating GWAS cleaning, imputation and analyses into one tool. The paper is structured as follows: first, we detail the main functionalities and the visualization tools of JASS; second, we discuss the performance optimization strategies we adopted; third, we provide some technical details of the package; and last, we present applications using real GWAS summary data performed using the public JASS server.

MATERIALS AND METHODS

Overview of JASS

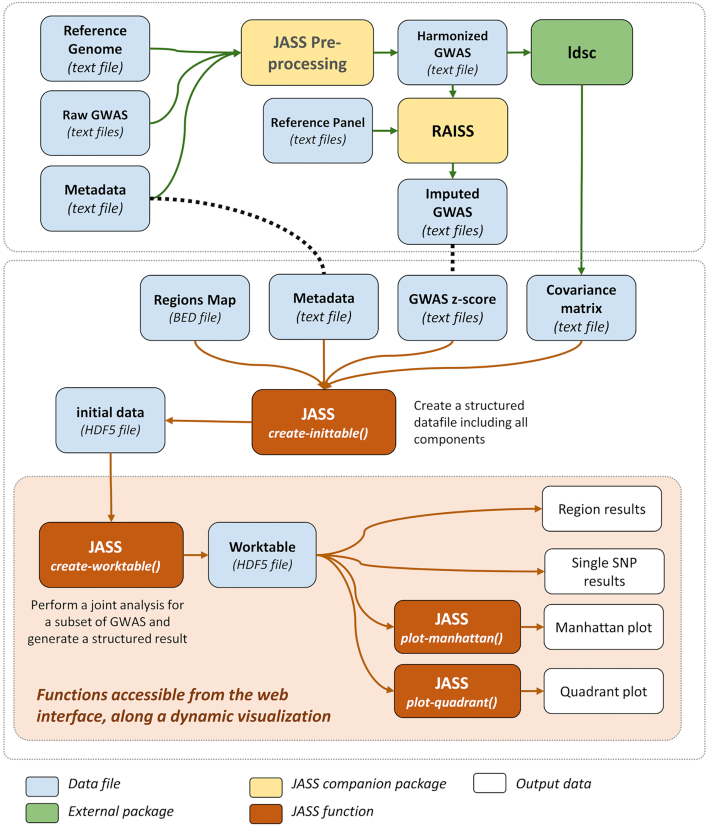
JASS is a Python package that handles the computation of joint statistics over sets of selected GWAS results through a command line interface and/or a web interface. The derivation of joint statistics, and the generation of static plots to display the results, as well as more advanced features such as the implementation of user-defined statistics, can be easily performed using the command line interface. Many of these functionalities can also be accessed through a web application embedded in the Python package, which also enables the exploration of the results through a dynamic JavaScript interface. The lists of available functions and features are provided in Supplementary Tables S1 and S2, respectively. Figure 1 shows a standard analysis workflow, including the steps performed through companion packages.

Figure 1.

JASS workflow. The figure shows the main steps of an analysis with JASS, including the preprocessing steps performed using either companion packages (in yellow) or external software (in green).

Statistical tests implemented in JASS

A number of methods have been published for the joint analysis of correlated GWAS summary statistics. We implemented the two most common approaches that cover most of the existing joint tests, although users also have the possibility to implement their own joint statistic and plug it in the analysis. The first test is a standard omnibus approach that combines 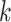single GWAS statistics to form 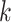degree of freedom (df) statistics. For a given SNP, the omnibus statistic can be expressed as

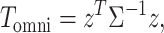(1)

where 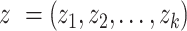is a vector of 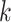Z-scores, derived from the available GWAS summary statistics as 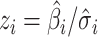, where 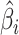and 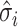are the estimated regression coefficient and its standard error for study 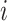; 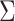is the covariance matrix between the Z-scores under the null and is assumed unique for all SNPs analyzed. Under the null hypothesis of no association between the SNP tested and any of the 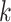phenotypes tested jointly, 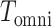follows a 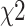distribution with  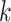df.

The second statistic is a weighted sum of Z-scores and has the following form:

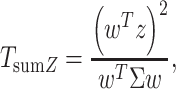(2)

where 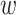is a vector of weights assigned to each GWAS, and applied uniformly to all SNPs analyzed. Under the null hypothesis of no association between the SNP tested and any of the 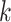phenotypes tested, 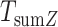follows a 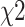distribution with 1 df. This joint test is the most discussed one in the literature, and variations of this approach mostly consist in optimizing the weighting scheme (e.g. 10,11). The users can specify their own weighting scheme via a command line option.

Note that whichever multivariate statistic is used, the estimation of 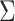is critical to ensure a correct type I error rate. As done in our real data application, we strongly recommend building that matrix using the intercept derived from univariate and bivariate LDscore regression described by Bulik-Sullivan et al. (6). However, users can provide their own estimation of the covariance matrix or use a default estimator provided by JASS. Note that we integrated the LDscore H₀ matrix computation in our nextflow pipeline (see the ‘Data pre- and postprocessing’ section).

Finally, besides approaches for the analysis of correlated GWAS statistics, we also implemented the Fisher's test and the standard inverse-variance meta-analysis for investigators interested in performing classic meta-analysis. However, we emphasize that the validity of both approaches requires univariate tests to be uncorrelated under the null, which in general means no sample overlap across the GWAS analyzed, or no correlation between the phenotypes considered. This hypothesis can be assessed by controlling the off-diagonal terms of 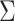 are close to 0.

JASS input and output

The JASS package requires for input a set of GWAS summary statistics, and some metadata about these GWAS (e.g. coded allele, sample size per SNP, etc.). Two additional key arguments can be provided: (i) a matrix of the covariance between statistics under the null hypothesis [i.e. 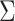, see Equations (1) and (2)]; and (ii) a map of regions that is used to create summary results. If the covariance matrix is not provided by the user, it will be derived based on the observed pairwise correlation between GWAS after filtering out SNPs with P-values below a significance threshold (P < 5 × 10⁻⁵), in order to remove likely associated variants (25). Note that the primary purpose of the region map file is to provide an overview of the main independent signals and to improve exploration and visualization of the results. It is not intended to provide a list of independently associated variants. The latter analysis should be conducted using suitable tools such as CO-JO (26). For meaningful interpretation of the region-based results, we strongly suggest to define the regions based on the SNPs’ linkage disequilibrium (LD) between variants. If not provided by the user, JASS will use regions based on LD recombination hotspot computed using the approach proposed by Berisa and Pickrell (27) for European populations. From these input data, the command line tool allows for multiple joint tests to be performed: (i) the omnibus approach [Equation (1)]; (ii) the sumZ approach [Equation (2)], where the user has to specify a vector of weights; and (iii) any other alternative statistics applicable to a vector of Z-scores.

Joint analysis results are stored into two tables. The most significant SNPs by region are reported in the region table. This table provides a simple way to count the number of independent significant loci. The results for all analyzed SNPs are stored in the SumStaTab. Two main static plots can then be generated from the joint analysis: (i) a so-called Manhattan plot, i.e. a scatter plot of genome-wide association signal showing the −log₁₀ of the P-value of each region, according to their position on the genome; and (ii) a quadrant plot, which allows for a fast comparison of association signal between the joint test and single GWAS results. In brief, the −log₁₀ of the minimum P-value of each region from the joint analysis is plotted as a function of the −log₁₀ of the minimum P-value from univariate GWAS analysis. The result is a four-quadrant scatter plot, where (i) the upper left quadrant contains all the regions where the joint analysis is significant when all the original GWAS are not, hence newly detected regions; (ii) the upper right quadrant contains all the significant regions identified with both strategies; (iii) the lower right quadrant contains all the regions that are significant for any one of the selected GWAS but not for the joint analysis; and (iv) the lower left quadrant displays the regions that contain no signals.

The web interface provides a complementary set of tools for both analysis and visualization. Note that it is applicable after all input data have been harmonized and merged along all required information (Figure 1), and it currently allows only for the omnibus test to be performed. Once a set of GWAS has been analyzed, the user can proceed to the exploration at the SNP level by clicking on a region. This action will trigger the representation of an SNP level heatmap of the Z-score across all GWAS analyzed jointly and a zoomed Manhattan plot of the joint test association results for that region. When implemented on a public server, the web interface also offers the possibility of sharing the results from an analysis through a ‘Share direct link’ button. It allows the user to generate a unique link for the joint analysis they performed, avoiding other investigators to replay the same analysis multiple times and an easy way to access additional details from a published study.

Data pre- and postprocessing

A critical issue to ensure a valid multi-GWAS analysis is the harmonization and cleaning of the input data. Raw GWAS data are usually heterogeneous in their content and format. To avoid the user series of time-consuming operations, we automatized all of these steps into a preprocessing Python package tool (jass_preprocessing) provided on behalf of JASS. This companion package addresses the following: (i) it maps heterogeneous column names to standard names (rsID, pos, A0, A1, Z); (ii) it derives Z-scores from P-values and signed statistics (log odds ratio or linear regression coefficients); (iii) when missing, it infers per-SNP sample size from the effect estimate standard deviation and the minor allele frequency; (iv) it filters SNPs with sample size <75% of the maximum; and (v) it aligns coded genetic variants with a reference panel. This reference panel should be filtered out for strand-ambiguous variants and variants with low frequency. In our example, we used 6 978 319 SNPs selected using the European ancestry samples from the 1KG project (28). This reference panel is available in the preprocessing package.

Importantly, joint statistics commonly require complete data to perform a statistical test. To increase the number of SNPs with complete data, we chose to perform the systematic imputation of GWAS included in our real data examples. Because of the complexity of the task, we developed a tool for the imputation of missing statistics in an independent study implemented in the RAISS package (29). The input and output formats of RAISS are the same as input format for the JASS package, so the imputation step can easily be integrated in a JASS pipeline. Nevertheless, the imputation of missing data can only be partial; therefore, JASS includes a computationally optimized procedure to derive joint statistics for each SNP only from the subset of GWAS with available data.

We integrated these preprocessing steps into a nextflow (24) pipeline, which provides several advantages for the user: (i) automated transmission of preprocessed data to subsequent analysis steps that greatly limit the number of input data left to the user; (ii) if executed on an HPC cluster, automatically parallelized subprocesses when possible; and (iii) a stable computing environment by assigning a docker container to each process.

Finally, despite careful preprocessing, it remains possible that some features susceptible to impact the validity of multivariate tests are missing from the input data. For example, GWAS might include summary results for imputed SNP with relatively low imputation quality score (e.g. 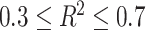). Such variants do not impact the validity of the univariate screening, but can harbor differences in their covariance 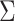as compared to the other SNPs. Such differences can induce false signals in a multivariate test. To handle such situations, we also propose a post-hoc filtering to remove likely outlier signal. It consists in removing SNPs with genome-wide significant multivariate signal (i.e. P-value <5 × 10⁻⁸) in the absence of other signal with a P-value below a user-specified threshold (10⁻⁶ by default) in the neighborhood of the target SNP.

Technical details

Architecture

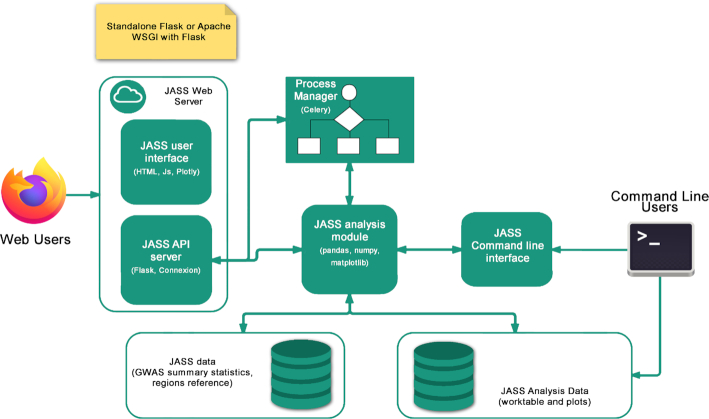
JASS is a Python package that can be run both as a command line tool and as an embedded web application, either on a local or on a public web server. An overview of its architecture is illustrated in Figure 2, which describes its primary components.

Figure 2.

JASS architecture. The JASS Python package is composed of a central ‘analysis module’ that defines computational features, enables reading input data and writing results to HDF files, and generating static plots as PNG files. These features can be accessed from a command line interface or from an embedded web application powered by a Flask server that uses the connexion library and a JavaScript user interface using the plotly library that enables the execution of joint analysis and the exploration of the results. In the latter case, the management of the analysis jobs requires the setup of a Celery server.

Data storage and computations

The analysis module of JASS uses the pandas library for data processing, allowing for convenient and fast computations over large datasets. Furthermore, pandas includes a native support for HDF5 files, which JASS uses to store both the initial data and the results of joint analyses. This format presents multiple advantages, including (i) generating cross-platform and compressed files, (ii) enabling indexing (which later reduces the access time when accessing the results during the interactive exploration) and (iii) storing multiple data frames in a single file.

Interactive web interface

The JASS web interface is implemented in JavaScript, HTML and SVG. To browse the results efficiently, we use a plotly library. This library enables the simultaneous display of very large numbers of points, as encountered in JASS, where the size of GWAS matrices to be explored can potentially reach hundred phenotypes per several million SNPs. It is already used in other GWAS analysis R packages, for example Manhattanly. The tables we use for selecting phenotypes and exporting results use the jquery datatable plugin.

Web server

The web server provides all functionalities (except for the initial data import), through a RESTful API. This API is described with OpenAPI, and connected to the Python JASS analysis module through the connexion library. It is used primarily by the web user interface, but could also be used to run JASS analyses remotely, or with other client frameworks. Contrarily to the command line API, the statistics computation and plot generation operation is launched asynchronously, to avoid the potential timeouts that can occur during its execution. The server uses the Celery task queue to run these operations.

RESULTS

Balancing resource usage

The amount of data that has to be managed and processed guided us to choose the architecture and the output format for JASS. As discussed in the previous sections, there are currently >3000 GWAS summary statistics available. These GWAS currently contain approximately between 300 000 and 10 million genetic variants. However, future studies including either additional imputed SNPs or sequence data can potentially bring this total to up to 100 million variants or more. Given these numbers, the loading and processing of a multi-GWAS analysis would be intractable when using either a standard laptop or a standard web server (which includes often <10 GB RAM). Therefore, emphasis has been put on optimizing the memory usage, while preserving reasonable execution times. This translated into two main components in the JASS implementation.

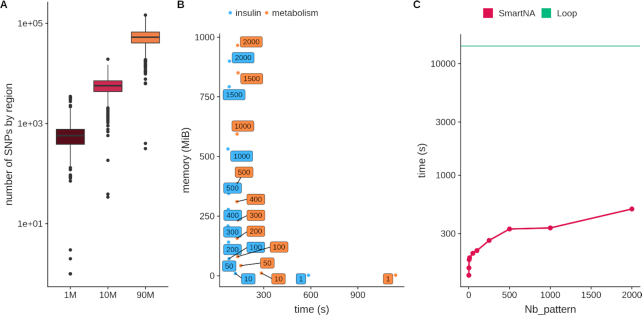
First, while the analysis is done on a single SNP basis, we constructed a region-based result on top of the single SNP results. In brief, we defined genomic regions based on the SNPs’ LD, and derived statistics and summary based only the most significant SNP from each region. This region-based result allows for both a very fast visualization at the genome level in the web interface and a preliminary count of independent signals, circumventing the loading of the whole genome results. Here, we propose using regions based on LD recombination hotspots computed using the approach proposed by Berisa and Pickrell (27). Note that JASS offers the possibility of using an alternative user-defined region map. The map we used in our examples includes 1703 regions. We derive in Figure 3A the distribution of the number of SNPs per region in three arbitrary scenarios: 1M SNPs from the Illumina Omni1-QuAd, 9.9M SNPs after imputation as available in (30) and 96M SNPs as available in the latest UK Biobank genotype panel after imputation (31). Overall, our approach shows a good scalability with an average of 590, 5812 and 54 664 SNPs per region, with maximum of 3470, 19 217 and 145 987 SNPs, respectively.

Figure 3.

Resource usage and computation time. (A) The distribution of the number of SNPs per region when using the recombination hotspot map proposed by Berisa and Pickrell (27) while using 1M SNPs from the Illumina Omni1-QuAd, 9.9M SNPs from a recent GWAS and 96M SNPs as available in the latest UK Biobank genotype panel after imputation. (B) The trade-off between memory usage and computation time. JASS omnibus statistics was computed for 4 traits and 3 192 045 SNPs (insulin) and 11 traits and 3 673 285 SNPs (metabolism). The y-axis is the peak in memory usage in megabytes and x-axis is the time (in seconds) to perform the task. Labels attached to data points give the number of genomic regions processed at once. For example the two boxes filled with a “2000" in the top left of the plot correspond to the case were the entire dataset is loaded in memory (as there is a total of 1703 regions in this example). Color represents the group of traits. (C) The computation time optimization. We computed the omnibus statistics for 3 673 285 SNPs for 11 traits; the y-axis is the time in seconds (logarithmic scale) and x-axis is the number of missing data in a pattern. The straight green line shows the result from a naïve computation loop approach over all SNPs, and the red line shows the results from our optimized algorithm.

Second, we implemented a strategy where the computation of the joint analysis is performed iteratively on chunks of 50 regions. The choice to process 50 regions at a time corresponds to an optimal trade-off between computation time and memory usage when analyzing multiple phenotypes (e.g. ≥20, Figure 3B). Processing less regions per iteration would increase computation time and processing more regions would increase dramatically memory usage. The maximum memory usage being reached when all regions are analysed in a single iteration. The resulting performance makes it possible to compute a joint analysis in less than a minute, while preserving the stability of the server. Note that computation time was not a major issue in our implementation, and this strategy addresses primarily memory usage burden due to the loading of the complete GWAS results. This process is particularly critical when using the JASS web server. Additionally, note that the Celery server is by default configured to queue and run sequentially the analyses launched potentially simultaneously on different datasets, to avoid excessive loads on the memory or CPU usage of the server. Finally, when analyzing jointly a large number of phenotypes (e.g. >100), command line on a local instance of JASS should be preferred.

Optimized algorithm for fast computation

It is well established that computation time of genome-wide screening can be decreased dramatically by using matrix product rather than through an iterative loop (e.g. (32). For illustration purposes, we considered an example of a real GWAS dataset including 11 traits and 3 673 285 SNPs after filtering out SNPs with missing data. The naïve loop-based implementation (computing the statistic for each SNP one by one and inverting the 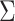matrix each time) took nearly 4 h. On the other hand, processing the same data with a matrix product took 127.1 s (Figure 3C). However, matrix-based derivation cannot be readily implemented in the presence of missing data. Missing values imply that the statistics will differ with rows according to which traits are missing. This is a particularly acute problem for the omnibus test, which requires the inversion of the covariance matrix for each SNP.

To solve this issue, we implemented an optimized algorithm that treats jointly genetic variants displaying the same missing value pattern. The computational cost of this operation can be factorized because values are generally not missing at random: missingness depends on the coverage of the genome by the technology used for the studies, the technology itself and the genotype imputation approach that was used. The algorithm first identifies patterns of missing values in the Z-score matrix and computes 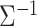only once for each pattern. Each set of SNPs harboring the same pattern is then analyzed using a matrix-based derivation. Figure 3C reports the execution time as a function of the number of missing value patterns in the data using the aforementioned real data example, after randomly incorporating an increasing amount of missing data. As shown in this figure, even with the number of missing value patterns set at its theoretical maximum (for 11 traits, this would be 2¹¹ = 2048 patterns), the execution time of the matrix-based computation is dramatically lower than the execution time of the naïve loop implementation (t = 499 s versus t = 14 365 s, respectively).

Comparison to the existing code to perform joint analysis

We compared the functionalities and computational performances of JASS against other approaches for the joint analysis of GWAS summary statistics. Out of the eight studies (Supplementary Table S3), two did not provide code (14,33), two provided loose R functions (11,12), one provided Python 2.7 scripts (3), one provided code in a non-open source software (9) and two provided R packages (10,13). The quality of documentation varied greatly from one method to another going from its absence to a wiki describing in depth routine usage. Only one package offered a command line interface. None of the advanced features offered in JASS, such as the management of missing values, an accompanying Python 3 package to harmonize and clean heterogeneous GWAS summary statistics and the possibility to deploy an interface server, were available in other approaches.

Finally, to compare the execution time of JASS with the HIPO (10) and MTAG (3) methods on a lipid example containing four traits and 1 818 293 SNPs, HIPO, MTAG and JASS ran, respectively, in 329, 212 and 33 s. To be fair with the HIPO methods, the reported running time includes the estimation of the genetic correlation matrix by the LDscore. Note that no option is provided in the function to avoid repeating the estimation for each analysis.

Detection of new associations with JASS

We deployed an online implementation of JASS that currently includes 154 publicly available GWAS summary statistics (http://jass.pasteur.fr/index.html, Supplementary Table S4). These GWAS cover several common diseases (e.g. asthma, type 2 diabetes, cardiovascular diseases) and quantitative traits (e.g. body mass index, total cholesterol). All GWAS were preprocessed using the JASS companion package and were aligned to a reference panel of European ancestry sample from the 1KG Project Phase 3 data (28). Rare (MAF < 1%), non-biallelic and strand-ambiguous SNPs were filtered out from the reference panel. These 154 GWAS represent only a fraction of all GWAS publicly available; however, there are already 2.3 × 10⁴⁶ possible combinations of phenotypes that can be analyzed jointly from this subset. As there is currently no established strategy to determine which specific set of phenotypes should be considered for joint test when addressing a specific biological question, it illustrates the strong need of disseminating to the community a fast and user-friendly tool for multi-GWAS analysis. Our package offers the possibility of performing multiple exploratory analyses extremely fast. To illustrate and demonstrate the potential of JASS, we performed three real data applications using these data.

Example 1

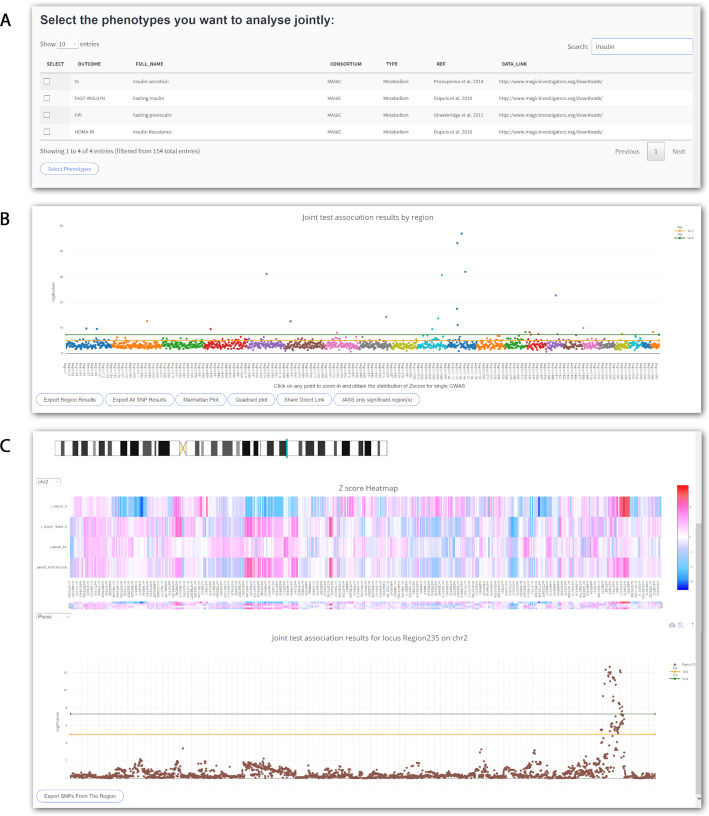
In this first example, we considered a simple scenario where an investigator is interested in complementing results from genome-wide genetic association studies of multiple insulin phenotypes. The goal is to perform a multivariate analysis to identify additional genetic variants associated with insulin phenotypes missed by the univariate analyses. Here, we performed the analysis using the online version of JASS, and as mentioned in the ‘Materials and Methods’ section, we generated a unique and publicly available link for this specific analysis (see the Data Availabitity section). We ran the omnibus test for the four insulin phenotypes from the MAGIC consortium (insulin resistance, fasting insulin, insulin secretion and fasting proinsulin) available (Supplementary Table S4). The main steps and corresponding screenshots of the analysis are presented in Figure 4. After imputation and filtering SNPs with data on at least two phenotypes, a total of 3 144 808 SNPs were available for the analysis.

Figure 4.

Screenshot JASS interface for example 1. We present screenshots from the web interface of the three main steps for the analysis performed in application 1. (A) Insulin-related GWAS available in the database are selected (insulin resistance, fasting insulin, insulin secretion and fasting proinsulin), (B) the genome-wide results from the joint test are presented in a Manhattan-like plot of the omnibus test, showing the top −log₁₀(P) per genomic region, and (C) when a region of interest is selected, a dynamic heatmap of the Z-scores of the previously selected phenotypes is generated along a zoom on the Manhattan plot showing the −log₁₀(P) single SNP signal for the joint analysis.

The univariate analyses identified 20 regions of interest (Table 1). All except four were also significant with the joint test (minimum P_JASS was in the range [1.0 × 10⁻⁷; 6.9 × 10⁻⁷] for those four regions). Conversely, the omnibus approach identified seven new regions. Several of these association signals map to genes with established links to insulin. For example, rs12718928 (P_JASS = 7.2 × 10⁻⁹) is 10 kb upstream the GRB10 gene, which encodes a growth factor receptor-binding protein that interacts with insulin receptors and insulin-like growth factor receptors (34). The minimum P-value from the univariate analyses for this variant was 1.0 × 10⁻⁶ for insulin resistance. Another example is variant rs560887 (P_JASS = 2.6 × 10⁻¹³), an intron of gene G6PC2, which has been reported to be associated with multiple phenotypes, including in particular elevated fasting plasma glucose and increased insulin release after oral and intravenous glucose loads (35). None of the P-value for the univariate test was nominally significant for that variant (P-values are 0.44, 0.10, 0.11 and 0.52 for insulin resistance, fasting insulin, insulin secretion and fasting proinsulin, respectively). The difference in significance between univariate and multivariate association for that variant suggests a genetic effect on a combination of the original phenotypes (e.g. difference or ratio between two insulin traits).

Table 1.

Top associated SNPs from example 1

RSIDa	Chr.	Geneb	Position	Ref.	Alt.	P  IR	P  FASTING	P  IS	P  FPI	P  JASS
rs4298759	1	SNX7	99 194 323	A	C	0.53	0.92	0.39	1.2 × 10−11	1.9 × 10−10
rs10913737	1	AXDND1	179 343 202	A	G	1.7 × 10−8	1.8 × 10−10	0.088	0.043	2.6 × 10−10
rs578763	2	G6PC2	169 776 360	G	T	0.43	0.096	0.13	0.34	2.2 × 10−13
rs10026163	4	LINC02438	19 533 790	T	C	6.3 × 10−10	1.4 × 10−6	0.87	0.35	3.3 × 10−10
rs13169290	5	PCSK1	95 729 406	A	G	0.66	0.62	0.60	3.4 × 10−34	7.8 × 10−32
rs56676529	6	CDKAL1	20 661 837	A	C	0.18	0.061	8.3 × 10−14	0.13	5.9 × 10−13
rs12718928	7	GRB10	50 866 921	A	G	1.1 × 10−6	1.3 × 10−5	2.8 × 10−5	–	7.2 × 10−9
rs11558471	8	SLC30A8	118 185 733	G	A	0.71	0.21	0.00058	4.2 × 10−13	5.0 × 10−15
rs1840780	10	SLC9B1P3	38 984 149	T	C	0.16	0.11	7.5 × 10−9	0.14	1.1 × 10−7
rs7924036	10	JMJD1C	65 191 645	G	T	2.7 × 10−6	5.5 × 10−5	9.0 × 10−6	0.0039	3.5 × 10−10
rs7096101	10	KIF11	94 362 928	G	A	0.46	0.085	3.0 × 10−13	0.033	2.2 × 10−14
rs4575195	10	TCF7L2	114 765 747	A	C	0.0098	4.4 × 10−4	0.0010	9.6 × 10−28	2.4 × 10−31
rs11038913	11	AMBRA1	46 559 730	C	T	0.071	0.028	0.12	4.9 × 10−18	1.5 × 10−17
rs11039182	11	MADD	47 346 723	C	T	0.81	0.55	–	3.4 × 10−45	6.2 × 10−44
rs10901988	11	LINC02750	50 561 635	T	C	0.033	0.76	0.12	3.3 × 10−6	7.8 × 10−12
rs57614870	11	ARAP1	72 435 983	G	A	0.0059	4.1 × 10−4	0.14	4.1 × 10−46	1.2 × 10−47
rs11020114	11	MTNR1B	92 682 604	C	T	0.017	0.83	3.2 × 10−17	1.7 × 10−4	1.1 × 10−32
rs703538	12	IGF1	102 900 185	A	G	3.6 × 10−9	1.1 × 10−9	0.52	0.98	1.4 × 10−7
rs1146937	13	SPRY2	80 797 107	C	T	0.76	0.96	0.42	1.7 × 10−8	6.9 × 10−7
rs336247	13	IRS2	110 476 671	A	G	0.61	0.30	4.4 × 10−10	0.18	4.2 × 10−9
rs8013954	14	EAPP	34 997 280	T	C	0.0023	0.28	0.77	0.49	5.5 × 10−9
rs2626454	14	LRFN5	42 879 735	C	T	0.021	0.034	0.80	4.6 × 10−9	4.9 × 10−8
rs11856307	15	C2CD4A	62 399 093	C	A	0.49	0.087	3.0 × 10−6	7.7 × 10−19	2.0 × 10−23
rs12438204	15	LARP6	71 126 593	G	A	0.079	0.032	0.79	4.0 × 10−8	2.7 × 10−7
rs4790332	17	SGSM2	2 262 611	A	G	0.011	0.028	0.26	5.8 × 10−11	2.1 × 10−10
rs11668296	19	ZNF254	24 177 790	T	C	1.7 × 10−5	5.0 × 10−6	4.2 × 10−5	0.035	2.2 × 10−8
rs113781727	22	SGSM1	25 218 120	T	C	2.1 × 10−6	7.6 × 10−6	6.0 × 10−6	–	4.6 × 10−9

^bFor each significant region, we report P-values for the most associated SNP across all five tests (the joint test and the four univariate tests).

^bNearest gene.

Genome-wide significant P-values are indicated in bold.

Missing values are coded as ‘–’.

Example 2

In this example, we assume an investigator wants to analyze jointly many phenotypes while assuming a strong a priori on the expected multitrait association pattern. Here, we used a set of 20 phenotypes related to metabolism and displaying substantial genetic correlation (Supplementary Figure S1). We applied the sumZ test from the command line version of JASS while using the weights based on the loading of the top 10 principal components (PCs) of the genetic correlation matrix), as proposed in the HIPO method (10). Genetic and null correlations were derived using the LDscore approach (6). Each of the 10 analyses took <3 min, illustrating the strong usability of JASS for a fast exploration of various alternative multivariate tests. For illustrating purposes, we present in Figure 5 the quadrant plot resulting from the analysis based on PC1.

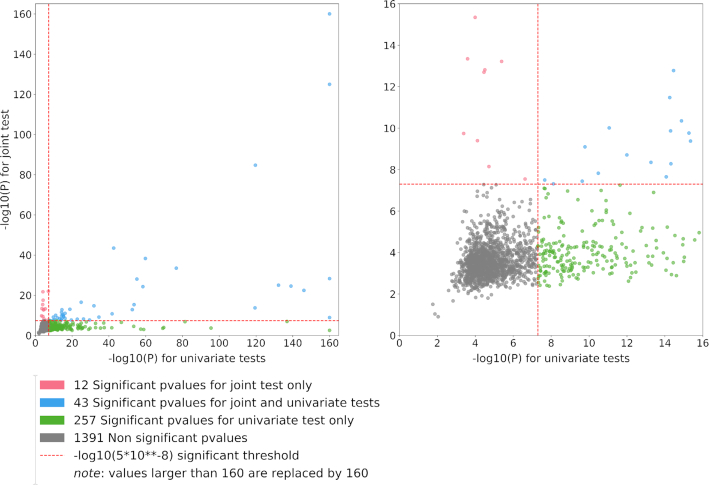
Figure 5.

Quadrant plots derived from example 2. The quadrant plot shows the best signal per region from the multivariate test (y-axis) as a function of the best signal for the same region from the univariate analysis (x-axis). We focused on the sumZ test using weights defined as the loadings of the first PC of the genetic correlation matrix times the inverse of the covariance matrix. Green dots represent regions identified by the univariate test only, red dots represent regions identified by the multivariate test only and blue dots are regions identified by both approaches. Left panel includes all regions [note that −log₁₀(P-value) >160 has been replaced by 160]. Right panel is a zoom centered around the genome-wide significance level (P = 5 × 10⁻⁸).

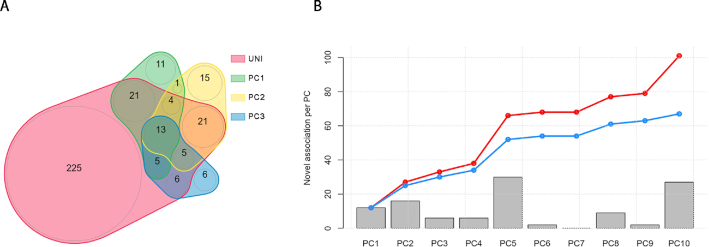
The univariate GWAS identified a total of 300 associated loci. Overall, each single PC analysis detected a few additional loci while missing approximately two-thirds of those identified by the univariate screenings. As shown in Figure 6A for the first three PCs, the overlap across each PC was relatively strong. We summarize in Figure 6B the detection of new loci identified for each PC, and the cumulative number when using an increasing number of PCs. With 10 PCs, the total number of new loci equals 101 if using the standard P-value threshold (5 × 10⁻⁸), or 67 if using a more stringent threshold accounting for the 10 tests performed (i.e. 5 × 10⁻⁹).

Figure 6.

Overview of results from example 2. We performed the sumZ test for the analysis of 20 phenotypes while using weights inspired from the HIPO approach, i.e. using the loadings from the 10 first PCs of the genetic correlation matrix, weighted by the inverse of the covariance matrix. (A) The overlap of identified loci across the univariate screening and the top 3 PCs. (B) The number of loci found associated for each PC on top of those identified by the univariate screening at a P-value threshold of 5 × 10⁻⁸. The red line indicates the cumulative number of additional signals when merging new signals from an increasing number of PCs. The blue line indicates the same cumulative number of new signals after applying Bonferroni correction accounting for the total number of PCs analyzed.

Example 3

In the last example, we consider a scenario where an investigator wants to confirm the relevance of SNPs near genome-wide significance for Crohn's disease (CD) through in silico replication of association across three other inflammatory conditions: ulcerative colitis (UC), rheumatoid arthritis (RA) and asthma. We show that performing multitrait analysis on these phenotypes related to the primary outcome can improve the validation of these variants. All analyses were performed using summary statistics from the aforementioned traits described in Supplementary Table S4. In practice, we first extracted for CD the most associated SNP for each of the 1704 regions from (27) and classified those top SNPs in three categories: (i) those with P-value below genome-wide significance; (ii) those suggestive for significance (i.e. having a P-value between 1 × 10⁻⁶ and 5 × 10⁻⁸); and (iii) those not significant. There were 33 candidate suggestive significant SNPs [group (ii), Supplementary Table S5] for our replication analysis. For each of these SNPs, we extracted the P-value for association for the three other phenotypes and from the omnibus test derived using the command line version of JASS.

Of the 33 SNPs, 24% (N = 8), 18% (N = 6) and 61% (N = 20) were replicated at the Bonferroni corrected P-value threshold of 0.0015 (i.e. 0.05/33), for asthma, RA and UC, respectively. The omnibus test outperformed all individual univariate signals with an overall replication of 76% (N = 25), while performing a single test instead of three. Overall, 7 out of the 33 SNPs had P-values below the genome-wide significance threshold (P < 5 × 10⁻⁸) with at least one of the approach (Table 2). The omnibus test highlighted in particular two SNPs not identified by the three individual GWAS. The first one, rs3184504, is a missense mutation in SH2B3. This variant is cited in >40 publications, many of them related to T1D, celiac disease and other autoimmune disorders. The second variant, rs267949, is an intron variant of DAP on chromosome 5. While not identified in the univariate GWAS we used, a previous study found association between the DAP gene and UC (36).

Table 2.

Validation of SNPs from example 3

RSID	Chr.	Position	Ref.	Alt.	Gene	P  CD	P  Asthma	P  RA	P  UC	P  JASS
rs7514098	1	8 177 632	A	G	LOC107984915	9.8 × 10−8	0.64	0.027	4.1 × 10−11	3.3 × 10−9
rs4845604	1	151 801 680	A	G	RORC	6.1 × 10−7	0.16	0.37	1.6 × 10−11	2.3 × 10−9
rs267949	5	10 743 929	T	C	DAP	1.3 × 10−7	0.063	9.3 × 10−7	4.9 × 10−5	1.5 × 10−8
rs174564	11	61 588 305	G	A	FADS2	7.1 × 10−7	1.4 × 10−8	5.7 × 10−4	0.061	6.0 × 10−10
rs3184504	12	111 884 608	T	C	SH2B3	5.7 × 10−7	8.5 × 10−5	3.0 × 10−7	5.5 × 10−6	1.2 × 10−12
rs2836881	21	40 466 299	T	G	LOC107985484	5.7 × 10−7	0.31	0.41	1.1 × 10−32	3.5 × 10−27
rs138788	22	35 729 721	G	A	TOM1	7.2 × 10−8	0.14	0.58	2.9 × 10−8	1.4 × 10−6

Genome-wide significant P-values are indicated in bold.

DISCUSSION

The past few years saw a dramatic increase in the number of publicly available GWAS summary statistics for a broad range of phenotypes. This wealth of data is coming along a strong interest from the community for multitrait analysis, and multitrait association testing in particular. In this study, we present JASS, a command line and web-based package dedicated to the joint analysis of GWAS summary statistics. JASS addresses the need for a fast and user-friendly tool to perform various joint analyses of summary statistics. Our package includes the two most popular multivariate approaches, an omnibus test and a weighted sum of Z-scores, but allows for alternative approaches to be implemented by advanced users. JASS also includes several complementary functions both for a dynamic synthesis and visualization of large-scale results and for the preprocessing of heterogeneous GWAS data, a critical step for valid multivariate analysis.

Using existing GWAS summary statistics, we showed the flexibility and strong computational performances of our package as compared to the existent. We further performed three arbitrary real data applications to demonstrate the potential of JASS. These examples cover various scenarios, including the joint analysis of related phenotypes for the identification of new associated loci missed by univariate analyses, the exploratory analysis of alternative weighting schemes to identify specific genetic components across a large number of traits and the validation of suggestive associations for a given phenotype using multivariate analysis applied to correlated phenotypes. We also deployed a publicly available web instance of JASS (http://jass.pasteur.fr) currently including 154 preprocessed and harmonized GWAS summary statistics, and covering several common diseases and quantitative traits. This installation-free instance of JASS allows nonexperts to performed various complementary analyses relevant to their specific study.

Our JASS software is complementary to standard meta-analysis approaches, as implemented, for example, in METAL (37) or GWAMA (38). These meta-analysis tools focus on combining association results from independent GWAS performed for the same phenotypes, and are typically used in consortium data. They incorporate approaches for the combined analysis of effect estimates, such as the inverse-variance weighted meta-analysis, or P-values, such as the Fisher's test, whose validity relies on the assumption of independence between GWAS. The primary objective of JASS is to combine statistics from multiple phenotypes from potentially correlated GWAS, and is therefore a generalized version of the aforementioned approach. For example, the inverse-variance weighting meta-analysis is a special case of the sumZ test using the square root of the sample size as weight. Similarly, the Fisher's test should be approximately similar to the omnibus test in the special case of no correlation between GWAS. On the other hand, meta-analysis tools often include a number of quality control (QC) functions applicable to univariate GWAS (e.g. filtering SNPs based on imputation quality or the significance of the test for Hardy–Weinberg equilibrium). Because JASS addresses follow-up analysis of validated published GWAS, it does not include such QC functions. However, our pipeline does address potential QC issues that are specific to the joint analysis of summary statistics. For example, we incorporate our recently developed RAISS (29) approach for the imputation step, as well as filtering based on the sample size used per SNP.

There are various multivariate analyses that can be performed from a given set of GWAS summary statistics. Different tests (e.g. omnibus or sumZ, as implemented in JASS), different parameters (e.g. alternative weighting scheme for sumZ) and the choice of a subset of phenotypes to be analyzed jointly will lead to the identification of different loci. To our knowledge, there are no established guidelines for setting an optimal approach. Moreover, as discussed in previous studies, alternative models likely capture complementary components of the genetic architecture of the traits under study. The JASS packages not only offers the possibility to explore quickly a range of alternative models, but is also a first step toward building an integrated platform including both multitrait association testing and the generation of biological hypothesis on the underlying genetic structure.

DATA AVAILABILITY

A JASS public server currently including 154 clean and harmonized GWAS is available at http://jass.pasteur.fr For local use, the source code of JASS can be found at https://gitlab.pasteur.fr/statistical-genetics/jass. Installation, configuration and data import instructions are included and linked from the README.md file. The JASS software is released under the terms of the MIT license (see https://gitlab.pasteur.fr/statistical-genetics/jass/blob/master/LICENSE). The preprocessing package is available at https://gitlab.pasteur.fr/statistical-genetics/JASS_Pre-processing. The imputation package is available at https://gitlab.pasteur.fr/statistical-genetics/raiss. The nextflow pipeline integrating all JASS preprocessing steps (GWAS harmonization, GWAS imputation and H₀ covariance matrix computation) is available at https://gitlab.pasteur.fr/statistical-genetics/jass_suite_pipeline. Finally, the link to the analysis of insulin phenotype is: http://jass.pasteur.fr/directLink.html?phenotypes=z_MAGIC_HOMA-IR,z_MAGIC_FAST-INSULIN,z_MAGIC_IS,z_MAGIC_FPI.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

National Institute of Dental & Craniofacial Research (NIDCR) [R03DE025665]; Investissement d’Avenir grant [ANR-16-CONV-0005].

Conflict of interest statement. None declared.