Ligand Field Theory and Angular Overlap Model Based Analysis of the Electronic Structure of Homovalent Iron–Sulfur Dimers

Abstract

The electronic structure of multinuclear transition metal complexes is a highly challenging problem for quantum chemical methods. The problems to be solved for a successful analysis include the following: (1) many unpaired electrons leading to “highly entangled” wave functions that cannot be calculated by standard electronic structure methods, (2) drastic differences between the one-particle and many-particle spectra and a high density of low-lying states, and (3) the interpretation of such highly complex wave functions in chemical terms. In this work, we continue our research on oligonuclear clusters by presenting an in-depth analysis of the electronic structure of a prototypical iron–sulfur (Fe₂S₂) dimer. Accurate wave functions are obtained from a variety of advanced wave function based methods. The wave function results are interpreted in terms of an effective Hamiltonian that in turn is parametrized in terms of the angular overlap model (AOM) that provides the chemical insights that we are striving for. A hierarchical analysis allows us to interpret the local electronic structure in terms of the thiolate, sulfide ligands, and metal–metal interaction strengths. The many-particle spectrum is analyzed in terms of configurations involving ligand and metal centers. Finally, we are able to derive simple yet effective interpretations of ligand interaction strengths, the metal–metal interaction strength, and the low-lying many-particle spectrum of the Fe₂S₂ dimer.

Short abstract

We present an analysis of the electronic structure of a homovalent iron−sulfur (FeS) dimer via ab initio ligand field and angular overlap models. The metal−thiolate and −sulfide ligand interaction strengths are compared to metal−metal interactions, underscoring the importance of changes upon going from FeS monomers to dimers. The many-particle spectrum is analyzed to understand the nature of the exchange coupling. Finally, analysis of the excited states in terms of various charge transfer configurations is presented.

1. Introduction

Iron–sulfur (FeS) active sites are well-known in nature to act as electron transfer agents in proteins.^1,2 The FeS dimer containing ferrodoxin proteins, which are recognized as model systems that carry out electron transfer, also show interesting magnetic properties.³⁻⁶ FeS dimers occur in the homovalent state with two equivalent tetrahedral Fe(III) sites,² whereas in its one-electron reduced state the dimer can occur as a mixed-valent localized (classes I and II) Fe(II)–Fe(III) and a mixed-valent delocalized Fe(2.5)–Fe(2.5) dimer.⁷ In order to understand the origin of the magnetic properties and the variation of such properties in various types of ferredoxins, one requires an in-depth understanding of the electronic properties of homovalent and mixed-valent dimers. The Fe(III) and Fe(II) centers in such proteins occur as locally high spin S = 5/2 or S = 2 spin-centers, respectively, due to the relatively small ligand field splitting imposed by the four thiolate and two sulfide ligands. The presence of a large number of unpaired electrons enforces a complex representation of their electronic ground- and excited-state wave functions. Therefore, in order to simplify the study of such systems, one needs good model Hamiltonians, such as the ligand field model⁸⁻¹⁰ (LFT) and the angular overlap model¹¹⁻¹³ (AOM), in order to present a simple yet qualitatively correct interpretation of the electronic structure.

In a previous work, ref (14), we performed a detailed analysis of FeS monomers. In the present work, we carry out a detailed ab initio analysis of the many-particle spectrum of the Fe₂S₂ dimer. This work is organized as follows: In section 2, we give a brief summary of the methodology and computational details employed for this study. In section 3 we present the main results of this work. The emphasis is placed on a hierarchical understanding of the electronic structure upon going from the FeS monomer to the dimer. The main changes in the electronic structure between the monomer and dimer are divided into two parts. First, the effect of the thiolate vs the sulfide ligand upon the local ligand field of the Fe center is analyzed using LFT. This is followed by the AOM analysis of the wave function in order to extract ligand interaction parameters (e_σ, e_π), which can be related to experimental observables. Second, the effect of the metal–metal interaction on the electronic structure is presented by using our recently developed open-shell coupled cluster method.^15,16 In section 3.3, we present the many-particle spectrum of the dimer where the term “many-particle spectrum” is used to refer to the ab initio calculated eigenvalues of the Born–Oppenheimer Hamiltonian operator. This distinction is made in order to differentiate it from the spectrum of orbital energies (referred to as the one-particle spectrum). Finally, we summarize the major points in the conclusion.

2. Computational Approach

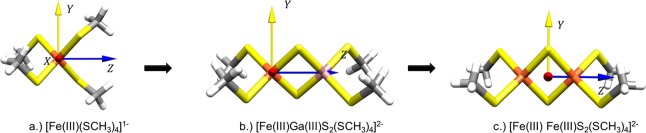
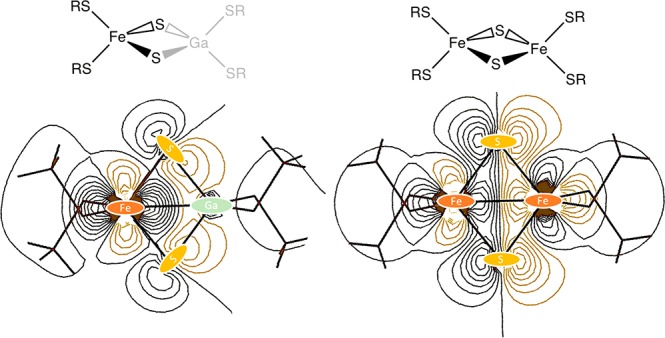
In order develop a stepwise understanding of the electronic structures of Fe₂S₂ dimers, we have followed a hierarchical approach separating two types of interaction in the dimers. First, the changes in the local ligand field splitting due to the replacement of thiolate ligands with bridging sulfide ligands is analyzed; second, the nature of the metal–metal interaction is presented. This is schematically shown in Figure 1.

Figure 1.

Schematic of the three models studied going from the FeS monomer to the Fe₂S₂ dimer. The gallium substituted FeGaS₂ “dimer” serves to analyze the change in the metal–ligand interaction between the thiolate and the sulfide ligands.

2.1. Geometric Structure Comparison

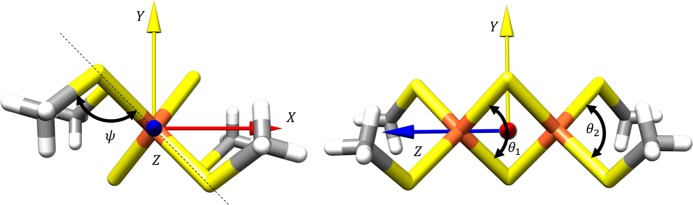
The structure of the Fe₂S₂ dimer that has been taken from crystallographic data¹⁷ is shown in Figure 2. The 2,2′-bis(benzo[d]thiazoline)-4,4′-dinitrophenyl disulfide ligand was simplified by replacing the benzo[d]thiazoline with a methyl group in order to reduce computational effort. The geometry was further symmetrized to the highest possible point group (C_2h) while preserving the main geometric features. The main geometry parameters for the dimer are compared to that of [Fe(SR)₄]⁻ monomer (CSD code, BOSTOS, where SR = 2,3,5,6-tetramethylphenylthiolate) in Table 1. The definition of the two angles θ and ψ is shown in Figure 2. The symmetrized geometry was used for the analysis of the molecular orbitals (MOs) and wave function resulting from the ab initio calculations.

Figure 2.

Geometry parameters of the model Fe₂S₂ dimer. The ψ angle represents the dihedral angle between C–S–Fe–S atoms and θ angle corresponds to the tetrahedral angle between the S–Fe–S atoms. The C_2h axis is along the Z axis (blue arrow) of the dimer molecule.

Table 1. Comparison of the Main Geometry Parameters of the FeS monomer and Fe₂S₂ dimer^A.

		[Fe2S2]2+
	[Fe(SR)4]−	X-ray	C2h
Fe–Fe (Å)		2.70	2.70
θ1 (deg)	57.12	55.57	55.51
θ2 (deg)		52.38	52.36
ψ (deg)	54.56	62.5	64.38
Fe–S–CH3 (deg)	102.34	110.67	110.68
Fe–SR (Å)	2.264	2.303	2.310
Fe−μS (Å)		2.202	2.199
S–C (Å)	1.845	1.774	1.779

^AA comparison of the C_2h symmetrized geometry is also given.

2.2. Computational Protocol

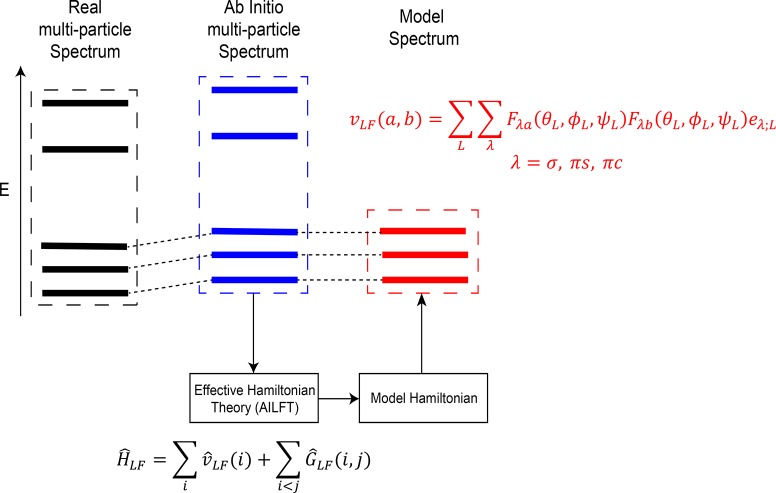
We have used the same procedure as in ref (14) for the elucidation of the electronic structure of iron–sulfur dimers. In brief, first, an accurate ab initio spectrum is calculated and compared to the experimental spectrum where available. Second, a phenomenological model Hamiltonian for low energy states is established in order to quantify experimentally relevant interactions in the molecule. Finally, chemically meaningful parameters are extracted and compared to the experimental ones. Therefore, a complex many-particle spectrum is rationalized via a phenomenological model Hamiltonian with chemically meaningful parameters that can subsequently be related to the geometry of the molecule. A schematic of this protocol is presented in Figure 3.

Figure 3.

Schematic of the protocol for the analysis of the many-particle spectrum of iron–sulfur molecules.

2.3. Comment on Level of Theory

In the present work, we have used three computational protocols individually adapted for the specific types of properties that we wanted to describe. In the following, we give a brief description of the three computational protocols and the justification for their choice.

(A) First, we studied the local ligand field splitting of the iron center via the previously established protocol.¹⁴ Such a study requires a state-averaged complete active space self-consistent field (CASSCF) calculation¹⁸⁻²⁰ with five electrons in five orbitals (5e,5o) followed by the N-electron Valence State Perturbation theory (NEVPT2) correction.²¹⁻²⁴ The AILFT module in ORCA is then used to extract the LFT parameters v_ij, B, and C using the CASSCF/NEVPT2 transition energies. Here the v_ij’s are the 14 one-electron parameters as shown in Figure 3. Such a procedure has been demonstrated to be useful for the understanding of local properties of transition metal systems.²⁵

(B) Second, for a comparison of properties of molecules with one vs two Fe centers one must use methods which are capable of consistently describing systems with a varying number of interacting electrons. The coupled cluster method is such a size consistent electron correlation method; therefore, natural orbitals obtained using the open-shell coupled cluster singles and doubles method^15,16 (CCSD) can be used to compare the changes that occur in a molecule containing one vs two Fe centers.

(C) Finally, a calculation of transition energies of states involving excitations from the ligand to metal orbitals or vice versa require the inclusion of ligand-based occupied and virtual orbitals in the CAS space. Such a CAS space would consist of CAS(38e,24o) with all 14 occupied ligand p-orbitals and CAS(10e,22o) which includes 12 ligand unoccupied orbitals. A detailed description of the active space is given in section 3.3. Such large CAS spaces cannot be treated by a full configuration interaction (FCI) procedure due to their large Hilbert spaces, and one has to resort to approximate CI calculations. Such a near FCI estimate of the transition energies can be obtained using the configuration interaction by perturbation with a multiconfigurational wave function Selected by the iterative process (CIPSI) scheme^26,27 implemented in ORCA as the iterative configuration expansion (ICE) algorithm. Note that the open-shell CCSD procedure cannot be used for the calculation of such highly excited states due to their multireference character, given that the open-shell CCSD procedure described above is a single-reference method.

All calculations reported in this work were done with a development version of the ORCA program package²⁸ prior to the release of orca version ORCA 4.1. Hydrogen atom positions of the methyl group were optimized using density functional theory (DFT) implementation in the ORCA program package²⁹ (BP86 functional along with the Grimme’s D3 dispersion correction).^30,31 The def2-SVP and def2-TZVP basis sets³² were employed for the DFT and CASSCF calculations, while def2-SVP basis was employed for the open-shell CCSD treatment. The downscaling of the basis set in the CCSD calculations was necessary due to computational restrictions. The resolution of identity (RI) approximation was used for the calculation of molecular integrals using the AutoAux procedure.³³ The details of the theoretical description of the AILFT and AOM procedure are presented in section 1 of the Supporting Information (SI).

3. Results and Analysis

As presented in the Introduction, we have followed a stepwise approach to describe the changes in the electronic structure of FeS monomers and dimers as shown in Figure 4. The first part consists of a comparison of the FeS monomer with the diamagnetically substituted FeGaS₂ dimer. The diamagnetic substitution of one Fe in the dimers serves to deactivate metal–metal interaction by removing metal–metal charge transfer excitations. Thus, isolating the changes in the local electronic structure to the ligand environment and the geometry changes between the [Fe₂SR₄]⁻ monomer and [FeGaS₂(SR)₄]^2– dimer. The second part of the analysis compares [FeGaS₂(SR)₄]^2– dimer with the [Fe₂S₂(SR)₄]^2– dimer in order to estimate metal–metal interaction effects on the metal–ligand interaction and the global electronic structure.

Figure 4.

Outline for the analysis of the changes in the local ligand field surrounding the Fe center upon going from the FeS monomer to the [Fe₂S₂SR₄]^2– dimer. The axis orientations are kept constant in order to be able to compare the changes due to the ligand environment.

3.1. Analysis of the Metal–Ligand Interaction

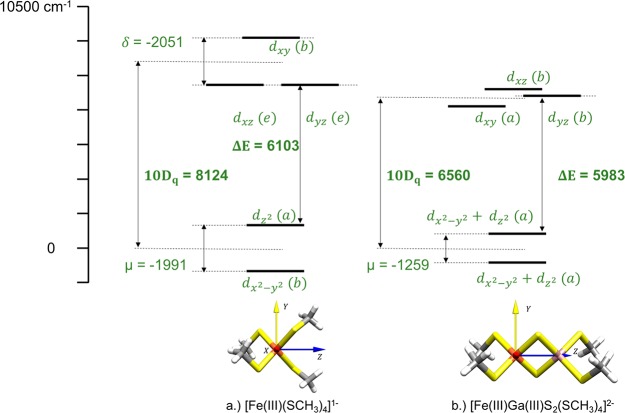
In this section, we present a comparison of the metal–ligand interaction strength of thiolate and sulfide ligands. Ligand field analysis has been carried out using the AILFT implementation in ORCA. Using this technique, the local ligand field splitting (LF) of the lone iron center in the [FeGaS₂(SR)₄]^2– dimer can be calculated. The resulting LF splitting is given in Figure 5, where the LF splitting of the [Fe(SCH₃)₄]⁻ monomer taken from ref (14) is also shown for comparison. The def2-TZVP basis set has been used for both the [Fe(SCH₃)₄]⁻ monomer and the [FeGaS₂SR₄]^2– dimer molecules. The AILFT extraction has been performed with a CAS(5e,5o) calculation including the NEVPT2 correction following the protocol of ref (14).

Figure 5.

Comparison of the ligand field splitting of the [Fe(SCH₃)₄]^1– monomer (a) and the iron center in the [FeGaS₂SR₄]^2– dimer (b). The ligand field parameters 10D_q, μ, and δ have been extracted from the AILFT calculation with a CAS(5e,5o) along with the NEVPT2 correction. The symmetry of the orbitals are also shown in the local S₄ and C₂ point group for [FeSR₄]^1– and [FeGaS₂(SR)₄]^2–, respectively. All values are in cm^–1.

One distinguishing feature between the [Fe(SCH₃)₄]⁻ monomer and the [FeGaS₂SR₄]^2– dimer is the asymmetric ligand environment around the iron atom in the case of the [FeGaS₂SR₄]^2– dimer. The influence of this change is reflected in a decrease in the ligand field splitting. A second reason for the decrease is the increase in the π-interaction upon going from the thiolate to sulfide ligands. This increase is due both to an increased total charge on the sulfide ligand and the absence of additional covalent bonds.

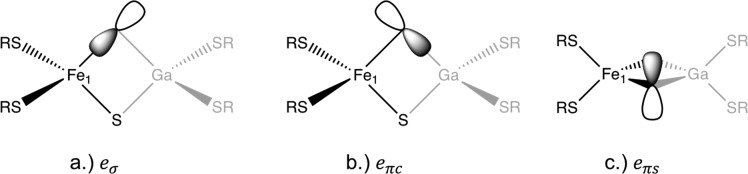
The reason for this increase can be quantified by using the AOM analysis. In order to perform the AOM analysis, two sets of parameters need to be defined: one for the thiolate ligands and one for the sulfide ligands. The AOM parameters for the sulfide ligands will consist of the standard e_σ, e_πs, and e_πc parameters, whereas, for the thiolate ligands, one needs to include the e_σπs parameter, due to the bent RC–S–Fe bond, along with the e_σ, e_πs, and e_πc parameters. A schematic of the type of interactions described by e_σ, e_πs, and e_πc parameters is shown in Figure 6. Therefore, the AOM parametrization involves seven parameters and the extraction of these seven parameters can be carried out by a least-squares fit of the 5 by 5 one-electron d-orbital interaction matrix obtained from the AILFT calculation on the [FeGaS₂SR₄]^2– dimer. In order to estimate the relative magnitudes of the AOM parameters for the thiolate and sulfide ligands, we have carried out an analysis on a series of simple model molecules consisting of sulfide and thiolate ligands. The analysis with the parameter estimates is presented in section 2.1 of the SI. This analysis has been used to obtain starting guess values for fitting the AOM parameters of the [FeGaS₂SR₄]^2– dimer. The AOM parameters of the [FeGaS₂SR₄]^2– dimer are presented in Table 2.

Figure 6.

Schematic of the type of interaction modeled by the AOM e_σ, e_πc, and e_πs parameters.

Table 2. Comparison of the AOM Model Parameters for the Ferric Center in the [FeSR₄]⁻ Monomer and [FeGaS₂SR₄]^2– Dimer Molecule^a.

		eσ	eπs	eπc	eσπc	total
[FeIII(SCH3)4]−
CASSCF	thiolate	6304.1	2315.6	∼1	–232.0	8852.2
NEVPT2		7020.3	2533.4	∼1	–247.0	9306.7
[FeIIIGaIIIS2(SCH3)4]2–
CASSCF	thiolate	6082.4	1191.3	6.2	186.5	7466.4
	sulfide	7089.4	3175.0	2159.5	-	12423.9
NEVPT2	thiolate	6448.9	1184.1	5.6	200.8	7839.4
	sulfide	7409.1	3235.3	2154.7	-	12799.1

^aThe AOM parameters for fits to the LF matrix elements at the CASSCF and NEVPT2 levels are shown. All values are given in cm^–1.

The replacement of two of the thiolate ligands with μ-sulfide ligands results in a decrease in the ligand field splitting 10D_q by about 1500 cm^–1. This can be estimated by looking at the expression for 10D_q of a tetrahedral ligand field given by 4/9 (3e_σ – 4e_π). Therefore, an increase in the _π interaction due to the replacement of thiolate ligands with sulfide (as evidenced in Table 2) leads to a net decrease in 10D_q. A second consequence of this replacement is a decrease in the local symmetry. This decrease in the local symmetry from S₄ in the monomer to C₂ in the dimer enables the mixing of the d_x² – d_y² and d_z² orbitals as well as a lifting of the degeneracy in the d_xz, d_yz orbital pair. The analysis of the AOM results for the dimers can be summarized in the following points:

(A) As anticipated, the σ-donor strength of the thiolate ligands (represented by their corresponding AOM parameters) in the [FeGaS₂SR₄]^2– dimer is close to that in the [FeSR₄]^1– monomers (cf. Table 2). This shows the consistency of the AOM treatment.

(B) There is a significant change in e_πs (i.e., π donor strength) of the thiolate ligands in the [FeGaS₂SR₄]^2– dimer compared to the [FeSR₄]⁻ monomers. This is due to the competition among the π-interaction between the thiolate/sulfide π orbitals and the Fe d-orbitals. A larger strength of the π-interaction between the sulfide and Fe d-orbitals results in an equivalent reduction in the π-interaction of the thiolate ligands. Such a decrease is not observed for the σ-interaction due to the fact that the d-orbitals showing σ-interaction are of a different symmetry with respect to thiolate and sulfide σ-orbitals.

(C) The μ-sulfide ligand behaves overall as a stronger donor than the thiolate with a ratio for the total interaction strength of 1.66 for sulfide vs thiolate. This increase in metal–ligand interaction for the μ-sulfide ligand has also been observed in S K-edge X-ray absorption studies of iron–sulfur-based molecules.³⁴

(D) The strength of the e_π-interaction is significantly larger for the μ-sulfide ligand than the thiolate ligand. This increase in the π bonding interaction of the μ-sulfide ligands is due to the absence of additional bonds (contrary to the case of the thiolate ligands) allowing a larger interaction of the π-orbitals with the metal d-orbitals.

(E) Due to the increase in the total π-interaction, there is an apparent reduction of the local ligand field splitting for the [FeGaS₂SR₄]^2– dimer compared to that of the [FeSR₄]⁻ monomer.

It should be mentioned that the replacement of the second Fe(III) atom with Ga(III) will influence the metal–ligand interaction of the bridging sulfide ligand. The extent of this effect is the subject of analysis of the next section.

3.2. Analysis of the Metal–Metal Interaction

To understand the metal–metal interaction, one needs to treat the full [Fe₂S₂SR₄]^2– dimer molecule. Such a calculation will require one to account for the 10 d-orbitals of both metal centers at least. Therefore, a minimal complete active space (CAS) would consist of the 10 d-orbitals and the 10 electrons of the two Fe(III) centers. Here the results of the CAS(10e,10o) calculation will be presented and analyzed.

A qualitative estimate of the metal–metal interaction on the one-particle spectrum can be obtained by looking at the CASSCF state-averaged natural orbitals, averaged over the lowest root of the six spin-states S = 0 to S = 5. The 10 metal d-based MOs can be ordered according to the magnitude of the diagonal elements of the state-averaged Fock matrix (F_ii). The symmetry of each MO and its Loewdin population is given in Table 3. A schematic of the MOs is presented in Figure 7, where the diagonal element of the total Fock matrix was used for ordering as in Table 3 despite the fact that natural orbitals do not have a well-defined orbital energy. As we can see from Table 3 the CASSCF MOs are very ionic with about 90% metal character. This is due to the nature of the CASSCF procedure which give a too ionic wave function. As we shall show below, this can be partly corrected for by accounting for dynamic correlation effects via the coupled cluster approach.

Table 3. 10 Symmetry Adapted Natural MOs Resulting from the State-Average CAS(10e,10o) Calculation along with Their Composition and Irreproducible Representations (Irrep)^a.

				weight (%)
irrep	composition	Fii (cm–1)	occupation	Fe	SR–	S2–
2bu	dxz	26388.3	0.92	86.6	0.4	13.0
3au	dx2–y2 + dz2	25527.9	0.91	88.0	3.2	8.8
1bu	dyz	19593.5	0.97	85.8	7.6	6.6
3ag	dxy	14865.3	0.96	93.8	0.0	6.2
2ag	dx2–y2 – dz2	13048.5	0.99	94.0	3.6	2.4
2bg	dyz	11845.8	1.03	94.0	6.0	0.0
2au	dx2–y2 + dz2	9859.6	1.01	96.4	3.2	0.4
1bg	dxz	3972.1	1.08	96.4	0.8	2.8
1au	dxz	3648.3	1.04	99.2	0.0	0.8
1ag	dx2–y2 – dz2	0.0	1.09	98.2	1.2	0.6

^aThe ordering has been defined according to the diagonal elements of the Fock matrix (F_ii). The lowest F_ii MO (a_g) has been taken as the zero, and F_ii of the other orbitals is given relative to this orbital. The Loewdin orbital composition of the MOs in terms of percentage of metal and ligand orbitals (thiolate and sulfide) is also presented.

Figure 7.

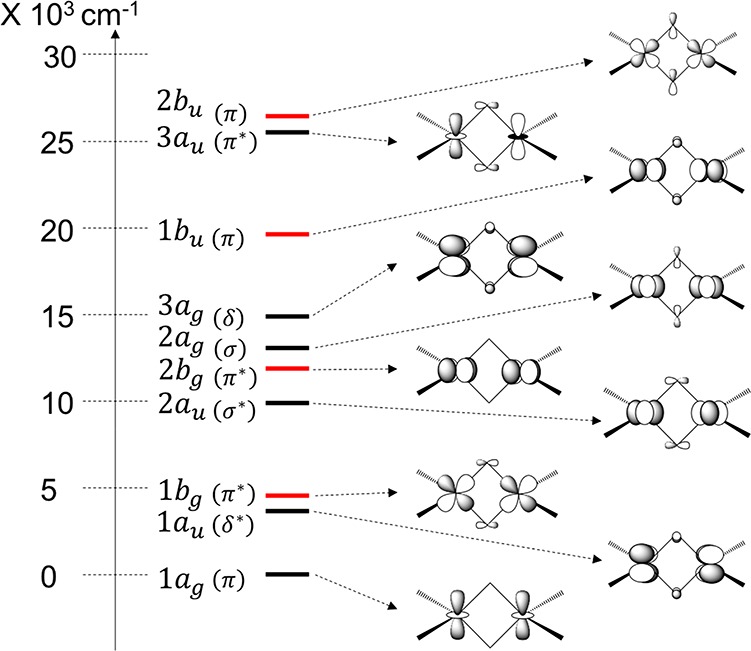
Symmetry adapted natural molecular orbitals. The natural orbital “energies” correspond to the diagonal elements of the state-averaged Fock matrix taken from a state-averaged CAS(10e,10o) calculation. The orbitals represented by black lines belong to a symmetry and red b symmetry in the C₂ point group. Only a schematic of the symmetry adapted orbitals along with the [Fe₂S₂SR₄]^2– backbone is shown for simplicity.

A comparison of the influence of two metal centers on the metal–ligand interaction can be made using the open-shell coupled cluster singles doubles (CCSD) natural orbital analysis.^15,16 In this procedure, the high-spin open-shell CCSD density was obtained starting from state-averaged orbitals for both the gallium substituted dimer [FeGaS₂SR₄]^2– and the homovalent dimer [Fe₂S₂SR₄]^2–, and the natural orbitals were calculated. These natural orbitals can then be analyzed to understand changes in the metal–ligand interaction due to the presence of one and two metal centers. A comparison of the CASSCF natural orbitals and the CCSD natural orbitals in terms of orbital Loewdin population is shown in Table 4. The metal–ligand orbital mixing shows a 2-fold increase upon going from CASSCF natural orbitals to CCSD natural orbitals. This is the usual behavior observed for a CASSCF analysis, which tends to emphasize the ionic nature of the orbitals (see Table 3). As we can see from Table 4, this ionic nature was corrected at least partly by the CCSD procedure. The final mixing between the iron d-orbitals and the ligand orbitals ranges from 37 to 3% depending on the nature of the d-orbital. The largest mixing is observed for the t₂ orbital of 37% and smallest for the e type orbital of 3%. Additionally, for the gallium substituted dimer, the sulfide ligands and thiolate ligands show equal mixing with d-orbitals (see Table 4) at the CASSCF level of 1:1 which is enhanced at the CCSD level to 1.3:1 ratio for sulfide vs thiolate contributions. A similar trend is observed for the full dimer for which a 1:1 mixing is enhanced to 1.5:1 at the CCSD level for the sulfide vs thiolate ligands. This can be compared with the AOM analysis above, which gave the sulfide vs thiolate contribution of about 1.66:1. The MO contributions again show a more important contribution of the sulfide ligands compared to the thiolate ligands in line with their larger contribution in the AOM analysis (see Table 2).

Table 4. Comparison of the CASSCF and CCSD Natural Orbitals for the [FeGaS₂SR₄]^2– and [Fe₂S₂SR₄]^2– Dimers^a.

CASSCF				CCSD
	Fe	S2–	SR–		Fe	S2–	SR–
FeIIIGaIII
dxz	92	2	6	dxz	75	14	11
dyz	86	5	8	dyz	76	14	10
dxy	88	6	5	dxy	77	10	13
dx2–y2	91	7	1	dx2–y2	85	13	2
dz2	90	8	2	dz2	89	4	7
FeIIIFeIII
3au (dz2)	88	9	3	dz2	84	9	7
3ag (dxy)	93	6	0	dxy	80	7	13
2bg (dyz)	93	0	6	dyz	84	0	16
2au (dx2–y2)	96	0	3	dx2–y2	76	24	0
2ag (dz2)	93	2	4	dz2	87	10	3
1ag (dx2–y2)	98	1	1	dx2–y2	97	1	2
1bg (dxz)	95	4	1	dxz	82	13	5
2bu (dxz)	86	13	0	dxz	69	27	4
1bu (dyz)	85	7	8	dyz	63	22	15
1au (dxy)	99	0	0	dxy	91	1	8

^aThe Loewdin population of the 5 and 10 singly occupied orbitals respectively is presented in terms of the percent of metal and ligand contributions. The CCSD calculations and CASSCF calculations have been performed with the def2-SVP basis set.

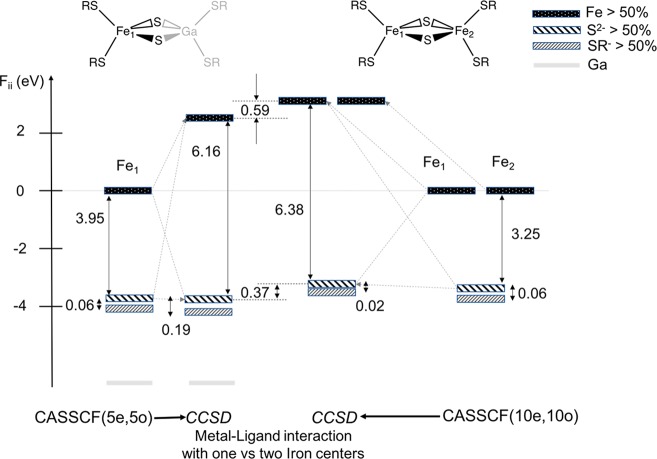
Although orbital energies have no precise meaning for natural orbitals, one can nonetheless obtain an indication about the nature and strength of the interaction by comparing the diagonal elements of the Fock matrix of the CCSD natural orbitals. Such an analysis will shed light on the influence of the metal–metal interaction on the global electronic structure. Using the diagonal elements of the Fock matrix (F_ii), a MO diagram can be made such as that shown in Figure 8. The presence of a second metal center results in a net reduction of the average metal–sulfide interaction compared to the [FeGaS₂SR₄]^2– dimer. This is due to a sharing of the electron density on the bridging sulfide between two Fe(III) atoms. This reduction of the effective metal–sulfide interaction is accompanied by an increase in the net metal–thiolate interaction evidenced by a relative lowering of thiolate “energies” by 0.05 eV compared to the gallium substituted dimer. Note that this lowering of the thiolate energies is in comparison to the Fe d-orbitals of the same molecules and not the thiolate energies between the [FeGaS₂SR₄]^2– and [Fe₂S₂SR₄]^2– molecules. As a result, the local properties of one metal center could be influenced by the second metal center albeit via the bridging sulfide ligand. The full list of the metal and ligand energies is given in Table S2 of the SI.

Figure 8.

Molecular orbital diagram of the interaction between the metal d-orbitals, the bridging sulfide orbitals and the thiolate orbitals for the [FeGaS₂SR₄]^2– and [Fe₂S₂SR₄]^2– dimers. Fock matrix diagonal elements have been used as energies for comparison purposes. The barycenter of energy has been used for the five metal d-based molecular orbitals as well as the six p-orbitals of the bridging ligands in order to simplify the figure. The barycenter of the 12 (4 × 3) thiolate p-orbitals is chosen to represent a net thiolate “energy”. All values are given in eV.

The metal–metal interaction can be quantitatively estimated using the so-called hopping integral.35,36 In order to define the hopping from one Fe center to another, a unique local orbital basis has to be defined. For this purpose, we have used the state-averaged local Fock basis as defined in section 1.3 of the SI. On the basis of local Fock orbitals, the hopping integral between the dx2–y21 orbital on the left iron center (Fe1) and the dx2–y2 orbital on the right iron center (Fe2) can be defined as shown below: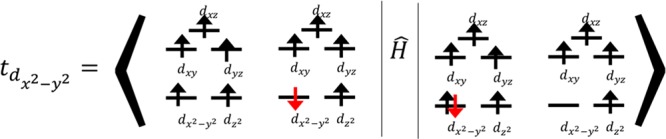where Ĥ represents the full Born–Oppenheimer Hamiltonian and the metal to metal charge transfer (MMCT) determinant is represented on the ket. We have extracted the values of the hopping integral between the five d-orbitals. These values along with the energies of MMCT configurations are given in Table 5. The main conclusions for the metal–ligand and metal–metal interaction analysis are the following:

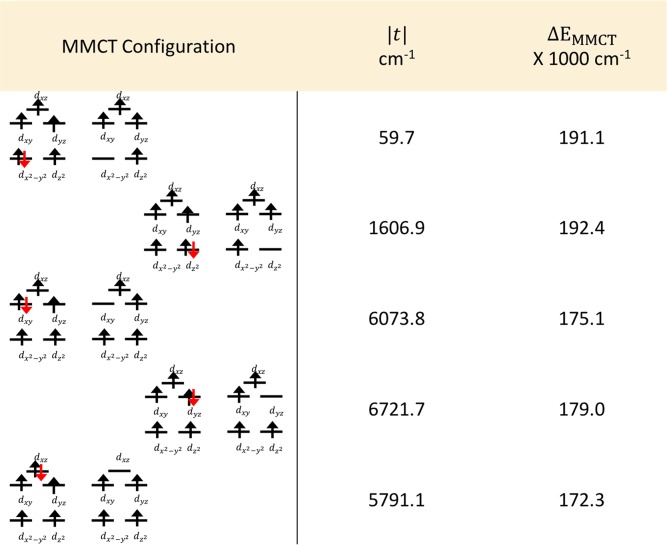
Table 5. Tabulated One-Electron Matrix Elements between the Various MMCT Configurations and Neutral Determinant^a.

^aHere t represents the matrix element between two configurations involving electron hopping. The energy difference between the corresponding MMCT configuration and the S = 4 ground state is also given.

(A) There is a large intersite interaction between the d-orbitals of the two Fe centers as evidenced by the hopping integral t. The hopping integral contains both the direct metal–metal interaction and the metal–ligand–metal interaction mediated via the sulfide ligands. It is interesting to note that the magnitude of the hopping integral is similar to the magnitude of the AOM parameters for the sulfide ligands. Only the d_x²–y² orbital shows a considerably smaller hopping of ∼60 cm^–1.

(B) The mixing between the d_z² and d_x²–y² orbitals is of about 30:50 and 50:30 for the gerade and ungerade MOs, respectively. This shows that there is considerable mixing between the local d orbitals of a symmetry. This factor will become important during the analysis of the mixed-valent dimer molecule.

(C) The difference in the covalency between the thiolate and sulfide ligands can also be seen in the MO contributions (cf. Tables 3 and 4). The mixing of the sulfide ligand orbitals is larger than that of the thiolate ones despite the presence of two thiolate ligands per sulfide ligand. This is consistent with the AOM analysis showing that the sulfide ligands are about two times more covalent than the thiolate ligands.

(D) The presence of metal–metal interaction has a 2-fold effect. First, there is a decrease in the individual metal–sulfide interaction due to the sharing of the electron density of the sulfide ligands between the two metal atoms. This decrease is accompanied by an increased metal–thiolate interaction. Second, the direct metal–metal interaction has an impact similar to the metal–ligand interaction as evidenced by the natural orbital Fock matrix elements, as well as the hopping integral t.

3.3. Many-Particle Spectrum

In the present section, we focus on the many-particle states of the [Fe₂S₂(SCH₃)₄]^2–dimer molecule. The many-particle spectrum can be divided into two sets of states: First is the low-energy spectrum (<5000 cm^–1) which is made up of states that are dominated by configurations that respect local S = 5/2 spin on each iron center (Hund states). There are six such Hund states, one for each of the spin-states S_t = 0–5. These Hund states also correspond to the lowest energy root of each spin-subspace. The CASSCF and NEVPT2 energy differences of these states with respect to the lowest singlet state ¹A_g are shown in Figure 9. The wave function of these states in terms of the dominant configurations is given in Table 6.

Figure 9.

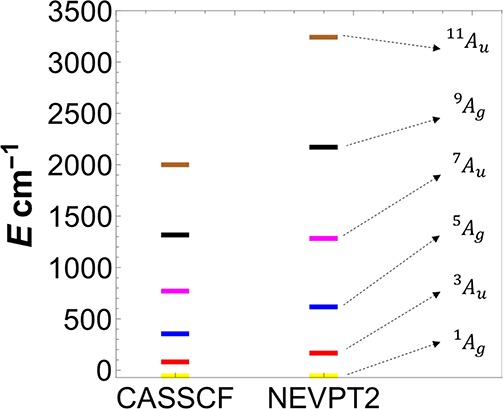
CASSCF and NEVPT2 spin-spectrum calculated with the CAS(10e,10o) active space. The singlet ground state ¹A_g is taken as the zero of energy.

Table 6. Wavefunction of the Six Spin-States in Terms of the Percentage Weights of the Various Types of Configurations.

spin	Hund	(spin–flip) non-Hund	(d–d) non-Hund	MMCT	E (cm–1)
S = 0	97.0	1.0	0.0	2.0	0
S = 1	97.2	0.9	0.0	1.9	224.6
S = 2	97.6	0.8	0.0	1.6	672.2
S = 3	98.2	0.6	0.0	1.2	1340.8
S = 4	99.0	0.3	0.0	0.6	2225.1
S = 5	100.0	0.0	0.0	0.0	3295.5

The six spin-states can be modeled using the usual Heisenberg Hamiltonian as shown in Table 7. It is interesting to observe that the Landé spin-ladder is not exactly reproduced by the NEVPT2 energies. There is a deviation of 5 cm^–1 in the J value calculated from the energy difference of the lowest two spin-states (S = 0, 1) and the highest two spin-states (S = 4, 5) (see Table 7). This deviation has a physical origin in the nature and the mechanism of the magnetic coupling between the Fe centers. This deviation can be modeled by the inclusion of a bi-quadratic term in the model Hamiltonian as proposed by Falk et al.³⁷ and applied by Bastardis et al.^35,36,43 and Sharma et al.³⁸ for iron–sulfur clusters. The Heisenberg Hamiltonian with the bi-quadratic term is given below:

The effect of the bi-quadratic term λ on the Landé spin-ladder is given in Table 7. It can be clearly seen that λ makes the energy differences deviate from the Landé pattern, having the effect of decreasing the energy difference between the S = 5 and S = 4 spin-states, while increasing the difference between the S = 0 and S = 1 spin-states for a negative λ. The best fit solution gives J = −109.6 cm^–1 and 4λ = −0.44 cm^–1. Therefore, although present, the bi-quadratic term is found to be small at least at the NEVPT2 level of theory.

Table 7. Comparison of the Heisenberg and the Heisenberg + Bi-quadratic Spin-Ladder Spectrum^a.

	model		ab initio
	Heisenberg	Heisenberg + bi-quadratic	NEVPT2 energies	Heisenberg fit J = 110.5 cm–1	Heisenberg + bi-quadratic
S = 5	–30J	–30J + 90λ	3295.5	3314.1	3277.6
S = 4	–20J	–20J + 260λ	2225.1	2209.4	2162.7
S = 3	–12J	–12J + 252λ	1340.8	1325.6	1287.0
S = 2	–6J	–6J + 162λ	672.2	662.8	639.5
S = 1	–2J	–2J + 62λ	224.6	221.0	212.3
S = 0	0	0	0	0	0

^aAll values are given in cm^–1.

The second set of states will be made up of configurations which either do not obey Hund’s rule or configurations which involve ligand to metal charge transfer or metal to metal charge transfer. Here, we briefly describe these types of configurations and their importance in the understanding of the electronic structure. The first is the MMCT type of configurations where one or more electrons are transferred from one metal center to the other. These types of configurations contribute to the kinetic exchange mechanism of coupling of the two iron centers. Second, there are non-Hund configurations are of the “d–d” type, where the total charge on each iron center is maintained to Fe(III) each but the local spin and electronic configuration are modified to give a local S = 3/2 spin-state by a de-excitation of a t₂ electron to the e set of orbitals. The second class of non-Hund configurations is of the spin–flip type; such configurations are made up of two Fe(III) centers with five singly occupied d-orbitals each, albeit the spin-couplings of the five electrons gives rise to local S = 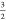spin-configuration on the iron center. Such configurations do not respect Hund’s rule due to a change in the spin-coupling and are therefore called spin–flip non-Hund (NH) configurations. Note that these non-Hund configurations involve a local S = 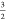spin-state which is a linear combination of the five Ms = 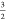determinants and are therefore multideterminental configurations. Importantly, the d–-d non-Hund configurations involve a change in the electron distribution, whereas the spin–flip non-Hund configurations do not. The LMCT configurations constitute the third type of configurations involving an electron transfer from a ligand DOMO such as the μS(π) orbital to a metal d-orbital. Such types of configurations contribute to the superexchange mechanism.^39,40 Finally, there are MLCTs which involve electron transfer from the metal d-orbitals to the unoccupied ligand orbitals such as the μS(π*) 4s and 4p orbitals of the bridging sulfide ligands. A schematic of these five types of configurations is given in Figure 10. Estimates of energy differences between these five class of states have been obtained as follows:

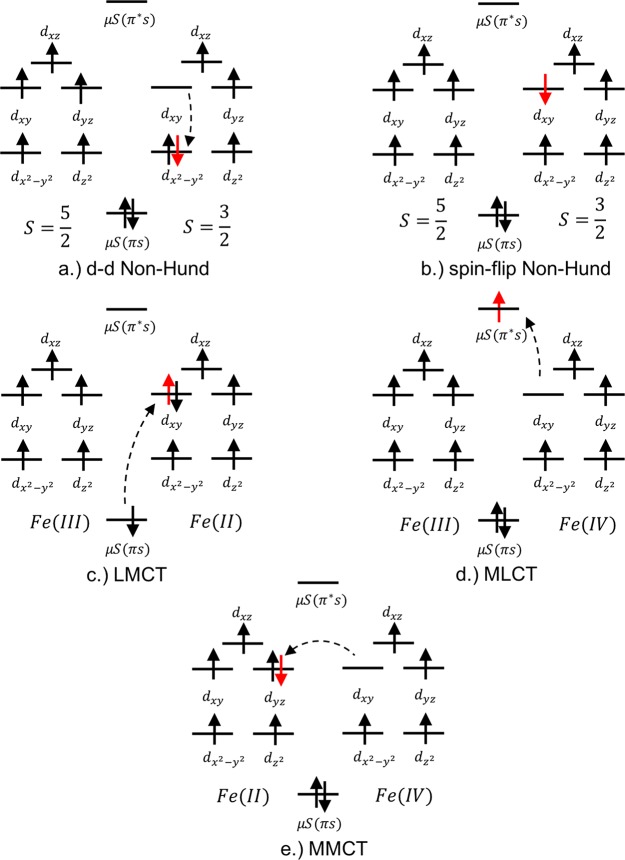
Figure 10.

Five types of configurations mediating the magnetic coupling between the metal centers. The abbreviations LMCT and MLCT refer to ligand to metal charge transfer and metal to ligand charge transfer, respectively. MMCT refers to metal to metal charge transfer. The d–d non-Hund label refers to the non-Hund configuration produced by an intrairon d to d excitation and the spin-flip non-Hund label refers to the non-Hund configuration resulting from a change in the local spin-coupling at the iron center.

(A) The energy estimates of the d–d non-Hund, spin–flip non-Hund, and MMCT states can be obtained from a CAS(10e,10o)/NEVPT2 calculation asking for all roots for the S = 4 spin-state. There are a total of 40 d–d non-Hund states, 8 spin–flip non-Hund states, and 50 MMCT states in the S = 4 spin-subspace making a total of 99 roots including the one Hund state.

(B) The energies of the S = 4 LMCT states have been obtained using an approximate ICE-CI CIPSI^26,27 calculation employing CAS(38e,24o) including all of the six bridging sulfide p-orbitals and the eight terminal thiolate p-orbitals (one σ and π each). This gives a total of 1260 LMCT states belonging to the S = 4 spin-subspace.

(C) Similarly, the MLCT bands have been calculated using an approximate ICE-CI CIPSI calculation including all the 4s and 3d virtual ligand orbitals of the bridging ligands making a CAS(10e,22o). Only 28 MLCT states with spin S = 4 corresponding to transition energies <200,000 cm^–1 were calculated.

The energies of the states up to 200,000 cm^–1 along with their type are given in Figure 11 below. The wave function of the many-particle states in terms of these five states is given in Table S3 of the SI. Note that, in the calculation of the energy differences, we have only accounted for static electron correlation, we hope that the inclusion of dynamic correlation effects will not qualitatively change the analysis.

Figure 11.

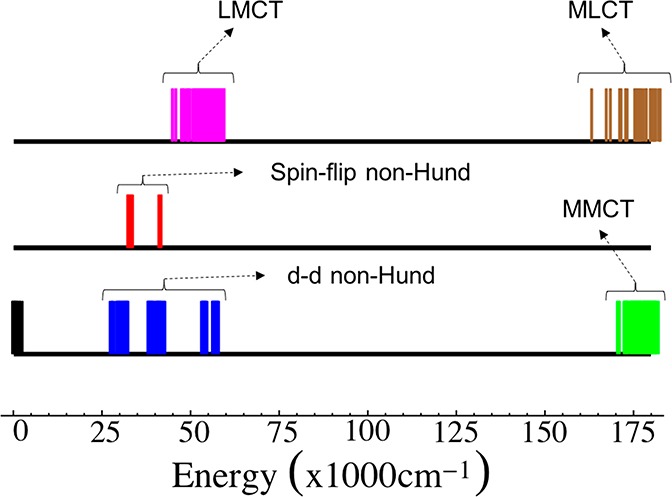
Energies of the S = 4 excited states for the Fe₂S₂ dimer. The black sticks correspond to the Hund set of states. The blue sticks represent the d–d non-Hund configurations and the green sticks the MMCT. The magenta sticks represent the LMCT and the brown sticks represent the MLCT energies. The singlet ground state ¹A_g is taken as the zero of energy.

The main observations have been summarized below:

(A) As expected from the classical Anderson model, there is a significant interaction of the Hund configuration with the MMCT configurations (cf. Table 6). This is due to the large hopping matrix elements between the Hund and the MMCT configurations as shown in Table 5. The MMCT states are the highest in energy among the CAS states starting from 172,573 cm^–1 which is almost 100,000 cm^–1 higher than the d–d and spin–flip non-Hund states. The spin–flip non-Hund configurations also have a non-negligible interaction with the Hund configurations, whereas the d–d non-Hund configurations have vanishingly small interaction with the Hund configurations.

(B) The next three set of states corresponding to d–d non-Hund, spin–flip non-Hund and LMCT occur at about the same energy range of 25,000 to 75,000 cm^–1. Note that here we have only calculated the S = 4 set of states. This region will also contain transitions corresponding to S = 3 through S = 0 set of states.

(C) Not surprisingly, the lowest d–d non-Hund state is lower in energy than the lowest spin–flip non-Hund state. This is consistent with the ordering among these states calculated for the monomers in ref (14) and experimentally demonstrated by Gebhard et al.⁴¹

(D) Due to the close proximity of the LMCT, spin–flip non-Hund, and d–d non-Hund configurations, there is a considerable mixing between them. This can be seen from their wave functions given in Table S3 of the SI. Especially the mixing between the LMCT and d–d non-Hund configurations is large going up to 40% and is twice as that of the spin–flip non-Hund configurations. This suggests that a mechanism involving LMCT configurations and non-Hund configurations might have an equal or dominant contribution as opposed to the conventional magnetic coupling mechanism which involves both the LMCT and MMCT configurations.⁴¹

(E) The MLCT states are expected to occur at energies higher than the MMCT due to the high-lying unoccupied ligand antibonding orbitals. Nevertheless, we observe that the MLCT states occur at about the same transition energy as the MMCT states at 163,169 cm^–1.

4. Conclusion

In the present work, we have carried out a detailed analysis of the electronic structure of the iron–sulfur dimer. We have focused upon the changes in the metal–ligand interactions that occur upon going from a FeS monomer to dimer. The influence of the metal–metal interaction has also been analyzed. The main conclusions of the work can be summarized as follows:

(A) The ligand field splitting of the iron center in the FeS dimers shows a net decrease compared to the monomer. This is due to a combined effect of the increase in the metal–ligand π-interaction (which destabilizes the e set of orbitals to a larger extent compared to the t₂ set) and the lowering of symmetry due to the presence of thiolate and sulfide ligands.

(B) The decrease in the LF splitting can be quantitatively rationalized by the AOM model parameters e_σ and e_π. The sulfide ligands show a net increase in the e_π-interaction compared to the thiolate ligands of about 4000 cm^–1. This leads to a decrease in the 10D_q of about 1500 cm^–1. Additionally, the presence of two different ligands in the case of the FeS dimer leads to a splitting of the t₂ and e set of orbitals.

(C) Next, we have analyzed the changes that occur due to the presence of a second metal center. There are two main effects: first, the presence of the second metal center leads to a decrease in the individual metal–sulfide interaction. This is due to the equal sharing of the sulfide electron density among the two metal centers. This net decrease in the metal–sulfide interaction leads to a small, but significant, increase in the metal–thiolate interaction, compensating the total metal–ligand covalency.

(D) Second, there is a significant metal–metal interaction which is of the same order of magnitude as the metal–ligand interaction of about 4000 cm^–1. This shows that there is a strong interplay between the metal–ligand and metal–metal interaction strengths. Such an interaction could communicate changes near one metal center to the second.

(E) The CCSD natural orbital shows that there is significant orbital mixing with the sulfide and thiolate ligands of about 23%. In accordance with the AOM parameters, the sulfide ligand shows a stronger orbital mixing compared to the thiolate ligand by about 1.5:1. The t₂ family of orbitals show a larger mixing compared to the e set of orbitals.

(F) The many-particle spectrum up to 4000 cm^–1 follows the Heisenberg Hamiltonian and the CASSCF wave function shows significant influence of both the spin–flip non-Hund configurations and the MMCT configurations.

(G) The spectrum above 4000 cm^–1 and up to 100,000 cm^–1 contains a dense manifold of states originating from the d–d and spin–flip non-Hund states and the LMCT states. The close proximity of the LMCT states and the non-Hund states leads to their strong mixing which might contribute to the global magnetic exchange coupling mechanism along with the usual mechanism involving MMCT states.⁴²

(H) The spectrum beyond 100,000 cm^–1 is made up of MMCT states which are closely followed by the MLCT. The presence of a large number of states of LMCT, MLCT, and MMCT family in the spectrum up to 175,000 cm^–1 leads to a complex electronic structure which is a characteristic of FeS molecules.

Finally, the present work gives an indication of the sensitivity of the electronic structure to changes in the local ligand environment of the dimers. We have shown that the metal–ligand and metal–metal interactions together play an important role in describing the electronic structure. Such a synergistic interaction will be an important aspect of the description of the electronic structure of mixed-valent FeS dimers, which is the subject of the forthcoming work in this series.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.inorgchem.9b00974.

• Detailed description of the methodology along with additional results on the AOM and wave function analysis; input files and geometries for the various calculations (PDF)

The authors declare no competing financial interest.