Intermittent Failure of Spike Propagation in Primary Afferent Neurons during Tactile Stimulation

Abstract

Primary afferent neurons convey somatosensory information to the CNS. Low-threshold mechanoreceptors are classified as slow-adapting (SA) or rapid-adapting (RA) based on whether or not they spike repetitively during sustained tactile stimulation; the former are subclassified as Type 1 or 2 based on the regularity of their spiking. Recording in vivo from DRGs of mice, we observed irregular- and regular-spiking units consistent with SA1 and SA2 low-threshold mechanoreceptors, but some units, which we labeled “semiregular,” did not fit cleanly into the existing classification scheme. Analysis of their spiking revealed integer-multiple patterning in which spike trains comprised a fundamental interspike interval and multiples thereof. Integer-multiple-patterned spiking was reproduced by randomly removing spikes from an otherwise regular spike train, suggesting that semiregular units represent SA2 units in which some spikes are “missing.” We hypothesized that missing spikes arose from intermittent failure of spikes to initiate or to propagate. Intermittent failure of spike initiation was ruled out by several observations: integer-multiple-patterned spiking was not induced by intradermal lidocaine, was independent of stimulus modality (mechanical vs optogenetic), and could not be reproduced in a conductance-based model neuron given constant input. On the other hand, integer-multiple-patterned spiking was induced by application of lidocaine to the DRG, thus pinpointing intermittent failure of spike propagation as the basis for integer-multiple-patterned spiking. Indeed, half of all SA2 units exhibited some missing spikes, mostly at low rate (<5%), which suggests that axons are efficient in using the lowest safety factor capable of producing near-perfect propagation reliability.

SIGNIFICANCE STATEMENT The impedance mismatch at axon branch points can impede spike propagation. Reliability of spike propagation across branch points remains an open question and is especially important for primary afferents whose spikes must cross a T-junction to reach the CNS. Past research on propagation reliability has relied almost entirely on simulations and in vitro experiments. Here, recording in vivo, we linked a distinctive pattern of spiking to the intermittent failure of spike propagation at the T-junction. The rarity of failures argues that safety factor is high under physiological conditions, yet the occurrence of such failures argues that safety factor is just high enough to ensure near-perfect reliability, consistent with a good balance between propagation reliability and energy efficiency.

Introduction

Primary afferent neurons convey somatosensory information to the CNS. Unlike central neurons, whose spikes are initiated in the axon initial segment, primary afferent spikes originate in axon terminals innervating skin or other peripheral tissue. On their way to the CNS, spikes cross a T-junction in the DRG where the axon from the soma bifurcates to form peripheral and central branches. Because of the impedance mismatch associated with branch points (Goldstein and Rall, 1974), the T-junction has long been recognized as a site where spike propagation may fail (Dun, 1955; Ito and Saiga, 1959; Stoney, 1985, 1990; Lüscher et al., 1994a,b; Djouhri et al., 2001; Zhou and Chiu, 2001; Coleman et al., 2003; Fang et al., 2005; Gemes et al., 2013; Sundt et al., 2015). This could dramatically affect somatosensation by reducing the number of spikes reaching the CNS. Studies in central neurons indicate that propagation reliability is usually high (Allen and Stevens, 1994; Mackenzie et al., 1996; Cox et al., 2000; Koester and Sakmann, 2000; Raastad and Shepherd, 2003; Engel and Jonas, 2005; Foust et al., 2010; Apostolides et al., 2016; Radivojevic et al., 2017) but can vary (Swadlow et al., 1980; Bucher and Goaillard, 2011). Most experiments on propagation reliability, including those in afferents, have been conducted in vitro using cultured neurons (e.g., Lüscher et al., 1994a,b) or reduced, ex vivo preparations (e.g., Djouhri et al., 2001; Gemes et al., 2013) to facilitate electrophysiological recordings and/or imaging. Based on in vivo recordings initially conducted for purposes unrelated to spike propagation, we observed a distinctive pattern of spiking that we demonstrate to arise from propagation failure, thus providing a unique and complementary perspective on propagation reliability in vivo.

Low-threshold mechanoreceptors (LTMRs) are a subset of primary afferent neurons that encode innocuous tactile stimuli (Johansson and Vallbo, 1979; Lumpkin and Caterina, 2007; Abraira and Ginty, 2013). Adrian and Zotterman (1926) were the first to show that some LTMRs spike repetitively during sustained tactile stimulation, whereas others spike only at stimulus onset and offset. Neurons were respectively classified as slow-adapting (SA) or rapid-adapting (RA). The former are subclassified as SA1 or SA2 based on criteria that include spontaneous spiking, response to stretching, and the regularity of spiking (Chambers and Iggo, 1967). Criteria have evolved (Horch et al., 1977) with recent studies focusing on spiking regularity in part because of the difficulty applying stretch stimuli in rodents (Leem et al., 1993; Wellnitz et al., 2010). SA2 neurons spike more regularly than SA1 neurons.

To study LTMR coding properties, we applied sustained tactile stimuli to the glabrous skin of the mouse hindpaw and recorded extracellularly from LTMR somata in DRG. We observed units with irregular or regular spiking, consistent with SA1 and SA2 neurons, but we also observed units that seemed not to fit into the existing classification scheme. Analyzing these “semiregular” units revealed integer-multiple patterning: a fundamental interspike interval (ISI) predominates, but longer ISIs, corresponding to multiples of the fundamental ISI, also occur due to missing spikes. This suggests that semiregular units represent SA2 units in which some spikes are missing. Missing spikes could be due to the intermittent failure of spikes to initiate (Braun et al., 1994; Xing et al., 2001) or to propagate (Smith and Hatt, 1976; Matzner and Devor, 1993).

We sought to identify which of these two mechanisms, intermittent failure of spike initiation or propagation, accounts for the integer-multiple-patterned spiking that we observed in some LTMRs during tactile stimulation. Using a combination of computer simulations and experiments, we determined that integer-multiple-patterned spiking results from intermittent failure of spikes to propagate through the axon bifurcation (T-junction) in the DRG. Our data demonstrate that, in vivo, safety factor is high enough that nearly all spikes are reliably propagated but is low enough that failures occasionally occur. This suggests that excitability is optimized to ensure faithful yet efficient spike propagation under physiological conditions.

Materials and Methods

Transgenic mice.

All procedures were approved by the Animal Care Committee of The Hospital for Sick Children. Advillin-Cre mice (gift from Fan Wang, Duke University) were crossed with Ai32 mice (The Jackson Laboratory, #024109) to create Advillin^Cre/+;ChR2^loxP/+ mice in which channelrhodopsin-2 (ChR2) is expressed in all types of primary afferent neurons, as previously described (Zhu et al., 2015). For Figure 3C, we included data from PV^Cre/+;ChR2^loxP/+ mice, which express ChR2 in a subset of primary afferent neurons (de Nooij et al., 2013). These mice were created by crossing B6 PV-Cre (The Jackson Laboratory, #017320) with Ai32 mice. All optogenetics data reported in Figure 8 come from Advillin^Cre/+;ChR2^loxP/+ mice.

Figure 3.

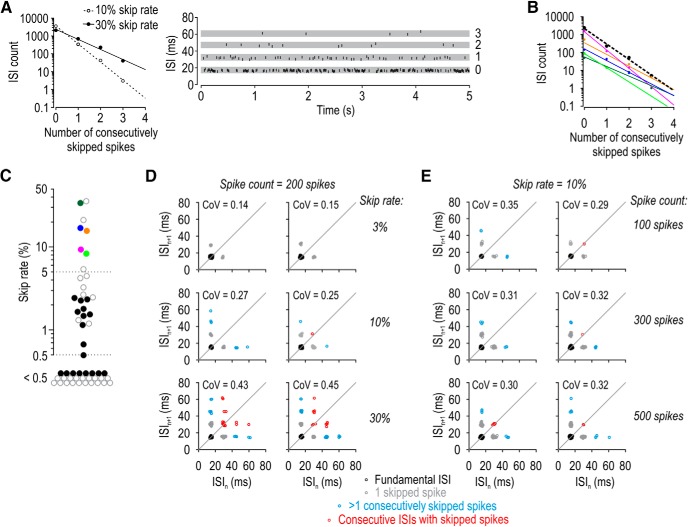
Spikes are skipped randomly. A, For synthetic spike trains with 10% or 30% of their spikes randomly removed (open and filled symbols, respectively), the ISI count decayed exponentially as a function of the number of consecutively skipped spikes. The slope of lines fitted to the log-transformed ISI counts reflects the skip rate. Inset, How ISIs were classified. The number next to each gray strip indicates the number of consecutively skipped spikes. B, ISI counts decayed exponentially for all five semiregular units, each shown in a different color; fits were excellent in each cell (r² > 0.93). Dashed line indicates fit to ISI counts pooled across all 5 semiregular units. C, The proportion of spikes skipped in all regular and semiregular units (n = 23) tested with 5-s-long stimuli (filled symbols; colors correspond to units in B). Open symbols represent additional regular and semiregular units (n = 29) tested with 1-s-long stimuli. D, Return plots for synthetic spike trains in which 3%, 10%, or 30% of spikes were removed from a train of 200 spikes. Because long ISIs caused by consecutively skipping >1 spike (blue points) and consecutive ISIs with missing spikes (red points) occur infrequently, such events may not be observed when the skip rate is low. Two sample return plots are shown for each condition to illustrate the variability. E, Same analysis as in D, but with 10% of spikes randomly removed from trains of 100, 300, or 500 spikes to illustrate that rare events may not be observed when spike count is low.

Figure 8.

Propagation failure rate is independent of stimulus modality. A, Integer-multiple-patterned spiking in the same neuron illustrated in Figure 7, but now stimulated optogenetically with 2 mW/mm² blue (455 nm) light applied to the hindpaw, which evoked 52 spikes/s. Corresponding ISI return map is shown. Based on all responses from the unit shown in A, (B) the skip rate did not differ significantly between early- and late-phase responses (t₍₃₎ = −0.83, p = 0.47, paired t test) and (C) the slope of the regression line did not differ significantly from horizontal (slope = −0.022, p = 0.10, one-sample t test). D, Sample of optogenetically evoked spiking in another unit. Because of the high skip rate, ISIs with >1 consecutively skipped spike and consecutive ISIs with skipped spikes are evident. E, Based on analysis of 10 units responsive to mechanostimulation and photostimulation, there was no significant difference in the skip rate between stimulus modalities (Z = −0.31, p = 0.84, signed rank test) (left). The skip rate during photo- and mechano-evoked spiking expressed as a ratio (right) did not differ significantly from unity (t₍₅₎ = 0.038, p = 0.97, one-sample t test) but did differ significantly from zero (t₍₅₎ = 3.60, p = 0.016). The 95% CI is shown. Overall, these data argue in favor of skipping due to intermittent failure of spike propagation, and against skipping due to intermittent failure of spike initiation.

Surgery.

Mice of either sex (∼12–16 weeks old) were anesthetized with urethane (1.6 g/kg i.p.). A tracheotomy was performed to mitigate breathing problems. Briefly, the trachea was exposed through a midline incision (∼15 mm) between the lower jaw and upper thorax. The trachea was incised just below the larynx, and a short length of PE60 tubing (Becton Dickinson) was inserted and fixed in place with a knot. The incision was sutured. No ventilation was applied. A laminectomy was then performed to expose the L4 DRG and adjacent spinal cord. L4 DRG was targeted because it is the largest DRG in mouse, and is a major contributor to the sciatic nerve, which innervates the hindpaw (Rigaud et al., 2008).

In vivo extracellular single-unit recording.

A parylene-insulated tungsten microelectrode (A-M Systems, #573500) was inserted into the L4 DRG. Signals were amplified, digitized at 40 kHz, and high-pass filtered at 300 Hz using an OmniPlex Data Acquisition System (Plexon). Single units were isolated using Offline Sorter version 4 software (Plexon) (for details, see Fig. 4) and analyzed with MATLAB (The MathWorks).

Figure 4.

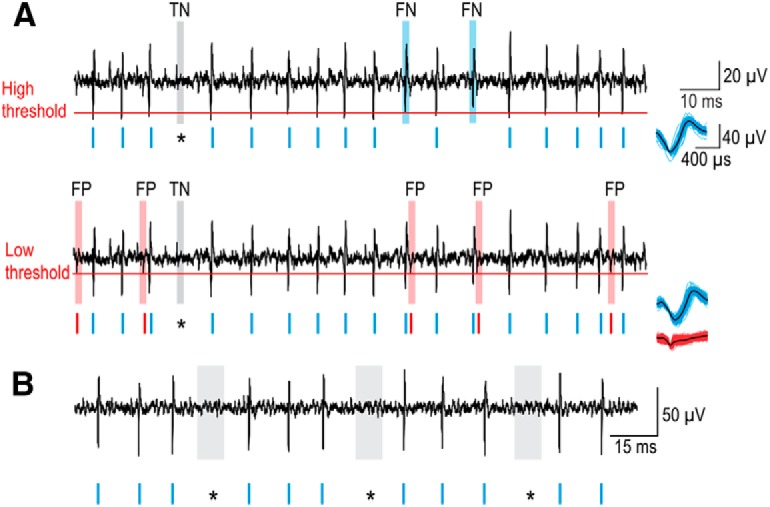
Methodology to ensure that skipped spikes are not an artifact. A, Spikes (blue rasters) were identified by applying a threshold (red line) to the continuous voltage recording (black). A high threshold (top) correctly detects spikes (true positives) but may fail to detect some spikes (false negatives, FN, blue shading). True negatives (TN, gray shading) correspond to where an expected spike is missing. Lowering the threshold (bottom) prevents false negatives but leads to detection of nonspikes (red rasters and shading). These false positives (FP) are distinguished from true positives based on their waveform, as shown on the right. Thus, using a low threshold to avoid false negatives and spike sorting to separate true and false positives, we verified that gaps (*) in otherwise regular spiking were indeed true negatives (i.e., no spike occurred). B, A continuous recording from another unit showing that gaps contain no undetected spikes. Smaller-than-normal spikes (as might occur if spike propagation failed close to the soma) are not evident during gaps.

Stimulation.

Gentle brushing was used as a search stimulus to identify LTMRs innervating the glabrous skin of the hindpaw. The receptive field was subsequently mapped with von Frey filaments. Precise and reproducible mechanostimulation was applied using a computer-controlled mechanical stimulator (Aurora Scientific, model 300C-I) positioned with a micromanipulator (tip diameter = 1 mm). Photostimulation was provided by a fiber-coupled 455 nm LED (Thorlabs) positioned with a micromanipulator. The timing and intensity of both types of stimuli were controlled by a Power1401 computer interface and Signal version 5 software (Cambridge Electronic Design). The timing of each stimulus was sent as a trigger to Plexon to align neural responses to stimuli. Conduction velocity was calculated by dividing the distance between the stimulation and recording sites by the latency to the first spike from the onset of the strongest mechanical stimulus that was tested.

Spike train analysis.

The coefficient of variation (CoV) $\left(\text{CoV}=\frac{{\text{SD}}_{\text{ISI}}}{{\text{mean}}_{\text{ISI}}}\right)$ was calculated from the ISIs measured from recorded spike times. ISI return maps show each ISI (designated n) plotted against the next ISI (designated n + 1) to depict the relationship between consecutive ISIs (Siegel and Read, 1993; Szucs, 1998). Skip rate was calculated as follows:

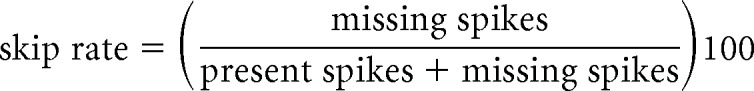Synthetic spike trains.

We used the gamma distribution probability function to specify different distributions from which we randomly drew ISIs to generate synthetic spike trains (Maimon and Assad, 2009). ISI distributions are generally well fit by a gamma distribution probability function defined as follows:

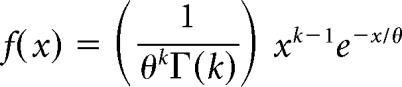where k is the shape parameter, θ is the scale parameter, and Γ is the gamma function, as follows:

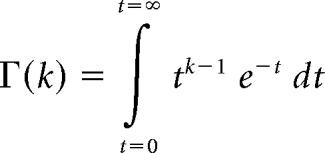Increasing k generates a narrower distribution (lower CoV). Dividing θ by k keeps the mean ISI constant as k is varied. Synthetic spike trains were generated from consecutively drawn ISI values. Thereafter, a subset of spikes was randomly removed to generate integer-multiple-patterned spiking.

Biophysical model for spike initiation.

We used the Morris–Lecar model with parameters set to produce a neuronal oscillator with Class 2 excitability (Prescott et al., 2008). The model is defined as follows:

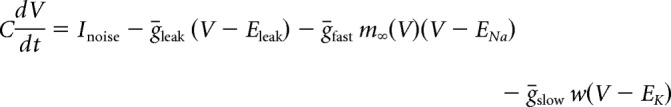where C is capacitance, V is membrane potential, I_noise represents noisy fluctuations in current and, as follows:

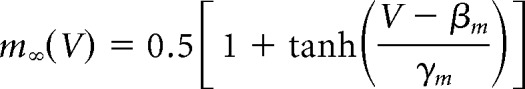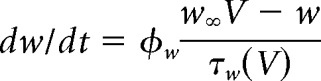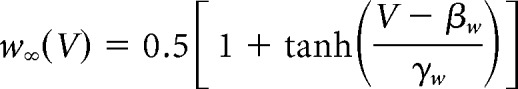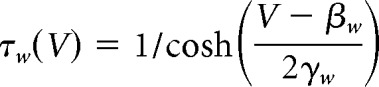The sodium conductance g_Na is assumed to activate instantaneously with changes in V, whereas the potassium conductance g_K is gated by the slower recovery variable w. Parameter values were as follows: E_Na = 50 mV, E_K = −100 mV, E_leak = −70 mV, ḡ_fast = 20 mS/cm², ḡ_slow = 20 mS/cm², g_leak = 2 mS/cm², φ_w = 0.15, C = 2 μF/cm², β_m = −1.2 mV, γ_m = 18 mV, γ_w = 10 mV, β_w = −13 mV. Noisy fluctuations in current were produced through an Ornstein–Uhlenbeck process as follows:

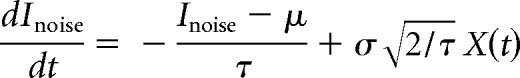where the current I_noise drifts back to the average μ with time constant τ = 1 ms, and X is a random number drawn from a normal distribution with 0 mean and unit variance, which is then scaled so that the SD of I_noise corresponds to σ.

Statistical analysis.

Statistical analysis was performed using SigmaPlot version 11.0. An appropriate parametric test was used when data were normally distributed (according to the Shapiro–Wilk test); otherwise, the comparable nonparametric test was used. Each test is identified in Results. For comparisons between CoV of three separate groups, a one-way ANOVA and post hoc Holm–Sidak tests were used (see Fig. 1E). For comparisons between two groups, an unpaired t test (subset of Fig. 1E) or Mann–Whitney test (see Fig. 1F) was used. For comparisons within the same group, paired t tests (see Figs. 7B,D, 8B) or the signed ranks test (see Figs. 7D, 8E) were used. To determine whether the skip rate varied significantly with firing rate (see Figs. 7C,E, 8C), the slope of the fitted line was compared with horizontal (slope of 0) using a one-sample t test. To determine whether the skip rate ratio differed significantly from unity for early- and late-phase spiking (see Fig. 7D, right) or for mechano- and photo-evoked spiking (see Fig. 8E, right), a one-sample t test was used to compare to unity or to 0, as reported in Results.

Figure 1.

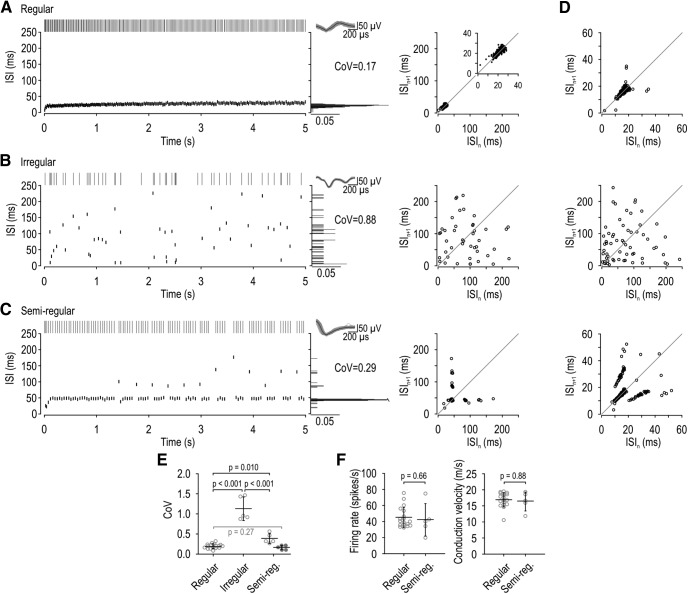
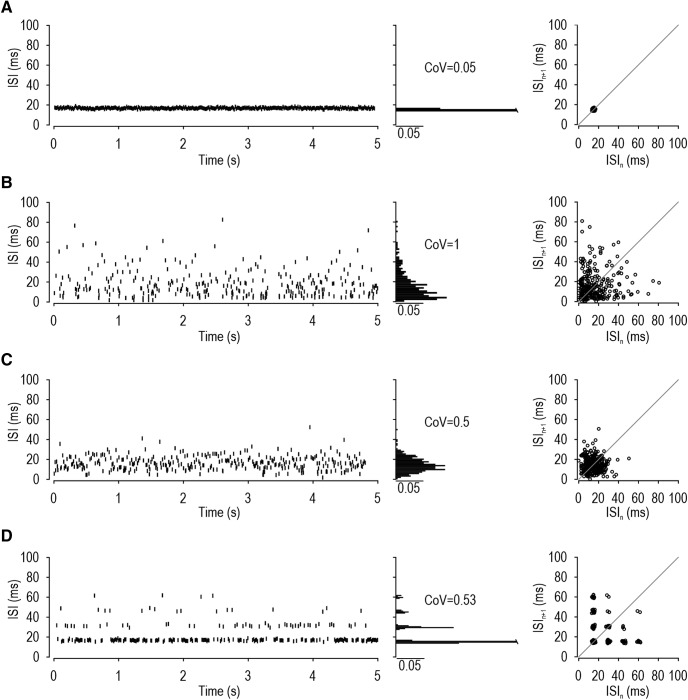
Spike patterns in LTMRs evoked by 5-s-long steps of constant force applied to the hindpaw. A–C, Top left, Rasters show representative spike trains. Bottom left, Corresponding ISIs are plotted against time. Right, Spike waveform. Middle, Histograms show ISI distribution and the CoV. Right, ISI return maps show the relationship between consecutive ISIs by plotting ISI_n against ISI_n+1. A, In regular units, ISIs are tightly clustered on the ISI histogram and return plot. B, In irregular units, ISIs are broadly distributed. C, In semiregular units, there is a dominant ISI, but some spikes occur with an ISI 2–3 × longer than (i.e., an integer multiple of) the dominant ISI. This leads to a conspicuous multimodal distribution on the ISI histogram and to clusters on the ISI return plot. D, Additional sample ISI return plots from a regular (top), irregular (middle), and semiregular (bottom) unit. E, Summary of the CoV measured from the maximal response of each unit. Based on spike patterns illustrated in A–C, 18 neurons were classified as regular (0.19 ± 0.01, mean CoV ± SEM), 5 as irregular (1.13 ± 0.13), and 5 as semiregular (0.38 ± 0.06). CoV differed significantly across groups (p < 0.001, one-way ANOVA). Results of post hoc Holm–Sidak tests are reported in black on the graph. Removing ISIs with one or more missing spikes and recalculating the CoV in semiregular units (filled symbols) yielded a lower CoV (0.16 ± 0.02) that was not significantly different from the CoV in regular units (t₍₂₁₎ = 1.13, p = 0.27, unpaired t test). F, There was no significant difference in the firing rate (U = 38.5, p = 0.66, Mann–Whitney test) or conduction velocity (U = 42.5, p = 0.88, Mann–Whitney test) between regular and semiregular units.

Figure 7.

Spike propagation failure is not activity-dependent at physiological firing rates. The activity dependence of skipping was assessed in two ways: by comparing the early and late phase of each response (B,D) and by assessing changes in skip rate as a function of firing rate (C,E). A, Sample responses from a semiregular unit to 10 g (top) and 20 g (bottom) mechanical stimulation. Average firing rate (calculated as number of spikes/period until last spike) was 50 and 60 spikes/s, respectively. Early and late phase of responses are indicated. Right, Corresponding ISI return maps. Based on all responses from the unit shown in A, (B) skip rate did not differ significantly between early- and late-phase responses (t₍₇₎ = 1.24, p = 0.26, paired t test), and (C) skip rate did not vary with firing rate; that is, the slope of the regression line (0.16) did not differ significantly from horizontal (p = 0.12, one-sample t test). D, Based on the maximal response of each unit, the skip rate did not differ significantly between the early- and late-phase responses of semiregular units (t₍₄₎ = 1.50, p = 0.21, paired t test, black), regular units (t₍₁₇₎ = −1.00, p = 0.33, paired t test, gray), or all units combined (Z = 1.21, p = 0.24, signed rank test) (left). Right, Skip rates replotted as a ratio of late versus early phase responses; units without skipping were excluded. This ratio did not differ significantly from unity (t₍₁₄₎ = 1.40, p = 0.18, one-sample t test), but since that test was underpowered (d = 0.26), it is helpful to consider the 95% CI, which tells us that any activity-dependent increase in skip rate must be <134%. E, Also based on the maximal response of each unit, the slope of the regression line did not differ significantly from horizontal (slope = −0.013, p = 0.25, one-sample t test). Skip rate was log transformed before the linear regression, and firing rate was corrected for the number of missing spikes so that variations in skip rate do not confound the analysis.

Results

In vivo single-unit recordings reveal three spike patterns among SA LTMRs

Recording in vivo from mouse DRG, we thoroughly characterized 35 SA LTMRs using a 5-s-long stimulus protocol. The conduction velocity of 15.3 ± 0.6 m/s (mean ± SEM) is consistent with Aβ fibers (Walcher et al., 2018). Seven of these SA units were excluded because they produced too few spikes to ensure reliable analysis; specifically, excluded cells did not sustain firing for >1 s or had a maximal firing rate <5 spikes/s, which amounted to <25 spikes/trial. RA units were also recorded but are not considered in this study.

Three spike patterns were observed. The majority of units (64%; 18 of 28 cells) had a regular pattern (Fig. 1A) consistent with SA2 classification. Their ISI distributions were narrow and unimodal (low CoV), and ISI return plots exhibited points tightly clustered near the diagonal. Other units (18%; 5 of 28 cells) displayed an irregular spike pattern (Fig. 1B) consistent with SA1 classification. Their ISI distributions were broad (high CoV), and ISI return plots exhibited widely scattered points. All SA1 units had receptive fields in the digits, consistent with past observations (Johansson and Vallbo, 1979; Leem et al., 1993), but we tended to search for units with receptive fields located farther back on the paw because of the difficulty positioning the mechanical stimulator on digits, thus explaining the disproportionate representation of SA2 units in our sample. The remaining units (18%; 5 of 28 cells) exhibited a spiking pattern that we tentatively labeled “semiregular” (Fig. 1C). These neurons exhibited ISIs with a relatively low CoV; otherwise, regular spiking was punctuated by gaps that were 2, 3, or sometimes 4 times wider than the typical ISI, consistent with integer-multiple patterning (see Introduction). The occurrence of longer-than-expected ISIs is evident in the multimodal ISI distribution and the appearance of multiple clusters on the ISI return plot. Figure 1D shows return plots from additional units representing each spike pattern. The top and bottom panels illustrate how the distribution of points can “smear” along the diagonal due to slow changes in firing rate caused by adaptation. The top panel also shows that regular units occasionally exhibit data points that deviate from the diagonal, but such points are too few to produce a conspicuous integer-multiple pattern. Although the spiking patterns described here suggest that units fall into three groups, other analyses ultimately reveal that regular and semiregular units fall along a continuum (see below).

Figure 1E summarizes the CoV for each unit (calculated from its maximal response) and group averages. The average CoV varied significantly across units with different spiking patterns (F_(2,25) = 91.44, p < 0.001, one-way ANOVA). Post hoc Holm–Sidak tests showed that the CoV in irregular units (1.13 ± 0.13) is significantly higher than in regular units (0.19 ± 0.01; p < 0.001) or semiregular units (0.38 ± 0.06; p < 0.001). The CoV of regular and semiregular units also differed significantly (p = 0.01), although most semiregular units would be classified as regular if an arbitrary criterion of CoV < 0.5 was applied. That said, when the CoV for semiregular units was recalculated after removing longer-than-expected ISIs (Fig. 1E, filled symbols), their CoV (0.16 ± 0.02) was no longer significantly different from regular units (t₍₂₁₎ = 1.13, p = 0.27, unpaired t test), thus revealing that longer-than-expected ISIs account for the modestly elevated CoV seen in semiregular units. This led us to suspect that semiregular units represent regular units in which some spikes are “missing” (see below). Consistent with this hypothesis, regular and semiregular units did not differ significantly in their maximal firing rate (U = 38.50, p = 0.66, Mann–Whitney test) or conduction velocity (U = 42.50, p = 0.88, Mann–Whitney test) (Fig. 1F), nor did we notice obvious differences in any other response properties (e.g., receptive field distribution).

Integer-multiple-patterned spiking is explained by randomly missing spikes

To compare with the experimentally observed spiking patterns summarized in Figure 1, we created synthetic spike trains. By drawing ISI values from differently shaped gamma distributions, as defined by k (see Materials and Methods), we generated spike trains with varying degrees of regularity: k = 500 yielded regular spiking (CoV = 0.05; Fig. 2A), k = 1 yielded irregular spiking (CoV = 1.0; Fig. 2B), and k = 4 yielded spiking with intermediate regularity (CoV = 0.5; Fig. 2C). None of these spike trains reproduced the multimodal ISI distributions evident on the ISI histograms or return plots of semiregular units. The only way we could reproduce integer-multiple-patterned spiking was by randomly removing spikes from a regular spike train (Fig. 2D). Although the CoV for spike trains in Figure 2C, D are nearly identical, the ISI histograms and return maps are distinct. Moreover, randomly removing 30% of spikes from a regular train increased the CoV from 0.05 to 0.53, consistent with our observation that missing spikes account for the difference in CoV between regular and semiregular units (Fig. 1E).

Figure 2.

Reproduction of different spiking patterns in synthetic spike trains. Spike trains were generated by randomly drawing ISI values from a gamma distribution whose shape is controlled by parameter k. A, Regular pattern: k = 500, CoV = 0.05. B, Irregular pattern: k = 1, CoV = 1.0. C, Intermediate regularity: k = 4, CoV = 0.5. Despite an elevated CoV value, this spike train did not reproduce the multimodal ISI histogram or patterned ISI return plot characteristic of semiregular units (compare with Fig. 1C,D). D, The semiregular (integer-multiple) spike pattern was reproduced by randomly removing 30% of spikes from the regular (k = 500) spike train. Removing spikes caused the CoV to increase to 0.53.

These results show that randomly removing spikes can produce integer-multiple patterning, but the random nature of skipping has additional implications for the ISI distribution. Consider that if 30% of spikes are randomly removed, the probability of removing n consecutive spikes is 0.3ⁿ; in other words, the probability of observing ISIs formed by skipping n consecutive spikes falls off exponentially. With ISI counts plotted on a log scale, this relationship is described by a line whose slope corresponds to the logarithm of the skip rate (Fig. 3A). Exponential relationships were observed in experimental data (Fig. 3B) based on all trials for each semiregular unit (solid colored lines) and for data pooled across all units (dashed line), which argues that the skipping observed in real neurons is random. Other relationships arise when skipping is nonrandom (Gu et al., 2011).

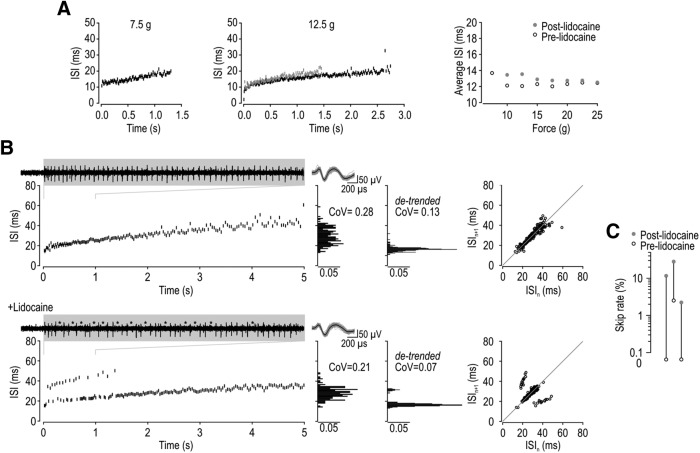
Figure 3C summarizes the proportion of skipped spikes for all regular and semiregular units and includes data from an additional 29 SA2 units tested with shorter (1-s-long) tactile stimuli. All 8 units identified as semiregular based on their conspicuous integer-multiple-patterned spiking fell at one end of the distribution, with a skip rate >5%. Half of all units (52%, 27 of 52) exhibited a skip rate <0.5%, whereas one-third (33%, 17 of 52) exhibited a skip rate between 0.5% and 5%. From this, we conclude that semiregular units are indeed SA2 units with a high skip rate, but many SA2 units exhibit some skipping.

Next, we sought to address subtle differences between the integer-multiple patterning in our initial simulations versus experiments. Specifically, the return plot in Figure 2D shows ISIs in which >1 spike is consecutively skipped and ISI sequences in which consecutive ISIs have skipped spikes, but such events were not obvious in experimental data (compare with Fig. 1). This is because the probability of such events diminishes rapidly as the skip rate and/or spike count are reduced, as illustrated by additional simulations in which these parameters were systematically varied (Fig. 3D,E), and as expected from the exponential relationship described above. Accordingly, ISIs with >1 consecutively skipped spikes or consecutive ISIs with skipped spikes may not occur during a typical response of ∼200 spikes and a skip rate <30%, but such events are evident under the appropriate conditions (see Fig. 8D).

Having established that half of all SA2 units experience skipped spikes, and that randomly skipped spikes can account for integer-multiple patterning, the remainder of our study focused on identifying the basis for skipped spikes.

Skipped spikes are not an artifact of failed spike detection

Figure 4A shows a sample recording to illustrate that integer-multiple-patterned spiking could arise from failure to detect some spikes (false negatives) if the detection threshold is set too high (Fig. 4A, top). We prevented this by setting the detection threshold low (Fig. 4A, bottom), but that can result in the detection of noisy voltage fluctuations (false positives). False positives were separated from true positives by clustering the waveforms of all detected events (Fig. 4A, right). The timing of events thus classified as true or false positives was then visually compared with the original voltage recordings to verify that the gaps responsible for integer-multiple patterning contained no undetected spike and were, therefore, true negatives. Our multistep analysis ensured that skipped spikes are authentic, not an artifact of poor spike detection/sorting. The same detection/sorting/verification process was applied to all regular and semiregular units. Figure 4B shows another example (see also Fig. 6B).

Figure 6.

Intermittent failure of spike propagation accounts for integer-multiple-patterned spiking. A, Injection of 1%–2% lidocaine intradermally into the hindpaw increased the mechanical threshold for spiking and reduced the duration and rate of spiking in 3 of 3 units tested, but it did not induce skipping in any units. Sample ISI plots are shown for a typical unit during 7.5 and 12.5 g stimulation before (black) and after (gray) 2% lidocaine. Right, Average ISI calculated from the initial 1 s of spiking for all forces applied. B, Application of 1%–2% lidocaine directly onto the DRG converted regular spiking (top) into semiregular spiking (bottom) in 3 of 3 units tested. Lidocaine initially blocked all spikes, but skipped spikes were evident during recovery. Insets, Continuous recording over interval indicated on ISI plot with skipped spikes indicated by asterisks. In the illustrated unit, adaptation during the response caused progressive lengthening of the ISI, causing peaks on the ISI histogram to “smear.” Smearing was corrected in histograms on the right by detrending the response (i.e., subtracting the slow change estimated by a fitted monoexponential curve). Return plots still show clusters despite smearing. C, Proportion of skipped spikes before and after adding lidocaine.

Intermittent failure of spike initiation does not account for the pattern of skipped spikes

Integer-multiple-patterned spiking can arise if membrane potential periodically approaches threshold closely enough that threshold crossings occur probabilistically under noisy conditions: noise can either encourage spike initiation during a subthreshold oscillation or discourage spike initiation during a suprathreshold oscillation. Either way, threshold crossings occur preferentially near the peak of each perithreshold oscillation, but not on every cycle, thus causing spikes to occur at intervals that correspond to multiples of the oscillation period (Braun et al., 1994; Xing et al., 2001). Membrane potential oscillations could arise through oscillatory input (Rose et al., 1967; Longtin, 1991) and/or oscillatory spike initiation dynamics (Braun et al., 1994; Xing et al., 2001). Since we applied mechanical stimuli as steps of constant force rather than as an oscillation (e.g., vibration) or pulse train, our stimuli lack an oscillatory component. It is conceivable that a rhythmic process, such as blood flow, could change the biomechanical properties of the skin and thus modulate the effective stimulus force in an oscillatory manner, but we consider this unlikely, especially since skipping is observed over a broad range of firing rates and stimulus intensities (see Fig. 7), and during optogenetic stimulation (see Fig. 8). On the other hand, the inability of SA neurons to maintain repetitive spiking below a critical frequency, evident from spike trains ending abruptly during adaptation (see Fig. 7A, top), points to spike initiation through a subcritical Hopf bifurcation (Prescott et al., 2008), which is associated with noise-induced membrane potential oscillations (Rho and Prescott, 2012; Ratté et al., 2014). In other words, SA2 afferents appear to have oscillatory spike initiation dynamics.

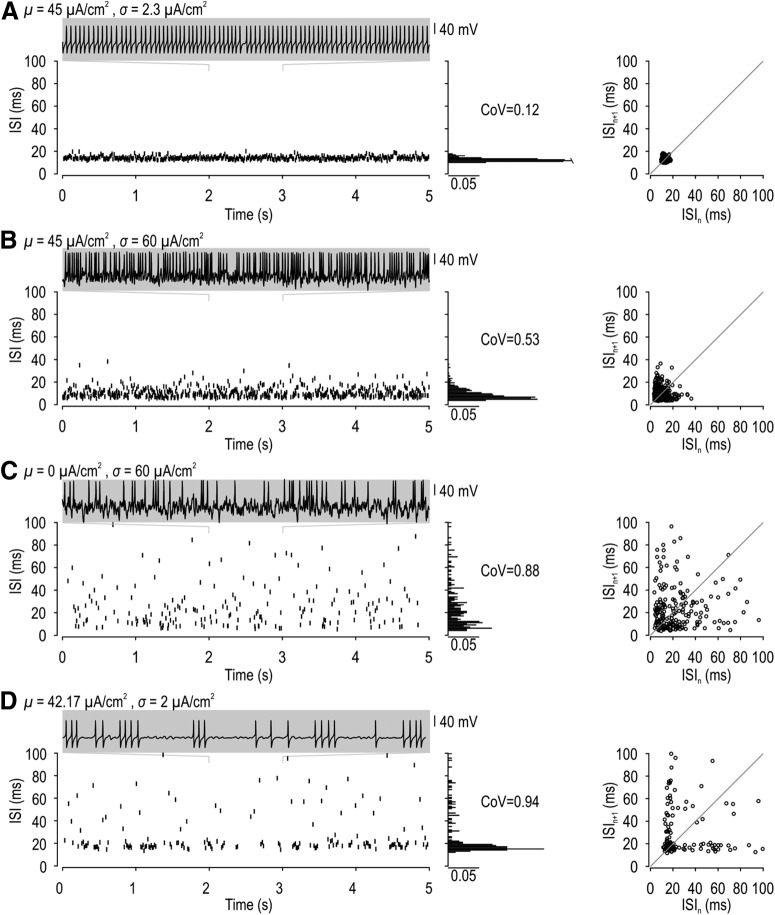
To test whether intermittent failure of spikes initiated through a subcritical Hopf bifurcation could account for integer-multiple-patterned spiking under noisy conditions, we tried to reproduce the skipping pattern in a conductance-based model with Class 2 excitability (see Materials and Methods). The model neuron was stimulated with noisy current defined by an average intensity μ and SD σ. When average current was suprathreshold, spiking was regular in the presence of weak noise (Fig. 5A) but became irregular as noise was increased (Fig. 5B). High-intensity noise added to average subthreshold current caused even greater irregularity (Fig. 5C). Regardless of whether noise disrupted repetitive spiking driven by suprathreshold input (Fig. 5B) or evoked spiking by adding fluctuations to subthreshold input (Fig. 5C), the ISI distribution was broadened (like Fig. 2C) but remained unimodal (unlike Fig. 2D). We retested the model neuron with diverse combinations of μ and σ to identify any conditions under which integer-multiple-patterned spiking could occur. The only other spiking pattern we observed was bursting when average current was exquisitely close to threshold and noise was weak (Fig. 5D). Unlike integer-multiple-patterned spiking, bursting comprised periods of regular spiking interrupted by long periods of quiescence that are inconsistent with the low probability of consecutively skipped spikes when skipping occurs randomly (Fig. 3). These long interburst gaps translate into a skewed ISI distribution, consistent with intermittent switching between two bistable states, namely, quiescence and repetitive spiking, rather than a multimodal ISI distribution. Furthermore, bursting was observed in the model neuron only within an exquisitely narrow stimulus range, consistent with previous studies (Huaguang et al., 2015), but inconsistent with our observation of this integer-multiple patterning over a broad range of stimulus intensities (see below). All of this argues against integer-multiple-patterned spiking being due to the intermittent failure of spike initiation under the stimulus conditions we tested.

Figure 5.

Conductance-based model cannot reproduce integer-multiple-patterned spiking based on intermittent failure of spike initiation. Noisy current with different average (μ) and SD (σ) was applied to a conductance-based model that behaves as an oscillator (see Materials and Methods). A, With suprathreshold stimulation (μ = 45 μA/cm²) plus weak noise (σ = 2.3 μA/cm²), spikes occur with a regular pattern (CoV = 0.12). B, With suprathreshold stimulation (μ = 45 μA/cm²) plus strong noise (σ = 60 μA/cm²), spikes occur irregularly (CoV = 0.53). C, With subthreshold stimulation (μ = 0 μA/cm²) plus strong noise (σ = 60 μA/cm²), spikes also occur irregularly (CoV = 0.88). D, With perithreshold stimulation (μ = 42.17 μA/cm²) and weak noise (σ = 2 μA/cm²), spikes occurred in bursts defined by periods of regular, high-rate spiking interrupted by long periods of quiescence. The long periods of quiescence are inconsistent with random spike skipping (Fig. 3) and yield an L-shaped distribution on the ISI return plot rather than discrete clusters. Integer-multiple-patterned spiking was not observed in this model under any stimulus condition.

To experimentally test the effects of modulating spike initiation, we injected lidocaine (1%–2%, 10 μl) intradermally to partially block sodium channels in the axon terminals where spikes are normally initiated. Instead of inducing integer-multiple-patterned spiking, peripheral lidocaine increased the stimulus intensity required to evoke spiking and reduced the spike rate evoked by a given stimulus (Fig. 6A). These effects were observed in 3 of 3 neurons tested, and affirm that intermittent failure of spike initiation does not account for skipped spikes during sustained, nonoscillating tactile stimulation.

Intermittent failure of spike propagation accounts for the pattern of skipped spikes

Integer-multiple patterning has also been linked to intermittent failure of spike propagation (Smith and Hatt, 1976; Matzner and Devor, 1993): spikes are initiated at regular intervals, but some of those spikes ultimately fail to propagate to the recording site. We therefore tested whether intermittent failure of spike propagation accounts for integer-multiple patterning. To this end, we applied lidocaine to the exposed DRG to discourage spike propagation by partially blocking sodium channels in and around the T-junction. In 3 of 3 neurons tested, integer-multiple-patterned spiking was induced in neurons that spiked regularly before lidocaine (Fig. 6B). Specifically, spiking was completely blocked shortly after lidocaine application, but, as the local lidocaine concentration decreased over time, integer-multiple-patterned spiking was observed before the cell returned to its original regular-spiking pattern. Figure 6C summarizes the skip rate before lidocaine injection and during the post-lidocaine trial exhibiting integer-multiple patterning. These data demonstrate that partial blockade of sodium channels near the T-junction is sufficient to cause intermittent failure of spike propagation, and that this reproduces the integer-multiple patterning seen in semiregular units. These results support the view than semiregular units are simply regular (SA2) units that have a high skip rate.

Propagation failure is not activity-dependent at physiological firing rates

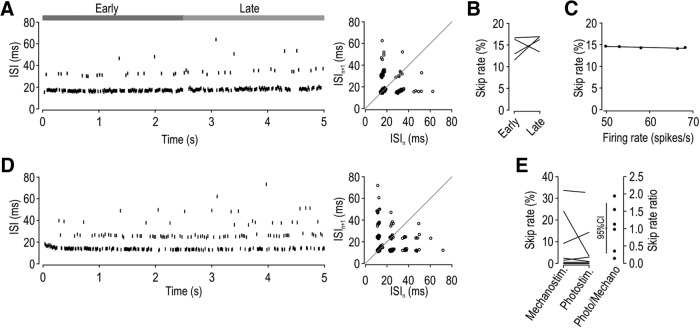
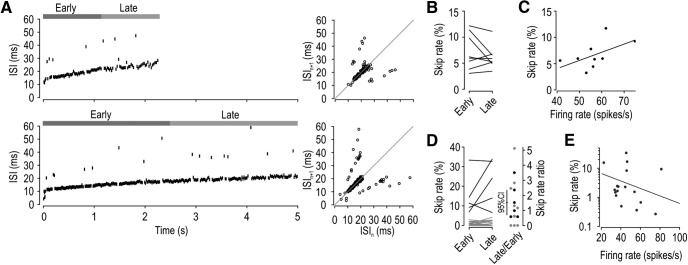
By stimulating neurons with high-rate pulse trains to determine how fast neurons can initiate and propagate a spike in response to each stimulus pulse, past studies found that spike propagation failure is activity-dependent (for review, see Debanne et al., 2011). To investigate this in our dataset, we asked whether the skip rate differs between the early and late phase of each response or whether it varies with firing rate (evidenced by comparing across responses to different stimulus intensities). Figure 7A illustrates sample responses from a unit with a high skip rate. Analysis of this unit revealed that the skip rate did not differ significantly between the early and late phase of each response (t₍₇₎ = 1.24, p = 0.26, paired t test) (Fig. 7B), nor did it vary significantly with firing rate; that is, the slope (0.16) of the regression line did not differ significantly from horizontal (t = 1.75, p = 0.12, one-sample t test) (Fig. 7C). Based on the maximal response from each unit, we found that skip rate did not differ significantly between the early and late phase of responses in semiregular units (t₍₄₎ = 1.50, p = 0.21, paired t test), regular units (t₍₁₇₎ = −1.00, p = 0.33, paired t test), or the group as a whole (Z = 1.21, p = 0.24, signed ranks test) (Fig. 7D). Consistent with this, the ratio of skip rates during early versus late phase responses did not differ significantly from unity (t₍₁₄₎ = 1.40, p = 0.18, one-sample t test), nor did skip rate vary significantly with firing rate; that is, the slope (−0.01) of the regression line did not differ significantly from horizontal (t = −1.20, p = 0.25, one-sample t test) (Fig. 7E). Unlike the variability in skip rate across neurons (Fig. 3C), data in Figure 7 demonstrate that the skip rate within a given neuron is consistent over time and across stimulus intensities. This argues that the T-junction does not operate as a low-pass filter at physiological firing rates, but our data do not rule out that skipping may increase when neurons are driven to spike at higher-than-normal rates (see Discussion).

Propagation failure is independent of stimulus modality

In some units, spikes could be evoked optogenetically via photostimulation of channelrhodopsin-2 (ChR2) (see Materials and Methods). The mechanopotential experienced by peripheral LTMR axon terminals remains unclear because of the prohibitive difficulty recording intracellularly from the axon, but the photopotential induced by ChR2 activation is known to be sustained and nonoscillatory. Such depolarization is not associated with intermittent failure of spike initiation (Fig. 5); therefore, we predicted that (1) skipped spikes should not occur during photo-evoked spiking if skipping is due to intermittent failure of spike initiation. On the other hand, we predicted that (2) the skip rate should, for a given neuron, be similar for each stimulus modality if skipping is due to intermittent failure of spike propagation.

Figure 8A shows integer-multiple-patterned spiking evoked by photostimulation in the same unit shown in Figure 7. Like for mechanically evoked spiking, the proportion of skipped spikes did not differ significantly between the early and late phase of each response (t₍₃₎ = −0.83, p = 0.47, paired t test) (Fig. 8B), nor did it vary significantly with firing rate: that is, the slope (−0.02) of the fitted line did not differ significantly from horizontal (t = −2.36, p = 0.10, one-sample t test) (Fig. 8C). Figure 8D illustrates another sample response evoked optogentically in a different unit; because of the high skip rate, the return plot exhibits ISIs with >1 consecutively skipped spikes and consecutive ISIs with skipped spikes, as in simulation data (compare with color points on Fig. 3D,E). Based on all regular and semiregular spiking units that responded to photostimulation (n = 10), the skip rate within a given unit did not differ significantly between stimulus modalities (Z = −0.31, p = 0.84, signed rank test) (Fig. 8E). The skip rate during photo- and mechano-evoked spiking expressed as a ratio did not differ significantly from unity (t₍₅₎ = 0.038, p = 0.97, one-sample t test), consistent with Prediction 2, but it did differ significantly from zero (t₍₅₎ = 3.60, p = 0.016, one-sample t test), inconsistent with Prediction 1. Overall, these results support our conclusion that skipping is due to intermittent failure of spike propagation and that the skip rate is consistent within a given neuron, across stimulus intensities and modalities, despite its variability across neurons.

Discussion

This study was triggered by our observation of integer-multiple-patterned spiking in a subset of LTMRs recorded in vivo. We show that integer-multiple patterning results from the random “skipping” of spikes in an otherwise regular spike train (Fig. 2). Several pieces of evidence point to the intermittent failure of spike propagation, rather than spike initiation, as the basis for this distinctive pattern. First, partial blockade of sodium channels in the DRG induced skipping, whereas sodium channel blockade in axon terminals did not (Fig. 6). Second, a neuron oscillator model stimulated with nonoscillatory input could not initiate spikes with the appropriate skipping pattern (Fig. 5). Third, different stimulus modalities, mechanical and optogenetic, evoked the same proportion of skipped spikes in a given neuron (Fig. 8), consistent with skipping that originates downstream of the transduction step. By identifying intermittent failure of spike propagation as the basis for integer-multiple-patterned spiking, our results provide new insights into the reliability of spike propagation in vivo.

Reliable spike propagation in primary afferents

On their way to the CNS, spikes originating in peripheral axon terminals must cross a T-junction located in the DRG. The T-junction and soma both pose a challenge for spike propagation. Propagation failure near the soma prevents a full-sized somatic spike, but somatic depolarization still occurs because of electrotonic current spread (Gemes et al., 2013). The absence in our recordings of smaller-than-normal events coincident with skipped spikes (Fig. 4), though potentially difficult to record extracellularly, suggests that propagation failed farther away (Stoney, 1985). Consistent with this interpretation, and with work on propagation slowing (Dun, 1955), propagation failures occur most commonly at the T-junction (Gemes et al., 2013). Amir and Devor (2003) showed with simulations that spikes can propagate down the central branch, even if they fail to propagate toward the soma, consistent with observations by Ito and Saiga (1959) during repetitive activation (see also Parnas and Segev, 1979), but this is a moot point if most spikes reach the soma, as our data indicate.

Many past studies have focused on measuring the maximal frequency (or minimal interval) at which spikes reliably propagate through the T-junction (e.g., Lüscher et al., 1994a; Djouhri et al., 2001; Gemes et al., 2013). This involves driving the neuron to fire at higher-than-normal rates. Moreover, almost all past experiments on spike propagation have been conducted on reduced (ex vivo) preparations or in cultured neurons (see Introduction), and many recordings from DRG neurons have used sharp electrodes, which risk introducing a significant leak at the recording site that could exacerbate the impedance mismatch and alter resting membrane potential (Staley et al., 1992). All of this to say that past studies have elucidated the many factors (e.g., axon diameter, channel densities, and gating) that affect spike propagation, but what fraction of spikes make it past the T-junction under natural conditions has remained largely untested. Notably, Coleman et al. (2003) found no evidence of propagation failure at the T-junction based on in vivo recordings. Notwithstanding concerns about whether they recorded centrally and peripherally from the same fibers, the reliability they observed is consistent with our own findings and with other data from central axons (see Introduction).

By recording extracellularly from an intact DRG in vivo while monitoring responses to tactile stimuli that evoked physiologically relevant firing rates, we found that propagation is reliable but that failures do occur. The regularity of spiking in SA2 units was crucial for allowing us to recognize that some spikes were “skipped”; similar analysis is not feasible in SA1 units because their repetitive spiking is irregular, or in RA units because their spiking is transient. By applying stimuli as sustained steps, rather than as trains of short pulses, we avoided confusion that might arise from the intermittent failure of spike initiation in response to each pulse; for instance, similar skipping has been observed during vibrotactile stimulation (Coleman et al., 2003; Cheng et al., 2013) but may be due to intermittent failure of spike initiation. Reliable spike initiation can be achieved with supramaximal pulses, but strong pulses risk causing unnaturally synchronized spiking that can lead to ephaptic effects (Jefferys, 1995) or other forms of cross-excitation (Devor and Wall, 1990). Although propagation reliability is high under normal conditions, this may not remain true under pathological conditions. Moreover, given that safety factor is just high enough to support reliable propagation under normal conditions (see below), we expect the skip rate to eventually increase if firing rate is increased above physiological levels.

Reliable yet efficient spike propagation

Integer-multiple-patterned spiking was conspicuous in a subset of SA2 units that exhibited a high proportion of skipped spikes (>5%), but many other SA2 units exhibited a lower, non-zero rate of skipping (Fig. 3C). This suggests that safety factor is high enough to guarantee reliable propagation of most spikes, even in semiregular units, yet is low enough that some failures occur. This is an efficient solution: a decrease in safety factor would substantially reduce reliability, whereas an increase in safety factor would yield little improvement (Fig. 9). Although often overlooked, neural coding is constrained by energy usage (Laughlin, 2001; Niven and Laughlin, 2008). Remme et al. (2018) recently showed, in the context of coincidence detection in the auditory system, that neurons use the most energy efficient solution that does not compromise function. Our data point to a comparable balance in the context of propagation reliability. Action potentials vary widely in their energy efficiency, depending on sodium and potassium channel densities and how long those channels are simultaneously open during a spike (Carter and Bean, 2009; Hasenstaub et al., 2010; Sengupta et al., 2010; but see also Ju et al., 2016). Hallermann et al. (2012) compared the metabolic costs of a spike in axon versus dendrites and found that the axon is less efficient per unit of area. This fits with other data showing that propagation reliability is higher in the axon than in dendrites (Mackenzie et al., 1996). Indeed, Hallermann et al. (2012) concluded that a certain degree of inefficiency was necessary to ensure reliable propagation at high firing rates. Separate work has shown that mossy fibers are relatively efficient in their spiking (Alle et al., 2009). Notwithstanding differences in efficiency, it appears that axons trade off energy efficiency and propagation reliability. Our results argue that peripheral axons, at least SA2 LTMRs, are no different in this regard.

Figure 9.

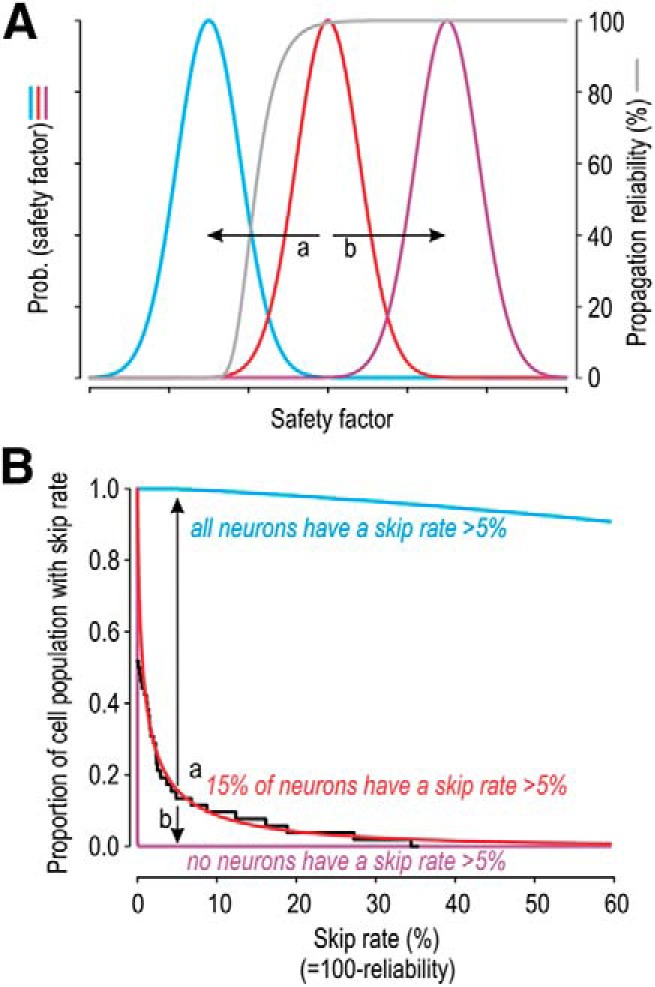
Theoretical relationship between safety factor and propagation reliability. A, Gray curve indicates propagation reliability as a function of safety factor. Colored curves indicate the variation in safety factor across three separate populations of cells. B, Convolving the gray curve with the cumulative probabilities corresponding to each colored curve (in A) yields the proportion of cells exhibiting different skip rates. Reliability is high for all purple cells but is low for all blue cells (i.e., the skip rate is uniformly low or high, respectively). In contrast, for cells shown in red, 15% of the population have a skip rate >5% (which produces conspicuous integer-multiple-patterned spiking), but most cells are very reliable. Data from Figure 3C (shown in black) are well fit by the red curve. Relative to the red distribution, a small reduction in safety factor (arrow a) dramatically reduces propagation reliability, whereas a small increase (arrow b) conveys little improvement, therein showing that an optimal solution is achieved by using a safety factor near the elbow of the gray curve.

Integer-multiple-patterned spiking and noise

Even when spikes are skipped at a relatively high rate, as in the initial five units that led us to recognize integer-multiple patterning, skipping may go undetected if individual ISI values are not measured and appropriately visualized. Indeed, the CoV values of semiregular units were only modestly higher than in regular units (Fig. 1E). Moreover, if propagation failures occur at the T-junction, skipped spikes would not occur in recordings from peripheral nerve, consistent with many publications (Koltzenburg et al., 1997; Cain et al., 2001; Zimmermann et al., 2009; Wellnitz et al., 2010). Skipped spikes would have been expected in those datasets if skipping originated at the spike initiation step. Notably, we observed integer-multiple-patterned spiking across a broad range of stimulus intensities and to different stimulus modalities, all of which is consistent with intermittent failure of spike propagation (Smith and Hatt, 1976; Matzner and Devor, 1993), but integer-multiple-patterned spiking may be due to intermittent failure of spike initiation under other stimulus conditions (Freeman and Johnson, 1982; Gang et al., 1993; Braun et al., 1994; Xing et al., 2001; Coleman et al., 2003; Amir et al., 2005; Cheng et al., 2013).

The intermittency, or randomness, of propagation failure (Fig. 3) points to a stochastic process. The most likely explanation is channel noise (Schneidman et al., 1998) given that the number of channels at the T-junction is possibly quite small. Although Schneidman et al. (1998) described missing spikes that might be equated with our missing spikes, the spiking patterns they show are consistent with switching between two attractors, quiescence and repetitive spiking, in a bistable system, as in our simulations in Figure 5D. This does not reproduce the exponential distribution of consecutively skipped spikes that we observed experimentally (Fig. 3B). Faisal and Laughlin (2007) observed a small number of skipped spikes in their simulations of channel noise in unmyelinated axons. To the best of our knowledge, past simulations of propagation through the T-junction have not modeled stochastic channel gating or included any noise. This, together with the energetic considerations discussed above, are important factors to incorporate into future computational work in this area.

In conclusion, our experiments have demonstrated intermittent failure of spike propagation at the T-junction of primary afferent neurons. But such failures are actually quite rare. The vast majority of spikes make it through the T-junction to reach the soma, and presumably also reach the CNS. That said, our observation that a small minority of spikes fail to reach the soma reveals that the safety factor is not exceedingly high, which in turn suggests that the T-junction has found an efficient solution for reliable propagation, similar to the emerging picture in central axons.