Abstract
Sensory systems encounter remarkably diverse stimuli in the external environment. Natural stimuli exhibit timescales and amplitudes of variation that span a wide range. Mechanisms of adaptation, a ubiquitous feature of sensory systems, allow for the accommodation of this range of scales. Are there common rules of adaptation across different sensory modalities? We measured the membrane potential responses of individual neurons in the visual, somatosensory, and auditory cortices of male and female mice to discrete, punctate stimuli delivered at a wide range of fixed and nonfixed frequencies. We find that the adaptive profile of the response is largely preserved across these three areas, exhibiting attenuation and responses to the cessation of stimulation, which are signatures of response to changes in stimulus statistics. We demonstrate that these adaptive responses can emerge from a simple model based on the integration of fixed filters operating over multiple time scales.
SIGNIFICANCE STATEMENT Our recent sensations affect our current expectations and perceptions of the environment. Neural correlates of this process exist throughout the brain and are loosely termed adaptation. Adaptive processes have been described across sensory cortices, but direct comparisons of these processes have not been possible because paradigms have been tailored specifically for each modality. We developed a common stimulus set that was used to characterize adaptation in somatosensory, visual, and auditory cortex. We describe here the similarities and differences in adaptation across these cortical areas and demonstrate that adaptive responses may emerge from a set of static filters that operate over a broad range of timescales.
Keywords: adaptation, auditory cortex, neural coding, somatosensory cortex, visual cortex
Introduction
Natural stimuli encompass, across all sensory modalities, a very wide range of amplitudes, and share structure at many spatial and temporal scales (Simoncelli and Olshausen, 2001; Fairhall, 2014). We suggest that, as a consequence, all sensory systems are subject to multiple mechanisms of adaptation that modulate their response properties over a variety of timescales ranging from milliseconds to hundreds of seconds. These adaptive modulations are driven by a number of factors, such as the history of variations in input, statistical properties of the stimulus, and the overall activity of the system. As a result, an encoding model developed for a given set of stimulus dynamics often fails to predict responses when the statistics of the stimulus change (Ozuysal and Baccus, 2012; Mease et al., 2014; Heitman et al., 2016; McIntosh et al., 2016; Weber et al., 2019).
While the statistical details differ across sensory modalities, natural stimuli all exhibit temporal fluctuations that are distributed across timescales. One may therefore expect the adaptive properties of sensory systems to be tuned to address these temporal fluctuations (Fairhall, 2014). Circuitry and cell types are similar across cortical fields as well, raising the question whether these similarities lead to common adaptive properties across different sensory areas. With this in mind, we explore here temporal properties of adaptation, documenting the dynamics of response sensitivity across sensory modalities.
To examine sensory adaptation across the neocortex, we investigated three sensory modalities: somatosensory, visual, and auditory. A major challenge in previous work has been that, while the descriptions of adaptation for each of these systems are extensive, they are difficult to compare due to disparate experimental paradigms. Our goal here was to characterize neuronal responses across the sensory cortex to a common stimulus set, allowing us to move beyond modality-specific descriptions. Due to the inherent difficulty in comparing stimulus intensities across modalities, we focused here on responses to common temporal statistics. To this end, we studied sequences of discrete punctate pulses (in the form of monitor flashes, auditory clicks, and transient whisker deflections) delivered both at fixed frequencies and in Poisson-noise sequences. For each stimulus modality, we performed in vivo whole-cell recordings in the respective cortical area (V1, S1, and A1).
We uncover a set of underlying fixed sensory filters that allows sensory neurons to adjust their sensitivity to temporally varying stimulus conditions. While the dynamics of neuronal responses appears to depend on stimulus conditions, we demonstrate that a common model, composed of filters with multiple timescales, can account for their emergent behavior. We found that major adaptive features of the membrane potential responses to fixed frequency stimuli are generally conserved across different cortical sensory modalities, although they differed in the degree to which they are expressed. These include a shift in the complexity of individual responses with the rate of stimulation, a reduction in response amplitude with the rate of stimulation, and a termination response at the end of high-frequency stimulation. All of these components of the adaptive responses obtained from sensory neurons are predicted by a fixed, time-invariant model, indicating that adaptive processes for different sets of stimuli can be accounted for through the integration of multiple timescales of static sensory filters.
Materials and Methods
Physiology.
Physiological procedures for mouse recordings are based on those previously described (Scholl et al., 2013). All of our experiments were conducted using adult C57BL/6 or ChR2-GAD mice (n = 27) P28-P90 to avoid the hearing loss that develops in older mice of this strain of both sexes. Mice used in V1 experiments were P35 and older to avoid the visual critical period. Mice were anesthetized with 1000 mg/kg urethane and 10 mg/kg chlorprothixene via intraperitoneal injection. A further intraperitoneal injection of 20 mg/kg dexamethasone was administered to prevent brain edema. During the course of the experiment, body temperature was monitored and maintained at 37°C. A tracheotomy was performed, and the head was secured using custom-made head holders. A craniotomy and durotomy were performed over the appropriate area of sensory cortex. A1, S1, and V1 were located using standard techniques. Mouse eyes were kept moist with artificial tears or a thin layer of silicone oil. The cortical surface was kept moist with saline or 4% agarose in normal saline. All animal procedures were approved by the University of Texas at Austin Institutional Animal Care and Use Committee and by Animal Care and Use Committees at Hebrew University and the Weizmann Institute. Hebrew University is an Association for Assessment and Accreditation of Laboratory Animal Care-approved institution.
After the identification of the relevant area of sensory cortex, we performed in vivo whole-cell recordings using the blind patch method. A silver-silver chloride wire was inserted into muscle near the base of the skull and used as a reference electrode. For V1 and A1 recordings, pipettes (5–10 mΩ) were pulled from 1.2 mm outer diameter, 0.7 mm inner diameter KG-33 borosilicate glass capillaries (King Precision Glass) on a P-2000 micropipette puller (Sutter Instruments). Pipettes were filled with the following (in mm): 135 K-gluconate, 4 NaCl, 0.5 EGTA, 2 MgATP, 10 phosphocreatine disodium, and 10 HEPES, pH adjusted to 7.3 with KOH (Sigma-Aldrich). For S1 recordings, pipettes (1.5 mm outer diameter, 0.86 inner diameter, BF150–86-10, Sutter Instruments) were pulled on a PC-10 vertical puller (Narashige) and were filled with the following (in mm): 136 K-gluconate, 10 KCl, 5 NaCl, 10 HEPES, 1 MgATP, 0.3 NaGTP, and 10 phosphocreatine (310 mOsm/L). Neurons were recorded 150–500 μm below the cortical surface. Current-clamp recordings were performed with a MultiClamp 700B patch-clamp amplifier (Molecular Devices). Current flow out of the amplifier into the patch pipette was considered positive.
Stimuli.
We constructed stimuli consisting of sequences of discrete 20 ms pulses, delivered as light flashes, auditory clicks, or whisker deflections. Each trial was composed of pulses presented at fixed frequencies or following a homogeneous Poisson process with rates ranging from 0.5 to 20 pulses/s. Fixed frequency stimulation was set at a 4 s duration per trial while Poisson trials varied in their length. An additional stimulus for model validation was generated as an inhomogeneous Poisson process with a slowly varying rate (time constant of 1 ms) ranging from 0.5 to 20 pulses/s. The fixed frequency stimulus set was designed to directly measure how the dynamics of the response systematically change with stimulation frequency. The Poisson stimulus sets were used to fit linear/nonlinear models applying maximum likelihood techniques to predict the responses to the range of fixed frequencies.
Visual: Full-field monitor flashes were presented monocularly at full contrast on a black screen. All stimuli were generated via the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) for MATLAB (The MathWorks) on a Macintosh (Apple) computer. Stimuli were presented on a calibrated CRT monitor (Sony, FDM-520) placed 25 cm in front of the animal's eyes with a refresh rate of 100 Hz and a spatial resolution of 1204 × 768 pixels. The mean luminance of the monitor was 40 cd/cm2.
Somatosensory: For whisker deflection, the principal whisker (trimmed to 10–20 mm) was inserted into a 21G needle attached to a galvanometer servo-control motor (6210H; Cambridge Technology) with a matching servo driver and a controller (MicroMax 677xx, Cambridge Technology). A fast-rising voltage command was used to evoke a fast whisker deflection with a constant rise time of 1 ms followed by a 20 ms ramp down signal to prevent an off response for each stimulus. Because of the fixed rise time, amplitude and speed of deflection grow together following a quasi-linear relationship.
Auditory: Click stimuli consisted of 20 ms bursts of broadband noise (5 ms linear rise/fall ramps). They were transduced to analog signals with a high-quality sound card (RME HDSP-9632), attenuated (TDT PA5), and presented to the contralateral ear (TDT EC1). The noise was generated with a spectrum level of −50 dB/sqrt(Hz) and had a bandwidth of 60 kHz. For acoustic calibration, pure tones were used. Typically, a pure tone at 0 dB attenuation produced a sound level of 100 dB SPL, with variations of up to 10 dB across frequency.
Data analysis.
Spikes were identified and removed by passing membrane potential data through a 10 ms median filter or by interpolation (Meir et al., 2018). The mean membrane potential was computed by averaging all trials for each stimulus frequency.
Response amplitude was assessed for each individual pulse (whisker deflection, monitor flashes, or single noise bursts) in the stimulus train. The peak membrane potential was obtained for each stimulus period, and the baseline membrane potential at the time of the stimulus pulse was subtracted away to obtain the response amplitude. These responses were then normalized so that the value of the response to the initial pulse was one and a lack of response was considered 0. Adaptation ratios were obtained by dividing the amplitude of the response to the last pulse by the amplitude of the first response (Meir et al., 2018).
As described below, we found that sensory stimulation sometimes evoked a complex biphasic or multiphasic response consisting of an initial rapid phase followed by a dip and then a second response phase. We defined cells as containing a multiphasic response by initially identifying the initial peak response that occurs after the stimulus. We then identified the time point following the initial peak at which the response significantly declined from the peak and arrived at a minimal value for 10 ms. We next measured whether a second response depolarization occurs following this minimum by measuring whether the response significantly increased after the minimum time point. Those cells and conditions in which response was significantly larger than the trough were marked as multiphasic. Significant differences were determined by a one-sided t test (p < 0.05).
Termination responses were defined as significant depolarizations following the cessation of the stimulus. To test for the presence of termination responses, we compared the mean membrane potential before the stimulus train with the mean membrane potential 300–800 ms after the final stimulus pulse with a Wilcoxon rank-sum test. These were distinct from the response to the last stimulus as they occurred a few hundred milliseconds after the last stimulus pulse. Termination response amplitudes were defined at the peak of the trial-averaged response. Latencies were defined as the time from the last stimulus pulse to the peak of the termination response.
Modeling.
We fit our model to all Poisson trials (excluding the repeated Poisson noise stimulus). For each trial, we fit the voltage recorded from 50 ms before the stimulus window onset to 1500 ms after the stimulus window offset. Because the adaptive response dynamics we modeled occurred on timescales >10 ms, we downsampled the median-filtered voltage to 10 ms bins. The models were fit using between 21 and 229 Poisson noise trials (mean 88.9 trials).
We modeled the voltage as a sum of linear–nonlinear subunits. Our approach is similar to previous models of spiking activity in the lateral geniculate nucleus (McFarland et al., 2013) and retina (Freeman et al., 2015; Maheswaranathan et al., 2018). The bank of nonlinear subunits could approximate the input received from distinct presynaptic sources (e.g., excitatory and inhibitory neurons), which are rectified by synaptic transmission. For time step t on trial i, the voltage is modeled as follows:
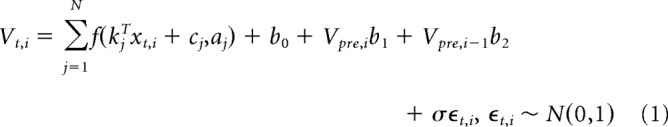 |
The stimulus before time t is given by the vector xt,i. The N linear filters are the vectors kj, and the baseline level for each subunit is cj. The nonlinearity is a variation on the logistic function as follows:
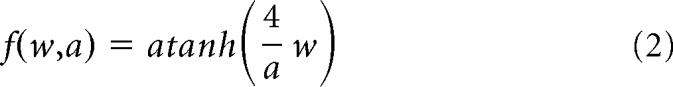 |
where a is the subunit's scale, which was restricted to be >1. This formulation gives f(0, a) = 0 and the derivative fw(0, a) = 1, so that the filters can approximately be viewed in units of mV/pulse, regardless of the scale parameter a.
The model accounts for slow drift in baseline voltage occurring over trials by incorporating the voltage in a 400 ms window occurring 450–50 ms before stimulus onset. The value Vpre,i is the lower fifth percentile value of the voltage in that window as an estimate of the baseline voltage. We also use the baseline estimate from the previous trial, Vpre,i-1, to enhance this estimate. The Vpre estimates are weighted by b1 and b2. The final baseline term is b0, which is constant across all trials and times. The noise variance is σ2.
To reduce the model complexity and promote smoothness in the linear filters, we parameterized the linear filters using a raised cosine basis (Pillow et al., 2005, 2008) of the following form:
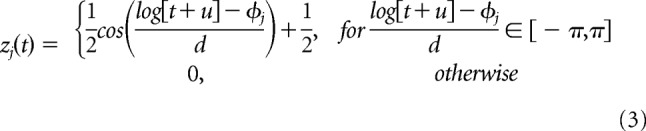 |
The φj are spaced linearly from φ1 = log (tstart + u) to φM = log (tend + u). For V1 and S1 cells, we used M = 16 basis functions with tstart = 0.01s, tend = 2s, and u = 0.3. For the A1 cells, we used M = 20 basis functions with tstart = 0.01s, tend = 2s, and u = 0.1 to account for fast timescale responses. For fitting, the basis was orthonormalized. The total number of free parameters in the model was 4 + N(M + 2), where N is the number of filters. For the model fits with four filters, this gives 76 parameters for the V1 and S1 cells and 92 parameters for the A1 cells.
We placed an independent Gaussian prior on each term in the filter parameters and the history terms as follows:
We set ω2 = 52. This choice of prior regularizes the filter estimates by shrinking the filters toward 0 and keeps the per-pulse deviations in voltage within a biophysically realistic range: a priori, the mean maximum deviation per pulse for a single filter is 4.44 mV with an SD of 1.58 mV for the V1 and S1 bases. Similar results were achieved for different choices of the shrinkage parameter. The other prior used was for the noise term . Uniform priors were placed over b0 an cj.
We obtained maximum a posteriori estimates of the model parameters using a trust-region algorithm. Because this nonlinear model is not convex, we fit the model to each cell 1000 times using random initialization points and selected the fit with the largest log posterior value. The initial conditions were generated according to the following distributions:
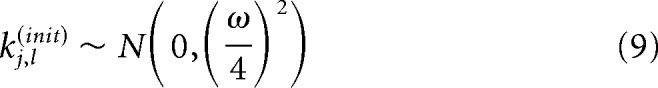 |
 |
The linear terms b0, b1, and b2 were set to the maximum likelihood estimate computed by normal least squares, keeping the other parameters fixed. Similarly, σ2 was set to the maximum a posteriori estimate given all other parameters.
We evaluated model performance by predicting the voltage recorded in response to stimuli that had not been used for model fitting. For those stimuli, we tested the model's ability to predict the average voltage recorded in response to the stimulus instead of predicting single trials. We evaluated model performance using the Pearson's correlation coefficient between the true and predicted voltages and the percentage variance explained the following:
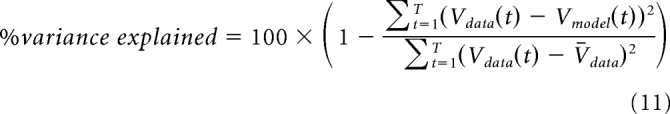 |
To analyze the model response to frequency changes, we ran model simulations (see Fig. 7) composed of stimuli in which two stimulus frequencies were presented. The initial frequencies ranged from 1 to 15 Hz and were then changed to a new value between 1 and 15 Hz after 3 s. For these simulations, the stimulus pulse times were randomized. Each combination of stimulus frequencies was simulated 5000 times using distinct pulse times, and these resulting model outputs were averaged. Frequency transition responses were calculated as the mean 200 ms around the peak of the response. The mean steady-state amplitude 200 ms before the transition was then subtracted from this value to obtain the transition response amplitude.
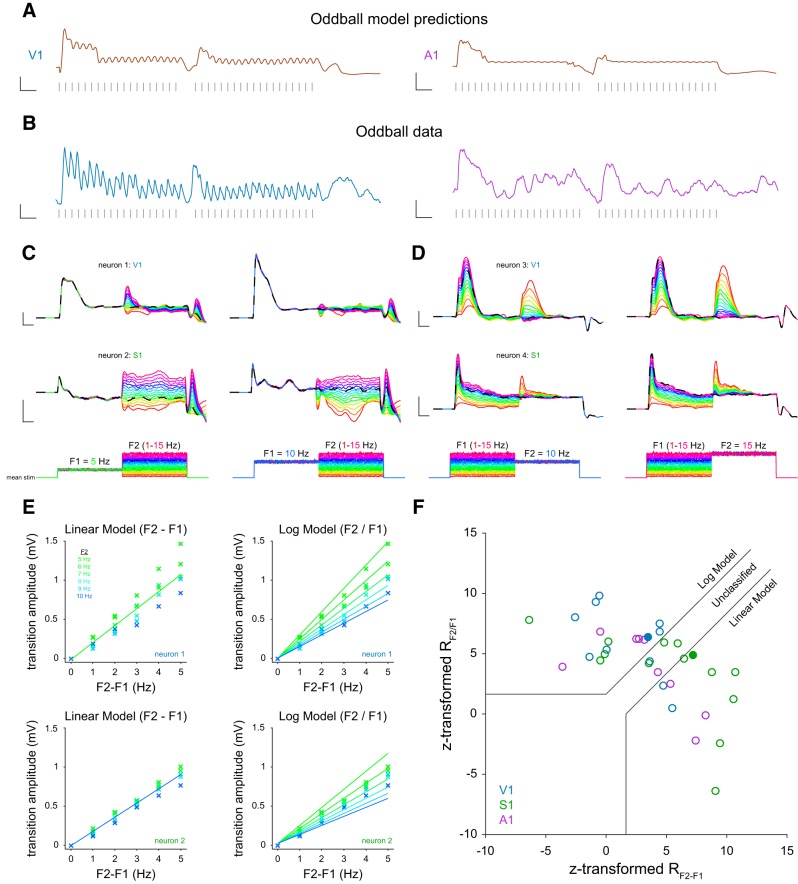
Figure 7.
Responses to frequency transitions. A, Model predictions for two neurons (V1, A1) for an oddball stimulus. One or two stimulus pulses was removed in the middle of the stimulus train. Calibration: y axis, 5 mV change; x axis, 250 ms duration. B, Membrane potential data for the oddball stimulus. Calibration: y axis, 5 mV change; x axis, 250 ms duration. C, Model simulations for two cells. Initial mean stimulus frequency was 5 Hz (top) or 10 Hz (bottom) for all traces. This then transitioned to all frequencies between 1 and 15 Hz. Dotted line indicates no frequency transition. Calibration: y axis, 2 mV change; x axis, 500 ms duration. D, Same as in C, but the second frequency was held constant and the first frequency was changed. E, Model predictions for a linear and log frequency transition signal. Solid bars represent prediction. x vales indicate data. F, Scatter plot of z-scored partial correlations. Solid lines indicate significance at 95%. Filled circles are example cells from C.
Results
To examine the adaptive properties of sensory neurons across modalities, we constructed a stimulus set consisting of temporal sequences of constant amplitude, discrete punctate pulses: monitor flashes, auditory clicks, or transient whisker deflections. These temporal sequences were either Poisson point processes or fixed-interval trains presented at multiple frequencies. We recorded the membrane potential responses in three regions of mouse sensory cortex (A1: n = 9, S1: n = 14; V1: n = 11) using whole-cell recordings.
In response to temporal sequences composed of fixed intervals, the membrane potential exhibited a number of dynamical properties that appear to be generally conserved across sensory cortex (Fig. 1). First, increasing stimulus frequency entailed more adaptation, leading to a systematic reduction in response amplitude toward the end of the train. Second, we observed that the reduction in stimulus-evoked response when stimulus frequency increases is accompanied by a systematic shift in the complexity of the response to individual pulses: at low frequencies, individual responses are long-lasting and multiphasic, whereas they become briefer and monophasic at higher frequencies. Finally, we found that a response occurs at the cessation of a high-frequency stimulus, which we term a termination response. Neurons across modalities varied in the degree to which they expressed these properties to fixed interval stimulation, as detailed below, but these motifs persisted across our sample database.
Figure 1.
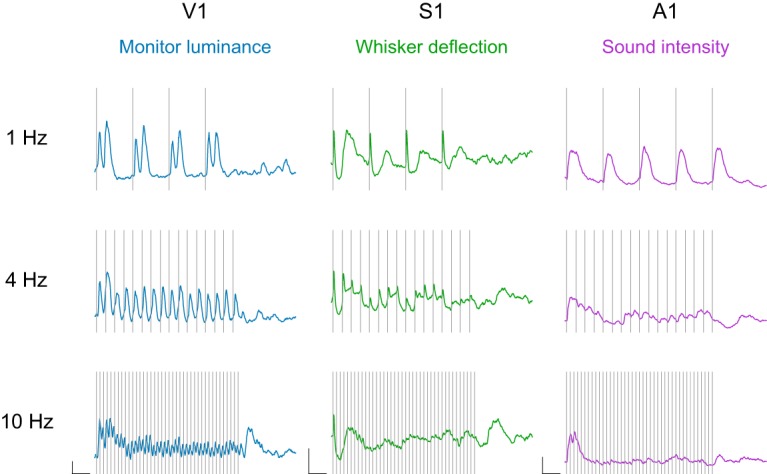
Fixed-interval stimulus responses across sensory cortex. Example V1 (blue), S1 (green), and A1 (purple) membrane potential responses to fixed-interval stimuli delivered at 1, 4, and 10 Hz. Calibration: y axis, 5 mV change in membrane potential; x axis, 500 ms duration. Gray bars represent an individual pulse in the stimulus train.
One way features could arise is if the state of the system changes as a result of being driven by stimuli with different statistics (Garrido et al., 2009). For instance, an increase in stimulus frequency could alter response time constants, resulting in a more monophasic response to the individual stimuli. Such a possibility could arise from the recruitment of slow inhibitory inputs (Dealy and Tolhurst, 1974). This would render any attempt to predict responses across stimulus frequencies from a fixed model fruitless, as model parameters would need to be adjusted with the stimulus statistics. Alternatively, varying stimulus statistics may evoke different components of a fixed but complex response. In this case, changes in response due to altered stimulus statistics can emerge from the combination of a single set of sensory filters.
To determine whether a single set of filters can account for the responses seen across stimulus frequencies, for the same cells, we additionally recorded membrane potential responses to Poisson pulse trains that varied widely in their rates, where the amplitude and shape of each stimulus were identical to those used for the fixed-frequency stimulation. We then fit these data within a linear–nonlinear modeling framework. Our model was composed of a bank of linear filters that were followed by output nonlinearities (see Materials and Methods; Fig. 2B). The outputs of the linear–nonlinear components were then summed to give the estimated membrane potential. This architecture provides flexibility by allowing multiple contributions to membrane voltage, or temporal “subunits,” with independent nonlinearities. We used maximum a posteriori methods to estimate the parameters of this linear–nonlinear subunit model (Eq. 1) using each cell's responses to Poisson trains with a wide range of mean stimulation rates. Because the pulse stimuli are non-Gaussian, we used maximum likelihood fitting instead of an approach like spike-triggered covariance, which is most appropriate for Gaussian stimuli (de Ruyter van Steveninck and Bialek, 1988; Brenner et al., 2000; Schwartz et al., 2006; Park et al., 2013; Aljadeff et al., 2016).
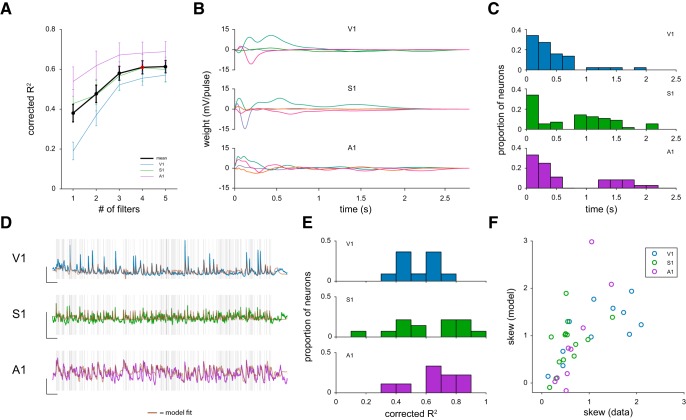
Figure 2.
Modeling framework. A, Corrected R2 values to a withheld stimulus generated by an inhomogeneous Poisson process by number of filters included in the model. Data are mean ± SE. B, Example filters for individual neurons for all three sensory systems. C, Histograms of filter timescales across the population. D, Model fits obtained from the example filters shown in B to a fixed Poisson-process stimulus. Calibration: y axis, 10 mV; x axis, 1 s. Brown traces represent model fits. Gray bars represent individual stimulus pulses. E, Histogram of variance accounted for in the fixed Poisson stimulus for V1, S1, and A1. F, Scatterplot comparing the skew of the responses to the fixed Poisson-process stimuli for the data and the model simulations.
We first examined how the number of subunit filters included affected the model's ability to capture responses to Poisson stimuli for individual neurons. We assayed the model performance by examining how well it could account for the average response to a separate (held-out) Poisson sequence that had been repeated many times (Fig. 2D). Across V1, S1, and A1, models composed of 4 filters accounted for a significant amount of the explainable response variance to the repeated Poisson sequence (R2: V1 = 0.47 ± 0.04; S1 = 0.4 ± 0.06; A1 = 0.50 ± 0.07; values indicate mean ± SE across neurons), demonstrating that this modeling framework can largely account for sensory responses in cortex. To estimate the fraction of explainable variance the model accounts for, we used a method developed by Sahani and Linden (2003), which takes into account the number of stimulus repeats and the variation between trials (see Sahani and Linden, 2003; Mohanty et al., 2012). This correction factor only modestly increased the variance accounted for by our model (see Fig. 2E; corrected R2: V1 = 0.56 ± 0.04; S1 = 0.61 ± 0.07; A1 = 0.68 ± 0.06). Increasing the number of filters systematically improved the model's performance, although performance increases from using >4 filters were minimal (Fig. 2A). Beyond overall performance, a model composed of a single filter failed to account for specific features of the adaptive response to fixed frequency stimuli (see Fig. 8), as detailed in the following sections. To standardize our analyses across neurons and modality, we fixed the number of filters used to 4.
Figure 8.
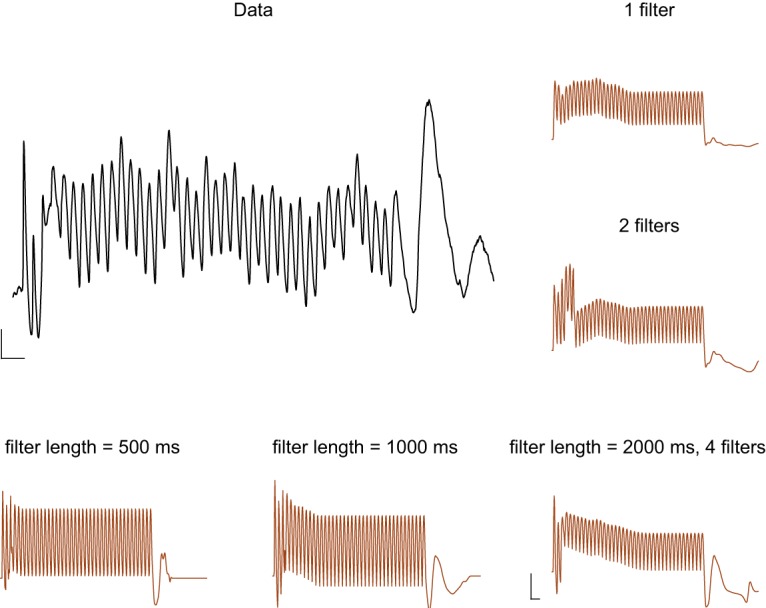
Impact of model parameters of response properties. Model simulations (brown) generated by changing the number of filters (right column) and the filter length (bottom row). Data are shown in black. Calibration: x axis, 250 ms; y axis, 2 mV.
To characterize how the model is able to match the responses to Poisson sequences, we examined the properties of the subunits used to generate the model. We extracted the temporal envelope of each subunit filter by performing an autocorrelation and quantifying the time over which it was above a threshold value, chosen to be 0.2 (Shelhamer, 2007). For individual neurons, these subunit timescales could vary from 60 ms to >2 s. Most subunit filters had short envelopes, forming an exponential distribution of timescales (Fig. 2C). Each neuron had filters that varied in time scale. The median difference between the fastest and slowest time scale was >1 s. The average ratio of the time of the longest and shortest filter for each cell was 8.48 ± 1.24 (geometric mean). Because of these subunit time scales, we set a maximum filter length of 2.5 s for each subunit of our model.
We next sought to determine how well the model could account for a membrane potential skew. We chose skew because this metric of the response distribution encapsulates the degree of neuronal selectivity, particularly when a broad stimulus range is used. Neurons that respond to specific stimulus conditions have higher skews, whereas those that respond more broadly have lower skews (Ringach and Malone, 2007). The model was largely able to predict the skew of the membrane potential response to the left-out Poisson sequence across sensory areas (Fig. 2F; correlation coefficient of skew (r): V1 = 0.70; S1 = 0.46; A1 = 0.84)
We tested whether the subunit model, fitted from noise sequences, was able to capture the membrane potential fluctuations observed in response to fixed interval sequences (Fig. 1). The subunit model provided predictions that were highly correlated with the measured responses of the neurons (corrected R2: V1 = 0.68 ± 0.04, S1 = 0.73 ± 0.05, A1 = 0.83 ± 0.05). These high correlations demonstrate that, in general, the model predicts the membrane potential responses observed in the fixed interval data.
We next focused our analysis on specific components of the adaptive response. We examined whether the model could recapitulate the three prominent adaptive aspects of the responses highlighted above: (1) the decay of response amplitude with increasing stimulus frequency, (2) the shift in complexity of a single-pulse response from biphasic to monophasic as stimulus frequency increases, and (3) the presence of a termination response following the cessation of a high-frequency stimulus train (Fig. 1).
Response attenuation with stimulus frequency
A prominent feature of sensory adaptation is that the degree of response attenuation is linked to the rate of sensory stimulation: higher frequency stimulation leads to stronger amplitude attenuation (Chung et al., 2002; Khatri et al., 2004; Martin-Cortecero and Nuñez, 2014; Kheradpezhouh et al., 2017). We find this common pattern in our V1, S1, and A1 responses (Fig. 3A). The responses of neurons at 1 Hz stimulation were only weakly attenuated, whereas the responses to 10 Hz stimuli were strongly attenuated. To determine the degree of attenuation to each fixed-frequency stimulus, we quantified the membrane potential response to each pulse in the train (Fig. 3B; see Materials and Methods). We first quantified the membrane potential response to a single stimulus pulse by subtracting the baseline value before the pulse from the peak of the response. Overall values varied widely both within and between modality (V1 = 18.2 ± 23 mV; S1 = 6.5 ± 0.8 mV; A1 = 8.6 ± 0.5 mV). It is not clear whether or not these differences are due to potential differences in stimulus intensity across the different modalities and individuals (see Discussion) or to properties of the different systems and cells recorded from.
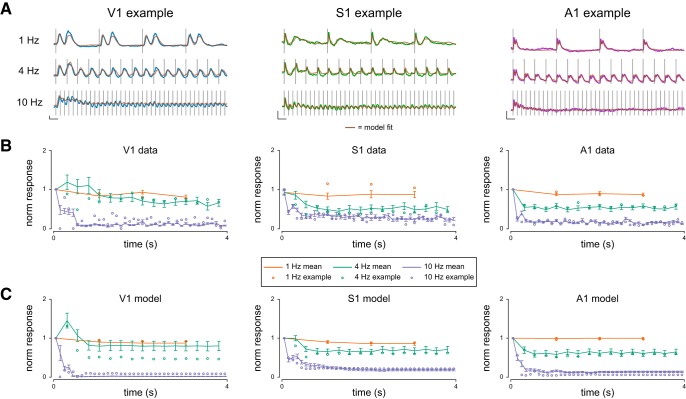
Figure 3.
Response attenuation increases with stimulus frequency. A, Example V1, S1, and A1 membrane potential responses to fixed interval stimuli delivered at 1, 4, and 10 Hz. Brown traces represent model fits to these responses. Calibration: y axis, 5 mV change in membrane potential; x axis, 200 ms duration. B, Normalized mean peak membrane potential responses to each pulse in a stimulus train at the three frequencies shown in A. Open circles are data from the example cells in A. Error bars indicate SEM. C, Same as in B, but for model fits.
To calculate the degree of response attenuation, we measured the peak membrane potential response to each stimulus pulse relative to the baseline membrane potential immediately before the pulse to determine the change in membrane potential elicited by each pulse in the stimulus train. In these example neurons, response amplitude systematically declines as a function of stimulus frequency and the location of the pulse in the train (Fig. 3). These example neurons reflect the typical responses found in each modality, in which low-frequency stimulation evokes little response attenuation and high-frequency stimulation evokes large attenuation.
To quantify the frequency dependence of this attenuation in our dataset, we computed the adaptation ratio, defined as the ratio of the response amplitude of the last stimulus in our train and the response to the first stimulus, for each stimulus frequency (Meir et al., 2018). Although there was considerable variability in adaptation across and within sensory systems, a pattern emerges when looking at the population. For 1 Hz, the adaptation ratio was similar across V1, S1, and A1 neurons (Fig. 4). As frequency increased, these adaptation ratios systematically declined, such that, at 10 Hz, the adaptation ratios were much closer to 0. Neurons attenuate in a similar manner within a modality, and the same trend of greater attenuation with higher stimulation frequency is observed across modalities. Hence, under comparable experimental conditions, response attenuation follows a similar pattern for these 3 sensory modalities.
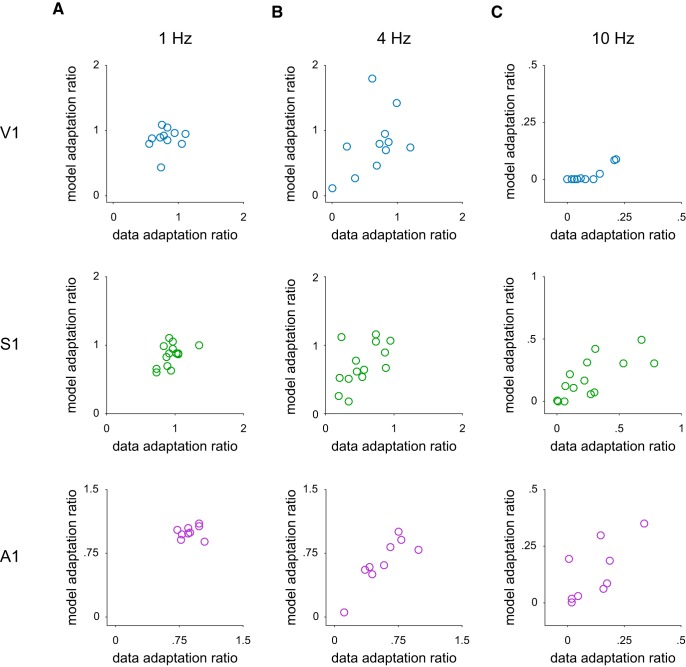
Figure 4.
Model fits account for response attenuation adaptation ratios. A, Scatterplot comparing the adaptation ratios of neurons for the data (x axis) and model fits (y axis) in response to a 1 Hz stimulus for V1, S1, and A1. B, Same as in A, but for 4 Hz stimulus. C, Same as in A, but for a 10 Hz stimulus.
We tested whether our model could account for these findings by simulating responses to the 1, 4, and 10 Hz stimuli for each cell in our dataset (Fig. 3A, brown traces) using the filters that were obtained from Poisson stimulation. We then performed the same analysis on these model fits to determine whether they exhibit the same response attenuation (Fig. 3C). Adaptation ratios of model fits were highly correlated with their data counterparts (r = 0.80 (V1), 0.68 (S1), 0.95 (A1); Fig. 4). These data indicate that our model is able to capture the stimulus frequency dependence of response attenuation across three areas of sensory cortex. Not only is the model able to capture the broad response attenuation observed in our dataset, but it predicts differences in response attenuation across modalities. For example, we find that S1 neurons attenuate less at 10 Hz than either A1 or V1 neurons, which matches model predictions.
Change in response complexity with stimulus frequency
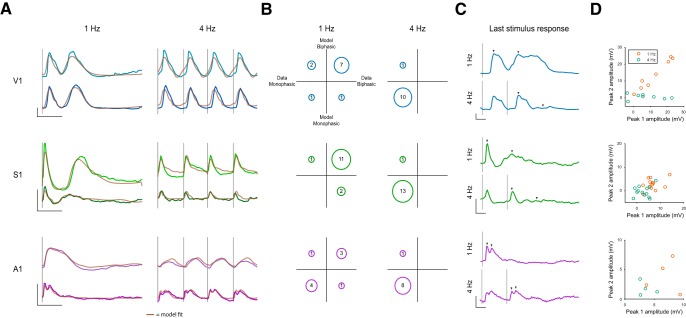
The second adaptive feature we noticed was that the shape of the membrane potential response is often altered by stimulus frequency. Visual inspection revealed a characteristic shift in the complexity of the response to individual stimuli as stimulus frequency increased in a large proportion of visual and somatosensory neurons (Fig. 5A). At lower frequencies (<4 Hz), complex biphasic responses were common in S1 and V1, as has been previously reported in rodents and humans (Sachidhanandam et al., 2013; Funayama et al., 2015, 2016). We found, however, that these multiphasic responses shifted to simple, monophasic responses as stimulus frequency increased to 4 Hz. We classified whether the responses were significantly multiphasic by determining whether responses followed a pattern of initial depolarization, a decline in membrane potential followed by a second depolarization that is significantly larger than the decline. The multiphasic responses apparent at low stimulus frequencies follow this pattern, responding with a significant depolarization following the dip. Low-frequency stimuli evoked membrane potential responses that were deemed multiphasic for the majority of V1 (73%) and S1 (93%) neurons (Fig. 5B), but only the minority of A1 neurons (44%). A1 neurons exhibited a somewhat different type of biphasic response, with much shorter latencies between the two components of the response (Fig. 5A, bottom). When the stimulus rate was increased to 4 Hz, the responses of V1, S1, and A1 neurons became less multiphasic and none exhibited multiphasic responses.
Figure 5.
Change in response complexity with increasing stimulus frequency. A, Example V1, S1, and A1 membrane potential responses to fixed interval stimuli delivered at 1 and 4 Hz. Two example cells per sensory system are shown. Brown represents model fits to these responses. Calibration: y axis, 10 mV change in membrane potential; x axis, 200 ms duration. B, Count of neurons and model fits whose responses are significantly biphasic in V1, A1, and S1. The x axis categorizes data as monophasic (left) or biphasic (right). The y axis categorizes model fits as monophasic (bottom) or biphasic (top). C, Example membrane potential responses to fixed interval stimuli delivered at 1 and 4 Hz. Traces represent the end of the stimulus train. Arrows indicate identified peaks. Calibration: y axis, 5 mV change in membrane potential; x axis, 100 ms duration. D, Scatterplots of peak amplitude for both peaks of the biphasic response. Peak locations were determined from the 1 Hz trace and were then measured on the 4 Hz stimulus from the time of last stimulation.
Not only did the response complexity change with stimulus frequency, response duration also shifted with stimulus frequency. We quantified response duration by measuring the envelope of time over which responses deviated from the baseline membrane potential (see Materials and Methods). We examined the response to stimulus pulses that occurred 2 s after the stimulus train began to be sure that the cell had adapted to the stimulus frequency. Responses to 4 Hz stimuli were considerably shortened in V1 and S1 neurons (V1 = 126 ± 39 ms, S1 = 101 ± 65 ms) relative to response to 1 Hz stimuli (V1 = 505 ± 138 ms, S1 = 435 ± 237). Responses for A1 neurons, however, were similar between the two frequencies (1 Hz = 158 ± 101 ms, 4 Hz = 158 ± 56 ms).
We next sought to determine whether the subunit model could account for these response dynamics (Fig. 5A, brown traces). As with the recordings of the membrane potential, we measured whether model responses were significantly multiphasic. The model successfully recapitulated the multiphasic responses in V1, S1, and A1 at low frequencies (V1 = 82%, S1 = 86%, A1 = 44%) as well as the shift to monophasic responses at higher frequencies (V1 = 9%, S1 = 7%, A1 = 11%; Fig. 5B). Furthermore, the results revealed that, in general, the neural responses and their model fits received the same classification (Fig. 5B). The model also captured the large shift in response duration in V1 (1 Hz = 507 ± 118 ms, 4 Hz = 146 ± 27) and S1 (1 Hz = 507 ± 227, 4 Hz = 151 ± 58 ms) and the weak shift in A1 responses (1 Hz = 216 ± 132 ms, 4 Hz = 137 ± 58 ms). Across modalities, the subunit model resulted in response durations that were correlated to those measured in V1, S1, and A1 (r: V1 = 0.92; S1 = 0.77; A1 = 0.70).
One possibility is that responses seemed monophasic at higher frequencies because the biphasic portion of the response was interrupted by the next stimulus pulse. To control for this, we focused our analysis on the last pulse in the stimulus train (Fig. 5C). We first measured the mean amplitude 10 ms around the first and second peak of biphasic responses using the indices we obtained previously. The amplitude of the two peaks was highly related in V1 neurons (Fig. 5D, r = 0.98) where the amplitude of the two peaks was generally on the same scale (mean amplitude: first peak 12.3 ± 3.2 mV; second peak 13.6 ± 3.1; t test, p > 0.05). S1 responses tended to have weaker second peaks (first peak = 6.8 ± 0.9 mV, second peak = 2.8 ± 0.6 mV; t test, p < 0.001), which resulted in a weaker correlation (r = 0.36).
We then used these indices to measure the amplitude evoked by a 4 Hz stimulus at the end of the stimulus train. As previously shown (see previous section), the amplitudes of the first peak were smaller in the 4 Hz condition compared with the 1 Hz condition (V1 = 7.5 ± 3.4 mV; S1 = 2.9 ± 0.8 mV; t test, V1: p = 0.02; S1: p = 0.003). Using the latencies (defined as the time between the peak values of each phase of the response) obtained from the 1 Hz responses, we measured the amplitude of the “second peak” of the 4 Hz responses to the last stimulus in the train. As expected, amplitudes were near 0, indicating a lack of a biphasic response (V1 = 0.6 ± 0.5 mV; S1 = −0.3 ± 0.6 mV). Furthermore, the amplitude of the first 4 Hz peak exhibited weak and nonsignificant correlations with that of the second (r: V1 = −0.25, p > 0.05; S1 = 0.23, p > 0.05). These results indicate that 4 Hz responses truly shift to a monophasic shape and are not an artifact of our protocol and analysis. A1 data are not summarized here due to the low number (4) of biphasic neurons, but data are shown in Figure 5C, D (bottom row).
Termination responses
Paradigms using periodic stimuli have consistently found a large response at the end of a stimulus train or when a stimulus is omitted or changed (Näätänen et al., 1978; Bullock et al., 1990; Karamürsel and Bullock, 1994; Schwartz et al., 2007; Hamm and Yuste, 2016; Li et al., 2017). These phenomena have been reported at multiple levels of analysis, including EEG (see Näätänen et al., 1978) and in single-unit recordings (see Schwartz et al., 2007) in multiple sensory systems. Although the terms (mismatch negativity, omitted stimulus response, echo response, etc.) and the underlying mechanisms of these responses may differ, their descriptions and interpretations share a number of common features (Bullock et al., 1993; Schwartz et al., 2007; Stefanics et al., 2014).
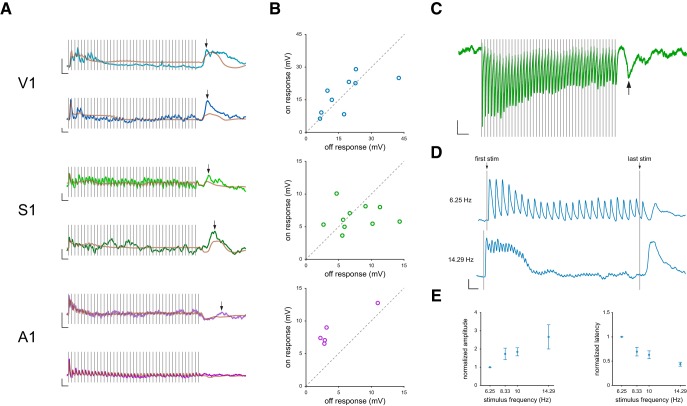
We also found transient membrane potential depolarizations following the termination of the high-frequency stimulus trains across the three sensory modalities and term these deflections “termination responses” (Fig. 6A). These termination responses are easily distinguished from a response to the last stimulus of the train as they start hundreds of milliseconds after the termination of the stimulus train. To determine whether these depolarizations were statistically significant, we compared the mean membrane potential 300–700 ms after the response to the last pulse in the stimulus train to the membrane potential before sensory stimulation. We found that termination responses were present in the majority of V1 (9 of 11) and S1 (10 of 14) cells at a stimulation frequency of 10 Hz. Termination responses were found in a smaller proportion of A1 cells (3 of 9). While termination responses were common at high frequencies, they were less prevalent at lower frequencies, such as 4 Hz (V1, 3 of 11; S1, 2 of 14; A1, 0 of 9; Fig. 1). We quantified the latency and amplitude of the termination responses for all of the intracellular records. The latency of the termination response (defined from the last stimulus to the peak) was generally long (V1 = 367 ± 79 ms, S1 = 446 ± 102 ms, A1 = 642 ± 284 ms; see Materials and Methods), and its amplitude was large, on generally the same scale as the response to the first stimulus (V1 = 17.9 ± 11.2 mV, S1 = 7.6 ± 3.5 mV, A1 = 4.4 ± 3.7 mV; Fig. 6B). To determine the role of synaptic input in generating these termination responses, we performed recordings while voltage-clamping neurons near the reversal potential of inhibition. Voltage-clamp recordings indicate a large current after the end of stimulation that indicates a synaptic origin for these responses (Fig. 6C).
Figure 6.
Termination responses. A, Example V1, S1, and A1 membrane potential responses to fixed interval stimuli delivered at 10 Hz. Two example cells per sensory system are shown. Brown represents model fits to these responses. Calibration: y axis, 5 mV change in membrane potential; x axis, 200 ms duration. Arrow indicates the location of the termination response. B, Scatter plots comparing the amplitude of the termination response and the on response for V1, S1, and A1. C, Example S1 voltage-clamp recording while the neuron was held at the reversal potential of inhibition. Arrow indicates location of termination response. Gray bars represent individual stimulus pulses. Calibration: y axis, 20 pA; x axis, 250 ms change. D, Example neuron membrane responses to two different stimulus frequencies. Calibration: y axis, 5 mV change in membrane potential; x axis, 250 ms duration. E, Mean normalized termination response amplitude and latency at four stimulus frequencies. Responses are normalized to the termination response at 6.25 Hz for each cell. Error bars indicate SEM.
The subunit model successfully accounted for the depolarizations at the termination of high-frequency stimulus trains for those neurons with significant termination responses. Despite predicting the presence of a termination response to the high-frequency data, our models consistently underestimated the response amplitude at the end of the stimulus train (Fig. 6A; r = 0.59, slope = 0.14). The model did predict the long latency of these termination responses, although the individual variation in termination latency was only weakly correlated with estimates of termination response latency from our measurements (r = 0.414, slope = 0.41). Some of the difference in latencies between the model and measurements reflects the difficulty assigning a single latency value to responses that extend and slowly depolarize over hundreds of milliseconds.
We focused our comparison of the termination response on two frequencies that either lacked a termination response (4 Hz) or consistently exhibited a termination response (10 Hz). To expand our analysis to include multiple frequencies that exhibited a termination response, we performed additional V1 recordings with a wider range of higher stimulus frequencies (Fig. 6D). We found that the termination responses exhibit changes in amplitude and latency that are related to the stimulus frequency. In particular, the amplitude of the termination response monotonically increased with stimulation frequency (Fig. 6E). Not only was there a smooth dependence of termination amplitude on stimulation frequency, we also uncovered a systematic change in termination latency on stimulation frequency such that higher frequency stimuli, to which neurons exhibited the strongest adaptation, resulted in shorter latencies and larger amplitudes (Schwartz et al., 2007). These observations indicate that adaptive processes carry information about changes in the temporal statistics of temporal sequences, that is, the termination of the stimulus.
Signals for changes in temporal statistics
To explore how adaptation might shape signals related to a change in the temporal statistics of our stimuli, we explored two distinct paradigms in which the sequences of punctate stimuli are varied. Because the model predicted responses to the absence of stimuli at the end of a sequence, we reasoned that the model may also predict responses when stimuli are removed during a stimulus sequence. Indeed, we find that our models consistently predict a response to an omitted stimulus, or an enhanced response to subsequent stimuli (Fig. 7A). This model prediction is exhibited in the responses of individual neurons when presented with the same stimulus train (Fig. 7B). Indeed, such omitted stimuli are particularly salient perceptually (Näätänen, 2018), mirroring the changes in activity we observe and predict from the model.
We next explored how model neurons respond to changes in the frequency of stimulation f, anticipating that signal strength may be related to the degree of frequency change should be present. We simulated responses from model neurons using filters fit from data to stimuli composed of an initial frequency (F1), which ranged between 1 and 15 Hz. Once the neuron had adapted to the initial frequency, the frequency switched abruptly to a new value, which also ranged between 1 and 15 Hz (F2; see Materials and Methods). Frequency increases resulted in changes in membrane potential depolarization with amplitudes that were related to the size of the frequency increase (Fig. 7C). We noticed two distinct response types in our dataset. When holding F1 constant and varying F2, some cells exhibited a transient response depending on F2 which then quickly settled to a common steady-state level (Fig. 7C, neuron 1). Other neurons exhibited a similar depolarization, but rather than repolarizing, maintained an elevated membrane potential for the duration of the stimulation, continuously conveying information about the value of F2 (Fig. 7C, neuron 2). When holding F2 constant while varying F1, similar patterns emerged (Fig. 7D). Surprisingly, in some neurons, although they settled to a common response amplitude independent of F1, they responded with distinct amplitudes when the frequency transitioned to the common F2 (Fig. 7D, neuron 3), showing that information about F1 was retained in the system's state, even though it was not manifest in the membrane potential. Furthermore, the effects of the distinct F1 rates lingered for nearly 2 s while responding to the common F2 (Fig. 7D, neuron 4). These transition responses suggest that stimulus history can affect dynamics at the membrane potential level for a long time, on the order of seconds.
How might stimulus history and the amplitude of the transition response be related? One possible model is that the change in overall frequency (F2-F1) determines the size of the response, which we term the linear model. In this case, the responses scale linearly with ΔF, regardless of the initial frequency. Another possibility is that the transition amplitude follows Weber's law. In the Weber model, the response to frequency change scales with respect to the ratio of F2 and F1 (F2/F1). In this case, the response to a frequency change depends on Δlog(F), regardless of the initial frequency (logarithmic model).
To determine whether the responses follow the linear or logarithmic model, we quantified the transition response amplitude to each frequency change (see Materials and Methods). We focused our analysis on values of F1 that ranged from 5 to 10 Hz and F2 values that increased F1's value by 1–5 Hz. We then performed a least-squares fit to each model. We obtained the slope (mln) and y intercept (bln) of the best fit line to the transition response amplitudes from an initial frequency of 5 Hz on a linear (F2-F1) x axis. The linear model was defined using the following equation (Fig. 7E):
A similar procedure was then performed to obtain the Weber's law slope (mwb) and y intercept (bwb) using the same response amplitudes as before on a Weber-like (F2/F1) x axis. The logarithmic model was defined using the following equation (Fig. 7F):
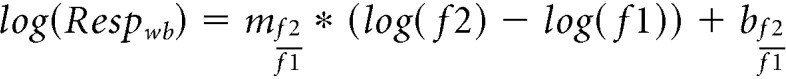 |
These two examples show that Neuron 2 exhibited linear responses, whereas Neuron 1 showed more logarithmic-like responses. To classify each neuron as following either the linear model, logarithmic model or neither, we used a correlation analysis, which removes shared correlation (Fig. 7F) (Movshon et al., 1986). We calculated partial correlations using the actual and predicted responses from each model to each stimulus condition using the following equations:
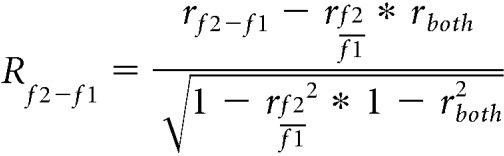 |
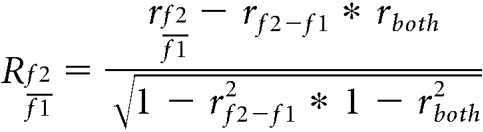 |
where rf2-f1 and rf2/f1 are the correlation between the respective model predictions and responses, and rboth is the correlation between the two model predictions. We then calculated Fisher z-transformed partial correlations using the following equations:
This analysis reveals that a sizeable proportion of the fitted neurons follow either the logarithmic or linear model (29 of 34: V1: 10 of 11; S1: 11 of 14; A1: 8 of 9). Of these, 59% (V1: 80%, S1: 36%, A1: 63%) significantly followed the logarithmic model. However, we found neurons in each sensory modality that carry signals related to linear changes in frequency as well as relative changes in frequency and that these distinctions reflect differences in our population in degree rather than category.
How do the response properties we observe emerge from our model? In our previous analysis, our model was composed of 4 filters and the filter timescales were set to a maximum of 2 s. How might changing these parameters affect the adaptive responses captured by our model? Figure 8 demonstrates the effect of these parameter choices on the predicted responses to a 10 Hz stimulus of an example fitted S1 neuron. For this neuron, as the number of filters increases (right hand column), the termination response emerges and approaches the amplitude observed in the data only using 4 filters. As filter length is varied (Fig. 8, bottom row), response attenuation is largely absent for 500 ms filters and only marginally, if at all, increases at 1000 ms, requiring 2000 ms filters to approach the experimental results. Although different neuron fits show different specific characteristics, this example demonstrates that both multiple filters and the long timescales used are required to capture the multiple components of the experimental responses.
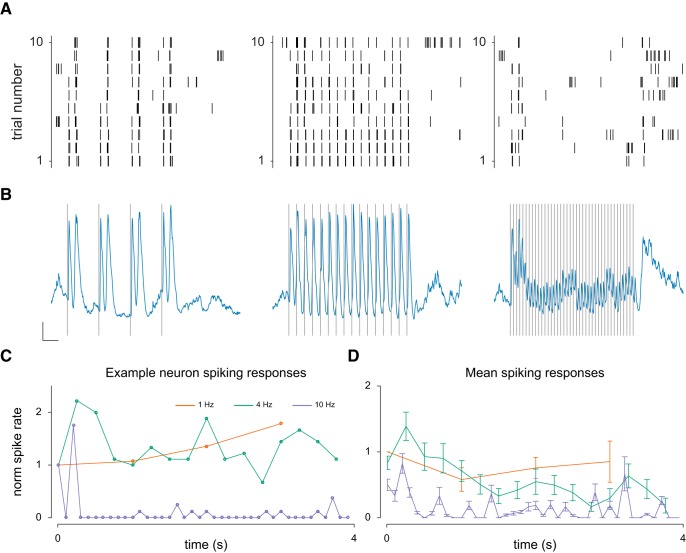
How does the adaptation observed in the membrane potential responses impact the spiking response? To investigate this, we measured response attenuation of spiking responses in 6 V1 neurons that had robust spiking responses (Fig. 9). The analysis was performed as before (see above section); however, because some neurons did not spike in response to the first stimulus pulse, responses were normalized to the first spiking response. Spiking responses exhibited similar patterns of response attenuation as the membrane potential (Fig. 9A,B), showing a decrease in response amplitude with higher stimulus frequencies (Fig. 9C,D).
Figure 9.
Adaptation of spiking responses. A, Example raster plots for a V1 neuron in response to a 1, 4, and 10 Hz stimulus. B, Average membrane potential responses of the example neuron from B. Calibration: y axis, 5 mV change; x axis, 500 ms. C, Normalized mean peak spiking rate responses to each pulse in a stimulus train at the three frequencies shown in A, B for the example neuron. D, Same as for C, but for the mean of 6 V1 neurons.
Discussion
We examined adaptation in visual, somatosensory, and auditory cortex using a common stimulus framework to uncover and compare their adaptive response properties.
In sensory coding, one aims to find a model that transforms recent sensory inputs into neural responses. While such transformations can account for some neural responses, adaptive changes occur over longer time scales that lead to systematic changes in the mapping of sensory inputs to neural responses. One approach to incorporate longer timescale changes is to create a model in which the function that transforms inputs to responses depends on the adaptive state of the network. Such a model is composed of two components: one that is sensitive to the recent sensory stimulation and another that is sensitive to the adaptive state of the system and whose value modulates the effects of the fast-varying component (Weber et al., 2019). We take an alternative approach: we integrate these two components directly into a single model in which the adaptive state of the network is not explicitly represented. This modeling framework mirrors that of the biophysical properties of neurons, which do not segregate into distinct adaptive and responsive components. For example, the short-term synaptic depression exhibited at the thalamocortical and cortical synapses acts on both fast and slow timescales (Abbott et al., 1997; Tsodykes and Markram, 1997). Short-term synaptic dynamics act both to transmit information at high frequencies and to store a trace of the stimulation history in the probability of the release of synaptic transmitter. As with these biophysical properties, the temporal filters we extracted from our neural data exhibit both short- and long-time scale features. We found this framework to be surprisingly effective in predicting the complex adaptive effects seen in our responses. Our results extend upon previous studies that have shown that many nonlinear properties of neural responses can be captured by summing independent subunits (Ozuysal and Baccus, 2012; McFarland et al., 2013; Freeman et al., 2015; Vintch et al., 2015; Harper et al., 2016). We find that, for each neuron, a fixed set of four filters spanning multiple timescales accounts for response dynamics across stimulation frequency, demonstrating that a single static model accounts for responses under distinct sensory contexts. Therefore, these adaptive changes can be compactly accounted for by modeling adaptation as an emergent property of fixed, but complex, neural responses.
We focused on three components of the adaptive sensory response: decreased response amplitude with increasing stimulus frequency, a shift in response complexity as stimulus frequency increases, and a termination response at the cessation of a high-frequency stimulus. We used common stimulus sets and analysis tools to study these response features across modalities, allowing us to demonstrate which are common across modalities and which are more specific. We find, for example, that decreases in response amplitude with increased stimulus frequency are shared across modalities but vary in degree. The frequency dependence of response complexity was common to both S1 and V1. While individual A1 neurons had distinct response dynamics, we did not find a frequency-dependent shift in those dynamics. Finally, all modalities demonstrated a termination response following the end of stimulation in at least some of the neurons.
These response characteristics emerge from our model. We demonstrate that a general model built from responses to stochastic stimuli, sampled over a broad statistical range, can dissect complex neural responses to fixed-interval stimuli into simpler components to reveal general features of sensory adaptation. The emergence of these adaptive features relies on a model composed of multiple filters. When a model composed of a single filter is used, overall model performance sharply declines. The specific adaptive responses to fixed frequency seen in our data are absent from single-filter model responses. The use of multiple filters with associated nonlinear transformations accounts for the ability of our model to generate these adaptive responses. Adaptive changes have been demonstrated to exist on multiple timescales and in a large variety of contexts (e.g., visual contrast adaptation, auditory stimulus-specific adaptation). While adaptation is typically studied relative to controlled changes in defined stimulus statistics, such as contrast, here we propose relevant stimulus statistics in an unsupervised way through its sensory filters. Our fixed-filter model offers a parsimonious description of the membrane potential responses that does not require explicitly modeling different adaptation or network states and estimating the stimulus–response function in each state.
Sensory adaptation has been shown to enhance change detection in behavioral tasks (Goble and Hollins, 1993; Tannan et al., 2007; Musall et al., 2014). Here, we uncovered frequency transition responses whose amplitude and length are related to the neurons' stimulus history. Neurons in our dataset showed a transition response amplitude in a pattern that varied between a linear or a Weber's law-like response across all modalities. These results demonstrate how adaptive processes act to preserve essential frequency information across long timescales.
There was a noticeable degree of variation both between and within modalities. For instance, A1 neurons did not display the same changes in response complexity and envelope with stimulus frequency that occur in V1 and S1 neurons. Some differences across sensory modality, such as these, should be expected, as each system is likely calibrated to deal with the specific statistics of its relevant sensory information. Our simple model, however, was able to capture these differences in response dynamics.
Our recordings were all performed in primary sensory areas in cortex. It is likely, however, that some of the effects described either originate or are influenced by subcortical areas, potentially as far back as the receptors themselves. Work using similar stimuli while recording from retinal ganglion cells has found some similar phenomena to those we described, notably the termination response (Schwartz et al., 2007; Schwartz and Berry, 2008). This may differ by sensory system, as a recent study using fiber photometry failed to find a termination (or echo) response in the auditory thalamus (Li et al., 2017). Both the biphasic response to individual pulses (or low-frequency stimulation) and response attenuation at high stimulus frequencies have also been reported subcortically (Chung et al., 2002; Martin-Cortecero and Nuñez, 2014; Funayama et al., 2016). In the visual system, a recent study found that biphasic responses exist in the LGN, but not in the retina (Funayama et al., 2016). Adaptation cascades through sensory streams, which may occur between cortical layers (Dhruv and Carandini, 2014), which we cannot directly address. Such an analysis might be complicated by the distinct thalamic projections that converge on layer 2/3 and layer 4 neurons (Wise and Jones, 1978; Huang and Winer, 2000; Jones, 2009; Krahe et al., 2011; Cruz-Martín et al., 2014; Bickford et al., 2015; Ji et al., 2016).
Another possible factor that may explain differences across modalities is the intensity of stimulation, which was not calibrated to evoke similar response magnitude across systems. Indeed, our previous studies of the somatosensory system showed that stimulus intensity entails different adaptation profiles, already observed in the trigeminal nerve (Ganmor et al., 2010; Mohar et al., 2013). Cortical mechanisms, and specifically inhibition, can determine the degree of recovery from adaptation (Cohen-Kashi Malina et al., 2013). Inhibitory effects can vary across cortical areas and thus differently shape their adaptation behavior. It is also possible that adaptation is altered by the urethane anesthesia used in our experiments. Studies examining general sensory properties in visual cortex have found little effect of urethane on response properties (Durand et al., 2016), although effects may exist in other modalities.
A key aspect of our approach is the standardization of experimental paradigms across sensory modalities. This allows investigation to go beyond modality-specific analysis of neuronal computations to that of the underlying algorithms used across systems. Here we focused on adaptation, but this approach may have value in the study of other processes common in sensory cortex. For example, forms of contrast gain control, which has historically been studied in the visual cortex (Sclar et al., 1985), have been reported in the auditory (Rabinowitz et al., 2011; Cooke et al., 2018) and somatosensory cortices (Garcia-Lazaro et al., 2007). Understanding of this phenomenon may benefit from a cross-modal approach, such as the one used here. Recent decision-making paradigms in rodents have used similar punctate stimuli in auditory, visual, and multisensory tasks, but these experiments have focused on higher-order cortical computations rather than primary sensory representations (Brunton et al., 2013; Raposo et al., 2014; Hanks et al., 2015).
The homology of cortical circuits had led many to hypothesize that different regions of cortex share a computational framework (Douglas and Martin, 2004). A certain degree of specialization among cortical areas is to be expected (Yang and Zador, 2012), but it is possible that one defining difference among cortical areas is simply the input each region receives (Sharma et al., 2000). Our results demonstrate that each of these primary sensory areas integrates information across multiple comparable timescales, yielding complex response dynamics. A change in the state of the network is therefore not required for these complex dynamics to occur, but rather can be understood as the interplay of multiple static sensory filters that span a range of relevant time scales.
Footnotes
This work was supported by the Human Frontiers Science Program to A.L.F., I.L., I.N. and N.J.P., and the Washington Research Foundation, University of Washington Institute of Neuroengineering to A.L.F. A.L.F. thanks Máté Lengyel for helpful discussions.
The authors declare no competing financial interests.
References
- Abbott LF, Varela JA, Sen K, Nelson SB (1997) Synaptic depression and cortical gain control. Science 275:220–224. 10.1126/science.275.5297.221 [DOI] [PubMed] [Google Scholar]
- Aljadeff J, Lansdell BJ, Fairhall AL, Kleinfeld D (2016) Analysis of neuronal spike trains, deconstructed. Neuron 91:221–259. 10.1016/j.neuron.2016.05.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickford ME, Zhou N, Krahe TE, Govindaiah G, Guido W (2015) Retinal and tectal “driver-like” inputs converge in the shell of the mouse dorsal lateral geniculate nucleus. J Neurosci 35:10523–10534. 10.1523/JNEUROSCI.3375-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. (1997) The psychophysics toolbox. Spat Vis 10:433–436. 10.1163/156856897X00357 [DOI] [PubMed] [Google Scholar]
- Brenner N, Bialek W, de Ruyter van Steveninck R (2000) Adaptive rescaling maximizes information transmission. Neuron 26:695–702. 10.1016/S0896-6273(00)81205-2 [DOI] [PubMed] [Google Scholar]
- Brunton BW, Botvinick MM, Brody CD (2013) Rats and humans can optimally accumulate evidence for decision-making. Science 340:95–98. 10.1126/science.1233912 [DOI] [PubMed] [Google Scholar]
- Bullock TH, Hofmann MH, Nahm FK, New JG, Prechtl JC (1990) Event-related potentials in the retina and optic tectum of fish. J Neurophysiol 64:903–914. 10.1152/jn.1990.64.3.903 [DOI] [PubMed] [Google Scholar]
- Bullock TH, Karamürsel S, Hofmann MH (1993) Interval-specific event related potentials to omitted stimuli in the electrosensory pathway in elasmobranchs: an elementary form of expectation. J Comp Physiol A 172:501–510. 10.1007/BF00213532 [DOI] [PubMed] [Google Scholar]
- Cohen-Kashi Malina K, Jubran M, Katz Y, Lampl I (2013) Imbalance between excitation and inhibition in the somatosensory cortex produces postadaptation facilitation. Journal of Neuroscience 33:8463–8471. 10.1523/jneurosci.4845-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung S, Li X, Nelson SB (2002) Short-term depression at thalamocortical synapses contributes to rapid adaptation of cortical sensory responses in vivo. Neuron 34:437–446. 10.1016/S0896-6273(02)00659-1 [DOI] [PubMed] [Google Scholar]
- Cooke JE, King AJ, Willmore BD, Schnupp JW (2018) Contrast gain control in mouse auditory cortex. J Neurophysiol 120:1872–1884. 10.1152/jn.00847.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cruz-Martín A, El-Danaf RN, Osakada F, Sriram B, Dhande OS, Nguyen PL, Callaway EM, Ghosh A, Huberman AD (2014) A dedicated circuit links direction-selective retinal ganglion cells to the primary visual cortex. Nature 507:358–361. 10.1038/nature12989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dealy RS, Tolhurst DJ (1974) Is spatial adaptation an after-effect of prolonged inhibition? J Physiol 241:261–270. 10.1113/jphysiol.1974.sp010652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Ruyter van Steveninck R, Bialek W (1988) Real-time performance of a movement-sensitive neuron in the blowfly visual system: coding and information transfer in short spike sequences. Proc R Soc Lond B Biol Sci 234:379–414. 10.1098/rspb.1988.0055 [DOI] [Google Scholar]
- Dhruv NT, Carandini M (2014) Cascaded effects of spatial adaptation in the early visual system. Neuron 81:529–535. 10.1016/j.neuron.2013.11.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas RJ, Martin KA (2004) Neuronal circuits of the neocortex. Annu Rev Neurosci 27:419–451. 10.1146/annurev.neuro.27.070203.144152 [DOI] [PubMed] [Google Scholar]
- Durand S, Iyer R, Mizuseki K, de Vries S, Mihalas S, Reid RC (2016) A comparison of visual response properties in the lateral geniculate nucleus and primary visual cortex of awake and anesthetized mice. J Neurosci 36:12144–12156. 10.1523/JNEUROSCI.1741-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fairhall AL. (2014) Adaptation and natural stimulus statistics. In: The cognitive neurosciences (Gazzaniga MS, Mangun GR, eds). Cambridge, MA: Massachusetts Institute of Technology. [Google Scholar]
- Freeman J, Field GD, Li PH, Greschner M, Gunning DE, Mathieson K, Sher A, Litke AM, Paninski L, Simoncelli EP, Chichilnisky EJ (2015) Mapping nonlinear receptive field structure in primate retina at single cone resolution. Elife 4:e05241. 10.7554/eLife.05241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funayama K, Minamisawa G, Matsumoto N, Ban H, Chan AW, Matsuki N, Murphy TH, Ikegaya Y (2015) Neocortical rebound depolarization enhances visual perception. PLoS Biol 13:1–25. 10.1371/journal.pbio.1002231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funayama K, Hagura N, Ban H, Ikegaya Y (2016) Functional organization of flash-induced V1 offline reactivation. J Neurosci 36:11727–11738. 10.1523/JNEUROSCI.1575-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganmor E, Katz Y, Lampl I (2010) Intensity-dependent adaptation of cortical and thalamic neurons is controlled by brainstem circuits of the sensory pathway. Neuron 66:273–286. 10.1016/j.neuron.2010.03.032 [DOI] [PubMed] [Google Scholar]
- Garcia-Lazaro JA, Ho SS, Nair A, Schnupp JW (2007) Shifting and scaling adaptation to dynamic stimuli in somatosensory cortex. Eur J Neurosci 26:2359–2368. 10.1111/j.1460-9568.2007.05847.x [DOI] [PubMed] [Google Scholar]
- Garrido MI, Kilner JM, Stephan KE, Friston KJ (2009) The mismatch negativity: a review of underlying mechanisms. Clin Neurophysiol 120:453–463. 10.1016/j.clinph.2008.11.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goble AK, Hollins M (1993) Vibrotactile adaptation enhances amplitude discrimination. J Acoust Soc Am Sci 93:418–424. 10.1121/1.405621 [DOI] [PubMed] [Google Scholar]
- Hamm JP, Yuste R (2016) Somatostatin interneurons control a key component of mismatch negativity in mouse visual cortex. Cell Rep 16:597–604. 10.1016/j.celrep.2016.06.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks TD, Kopec CD, Brunton BW, Duan CA, Erlich JC, Brody CD (2015) Distinct relationships of parietal and prefrontal cortices to evidence accumulation. Nature 520:220–223. 10.1038/nature14066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper NS, Schoppe O, Willmore BD, Cui Z, Schnupp JW, King AJ (2016) Network receptive field modeling reveals extensive integration and multi-feature selectivity in auditory cortical neurons. PLoS Comput Biol 12:e1005113. 10.1371/journal.pcbi.1005113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitman A, Brackbill N, Greschner M, Sher A, Litke AM, Chichilnisky EJ (2016) Testing pseudo-linear models of responses to natural scenes in primate retina. bioRxiv. Advance online publication. Retrieved December 7, 2016 Doi: 10.1101/045336. [DOI] [Google Scholar]
- Huang CL, Winer JA (2000) Auditory thalamocortical projections in the cat: laminar and areal patterns of input. J Comp Neurol 427:302e331. [DOI] [PubMed] [Google Scholar]
- Ji XY, Zingg B, Mesik L, Xiao Z, Zhang LI, Tao HW (2016) Thalamocortical innervation pattern in mouse auditory and visual cortex: laminar and cell-type specificity. Cereb Cortex 26:2612–2625. 10.1093/cercor/bhv099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones EG. (2009) Synchrony in the interconnected circuitry of the thalamus and cerebral cortex. Ann N Y Acad Sci 1157:10–23. 10.1111/j.1749-6632.2009.04534.x [DOI] [PubMed] [Google Scholar]
- Karamürsel S, Bullock TH (1994) Dynamics of event-related potentials to trains of light and dark flashes: responses to missing and extra stimuli in elasmobranch fish. Electroencephalogr Clin Neurophysiol 90:461–471. 10.1016/0013-4694(94)90138-4 [DOI] [PubMed] [Google Scholar]
- Khatri V, Hartings JA, Simons DJ (2004) Adaptation in thalamic barreloid and cortical barrel neurons to periodic whisker deflections varying in frequency and velocity. J Neurophysiol 92:3244–3254. 10.1152/jn.00257.2004 [DOI] [PubMed] [Google Scholar]
- Kheradpezhouh E, Adibi M, Arabzadeh E (2017) Response dynamics of rat barrel cortex neurons to repeated sensory stimulation. Sci Rep 7:1–10. 10.1038/s41598-017-11477-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krahe TE, El-Danaf RN, Dilger EK, Henderson SC, Guido W (2011) Morphologically distinct classes of relay cells exhibit regional preferences in the dorsal lateral geniculate nucleus of the mouse. J Neurosci 31:17437–17448. 10.1523/JNEUROSCI.4370-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Liao X, Zhang J, Wang M, Yang N, Zhang J, Lv G, Li H, Lu J, Ding R, Li X, Guang Y, Yang Z, Qin H, Jin W, Zhang K, He C, Jia H, Zeng S, Hu Z, et al. (2017) Primary auditory cortex is required for anticipatory motor response. Cereb Cortex 27:3254–3271. 10.1093/cercor/bhx079 [DOI] [PubMed] [Google Scholar]
- Maheswaranathan N, Kastner DB, Baccus SA, Ganguli S (2018) Inferring hidden structure in multilayered neural circuits. PLoS Comput Biol 14:e1006291. 10.1371/journal.pcbi.1006291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin-Cortecero J, Nuñez A (2014) Tactile response adaptation to whisker stimulation in the lemniscal somatosensory pathway of rats. Brain Res 1591:27–37. 10.1016/j.brainres.2014.10.002 [DOI] [PubMed] [Google Scholar]
- McFarland JM, Cui Y, Butts DA (2013) Inferring nonlinear neuronal computation based on physiologically plausible inputs. PLoS Comput Biol 9:e1003143. 10.1371/journal.pcbi.1003143 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh LT, Maheswaranathan N, Nayebi A, Ganguli S, Baccus SA (2016) Deep learning models of the retinal response to natural scenes. Adv Neural Inf Process Syst 29:1369–1377. [PMC free article] [PubMed] [Google Scholar]
- Mease RA, Lee S, Moritz AT, Powers RK, Binder MD, Fairhall AL (2014) Context-dependent coding in single neurons. J Comput Neurosci 37:459–480. 10.1007/s10827-014-0513-9 [DOI] [PubMed] [Google Scholar]
- Meir I, Katz Y, Lampl I (2018) Membrane potential correlates of network decorrelation and improved SNR by cholinergic activation in the somatosensory cortex. J Neurosci 38:1159–1218. 10.1523/JNEUROSCI.1159-18.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohanty D, Scholl B, Priebe NJ (2012) The accuracy of membrane potential reconstruction based on spiking receptive fields. J Neurophysiol 107:2143–2153. 10.1152/jn.01176.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohar B, Katz Y, Lampl I (2013) Opposite adaptive processing of stimulus intensity in two major nuclei of the somatosensory brainstem. J Neurosci 33:15394–15400. 10.1523/jneurosci.1886-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Adelson EH, Gizzi MS, Newsome WT (1986) The analysis of oving visual patterns. Exp Brain Res [Suppl 2]:117–151. 10.1007/978-3-662-09224-8_7 [DOI] [Google Scholar]
- Musall S, von der Behrens W, Mayrhofer JM, Weber B, Helmchen F, Haiss F (2014) Tactile frequency discrimination is enhanced by circumventing neocortical adaptation. Nat Neurosci 17:1567–1573. 10.1038/nn.3821 [DOI] [PubMed] [Google Scholar]
- Näätänen R. (2018) Attention and brain function. Routledge: London, New York. [Google Scholar]
- Näätänen R, Gaillard AW, Mäntysalo S (1978) Early selective-attention effect on evoked potential reinterpreted. Acta Psychol 42:313–329. 10.1016/0001-6918(78)90006-9 [DOI] [PubMed] [Google Scholar]
- Ozuysal Y, Baccus SA (2012) Linking the computational structure of variance adaptation to biophysical mechanisms. Neuron 73:1002–1015. 10.1016/j.neuron.2011.12.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park IM, Archer EW, Priebe N, Pillow JW (2013) Spectral methods for neural characterization using generalized quadratic models. Adv Neural Inf Process Syst 2454–2462. Lake Tahoe, California. [Google Scholar]
- Pelli DG. (1997) The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis 10:437–442. 10.1163/156856897X00366 [DOI] [PubMed] [Google Scholar]
- Pillow JW, Paninski L, Uzzell VJ, Simoncelli EP, Chichilnisky EJ (2005) Prediction and decoding of retinal ganglion cell responses with a probabilistic spiking model. J Neurosci 25:11003–11013. 10.1523/JNEUROSCI.3305-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, Simoncelli EP (2008) Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 454:995–999. 10.1038/nature07140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabinowitz NC, Willmore BD, Schnupp JW, King AJ (2011) Contrast gain control in auditory cortex. Neuron 70:1178–1191. 10.1016/j.neuron.2011.04.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raposo D, Kaufman MT, Churchland AK (2014) A category-free neural population supports evolving demands during decision-making. Nat Neurosci 17:1784–1792. 10.1038/nn.3865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringach DL, Malone BJ (2007) The operating point of the cortex: neurons as large deviation detectors. J Neurosci 27:7673–7683. 10.1523/JNEUROSCI.1048-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachidhanandam S, Sreenivasan V, Kyriakatos A, Kremer Y, Petersen CC (2013) Membrane potential correlates of sensory perception in mouse barrel cortex. Nat Neurosci 16:1671–1677. 10.1038/nn.3532 [DOI] [PubMed] [Google Scholar]
- Sahani M, Linden JF (2003) How linear are auditory cortical responses? Adv Neural Inf Process Syst 125–132. Vancouver, British Columbia, Canada. [Google Scholar]
- Scholl B, Tan AY, Corey J, Priebe NJ (2013) Emergence of orientation selectivity in the mammalian visual pathway. J Neurosci 33:10616–10624. 10.1523/jneurosci.0404-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz G, Berry MJ 2nd (2008) Sophisticated temporal pattern recognition in retinal ganglion cells. J Neurophysiol 99:1787–1798. 10.1152/jn.01025.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz G, Harris R, Shrom D, Berry MJ 2nd (2007) Detection and prediction of periodic patterns by the retina. Nat Neurosci 10:552–554. 10.1038/nn1887 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz O, Pillow JW, Rust NC, Simoncelli EP (2006) Spike-triggered neural characterization. J Vis 6:484–507. 10.1167/6.4.13 [DOI] [PubMed] [Google Scholar]
- Sclar G, Ohzawa I, Freeman RD (1985) Contrast gain control in the cat's visual system. J Neurophysiol 54:668–675. 10.1152/jn.1985.54.3.668 [DOI] [PubMed] [Google Scholar]
- Sharma J, Angelucci A, Sur M (2000) Induction of visual orientation modules in auditory cortex. Nature 404:841–847. 10.1038/35009043 [DOI] [PubMed] [Google Scholar]
- Shelhamer M. (2007) Nonlinear dynamics in physiology: a state-space approach. Singapore: World Scientific. [Google Scholar]
- Simoncelli EP, Olshausen BA (2001) Natural image statistics and neural representation. Annu Rev Neurosci 24:1193–1216. 10.1146/annurev.neuro.24.1.1193 [DOI] [PubMed] [Google Scholar]
- Stefanics G, Jan Kremlácek J, Czigler I (2014) Visual mismatch negativity: a predictive coding view. Front Hum Neurosci 8:666. 10.3389/fnhum.2014.00666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tannan V, Simons S, Dennis RG, Tommerdahl M (2007) Effects of adaptation on the capacity to differentiate simultaneously delivered dual-site vibrotactile stimuli. Brain Res 1186:164–170. 10.1016/j.brainres.2007.10.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodykes M, Markram R (1997) The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci U S A 94:719–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vintch B, Movshon JA, Simoncelli EP (2015) A convolutional subunit model for neuronal responses in macaque V1. J Neurosci 35:14829–14841. 10.1523/JNEUROSCI.2815-13.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber AI, Krishnamurthy K, Fairhall AL (2019) Coding principles in adaptation. Annu Rev Vis Sci 5:427–449. 10.1146/annurev-vision-091718-014818 [DOI] [PubMed] [Google Scholar]
- Wise SP, Jones EG (1978) Developmental studies of thalamocortical and commissural connections in the rat somatic sensory cortex. J Comp Neurol 178:187–208. 10.1002/cne.901780202 [DOI] [PubMed] [Google Scholar]
- Yang Y, Zador AM (2012) Differences in sensitivity to neural timing among cortical areas. J Neurosci 32:15142–15147. 10.1523/JNEUROSCI.1411-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]