Deep Learning Benchmarks on L1000 Gene Expression Data

Abstract

Gene expression data can offer deep, physiological insights beyond the static coding of the genome alone. We believe that realizing this potential requires specialized, high-capacity machine learning methods capable of using underlying biological structure, but the development of such models is hampered by the lack of published benchmark tasks and well characterized baselines.

In this work, we establish such benchmarks and baselines by profiling many classifiers against biologically motivated tasks on two curated views of a large, public gene expression dataset (the LINCS corpus) and one privately produced dataset. We provide these two curated views of the public LINCS dataset and our benchmark tasks to enable direct comparisons to future methodological work and help spur deep learning method development on this modality.

In addition to profiling a battery of traditional classifiers, including linear models, random forests, decision trees, K nearest neighbor (KNN) classifiers, and feed-forward artificial neural networks (FF-ANNs), we also test a method novel to this data modality: graph convolutional neural networks (GCNNs), which allow us to incorporate prior biological domain knowledge.

We find that GCNNs can be highly performant, with large datasets, whereas FF-ANNs consistently perform well. Non-neural classifiers are dominated by linear models and KNN classifiers.

I. Introduction

GENE expression data offers a view beyond the static genome into the dynamic workings of the cell. The potential utility of this data modality is staggering, and biologists have accrued a mass of domain knowledge regarding how gene expression is regulated, providing extensive, if complicated and uncertain, structure around these data. Further, the availability of large-scale, heterogeneous gene expression datasets is rapidly on the rise, fueled both by falling costs and development of new gene expression profiling technologies [1].

Simultaneous with the increasing availability of gene expression data, deep learning techniques have grown vastly more powerful and popular—showing advances in image processing [2]–[4], natural language processing [5]–[7], and speech recognition/generation [8], [9], among other fields. In some limited areas, these advances have also translated into the biomedical domain—for example, in analyzing mass spectrometry spectra [10], DNA sequences [11], amino acid sequences [12]–[14], or biomedical images [2], [3].

However, among non-sequential, non-imaging modalities, such as gene expression data, “deep” learning methods generally remain limited to simple, unstructured, shallow modeling techniques. In particular, while large-scale benchmarks such as the ImageNet challenge¹ and the existence of an underlying mathematical structure have fueled the development of convolutional neural networks (CNNs) for image processing or recurrent neural network (RNNs) for sequential analysis, bioinformaticians are limited to unstructured feed-forward artificial neural networks (FF-ANNs), which are known to be relatively inefficient learners [17].

In this work, we aim to lay a foundation that will help deep learning succeed for gene expression data as it has in these other domains by providing a fixed definition of success via benchmarks and offering a potential avenue for using structure to create more intelligent modeling approaches. In particular, we define three biologically motivated benchmarking tasks over two curated views² of the public L1000 LINCS dataset and one privately produced gene expression dataset. On each task, we profile K nearest neighbor (KNN) classifiers, decision trees, random forests (RFs), linear classifiers, and two neural classifiers: feed-forward artificial neural networks (FF-ANNs) and graph convolutional neural networks (GCNNs). GCNNs generalize the notion of convolutional neural networks (CNNs) onto data structured over arbitrary graphs and allow us to use prior biological knowledge, namely regulatory relationships between pairs of genes, to more intelligently model these data. To the best of our knowledge, this is the first work that uses these techniques to classify gene expression profiles.

We find that GCNNs can be performant, but require large amounts of data, excelling at all tasks on our largest dataset, but under-performing FF-ANNs on our smaller datasets. Of other methods, FF-ANNs perform best, followed consistently by linear classifiers, then random forests, then decision trees. KNN classifiers perform very well on our larger datasets, nearly matching FF-ANNs, but they underwhelm on our smaller datasets.

Gene expression datasets often contain many samples spanning a much smaller set of subjects, as a single subject’s gene expression profile may be taken many times under varying conditions (e.g., drugs, etc.). As such, an important, distinct measure from traditional performance metrics (e.g., per-sample accuracy, which is appropriate for model development but not pre-deployment assessments) is per-subject accuracy(i.e., generalization to unseen subjects). In addition to our per-sample benchmarks on the LINCS corpus, we assess per-subject accuracy on a private, smaller L1000 corpus and find that all methods struggle to generalize to unseen subjects, showing performance drops ranging from 10 to 18 percent of their per-sample accuracies.

In sum, in this work we make the following contributions:

1. We establish biologically meaningful classification benchmarks at deep learning scale on the largest publicly available gene expression dataset. This is important because absent a shared, consistent view of the data and definition of success, deep learning method development is severely hampered.

2. We profile a number of classifiers on these tasks, including non-neural methods and two variants of neural networks, one of which incorporates prior biological knowledge and, to the best of our knowledge, has never been profiled on this data modality.

3. We profile these same classifiers on a similar task on a smaller, privately produced gene expression corpus to assess which techniques work well in data-starved environments.

4. We assess how well these techniques transfer to unseen subjects to assess population-level generalizability.

II. Background & Related Work

A. Gene Expression Data

1). The Biology:

The cellular system is governed by the genome: the sequence of DNA base pairs that encode all information necessary for the cell’s development and functioning. In order to process DNA into useful cellular work, the cell first transcribes genes into messenger RNA (mRNA), which is then shuttled towards cellular organelles that translate mRNA sequences into proteins: amino-acid built macromolecules that carry out all of the necessary functions of the cell. A cell’s gene expression profile quantifies how actively these genes are being expressed (i.e., transcribed and translated into proteins) and thus provides a view into the dynamic state of the cell beyond the fixed picture offered by the genome alone.

A single cell’s gene expression patterns will vary over time and in response to environmental conditions, such as exposure to drugs, along with intracellular factors, such as the other proteins in the cellular environment. Understanding the genetic regulatory network (i.e., which factors govern transcription of what and how) is a topic of intense study [18].

2). Measuring Gene Expression/Transcriptomics:

Gene expression can be quantified in many ways. Two broad categories of gene expression data are proteomics, which directly measures the quantities of produced proteins within the cell, and transcriptomics, which measures the quantities of produced mRNA transcripts within the cell (Figure 1). Transcriptomic gene expression is far more easily measured and will be our focus in this work [19], [20].

Fig. 1.

Transcriptomics data is measured by quantifying the mRNA produced during transcription. The output of this process is a vector with each dimension quantifying the expression of a particular gene. Both technical (e.g., misplaced reads) and biological (e.g., tissue type) factors add variance to these data. Images: [21], [22]

Note that there is not a direct correspondence between these two measurement techniques. Protein production is heavily regulated post-transcription, and in using transcriptomic data, we ignore these additional layers of biological processing in favor of the increased availability of data.

3). Measurement Techniques:

Transcriptomics data itself can be measured by many techniques, including RNA-Seq, single-cell RNA-Seq, and the L1000 platform, which we focus on here. The L1000 platform [1] is notably cheaper per-sample than other transcriptomics techniques, but both measures fewer genes³ than other technologies, focusing on only 978 “landmark genes,” and is noisier than some alternatives as it requires additional layers of processing which instills greater technical variability. Despite these problems, the low price point of L1000 has enabled the creation of large scale public datasets, such as the approximately 1.3M sample LINCS dataset, which is available on GEO at accession number GSE92742.⁴

L1000 data is often used at one of two levels of pre-processing:

a). Level 4 (a.k.a. Roast):

Level 4 data is fully normalized, plate-controlled, and z-scored, and presented at the level of one profile per sample.

b). Level 5 (a.k.a. Brew):

Level 5 data takes the Level 4 data and aggregates samples under identical technical conditions into a single averaged view of that profile (see [1] for full details). This process reduces variance, but also severely reduces dataset size. This variance reduction is useful for traditional bioinformatics, but it is not clear how helpful it should be for deep learning methods which generally prefer to automatically learn how to extract features from the most raw view of data possible. We would like our classifiers to be able to fully account for the technical variability inherent between repeated measurements, but using Level 5 data would deprive us of that opportunity while costing a significant number of input samples. On the other hand, Level 5 data may be of higher quality.

4). Experimental Pipelines:

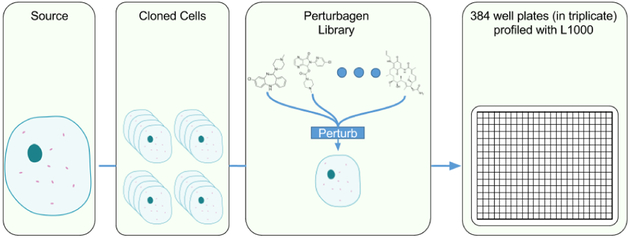
Often (though not universally) experimental pipelines producing large corpora of gene expression data work by acquiring some base cellular sample, either subject derived or via a stock cell line, cloning that cell line extensively, then perturbing a number of samples and profiling them (Figure 2). In this way, these datasets often have many more samples than cellular sources. This can lead to population-specific over-fitting, where a model specializes only to the population within the corpus and, despite generalizing to unseen samples within the corpus, the model will fail to generalize to unseen cellular sources.

Fig. 2.

Gene expression corpora are often produced by cloning a small number of cellular sources, then perturbing and profiling those clones. Image:[21].

Experimental pipelines also often show highly skewed distributions of perturbagen frequency, as common perturbagens may be profiled across many cell sources but more niche perturbagens will be profiled in isolation only on some smaller subset of cell lines. This problem is even more extreme considering “control” substances, such as DMSO, which are often profiled many more times than other compounds to provide a rigid baseline. As a result, attempting to evaluate machine learning models across perturbagens can be difficult as one must account for these biases in the dataset.

B. Deep Learning on Gene Expression Data

Deep learning techniques have been applied widely in the biomedical domain, using both structured, truly deep modeling frameworks on imaging or sequential modalities as well as unstructured models on other domains [23]. In this section, we will explore in greater depth those applications of neural network techniques on gene expression data.

1). Traditional Analyses:

Traditional analyses on these data focus on statistical or geometric tests for differential gene expression [24], gene set enrichment analyses (GSEA) [25], and (for the L1000 platform specifically) signature based analyses [1], [26]. Some have also used tensor decomposition/completion to disentangle cell-type from perturbagen effects [27], [28], and explored traditional classifiers for adverse drug event prediction [29].

2). Neural Representation Learning:

Other authors have used neural network models to build embeddings of gene expression data. In [30], the authors use a twin network architecture to represent gene expression profiles as 100 diensional bar-codes. They actually use the inherently high technical variability of this modality as a learning signal, by training their network to learn an embedding that minimizes distances between replicated samples. In [31], the authors use a sparse autoencoder to analyze binarized yeast differential gene expression microarray data. Post-training analyses found overlaps between transcription-factor mediated regulatory relationships and the connections trained by their network between the first two layers. In [32], the authors explore neural network mediated dimensionality reduction for single cell RNA-Seq data, augmenting traditional networks by adding nodes to the first hidden layer according to known transcription factor or protein-protein interactions, and only connecting input gene nodes to those regulatory or interaction nodes as dictated by prior biological knowledge.

3). Neural Classification & Regression:

In [33], authors use a FF-ANN to classify profiles into categories based on the therapeutic effect of the generating perturbagen. Researchers have also explored neural techniques for extrapolating the L1000 set of landmark genes to the full transcriptome. In [34] and [35], authors use a 3 hidden layer feed forward network to perform gene expression extrapolation from the L1000 landmark set.

Some authors have also attempted to use other modeling techniques on gene expression Data. In [36], the authors first reindex the gene expression vector according to chromosome position, reasoning that genes near one-another on the chromosome are more likely to interact, then reshape this one-dimensional vector into a two-dimensional square image and process it with a two dimensional convolutional neural network (CNN). This approach is very misguided as it asserts a set of spatial invariances (locality, translation, etc.) which CNNs require and are satisfied in image processing but do not apply to arbitrarily reshaped gene expression data. Nevertheless, as this approach allows the authors to model non-linear affects, it does offer strong performance on their task.

C. Structured Models via Graph Convolutional Networks

1). Regulatory Graphs:

As stated in Section II-A1, gene expression is regulated by complex processes and is a topic of intense study. What we do know of gene expression regulation is often envisioned as a graph (such as in Figure 3) with genes forming the vertices of this graph and edges between genes representing regulatory relationships between those two genes.

Fig. 3.

The regulatory relationships between L1000 landmark genes, as determined according to [37]. Nodes (red dots) are genes and edges between them represent known or suspected regulatory interactions. Note that many genes only have one known edge connecting them to much denser clusters within the center of the graph. This may reflect biological processes, or that some proteins are studied much more than others.

Many of these relationships are only suspected, and as biologists have yet to study all possible interactions between sets of genes, these graphs are biased towards representing commonly studied proteins. Additionally, regulatory relationships themselves depend on cell type and, even within a single cell, they change in response to perturbations and environmental conditions, among other factors. Nonetheless, these “regulatory graphs” present at least a partial encoding of the biological understanding of relationships between different genes, and we use them here to augment neural classifiers with domain knowledge via GCNNs. Regulatory graphs are usually directed, but in this work we consider them as undirected graphs for simplicity.

2). Graph Convolutional Networks in Theory:

GCNNs are extensions of CNNs onto data defined over arbitrary graphs. Qualitatively, we can think of these networks as attempting to analyze data whose features are nodes in a graph by repeatedly summarizing the features within local neighborhoods of the graph, before aggregating those features into higher level signals spanning larger regions of the graph. This is directly analogous to how convolutional neural networks for image processing learn featurizations of local patches of the image, then pool those signals over larger windows.

There are two main strategies to generalize a CNN to other domains: the spectral approach, which generalizes the notion of a Fourier transform onto a graph via the graph Laplacian, and the locality approach, which uses the idea of processing data defined in local patches via neighborhoods in the graph more directly. GCNNs must also generalize the notion of “pooling” onto graphs, which they generally do via graph clustering algorithms, using the resulting node clusters to determine pooling neighborhoods.

GCNNs promise to bring the normalization obtained via weight sharing over consecutive convolution and pooling operations to features defined over any arbitrary graph, but they present their own challenges. Both local and spectral methods present computational challenges, and efficient graph pooling algorithms must use approximate solutions for NP-hard graph clustering problems. In practice, many operations are approximated, which affects the power of these models.

3). Graph Convolutional Networks in Practice:

Graph convolutional networks are often used in forming predictions at the node level, or in classifying whole graphs. For example, [38] explored node classification on knowledge and citation graphs. In this vein, GCNNs have also been used in several biological tasks. For example, [39] classifies proteins viewed as nodes in varying tissue-specific protein protein interaction graphs, [40] learns representations of molecular compounds interpreted as unique graphs with vertices determined by atoms and edges by bonds, [41] classifies polypharmacological interactions as edges of a drug and protein interaction graph, and [42] learns representations of graphs defined by protein three dimensional structure for protein interface prediction.

These node classification tasks differ from our context, where we wish to make predictions over a set of gene expression profiles, each of whose individual feature dimensions (the expression level of a particular gene) can be seen as a node on a static graph (a regulatory network such as Figure 3). Spectral methods are enticing for use in this context. In fact, this picture is so appealing that many papers describing novel GCNN algorithms use this example to frame the impact of their ideas [43]–[46]. However, to the best of our knowledge, no work yet has profiled how these ideas actually serve on gene expression data in practice. We fill that lack here, and profile the work of [43], with minor technical modifications⁵ to support multi-component graphs, on gene expression data backed by both tissue-independent and tissue-specific genetic regulatory networks culled from the literature.

III. Methods

A. Datasets

1). Curated Views of the Public LINCS Corpus:

The full Level 4 LINCS dataset contains approximately 1.3 M gene expression profiles over 76 cell lines, ranging in frequency from VCAP, profiled over 200,000 times to NCIH716 with only 43 samples. Each cell line is profiled in diverse conditions—for example, within prostate tissue (the most frequently sampled tissue type) over 40,000 unique perturbagens were tested (including both drugs and genetic knockout or over-expression perturbagens), many sampled only a single time. To be clear, each sample in this dataset is a complete gene expression profile over the landmark genes—i.e., it is a 978 dimensional vector where each number quantifies the expression level of a particular gene in the genome.

On this dataset, we formed three supervised learning tasks:

a). Primary Site:

Predicting primary site (e.g., “breast tissue” or “large-intestine”) forces the classifier to examine deviations within a gene expression profile indicative of the tissue type, and would have applications to quality control within cell differentiation pipelines. Primary site is cell-line specific.

b). Subtype:

Subtype (e.g. “malignant melanoma” or “myoblast”) is also cell-line specific and speaks to disease state and provides another way of aggregating the many disparate cell lines within LINCS into useful predictive categories.

c). MOA:

Predicting drug mechanism of action (MOA, e.g. “ATPase inhibitor” or “Sodium channel blocker”) speaks to drug re-purposing and discovery applications and aggregates many disparate perturbagens into meaningful predictive categories. However, note that though we treat this as a standard multi-class classification problem, in reality many drugs have multiple known MOAs, a distinction we ignore here for simplicity. To ensure this simplifying assumption adds minimal noise to our classification task, we only exclusively include compounds with only a single known MOA.

B. Dataset Curation Procedure

We chose to reduce the LINCS dataset to a single curated view simultaneously suitable for all three of these tasks rather than forming a separate view per task. This causes us to lose some samples which only meet inclusion criteria for a subset of our tasks, but it is much more convenient to work with and disseminate. In that pursuit, we reduced the dataset to only those samples perturbed by compounds (not genetic knock-out or over-expression perturbations), and further only those samples perturbed by compounds with a single known MOA. We further restricted the dataset to only those samples corresponding to MOAs, primary sites, and subtypes that occurred more than 1000 times within the overall dataset, to ensure sufficient training examples for all classes for our classifiers. We performed these filtering steps independently—i.e., we removed all gene expression profiles belonging to a class in any of our three tasks that lacked 1000 full examples at the start. This resulted in some few classes in some of our tasks having fewer than 1000 examples (because, at the beginning of the process, they had over 1000 measurements, but after removing some samples due to their class membership for another task, the class then had fewer than 1000 measurements).

This formed one curated view of our data, and three classification tasks. One qualm some might have with this dataset is that it is very heterogeneous in terms of cell type—perhaps it is better to classify samples only derived from a single tissue type. To that end, we also formed a dataset containing only samples from prostate tissue (chosen as it was the most frequently sampled tissue type). As in our full dataset, here we restrict the samples to only those perturbed by compounds with a single known MOA that occurred at least 1000 times. This formed our “Prostate Only” dataset, on which we predict MOA only.

Full final dataset sizes, heterogeneity (among cell type) statistics, task statistics (e.g., class imbalance, number of classes) are shown in Table I. Note that there is significant class imbalance in this dataset–an unavoidable reflection of the corpus’s original makeup–but by filtering to a baseline number of examples per class we assert that there are at least a significant number of samples for every label ensuring learning power. We have made both of these datasets (though derived from fully public data), along with the cross-validation folds used in all of our experiments, publicly available,² so that others can most easily compare novel methodologies against our benchmarks.

TABLE I.

Population Statistics for Our Datasets and Tasks.

Dataset Statistics:
Dataset	Number of Samples	# Cell Lines	Most Frequent Cell Line	Least Frequent Cell Line
Full LINCS	156,461	36	MCF7 (26,546)	NCIH716 (8)
Prostate Only LINCS	25,565	2	PC3 (13,625)	VCAP (11,940)
MGH NeuroBank (Level 4)	5602	5	N/A (1133)	N/A (1109)
MGH NeuroBank (Level 5)	1894	5	N/A (380)	N/A (377)

Task Statistics:
Dataset	Task	# Classes	Most Frequent Class	Least Frequent Class
LINCS (Full)	Primary Site	12	Prostate (43,686)	Ovary (415)
	Subtype	14	Adenocarcinoma (53,245)	Embryonal Kidney (1384)
	MOA	49	DMSO (25,638)	IKK Inhibitor (828)
LINCS (Prostate Only)	MOA	9	DMSO (8833)	Serotonin Receptor Antagonist (1029)
MGH NeuroBank (Level 4)	Perturbagen	60	DMSO (383)	Ruboxistaurin (78)
MGH NeuroBank (Level 5)	Perturbagen	60	DMSO (130)	Ruboxistaurin (27)

We do not claim that these benchmark tasks or views of the data are the best benchmarks available. But these are biologically meaningful benchmarks on an important data modality that currently has none. We hope that as future methods evolve to better suit this methodology, we can also derive better benchmark tasks. Note here that we do not mean to claim that no machine learning tasks have been used on this modality previously, but rather that no set of systematized, very large sample size tasks for methodology development currently exist.

Given the very large ratio of samples to cellular sources (e.g. 156k to 36) and the very large skew in perturbagen frequency (e.g. DMSO accounting for approximately 1/6th of all data), as well as the lack of independence between perturbagen and cell type, we measure all accuracies on these datasets as per-sample accuracy, not per-subject, per-drug, or even per-experimental condition (as different experimental conditions are repeated to varying degrees). This means that our results on these data should not be interpreted to speak to true generalization outside the LINCS covariate space, but rather should be viewed only in their capacity to enable rigorous methodological comparisons.

1). MGH NeuroBank Corpus:

Our private corpus of L1000 data was measured on a collection of subject-derived neural progenitor cells, which were perturbed with one of 60 different small-molecule bioactives at varying doses. Some of these compounds are known to have consistent gene-expression signatures (e.g., HDAC inhibitors), whereas others have known clinical utility but a less well understood transcriptomic profile (e.g., clozapine), and still others were unknown on all counts.

These cells come from a population of five individuals, two healthy control subjects, one with Bipolar Disorder, and two with Schizophrenia (all diagnostic labels are DSM-IV diagnoses confirmed by structured clinical interview). All individuals’ cells were treated with the same compounds. On this data, we predict perturbagen identity. Note that each perturbagen was profiled at one of several doses, which we ignore here. We also use this dataset to profile how well classifiers do on Level 4 vs. Level 5 data and make a first attempt at assessing per-subject generalizability, by training a model on only four of the five subjects, then testing on the data for the fifth subject.

Full details for this corpus are also found in Table I.

C. Models

We compare a variety of standard classifiers, all save GCNNs implemented via scikit-learn [47] for maximal reproducibility and ease of use. GCNNs, as previously stated, were implemented via the method of [43].

In the interest of space, we will not provide a primer on each of the standard methods mentioned below in this work, but instead make clear why they were chosen to benchmark for this task and indicate which scikit-learn class was used to implement them. For a description of GCNNs see Section II-C.

1). Classifiers Tested:

a). Feed-forward artificial neural network (FF-ANN) classifiers:

FF-ANNs are a common, powerful, non-linear modelling technique, and were used in many of the prior works on gene expression data. However, partly as they do not assume any particular structure of their input and are thus least constrained, they are relatively inefficient learners. Some postulate that this inefficiency is due to simply their larger parameter overhead; however, the full reason is not yet known. Implemented via the MLPClassifier class.

b). Linear classifiers:

Linear classifiers, subsuming both logistic regression (LR) and support vector classifiers (SVCs), are extremely common across all domains, including traditional bioinformatics analyses, and are interpretable. Implemented via the SGDClassifier class.

c). Random forests:

Random forests are not as commonly used in traditional bioinformatics use cases, but are thought to often provide a compelling non-neural but still non-linear baseline. They are composed of many bagged random decision trees. Implemented via the RandomforestClassifier class.

d). K nearest neighbors classifiers:

KNN methods are commonly used in this domain for clustering analyses, and we hope that investigating their performance here can help inform further choices for those and other analyses in these domains. They also shed some light on appropriate distance metrics. Implemented via the KNeighborsClassifier class. Index construction, often a computationally intensive task on large datasets, was done via either brute force search, the construction of a KDTree, or the construction of a Ball Tree, as determined by scikit-learn’s ‘algorithm=auto’ setting.

e). Decision trees:

Decision trees are low powered, but extremely mechanistically interpretable. Implemented via the DecisionTreeClassifier class.

f). GCNNs:

Lastly, we tested GCNNs—in particular, the spectral approach defined by [43]. We encourage interested readers to refer to the primary source for full details regarding this algorithm, but we provide a brief explanation of the method here. In particular, this method of graph convolutional processing approximates localized filters in the graph fourier space via polynomials of the graph Laplacian. As follows from the graph theoretical nature of the Laplacian, restricting the order of these polynomials yields a localized radius of effect when impacting on the featurization of each graph node. These polynomials are realized in an efficient manner by relying on the stable recurrence relation of the Chebyshev polynomials, which form an orthogonal basis of a relevant Hilbert space and have been used historically in graph signal analysis for approximate wavelet analysis. Ultimately, this yields a means of producing fast, localized, graph convolutional filters. Graph pooling is implemented via the coarsening phase of the Gracus multilevel clustering algorithm [48].

We use the code of [43] with minor modifications to support multi-component graphs. We considered a number of potential regulatory graphs, both tissue specific and tissue independent. Our tissue-independent regulatory network is a network of transcription-factor and micro-RNA mediated regulatory relationships summarized from 25 literature defined external datasets [37].⁶ Our tissue-dependent regulatory network is built from a probabilistic model of tissue-specific gene-gene correlations [49].⁷ Interested readers should refer to the primary sources to determine the details of the graph constructions—for our purposes it suffices to note that they are constructed to capture known or suspected genetic regulatory relationships as in Figure 3. We treated all graphs as undirected, allowing them to capture merely a notion of regulatory interaction rather than any directed up- or down-regulation. This is certainly a simplification, and one we plan to extend in the future, but it yield significant technical simplifications for this work enabling these graphs to work natively within our chosen graph convolutional framework.

The tissue independent graph has edges determined from the literature and is unweighted. For our tissue specific graphs, we considered a neuron graph for the MGH NeuroBank tissue, and a prostate gland graph for the prostate only LINCS dataset. All graphs were undirected. Tissue independent graphs were unweighted, while tissue-specific graphs come with edge weights determined via an estimated confidence in the true existence of that edge, determined via a probabilistic model. When working with these weighted graphs, we culled all edges with confidence below a cutoff weight, which was tuned with all other hyperparameters.

g). Other Classifiers Considered:

We also tested Näıve Bayes classifiers, Gaussian Processes Classifiers, Quadratic Discriminant Analysis, Boosted methods via Adaboost, and Kernel Support Vector Classifiers, but these classifiers were removed from our experimental lineup for reasons varying from poor performance, non-insightful new results, computational intensivity, or combinations therein.

D. Hyperparameter Search & Technical Setup

Hyperparameters for all classifiers were determined by a random search [50] over all possible parameters and tasks, including over the number and sizes of hidden layers for FF-ANNs and number of graph convolution layers/filter sizes/pooling sizes, loss types, etc. In addition to random search, we also rotated the discovered optimal hyperparameters across tasks during various stages of the search procedure and made certain manual tweaks in pursuit of obtaining strong performance metrics for all models, particularly baseline methods. One notable disparity in the hyperparameter space searched is that the Scikit Learn FF-ANNs do not support dropout (only L2 regularization, which was included in our search), whereas the GCNNs do. To compensate for this potential bias, we took the optimal FF-ANN models found via the hyperparameter search and re-implemented them in Keras, as identically as possible, then performed a miniature grid-search over dropout within these models. This procedure induced a mild performance gain, but not enough to upset the observed model ordering on any tasks where GCNNs performed the best. We also did not hyperparameter optimize over batch size for FF-ANNs, but we did optimize over learning rate, a heavily related parameter, and we also tested several smaller batch sizes with our final models to ensure that we were not biasing the results against this baseline.

For GCNNs, we notably did not hyperparameter search over the number of epochs, but rotated progressively through a very limited fixed set of number of epochs for computational reasons. Additionally, GCNNs only supported a single optimizer, whereas FF-ANNs offered several options. The search process was, however, run over various considered graphs, as well as over the graph edge weight cutoff, which we used to cull irrelevant edges from our graphs.

For our benchmarking tasks, a full list of all hyperparameters tested, the distributions used to back our random search, and the final, chosen hyperparameters are available with our provided code.² Additionally, the optimal hyperparameters for all methods across all datasets and tasks can be found in the Appendix.

This random search was performed over 10 fold cross validation on the full LINCS dataset, and 15 fold cross validation on the private L1000 dataset (as that dataset is smaller, it warrants additional folds to improve accuracy). In each case, one fold was held out for testing, one for hyperparameter optimization, and the remaining used for training. The hyperparameter search optimized for mean accuracy over all folds, though we also report macro-F1⁸ in our test set results below, as some tasks present significant class imbalance. We chose these two metrics to offer first, a comparatively understandable metric (accuracy) which allows for a clear baseline measure (majority class performance) but is often overly forgiving for tasks with large class imbalance, and second, a less overt, but still commonly used, metric which compensates for class imbalance. We chose not to use AUC as it is less immediately understandable than accuracy while also not accounting for class imbalance as directly as macro-F1, and to avoid having too many evaluation metrics and thereby diluting our comparisons. For all results, statistical significance was assessed using paired t-test across all folds, followed by Benjamini-Hochberg multiple tests FDR adjustment within experimental conditions.

As different classifiers required different amounts of computational time to run, we did not run all classifiers for the same number of samples—this induces a mild bias towards the fastest running classifiers, as they will have had the opportunity to test additional hyperparameter settings. We did, however, ensure that we measured at least 60 samples for the standard FF-ANN classifier and linear models to ensure that we did not conclude any model better than those traditionally strong baselines simply due to lack of appropriate sampling. Graph convolutional networks, being highly computationally intensive, in particular on the larger datasets, were under-sampled compared to the other methods—it is possible that with more compute time their performance would improve. Note the direction of this bias: were more samples to improve the performance of the GCNN methods further, it would only strengthen the performance gap observed on the largest datasets, and potentially render them more performant than the simpler models on our smaller datasets. Because this bias is in favor of our baselines, rather than the more exotic, structured GCNN models, we feel comfortable still reporting these results even though they may improve later.

For our data-flush regimes (the tasks over the full and prostate only LINCS datasets), we used only the Level 4 data. This data is less processed, but presents 3 times as much data as the analogous Level 5 data. Note that had we used Level 5 data, our filtering procedure eliminating classes with less than 1000 examples would have eliminated many classes and made the overall task much easier. For our data-sparse tests (the task on our private L1000 corpus), we tested methods on both datasets, wondering whether in this data-sparse regime, the more processed data might prove more valuable than the relatively small increase in dataset size. Additionally, as in neither dataset on the MGH corpus did we filter out infrequent classes (given the dataset size, all classes are infrequent by our standards for the full LINCS data), this change from Level 5 to Level 4 can be done more transparently than on the full LINCS datasets.

Along with our code, the results of these hyperparameter searches are all publicly available.²

IV. Results & Discussion

A. LINCS Corpus

1). Full Corpus:

Final results are shown in Table II. Accuracies and macro F1s are reported averaged across unseen test folds, using hyperparameters found via a separate validation fold. Included in the results are those obtained using a majority class classifier, which simply predicts the most frequent class with probability equal to that found in the training set. This was tested across the same folds and is reported here to ground all other reported results and variances. Observed differences between mean performance of any pair of classifiers were statistically significant (p ≤ 0.05).

TABLE II.

Performance (mean ± standard deviation) for the full, tissue-heterogenous LINCS corpus

Task	Classifier Name	Accuracy	Macro F1
Primary Site	GCNN	93.9 ± 0.28	90.5 ± 0.82
	FF-ANN	90.6 ± 0.44	85.6 ± 0.97
	KNNs	89.6 ± 0.30	87.2 ± 0.61
	Linear Classifier	60.9 ± 0.50	47.6 ± 0.63
	Random Forest	57.2 ± 0.48	40.2 ± 0.77
	Decision Tree	44.4 ± 0.70	24.7 ± 2.22
	Majority Class	27.9 ± 0.16	3.63 ± 0.02
Subtype	GCNN	93.5 ± 0.34	91.7 ± 2.1
	FF-ANN	90.5 ± 0.30	88.5 ± 0.54
	KNNs	89.8 ± 0.13	90.2 ± 0.27
	Linear Classifier	62.6 ± 0.62	56.3 ± 1.06
	Random Forest	51.7 ± 0.37	22.3 ± 0.49
	Decision Tree	41.1 ± 0.21	18.4 ± 0.62
	Majority Class	34.0 ± 0.21	3.62 ± 0.02
MOA	GCNN	46.4 ± 0.35	31.6 ± 0.65
	FF-ANN	45.9 ± 0.43	29.6 ± 0.60
	KNNs	43.5 ± 0.50	29.5 ± 0.58
	Linear Classifier	39.1 ± 0.29	20.6 ± 0.39
	Random Forest	32.3 ± 0.40	11.5 ± 0.31
	Decision Tree	28.7 ± 0.31	8.5 ± 0.29
	Majority Class	16.4 ± 0.16	0.57 ± 0.005

We note that on all of the tested tasks, GCNNs perform best, by notable margins in accuracy and macro F1 on both primary site and subtype prediction. The margin of accuracy in MOA prediction is smaller, but still statistically significant. KNNs performed surprisingly well on all three tasks, offering competitive performance even with the FF-ANNs. Investigations of why they performed so well revealed two findings:

1. KNN classifiers strongly prefer traditional distance metrics (e.g., Euclidean) over correlative based “distance metrics.” This is notable because correlation is often used as a signal of biological similarity on these data, which may be contraindicated by these results.

2. Our hyperparameter search method also changed the distance metric underlying the KNN method. Across all tasks and datasets, the optimal distance metric was the “Canberra” distance, defined via

   $$d\left(\mathit{x},\mathit{y}\right)=\sum _i\frac{\left|{\mathit{x}}_i-{\mathit{y}}_i\right|}{\left|{\mathit{x}}_i\right|+\left|{\mathit{y}}_i\right|}.$$

   Using this distance metric induced performance gains over correlative and traditional, euclidean distance measures. The Canberra distance is traditionally used for integer valued vectors and we are unsure why it would be preferred here. We have not performed analyses to determine if this apparent distance metric preference is statistically significant.

Linear classifiers robustly performed well. On the MOA task, hyperparameter search selected a logistic regression model (via the log loss in scikit-learn), whereas on the Subtype and Primary Site tasks, the optimal setting used a modified_huber loss, which is a smooth loss that is tolerant to outliers.

Random forests and decision trees both yielded under-whelming results, particularly with respect to Macro F1. One hypothesis as to why this may be is that Random forests were less sampled in the hyperparameter search than linear models. Alternatively, these results may suggest that absolute feature values are less meaningful in our data than are relationships between feature values—an idea that meshes well with the fact that this dataset is very heterogenous with respect to cell (e.g., tissue) type, and the same expression level of any individual gene may mean very different things in different tissue types. Some might postulate that this is perhaps due to a poor search space of some critical hyperparameters; we intentionally ensured our hyperparameter search space was very broad especially over these critical parameters. For number of trees, we searched over an equal mixture of Poisson distributions centered at 50, 200, and 400, respectively, and the optimal hyperparameters (shown in the appendix) showed a mix over this entire range. All regularization parameters were also included in our search space.

2). Prostate Only Corpus:

Final results for prediction of prostate MOA are shown in Table III. All classifier comparisons were statistically significant (p = 0.05). Here, FF-ANNs perform best, though GCNNs are quite competitive. Note that GCNNs still preferred tissue non-specific regulatory graphs, rather than prostate specific graphs. Again, KNNs perform well. Here, RFs and decision trees still under-perform the other methods, but perform better with respect to macro F1 than they do on the more heterogeneous full LINCS corpus, suggesting again that perhaps they may be more appropriate on more homogeneous data sources.

TABLE III.

Performance (mean ± standard deviation) on the prostate LINCS corpus and MOA prediction task.

Classifier Name	Accuracy	Macro F1
GCNN	67.7 ± 0.76	46.0 ± 0.42
FF-ANN	68.3 ± 0.60	50.4 ± 0.71
KNNs	66.5 ± 0.71	46.2 ± 0.89
Linear Classifier	63.8 ± 0.52	42.6 ± 1.03
Random Forest	60.4 ± 0.48	37.4 ± 0.41
Decision Tree	53.2 ± 1.16	32.6 ± 0.91
Majority Class	34.54 ± 0.05	5.71 ± 0.01

As indicated in Section III-C1, we tested both tissue-specific and tissue-independent regulatory graphs. Surprisingly, on the prostate corpus, the GCNN performed better using the tissue independent regulatory network than it did using the prostate specific regulatory graph. This may indicate that our tissue-specific graphs suffer from some unknown problem, or that tissue-independent graphs are simply more performant overall.

Similar to the full system MOA task, the optimal linear model here was a logistic regression model.

B. MGH NeuroBank Corpus

1). Raw Performance Results:

Final results for perturbagen identification on the MGH NeuroBank corpus are shown in Table IV. Results were not statistically significantly different at p = 0.05 between the Level 5 data and Level 4 data for any classifier save the GCNN. All within-level classifier comparisons were statistically significant (p = 0.05) save between Level 5 GCNNs and RF, GCNNs and KNNs, and KNNs and RFs.

TABLE IV.

Performance (mean ± standard deviation) on the perturbagen identity task on the MGH NeuroBank Corpus.

Classifier Name	Level 5		Level 4
	Accuracy	Macro F1	Accuracy	Macro F1
GCNN	46.0 ± 9.90	44.0 ± 10.8	54.6 ± 3.94	56.4 ± 3.94
FF-ANN	63.2 ± 10.3	62.7 ± 10.8	57.3 ± 4.12	58.9 ± 4.00
KNNs	46.9 ± 8.13	44.7 ± 9.15	44.9 ± 3.74	45.7 ± 3.61
Linear Classifier	52.3 ± 9.61	51.4 ± 10.0	49.1 ± 3.98	50.2 ± 3.63
Random Forest	48.0 ± 8.96	44.7 ± 9.15	43.2 ± 4.87	42.7 ± 4.75
Decision Tree	26.7 ± 8.07	25.6 ± 7.45	27.0 ± 2.02	26.4 ± 1.79
Majority Class	7.56 ± 2.37	0.23 ± 0.07	6.88 ± 0.77	0.21 ± 0.02

Here, FF-ANNs lead in performance by a wide margin compared to other methods. We interpret their strong success here relative to GCNNs to be indicative of a strong need for very large datasets for the GCNN models. Recall that this dataset is significantly smaller than our other datasets (see Table I). This intuition is supported by two observations: 1) the apparent slope in GCNN performance relative to dataset size is quite steep, exceeding at all tasks on the largest dataset, nearly matching on the prostate only dataset, and failing by a large margin here, and 2) GCNNs show a statistically significant preference for the larger Level 4 data, whereas no other classifier cares between the two modalities in a statistically significant manner.

It is also possible that GCNNs are less appropriate on this corpus than on the larger corpora due to this dataset’s strong neural focus. Or, it may be that GCNNs are most appropriate in heterogeneous datasets spanning many cell types.

Among the other classifiers, linear classifiers perform well, followed by KNNs and RFs, then, much worse, by decision trees. No classifier save GCNNs shows a statistically significant preference for Level 5 data over Level 4 data, but all save GCNNs do show a (again, statistically insignificant) preference for Level 5 data in terms of absolute measure.

2). Generalization Experiments:

We also used the MGH NeuroBank Corpus to assess population level generalizability, by training on four of our subjects and testing on the fifth subject. As the MGH NeuroBank Corpus contains only one subject with Bipolar Disorder, we do not ever test on this subject’s data—absent more examples of any subject data in this diagnostic category, we would not expect a classifier to generalize well to this subject. Including their results causes a mild but consistent drop in mean generalization accuracy across almost all classifiers tested. We report all results here using Level 4 data as no classifier statistically significantly preferred Level 5, but the relative drops in performance observed were similar for that modality.

Results for this experiment are shown in Table V. All methods showed a notable drop in accuracy on unseen subjects, ranging from a 10.2% drop for linear classifiers to an 18.5% drop for decision trees (percentages taken of per-sample accuracies, not raw percentage points). This indicates a definite unmet need for either a) more diverse datasets or b) novel methods able to better generalize to unseen subjects. Note, though, that the MGH NeuroBank corpus only contains 5 total subjects to begin with, so it may be the case that these numbers would improve significantly were we to have even a only marginally larger subject pool. Note that on a dataset like LINCS, which is much larger and thus more amenable to higher-capacity learning yet has relatively fewer cellular sources (and with those cellular sources often differing by tissue type or primary diagnosis no less), it is reasonable to imagine that this observed population specific overfitting could forseeably be even worse than what we observe on the MGH dataset—this point is critical given that this dataset has been used historically for many machine learning investigations with clinically generalizable aspirations, unlike our work where the tasks are designed to aid primarily in method development.

TABLE V.

Per (Non-BD) Subject Generalization Accuracy (mean ± standard deviation) on the MGH NeuroBank Corpus.

Classifier Name	Accuracy	Macro F1
GCNN	47.7 ± 6.78	48.9 ± 7.40
FF-ANN	48.7 ± 7.85	50.1 ± 8.34
KNNs	37.9 ± 5.39	39.0 ± 6.68
Linear Classifier	44.1 ± 4.03	44.7 ± 4.21
Random Forest	38.8 ± 5.37	38.3 ± 6.76
Decision Tree	22.0 ± 3.85	21.8 ± 3.59

V. Conclusion

In this work we aimed to make the following contributions:

a). Establish biologically meaningful benchmark tasks for gene expression data:

With the curation of the full and prostate-specific views of the LINCS dataset and specification of the Primary Site, Subtype, and MOA tasks, we meet this goal.

b). Provide robust benchmarks:

We provide benchmarks on the tasks defined above for 6 different types of classifiers. We establish that graph convolutional neural networks, which incorporate prior biological knowledge via genetic regulatory graphs, perform very well when dataset size is very large, and feed-forward artificial neural networks offer good performance across all dataset sizes. Additionally, we profile non-neural classifiers, including K nearest neighbor methods, random forests, linear classifiers and decision trees. K nearest neighbor methods provide surprisingly strong performance in data rich environments using the Canberra distance.

c). Assess how these classifiers function in data-scarce regimes:

We profile these same classifiers on a similar task on the smaller, privately produced MGH NeuroBank corpus. Here, we find that graph convolutional neural networks no longer offer competitive performance, but feed-forward artificial neural networks continue to perform well, as do linear models.

d). Assess population level generalizability:

We demonstrate that subject level generalizability remains an important challenge in this domain. Linear classifiers generalize best, losing only 10.2% of their per-sample accuracy, while decision trees generalize worst, losing 18.5%. It is important to note that we were only able to assess this on our smallest dataset, the MGH NeuroBank Corpus, as differing cell lines represented too divergent demographic conditions in the full LINCS dataset, so this may simply be a reflection of the small dataset size, or indicative of a more chronic problem due to the fact that gene expression corpora contain many samples per subject.

VI. Future Work

There are several notable directions for future work. First, a notable absent classifier is a self-normalizing neural network (SNNN) [17]. Introduced in late 2017, SNNNs have demon-strated improvements in a battery of different tasks and warrant inclusion here. Other types of classifiers capable of using graph structures would also warrant inclusion. Additionally, there are other graph convolutional networks one could use, [39], [44], as well as other sources for our regulatory graphs. One notable contender in that domain is HuRI: The Human Reference Protein Interactome Mapping Project⁹ which has several large databases of protein-protein interactions found experimentally through yeast two-hybrid screening methods [42], [51]. Additionally, incorporating directional information in our regulatory graphs would also enable significantly more nuanced processing. Finally, we would also like to establish other types of machine learning benchmark tasks, most notably clustering tasks, or other tasks that can better assess generalizability across subjects, drugs, or even measurement technologies. More investigation into what drove the success of GCNNs here, perhaps by running dataset size ablation experiments, would also help clarify their strengths. Similarly, more investigations into the failings of random forest models or the relative strengths of differing distance metrics would also be informative.

Biography

Matthew McDermott Matthew McDermott is a PhD student in the Massachusetts Institute of Technology Clinical Decision Making Group, studying clinical and biomedical machine learning. He also holds a B.S. degree in Mathematics from Harvey Mudd College.

Jennifer Wang Jen has BA in Mathematics and a BS in Physics from the University of California, San Diego. She earned her PhD in Neuroscience from the Massachusetts Institute of Technology where she studied neural circuits in-vitro using electrophysiology and optogenetics. She did a fellowship at MGH reprogramming patient cell models to identify psychiatric disease phenotypes. She now continues this work as a senior research scientist at the MGH Center for Quantitative Health.

Wen-Ning Zhao Wen-Ning Zhao has a BS in Biochemistry from Nanjing University, a PhD in Biochemistry from The University of Texas Health Science Center at San Antonio, and received post-doctoral training in the Dept. of Neurobiology at the Harvard Medical School. Dr. Zhao is now a senior research scientist/group leader at the Chemical Neurobiology Laboratory, Center for Genomic Medicine at MGH.

Steven D. Sheridan Dr. Sheridan received his PhD in Molecular Genetics at the University of California, Irvine and followed-up with post-doctoral training in genetic engineering at Harvard University. Dr. Sheridan is now a senior research investigator and director of the Platform for Cellular Modeling of Neuropsychiatric Disease (cMiND).

Peter Szolovits Peter Szolovits received a PhD from Caltech and is now Professor of Computer Science and Engineering and head of the Clinical Decision-Making Group within CSAIL. Professor Szolovits is also an associate member of the MIT Institute for Medical Engineering and Science (IMES) and on the faculty of the Harvard/MIT Health Sciences and Technology program.

Isaac Kohane Isaac Kohane, MD, PhD is the inaugural Chair of the Department of Biomedical Informatics at Harvard Medical School. He develops and applies computational techniques to address disease at multiple scales: From whole healthcare systems as living laboratories to the functional genomics of neurodevelopment with a focus on autism.

Stephen J. Haggarty Dr. Haggarty received a B.Sc. in genetics from the University of British Columbia, Vancouver, and a Ph.D. in biochemistry from Harvard University. Dr. Haggarty is a faculty member in the Department of Neurology at Harvard Medical School and the Center for Genomic Medicine at Massachusetts General Hospital, where he is the Director of the Chemical Neurobiology Laboratory (CNL) as well as the Head of Neuropharmacology for the MGH Center for Experimental Drugs & Diagnostics in the Department of Psychiatry

Roy H. Perlis Dr. Perlis is Director of the Center for Quantitative Health at Massachusetts General Hospital and Professor of Psychiatry at Harvard Medical School. He is a graduate of Brown University, Harvard Medical School, and the Harvard School of Public Health. His lab is focused on developing clinical and genomic predictors of treatment response and on developing novel therapeutics based on cellular models of brain disease.

Appendix

TABLE VI.

Optimal Hyperparameters for LINCS Full MOA

GCNN	regularization	1.09e–2
	num_epochs	350
	Fs	[[9]]
	M	[137, 49]
	Ks	[[7]]
	batch_size	92
	pool	apool1
	learning_rate	1.23e–3
	decay_steps	405
	decay_rate	9.91e–1
	dropout	6.98e–1
	momentum	8.79e–1
	ps	[[2]]
FF-ANN	activation	relu
	alpha	1.69
	power_t	3.30e–1
	learning_rate_init	1.09e–1
	hidden_layer_sizes	[955]
	learning_rate	adaptive
	momentum	8.64e–1
	early_stopping	True
	nesterovs_momentum	True
KNNs	weights	distance
	metric	canberra
	n_neighbors	12
Linear Classifier	penalty	l1
	l1_ratio	4.06e–1
	alpha	1.23e–3
	loss	log
	n_jobs	−1
	tol	1.00e–5
	learning_rate	invscaling
	eta0	3.17e–4
	power_t	1.84e–1
Random Forest	max_depth	100
	max_leaf_nodes	None
	criterion	gini
	n_estimators	211
	min_samples_split	2
	min_weight_fraction_leaf	1.27e–6
	min_impurity_decrease	1.70e–5
	min_samples_leaf	1
Decision Tree	max_features	None
	criterion	entropy
	max_depth	10
	splitter	best
	min_samples_leaf	2
	min_impurity_decrease	1.23e–3
	min_samples_split	2
	max_leaf_nodes	None
	min_weight_fraction_leaf	2.08e–3

TABLE VII.

Optimal Hyperparameters for LINCS Full Subtype

GCNN	regularization	5.42e–3
	num_epochs	300
	pool	mpool1
	M	[150, 150, 14]
	batch_size	88
	Fs	[[43]]
	momentum	9.73e–1
	learning_rate	2.95e–3
	ps	[[2]]
	decay_steps	362
	decay_rate	9.76e–1
	Ks	[[8]]
	dropout	4.54e–1
FF-ANN	activation	relu
	nesterovs_momentum	True
	hidden_layer_sizes	[997]
	learning_rate	invscaling
	early_stopping	False
	learning_rate_init	5.53e–2
	power_t	2.26e–1
	alpha	8.20e–1
	momentum	8.67e–1
KNNs	metric	canberra
	weights	uniform
	n_neighbors	1
Linear Classifier	learning_rate	invscaling
	alpha	3.63e–1
	power_t	1.14e–1
	l1_ratio	7.37e–1
	penalty	l2
	eta0	9.91e–5
	loss	modified huber
Random Forest	criterion	gini
	max_depth	25
	min_samples_leaf	1
	max_leaf_nodes	500
	n_estimators	411
	min_weight_fraction_leaf	4.33e–4
	min_samples_split	2
	min_impurity_decrease	3.64e–5
Decision Tree	min_impurity_decrease	3.19e–5
	criterion	entropy
	min_weight_fraction_leaf	1.12e–2
	max_leaf_nodes	100
	min_samples_leaf	1
	min_samples_split	2
	max_depth	5
	splitter	best
	max_features	None

TABLE VIII.

Optimal Hyperparameters for LINCS Full Primary Site

GCNN	regularization	3.08e–3
	num_epochs	350
	Fs	[[41]]
	batch_size	68
	M	[135, 12]
	ps	[[2]]
	decay_steps	380
	momentum	9.45e–1
	learning_rate	3.13e–3
	pool	apool1
	decay_rate	9.89e–1
	Ks	[[5]]
	dropout	5.62e–1
FF-ANN	learning_rate_init	5.53e–2
	activation	relu
	momentum	8.67e–1
	nesterovs_momentum	True
	learning_rate	invscaling
	power_t	2.26e–1
	early_stopping	False
	hidden_layer_sizes	[997]
	alpha	8.20e–1
KNNs	n_neighbors	11
	metric	canberra
	weights	uniform
Linear Classifier	learning_rate	invscaling
	l1_ratio	7.85e–1
	power_t	8.51e–2
	loss	modified-huber
	penalty	l2
	eta0	2.99e–6
	alpha	4.94e–1
Random Forest	criterion	entropy
	max_depth	100
	min_samples_leaf	1
	min_weight_fraction_leaf	3.87e–4
	n_estimators	401
	max_leaf_nodes	None
	min_samples_split	4
	min_impurity_decrease	2.89e–4
Decision Tree	max_depth	100
	min_samples_leaf	1
	min_weight_fraction_leaf	2.53e–3
	min_samples_split	2
	criterion	gini
	min_impurity_decrease	7.73e–5
	max_features	250
	splitter	best
	max_leaf_nodes	None

TABLE IX.

Optimal Hyperparameters for LINCS Prostate Only MOA

GCNN	regularization	4.00e–3
	num_epochs	200
	Fs	[[25]]
	batch_size	55
	M	[168, 14, 9]
	Ks	[[15]]
	ps	[[2]]
	pool	mpool1
	learning_rate	5.00e–3
	decay_steps	415
	decay_rate	9.50e–1
	momentum	9.70e–1
	dropout	5.00e–1
FF-ANN	learning_rate	invscaling
	nesterovs_momentum	True
	hidden_layer_sizes	[997]
	learning_rate_init	5.53e–2
	momentum	8.67e–1
	early_stopping	False
	alpha	8.20e–1
	power_t	2.26e–1
	activation	relu
KNNs	metric	canberra
	weights	distance
	n_neighbors	13
Linear Classifier	eta0	3.17e–4
	l1_ratio	4.06e–1
	tol	1.00e–5
	penalty	l1
	learning_rate	invscaling
	alpha	1.23e–3
	n_jobs	−1
	power_t	1.84e–1
	loss	log
Random Forest	min_samples_split	2
	criterion	entropy
	min_weight_fraction_leaf	6.01e–5
	min_samples_leaf	2
	max_depth	None
	min_impurity_decrease	3.68e–4
	max_leaf_nodes	None
	n_estimators	53
Decision Tree	min_impurity_decrease	1.46e–3
	min_samples_leaf	1
	min_weight_fraction_leaf	1.81e–4
	max_depth	25
	max_features	250
	criterion	entropy
	max_leaf_nodes	None
	min_samples_split	2
	splitter	best

TABLE XI.

Optimal Hyperparameters for MGH NeuroBank Corpus Level 5

GCNN	regularization	5.00e–2
	decay_steps	400
	learning_rate	1.00e–3
	pool	apool1
	momentum	9.00e–1
	num_epochs	350
	batch_size	20
	M	[100, 60]
	ps	[[2]]
	decay_rate	9.60e–1
	Ks	[[7]]
	Fs	[[25]]
	dropout	5.00e–1
FF-ANN	hidden_layer_sizes	[946, 193]
	alpha	1.11
	power_t	8.87e–1
	early_stopping	False
	learning_rate_init	9.86e–1
	nesterovs_momentum	True
	learning_rate	constant
	momentum	8.76e–1
	activation	relu
KNNs	n_neighbors	7
	metric	canberra
	weights	distance
Linear Classifier	learning_rate	invscaling
	tol	1.00e–5
	n_jobs	−1
	power_t	1.84e–1
	penalty	l1
	eta0	3.17e–4
	loss	log
	l1_ratio	4.06e–1
	alpha	1.23e–3
Random Forest	max_depth	25
	max_leaf_nodes	500
	min_weight_fraction_leaf	4.33e–4
	min_samples_split	2
	min_samples_leaf	1
	n_estimators	411
	criterion	gini
	min_impurity_decrease	3.64e–5
Decision Tree	min_samples_split	2
	max_depth	10
	criterion	entropy
	min_impurity_decrease	1.23e–3
	max_leaf_nodes	None
	min_weight_fraction_leaf	2.08e–3
	min_samples_leaf	2
	max_features	None
	splitter	best

TABLE X.

Optimal Hyperparameters for MGH NeuroBank Corpus Level 4

GCNN	regularization	2.65e–2
	decay_steps	410
	learning_rate	1.01e–2
	pool	mpool1
	momentum	8.14e–1
	num_epochs	350
	batch_size	25
	M	[138, 60]
	ps	[[2]]
	decay_rate	9.98e–1
	Ks	[[26]]
	Fs	[[31]]
	dropout	6.22e–1
FF-ANN	hidden_layer_sizes	[976]
	alpha	1.16
	power_t	3.21e–1
	activation	relu
	learning_rate_init	4.05e–1
	early_stopping	False
	momentum	9.07e–1
	tol	1.00e–5
	nesterovs_momentum	True
	learning_rate	invscaling
KNNs	n_neighbors	6
	metric	canberra
	weights	distance
Linear Classifier	learning_rate	invscaling
	tol	1.00e–5
	n_jobs	−1
	power_t	1.84e–1
	penalty	l1
	eta0	3.17e–4
	loss	log
	l1_ratio	4.06e–1
	alpha	1.23e–3
Random Forest	max_depth	25
	max_leaf_nodes	500
	min_weight_fraction_leaf	4.33e–4
	min_samples_split	2
	min_samples_leaf	1
	n_estimators	411
	criterion	gini
	min_impurity_decrease	3.64e–5
Decision Tree	min_samples_split	2
	max_leaf_nodes	None
	criterion	gini
	min_impurity_decrease	7.73e–5
	min_weight_fraction_leaf	2.53e–3
	min_samples_leaf	1
	max_features	250
	max_depth	100
	splitter	best