Abstract
Influenza A Virus (IAV) replications start from the deposition of inhaled virus-laden droplets on the epithelial cells in the pulmonary tracts. In order to understand the local deposition patterns and within-host dynamics of infectious aerosols, accurate information of high-resolution imaging capabilities, as well as real-time flow cytometry analysis, are required for tracking infected cells, virus agents, and immune system responses. However, clinical and animal studies are in deficit to meet the above-mentioned demands, due to their limited operational flexibility and imaging resolution. Therefore, this study developed an experimentally validated multiscale epidemiological computational model, i.e., the Computational Fluid-Particle Dynamics (CFPD) plus Host Cell Dynamics (HCD) model, to predict the transport and deposition of the low-strain IAV-laden droplets, as well as the resultant regional immune system responses. The hygroscopic growth and shrinkage of IAV-laden droplets were accurately modeled. The subject-specific respiratory system was discretized by generating the new polyhedral-core mesh. By simulating both mouth and nasal breathing scenarios, the inhalations of isotonic IAV-laden droplets with three different compositions were achieved. It is the first time that parametric analysis was performed using the multiscale model on how different exposure conditions can influence the virus aerodynamics in the lung and the subsequent immune system responses. Numerical results show a higher viral accretion followed by a faster immune system response in the supraglottic region when droplets with the higher salt concentration were inhaled. Consequently, more severe symptoms and longer recovery are expected at the pharynx. Furthermore, local deposition maps of IAV-laden droplets and post-deposition infection dynamics provide informative and direct evidence which significantly enhance the fundamental understanding of the underlying mechanisms for upper airway and lower airway infections.
Keywords: Influenza A Virus (IAV) Laden Droplets, Computational Fluid Particle Dynamics (CFPD), Host Cell Dynamics (HCD), Adaptive Immune System, Innate Immune System
1. Introduction
Influenza A virus (IAV) is highly transmissible as one of the leading causes of pulmonary infections such as pneumonia, and 5 to 20 percents of the population in the United States contract influenza every year (Boianelli et al., 2015). Three circulating subtypes, i.e., type A/H1N1, type A/H3N2, and type B, can infect humans and cause massive global epidemics. IAVs pass among individuals through the air in droplets when someone sneezes or coughs. The airborne transmission of infectious substances expelled by the respiration system of an infected patient is commonly known to be the key contagion mechanism (Eames et al., 2009). Subsequently, influenza virus replicates in the epithelial cells throughout the lung airways, with the virus being recoverable from both the upper and lower respiratory tract naturally or experimentally infected. The epithelial cells in the tracheobronchial tree were the primary sites of IAV replication. The pulmonary deposition of virus-laden droplets impose warning signals to the immune system, which is a complex and nonlinear interaction of the host cells and antigen structure. Lower airway infections can result in the flooding of alveolar sacs, developing acute respiratory distress syndrome, and causing fatalities from respiratory failure. Airborne transmission of the IAV-laden droplets occurs when the viral load migrates through nasal and mouth breathing or paranasal sinuses (ocular route) to the airways. The airborne transmission of infectious substances expelled by an infected subject is commonly known to be the decisive contagion mechanism. Meanwhile, the underlying principles of how IAVs cause different pathogenic profiles is not well studied. Investigating local deposition patterns and within-host dynamics require high-resolution imaging capabilities as well as real-time flow cytometry analysis of the infected cells, virus agents, and immune system responses. However, clinical and animal studies are in deficit to meet such demands. Therefore, the objective of this study is to develop a new multiscale model by integrating the computational fluid-particle dynamics (CFPD) model and the host cell dynamics (HCD) model, to simulate the transport and deposition of IAV-laden droplets and predict the regional immune system responses of infected host cells. Deposition patterns of IAV-laden droplets and post-deposition infection dynamics provide informative data, which will significantly enhance the fundamental understanding of how exposure to the airborne IAV-laden aerosols can lead to the lower airway infection.
Research efforts and general findings from early studies are summarized as follows. To the best of our knowledge, there is no existing multiscale model which is capable of simulating the transport and deposition of virus-laden droplets, as well as the resultant immune system responses together. However, many numerical studies have been done separately focusing on modeling either the droplet transport dynamics in lung or the viral dynamics in host cells. Lambert et al. (2011) performed a multiphase flow simulations of the transport of pure water droplets with a constant diameter of 2.5 μm. Exposure through mouth breathing showed a higher deposition at the upper airway and the primary bifurcation. Using the CFPD models, (Kreidenweis et al., 2005; Mikhailov et al., 2004) determined the particles greater than 6 μm deposited in the upper respiratory tract. Those particles between 2 to 6 μm mostly deposited in the 2nd generation (G2), and smaller particles would reach lower lobes (Darquenne, 2012; Ou et al., 2017). As a key mechanism, the hygroscopic growth and shrinkage of particulate matters in humid air were initially modeled and investigated in climate science. Aerosol size change dynamics were studied in idealized upper airway geometries (Feng et al., 2016; Zhang et al., 2006), in the subject-specific human upper airway geometry excluding the nasal cavity (Worth Longest & Xi, 2008), and the nasal cavity only (Schroeter et al., 2016). The results showed the evaporation and condensation of droplets were dependent on the droplets composition and the ambient relative humidity (RH), temperature, and pressure. Droplet trajectory also depends on the surrounded airflow patterns. Specifically, breathing through mouth or nose changes the local airflow and consequently the droplet heat and mass transfer.
Once the droplets deposit on the mucus layer, IAVs will bind to the surface of targeted epithelial cells. The endocytosis of the virions inside the epithelial cell occurs after 20 minutes post-infection (Oguin et al., 2014). At this stage, the virus binds to the epithelial cell for cloning and reproducing copies of RNA and viral proteins, which is also known as the incubation period. Eclipse phase (Pinilla et al., 2012) is the period between post-infection and reproducing stage. The duration of this phase is predicted from 5 to 12 hours post-infection (Beauchemin & Handel, 2011) and can reach its peak value after 2 to 3 days post-infection (dpi) (Boianelli et al., 2015). Accordingly, the innate and adaptive immune systems (IIS and AIS respectively) will be activated and interfere with the antigen replication. Mathematical models for the viral dynamics within the host, i.e., host cell dynamics (HCD) models, were developed with various considerations for the interactions between the targeted cell, immune system, and viral agents (Beauchemin & Handel, 2011; Smith & Perelson, 2011). The first attempt to numerically represent the HCD was done by Larson et al. (1976) after fitting the data from IAV H3N2 infected Swiss-ICR mice. The viral doses in the lung, trachea, and nasopharynx were investigated with five associated rate parameters. Formulating the HCD using target cell models (Nowak & May, 2000) paved a new roadmap on the IV infection study. Baccam et al. (2006) adopted target cell models by including susceptible cell, infected cell, and virus to fit a model with the in vivo data of the virus A/Hong Kong/123/77 (H1N1) infected human. Specifically, eclipse phase was included by considering a latent phase for the infected cell before becoming productive. Their numerical results indicate that the virus reproduction started at 6 hours post-infection and the infected cells lifetime was 11 hours. Holder & Beauchemin (2011) investigated the same mathematical model for validation of in vitro study and suggested a more complex parameter for the infected cells in delayed phase. Petrie et al. (2013) developed a double target cell model for human infections with avian strain by differentiating target cells into two fractions, i.e., default and secondary cells. The response from the immune system by proposing the effect of Abs and CD8+ T cells was first introduced into the model by Bocharov & Romanyukha (1994). Baccam et al. (2006) included the (IFN)-I dynamics and their results show double peaks in viral titer data. Moreover, the additional factor of NK cells was introduced to the target cell models by Canini & Carrat (2011), where the NK activation is induced by (IFN)-I. Specifically, the virus kinetics and symptom dynamics population have been utilized to estimate infection parameters. Attempts on including the AIS with CD8+ T cells and Abs into the cell population models were projected by Lee et al. (2009). Specifically, a lymphatic compartment was considered to represent the activation of T and B cells. In this regard, 10 equations for the kinetic of AIS components at a different stage were added to the target model and the optimum time of antiviral drug administration was proposed to be at 2 dpi. In addition, existing in vitro and in vivo studies have categorize well on the key mechanisms that need to be modeled in the HCD model (Male et al., 2006; Baccam et al., 2006; De Andrea et al., 2002; Miller & Mitchell, 1969). Specifically, immune subsystem responses and processes are in a collocative multi-directional state compared to each other that any changes in a factor would influence intensively on the enhancement or suppression of the others. The immune response processed by lymphoid tissues and leukocytes in a process that can be explained by recalling two lines of defense: (1) Innate immune system response (IISR): released interferons (IFN)-I from the invaded cells and Natural Killers (NK) cells; and (2) adaptive immune system response (AISR): humoral response (antibody mediated) and cytotoxic lymphocytes agents (Cytotoxic and Helper T cells, B cells) with the activation dependency on dendritic cell and IAV population.
Since the infection replication is significantly dependent on the population of the above-mentioned agents, it is necessary to combine the CFPD model and the HCD model. The rational is that, the CFPD model is able to address the deficiency of the HCD model by providing accurate predictions of the regional IAV deposition data in human respiratory systems under realistic exposure conditions, which are not achievable by the current models available. Therefore, in this study, an experimentally validated multiscale model, i.e., a CFPD-HCD model was employed in this study to simulate the transport of the respired IAV-laden droplets, and predict the immune system response at a time span of 12 days post-infection (dpi). To the best of our knowledge, this is the first time that virus-laden droplet transport, size change dynamics, deposition, and replication, as well as the resultant immune system responses, have been systematically studied in a subject-specific human respiratory system under various exposure conditions using a validated noninvasive multiscale CFPD-HCD model.
2. Methodology
An experimentally validated multiscale model, i.e., the CFPD-HCD model was developed and employed to simulate the transport of inhaled IAV-laden droplets and the resultant immune system response at a time span of 12 dpi. The CFPD-HCD model consists of two simulation layers connected at the airway mucosa lining, based on the fact that the viral replications started from the deposition of inhaled fomites on the epithelial cells. Since the infection replication is significantly dependent on the host cell population and immune system agents at each region, the CFPD model with the Euler-Lagrange scheme was adopted to simulate the virus-laden droplets aerodynamics in lung, which provides more realistic regional lung uptakes than the numerical studies with the HCD model only. Localized deposition patterns were simulated and transferred as the inputs to the HCD model for the determination of the regional host dynamic responses.
Figure 1 shows the schematic of the workflow for the CFPD-HCD model. Instead of tetra-core meshes used in early studies (Feng et al., 2018, 2016; Zhang et al., 2006), the poly-core mesh was generated considering the better computational efficiency and stability. The final mesh has 18,453,311 elements including near-wall prism layers (see SI for the mesh independence test details). The inhaled number concentration of IAV-laden droplets after the exposure to sneezing events by the infected subject was estimated based on a separation distance of 3 feet (Hamborsky et al., 2015; Liu et al., 2017). The indoor condition with artificial heating at the winter time is set up for the inhalation condition (Knight, 1980). The unimodal droplet size distribution was defined using 6 size bins based on the statistics reported by Duguid (1946). Two inhalation patterns, i.e., mouth and nasal breathings, were simulated using realistic human breathing waveforms of complete inhalation-exhalation cycles. Moreover, the condensation and evaporation between droplets and the surrounding humid air were modeled by solving the energy and mass balance equations for each droplet. Since the hygroscopic growth behavior of droplets is highly dependent on their compositions (Feng et al., 2016; Zhang et al., 2006), three compositions were selected for the parametric analysis on how droplet initial compositions can influence the droplet size change dynamics and the resultant transport and deposition in human respiratory systems and the immune system responses. Based on the fact that NaCl and water are the two major components of the coughing or sneezing droplets (Effros et al., 2002), NaCl-water binary mixtures are assumed for the droplet composition. The investigated cases with different breathing patterns and droplet compositions in mass fractions are listed as follows:
Figure 1:
The framework of the multiscale CFPD-HCD model for the human-to-human IAV infection with a subject-specific airway geometry. The description of the HCD model is given in Section 3.2. The detail of the final polyhedral-core mesh is provided at the right nostril and a lobar outlet (RUL: right upper lobe, RML: right middle lobe, RLL: right lower lobe, LUL: left upper lobe, LLL: left lower lobe).
- Realistic nasal breathing (NB) exposed to a sneezing event:
- Case 1: 100.0% water 0.0% NaCl,
- Case 2: 93.2% water 6.8% NaCl (Schaffer et al., 1976),
- Case 3: 89.6% water 10.4% NaCl (Yang & Marr, 2011),
- Realistic mouth breathing (MB) exposed to a sneezing event:
- Case 4: 100.0% water 0.0% NaCl,
- Case 5: 93.2% water 6.8% NaCl,
- Case 6: 89.6% water 10.4% NaCl.
3. Governing Equations
3.1. Computational Fluid-Particle Dynamics (CFPD)
The transport of IAV-laden droplets in the subject-specific human respiratory system starts from inhaling airborne IAV aerosols sneezed/coughed out from an infected subject. Due to the low volume fraction of IAV-laden droplets in air, the one-way coupled Euler-Lagrange scheme is adopted in this study (Feng et al., 2018). The liquid-vapor interaction was considered by predicting the droplet size change dynamics during their transport in the respiratory system. These effects were modeled by solving supplemetary equations, i.e., heat and mass balance equations for each droplets and vapor phases. Details are provided as follows:
3.1.1. Eulerian Phase: Airflow
Based on the fact that the laminar-to-turbulence transitional flow regime exists at the nasopharynx and the onset of the epiglottis in subject-specific human respiratory systems (Feng et al., 2018), turbulence models that can capture the transitional sites need to be employed. Indeed, precise predictions of the airflow field is important to determine deposition patterns in lung airways (Ma & Lutchen, 2009). In this study, Transition Shear Stress Transport (SST) model (Menter, 1994; Feng et al., 2018) is employed that takes the ability of the k − ω model in representing the near-wall boundary layers and is combined with the k − ϵ model to solve the free-stream airflow (Langtry & Menter, 2009). The 4-equation SST model is presented as follows:
Averaged Navier-Stokes (N-S) Equation
| (1) |
Transition Shear Stress Transport Model
| (2) |
| (3) |
| (4) |
| (5) |
where ρ is density of the Euler phase mixture, ui is the mixture stream velocity vector, and μ is the gas mixture molecular dynamic viscosity. In addition, μt is the turbulent viscosity given as μt = ρcμfμk/ω and fμ is a function of RT = ρk/(μω) and other turbulence constants reported by Wilcox et al. (1998). In Eqs. (2)–(5), G and Y account for the production and dissipation of the turbulence kinetic energy (k) and the rate of dissipation of k into internal thermal energy (ω) due to turbulence. Also, σk and σω are turbulent Prandtl numbers, which are equal to 0.85 and 0.75 respectively. The calculation of intermittency generation term in Eq. (4) (Gγ) is performed by the transported Reynolds number () in Eq. (5).
The Advection-Diffusion Equation
Governing equations for the mass conservation of the air-water vapor mixture are:
| (6) |
in which Ys is the vapor species mass fraction. The mixture is a combination of air, water vapor, and a negligible amount of NaCl in vapor form. Js is the mass diffusion flux of species due to concentration gradient. To calculate Js, the Fick’s Law can be used and given as:
| (7) |
where is the molecular diffusivity of the species in the Euler phase. Sct is the turbulent Schmidt number, i.e., Sct = μt/(ρDt) and Dt is the turbulent diffusivity. In this study, Sct is assumed to be 0.9 (Zhang et al., 2012a). In Eq. (6) is the mass source term, i.e., the rate of species mass transfer between liquid and vapor phases.
Energy Balance Equation
The conservation of energy for the air-water vapor mixture can be given as:
| (8) |
where cp, T, Φvd, kc, and kc,t are the gas mixture specific heat, cell center temperature, viscous dissipation, gas mixture turbulent conductivity, and turbulent thermal conductivity, respectively. Moreover, kc,t = cpμt/P rt, in which the turbulent Prandtl number is Prt = cpμ/kc. hs is the sensible enthalpy of the species calculated by considering 298.15 K as the reference temperature.
With the unsteady particle tracking in a local control volume (dV), two different time steps are defined. tf is the flow time step and td is the discrete droplet time step. Transient simulations of the inter-phase source terms using implicit solver is performed by advancing the DP at the beginning of the flow time step. The mass source term can be defined as:
| (9) |
where Nd/parcel is the number of droplets in each “parcel”, i.e., a combination of droplets with the same diameter existing in the same volume control.
The energy source term ST [W/m3] was calculated by considering the latent heat of evaporation/condensation between phases:
| (10) |
| (11) |
where Hlat is the latent heat of energy exchange between the phases. The subscripts of and show the flow time step at the inlet and outlet of the control volume. In addition, to distribute the effect of the parcel’s mass and energy source terms to neighboring mesh nodes, the nodes-per-cell averaging was performed for the continuous phase by dividing and ST by the number of mesh nodes at each control volume. The advanced averaging technique results in better stability in the calculation of mass and energy equations.
3.1.2. Lagrangian Phase: IAV-laden Droplets Transport and Size Change Dynamics
With the dilute suspension assumption and the negligible droplet rotational motion, the unsteady DP tracking is performed by calculating a series of equations, i.e., the translational equation, as well as the mass and energy conservation equations for each droplet.
Translational Equation
| (12) |
The superscripts of D, L, BM, and G represent drag force, Saffman lift force, Brownian motion force, and gravity, respectively. The details of each force acting on the spherical droplet can be found in Feng et al. (2018).
Forces acting on the droplets can be accurately predicted by recovering the local turbulence fluctuation velocity components (Feng & Kleinstreuer, 2013). In detail, the eddy lifetime model is employed, which assumes the interaction of particles with turbulence eddies is identified by the Gaussian probability distribution of fluctuation velocity () and the lifetime of the turbulence eddies can be given as (Daly & Harlow, 1970):
| (13) |
However, the default eddy lifetime model can overestimate the near-wall fluctuation velocity by neglecting the anisotropic fluctuation velocity components in different directions (Feng & Kleinstreuer, 2013). Thus, the near-wall correction is employed by introducing a damping function (Wang et al., 1999; Feng & Kleinstreuer, 2013).
Mass Balance Equation
| (14) |
where Ys,S and Ys,∞ are the mass fraction of species s at the droplet surface and at the surrounding continuous phase, i.e., the center of the cell where the droplet is residing. Ad is the droplet surface and Kmc is the mass transfer coefficient [m/s] given as:
| (15) |
In Eq. (15), the first parameter shows the non-continuum effect for the submicron droplets, where αm = 1 is the mass accommodation coefficient (Hinds, 2012) and the Knudsen number is defined as , in which λ is the mean free path of the continuous phase gas mixture and is the droplet diameter. In addition, the Sherwood number (Sh) can be calculated by (Whitaker, 1972):
| (16) |
where Red is the droplet Reynolds number. Also, μ and μd,S are the gas mixture viscosities at the droplet ambient temperature and droplet surface temperature, respectively.
The threshold between the evaporation and condensation processes is defined by the thermodynamic properties of the droplet, i.e., equilibrium partial vapor pressures, the temperature at the dew point, and mass fraction of droplet components. For evaporation, any droplet that shrinks under , i.e., 0.05% of the IAV minimum diameter, is considered to be completely evaporated.
The partial vapor pressure at the droplet surface can be significantly influenced by two effects: (1) the Kelvin effect, and (2) the solute effects. Based on the cloud physics for the multicomponent droplet with an ionic solute, the Köhler theory is employed to update the droplet compositions (Mikhailov et al., 2004; Kreidenweis et al., 2005). Specifically, the mass fraction can be calculated by:
Hygroscopic Growth and Shrinkage Dynamic Equation
| (17) |
where Ps,S and P0(T) are the vapor pressure at the droplet surface and the saturation vapor pressure of the transferred species at the temperature of the control volume where the droplet is located. σd is the surface tension of the droplet solution, R is the universal gas constant, γs is the species activity coefficient, and is the partial molar volume of solute NaCl. It can be estimated by the following equations:
| (18) |
| (19) |
In Eqs. (18) and (19), MWs represents the species molecular weight, ρsol is the droplet solution density, ϑd,s is the stoichiometric dissociation number of the solute (ϑd,s=2 for NaCl), and Φd,s is the molal osmotic coefficient of the solute in solution. Also, is the molality (m) of the solution. The solute effect is represented in the formulation of activity coefficient and the Kelvin effect is showed in Eq. (17). It is worth mentioning that for a dilute solution, Eqs. (18) and (19) can be simplified as:
| (20) |
| (21) |
where ϱ is the van’t Hoff factor. xd,water is the mole fraction of water and can be calculated by:
| (22) |
In Eqs. (17)–(20), parameters are extensively dependent on the temperature and composition of the droplet. Correlations and experimental data that were utilized to calculate these parameters are listed in Table 4.
Table 4:
IAV-laden droplet properties in the expelled aerosol by sneezing and the initial and boundary conditions for the CFPD model.
| Sneezing Event | Distribution Bins (Duguid, 1946) | Droplet Diameter (dd) [μm] | Number of Expelled Droplets |
| 1–2 | 26,000 | ||
| 2–4 | 160,000 | ||
| 4–10 | 420,000 | ||
| 10–25 | 26,000 | ||
| 25–50 | 58,375 | ||
| 50–100 | 14,500 | ||
| +100 | fall to the ground | ||
| texp [s] | 0.3–0.7 | Han et al., 2013 | |
| Qexp [m3/s] | 21.5 | Scharfman et al., 2016 (from Reynolds number) | |
| Properties | Droplet Density f(Td, YNaCI) | Correlation | Simion et al., 2015 |
| Diffusivity f(T) | Correlation | Treybal, 1980 | |
| Surface Tension f(Td, YNaCl) | Correlation | Weissenborn et al., 1996 | |
| Mean Free Path [m] | 9.85E-08 | water vapor - air | |
| Inlet Temperature [K] | 310.15 | ||
| RH% | inlet airflow: 40 | airway walls: 99.5 | |
| Regional Surface Area [m2] | Oral Cavity | 4.61E-03 | |
| Nasal Cavity | 1.37E-02 | ||
| Oropharynx | 2.21E-03 | ||
| Nasopharynx | 1.56E-03 | ||
| Glottis | 5.00E-03 | ||
| Trachea | 6.66E-03 | ||
| Lobes (B1-G6) | 4.25E-02 | ||
Droplet Energy Balance Equation
| (23) |
where Khc is the heat transfer coefficient. Lewis number is assumed to be equal to 1, and a negligible influence of the evaporated/condensed species in DP on the gas mixture specific heat result in:
| (24) |
In Eq. (24), Nu is the Nusselt number given as:
| (25) |
Eq. (23) is based on the assumption that the droplet is at a uniform temperature and DP has a negligible internal resistance to the heat transfer. Also, detailed derivation and validation of Eqs. (14) and (23) are provided by Miller et al. (1998).
3.2. The Host Cell Dynamics (HCD) Model
Being targeted by the IAVs, epithelial cells are also the first contacting sites for the inhaled IAV-laden droplets. The AIS activation occurs in the lymphoid structure of the pulmonary system carried by the extra-pulmonary lymphatic vessels. Handel et al. (2007) studied the in silico IAV infection in humans and provided a model with seven variables for the virus, cell, and the combination of IIS and AIS. The parameter tuning was performed by fitting the virus titer experiments. In Handel et al. (2007) model, the uninfected cells were controlled by the infection rate and were decreased by a death rate, i.e., a factor of the lag time and the initial immune response. The inclusion of the IIS in the HCD model was proposed by Pawelek et al. (2012). The target cells conversion to the refractory state, i.e., cells that become refractory to infection, was represented by the infection decreasing frequency and the rate of antiviral release. The production of infected cells was presented by the rate of infection subtracted from the response from the NK cells. A constant AIS response rate was assumed before the emergence of AIS agents and then was exponentially increased to the maximum response. The virus growth rate was determined by the rate of change from the susceptible phase to the infected state, i.e., interfered by an increase in the population of (IFN)-I cytokines. Moreover, a simplified action of infected cell cytolysis by NK was introduced by considering a mass action term. The model proposed by Lee et al. (2009) showed the effect of AIS with considering dendritic cells as the intermediate agent between IIS and AIS. The similarity and incongruity of the three models are expressed in Figure 2.
Figure 2:
Comparison of existing IAV infection HCD models (Handel et al., 2007; Pawelek et al., 2012; Lee et al., 2009).
In this study, features of early HCD modelsHandel et al. (2007); Pawelek et al. (2012); Lee et al. (2009) are critically reviewed, combined, and optimized (see Table 1 for the underlying processes). The current HCD model variables and parameters are stated with underbars to be differentiate from the CFPD variables and parameters. The schematic of the interactions in the host cells is presented in Figure 1.
Table 1:
The variable list for host cells, pathogen, IIS and AIS agents of the current HCD model
| Refractory Cells | |
| Infected Cells |
|
| Virus | |
| Dendritic Cells | |
| Helper T Cells | |
| B Cells | |
| Antibody | |
| Interferon |
After inhaled IAV-lade droplets touch epithelial cells (TT), viral reproduction process starts immediately. By the secretion of interferons (F), the neighboring epithelial cells become refractory (R) to the infection. The virus titer (V) and the infected cell (I) count are connected by the rate of virus replication (βE). TT are infected at the rate of βTTV and are converted to two states of R and susceptible (TT) which is controlled by the production of F, represented as πFTT. In addition, to enhance the reverse action, a rate is introduced for conversion back to the susceptible phase (ζRR). The effect of NK cells is incorporated into the interfering action of F as κFIF. The influence of cytotoxic CD8+ T cells is represented by defining the time of emergence (τA) and the migration factor (γ). Other unknown sources of IIS and AIS responses are added to the infected cell equation (δXI) with a constant value (δI) for IIS and a transient parameter with the growth rate of σ for the AIS. The V production rate is represented as βE and the death rate of infection is defined by δV. Also, the effect of the antibodies (A), i.e., produced by the mature B cells, on the virus reproduction deactivation is represented by the rate of (κV).
Subsequently, the DM processes antigen and present it on the AIS components. The critical agents simplify the AIS action, i.e., CD8+ T cell (TC), CD4+ T cell (TH), and B cell (B). The activation of the AIS components is considered as a function of the dendritic cell (DM) count (Lee et al., 2009). The CD8+ T cell starts the apoptosis of infected cells and B cell generates the antibodies to stop the functionality of the virus with T helper cells. Logistic growth is selected for the operation of AIS components and the maximum values for the logistic profiles are adapted from the study by Lee et al. (2009) and compared with the predicted profile for the human infection by Handel et al. (2007). Finally, the antibody and interferon population balance are presented by considering a growth rate (πA and δA, respectively) and death rate (βF and κA, respectively) for each of them.
The optimized parameters with detailed description and the reported data from previous works have been provided in Table 2. Some of the parameters lack the physical meaning and the optimization variables were set up with the range of 1e-2 to 1e+3 compared to the data reported by the previous studies. Genetic Algorithm (GA) is used to optimize the HCD mathematical system with a vast number of constraints. GA classifies under probabilistic optimization algorithm which characterized as methods that encounter with the complicated and nebulous relation between a solution and its fitness (Weise, 2009). The evolution usually starts from a population of randomly generated individuals. The fitness of every individual is evaluated, and the best individuals are selected from the current population. Next, each genome is modified by replacing one or more individuals with new solutions, which are created either by combining two individuals (crossover) or by changing an individual (mutation) to form a new generation (Edgar et al., 2001). Practically, by considering the appropriate generation, the population explorer of the possible domain of an optimal solution is obtained. In this research, non-sorting genetic algorithm II (NSGAII) is selected to solve the developed optimization problem. Based on the results of the non-sorting genetic algorithm, Pareto-front is developed, and a single set of parameters is selected based on developed Pareto-front and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) as an efficient decision-making method. The objectives are the absolute error between the experimental data and the HCD model for the viral titer and the IFN count (see 5.2). Optimized parameters, i.e., at the biologically feasible range, are changing regarding each other and the data probing has been investigated on the global domain. The optimization and decision-making processes are executed using MATLAB (“optimtool”) and in-house 4th order Runge-Kutta method ODE solver.
Table 2:
Optimized parameters of the HCD model
| Parameter | Definition | Reference Values | Optimized Value |
|---|---|---|---|
| Infection rate | 9.9e-2† ml/day.TCID50 4.7e-5‡* (RNA copy)−1ml NS day−1 7e-5§ day−1 (EID50/ml)−1 |
9.89e-3 | |
| IFN-induced antiviral efficacy | 3.3e-1‡* (IFN fold change)−1day−1 | 5.01e-1 | |
| Reversion rate from refractory | 2.6‡* day−1 | 1.15 | |
| Killing rate of infected cells by NK cells | 4.2‡* (IFN fold change)−1day−1 | 1.24e-2 | |
| Killing rate of infected cells by CD8+ T cells | 1.19e-3§ day−1 | 1.29e-2 | |
| CD8+ T cells migration factor | 0.15§ | 0.925 | |
| Infected cell death rate | 5.0e-1† day−1 2‡ day−1 1.2§ day−1 |
5.02e-1 | |
| Death rate increases factor | 0.99‡* | 0.98 | |
| Time at which AIS become fully functional | 4.87‡* day | 1.5 | |
| Virus production rate | 1.2e-5† TCID50day−1ml−1 5.3e-3‡* RNA copies (ml NS)−1day−1cell−1 1.9 EID50day−1ml−1 |
1.80e-5 | |
| Clearance rate of free virions | 8.1e-2† day−1 15‡* day−1 1§ day−1 |
9.85e-1 | |
| Rate of IAV neutralization by unit anti-IAV antibody | 4e-3§ day−1titer−1 | 6e-3 | |
| Infection rate of Dendritic cells by unit IAV | 1e-2§ day−1(EID50/ml)−1 | 1.04e-2 | |
| Max. value of the Dendritic cells | 1e+5§ | 1e+5 | |
| Death rate of mature dendritic cells | 5e-1§ day−1 | 10e-1 | |
| Max. activation rate of naive CD4+ T cells | 1.5§ day−1 | 1.85 | |
| No. of Dendritic cells for half-maximal activation of naive CD4+ T cells | 1e+2§ | 1e+2 | |
| Max. value of the activated CD4+ T cells | 1e+5§ | 1.1e+5 | |
| Max. clearance rate of effector CD4+ T cells | 4e-1§ day−1 | 0.48 | |
| No. of Dendritic cells for half-maximal clearance of effector CD4+ T cells | 1§ | 1 | |
| Max. activation rate of naive CD8+ T cells | 3§ day−1 | 2.94 | |
| No. of Dendritic cells for half-maximal activation of naive CD8+ T cells | 1e+2§ | 9e+2 | |
| Max. value of the activated CD8+ T cells | 1e+5§ | 1e+5 | |
| Max. clearance rate of effector CD8+ T cells | 75e-2§ day−1 | 0.95 | |
| No. of Dendritic cells for half-maximal clearance of effector CD8+ T cells | 1§ | 1 | |
| Max. activation rate of naive B cells | 3§ day−1 | 3.02 | |
| No. of Dendritic cells for half-maximal activation of naive B cells | 1e+4§ | 1e+4 | |
| Max. value of the activated B cells | 1e+5§ | 1e+5 | |
| Clearance rate of activated B cells | 9e-1§ day−1 | 0.9 | |
| Secretion rate of antibody titer by unit short-lived plasma cell | 6e-2§ day−1 | 0.9 | |
| Clearance rate of antibody | 4e-2§ day−1 | 4e-3 | |
| Production rate of IFN | 9.6e-10‡* (IFN fold change) day−1cell−1 | 6.20e-7 | |
| Decay rate of IFN | 1.9‡* day−1 | 4.6e-1 |
Avg values reported by Pawelek et al., 2012
4. Numerical Setup
4.1. Geometry
The subject-specific upper airway geometry excluding the nasal cavity was reconstructed from the Magnetic Resonance Imaging (MRI) scanned data (Zhang et al., 2012b). The nasal cavity geometry acquired from the MRI scanned data set by Guilmette et al. (1989) contains two passages, which are separated by the nasal septum and merged at the posterior nasal aperture. The two geometries were connected at the soft palate between nasopharynx and oropharynx. Therefore, the upper airway, starting from the nares to the first six bronchial tree generations (G6) was modeled as a single domain. To avoid unrealistic reversed flow at outlets, extending cylindrical tubes were added to the lobar outlets.
4.2. Initial and Boundary Conditions
4.2.1. The CFPD Model
As the two common inhalation patterns, mouth breathing (MB) and nasal breathing (NB) were considered. The realistic breathing waveforms were assigned as customized mouth inlet boundary conditions using UDFs. The transient volumetric flow rate data set were obtained from Scheinherr et al. (2015) for MB and Rennie et al. (2011) for NB. Both profiles represent the breathing patterns healthy human subjects at rest. For the MB waveform, an 8-term Fourier series was used to fit the experimental data (see Figure 3(b) and Table 3 (a)). For the NB waveform, two 7-term sinusoidal function series were used to fit to the breathing profile data at left and right nostrils separately (see Figure 3 (a) and Table 3 (b)).
Figure 3:
Subject-specific nasal and mouth breathing patterns. (a) NB at each nostril: the average data is collected and is fitted with the summation of sines with 7-term; (b) MB is fitted with 8-term Fourier series.
Table 3:
Fitted equations for the realistic breathing patterns (MB and NB).
| Fourier Series with 8 Terms |
Sum of Sines with 7 Terms |
|||||
|---|---|---|---|---|---|---|
| i | ai | bi | i | ai | bi | ci |
| 0 | −1.462 | N/A | 1 | 263.7 | 0.6369 | 3.015 |
| 1 | 19.55 | 60.38 | 2 | 330.7 | 0.1254 | −3.727 |
| 2 | −10.90 | −0.9638 | 3 | 73.19 | 4.86 | −0.7755 |
| 3 | −1.6 | 7.435 | 4 | 48.58 | 7.822 | −0.7588 |
| 4 | −2.737 | 1.096 | 5 | 16.06 | 13.33 | 0.03013 |
| 5 | −2.057 | −0.4919 | 6 | 253.6 | 2.011 | −0.4039 |
| 6 | −0.4734 | 0.7077 | 7 | 43.69 | 10.85 | −1.085 |
| 7 | −0.4042 | −0.8452 | ||||
| 8 | 0.08115 | 0.6936 | ||||
| W=1.561 | ||||||
For the sneezing event, the dispersed droplets number and diameter in the expelled aerosol were acquired from the experimental dataset proposed by Duguid (1946). The droplet size distribution was divided into 6 bins that encompass droplet diameters from 1 to 100 μm. The time duration (texp) and volumetric flow rate (Qexp) of expelled IAV-laden droplets carried by the airflow, are defined as 0.7 s (Han et al., 2013) and 21.5 m3(Scharfman et al., 2016), respectively. A 1 meter high circular cone was used to estimate the total aerosol volume (Vdis) at the time that the subject starts to be in contact with the expelled IAV-laden droplets from the infected subject. Specifically, the vertex of the cone is at mouth/nose region of the infected subject, and the axis of the cone is assumed to be parallel to the ground. The properties of the IAV-laden droplets and the initial and boundary conditions for the CFPD model are given in Table 4.
4.2.2. The HCD Model
For the HCD model, initial conditions were obtained from early studies (see Table 5). For estimating the epithelial cell population at each region, the mean cell size of 2.5e-7 cm2 reported by Farmer (1991) is considered. To obtain eligible inputs from the lung deposition data predicted by the CFPD model for the the post-deposition analysis using the HCD model, the number of inhaled IAV-laden droplets that can represent one 50% tissue culture infectious dose (TCID50)need to be determined. The biological decay of the IAV-laden droplet is also considered in the modeling process. Tellier (2009) showed 150–650 RNA copies of IAV represent 1 TCID50. Yang et al. (2011) had estimated 2.1e+3 and 452 genome copies per TCID50 of A/PR/8/34 (H1N1) and A/California/04/2009 (H1N1) strains, respectively. On average, the results showed the 1-hour exposure to 1.6e+4 genome copies per m3 represents 35.4 ± 21.0 TCID50 per m3. In this study, the experimental data by Ward et al. (2004) is used where it showed that one TCID50ml−1 holds 1000 copies of the viral genome and also each viral particulate ( < 1 μm) was expected to hold one viral agent (Knight, 1980).
Table 5:
Initial conditions and simulated variable definitions of the HCD model.
| Variable | Definition | Initial Value [unit] |
|---|---|---|
| Uninfected epithelial cells | 4e+8† [cells] | |
| R | Epithelial cells in the refractory state | 0‡ [cells] |
| V | Infected epithelial cells | 0† [cells] |
| V | Virus titer | Regional Deposition form the CFPD model 5[TCID50ml−1] |
| Mature Dendritic cells | 1e+3§ [cells] | |
| Effector CD4+ T cells | 0§ [cells] | |
| Effector CD8+ T cells | 0§ [cells] | |
| B | Activated B cells | 0§ [cells] |
| A | Antiviral antibody titer | 110.2§ [titers] |
| F | Interferon | 10* [IFN fold change] |
5. Model Validations
5.1. CFPD Model Validations
The CFPD model has been well validated in early studies by the airflow field and regional particle deposition comparisons with benchmark experimental data (Haghnegahdar et al., 2018; Feng et al., 2018). The advanced DPM modeling capability in this study, the accuracy of droplet size change dynamics prediction is extensively validated. The validation was done by comparing the size changes of two different scenarios of dilute aqueous droplet evaporation and a dry NaCl particle condensation with experimental data (El Golli et al., 1977; Li et al., 1992).
For validating the droplet evaporation, the simulation results were compared with the experimental data by El Golli et al. (1977). Figure 4 (a) shows the influence of the initial compositions of the droplet on its evaporation and the comparison between the CFPD model with the experimental data. The droplets were injected with the initial diameter of 16 μm to the airflow stream with the relative humidity RH=70%. Specifically, water-NaCl droplets with different molalities (m=mol/kg) are simulated and visualized. Figure 4 (b) further shows the influence of the ambient RH, the initial droplet diameter, and the initial NaCl molality in droplets on the droplets evaporation characteristics. Specifically, it can be observed in Figure 4 (b) that the increase in ambient RH will lower the initial water partial pressure gradient for evaporation cases, thereby lower the initial evaporation rate of the droplets. Good agreements can be found in Figures 4 (a) and (b) between the CFPD modeling results in this study and the experimental data, indicating the reliability of the CFPD model to predict droplet evaporation dynamics accurately. For validating the droplet condensation, the simulation results were extensively compared with the experimental data by Li et al. (1992). Figure 4 (c) shows the comparison of the droplet hygroscopic growth rate versus the initial droplet diameter with various airflow RH and temperature. For the dry NaCl particle simulations, the initial diameter is equal to 200 nm released into the domain with RH=99.5% and T=295.15 K. Specifically, a small increase in RH (from 99% to 99.5%) resulted in a substantial increase in the droplet size growth. Therefore, the agreement between the numerical and experimental data is acceptable and the differences are due to the experimental errors by controlling the ambient RH. Thus, the predictive capability of the CFPD model can be validated too.
Figure 4:
The CFPD-HCD model validations: (a-b) Droplet dynamics validation at different molality (m), RH, and T (El Golli et al., 1977); (c) The validation of dry NaCl particle hygroscopic growth at different RH and T; (d) In-house HCD modeling results of the concentration time courses for the targeted cell, infected cell, and refractory cell; (e) Comparisons of the mean viral titer [TCID50 ml−1] for the HCD model validation; and (f) Comparisons of the IFN data in early studies Fritz et al. (1999); Hayden et al. (1998, 1996).
5.2. HCD Model Validations
The validation of the HCD model was executed by comparing the HCD simulation data with the viral titer of the IAV H1N1 infection by Fritz et al. (1999); Hayden et al. (1998) as well as the average IAV H3N2 viral titer data provided by Hayden et al. (1996) (Figure 4 (f)). Furthermore, the Interferon (IFN) data by Fritz et al. (1999) was also used to validate the prediction of IFN time courses (Figure 4 (f)). Figure 4 (e) shows the viral titer data for TCID50/ml of nasal wash. One TCID50 corresponds to a single infectious virion (Handel et al., 2007). The initial value of the virus titer is considered as 5 (Lee et al., 2009) (see Table 5). Figure 4 (d) shows the predicted HCD for the target and refractory cells. The numerical time courses match experimental data well, which provides the direct evidence as the HCD model validation.
6. Results and Discussion
6.1. Airflow Velocity Field
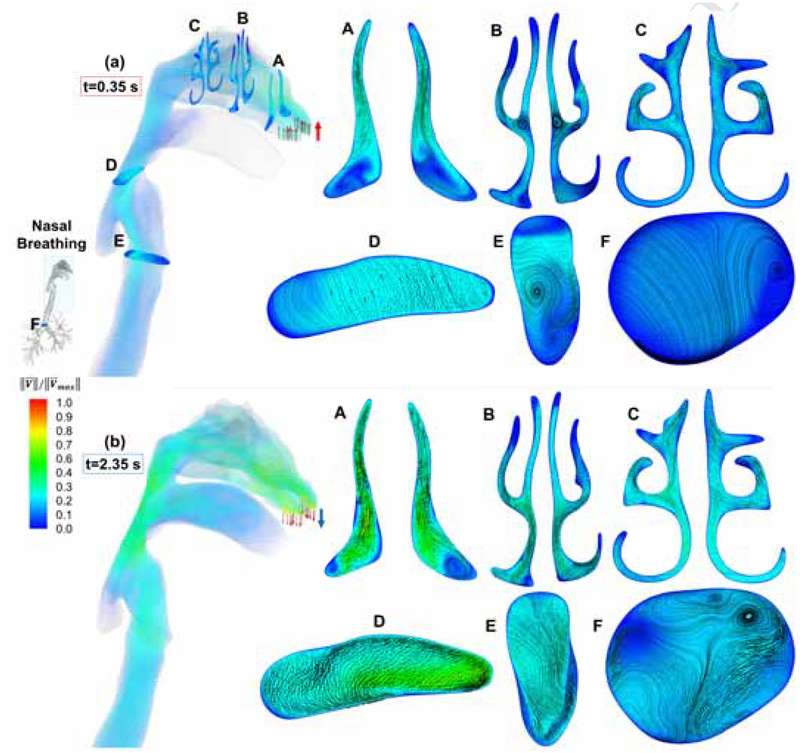
Figures 5 and 6 show the volume rendering of the normalized airflow velocity magnitude and contours at the multiple cross-sections. The normalization for the NB case were done by dividing the velocity magnitude by which is at the time of peak exhalation (t=2.35 s) at the inferior nasal aperture both in the left and right nasal passages. For the MB case, the normalization was done by dividing the velocity magnitude by which is generated at t=0.56 s on the onset of the epiglottis and the laryngeal jet core.
Figure 5:
Airflow velocity contours and volume rendering in the human respiratory system at t=0.35 s (the peak inspiratory velocity) and t=2.35 s (the peak expiratory velocity) for the NB case.
Figure 6:
Airflow velocity contours and volume rendering in the human respiratory system at t=0.56 s (the peak inspiratory velocity) and t=2.48 s (the peak expiratory velocity) for the MB case.
For the NB case, the mainstream distributions are visualized at 6 cross-sections and the secondary flows are shown by in-plane streamlines and velocity vectors (see Figure 5). In Figure 5, the top row shows the results at the time when the peak inspiratory velocity (t=0.35 s) is reached, and the bottom row shows the results at the peak exhalation (t=2.35 s). Nasal inlet jets are hitting the superior conchae and the resultant lower pressure next to the inferior concha drives the secondary flow and clockwise (CW) vortices at cross-section A (Figure 5 (a)-A). At t=0.35 s, the Reynolds number (Re) at the right nostril is 3,695 and recirculation zones are formed in the cavity between the inferior turbinate and the nasal septum. Moving forward in the nasal passages, the middle turbinate appears which changed L-shaped passage (see Figure 11 (a)-A) to Y-shaped (see Figure 11 (a)-B) spacing. The flow was separated into three fissures. The pressure drop at the cavity next to the bifurcating point of the Y-shaped opening caused the recirculations to form, i.e., CW in the left passage and counter-clockwise (CCW) in the right passage (Figure 5 (a)-B). Towards the posterior nasal apertures, the two passages deform to ξ-shaped passage when superior turbinate appears and the recirculation intensities were dissipated (Figure 5 (a)-C). These two passages merge into the nasopharynx. The velocity vectors showed the backward direction as the merged flow from the nasal cavity hits the posterior wall of the oropharynx (Figure 5 (a)-D). The same patterns exist until the mainstream airflow enters the trachea. At the glottis, due to the pressure drop at the dead volumes of the laryngopharynx (piriform recesses) a CCW recirculation region is formed (Figure 5 (a)-E), being accompanied by the laryngeal jet. In the trachea, Re is reduced from 2,628 at the glottis to 1,760 when reaching G1 which indicates the re-laminarization from the turbulence near the glottis (Figure 5 (a)-D and F).
Figure 11:
Regional virus titer predictions using the CFPD-HCD model: (a-c) The HCD in the nasal cavity (NC) and the pharynx (PY) for droplets inhalation using nose (NB) with different NaCl concentrations (YNaCl=0 and YNaCl=0.104);and (d-f) The HCD in the oral cavity (OC) and the pharynx (PY) for droplets inhalation using mouth (MB) with different NaCl concentrations (YNaCl=0 and YNaCl=0.104).
At the peak of nasal exhalation, the flow develops from airstream discharges from the lung and Re is 3,871 at cross-section F (Figure 5 (b)-F). As a result, incipient turbulence is expected. Vortices are formed, and the flow deviated to the anterior wall of the trachea (Figure 5 (b)-F). As the expiratory flow reached the glottis, the turbulence intensity is reduced and Re is 3,520. In the nasopharynx, the stream separated into two parts by uvula and headed toward the nasal and oral cavity. As the mouth is closed, static pressure differences near the lips provide resistance to the airflow entered the oral cavity, leading to the recirculating flow patterns shown by the volume rendering graph at t=2.35 s. Following the flow in the nasal cavity, the superior section of the nasopharynx, i.e., where the pharyngeal tonsil is located, directed the airflow into the nasal passages.
Figure 6 represents the velocity field at the time stations with the peak inhalation and exhalation flow rates, of the MB profile, i.e., t=0.56 s and t=2.48 s. It can be observed that the high-velocity jet core enters the oral cavity and stays near the lower palate. At t=0.56 s, due to low static pressure near the central part of the lower palate, induced by the high-velocity airflow, two counter-rotating vortices are generated near the upper palate which are visualized at cross-section A (see Figure 6 (a)-A). With the airflow progressing to cross-section B near the 90-degree bend between the oral cavity and pharynx, the triangular lower wall was deformed to a symmetrical geometry with a flat lower wall (Figure 6 (a)-B). As the result, recirculations on the left side of cross-section B are extended and cause deviation the vortex core on the right side from the centerline. It also creates a CW vortex in the oropharynx and the mainstream moves further towards the right side at cross-section C. Passing the glottis, a laryngeal jet is formed and impacts the posterior side of the trachea. During the mouth exhalation phase shown in Figure 6 at t=2.48 s, the expiratory laryngeal jet was generated and touched the larynx. The maximum airflow velocity was generated at the constriction of the oropharynx (Figure 6 (b)-C). A portion of the flow entered the posterior nasal cavity, but was not able to penetrate further into the front part. Such a phenomenon is due to the momentum loss of the airflow which failed to overcome the high resistance in the nasal cavity. In contrast to the observation that the high-velocity airflow is close to the lower palate during the mouth inhalation phase, part of the expiratory airflow entered the oral cavity and directly impacted the upper palate.
The comparison of the airflow fields between NB and MB cases indicate that the nasal passage can significantly reduce the airflow momentum at the post-nasal region. During the NB inhalation, the core of laryngeal jet has lower turbulence strength that results in a weaker impaction of flow to the posterior tracheal wall compared to the MB case. As a result, lower inertial impaction and droplet deposition is expected for the NB case at the trachea. However, there are similarities between the flow pattern at the subglottal regions between the MB and NB. During the inhalation, the flow pattern at the mid trachea is similar between MB and NB (see Figures 5 (a)-E and 6 (a)-F). During the exhalation, the secondary flow at the mid trachea and glottis are similar between NB and MB. The similarity of the flow patterns at the subglottal airways for both cases implies that the glottal contraction can re-regulate the airflow patterns and diminish the flow characteristics induced by different ways of breathing via mouth or nose, as well as the superglottal anatomical variability.
6.2. Relative Humidity Distributions
The airflow relative humidity (RH) is calculated by having the local temperature, pressure, and mass fraction of the water vapor. Figure 7 shows the RH in percentage for both NB (the top row) and MB (the bottom row) cases. The contours are at the onset of inhalation (t=0.10 s), the peak inhalation (t=0.35 s for NB and t=0.56 s for MB), and at the end of inhalation (t=1.60 s for NB and t=0.56 s for MB). The ambient water vapor mass fractions were determined based on the standard condition, i.e., T=310 K and RH=40% at 1 atm. The initial RH in the human respiratory system is assumed to be constant and equal to 99.5% and the airway walls were considered nearly saturated at which RH=99.5% (Ferron, 1977). Simulation results show that during the inhalation phase of NB, dry ambient air entering the nasal cavity started to lower the local RH. Due to the large ratio between surface area and passage length in the nose, high RH at the saturated airway walls can create sufficiently high gradients to compensate the loss of water vapor. Therefore, at the peak inhalation flow rate (t=0.35 s), RH is still higher than 90% from the nasopharynx to the mid trachea. It can also be observed that the RH distributions are significantly influence by the localized airflow patterns shown in Figure 5. Specifically, RH in recirculation regions are higher because of the longer residence time of the trapped dry airs than those in the mainstreams. Additionally, because of the reduced convection effect at the end of nasal inhalation (t=1.60 s), RH in the upper airways (shown in Figure 7 (a)) recovers to 99.5% due to the dominant water vapor diffusion from the saturated airway walls to the bulk region in the nasal cavity. For the MB case at t=0.10 s, the inhaled dry air stream has already influenced the entire oral cavity. As the flow impacts the lower palate, the low RH flow deviates towards the upper palate and reduced the localized water vapor mass fractions. At t=0.56 s, i.e., the peak inhalation flow rate, the influence of dry air on the RH reaches the mid trachea. Comparing with the velocity profile shown in Figure 6 (a)-A, the recirculation zones created by the two vortices near the mouth front results in higher local RH values. In detail, the average RHs at oropharynx and glottis are 54.3% and 61.6%, respectively. At the end of inhalation for the MB case (t=1.76 s), RH values in the upper airway did not recover as prompt as the NB case. Comparisons between NB and MB cases show that the inhaled airflow with lower RH can make the airway dryer with MB than with NB. The high ratio between the surface area and passage distance of the nasal cavity provide significant compensation of the humidity and restrict the influence of dry air more efficiently than the oral cavity.
Figure 7:
Local RH distribution of the respired airflow with RH=40% during NB and MB at different time stations of inhalation.
6.3. Size Change Dynamics and Deposition Patterns of Inhaled IAV-Laden Droplets
Figure 8 shows the positions of suspending droplets at t=1.6 s for NB and t=1.76 s for MB, i.e., the time stations of the transitions between inhalation and exhalation. Three compositions of the water-NaCl droplets were investigated (see Section 2 for droplet compositions). In Figure 8, droplets are colored based on their diameters. To visualize and compare droplet size change dynamics with better clarity, only droplets with initial diameter equal to 7 μm are shown. For the inhalation of pure water droplets in the NB case, it can be observed that droplets were undergoing evaporation. Fast droplet size reduction due to water evaporation happens in the nasal cavity, because of the relatively lower regional RH (see Figure 7 (a)). Specifically, based on the observation that the RH decreases in the nasal cavity during the inhalation phase of the NB, significant water liquid droplets evaporation occurs accordingly in superglottal regions. In contrast, during MB inhalation of the pure water droplets, RH is much lower in the entire upper airway compared to the NB case. Therefore, evaporation in the mouth inhalation has higher rates due to the higher partial pressure gradients of water. Specifically, the highest mass exchange occurred in the oropharynx and continued in the trachea. As a result, lower droplet diameters can be observed in the MB case than the NB case (see Figures 8 (a) and (d)).
Figure 8:
The suspending droplets distribution at t=1.60 s for NB and at t=1.76 s for MB (droplet initial diameter: 7 μm).
For droplets containing 6.8% NaCl inhaled via NB (see Figure 8 (b)), evaporation and the resultant decrease in droplet diameters can be observed near the nostrils. The size change dynamics is because the inlet jet increases the droplets Reynolds number and consequently the heat and mass transfer due to the higher Sh and Nu, respectively. Also, lower RH of the inlet flow resulted in an elevated mass exchange between the droplets and the surrounding gas mixture. With the droplets transporting into the high-RH regions, ambient water vapor started to condensate on droplets and initiated the hygroscopic growth. During the inhalation (see Figure 8 (b)), some droplets entered and stayed in the nasal cavity with larger diameters than other droplets. Since droplets suspending in the domain has the same residence time, i.e.,1.6 s, such differences in size growth is due to the higher condensation mass rate induced by higher local RH in the nasal cavity (RH=99.5%). A similar trend could be observed for the MB case on the transport of droplets with 6.8% NaCl (see Figure 8 (e)). However, due to the lower RH distributions in the MB case compared with the NB case, the partial pressure gradient is smaller and the condensation rate is lower. Therefore, the average droplet size visualized is smaller than the NB case. For droplets with 10.4% NaCl, the high NaCl concentration lowered the water partial pressure and increased the concentration rate. Thus, the stronger hygroscopic growth happens for droplets with 10.4% NaCl than those with 6.8% NaCl (compare Figures 8(b) and (c) for the NB case and Figures 8 (e) and (f) for the MB case).
Deposition patterns of droplets with different initial compositions during the inhalation phase and the exhalation phase are visualized in Figure 9 for both the MB and NB cases. Droplets are colored by their final diameters at deposition sites. During MB of the pure water droplets, 20–80 μm droplets deposit mainly at the back of the oral cavity and oropharynx due to dominant inertial impaction effect. Additionally, dispersed deposition patterns of nanoscale droplets can be found in the oral cavity due to the dominant influence of Brownian motion and interception. Moreover, the oral cavity is the main deposition site for droplets with smaller initial diameters. Indeed, small droplets that did not deposit in the oral cavity will evaporate completely into vapors. Deposition patterns also show gradually decreasing final droplet diameters from the pharynx to lower airways due to the continuous evaporation effect. During the expiration, evaporation continues and returned droplets become nanoscale and deposit in the oral cavity. Similarly, during the NB of pure water droplets, direct impactions of large droplets happened at the superior conchae right at the top of nares and due to the narrower passage at the nasal cavity. As a result of high filtration efficiency of the nasal cavity, only the smaller droplets were able to avoid depositing in the nasal cavity and entered the pharynx and small airways. For droplets with 10.4% NaCl, the deposition patterns show a more uniform distributions of the final droplet diameter.
Figure 9:
Local deposition patterns of the pure water and isotonic aqueous droplets (YNaCl=10.4%) with polydispersed droplet injections at different time stations for the NB and MB cases.
The hygroscopic growth and shrinkage of droplets is a key mechanism that can influence the droplet trajectory and deposition locations (Feng et al., 2016). To investigate such effect on deposition patterns, the regional and total droplet deposition fractions (DF) (Haghnegahdar et al., 2018) are provided in Figure 10 for 6 different exposure conditions (also see Section 2 for case details). NB cases show higher DF in the nasal cavity compared with the MB cases, indicating the better filtration efficiency of the nasal cavity than the oral cavity. Furthermore, the better filtration performance of nose prohibits IAV-droplet entering the pharynx, which can be demonstrated by the lower DF in pharynx for the MB cases. In addition, the total DF of NB cases are slightly higher than MB cases due to an increased deposition of small droplets when they pass the narrow nasal passages. DF comparisons for droplets with compositions show an increase in the total deposition with the increase in NaCl concentration. Due to the higher initial NaCl concentration in droplets, higher water vapor absorption and higher droplet growth are expected. Hence, the deposition increases accordingly in the upper airways. However, DFs at the primary regions of contact, i.e., the oral cavity for MB and nasal cavity for NB, was higher for pure water droplets than the other two types of droplets with NaCl. Specifically, the quantitative data of regional and total DF comparisons show that for MB cases, with a 53% increase in the NaCl content (from 6.8% to 10.4% NaCl), the total deposition increases by 6.72%. The pharynx DF increases by 8.85% and the oral cavity DF increases by 2.22%. However, comparisons between the 6.8% NaCl containing droplets and pure water droplets show that the increase in NaCl composition leads to an increase of the total DF by 2.2% and the increase of the pharyngeal DF by 26.54%. Also, it results in a 10.6% decrease of the regional DF in the oral cavity. Similarly for NB cases, with a 53% increase in the NaCl content (from 6.8% to 10.4% NaCl), the total deposition increases by 6.89%. The pharynx DF increases by 14.3% and the nasal cavity DF increases by 5.22%. However, comparisons between the 6.8% NaCl containing droplets and pure water droplets show that the increase in NaCl composition leads to an increase of the total DF by 1.4% and the increase of the pharyngeal DF by 39.74%. Also, it results in a 5.95% decrease of the nasal cavity DF. In addition, figure 10 shows that mean diameters of the deposited droplets in the MB cases are lower than NB cases. There are several possible reasons: (1) The nasal cavity can trap large droplets more efficiently than the oral cavity; (2) the relatively lower RH in upper airways of MB cases restrict the condensation rate while enhance the evaporation rate. In contrast, due to the smaller size of the droplets, the number of escaped droplets to the distal sections of the lung was higher for mouth breathers. As a result, more IAV-laden droplets are able to enter and infect lower airways for the MB cases.
Figure 10:
Regional deposition fractions (RDFs) of droplets with different initial compositions colored by the mean diameter of deposited droplets
6.4. After-Deposition Dynamics of IAV-laden Droplets
Compared with previous studies which are without accurate IAV lung dosimetry predictions, the multiscale CFPD-HCD model in this study provides the unique modeling capability to predict immune system responses after IAV infection with realistic exposure conditions and lung depositions. Specifically, the local within-host cell dynamics and the virus replication help to determine the local infection site and the immune system response in the respiratory system. The deposition of the IAV-laden droplets shows the population of active virus agents in the human respiratory system. Exposure to a sneezing event with a distance of 3 feet prompted an acute infection for IAV (Knight, 1980). Figure 11 shows the host cells (TT and R) dynamics and 50% human infectious dose [HID50] in the unit of TCID50 per secretion volume, as well as the resultant IFN (F). A timespan of 12 dpi was simulated using the CFPD-HCD model, during the NB at the nasal cavity (NC) and pharynx (PY), and during the MB at the oral cavity (OC) and pharynx (PY). The local threshold of clinical symptoms was determined as the time once 10% of the epithelium are desquamated (Bocharov & Romanyukha, 1994) until I has reached 5% of its lowest population.
For the NB case, the highest DFs are in NC and PY are independent of the droplet composition. The numbers of virus-laden droplets deposited in the NC are close between droplets with YNaCl = 0 and YNaCl = 0.104. For the deposition in the PY, droplets with YNaCl = 0.104 deposit 38% higher more than droplets with YNaCl = 0. As a result of higher DFs, higher viral loads are expected to be available to the local epithelium, but is negligible when the deposited IAV masses were converted into TCID50. The local HCD of NC and PY show that the high DF and epithelial cells at NC lead to more than 2 times conversion of susceptible cells to refractory state (Figure 11 (a)). More IFNs were released at NC with 1.14 times higher amount with longer duration(0.35 days) compared to PY (Figure 11 (c)). However, the TT profile shows a similar minimum value between PY and NC, because the higher surface area at the NC provides more immune system agents. Thus, the infection was prevented from causing severe damage to the tissue layers (Figure 11 (b)). Also, the virus titer shows comparable infection severity at PY and NC during NB. As IIS and AIS were being removed the virus progenies, the cells were shifting back to the susceptible state, and the total apoptosis of epithelium at 12 dpi are 76.4% and 78.7% of the initial cell population at NC and PY respectively (see Figure 11 (a)). The regional respiratory symptom threshold was determined at 0.91 to 5.24 dpi in NC, and 0.85 to 5.26 dpi in PY. The systemic symptom was predicted to be initiated with a 1-day delay from the respiratory symptom threshholds based on symptom score data provided by Knight (1980); Carrat et al. (2008). As a result, the systemic symptom threshold in NC is between 1.91 to 6.24 dpi, and 1.85 to6.26 dpi in PY during NB. The duration of symptom in PY is longer than NC, since the AIS and IIS are more available in NC.
Once the IAVs are inhaled via MB, the highest DFs are in OC and PY. Similar to NB cases, droplet composition difference does not impose a significant change on the local viral load. The comparison of local HCD in OC and PY show a higher epithelial cell population in PY but similar DFs. The maximum population of the refractory cell is 1.87 times higher and IFN cytokine release is 2.01 times more in PY compared to OC (see Figures 11 (d) and (e)). The duration of IFN release was similar due to the similarity between the surface area at PY and OC. The same TT minimum value between PY and NC are due to the similarity on the viral load and the responses from immune systems agents (Figure 11 (d)). The virus titer showed a similar trend but slightly higher peak infection titer in PY compared with in OC due to the 15.3% higher DF of IAV-laden droplets with YNaCl = 0.104 in PY, leading to the elevated infection in PY and OC. By increasing the IIS and AIS agents populations, the refractory cells shifted back to the susceptible state, and the total apoptosis of epithelium at 12 dpi was predicted as 74.7% in PY and 68.6% in OC of the initial cell population (see Figure 11 (d)). The local respiratory symptom threshold is at 0.62 to 5.44 dpi in OC and 0.66 to 5.56 dpi in PY. The threshold of the systemic symptom is from 1.62 to 6.44 dpi in OC and from 1.66 to 6.26 dpi in PY during NB.
Inhalations of IAV-laden droplets via MB and NB lead to different depositions, infections, and immune system responses. In this study, the mucus clearance in OC and NC were neglected. In both cases, the virus titer decreases below the value at 5.6 dpi which represents an increased level of relief from flu symptoms (see Figures 11 (b) and (e)). Comparatively, infections in PY induced by the inhaled IAV-laden droplets via NB and MB show higher virus titers. The clinical symptom was predicted to appear in the OC faster than NC due the the less amount of available immune system agents. It also indicates a more extended recovery period. As demonstrated by this in-silico study, low strain (H1N1 and H3N2) IAV replications happened in the upper airway tissues which agreed with experiments. Therefore, higher accumulation of activated dendritic cells as representative of adaptive immune system activation can be identified in PY regions.
7. Conclusions
A multiscale CFPD-HCD model is developed and the in-silico epidemiological study is presented to investigate the transport, deposition, and resultant immune system responses of the low-strain IAV laden droplets in a subject-specific human respiratory system. Both mouth and nasal breathing patterns were employed. The hygroscopic growth and shrinkage behaviors of droplets with different water-NaCl compositions were simulated and compared. The CFPD-HCD model shows the capability of predicting the local virus replication and population variations of the relative tissue agents. According to the parametric analyses in this study, the quantitative conclusions are listed as follows:
The CFPD-HCD modeling results demonstrate that low-strain (H1N1 and H3N2) IAV replication occurs in the upper airway tissues which agrees with existing experimental discovery.
For the mouth breathing (MB) case, the droplet deposition fraction in the oral cavity was 26.4%, 23.7%, and 24.1% for droplets with NaCl mass fraction of 0, 0.068, and 0.104, respectively. No monotonic trend of the regional deposition can be identified with the increase of NaCl mass fraction in droplets.
For the nasal breathing (NB) case, the droplet deposition fraction in the nasal cavity was 48.1%, 45.2%, and 47.6% for droplets with NaCl mass fraction of 0, 0.068, and 0.104, respectively. No monotonic trend of the regional deposition can be identified either with the increase of NaCl mass fraction in droplets.
Due to the high filtration efficiency of the nasal cavity compared with the oral cavity, only the smaller droplets were transferred to the pharynx and distal sections. Specifically, the pharynx deposition fraction was significantly lower during the mouth breathing compared to the nasal breathing.
For the mouth breathing (MB) case, the average diameter of deposited droplets is less than the one for the nasal breathing (NB) case.
Higher accumulation of activated dendritic cells as representative of adaptive immune system activation was identified in the pharynx and oral cavity for the mouth breathing (MB) case and similarly in the pharynx and nasal cavity for the nasal breathing (NB) case.
In the absence of mucus clearance, the average onset of systemic symptom was estimated at 1.88 dpi for NB and 1.64 dpi for MB. It indicates the faster infection distribution and immune system response for the MB case because of the less efficient filtration effect in the oral cavity than the nasal cavity in the NB case.
8. Limitations and Future Work
The biological system can be affected by a vast number of factors that makes the numerical simulation highly complex and challenging (Dobrovolny et al., 2013). Hence, an advanced in-silico 3D cell culture media model is needed to consider the inter-cellular communication in the realistic physiology of the tissue. More in vitro and in vivo data regarding the host cell and immune system responses are also necessary for the model optimization using machine learning approaches in the future. To develop a more advanced CFPD-HCD model, future research tasks include:
Considering the subject-specific human airway configurations for with pre-existing lung diseases, e.g., emphysema and COPD.
Employing the glottal adduction motion, which may significantly influence the transport and deposition of IAV-laden droplets and the resultant local IAV deposition and replication.
Including the movement of the periciliary fluid layer by modeling cilia propulsions and in tissue spatial distribution of the cell population, e.g., T cell movement within lymph nodes, via employing the agent-based model.
Modeling the resuspension of IAV from the periciliary fluid layer and investigating the enhancement of the transport of the viral agent to small airways. The same framework can be employed for the evaluation of HID50 in the human exhalation at different times post-infection.
Supplementary Material
Highlights.
A multiscale model to predict pulmonary IAV-laden droplet dynamics with hygroscopic growth
An integrated in-host dynamics model to predict after-infection response
Polyhedral-core mesh employment with enhanced computational efficiency
Realistic transient mouth and nose breathing patterns
Acknowledgments
This work was supported by the National Institute of General Medical Sciences of the National Institute of Health under Award Number P20GM103648. The use of ANSYS software (Canonsburg, PA, USA) as part of the ANSYSCBBL academic partnership agreement is gratefully acknowledged (Dr. Thierry Marchal, Global Industry Director).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Baccam P, Beauchemin C, Macken CA, Hayden FG, & Perelson AS (2006). Kinetics of influenza a virus infection in humans. Journal of virology, 80, 7590–7599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beauchemin CA, & Handel A (2011). A review of mathematical models of influenza a infections within a host or cell culture: lessons learned and challenges ahead. BMC public health, 11, S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bocharov G, & Romanyukha A (1994). Mathematical model of antiviral immune response iii. influenza a virus infection. Journal of Theoretical Biology, 167, 323–360. [DOI] [PubMed] [Google Scholar]
- Boianelli A, Nguyen VK, Ebensen T, Schulze K, Wilk E, Sharma N, Stegemann-Koniszewski S, Bruder D, Toapanta FR, Guzmán CA et al. (2015). Modeling influenza virus infection: a roadmap for influenza research. Viruses, 7, 5274–5304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canini L, & Carrat F (2011). Population modeling of influenza a/h1n1 virus kinetics and symptom dynamics. Journal of virology, 85, 2764–2770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrat F, Vergu E, Ferguson NM, Lemaitre M, Cauchemez S, Leach S, & Valleron A-J (2008). Time lines of infection and disease in human influenza: a review of volunteer challenge studies. American journal of epidemiology, 167, 775–785. [DOI] [PubMed] [Google Scholar]
- Daly BJ, & Harlow FH (1970). Transport equations in turbulence. The Physics of Fluids, 13, 2634–2649. [Google Scholar]
- Darquenne C (2012). Aerosol deposition in health and disease. Journal of aerosol medicine and pulmonary drug delivery, 25, 140–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Andrea M, Ravera R, Gioia D, Gariglio M, & Landolfo S (2002). The interferon system: an overview. European Journal of Paediatric Neurology, 6, A41–A46. [DOI] [PubMed] [Google Scholar]
- Dobrovolny HM, Reddy MB, Kamal MA, Rayner CR, & Beauchemin CA (2013). Assessing mathematical models of influenza infections using features of the immune response. PloS one, 8, e57088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duguid J (1946). The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. Epidemiology & Infection, 44, 471–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eames I, Tang J, Li Y, & Wilson P (2009). Airborne transmission of disease in hospitals. [DOI] [PMC free article] [PubMed]
- Edgar TF, Himmelblau DM, & Lasdon LS (2001). Optimization of chemical processes. McGraw-Hill,. [Google Scholar]
- Effros RM, Hoagland KW, Bosbous M, Castillo D, Foss B, Dunning M, Gare M, Lin W, & Sun F (2002). Dilution of respiratory solutes in exhaled condensates. American Journal of Respiratory and Critical Care Medicine, 165, 663–669. [DOI] [PubMed] [Google Scholar]
- El Golli S, Arnaud G, Bricard J, & Treiner C (1977). Evaporation of volatile solvent from saline multi-component droplets carried in a stream of air. Journal of Aerosol Science, 8, 39–54. [Google Scholar]
- Farmer S (1991). The airway epithelium: physiology, pathophysiology, and pharmacology volume 55 Marcel Dekker. [Google Scholar]
- Feng Y, & Kleinstreuer C (2013). Analysis of non-spherical particle transport in complex internal shear flows. Physics of Fluids, 25, 091904. [Google Scholar]
- Feng Y, Kleinstreuer C, Castro N, & Rostami A (2016). Computational transport, phase change and deposition analysis of inhaled multicomponent droplet–vapor mixtures in an idealized human upper lung model. Journal of Aerosol Science, 96, 96–123. [Google Scholar]
- Feng Y, Zhao J, Kleinstreuer C, Wang Q, Wang J, Wu DH, & Lin J (2018). An in silico inter-subject variability study of extra-thoracic morphology effects on inhaled particle transport and deposition. Journal of Aerosol Science,. [Google Scholar]
- Ferron G (1977). The size of soluble aerosol particles as a function of the humidity of the air. application to the human respiratory tract. Journal of Aerosol Science, 8, 251–267. [Google Scholar]
- Fritz RS, Hayden FG, Calfee DP, Cass LM, Peng AW, Alvord WG, Strober W, & Straus SE (1999). Nasal cytokine and chemokine responses in experimental influenza a virus infection: results of a placebo-controlled trial of intravenous zanamivir treatment. The Journal of infectious diseases, 180, 586–593. [DOI] [PubMed] [Google Scholar]
- Guilmette RA, Wicks JD, & Wolff RK (1989). Morphometry of human nasal airways in vivo using magnetic resonance imaging. Journal of Aerosol Medicine, 2, 365–377. [Google Scholar]
- Haghnegahdar A, Feng Y, Chen X, & Lin J (2018). Computational analysis of deposition and translocation of inhaled nicotine and acrolein in the human body with e-cigarette puffing topographies. Aerosol Science and Technology, 52, 483–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamborsky J, Kroger A, Wolfe S, for Disease Control, C., Prevention et al. (2015). Epidemiology and prevention of vaccine-preventable diseases. US Department of Health & Human Services, Centers for Disease Control and Prevention. [Google Scholar]
- Han Z, Weng W, & Huang Q (2013). Characterizations of particle size distribution of the droplets exhaled by sneeze. Journal of The Royal Society Interface, 10, 20130560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handel A, Longini IM Jr, & Antia R (2007). Neuraminidase inhibitor resistance in influenza: assessing the danger of its generation and spread. PLoS Computational Biology, 3, e240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayden FG, Fritz R, Lobo MC, Alvord W, Strober W, & Straus SE (1998). Local and systemic cytokine responses during experimental human influenza a virus infection. relation to symptom formation and host defense. The Journal of clinical investigation, 101, 643–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayden FG, Treanor JJ, Betts RF, Lobo M, Esinhart JD, Hussey EK et al. (1996). Safety and efficacy of the neuraminidase inhibitor gg167 in experimental human influenza. Journal of the American Medical Association, 275, 295–299. [PubMed] [Google Scholar]
- Hinds WC (2012). Aerosol technology: properties, behavior, and measurement of airborne particles. John Wiley & Sons. [Google Scholar]
- Holder BP, & Beauchemin CA (2011). Exploring the effect of biological delays in kinetic models of influenza within a host or cell culture. BMC Public Health, 11, S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight V (1980). Viruses as agents of airborne contagion. Annals of the New York Academy of Sciences, 353, 147–156. [DOI] [PubMed] [Google Scholar]
- Kreidenweis S, Koehler K, DeMott P, Prenni A, Carrico C, & Ervens B (2005). Water activity and activation diameters from hygroscopicity data-part i: Theory and application to inorganic salts. Atmospheric Chemistry and Physics, 5, 1357–1370. [Google Scholar]
- Lambert AR, O’shaughnessy PT, Tawhai MH, Hoffman EA, & Lin C-L (2011). Regional deposition of particles in an image-based airway model: large-eddy simulation and left-right lung ventilation asymmetry. Aerosol Science and Technology, 45, 11–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langtry RB, & Menter FR (2009). Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA journal, 47, 2894–2906. [Google Scholar]
- Larson EW, Dominik JW, Rowberg AH, & Higbee GA (1976). Influenza virus population dynamics in the respiratory tract of experimentally infected mice. Infection and immunity, 13, 438–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee HY, Topham DJ, Park SY, Hollenbaugh J, Treanor J, Mosmann TR, Jin X, Ward BM, Miao H, Holden-Wiltse J et al. (2009). Simulation and prediction of the adaptive immune response to influenza a virus infection. Journal of virology, 83, 7151–7165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Montassier N, & Hopke P (1992). A system to measure the hygroscopicity of aerosol particles. Aerosol science and technology, 17, 25–35. [Google Scholar]
- Liu L, Li Y, Nielsen PV, Wei J, & Jensen RL (2017). Short-range airborne transmission of expiratory droplets between two people. Indoor air, 27, 452–462. [DOI] [PubMed] [Google Scholar]
- Ma B, & Lutchen KR (2009). Cfd simulation of aerosol deposition in an anatomically based human large–medium airway model. Annals of biomedical engineering, 37, 271. [DOI] [PubMed] [Google Scholar]
- Male D, Brostoff J, Roth D, & Roitt I (2006). Immunology. 7th ed.Elsevier. [Google Scholar]
- Menter FR (1994). Two-equation eddy-viscosity turbulence models for engineering applications. AIAA journal, 32, 1598–1605. [Google Scholar]
- Mikhailov E, Vlasenko S, Niessner R, & Pöschl U (2004). Interaction of aerosol particles composed of protein and saltswith water vapor: hygroscopic growth and microstructural rearrangement. Atmospheric Chemistry and Physics, 4, 323–350. [Google Scholar]
- Miller J, & Mitchell G (1969). Thymus and antigen-reactive cells. Immunological Reviews, 1, 3–42. [DOI] [PubMed] [Google Scholar]
- Miller R, Harstad K, & Bellan J (1998). Evaluation of equilibrium and non-equilibrium evaporation models for many-droplet gas-liquid flow simulations. International Journal of Multiphase Flow, 24, 1025–1055. [Google Scholar]
- Nowak M, & May RM (2000). Virus dynamics: mathematical principles of immunology and virology: mathematical principles of immunology and virology. Oxford University Press, UK. [Google Scholar]
- Oguin TH, Sharma S, Stuart AD, Duan S, Scott SA, Jones CK, Daniels JS, Lindsley CW, Thomas PG, & Brown HA (2014). Phospholipase d facilitates efficient entry of influenza virus, allowing escape from innate immune inhibition. Journal of Biological Chemistry, 289, 25405–25417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou C, Li Y, Wei J, Yen H-L, & Deng Q (2017). Numerical modeling of particle deposition in ferret airways: A comparison with humans. Aerosol Science and Technology, 51, 477–487. [Google Scholar]
- Pawelek KA, Huynh GT, Quinlivan M, Cullinane A, Rong L, & Perelson AS (2012). Modeling within-host dynamics of influenza virus infection including immune responses. PLoS computational biology, 8, e1002588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrie SM, Guarnaccia T, Laurie KL, Hurt AC, McVernon J, & McCaw JM (2013). Reducing uncertainty in within-host parameter estimates of influenza infection by measuring both infectious and total viral load. PLoS One, 8, e64098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinilla LT, Holder BP, Abed Y, Boivin G, & Beauchemin CA (2012). The h275y neuraminidase mutation of the pandemic a/h1n1 influenza virus lengthens the eclipse phase and reduces viral output of infected cells, potentially compromising fitness in ferrets. Journal of virology, 86, 10651–10660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rennie CE, Gouder KA, Taylor DJ, Tolley NS, Schroter RC, & Doorly DJ (2011). Nasal inspiratory flow: at rest and sniffing In International forum of allergy & rhinology (pp. 128–135). Wiley Online Library; volume 1. [DOI] [PubMed] [Google Scholar]
- Schaffer F, Soergel M, & Straube D (1976). Survival of airborne influenza virus: effects of propagating host, relative humidity, and composition of spray fluids. Archives of virology, 51, 263–273. [DOI] [PubMed] [Google Scholar]
- Scharfman B, Techet A, Bush J, & Bourouiba L (2016). Visualization of sneeze ejecta: steps of fluid fragmentation leading to respiratory droplets. Experiments in Fluids, 57, 24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheinherr A, Bailly L, Boiron O, Lagier A, Legou T, Pichelin M, Caillibotte G, & Giovanni A (2015). Realistic glottal motion and airflow rate during human breathing. Medical engineering & physics, 37, 829–839. [DOI] [PubMed] [Google Scholar]
- Schroeter JD, Asgharian B, Price OT, Kimbell JS, Kromidas L, & Singal M (2016). Simulation of the phase change and deposition of inhaled semi-volatile liquid droplets in the nasal passages of rats and humans. Journal of Aerosol Science, 95, 15–29. [Google Scholar]
- Smith AM, & Perelson AS (2011). Influenza a virus infection kinetics: quantitative data and models. Wiley Interdisciplinary Reviews: Systems Biology and Medicine, 3, 429–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tellier R (2009). Aerosol transmission of influenza a virus: a review of new studies. Journal of the Royal Society Interface, (p. rsif20090302). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, James P et al. (1999). On the effect of anisotropy on the turbulent dispersion and deposition of small particles. International Journal of Multiphase Flow, 25, 551–558. [Google Scholar]
- Ward C, Dempsey M, Ring C, Kempson R, Zhang L, Gor D, Snowden B, & Tisdale M (2004). Design and performance testing of quantitative real time pcr assays for influenza a and b viral load measurement. Journal of Clinical Virology, 29, 179–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weise T (2009). Global optimization algorithms-theory and application. Self-published, 2. [Google Scholar]
- Whitaker S (1972). Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles. AIChE Journal, 18, 361–371. [Google Scholar]
- Wilcox DC et al. (1998). Turbulence modeling for CFD volume 2 DCW industries; La Canada, CA. [Google Scholar]
- Worth Longest P, & Xi J (2008). Condensational growth may contribute to the enhanced deposition of cigarette smoke particles in the upper respiratory tract. Aerosol Science and Technology, 42, 579–602. [Google Scholar]
- Yang W, Elankumaran S, & Marr LC (2011). Concentrations and size distributions of airborne influenza a viruses measured indoors at a health centre, a day-care centre and on aeroplanes. Journal of the Royal Society Interface, (p. rsif20100686). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W, & Marr LC (2011). Dynamics of airborne influenza a viruses indoors and dependence on humidity. PloS one, 6, e21481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Kim CS, & Kleinstreuer C (2006). Water vapor transport and its effects on the deposition of hygroscopic droplets in a human upper airway model. Aerosol Science and Technology, 40, 1–16. [Google Scholar]
- Zhang Z, Kleinstreuer C, & Feng Y (2012a). Vapor deposition during cigarette smoke inhalation in a subject-specific human airway model. Journal of Aerosol Science, 53, 40–60. [Google Scholar]
- Zhang Z, Kleinstreuer C, & Hyun S (2012b). Size-change and deposition of conventional and composite cigarette smoke particles during inhalation in a subject-specific airway model. Journal of Aerosol Science, 46, 34–52. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.