Quantifcation of Trans-synaptic Protein Alignment: A Data Analysis Case for Single-molecule Localization Microscopy

Abstract

Nanoscale distribution of proteins and their relative positioning within a defined subcellular region are key to their physiological functions. Thanks to the super-resolution imaging methods, especially single-molecule localization microscopy (SMLM), mapping the three-dimensional distribution of multiple proteins has been easier and more efficient than ever. Nevertheless, in spite of the many tools available for efficient localization detection and image rendering, it has been a challenge to quantitatively analyze the 3D distribution and relative positioning of proteins in these SMLM data. Here, using heterogeneously distributed synaptic proteins as examples, we describe in detail a series of analytical methods including detection of nanoscale density clusters, quantification of the trans-synaptic alignment between these protein densities, and automatic en face projection and averaging. These analyses were performed within customized Matlab routines and we make the full scripts available. The concepts behind these analytical methods and the scripts can be adapted for quantitative analysis of spatial organization of other macromolecular complexes.

1. Introduction

Neuronal communication via synaptic transmission is a complex biological process that must coordinate specialized protein structures within connected cells. Proteins in the presynaptic active zone mediate the release of neurotransmitters which diffuse within the synaptic cleft and activate postsynaptic receptors[1]. In spite of their significant impacts on synaptic transmission[2–5], subsynaptic structure and protein interactions are still unclear. This is chiefly because synapses are too small (hundreds of nanometers in diameter), existing beyond the limitation of optical diffraction of the conventional light microscope. Electron microscopy provides high enough resolution[6], but it is difficult to specifically mark and accurately recognize particular protein species, and cannot be applied in living cells. Recently developed methods of single molecule localization microscopy (SMLM) [7–9] provides the best opportunity for visualizing the protein distribution at structures such as synapses.

SMLM includes a variety of super-resolution imaging techniques that localize isolated fluorescent molecules with precision well beyond the diffraction limit by fitting their images with a version of the microscope’s point spread function. Application of these methods, especially stochastic optical reconstruction microscopy (STORM)[9, 10], photoactivated localization microscopy (PALM)[8, 11] and point accumulation for imaging in nanoscale topography (PAINT)[12], has led to series of discoveries of new biological structures and processes[13–18]. Specifically in neuroscience, these methods have revealed a new layer of protein organization at nanometer scale that is critical for modulation of synaptic functions. Postsynaptic scaffolding proteins are organized in nanoclusters enriched with AMPA receptors[19,20], while the presynaptic vesicle fusion sites are guided by nanoclusters of active zone proteins RIM[21] and Munc13[22]. Most surprisingly, nanoclusters of postsynaptic scaffolds and receptors were found to be spatially aligned with presynaptic RIM nanoclusters, suggesting a trans-synaptic nanocolumn structure[21] that couples presynaptic transmitter release to the densities of postsynaptic receptors and optimizes the synaptic transmission[4, 5, 19, 23]. The reorganization of nanocolumns in synapses may underlie the tuning of synaptic strength during plasticity and pathological conditions[4, 24].

Despite the magnificent details SMLM has provided, performing quantitative analysis on this data has proven to be a challenge. This has become a barrier for the efficient application of SMLM in the biomedical field, especially since more sophisticated and customized analyses are often required to meet the demands of most specific projects than the image processing capabilities of most general software packages[25]. Indeed, many reports rely heavily simply on presenting images rather than exploiting the wealth of information present in them. Here, we describe detailed analytical methods on quantification of trans-synaptic alignment on three-dimensional STORM data with the full Matlab script attached. Compared with the previous work of Tang et al[21 ], we have made several new improvements besides developing new analytical methods. Specifically, the nanocluster detection function was re-written and its performance was greatly improved so it could cover a larger range of overall density and give lower false positive rate. The cross-cleft translation, paired cross-correlation and enrichment analysis were revised in minor details to increase the efficiency. The automated detection of cleft plane and 2D projection were newly developed. Some of the methods could be easily adapted to analysis of other biological structures.

2. Result

To begin, we assume that all the three-dimensional coordinates of localized fluorophores labeling the proteins of interest were previously determined, using Gaussian fitting or other methods[26]. Numerous prior works and reviews cover details of the localization process, and we will not address it here[10, 27]. Synapses are structurally unique, with presynaptic active zone (AZ) and postsynaptic density (PSD) always symmetrically aligned across the synaptic cleft, as is clearly visible under the electron microscope[28]. Therefore, when one AZ protein and one PSD protein are separately labeled, synapses can be efficiently identified as sandwich-shaped structures in the scatter plot of localizations[13]. Then we applied the DB-SCAN method[29] on the localizations in selected ROI by using Matlab function ‘DBSCAN.m’ created by S. Mostapha Kalami Heris to define the final synaptic boundaries, which we term the “synaptic cluster”. Only those localizations with a minimum of 60 localizations (MinPts=60) within a radius of 5 times mean minimal distance (epsilon = 5 x MMD ≈ 100-120 nm) were considered members of the synaptic cluster. With the same epsilon, MinPts varying from 20 to 80 could pick up the cluster with differences of only a small set of localizations around the boundary.

2.1. The detection of high-density nanoclusters.

Basic strategy

Within the synaptic cluster are frequently found further smaller clusters of protein, which we term “nanoclusters”[21] or nanodomains[19, 20]. To automatically identify nanoclusters, we segmented the localizations within a cluster based on their local density, thus defining nanoclusters as groupings of particularly high-density localizations. Thus, accurately calculating the density threshold of nanoclusters is the most critical step. This is made more difficult because although the border of the synaptic cluster is often abrupt and steep, most synaptic proteins are not distributed with a high-density contrast between nanoclusters and the background within the synaptic cluster, and the finite imaging resolution blurs apparent nanocluster borders.

We took a strategy similar to the DB-SCAN method[29]to calculate the local density (LD) of localizations by counting the number of localizations within a certain distance (d) from each localization. To account for the variation in localization density across different synaptic clusters, we defined d as T _x MMD instead of a fixed value[19, 21], where MMD is the mean minimal distance of all localizations within the synaptic cluster, and T is a scalar multiplying factor. The appropriate value for T was determined empirically, as shown below. The threshold of local density for nanocluster detection was defined as Mean(LDO) + 4 × Std(LD0), where LD0 is the local density of a randomized cluster with the same overall density as the synaptic cluster. We set up the threshold based on two major considerations: first, to minimize the detection of nanoclusters in clusters with randomized uniform distribution, and second, to maximize the number of nanoclusters detected in labeled protein clusters with different total densities. The threshold we used represented the 99.95% confidence that the measured density differs from chance. With this high threshold, the occurrence of false positives is greatly reduced, and all localizations with a local density larger than this threshold were considered within nanoclusters.

These positions are then divided into sub-clusters using a “top-down” splitting strategy. We ranked all localizations with an above-threshold local density based on their local density in a descending order, and then assigned each localization sequentially as the peak of a new nanocluster or a part of an existing nanocluster based on whether it’s further enough from peaks of all existing nanoclusters. The localization with highest local density, if above the threshold, was defined as the peak of the first nanocluster. The second-highest-density localization would be considered as the peak of another potential nanocluster. If the distance between the first peak to this potential second peak was larger than the defined cutoff distance, we consider the second localization the peak of the second nanocluster; otherwise, the second localization was considered a part of the first nanocluster. According to the previously measured average nanocluster diameter 80 nm, the minimum peak-to-peak distance is 80 nm, which is about the average size of synaptic nanoclusters[21]. With this, even if the valley between two local peaks has a density much higher than the threshold, as long as the distance between the two peaks is far enough, they will organize two different nanoclusters.

Then, each potential nanocluster was further divided into sub-clusters based on the point-to-point distance with a cutoff of 2 x Mean(MMD) using Matlab function ‘clusterdata’, and only the sub-cluster having the original peak localization of this potential nanocluster was selected. This step was designed to deal with situations when there were multiple “nanoclusters” within an 80-nm-dimeter region. This was more common in our simulations when overall density was high. The cutoff distance of 2 x Mean(MMD) was decided based on a series of tests on measured data and randomized simulations. Finally, to be accepted as a nanocluster, the subclusters had to include at least 4 localizations which is the minimal number to define a 3D structure.

Practical example

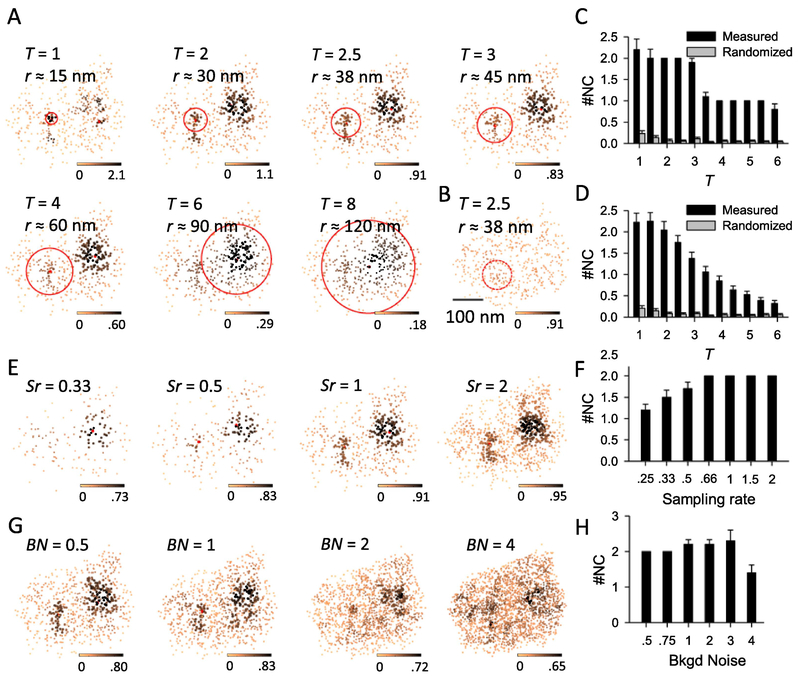
We labeled the postsynaptic scaffold protein PSD-95 in cultured hippocampal neurons with antibodies conjugated with Alexa647 and used 3D-STORM to map its distribution[10, 30]. We integrated all the above processes into one MATLAB function nanocluster_detection_3d.m and used it to detect nanoclusters by varying the parameter T (Figure 1A). At the same time, we also randomized the distribution of localizations within the measured borders of the cluster and used the same function to detect any “false positive” nanoclusters (figure 1B). When T was small, i.e. local density was calculated within a smaller radius, the algorithm was too sensitive to the localization distribution within a very close vicinity and therefore the nanocluster number and their peak positions showed a larger variation; when T was too large, local densities were more washed out due to a larger averaging radius and therefore some visually identifiable nanoclusters were missing from the result, and the detected peak of a nanocluster (red dots in Figure 1A) did not represent the intuitive peak (Figure 1A, T = 8). At almost all values of T, the rate of detecting false-positives was very low (Figure 1C–D). For the example PSD-95 cluster, the nanocluster number was constant and the result matched our visual expectation with T 1~3 (figure 1C). When results from more PSD-95 clusters (n = 59) were pooled together, the nanocluster number was stable for T 1~2 and then started reducing with higher T (figure1D). Based on these, we chose T of 2.5 for all our analysis.

Figure 1. The detection of nanocluster and its robustness.

A. Detected nanoclusters from the same PSD-95 cluster with different T values as labeled. PSD-95 localizations are shown in the enface angle, with the color scale coding local density and the red point representing the peak of a nanocluster, i.e. localization with highest local density within a nanocluster. Note that the peak of a nanocluster is not necessarily around its center. Red circles represent the region within which the local density was calculated for nanocluster detection, with the radius (r) roughly calculated and labeled. Scale 100 nm. B. Typical example of homogenized cluster of the same one in a, with the same color scale as its comparable control in A. C. Pooled results of detected nanocluster number in the example cluster in A from 20 rounds of computation. D. Pooled results of detected nanocluster number from 59 PSD-95 clusters. Note that in the full parameter space, the nanocluster number in measured protein was significantly higher than that of the randomized protein (p < 0.001 at all bins, one-way ANOVA on ranks with pairwise comparison procedures).E.Nanocluster detection in simulated synaptic clusters with different sample rate (Sr). The cluster was generated by a random subset of localizations (for Sr < 1) or adding more localizations with an error within 30 nm in each dimension (for Sr >1). F. Number of detected nanoclusters with varied sample rate. Data were averaged from 10 simulations. G-H. Nanocluster detection in simulated clusters with extra background noise by adding randomized localizations. BN or background noise denotes the ratio of added localization number to the original. Data were pooled from 10 simulations.

To further test the performance of our algorithm for clusters with various localization density and background noise, we performed nanocluster detection on two sets of simulated synaptic clusters. First, we randomly selected a subset of localizations to form low-density clusters and added a random subset of localizations with an extra −30 to 30 nm error in each dimension to generate high-density clusters (figure 1E). The results showed that the number of nanoclusters detected is consistent for clusters with a density of 0.66 to 2 times the original density. When the density is lower, less dominant nanoclusters are less likely to be reliably detected (figure 1F). At the same time, we added randomly distributed localizations in the cluster to increase the background noise (figure 1G) and found that when added noise was less than the original overall density, detection of nanoclusters was consistent and reliable. When the noise level was equal to or higher than the original density, detected nanoclusters became less reliable (figure 1H). Together, these tests further demonstrated the robustness of our nanocluster detection algorithm.

Discussion

The key parameter T was decided 2.5 as a tradeoff between two errors for this binary classification. First, we would like to reduce the false negative error, which is favored by a lower T and a lower initial density threshold. Second, we want to minimize the false positive error, which requires a parameter set in the opposite direction. In our case, especially for the following protein enrichment analysis, the false positives would greatly affect the result by diluting the potential enrichment, while the impact of false negatives on enrichment is minimal and the main risk is reducing the number of observations. Accordingly, we set the parameters to favor a lower false positive error, and as a result, we may have underestimated the nanocluster numbers within synapses. In cases that the false negative is more critical, a lower T and a lower initial density threshold should be considered.

Overcounting represents a great challenge for most analysis on data of localization microscopy[31–33]. In our case, though we have combined those peaks lasting for multiple frames into single localizations (temporal grouping) to minimize the overcounting error, this problem cannot be fully eliminated due to the use of highly reversible probes. Therefore, there is a possibility that the multiple blinkers would create some artificial nanoclusters. In our previous study[21], we have taken multiple experimental and numerical approaches to argue that in spite of the possible contamination by overcounting, the large majority of our detected nanoclusters arise from local densities of synaptic proteins. One clear test is that the normalized auto-correlation of putative synaptic nanoclusters was very different than that of either measured or simulated repetitively activated single emitters. Due to the large variation of nanocluster size, it is hard to estimate what proportion of detected nanoclusters arose from overcounting. However, this proportion appears to be quite small, because the nanocluster detection-dependent enrichment analysis showed a significant co-enrichment of multiple synaptic proteins across the cleft, and the analysis was sensitive to discern subtle changes of protein enrichment during plasticity.

This algorithm can also obtain some detailed information regarding the nanoclusters themselves, including their volume and the internal localization density. Since the number of localizations in one nanocluster was typically small, using a convex hull or alpha shape to delineate it would greatly under-estimate the nanocluster volume due to the boundary effect. Therefore, following published suggestions[34], we tessellated the synaptic cluster with polyhedrons using Matlab function voronoin(), with each Voroni cell containing one localization. The nanocluster volume was calculated as a summation of volumes of all polyhedrons containing the nanocluster localizations. To avoid unexpected unbounded Voronoi cells and over-estimating the volume of cells near the cluster surface, we introduced ~10% background noise by adding randomly distributed localizations around the cluster. Polyhedron volume for each localization was averaged across ten independent simulations. The nanocluster is not a discrete structure but a density gradient, and therefore this threshold-based algorithm would have a certain degree of arbitrariness. However, by applying the same set of detection parameters to different proteins or treatments, the method is sensitive enough to pick up differences in nanocluster number, volume, or interior localization density[21].

For subsequent analysis below, it is not critical what method is used to delineate the borders of subsynaptic nanoclusters. Indeed, there have been several methods well established for nanocluster detection in 2D data, including those based on DB-SCAN[19, 20] or Voronoi tessellation[34], and these could be expanded to operate on 3D localizations[35]. No matter which method is used, the localizations near cluster boundaries would have under-estimated local densities and as a result they are more likely to be excluded from the detected nanoclusters. We have tried to correct this bias by normalizing the calculated local density with the density at the same positions when all other localizations were randomly distributed within the synaptic cluster. This worked in most cases except that sometimes the boundary-defining localizations, especially those at sharp corners, got over-estimated densities due to small in-cluster volume around them. However, the majority of these localizations cannot generate nanoclusters owing to our strict criteria in the detection function. We compared the nanocluster detection based on original local density and normalized density and got very similar results; the only differences were some nanoclusters close to synapse edge that might include a small extra number of localizations when detected with the later method, suggesting under our experimental conditions, nanoclusters were naturally away from synaptic boundaries[21]. Therefore, we used the original instead of normalized local density for nanocluster detection to increase the computation efficiency.

2.2. Analysis of trans-synaptic protein alignment

To quantify the alignment of protein distributions across the synapse, we provide two independent methods: 1) 3D paired cross-correlation function (PCF) analysis to quantify the overall correlation of protein densities, and 2) a protein enrichment analysis to calculate the local protein density at positions opposing a given nanocluster on the other side of synapse[21, 31]. Both methods were based on the assumption that the high densities within two proteins are distributed at similar positions within their own cluster, i.e. if the two synaptic clusters are overlapping, the two sets of high densities should be colocalized. However, the pre- and postsynaptic proteins are distributed at different sides of synaptic cleft with a distance of 50-200 nm[13]. Therefore, before performing these analyses of alignment, we first have to translate one cluster to overlap with the other without bias towards local densities.

2.2.1. Overlapping pre- and postsynaptic clusters without bias towards local densities.

Basic strategy

Though in EM images we cannot distinguish the protein identity or local density of specific proteins within active zones and postsynaptic densities, AZs and PSDs were always aligned well across the cleft[36], i.e., the AZ and PSD are two disc-shaped structures of the same size, paralleled with each other. Thus for proteins distributed within these two regions, such as RIM1/2 in AZ and PSD-95 in PSD, the space they take under 3D STORM should be similar in volume and shape[13, 21]. Therefore, we could translate one cluster along a certain direction across a certain distance and get a good overlap with the other. It is worth emphasizing that this overlapping is for the general shape of the two synaptic clusters, as if aligning the edges of AZ and PSD in EM images. To guarantee that, we set a density ceiling of ρ/4 for the density matrix of both clusters, where ρ is the average localization density within synaptic clusters. Without a density ceiling, the cross-correlation would be dominated by those high-density sub-regions and the translation would preferentially overlap high-density nanoclusters of the two proteins, which would result in strong artificial enrichment, so the effect of local high density within the synaptic boundary should be minimized. The ρ/4 density ceiling was chosen based on series of simulations by randomly shuffling all nanocluster positions within the synaptic boundary. We tested different density ceiling values and found that with a ceiling of ρ/4 the positioning of nanoclusters inside the synapse had very little impact on the translation. However, if the ceiling was too low, the translation was too sensitive to the boundary definition and including one or two extra localizations on edges was able to greatly reshape the full cluster and dramatically affect the translation. For this consideration, a higher ceiling could reduce the impact of those low-density localizations around edges on the translation. A density ceiling of ρ/4 was a good compromise. The magnitude and direction of the translation were then defined as the vector from the center to the peak in the cross-correlation space calculated with the density matrix of the two clusters[21].

Practical example

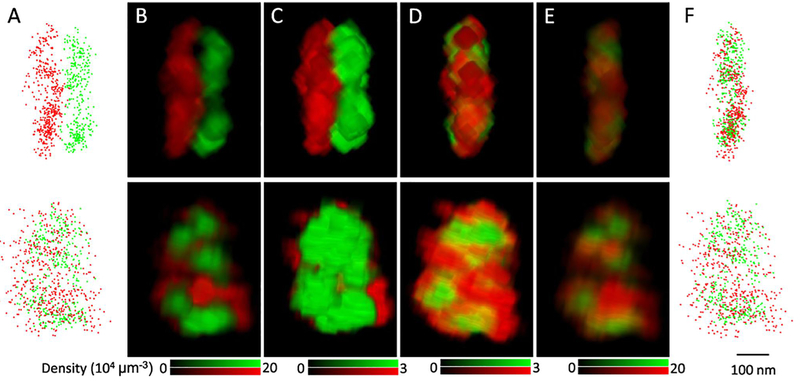
RIM1/2 and PSD-95 are key proteins in AZ and PSD[4–6], so we labeled these two proteins with antibodies conjugated with Alexa647 and Cy3, respectively, and used STORM to map their 3D distribution (Figure 2A)[9, 10, 30]. 3D density matrices were built for each cluster with a voxel size of 5 nm, and a 3D convolution with kernel size of 11 was applied to smooth the matrices (Figure 2B). As mentioned above, the maximal density in a matrix was set to a quarter of the average density to eliminate the major heterogeneity inside the synapse (Figure 2C). With these largely homogenized matrices, the vector could be calculated, and the two matrices could be translated to have an optimal overlap based on their general shapes (Figure 2D). Finally, the overlapping original protein densities were restored to the state of measurement for the following quantitative analysis (Figure 2E–F). This part of the process was coded into the same Matlab script with the following paired cross-correlation function.

Figure 2. Translation of synaptic clusters to overlap pre- and postsynaptic clusters without bias towards local densities.

A. Scatter plot of RIM1/2 (red) and PSD-95 (green) localizations with the side (top) and enface (bottom) view angles. B-E. Volume views of the original synaptic density matrix (B), matrix with a low density ceiling(C), matrix with density ceiling after the translation (D), and matrix with the original density after the translation (E). The density matrix was constructed with a voxel size of 5 nm and a 13x13 convolution was applied. Images were made with the 3D viewer plugin in Fiji ImageJ. F. Scatter plot of the two clusters after the translation. Scale 100 nm.

Discussion

The translation was based on the assumption that the two clusters were proteins marking the AZ or PSD, that is, the protein structures attached to the synaptic membrane and thus fairly planar. So, extra caution should be taken for synaptic proteins with substantial presence away from the membrane, such as the protein synapsin which is associated with synaptic vesicles and thus fills almost the whole bouton[37, 38].

In the defined function, we set one parameter to constrain the distance range of the translation (distance in get_crosscorr_3d.m). For major synaptic protein pairs, the range could be estimated based on previous STORM study by Dani et al[ 13]. Depending on the imaging system, there may be a channel registration error. Therefore, the range of translation distance should be expanded accordingly. For both the following alignment analysis, the computation was performed on the overlapped cluster pair after the translation. In this case, as long as the channel registration error was linear and not too large to attain the cluster-shape-dependent translation, it won’t impact the alignment analysis.

2.2.2. Paired cross-correlation analysis

Basic strategy

Pair correlation function has been used to quantify heterogeneity within an organization or colocalization between systems[31, 39, 40]. The pair cross-correlation function, g(r), reports the increased probability of finding a similar localized signal in system 2 at a distance r away from a given localized signal in system 1.

$$g\left(\overrightarrow{r}\right)=\mathrm{Re}\left\{\frac{FF{T}^{-1}\left(FFT\left(I_1\right)\times conj\left[FFT\left(I_2\right)\right]\right)}{{\rho }_1{\rho }_{2}FF{T}^{-1}\left(FF{T}^{-1}\left(W_1\right)\times conj\left[FFT\left(W_2\right)\right]\right)}\right\}$$

The function describes the cross-correlation of the two constructed density matrices (I₁, I₂) of the two sets of STORM localizations normalized with the cross-correlation of the two window functions (W₁, W₂) for I₁ and I₂, respectively. W has the value of 1 inside the corresponding cluster and 0 outside. The cross-correlation is tabulated in Matlab using Fast Fourier Transforms (FFTs), conj[] indicates a complex conjugate, ρ₁ and ρ₂ are the average densities of matrix I₁ and I₂ respectively, and Re indicates the real part. This normalization is critical as it removes all the effects coming from complex boundary shapes and makes the function account only for the internal density distributions within the two matrices. $g\left(\overrightarrow{r}\right)\approx 1$ represents a random correlation between the two structures, and the colocalization of any high-density structures would result in $g\left(\overrightarrow{r}\right)>1$.

Practical example

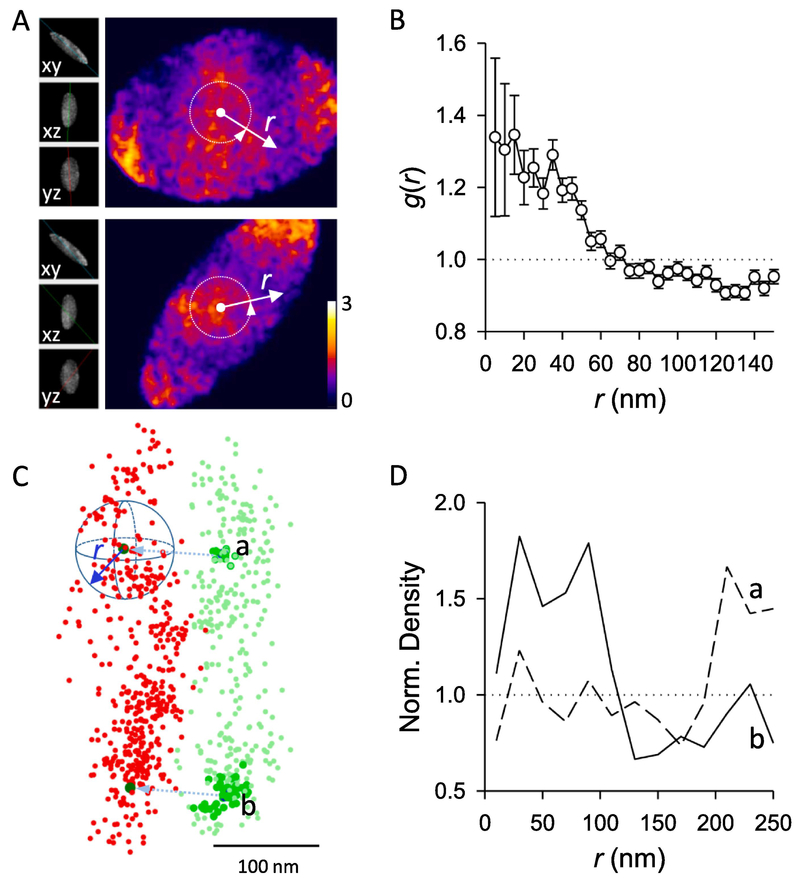
We used the same RIM1/2 and PSD-95 cluster pair as example. Density matrix (I₁ and I₂) were built with a voxel size of 5 nm and the window functions W₁ and W₂ were defined as the same set of matrices with voxels set to 1 inside the cluster defined with an alpha shape (α = 150 nm). In the three-dimensional $g\left(\overrightarrow{r}\right)$ matrix (Figure 3A), the voxels in the center region showed significant higher values, as shown clearly with the circularly averaged one-dimensional distribution (Figure 3B). The g(r) between the measured proteins was significantly larger than 1 within a certain radius range (with ANOVA), suggesting the internal densities of RIM1/2 and PSD-95 at this synapse had a significant alignment.

Figure 3. Paired cross-correlation and protein enrichment analysis.

A. Two sections of the 3D paired cross-correlation matrix $g\left(\overrightarrow{r}\right)$. Inserts on the left represent the sectioning angles, and the color coded the normalized coefficients of paired correlation between density matrixes of RIM1/2 and PSD-95 after translation. Note the heated color near the center of matrix. Images were made with the volume viewer plugin in Fiji ImageJ. The color-coded are divided according to the degree of heat, and the left side shows different three-dimensional angles, r represents the size of the region between the various angles deviating from the best correlation value. B. The paired correlation function distribution g(r) averaged over all angles along distances from the center of matrix $g\left(\overrightarrow{r}\right)$, as shown with the white arrows in A. Note g(r) is significantly higher than 1 within certain radius. C. Strategy of the protein enrichment analysis. From the projected peaks of PSD-95 nanoclusters (dark green), local density of RIM1/2 (red) was averaged over all angles along distances. In case of a positive alignment, a higher averaged density is expected at distances around 0. D. Spatial profile of normalized RIM1/2 density along distances from projected peaks of PSD-95 nanocluster a and b. Note the significant enrichment of RIM1/2 to nanocluster b but not to a.

All these computations were incorporated in a defined Matlab function get_crosscorr_3d.m together with the cluster translation in part 2.2.1. Besides the 3D coordinates of the two localization sets as inputs, the other parameters included voxel size, radius range for g(r) calculate, cluster translation vector, and distance range of the translation. If the cluster translation vector was set as null ([] in Matlab), the function would calculate the vector as described in 2.2.1, which would be skipped if there was a valid input for cluster translation vector.

Discussion

Theoretically, a 2D cross-correlation in the plane of the cleft could provide a better approach for this analysis. Though 2D and 3D correlation become equal when the thickness of both clusters is close to 0, our data cannot be considered to be close to this limit due to the limitations of the biological structure of the synapse and the imaging resolution. Our employment of 3D cross-correlation has a potential risk of including certain contribution of “out-of-plane” distributions to g(r) at distances within half the cluster thickness. However, several considerations indicate that 3D cross-correlation provides better results here for testing the trans-synaptic alignment of synaptic proteins. We discuss this in detail in section 2.3.

The application of the paired cross-correlation method is not limited to the analysis of two neighboring or overlapped protein clusters, but can be expanded to many occasions for colocalization or alignment analysis such as the three-dimensional distribution of two proteins in a defined space with varied volumes. However, when distributions over a large volume are analyzed with a small voxel size, i.e. when there are a large voxel number in the constructed density matrix, running the function may be extremely memory-intensive in current versions of Matlab. In this case, an alternate computing strategy should be employed[41].

The paired cross-correlation method determines whether two three-dimensional clusters have correlated internal density structures[31, 39]. It does not rely on the detection of high-density nanoclusters therefore won’t be affected by potential errors during nanocluster detection as discussed in part 2.1. For the same reason, this method cannot provide any detailed information about the alignment of individual nanoclusters and therefore it may not be sensitive enough to detect all potential alignment, especially when there are multiple high-density peaks. Ideally, we need an analysis that could test the alignment for each individual nanocluster – therefore, we developed the protein enrichment analysis.

2.2.3. Protein enrichment analysis

Basic strategy

This analysis is based on the prediction that if the pre- and postsynaptic nanoclusters align across the cleft, the presence of a nanocluster on one side will predict a higher local protein density around its projected point on the other side. To quantitatively test this, we calculated the average local density of protein A over the distance from the projected peak of a protein B nanocluster. In case of a positive alignment, this curve would start from a local density significantly higher than the average at the small distance and then decay to the average.

Practical example

We explored the degree of RIM1/2 enrichment relative to the two PSD-95 nanoclusters in the same example synapse. The PSD-95 nanoclusters were detected as described in 2.1 and the PSD-95 cluster together with the two nanocluster peaks was projected to have a best overlap with RIM1/2 cluster as in 2.2.1. The number of RIM1/2 localizations were counted within binned distance ranges from the projected peaks (Figure 3C). However, the volumes corresponding to the bins do not follow the simple cubic power distance, but are affected by cluster boundaries and depend heavily on cluster shapes and positions of the nanoclusters. Without volumes, local densities could not be calculated and the data from different clusters or even from different nanoclusters in the same synapse could not be averaged. To measure these volumes, we randomized the RIM1/2 localizations within its cluster boundary, and the distribution of randomized localizations along the same distance represented the volumes corresponding to the distance bins. A simple ratio of these two distributions gave the normalized local densities along distances from the PSD-95 nanocluster center. If there was a RIM1/2 nanocluster aligning to a given PSD-95 nanocluster, we would expect a normalized density significantly larger than 1 within a certain small range of r, such as for nanocluster b in Figure 3C–D. This r range was determined as r < 60 nm based on pooled enrichment, and an enrichment index could be defined as the averaged density within the range for further statistical tests[21]. Otherwise, the normalized density would be around 1, which suggests a random distribution, as can be seen for nanocluster a in Figure 3C–D, or below 1, which would suggest that molecules are de-enriched in regions closely aligned with the nanocluster. To simplify the quantification, we defined an enrichment index by averaging the normalized density within 60 nm from the projected peak. The radius of 60 nm was chosen based on the fact that most key synaptic proteins are significantly enriched in the nanocolumn within this radius[21]. Whether RIM1/2 is enriched to a given PSD-95 nanocluster could be determined via comparison with the enrichment indices of multiple randomized RIM1/2 clusters. With this, the percentile of PSD-95 nanoclusters that were enriched with RIM1/2 could be quantified[21].

Discussion

Enrichment analysis and paired cross-correlation function are two independent tests on whether two clusters have spatially correlated internal density structures. While the paired cross-correlation compares the overall degree of correlation between internal distributions of two proteins, the enrichment analysis provides more detailed information by quantifying the local density of protein A relative to a defined B sub-region. While in our case of nanoscale alignment between high density peaks the sub-region of protein B is the defined nanoclusters, the same analysis could be easily adapted to other forms of sub-structures such as hollow spots or inverse density peaks depending on the demand of specific scientific questions. Since the enrichment analysis is based on the positions of sub-regions, the false-negatives of the nanocluster detection would have a great impact by diluting the distribution profile. Therefore, the analysis will benefit from stricter criteria on nanocluster detection.

Due to the discrete nature of SMLM data, the boundary effect could dominate the result in special occasions, especially when a ratiometric measurement is made. In our case, depending on the cluster shape and the position of the nanocluster, the valid volumes for some bins may be very small. Even though we randomized the cluster with a density 10 times the original, which was equivalent to averaging across 10 simulations, the numbers of randomized localizations within these volumes were still not representative, which would result in an extremely large ratio or even an invalid calculation. If a bin showed an infinite ratio, its neighboring bins usually suffered from this boundary effect. We exclude these bins when pooling the data to reduce potential contamination.

2.3. Automatic enface projection and averaging of synapses

While the enrichment analysis provides detailed spatial distribution of one protein along distances from defined points such as peaks of nanoclusters of the reference protein, it would be helpful if similar information can be represented as images. Here we present an automatic method to make a projection of the three-dimensional synaptic structure to a defined plane such as synaptic cleft to generate an enface view of the protein distribution. This projection would make it possible to average the enface profile of protein densities or even analyze the relative spatial distribution patterns of pre- and postsynaptic nanoclusters.

Basic strategy

With one presynaptic AZ protein and one postsynaptic PSD protein labeled with two fluorophores, a typical synapse would be a sandwich shape, or a flat disc after one set of localizations were translated to overlay with the other (Figure 2). A plane parallel to the cleft can be defined by fitting all localizations after the translation (least square of the normal distance to the plane). The two-dimensional enface projection can be achieved with calculation of the projected coordinates of all localizations along the fitted plane.

Practical example

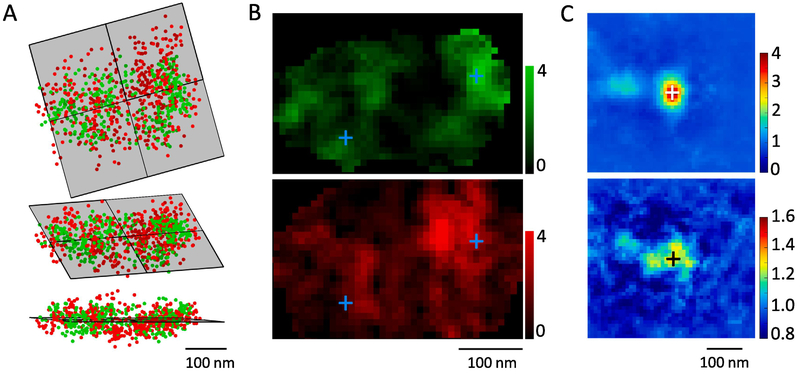
We use the same synapse as example. After overlaying the two cluster together as in Figure 2, we calculated the enface plane (Figure 4A) with the defined Matlab function get_2D_projection.m based on the affine_fit.m function by Adrien Leygue. The same function also yielded the projected 2D coordinates so we could generate the enface density map. To rule out the effect of cluster thickness along the projection direction on the local density, we randomized all localizations within the original clusters and performed a similar projection to get a map coding the thickness information. Using this as a normalizing factor, we obtained a map coding the related local density (Figure 4B).

Figure 4. Automatic enface projection and averaging of synapses.

A. Calculation of the enface plane by fitting all overlapped localizations after translation. RIM1/2 is in red, PSD-95 in green. Top shows the top-view, lower the side-view and middle the elevated view. B. Local density distribution after the projection. Crosses present the peaks of two PSD-95 nanoclusters. C. Averaged PSD-95 nanocluster in projection plane and the corresponding density distribution of RIM1/2 across 103 nanoclusters from 59 synapses.PSD-95 distribution was rotated to get the best fit of the internal distribution to the original template. Note the second nanocluster ~120 nm from the center of the averaged nanocluster. RIM1/2 was rotated with the same angle as PSD-95 from the same synapse. Note the significant higher density around the averaging center.

To visualize the enface distribution of both RIM1/2 and PSD-95 around PSD-95 nanoclusters, we averaged both normalized density maps centered around the projected peaks of PSD-95 nanoclusters (crosses in Figure 4B–C). To further test whether there are secondary density structures around the nanoclusters, we performed a free 360-degree rotation around the nanocluster peak to find the best correlation with a template (density map around the first nanocluster for the first correlation, and the averaged density map for the following). Note that this correlation was computed in a similar way as in part 2.1.2 to eliminate the effect of cluster boundaries border, i.e. only the internal density structures mattered for the correlation. Meanwhile, to avoid any artifact created by the bordering effect, all values outside the synaptic cluster were replaced with 1 before averaging was performed. This process was incorporated in a defined function get_bestfit_rotate.m. While PSD-95 maps were freely rotated, the rotation angles of RIM1/2 maps were kept the same as that of PSD-95 in the same synapse to maintain the relative positioning of the two clusters. In the averaged density maps in Figure 4C, besides the center PSD-95 nanocluster, there was a secondary but weaker nanocluster, which is a result of freely-rotating averaging across the maps of synapses with 2 or more PSD-95 nanoclusters. The distance of ~120 nm from the image center suggests an average distance between two neighboring nanoclusters for PSD-95. As expected, the averaged map of RIM1/2 also showed a significant higher density around the center, representing the enrichment between the two proteins.

Discussion

Theoretically, the translation vector should be vertical to the fitted plane and therefore we could simply use that vector to make projections. However, the vector was often contaminated by the two-channel registration error, so its direction was not as reliable for projection. The current method benefited from the fact that the registration error was largely reduced by the overlapping translation, and therefore provided not only a more accurate projecting direction but also less error for the 2D enrichment distribution, as demonstrated by the secondary PSD-95 nanocluster and the significant enrichment of RIM1/2 around the image center (Figure 4C).

Similar with the overlapping translation, the fitting of the enface plane assumed that the clusters were representing the disc shape of AZ or PSD. If one protein had a strong distribution outside these two specialized compartments, such as presynaptic synapsin and postsynaptic actin or mGluRs[38, 42], it should not be included in fitting process. In this case, the enface plane could be fitted with only the other protein. Moreover, for large synapses, this algorithm may fail if complex border structure in the 2D projection of either presynaptic or postsynaptic shape dominates the projection.

As we discussed in section 2.2.2, the 2D and 3D cross-correlations only become equal when the slice thickness approaches 0, that our data should not be treated as near that limit. In this case, the axial density distribution may contribute to a certain extent to the shape of averaged g(r); however, the magnitude of the effect is hard to quantify directly. To address this concern, we tried measuring the effect indirectly by comparing the 3D cross-correlation of 63 synapses with that of the 2D projections with and without the normalization of cluster thickness (data not shown). Though g(r) from the three methods varied a little in shape and the extent over which it remained above the chance level, the averaged g(r<40 nm) correlate well with each other, suggesting they are equally effective for the purpose of generally testing the correlation between two density distributions. Therefore, 3D cross-correlation works as well as the 2D correlation in testing the trans-synaptic alignment of synaptic proteins.

However, the 3D cross-correlation has a few advantages that make it more suitable in our analysis. First, defining the synaptic cleft based on two synaptic clusters is frequently difficult. While we often consider the synaptic clusters as a sandwich shape, a non-flat cleft is more common in real synapses. For such synapses, 2D projection as a simplified approximation is very likely to over-estimate the local density. Further, while it is biologically sensible to restrict the analysis to a thin slice near the cleft, the observed geometry makes it difficult and probably unreliable to attempt this. The 3D paired correlation, on the other hand, does not require the definition of the cleft and therefore better deals with this situation. Second, the density map of 2D projection suffers from the variation in cluster thickness. Although we could try removing this effect by normalizing with a randomized cluster, this normalization is very sensitive to the definition of cluster boundaries. Taken together, we conclude that 3D paired cross-correlation is a better compromise between accuracy and reliability.

3. Conclusions

Imaging with single molecule localization microscopy provides a wealth of information on subcellular structures and protein organizations which underlay their specialized functions. To exploit them requires more detailed sophisticated quantitative analyses rather and image processing than most general software packages provide. We have described a set of detailed analytical methods for quantification of trans-synaptic alignment on three-dimensional STORM data and have made all the Matlab scripts available. Some could be easily adapted to analysis of other biological structures. We hope our methods could be helpful and inspiring for others to design automated and quantitative analysis on their SMLM data.

Highlights:

• Localization microscopy provides abundant data for precise quantitative analysis.

• An algorithm to identify local density peaks within a 3D localization cluster.

• New methods for quantitative analysis of trans-synaptic protein alignment and enrichment.

• These algorithms can be easily adapted to analysis of other subcellular organizations.