Wavelet-based Computationally-Efficient Computer-Aided Characterization of Liver Steatosis using Conventional B-mode Ultrasound Images

Abstract

Hepatic steatosis occurs when lipids accumulate in the liver leading to steatohepatitis, which can evolve into cirrhosis and consequently may end with hepatocellular carcinoma. Several automatic classification algorithms have been proposed to detect liver diseases. However, some algorithms are manufacturer-dependent, while others require extensive calculations and consequently prolonged computational time. This may limit the development of real-time and manufacturer-independent computer-aided detection of liver steatosis. This work demonstrates the feasibility of a computationally-efficient and manufacturer-independent wavelet-based computer-aided liver steatosis detection system using conventional B-mode ultrasound (US) imaging. Seven features were extracted from the approximation part of the second-level wavelet packet transform (WPT) of US images. The proposed technique was tested on two datasets of ex-vivo mice livers with and without gelatin embedding, in addition to a third dataset of in-vivo human livers acquired using two different US machines. Using the gelatin-embedded mice liver dataset, the technique exhibited 98.8% accuracy, 97.8% sensitivity, and 100% specificity, and the frame classification time was reduced from 0.4814 s using original US images to 0.1444 s after WPT preprocessing. When the other mice liver dataset was used, the technique showed 85.74% accuracy, 84.4% sensitivity, and 88.5% specificity, and the frame classification time was reduced from 0.5612s to 0.2903 s. Using human liver image data, the best classifier exhibited 92.5% accuracy, 93.0% sensitivity, 91.0% specificity, and the classification time was reduced from 0.660 s to 0.146 s. This technique can be useful for developing computationally-efficient and manufacturer-independent noninvasive CAD systems for fatty liver detection.

1. Introduction

The non-alcoholic fatty liver disease (NAFLD) is a common liver disease with 20–30% prevalence in Western countries, comparable prevalence in the Middle East, and 2–4% worldwide [1]. The prevention of NAFLD is crucial in Asian countries and particularly in the Gulf countries because of the high prevalence of obesity, diabetes and metabolic syndrome (MS) [1]. Liver fat accumulation occurs due to hyperinsulinemia and insulin resistance, and hepatic accumulation of triglycerides (TG) producing an imbalance between increased free fatty acid (FFA) flux from adipose tissues to the liver, increased caloric intake, and increased de novo lipogenesis in the liver and liver handling and export of the extra fat [2].

Liver fibrosis, which is considered the most common chronic liver disease, is caused by the accumulation of extracellular matrix proteins including collagen. NAFLD is among the main reasons of chronic liver diseases in addition to Hepatitis B viruses (HBV), hepatitis C viruses (HCV), and alcoholic fatty liver disease (FLD) [3]. If hepatic fibrosis is left untreated, fibrosis typically progresses to liver cirrhosis that cannot be treated and may increase the chance of mortality. The prevalence of liver disease in patients with central obesity, diabetes mellitus, dyslipidemia, and high blood pressure are respectively 32, 31, 22 and 23 folds higher than the liver disease prevalence in other people [4].

Liver biopsy (LB) is the gold-standard procedure for diagnosing fatty liver disease. However, LB is invasive, painful and bears the risk of infection and bleeding. Thus, LB may not be a preferred choice for many patients. Instead, non-invasive methods using medical imaging techniques represent suitable replacements of LB. Medical imaging modalities include ultrasound (US), computed tomography (CT) and magnetic resonance imaging (MRI) [5].

US grayscale brightness mode (B-mode) imaging may be considered the first choice for clinicians to non-invasively diagnose liver disease because of its safety, cost effectiveness, and wide availability. However, US imaging is both operator and machine dependent, and can only detect livers with more than 30% steatosis [6]. CT provides a reliable tool for the examination of diffuse and focal fatty livers, but it uses ionizing radiation and is strongly influenced by the iron deposition in the liver leading to misdiagnosis. Although MRI is a very useful imaging modality, it is not commonly used due to the expensive exam cost, limited availability, and lack of standardization [7]. Several US-based techniques can be used to improve the diagnostic process in combination with conventional imaging.

Transient elastography (TE) is an important non-invasive US method that measures stiffness changes in liver tissues to detect cirrhosis in patients with chronic liver disease. Liver stiffness was found to be significantly correlated with the clinical, biological, and morphological parameters of liver fibrosis [8]. TE was shown to reduce the need for LB in the follow up of chronic liver disease [9]. Also, TE exhibited good sensitivity and specificity for cirrhosis, but lower ability for mild degrees of fibrosis [10]. However, TE has not shown enough accuracy to assess various stages of fibrosis. TE classifies liver diseases through liver stiffness that is correlated with shear wave speed in the liver. Hence, any other conditions that may increase liver stiffness measurement (LSM) other than fibrosis can mislead the diagnosis of liver fibrosis [11]. Shear wave elastography (SWE) may be more suitable than TE [12]. Shear wave velocity generated by focused US beams is directly related to liver stiffness [13]. The use of SWE as a non-invasive technique in the diagnosis and staging of liver fibrosis has been increasing. However, for patients with a high body mass index, erroneous values may be obtained, and the diagnosis of liver fibrosis can be confounded by edema, inflammation, cholestasis and congestion [14].

US thermal strain imaging (TSI) is a noninvasive technique that can be adopted for liver tissue characterization. It is based on the physical observation of changes in sound speed with temperature [15]. For tissue characterization, the change in temperature can be relatively small (≤ 3°C) compared to human body temperature (37°C). This change does not cause significant tissue thermal expansion [16]. Mahmoud et al. [17] showed the feasibility of US-TSI in the discrimination between fatty and normal livers using two US systems. Although the study demonstrated the feasibility of USTSI as a non-invasive technique for hepatic steatosis diagnosis, US-TSI can be easily affected by physiological motions such as respiratory and cardiac motions and/or thermal diffusion [16]. The complexity of current TSI systems and the precautions that must be taken for classifying liver fibrosis limit US-TSI applicability in clinics compared to the CAD techniques that uses conventional B-mode images. Computer-aided diagnosis (CAD) methods based on conventional B-mode US images can improve the diagnosis of liver steatosis, decrease user dependency, and help quantifying percentage liver fats [18].

The progress in computer technology and machine learning has promoted the use of CAD systems in the clinical field. Feature extraction plays an important role in CAD system design due to its direct effect on the accuracy and computational time [18]. Some features can be evaluated by considering the spatial relationship between pixels over small neighborhoods [19] such as grey-level co-occurrence matrices (GLCM) [20], gray-level difference statistics (GLDS), gray-level run-length matrices (GLRLM), statistical feature matrices (SFM), local binary patterns (LBP) [21], etc. Another way to extract features is the transformation of images into other domains, followed by the analysis of the transform coefficients over different scales using multiresolution patterns. Examples of transform features are those of the Fourier power spectrum (FPS), discrete wavelet transform (DWT) [22], wavelet packet transform (WPT), Gabor wavelet transform (GWT), etc. In particular, WPT performs a multiresolution analysis in all frequency bands. Extracted WPT features are robust since they contain valuable information in the middle and high frequency bands [23]. However, the transformation process itself costs additional computations and time.

Several CAD systems have been proposed for fatty liver classification. Ricardo and Sanches [24] used intensity and texture features to classify normal and fatty hepatic parenchyma using 10 subjects (20 images). A region of interest (ROI) of 128 × 128 pixels in size was selected manually. They achieved 95% overall accuracy using a Bayesian classifier. Wan and Zhou [25] applied WPT to classify normal and cirrhotic livers using the mean and energy features, and then applied SVM for classification to reach an accuracy of 85.5%. Virmani et al. [23] aimed to characterize normal and cirrhotic livers, and hepatocellular carcinoma (HCC) using SVM on 56 US images. The multiresolution wavelet packet texture descriptor was constructed from the mean, standard deviation, and energy, and achieved an accuracy of 88.8%. Acharya et al. [26] trained a decision tree classifier using a combination of features based on the texture wavelet transform, and higher order spectra from 100 liver US images. An accuracy of 93.3% was achieved. Singh et al. [27] used a set of seven texture features, namely the spatial gray-level co-occurrence matrix, gray-level difference statistics, first-order statistics, Fourier power spectrum, statistical feature matrix, Laws’ texture energy measures, and fractal features. Using the linear discriminant analysis (LDA), an accuracy of 95% was achieved. Owjimehr et al. [28] used completed local binary patterns (CLBP) for the discrimination of fatty, normal, and heterogeneous livers. They selected the ROIs automatically and applied SVM and reached 89.66% accuracy. Later, Owjimehr et al. [29] used the same dataset and improved the classification technique using median, standard deviation, and interquartile range to reach an accuracy of 97.7%. Alivar et al. [30] used the same dataset with different feature descriptors of GLCM, CLBP, WPT, and Gabor filter banks and achieved 97.73% accuracy.

Quantitative ultrasound (QUS) techniques such as acoustic attenuation backscatter coefficient, speed of sound (SOS), envelope statistics, scatterer size or diameter, and tissue elasticity can be used for tissue characterization [31]. In particular, the mean scatterer spacing (MSS), which is the average spacing among coherent scatterers, provides a direct assessment of microstructures. For liver tissue characterization, the liver contains two types of scatterers including diffuse and quasi-periodic scatterers. Liver fibrosis alters the value of the MSS compared to normal livers. MSS can be evaluated using the wavelet transform directly from US images [31].

In this work, a different approach for CAD system design is proposed. WPT was applied to US B-mode images as a pre-processing step to produce a quarter-size approximation replica of the original image that will be used for further classification analyses. This approximation image includes the low-frequency components of the original image, which preserves major information needed for the proposed feature extraction and classification [32]. Most of the above-mentioned CAD techniques that use conventional US B-mode images are computationally expensive and consequently require prolonged computational time and power. A crucial factor that directly affects the computational power is the data size [33].

In this work, we investigate the feasibility of a computationally-efficient and manufacturer-independent wavelet-based technique that can be used to characterize liver tissues and detect fatty livers. The technique adopts quarter-size wavelet decompositions of US B-mode images for liver classification instead of using original images. Ex-vivo animal and in-vivo human experiments were performed using commercially available US machines to test the proposed CAD system on several datasets of liver images. Our goal is to reduce hardware complexity (memory space), computational power, and consequently processing time, while keeping the main information needed for accurate classification. The rest of the paper is organized as follows. Section 2 describes the methods including region-of-interest (ROI) selection, feature extraction, and classification methods. Then, experimental results are shown (Section 3) and discussed (Section 4). Finally, conclusions are given in Section 5.

2. Methods

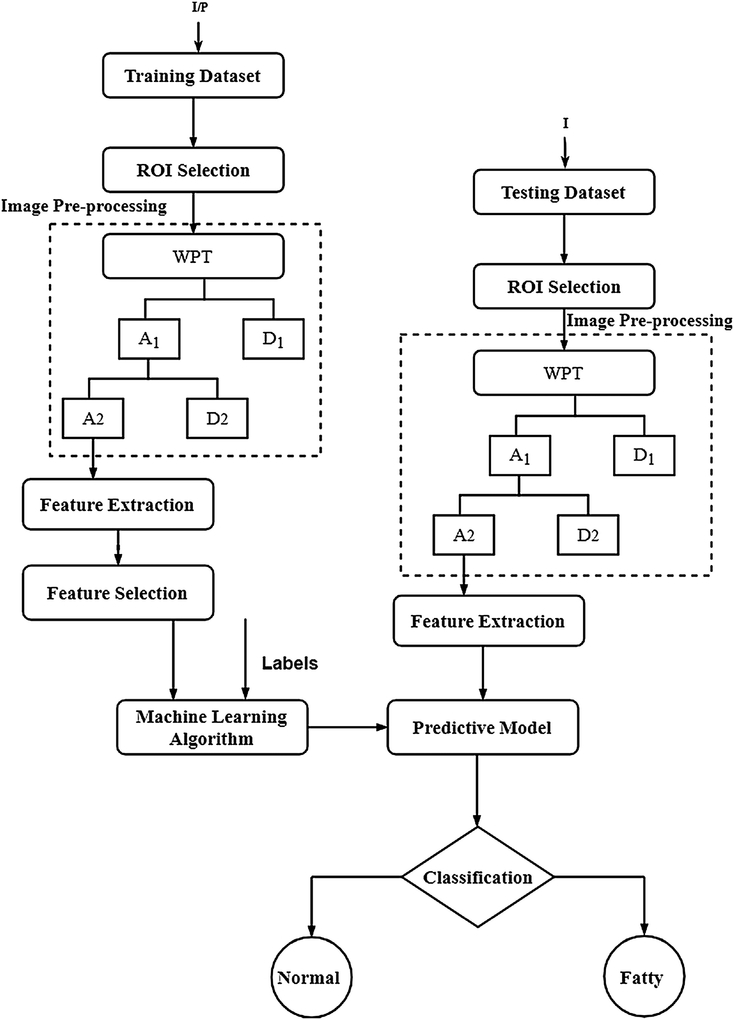
The block diagram of the proposed fatty liver CAD system is described in figure 1. The system is divided into learning and testing stages. For each US B-mode image, a region of interest (ROI) is selected. Several features are extracted after applying two-level wavelet packet transform (WPT). A feature selection criterion is then applied to reduce the number of features and improve the computational efficiency for both training and testing images. A robust predictive model was built using supervised learning to classify fatty and normal liver images. In the following, the main components of the block diagram are described in detail. All algorithms were developed using MATLAB R2015b on a PC with a Core i5 processor and a 4GB RAM.

Figure 1:

Block diagram of the proposed CAD system to classify normal and fatty liver using conventional ultrasound (US) B-Mode images. I/P is the training US images of EXMLG, EXML and INHL datasets, and I is the testing US images.

2.1. Image Acquisition

The proposed CAD system was trained to classify fatty and normal livers of both animals and humans. Two animal studies were conducted to acquire normal and fatty livers of mice. Animal studies were performed according to a protocol approved by the University of Pittsburgh Institutional Animal Care and Use Committee (IACUC), while the human pilot study was performed at the Endemic Medicine Department and Liver Unit, Faculty of Medicine, Cairo University. The Research Ethics Committee (REC) at Cairo University has approved the study protocol with IRB code (N-58–2016). Each patient signed an informed consent form.

2.1.1. Animal Data

US images of mice livers were acquired using a high-frequency linear US imaging transducer (13–24 MHz) (Vevo2100, FUJIFILM VisualSonics Inc., Canada) and the operating parameters were kept constant throughout experiments (center frequency: 21 MHz, dynamic range: 75 dB, and gain ~50%). Further details about the experimental setup can be found in [17]. The size of each image was 900×1200 pixels. The study was conducted using two different datasets collected in different experiments.

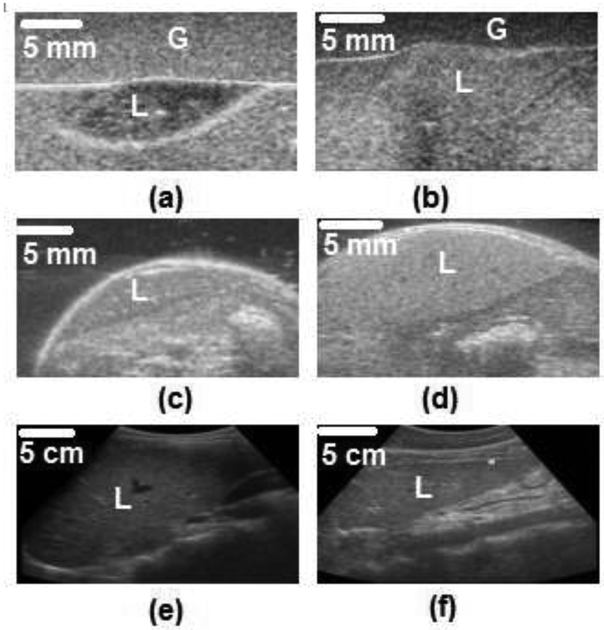
The first dataset is for ex-vivo mice livers embedded in gelatin (EXMLG) and consists of 164 frames including 82 for training (46 control, 36 fatty) and 82 for testing (46 control, 36 fatty). Control livers were extracted from 6 wild-type (C57B6) mice (7–13 weeks old) fed with normal diet, whereas fatty livers were extracted from 6 obese (ob/ob) mice (7–13 weeks old). These livers were embedded in 6% gelatin blocks with approximate dimensions of 13.5 × 11.5 × 4.8 cm (G-2500, Sigma Aldrich Corp., St. Louis, MO) mixed with 1% cellulose (S3504, Sigma Aldrich Corp., St. Louis, MO) by weight in the role of US scatterers [17]. Figures 2(a) and 2 (b) show, respectively, typical US images for control and fatty livers embedded in gelatin blocks.

Figure 2: Sample B-mode US images of different datasets for normal and control livers (L).

(a) control and (b) fatty mouse livers embedded in gelatin (G) of the EXMLG dataset, (c) control and (d) fatty mouse livers of the EXML dataset, and (e) control and (f) fatty human livers of the INHL dataset.

The second dataset is for ex-vivo mice livers (EXML), where imaging was performed transcutanously right after euthanasia. This dataset consists of 1200 frames including 700 images used for training (200 control, 500 fatty) and 500 images for testing (150 control, 350 fatty). Control livers were extracted from 5 wild-type (C57BJ6) mice, while fatty livers were extracted from 4 (ob/ob) mice with various degrees of steatosis. Original frames were extracted as RF frames, then processed to obtain B-mode images. Figures 2(c) and 2(d) show sample US images of control and fatty livers, respectively, reconstructed from RF data.

2.1.2. Human Data

US images of human livers were acquired using a dual frequency convex US transducer (3.0–3.75 MHz) connected to US equipment (Famio5 portable, Toshiba Medical Systems Corporation, Japan). The operating parameters were kept constant throughout the experiments. The size of each image was 768 × 1366 pixels.

The dataset of in-vivo human livers (INHL) consists of 57 frames including 37 for training (15 control, 22 Fatty), and 20 for testing (10 control, 10 Fatty) from 23 human patients. Control liver images were acquired from 11 patients (5 men, 6 women) whose ages ranged from 25 to 49 years old, while fatty livers were imaged from 12 patients (5 men, 7 women) whose ages ranged from 29 to 56 years old. The body mass index ranged between 20 – 25 kg / m². Figures 2 (e) and 2 (f) show typical B-mode images for human control and fatty livers, respectively.

2.2. Region of Interest Selection

ROIs were selected away from non-homogenous structures like blood vessels and hepatic ducts. For reliable statistics, a proper ROI size must be selected. It has been reported that the minimum number of pixels needed for a proper ROI is about 800 pixels [34]. In another report, a ROI size of at least 1,000 pixels was recommended [35]. However, different sizes ranging from 10×10 [36], 30×30 [27], 64×64 [37] and 128×128 pixels [26] have been used for classification of liver diseases.

In this work, ROIs of equal physical dimensions were used. A ROI size of 3 mm × 2 mm was used for mouse livers. The average size of mice livers used in this study is approximately 15 mm × 5 mm. The same procedures were followed for ROIs in human livers, where a square region of 2 cm × 2 cm was used for an average size of human livers of approximately 9 cm × 9 cm [38]. This corresponds to ROI size of 60 × 160 pixels for animal images and 100 × 170 pixels for INHL images.

2.3. Image Pre-processing

A two-level WPT was applied using the Daubechies 6 wavelet. The approximation part of WPT was used to reduce the number of pixels required for feature calculations and consequently reduce the processing time, while keeping important information. The detailed part was neglected. Daubechies 6 is considered the most common wavelet family supporting orthonormal wavelets, which makes discrete wavelet analysis practicable [39]. Additionally, Daubechies wavelets provide higher signal-to-noise ratios and lower mean square error than other wavelet families [40]. Dogra et al. compared different wavelet families on bone vessel fusion and reported that the Daubechies wavelets outperformed other wavelet families [41].

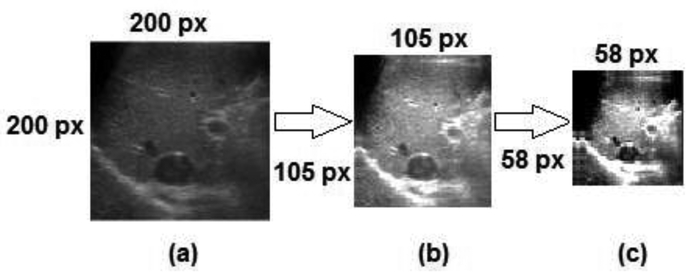
Each original US image (Figure 3(a)) is decomposed into 4 bands after applying WPT. The first band is the approximation part of the first level (Figure 3(b)) where the main information of the original image exists. Figure 4(c) shows the approximation part of the second-level of quarter-size the original image. It was observed that the details parts contain high-frequency components that may not add substantial information for discriminating benign and malignant tumors.

Figure 3:

Liver US B-mode images after applying wavelet packet decomposition: (a) Original image, (b) approximation coefficients of the first-level, (c) approximation coefficients of the second-level. Numbers beside each image indicate the image size in pixels (px)

Figure 4:

Accuracy for the most common wavelet families using kNN classifier

WPT is preferred in the analysis of nonstationary signals because the same frequency bandwidths can provide good resolution regardless of high and low frequencies [42]. There are two main reasons to extract features in the wavelet domain. First, textural properties of the US image can be analyzed easily in the decomposed image at different frequency levels. This textural information is much more reliable for the human visual system [23]. Second, the use of WPT sublevels reduces the computational cost of the classification technique since only the approximation (low-frequency) part of the image whose size is quarter of the size of the original image was used. This keeps the essential information required for feature extraction [25].

2.4. Feature Extraction

In conventional B-mode images, sonographers or radiologists may observe pathological changes qualitatively as a coarseness, inhomogeneity, or heterogeneity. To quantify these changes, a ROI within the liver is selected as previously explained and several features are calculated from the approximation part of WPT as will be described.

2.4.1. First-Order Gray Level Parameters (FOP)

According to clinical reports, a normal liver has relatively darker B-mode images compared to fatty or cirrhotic livers due to the uniform acoustic impedance [43]. Thus, the first-order gray level parameters of a normal liver image are supposed to be smaller than those of fatty or cirrhotic livers. These parameters are the mean, variance, skewness and kurtosis.

2.4.2. Gray - Level Co-occurrence Matrix (GLCM)

The GLCM is commonly used for estimating second-order textural features. There are more than 20 features that are typically calculated from the GLCM [44]. We selected features that consider the spatial relationship of pixels known as the gray-level spatial dependence matrix. These features include contrast, correlation, angular second moment, and homogeneity.

2.4.3. Local Binary Patterns (LBP)

Textural information encoded by means of local binary patterns (LBP) has also been applied to identify textural uniformity patterns of US images. LBP is a non-parametric gray-scale invariant texture analysis model [45]. LBP is computationally simple and efficient for texture analysis.

2.5. Feature Selection and Reduction

Feature selection is used to eliminate redundant and irrelevant features. Feature selection improves the classifier performance and provides faster and cost-effective models throughout specific metrics calculated from the dataset to determine the best feature combination [46]. Wilcoxon rank-sum test is a statistical hypothesis test used to compare two interrelated samples on a solitary sample to evaluate whether their population means differ in terms of mean ranks [47]. We used this test in our work due to the non-parametric nature of data. Nonparametric methods do not require any assumptions to be made about the data format [48]. A low p-value (<0.05) indicates the rejection of the null hypothesis, which implies that the mean values of two classes are significantly different, and hence, the feature is significant [48].

The purpose of the dimensionality reduction techniques is to decompose a signal into significant components that are optimal for a given classification task. Principal component analysis (PCA) was adopted as one of the most popular dimensionality reduction techniques [49]. PCA is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components. The number of principal components is less than or equal to the number of original variables [50]. It explains the maximum amount of variance with the minimum number of principal components through projection of given data points in a higher-dimensional space into a lower-dimensional space, while preserving as much information as possible [49].

2.6. Classification

Classification models are predictive models built from an input dataset by adopting supervised, unsupervised, or manifold learning algorithms that help in identifying the class of a test dataset. The proposed technique is based on non-parametric supervised learning models such as kNN, linear SVM, kernel-based SVM and LDA. In this work, several classifiers were tested and compared.

The k-nearest neighbors (kNN) classifier is a non-parametric classifier that uses occurrence-based learning to classify samples. The unclassified data is compared with the training data to determine the k-nearest neighbors. The class of the majority of the k-nearest neighbors is used to predict the class of a new sample [51].

Support vector machines (SVM) use information from two classes to determine a maximum-margin hyperplane that distinguishes the two classes according to intuition and the probably approximately correct learning (PAC) framework [52]. SVM can efficiently apply non-linear classification kernels via mapping their inputs into high-dimensional feature spaces [53]. Linear SVM (LSVM) and kernel-based SVM were applied for non-linear classification. That kernels include the Gaussian radial basis function (RBF) kernel, the multilayer perceptron (MLP) kernel, and the quadratic kernel.

Linear discriminant analysis (LDA) is used to find a linear combination of features that characterizes or separates two or more classes of objects or events. LDA extracts low dimensional features of the most sensitive discriminant ability from high dimensional feature space [54].

For each classifier, performance parameters such as accuracy, sensitivity, specificity, area under the curve (AUC), and the processing time were computed and compared to investigate the effect of using wavelet pre-processing in reducing the processing time. These performance parameters are defined as follows:

$$\text{Sensitivity}=\frac{\text{True positive}}{\sum \text{condition positive}}=\frac{\text{TP}}{\text{TP+FN}}$$ (2.7.1)

$$\text{Specificity}=\frac{\text{True negative}}{\sum \text{condition negative}}=\frac{\text{TN}}{\text{FP+TN}}$$ (2.7.2)

$$\text{Accuracy}=\frac{\text{True positive+True negative}}{\sum \text{total population}}=\frac{\text{TN+TP}}{\text{TP+TN+FN+FP}}$$ (2.7.3)

where for the true positive (TP) samples the disease is present and the test shows the presence of disease, for the true negative (TN) samples the disease is absent and the test shows the absence of disease, for the false negative (FN) samples the test shows the absence of disease but in fact the sample has the disease, and for the false positive (FP) samples the test shows the presence of disease but in fact there is no such disease [55].

The area under the receiver operator characteristic (ROC) is called the area under the curve (AUC). The curve is generated by plotting TP rates and FP rates at different threshold values [56]. The diagonal divides the ROC space. As the AUC approaches 1, the classifier becomes better [26].

3. Results

3.1. Wavelet Technique

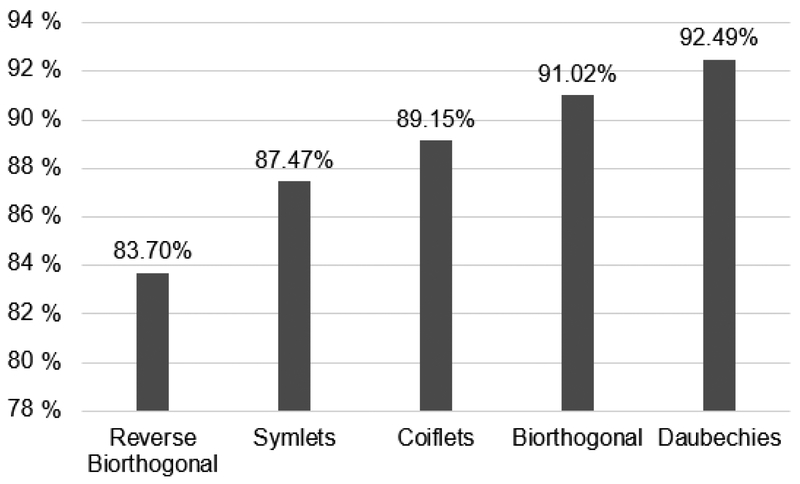
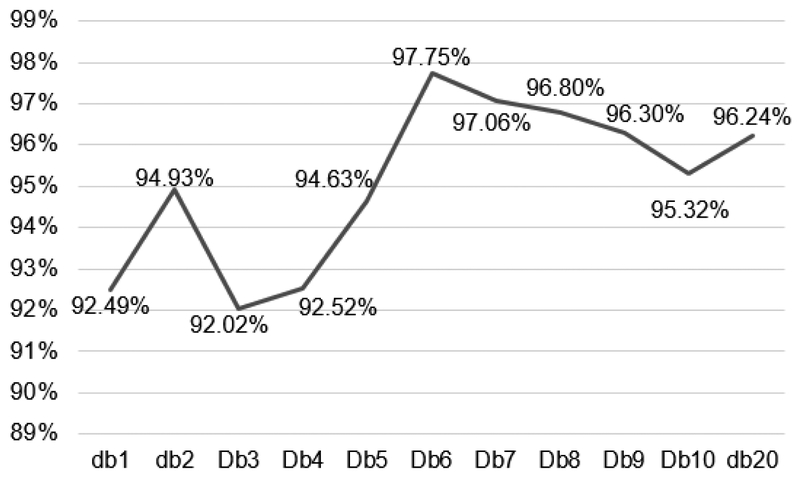
In a pilot study using the kNN classifier applied on the EXMLG dataset, Daubechies wavelet was compared with the most common Wavelet families using the first coefficient for image decomposition. Figure 4 shows the results of classification accuracies, where Daubechies exhibited the highest accuracy of 92.49%, followed by Biorthogonal (91.02%), Coiflets (89.15%), Symlets (87.47%), and reverse Biorthogonal (83.70%). No significant difference was found in processing time. Additionally, in order to determine the optimum number of Daubechies moments/coefficients, the same experiment was performed using different number (N) of Daubechies moments/coefficients (dbN). It was observed that db6 exhibited the highest accuracy of 97.75 % (Figure 5) with no significant difference in time.

Figure 5:

Accuracy for different db coefficients

3.2. Experimental results

Table 1 summarizes the results of four experiments when the proposed CAD system was applied on different datasets of liver images with and without WPT. The kNN and MLP-kernel SVM classifiers exhibited very good accuracies of 98.78% and 96.3%, respectively, using the original EXMLG dataset (without WPT). When WPT was applied, accuracies were slightly reduced by ~1% for both classifiers. However, there was a drastic reduction in the image classification times after incorporating WPT. The classification time was 0.4814s when features were extracted from original US images, while it was reduced to one-third (0.1444s) when the same features were extracted from the approximation image (with WPT) using the kNN classifier. The MLP-kernel SVM classifier showed similar results. Using the EXML dataset, both classifiers exhibited similar performance to that of the EXMLG dataset, but with lower accuracies (85.74% using the kNN classifier) and longer classification times. However, a significant reduction was observed in classification time. The time was reduced from 0.5612s without WPT to 0.2903s with WPT. When the MLP-kernel SVM was applied to the EXMLG dataset, the frame classification time was reduced from 0.8296s to 0.3109 s without and with adopting WPT, respectively.

Table 1:

Performance evaluation with (w/) and without (w/o) WPT of four different experiments when the kNN and MLP-kernel SVM classifiers were used.

Data Set	w/ & w/o WPT preprocessing	MLP-kernel SVM		kNN
		Accuracy	Classification Time (s)	Accuracy	Classification Time (s)
EXMLG	w/o	96.3%	0.5649	98.78%	0.4814
	w/	95.12%	0.1621	97.75%	0.1444
EXML	w/o	76.25%	0.8296	85.74%	0.5612
	w/	72.00%	0.3109	84.23%	0.2903
EXMLG-EXML	w/o	96.14%	0.5649	97.94%	0.4814
	w/	95.05%	0.1622	96.23%	0.1443
INHL	w/o	91.10%	0.5512	92.50%	0.6600
	w/	89.80%	0.1590	91.80%	0.1460

In a further experiment using the animal datasets, the EXMLG and EXML datasets were combined (EXMLG – EXML), where the EXMLG dataset was used for training and images from the EXML dataset were used for testing. There was not a noticeable change in the classification time compared to the EXMLG experiment. After applying WPT, a similar behavior was observed where the accuracy dropped slightly while there was a major reduction in the classification time without and with WPT. The classification accuracies when the kNN and MLP-kernel SVM were applied on the INHL dataset slightly decreased from 92.5% to 91.8%, and from 91.1% to 89.8%, without and with WPT, respectively. However, the computation time was significantly reduced to less than one-third (0. 1460s and 0. 1590s) when the WPT was applied using the kNN and MLP-kernel classifiers, respectively.

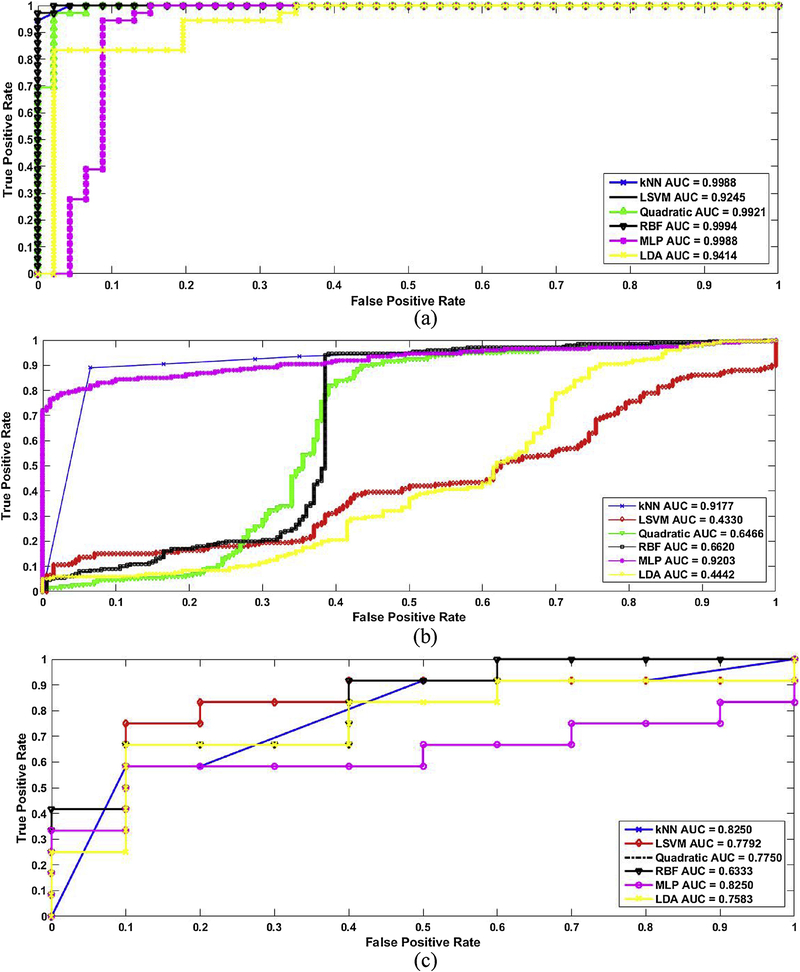
The ROC curves in Figure 6 (a) show the performance parameters when the six classifiers were applied on the EXMLG dataset w/o WPT. The kNN exhibited an AUC of 0.9988. At the optimal point, the sensitivity and specificity were 100% and 97.83%, respectively. For the LSVM, the AUC was 0.9245, and the specificity and sensitivity were 94.44 % and 97.83%, respectively. When the MLP-kernel SVM was used, the AUC was 0.9988, and the specificity and sensitivity were 98.23% and 90.74%, respectively. For the RBF-kernel SVM, the AUC was 0.9994, and the specificity and sensitivity were 100 % and 97.32%, respectively. For the Quadratic-kernel SVM, the AUC was 0.9921, and the specificity and sensitivity were 98.23 % and 98.5%, respectively. For the LDA, the AUC was 0.9914, and the specificity and sensitivity were 83.44 % and 89.13%, respectively.

Figure 6:

The ROC curves of 6 classifiers applied on different datasets including (a) EXMLG (b) EXML (c) INHL.

The ROC curves in figure 6 (b) show the performance parameters when the six classifiers were applied on EXML dataset w/o WPT. The kNN exhibited an AUC of 0.9177. At the optimal point, the sensitivity and specificity were 90% and 95.83%, respectively. For the LSVM, the AUC was 0.4330, and the specificity and sensitivity were 40.44 % and 55.83%, respectively. When the MLP-kernel SVM was used, the AUC was 0.9203, and the specificity and sensitivity were 78% and 98.74%, respectively. For the RBF-kernel SVM, the AUC was 0.6620, and the specificity and sensitivity were 98 % and 67.32%, respectively. For the Quadratic-kernel SVM, the AUC was 0.6466, and the specificity and sensitivity were 82 % and 68.5%, respectively. For the LDA, the AUC was 0.4442, and the specificity and sensitivity were 89.44 % and 27.13%, respectively.

The ROC curves in figure 6 (c) show the performance parameters when the six classifiers were applied on INHL dataset w/o WPT. The kNN exhibited an AUC of 0.8250. At the optimal point, the sensitivity and specificity were 60% and 90 %, respectively. For the LSVM, the AUC was 0.7792, and the specificity and sensitivity were 78.69 % and 90%, respectively. When the MLP-kernel SVM was used, the AUC was 0.8250, and the specificity and sensitivity were 60% and 90.23%, respectively. For the RBF-kernel SVM, the AUC was 0.6333, and the specificity and sensitivity were 42 % and 100%, respectively. For the Quadratic-kernel SVM, the AUC was 0.7750, and the specificity and sensitivity were 78.69 % and 90%, respectively. For the LDA, the AUC was 0.7583, and the specificity and sensitivity were 67.77 % and 90.32%, respectively.

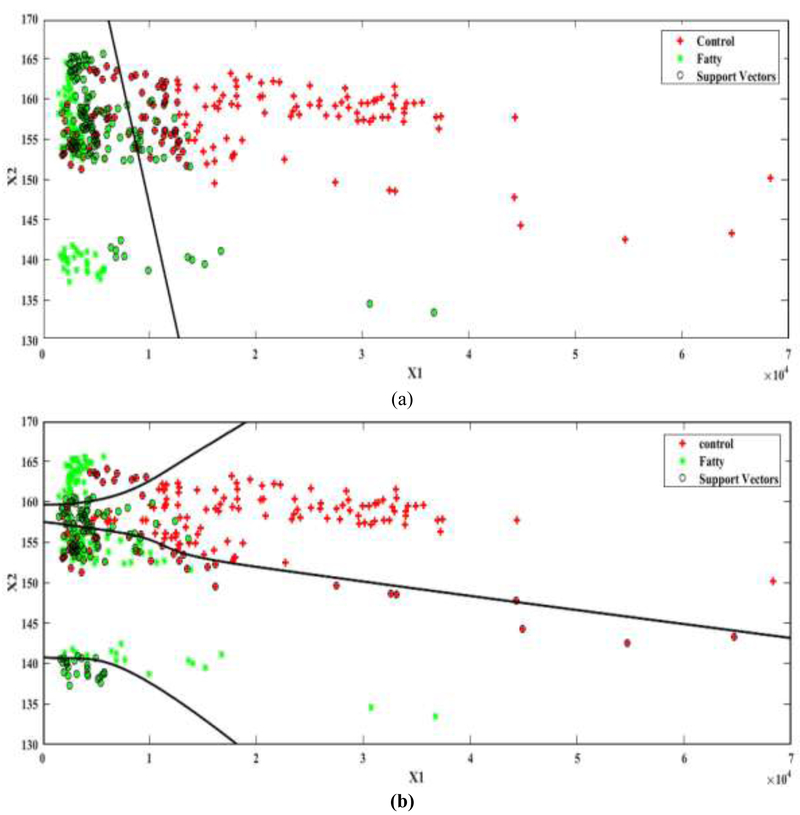
The performance of different SVM kernel functions was compared when the EXML dataset was used as it was hardly separable by a linear plane. The accuracy and the processing time were evaluated for each kernel. All SVM kernel functions exhibited the same computational time. When the linear kernel (LSVM) was used (Figure 7(a)), the accuracy was 57%. When the MLP kernel was applied with the default scale of [1 –1] (Figure 7(b)), the accuracy increased to 75%.

Figure 7:

The separating plane between the two principal components (x₁, x₂) used for classification by SVM on the EXML dataset. (a) LSVM (b) Multilayer perceptron.

4. Discussion

4.1. Implementation details

High performance classification performance is usually evaluated by memory cost, speed, and accuracy. Currently, many CAD systems for US-based liver classification are computationally and memory intensive, which limits their practicality and common use. For example, it is difficult to integrate resource-intensive algorithms into US devices for real-time applications. In some resource-limited regions or countries, many lives were lost because of unavailability of accurate and low-cost fatty liver detection techniques and devices; high performance approaches consume much less resources than traditional approaches, and is vitally important to provide an affordable means for early detection of fatty liver disease [57].

This work investigated the feasibility of characterizing hepatic steatosis using a computationally-efficient wavelet-based CAD system. The technique was applied on conventional B-mode liver images of three datasets acquired using two different US systems. Two datasets of mice livers were acquired using a high-frequency small-animal imaging system, while the last dataset of human liver images was acquired using a clinical US system. Generally, it was observed that extracting features from US B-mode images after WPT preprocessing did not have a significant effect on the classification accuracy (~ 1% reduction), while there was a major reduction in the average processing time of more than 3 folds. Without this WPT preprocessing, it would be necessary to search through the entire image, which could be more time consuming and a complex system would be needed for a manufacturer-independent noninvasive software solution.

To build a machine learning technique for classification, the training and testing datasets must be collected under the same conditions, but US imaging is operator-dependent. To demonstrate that the proposed technique minimizes the manufacturer and user dependencies, the experiments of this study were performed in two different places where datasets were collected by different operators. The operating parameters (central frequency, gain, depth, dynamic range) were kept similar for animal studies.

Wavelets is a powerful tool that can be used for a wide range of applications including image de-noising, feature extraction, and face detection [58]. It can be used for image compression to remove redundancy in the data, where it determines which data is kept to enable image reconstruction using a smaller number of bits [56]. Doukas et al. [59] designed a Picture Archiving and Communication Systems (PACS) application designed for viewing DICOM compliant medical images using wavelet compression with ROI coding support on mobile devices. We also studied the usage of WPT as a classification feature not as a pre-processing step and we observed higher performance parameters of our proposed system versus using WPT coefficients as classification features.

4.2. Speed-accuracy tradeoff

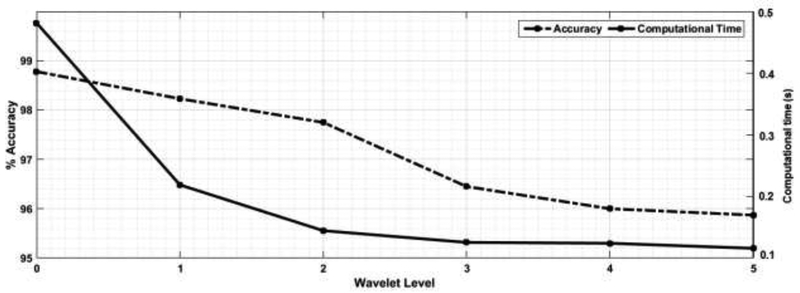
The reduction in ultrasound classification accuracy associated with the reduction in the computational time cost is an example of the speed-accuracy tradeoff (SAT) [60]. This phenomenon, namely the covariance of the decision speed with the decision accuracy, is exhibited by living organisms such as insects, rodents, and primates [61]. Liu and Watanabe [62] argued for the importance of accounting for both accuracy and response time in perceptual learning experiments. Moreover, this tradeoff is demonstrated in artificial intelligent agents and has been receiving growing attention. For example, Collingwood and Wilkerson [63] analyzed the accuracy and efficiency tradeoffs of supervised machine learning systems for large-scale text classification problems, where the marginal improvements in performance may be outweighed by the additional time costs. Huang et al. [64] explored different deep learning schemes that balance speed, memory, and accuracy requirements for different applications and platforms. Also, Xie et al. [65] restructured complex deep learning architectures to achieve a better speed-accuracy tradeoff in video classification. For medical ultrasound imaging, the speed-accuracy tradeoff was investigated in the construction of ultrasound images [66], [67]. Careful consideration of this tradeoff should be made as big data and deep learning methodologies emerge in ultrasound signal processing. Our work is one stepping stone in this direction. We seek a balance between speed and accuracy by building an effective and efficient US classification system through determining how best to tradeoff model complexity with speed [68] via selecting the optimum level of db6. Figure 8 shows this tradeoff as the level of WPT increase the classification accuracy reduced with more than 4 % but the time reduction become minimal. So 2^nd level of db6 was the optimum to give the balance between accuracy and computational time for classification.

Figure 8:

Accuracy vs classification time trade-off for different db6 orders

The significance of the proposed features in classifying normal and fatty livers were assessed individually via the Wilcoxon rank-sum test (p<0.05). Features such as the mean, variance, contrast, correlation, angular second moment, homogeneity, and LBP exhibited p-values < 0.001, while the p-values for skewness and kurtosis were 0.1749 and 0.4705, respectively. Both skewness and kurtosis were hence excluded.

This wavelet-based technique classified fatty livers in the EXMLG dataset within 0.1444 s with 97.75% accuracy and an AUC of 0.9988 using the kNN classifier. The sample size of the EXML dataset was 1200 frames of mice livers acquired transcutaneously right after euthanizing the mice. Results supported our hypothesis that the application of WPT as a preprocessing step before feature extraction in combination with kNN shall reduce the computational time drastically while keeping other performance parameters almost the same and exhibited a frame characterization computation time in the range of milliseconds (0.2903 s). For human liver classification, the CAD system exhibited an accuracy of 91.80% and an average computational time of 0.146s.

One major challenge of the proposed technique is the reliability of the dataset used for building the machine learning system. The dataset can influence the system response as observed from the difference in performance parameters between the EXMLG and EXML datasets. This may have occurred because the EXML dataset was acquired from the US machine as RF frames, then we applied envelop detection and logarithmic compression to render B-Mode images rather than using conventional B-Mode images (EXMLG dataset). Hence, the accuracy was reduced from 98.78% to 85.74%. Also, the ROC curves in Figures 6 (a) and 6 (b) showed how the AUC was reduced using EXMLG dataset compared to the EXML for all classifiers. This can be minimized via following the standard processing algorithms for B-mode reconstruction and/or incorporating large number of B-mode images from several US machines in the training and testing datasets.

Despite these limitations, one of the key findings of the proposed CAD technique is that conventional US liver images are the only input required. To the best of our knowledge, this study is considered the first to exploit the use of WPT as a pre-processing step not as a classification feature and it showed a superior effect in reducing the complexity of the system by making the entire process computationally less complex and cost effective. A high classification accuracy has been obtained (98.78%) with 164 samples within 0.15 second.

4.3. Comparison with the existing techniques

Table 2 compares the proposed technique with few recent studies that described various CAD techniques for liver image classification sorted by publication year. Ribeiro et al. [24] used intensity and texture features to classify normal and fatty hepatic parenchyma from 10 subjects (20 images). ROI was selected manually of 128 × 128 pixels, achieving 95% overall accuracy using Bayesian classifier. Wan et al. [25] applied wavelet packet transform to classify normal and cirrhosis one using mean and energy features then applied SVM and got 85.5%. Virmani et al. [23] aimed to characterize normal liver, cirrhotic liver and HCC using SVM from 56 US image. The multiresolution wavelet packet texture descriptor constructed from mean, standard deviation and energy were calculated and achieved accuracy of 88.8%. Acharya et al. [26] used a combination of features based on the texture wavelet transform, and higher order spectra from 100 liver US images using decision tree classifier. They were able to achieve 93.3% accuracy. Singh et al. [27] used a set of seven texture features which are: spatial gray level co-occurrence matrix, gray level difference statistics, first order statistics, Fourier power spectrum, statistical feature matrix, law’s texture energy measures and fractal features. Based upon the results of Linear Discriminative Analysis (LDA) they achieved accuracy of 95%. Owjimehr et al. [28] used CLBP for fatty, normal and heterogeneous liver discrimination. They selected the ROI fully automatically and applied SVM then they got 89.66% accuracy. In the following year, the same group [29] used the same dataset and improved the classification technique using Median, standard deviation, and interquartile range and the accuracy was improved to 97.7%. Alivar et al. [30] used the same data set used by Owjimehr [28] with different feature descriptors GLCM, CLBP, Wavelet packet transform, Gabor filter bank and achieved 97.73% accuracy.

Table 2:

Summery of recent studies that presented various CAD techniques for liver image classification sorted by publication year

Author/Year	Sample size	Features	Classifier (s)	Accuracy
Riberiro et. al/2009 [24]	10 normal 10 fatty	Intensity and texture feature	Bayes classifier	95%
Wan and Zhou/2010 [25]	390 normal 200 cirrhosis	Mean and Energy	SVM	85.5%
Virmani et. al/2012 [23]	15 Normal 16 cirrhotic 25HCC	Mean, standard deviation and energy	SVM	88.8%
Acharya et. al/2012 [261	58 abnormal 42 normal	Texture, wavelet transform, and higher order spectra	Decision tree classifier	93.3%
Singh et. al/2013 [27]	40 Normal 60 Fatty	GLCM, Gray Level Difference Statistics, Fourier Power Spectrum, Statistical Feature Matrix, Fractal Features	LDA	95%
Owjimehr et. al/2014 [69]	39 normal 30 fatty 19 heterogeneous	CLBP	SVM	89.66%
Owjimehr et. al/2015 [29]	39 normal 30 fatty 19 heterogeneous	Median, standard deviation, and interquartile range.	SVM	97.7%
Alivar et. al/2017 [30]	39 normal 30 fatty 19 heterogeneous	GLCM. CLBP, Wavelet packet transform Gabor filter bank	SVM	97.72%
The proposed technique	46 normal 36 Fatty	FOP GLCM LBP	kNN MLP-kernel SVM	98.78% 97.56%

The proposed CAD system exhibited a superior accuracy using the EXMLG dataset. It was difficult to perform a fair comparison between our results and recently published CAD studies due to the differences in the sample size, target classes, cross-validation technique, and the evaluation criteria. To overcome this problem, based on the summery in table 2, the technique described by Owjimehr et al. [29] and Alivar et. al [30] showed the highest accuracy, so we implemented them. Table 3 describes the results of this comparison, where our algorithm achieved higher accuracy, sensitivity and specificity using both datasets compared to the technique by Owjimehr et al. [29] who reported superior performance parameters (97.7% Accuracy, 100% sensitivity) in their previous studies using their dataset. We tested their technique on our EXMLG and INHL datasets. WPT was applied as a pre-processing step before feature extraction and showed a significant effect on reducing the computation time with minimal degradation in performance parameters. However, the processing time reported by Owjimehr et al. was shorter than the time taken by our technique. This was due the smaller number of features that Owjimehr et al. used. However, when WPT was applied to the method of Owjimehr et al., there was a major reduction in their computational time with a slight degradation in performance. This comparison demonstrates the tradeoff between the number of effective features and processing time as it is not favored to achieve a quicker decision with lower accuracy. Owjimehr et al.’s technique was slightly faster (0.1413s) than our proposed CAD system (0.1443s) since they are using a fewer number of features including only the median, standard deviation, and interquartile range that are very simple features. Whereas, the accuracy of our proposed technique was higher (91.8%) than the algorithm in [29] (88.6%).

Table 3:

Performance parameters of the proposed technique versus Owjimehr et al. [29] and Alivar et. Al [30] with and without applying WPT as a pre-processing step.

	Dataset	Accuracy (%)		Sensitivity (%)		Specificity (%)		Time (s)
		w/o	w/	w/o	w/	w/o	w/	w/o	w/
Proposed technique	EXMLG	98.78	97.75	97.8	97	100	99.3	0.4800	0.1443
	INHL	92.5	91.8	93	92.7	91	90	0.6600	0.1480
Owjimehr et al. [29]	EXMLG	95.5	95	96	95	96.5	95.2	0.5300	0.1413
	INHL	89.2	88.6	90	89	89.4	89	0.6100	0.1140
Alivar et. al [30]	EXMLG	98.84	98.02	100	99.02	99.7	98.2	5.236	2.782
	INHL	94.5	93.8	95.6	95.2	96.3	95.8	5.489	2.258

Alivar et. al [30] combined the spatial and wavelet domains for feature extraction. GLCM and completed local binary pattern features were used as spatial domain features and a number of statistical features of 2-D wavelet packet transform sub-images which are the median, standard deviation, and interquartile range and 2-D Gabor filter banks transformed images as transform domain features with five frequencies and six orientations. As a result, there would be a feature vector with 62 elements that is attained from 30 Gabor transformed images and the original ROI image, totally 31 images that each has two features for Gabor filter bank. Ended up with a complex feature vector of 71 elements obtained from the spatial and transformed domains. Both spatial and transform domain based features are used in the classification, since they have positive effects on the classification accuracy. However, the complexity of the system increased and the processing time is the largest through all the technique. Still the extraction of all the feature from the transformed domain is more suitable due to massive reduction as ~ 3 folds.

5. Conclusion

This study demonstrated the feasibility of a wavelet-based algorithm to detect hepatic steatosis using conventional US images combined with a computer-aided diagnostic system. The use of the second-level wavelet packet transform (WPT) of B-mode images for feature extraction utilized less memory and accelerated the classification process of liver images by a factor more than 3 folds compared to directly using B-mode images. Meanwhile, the algorithm using original B-mode image exhibited a high accuracy (98.8%), sensitivity (97.8%) and specificity (100%), and the classification time was reduced from 0.4818s to 0.1444s using WPT and an accuracy of 97.75%, sensitivity (97%) and specificity (99.3%) compared to state-of-the-art methods. Additionally, the proposed CAD system demonstrated a vendor independency as it was tested using both animal and human datasets using two different US systems and several users. Such speed and accuracy may pave the road for implementing real-time algorithms for standard US scanners. Currently, an ongoing study on this technique focuses on developing an add-on smart software solution for characterizing liver tissues that can be used with a wide range of commercial US machines and can be used easily in clinical practice.

Highlights.

• This work develops a computationally-efficient technique to classify fatty livers using conventional B-mode ultrasound images.

• The technique relies on extracting features from the Wavelet domain using the approximation part of ultrasound images.

• The technique was tested ex vivo on mice livers using two different datasets and in vivo on human livers using different ultrasound machines.

• This technique shall improve the implementation of manufacturer-independent real-time techniques for fatty liver classification.