A computational model of the Cambridge gambling task with applications to substance use disorders

Abstract

Background:

Impulsivity is central to all forms of externalizing psychopathology, including problematic substance use. The Cambridge Gambling task (CGT) is a popular neurocognitive task used to assess impulsivity in both clinical and healthy populations. However, the traditional methods of analysis in the CGT do not fully capture the multiple cognitive mechanisms that give rise to impulsive behavior, which can lead to underpowered and difficult-to-interpret behavioral measures.

Objectives:

The current study presents the cognitive modeling approach as an alternative to traditional methods and assesses predictive and convergent validity across and between approaches.

Methods:

We used hierarchical Bayesian modeling to fit a series of cognitive models to data from healthy controls (N = 124) and individuals with histories of substance use disorders (Heroin: N = 79; Amphetamine: N = 76; Polysubstance: N = 103; final total across groups N = 382). Using Bayesian model comparison, we identified the best fitting model, which was then used to identify differences in cognitive model parameters between groups.

Results:

The cognitive modeling approach revealed differences in quality of decision making and impulsivity between controls and individuals with substance use disorders that traditional methods alone did not detect. Crucially, convergent validity between traditional measures and cognitive model parameters was strong across all groups.

Conclusion:

The cognitive modeling approach is a viable method of measuring the latent mechanisms that give rise to choice behavior in the CGT, which allows for stronger statistical inferences and a better understanding of impulsive and risk-seeking behavior.

1. Introduction

Impulsivity is a multidimensional, heritable trait that confers liability to progression along the externalizing spectrum, which spans from attention-deficit/hyperactivity disorder in early childhood on toward substance use disorders in adulthood (Beauchaine and McNulty, 2013; Beauchaine et al., 2017). Defined as a preference for immediate over delayed rewards, action taken without forethought, and/or deficient self-control, many behavioral tasks are used to make inferences on impulsivity given individuals’ behavior. Recently, the use of behavioral tasks in combination with neuroimaging technologies such as functional magnetic resonance imaging (fMRI) has revealed neurocognitive mechanisms that give rise to risky and impulsive behaviors (Robbins et al., 2012). Importantly, neuroimaging work has made it clear that impulsive behavior is equifinal, where different cognitive mechanisms can give rise to similar observable behaviors (e.g., Turner et al., 2018). Traditional methods of analyzing behavioral task data rely on behavioral summary statistics, which ignore the equifinal nature of impulsive behavior and may subsequently decrease power in detecting differences in quality of decision making and impulsive behavior among groups.

Cognitive modeling is an alternative to traditional summary methods which allows us to identify separable effects of latent cognitive variables that are difficult to observe directly from behavioral data alone (e.g. Ahn and Busemeyer, 2016; Busemeyer and Stout, 2002). Therefore, cognitive modeling has the potential to more reliably estimate individual decision-making differences and subsequently increase statistical power to detect subtle differences across groups. Yechiam et al. (2005), for instance, used a cognitive model of the Iowa Gambling Task to identify distinct “cognitive profiles” of several clinical groups, such as individuals with bilateral lesions in ventromedial prefrontal cortices, patients with Huntington’s or Parkinson’s disease, and various subtypes of substance users (cannabis, cocaine, alcohol, and polysubstance users), despite traditional analyses finding little evidence of group differences. Many others have followed suit (Ahn and Busemeyer, 2016; Busemeyer and Stout, 2002; Neufeld, 2015; Stout et al., 2004; for a review of cognitive modeling, see Ahn and Busemeyer, 2016; Ahn et al., 2016), and it has become clear that cognitive modeling can lead to greater predictive validity and reliability than traditional methods (Wiecki et al., 2015). That is, parameter estimates from cognitive models tend to be more reliable and correlate better with expected, external measures, as cognitive models tend to base their estimates on the entire data set for each participant, as opposed to simply analyzing the means (Busemeyer and Diederich, 2010). Here, we adopt the cognitive modeling approach and apply it to the Cambridge Gambling Task (CGT; Rogers et al., 1999), which is commonly used for neuropsychological assessment in clinical populations (Kräplin et al., 2014; Lawrence et al., 2009; Sørensen et al., 2017; Wu et al., 2017), including for individuals with substance use disorders (e.g., Ahn and Vassileva, 2016; Ahn et al., 2017; Baldacchino et al., 2015; Lawrence et al., 2009; Passetti et al., 2008). To our knowledge, this is the first cognitive model developed for the CGT. Below, we describe the CGT and common methods of summarizing CGT performance before explaining the cognitive modeling approach.

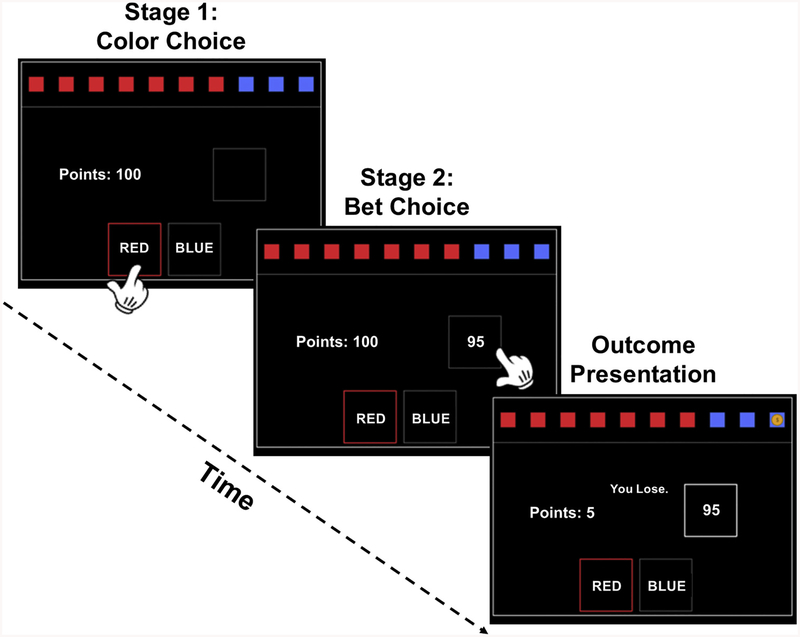
The CGT was developed to assess decision-making and risk-taking outside a learning context. In the CGT, a yellow token is hidden in one of ten boxes that appear on a computer screen. Some of the boxes are red, others are blue, and the ratio between red and blue boxes can range from one red (nine blue) to nine red (one blue) boxes, with each (red, blue)-pair having an equal chance of occurring. The CGT proceeds in two stages, where the participant: (1) predicts the color of the box hiding the token, and then (2) bets a proportion of their accumulated points (see Fig. 1) based on the certainty of their decision. The bet proportions are fixed across trials (.05, .25, .5, .75, .95) and presented sequentially with delays such that participants must wait to select their preferred bet. Importantly, the presentation order is varied across conditions, where ascending and descending blocks present the lowest (5%) and highest (95%) bet first, respectively.

Fig. 1.

Stages of the CGT.

The CGT progresses through two stages before the outcome of the token (and subsequently of the chosen bet) is revealed. First, participants must guess which color hides the token. Once a color is chosen, bet proportions (.05, .25, .5, .75, .95) are shown in either ascending or descending order, where each bet is shown for 5 s in total. Note that the “bet box” shows the number of points that can be gained/lost for each bet proportion rather than the bet proportions themselves.

Traditionally, performance on the CGT is probed with multiple indices that capture different facets of decision-making. The CGT has a number of behavioral measures, including: (1) quality of decision-making, (2) impulsivity/delay aversion, (3) risk-taking, (4) deliberation time, (5) risk adjustment, and (6) overall proportion bet. First, quality of decision-making (QDM) is the percentage of trials where a participant chooses the color with more boxes. The first study using the CGT revealed a dissociation between amphetamine and opiate users such that amphetamine, but not opiate users, showed lower QDM relative to healthy controls (Rogers et al., 1999). However, later studies using more participants showed that QDM is similar across individuals with opiate and amphetamine use disorders (Vassileva et al., 2014; Wilson and Vassileva, 2018). Other studies consistently show that individuals with alcohol use disorder have QDM scores that are indistinguishable from healthy controls (e.g., Bowden-Jones et al., 2005; Lawrence et al., 2009; Monterosso et al., 2001; Zois et al., 2014), which could be due to no true difference or measurement error. Altogether, because QDM findings are inconsistent, the external and predictive validity of QDM is unclear².

Second is impulsivity (IMP), or delay aversion, which is operationalized as the difference in average betting ratios chosen across ascending and descending conditions (E[A − D]; Rogers et al., 1999), but only counting the optimal trials (i.e., where the participant chose the color that had the greater number of boxes). Large, negative differences between conditions correspond to more rapid, impulsive betting. For example, someone betting impulsively would be expected to choose the “sooner” bets (those shown first) more frequently than the “later” bets. Therefore, IMP can be considered an index of intertemporal choice (Dai and Busemeyer, 2014) and is conceptually similar to measures of impulsivity derived from delay discounting tasks (DDT; Green and Myerson, 1993; Mazur, 1987; Myerson and Green, 1995; Reynolds, 2006). Importantly, individuals with substance use disorders consistently show steeper discounting of future rewards relative to healthy controls (Bickel et al., 2007; Dai et al., 2016; Green and Myerson, 1993; Johnson et al., 2015; Mazur, 1987; Miedl et al., 2014; Myerson and Green, 1995; Reynolds, 2006; Wilson and Vassileva, 2016), a pattern that has also been observed in IMP with problem gamblers (e.g., Kräplin et al., 2014; Lawrence et al., 2009; Zois et al., 2014; but see Monterosso et al., 2001). Like QDM, however, findings regarding differences in IMP among individuals with substance use disorders are inconsistent. For example, alcohol dependence has been linked to higher IMP relative to controls (Lawrence et al., 2009), but other studies have revealed no differences (Czapla et al., 2016; Monterosso et al., 2001; Zois et al., 2014).

We hypothesize that the inconsistent findings using QDM and IMP result, in part, because they ignore the equifinal nature of behavior (i.e. the underlying mechanisms). Specifically, summary statistics like QDM and IMP are dependent on multiple cognitive mechanisms, which may each contribute to measurement error. Using IMP as an example, compare an individual who selects (A) all 5% bets, versus someone selecting (B) all 95% bets. Here, both individuals are given the same IMP score despite showing clear differences in risk valuation (i.e. A is risk-averse while B is risk-seeking). Because risk sensitivity, temporal discounting, and other cognitive mechanisms all jointly determine which bet proportion participants choose (see eq.’s 4–8 in the Supplementary Materials [SM]³), impulsivity as traditionally measured in the CGT is inherently confounded with the effects of other cognitive mechanisms. As in temporal discounting paradigms, IMP should provide an independent measure of how much the expected utility is discounted with each delayed bet. Cognitive modeling allows for the specification of such a measure, which should provide a more precise measurement of IMP that can better differentiate groups.

Risk taking (Risk) is a third measure often used to assess decision-making in the CGT. However, unlike QDM and IMP, Risk is often operationalized in different ways across studies. For example, some studies define Risk as the average betting ratio only on those trials where participants choose the optimal color (Risk+; e.g. Kräplin et al., 2014; Zois et al., 2014); others as the average betting ratio across all trials (Risk-Avg or Overall Proportion Bet; e.g. Bowden-Jones et al., 2005; Lawrence et al., 2009); and still others as the average betting ratio for trials in which participants choose the less optimal color (Risk-, e.g. Baldacchino et al., 2015). Based on our literature review, we chose to operationalize risk-taking as the Risk + definition above due to its more widespread use (which is typically called ‘Risk Taking’).

As mentioned earlier, there are a number of additional measures from the CGT: Deliberation time is the time between the beginning of the trial and the bet choice; overall proportion bet records the average betting ratio chosen across all trials, including non-optimal trials and trials in which the proportion of red and blue boxes are the same; risk adjustment captures the tendency for participants to bet more when the odds are in their favor. While we also assess the models’ capabilities to capture trends in these data, as well as report on these data, these additional measures are not as common, or are very similar to the first three measures, and so our focus will be mostly on the three main measures of QDM, Risk+, and IMP.

Because parameters from cognitive models are often difficult to estimate, we use hierarchical Bayesian analysis (HBA; Kruschke, 2014; Wagenmakers et al., 2018). HBA has many advantages over traditional approaches (e.g., maximum likelihood estimation) and is particularly well-suited for estimating group-level effects while accounting for individual-level variation. Specifically, HBA uses estimates of participant-level parameters to inform the group-level estimate, which leads to pooling of information across subjects within each group. Once estimated, group-level parameters can then be directly compared to identify differences in cognitive mechanisms between groups (Kruschke, 2014; Wagenmakers et al., 2018)

In sum, the explanatory power of the behavioral CGT data in isolation is quite restricted, and here we offer a cognitive model of the CGT as a partial solution. We develop models based on both expected utility theory (von Neumann and Morgenstern, 1944) and ideas from prospect theory (Kahneman and Tversky, 2013/1979) and use Bayesian model comparison to determine which model is most generalizable. Further, we evaluate the predictive validity of the model relative to traditional behavioral summary methods (QDM, IMP, Risk+, etc.) by comparing model parameters and traditional measures of CGT behavior across control participants and multiple groups of currently abstinent individuals with a history of pure amphetamine, pure heroin, and polysubstance use disorders. Additionally, we examine convergent validity between traditional methods and our proposed alternatives. We expect to find steeper delay discounting of bets in all substance using groups relative to healthy controls. Further, we hypothesize that cognitive modeling will reveal differences in the groups’ parameter estimates that many of the behavioral measures will fail to detect.

2. Methods

2.1. The cognitive models

The full mathematical details for each model are relegated to the SM (see S1 Table for complete mathematical details⁴), but we provide a verbal description here. All models assume that a color and bet is chosen based on its “strength” (i.e., expected utility) relative to all other options (von Neumann and Morgenstern, 1944). Comparing the strength of each possible choice to the summed strength of all choices (Luce’s choice rule; Busemeyer and Stout, 2002) yields a probability of choosing that particular option, so that our models output probability mass functions for each stage of the task. In particular, the probability of choosing a betting option is proportional to the expected utility of that option. Note also that the expected utility of each option is conditioned on the color choice. The color choice will be based on distortions of the available color data during the task, where the distorted values are our “expected utilities” in this context.

We tested a total of 12 different models that varied assumptions regarding the color and bet utility functions. Below, we limit our discussion to what we term the Cumulative model (CM), which provided the best fit to the data relative to competing models and was deemed more generalizable⁵. The CM bases the expected utility on the accumulated points up to the given trial (i.e. based on what the resulting “Point” value would be in Fig. 1), contrasting models such as in Prospect Theory which assume that only the potential outcomes determine an option’s expected utility⁶. Additionally, we assume that both the color choice probabilities and bet proportions are used to determine the expected utility for each option (the assumed dependence). Formally, we can represent the expected utility of each option as:

$$EU\left(X|\mathit{\text{Color}}\right)=P\left(\mathit{\text{Color Chosen Wins}}\right)\cdot \mathit{\text{Utility}}\left(\mathit{\text{Points After Gain}}\right)+P\left(\mathit{\text{Opposite Color Wins}}\right)\cdot \mathit{\text{Utility}}\left(\mathit{\text{Points After Loss}}\right)$$

That is, the expected utility of option X, given the chosen color, is a weighted average of the utility of the cumulative point values across gaining or losing points on the current trial. We assume that the Expected Utility (EU) is computed for each of the possible bets, the strength of which determines the probability of bet choice.

The CM has a total of 5 free parameters that are estimated for each participant/group. First, subjective probabilities for the color choice are captured by α (0 ≤ α ≤ 5), which “distorts” the objective probabilities of the token being under a red versus blue box. Higher values for α indicate underweighting of low and overweighting of high probabilities, which leads to more optimal color choices. A value of α = 1 indicates objective probability weighting. Therefore, probability distortion is our proposed cognitive mechanism that captures what is traditionally referred to as QDM. To account for biases that participants might have toward one color (which can introduce noise in estimation of probability distortion), we also include a color bias parameter c (0 ≤ c ≤ 1) where values closer to 1 indicate a bias for red. Note that CM uses the “distorted” color probabilities to generate color choice probabilities, but the objective color probabilities are used to weight the bets in the EU equation above⁷.

For calculating the value of gaining/losing a bet, we include a utility parameter ρ (0 ≤ ρ < + ∞) which governs how sensitive participants are to losses relative to gains. Specifically, we set ρ = 1 for gains and freely estimated ρ for losses, which allows for ρ to capture variations in loss sensitivity that can lead to risk-seeking (ρ < 1) or risk-averse (ρ > 1) behavior. Therefore, ρ should (anti-)align with traditional measures of Risk (i.e., Risk+⁸).

To capture the tendency to select immediate over delayed bets, the expected utility is then “discounted” for the time delay for each bet option. Specifically, the CM assumes that waiting for an option diminishes its subjective value linearly. The slope of this linear descent is given by β (0 ≤ β < + ∞), which is interpreted here as the impulsivity parameter (IMP) and is akin to the discounting rate measured in delay discounting paradigms. Greater descent in value due to time delays (higher β) indicates higher impulsivity. Finally, the discounted expected utilities for each bet option are exponentiated, scaled with γ (0 ≤ γ < + ∞), and then compared to the utility of other bet options to generate a probability of selecting a given bet (known as Luce’s choice rule, Busemeyer and Stout, 2002). Higher (lower) values for γ indicate that participants are making more deterministic (random) choices with respect to their model-predicted expected value for each option. Table 1 summarizes each of the CM’s parameters and their respective psychological interpretations.

Table 1.

The parameters in the model.

Parameter	Range of Values	Interpretation
α	0 ≤ α ≤ 5	Color probability weighting
ρ	0 ≤ ρ < + ∞	Risk aversion
c	0 ≤ c ≤ 1	Bias for choosing RED
β	0 ≤ β < + ∞	Impulsivity
γ	0 ≤ γ < + ∞	Variability/noise in betting choice

A compendium of the parameters in the models. The second column gives the permissible values for that particular parameter (note that β and γ are not bounded above). The final column gives the psychological interpretation of the parameter based on how its values affect the output of the models. See section 2 for more details.

2.2. Experimental details

Because the experimental details have been explained elsewhere (Ahn and Vassileva, 2016; Vassileva et al., 2014; Wilson and Vassileva, 2016), we only touch on some highlights here. More information can be found in the SM⁹.

First, our final sample consisted of 124 healthy controls¹⁰ (i.e., those not having current or lifetime diagnosis of substance dependence) and three groups of participants with a history of substance-dependence based on DSM-IV criteria: (a) a “pure” (i.e., mono-dependent) heroin dependent group (N = 79); (b) a “pure” amphetamine dependent group (N = 76); and (c) a polysubstance dependent group (N = 103). This final sample excludes eighteen participants across the four groups for reasons we elaborate below. The majority of substance dependent participants were in protracted abstinence, i.e. in DSM-IV sustained full remission for twelve months or longer (heroin: 78%; amphetamine: 59%; polysubstance: 64%). All participants were recruited in Sofia, Bulgaria, as part of a larger study on impulsivity among substance users. All participants provided informed consent. The demographic data for the final sample is found in Table 2; more information on the procedures can be found in (Ahn and Vassileva, 2016; Vassileva et al., 2014) and in the SM¹¹.

Table 2.

Participant demographics and Behavioral Indices. Demographics, Substance Use, and Behavioral Measures for the Cambridge Gambling Task.

Measure	Controls	Heroin	Amphetamine	Polysubstance
N*	124	79	76	103
Age	26.02 (6.11)	30.28 (4.89)	24.59 (4.85)	27.25 (5.53)
Percent Male	63.71%	74.36%	67.11%	82.35%
Education	14.15 (2.85)	13.03 (2.45)	13.40 (2.23)	13.12 (2.48)
Last Alcohol	45.07 (188.05)	257.23 (592.08)	25.04 (81.14)	159.07 (262.55)
Last Drug	1032.1 (1347.6)	771.3 (993.9)	273.4 (1039.3)	339.5 (628.9)
Delay Aversion	.29 (.23)	.37 (.21)	.33 (.18)	.33 (.21)
Deliberation Time	2316.8 (690.5)	2271.0 (678.3)	2470.8 (804.6)	2396.8 (794.8)
Overall Proportion Bet	.53 (.14)	.54 (.13)	.56 (.12)	.57 (.13)
Quality of Decision Making	.89 (.12)	.87 (.15)	.87 (.11)	.87 (.13)
Risk Adjustment	1.07 (0.93)	.97 (.88)	.97 (.79)	.91 (.76)
Risk-Taking/Risk+**	.57 (.15)	.58 (.14)	.60 (.13)	.62 (.14)

Demographics, substance use, and behavioral data of the substance-using groups and controls. The statistics are given as: Mean (Standard Deviation). ‘Last Alcohol’ represents how many days since the participant had alcohol; similarly for ‘Last Drug.’ The behavioral measures are defined in the Introduction in the text. Controls have a non-zero value in ‘Last Drug’ because they were allowed to have used cannabis in the past, while not meeting dependence criteria. Numbers in bold represent a significant difference after a Bonferroni correction.

^*One heroin user and one polysubstance user had missing demographic and summary data, but complete trial-by-trial data.

^**ANOVA reported p < .05.

We administered the CGT using the CANTAB® battery (Cognition, 2016) to all participants. We excluded 18 participants due to clear signs of boredom (details in the SM¹²): (i) Controls = 7; (ii) HeroiN = 5; (iii) Amphetamine = 2; (iv) Polysubstance = 4. Our initial sample consisted of 437 participants; 18 of whom needed to be removed due to clear signs of boredom, and an additional 37 control participants were removed because, after further inspection, they were found to be ineligible¹³. Additionally, 2 participants had missing summary CGT data (as outputted by CANTAB) and demographic data but complete trial-by-trial data (which is used in the models). This leaves us with a final sample of N = 382 participants, with two people missing summary and demographic data. The behavioral results below used those with complete summary CGT data (N = 380).

3. Results

3.1. Behavioral results

We performed an ANOVA on each of the behavioral measures available to us from the CGT: (1) QDM, (2) IMP/delay aversion, (3) Risk +/Risk-Taking, (4) Deliberation Time, (5) Risk Adjustment, and (6) Overall Proportion Bet (OPB).

There were no significant group differences on: QDM, with F(3, 376) = 0.54, ns (p = 0.66); Delay Aversion/IMP, with F(3, 376) = 2.30, p = 0.08; Deliberation time, with F(3, 376) = 1.17, p = 0.32; Overall Proportion Bet, with F(3, 376) = 2.38, p = 0.07; and Risk Adjustment, with F(3, 376) = 0.74, p = 0.53. Note that the degrees of freedom are two less than they should be given a total N of 392, since one polysubstance and one heroin participant had missing summary data.

However, Risk+ (Risk-Taking) was found to be significant, with F(3, 376) = 2.79, p = 0.04. A Bonferroni correction on Risk+, with 3 comparisons and an alpha-level set at 0.05, revealed that only the comparison between controls and polysubstance users was significant, t(224) = −2.66, p = 0.0083; the negative t statistic indicates that polysubstance users were higher in Risk + than controls.

Thus, most of the behavioral measures suggest that there is minimal evidence of group differences on the task, with the exception of Risk+, where polysubstance users scored significantly higher than controls on both measures. Thus, while there are multiple measures of risk in the CGT, for simplicity we focus on the comparison between ρ and Risk+, as Risk + was the only measure to have a significant difference.

3.2. Cognitive modeling results

Details on the procedures used to fit, check and determine the best model are included in the SM¹⁴. Briefly, we fit twelve competing models to each group separately, resulting in both group and individual-level posterior estimates for each model and group (see S1 Table for mathematical details¹⁵). We checked convergence to target distributions using both graphical and quantitative measures (Gelman and Rubin, 1992), and then used the leave-one-out information criterion to determine which model described the data best while penalizing for model complexity (Vehtari et al., 2017).

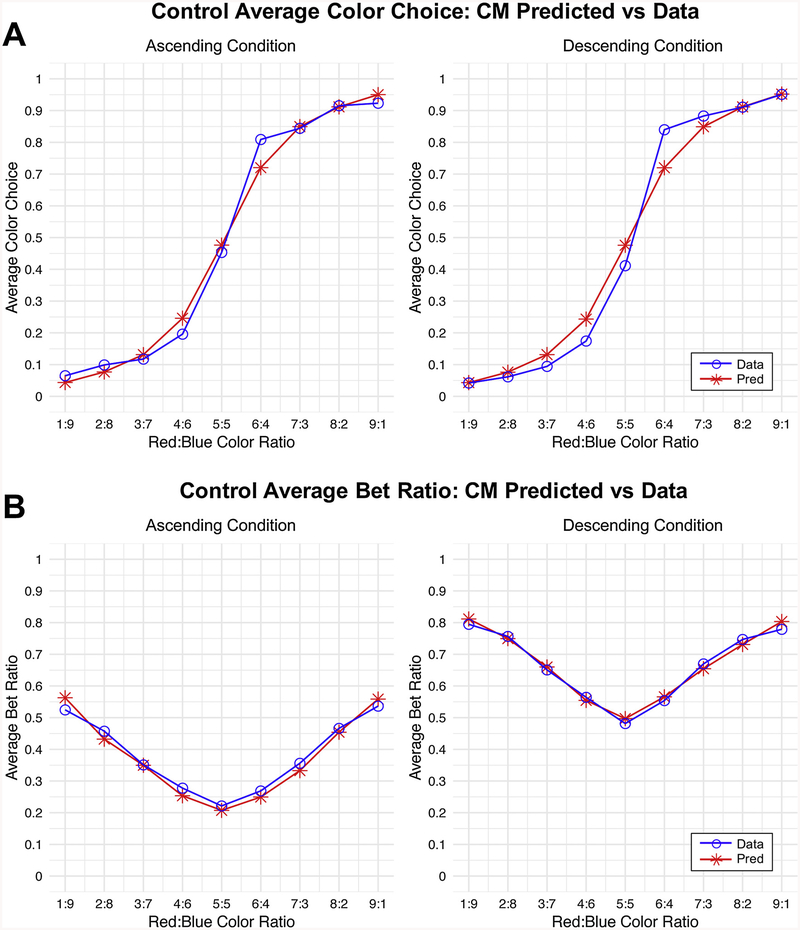
Additionally, we conducted posterior predictive simulations to check how well the CM could describe each groups’ choice patterns across different color ratios and conditions. Fig. 2 shows that the CM provided an excellent fit to both the color choice and bet proportions across conditions in the control group. Results were similar for the other groups (see S2 and S3 Tables for mean squared error measures across all models and groups¹⁶). (Note that the model follows the hypothesized effect of color ratio on betting choice.) Because the CM provided an accurate account of all groups’ color choice and betting behavior, we used it to infer substance-specific differences in cognitive mechanisms between groups.

Fig. 2.

Comparison of Posterior Predictive Simulations versus Actual Average Choices.

Posterior predictive simulations generated from the best fitting model (CM with log valuation function; Model 12 in the Supplementary Text). Simulations from the model were generated for each individual after fitting the model, conditional on their actual choices. Resulting individual level predictions were then averaged across participants within groups and plotted against the actual behavioral choices averaged across participants within groups. Note that these graphs depict only healthy control data, though results were consistent across groups. We refer the reader to S2 and S3 Tables for comparison of posterior predictive simulations across models and groups. (A) Simulations versus actual behavioral data for color choices. Note that a choice of blue was coded as 0, and a choice of red was coded as 1. Thus, averages close to zero indicate more choices of blue, and those closer to 1 indicate more choices of red. (B) Simulations versus actual behavioral data for bet choices. The y-axis here now represents the average betting ratio that was chosen versus predicted. Note that while the shapes for the ascending and descending cases are similar, the descending graph is shifted upward relative to the ascending graph—this difference indicates impulsivity and is captured by β in the CM model.

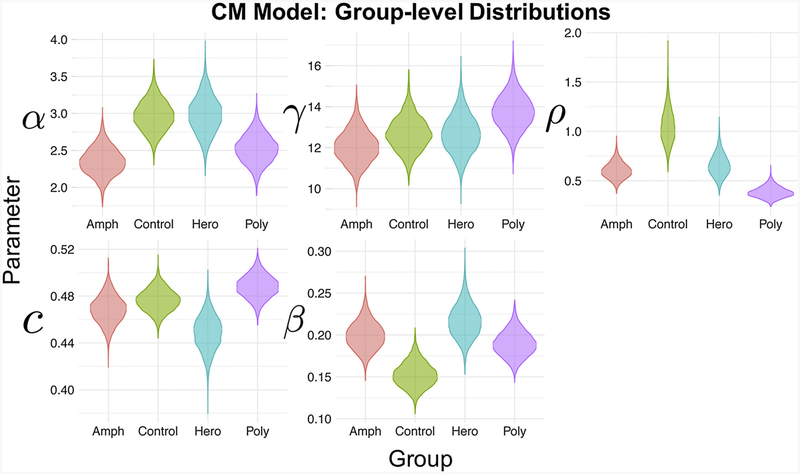
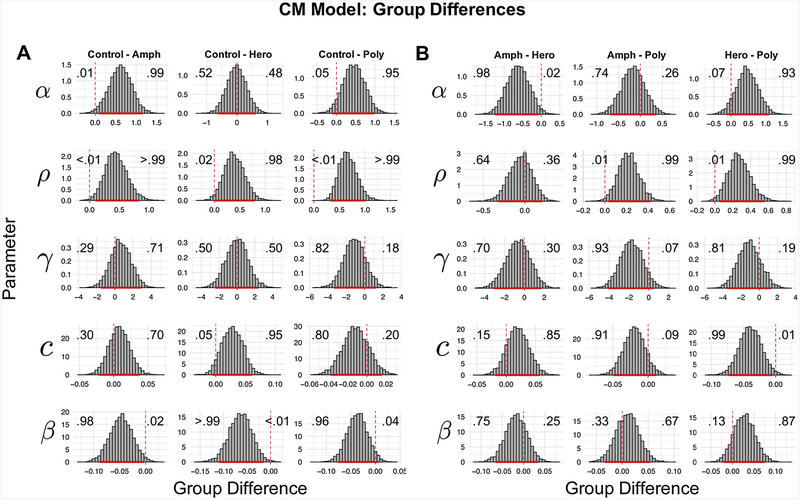
Fig. 3 shows the group-level posterior estimates for the CM for each group. Note that posterior distributions reflect uncertainty in the parameter estimates, where areas of higher density reflect more probable parameter values. To compare groups in a Bayesian manner, we computed differences between group-level parameters (see Fig. 4A and 4B). For brevity, we focus on reporting comparisons where the 95% highest density interval (HDI) of the difference between group parameters excludes/nearly excludes 0 (Kruschke, 2014). However, we do not endorse binary interpretations of “significant differences” using this threshold and instead refer the reader to the graphical comparisons to judge whether parameter differences are meaningful. In particular, the Bayesian method of analysis allows us to make statements about the probability of certain parameter comparisons. The probabilities within Fig. 4 demonstrate those probabilities of interest.

Fig. 3.

Posterior Distributions for the Means of Each Parameter Across Groups.

The posterior densities (distributions) for the means of each parameter, color-coded by group. Note that parameters are estimated from the CM model with a log valuation function (Model 12 in the Supplementary Text).

Fig. 4.

Group Differences in Posterior Estimates of Parameters Using Model 12.

(A) Posterior distribution of differences in estimated parameters between groups, using the best-fitting model (CM model with log valuation function; termed M12 in Supplementary Text). Each column shows the difference distributions between Controls and one of the substance-using groups. These differences are comparing each of the CM model hyper-parameters (i.e. the parameters reflecting group-level means). The solid red bars indicate the 95% Highest Density Interval (HDI) for each difference, meaning where 95% of the “mass” of the posterior distribution lies. Note that we do not endorse binary interpretations of significance using HDIs, and instead interpret the posterior distributions as continuous measures of evidence. The vertical dashed lines show where zero lies in each graph. The numbers overlaying each subplot indicate the proportion of the posterior distribution above and below 0, which can be interpreted as the model-estimated probability of a difference in parameter values between groups (where .50 indicates no evidence for a difference, and more peaked and diffuse distributions indicate more and less certainty in the inferred difference, respectively). (B) Posterior distributions of the differences in group-level CM model parameters between substance use groups. Solid and dashed lines and overlaying numbers are interpreted in the same way as for (A).

Overall, we found strong evidence for large differences between controls and substance users. First, amphetamine users, and polysubstance users to a lesser extent, showed evidence for less probability distortion (lower α) than healthy controls, which reflects a greater willingness to make less optimal bets (analogous to QDM). Additionally, amphetamine and heroin users, and polysubstance users to a lesser extent, showed evidence for larger β parameters compared to the healthy controls, which is indicative of higher impulsivity (i.e. greater discounting of time delay when placing bets) in the substance using groups. Specifically, all substance using groups had an estimated 96% or greater probability of having higher β parameters relative to controls, as seen in Fig. 4. Furthermore, all substance using groups showed greatly reduced sensitivity to loss (lower ρ) relative to controls (estimated 98% or greater probability of lower ρ relative to controls), which leads to taking more risky bets. This follows since reduced sensitivity makes losses less painful, and hence the person will be more willing to take riskier bets¹⁷. Notably, a difference in ρ between polysubstance users and controls is consistent with our findings using traditional measures of Risk+.

In addition to identifying differences between healthy controls and substance users, the CM differentiated well among substance using groups (Fig. 4B). For example, amphetamine users showed evidence of lower probability distortion of color choices (α) relative to heroin users (98% of the posterior samples were greater than 0) possibly indicating a quantitatively worse decision-making process in the color choice. Specifically, amphetamine users appear to probability match to a some-what greater degree than heroin users, where probability matching is the less optimal strategy in this situation (Shanks et al., 2002). Additionally, pure substance users (i.e. pure amphetamine and pure heroin users) showed more risk-sensitivity to losses (ρ) relative to polysubstance users (estimated 99% or greater probability). Notably, there were no strong differences in impulsivity (β) among substance using groups. Finally, heroin users showed a smaller bias for the red color choice (c) relative to polysubstance users. That is, the heroin users had a greater propensity to choose blue over red than polysubstance users. While not theoretically important, this result underscores the importance of modeling choice biases that could obscure inferences on more meaningful model parameters¹⁸. In fact, such biases may be partly responsible for inconsistent findings using traditional measures of QDM and IMP. Further, our finding that ρ differed between substance using groups shows that the CM is more sensitive to differences in risk sensitivity compared to traditional measures in the CGT (Risk+).

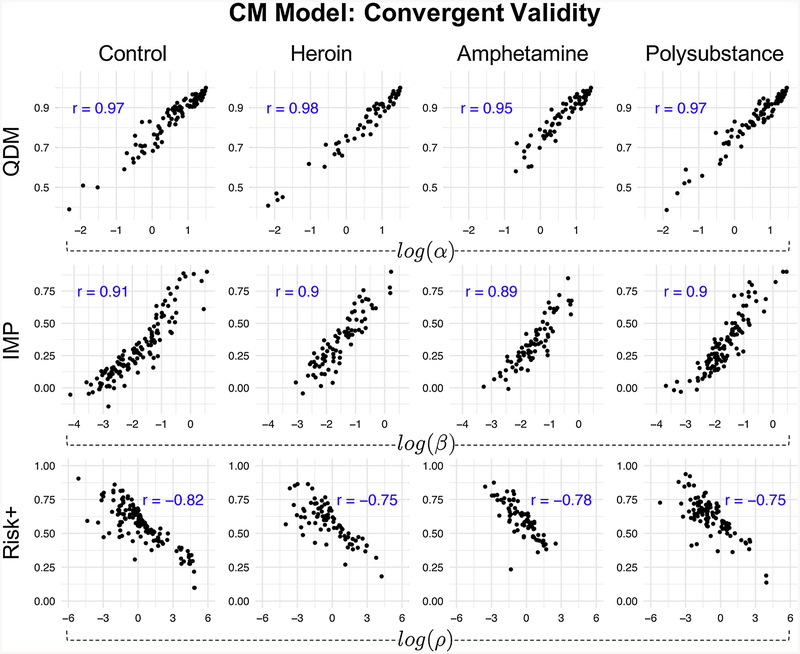
Finally, to test convergent validity between QDM, IMP, and Risk + to similar corresponding measures offered by the CM, we computed the posterior means for each participant’s α, β, and ρ parameters and compared them to each participant’s QDM, IMP, and Risk + scores, respectively. Fig. 5 shows the Pearson’s correlations between cognitive model parameters and traditional behavioral summary measures. Notably, correlations were high across all groups and measures (all |r|s ≥.75), suggesting that the CM captures facets of decision-making similar – but not identical – to those inferred using traditional summary statistics derived from the CGT. Importantly the CM maintained strong convergent validity with traditional measures while also identifying group differences to which traditional measures/analyses were not sensitive.

Fig. 5.

Convergent validity between traditional metrics and cognitive model parameters.

Convergent validity between traditional measures of QDM, IMP, and Risk + and corresponding cognitive model parameter alternatives. The α parameter captures distortion of color choice probabilities, which leads to more or less optimal color choices and is analogous to traditional measures of QDM. The β parameter captures how much participants discount the utility of each bet with the passing of time and is analogous to traditional measures of IMP. The ρ parameter captures risk sensitivity, where values of ρ < 1 indicate less sensitivity to losses than gains and values of ρ > 1 have the opposite interpretation. Therefore, ρ < 1 reflects risk-seeking behavior, and ρ > 1 indicates risk-averse behavior. Note that the correlations between ρ parameters and Risk + scores are negative because ρ is specific to losses, so the interpretation is reversed. The cognitive model parameters are log-transformed. All p-values < < 0.001.

4. Discussion

We have presented a modeling perspective on measuring latent cognitive mechanisms that give rise to choice behavior in the Cambridge Gambling Task (CGT). Specifically, we developed a suite of cognitive models that made different assumptions about how individuals make choices on the CGT, and we used hierarchical Bayesian modeling and Bayesian model comparison to identify the model that provided the best fit to empirical data collected from both healthy controls and multiple groups of individuals with histories of substance use disorders. Finally, we probed the best-fitting model to determine which cognitive mechanisms varied across groups. The model that performed the best (CM; coded as M12 in the SM) used a slowly-growing (i.e. logarithmic), cumulative utility function, and it demonstrated expected differences among the groups in its proxy measure of impulsivity (β). In particular, we found that all the substance dependent groups showed evidence of higher β’ s than the healthy controls, an indication of greater impulsivity (i.e. greater discounting of delayed bets) within these groups than in controls. The CM further demonstrated differences among substance using groups that are consistent with prior literature. For example, we found that amphetamine use was linked to lower probability distortion (α) relative to heroin use, which indicates less optimal color choices, and is consistent with elevated sensation seeking predicting amphetamine rather than heroin use (Ahn and Vassileva, 2016). We additionally found evidence for differences in risk-seeking behavior across the groups, and even within the substance-using groups (e.g. monosubstance users not differing, but evidence for a difference between mono- and polysubstance users).

The models developed in this article were an initial attempt to model the CGT, and so there is certainly room for improvement. For instance, it may be that our proxy measure of impulsivity is too crude, and may conflate related but distinct constructs such as sensation-seeking, novelty-seeking, and various types of trait impulsivity, to name a few (Magid et al., 2007). Possible improvements could see how these different forms of impulsivity could be implemented into the model. In addition, because the functional form of the bet utility function of the CM is specific to loss sensitivity, we caution readers and those interested in employing the model that the CM risk aversion parameter should not be interpreted in the same manner as risk aversion traditionally measured in economic tasks. In particular, the risk aversion parameter is: (1) opposite in direction to that of traditional measures of risk aversion, and (2) estimated using an unorthodox function – which provided the best fit to all groups in the current study. Therefore, those interested in traditional measures of risk aversion should not rely wholly on our CGT model (more on this can be found in the SM¹⁹).

There are some limitations to this study that should be kept in mind. First, the design of the CGT complicates not only any design for a model, but also the interpretation of results from such a model. The design allows multiple cognitive components of decision-making to be assessed at once, in a fairly realistic gambling simulation; however, this possibly comes at the cost of “watering down” any possible assessment of these components individually. If we accept that cognitive models lead to more reliable and valid results, then these comments easily apply to any traditional measures of the CGT as a corollary. Indeed, as the CGT engages a variety of cognitive processes that may not be reliably assessed, this may partially explain the inconsistent results in the literature. While the CGT may arguably give a more ecologically valid assessment of decision-making processes, this comes at the cost of lower reliabilities for any measures derived from it.

Finally, these results came from a rare group of former pre-dominantly mono-dependent substance users, currently in protracted abstinence. It has been suggested that long-term recovery from addiction may involve developing capacities such as unusually strong impulse control, that may exceed those of individuals who have never been addicted (Humphreys and Bickel, 2018). However, it is unclear if factors other than type of substance use could have driven the results we observed, e.g. the gender imbalance in our sample (mostly male), length of abstinence, individual differences in history and severity of substance use, or co-occurring psychopathology. These factors may have differed across our groups, which may have affected our results. Future studies should examine the influence of these potentially confounding variables on CGT model parameters.

Nonetheless, these results potentially testify to the long-term effects of chronic substance use on decision-making capabilities; while it is certainly possible that diminished decision-making capabilities could have caused the substance use in our sample, our experimental design does not allow us to determine the direction of causality. However, our results are congruent with a meta-analysis of the long-term effects of alcohol use disorder (Stavro et al., 2013) and opioid use disorder (Biernacki et al., 2016). Our sample being mostly in protracted abstinence may also explain why we only found a marginally non-significant behavioral difference among groups in the raw data, whereas others have found significant differences (Kräplin et al., 2014; Lawrence et al., 2009; Zois et al., 2014). Indeed, cognitive functioning has been shown to improve gradually with abstinence (Garavan et al., 2013; Stavro et al., 2013). Therefore, future research should determine if our results generalize to groups of active substance users or whether they are specific to substance users in protracted abstinence.

5. Conclusion

Cognitive modeling offers a powerful, valid alternative to traditional summary measures of behavioral performance on the CGT. We used hierarchical Bayesian modeling to develop and test multiple cognitive models on CGT data from healthy controls and several groups of substance users in protracted abstinence. Further, we used Bayesian model comparison to determine the best-fitting, most generalizable model. To our knowledge, this is the first cognitive model developed specifically for the CGT. We added the best-fitting model to hBayesDM, an R package that will allow interested researchers to easily apply the CM to data collected from the CGT (Ahn et al., 2017). We refer interested readers to the tutorial on our GitHub repository (https://github.com/CCS-Lab/hBayesDM) for details on installing and using hBayesDM to fit the CM to CGT data.