ChaRTr: An R toolbox for modeling choices and response times in decision-making tasks

Chandramouli Chandrasekaran; Guy E Hawkins

doi:10.1016/j.jneumeth.2019.108432

. Author manuscript; available in PMC: 2020 Jan 24.

Published in final edited form as: J Neurosci Methods. 2019 Oct 3;328:108432. doi: 10.1016/j.jneumeth.2019.108432

ChaRTr: An R toolbox for modeling choices and response times in decision-making tasks

Chandramouli Chandrasekaran ^a,^b,^c,^*, Guy E Hawkins ^d

PMCID: PMC6980795 NIHMSID: NIHMS1547435 PMID: 31586868

Abstract

Background

Decision-making is the process of choosing and performing actions in response to sensory cues to achieve behavioral goals. Many mathematical models have been developed to describe the choice behavior and response time (RT) distributions of observers performing decision-making tasks. However, relatively few researchers use these models because it demands expertise in various numerical, statistical, and software techniques.

New method

We present a toolbox — Choices and Response Times in R, or ChaRTr — that provides the user the ability to implement and test a wide variety of decision-making models ranging from classic through to modern versions of the diffusion decision model, to models with urgency signals, or collapsing boundaries.

Results

In three different case studies, we demonstrate how ChaRTr can be used to effortlessly discriminate between multiple models of decision-making behavior. We also provide guidance on how to extend the toolbox to incorporate future developments in decision-making models.

Comparison with existing method(s)

Existing software packages surmounted some of the numerical issues but have often focused on the classical decision-making model, the diffusion decision model. Recent models that posit roles for urgency, time-varying decision thresholds, noise in various aspects of the decision-formation process or low pass filtering of sensory evidence have proven to be challenging to incorporate in a coherent software framework that permits quantitative evaluation among these competing classes of decision-making models.

Conclusion

ChaRTr can be used to make insightful statements about the cognitive processes underlying observed decision-making behavior and ultimately for deeper insights into decision mechanisms.

Keywords: Decision making, Choice, Response time (RT), Diffusion decision model, DDM, Urgency gating, AIC, BIC, Model selection

1. Introduction

Perceptual decision-making is the process of choosing and performing appropriate actions in response to sensory cues to achieve behavioral goals (Freedman and Assad, 2011; Hoshi, 2013; Shadlen and Newsome, 2001; Gold and Shadlen, 2007; Shadlen and Kiani, 2013; O’Connell et al., 2018a). A sophisticated research effort in multiple fields has led to the formulation of cognitive process models to describe decision-making behavior (Donkin and Brown, 2018; Ratcliff et al., 2016). The majority of these models are grounded in the “sequential sampling” framework, which posits that decision-making involves the gradual accumulation of noisy sensory evidence over time until a bound (or criterion/threshold) is reached (Forstmann et al., 2016; Ratcliff et al., 2016; Shadlen and Kiani, 2013; Brunton et al., 2013; Ratcliff and Rouder, 1998; Ratcliff and McKoon, 2008; Gold and Shadlen, 2007; Hanks et al., 2014). Models derived from the sequential sampling framework are typically elaborated with various systematic and random components so as to implement assumptions and hypotheses about the underlying cognitive processes involved in perceptual decision-making (Ratcliff et al., 2016; Diederich, 1997).

The most prominent sequential sampling model of decision-making is the diffusion decision model (DDM), which has an impressive history of success in explaining the behavior of human and animal observers (e.g., Forstmann et al., 2016; Ratcliff et al., 2016; Palmer et al., 2005; Tsunada et al., 2016; Ding and Gold, 2012a,b). However, recent studies propose alternative sequential sampling models that do not involve the integration of sensory evidence over time. Instead, novel sensory evidence is multiplied by an urgency signal that increases with elapsed decision time, and a decision is made when the signal exceeds the criterion (Ditterich, 2006a; Thura et al., 2012; Cisek et al., 2009). Another line of research proposes that observers aim to maximize their reward rate and suggests that the decision boundary dynamically decreases as the time spent making a decision grows longer. Such a framework has been argued to provide a better explanation for decision-making behavior in the face of sensory uncertainty (Drugowitsch et al., 2012).

One approach to distinguish between these different models is to systematically manipulate the stimulus statistics and/or the task structure and then test whether behavior is qualitatively consistent with one or another sequential sampling model (Cisek et al., 2009; Thura and Cisek, 2014; Carland et al., 2015; Brunton et al., 2013; Scott et al., 2015). An alternative approach is to quantitatively analyze the choice and RT behavior with a large set of candidate models, and then carefully use model selection techniques to understand the candidate models that best describe the data (e.g., Hawkins et al., 2015b; Chandrasekaran et al., 2017; Purcell and Kiani, 2016; Evans et al., 2017). The quantitative modeling and model selection approach allows the researcher to determine whether a particular model component (e.g., an urgency signal, or variability in the rate of information accumulation) is important for generating the observed behavioral data. It also provides a holistic method for testing model adequacy because the proposed model is judged on its ability to account for all available data (e.g., Evans et al., 2017), rather than focusing on a specific subset of the data.

Despite the apparent benefits of model selection, there are technical and computational challenges in the application of decision-making models to behavioral data. Some researchers have surmounted these issues by simplifying the process: using analytical solutions for the predicted mean RT and accuracy from the simplest form of the DDM, applied to participant-averaged behavioral data (Palmer et al., 2005; Tsunada et al., 2016). However, the complete distribution of RTs is highly informative, and often necessary, to reliably discriminate between the latent cognitive processes that influence decision-making (Forstmann et al., 2016; Ratcliff and McKoon, 2008; Ratcliff et al., 2016; Luce, 1986). Until recently, applying sequential sampling models like the DDM to the joint distribution over choices and RT required bespoke domain knowledge and computational expertise. This has hindered the widespread adoption of quantitative model selection methods to study decision-making behavior.

Some recent attempts have demystified the application of cognitive models of decision-making to behavioral data, providing a path for researchers to apply these methods to their own research questions. For instance, Vandekerckhove and Tuerlinckx (2008) developed the Diffusion Modeling and Analysis Toolbox (DMAT), and Voss and Voss (2007) developed the diffusion model toolbox (fast-dm; for an updated version see fast-dm-30, Voss et al., 2015). Other modern toolboxes have improved the parameter estimation algorithms and can leverage multiple observers to perform hierarchical Bayesian inference (Wiecki et al., 2013). In hBayesDM (Ahn et al., 2017) and Dynamic Models of Choice (Heathcote et al., 2018) researchers can apply a range of models to behavior from a wide variety of decision-making paradigms ranging from choice tasks to reversal learning and inhibition tasks.

A common feature across all of the excellent toolboxes currently available is that they provide code to apply the DDM to data, or the DDM in addition to a few alternative models. As a consequence, the toolboxes provide no pathway for a researcher to rigorously compare the quantitative account of the DDM to alternative theories of the decision making process including models with an urgency signal (Ditterich, 2006a), urgency-gating (Cisek et al., 2009), or collapsing bounds (Hawkins et al., 2015b). Simply put, we currently have no openly available and extensible toolbox for understanding choice and RT behavior using the many hypothesized models of decision-making. We believe there is a critical need for examining how these different models perform in terms of explaining decision-making behavior.

The objective of this study was to address this need and provide a straightforward framework to analyze a range of existing sequential sampling models of decision-making behavior. Specifically, we aimed to provide an open-source and extensible framework that permits quantitative implementation and testing of novel candidate models of decision-making. The outcome of this study is ChaRTr, a novel toolbox in the R programming environment that can be used to analyze choice and RT data of humans and animals performing two-alternative forced choice tasks that involve perceptual or other types of decision-making. R is an open source language that enjoys widespread use and is maintained by a large community of researchers. ChaRTr can be used to analyze choice and RT behavior from the perspective of a (potentially large) range of decision-making models and can be readily extended when new models are developed. These new models can be incorporated into the toolbox with minimal effort and require only basic working knowledge of R and C programming; we explain the required skills in this manuscript. Similarly, new optimization routines that are readily available as R packages can be implemented if desired.

2. Methods and materials

The methods are focused on the specification of various mathematical models of decision-making, and the parameter estimation and model selection processes. For reference, the symbols we use to describe the models are shown in Table 1. The naming convention for the models we have developed in ChaRTr is to take the main architectural feature of the model and use it as a prefix to the model.

Table 1.

List of symbols used in the decision-making models implemented in ChaRTr.

Parameter	Description
x(t)	State of the decision variable at time t.
Δt	Time step of the decision variable.
z, s_z	Starting state of the decision variable (i.e., x(0) = z), and decision-to-decision variability in starting state. s_z is the range of a uniform distribution with mean (midpoint) z.
v_i, s_v	Rate at which the decision variable accumulates decision-relevant information (drift rate, v) in condition i, and decision-to-decision variability in drift rate. s_v is the standard deviation of a normal distribution with mean v_i.
γ(t)	Urgency signal that dynamically modulates the decision variable as a function of t. Can take different functional forms in different models.
a_upper, a_lower	Upper and lower response boundaries that terminate the decision process.
a_upper(t), a_lower(t)	Upper and lower response boundaries that vary as a function of t.
T_er, s_t	Time required for stimulus encoding and motor preparation/execution (non-decision time), and decision-to-decision variability in non-decision time. s_t is the range of a uniform distribution with mean (midpoint) T_er.
s	Within-decision variability in the diffusion process. Represents the standard deviation of a normal distribution. By convention, set to a fixed value to satisfy a scaling property of the model.
E(t)	Momentary sensory evidence at time t.
b, s_b	Intercept and variability of the intercept in urgency based models with linear urgency signals.
$N (0, 1)$	Normal distribution with zero mean and unit variance.
$U (l_{1}, l_{2})$	Uniform distribution over the interval l₁ and l₂.

Open in a new tab

The diffusion decision model, henceforth DDM, refers to the simplest sequential sampling model.
cDDM refers to a DDM with collapsing boundaries (Hawkins et al., 2015b).
cfkDDM refers to a DDM with collapsing boundaries and a fixed parameter for the function defining the collapsing boundary (Hawkins et al., 2015b).
uDDM refers to a DDM with a linear urgency signal with a slope and an intercept.
dDDM refers to a DDM with urgency signal defined by Ditterich (2006a).
UGM refers to an Urgency Gating Model (Cisek et al., 2009; Thura et al., 2012).
bUGM refers to a UGM with a linear urgency signal composed of a slope and an intercept (Chandrasekaran et al., 2017).

For reference, the models being considered, the parameters for the models and the number of parameters in each model are shown in Table 2.

Table 2.

List of the 37 models available in ChaRTr along with the individual parameters in each model and the total number of parameters. n refers to the number of stimulus conditions used. a_U is the short form of a_upper.

Abbreviation	Parameters	N
Diffusion decision model (DDM)
References: Ratcliff (1978), Ratcliff and Rouder (1998),Ratcliff, 1978,Ratcliff (1978), Ratcliff and Rouder (1998)
DDM	v_1...n, a_U, T_er	n + 2
DDMS_v	v_1...n, a_U, T_er, S_v	n + 3
DDMS_t	v_1...n, a_U, T_er, S_t	n + 3
DDMS_vS_z	v_1...n, a_U, T_er, S_v, S_z	n + 4
DDMS_vS_t	v_1...n, a_U, T_er, S_v, S_t	n + 4
DDMS_vS_zS_t	v_1...n, a_U, T_er, S_v, S_z, S_t	n + 5
Collapsing diffusion decision model (cDDM)
References: Drugowitsch et al. (2012), Hawkins et al. (2015b),Drugowitsch et al., 2012,Drugowitsch et al. (2012), Hawkins et al. (2015b)
cDDM	v_1...n, a_U, T_er, a′, k	n + 4
cDDMS_v	v_1...n, a_U, T_er, a′, k, S_v	n + 5
cDDMS_t	v_1...n, a_U, T_er, a′, k, S_t	n + 5
cDDMS_vS_z	v_1...n, a_U, T_er, a′, k, S_v, S_z	n + 6
cDDMS_vS_t	v_1...n, a_U, T_er, a′, k, S_v, S_t	n + 6
cDDMS_vS_zS_t	v_1...n, a_U, T_er, a′, k, S_v, S_z, S_t	n + 7
Collapsing diffusion decision model with fixed k (cfkDDM)
References: Hawkins et al. (2015b)
cfkDDM	v_1...n, a_U, T_er, a′	n + 3
cfkDDMS_v	v_1...n, a_U, T_er, a′, S_v	n + 4
cfkDDMS_t	v_1...n, a_U, T_er, a′, S_t	n + 4
cfkDDMS_vS_t	v_1...n, a_U, T_er, a′, S_v, S_t	n + 5
cfkDDMS_vS_zS_t	v_1...n, a_U, T_er, a′, S_v, S_z, S_t	n + 6
Linear urgency diffusion decision model (uDDM)
References: Ditterich (2006a), O’Connell et al. (2018b)
uDDM	v_1...n, a_U, T_er, b, m	n + 4
uDDMS_v	v_1...n, a_U, T_er, b, m, S_v	n + 5
uDDMS_t	v_1...n, a_U, T_er, b, m, S_t	n + 5
uDDMS_vS_t	v_1...n, a_U, T_er, b, m, S_v, S_t	n + 6
uDDMS_vS_b	v_1...n, a_U, T_er, b, m, S_v, S_b	n + 6
uDDMS_vS_bS_t	v_1...n, a_U, T_er, b, m, S_v, S_b, S_t	n + 7
Ditterich urgency diffusion decision model (dDDM)
References: Ditterich (2006a)
dDDM	v_1...n, a_U, T_er, s_x, s_y, d	n + 5
dDDMS_v	v_1...n, a_U, T_er, s_x, s_y, d, S_v	n + 6
dDDMS_t	v_1...n, a_U, T_er, s_x, s_y, d, S_t	n + 6
dDDMS_vS_t	v_1...n, a_U, T_er, s_x, s_y, d, S_v, S_t	n + 7
dDDMS_vS_zS_t	v_1...n, a_U, T_er, s_x, s_y, d, S_v, S_z, S_t	n + 8
Urgency gating model (UGM)
References: Cisek et al. (2009), Thura et al. (2012),Cisek et al., 2009,Cisek et al. (2009), Thura et al. (2012)
UGM	v_1...n, a_U, T_er	n + 2
UGMS_v	v_1...n, a_U, T_er, S_v	n + 3
UGMS_t	v_1...n, a_U, T_er, S_t	n + 3
UGMS_vS_t	v_1...n, a_U, T_er, S_v, S_t	n + 4
Urgency gating model with intercept (bUGM)
(Chandrasekaran et al., 2017)
bUGM	v_1...n, a_U, T_er, b	n + 3
bUGMS_v	v_1...n, a_U, T_er, b, S_v	n + 4
bUGMS_vS_t	v_1...n, a_U, T_er, b, S_v, S_t	n + 5
bUGMS_vS_b	v_1...n, a_U, T_er, b, S_v, S_b	n + 5
bUGMS_vS_bS_t	v_1...n, a_U, T_er, b, S_v, S_b, S_t	n + 6

Open in a new tab

2.1. Mathematical models of decision-making

Sequential sampling models of decision-making assume that RT comprises two components (Ratcliff and McKoon, 2008; Ratcliff et al., 2016). The first component is the decision time, which encompasses processes such as the accumulation of sensory evidence and additional decision-related factors such as urgency. The second component is the non-decision time (or residual time), which involves the time required for processes that must occur to produce a response but fall outside of the decision-formation process, such as stimulus encoding, motor preparation and motor execution time.

We introduce various models of the decision-making process in approximately increasing level of complexity, beginning with the simple DDM.

2.1.1. Simple diffusion decision model (DDM)

The diffusion decision model (or DDM) is derived from one of the oldest interpretations of a statistical test – the sequential probability ratio test (Wald and Wolfowitz, 1948) – as a model of a cognitive process – how decisions are formed over time (Stone, 1960). The DDM provides the foundation for the decision-making models implemented in ChaRTr and assumes that decision-formation is described by a one-dimensional diffusion process (Fig. 1A) with the stochastic differential equation

x (t + Δ t) = x (t) + v Δ t + s \sqrt{Δ t} N (0, 1)

(1)

where x(t) is the state of the decision-formation process, known as the decision variable, at time t; v is the rate of accumulation of sensory evidence, known as the drift rate; Δt is the step size of the process; s is the standard deviation of the moment-to-moment (Brownian) noise of the decision-formation process; $N (0, 1)$ refers to a random sample from the standard normal distribution. A response is made when x (t + Δt) ≥ a_upper or x(t + Δt) ≤ a_lower. Whether a response is correct or incorrect is determined from the boundary that was crossed and the valence of the drift rate (i.e., v > 0 implies the upper boundary corresponds to the correct response, v < 0 implies the lower boundary corresponds to the correct response). In Fig. 1A, and in all DDM models in ChaRTr, we specify a_lower = 0 and a_upper = A, without loss of generality. z represents the starting state of the evidence accumulation process (i.e., the position of the decision variable at x(0)) and can be estimated between a_lower and a_upper. When we assume there is no a priori response bias, z is fixed to the midpoint between a_lower and a_upper (i.e., A/2). The decision time is the first time step t at which the decision variable crosses one of the two decision boundaries. The predicted RT is given as a sum of the decision time and the non-decision time T_er.

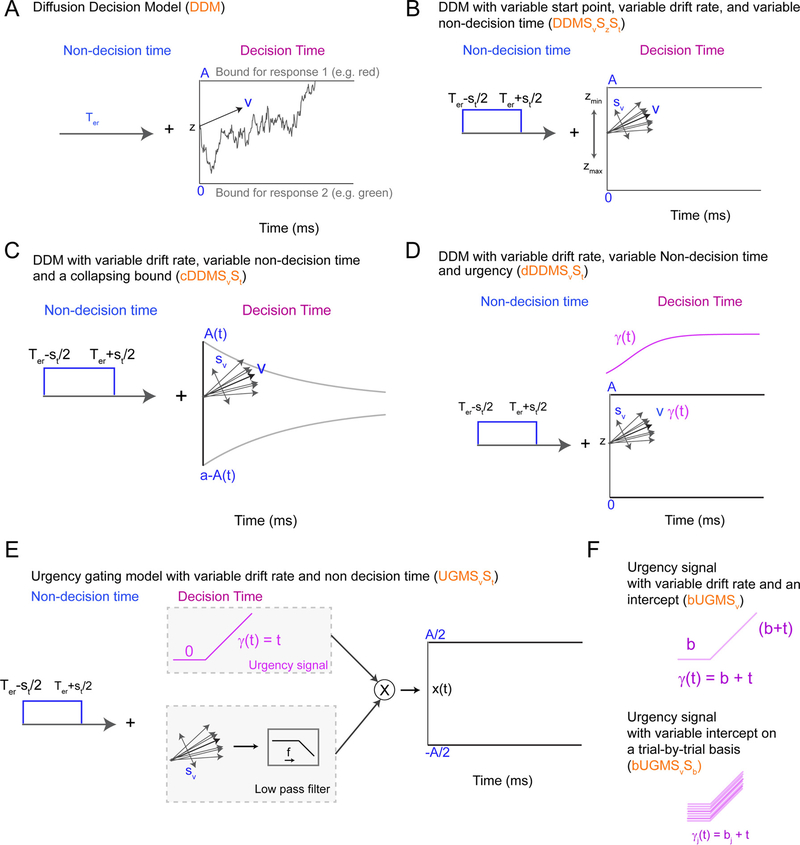
Fig. 1. — Schematic of some sequential sampling models of decision-making incorporated in *ChaRTr*. (A) The DDM model is the simplest example of a diffusion model of decision-making. (B) A variant of the DDM with variable non-decision time (S_t), variable drift-rate (S_v) and a variable start point (S_z). (C) A DDM with collapsing bounds and variability in the non-decision time and drift rate. The function A(t) takes the form of a Weibull function as defined in Eq. (6). (D) A variant of the DDM with variable non-decision time and drift rate, and an “urgency signal”. This urgency signal grows with elapsed decision time, which is implemented by multiplying the decision variable by the increasing function of time γ(t) (Eq. (10), following Ditterich, 2006a). (E) UGM with variable drift rate (S_v) and variable non decision time (S_t). In the standard UGM, the urgency signal is only thought to depend on time and thus starts at 0. The sensory evidence is passed through a low pass filter (typically a 100–250 ms time constant, Carland et al., 2015; Thura et al., 2012). The sensory evidence is then multiplied by the urgency signal to produce a decision variable that is compared to the decision boundaries. (F) Schematic of urgency signals with an intercept (top panel) and a variable intercept (bottom panel).

2.1.2. DDM with variable starting state, variable drift rate, and variable non-decision time

The (simple) DDM assumes a level of constancy from one decision to the next in various components of the decision-formation process: it always commences with the same level of response bias (z), the drift rate takes a single value (v_i, for trials in experimental condition i), and the non-decision time never varies (T_er).

None of these simplifying assumptions are likely to hold in experimental contexts. For example, the relative speed of correct and erroneous responses can differ, and participants’ arousal may exhibit random fluctuations over time, possibly due to a level of irreducible neural noise. Decades of research into decision-making models suggests that these effects, and others, are often well explained by combining systematic and random components in each of the starting state, drift rate, and non-decision time (Fig. 1B). In ChaRTr, we provide variants of the DDM where all of these parameters can be randomly drawn from their typically assumed distributions over different trials,

x_{j} (t + Δ t) = x_{j} (t) + v_{ij} Δ t + s \sqrt{Δ t} N (0, 1)

(2)

x_{j} (0) \sim U (z - \frac{s_{z}}{2}, z + \frac{s_{z}}{2})

(3)

v_{ij} \sim N (v_{i}, s_{v})

(4)

T_{er, j} \sim U (T_{er} - \frac{s_{t}}{2}, T_{er} + \frac{s_{t}}{2})

(5)

where i denotes an experimental condition; j denotes an exemplar trial; $U$ denotes the uniform distribution. ChaRTr provides flexibility to the user such that they can assume the decision-formation process involves none, some or all of these random components. Furthermore, it provides flexibility to assume distributions for the random components beyond those that have been typically assumed and studied in the literature. For example, one could hypothesize that non-decision times are exponentially distributed rather than uniformly distributed (Ratcliff, 2013).

2.1.3. DDM with collapsing decision boundaries (cDDM)

The DDM with collapsing boundaries generalizes the classic DDM by assuming that the sensory evidence required to commit to a decision is not constant as a function of elapsed decision time. Instead, it assumes that the decision boundaries gradually decrease as the decision-formation process grows longer (e.g., Bowman et al., 2012; Drugowitsch et al., 2012; Hawkins et al., 2015a; Milosavljevic et al., 2010; Tajima et al., 2016). Collapsing boundaries terminate trials with weak sensory signals (i.e., lower drift rates) at earlier time points than models with ‘fixed’ boundaries (i.e., simple DDM) and otherwise equivalent parameter settings. The net result of collapsing boundaries is a reduction in the positive skew (right tail) of the predicted RT distribution relative to the fixed boundaries DDM. This signature in the predicted RT distribution holds whether there is variability in parameters across trials (Section 2.1.2) or not (Section 2.1.1).

Collapsing boundaries allow the observer to implement a decision strategy where they do not commit an inordinate amount of time to decisions that are unlikely to be correct (i.e., decision processes with weak sensory signals). This allows the observer to sacrifice accuracy for a shorter decision time, so they can engage in new decisions that might contain stronger sensory signals and hence a higher chance of a correct response. When a sequence of decisions varies in signal-to-noise ratio from one trial to the next, like a typical difficulty manipulation in decision-making studies, collapsing boundaries are provably more optimal than fixed boundaries in the sense that they lead to greater predicted reward across the entirety of the decision sequence (Drugowitsch et al., 2012; Tajima et al., 2016). In this type of decision environment, collapsing boundaries have provided a better quantitative account of animal behavior, including monkeys, who might be motivated to obtain rewards to a greater extent than humans, possibly due to the operant conditioning and fluid/food restriction procedures used to motivate these animals (Hawkins et al., 2015a). Whether humans also aim to maximize reward via collapsing boundaries is less clear (e.g., Evans et al., 2019).

Fig. 1C shows a schematic of a collapsing boundaries model. In ChaRTr we assume the collapsing boundary follows the cumulative distribution function of the Weibull distribution, following Hawkins et al. (2015a). The Weibull function is quite flexible and can approximate many different functions that one might wish to investigate, including the exponential and hyperbolic functions. We assume the lower and upper boundaries follow the form

a_{lower} (t) = a (1 - \exp (- {(\frac{t}{λ})}^{k})) (\frac{1}{2} - a^{'})

(6)

a_{upper} (t) = a - a_{lower} (t)

(7)

where a_lower(t) and a_upper(t) denote the position of the lower and upper boundaries at time t; a denotes the position of upper boundary at t = 0 (initial boundary setting, prior to any collapse); a′ denotes the asymptotic boundary setting, or the extent to which the boundaries collapsed (the maximal possible collapse – where the upper and lower boundaries meet – can occur when a′ = 1/2); λ and k denote the scale and shape parameters of the Weibull distribution.

The collapsing boundaries are denoted in ChaRTr as cDDM. When the k parameter is fixed to a particular value to aid stronger identifiability in parameter estimation (Hawkins et al., 2015a), we refer to the architecture as cfk to denote a fixed k value (cfkDDM), here chosen to be 3 but can be modified in user implementations.

The collapsing boundaries, as implemented here, are symmetric, though they need not be; ChaRTr provides flexibility to modify all features of the boundaries, including symmetry for each response option, and the functional form. For instance, one might hypothesize that linear collapsing boundaries are a better description of the decision-formation process than nonlinear boundaries (O’Connell et al., 2018a; Murphy et al., 2016). ChaRTr also permits DDMs with collapsing boundaries to incorporate any combination of variability in starting state, drift rate, and non-decision time (e.g., models of the form cDDMS_vS_zS_t and cfkDDMS_vS_zS_t).

2.1.4. DDM with an urgency signal (uDDM)

The DDM with an urgency signal assumes that the input evidence – consisting of the sensory signal and noise – is modulated by an “urgency signal”. This urgency-modulated sensory evidence is accumulated into the decision variable throughout the decision-formation process. As the process takes longer, the urgency signal grows in magnitude, implying that sensory evidence arriving later in the decision-formation process has a more profound impact on the decision-variable than information arriving earlier (Fig. 1D). To make the distinction between an urgency signal and collapsing boundaries clear, the DDM with an urgency signal assumes a dynamically modulated input signal combined with boundaries that mirror those in the classic DDM; the DDM with collapsing boundaries assumes a decision variable that mirrors the classic DDM combined with dynamically modulated decision boundaries.

As with the collapsing boundaries, the urgency signal can take many functional forms; we have implemented two such forms in ChaRTr. The general implementation of the urgency signal is

E (t) = v Δ t + s \sqrt{Δ t} N (0, 1)

(8)

x (t + Δ t) = x (t) + E (t) γ (t)

(9)

where E(t) denotes the momentary sensory evidence at time t; γ(t) denotes the magnitude of the urgency signal at time t. Note that with increasing decision time the urgency signal magnifies the effect of the sensory signal (vΔt) and the sensory noise $(s \sqrt{Δ t} N (0, 1))$ .

The first urgency signal implemented in ChaRTr follows a 3 parameter logistic function with two scaling factors (s_x, s_y) and a delay (d), originally proposed by Ditterich (2006a, dDDM)Ditterich, 2006a,Ditterich (2006a, dDDM):

S_{1} (t) = \exp (s_{x} (t - d))

(10)

S_{2} (t) = \exp (- s_{x} d)

(11)

γ (t) = \frac{s_{y} S_{1} (t)}{1 + S_{1} (t)} + \frac{1 + (1 - s_{y}) S_{2} (t)}{1 + S_{2} (t)}

(12)

The second form of urgency signal implemented in ChaRTr follows a simple, linearly increasing function (uDDM)

γ (t) = b + mt

(13)

where b is the intercept of the urgency signal and m is the slope.

As with the DDMs described above, urgency signal models can incorporate any combination of variability in starting state, drift rate and non-decision time, giving rise to a family of different decision-making models. We also allow for the possibility of variability across decisions in the intercept term of the linear urgency signal,

γ_{j} (t) = b_{j} + mt

(14)

b_{j} \sim U (b - \frac{s_{b}}{2}, b + \frac{s_{b}}{2})

(15)

where j denotes an exemplar trial, and b and s_b denote the mean (i.e., midpoint) and range of the uniform distribution assumed for the urgency signal respectively.

In ChaRTr, we have assumed that the urgency signal exerts a multiplicative effect on the sensory evidence (Eq. (9)). One variation of urgency signal models proposed in the literature posits that urgency is added to the sensory evidence, rather than multiplied by it (Hanks et al., 2011, 2014). In the one-dimensional diffusion models considered here, additive urgency signals make predictions that cannot be discriminated from a DDM with collapsing boundaries (Boehm et al., 2016). That is, for any functional form of an additive urgency signal, there is a function for the collapsing boundaries that will generate identical predictions. For this reason we do not provide an avenue for simulating and estimating additive urgency signal models in ChaRTr, and instead recommend the use of the DDM with collapsing boundaries.

2.1.5. Urgency gating model (UGM)

In a departure from the classic DDM framework, the urgency gating model (UGM) proposes there is no integration of evidence, at least not in the same form as the DDM (Cisek et al., 2009; Thura et al., 2012; Thura and Cisek, 2014). Rather, the UGM assumes that incoming sensory evidence is low-pass filtered, which prioritizes recent over temporally distant sensory evidence, and this low-pass filtered signal is modulated by an urgency signal that increases linearly with time (Eq. (13)).

Implementation of the UGM in ChaRTr uses the exponential average approach for discrete low-pass filters (smoothing). The momentary evidence for a decision is a weighted sum of past and present evidence, which gives rise to the UGM’s pair of governing equations

α = \frac{τ}{τ + Δ t}

(16)

E (t) = α E (t - 1) + (1 - α) (v Δ t + s \sqrt{Δ t} N (0, 1))

(17)

where τ is the time constant of the low-pass filter, which has typically been set to relatively small values of 100 or 200 ms in previous applications of the UGM, and α controls the amount of evidence from previous time points that influences the momentary evidence at time t. For instance, when α = 0 there is no low-pass filtering, and when τ = 100 ms (and Δt is 1 ms) the previous evidence is weighted by 0.99 and new evidence by 0.01.

The decision variable at time t is now given as

γ (t) = b + mt

(18)

x (t) = E (t) γ (t) .

(19)

The intercept and slope of the urgency signal are set to particular values in standard applications of the UGM (b = 0, m = 1), reducing Eq. (19) to

x (t) = E (t) t .

(20)

In ChaRTr, we allow for variants of the UGM where the parameters of the urgency signal are not fixed. For instance, similar to the DDM with an urgency signal, we can test a UGM where the intercept (b) is freely estimated from data (bUGM), and even an intercept that varies on a trial-by-trial basis (Eq. (14)).

2.2. Fitting models to data

2.2.1. Parameter estimation

In ChaRTr, we estimate parameters for each model and participant independently, using Quantile Maximum Products Estimation (QMPE; Heathcote et al., 2002; Heathcote and Brown, 2004). QMPE uses the QMP statistic, which is similar to χ² or multinomial maximum likelihood estimation, and produces estimates that are asymptotically unbiased and normally distributed with asymptotically correct standard errors (Brown and Heathcote, 2003). QMPE quantifies agreement between model predictions and data by comparing the observed and predicted proportions of data falling into each of a set of inter-quantile bins. These bins are calculated separately for the correct and error RT data. In all examples that follow, we use 9 quantiles calculated from the data (i.e., split the RT data into 10 bins), though the user can specify as many quantiles as they wish. Generally speaking, we recommend no fewer than 5 quantiles, to prevent loss of distributional information, and no more than approximately 10 quantiles, to prevent noisy observations in observed data especially at the tails of the distribution potentially bearing undue influence on the parameter estimation routine.

Many of the models considered in ChaRTr have no closed-form analytic solution for their predicted distribution. To evaluate the predictions of each model, we typically simulate 10,000 Monte Carlo replicates per experimental condition during parameter estimation. Once the parameter search has terminated, we use 50,000 replicates per experimental condition to precisely evaluate the model predictions and perform model selection. In ChaRTr, the user can vary the number of replicates used for parameter estimation and model selection; in previous applications, we have found these default values provide an appropriate balance between precision of the model predictions and computational efficiency. To simulate the models, we use Euler’s method, which approximates the models’ representation as stochastic differential equations.

Alternatives to our simulation-based approach exist, such as the integral equation methods of Smith (2000) or others that use analytical techniques to calculate first passage times (Gondan et al., 2014; Navarro and Fuss, 2009), to generate exact distributions. We do not pursue those methods in ChaRTr owing to the model-specific implementation required, which is inconsistent with ChaRTr’s core philosophy of allowing the user to rapidly implement a variety of model architectures.

We estimate the model parameters using differential evolution to optimize the goodness of fit (DEoptim package in R, Mullen et al., 2011). For the type of non-linear models considered in ChaRTr, we have previously found that differential evolution more reliably recovers the true data generating model than particle swarm and simplex optimization algorithms (Hawkins et al., 2015a). DEoptim also allows easy parallelization and can be used readily in clusters and the cloud with large number of cores to speed the process of model estimation. However, we again provide flexibility in this respect; the user can change this default setting and specify their preferred optimization algorithm (s).

2.2.2. Model selection

ChaRTr provides two metrics for quantitative comparison between models. Each metric is based on the maximized value of the QMP statistic, which is a goodness-of-fit term that approximates the continuous maximum likelihood of the data given the model.

The DDM is a special case of most of the model variants considered and will almost always fit more poorly than any of the other variants. We provide model selection methods that determine if the incorporation of additional components such as urgency or collapsing bounds provide an improvement in fit that justifies the increase in model complexity.

The raw QMP statistic, as an approximation to the likelihood, can be used to calculate the Akaike Information Criterion (AIC Akaike, 1974) and the Bayesian Information Criterion (BIC; Schwarz, 1978). We provide methods to compute AIC and BIC owing to the differing assumptions underlying the two information criteria (Aho et al., 2014), and differing performance with respect to the modeling goal (Evans, 2019b).

ChaRTr also provides functionality to transform the model selection metrics into model weights, which account for uncertainty in the model selection procedure and aid interpretation by transformation to the probability scale. The weight w for model i, w(M_i), relative to a set of m models, is given by

w (M_{i}) = \frac{\exp (- \frac{1}{2} Z (M_{i}))}{\sum_{j = 1}^{m} \exp (- \frac{1}{2} Z (M_{j}))}

(21)

where Z is AIC, BIC, or the deviance (−2× log-likelihood; that is, −2× QMP statistic). The model weight is interpreted differently depending on the metric Z:

Where Z is the log-likelihood, the model weights are relative likelihoods. The log-likelihood should only be used in the model weight transformation when all models under consideration have the same number of freely estimated parameters.
Where Z is the AIC, the model weights become Akaike weights (Wagenmakers and Farrell, 2004).
Where Z is the BIC, and the prior probability over the m models under consideration is uniform (i.e., each model is assumed to be equally likely before observing the data), the model weights approximate posterior model probabilities (p(M|Data), Wasserman, 2000).

Although AIC and BIC are provided and easily computed in ChaRTr, their use for discriminating between models requires careful consideration from the researcher. Our perspective is influenced by an excellent paper that describes the worldviews for the two metrics (Aho et al., 2014). Here, we provide a succinct summary of the recommendations from Aho et al. (2014). Ultimately, whether AIC or BIC are used depends on the goals of the researcher.

If a researcher believes that all of the models implemented in ChaRTr or novel models they develop are all wrong but provide useful descriptions of choice and RT data, then AIC is more appropriate for model selection. In this scenario, the goal of model selection is to assess which model will provide the best predictions for new data. In this sense, AIC is closely linked to cross validation. As more and more data are collected, the assumption under AIC is that the model that produces the best predictions will become more and more complex.

In contrast, if a researcher believes that the true model is implemented in ChaRTr or in the set of novel models they develop, then BIC is likely to be the better tool. In this scenario, the goal of model selection is to address the question “Which of these models is correct?”. As more and more data are collected, the assumption under BIC is that the correct model will be identified. BIC is thus ideally suited to answer questions about identifying which model was most likely to have generated the data.

The only difference between AIC and BIC is the size of the penalty term correcting for model complexity. AIC considers false negatives (“Type II” errors) worse than false positives and errs on the side of selecting more complex models, and thus can be perceived as favoring “overfitting” models. In contrast, BIC is more conservative and considers false positives (“Type I” errors) worse than false negatives and errs on the side of the selecting simpler models, and thus could be perceived as favoring “underfitting” models. Both are valid perspectives and our opinion is that claiming one is better than the other is not a particularly fruitful endeavor.

Thus, our position is that both metrics have utility when a researcher applies ChaRTr to real data. Practically, we recommend using both AIC and BIC for model comparison as a method for identifying a set of likely models. We take this approach in the case studies described below, which leads us to some nuanced conclusions. Throughout this paper, and in other papers (Chandrasekaran et al., 2018), we argue that using model selection techniques such as AIC and BIC to identify a single best model might not be the best approach. Rather, we suggest researchers use these metrics judiciously to guide their analyses and ultimately new experiments.

2.2.3. Visualization: quantile probability plots

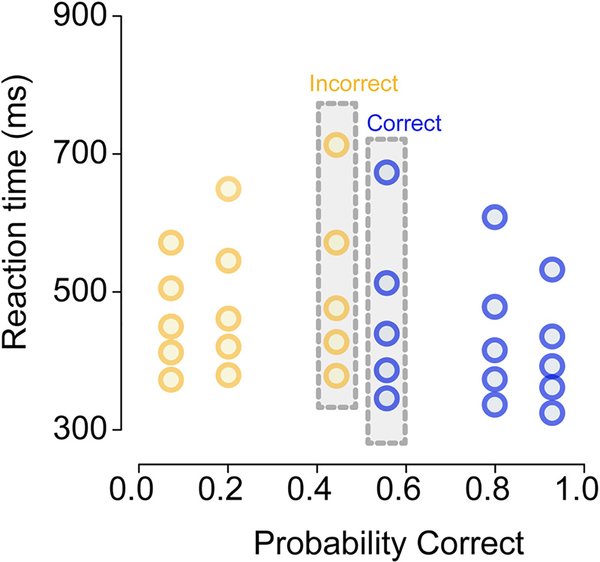
Visualization of choice and RT data is critical to understanding observed and predicted behavior. Such visualization can prove challenging in studies of rapid decision-making because each cell of the experimental design (e.g., a particular stimulus difficulty) yields a joint distribution over the probability of a correct response (accuracy) and separate RT distributions for correct and error responses. Since most decision-making tasks manipulate at least one experimental factor across multiple levels, such as stimulus difficulty, each data set is comprised of a family of joint distributions over choice probabilities and pairs of RT distributions (correct, error). Following convention and recommendation (Ratcliff et al., 2016; Ratcliff and McKoon, 2008), we visualize these joint distributions with quantile probability (QP) plots. QP plots are a compact form to display choice probabilities and RT distributions across multiple conditions.

In a typical QP plot, quantiles of the RT distribution of a particular type (e.g., correct responses) are plotted as a function of the proportion of responses of that type. Consider a hypothetical decision-making experiment with three different levels of stimulus difficulty; Fig. 2 provides a plausible example of the data from such an experiment. Now assume that for one of the experimental conditions, the accuracy of the observer was 55%. To display the choice probabilities, correct RTs and error RTs for this condition, the QP plot shows a vertical column of N markers above the x-axis position ~0.55, where the N markers correspond to the N quantiles of the RT distribution of correct responses (rightmost gray bar in Fig. 2). The QP plot also shows a vertical columns of N markers at the position 1 − 0.55 = 0.45, where this set of N markers correspond to the N quantiles of the distribution of error RTs (leftmost gray bar in Fig. 2). This means that RT distributions shown to the right of 0.5 on the x-axis reflect correct responses, and those to the left of 0.5 on the x-axis reflect error responses.

Fig. 2. — A quantile probability (QP) plot of choice and RT data from a hypothetical decision-making experiment with three levels of stimulus difficulty. The three difficulty levels are represented as vertical columns mirrored around the midpoint of the x-axis (0.5). In this example, the lowest accuracy condition had ~55% correct responses, so the RTs for correct responses in this condition are located at 0.55 on the x-axis and the corresponding RTs for error responses are located at 1 − 0.55 = 0.45 on the x-axis; these two RT distributions are highlighted in gray bars. For each RT distribution we plot along the y-axis the 10th, 30th, 50th, 70th, 90th percentiles (i.e., 0.1, 0.3, 0.5, 0.7, 0.9 quantiles), separately for correct and error responses in each of the three difficulty levels. For clarity, correct responses are shown in blue and error responses are shown in yellow. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The default ChaRTr QP plot displays 5 quantiles of the RT distribution: 0.1, 0.3, 0.5, 0.7 and 0.9 (sometimes also referred to as five percentiles: 10th, 30th, 50th, 70th, 90th). The .1 quantile summarizes the leading edge of the RT distribution, the 0.5 quantile (median) summarizes the central tendency of the RT distribution, and the 0.9 quantile summarizes the tail of the RT distribution. The goal of visualization with QP plots, or other forms of visualization, is to enable comparison of the descriptive adequacy of a model’s predictions relative to the observed data.

3. Results

The results section first provides guidance on the use of ChaRTr and how to apply the various models of the decision-making process to data. The second part of the results section illustrates the use of ChaRTr to analyze choice and RT data from hypothetical observers, followed by a case study modeling data from two non-human primates (Roitman and Shadlen, 2002). Code for the ChaRTr toolbox is available at Chartr.chandlab.org/ or directly from github at https://github.com/mailchand/ChaRTr and will eventually be released as an R library.

3.1. Toolbox flow

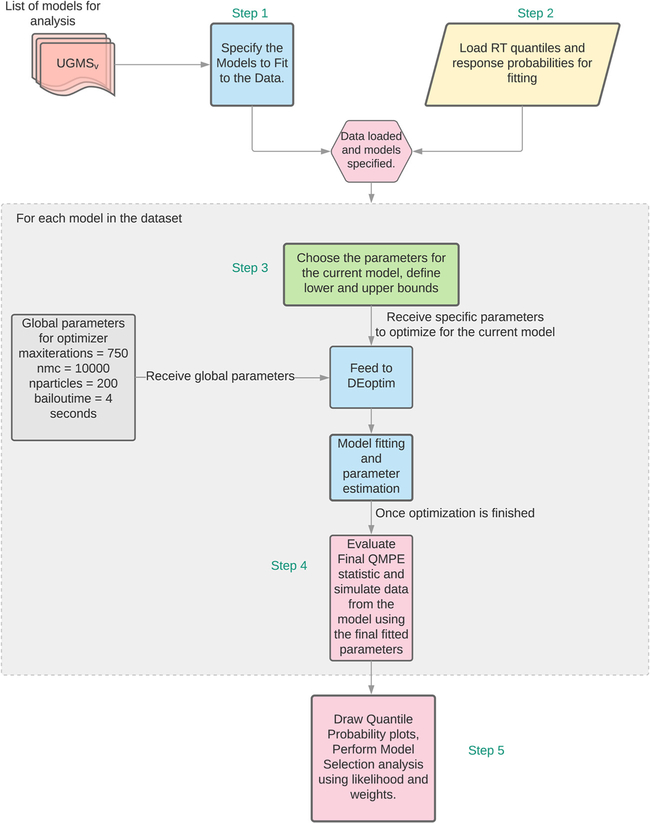
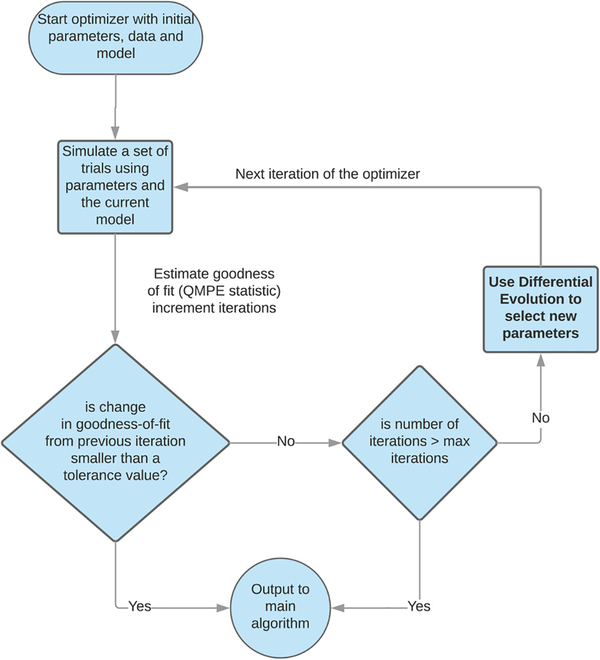
Figs. 3 and 4 provide flowcharts for ChaRTr. Fig. 3 provides an overview of the five main steps involved in the cognitive modeling process. Fig. 4 provides a schematic overview of the steps involved in the parameter estimation component of the process, which uses the differential evolution optimization algorithm (Mullen et al., 2011).

The typical steps in ChaRTr for estimating the parameters of a decision-making model from data are as follows:

Model Specification: Specify models in the C programming language, and compile the C code to create the shared object, Chartr-ModelSpec.so, that is dynamically loaded into the R workspace. Future versions of ChaRTr will use the Rcpp framework and will not require the compilation and loading of shared objects (Eddelbuettel and François, 2011).
Formatting and Loading Data: Convert raw data into an appropriate format (choice probabilities, quantiles of RT distributions for correct and error trials). Save this data object for each unit of analysis (e.g., a participant, different experimental conditions for the same participant). Load this data object into the R workspace.
Parameter Specification: Choose the parameters of the desired model that need to be estimated along with lower and upper boundaries on those parameters (i.e., the minimum and maximum value that each parameter can feasibly take).
Parameter Estimation: Pass the parameters, model and data to the optimization algorithm (differential evolution). The algorithm iteratively selects candidate parameter values and evaluates their goodness of fit to data. This process is repeated until the goodness of fit no longer improves (Fig. 4).
Model Selection: The parameter estimates from the search termination point (i.e., the point where goodness of fit no longer improves), the corresponding goodness of fit statistics and model predictions are saved for subsequent model selection and visualization.

These 5 steps are repeated for each model and each participant under consideration. In the next few sections, we elaborate on each of the steps with examples to illustrate their implementation in ChaRTr. We note that use of ChaRTr requires a basic knowledge of R programming, and if one wishes to design and test a new decision-making model then also C programming. Owing to the many excellent online resources for both languages (a simple search of “R program tutorial” will return many helpful results), we do not provide a tutorial for either language here.

3.1.1. Model specification

The difference equation for the model variants implemented in ChaRTr is specified in C code in the file “Chartr-ModelSpec.c”. An example algorithm for the DDM (Section 2.1.1) is shown in Algorithm 1. The functions take as input the various parameters that are to be optimized along with various constants such as the maximum number of time points to simulate as well as the time step.

Once the C code has been specified for the model, the code is compiled using the following command that uses the SHLIB framework (R Core Team, 2019) at the terminal (usually ITERM in mac, Terminal Emulator in linux). The command shown in Listing 1 calls the appropriate compiler (clang on mac, gcc on linux), identifies the appropriate compiler to run, and loads the appropriate libraries and ensures the correct options are applied during compilation to create the architecture-specific shared object.

Listing 1.

Creating a shared library for loading the specified models into R.

$ R CMD SHLIB chartr-ModelSpec.c

Open in a new tab

The output of the compilation is a shared object called Chartr-ModelSpec.so that is dynamically loaded into R for use with the differential evolution optimizer. We anticipate that future versions of ChaRTr will use the Rcpp framework (Eddelbuettel and François, 2011), which will obviate the need for compiling and loading shared object libraries.

3.1.2. Formatting and loading data

To estimate the parameters of decision-making models in ChaRTr, the data need to be organized in a separate comma separated values (CSV) file for each participant in a simple three column format: “condition, response, RT”. “condition” is typically a stimulus difficulty parameter, “response” is correct (1) or incorrect (0), and RT is the response time (or reaction time when response time and movement can be separated). For example, in a typical file, data for a single stimulus difficulty (e.g., one level of motion coherence in a random dot motion task) would look like Listing 2.

Listing 2.

The required raw data format for parameter estimation in ChaRTr.

condition, response, RT

90,1,0.573

90,1,0.472

90,1,0.556

.

90,0,0.406

90,0,0.429

90,0,0.57

Open in a new tab

The raw data are converted in “chartr-processRawData.r” to generate 9 quantiles (10 bins) of correct and error RTs to be used in the parameter estimation process. It also stores the data as a R list named dat, which includes four fields: n, p, q, pb.

n is the number of correct and error responses in each condition.
p is the proportion of correct responses in each condition (derived from n).
q is the quantiles of the correct and error RT distributions in each condition.
pb is the number of responses in each bin of the correct and error RT distributions in each condition (derived from n).

dat is saved to disk as a new file. The dat file is loaded into the R workspace as required for the model estimation procedure.

3.1.3. Parameter specification

The next step in model estimation is, for each model, to specify a list of parameters that can be freely estimated from data along with each parameter’s lower and upper bound; we provide default suggestions for the lower and upper boundaries in ChaRTr. Model parameters can be generated by calling the function paramsandlims with two arguments: model name and the number of stimulus difficulty levels in the experiment. The number of stimulus difficulties is internally converted into drift rate parameters; for example, if there are n stimulus difficulties, then paramsandlims will estimate n independent drift rate parameters. There is also functionality in ChaRTr to specify fixed (non-estimated) values of some parameters, such as a drift rate of 0 for conditions with non-informative sensory information (e.g., 0% coherence in a random dot motion experiment). paramsandlims returns a named list with the following fields: lowers, uppers, parnames, fitUGM. These variables are used internally in the parameter estimation routines.

3.1.4. Parameter estimation

Steps 1–3 loaded the required data, identified the desired model to fit and specified the parameters of the model to be estimated. This information is now passed to the optimization algorithm (differential evolution). Parameter optimization is an iterative process of proposing candidate parameter values, accepting or rejecting candidate parameter values based on their goodness of fit, and repeating. This process continues until the proposed parameter values no longer improve the model’s goodness of fit. These are assumed to be the best-fitting parameter values, or the (approximate) maximum likelihood estimates. Fig. 4 provides an overview of the steps involved in parameter estimation when using the differential evolution optimization algorithm (Mullen et al., 2011).

The accompanying file “Chartr-DemoFit.r” provides a complete code example for estimating the parameters of a model with urgency.

3.1.5. Model selection

Once the best-fitting parameters have been estimated from a set of candidate models, the final step is to use this information to guide inference about the relative plausibility of each of the models given the data. Many different levels of questions can be asked of these models. The best practices for model selection are described generally in Aho et al. (2014) and for the specific problem of behavioral modeling in Heathcote et al. (2015).

In ChaRTr, we provide functions for converting the raw QMP statistic that approximates the likelihood. The likelihood is a goodness-of-fit statistic that can be combined with penalized model comparison metrics. This could entail comparison between two models at multiple levels of granularity. For instance, the question could be “which of the models considered provides the better description of the data”, or “is a DDM with variable baseline better than a DDM without a variable baseline”. It could also be used to compare between a model with collapsing boundaries and a model with drift-rate variability (O’Connell et al., 2018a) or between models with different forms of collapsing boundaries (Hawkins et al., 2015a). All of these questions can be answered using ChaRTr. As a guide, we provide illustrations of model selection analyses using ChaRTr in two case studies presented in Section 3.4. We also apply the model selection analyses to the behavior of monkeys performing a decision-making task (Roitman and Shadlen, 2002).

3.2. Extending ChaRTr

ChaRTr is designed with the goal of being readily extensible, to allow the user to specify new models with minimal development time. This frees the user to focus on the models of scientific interest while ChaRTr takes care of the model estimation and selection details behind the scenes. Here, we provide an overview of the steps required to add new models to ChaRTr.

Add a new function to “Chartr-ModelSpec.c” with the parameters needed to be estimated for the model. Specify the model in C code, following the structure of the pseudo-code example given in Algorithm 1. Provide the new model with a unique name (i.e., not shared with any other models in the toolbox), preferably using the convention defined in Table 2.
Add any new parameters of the model to the function makeparamlist, and to the paramsandlims function in script “Chartr-HelperFunctions.r”.
Add the name of the model to the function returnListOfModels, in script “Chartr-HelperFunctions.r”.
Make sure additional parameters are passed to the functions diffusionC and getpreds, in scripts “ChaRTr-HelperFunctions.r” and “ChaRTr-FitRoutines.r”, respectively.
Finally, specify in function diffusionC the code for generating choices and RTs to use for model fitting. For example, the code for generating the choices and RTs for DDMS_vS_zS_t is shown in Listing 3.

Listing 3. R Code for simulating choices and RTs for the model DDMS_vS_zS_t.

3.3. Simulating data from models in ChaRTr

Once models are specified, they can be used to generate simulated RTs and discrimination accuracy for each condition. Simulated data help refine quantitative hypotheses. They also provide much greater insight into the dynamics of different decision-making models and how different variables in these models modulate the predicted RT distributions for correct and error trials (Ratcliff and McKoon, 2008).

ChaRTr provides straightforward methods to simulate data from decision-making models and generate quantile probability plots to compactly summarize and visualize RT distributions and accuracy. The function paramsandlims, used above in the parameter estimation routine, can also be used to generate hypothetical parameters to be passed to the function simulateRTs, which generates a set of simulated RTs and choice responses. By hypothetical parameters, we mean a set of reasonable starting values. An example is shown in Listing 4. These parameters can be changed by the user.

Listing 4.

R code for simulating RT and choice responses from the simple diffusion decision model (DDM).

source(“chartr-HelperFunctions.r”)

nCoh = 5

nmc = 50000

model = “DDM”

fP = paramsandlims(model, nCoh, hypoPars = TRUE)

currParams = fP$hypoParams

R= simulateRTs(model, currParams, n=nmc, nds=nCoh)

Open in a new tab

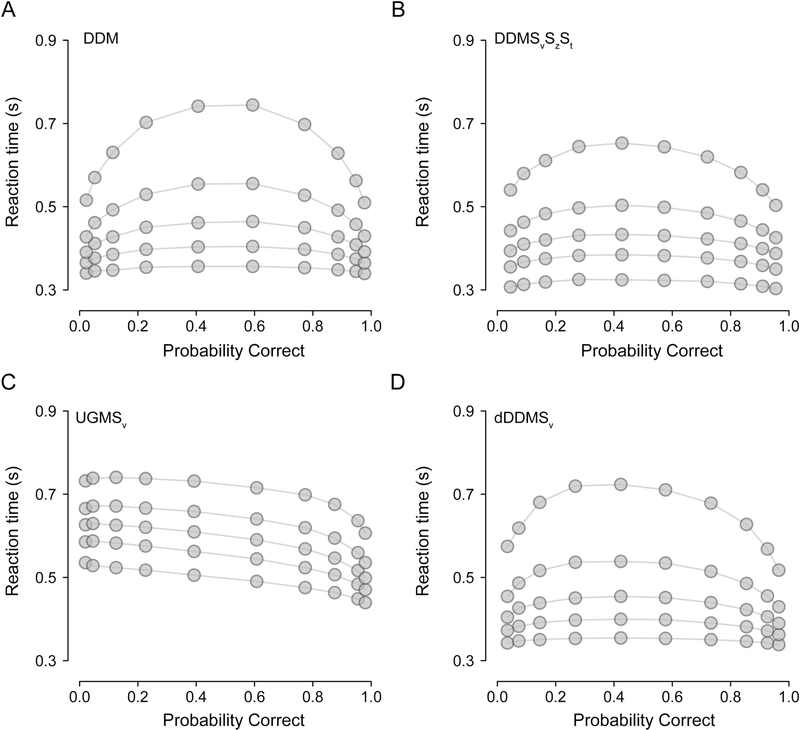
Fig. 5 shows the output of “Chartr-Demo.r”, which simulates and visualizes choice and RT data from four models in ChaRTr: DDM, DDMS_vS_zS_t, UGMS_v, and dDDMS_v. Fig. 5A shows predictions of the simple DDM (see Section 2.1.1), a symmetric, inverted-U shaped QP plot (Ratcliff and McKoon, 2008); the symmetry implies that correct and error RTs are identically distributed. As variability is introduced to the DDM’s starting state (S_z) and/or drift-rate (S_v; see Section 2.1.2), the QP plot loses its symmetry (Fig. 5B); relative to correct RTs, error RTs can be faster (due to S_z) or slower (due to S_v). Fig. 5B also introduced variability in non-decision time (S_t), which increases the variance of the fastest responses.

Fig. 5C shows predictions of a standard variant of the UGM model (UGMS_v) that assumes variable drift rate, zero intercept, a slope (β) of 1 and a time constant of 100 ms (see Section 2.1.5). The urgency gating mechanism in this model reduces the positive skew of the RT distributions, and leads to the prediction that error RTs are always slower than correct RTs (Fig. 5C; Hawkins et al., 2015b). Like the UGM, the dDDMS_v model, another model of urgency (see Section 2.1.4), also predicts reduced positive skew of the RT distributions. Unlike the standard UGM, however, it can also predict error RTs that are faster or slower than correct RTs (Fig. 5D).

It is clear from Fig. 5 that various features in data discriminate between various features of the decision-making models: the relative speed of correct and error RTs, and critically the shape of complete RT distributions. We now provide three illustrative case studies that take advantage of the differential predictions of the models, demonstrating the use of ChaRTr for parameter estimation and selection amongst sets of competing models.

3.4. Case studies

To illustrate the utility of the toolbox, we provide three case studies where we simulated data from decision-making models in ChaRTr (case studies 1 and 2) or use ChaRTr to model data collected from monkeys performing a decision-making task (case study 3). We use the case studies to demonstrate the typical model estimation and selection analyses. The case studies also provide a modest test of model and parameter recovery. That is, whether ChaRTr reliably suggests that the true data-generating model is in the set of candidate models, and whether it reliably estimates the parameters of the true data-generating model.

3.4.1. Case study 1: hypothetical data generated from a DDM with variable drift rate and non-decision time (DDMS_vS_t)

For our first case study, we assumed the data came from hypothetical observers who made decisions in a manner consistent with a DDM with variable drift rate (S_v) and variable start times (S_t). In ChaRTr, this corresponds to simulating data from the model DDMS_vS_t, where an observer’s RTs exhibit variability due to both the decision-formation process and the non-decision components. We simulated 300 trials for each of 5 stimulus difficulties, for 5 hypothetical participants.

For each model and hypothetical participant, we repeated the parameter estimation procedure 5 times, independently. We strongly recommend this redundant-estimation approach as it greatly reduces the likelihood of terminating the optimization algorithm in local minima, which can arise in simulation-based models like those implemented in ChaRTr. Variability occurs due to randomness in simulating predictions of the model at each iteration of the optimization algorithm, and randomness in the optimization algorithm itself (for a similar approach see Hawkins et al., 2015a,b). We then select the best of the 5 independent parameter estimation procedures (or ‘runs’) for each model and participant (i.e., the ‘run’ with the highest value of the QMP statistic). If computational constraints are not an issue, then we encourage as many repetitions as possible of the parameter estimation procedure.

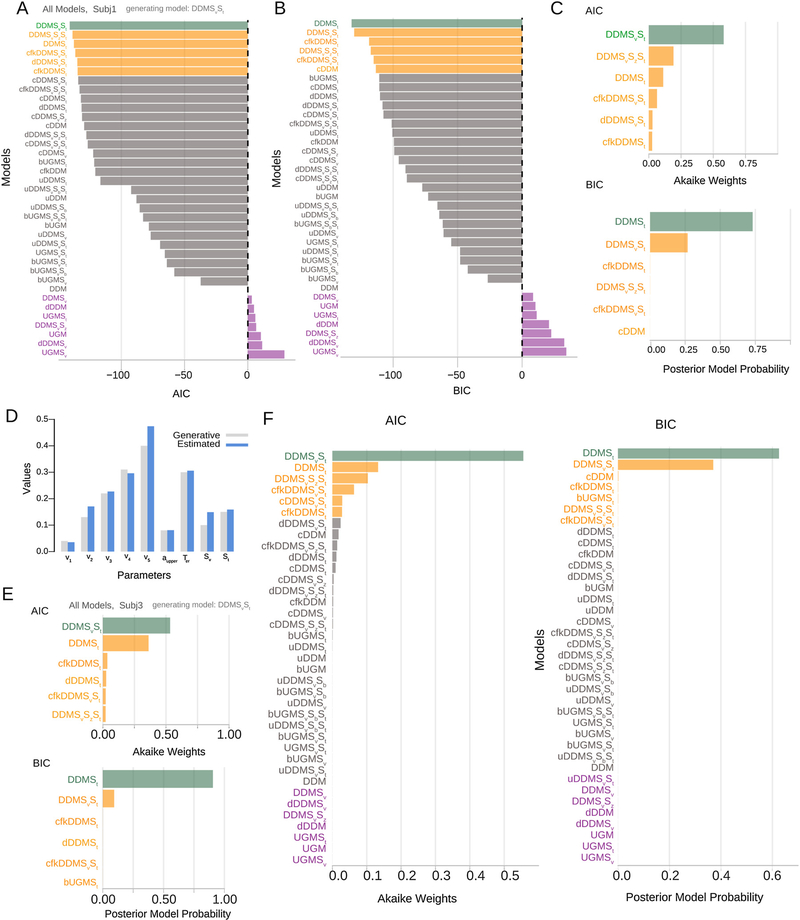
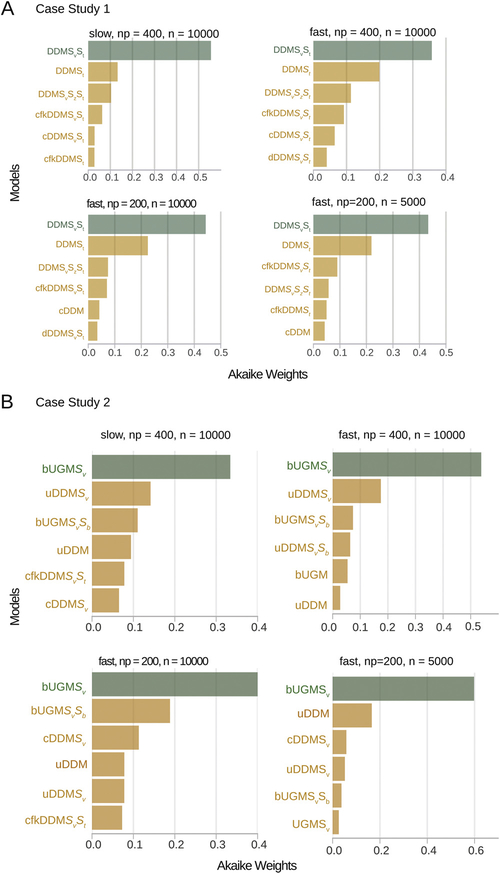
Fig. 6A and B shows the AICs and BICs for a set of models, obtained after using ChaRTr to fit the choice and RT data from one of the hypothetical observers. Both information criteria (ICs) are reported with reference to the DDM (i.e., as difference scores relative to the DDM). Thus, negative values suggest a more parsimonious account of the data than the DDM, and positive values suggest the opposite. Fig. 6C shows the Akaike weights and BIC-based approximate posterior model probabilities (Eq. (21)) for the top six models.

The AIC scores/weights suggest that DDMS_vS_t provides the best account of the data; by ‘best account’, we mean the model that provided the most appropriate tradeoff between model fit and model complexity among the specific set of models under consideration, according to AIC. This suggests that ChaRTr reliably recovers the generating model as one of the candidate models – a necessary test for any parameter estimation and model selection analysis. We strongly recommend this form of model recovery analysis when developing and testing any proposed cognitive model; if a data-generating model cannot be successfully identified as a set of candidate models in simulated data, where the true model is known, it is not a useful measurement model for real data.

The BIC scores/weights also suggest that DDMS_vS_t and DDMS_t are the best models for describing the data. However, interestingly, BIC ranks DDMS_t higher than DDMS_vS_t. This result does not suggest that ChaRTr is failing to recover the data generating model. Instead, our interpretation of the results is that both DDMS_vS_t and DDMS_t should be considered candidate explanations for the data and that they are very close in terms of explanations for the choice and response time data. That is, the most likely explanation for the data is a DDM with variable non-decision time. There might also be a contribution from drift rate variability. As we explained in the methods, AIC is more focused on false negatives and thus places a lower penalty on complexity. BIC is more focused on false positives and thus places a higher penalty on complexity.

The models ChaRTr ranked 3rd to 6th using both AIC and BIC were sensibly related to the data-generating model. These models all assumed that observed RTs were influenced by factors other than sensory evidence (such as growing impatience), which might mimic the data-generating model’s RT variability that arose due to factors external to the decision-formation process (variable non-decision time). The results serve as an important reminder that model selection should not be used to argue for the “best” model in an absolute sense. Rather, when considering the collection of the highest ranked models (e.g., models in green and orange in Fig. 6A and B) it can be most constructive to rank useful hypotheses/explanations of the data that can then guide further study (Burnham et al., 2011), which is the approach we have used here. For instance, considering this set of highly-ranked models provides strong evidence that the true decision process involves perfect information integration (as opposed to low-pass filtering of sensory evidence, as in the UGM) and includes variability in non-decision time components, which were both components of the data-generating model.

Fig. 6D shows the estimated parameter values for the DDMS_vS_t model. The parameter estimates were very similar to the data-generating values, with some minor over- or under-estimation of the drift rate parameters. This suggests that ChaRTr can reasonably recover the data-generating model and parameters. As above, we also strongly recommend this form of parameter recovery analysis when developing and testing any proposed cognitive model.

Fig. 6E shows the model selection outcomes from another hypothetical observer. When using AIC, ChaRTr again identifies the best fitting model as DDMS_vS_t and the next best model as DDMS_t. BIC again prefers DDMS_t over DDMS_vS_t. A few other models also provided good accounts of the data. As was the case for observer 1, these models predict variability in RTs due to mechanisms outside the decision-formation process.

In the three other hypothetical observers that we simulated, the pattern of results returned by ChaRTr was consistent with the results shown for the two hypothetical observers in Fig. 6: DDMS_vS_t was chosen as the best fitting model for all observers by AIC. If we assume the set of observers are independent, which is true in the case of our hypothetical example and usually in experiments, we can average the individual-participant posterior model probabilities to obtain a group-level estimate. As shown in Fig. 6F, across the set of observers DDMS_vS_t is identified as the most plausible model for the data, indicating reasonably good model recovery; the next-best models are the same as those described earlier. The results from BIC were again consistent, preferring the DDMS_t model over DDMS_vS_t for this group of hypothetical observers.

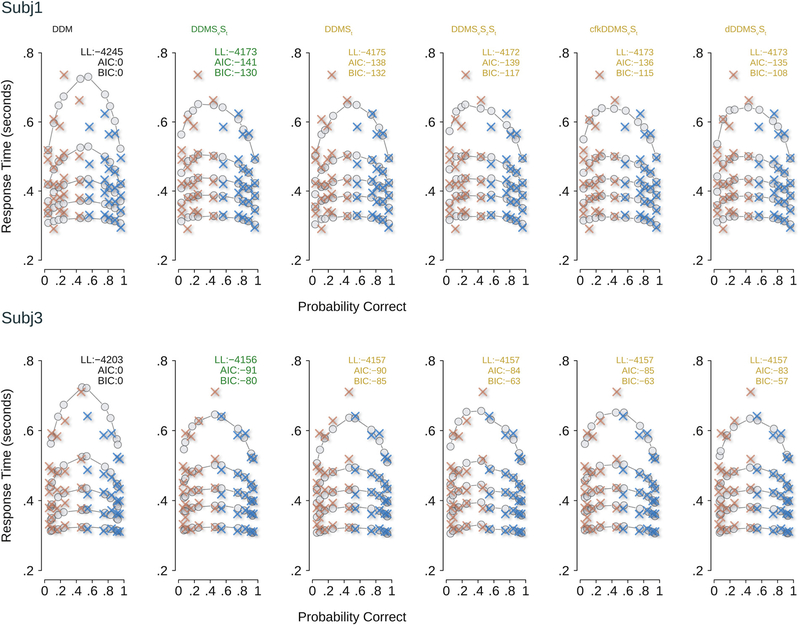
Fig. 7 shows QP plots of the data from two hypothetical observers overlaid on the predictions from a range of models. The simple DDM predicted greater variance than was observed in data, and therefore provided a poor account of the data. When the DDM is augmented with S_t and both S_v and S_t, it provided a much improved account of the data, capturing most of the RT quantiles and the accuracy patterns. Three other models provided an almost-equivalent account of the data in terms of log-likelihoods (DDMS_vS_zS_t, cfkDDMS_vS_t, dDDMS_vS_t), but they did so with the use of more model parameters than DDMS_vS_t and DDMS_t. This led to a larger complexity penalty for those models and thus larger AICs and BICs in comparison to the DDMS_vS_t model, as shown in the model selection analysis in Fig. 6.

Together, this case study highlights the power of ChaRTr in discriminating between 37 albeit overlapping models of decision-making and ranking the most likely models. As we have emphasized, the models selected by AIC and BIC will differ slightly because of the different penalties assumed for the two methods which underlie their different philosophies. If we obtained this result in real data, our interpretation would be that for this population of subjects, the data are consistent with a model that involves a DDM and variable non-decision time and that there is also the possibility of variability in the drift rate parameter. We would also conclude that the most likely models are DDMs without a dynamic component such as an urgency signal, since the DDMs performed better than models with collapsing boundaries or urgency.

3.4.2. Case study 2: hypothetical data generated from a UGM with variable intercept (bUGMS_v)

In a second case study we simulated data from hypothetical observers whose decision-formation process was controlled by an urgency gating model (Cisek et al., 2009; Thura et al., 2012) with a variable drift rate and an intercept (Chandrasekaran et al., 2017), termed bUGMS_v in ChaRTr. We again assumed five hypothetical subjects, five stimulus difficulties and simulated 500 trials for each of them. We then fit the data with the redundant-estimation approach as in case study 1 and evaluated the results of the model selection analysis, all using routines contained in ChaRTr.

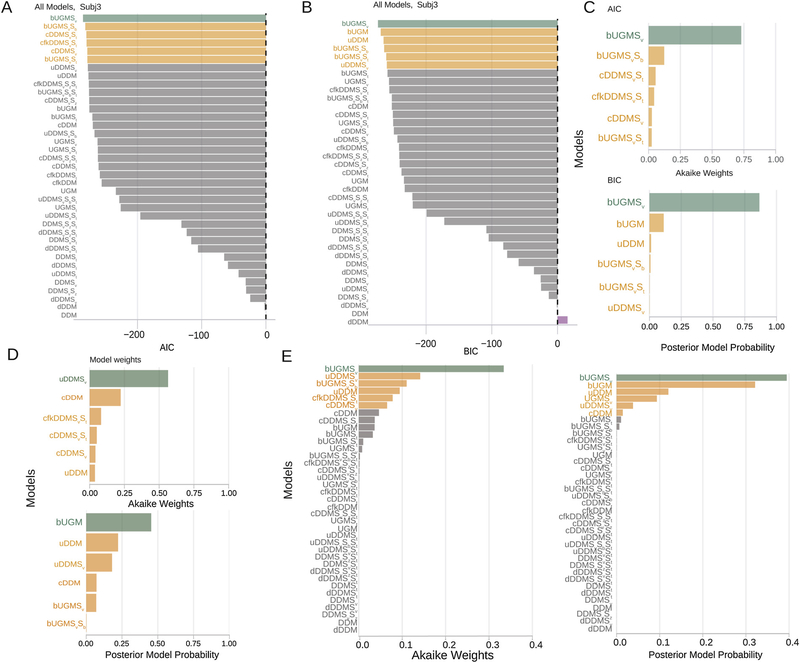
Fig. 8A and B shows the AICs and BICs for the set of models considered for one hypothetical observer’s data, again referenced to the DDM (i.e., as difference scores relative to the DDM). Negative values suggest a more parsimonious account of the data than the DDM, and positive values suggest the opposite. Fig. 8C shows the Akaike weights and posterior model probabilities for the top six models. bUGMS_v provides the best account of the data for this hypothetical observer according to both AIC and BIC.

The models ChaRTr ranked 2nd to 6th were also sensibly related to the data-generating model; they all assumed the decision-formation process was influenced by factors other than sensory evidence, such as growing impatience or other variants of the urgency gating model. The second case study reaffirms our conclusion from the first case study that model selection may not be put to best use when arguing for a single “best” model in an absolute sense. This is especially true when the data-generating model is not decisively recovered from data.

For example, Fig. 8D shows the top six models identified by ChaRTr using AIC and BIC as providing the best account of another of the hypothetical observers’ data. For this particular hypothetical dataset, many other models provided a better account than the generative model bUGMS_v. This result highlights two important points. First, some models under some circumstances can mimic each other (i.e., generate similar predictions), which makes their identification in data difficult. Second, some models may not be mimicked, but they may require very many data points to reliably recover. We note that these points are not specific to ChaRTr – they are properties of quantitative model selection in general and are an important reminder of the necessary careful steps needed when aiming to select between models (Chandrasekaran et al., 2018).

Fig. 8E shows the Akaike weights (left panel) and posterior model probabilities (right panel) for the different models averaged over all five observers considered. Reassuringly, the most plausible model across the set of observers is the generative model bUGMS_v for both AIC and BIC. For AIC, the next five best models are all conceptually related to the data generating model. For instance, the next best model was uDDMS_v which is a DDM with urgency but no gating. The third best model was bUGMS_vS_b which is an urgency gating model with variable intercept.

Similarly, when using posterior model probabilities, the most plausible model across the set of observers is the generative model bUGMS_v. Again the next five best models are all conceptually related to the data generating model. For instance, the next best model was bUGM which is an urgency gating model with an intercept and no drift rate variability. The third best model was uDDM which is a DDM with an urgency signal but no gating.

Together these results serve as another reminder of the utility of ChaRTr in the analysis of decision-making models, including the ability to quantitatively assess a large set of conceptually similar and dissimilar models. If we were to obtain results like the case study in a hypothetical experiment, we would reject a simple DDM as an explanation for our data and suggest that a model with an urgency signal containing an intercept is a more likely model to explain the data. We would also likely suggest the presence of a gating component in the data but qualify our conclusions by saying that additional subjects and larger number of trials per subject would be needed for more confidence in the result.

3.4.3. Case study 3: behavioral data from monkeys reported in Roitman and Shadlen (2002)

To demonstrate the utility of ChaRTr in understanding experimental data, we model the freely available choice and RT data from two monkeys performing a random dot motion decision-making task (Roitman and Shadlen, 2002). In this classic variant of the random-dot motion task, the monkeys were trained to report the direction of coherent motion with eye movements. The percentage of coherently moving dots was randomized from trial to trial across six levels (0%, 3.2%, 6.4%, 12.8%, 25.6% and 51.2%). Monkey b completed 2614 trials and Monkey n completed 3534 trials.

We demonstrate that ChaRTr replicates key findings from past analyses of these behavioral data. Roitman and Shadlen (2002)’s behavioral (and neural) data were originally interpreted as a neural correlate of the DDM. Later studies suggested a stronger role for impatience/urgency in these data (Ditterich, 2006a; Hawkins et al., 2015b). This is the first result we wish to reaffirm using ChaRTr. The second result we aim to reaffirm is that Hawkins et al. (2015a) showed the urgency gating model provides a better description of the data than the DDM. We note that recent work suggests the evidence for impatience/urgency in Roitman and Shadlen (2002)’s data might be the result of the particular training regime their monkeys experienced that is not shared by other monkey training protocols (Evans and Hawkins, 2019).

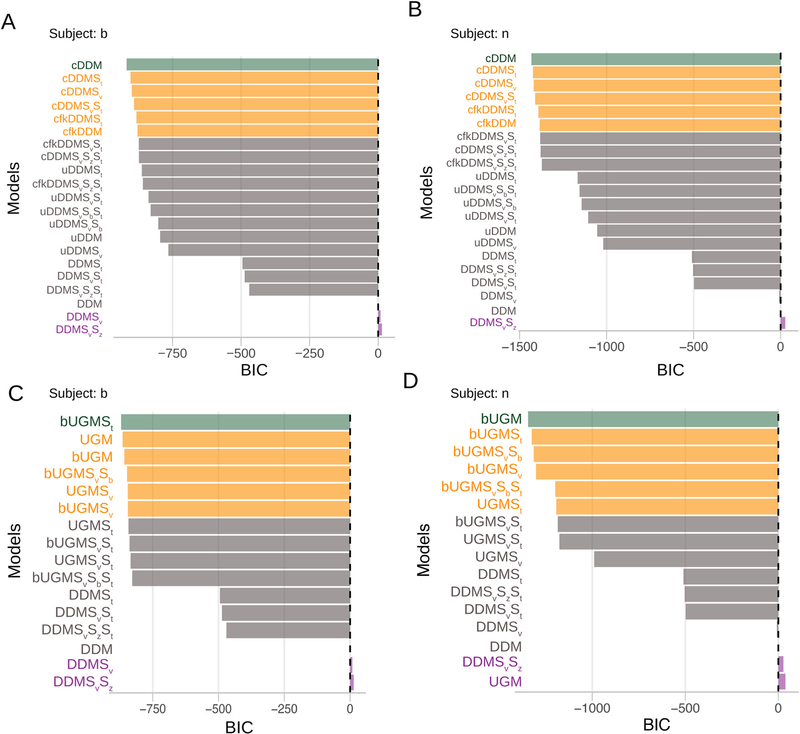
Fig. 9A and B shows the results from ChaRTr. For both monkeys, the four best-performing models all included a DDM with collapsing bounds, and the worst performing models were largely DDMs without any form of urgency. As mentioned above, for any functional form of a collapsing boundary there is a form of additive urgency signal that can generate identical predictions. So finding that collapsing bound models describe the data better is consistent with prior observations that (additive) urgency is an important factor. Together, the results are broadly consistent with those of Ditterich (2006a) and Hawkins et al. (2015b) who reported that models with forms of impatience are systematically better than models without it, for Roitman and Shadlen (2002)’s data. Fig. 9C and D shows that when the comparison is restricted to a subset of the ChaRTr models – UGMs and DDMs – variants of the UGM better explain the behavior of the monkeys than variants of the DDM, which is consistent with the findings of Hawkins et al. (2015a).

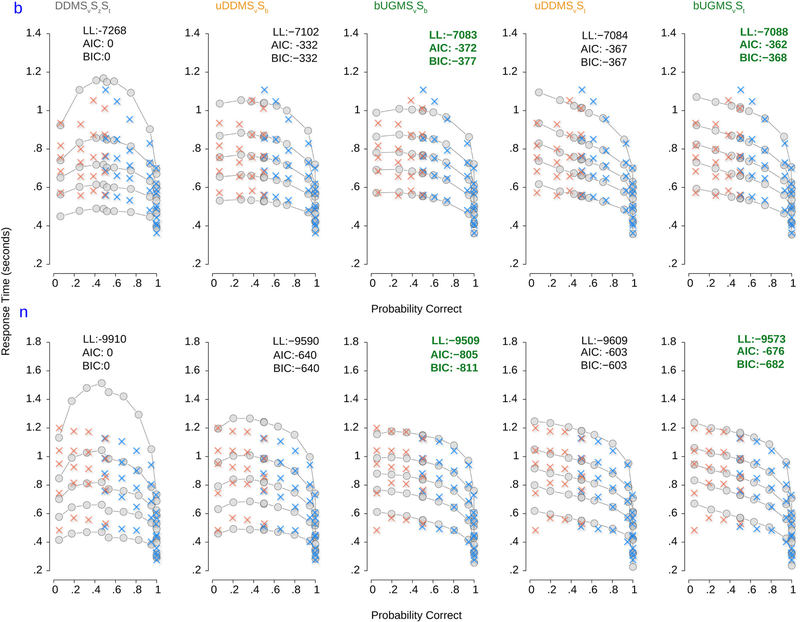
We can use ChaRTr to derive more insights into the behavior of the monkeys in this decision-making task, by examining whether urgency or the time constant of integration is a more important factor in explaining their behavior. Fig. 10 shows quantile probability plots for five models: DDMS_vS_zS_t, a model from the DDM class without urgency but elaborated with variability in various parameters (S_v, S_z, S_t), two models with urgency and variability in some parameters (uDDMS_vS_t, uDDMS_vS_b), and two UGM models with variability in parameters (bUGMS_vS_b, bUGMS_vS_t). As was shown in the model selection outcomes in Fig. 9, the addition of urgency dramatically improved the ability of the models to account for the decision-making behavior of the two monkeys.

Fig. 10. — Quantile probability (QP) plots showing data in blue (corrects) and yellow crosses (errors) for the two monkeys from Roitman and Shadlen (2002), along with the model predictions (gray dots). Predictions from DDMS_vS_zS_t are shown along with four other models uDDMS_vS_b, bUGMS_vS_b, uDDMS_vS_t, bUGMS_vS_b. Numbers at the top of each plot show the Log likelihood, the AIC and the BIC for the model under consideration. Higher, that is, more positive values of log likelihood are better. AIC and BIC are reported assuming DDMS_vS_zS_t as the base (reference) model. For both monkeys the model bUGMS_vS_b is the best model for describing the data out of these candidate set of models. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We next used ChaRTr for a preliminary analysis of whether the gating component of the urgency gating model improves model predictions over and above urgency alone. In both monkeys, we found that the data are slightly more consistent with models such as bUGMS_vS_b and bUGMS_vS_t, models that involve urgency and gating with a 100 ms time constant of integration (Fig. 10). These observations provide hypotheses for further analyses of the neural data and further targeted model selection. Together, our conclusions would be that urgency is the more important factor. However, there might be a modest role for imperfect integration as well (especially in monkey n).

Together, the results in Figs. 9 and 10 highlight the ease with which ChaRTr can be used to make insightful statements about the latent cognitive processes underlying behavior in decision-making tasks and ultimately may be a stepping stone for deeper insights into mechanism (Krakauer et al., 2017).

3.5. Performance

In this final section we discuss computational requirements for a full ChaRTr model selection analysis. Fig. 11A–C shows that the average time to estimate the set of 37 ChaRTr models for a single run for a single subject is approximately 88 h. This estimate is based on tests on a node of the Boston University Shared Computing Cluster (BU SCC, two 14 core 2.4 GHz Xeon E5–2680V4 processors, 256 GB RAM) for an implementation with 400 particles in the differential evolution optimizer, 10,000 Monte Carlo replicates per experimental condition, and un-optimized random number generators. We consider this the baseline performance of ChaRTr as it reflects the initial implementation of the code.

We also investigated factors that influenced computation time for the models. As might be expected, computation time increases as model complexity (number of parameters) increases, though this is not the sole driver of the time required for the model fitting analysis. Our parameter estimation approach (QMPE) is based on quantiles of the RT data, meaning that the size of the data set does not influence run speed. This is different to alternative estimation schemes such as maximum likelihood estimation that scales directly with the size of the data set. However, three other factors that we loosely term “hyperparameters” increase computational time in ChaRTr: the random number generators, the number of particles used in the differential evolution algorithm, and the number of Monte Carlo replicates per experimental condition (i.e., number of simulated trials). Optimizing these hyperparameters increases the speed of the model fits. Below we outline how changing these parameters improves the computational performance of ChaRTr.

In a recent study, Evans (2019a) analyzed models similar to those in ChaRTr and found that a relatively large amount of time is spent generating random numbers for simulating the models (in particular, sampling the diffusion noise on each time step of each simulated trial). In our C implementation, random number generation is performed using the norm_rand() function, and it is the most time consuming component of the simulation. To reduce the time required for random number generation, Evans (2019a) recommended replacing the norm_rand() function of the random number generation process with Lookup Tables (LUTs). We implemented the recommended LUTs and compared them to the speed of our original implementation on the same compute nodes (BU SCC, 28 core systems). Using LUTs for random number generation decreased simulation time: For the 37 models we considered, the revised implementation was performed in ~56 h (compare “slow” to “fast” in Fig. 11A–C). This is ~36% faster than the standard implementation.

Second, we considered the number of particles used to explore the parameter space in the differential evolution optimization algorithm. In general, a higher number of particles is better as it minimizes the risk of falling into local minima, though this comes at the cost of computational time. We reduced the number of particles from 400 to 200 and found that computation time again halved (Fig. 11A–C). The general rule of thumb proposed for the number of particles is 10 times the number of parameters to be estimated; 200 particles is consistent with the rule of thumb for the models implemented in ChaRTr.

Finally, a key component of the parameter estimation routine is to simulate thousands of trials for a given set of parameters (i.e., one particle for one iteration of the differential evolution algorithm) and then assess whether the simulated data are in close agreement with the observed data. The speed-up obtained when we halved the number of simulated trials from our standard of 10,000 to 5000 was ~50% (Fig. 11A–C). For these hyperparameter settings — LUT random number generation, 200 particles for the differential evolution optimizer, and 5000 trials for the simulation of the models — a full model selection analysis was performed in approximately 16 h.

One concern is that altering the hyperparameters of the estimation routine might be detrimental to model selection. This did not occur in either of our case studies involving simulated data: when using Akaike weights, the data-generating model and the next most likely models were broadly consistent even when we used LUTs for the random number generation, combined LUTs with a smaller number of particles, or combined LUTs, smaller number of particles, and smaller number of simulated trials (Fig. 12A and B). Similar results were observed with posterior model probabilities (not shown).

Fig. 12. — Optimizing computational speed is not detrimental to model selection analysis in *ChaRTr*. Akaike weights averaged over five hypothetical subjects in a model selection analysis with different settings of the random number generator, number of particles, and number of simulated trials per particle for case study 1 (A) and case study 2 (B). For both case studies, *ChaRTr* reliably identifies the correct data-generating model and in many cases agrees on the second best model for the data. We also note that the exact ranking of the models slightly differ across hyperparameter settings, but the set of identified models is consistent.

This reliability across different hyperparameter settings suggests that when large computing resources are not available, one could perform an initial fast assessment using the hyperparameter settings that provide the fastest model selection analysis to identify a candidate set of models. After that first phase, a subset of the models that performed best could be re-estimated with more conservative hyperparameter settings to refine and confirm the results of the initial assessment.

Such an approach may also be particularly important when cross validation is used instead of model selection metrics. Given the necessity to run the model fitting code many times with different random seeds to avoid local minima, even a 10 fold cross validation would lead to enormous numbers of model fitting runs. For instance for five repeats and 10 fold cross validation, it would take nearly 50 such repeats which might be very time consuming if the researcher wishes to test every single model in this process. Using the model selection metrics to pare down to the most likely set of models and then pursuing cross validation and different hyperparameter settings is likely advisable. We leave the judicious choice of these settings to the users of ChaRTr.

4. Discussion

Advances in our understanding of decision making have come from three fronts: (1) through novel experimental manipulations of sensory stimuli (Brody and Hanks, 2016; Cisek et al., 2009; Ratcliff, 2002; Ratcliff and Rouder, 2000; Smith and Ratcliff, 2009; Thura and Cisek, 2014) and/or task manipulations (Hanks et al., 2014), (2) recording neural data in a variety of decision-related structures in multiple model systems (Shadlen and Newsome, 2001; Schall, 2001; Chandrasekaran et al., 2017; Thura et al., 2014; Coallier et al., 2015; Ding and Gold, 2012a; Hanks et al., 2015), and (3) developing and testing quantitative cognitive models of choices, RTs, and other behavioral readouts from animal and human observers performing decision-making tasks (Ratcliff and Smith, 2015). Quantitative modeling is a lynchpin in generating novel insights into cognitive processes such as decision-making. However, it has posed significant technical and computational challenges to the researcher. Widespread and rapid uptake of quantitative modeling requires software toolboxes that can easily implement the many sophisticated models of decision-making proposed in the literature.

We argue that the ideal toolbox for developing and implementing cognitive process models of decision-making and evaluating them against choice and RT data should be simple to use, offer a plurality of cognitive models, provide model estimation and model selection procedures, provide simple simulation and visualization tools, and be easily extensible when new hypotheses are developed. Such a view is broadly consistent with recent research that lays out the best practices for computational modeling of behavior (Wilson and Collins, 2019; Heathcote et al., 2015). Ready adoption is also facilitated when the toolbox is implemented in an open-source, free programming language obviating the need for expensive licenses. The added benefit of an open source toolbox is that researchers can look “under the hood”, which has at least three benefits: (1) allow a deeper level of understanding of the models, (2) readily permit extension of the toolbox, and (3) catch errors in implementation. At the time of development of this toolbox and submission of this study, no existing toolbox has satisfied all of these criteria.

ChaRTr was guided by these pragmatic principles, and is our attempt to provide a practical toolbox that encompasses a range of cognitive models of decision-making. Some of the models are grounded in classic random walk and diffusion models (Ratcliff, 1978; Stone, 1960). Others incorporate modern hypotheses that decision-making behavior might involve signals such as urgency (Ditterich, 2006a), collapsing boundaries (Drugowitsch et al., 2012), and variable non-decision times (Ratcliff and Tuerlinckx, 2002). Since all of the source code is freely available, the toolbox thus provides a framework where models that are proposed into the future can also be implemented and contrasted against existing models. We provide a suite of functions for estimating the parameters of decision-making models, methods to compare log-likelihoods, and calculating penalized information criteria from these different models. Finally, the toolbox is developed in the R Statistical Environment, an open source language that is maintained by an active community of scientists and statisticians (R Core Team, 2016).

We anticipate that ChaRTr will provide a pathway to standardizing quantitative comparisons between models and across studies, and ultimately serve as one of the reference implementations for researchers interested in developing and experimentally testing candidate models of decision-making processes. ChaRTr also codifies the various parameters of decision-making models, which reflects the hypothesized latent constructs and how they interact, and provides easy access to many models of behavioral performance in decision-making tasks including variants of the diffusion decision model, the urgency gating model, diffusion models with urgency signals, and diffusion models with collapsing boundaries. ChaRTr also offers pedagogical value because it allows the user to effortlessly simulate the many different models of decision-making and generate choice and RT data from hypothetical observers. ChaRTr will also allow quantitative evaluation of the predictions of various decision-making models and help move away from qualitative intuition-based predictions from these models. Finally, ChaRTr is also sufficiently flexible that users can implement novel models with their own specific assumptions.

ChaRTr provides researchers with the resources to apply and test more than 30 different, albeit overlapping, variants of decision-making models. We have argued throughout that model selection techniques ought to be used as a tool for selecting families of models to guide the next generation of experiments and further analyses, which is in the spirit of Burnham et al. (2011); we do not believe model selection should be used to justify categorical answers (“the best model”). In this sense, model selection is one tool in the whole gamut of tools that are needed to understand decision-making (Chandrasekaran et al., 2018).

The most promising approaches for advancing our understanding of decision-making will combine the rigorous model selection techniques we advocate here with novel experimental manipulations of stimulus statistics (Brody and Hanks, 2016; Cisek et al., 2009; Evans et al., 2017; Thura et al., 2014), task contingencies (Heitz and Schall, 2012; Hanks et al., 2014; Thura and Cisek, 2016; Murphy et al., 2016), and a range of other factors. We believe that validating and advancing models of decision-making will be facilitated by data that is freely available for the kinds of model estimation and model selection analyses we have performed here. Here, we took advantage of the freely available dataset from Roitman and Shadlen (2002). We anticipate the application of ChaRTr to many more decision-making datasets will help to form a coherent picture of how various latent cognitive processes affect the behavior of animal and human decision-making. This deeper understanding of decision-making behavior (Krakauer et al., 2017) will in turn facilitate a deeper understanding of decision-related neural responses (Murphy et al., 2016; Thura et al., 2012; Cisek et al., 2009; Churchland et al., 2008; Purcell and Kiani, 2016; Chandrasekaran et al., 2017; O’Connell et al., 2018a).

Rigorous model selection techniques are even more relevant if we wish to make further inroads into understanding the neural correlates of decision-making. In particular, discriminating between multiple candidate models of decision-making is critical for neurophysiological studies of decision-making that attempt to relate neural responses in decision-related structures to the features of sequential sampling models (Ditterich, 2006a,b; Shadlen and Newsome, 2001; Gold and Shadlen, 2007; Ratcliff et al., 2003, 2007; Heitz and Schall, 2012; Hanes and Schall, 1996). For example, one of the most well-established tenets of the neural basis of decision-making is the gradual ramp-like increase in the firing rates of individual neurons in decision-related structures such as the lateral intraparietal area (Shadlen and Newsome, 2001; Roitman and Shadlen, 2002), frontal eye fields (Ding and Gold, 2012a; Hanes and Schall, 1996), superior colliculus (Ratcliff et al., 2003, 2007), prefrontal cortex (Kim and Shadlen, 1999) and dorsal premotor cortex (Chandrasekaran et al., 2017; Thura et al., 2014; Coallier et al., 2015). However, questions still remain; for example, is the ramp in a neuron’s response a signature of the evidence integration process posited by a DDM or is it more consistent with the presence of, say, an increasing urgency signal. It can be challenging to neurally discriminate between frameworks without (1) a detailed and ideally quantitative understanding of the behavior (Krakauer et al., 2017; O’Connell et al., 2018a), and (2) a clear hypothesis about the mapping from the underlying neural mechanisms to the observed behavior (Schall, 2004). We believe ChaRTr and other toolboxes of its ilk will play a critical role in further advancing our understanding of the neural correlates of decision-making.

4.1. Future directions

ChaRTr provides a powerful framework for estimating and discriminating between candidate decision-making models. Nevertheless, there is considerable scope for extending its capabilities. Here, we outline a few future directions we believe would make ChaRTr, and other toolboxes that come in its wake, even more useful for decision-making researchers.

First, ChaRTr provides options to estimate sequential sampling models that assume relative evidence is accumulated over time. A related and compelling line of research assumes a race model architecture where a choice between n options is represented as a race between n evidence accumulators. The n ≥ 2 accumulators collect evidence in favor of their respective response options as a dynamic race toward their respective thresholds. The first accumulator to reach the threshold triggers a decision for the corresponding response option. There are a range of race models that differ in details, including accumulators that are independent (e.g., Brown and Heathcote, 2008; Reddi and Carpenter, 2000) or dependent (e.g., Usher and McClelland, 2001). Naturally, these models can be elaborated with many features of the relative evidence accumulation models implemented in ChaRTr, including variable non-decision times and urgency (though see Zhang et al., 2014; Bogacz et al., 2006, for demonstration of the equivalence between relative and absolute evidence accumulation models under certain circumstances). Incorporation of race models in ChaRTr will be a useful extension into the future.

Second, the current instantiation of ChaRTr assumes that observers are independent. Recent efforts have proposed the use of hierarchical Bayesian methods for the DDM and other decision-making models (Ahn et al., 2017; Heathcote et al., 2018; Wiecki et al., 2013). Bayesian estimation methods provide at least two advantages over the current framework provided in ChaRTr. First, Bayesian methods incorporate prior knowledge into the plausible distribution of parameter values and they provide full posterior distributions for all model parameters. ChaRTr currently provides only the most likely value for a parameter without any measure of its uncertainty, whereas the full posterior distribution provides uncertainty in the estimate for each parameter, thus reducing the likelihood of drawing over-confident conclusions. Second, Bayesian methods are advantageous when used in contexts where there are only modest numbers of trials per observer. Hierarchical Bayesian models in particular can enhance statistical power by providing opportunities for simultaneous estimation of the parameters of individual observers as well as the population-level distributions from which they are drawn.

Despite these benefits, we emphasize that it is far from straightforward to extend the models implemented in ChaRTr to Bayesian parameter estimation methods. The goal of ChaRTr is simple and rapid implementation and testing of new models, which takes place via simulation-based techniques. Bayesian methods require model likelihood functions, which can be challenging to derive and may not even exist for some of the models implemented in ChaRTr, and as such the extension to Bayesian methods is not trivial. In future work, we aim to extend the parameter estimation routines in ChaRTr to make use of approximate Bayesian techniques.

Third, the framework in ChaRTr is currently only amenable for analyzing behavior from decision-making tasks where the sensory stimulus provides constant evidence over time, albeit with noise, and varies along a single dimension. However, previous research suggests that a powerful way to dissociate between different models of decision-making is to use time-varying stimuli (Brunton et al., 2013; Brody and Hanks, 2016; Cisek et al., 2009; Ratcliff, 2002; Ratcliff and Rouder, 2000; Smith and Ratcliff, 2009; Thura et al., 2014; Usher and McClelland, 2001). In a related vein, there has been increased interest in combining frameworks that posit sensory stimuli are optimally combined and could drive multisensory decision-making models (Drugowitsch et al., 2014; Chandrasekaran, 2017). Future versions of ChaRTr will provide opportunities for implementing and testing models in contexts where the sensory stimuli have temporal structure (Evans et al., 2017), or involve multi-sensory integration (Chandrasekaran, 2017; Chandrasekaran et al., 2019).

Fourth, in ChaRTr, we have largely focused on the use of model-selection metrics rather than predictive tests such as cross validation. However, cross validation is a powerful tool to guard against over-fitting and for predicting generalization performance on held out data and does not explicitly include a penalty term. If one intends to use cross validation, one could subset the data that is passed into the parameter estimation routines; say, retain 80% of the data and hold out 20% of the data. Parameter estimation would then operate on the training data as described below. Once the best-fitting parameters are identified they could be passed with the held out 20% of the data to the same functions as the training phase to calculate the out-of-sample goodness of fit. This process could then be repeated, say, 10 times, to obtain an estimate of the average out-of-sample goodness of fit. We anticipate implementing cross validation as an additional approach in future versions of ChaRTr.

Finally, ChaRTr currently allows the quality of the evidence signal (drift rate) to vary with an experimental factor (stimulus difficulty). In future versions of ChaRTr, we will provide capabilities for different model parameters to vary with different experimental factors. There are a range of other experimental manipulations whose effect will likely appear in model parameters other than the drift rate; for example, emphasizing the speed or accuracy of decisions is most likely to affect the decision boundary, or the speed with which a boundary collapses. Future versions of ChaRTr will allow researchers to test and discriminate between these hypotheses.

Acknowledgments

CC was supported by a NIH/NINDS R00 award 4R00NS092972-03. GH was supported by an Australian Research Council (ARC) Discovery Early Career Researcher Award (DECRA, award DE170100177) and an ARC Discovery Project (award DP180103613). Some of the model fits for simulated and real data were performed on the Shared Computing Cluster funded by an ONR DURIP N00014-17-1-2304 grant to Boston University. Some of the work was done under the auspices of Prof. Krishna Shenoy at Stanford University. We thank Prof. Shenoy for helpful discussions and advice, and Jessica Verhein and Megan Wang for insightful discussions.

References

Ahn WY, Haines N, Zhang L, 2017. Revealing neurocomputational mechanisms of reinforcement learning and decision-making with the hbayesdm package. Comput. Psychiatry 1, 24–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
Aho K, Derryberry D, Peterson T, 2014. Model selection for ecologists: the worldviews of AIC and BIC. Ecology 95, 631–636. [DOI] [PubMed] [Google Scholar]
Akaike H, 1974. A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723. [Google Scholar]
Boehm U, Hawkins GE, Brown S, van Rijn H, Wagenmakers EJ, 2016. Of monkeys and men: impatience in perceptual decision-making. Psychon. Bull. Rev 23, 738–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD, 2006. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced choice tasks. Psychol. Rev 113, 700–765. [DOI] [PubMed] [Google Scholar]
Bowman NE, Kording KP, Gottfried JA, 2012. Temporal integration of olfactory perceptual evidence in human orbitofrontal cortex. Neuron 75, 916–927. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brody CD, Hanks TD, 2016. Neural underpinnings of the evidence accumulator. Curr. Opin. Neurobiol 37, 149–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brown SD, Heathcote A, 2008. The simplest complete model of choice reaction time: linear ballistic accumulation. Cogn. Psychol 57, 153–178. [DOI] [PubMed] [Google Scholar]
Brown S, Heathcote A, 2003. QMLE: fast, robust, and efficient estimation of distribution functions based on quantiles. Behav. Res. Methods Instrum. Comput 35, 485–492. [DOI] [PubMed] [Google Scholar]
Brunton BW, Botvinick MM, Brody CD, 2013. Rats and humans can optimally accumulate evidence for decision-making. Science 340, 95–98. [DOI] [PubMed] [Google Scholar]
Burnham KP, Anderson DR, Huyvaert KP, 2011. AIC model selection and multi-model inference in behavioral ecology: some background, observations, and comparisons. Behav. Ecol. Sociobiol 65, 23–35. [Google Scholar]
Carland MA, Thura D, Cisek P, 2015. The urgency-gating model can explain the effects of early evidence. Psychon. Bull. Rev 22, 1830–1838. [DOI] [PubMed] [Google Scholar]
Chandrasekaran C, 2017. Computational principles and models of multisensory integration. Curr. Opin. Neurobiol 43, 25–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chandrasekaran C, Peixoto D, Newsome WT, Shenoy KV, 2017. Laminar differences in decision-related neural activity in dorsal premotor cortex. Nat. Commun 8, 614. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chandrasekaran C, Soldado-Magraner J, Peixoto D, Newsome WT, Shenoy K, Sahani M, 2018. Brittleness in model selection analysis of single neuron firing rates. bioRxiv. [Google Scholar]
Chandrasekaran C, Blurton SP, Gondan M, 2019. Audiovisual detection at different intensities and delays. J. Math. Psychol 91, 159–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
Churchland AK, Kiani R, Shadlen MN, 2008. Decision-making with multiple alternatives. Nat. Neurosci 11, 693–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cisek P, Puskas GA, El-Murr S, 2009. Decisions in changing conditions: the urgency-gating model. J. Neurosci 29, 11560–11571. [DOI] [PMC free article] [PubMed] [Google Scholar]
Coallier É, Michelet T, Kalaska JF, 2015. Dorsal premotor cortex: neural correlates of reach target decisions based on a color-location matching rule and conflicting sensory evidence. J. Neurophysiol 113, 3543–3573. [DOI] [PMC free article] [PubMed] [Google Scholar]
Diederich A, 1997. Dynamic stochastic models for decision making under time constraints. J. Math. Psychol 41, 260–274. [DOI] [PubMed] [Google Scholar]
Ding L, Gold JI, 2012a. Neural correlates of perceptual decision making before, during, and after decision commitment in monkey frontal eye field. Cereb. Cortex 22, 1052–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ding L, Gold JI, 2012b. Separate, causal roles of the caudate in saccadic choice and execution in a perceptual decision task. Neuron 75, 865–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ditterich J, 2006a. Evidence for time-variant decision making. Eur. J. Neurosci 24, 3628–3641. [DOI] [PubMed] [Google Scholar]
Ditterich J, 2006b. Stochastic models of decisions about motion direction: behavior and physiology. Neural Netw. 19, 981–1012. [DOI] [PubMed] [Google Scholar]
Donkin C, Brown SD, 2018. Response times and decision-making. Stevens’ Handb. Exp. Psychol. Cogn. Neurosci. Methodol 349. [Google Scholar]
Drugowitsch J, Moreno-Bote R, Churchland AK, Shadlen MN, Pouget A, 2012. The cost of accumulating evidence in perceptual decision making. J. Neurosci 32, 3612–3628. [DOI] [PMC free article] [PubMed] [Google Scholar]
Drugowitsch J, DeAngelis GC, Klier EM, Angelaki DE, Pouget A, 2014. Optimal multisensory decision-making in a reaction-time task. Elife 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Eddelbuettel D, François R, 2011. Rcpp: seamless R and C++ integration. J. Stat. Softw 40, 1–18. [Google Scholar]
Evans NJ, 2019a. A method, framework, and tutorial for efficiently simulating models of decision-making. Behav. Res. Methods 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
Evans NJ, 2019b. Assessing the practical differences between model selection methods in inferences about choice response time tasks. Psychon. Bull. Rev 26 (4), 1070–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
Evans NJ, Hawkins GE, 2019. When humans behave like monkeys: feedback delays and extensive practice increase the efficiency of speeded decisions. Cognition 184, 11–18. [DOI] [PubMed] [Google Scholar]
Evans NJ, Hawkins GE, Boehm U, Wagenmakers EJ, Brown SD, 2017. The computations that support simple decision-making: a comparison between the diffusion and urgency-gating models. Sci. Rep 7, 16433. [DOI] [PMC free article] [PubMed] [Google Scholar]
Evans NJ, Hawkins GE, Brown S, 2019. The role of passing time in decision-making. J. Exp. Psychol.: Learn. Mem. Cogn (in press). [DOI] [PubMed] [Google Scholar]
Forstmann BU, Ratcliff R, Wagenmakers EJ, 2016. Sequential sampling models in cognitive neuroscience: advantages, applications, and extensions. Annu. Rev. Psychol 67, 641–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
Freedman DJ, Assad JA, 2011. A proposed common neural mechanism for categorization and perceptual decisions. Nat. Neurosci. 14, 143. [DOI] [PubMed] [Google Scholar]
Gold JI, Shadlen MN, 2007. The neural basis of decision making. Annu. Rev. Neurosci 30, 535–574. [DOI] [PubMed] [Google Scholar]
Gondan M, Blurton SP, Kesselmeier M, 2014. Even faster and even more accurate first-passage time densities and distributions for the Wiener diffusion model. J. Math. Psychol 60, 20–22. [Google Scholar]
Hanes DP, Schall JD, 1996. Neural control of voluntary movement initiation. Science 274, 427–430. [DOI] [PubMed] [Google Scholar]
Hanks T, Kiani R, Shadlen MN, 2014. A neural mechanism of speed-accuracy tradeoff in macaque area LIP. Elife 3. 10.7554/eLife.02260. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hanks TD, Mazurek ME, Kiani R, Hopp E, Shadlen MN, 2011. Elapsed decision time affects the weighting of prior probability in a perceptual decision task. J. Neurosci 31, 6339–6352. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hanks TD, Kopec CD, Brunton BW, Duan CA, Erlich JC, Brody CD, 2015. Distinct relationships of parietal and prefrontal cortices to evidence accumulation. Nature 520, 220. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hawkins GE, Forstmann BU, Wagenmakers EJ, Ratcliff R, Brown SD, 2015a. Revisiting the evidence for collapsing boundaries and urgency signals in perceptual decision-making. J. Neurosci 35, 2476–2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hawkins GE, Wagenmakers EJ, Ratcliff R, Brown SD, 2015b. Discriminating evidence accumulation from urgency signals in speeded decision making. J. Neurophysiol 114, 40–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heathcote A, Brown SD, 2004. Reply to Speckman and Rouder: a theoretical basis for QML. Psychon. Bull. Rev 11, 577–578. [DOI] [PubMed] [Google Scholar]
Heathcote A, Brown SD, Mewhort DJK, 2002. Quantile maximum likelihood estimation of response time distributions. Psychon. Bull. Rev 9, 394–401. [DOI] [PubMed] [Google Scholar]
Heathcote A, Brown SD, Wagenmakers EJ, 2015. An introduction to good practices in cognitive modeling. In: Forstmann BU, Wagenmakers EJ (Eds.), An Introduction to Model-Based Cognitive Neuroscience. Springer, New York. [Google Scholar]
Heathcote A, Lin YS, Reynolds A, Strickland L, Gretton M, Matzke D, 2018. Dynamic models of choice. Behav. Res. Methods. [DOI] [PubMed] [Google Scholar]
Heitz RP, Schall JD, 2012. Neural mechanisms of speed-accuracy tradeoff. Neuron 76, 616–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hoshi E, 2013. Cortico-basal ganglia networks subserving goal-directed behavior mediated by conditional visuo-goal association. Front. Neural Circuits 7, 158. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kim JN, Shadlen MN, 1999. Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat. Neurosci 2, 176. [DOI] [PubMed] [Google Scholar]
Krakauer JW, Ghazanfar AA, Gomez-Marin A, MacIver MA, Poeppel D, 2017. Neuroscience needs behavior: correcting a reductionist bias. Neuron 93, 480–490. [DOI] [PubMed] [Google Scholar]
Luce RD, 1986. Response Times. Oxford University Press, New York. [Google Scholar]
Milosavljevic M, Malmaud J, Huth A, Koch C, Rangel A, 2010. The drift diffusion model can account for the accuracy and reactime of value-based choices under high and low time pressure. Judgment Decis. Making 5, 437–449. [Google Scholar]
Mullen K, Ardia D, Gil D, Windover D, Cline J, 2011. DEoptim: an R package for global optimization by differential evolution. J. Stat. Softw 40, 1–26. [Google Scholar]
Murphy PR, Boonstra E, Nieuwenhuis S, 2016. Global gain modulation generates time-dependent urgency during perceptual choice in humans. Nat. Commun 7, 13526. [DOI] [PMC free article] [PubMed] [Google Scholar]
Navarro DJ, Fuss IG, 2009. Fast and accurate calculations for first-passage times in wiener diffusion models. J. Math. Psychol 53, 222–230. [Google Scholar]
O’Connell RG, Shadlen MN, Wong-Lin K, Kelly SP, 2018a. Bridging neural and computational viewpoints on perceptual decision-making. Trends Neurosci. [DOI] [PMC free article] [PubMed] [Google Scholar]
O’Connell RG, Shadlen MN, Wong-Lin K, Kelly SP, 2018b. Bridging neural and computational viewpoints on perceptual decision-making. Trends Neurosci. [DOI] [PMC free article] [PubMed] [Google Scholar]
Palmer J, Huk AC, Shadlen MN, 2005. The effect of stimulus strength on the speed and accuracy of a perceptual decision. J. Vis 5, 376–404. [DOI] [PubMed] [Google Scholar]
Purcell BA, Kiani R, 2016. Neural mechanisms of post-error adjustments of decision policy in parietal cortex. Neuron 89, 658–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
R Core Team, 2016. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
R Core Team, 2019. SHLIB: Build Shared Object/dll for Dynamic Loading.
Ratcliff R, 1978. A theory of memory retrieval. Psychol. Rev 85, 59–108. [Google Scholar]
Ratcliff R, 2002. A diffusion model account of response time and accuracy in a brightness discrimination task: fitting real data and failing to fit fake but plausible data. Psychon. Bull. Rev 9, 278–291. [DOI] [PubMed] [Google Scholar]
Ratcliff R, Cherian A, Segraves M, 2003. A comparison of macaque behavior and superior colliculus neuronal activity to predictions from models of simple two-choice decisions. J. Neurophysiol 90, 1392–1407. [DOI] [PubMed] [Google Scholar]
Ratcliff R, Hasegawa YT, Hasegawa YP, Smith PL, Segraves MA, 2007. Dual diffusion model for single-cell recording data from the superior colliculus in a brightness-discrimination task. J. Neurophysiol 97, 1756–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ratcliff R, McKoon G, 2008. The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput. 20, 873–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ratcliff R, Rouder JN, 1998. Modeling response times for two-choice decisions. Psychol. Sci 9, 347–356. [Google Scholar]
Ratcliff R, Rouder JN, 2000. A diffusion model account of masking in two-choice letter identification. J. Exp. Psychol.: Human Percept. Perform. 26, 127–140. [DOI] [PubMed] [Google Scholar]
Ratcliff R, Smith P, 2015. Modeling simple decisions and applications using a diffusion model. In: Busemeyer JR, Wang Z, Townsend JT, Eidels A (Eds.), The Oxford Handbook of Computational and Mathematical Psychology. Oxford University Press, pp. 35–62. [Google Scholar]
Ratcliff R, Smith PL, Brown SD, McKoon G, 2016. Diffusion decision model: current issues and history. Trends Cogn. Sci 20, 260–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ratcliff R, Tuerlinckx F, 2002. Estimating parameters of the diffusion model: approaches to dealing with contaminant reaction times and parameter variability. Psychon. Bull. Rev 9, 438–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ratcliff R, 2013. Parameter variability and distributional assumptions in the diffusion model. Psychol. Rev 120, 281. [DOI] [PMC free article] [PubMed] [Google Scholar]
Reddi BAJ, Carpenter RHS, 2000. The influence of urgency on decision time. Nat. Neurosci 3, 827–830. [DOI] [PubMed] [Google Scholar]
Roitman JD, Shadlen MN, 2002. Responses of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci 22, 9475–9489. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schall JD, 2001. Neural basis of deciding, choosing, and acting. Nat. Rev. Neurosci 2, 33–42. [DOI] [PubMed] [Google Scholar]
Schall JD, 2004. On building a bridge between brain and behavior. Annu. Rev. Psychol 55, 23–50. [DOI] [PubMed] [Google Scholar]
Schwarz G, 1978. Estimating the dimension of a model. Ann. Stat 6, 461–464. [Google Scholar]
Scott BB, Constantinople CM, Erlich JC, Tank DW, Brody CD, 2015. Sources of noise during accumulation of evidence in unrestrained and voluntarily head-re-strained rats. Elife 4, e11308. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shadlen MN, Kiani R, 2013. Decision making as a window on cognition. Neuron 80, 791–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shadlen MN, Newsome WT, 2001. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol 86, 1916–1936. [DOI] [PubMed] [Google Scholar]
Smith PL, 2000. Stochastic dynamic models of response time and accuracy: a foundational primer. J. Math. Psychol 44, 408–463. [DOI] [PubMed] [Google Scholar]
Smith PL, Ratcliff R, 2009. An integrated theory of attention and decision making in visual signal detection. Psychol. Rev 116, 283–317. [DOI] [PubMed] [Google Scholar]
Stone M, 1960. Models for choice-reaction time. Psychometrika 25, 251–260. [Google Scholar]
Tajima S, Drugowitsch J, Pouget A, 2016. Optimal policy for value-based decision-making. Nat. Commun 7, 12400. [DOI] [PMC free article] [PubMed] [Google Scholar]
Thura D, Beauregard-Racine J, Fradet CW, Cisek P, 2012. Decision making by urgency gating: theory and experimental support. J. Neurophysiol 108, 2912–2930. [DOI] [PubMed] [Google Scholar]
Thura D, Cisek P, 2014. Deliberation and commitment in the premotor and primary motor cortex during dynamic decision making. Neuron 81, 1401–1416. [DOI] [PubMed] [Google Scholar]
Thura D, Cisek P, 2016. Modulation of premotor and primary motor cortical activity during volitional adjustments of speed-accuracy trade-offs. J. Neurosci 36, 938–956. [DOI] [PMC free article] [PubMed] [Google Scholar]
Thura D, Cos I, Trung J, Cisek P, 2014. Context-dependent urgency influences speed-accuracy trade-offs in decision-making and movement execution. J. Neurosci.: Off. J. Soc. Neurosci 34, 16442–16454. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tsunada J, Liu ASK, Gold JI, Cohen YE, 2016. Causal contribution of primate auditory cortex to auditory perceptual decision-making. Nat. Neurosci 19, 135–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
Usher M, McClelland JL, 2001. On the time course of perceptual choice: the leaky competing accumulator model. Psychol. Rev 108, 550–592. [DOI] [PubMed] [Google Scholar]
Vandekerckhove J, Tuerlinckx F, 2008. Diffusion model analysis with MATLAB: a DMAT primer. Behav. Res. Methods 40, 61–72. [DOI] [PubMed] [Google Scholar]
Voss A, Voss J, 2007. Fast-dm: a free program for efficient diffusion model analysis. Behav. Res. Methods 39, 767–775. [DOI] [PubMed] [Google Scholar]
Voss A, Voss J, Lerche V, 2015. Assessing cognitive processes with diffusion model analyses: a tutorial based on fast-dm-30. Front. Psychol 6, 336. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wagenmakers EJ, Farrell S, 2004. AIC model selection using Akaike weights. Psychon. Bull. Rev 11, 192–196. [DOI] [PubMed] [Google Scholar]
Wald A, Wolfowitz J, 1948. Optimal character of the sequential probability ratio test. Ann. Math. Stat 19, 326–339. [Google Scholar]
Wasserman L, 2000. Bayesian model selection and model averaging. J. Math. Psychol 44, 92–107. [DOI] [PubMed] [Google Scholar]
Wiecki TV, Sofer I, Frank MJ, 2013. HDDM: hierarchical Bayesian estimation of the drift-diffusion model in Python. Front. Neuroinform 7. 10.3389/fninf.2013.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wilson RC, Collins A, 2019. Ten Simple Rules for the Computational Modeling of Behavioral Data. [DOI] [PMC free article] [PubMed]
Zhang S, Lee MD, Vandekerckhove J, Maris G, Wagenmakers EJ, 2014. Time-varying boundaries for diffusion models of decision making and response time. Front. Psychol 5, 1364. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R1] Ahn WY, Haines N, Zhang L, 2017. Revealing neurocomputational mechanisms of reinforcement learning and decision-making with the hbayesdm package. Comput. Psychiatry 1, 24–57. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] Aho K, Derryberry D, Peterson T, 2014. Model selection for ecologists: the worldviews of AIC and BIC. Ecology 95, 631–636. [DOI] [PubMed] [Google Scholar]

[R3] Akaike H, 1974. A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723. [Google Scholar]

[R4] Boehm U, Hawkins GE, Brown S, van Rijn H, Wagenmakers EJ, 2016. Of monkeys and men: impatience in perceptual decision-making. Psychon. Bull. Rev 23, 738–749. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD, 2006. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced choice tasks. Psychol. Rev 113, 700–765. [DOI] [PubMed] [Google Scholar]

[R6] Bowman NE, Kording KP, Gottfried JA, 2012. Temporal integration of olfactory perceptual evidence in human orbitofrontal cortex. Neuron 75, 916–927. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] Brody CD, Hanks TD, 2016. Neural underpinnings of the evidence accumulator. Curr. Opin. Neurobiol 37, 149–157. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Brown SD, Heathcote A, 2008. The simplest complete model of choice reaction time: linear ballistic accumulation. Cogn. Psychol 57, 153–178. [DOI] [PubMed] [Google Scholar]

[R9] Brown S, Heathcote A, 2003. QMLE: fast, robust, and efficient estimation of distribution functions based on quantiles. Behav. Res. Methods Instrum. Comput 35, 485–492. [DOI] [PubMed] [Google Scholar]

[R10] Brunton BW, Botvinick MM, Brody CD, 2013. Rats and humans can optimally accumulate evidence for decision-making. Science 340, 95–98. [DOI] [PubMed] [Google Scholar]

[R11] Burnham KP, Anderson DR, Huyvaert KP, 2011. AIC model selection and multi-model inference in behavioral ecology: some background, observations, and comparisons. Behav. Ecol. Sociobiol 65, 23–35. [Google Scholar]

[R12] Carland MA, Thura D, Cisek P, 2015. The urgency-gating model can explain the effects of early evidence. Psychon. Bull. Rev 22, 1830–1838. [DOI] [PubMed] [Google Scholar]

[R13] Chandrasekaran C, 2017. Computational principles and models of multisensory integration. Curr. Opin. Neurobiol 43, 25–34. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] Chandrasekaran C, Peixoto D, Newsome WT, Shenoy KV, 2017. Laminar differences in decision-related neural activity in dorsal premotor cortex. Nat. Commun 8, 614. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] Chandrasekaran C, Soldado-Magraner J, Peixoto D, Newsome WT, Shenoy K, Sahani M, 2018. Brittleness in model selection analysis of single neuron firing rates. bioRxiv. [Google Scholar]

[R16] Chandrasekaran C, Blurton SP, Gondan M, 2019. Audiovisual detection at different intensities and delays. J. Math. Psychol 91, 159–175. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] Churchland AK, Kiani R, Shadlen MN, 2008. Decision-making with multiple alternatives. Nat. Neurosci 11, 693–702. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] Cisek P, Puskas GA, El-Murr S, 2009. Decisions in changing conditions: the urgency-gating model. J. Neurosci 29, 11560–11571. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] Coallier É, Michelet T, Kalaska JF, 2015. Dorsal premotor cortex: neural correlates of reach target decisions based on a color-location matching rule and conflicting sensory evidence. J. Neurophysiol 113, 3543–3573. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Diederich A, 1997. Dynamic stochastic models for decision making under time constraints. J. Math. Psychol 41, 260–274. [DOI] [PubMed] [Google Scholar]

[R21] Ding L, Gold JI, 2012a. Neural correlates of perceptual decision making before, during, and after decision commitment in monkey frontal eye field. Cereb. Cortex 22, 1052–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] Ding L, Gold JI, 2012b. Separate, causal roles of the caudate in saccadic choice and execution in a perceptual decision task. Neuron 75, 865–874. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] Ditterich J, 2006a. Evidence for time-variant decision making. Eur. J. Neurosci 24, 3628–3641. [DOI] [PubMed] [Google Scholar]

[R24] Ditterich J, 2006b. Stochastic models of decisions about motion direction: behavior and physiology. Neural Netw. 19, 981–1012. [DOI] [PubMed] [Google Scholar]

[R25] Donkin C, Brown SD, 2018. Response times and decision-making. Stevens’ Handb. Exp. Psychol. Cogn. Neurosci. Methodol 349. [Google Scholar]

[R26] Drugowitsch J, Moreno-Bote R, Churchland AK, Shadlen MN, Pouget A, 2012. The cost of accumulating evidence in perceptual decision making. J. Neurosci 32, 3612–3628. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] Drugowitsch J, DeAngelis GC, Klier EM, Angelaki DE, Pouget A, 2014. Optimal multisensory decision-making in a reaction-time task. Elife 3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Eddelbuettel D, François R, 2011. Rcpp: seamless R and C++ integration. J. Stat. Softw 40, 1–18. [Google Scholar]

[R29] Evans NJ, 2019a. A method, framework, and tutorial for efficiently simulating models of decision-making. Behav. Res. Methods 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] Evans NJ, 2019b. Assessing the practical differences between model selection methods in inferences about choice response time tasks. Psychon. Bull. Rev 26 (4), 1070–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] Evans NJ, Hawkins GE, 2019. When humans behave like monkeys: feedback delays and extensive practice increase the efficiency of speeded decisions. Cognition 184, 11–18. [DOI] [PubMed] [Google Scholar]

[R32] Evans NJ, Hawkins GE, Boehm U, Wagenmakers EJ, Brown SD, 2017. The computations that support simple decision-making: a comparison between the diffusion and urgency-gating models. Sci. Rep 7, 16433. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] Evans NJ, Hawkins GE, Brown S, 2019. The role of passing time in decision-making. J. Exp. Psychol.: Learn. Mem. Cogn (in press). [DOI] [PubMed] [Google Scholar]

[R34] Forstmann BU, Ratcliff R, Wagenmakers EJ, 2016. Sequential sampling models in cognitive neuroscience: advantages, applications, and extensions. Annu. Rev. Psychol 67, 641–666. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] Freedman DJ, Assad JA, 2011. A proposed common neural mechanism for categorization and perceptual decisions. Nat. Neurosci. 14, 143. [DOI] [PubMed] [Google Scholar]

[R36] Gold JI, Shadlen MN, 2007. The neural basis of decision making. Annu. Rev. Neurosci 30, 535–574. [DOI] [PubMed] [Google Scholar]

[R37] Gondan M, Blurton SP, Kesselmeier M, 2014. Even faster and even more accurate first-passage time densities and distributions for the Wiener diffusion model. J. Math. Psychol 60, 20–22. [Google Scholar]

[R38] Hanes DP, Schall JD, 1996. Neural control of voluntary movement initiation. Science 274, 427–430. [DOI] [PubMed] [Google Scholar]

[R39] Hanks T, Kiani R, Shadlen MN, 2014. A neural mechanism of speed-accuracy tradeoff in macaque area LIP. Elife 3. 10.7554/eLife.02260. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] Hanks TD, Mazurek ME, Kiani R, Hopp E, Shadlen MN, 2011. Elapsed decision time affects the weighting of prior probability in a perceptual decision task. J. Neurosci 31, 6339–6352. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] Hanks TD, Kopec CD, Brunton BW, Duan CA, Erlich JC, Brody CD, 2015. Distinct relationships of parietal and prefrontal cortices to evidence accumulation. Nature 520, 220. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Hawkins GE, Forstmann BU, Wagenmakers EJ, Ratcliff R, Brown SD, 2015a. Revisiting the evidence for collapsing boundaries and urgency signals in perceptual decision-making. J. Neurosci 35, 2476–2484. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] Hawkins GE, Wagenmakers EJ, Ratcliff R, Brown SD, 2015b. Discriminating evidence accumulation from urgency signals in speeded decision making. J. Neurophysiol 114, 40–47. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R44] Heathcote A, Brown SD, 2004. Reply to Speckman and Rouder: a theoretical basis for QML. Psychon. Bull. Rev 11, 577–578. [DOI] [PubMed] [Google Scholar]

[R45] Heathcote A, Brown SD, Mewhort DJK, 2002. Quantile maximum likelihood estimation of response time distributions. Psychon. Bull. Rev 9, 394–401. [DOI] [PubMed] [Google Scholar]

[R46] Heathcote A, Brown SD, Wagenmakers EJ, 2015. An introduction to good practices in cognitive modeling. In: Forstmann BU, Wagenmakers EJ (Eds.), An Introduction to Model-Based Cognitive Neuroscience. Springer, New York. [Google Scholar]

[R47] Heathcote A, Lin YS, Reynolds A, Strickland L, Gretton M, Matzke D, 2018. Dynamic models of choice. Behav. Res. Methods. [DOI] [PubMed] [Google Scholar]

[R48] Heitz RP, Schall JD, 2012. Neural mechanisms of speed-accuracy tradeoff. Neuron 76, 616–628. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] Hoshi E, 2013. Cortico-basal ganglia networks subserving goal-directed behavior mediated by conditional visuo-goal association. Front. Neural Circuits 7, 158. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Kim JN, Shadlen MN, 1999. Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat. Neurosci 2, 176. [DOI] [PubMed] [Google Scholar]

[R51] Krakauer JW, Ghazanfar AA, Gomez-Marin A, MacIver MA, Poeppel D, 2017. Neuroscience needs behavior: correcting a reductionist bias. Neuron 93, 480–490. [DOI] [PubMed] [Google Scholar]

[R52] Luce RD, 1986. Response Times. Oxford University Press, New York. [Google Scholar]

[R53] Milosavljevic M, Malmaud J, Huth A, Koch C, Rangel A, 2010. The drift diffusion model can account for the accuracy and reactime of value-based choices under high and low time pressure. Judgment Decis. Making 5, 437–449. [Google Scholar]

[R54] Mullen K, Ardia D, Gil D, Windover D, Cline J, 2011. DEoptim: an R package for global optimization by differential evolution. J. Stat. Softw 40, 1–26. [Google Scholar]

[R55] Murphy PR, Boonstra E, Nieuwenhuis S, 2016. Global gain modulation generates time-dependent urgency during perceptual choice in humans. Nat. Commun 7, 13526. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] Navarro DJ, Fuss IG, 2009. Fast and accurate calculations for first-passage times in wiener diffusion models. J. Math. Psychol 53, 222–230. [Google Scholar]

[R57] O’Connell RG, Shadlen MN, Wong-Lin K, Kelly SP, 2018a. Bridging neural and computational viewpoints on perceptual decision-making. Trends Neurosci. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] O’Connell RG, Shadlen MN, Wong-Lin K, Kelly SP, 2018b. Bridging neural and computational viewpoints on perceptual decision-making. Trends Neurosci. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] Palmer J, Huk AC, Shadlen MN, 2005. The effect of stimulus strength on the speed and accuracy of a perceptual decision. J. Vis 5, 376–404. [DOI] [PubMed] [Google Scholar]

[R60] Purcell BA, Kiani R, 2016. Neural mechanisms of post-error adjustments of decision policy in parietal cortex. Neuron 89, 658–671. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R61] R Core Team, 2016. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]

[R62] R Core Team, 2019. SHLIB: Build Shared Object/dll for Dynamic Loading.

[R63] Ratcliff R, 1978. A theory of memory retrieval. Psychol. Rev 85, 59–108. [Google Scholar]

[R64] Ratcliff R, 2002. A diffusion model account of response time and accuracy in a brightness discrimination task: fitting real data and failing to fit fake but plausible data. Psychon. Bull. Rev 9, 278–291. [DOI] [PubMed] [Google Scholar]

[R65] Ratcliff R, Cherian A, Segraves M, 2003. A comparison of macaque behavior and superior colliculus neuronal activity to predictions from models of simple two-choice decisions. J. Neurophysiol 90, 1392–1407. [DOI] [PubMed] [Google Scholar]

[R66] Ratcliff R, Hasegawa YT, Hasegawa YP, Smith PL, Segraves MA, 2007. Dual diffusion model for single-cell recording data from the superior colliculus in a brightness-discrimination task. J. Neurophysiol 97, 1756–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R67] Ratcliff R, McKoon G, 2008. The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput. 20, 873–922. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] Ratcliff R, Rouder JN, 1998. Modeling response times for two-choice decisions. Psychol. Sci 9, 347–356. [Google Scholar]

[R69] Ratcliff R, Rouder JN, 2000. A diffusion model account of masking in two-choice letter identification. J. Exp. Psychol.: Human Percept. Perform. 26, 127–140. [DOI] [PubMed] [Google Scholar]

[R70] Ratcliff R, Smith P, 2015. Modeling simple decisions and applications using a diffusion model. In: Busemeyer JR, Wang Z, Townsend JT, Eidels A (Eds.), The Oxford Handbook of Computational and Mathematical Psychology. Oxford University Press, pp. 35–62. [Google Scholar]

[R71] Ratcliff R, Smith PL, Brown SD, McKoon G, 2016. Diffusion decision model: current issues and history. Trends Cogn. Sci 20, 260–281. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] Ratcliff R, Tuerlinckx F, 2002. Estimating parameters of the diffusion model: approaches to dealing with contaminant reaction times and parameter variability. Psychon. Bull. Rev 9, 438–481. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] Ratcliff R, 2013. Parameter variability and distributional assumptions in the diffusion model. Psychol. Rev 120, 281. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] Reddi BAJ, Carpenter RHS, 2000. The influence of urgency on decision time. Nat. Neurosci 3, 827–830. [DOI] [PubMed] [Google Scholar]

[R75] Roitman JD, Shadlen MN, 2002. Responses of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci 22, 9475–9489. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R76] Schall JD, 2001. Neural basis of deciding, choosing, and acting. Nat. Rev. Neurosci 2, 33–42. [DOI] [PubMed] [Google Scholar]

[R77] Schall JD, 2004. On building a bridge between brain and behavior. Annu. Rev. Psychol 55, 23–50. [DOI] [PubMed] [Google Scholar]

[R78] Schwarz G, 1978. Estimating the dimension of a model. Ann. Stat 6, 461–464. [Google Scholar]

[R79] Scott BB, Constantinople CM, Erlich JC, Tank DW, Brody CD, 2015. Sources of noise during accumulation of evidence in unrestrained and voluntarily head-re-strained rats. Elife 4, e11308. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R80] Shadlen MN, Kiani R, 2013. Decision making as a window on cognition. Neuron 80, 791–806. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R81] Shadlen MN, Newsome WT, 2001. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol 86, 1916–1936. [DOI] [PubMed] [Google Scholar]

[R82] Smith PL, 2000. Stochastic dynamic models of response time and accuracy: a foundational primer. J. Math. Psychol 44, 408–463. [DOI] [PubMed] [Google Scholar]

[R83] Smith PL, Ratcliff R, 2009. An integrated theory of attention and decision making in visual signal detection. Psychol. Rev 116, 283–317. [DOI] [PubMed] [Google Scholar]

[R84] Stone M, 1960. Models for choice-reaction time. Psychometrika 25, 251–260. [Google Scholar]

[R85] Tajima S, Drugowitsch J, Pouget A, 2016. Optimal policy for value-based decision-making. Nat. Commun 7, 12400. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R86] Thura D, Beauregard-Racine J, Fradet CW, Cisek P, 2012. Decision making by urgency gating: theory and experimental support. J. Neurophysiol 108, 2912–2930. [DOI] [PubMed] [Google Scholar]

[R87] Thura D, Cisek P, 2014. Deliberation and commitment in the premotor and primary motor cortex during dynamic decision making. Neuron 81, 1401–1416. [DOI] [PubMed] [Google Scholar]

[R88] Thura D, Cisek P, 2016. Modulation of premotor and primary motor cortical activity during volitional adjustments of speed-accuracy trade-offs. J. Neurosci 36, 938–956. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R89] Thura D, Cos I, Trung J, Cisek P, 2014. Context-dependent urgency influences speed-accuracy trade-offs in decision-making and movement execution. J. Neurosci.: Off. J. Soc. Neurosci 34, 16442–16454. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R90] Tsunada J, Liu ASK, Gold JI, Cohen YE, 2016. Causal contribution of primate auditory cortex to auditory perceptual decision-making. Nat. Neurosci 19, 135–142. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R91] Usher M, McClelland JL, 2001. On the time course of perceptual choice: the leaky competing accumulator model. Psychol. Rev 108, 550–592. [DOI] [PubMed] [Google Scholar]

[R92] Vandekerckhove J, Tuerlinckx F, 2008. Diffusion model analysis with MATLAB: a DMAT primer. Behav. Res. Methods 40, 61–72. [DOI] [PubMed] [Google Scholar]

[R93] Voss A, Voss J, 2007. Fast-dm: a free program for efficient diffusion model analysis. Behav. Res. Methods 39, 767–775. [DOI] [PubMed] [Google Scholar]

[R94] Voss A, Voss J, Lerche V, 2015. Assessing cognitive processes with diffusion model analyses: a tutorial based on fast-dm-30. Front. Psychol 6, 336. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R95] Wagenmakers EJ, Farrell S, 2004. AIC model selection using Akaike weights. Psychon. Bull. Rev 11, 192–196. [DOI] [PubMed] [Google Scholar]

[R96] Wald A, Wolfowitz J, 1948. Optimal character of the sequential probability ratio test. Ann. Math. Stat 19, 326–339. [Google Scholar]

[R97] Wasserman L, 2000. Bayesian model selection and model averaging. J. Math. Psychol 44, 92–107. [DOI] [PubMed] [Google Scholar]

[R98] Wiecki TV, Sofer I, Frank MJ, 2013. HDDM: hierarchical Bayesian estimation of the drift-diffusion model in Python. Front. Neuroinform 7. 10.3389/fninf.2013.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R99] Wilson RC, Collins A, 2019. Ten Simple Rules for the Computational Modeling of Behavioral Data. [DOI] [PMC free article] [PubMed]

[R100] Zhang S, Lee MD, Vandekerckhove J, Maris G, Wagenmakers EJ, 2014. Time-varying boundaries for diffusion models of decision making and response time. Front. Psychol 5, 1364. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

ChaRTr: An R toolbox for modeling choices and response times in decision-making tasks

Chandramouli Chandrasekaran

Guy E Hawkins

Abstract

Background

New method

Results

Comparison with existing method(s)

Conclusion

1. Introduction

2. Methods and materials

Table 1.

Table 2.

2.1. Mathematical models of decision-making

2.1.1. Simple diffusion decision model (DDM)

Fig. 1.

2.1.2. DDM with variable starting state, variable drift rate, and variable non-decision time

2.1.3. DDM with collapsing decision boundaries (cDDM)

2.1.4. DDM with an urgency signal (uDDM)

2.1.5. Urgency gating model (UGM)

2.2. Fitting models to data

2.2.1. Parameter estimation

2.2.2. Model selection

2.2.3. Visualization: quantile probability plots

Fig. 2.

3. Results

3.1. Toolbox flow

Fig. 3.

Fig. 4.

3.1.1. Model specification

Listing 1.

3.1.2. Formatting and loading data

Listing 2.

3.1.3. Parameter specification

3.1.4. Parameter estimation

3.1.5. Model selection

3.2. Extending ChaRTr

3.3. Simulating data from models in ChaRTr

Listing 4.

Fig. 5.

3.4. Case studies

3.4.1. Case study 1: hypothetical data generated from a DDM with variable drift rate and non-decision time (DDMSvSt)

Fig. 6.

Fig. 7.

3.4.2. Case study 2: hypothetical data generated from a UGM with variable intercept (bUGMSv)

Fig. 8.

3.4.3. Case study 3: behavioral data from monkeys reported in Roitman and Shadlen (2002)

Fig. 9.

Fig. 10.

3.5. Performance

Fig. 11.

Fig. 12.

4. Discussion

4.1. Future directions

Acknowledgments

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

3.4.1. Case study 1: hypothetical data generated from a DDM with variable drift rate and non-decision time (DDMS_vS_t)

3.4.2. Case study 2: hypothetical data generated from a UGM with variable intercept (bUGMS_v)