Robust single-shot acquisition of high resolution whole brain ASL images by combining time-dependent 2D CAPIRINHA sampling with spatio-temporal TGV reconstruction

Abstract

For ASL perfusion imaging in clinical settings the current guidelines recommends pseudo-continuous arterial spin labeling with segmented 3D readout. This combination achieves the best signal to noise ratio with reasonable resolution but is prone to motion artifacts due to the segmented readout. Motion robust single-shot 3D acquisitions suffer from image blurring due to the T2 decay of the sampled signals during the long readout. To tackle this problem, we propose an accelerated 3D-GRASE sequence with a time-dependent 2D-CAIPIRINHA sampling pattern. This has several advantages: First, the single-shot echo trains are shortened by the acceleration factor; Second, the temporal incoherence between measurements is increased; And third, the coil sensitivity maps can be estimated directly from the averaged k-space data. To obtain improved perfusion images from the undersampled time series, we developed a variational image reconstruction approach employing spatio-temporal total-generalized-variation (TGV) regularization. The proposed ASL-TGV method reduced the total acquisition time, improved the motion robustness of 3D ASL data, and the image quality of the cerebral blood flow (CBF) maps compared to those by a standard segmented approach. An evaluation was performed on 5 healthy subjects including intentional movement for 2 subjects. Single-shot whole brain CBF-maps with high resolution3.1 × 3.1 × 3 mm and image quality can be acquired in 1min 46sec. Additionally high quality CBF- and arterial transit time (ATT) -maps from single-shot multi-post-labeling delay (PLD) data can be gained with the proposed method. This method may improve the robustness of 3D ASL in clinical settings, and may be applied for perfusion fMRI.

1. Introduction

Arterial Spin Labeling (ASL) is a non-invasive MRI technique for measuring perfusion that uses magnetically labeled blood water as an endogenous tracer (Detre et al., 1992). This technique provides the opportunity to quantify the cerebral blood flow (CBF) in absolute units which is coupled to brain metabolism and may be used as a marker of cerebrovascular diseases (Cha et al., 2013). Therefore, ASL is highly suitable for repetitive measures to trace disease progression and treatment effects especially for patients who are not suitable for contrast agent studies. However, ASL is a subtraction technique and the difference in signal intensity between control and label images is on the order of 1% (Petr et al., 2010). Therefore, the perfusion weighted image (PWI) has a low SNR. Since the introduction of ASL in 1992 (Detre et al., 1992), many different acquisition and labeling approaches have been proposed to improve the SNR and robustness of ASL images. This led to a recent consensus paper for acquiring ASL data in clinical settings from the ISMRM perfusion study group (Alsop et al., 2015). The recommended way to acquire ASL data in clinical settings is using a 3D acquisition such as turbo spin echo (TSE) stack of spirals (SoSP) (Vidorreta et al., 2013; Ye et al., 2000) or gradient and spin echo (GRASE) (Feinberg et al., 2002; Fernández-Seara et al., 2005; Günther et al., 2005) in combination with pseudo-continuous ASL (pCASL) (Dai et al., 2008). Besides the advantage of higher SNR and the incorporation of efficient background suppression (Maleki et al., 2012; Ye et al., 2000) to reduce physiological noise, 3D-acquisitions suffer from the drawback that the echo train length is much longer than the T2-relaxation of blood. This leads to strong blurring along the partition encoding direction. Different strategies were proposed to reduce the amount of blurring to a certain extent, e.g. using a variable flip angle approach (Liang et al., 2014; Zhao et al., 2018) or a retrospective deconvolution method in image space (Galazzo et al., 2014). Another more intuitive approach to reduce the echo train length and hence image blurring is to acquire the full 3D k-space in several shots or segments, as recommended by the consensus paper. However, this decreases the temporal resolution and hence increases the sensitivity to inter-segment motion, which is problematic for uncooperative subjects and patients. Improvements in motion robustness were achieved by using prospective motion correction strategies e.g. motion sensitive navigator echoes (Shao et al., 2017; Zun et al., 2014) or optical tracker systems (Aksoy et al., 2017). Besides the advantage of improved motion robustness, the drawback of a lower temporal resolution still remains, which limits its applications to perfusion based functional MRI or multi-delay ASL (Buxton et al., 1998).

Another way to improve the temporal resolution is to undersample the k-space and use parallel imaging methods such as SENSE and GRAPPA to reconstruct the images (Duhamel and Alsop, 2004; Vidorreta et al., 2017; Wang et al., 2013). However, only moderate acceleration factors of 2–3 are recommended by the consensus paper, because the SNR of the PWI is inherently low and decreases further with higher acceleration factors, due to the g-factor penalty. Recently, a 2D-CAIPIRINHA accelerated 3D-GRASE readout (Boland et al., 2018) and a 3D-accelerated TSE-SoSP readout (Chang et al., 2017) was employed for pCASL scanning with conventional reconstructions. These approaches allow the acquisition of whole brain ASL imaging with decent spatial and temporal resolutions, and provide an improvement in SNR compared to standard parallel imaging (e.g. GRAPPA) based reconstructions. This improvement in temporal resolution improves the robustness against motion. However, compared to the fully sampled acquisitions, the temporal signal to noise ratio (TSNR) is still reduced for both (accelerated 3D-GRASE and TSE-SoSP) approaches due to the g-factor penalty. As an alternative approach, we proposed a total generalized variation (TGV)-based reconstruction approach and showed improved image quality using retrospective undersampled data (Spann et al., 2018). This TGV-based reconstruction incorporated the averaging of ASL signals directly in the reconstruction of single post-labeling delay (PLD) images by using all raw data in one reconstruction process.

This study combines now CAIPIRINHA accelerated 3D-GRASE acquisition and an enhanced ASL-TGV framework allowing the reconstruction of the whole 3D time series in one compact procedure. Firstly, an accelerated 3D-GRASE sequence with a time-dependent 2D-CAIPIRINHA sampling pattern was implemented as a single-shot acquisition to improve the temporal resolution and robustness against motion. The time-dependent sampling pattern has the advantage that the temporal incoherence between control/label (C/L)-pairs is increased, and additionally allows the estimation of the coil sensitivities without an additional pre-scan. Secondly, the reconstruction algorithm was adapted to incorporate additional temporal regularization on the whole C/L-time series. The result of the reconstruction method is a 4D C/L-series which allows performing motion correction retrospectively in image space, and is capable of handling 4D ASL data. The purpose of this study is to present and evaluate the proposed acquisition and reconstruction approach by comparison with a standard segmented approach on numerical and in-vivo data.

2. Materials and methods

2.1. MRI pulse sequence

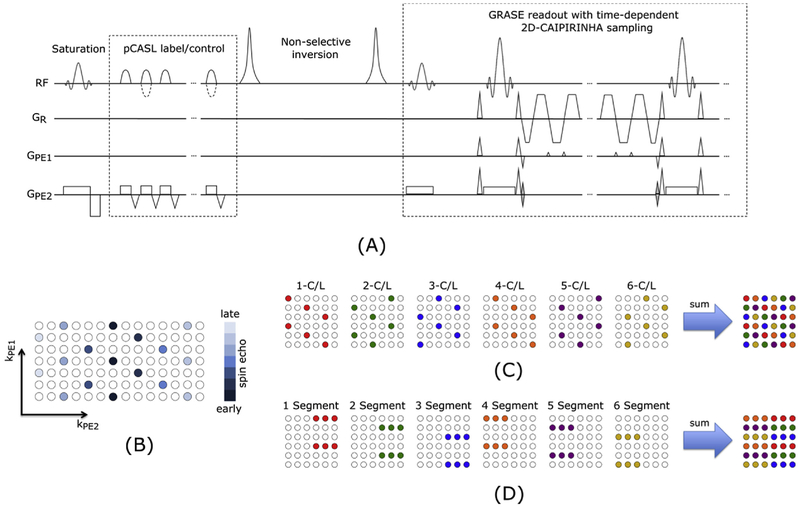
A pCASL sequence with background suppressed 3D-GRASE readout was developed and the pulse sequence diagram is shown in Fig. 1A. Background suppression was achieved by one pre-saturation pulse and two inversion pulses, and the timing for inversion pulses was optimized by numerical simulations (Shao et al., 2018). Parameters for the balanced pCASL scheme were: Hanning window-shaped RF pulse with duration of 500 μs and spacing of 360 μs, flip angle = 25°, slice-selective labeling gradient = 6 mT/m and the average labeling gradient amplitude was 0.6 mT/m (Wu et al., 2007).

Fig. 1.

(A) Sequence diagram for accelerated 3D-GRASE acquisition with variable 2D-CAIPIRINHA pattern and balanced pCASL labeling (dotted lines are modifications in control condition). The background suppression consists of a pre-saturation and 2 non-selective inversion pulses. The acquisition strategy is shown for a CAIPIRINHA 1 × 6⁽²⁾ pattern. A center out acquisition is used as illustrated in (B). For one C/L-pair the same 2D-CAIPIRINHA pattern is used. Between subsequent C/L-pairs the pattern is shifted in PE1 or PE2 direction as exemplary shown in (C). This variation increases the temporal incoherence between the C/L-pairs and additionally allows the estimation of the coil sensitivity maps directly from the summed data. Subfigure (D) shows for comparison the acquisition scheme of the fully sampled but segmented approach for the used settings.

To reduce the echo-train length of the 3D-GRASE readout 2D-CAIPI-RINHA sampling (Breuer et al., 2006) was implemented. More precisely, time-dependent 2D-CAIPIRINHA acceleration with an acceleration factor from 1 to 3 is supported along phase (PE1) and partition (PE2) directions respectively. For all acceleration factors a center out acquisition is used (Fig. 1B). The time-dependent 2D-CAIPIRINHA pattern is shifted between subsequent C/L-pairs in the PE1 and PE2 direction as exemplary shown in Fig. 1C. This shift in acquisition pattern increases the temporal incoherence between subsequent acquisitions and over time each point in k-space is sampled. Therefore, the coil sensitivity maps can be estimated directly from the averaged k-space. For comparison of the proposed 2D-CAIPIRINHA acquisition scheme the standard segmented 3D-GRASE acquisition is shown in Fig. 1D.

2.2. Reconstruction of ASL data

2.2.1. Theory

In variational MRI reconstruction the unknown image u is estimated from measured noisy data d by a regularized optimization procedure formulated in a general way as:

$$u^{*}\in \underset{u}{\text{argmin}}D(u,d)+R(u)$$ (1)

where D(u, d) represents the data-fidelity term and R(u) the regularization term. The data-fidelity term connects the measured data $d\in C^{N_{x}x{N}_{y}x{N}_{z}x{N}_{s}x{N}_t}$ with the estimated image $u\in C^{N_{x}x{N}_{y}x{N}_{z}x{N}_t}$ via a linear forward operator K. We denote by N_x x N_y x N_z the dimensions of image space, N_s the number of coils and by N_t the number of time frames. Here for the data-fidelity term, the L2-norm is an appropriate choice, due to the theoretical expectation of Gaussian noise statistics of the complex data:

$$D(u,d)=\frac{1}{2}\Vert K(u)-d{\Vert }_2^2.$$ (2)

The forward operator K includes the coil sensitivity profiles, the Fourier operator and the sampling pattern. For reconstruction of 3D-time dependent data with variable sampling pattern in the time-domain, the operator K is defined as follows:

$$K:u={\left(u_t\right)}_{\left\{t=1\dots N\right\}}\to {\left(F_t\left\{b_s{u}_t\right\}\right)}_{s,t}$$ (3)

where F_t defines the Fourier operator for each time-frame including the varying undersampling pattern over time (Schloegl et al., 2017), $b_s\in C^{N_{x}x{N}_{y}x{N}_z}$ describes the coil sensitivities for each coil s, and u_t the 3D volume at each time frame t.

The regularization term R(u) contains a-priori information about the structure of the estimated volume. Different spatio-temporal constraints exist like total variation (Rudin et al., 1992) or wavelets (Murphy et al., 2012). The choice of the regularization term is crucial and for MRI image it was shown that TGV (Bredies et al., 2010) is well suited (Knoll et al., 2011a). TGV enforces piece-wise smooth images and is defined as follows:

$$R(u)=TG{V}_{{\alpha }_1,{\alpha }_0,\beta }^2(u)$$ (4)

$$TG{V}_{{\alpha }_1,{\alpha }_0,\beta }^2(u)=\underset{v}{\text{min}}\left\{{\alpha }_1\cdot \Vert {\nabla }_{\beta }u-v{\Vert }_{1,2}+{\alpha }_0\cdot \Vert {\epsilon }_{\beta }v{\Vert }_{1,2}\right\}.$$ (5)

where ∇_βu = (β₁δ_xu, β₁δ_yu, β₁δ_zu, β₂δ_tu) and ${\epsilon }_{\beta }v=\frac{1}{2}\left({\nabla }_{\beta }v+{\left({\nabla }_{\beta }v\right)}^T\right)$ are the gradient and the symmetrized gradient respectively. In case of a spatio-temporal regularization an additional parameter $\beta =\frac{{\beta }_2}{{\beta }_1}$ is necessary to define the relation between spatial and temporal grid size as defined in (Schloegl et al., 2017).

2.2.2. Reconstruction setup

With the defined data-fidelity and regularization term in equations (2) and (5) respectively, the control volume time series can be reconstructed as follows:

$$c^{*}\in \underset{c}{\text{argmin}}\frac{{\lambda }_c}{2}\Vert Kc-d_c{\Vert }_2^2+TG{V}_{a_1,a_0,\beta }(c)$$ (6)

Since in ASL imaging always two different types of images are acquired the control and the label, the reconstruction approach for the control images formulated in equation (6) can be extended by including the label image time-series:

$$\left(c^{*},l^{*}\right)\in \underset{c,l}{\text{argmin}}\frac{{\lambda }_c}{2}\Vert Kc-d_c{\Vert }_2^2+\frac{{\lambda }_l}{2}\Vert Kl-d_l{\Vert }_2^2+TG{V}_{a_1,a_0,\beta }(l)+TG{V}_{a_1,a_0,\beta }(c)$$ (7)

However in ASL, the key quantity is the perfusion weighted image which is obtained by subtracting the label from the control image. Therefore, the goal of our reconstruction approach is to achieve a PWI with a good SNR and image quality. To this end an additional spatio-temporal constraint on the perfusion weighted image (Zhou et al., 2018) is set which results in the final minimization problem:

$$\left(c^{*},l^{*}\right)\in \underset{c,l}{\text{argmin}}\frac{{\lambda }_c}{2}\Vert Kc-d_c{\Vert }_2^2+\frac{{\lambda }_l}{2}\Vert Kl-d_l{\Vert }_2^2+{\gamma }_1(w)TG{V}_{a_1,a_0,\beta }(l)+{\gamma }_1(w)TG{V}_{a_1,a_0,\beta }(c)+{\gamma }_2(w)TG{V}_{a_1,a_0,\beta }(c-l)$$ (8)

Additionally a weight function γ (w) was introduced in the functional to balance between the TGV terms as suggested in (Schloegl et al., 2017; Spann et al., 2017),

$${\gamma }_1(\text{w})=\frac{w}{\text{min}(w,1-w)},{\gamma }_2(\text{w})=\frac{1-w}{\text{min}(w,1-w)}.$$ (9)

where ∈ (0,1).

2.2.3. Formulation as saddle-point problem

The minimization problem defined in equation (8) is non-smooth but convex and can be solved using a first-order primal-dual algorithm (Chambolle and Pock, 2011). This algorithm needs to reformulate the problem in equation (8) as a saddle point problem of the following form:

$$\underset{xy}{\text{minmax}}\langle Hx|y\rangle +G(x)-F^{*}(y)$$ (10)

This results in a simple and efficient implementation and ensures convergence to a global optimum. For details of the implementation the reader is referred to the Appendix. The proposed reconstruction method is from now on referred as “ASL-TGV” approach.

2.2.4. Implementation

The reconstruction algorithm was implemented in C++ with CUDA parallel processing using the AGILE (Knoll et al., 2011b) and AVIONIC (Schloegl et al., 2017) library. The model parameters for the TGV functional were set to $\frac{a_1}{a_0}=\frac{1}{\sqrt{3}}$ which proved to be a reasonable choice for MRI images. The number of iterations was set to 1000, and the following model parameters were used: w = 0.9 and β = 7. Despite the set of fixed model parameters, the proposed method requires the choice of the right regularization parameter λ. This parameter was set to 7/8/9/10 for 12/18/24/30 C/L-pairs and was optimized as described in section “2.6 Parameter optimization”.

2.3. Data acquisition

Five healthy volunteers (four men and one woman, age range: 28–34 years) were scanned on a 3T MR system (Prisma, Siemens Healthcare, Germany) using a 32 channel head coil and pCASL with 3D-GRASE readout after informed consent was obtained. For the standard fully sampled and segmented acquisition the following imaging parameters were used: FOV = 200 × 200 mm², matrix = 64 × 64 × 38, 20% slice oversampling, 3.1 × 3.1 × 3mm³ resolution, TE = 15 ms, TR = 4100 ms, refocusing FA = 180°, EPI-factor = 21, turbo-factor (TF) = 23, 6 segment labeling duration (LD) = 1800 ms, PLD = 1800 ms, resulting in an acquisition time of 4 min 30s for five C/L-pairs and one M₀-image. Furthermore, a 2D-CAIPIRINHA accelerated single-shot 3D-GRASE pCASL acquisition was performed with the same imaging parameters and LD/PLD as those for the segmented acquisition, but with a 6-fold acceleration using an adapted time dependent CAIPIRINHA 1 × 6⁽²⁾ pattern as shown in Fig. 1. For the accelerated acquisition, the M₀-image was acquired with a two-shot acquisition using pattern 1 and 5 as illustrated in Fig. 1. The acquisition time for the C/L-pairs between the fully sampled with segmented acquisition and the single-shot acquisition were matched to 4 min 6 s. Additionally, for the accelerated and non-accelerated acquisitions, a repeated scan was performed in 2 subjects, during which the subjects were asked to move the head in a consistent manner using acoustic cues which were presented every 4 s. The movement pattern was as follows: right - left - center followed by nodding up -nodding down - center. The movement pattern was repeated until the acquisition was finished.

One multi-delay ASL dataset was acquired using the same imaging parameters used for the single PLD data. Five PLDs were used: 500/1000/1500/2000/2500 ms. For the fully sampled acquisition 1 average per PLD was acquired and for the proposed single-shot method 6 averages per PLD were acquired within an acquisition time of 4 min 6 s.

Additionally from each subject, T1w-images were acquired using a 3D-MPRAGE sequence with the following imaging parameters: 1 mm isotropic resolution, FOV = 256 × 224 mm², 176 slices, TR/TE/TI = 1900/2.7/900 ms, flip angle = 9°, acquisition time = 5 min 58 s.

2.4. Synthetic dataset

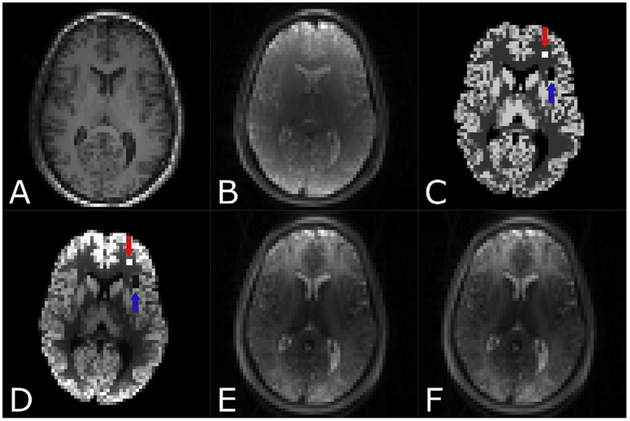
For validation of the proposed reconstruction method, a synthetic dataset was created in Matlab (MathWorks, Natick, MA, USA) based on a high resolution (1 mm isotropic) T1-weighted and an acquired fully sampled ASL dataset. In a first step, the high-resolution T1-weighted image was segmented into gray matter (GM) and white matter (WM) using Statistical Parameter Mapping (SPM)12¹ (Wellcome Trust Centre for Neuroimaging, University College London, UK) (Friston et al., 2007) and CAT12 (Gaser and Dahnke, 2016) software² (C. Gaser, Structural Brain Mapping Group, Jena University Hospital, Jena, Germany). The results of the segmentation process were tissue partial volume maps (PV-maps). The high resolution T1w-image and the GM- and WM-PV-maps were coregistered to the mean PWI as suggested by (Mutsaerts et al., 2018). Subsequently GM and WM values of 65 ml/100 g/min and 20 ml/100 g/min, reported for the normal human brain (Leenders et al., 1990; Zhang et al., 2014) were assigned to the GM and WM-PV-maps as described in (Spann et al., 2017). This leads to a more realistic CBF-map with partial volume effects and is illustrated in Fig. 2. Additionally a hyperperfusion (120 ml/100 g/min) and a hypoperfusion (0 ml/100 g/min) area which exactly match the ASL voxel space were added in the simulated CBF-map. These areas are displayed in Fig. 2. From the CBF-map a perfusion weighted image was calculated using the ASL model recommended by the consensus paper (Alsop et al., 2015):

$$CBF(x,y,z)=\frac{6000\cdot \lambda \cdot PWI(x,y,z)\cdot e^{\frac{PLD}{T{1}_b}}}{2\cdot \alpha \cdot M_0(x,y,z)\cdot T{1}_b\cdot \left(1-e^{-\frac{\tau }{T{1}_b}}\right)}$$ (11)

where α is the labeling efficiency and set to 0.85 (Dai et al., 2008), τ is the labeling duration and set to 1.800 s, PLD is set to 1.800 s (Alsop et al., 2015). M₀ is the acquired proton density weighted image, λ is the blood-brain partition coefficient and set to 0.9 ml/g (Herscovitch and Raichle, 1985), T1_b is the longitudinal relaxation time of blood at 3T and set to 1.650 s (Lu et al., 2004) and CBF(x,y,z) is the generated synthetic CBF-map. Afterwards the PWI was blurred using a Lorentzian-PSF (point spread function) by simulating the modulation transfer function (MTF) as described in (Vidorreta et al., 2017), assuming a TE of 15 ms and a T2 of blood of 186 ms (Chen and Pike, 2009). From the blurred PWI, the label (L) image was calculated by simple subtraction from the control (C) image.

Fig. 2.

Simulated ASL dataset in ASL space. (A) Co-registered T1w-image, (B) Proton-density weighted image (M0), (C) synthetic simulated noise-free CBF-map with a hyperperfusion area (120 ml/100 g/min) indicated with a red arrow and the hypoperfusion area (0 ml/100 g/min) indicated with a blue arrow, (D) PWI after blurring using a simulated modulation transfer function (MTF), (E) control image and (F) label image.

A time-series of 30 C/L-images were simulated. 3-D coil sensitivity maps, consisting of 32 coils equally spaced on a spherical surface, were computed using Biot-Savart’s law. The C/L-images were multiplied by the coil sensitivity profiles. Afterwards coil images were transformed in k-space and complex Gaussian noise was added.

2.5. Data processing

2.5.1. Structural data

For each subject the T1w images were segmented into GM and WM and coregistered to the native ASL image as described in section “2.4 Synthetic dataset”. A brain mask was generated by summing up the corresponding GM- and WM-PV-maps followed by a 3D dilation with a kernel element of size 3.

2.5.2. Raw data preprocessing of in-vivo data

The raw k-space data files were loaded into Matlab using MapVBVD³ software. Subsequent raw data preprocessing included: removing the readout-oversampling, EPI phase correction using the 3 reference line approach (Heid, 1997) and ramp sampling correction.

2.5.3. Image reconstruction and processing

In addition to the proposed reconstruction algorithm further data processing steps were performed with SPM, ASL-Toolbox (Wang, 2012; Wang et al., 2008) and Matlab. First, a coil compression was performed to reduce GPU-memory and reconstruction time using SVD with a cut-off of 0.1. Afterwards the coil sensitivity profiles were estimated from the averaged k-space data using ESPIRIT from the BART toolbox (Uecker et al., 2015). For comparison of our proposed reconstruction algorithm the ESPIRIT reconstruction with L2 regularization (ESP-L2) (Uecker et al., 2014) from the BART toolbox (Uecker et al., 2015), and additionally a single TGV reconstruction (Knoll et al., 2011a) was used, which has previously shown to outperform standard SENSE reconstruction. The single TGV reconstruction (sTGV) refers to an individual 3D reconstruction of the C and L images. The reconstructed images were motion-corrected using SPM and ASL-toolbox. Afterwards the averaged perfusion weighted image was calculated from the motion corrected time series. From this temporal averaged perfusion weighted image the CBF-maps were calculated using the recommended ASL model (equation (11)) with the parameters defined in section “2.4 Synthetic dataset”. For the multi-delay approach CBF and ATT were estimated by fitting the general kinetic model (Buxton et al., 1998) to the perfusion weighted time series using BASIL⁴ (Chappell et al., 2009; Groves et al., 2009) from the FSL (Jenkinson et al., 2012) toolbox.

2.6. Parameter optimization

The reconstruction parameters for the individual methods were optimized by maximizing the structural similarity index (SSIM) (Wang et al., 2004) between the ground-truth CBF-map and the calculated CBF-map for the simulated dataset. For the in-vivo dataset the same parameters employed for the simulated dataset were used due to the lack of noise free ground-truth.

2.7. Data evaluation

For the simulated dataset and in-vivo data a comparison between fully sampled but segmented acquisition and the proposed single-shot acquisition with different reconstruction algorithms was carried out. Additionally, for the proposed single-shot acquisition the corresponding C and L images were summed up to get a fully sampled k-space, e.g. control acquisition 1 to 6 gives the first fully sampled control k-space, control acquisition 7 to 12 the second fully sampled k-space for the control image, et cetera. This is now referred to as “accelerated sum”. For the simulated dataset the mean SSIM and peak signal to noise ratio (PSNR) were calculated between the noise free ground truth and the processed CBF-map. Furthermore, mean GM and WM CBF-values were calculated. For the single-PLD in-vivo data only mean GM and WM CBF as well as mean TSNR were reported due to the lack of noise free ground-truth. The TSNR for the reconstructed PWIs was calculated in the gray-, white-matter and whole brain respectively using equation (12). For the multi-PLD dataset mean GM and WM CBF as well as ATT were reported.

$$TSN{R}_{PWI}=\frac{\text{Mean}(PWI)}{SD(PWI)}$$ (12)

3. Results

3.1. Synthetic dataset

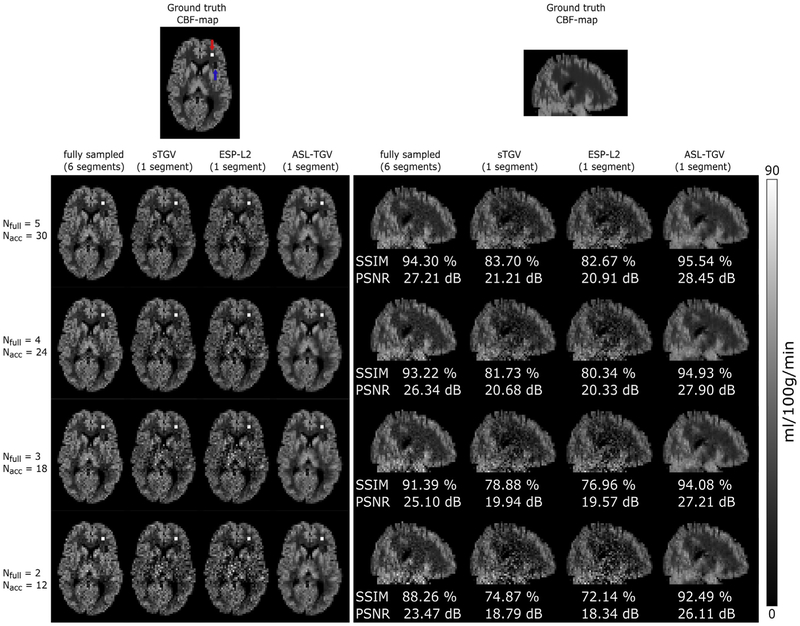
The reconstruction results of the fully sampled and accelerated synthetic dataset for a different number of C/L-pairs are shown in Fig. 3. Qualitative comparison of the CBF-maps shows a lower level of noise for the accelerated-dataset reconstructed with the proposed ASL-TGV algorithm compared to the CBF-maps generated from the fully sampled as well as from the sTGV and ESP-L2 reconstruction. Further, as expected the quality of the CBF-maps decreases with decreasing number of C/L-pairs. The proposed method yields high fidelity CBF-maps for the lowest number of 12 C/L-pairs, whereas for the sTGV and ESP-L2 method the noise is still dominant. This leads to the result that the hypoperfusion area, indicated with a blue arrow in Fig. 3, is only visible in the fully sampled as well as in the ASL-TGV images. However, the hyperperfusion area is clearly visible for all approaches due to the high SNR signal. This improvement in image quality is in accordance with the quantitative metrics of SSIM and PSNR, which were calculated over the whole brain. For 30 C/L-pairs the improvement is about 1% in SSIM and 1 dB in PSNR for the proposed method compared to the fully sampled but segmented approach, although the scan time for one PWI is reduced by a factor of 6. Furthermore, for a lower number of C/L-pairs (12) and hence a lower SNR, the improvement of the proposed method is about 4% (SSIM) and 3 dB (PSNR) compared to the fully sampled approach. In addition, the proposed method improves the SSIM by about 12% using 30 C/L-pairs and by 18% using 12 C/L-pairs, compared to the two separate reconstruction approaches (ESP-L2 and sTGV).

Fig. 3.

Transversal and sagittal view of one representative slice of CBF–map from the simulated synthetic dataset. Performance comparison of the fully sampled CBF-maps and the proposed accelerated 2D-time CAIPIRINHA acquisition using different reconstruction approaches and a different number of averages. In the transversal views the hyperperfusion (indicated with a red arrow) and hypoperfusion area (indicated with a blue arrow) are clearly visible in the segmented as well as in the CBF-maps using the proposed ASL-TGV method. The qualitative improvement in image quality and noise suppression is in concordance with the quantitative metrics SSIM and PSNR. Note that the SSIM and PSNR values in the sagittal views are calculated over the whole brain.

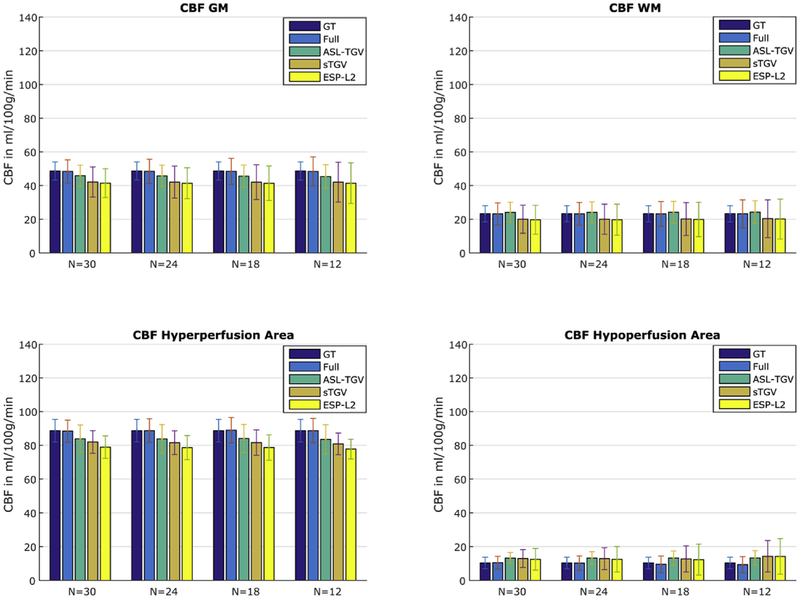
The mean CBF values for GM, WM, hyper- and hypoperfusion area are shown in Fig. 4. For all 4 methods the estimated CBF-values are close to the noise free ground truth (GT). The estimated CBF-values in the GM for fully sampled (Full), ASL-TGV, sTGV and ESP-L2 are 48.42 ± 6.9, 45.93 ± 6.2, 42.11 ± 8.9, 41.47 ± 8.6 ml/100 g/min respectively compared to the ground truth of 48.66 ± 5.4 ml/100 g/min. The ASL-TGV reconstruction approach shows a lower bias than the CBF-maps reconstructed using ESP-L2 or sTGV. As expected reducing the number of C/L-pairs increases the standard deviation due to the lower SNR but the mean values in GM and WM are still the same. The ASL-TGV has the lowest standard deviation and the increase is only slightly, from 6.2 using 30 C/L-pairs to 6.9 ml/100 g/min using 12 C/L-pairs.

Fig. 4.

Mean and standard deviation of CBF-values in four different areas of the synthetic CBF-map for the fully sampled (Full) and accelerated approach in dependence of different numbers of C/L-pairs. Note that the standard deviation in the noise free GT is due to blurring and incorporation of GM and WM values with a probability higher than 90%. Additionally, a N of 30 corresponds to 5 C/L-pairs for the fully sampled approach due to a 6-fold lower temporal resolution.

3.2. In-vivo dataset

3.2.1. Single-delay ASL data

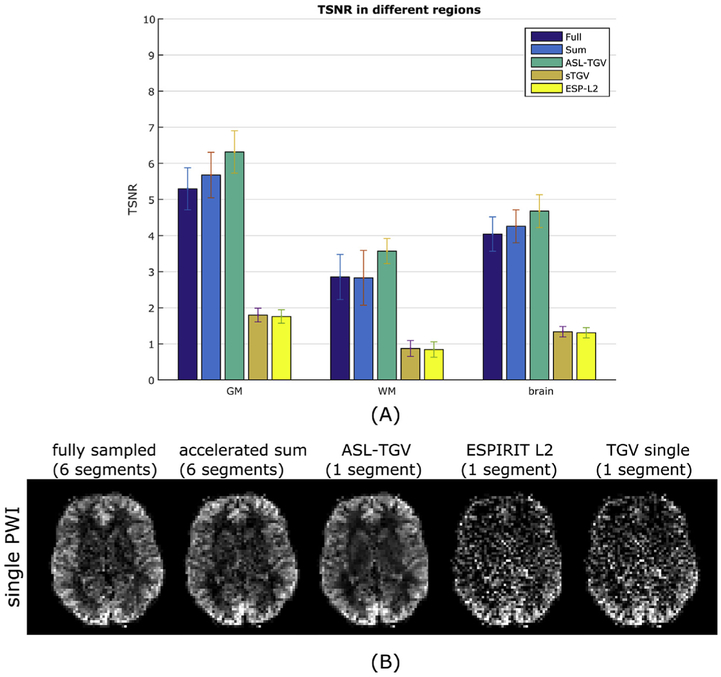
The mean TSNR_PWI values for GM, WM and whole brain averaged over all subjects shows an improvement of roughly 20%, 25% and 16% respectively for the accelerated ASL-TGV reconstruction results compared to the fully sampled but segmented approach. In comparison the standard single TGV reconstruction approach shows a TSNR decrease of 66% for GM, 69% for WM and 67% for the whole brain compared to the fully sampled data.

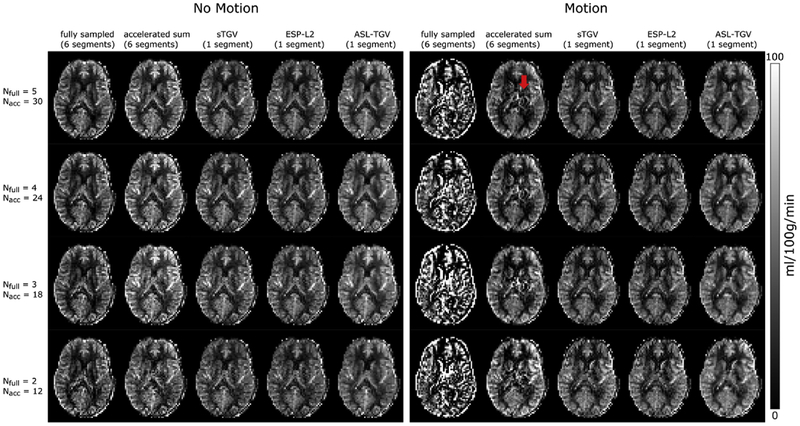
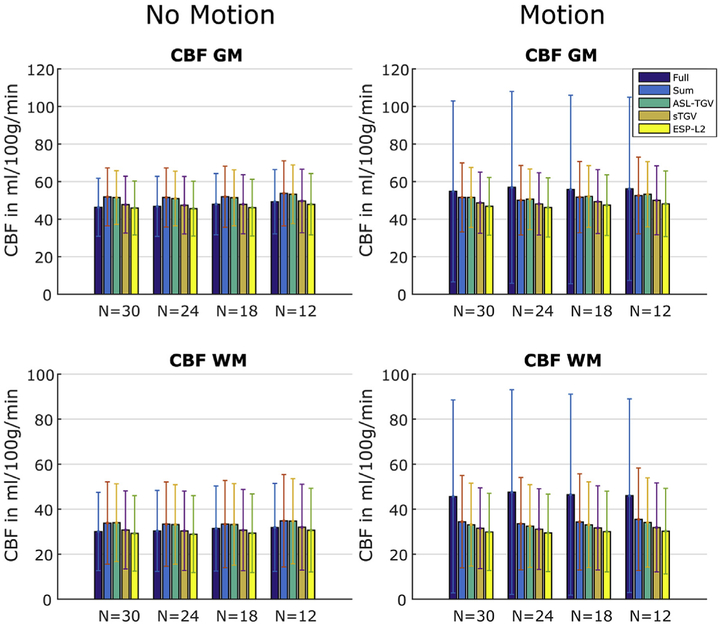
Compared to the fully sampled image, the TSNR is improved although the temporal resolution is increased by a factor of 6. This improvement in TSNR is visualized in Fig. 5B which shows the single perfusion weighted image from subject 5 for the different methods. This improvement in image quality is confirmed for the CBF-maps visible in Fig. 6, which shows results from the motionless data on the left side and the CBF-maps reconstructed form the motion-corrupted dataset on the right side. For the fully sampled data, the motion between segments leads to aliasing artifacts and low quality CBF-maps compared to the CBF-maps generated form the accelerated single-shot data. The proposed acquisition strategy shows an improved robustness to motion for the accelerated sum, however many residual motion-related artifacts remain (illustrated by the red arrow in Fig. 6). These motion-related artifacts can be suppressed by using a sTGV or ESP-L2 reconstruction but at the cost of decreased TSNR due to the g-factor penalty. Overall, the combination of the time-dependent 2D-CAIPIRINHA acquisition with the proposed spatio-temporal TGV reconstruction algorithm shows the best image quality for the motionless as well as motion-corrupted ASL data. Furthermore, for the single-shot acquisition the CBF-maps of the ASL-TGV are the most similar to the CBF-maps of the accelerated sum.

Fig. 5.

(A) Comparison of the TSNR of the PWIs averaged over all subjects for GM, WM and whole brain between different acquisition and reconstruction methods. The error bars shows the standard deviation. (B) Single perfusion weighted image from subject 5 for the segmented approaches (fully and accelerated sum) and the proposed single-shot method reconstructed with different algorithms.

Fig. 6.

One representative slice of CBF-map in dependence of different number of C/L-pairs of example subject 1. N_full is the number of C/L-pairs acquired for the fully sampled data and N_acc is the number of C/L-pairs acquired for the proposed accelerated single-shot data (N_full = 5/4/3/2; t_acq = 4 min 30sec/3 min 41sec/2 min 52sec/2 min 3sec, N_acc = 30/24/18/12; t_acq = 4 min 14sec/3min 25sec/2min 36sec/1min 46sec). On the left side are the CBF-maps where the subject was asked to lie as still as possible, whereas on the right side are the results from the subject moving his head during the acquisition. As expected the results of the segmented acquisition shows lots of artifacts for the motion case whereas the single-shot methods perform well and delivers CBF-maps with good image quality. The highest improvement in image quality is achieved with the proposed ASL-TGV approach. The red arrow indicates remaining motion artifacts for the accelerated sum approach.

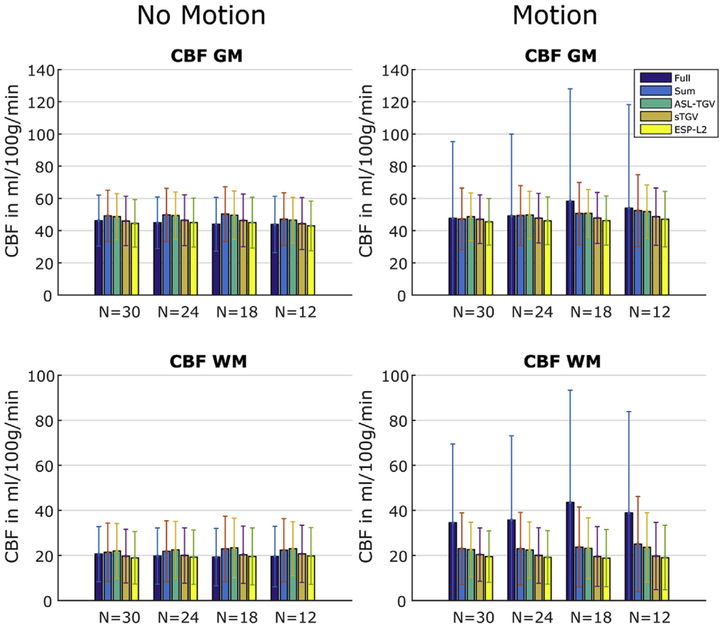
The CBF values in GM and WM for the motion-less and motion-corrupted data as a function of different numbers of C/L-pairs are shown in Fig. 7. In addition to visual improvements of the CBF image quality, the proposed method yields accurate quantitative CBF-values. In case of the fully sampled approach the motion leads to severe artifacts which result in a higher standard deviation and an additional bias in mean CBF values compared to the single-shot approaches. An increase in the standard deviations is also visible for the accelerated sum approach, whereas for the single-shot approaches the CBF-values are in high accordance between motion-less and motion-corrupted datasets.

Fig. 7.

Mean and standard deviation of CBF-values in GM and WM of subject 1 for the fully sampled approach (Full) and the proposed accelerated acquisition combined with different reconstruction methods using a different number of C/L-pairs. The error bars denote ±1 standard deviation.

Fig. 8 shows the CBF-maps of subject 2 for the different acquisition and reconstruction approaches respectively. The reconstruction results are in accordance with those of subject 1. The motion during the acquisition leads to artifacts in the CBF-maps, which are corrected in the proposed single-shot acquisition due to the retrospective motion correction. The corresponding mean GM and WM values of subject 2 are plotted in Fig. 9.

Fig. 8.

Different slices of CBF-maps for the highest and lowest number of averages (N_full = 5/2; t_acq = 4 min 30sec/2 min 3sec, N_acc = 30/12; t_acq = 4min 14sec/1min 46sec) of subject 2. The single-shot CBF-maps reconstructed with the ASL-TGV approach shows an improved image quality compared to fully sampled but segmented acquisition for the motionless acquisition. In case of subject movement, the CBF-maps of the segmented approach are not interpretable whereas for the single-shot method the motion can be corrected retrospectively, which results in CBF-maps with a good image quality.

Fig. 9.

Mean CBF-values in GM and WM of subject 2 for the fully sampled but segmented approach and the proposed accelerated single-shot acquisition in combination with different reconstruction approaches. The error bars denote ±1 standard deviation.

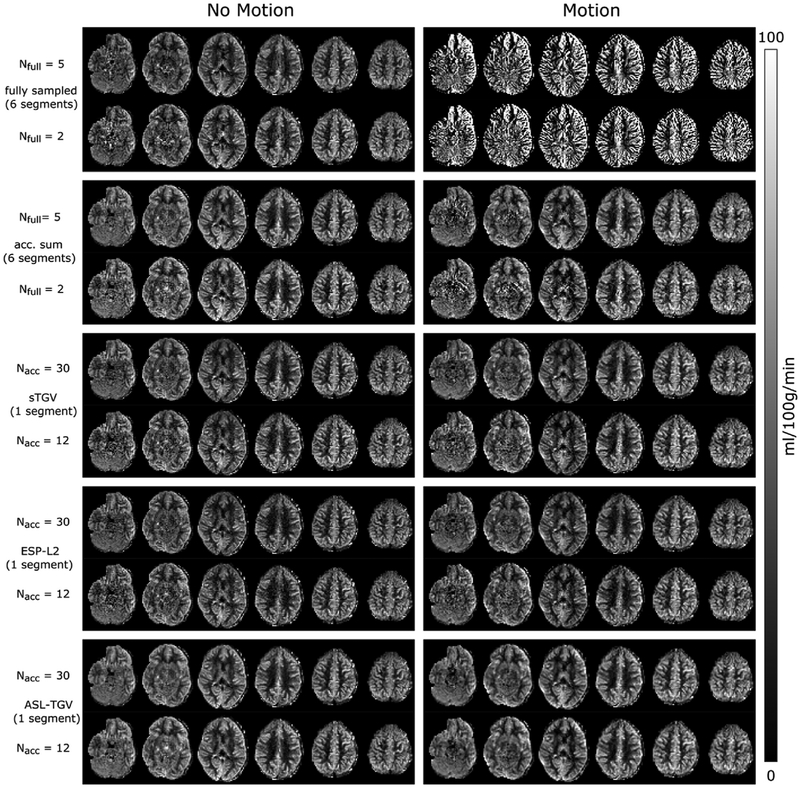
Supplementary Fig. S1 shows one representative CBF-map in transversal and sagittal plane of the remaining three subjects (subject 3 to subject 5) for the 5 acquisition and reconstruction approaches respectively. The results are in accordance with the results of subject 1 and 2 with an improved image quality for the proposed single-shot approach combined with the proposed ASL-TGV reconstruction compared to the rest approaches. This visual improvement is confirmed by the quantitative mean CBF values in the GM and WM which show the most accurate results for the proposed ASL-TGV approach as illustrated in Supplementary Fig. S2.

3.2.2. Multi-delay ASL data

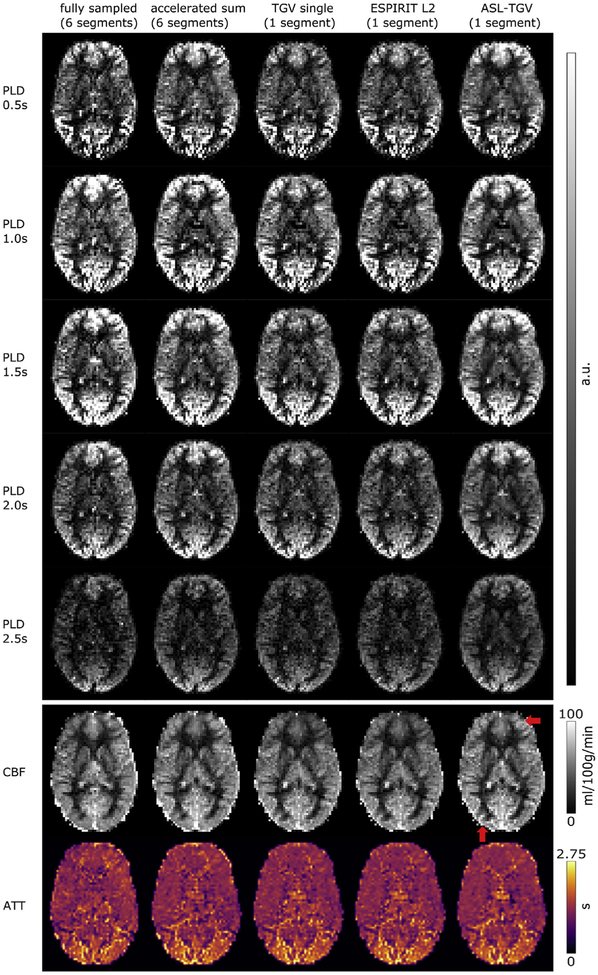
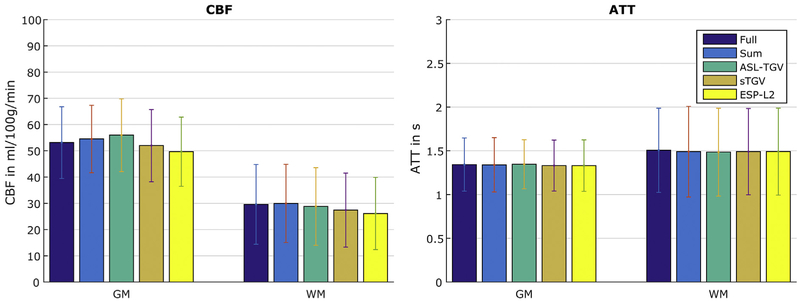
Fig. 10 shows the perfusion weighted images at different PLDs and the corresponding estimated CBF and ATT maps respectively. The perfusion weighted images reconstructed with the proposed ASL-TGV algorithm shows the highest quality. This improvement in SNR leads to sharper and more detailed CBF- and ATT-maps for the proposed method compared to the other methods (illustrated by the red arrow in Fig. 10). The corresponding mean CBF and ATT values in GM and WM are shown in Fig. 11.

Fig. 10.

One representative slice of PWI at different PLDs and the corresponding estimated CBF- and ATT-maps. The red arrow indicates areas where the ASL-TGV method provides more details in the CBF-map.

Fig. 11.

Mean CBF- and ATT-values in GM and WM for the fully sampled but segmented approach and the proposed accelerated single-shot acquisition in combination with different reconstruction approaches. The error bars denote ±1 standard deviation.

4. Discussion

In this study we present a novel single-shot 3D-GRASE acquisition with a time-dependent 2D-CAIPIRINHA sampling combined with a spatio-temporal reconstruction approach for pCASL scanning. Simulated synthetic and in-vivo single-PLD ASL datasets with a different number of C/L-pairs were considered. Both synthetic and in-vivo datasets show an improvement in noise-suppression and image-quality for ASL data compared to standard fully-sampled but segmented acquisition. The use of a time-dependent CAIPIRINHA sampling pattern allows the estimation of the coil-sensitivity maps directly from the averaged k-space data without the use of an additional pre-scan. Furthermore, the temporal incoherence is increased between each C/L-pair which is directly exploited in the proposed joint spatio-temporal reconstruction approach. This leads to a higher TSNR compared to the fully-sampled but segmented acquisition and also compared to the two single reconstruction methods. These results are in accordance with the results of (Boland et al., 2018), which reported a decrease of TSNR for accelerated 2D-CAIPIRINHA sequences with a fixed acquisition pattern compared to the fully sampled but segmented 3D-GRASE approach in combination with SENSE reconstruction. Similar results were reported by (Chang et al., 2017) for accelerated stack-of-spirals acquisitions with 3D-SPIRIT reconstruction. It should be noted that in our study the TSNR was not calculated in a time-equivalent manner between the fully sampled and accelerated acquisition. An additional incorporation of the number of averages in the TSNR calculation would result in a higher TSNR for the single as well as for the proposed ASL-TGV reconstruction method. In contrast to the aforementioned studies, the proposed acquisition and reconstruction method increases the TSNR, which results in an improved image quality. The increase in temporal resolution by a factor of 6 allows single-shot acquisition of the whole volume and hence improves the robustness to motion. Furthermore, the improved temporal resolution and TSNR could be very beneficial for perfusion based functional MRI (Wang et al., 2003). However, the potential and evaluation of the current approach for perfusion fMRI is out of scope of this study and will be part of future work.

For the proposed reconstruction approach the used model parameters are very robust and yield accurate results for simulated and in-vivo datasets with and without motion as well as for different number of C/L-pairs. However, the regularization parameter has to be adapted according to the noise level, but this is also the case for the sTGV or ESP-L2 approach where the regularization parameter has to be chosen accordingly. Compared to these single reconstruction approaches, our proposed method exploits the structural redundancy in the C/L-images as well as in the PWI. This leads to a higher SNR, better image quality as well as more accurate CBF-values compared to these two single reconstruction approaches. The accuracy of CBF-quantification is of high importance for quantitative analysis. Furthermore, the use of a spatio-temporal constraint on the PWI reduces noise and leads to a better detection of the hypoperfusion area, which vanishes for the two single reference reconstruction algorithms (Fig. 3). However, all three constrained reconstruction methods have a tendency to reduce the perfusion differences between adjacent regions with increasing regularization strength. The procedure for optimizing the regularization parameter with the SSIM is also sensitive to this effect and some bias remains. The present study, nevertheless, shows that for the proposed ASL-TGV method this bias is smaller than that of reconstruction approaches using only spatial regularization. For instance, the bias for the three methods ASL-TGV/sTGV/ESP-L2 is 5.5/7.6/11% respectively in the small hyperperfusion area for 30 C/L-pairs and 5.8/8.9/12.3% for 12 C/L-pairs. The remaining bias can be further reduced by using a debiasing method (Brinkmann et al., 2017; Deledalle et al., 2017) which could be performed in a future step. The additional incorporation of time information directly into the reconstruction approach strongly increases the TSNR and leads to CBF-maps with a higher image-quality. The fully sampled but segmented acquisition yields the lowest bias for the synthetic images. However, one should note that motion or physiological artifacts between segments are not simulated. Hence, the results for the accelerated sum approach are not shown for the synthetic data, because the difference between fully sampled and accelerated sum is only due to different Gaussian noise which is negligible. Physiological artifacts and motion can lead to misalignments in k-space which directly affects the reconstruction quality of the PWI and cannot be corrected retrospectively. This is exemplary illustrated in Figs. 6 and 7 where the subject moves the head during the acquisition with a maximum rotation of 3°and translation of 2 mm. As expected, the fully sampled but segmented approach results in CBF-maps with severe artifacts which are not interpretable. In contrast, the proposed accelerated single-shot acquisition provides high quality CBF-maps which are in high accordance with the “motionless” CBF-maps. This is important for clinical as well as research settings, where otherwise a rescan is necessary. Additionally, the quantitative CBF-values are in high accordance between motionless and motion corrupted data, which highlights the potential of the proposed approach for uncooperative subjects such as children and elderly.

In our study we additionally compared the fully sampled k-space of the accelerated acquisition, obtained by summing up the corresponding C/L-k-spaces, with the fully sampled standard GRASE acquisition. In Figs. 6 and 7 it is clearly visible that the proposed acquisition strategy is inherently more robust against motion than the standard segmented approach. This is due to the way how the 3D k-space is sampled. For the proposed method the whole k-space (PE1 and PE2) is sampled in an interleaved manner as illustrated in Fig. 1C. In contrast the standard segmented approach acquires the k-space points only interleaved along PE1 (Fig. 1D). In PE2 direction the first half of k-space (partition 24–46) is sampled with segment 1–3 and the second half (partition 1–23) is sampled with segment 4–6. In case of motion this leads to a higher inconsistency in the k-space symmetry along PE2 and hence to more severe motion artifacts. This result in lower TSNR values for the standard segmented GRASE acquisition compared to the accelerated sum method. The variability in CBF-values between those two acquisitions could be due to brain metabolism or physiological noise, e.g. motion, respiration or differences in cardiac cycle which can affect the mean CBF-values (Verbree and van Osch, 2018). For example in Fig. 6 some intravascular artifacts are clearly visible in the CBF-maps obtained from the accelerated sum. This explains the higher mean CBF-values in Fig. 7 compared to the fully sampled approach. In contrast, the mean CBF-values of subject 4 and 5 show higher CBF values for the fully sampled approach compared to the accelerated sum method. However, the variations in CBF between those two acquisitions are small and comparable to reported inter-scan variations in CBF (Heijtel et al., 2014; Xu et al., 2009). By comparing the CBF-values of the accelerated sum with the single reconstruction approaches (ESP-L2 and sTGV) a clear bias with an underestimation of the CBF-values for GM as well as WM is observable. This bias can be reduced by using the proposed ASL-TGV reconstruction method which uses spatio-temporal constraints on control, label and perfusion weighted images simultaneously. This leads to more accurate reconstruction results and hence in a high agreement of the CBF-values with the accelerated sum acquisition for all subjects.

The proposed single-shot acquisition has in comparison to the fully sampled approach the advantage that more PWIs can be acquired for one PLD and in combination with the ASL-TGV reconstruction the SNR can be improved (Fig. 10). A higher number of averages per PLD provides a better estimation of the noise and leads therefore to a more accurate setting of the spatial regularization of BASIL. This leads to improved perfusion images with sharper edges for the single-shot methods compared to the fully sampled approach (Fig. 10). The improved SNR of ASL-TGV allows additionally a weaker regularization of BASIL that further reduces smoothing and provides higher CBF-values (Fig. 11) for GM and lower CBF values for WM.

An improvement in temporal resolution provides a more flexible approach for multi-PLD ASL data and could be either used to increase the number of total sampling points (PLDs), which was recently shown to improve the accuracy of the quantification (Woods et al., 2019), or to shift the number of averages form high SNR acquisitions (short PLD) to low SNR acquisitions (long PLD) which will be investigated in a future work.

An additional benefit of the proposed single-shot method is the increased temporal resolution which results in a 6 fold increase in acquired C/L-pairs. This could be very beneficial in case of outliers. The elimination of a small number of C/L-pairs due to outliers has a negligible effect on the overall SNR, whereas for the fully sampled approach with only a few averages the exclusion of 1 or 2 images would have a big effect on the overall SNR.

The computation time for the sTGV reconstruction is ~13 s for one image which results in total in 780 s for 30 C/L-pairs using a Titan XP graphics card. In comparison for the proposed ASL-TGV method the reconstruction time of a whole 4D ASL dataset is approximately 250 s for 30 C/L-pairs. This is a decrease in computational time of 312% over the sTGV reconstruction method. However, one limitation of the reconstruction framework is the available GPU-memory and therefore the limited number of C/L-pairs. For the current dataset 36 C/L-pairs can be calculated simultaneously. Different strategies can be used to overcome this problem, e.g. using (mutli-threading) data streaming to multiple GPUs concurrently (Maier et al., 2019) or by reconstructing the 4D ASL-dataset in blocks.

The mean background suppression efficiency of the proposed method is 91.05 ± 1.2% in GM and 88.8 ± 1.5% in WM respectively. This leads to a TSNR improvement of approximately 365/338% in GM/WM compared to non-background suppressed ASL imaging (data not shown). Whereas a higher improvement in background suppression would lead to lower subtraction artifacts due to motion or temporal fluctuations this could lead to a loss in performance of all used reconstruction methods. This is due to a lower SNR in the C/L-images. However, we expected that our proposed ASL-TGV outperforms the other reconstruction algorithm because it incorporates information of the C/L as well as the PWI simultaneously. Additionally an even higher background suppression needs more background suppression pulses which would affect the labeling efficiency due to imperfections of the inversion pulse. Furthermore the lower SNR in the C/L images would affect additionally the quality of motion correction (Chappell et al., 2017). Hence, a strong background suppression with two pulses is recommended by the consensus paper (Alsop et al., 2015).

One limitation of the generated synthetic dataset is the shape of the hypo- and hyperperfusion ROI. They fit exactly in the voxels of the ASL images. A more realistic ROI would be a spherical region drawn in high resolution space which is than down sampled to ASL space. This would lead to more realistic hyper- and hypoperfusion areas with boards across the voxels.

In summary the results of this study highlights that the proposed accelerated time-dependent 2D-CAIPIRINHA sampling strategy combined with the proposed ASL-TGV reconstruction approach, which exploits spatial and temporal information of the C/L-images simultaneously, allows single-shot ASL acquisition of the whole brain. As a consequence, this method improves the robustness of ASL images against motion. Additionally due to the spatial and temporal constrains, it improves the SNR and image quality for simulation and in-vivo data with and without motion. Furthermore, it yields high quality quantitative CBF-maps from single-PLD data with only 12 C/L-pairs (t_acq = 1min 46sec) and high quality CBF- and ATT-maps from multi-PLD ASL data. This improvement addresses urgent clinical demands. A further improvement in the image quality could be expected by combining the proposed approach with a prospective motion correction strategy (Aksoy et al., 2017; Shao et al., 2017). Additionally, to reduce the amount of blurring in the final CBF images, which leads to an additional underestimation of the GM and an overestimation of WM-values, visible in the synthetic data, a variable-flip angle readout scheme (Liang et al., 2014) or a deblurring method (Galazzo et al., 2014) could be used. An additional improvement of the proposed acquisition method could be the use of a Hadamard encoding scheme (Guenther, 2007) to increase the number of sampling points of the kinetic curve.

5. Conclusion

The proposed time-dependent CAIPIRINHA sampling in combination with a spatio-temporal reconstruction approach adapted for ASL data provides high-quality CBF-maps from the whole brain with a single-shot 3D acquisition. It addresses important clinical demands in terms of scan-time reduction and motion-robustness compared to standard segmented 3D readouts. Furthermore, it increases the TSNR and reduces the acquisition time of one PWI by a factor of 6 compared to fully sampled but segmented 3D-GRASE pCASL acquisition. This makes this approach very promising for perfusion fMRI, multi-delay ASL data as well as for uncooperative subjects, patients or children.

Appendix A. Algorithm

For solving the problem defined in section “2.2 Reconstruction of ASL data” in equation (10) the primal dual algorithm is used (Chambolle and Pock, 2011). Therefore the reconstruction-problem has to be reformulated as a saddle-point problem. This is achieved by dualisation of the norms (Bredies, 2014), which introduces additional “dual” variables [p₂, p₃,q₂, q₃, r₂, r₃, y, z] and leads to the following form:

$$\begin{gathered} \underset{c,l,p_1,q_1,r_1}{\text{min}}\underset{p_2,p_3,q_2,q_3,r_2,r_3,y,z}{\text{max}}\langle Kc-d_c,y\rangle -\frac{1}{2{\lambda }_c}\Vert y{\Vert }_2^2+\langle Kl-d_l,z\rangle -\frac{1}{2{\lambda }_l}\Vert z{\Vert }_2^2 \\ +\langle {\nabla }_{\beta }(c-l)-p_1,p_2\rangle +\langle {\epsilon }_{\beta }{p}_1,p_3\rangle +\langle {\nabla }_{\beta }l-q_1,q_2\rangle +\langle {\epsilon }_{\beta }{q}_1,q_3\rangle \\ +\langle {\nabla }_{\beta }c-r_1,r_2\rangle +\langle {\epsilon }_{\beta }{r}_1,r_3\rangle -I_{{\alpha }_1,{\gamma }_2}\left(p_2\right) \\ -I_{{\alpha }_0,{\gamma }_2}\left(p_3\right)-I_{{\alpha }_1,{\gamma }_1}\left(q_2\right)-I_{{\alpha }_0,{\gamma }_1}\left(q_3\right)-I_{{\alpha }_1,{\gamma }_1}\left(r_2\right)-I_{{\alpha }_0,{\gamma }_1}\left(r_3\right) \end{gathered}$$

Setting x = (c, l, p₁, q₁, r₁) and y = (p₂, p₃, q₂, q₃, r₂, r₃, y, z) yields the following functions in the saddle-point formulation (equation (10)):

$$H=\left[\begin{array}{ccccc}{\nabla }_{\beta }& -{\nabla }_{\beta }& -Id& 0& 0\\ 0& 0& {\epsilon }_{\beta }& 0& 0\\ 0& {\nabla }_{\beta }& 0& -Id& 0\\ 0& 0& 0& {\epsilon }_{\beta }& 0\\ {\nabla }_{\beta }& 0& 0& 0& -Id\\ 0& 0& 0& 0& {\epsilon }_{\beta }\\ K& 0& 0& 0& 0\\ 0& K& 0& 0& 0\end{array}\right]$$

$$G(\mathit{x})=0$$

$$F^{*}(\mathit{y})=\langle d_c,y\rangle +\frac{1}{2{\lambda }_c}\Vert y{\Vert }_2^2+\langle d_l,z\rangle +\frac{1}{2{\lambda }_l}\Vert z{\Vert }_2^2+I_{{\alpha }_1,{\gamma }_2}\left(p_2\right)+I_{{\alpha }_0,{\gamma }_2}\left(p_3\right)+I_{{\alpha }_1,{\gamma }_1}\left(q_2\right)+I_{{\alpha }_0,{\gamma }_1}\left(q_3\right)+I_{{\alpha }_1,{\gamma }_1}\left(r_2\right)+I_{{\alpha }_0,{\gamma }_1}(r_3)$$

where $I_{{\alpha }_i,{\gamma }_i}(p)$ is the indicator function and de fined as follows:

$$I_{{\alpha }_i,{\gamma }_j}\left(p\right)=\{\begin{array}{cc}0,& {\Vert p\Vert }_{\infty }\le {\alpha }_i{\gamma }_j\left(w\right)\\ \infty ,& \mathit{\text{else}}\end{array}$$

With the defined functions the problem can be easily solved using the following iterative scheme:

$${\mathit{y}}^{n+1}={\left(I+\sigma \partial F^{*}\right)}^{-1}\left({\mathit{y}}^n+\sigma H{\overline{\mathit{x}}}^n\right)$$

$${\mathit{x}}^{n+1}={\left(I+\tau \partial G\right)}^{-1}\left({\mathit{x}}^n-\tau H^{*}{\mathit{y}}^{n+1}\right)$$

$${\overline{\mathit{x}}}^{n+1}=2{\mathit{x}}^{n+1}-{\mathit{x}}^n,$$

Dual Update:

$$p_2^{n+1}=P_{{\alpha }_1,{\gamma }_2}\left(p_2^n+\sigma \left({\nabla }_{\beta }{\overline{c}}^{\text{n}}-{\nabla }_{\beta }\stackrel{-\text{n}}{l}-{\overline{p}}_1^n\right)\right)$$

$$p_3^{n+1}=P_{{\alpha }_0,{\gamma }_2}\left(p_3^n+\sigma {\epsilon }_{\beta }{\overline{p}}_1^n\right)$$

$$q_2^{n+1}=P_{{\alpha }_1,{\gamma }_1}\left(q_2^n+\sigma \left({\nabla }_{\beta }\stackrel{-\text{n}}{l}-{\overline{q}}_1^n\right)\right)$$

$$q_3^{n+1}=P_{{\alpha }_0,{\gamma }_1}\left(q_3^n+\sigma {\epsilon }_{\beta }{\overline{q}}_1^n\right)$$

$$r_2^{n+1}=P_{{\alpha }_1,{\gamma }_1}\left(r_2^n+\sigma \left({\nabla }_{\beta }{\overline{c}}^{\text{n}}-{\overline{r}}_1^n\right)\right)$$

$$r_3^{n+1}=P_{{\alpha }_0,{\gamma }_1}\left(r_3^n+\sigma {\epsilon }_{\beta }{\overline{r}}_1^n\right)$$

$$y^{n+1}=P_{{\lambda }_c,\sigma }^2\left(y^n+\sigma \left(K{\overline{c}}^{\text{n}}-d_c\right)\right)$$

$$z^{n+1}=P_{{\lambda }_l,\sigma }^2\left(z^n+\sigma \left(K\stackrel{-\text{n}}{l}-d_l\right)\right)$$

Primal Update:

$$c^{n+1}=c^n-\tau \left({\nabla }_{\beta }^{*}{p}_2^{n+1}+{\nabla }_{\beta }^{*}{r}_2^{n+1}+K^{*}{y}^{n+1}\right)$$

$$l^{n+1}=l^n-\tau \left(-{\nabla }_{\beta }^{*}{p}_2^{n+1}+{\nabla }_{\beta }^{*}{q}_2^{n+1}+K^{*}{z}^{n+1}\right)$$

$$p_1^{n+1}=p_1^n-\tau \left(-p_2^{n+1}+{\epsilon }_{\beta }^{*}{p}_3^{n+1}\right)$$

$$q_1^{n+1}=q_1^n-\tau \left(-q_2^{n+1}+{\epsilon }_{\beta }^{*}{q}_3^{n+1}\right)$$

$$r_1^{n+1}=r_1^n-\tau \left(-r_2^{n+1}+{\epsilon }_{\beta }^{*}{r}_3^{n+1}\right)$$

Extrapolation step:

$${\overline{c}}^{n+1}=2c^{n+1}-c^n$$

$${\overline{l}}^{n+1}=2l^{n+1}-l^n$$

$${\overline{p}}_1^{n+1}=2p_1^{n+1}-p_1^n$$

$${\overline{q}}_1^{n+1}=2q_1^{n+1}-q_1^n$$

$${\overline{r}}_1^{n+1}=2r_1^{n+1}-r_1^n$$

In the above algorithm the operators $“P_{a_i,{\gamma }_j}(x)”\text{\hspace{0.17em}and\hspace{0.17em}}“P_{\lambda ,\sigma }^2(x)”$ correspond to proximal mappings and are given by:

$$P_{{\alpha }_i,{\gamma }_j}{\left(x\right)}_{k,l,m,t}=\frac{x_{k,l,m,t}}{max\left\{1,\frac{{\left|\left|x_{k,l,m,t}\right|\right|}_{1,2}}{{\alpha }_i,{\gamma }_j\left(w\right)}\right\}}$$

$$P_{\lambda ,\sigma }^2(x)=\frac{x}{1+\frac{\sigma }{\lambda }}$$

where ||v_k,_l,_m,_t ||_1,2 is defined for v ∈ R⁴ as:

$${\left|\left|v_{k,l,m,t}\right|\right|}_{1,2}=\sqrt{{\left|v_{k,l,m,t}^1\right|}^2+{\left|v_{k,l,m,t}^2\right|}^2+{\left|v_{k,l,m,t}^3\right|}^2+{\left|v_{k,l,m,t}^4\right|}^2}$$

and for v ∈ R¹⁰ as:

$${\left|\left|v_{k,l,m,t}\right|\right|}_{1,2}=\sqrt{{\left|v_{k,l,m,t}^1\right|}^2+{\left|v_{k,l,m,t}^2\right|}^2+{\left|v_{k,l,m,t}^3\right|}^2+{\left|v_{k,l,m,t}^4\right|}^2+2{\left|v_{k,l,m,t}^5\right|}^2+2{\left|v_{k,l,m,t}^6\right|}^2+2{\left|v_{k,l,m,t}^7\right|}^2+2{\left|v_{k,l,m,t}^8\right|}^2+2{\left|v_{k,l,m,t}^9\right|}^2+2{\left|v_{k,l,m,t}^{10}\right|}^2}$$

Here, the coefficients v are identified in the symmetric 4 × 4 matrices according to:

$$w=\left[\begin{array}{llll}v1\hfill & v5\hfill & v6\hfill & v7\hfill \\ v5\hfill & v2\hfill & v8\hfill & v9\hfill \\ v6\hfill & v8\hfill & v3\hfill & v10\hfill \\ v7\hfill & v9\hfill & v10\hfill & v4\hfill \end{array}\right]$$

Appendix B. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.neuroimage.2019.116337.