SUMMARY
During speech listening, the brain could use contextual predictions to optimize sensory sampling and processing. We asked if such predictive processing is organized dynamically into separate oscillatory timescales. We trained a neural network that uses context to predict speech at the phoneme level. Using this model, we estimated contextual uncertainty and surprise of natural speech as factors to explain neurophysiological activity in human listeners. We show, first, that speech-related activity is hierarchically organized into two timescales: fast responses (theta: 4–10 Hz), restricted to early auditory regions, and slow responses (delta: 0.5–4 Hz), dominating in downstream auditory regions. Neural activity in these bands is selectively modulated by predictions: the gain of early theta responses varies according to the contextual uncertainty of speech, while later delta responses are selective to surprising speech inputs. We conclude that theta sensory sampling is tuned to maximize expected information gain, while delta encodes only non-redundant information.
In Brief
Donhauser and Baillet use artificial neural networks and neurophysiological recordings to identify a mechanism for predictive speech processing in the brain. Fast and slow oscillations in auditory regions are modulated by the uncertainty of predictions and contextual surprise, respectively.
INTRODUCTION
In natural situations, the raw informational content of sensory inputs is astonishingly diverse and dynamic, which should be challenging to the computational resources of the brain. Internal representations of our sensory context could alleviate some of this ecological tension: through learning and life experiences, we develop internal models that are thought to issue contextual predictions of sensory inputs, yielding faster neural encoding and integration. Mechanistically, predictive coding from internal representations of the perceptual context would inhibit the responses of early sensory brain regions to predictable inputs; symmetrically, the gain of brain processes to sensory inputs would be increased in situations of greater contextual uncertainty, with the resulting non-redundant information subsequently updating higher-order internal representations (Rao and Ballard, 1999; Friston, 2005; Nobre and van Ede, 2018; Arnal and Giraud, 2012).
An example where predictive inferences may be key to a socially significant percept is the processing of human language. For instance, reading speed accelerates when context increases the predictability of upcoming words (Smith and Levy, 2013). Similarly, a word uttered in isolation (e.g., “house” versus “mouse”) can be ambiguous to recognize; in continuous speech, humans (Kalikow et al., 1977) and machines (Bahdanau et al., 2016) recognize words better when inferred from their context (as in “Today, I was cleaning my house”). These behavioral findings are supported by neurolinguistic evidence: semantic expectations are typically manipulated experimentally via the empirical probability of a closing word (cloze) from a sequence that primes its context. Less-expected sentence endings produce a deeper negative deflection of electroencephalographic (EEG) signals at least 400 ms (N400) after the onset of the closing word (Kutas and Hillyard, 1984; Frank et al., 2015; Kuperberg and Jaeger, 2016; Broderick et al., 2018).
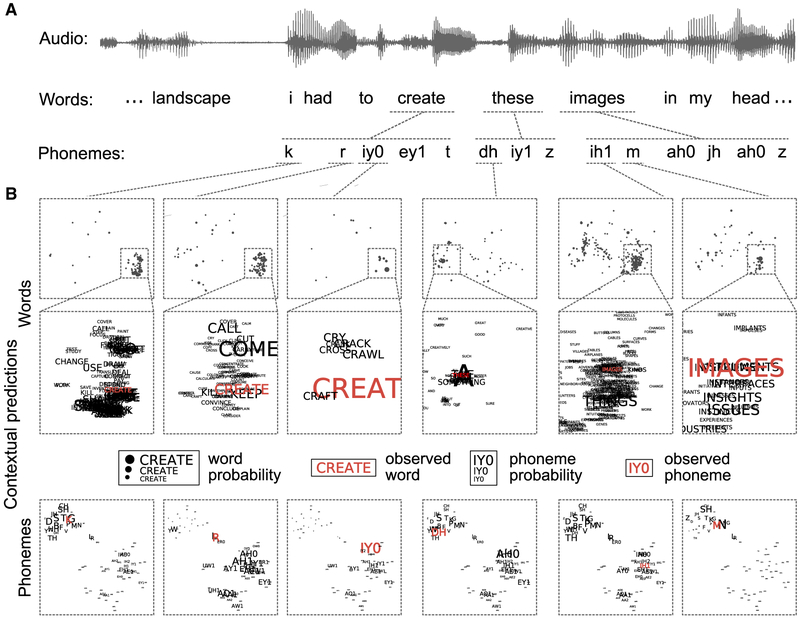
These effects point at relatively late brain processes occurring after the acoustic features of the last word are extracted. Thus, they can be explained as a posteriori brain responses to violations of semantic expectations (Van Petten and Luka, 2012; Kuperberg and Jaeger, 2016). However, based on predictive coding theory (Rao and Ballard, 1999; Friston, 2005), we would expect high-level semantic predictions to be channeled down to low-level phonetic predictions, thus affecting early brain processes as well. What is missing is a model of phonetic predictions that integrates both long-term (previous words) (Broderick et al., 2018; Frank et al., 2015) and short-term (previous phonemes within a word) (Brodbeck et al., 2018) contexts. For this reason, we trained an artificial neural network (ANN) as a proxy for human contextual language representations. The ANN was trained on a large corpus of 1,500 TED Talks to predict the upcoming phoneme and word from preceding phonemes and words and their respective timing in the speech streams. Figure 1 shows, by example, how the model continuously issues predictions and updates its internal representations with speech inputs at the phonetic timescale.
Figure 1. Contextual Speech Predictions at the Phonetic Timescale from an Artificial Neural Network.
(A) An example segment of speech presented to the human participants (Audio) is shown along with its word- and phoneme-level transcriptions.
(B) Outputs of the artificial neural network trained on spoken language: prior to each phoneme, the network estimates the respective probabilities of the upcoming phoneme and word. Contextual phoneme and word probabilities are visualized in two-dimensional plots (embeddings, projected using tSNE) (Maaten and Hinton, 2008) in which similar phonemes and words are grouped closely to each other. Probability values are represented by the size of phonemes, dots, and words. The actual observed phonemes and words are shown in red in the embedding maps. The predictions depend on the semantic and syntactic context and are updated after each observed phoneme. We produced a freely accessible web app (https://pwdonh.github.io/pages/demos.html) for everyone to explore the ANN predictions and the production of uncertainty and surprise measures over longer transcribed speech samples. See STAR Methods and Figure S1 for details on the network architecture and optimization.
If the human brain implements a similar predictive processing strategy, it requires an organizing principle to separate the fast sampling of sensory information from slower-evolving internal models that should be updated only with non-redundant information. Neural oscillations have been suggested as an organizational principle in the temporal domain (Giraud and Poeppel, 2012; Lakatos et al., 2005; Gross et al., 2013) due to their ability to parse the sensory input into packages of information. Beyond sensory parsing, here we hypothesize that different oscillatory timescales organize predictive speech processing across hierarchical stages of the auditory pathway. We expect from predictive coding theory that higher-order regions manifest slower neurophysiological dynamics as prediction errors are accumulated to update internal models (Bastos et al., 2012). Finally, we wish to clarify whether the fast sampling of sensory information in lower-order regions is in itself dependent on predictions from context.
RESULTS
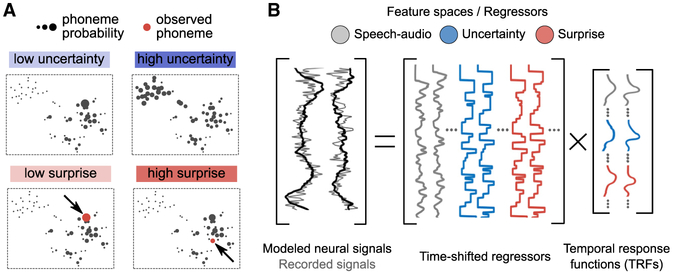
We recorded time-resolved ongoing neural activity from eleven adult participants using magnetoencephalography (MEG) (Baillet, 2017) while they listened to full, continuous audio recordings of public speakers (TED Talks). Using regression, we modeled the recorded neurophysiological signal fluctuations as a mixture of cortical entrainment by acoustic (Ding and Simon, 2012; Zion Golumbic et al., 2013) and contextual prediction features. The two contextual prediction features we derived at the phonetic timescale were “uncertainty” and “surprise” (Figure 2A). Contextual uncertainty is quantified by the entropy of the predictive distribution of the upcoming phoneme. Surprise is a measure of unexpectedness for the phoneme that is actually presented. These two measures are correlated. However, uncertainty uniquely quantifies the state of a predictive receiver before the observation of the next phoneme in the current context, and thus how much the predictive receiver has to rely on sensory information instead of predictions for correct perception. Surprise captures the actual added information carried by a phoneme after it has been observed in the same context.
Figure 2. Contextual Prediction Features for Neural Signal Regression.
(A) We illustrate the meaning of features “uncertainty” and “surprise” with example phoneme probabilities. Uncertainty is sensitive to the context before observing the next phoneme; surprise is inversely related to the probability of the actual observed phoneme in the present context.
(B) Neural signals are modeled with linear regression using three sets of time-resolved feature spaces: “speech-audio” (including the acoustic envelope of the speech stream), “uncertainty,” and “surprise” (see Figure S2B for a full list of regressors included in these feature spaces). Multiple time-shifted versions of the regressors are entered into the design matrix (see Figure S2C). The regression weights can be interpreted as temporal response functions (TRFs) showing the time course of the neural response to the feature of interest.
Speech-Related Neurophysiological Activity Is Hierarchically Organized in Theta and Delta Bands
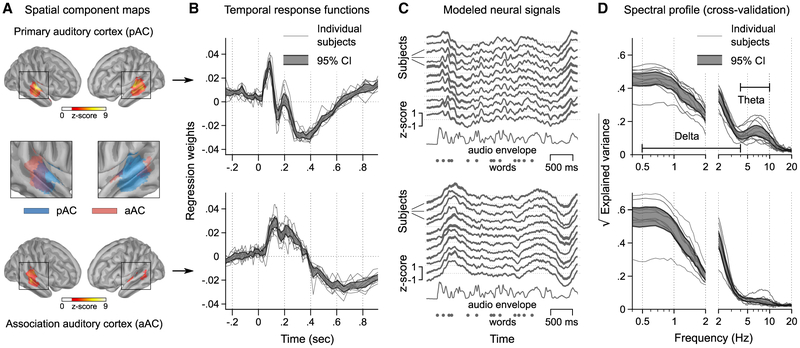
The analysis was first aimed at identifying the brain regions and oscillatory timescales of cortical activity driven by these speech features. We derived a regression model using a time-resolved temporal response function (TRF) approach (Huth et al., 2016; Di Liberto et al., 2015; Zion Golumbic et al., 2013). This approach entails estimating regression weights for multiple regressors and different lags on a training subset of the MEG data (Figure 2B). Due to high correlations between regressors, we used regularized (ridge) regression to stabilize the estimation of model parameters. We then used spatial component optimization (Donhauser et al., 2018) to identify subsets of brain regions whose neurophysiological activity was explained with similar TRFs in the regression model across participants (Figures S2 and S3). Figure 3A shows that bilateral portions of the superior temporal gyrus (STG) and of the superior temporal sulcus (STS) were identified by the mapping procedure. The first identified component comprised the primary auditory cortex (pAC). The second component included portions of the STG immediately anterior and posterior to primary auditory cortical regions, which are typical of the downstream auditory and language pathway (de Heer et al., 2017; Kell et al., 2018; Liegeois-Chauvel et al., 1994; Fontolan et al., 2014). We hereinafter refer to this second component as associative auditory cortex (aAC). The temporal profile (TRF) of pAC comprised rapid successions of peaks and troughs, starting as early as 85 ms after phoneme onset (then at 150 ms and 200 ms), akin to a damped wave in the theta frequency range, superimposed on a slower component with a pronounced trough around 400 ms (Figures 3B and 3C). In striking contrast, the dynamics of aAC were dominated by a slow wave that peaked after pAC (100–200 ms latency), with a subsequent trough 600 ms after phoneme onset.
Figure 3. Speech-Related Neurophysiological Activity Is Hierarchically Organized in Theta and Delta Bands.
(A) Two spatial components were extracted from the regression model in a data-driven manner. An optimization procedure identified components that were well-explained by speech-related features and showed functionally consistent responses across participants (see STAR Methods and Figures S2 and S3). The identified components corresponded to hierarchical levels of the auditory pathway: here we refer to them as primary auditory cortex (pAC, essentially comprising BA41/42) and association auditory cortex (aAC, comprising BA22). See Figure S3F for single subject cortical maps.
(B) Temporal response functions (TRFs) averaged across all features for pAC (top) and aAC (bottom), showing distinct temporal response profiles (CI: bootstrap confidence interval). Whereas pAC showed a sequence of early peaks and troughs resembling a damped theta wave, aAC was dominated by responses with the dynamics of a delta wave.
(C) Neural responses to the example speech segment predicted by the regression model show how the distinct temporal shapes of the TRFs translate into continuous time series with distinct spectral features.
(D) Performance of the regression model on held-out data across the frequency spectrum. Distinct spectral profiles can be seen that correspond to the temporal profiles in (B) and (C): we observed a peak in the theta range for pAC (top) in contrast to aAC (bottom), which showed more speech-related delta activity. The plots show coherence between the modeled and recorded neural responses (coherence2 = explained variance, spectral smoothing: 0.5 Hz & 3 Hz below & above 2 Hz) (Theunissen et al., 2001).
These two timescales were revealed in a complementary fashion by computing the variance explained by the regression model across the frequency spectrum in a test subset of the MEG data (using a cross-validation loop). Speech-related delta-range ([0.5,4] Hz) activity dominated in aAC, while faster theta ([4,10] Hz) activity was restricted to pAC (Figure 3D). These distinct coherence profiles were not due to differences in spectral power between the two components (Figure S3C).
Taken together, these first findings point at a temporal hierarchy of neural responses to ongoing spoken language (Giraud and Poeppel, 2012) and are compatible with a phenomenon of temporal downsampling in downstream regions (aAC) as expected from predictive coding theory (Bastos et al., 2012).
Contextual Uncertainty and Surprise Selectively Modulate Theta and Delta Band Responses
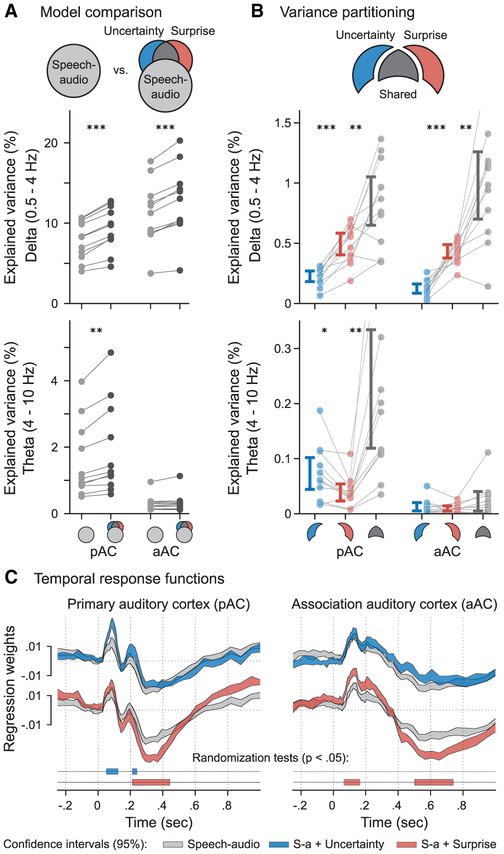
To assess whether this temporal hierarchy supports predictive speech processing, we tested the specific contributions of contextual uncertainty and surprise. First, we compared the full regression model (predictive-coding model) to a reduced alternative consisting of only acoustic features (speech-audio model). The analysis revealed that predictive-coding features explained a significant (F(1, 10) = 88.03, p < .001) portion of the variance of observed neurophysiological signals during speech listening: for the delta band, on average 17 and 12 percent (pAC and aAC, respectively), and for the theta band, 12 and 4 percent (Figure 4A). By comparing the ANN to simpler n-gram models, we show in Figure S4A that this effect is not explained by short-term transitional probabilities (phonotactics).
Figure 4. Contextual Uncertainty and Surprise Selectively Modulate Theta and Delta Band Responses.
(A) We compared cross-validation performances of the speech-audio model to those of a model with the predictive coding features “uncertainty” and “surprise.” Predictive coding outperformed the speech-audio model across both spatial components for the delta band and for pAC in the theta band.
(B) We showed (using variance partitioning) how much variance in the neural signal was explained uniquely by uncertainty and surprise, as well as shared contributions from both features. While the shared contribution was the largest (as expected, since the features are correlated), we found a remarkable difference between frequency bands: delta-band activity was better explained by surprise, while theta-band activity (which is dominant in pAC) was better explained by uncertainty. Error bars show 95% CIs.
(C) TRFs averaged for different feature spaces: these traces can be interpreted as neural responses to a speech input of low uncertainty and surprise (gray traces), high uncertainty (blue traces), and high surprise (red traces). Note that the effects of uncertainty and surprise complement the findings in the frequency domain: uncertainty enhances early theta-like responses in pAC (starting at 60 ms), and surprise enhances multiple delta-like peaks in aAC and pAC (starting at 80 ms). * p < .05, ** p < .01, *** p < .001. See also Figure S4.
Uncertainty and surprise are correlated in natural speech (r = 0.69 in the speech material used in the present study): when an upcoming stimulus is uncertain, it is also often surprising. We evaluated their respective contributions following a partitioning strategy (de Heer et al., 2017), separating the additional explained variance (predictive coding minus speech-audio model) into what was explained uniquely by uncertainty and surprise and what was shared between the two feature spaces (Figure S4). We compared the uncertainty, surprise, and shared variance partitions across the two spatiotemporal components (pAC and aAC) and two frequency bands revealed previously (3-way interaction, partition × components × frequency: F(2, 20) = 8.31, p = .002). As expected, the shared contribution of entropy and surprise was the largest of the variance partitions tested. But markedly, surprise was the strongest predictor of delta-band activity in pAC and aAC, and uncertainty was the strongest predictor of theta-band activity in pAC (2-way interaction, partition [uncertainty and surprise] × frequency: F(1, 10) = 60.82, p < .001) (Figure 4B). In Figure S4C, we show that this effect generalizes across the different types of regressors used in the full regression model (Figure S2B). Table S3 shows that this effect is not explained by differences in the spectral contents of regressors.
In the time domain, we compared the TRFs estimated in the full predictive-coding model (Figure 4C). We found that contextual uncertainty modulated the amplitude of early components of the pAC TRF (60–120 ms and 230 ms), which is consistent with the enhancement of a theta-wave response. We also found that the surprise induced by incoming phonemes enhanced a slightly later response from aAC (80–160 ms), followed by the deepening of a later trough (230–420 ms) in pAC (Figure 4C). This latter component is akin to the typical N400 response to low-probability endings (cloze) of word sequences observed in scalp EEG (Kutas and Hillyard, 1984; Frank et al., 2015; Broderick et al., 2018). The last detected effect of surprise was between 550 and 700 ms in pAC, akin to the late positivity observed in response to expectation violations, another EEG component (P600) well-studied in neurolinguistics (Van Petten and Luka, 2012). These findings are consistent with the enhancement of a delta-wave response.
Our data therefore suggest that contextual uncertainty increases the gain of early theta-band responses, whereas surprising inputs elicit subsequent delta responses of downstream areas, possibly to update internal models.
Reduction of Word-Level Uncertainty Is Explained by Phoneme Surprise
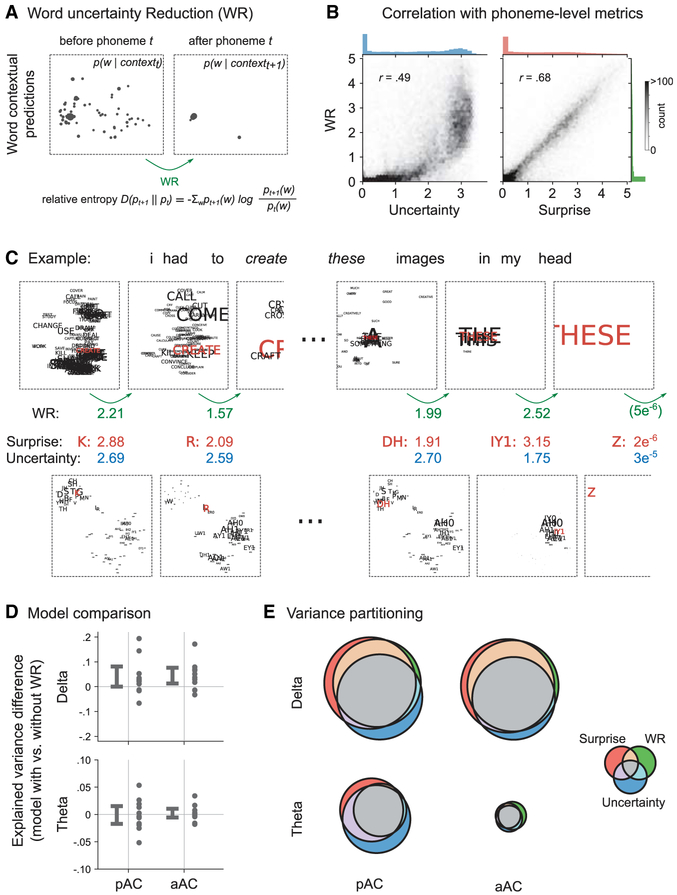
The ANN model (Figure 1) enables the quantification of specific aspects of the update of internal models during speech listening. For instance, the ANN can track how a current word is interpreted, as phonemes are perceived sequentially. The update to the internal model by a phoneme is quantified by the word uncertainty reduction (WR). WR is defined as the relative entropy between predictive word distributions before and after a given phoneme is presented (Figure 5A). Our data show that the WR metric correlates with phoneme surprise more strongly than with phoneme uncertainty (Figure 5B).
Figure 5. Reduction of Word-Level Uncertainty Is Explained by Phoneme Surprise.
(A) Two predictive distributions are shown as in Figure 1B: they illustrate word-level predictions before and after receiving a phoneme (the word “these” and the phoneme “DH”). We defined WR as the relative entropy between the two distributions.
(B) We show the association of WR with phoneme-level uncertainty and surprise across all phonemes in our stimulus set in a bivariate histogram alongside marginal histograms. WR has a stronger association to phoneme surprise.
(C) Illustration using the example sentence from Figure 1: shown are word- and phoneme-level predictive distributions (word-level is zoomed) along with the corresponding values of WR, uncertainty, and surprise. Note that for the word “create,” all three metrics are decreased for the second phoneme; in contrast, for the word “these,” there is less uncertainty about the second phoneme, but both the surprise and the associated WR are higher for the phoneme “IY1” (the number 1 signifies the stressed version of the phoneme “IY” in the CMU dictionary). This is because this phoneme constrains the interpretation of the word as “these,” whereas for the word “create” there are still multiple possible continuations of the phoneme sequence “K, R” in the given context.
(D) We show the relative performance of a regression model containing the feature space WR in addition to speech-audio, uncertainty, and surprise. We observe a moderate increase in performance for the delta band. Error bars show 95% CIs.
(E) We show the results of 3-way variance partitioning in the form of Venn diagrams. The areas of circles and their overlaps illustrate the average explained variance by the corresponding variance partition. We see that most of WR’s explanatory power is shared with phoneme surprise. Figure S5 further shows the consistency of the effect for single participants. Note that, as in Figure 4B, variance partitioning was performed after subtracting the variance explained by speech-audio regressors only.
Indeed, we observed that the effects of WR on neural activity are similar to the effects of phoneme surprise. Adding WR to the regression model leads to a moderate increase in explained variance in the delta band, but not for theta band (interaction model [with/without WR] × frequency: F(1, 10) = 7.05, p = .002, main effect of model for delta: F(1, 10) = 5.46, p = .04) (Figure 5D). We partitioned the variance explained by the full model into unique and shared variance components after subtracting the effect of speech-audio regressors, as in the analyses in Figure 4B. Most of the explanatory power of WR was shared with surprise, while surprise explains additional variance that is not accounted for by WR (see Figures 5E and S5). This suggests that contextual surprise at the phoneme level quantifies the relevance of the phoneme for the update of higher-level internal models, such as here, for the word-level interpretation.
DISCUSSION
We combined artificial neural network modeling with neurophysiological imaging to study hierarchical effects of natural speech predictability in the auditory/language pathway. Our findings bridge a gap between two views of brain responses to language stimuli, either as constructed from distinct event-related components (Kutas and Hillyard, 1984) or as modulations of ongoing oscillatory neurophysiological activity (Giraud and Poeppel, 2012; Lakatos et al., 2005; Gross et al., 2013). We show that during continuous speech listening, early event-related components emerge from stimulus-induced damped theta oscillations in primary auditory regions. Contextual uncertainty about the upcoming phoneme increases the gain of these early responses. This mechanism may provide downstream brain processing stages with higher signal-to-noise representations of speech sounds. In contrast, these subsequent brain processing stages are marked by stimulus-induced delta waves that are enhanced only when the incoming speech sound is informative (as quantified by surprise).
Our results thus suggest an intriguing organizing principle of speech processing for the learned allocation of brain processing resources to the most informative segments of incoming speech inputs. This result was enabled by a novel approach. (1) We view each elementary speech input (phoneme) in reference to a listener’s internal predictive model, which we approximate by an artificial neural network: this allows us to abstract across linguistic scales and calculate the expected (uncertainty) and actual (surprise) information gain of a given speech input in context. (2) We view neurophysiological responses as expressions of underlying oscillatory timescales: this provides a unifying view of several previously described temporally separated brain responses and instead reveals spectral separation between faster and slower neural timescales in the theta and delta ranges. (3) This spectral separation aligns with a functional division governed by the internal predictive model: sensory sampling based on expected information gain is implemented at a relatively rapid timescale, while updates of internal models based on actual information gain are implemented at a slower timescale.
Timescales in auditory and speech processing have been intensively studied, with the theta frequency range being viewed as key to the temporal sampling of sensory information (Gross et al., 2013; Teng et al., 2017; van Wassenhove et al., 2007). This process is suggested to be adaptive to the temporal contents of speech and the characteristics of the speech-motor apparatus (Ghazanfar et al., 2013; Chandrasekaran et al., 2009). Our findings reach beyond these low-level characteristics by suggesting that theta-rate sampling is optimized with respect to an internal predictive model, increasing sensory input gain in uncertain contexts. Temporal downsampling along the auditory/speech pathway has been suggested as a mechanism for hierarchical linguistic structure representations from sequential speech inputs (Giraud and Poeppel, 2012). For instance, a gradient of timescales in the temporal cortex was previously observed in electrophysiological recordings (Hamilton et al., 2018; Yi et al., 2019). Our present findings advance the comprehension of the neural mechanisms involved by specifically relating neural signals in the delta band to speech information deemed as non-redundant with the internal predictive model.
Temporal downsampling along the hierarchical neural pathways has been derived theoretically from predictive coding (Bastos et al., 2012). The theory has been used to explain spectral asymmetries in higher-frequency bands such as gamma and beta in the visual cortex (Bastos et al., 2015; Michalareas et al., 2016) and induced responses in the auditory cortex (Sedley et al., 2016). However, the theory is also applicable for lower-frequency ranges that we studied here: as discussed in the previous paragraph, speech has been found to be preferentially sampled at theta frequency ranges. Thus, the theory would indeed predict that this information is accumulated downstream in the delta frequency range to update internal models.
The effect of phoneme surprise and its relation to WR can be interpreted with reference to the sentence comprehension theory by Levy (2008). This theory considers the problem of interpreting the syntactic structure of a sentence incrementally word by word. It assumes that a perceiver holds a probability distribution p(T∣contextt) over multiple structures T that are compatible with the words processed so far and the context of the sentence. This distribution changes with every word: some interpretations become implausible, while some others become more plausible (see Figure 5C). Levy (2008) shows mathematically that the surprise of a given word in its context −logp(wt∣contextt) is equivalent to the uncertainty reduction in p(T) induced by the word t. The surprise incurred by a word thus directly quantifies how much it reduces the uncertainty with regards to the interpretation of a sentence.
Here we considered surprise at the phoneme level using an ANN trained to predict the next phoneme based on the context of the last 35 phonemes (~ 10 words). We should thus expect, in analogy to Levy’s theory, that the surprise incurred by a phoneme quantifies how much it reduces the uncertainty with regards to the current word w as well as the interpretation of the sentence T. From the ANN predictions, we could explicitly quantify the reduction of uncertainty with regards to the current word (WR). Indeed, we showed that WR is highly correlated to phoneme surprise, and most of its explanatory power with regards to neural signals is shared with phoneme surprise. Phoneme surprise explains more additional variance in the neural signals that cannot be accounted for by WR: this is to be expected, since a phoneme also reduces the uncertainty with regards to the interpretation of the sentence structure T. In our current model, we do not explicitly generate a distribution over possible sentence structures; instead, these are implicit in the ANN’s internal dynamics and lead to respective phoneme and word predictions.
The strong link between high-level internal models and lower-level surprise explains our findings of early effects of contextual predictability. Late effects previously reported with EEG (N400, P600) are typically interpreted as marking the increased processing demands induced by the occurrence of a surprising word (Kuperberg and Jaeger, 2016), thus the update of internal models as explained above. Here we also report early effects of contextual predictability on ongoing neurophysiological signals that cannot be explained only by a hierarchical feedforward process. These observations are compatible with the view that predictions formed in higher-level brain networks are channeled back and inhibit the responses of early sensory regions to predicted inputs (Rao and Ballard, 1999; Friston, 2005). So far, this view has been debated in the language domain (Kuperberg and Jaeger, 2016), and the reproducibility of supporting evidence has been questioned (Nieuwland et al., 2018; Nieuwland, 2019). We believe our study shows, using natural speech instead of trial-based presentation of words (Hamilton & Huth, 2018), combined with novel modeling and analysis approaches, robust effects of speech prediction starting from 60 up to 700 ms following a speech input.
In that respect, the human brain performs differently from current automatic speech recognition (ASR) systems, in which predictive language models intervene only relatively late in the speech-processing stream (Amodei et al., 2016; Bahdanau et al., 2016), selecting the most likely word instance a posteriori from a ranked list of possible transcriptions of the acoustic signal. The question remains whether these differences are imposed by the limited processing capacity of biological brains, or whether ASR systems could themselves benefit from a fully predictive processing strategy mimicking that of the human brain.
STAR★METHODS
LEAD CONTACT AND MATERIALS AVAILABILITY
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Peter Donhauser (peter.donhauser@mail.mcgill.ca).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Participants
11 healthy native English speakers were recruited (20-34 years; 5 female) as participants. The study was approved by the Montreal Neurological Institute’s ethics committee (NEU-11-036), in accordance with the Declaration of Helsinki. All participants gave written informed consent and were compensated for their participation. All participants had normal or corrected-to-normal vision and could comfortably read instructions presented to them during the MEG session. All participants reported normal hearing.
METHOD DETAILS
Speech dataset & MEG experimental stimuli
The speech data used in neural network training and the MEG experiment were taken from the TED-LIUM corpus (Rousseau et al., 2014). This corpus contains audio files and transcripts of 1495 / 8 / 11 publicly available TED talks for training / validation / test set, comprising 207 h / 96 min / 157 min of audio and 2.6 million / 17,868 / 27,814 words. Transcripts in the original corpus are temporally aligned with audio at the segment level. These segments were on average ~ 8 seconds long and contained ~ 28 words. We performed forced alignment using Prosodylab-Aligner (Gorman et al., 2011) to find the times when individual phonemes and words appear within the segments provided by the original corpus. The alignment procedure used the CMU pronouncing dictionary for North American English. Pronunciations for out-of-vocabulary words in the corpus were added manually to the dictionary. The symbols used for individual phonemes in this paper are the ones used by the CMU dictionary (Lenzo 2007) with numbers appearing after vowels indicating lexical stress (0: no stress, 1: primary stress, 2: secondary stress).
We selected the words that appeared at least 8 times in the training set, resulting in a vocabulary Vw containing 10,145 words. The less frequent words were replaced by an unk (unknown) token. The vocabulary for phonemes Vp contained 69 separate phonemes (24 consonants + 15 vowels × 3 levels of lexical stress).
We selected four talks out of the TED-LIUM test set as stimuli for the MEG experiment (see table S1), expected to appeal to most participants. Three of the talks were split up into two parts to produce a stimulus set for seven blocks of MEG recording less than ten minutes each. We manually verified the automatic (phoneme and word) alignment results for these four talks using the Praat speech analysis software (Boersma et al., 2002).
Language model
We trained a recurrent neural network with long short-term memory (LSTM) cells (Hochreiter and Schmidhuber 1997) using PyTorch (Paszke et al., 2017) on the speech dataset described above. Networks like these are usually trained e.g., to predict the next word in a sequence based on the history of previous words (Zaremba et al., 2014), whereas here we train to predict the next phoneme. We make two important additions to the basic architecture to adapt it to spoken language and phoneme-level modeling: First, we provide the network with timing information, namely the duration of phonemes and pauses. Since there is no punctuation in spoken language, this can provide important syntactic information. Second, we combine word- and phoneme-level inputs and predictions, since this helps the network hold semantic and syntactic information better than when training only from phonemes.
Importantly, the trained network outputs the contextual probability for each phoneme at t
| (1) |
where phoneme∈Vp and contextt = {phoneme1,..,t–1, duration1,..,t–1, pause1,..,t–1,word1,..,k–1}. Index t runs over phonemes, whereas index k runs over words. This allows us to compute the contextual uncertainty as the entropy of the phoneme prediction distribution at t as
| (2) |
as well as the surprise associated with the presented phoneme at t as
| (3) |
Neural network architecture
In the following we describe the additions made to the standard word-level network (Zaremba et al., 2014) step-by-step, comparing performances of networks using word, phoneme and timing information, namely:
word-only
words & timing
phonemes & timing
phonemes, words & timing
. In Figure S1 we show the architecture of the network that performed best at modeling the speech data at the phoneme level. For the different architectures explored, the input to the LSTM cells is encoded in the vector it and the output is the vector ot, both of which are of size S (S will be used to scale the network to different capacities). The LSTM cell at a given layer l = 1, .., L contains state variables (hidden state) and (cell state or memory cell) and computes the transition:
| (4) |
Layer l = 1 receives the input to the network, so: , whereas the last layer l = L computes the output, so: . We used two layers and dropout between the layers as a regularizer (the non-recurrent connections including connections to and from ot and it [Zaremba et al., 2014]).
In the standard, word-only version of the network (Zaremba et al., 2014) we have the previous word at t – 1 encoded in the input it of the network and the current word at t as the target. As is common in neural language models, the word at t – 1 is represented in an embedding layer (Bengio et al., 2003) that is jointly trained with the LSTM network: this means that each word in the vocabulary is mapped to a real-valued vector eWin[word] of size S. In the word-only network, the input to the first LSTM layer is it = eWin[wordt–1]. This can be formulated as a matrix multiplication, if we use the one-hot representation of a word: this is a vector of size V that contains a 1 at the word’s index and 0’s everywhere else. Thus, to obtain the input vector it, the one-hot representation is multiplied with the embedding matrix Ewin of size V × S, which contains all the words’ embeddings in its columns. The words’ embedding vectors represent a word within a multidimensional space (here of size S) in which semantic and syntactic relations between the words are represented by Euclidean distances. Similar words appear close to each other in this multidimensional space, and different dimensions in this space represent different features (semantic and syntactic) along which words can be similar or dissimilar. Please refer to Figure 1B for examples of embeddings.
The output of the last layer o is then conversely multiplied by the S × V output embedding Ewout followed by a softmax nonlinearity. The output of the softmax is a probability distribution over the vocabulary, quantifying
| (5) |
This probability can be influenced by the context of all words t = 1, .., t – 1 presented at test time, because this information is recurrently encoded in the hidden and cell states (see Equation 4) so we can say that
| (6) |
It is possible to tie the input and output word embeddings such that : this decreases the expressiveness of the network as a whole but decreases the number of parameters to be trained.
Because we train the network on spoken language, there is no punctuation; instead, important syntactic information can be carried by the timing of and pauses between words. In the words & timing network, we use the duration of the word at t – 1 and the duration of the following silence (durationt–1 and pauset–1) and encode them together with the word information in input vector it. The two time-variables are quantized into Q = 20 discrete bins logarithmically spaced between 50ms and 10sec and subsequently fed through a Q-dimensional real-valued embedding for durations edur and silences esil. We concatenate these time embedding vectors together with the word embedding vector to arrive at a (S + 2 × Q)-dimensional input vector it. The rationale for using quantization followed by an embedding (instead of just the continuous linear value in milliseconds) is that the network can learn similarities of different timings from the data: the difference between a 500 ms or a 1 s pause carries more information than the difference between a 19.5 s or a 20 s pause. This network thus quantifies
| (7) |
The phonemes & timing network is equivalent to the words & timing network described in the last section. Instead of words, we are providing the network with the phoneme at t – 1 as input and the phoneme at t as target, using input and output embeddings for phonemes epin and epout. Just as with word embeddings, the phoneme embeddings trained with this network encode similarities between phonemes (note the very obvious clustering into consonants and vowels in Figure 1B. This network quantifies
| (8) |
where index t runs over phonemes.
Theoretically, it should be possible for the phoneme-level network to discover higher-order structure like words, grammatical structure and semantics only from the (low-level) phoneme input. It is difficult in practice however. Hence we developed an architecture that makes combined use of phonetic and word-level information (phonemes, words & timing, Figure S1). Here, the input vector it encodes the phoneme at t – 1, its duration and subsequent silence, as before. In addition, it encodes the previous word: this word could have been several phonemes before, thus we introduce an additional index k to run over words rather than phonemes. We concatenate the embeddings corresponding to these four variables to produce a (2 × S + 2 × Q)-dimensional input vector it. Targets for training are the current phoneme as well as the current word: the output of the last layer o is separately fed through an output embedding for words Ewout and phonemes Epout followed by a softmax nonlinearity. The network thus quantifies
| (9) |
| (10) |
where index t runs over phonemes and index k runs over words. Refer to Figure 1A for contextual probabilities estimated by the network and Figure S1D for an example data sequence).
Parameters and neural network results
The state vectors and as well as embedding vectors eword and ephoneme are all of size S, and we tested different values of S together with different dropout probabilities (200/650/1500 and 0/0.5/0.65 respectively [Zaremba et al., 2014]). Each of the three parameter settings was tested with tied or separate weights for input and output embeddings. Weights as well as embedding vectors were initialized as uniformly random between −0.1 and 0.1 and biases set to zero. Hidden and cell states were initialized to zero at t = 0, but hidden and cell states were copied over to the next training batch (batch size: 20) to preserve long-term context. Backpropagation through time was used to train all networks, with gradients propagated through the last 35 inputs.
Results from the word-level networks in table S2 are shown in perplexity (PPL) which is derived from the average surprise per word under the given model: . We see, first, that larger networks (with higher dropout values) performed better (lower PPL), thus we are not overfitting the training data. Second, we can see that adding timing information to the input increases performance substantially, probably since it can provide similar syntactic cues to punctuation in written language. For this reason we used timing in the phoneme-level networks, as well as the highest value S = 1500.
The results of the phoneme-level networks are shown in bit-per-phoneme (BPP), which is the average surprise per phoneme under a given model, expressed in bits: . We see from table S2 that providing the network with additional word input increases performance (lowers BPP): likely, the network receiving only phoneme input has difficulty keeping higher-level information (syntax & semantics) in its memory. Tied embedding weights helped performance in the case of the word-level network: the lower number of parameters to be estimated was beneficial. In the phoneme-level network, tied weights led to decreased performance: here the flexibility of having different input and output embeddings was beneficial. For MEG analyses, we thus used the architecture phonemes, words & timing with non-tied weights to model predictions at the phonetic time-scale.
N-gram modeling
We generated a simpler model of phoneme predictions to compare against the ANN. This was to verify that observed effects of predictions could not be explained by short-term transition probabilities. The probability of a phoneme in context can be expressed as the proportion of times the phoneme in question has been following the preceding phoneme (in case of a bigram model) or the last two phonemes (in case of a trigram model) in the training data. The simplest model is a unigram model, which only considers the frequency of a given phoneme regardless of its context.
These models are very data greedy. In our case, we have 69 phoneme categories, hence for a bigram model there are 692 = 4,761 possible phoneme combinations to consider; for a trigram 693 = 328,509 and for a 4-g 694 = 22,667,121 combinations. Our training set in the TEDLIUM corpus contained around 8,000,000 phonemes, thus we fitted uni-, bi- and trigram models to have enough data for fitting.
We trained the models on the same data as the neural networks. The n-gram models did not model the TED-talk language data as well as the neural network (BPP: 5.13, 4.23 and 3.51 for uni-, bi- and trigams respectively, compared to 2.30 for the ANN used in the main text). For MEG analyses, we computed surprise and uncertainty from the predictive distributions obtained from bi- and trigram models (as in Equations 2 and 3). For unigram models we computed only surprise, since the predictive distribution is by definition equal for each phoneme.
Word uncertainty reduction
The ANN generates predictive distributions over both phonemes and words at each time point t (see Equation 10). We therefore computed how much the uncertainty w.r.t. the current word was reduced by the phoneme at time t. This value, called word-uncertainty reduction (WR), was derived from the Kullback-Leibler divergence or relative entropy between two predictive distributions
| (11) |
where pt+1(w) = p(wt+1∣contextt+1) and pt(w) = p(wt ∣ contextt).
Note the discontinuity at word boundaries: if t + 1 is the beginning of a new word, the probability p(wt+1∣contextt+1) is w.r.t. this new word and p(wt∣contextt) is the remaining uncertainty of the previous word before receiving its last phoneme. To reflect the assumption that the last phoneme in a word lifts the remaining uncertainty w.r.t the old word, we replaced D(pt+1∥pt) by where contains 1 for the word that finishes at t and zero for all other words. We can show from Equation 11 that this reduces to
| (12) |
which is the negative surprise of the word at time point t.
MEG experiment
Data acquisition
The participants were measured in a seated position using a 275-channel VSM/CTF MEG system with a sampling rate of 2400 Hz (no high-pass filter, 660 Hz anti-aliasing online low-pass filter). Three head positioning coils were attached to fiducial anatomical locations (nasion, left/right pre-auricular points) to track head movements during recordings. Head shape and the locations of head position coils were digitized (Polhemus Isotrak, Polhemus Inc., VT, USA) prior to MEG data collection, for co-registration of MEG channel locations with anatomical T1-weighted MRI. Eye movements and blinks were recorded using 2 bipolar electro-oculographic (EOG) channels. EOG leads were placed above and below one eye (vertical channel); the second channel was placed laterally to the two eyes (horizontal channel). Heart activity was recorded with one channel (ECG), with electrical reference at the opposite clavicle.
A T1-weighted MRI of the brain (1.5 T, 240 × 240 mm field of view, 1 mm isotropic, sagittal orientation) was obtained from each participant, either at least one month before the MEG session or after the session. For subsequent cortically-constrained source analyses, the nasion and the left and right pre-auricular points were first marked manually in each participant’s MRI volume. These were used as an initial starting point for registration of the MEG activity to the structural T1 image. An iterative closest point rigid-body registration method implemented in Brainstorm (Tadel et al., 2011) improved the anatomical alignment using the additional scalp points. The registration was visually verified.
The scalp and cortical surfaces were extracted from the MRI volume data. A surface triangulation was obtained using the Freesurfer (Fischl 2012) segmentation pipeline, with default parameter settings, and was imported into Brainstorm. The individual high-resolution cortical surfaces (about 120,000 vertices) were down-sampled to about 15,000 triangle vertices to serve as image supports for MEG source imaging.
Experimental procedure
Participants received both oral and written instructions on the experimental procedure and the task. In each of the seven blocks of recording, participants listened to one TED talk; the order of talks was counterbalanced between participants. Participants were instructed to fixate on a black cross presented on a gray background. At the end of each block, they were presented with several statements about the material presented to them. Participants judged with a button press whether the statements were true or false. Out of the 55 questions, the participants answered correctly on average 46 questions (individual participants: 50, 49, 46, 53, 39, 41, 41, 48, 47, 45, 48 correct answers), indicating that all participants listened to the talks attentively.
The audio signal was split and recorded as an additional channel with the MEG data such that audio and neural data could be precisely synchronized. To decrease the possibility of electromagnetic contamination of the data from the signal transducer, ~ 1.5 m air tubes between the ear and the transducer were used such that the transducer could be tucked into a shielded cavity on the floor (>1 m from the MEG gantry, behind and to the left of the participant).
MEG data processing
Artifact removal and rejection
We computed 40 independent components (ICA, Delorme et al., 2007) from the continuous MEG data filtered between 0.5 and 20 Hz and downsampled to 80 Hz. We identified components capturing artifacts from eye-blinks, saccades and heart-beats based on the correlation of ICA component time-series and ECG/EOG channels. We computed a projector from the identified mixing/unmixing matrices (Φ/Φ+) as I – ΦΦ+ and applied it to the raw unfiltered MEG data to remove contributions from these artifact sources. Subsequently, noisy MEG channels were identified by visually inspecting their power spectrum and removing those that showed excessive power across a broad band of frequencies. The raw data were further visually inspected to detect time segments with excessive noise e.g., from jaw clenching or eye saccades contamination not captured by any ICA component.
Data coregistration
Since our recording blocks were relatively long (~ 10 min, see Table S1), participants’ head position could shift over the course of a run. We used the continuous recordings of participants’ head position to cluster similar head positions: In each run we performed k-means clustering of the head-position time-series (9 time-series, x/y/z position for each coil) into eight clusters. We computed gain matrices Gc and source imaging operators Kc based on the average head position in each cluster c = 1, .., 8 * 7 (8 clusters for seven blocks).
Forward modeling of neural magnetic fields was performed using the overlapping-sphere model (Huang et al., 1999). A noise-normalized minimum norm operator (dSPM, Dale et al., 2000) was computed based on the gain matrix G of the forward model and a noise covariance matrix, which was estimated from same-day empty-room MEG recordings. The source space was defined by the cortical triangulation and at each vertex the source orientation was constrained to be normal to the cortical surface. This produced a 15000 (sources) × 275 (channels) source imaging operator K.
We then define the average (15000 × 15000) resolution matrix across head positions c
| (13) |
where nc is the number of time samples belonging to cluster c and perform singular value decomposition of this matrix . The M first singular vectors define the spatial basis for the coregistered data X used for the rest of the analyses, where M is the index of the singular value that cuts off 99.9% of the singular value spectrum. The MEG data are thus projected into a low-dimensional space as
| (14) |
Note that we can move back to the source (XUΓ) or the channel space () through a linear transformation of the data (see Figure S3). We finally downsampled the data matrix X to 150 Hz for faster data processing and applied a high-pass filter of 0.5 Hz to avoid slow sensor drifts. We refer to the projected data matrix X as coregistered MEG signals in this paper.
Ridge regression
The regression analysis described in the following was performed using custom code written in python using numpy and scipy. Some code was adapted from the Github repository alexhuth/ridge.
Let X and Xnew be the (N, Nnew) ×M data matrices for training and test set respectively, where (N, Nnew) are the number of samples in time and M is the number of signals. Let M and Mnew be the (N, Nnew)×K design matrices, where K is the number of features used for prediction. The MEG data are predicted as a linear combination of the design matrix columns (see Figure S2) as
| (15) |
In standard regression, the weights B are estimated as
| (16) |
from the singular value decomposition of the design matrix M = USVT. Instead of just inverting the singular values as done above, ridge regression adds a penalty β that regularizes the solution (Hoerl and Kennard 1970). We calculate
| (17) |
for each singular value Sj and fill the ridge diagonal matrix D = diag(d) to calculate the solution
| (18) |
To evaluate the prediction we then apply these weights to the design matrix of the test set
| (19) |
| (20) |
and compute a goodness-of-fit measure between predicted and recorded signals.
Optimizing spatial components
In MEG/EEG channel data, we observe linear mixtures of the underlying sources. Thus our goal is not to predict the data on the channel but on the level of physiological sources, which can be estimated by spatial filtering (Baillet et al., 2001; Blankertz et al., 2008). As we described in a previous paper (Donhauser et al., 2018), we can design spatial filters in a data-driven manner by specifying a quality function on the source signal s = Xw
| (21) |
that captures a hypothesized property of the source signal s. The spatial filters are optimized on the training set, as are the regression weights B.
In this paper we are interested in sources that are well explained by our model M. Thus we optimize f(s) as the ratio of explained variance to unexplained variance as
| (22) |
a value that is proportional to an F-statistic. This can be solved in the form of a generalized eigenvalue problem (GEP)
| (23) |
where and , resulting in a set of spatial filters W = [w1, w2, …, wM] ordered by the ratios λ. The regression model for the spatially filtered signals si, i = 1, …, M is thus given by
| (24) |
The matrix W = [w1, …, wM] performs the function of a spatial filter, whereas the fields generated by these sources (the spatial patterns) are given by the inverse (Haufe et al., 2014): P = W−1. We refer to the set of spatial filters/patterns and their corresponding signals as spatial components in the main text. We regularize the spatial filter optimization (Donhauser et al., 2018) by diagonal loading of matrices C1 and C2 parameterized by the regularization parameter α as
| (25) |
Group-optimized spatial components
The optimization procedure described above results in Mj spatial components for each participant j = 1, .., 11 in this study. These components are defined by the matrices containing spatial filters Wj and spatial patterns Pj. Associated with each component is a score that we use to select patterns that are well described by our regression model (the correlation between predicted and observed component signals). Retaining only components exceeding a certain correlation threshold (see below: Selecting hyperparameters) produces a set of components that form a low-dimensional subspace in MEG channel space (Donhauser et al., 2018). We define as the M×Lj dimensional spatial filter matrix, with Lj the number of spatial components retained for participant j. To compare components across participants we rotate the subspace axes in order to maximize the similarity of regression weights across participants, thus we find a rotation matrix Rj for each participant such that the resulting regression weights
| (26) |
are highly correlated across participants. This is achieved using canonical correlation analysis (CCA) for several sets of variables (Kettenring 1971) using an implementation in python (Bilenko and Gallant 2016). Note that the CCA is solved by invoking the GEP, as in the spatial component optimization procedure described above.
We obtained cortical maps for the rotated spatial components as ∣RTP*UΓ∣. These maps were smoothed with a 3mm kernel and projected to a high-resolution group template surface in Brainstorm (Tadel et al., 2011). Note that, while the regression weights (and thus the temporal response profile) of the identified components are optimized to be similar across participants, cortical maps can be different for each participant. To evaluate consistencies of cortical maps across the group, individual participants’ maps were averaged across the seven cross-validation runs and z-scored across space. At each cortical vertex we obtained a bootstrap distribution of the group mean; we then thresholded the maps by keeping the vertices where 99% of bootstrap values were greater than 1. The bootstrap-z-scores in Figure 3A are generated by taking the mean of the bootstrap distribution, subtracting 1, and dividing by the standard deviation of the bootstrap distribution. We show individual participant maps in Figure S3F that were generated equivalently by averaging and bootstrapping over the seven cross-validation runs and keeping vertices where 99% of bootstrap values had a mean >2.
Regressors
The regressors we used to model MEG data in response to TED talks are organized into three feature spaces: the speech-audio, uncertainty and surprise feature space (Figure S2).
The speech-audio feature space includes three regressors: the a) speech envelope extracted from the audio file that was presented to participants. The envelope was extracted by computing the square root of the acoustic energy in 5ms windows and linearly interpolating to the MEG data sampling rate (150 Hz). The b) speech on/off regressor is based on the results from the transcription alignment. A given time-point in the audio file is classified to be part of a phoneme, a non-speech sound, or a silence. The regressor includes a 1 if the time-point is part of a word/phoneme and zeros otherwise. The c) phoneme onset regressor includes a 1 at the start of a phoneme and 0’s otherwise.
The uncertainty and surprise feature spaces are based on the values defined in Equations 2 and 3. For both metrics we generate three different regressors, as shown in Figure S2: a step regressor including the uncertainty/surprise value throughout the duration of a phoneme, an impulse regressor, including the uncertainty/surprise value at the start of a phoneme and a regressor that features uncertainty/surprise values in interaction with the envelope (step regressor multiplied by speech envelope). To avoid extreme values (outliers) to drive the results, we bin uncertainty and surprise values into 10 separate bins according to their distribution across the speech material before producing the regressors.
Similar to other papers, we use what is called a TRF (in M/EEG, Di Liberto et al., 2015; Zion Golumbic et al., 2013) or voxel-wise modeling (in fMRI, Huth et al., 2016) approach. We replicate each regressor at different temporal lags τ to account for the a-priori unknown temporal response profile. Different from other studies, we use here a multi-resolution approach, where lags are densely spaced at short latencies and more widely spaced at long latencies (see Figure S2). This allows us to model also low-frequency components in the MEG signal (requiring long lags) while keeping the number of to-be-estimated regressors low. Note that the regression model remains unchanged by this approach and we still make predictions at the full sampling rate. A different way to reduce the number of to-be-estimated regressors would be to use a set of basis functions such as a wavelet basis to be convolved with the original regressors. Regression weights would then be estimated per basis function rather than per lag.
Cross-validation scheme
We perform cross-validation in a leave-one-block-out fashion, fitting the regression models on MEG data of six blocks (training set) and evaluating performance on one left out block (test set). Before performing the regression we remove all time samples marked as bad during preprocessing and then z-score the columns of the training set’s design matrix M and MEG data X. The same normalization is applied to the test set using means and standard deviation of the training set, since these can be seen as learned parameters. The cross-validation procedure is repeated and results are averaged across all seven blocks.
In each cross-validation run we use the training data (Xj and M) to estimate separate regression weights Bj for each participant j. More precisely, we fit four different models containing feature spaces:
speech-audio (speech-audio model)
speech-audio and uncertainty (uncertainty model)
speech-audio and surprise (surprise model)
speech-audio, uncertainty and surprise (predictive-coding model)
Subsequently, we extract subject-optimized and group-optimized spatial components ( and Rj, see above) using training data for the full predictive-coding model. Using a bootstrap procedure (see below: Selecting hyperparameters) we select 1) hyper-parameters for regression regularization and 2) the number of spatial components Lj to retain per participant.
We finally use the test data (Xj,new and Mnew) to estimate performance of the regression models by computing coherence between the predicted
| (27) |
and recorded signals
| (28) |
Coherence is computed as a spectrally resolved performance measure (Theunissen et al., 2001; Holdgraf et al., 2017) and is defined as
| (29) |
where and S[f] are the fourier coefficients at frequency f of the predicted and recorded signals respectively. For spectral estimation we used a multitaper procedure as implemented in MNE-Python (Gramfort et al., 2013) with a frequency smoothing of 0.5 Hz and 3 Hz for the two frequency ranges shown in Figure 3 (.4-2 and 2-20 Hz respectively).
Variance partitioning
Cross-validation gives us an estimate of how much variance in a given neural signal is explained by the different regression models (speech-audio, uncertainty, surprise & predictive-coding) computed as the squared correlation values R2. The regression models are, however, combinations of feature spaces. To evaluate how much explained variance is unique to or shared between the feature spaces of interest we used variance partitioning similar to the approach in de Heer et al. (2017)
The idea behind variance partitioning can be understood by the venn diagrams in Figure S4B that illustrate the set theoretic computations performed to obtain unique and shared variance components.
Since explained variance R2 is an empirical estimate in the cross-validation procedure, it is possible to obtain variance partitions that are not theoretically possible: e.g., when a joint model containing two feature spaces (due to overfitting during training) explains less variance than one of the individual feature spaces, we can and up with a negative unique variance component. We used the procedure described in de Heer et al. (2017) that considers the estimated explained variance of a model as a biased estimate and solves for the lowest possible bias values that produce no nonsensical results (a constrained function minimization problem).
We used magnitude squared coherence (the square of the measure defined in Equation 29) between predicted and observed signals as a measure of explained variance in the two frequency bands of interest (delta: 0.5-4 Hz; theta: 4-10 Hz) computed with multitaper frequency smoothing of 3 Hz. The unique and shared variance partitions were computed (according to the procedure described above) in and then averaged across each of the seven blocks.
Temporal response functions
The TRFs shown in this paper are derived from spatially filtered and rotated regression weights (, see Equation 26) which are reshaped to produce a time-series sampled at temporal lags τ In Figure 3B we averaged TRFs across all regressors in the model to illustrate the temporal response profile of the two spatial components. For Figure 4C, we averaged TRFs within each of the three feature spaces and displayed the resulting time-series for speech-audio as well as the summed time-series speech-audio + uncertainty and speech-audio + surprise to show the modulation of the basic waveform by uncertainty and surprise respectively.
Selecting hyperparameters
In each cross-validation run we estimate the best spatial regularization parameter α (Equation 25), and the best ridge regularization parameter β (Equation 17) and the number of subject-level spatial components Lj.We do this using a bootstrap procedure (Huth et al., 2016): we randomly draw 150 chunks of 600 time samples (4 s) from the training data to hold out and train on the rest of the training samples using a grid of 10 different α values logarithmically spaced between 10−4 to 10−0.5 and 20 different β values logarithmically spaced between 100.5 to 103.5. We test performance for each pair of regularization values on the held out samples by the correlation coefficient. We repeat this procedure 15 times and average correlations for each α, β and spatial component i to obtain correlations rα,β,i. We then take a weighted average of these correlation values as
| (30) |
and select the hyperparameters α* and β* that maximize this value. This way the hyperparameter selection is driven more strongly by the high-performing components. We then perform significance tests on the correlation values rα*,β*,j and select the number of spatial components Lj such that we can reject the null hypothesis
| (31) |
The above hyperparameter selection was conducted for the main results presented in Figures 3 and 4. To reduce computation time, we opted for a more restricted hyperparameter selection for the other analyses: 5 instead of 10 different α values logarithmically spaced between 10−4 to 10−0.5, 15 instead of 20 different β values logarithmically spaced between 100.5 to 103.5 and 5 instead of 15 bootstrap iterations. Note that for all model comparisons we report results obtained through equivalent hyperparameter selection procedures.
QUANTIFICATION AND STATISTICAL ANALYSIS
No participants were excluded from the analysis. All errorbars represent 95% bootstrap confidence intervals computed using 5999 bootstrap samples.
Cross-validation results
We compared performance of the full model (Speech-audio, Entropy & Surprise) to the speech-audio model using repeated-measures ANOVA in R. See main text and Figure 4A for results.
We evaluated the variance partitioning results using a three-way repeated-measure ANOVA in R with factors Partition (uncertainty unique, surprise unique, shared), Frequency band (delta, theta) and Spatial component (pAC, aAC). See main text and Figure 4B for results.
Temporal response functions
We performed a randomization procedure to evaluate the lags at which uncertainty and surprise modulate neural responses significantly (i.e., the regression weights exceed those computed for a null model). We estimated TRFs for the full predictive model on combined data from all blocks, once for the correct uncertainty and surprise values (observed TRFs) and 110 times while permuting pairs of uncertainty and surprise values randomly across phonemes in a block (null TRFs). We then check at which temporal lags τ the TRFs exceed (in absolute value) the null TRFs in at least 107 (p < .05, two-tailed) of randomization runs. This evaluates significance on the single-subject level. To obtain a group statistic, we refer to the prevalence test we described before (Donhauser et al., 2018). According to this test, in order to reject the majority null hypothesis (effect present in less than half of the population) at pmaj < .01, we require > = 10 out of 11 participants to show a significant effect. In Figure 4C we show the lags at which this majority null hypothesis is rejected for uncertainty and surprise.
DATA AND CODE AVAILABILITY
The phoneme and word alignments generated during this study for the TED-LIUM corpus are available at github.com/pwdonh/tedlium_alignments. The code for the artificial neural network training is available at github.com/pwdonh/tedlium_model. The raw MEG data generated during this study are available upon request from the lead contact Peter Donhauser (peter.donhauser@mail.mcgill.ca or peter.w.donhauser@gmail.com).
Supplementary Material
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| TED-LIUM corpus | Rousseau et al., 2014 | http://www.openslr.org/19/ |
| Software and Algorithms | ||
| Brainstorm | Tadel et al., 2011 | http://neuroimage.usc.edu/brainstorm/; SCR_001761 |
| PyTorch | Paszke et al., 2017 | https://pytorch.org/ |
| Praat | Boersma et al., 2002 | http://www.fon.hum.uva.nl/praat/; SCR_016564 |
| MNE-Python | Gramfort et al., 2013 | https://github.com/mne-tools/mne-python; SCR_005972 |
| Freesurfer | Fischl, 2012 | https://surfer.nmr.mgh.harvard.edu/; SCR_001847 |
| Prosodylab-aligner | Gorman et al., 2011 | https://github.com/prosodylab/Prosodylab-Aligner |
Highlights.
A neural network model was trained to generate contextual speech predictions
Contextual uncertainty and surprise of speech were estimated using this model
Human neurophysiological responses to speech showed a hierarchy of timescales
Theta and delta were modulated by uncertainty and surprise respectively
ACKNOWLEDGMENTS
We thank Benjamin Morillon, Shari Baum, Sebastian Puschmann, and Denise Klein for helpful comments on earlier versions of this manuscript and Elizabeth Bock and Heike Schuler for help in data acquisition. Supported by the NIH (R01 EB026299) and a Discovery grant from the Natural Sciences and Engineering Research Council of Canada (436355-13) to S.B. This research was undertaken thanks in part to funding from the Canada First Research Excellence Fund, awarded to McGill University for the Healthy Brains for Healthy Lives initiative.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information can be found online at https://doi.org/10.1016/j.neuron.2019.10.019.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Amodei D, Ananthanarayanan S, Anubhai R, Bai J, Battenberg E, Case C, Casper J, Catanzaro B, Cheng Q, Chen G, et al. (2016). Deep speech 2: end-to-end speech recognition in English and Mandarin. In International Conference on Machine Learning, pp. 173–182. [Google Scholar]
- Arnal LH, and Giraud A-L (2012). Cortical oscillations and sensory predictions. Trends Cogn. Sci 16, 390–398. [DOI] [PubMed] [Google Scholar]
- Bahdanau D, Chorowski J, Serdyuk D, Brakel P, and Bengio Y (2016). End-to-end attention-based large vocabulary speech recognition. In 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (IEEE), pp. 4945–4949. [Google Scholar]
- Baillet S (2017). Magnetoencephalography for brain electrophysiology and imaging. Nat. Neurosci 20, 327–339. [DOI] [PubMed] [Google Scholar]
- Baillet S, Mosher JC, and Leahy RM (2001). Electromagnetic brain mapping. IEEE Signal Process. Mag 18, 14–30. [Google Scholar]
- Bastos AM, Usrey WM, Adams RA, Mangun GR, Fries P, and Friston KJ (2012). Canonical microcircuits for predictive coding. Neuron 76, 695–711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastos AM, Vezoli J, Bosman CA, Schoffelen J-M, Oostenveld R, Dowdall JR, De Weerd P, Kennedy H, and Fries P (2015). Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron 85, 390–401. [DOI] [PubMed] [Google Scholar]
- Bengio Y, Ducharme R, Vincent P, and Jauvin C (2003). A neural probabilistic language model. J. Mach. Learn. Res 3, 1137–1155. [Google Scholar]
- Bilenko NY, and Gallant JL (2016). Pyrcca: regularized kernel canonical correlation analysis in python and its applications to neuroimaging. Front. Neuroinform 10, 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blankertz B, Tomioka R, Lemm S, Kawanabe M, and Muller K-R (2008). Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process. Mag 25, 41–56. [Google Scholar]
- Boersma P, et al. (2002). Praat, a system for doing phonetics by computer. Glot Int. 5, 341–345. [Google Scholar]
- Brodbeck C, Hong LE, and Simon JZ (2018). Rapid transformation from auditory to linguistic representations of continuous speech. Curr. Biol 28, 3976–3983.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broderick MP, Anderson AJ, Di Liberto GM, Crosse MJ, and Lalor EC (2018). Electrophysiological correlates of semantic dissimilarity reflect the comprehension of natural, narrative speech. Curr. Biol. 28, 803–809.e3. [DOI] [PubMed] [Google Scholar]
- Chandrasekaran C, Trubanova A, Stillittano S, Caplier A, and Ghazanfar AA (2009). The natural statistics of audiovisual speech. PLoS Comput. Biol 5, e1000436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Liu AK, Fischl BR, Buckner RL, Belliveau JW, Lewine JD, and Halgren E (2000). Dynamic statistical parametric mapping: combining fMRI and MEG for high-resolution imaging of cortical activity. Neuron 26, 55–67. [DOI] [PubMed] [Google Scholar]
- de Heer WA, Huth AG, Griffiths TL, Gallant JL, and Theunissen FE (2017). The hierarchical cortical organization of human speech processing. J. Neurosci 37, 6539–6557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A, Sejnowski T, and Makeig S (2007). Enhanced detection of artifacts in EEG data using higher-order statistics and independent component analysis. Neuroimage 34, 1443–1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Liberto GM, O’Sullivan JA, and Lalor EC (2015). Low-frequency cortical entrainment to speech reflects phoneme-level processing. Curr. Biol 25, 2457–2465. [DOI] [PubMed] [Google Scholar]
- Ding N, and Simon JZ (2012). Emergence of neural encoding of auditory objects while listening to competing speakers. Proc. Natl. Acad. Sci. USA 109, 11854–11859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donhauser PW, Florin E, and Baillet S (2018). Imaging of neural oscillations with embedded inferential and group prevalence statistics. PLoS Comput. Biol 14, e1005990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B (2012). FreeSurfer. Neuroimage 62, 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontolan L, Morillon B, Liegeois-Chauvel C, and Giraud A-L (2014). The contribution of frequency-specific activity to hierarchical information processing in the human auditory cortex. Nat. Commun 5, 4694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank SL, Otten LJ, Galli G, and Vigliocco G (2015). The ERP response to the amount of information conveyed by words in sentences. Brain Lang. 140, 1–11. [DOI] [PubMed] [Google Scholar]
- Friston K (2005). A theory of cortical responses. Philos. Trans. R. Soc. Lond. B Biol. Sci 360, 815–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghazanfar AA, Morrill RJ, and Kayser C (2013). Monkeys are perceptually tuned to facial expressions that exhibit a theta-like speech rhythm. Proc. Natl. Acad. Sci. USA 110, 1959–1963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giraud A-L, and Poeppel D (2012). Cortical oscillations and speech processing: emerging computational principles and operations. Nat. Neurosci 15, 511–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorman K, Howell J, and Wagner M (2011). Prosodylab-aligner: a tool for forced alignment of laboratory speech. Can. Acoust 39, 192–193. [Google Scholar]
- Gramfort A, Luessi M, Larson E, Engemann DA, Strohmeier D, Brodbeck C, Goj R, Jas M, Brooks T, Parkkonen L, and Hämäläinen M (2013). MEG and EEG data analysis with MNE-Python. Front. Neurosci 7, 267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Hoogenboom N, Thut G, Schyns P, Panzeri S, Belin P, and Garrod S (2013). Speech rhythms and multiplexed oscillatory sensory coding in the human brain. PLoS Biol. 11, e1001752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton LS, and Huth AG (2018).The revolution will not be controlled: natural stimuli in speech neuroscience. Lang. Cogn. Neurosci Published online July 22, 2018. 10.1080/23273798.2018.1499946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton LS, Edwards E, and Chang EF (2018). A spatial map of onset and sustained responses to speech in the human superior temporal gyrus. Curr. Biol 28, 1860–1871.e4. [DOI] [PubMed] [Google Scholar]
- Haufe S, Meinecke F, Görgen K, Dähne S, Haynes J-D, Blankertz B, and Bießmann F (2014). On the interpretation of weight vectors of linear models in multivariate neuroimaging. Neuroimage 87, 96–110. [DOI] [PubMed] [Google Scholar]
- Hochreiter S, and Schmidhuber J (1997). Long short-term memory. Neural Comput. 9, 1735–1780. [DOI] [PubMed] [Google Scholar]
- Hoerl AE, and Kennard RW (1970). Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 12, 55–67. [Google Scholar]
- Holdgraf CR, Rieger JW, Micheli C, Martin S, Knight RT, and Theunissen FE (2017). Encoding and decoding models in cognitive electrophysiology. Front. Syst. Neurosci 11, 61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang MX, Mosher JC, and Leahy RM (1999). A sensor-weighted overlapping-sphere head model and exhaustive head model comparison for MEG. Phys. Med. Biol 44, 423–440. [DOI] [PubMed] [Google Scholar]
- Huth AG, de Heer WA, Griffiths TL, Theunissen FE, and Gallant JL (2016). Natural speech reveals the semantic maps that tile human cerebral cortex. Nature 532, 453–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalikow DN, Stevens KN, and Elliott LL (1977). Development of a test of speech intelligibility in noise using sentence materials with controlled word predictability. J. Acoust. Soc. Am 61, 1337–1351. [DOI] [PubMed] [Google Scholar]
- Kell AJE, Yamins DLK, Shook EN, Norman-Haignere SV, and McDermott JH (2018). A task-optimized neural network replicates human auditory behavior, predicts brain responses, and reveals a cortical processing hierarchy. Neuron 98, 630–644.e16. [DOI] [PubMed] [Google Scholar]
- Kettenring JR (1971). Canonical analysis of several sets of variables. Biometrika 58, 433–51. [Google Scholar]
- Kuperberg GR, and Jaeger TF (2016). What do we mean by prediction in language comprehension? Lang. Cogn. Neurosci 31, 32–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutas M, and Hillyard SA (1984). Brain potentials during reading reflect word expectancy and semantic association. Nature 307, 161–163. [DOI] [PubMed] [Google Scholar]
- Lakatos P, Shah AS, Knuth KH, Ulbert I, Karmos G, and Schroeder CE (2005). An oscillatory hierarchy controlling neuronal excitability and stimulus processing in the auditory cortex. J. Neurophysiol 94, 1904–1911. [DOI] [PubMed] [Google Scholar]
- Lenzo K (2007). The CMU Pronouncing Dictionary (Carnegie Melon University; ). [Google Scholar]
- Levy R (2008). Expectation-based syntactic comprehension. Cognition 106, 1126–1177. [DOI] [PubMed] [Google Scholar]
- Liegeois-Chauvel C, Musolino A, Badier J, Marquis P, and Chauvel P (1994). Evoked potentials recorded from the auditory cortex in man: evaluation and topography of the middle latency components. Electroencephalogr. Clin. Neurophysiol 92, 204–214. [DOI] [PubMed] [Google Scholar]
- Maaten L.d., and Hinton G (2008). Visualizing data using t-SNE. J. Mach. Learn. Res 9, 2579–2605. [Google Scholar]
- Michalareas G, Vezoli J, van Pelt S, Schoffelen J-M, Kennedy H, and Fries P (2016). Alpha-beta and gamma rhythms subserve feedback and feedforward influences among human visual cortical areas. Neuron 89, 384–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwland MS (2019). Do ‘early’ brain responses reveal word form prediction during language comprehension? A critical review. Neurosci. Biobehav. Rev 96, 367–00. [DOI] [PubMed] [Google Scholar]
- Nieuwland MS, Politzer-Ahles S, Heyselaar E, Segaert K, Darley E, Kazanina N, Von Grebmer Zu Wolfsthurn S, Bartolozzi F, Kogan V, Ito A, et al. (2018). Large-scale replication study reveals a limit on probabilistic prediction in language comprehension. eLife 7, e33468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nobre AC, and van Ede F (2018). Anticipated moments: temporal structure in attention. Nat. Rev. Neurosci 19, 34–48. [DOI] [PubMed] [Google Scholar]
- Paszke A, Gross S, Chintala S, Chanan G, Yang E, DeVito Z, Lin Z, Desmaison A, Antiga L, and Lerer A (2017). Automatic differentiation in PyTorch. In NIPS Autodiff Workshop. [Google Scholar]
- Rao RP, and Ballard DH (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci 2, 79–87. [DOI] [PubMed] [Google Scholar]
- Rousseau A, Deléglise P, and Esteve Y (2014). Enhancing the TED-LIUM corpus with selected data for language modeling and more TED talks. In LREC, pp. 3935–3939. [Google Scholar]
- Sedley W, Gander PE, Kumar S, Kovach CK, Oya H, Kawasaki H, Howard MA III, and Griffiths TD (2016). Neural signatures of perceptual inference. eLife 5, e11476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith NJ, and Levy R (2013). The effect of word predictability on reading time is logarithmic. Cognition 128, 302–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tadel F, Baillet S, Mosher JC, Pantazis D, and Leahy RM (2011). Brainstorm: a user-friendly application for MEG/EEG analysis. Comput. Intell. Neurosci 2011, 879716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teng X, Tian X, Rowland J, and Poeppel D (2017). Concurrent temporal channels for auditory processing: Oscillatory neural entrainment reveals segregation of function at different scales. PLoS Biol. 15, e2000812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theunissen FE, David SV, Singh NC, Hsu A, Vinje WE, and Gallant JL (2001). Estimating spatio-temporal receptive fields of auditory and visual neurons from their responses to natural stimuli. Network 12, 289–316. [PubMed] [Google Scholar]
- Van Petten C, and Luka BJ (2012). Prediction during language comprehension: benefits, costs, and ERP components. Int. J. Psychophysiol 83, 176–190. [DOI] [PubMed] [Google Scholar]
- van Wassenhove V, Grant KW, and Poeppel D (2007).Temporal window of integration in auditory-visual speech perception. Neuropsychologia 45, 598–607. [DOI] [PubMed] [Google Scholar]
- Yi HG, Leonard MK, and Chang EF (2019). The encoding of speech sounds in the superior temporal gyrus. Neuron 102, 1096–1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaremba W, Sutskever I, and Vinyals O (2014). Recurrent neural network regularization. arXiv, arXiv:1409.2329 https://arxiv.org/abs/1409.2329. [Google Scholar]
- Zion Golumbic EM, Ding N, Bickel S, Lakatos P, Schevon CA, McKhann GM, Goodman RR, Emerson R, Mehta AD, Simon JZ, et al. (2013). Mechanisms underlying selective neuronal tracking of attended speech at a “cocktail party”. Neuron 77, 980–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The phoneme and word alignments generated during this study for the TED-LIUM corpus are available at github.com/pwdonh/tedlium_alignments. The code for the artificial neural network training is available at github.com/pwdonh/tedlium_model. The raw MEG data generated during this study are available upon request from the lead contact Peter Donhauser (peter.donhauser@mail.mcgill.ca or peter.w.donhauser@gmail.com).