The order associated with non-Kitaev interactions in a 3d layered honeycomb magnet is suppressed by a low magnetic field.
Abstract
Layered honeycomb magnets are of interest as potential realizations of the Kitaev quantum spin liquid (KQSL), a quantum state with long-range spin entanglement and an exactly solvable Hamiltonian. Conventional magnetically ordered states are present for all currently known candidate materials, however, because non-Kitaev terms in the Hamiltonians obscure the Kitaev physics. Current experimental studies of the KQSL are focused on 4d or 5d transition metal–based honeycombs, in which strong spin-orbit coupling can be expected, yielding Kitaev interaction that dominates in an applied magnetic field. In contrast, for 3d-based layered honeycomb magnets, spin-orbit coupling is weak, and thus, Kitaev physics should be substantially less accessible. Here, we report our studies on BaCo2(AsO4)2, for which we find that the magnetic order associated with the non-Kitaev interactions can be fully suppressed by a relatively low magnetic field, yielding a nonmagnetic material and implying the presence of strong magnetic frustration and weak non-Kitaev interactions.
INTRODUCTION
Unlike the quantum spin liquids (QSLs) found in geometrically frustrated quantum magnets, the Kitaev QSL (KQSL) arises from strong anisotropy and bond-dependent interactions that frustrate the spin configuration on a single site of a honeycomb lattice (1). The Kitaev model, which is an exactly solvable model of honeycomb lattice magnetism, has attracted considerable recent attention, as it gives rise to quantum and topological spin liquids and emergent Majorana quasiparticles (1). In real materials, the spin Hamiltonian for such systems can be expressed by the sum of three terms, with J, K, and Γ representing Heisenberg (J), Kitaev (K), and bond-dependent off-diagonal exchange interactions (Γ), respectively. This is known as the extended Kitaev-Heisenberg quantum spin model (2, 3).
To approach the ideal KQSL state, Kitaev interactions are required to dominate the spin Hamiltonian (4, 5). Such bond-dependent anisotropic Kitaev-type interactions are believed to dominate in materials with strong entanglement due to spin-orbit coupling (SOC) (6); thus, so far, most theoretical and experimental investigations of the KQSL state have been devoted to candidates with 4d and 5d transition metal–based honeycomb lattices, including α-RuCl3, A2IrO3 (A = Li and Na), and H3LiIr2O6 (7–10). Although Kitaev interactions are supposed to be strong for these materials, they are nonetheless not strong enough to stabilize the QSL state. Instead, the inevitable non-Kitaev interactions present in all these systems induce conventional magnetic order at finite temperatures (11–13), obscuring the signature (e.g., a half-integer quantized thermal Hall conductivity) of the Kitaev spin liquid state that is potentially present. Theoretical and experimental efforts have shown that the non-Kitaev terms can be suppressed by applying tuning parameters, such as a magnetic field (13–15), and that the ground state in that case may, in fact, be the exotic KQSL phase (16, 17).
In the search for the KQSL, recent theoretical studies (18, 19) have provided new ideas for extending the candidates to high-spin d7 electron configuration systems, especially those based on the 3d transition metal ion Co2+ (L = 1 and S = 3/2) (18). As potentially interesting systems, several Co-based materials with a honeycomb crystal structure are known, such as BaCo2(PO4)2 (20), BaCo2(AsO4)2 (21–23), Na3Co2SbO6 (24, 25), and Na2Co2TeO6 (24, 26). All of them exhibit conventional long-range or short-range magnetic ordering at low temperature. Here, motivated by recent theoretical models, we revisit one of these Co-based honeycomb materials, BaCo2(AsO4)2, well studied by neutron scattering in the 1970s. Through characterization of its magnetism, specific heat, and thermal conductivity, we find that it is an excellent candidate for the study of Kitaev physics in a 3d-based material. Our work on high-quality single crystals shows that the magnetic susceptibility is highly anisotropic, that the application of an appropriately orientated magnetic field of weak magnitude induces two consecutive magnetic phase transitions, and that the honeycomb magnet eventually attains a low-temperature nonmagnetic state at around 0.5 T. The behavior that we observe is similar to what is observed in the well-established 4d-based KQSL material α-RuCl3. We find that the magnetic phases present are extremely sensitive to a relatively weak in-plane field compared to the heavy transition metal honeycombs, which is a clear sign of weak nearest-neighbor Heisenberg interactions.
RESULTS
Crystal structure and anisotropic magnetic susceptibility
BaCo2(AsO4)2 crystallizes in the trigonal centrosymmetric space group R-3 (no. 148), with the lattice parameters a = b = 5.00 Å and c = 23.49 Å. Schematic plots of the crystal structure are shown in Fig. 1 (A and B). The material consists of Co-based magnetic honeycomb layers, packed with an ABC periodicity along the c axis (Fig. 1A). As shown in Fig. 1B, within the plane, the honeycomb structure is made of edge-sharing CoO6 octahedra. No stacking faults or twin domains are observable in this material from our single-crystal x-ray diffraction characterization owing to the fact that the magnetic honeycomb layers are stacked three-dimensionally through ionic bonding to the Ba and AsO4 tetrahedra. In contrast, van der Waals interlayer bonding, which is the case for α-RuCl3, can lead to honeycomb plane stacking faults and coexisting structural domains (27, 28). Compared to frequently studied Kitaev physics material α-RuCl3 then, our material is far simpler in terms of interpreting the magnetic and thermal properties. Our dark purple single crystals of BaCo2(AsO4)2 were obtained by the flux growth method, as shown in the inset of Fig. 1C.
Fig. 1. Crystal structure and anisotropic magnetic susceptibility.
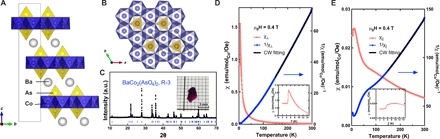
(A) Schematic of the BaCo2(AsO4)2 crystal structure, showing the honeycomb plane stacking along the c axis. (B) An individual honeycomb layer made of edge-sharing CoO6 octahedra; the [AsO4]3− tetrahedra sit in the middle of each honeycomb. The lines in (A) and (B) indicate the unit cell. (C) Room temperature x-ray diffraction pattern of the crushed BaCo2(AsO4)2 single crystals, indicating the high quality of the crystals. Calculated diffraction peak positions are marked by short blue ticks. The inset in (C) shows a photo of a dark pink single crystal. a.u., arbitrary units. (D and E) dc magnetic susceptibility χ and the inverse susceptibility 1/χ as a function of temperature measured for a BaCo2(AsO4)2 single crystal, under magnetic fields (0.4 T) applied both in plane [(D), H ⊥ c] and out of plane [(E), H ∥ c]. The magnetic transition is shown in detail in the insets. The CW fitting (black lines) results in Curie temperatures of Θ|| = −167.7 K and Θ⊥ = 33.0 K for out-of-plane and in-plane magnetic fields, respectively. emu, electromagnetic unit.
Anisotropic magnetization is usually found in layered magnetic oxides. To characterize the magnetic behavior of Co in the honeycomb layer of BaCo2(AsO4)2, we measured the magnetic susceptibility of a single crystal under both in-plane and out-of-plane fields [presented in Fig. 1 (D and E)]. For magnetic fields H applied parallel to the c axis, i.e., for field perpendicular to the honeycomb plane, the spin interactions are antiferromagnetic (AFM), as evidenced by a negative Curie-Weiss (CW) temperature Θ|| = −167.7 K. However, with a field applied within the honeycomb plane, a CW temperature of Θ⊥ = 33.8 K is derived from the fitting, indicating ferromagnetic magnetic coupling within the honeycomb planes. From these values, we estimate the exchange coupling constant J/kB to be 3.6 K [(29) and references therein]. The CW fit of the inverse susceptibility yields effective moments of μeff,|| = 5.91μB/Co and μeff,⊥ = 5.67μB/Co for H ∥ c and H ⊥ c, respectively. Clearly, these values are well above the spin-only value for the effective S = 1/2 spin configuration of Co2+ (1.73μB) because of the unquenched orbital contribution of the Co. Similarly, large μeff values have been observed in other compounds consisting of Co2+O6 octahedra, such as Na2BaCo(PO4)2 (30), which is an effective spin-1/2 system, evident by neutron scattering measurements. The strong magnetic anisotropy revealed by the susceptibility in BaCo2(AsO4)2 is consistent with that reported for α-RuCl3, which is believed to contribute to the anisotropic exchange interactions in the spin Hamiltonian (11, 31, 32).
Weak field manipulation of the magnetic states
The orientation-dependent M-T data in Fig. 1 (D and E) were obtained under a field of 0.4 T and indicate a clear AFM transition when the field is applied in the honeycomb plane. The magnetic behavior is greatly dependent on the magnitude of the applied field, reflecting the presence of field-induced magnetic phase transitions. We have also investigated the ac susceptibility, which is a more sensitive method for determining the onset of magnetic phase transitions (33), as illustrated in Fig. 2A. At each constant temperature, a small ac field of 5 Oe with a frequency of 5000 Hz is applied while sweeping the dc field within the honeycomb plane. At 1.8 K, two peaks in ac susceptibility are observed, corresponding to two separate magnetic phase transitions with two critical fields, Hc1 = 0.26 T and Hc2 = 0.52 T. Both critical fields are quite sensitive to temperature. The more obvious transition around 0.5 T displays a decreasing Hc2 with increasing temperature (Fig. 2A, left), while the one at the lower field displays more complicated behavior [in the expanded data (Fig. 2A, right), one can define Hc1 at two positions, within a narrow field range]. Magnetic hysteresis helps clarify the nature of those transitions. As illustrated in Fig. 2B, the magnetic hysteresis loop measured at 1.8 K has a zero coercivity and a dumbbell shape. Despite the fact that the overall magnetic interactions in this material are dominated by interplanar AFM coupling (Fig. 2B, inset), similar double hysteresis loops observed in the low field regime (<Hc1) have been previously reported for ferroelectrics (34) and, in this case, appear to result from in-plane ferromagnetic spin correlations. Previous neutron scattering studies (21, 22) reveal that the magnetic ground state of this system displays two-dimensional spiral order in zero applied field, consisting of weakly coupled quasi-ferromagnetic in-plane chains, which may result in the dumbbell-shape hysteresis observed below Hc1. At 5 K (Fig. 2C), the magnetic hysteresis associated with in-plane ferromagnetic correlations disappears but metamagnetic transitions at Hc1 = 0.155 T and Hc2 = 0.375 T are still observed. Thus, the field effect on the system can be understood by two consecutive AFM-type phase transitions, at Hc1 and Hc2, resulting in three magnetic phases, as marked in Fig. 2 (B and C). At low temperature, the in-plane ferromagnetic correlations result in magnetic hysteresis, leading to a difference in increasing and decreasing field behavior (23).
Fig. 2. Field-induced phase transitions.
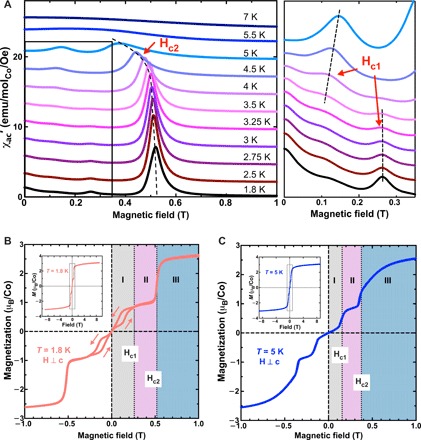
(A) Left: ac magnetic susceptibility as a function of in-plane dc field up to 1 T, measured at multiple temperatures. The dashed curve indicates the critical field Hc2 at different temperature, obtained from the peak positions of χ′ac. The box area has been zoomed into the right panel. Right: The dashed lines illustrate the critical field Hc1 at each temperature. (B and C) Magnetic hysteresis measured under an in-plane dc field |μ0H| ≤ 1 T at 1.8 K (B) and 5 K (C), respectively. The arrows in (B) indicate the field sweeping direction. Hc1 and Hc2 obtained in (A) at each temperature are indicated by the dashed lines, separating multiple magnetic phases with colorful shading. The two insets show the magnetic hysteresis at each temperature within a full field range of 9 T.
The temperature evolution of the magnetic system measured under multiple in-plane fields is illustrated in Fig. 3 (A and B), grouped by the field magnitude for clarity. As shown in Fig. 3A, at μ0H ≤ 0.26 T, a broad transition at lower temperature (TN1) and a sharp AFM transition at higher temperature (TN2) are observed (Fig. 3A). When μ0H > 0.26 T, only a single AFM phase transition at TN2 is seen. With increasing field, TN2 gradually shifts to a lower temperature and the transition is not detectable above μ0H ≈ 0.53 T (Fig. 3B). Similar behavior has been reported for other well-studied magnetic honeycombs such as A2IrO3 (A = Li and Na) (13) and α-RuCl3 (35), in which the zigzag AFM ground state turns into a nonmagnetic state at applied fields of 4 to 8 T. By contrast, the quantum phase transition observed in the BaCo2(AsO4)2 happens at a much lower field (0.5 T), a reflection of relatively weaker non-Kitaev interactions in the studied compound compared to other well-studied magnetic honeycombs.
Fig. 3. Weak in-plane field manipulation of the magnetic structure.
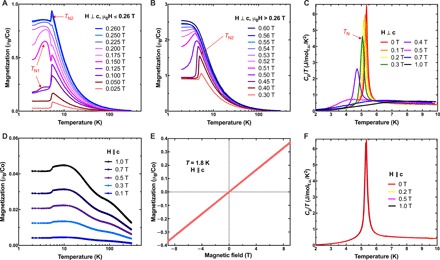
(A and B) Magnetization as a function of temperature, measured with an in-plane field (A) μ0H ≤ 0.26 T and (B) μ0H > 0.26 T. TN1 and TN2 with red arrows indicate both phase transitions. (C) Low-temperature specific heat Cp/T at several magnetic in-plane fields. TN with red arrow indicates the observed single peak at all temperatures associated with the first-order transition. (D) dc magnetization as a function of temperature measured under several out-of-plane fields. (E) Magnetic hysteresis loop measured under out-of-plane fields up to 9 T. (F) Low-temperature specific heat Cp/T measured with dc fields applied perpendicular to the hexagonal plane.
Specific heat measurements provide an additional perspective for understanding the magnetic phase transitions (as shown in Fig. 3C, the sharp, single transition further indicates the high quality of our single crystals, which have no stacking faults). The λ-peak associated with the long-range AFM ordering is rapidly suppressed by a relatively small in-plane field and appears to be fully absent above 0.5 T. The transition temperature TN observed in specific heat measurements agrees well with TN2 obtained from magnetization, which suggests that the transition at higher temperature (~5 K) is indeed due to a magnetic phase transition that involves heat exchange. However, the broad transition TN1 observed in magnetization does not result in a λ-shaped peak in specific heat, ruling out any typical first- or second-order transition. This broad transition sensitive to field may be associated with the realignment of the in-plane spins.
In contrast to the behavior in an in-plane magnetic field, the effect of the out-of-plane field on the magnetic system is negligible. With the external field applied perpendicular to the honeycomb plane, the magnetization is identical at different fields (Fig. 3D). The corresponding magnetization shows a linear dependence on the external field (Fig. 3E) and agrees well with expectations for A-type antiferromagnetism in which the interlayer coupling is dominated by the AFM interactions. In addition, as shown in Fig. 3F, specific heat measurements reveal a single phase transition that is unaffected by an out-of-plane field up to 1 T.
Strong temperature and field dependence of the thermal conductivity
Thermal conductivity was also used to characterize the honeycomb system in the vicinity of the phase transitions. Strong temperature and field dependence are observed. Representative data are shown in Fig. 4 (A and B). Figure 4A shows the temperature dependence of the thermal conductivity κxx for various in-plane applied magnetic fields. At temperatures above 5.4 K under 0 applied field, κxx/T decreases as temperature decreases. As the temperature drops below TN = 5.4 K, however, the material undergoes a phase transition, and a long-range AFM order starts to develop. This greatly enhances the thermal conductivity because of the suppression of the phonon-magnon scattering in the AFM ordered state, which is a common observation for magnets. This enhancement is suppressed with a magnetic field of 0.4 T and can no longer be seen with an applied field of 0.6 T, as the field suppresses AFM order and drives the sample into nonmagnetic states. The detailed field dependence of the thermal conductivity is shown in Fig. 4B. There is no field dependence of thermal conductivity at temperatures above 5.4 K. At 4 K, the thermal conductivity increases slightly as the external field reaches Hc1 and decreases markedly between Hc1 and Hc2 as the long-range order is continuously suppressed by an external in-plane field. The material eventually undergoes a metamagnetic phase transition into a nonmagnetic state as the external field goes beyond Hc2. In the field-induced nonmagnetic state, κxx increases with the magnetic field because of increasing magnon stiffness. Spin polarization enhances as field increases, resulting in weaker spin-phonon scattering and, thus, larger thermal conductivity. Similar observations have been reported for α-RuCl3, in which the thermal conductivity reaches a minimum at the critical field (36) and κxx is enhanced greatly with increasing field in the nonmagnetic state (37). The enhancement of κxx at low temperature may be attributed to the low-energy excitations of the field-induced spin liquid phase (38).
Fig. 4. Temperature and field dependence of the thermal conductivity.
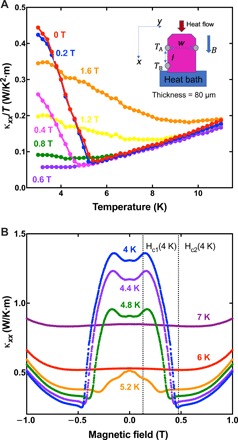
(A) Thermal conductivity over temperature κxx/T against temperature at various magnetic fields. The inset shows a schematic of the experiment setup. Two thermometers measuring temperature at A and B are marked as TA and TB. External field B is applied in-plane. w and l represent the sample’s width (1.5 mm) and length (3 mm), respectively. (B) Thermal conductivity κxx versus magnetic field at various temperatures. Hc1 and Hc2 marked in the figure are obtained from ac susceptibility shown in Fig. 2A. The magnetic field is applied in the ab plane for all thermal conductivity measurements.
Magnetic phase diagram
Using our data and data from the previous studies on the magnetic structure of BaCo2(AsO4)2, we generate a magnetic phase diagram for this honeycomb material, shown in Fig. 5. The spin spiral structure in the ground state of BaCo2(AsO4)2 can be easily eliminated through spin realignment driven by either temperature or an in-plane magnetic field. The resulting collinear AFM state may have one of several possible magnetic structures, i.e., zigzag, Néel, or stripy on the honeycomb lattice. The transition between these states at Hc1 results in the metamagnetism observed in M versus H (Fig. 2, C and D). Such a process involves no change in order parameter; thus, no peak was observed in the specific heat measurements. The detailed magnetic structures of the AFM phases I and II should be further clarified by neutron scattering. Eventually, the in-plane field suppresses the conventional Heisenberg interactions and drives the system to become a spin liquid state at TN2 (TN) and Hc2.
Fig. 5. A phase diagram showing the evolution of the AFM order under an in-plane field in BaCo2(AsO4)2.
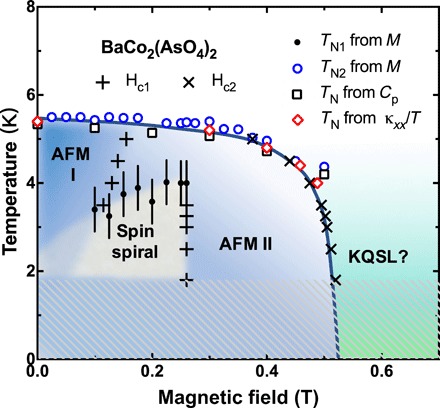
TN1 (black dots) is defined as the temperature where the low-temperature broad transition has a maximum in Fig. 3A. The corresponding error bars illustrate the full width at half maximum of the hump. The Néel temperature TN2 (blue circles) is determined from magnetization in Fig. 3B. TN is determined from specific heat data (black squares) shown in Fig. 3C or thermal conductivity measurements (red diamonds) shown in Fig. 4A. The boundary between different phases, Hc1 and Hc2, is determined from the ac susceptibility in Fig. 2A.
Similar observations have been reported for α-RuCl3 (39–41), which show that the zigzag order within the honeycomb planes is continuously suppressed with increasing in-plane field until completely being washed out around 8 T. Supported by the nuclear magnetic resonance (13, 37), thermal Hall conductivity (42), and inelastic neutron scattering (16, 17) measurements on that material, the field-induced nonmagnetic phase is attributed to the KQSL state. Other Kitaev systems are also revealed to be excellent candidates for field-induced QSLs, such as Na2IrO3 (43) and β-Li2IrO3 (13). Compared to the known magnetic honeycomb materials, BaCo2(AsO4)2 exhibits similar effects, although at a much weaker magnitude of applied field that is easily accessible in most experimental approaches. The phenomenological similarities in BaCo2(AsO4)2 imply that the field-induced spin liquid phase may be dominated by the Kitaev interaction as well, leading to an excitement on further determinations of the possible KQSL state.
The connection between the magnetic field sensitivity and non-Kitaev (Heisenberg and other) interactions is evident. In the Ru or Ir honeycombs, even with strong SOC and a prominent Kitaev term in the spin interactions, the Kitaev physics is not sufficient to stabilize the KQSL ground state because of the existence of the strong Heisenberg interactions. Thus, extra tuning parameters such as external fields that kill these nontrivial interactions are necessary to realize the pure Kitaev physics. In BaCo2(AsO4)2, in contrast, we find a complex multiphase transition and that the magnetic ordering can be totally washed out by a weak field of ~0.5 T, indicating the presence of weak nearest-neighbor Heisenberg and other non-Kitaev interactions, likely because of strong magnetic frustration.
DISCUSSION
Since the two essential elements for the Kitaev interaction are the bond-dependent exchange coupling and its anisotropy, honeycomb materials based on the 3d transition metal Co2+ are good candidates; the orbital degeneracy derived from the unquenched orbital contribution to the magnetic moment is responsible for the interaction anisotropy (18, 19). In addition, the relativistic SOC λ is large compared to the Jahn-Teller (JT) coupling EJT and exchange interaction J, giving rise to the relatively large SOC in 3d transition metal Co compounds (14). Compared to the widely studied low-spin d5 ions, the additional ferromagnetic spin exchange of the eg electrons in the d7 configuration (i.e., as seen for Co2+) may largely compensate for the AFM contribution of the Heisenberg term (18) in the Hamiltonian, leading to a proximate KQSL state. Therefore, in addition to the widely discussed heavy transition metal systems based on Ir and Ru, Co-based honeycombs can also be promising candidates in the search for the KQSL state.
Thus, cobalt honeycomb lattice materials may host Kitaev interaction. However, they are not necessarily dominated by Kitaev interaction under a magnetic field, as the conventional Heisenberg term in the Hamiltonian is usually dominant. Here, however, we characterize a Co-based honeycomb system that displays interesting behavior under an appropriately oriented magnetic field. With a rather weak field applied in the honeycomb plane, the magnetic ordering melts to a disordered state, evident by magnetization, specific heat, and thermal conductivity measurements, summarized in the H-T phase diagram (Fig. 5). In Co-based transition metal compounds with residual orbital angular momenta, the large degeneracy of the unquenched orbital leads to frustrating interactions and anisotropic magnetic properties, which results in multiple competing phases with similar energy scale (44). This is further proved by the observed sensitivity of such competing phases to the field.
In this work, we study a known Co-based honeycomb material, BaCo2(AsO4)2, from the perspective of Kitaev physics by performing measurements on high-quality single crystals. We observe a field-tuned low-temperature spin liquid state, which shows a similar behavior to α-RuCl3 and other Kitaev systems with regard to magnetization, specific heat, and thermal conductivity, making this system an excellent candidate for a field-induced QSL state. These features observed in a 3d element–based honeycomb extend the current interest on extensively studied heavy element systems into a new regime.
Our results are strong support for the theoretical predictions about the possibility to realize a KQSL in a Co-based honeycomb material. The relatively weak critical field of ~0.5 T and the availability of single crystals will motivate wider studies. We hope that this study will inspire the search for the signature of the KQSL state, such as half-integer quantized thermal Hall conductivity and fractionalized spin excitations in inelastic neutron scattering, to clarify the nature of the field-induced nonmagnetic state.
MATERIALS AND METHODS
Crystal growth
Because of the toxicity and low boiling point of the starting material As2O5, a powder sample of BaCo2(AsO4)2 was prepared by solid-state reaction before the single-crystal growth by the flux method. Stoichiometric mixtures of powder of BaO (99.9%), CoO (99%), and As2O5 (99.99%) were ground and packed into an alumina crucible, and the crucible was then carefully sealed in a quartz tube. The whole process was performed in an inert gas glove box to avoid the inhalation of a toxic substance as well as the deterioration of air-sensitive BaO. The sealed starting materials were heated at 300°C for 12 hours and then heated to 850°C for 24 hours. The powder obtained was then mixed and ground well with flux medium NaCl in a molar ratio of 1:5. The mixed materials were loaded into a capped alumina crucible, kept at 900°C for 2 hours, and then slowly cooled down to 700°C at a rate of 3°C/hour. Then, the whole furnace was quickly cooled down to room temperature. The crystals can be separated from the flux by dissolving in hot water.
Magnetization and thermodynamic measurements
The dc and ac magnetic susceptibility and specific heat were measured on single crystals in a physical property measurement system (PPMS) that cooled to 1.8 K (PPMS DynaCool, Quantum Design), equipped with a vibrating sample magnetometer option. Heat capacity measurements were conducted on a Quantum Design PPMS Evercool II with an applied magnetic field of up to 1 T. All measurements were carried out with a designed crystal orientation.
Thermal conductivity
For thermal transport measurements, we reduced the sample thickness to 80 μm by polishing with diamond paper. The size of the sample was approximately 3 mm by 4 mm by 0.08 mm. Lakeshore ruthenium oxide thermometers (Rx-102) were used for negligible field-induced corrections. The thermometers were attached to the sample via two thick gold wires with silver paint to provide a good thermal connection. The thermometer resistance was measured using a four-wire geometry with phosphor bronze wire to minimize the heat leak. The sample chamber was evacuated below 10−6 mbar. The field sweep rate was limited to 0.02 T/min to minimize the eddy current heating and magnetocaloric effect. The experiments were conducted in two ways: temperature scanning with fixed field and field sweeping with constant heating power.
Acknowledgments
Funding: The materials synthesis, magnetic, and thermodynamic characterization was supported by the Gordon and Betty Moore EPiQS program (grant GBMF-4412). The thermal conductivity research was supported by the Department of Energy (grant DE-SC0017863) and a U.S. National Science Foundation MRSEC award (grant DMR 1420541). Author contributions: R.J.C. and N.P.O. conceived the experiment. R.Z. synthesized the materials. R.Z. and T.G. performed the experiments and analyzed the data. All authors contributed to the writing of this paper. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper. Additional data related to this paper may be requested from the authors.
REFERENCES AND NOTES
- 1.Kitaev A., Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006). [Google Scholar]
- 2.Rau J. G., Lee E. K.-H., Kee H.-Y., Generic spin model for the honeycomb iridates beyond the Kitaev limit. Phys. Rev. Lett. 112, 077204 (2014). [DOI] [PubMed] [Google Scholar]
- 3.Chaloupka J., Khaliullin G., Magnetic anisotropy in the Kitaev model systems Na2IrO3 and RuCl3. Phys. Rev. B 94, 064435 (2016). [Google Scholar]
- 4.Chaloupka J., Jackeli G., Khaliullin G., Kitaev-Heisenberg model on a honeycomb lattice: Possible exotic phases in iridium oxides A2IrO3. Phys. Rev. Lett. 105, 027204 (2010). [DOI] [PubMed] [Google Scholar]
- 5.Singh Y., Manni S., Reuther J., Berlijn T., Thomale R., Ku W., Trebst S., Gegenwart P., Relevance of the Heisenberg-Kitaev model for the honeycomb lattice iridates A2IrO3. Phys. Rev. Lett. 108, 127203 (2012). [DOI] [PubMed] [Google Scholar]
- 6.Jackeli G., Khaliullin G., Mott insulators in the strong spin-orbit coupling limit: From Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009). [DOI] [PubMed] [Google Scholar]
- 7.Rau J. G., Lee E. K.-H., Kee H.-Y., Spin-orbit physics giving rise to novel phases in correlated systems: Iridates and related materials. Annu. Rev. Condens. Matter Phys. 7, 195–221 (2016). [Google Scholar]
- 8.Winter S. M., Tsirlin A. A., Daghofer M., van den Brink J., Singh Y., Gegenwart P., Valenti R., Models and materials for generalized Kitaev magnetism. J. Phys. Condens. Matter 29, 493002 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Ran K., Wang J., Wang W., Dong Z.-Y., Ren X., Bao S., Li S., Ma Z., Gan Y., Zhang Y., Park J. T., Deng G., Danilkin S., Yu S.-L., Li J.-X., Wen J., Spin-wave excitations evidencing the Kitaev interaction in single crystalline α-RuCl3. Phys. Rev. Lett. 118, 107203 (2017). [DOI] [PubMed] [Google Scholar]
- 10.Kitagawa K., Takayama T., Matsumoto Y., Kato A., Takano R., Kishimoto Y., Bette S., Dinnebier R., Jackeli G., Takagi H., A spin-orbital-entangled quantum liquid on a honeycomb lattice. Nature 554, 341–345 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Kubota Y., Tanaka H., Ono T., Narumi Y., Kindo K., Successive magnetic phase transitions in α-RuCl3: XY-like frustrated magnet on the honeycomb lattice. Phys. Rev B 91, 094422 (2015). [Google Scholar]
- 12.Chun S. H., Kim J.-W., Kim J., Zheng H., Stoumpos C. C., Malliakas C. D., Mitchell J. F., Mehlawat K., Singh Y., Choi Y., Gog T., Al-Zein A., Sala M. M., Krisch M., Chaloupka J., Jackeli G., Khaliullin G., Kim B. J., Direct evidence for dominant bond-directional interactions in a honeycomb lattice iridate Na2IrO3. Nat. Phys. 11, 462–466 (2015). [Google Scholar]
- 13.Ruiz A., Frano A., Breznay N. P., Kimchi I., Helm T., Oswald I., Chan J. Y., Birgeneau R. J., Islam Z., Analytis J. G., Correlated states in β-Li2IrO3 driven by applied magnetic fields. Nat. Commun. 8, 961 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chaloupka J., Jackeli G., Khaliullin G., Zigzag magnetic order in the iridium oxide Na2IrO3. Phys. Rev. Lett. 110, 097204 (2013). [DOI] [PubMed] [Google Scholar]
- 15.Janssen L., Andrade E. C., Vojta M., Honeycomb-lattice Heisenberg-Kitaev model in a magnetic field: Spin canting, metamagnetism, and vortex crystals. Phys. Rev. Lett. 117, 277202 (2016). [DOI] [PubMed] [Google Scholar]
- 16.Banerjee A., Bridges C. A., Yan J.-Q., Aczel A. A., Li L., Stone M. B., Granroth G. E., Lumsden M. D., Yiu Y., Knolle J., Bhattacharjee S., Kovrizhin D. L., Moessner R., Tennant D. A., Mandrus D. G., Nagler S. E., Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet. Nat. Mater. 15, 733–740 (2016). [DOI] [PubMed] [Google Scholar]
- 17.Banerjee A., Yan J., Knolle J., Bridges C. A., Stone M. B., Lumsden M. D., Mandrus D. G., Tennant D. A., Moessner R., Nagler S. E., Neutron scattering in the proximate quantum spin liquid α-RuCl3. Science 356, 1055–1059 (2017). [DOI] [PubMed] [Google Scholar]
- 18.Liu H., Khaliullin G., Pseudospin exchange interactions in d7 cobalt compounds: Possible realization of the Kitaev model. Phys. Rev. B 97, 014407 (2018). [Google Scholar]
- 19.Sano R., Kato Y., Motome Y., Kitaev-Heisenberg Hamiltonian for high-spin d7 Mott insulators. Phys. Rev. B 97, 014408 (2018). [Google Scholar]
- 20.Nair H. S., Brown J. M., Coldren E., Hester G., Gelfand M. P., Podlesnyak A., Huang Q., Ross K. A., Short-range order in the quantum XXZ honeycomb lattice material BaCo2(PO4)2. Phys. Rev. B 97, 134409 (2018). [Google Scholar]
- 21.Regnault L.-P., Burlet P., Rossat-Mignod J., Magnetic ordering in a planar X-Y model: BaCo2(AsO4)2. Phys. B Condens. Matter 86, 660–662 (1977). [Google Scholar]
- 22.Regnault L.-P., Boullier C., Lorenzo J. E., Polarized-neutron investigation of magnetic ordering and spin dynamics in BaCo2(AsO4)2 frustrated honeycomb-lattice magnet. Heliyon 4, e00507 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Regnault L.-P., Rossat-Mignod J., Effect of a magnetic field on the magnetic ordering of BaCo2(AsO4)2. J. Magn. Magn. Mater. 14, 194–196 (1979). [Google Scholar]
- 24.Viciu L., Huang Q., Morosan E., Zandbergen H. W., Greenbaum N. I., McQueen T., Cava R. J., Structure and basic magnetic properties of the honeycomb lattice compounds Na2Co2TeO6 and Na3Co2SbO6. J. Solid State Chem. 180, 1060–1067 (2007). [Google Scholar]
- 25.J.-Q. Yan, S. Okamoto, Y. Wu, Q. Zheng, H. D. Zhou, H. B. Cao, M. A. McGuire, Magnetic order in single crystals of Na3Co2SbO6 with a honeycomb arrangement of 3d7 Co2+ ions. arXiv: 1905.09365 [cond-mat.str-el] (2019).
- 26.Lefrancois E., Songvilay M., Robert J., Nataf G., Jordan E., Chaix L., Colin C. V., Lejay P., Hadj-Azzem A., Ballou R., Simonet V., Magnetic properties of the honeycomb oxide Na2Co2TeO6. Phys. Rev. B 94, 214416 (2016). [Google Scholar]
- 27.Johnson R. D., Williams S. C., Haghighirad A. A., Singleton J., Zapf V., Manuel P., Mazin I. I., Li Y., Jeschke H. O., Valenti R., Coldea R., Monoclinic crystal structure of α-RuCl3 and the zigzag antiferromagnetic ground state. Phys. Rev. B 92, 235119 (2015). [Google Scholar]
- 28.Cao H. B., Banerjee A., Yan J.-Q., Bridges C. A., Lumsden M. D., Mandrus D. G., Tennant D. A., Chakoumakos B. C., Nagler S. E., Low-temperature crystal and magnetic structure of α-RuCl3. Phys. Rev. B 93, 134423 (2016). [Google Scholar]
- 29.Ma Z., Wang J., Dong Z.-Y., Zhang J., Li S., Zheng S.-H., Yu Y., Wang W., Che L., Ran K., Bao S., Cai Z., Cermak P., Schneidewind A., Yano S., Gardner J. S., Lu X., Yu S.-L., Liu J.-M., Li S., Li J.-X., Wen J., Spin-glass ground state in a triangular-lattice compound YbZnGaO4. Phys. Rev. Lett. 120, 087201 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Zhong R. D., Guo S., Xu G., Xu Z., Cava R. J., Strong quantum fluctuations in a quantum spin liquid candidate with a Co-based triangular lattice. Proc. Natl. Acad. Sci. U.S.A. 116, 14505–14510 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Majumder M., Schmidt M., Rosner H., Tsirlin A. A., Yasuoka H., Baenitz M., Anisotropic Ru2+4d5 magnetism in the α-RuCl3 honeycomb system: Susceptibility, specific heat, and zero-field NMR. Phys. Rev. B 91, 180401 (2015). [Google Scholar]
- 32.Lampen-Kelley P., Rachel S., Reuther J., Yan J.-Q., Banerjee A., Bridges C. A., Cao H. B., Nagler S. E., Mandrus D., Anisotropic susceptibilities in the honeycomb Kitaev system α-RuCl3. Phys. Rev. B 98, 100403 (2018). [Google Scholar]
- 33.Balanda M., AC susceptibility studies of phase transitions and magnetic relaxation: Conventional, molecular and low-dimensional magnets. Acta Phys. Pol. A 124, 964–976 (2013). [Google Scholar]
- 34.Srivastava N., Weng G. J., A theory of double hysteresis for ferroelectric crystals. J. Appl. Phys. 99, 054103 (2006). [Google Scholar]
- 35.Ma Z., Ran K., Wang J., Bao S., Cai Z., Li S., Wen J., Recent progress on magnetic-field studies on quantum-spin-liquid candidates. Chin. Phys. B 27, 106101 (2018). [Google Scholar]
- 36.Yu Y. J., Xu Y., Ran K. J., Ni J. M., Huang Y. Y., Wang J. H., Wen J. S., Li S. Y., Ultralow-temperature thermal conductivity of the Kitaev honeycomb magnet α-RuCl3 across the field-induced phase transition. Phys. Rev. Lett. 120, 067202 (2018). [DOI] [PubMed] [Google Scholar]
- 37.Hentrich R., Wolter A. U. B., Zotos X., Brenig W., Nowak D., Isaeva A., Doert T., Banerjee A., Lampen-Kelley P., Mandrus D. G., Nagler S. E., Sears J., Kim Y.-J., Buchner B., Hess C., Unusual phonon heat transport in α-RuCl3: Strong spin-phonon scattering and field-induced spin gap. Phys. Rev. Lett. 120, 117204 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Leahy I. A., Pocs C. A., Siegfried P. E., Graf D., Do S.-H., Choi K.-Y., Normand B., Lee M., Anomalous thermal conductivity and magnetic torque response in the honeycomb magnet α-RuCl3. Phys. Rev. Lett. 118, 187203 (2017). [DOI] [PubMed] [Google Scholar]
- 39.Baek S.-H., Do S.-H., Choi K.-Y., Kwon Y. S., Wolter A. U. B., Nishimoto S., van den Brink J., Büchner B., Evidence for a field-induced quantum spin liquid in α-RuCl3. Phys. Rev. Lett. 119, 037201 (2017). [DOI] [PubMed] [Google Scholar]
- 40.Zheng J., Ran K., Li T., Wang J., Wang P., Liu B., Liu Z.-X., Normand B., Wen J., Yu W., Gapless spin excitations in the field-induced quantum spin liquid phase of α-RuCl3. Phys. Rev. Lett. 119, 227208 (2017). [DOI] [PubMed] [Google Scholar]
- 41.Sears J., Zhao Y., Xu Z., Lynn J. W., Kim Y.-J., Phase diagram of α-RuCl3 in an in-plane magnetic field. Phys. Rev. B 95, 180411 (2017). [Google Scholar]
- 42.Kasahara Y., Ohnishi T., Mizukami Y., Tanaka O., Ma S., Sugii K., Kurita N., Tanaka H., Nasu J., Motome Y., Shibauchi T., Matsuda Y., Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 559, 227–231 (2018). [DOI] [PubMed] [Google Scholar]
- 43.Patel N. D., Trivedi N., Magnetic field-induced intermediate quantum spin liquid with a spinon Fermi surface. Proc. Natl. Acad. Sci. U.S.A. 116, 12199–12203 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Khaliullin G., Okamoto S., Quantum behavior of orbitals in ferromagnetic titanates: Novel ordering and excitations. Phys. Rev. Lett. 89, 167201 (2002). [DOI] [PubMed] [Google Scholar]


