Accumulators, Neurons, and Response Time

Abstract

The marriage of cognitive neurophysiology and mathematical psychology to understand decision-making has been exceptionally productive. This interdisciplinary area is based on the proposition that particular neurons or circuits instantiate the accumulation of evidence specified by mathematical models of sequential sampling and stochastic accumulation. This linking proposition has earned widespread endorsement. Here, a brief survey of the history of the proposition precedes a review of multiple conundrums and paradoxes concerning the accuracy, precision, and transparency of that linking proposition. Correctly establishing how abstract models of decision-making are instantiated by particular neural circuits would represent a remarkable accomplishment in mapping mind to brain. Failing would reveal challenging limits for cognitive neuroscience. This is such a vigorous area of research because so much is at stake.

Linking propositions for response time

The goal of cognitive neuroscience, including neuroimaging and electrophysiology with humans and neurophysiology with animals, is to understand how neural processes produce behavior and how they instantiate associated cognitive representations and transformations. A pivotal example was Helmholtz’s measurements, circa 1850, of the conduction time of the nerve impulse in frog legs [1]. Discovering how slow the conduction was led quickly to research on the limits of human response time (RT) by Wundt, Donders and others [2]. Meanwhile, du Bois-Reymond performed the first measurement of the nerve current, known today as the action potential [3]. How do we know that the nerve impulse, the event triggered by irritation of a nerve that produces muscle contraction, is identical to an action potential, the transient exchange of ions that propagates in axons? The equivalence was not self-evident around 1950, for Huxley and Stämpfli performed an experiment to conclude, “This demonstrates that the transmission of the nervous impulse depends on currents flowing outside the myelin sheath…” [4].

Establishing the equivalence of the behavioral nerve impulse and the mechanistic action potential is one example of a linking proposition: a formal articulation of the relationship between a neural process and a behavior or cognitive process [5, 6]. Linking propositions can have different degrees of specificity, from identity (the nerve impulse is an action potential), to similarity (variation of the discharge rates of particular neurons parallel the parameters of a computational process), to analogy (the appearance of a computational process resembles the appearance of a neural process). To establish the identity linking proposition, particular criteria must be satisfied. For example, the neurons must have proper inputs and outputs to do the ascribed function. Also, the model and neural processes must be concomitant in duration, simultaneous in occurrence, and commensurate in magnitude. Inherent in the identity linking proposition is an explanation of how the mapping is the case. Consequently, integral to the similarity linking proposition and more so the analogy proposition is uncertainty about whether the observed relationship is necessary or fortuitous.

Rigorous linking propositions for higher order functions like language and consciousness are beyond the scientific horizon, many would argue, but surely an elementary behavioral measure like RT and the associated perceptual, cognitive, and motor processes should be within reach. Experimental psychology began with investigations of psychophysics and RT. To explain the systematic variation of RT across tasks with different degrees of difficulty, the first mechanistic hypothesis conjectured that RT is occupied by different stages of processing [7]. This hypothesis led naturally to investigations designed to determine the number and duration of such stages. However, by the 1930s the viability of research on RTs was questioned, “[Since] we cannot break up the reaction into successive acts and obtain the time of each act, of what use is the reaction time?” [8]

Interest in mental chronometry renewed in the 1960s and 1970s with the establishment of a new theoretical perspective [9], new experimental approaches [10], and theories of signal detection, sequential sampling, and stochastic processes, which led to a new hypothesis that the duration and variation of RT was the outcome of stochastic processes [11, 12, 13, 14, 15]. Through the 1990s and into the 2000s, the landscape of stochastic processes explaining RT became more complex and comprehensive including noisy diffusion between two barriers [16], linear accumulators [17, 18], leaky competition [19], and races among options [20, 21], all of which could be optimized to satisfy goals [22]. The proliferation of models led to a problem of mimicry – models with different architectures made indistinguishable predictions. Indeed, some alternative architectures are mathematically equivalent [23]. In spite of this uncertainty, the stochastic accumulator framework has proven powerful at characterizing human performance and identifying subtle quantitative differences associated with development, aging, and disease [24].

Meanwhile, through the 1970s to 1990s, other than Jean Requin [25], nonhuman primate neurophysiology researchers were largely uninterested in RT tasks and even avoided them. A 1996 publication, however, not only described a neural basis of the stochastic variation of RT but also conjectured that the form of that neural process could resolve the mimicry between alternative mathematical models of RT [26].

This conjecture sparked the productive line of research linking the mathematical psychology of RT with neurophysiology and neuroimaging during RT tasks [27, 28]. Multiple lines of evidence by many research groups produced evidence that particular neurons in primates could be identified with stochastic accumulators, predominantly in two-alternative perceptual discrimination tasks [29, 30]. While this framework has guided research with rodents as well [31, 32], differences between rodents and primates in brain organization [33] and performance strategies [34] confound simple integration of findings across mammalian clades.

In nonhuman primates, neural recording and computational modeling has indicated modulation in pattern and time corresponding to the drift-diffusion process for neurons in posterior parietal cortex area LIP [35] and in prefrontal area FEF [36] (Figure 1) (Box 1). But the linking proposition mapping neural activity patterns to stochastic accumulators appears to hold for other tasks. For example, neural recording and computational modeling has demonstrated that presaccadic movement neurons in FEF and SC modulate in pattern and time to instantiate the GO race process during a saccade countermanding task [37, 38]. Likewise, empirical and theoretical work has also demonstrated that the same presaccadic movement neurons modulate in pattern and time sufficient to instantiate the accumulation of visual search item salience [39, 40, 41] (Figure 1). Corresponding claims have been made with noninvasive measures of EEG and fMRI [29, 30]. Hence, the linking proposition that (certain) neurons are stochastic accumulators seems to have persuasive explanatory power (Box 2).

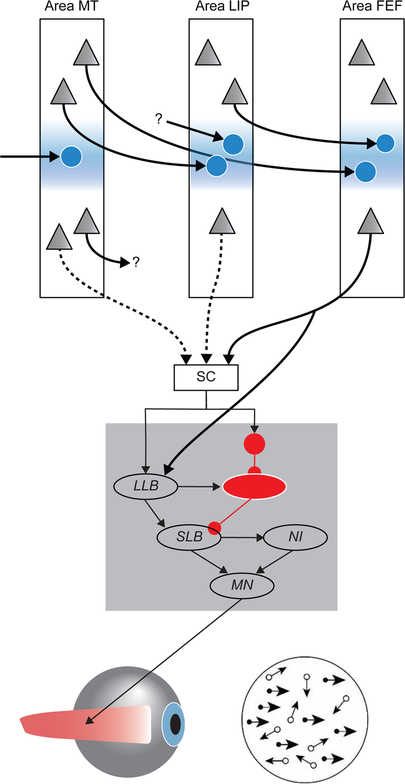
Figure 1.

Linking propositions for motion discrimination and visual search. (A) Diagram of visual displays. For the motion discrimination task, a field of randomly moving dots appears. Monkeys signal the perceived direction of motion by shifting gaze to one of two peripheral stimuli (rightward arrow). For a visual search task multiple fields of randomly moving dots appear. Monkeys signal the location of the stimulus moving in the direction opposite all of the others by shifting gaze to it (rightward arrow). (B) Discharge rate in visual processing area MT as a function of time from stimulus presentation. Diagram of encoding of preferred (thick) and non-preferred (thin) motion directions. As far as we know, the encoding is equivalent across tasks. (C) Discharge rate in parietal area LIP. During the motion discrimination task (left), neurons in LIP on average exhibit a transient suppression followed by progressively increasing activity that reaches a particular level (dashed horizontal line labeled A_RT to indicate the level of activity at RT). The rate of this accumulation varies from rapid (thicker) to slower (thinner) according to the clarity of the motion stimulus. This is often interpreted as accumulating the evidence provided by area MT neurons. However, as indicated by the thin vertical line spanning left panels B and C, the accumulation begins well after area MT neurons have encoded motion direction. During visual search tasks (right), neurons in LIP show an initially indiscriminate response followed by elevated discharge rate if the oddball stimulus is in the receptive field (thick) and reduced discharge rate otherwise (thin). This is interpreted as representing the salience of the objects in the array. (D) Discharge rate of presaccadic movement neurons in ocular motor structures FEF and SC. According to a model of the motion discrimination task [100], when discharge rates of LIP neurons reach A_RT, a subsequent process is triggered that produces the saccade after a stochastic period of accumulating discharge rate occupying ~150 ms. The model identifies this process with the activity of presaccadic movement neurons in FEF and SC, which project to the brainstem saccade generator and initiate saccades 10 ms after reaching A_RT. According to a model of the visual search task [40], the dynamics of the presaccadic movement neurons correspond to the accumulation of salience evidence. The colored arrows highlight questions about relationships that are elaborated in the text. Cyan, how can neurons represent the evidence in one task and accumulate evidence in another task? Green, how does the reaching of A_RT by neurons in LIP reliably initiate the subsequent response preparation process? Yellow, how can neurons be the response stage after evidence accumulation in one task and do evidence accumulation (followed by another response stage?) in another task?

Box 1. Neural circuits representing evidence and doing stochastic accumulation.

Much is known and not known about the neuroanatomical circuitry supporting perceptual decision-making tasks with eye movement responses. Figure I summarizes some of what is known and unknown.

The gray square illustrates the basic circuitry in the brainstem responsible for initiating and producing saccadic eye movements. Descending inputs activate long-lead burst neurons (LLB) and inhibit omnipause (OPN) neurons. This permits rapid activation of short-lead burst neurons (SLB) to generate the pulse of force producing the saccade through the extraocular motor neurons (MN). A circuit known as the neural integrator (NI) converts the velocity pulse into the step of force needed to hold gaze at an eccentric angle. The structure-function linking propositions for this circuit offer unique clinical utility. Where and when to shift gaze are specified by inputs to the brainstem saccade generator from the superior colliculus (SC) and frontal eye field (FEF). Cortical areas are comprised of different kinds of neurons organized across layers that are distinguished by different inputs and outputs. Layer 4 is comprised of small stellate neurons (symbolized by circles), and layers 2, 3, 5, and 6 consist of pyramidal neurons (symbolized by triangles). Inhibitory interneurons are ignored in the schematic. Also ignored is the spatial mapping within and between areas to translate the properties of a stimulus at one location to a saccade to that or another location. For perceptual decision-making, the features of visual stimuli must be encoded, as neurons in area MT encode the direction of motion. Area MT receives inputs from earlier visual areas including primary visual cortex (indicated by the arrow ending on the stellate neuron in layer 4). Some neurons in area MT project to the lateral intraparietal area (LIP) (indicated by arrow ending on stellate neuron in layer 4), underlying the model that signals from area MT are integrated in area LIP. Different neurons in area MT project to FEF (indicated by arrow ending on stellate neuron in layer 4). Yet other neurons in area MT project to other cortical (represented by the arrow ending in question mark) and subcortical structures (arrow from L5 to SC, being dashed to signify that the projection from area MT to SC does not contribute directly to saccade production). Given the diversity of neurons in area MT, we do not know which encode motion for integration in area LIP and in FEF. Area LIP receives inputs from areas other than area MT (represented by the arrow beginning at the question mark). The contribution of such signals to the motion discrimination task is unknown. Area LIP projects to cortical areas like FEF (indicated arrow) and to subcortical sites like SC (arrow from L5 to SC, also dashed to signify its uncertain contribution to saccade production). Neurons in L2/3 of FEF are visually responsive neurons that select the target of visual search arrays. Neurons in L5 of FEF are presaccadic movement neurons with build-up activity that parallels the build-up activity of SC neurons. Saccades are initiated as soon as the activity of these neurons reaches a critical level. However, the relation is uncertain between the FEF and SC neurons reaching that critical discharge rate and OPN inhibition releasing the saccade measured as the RT.

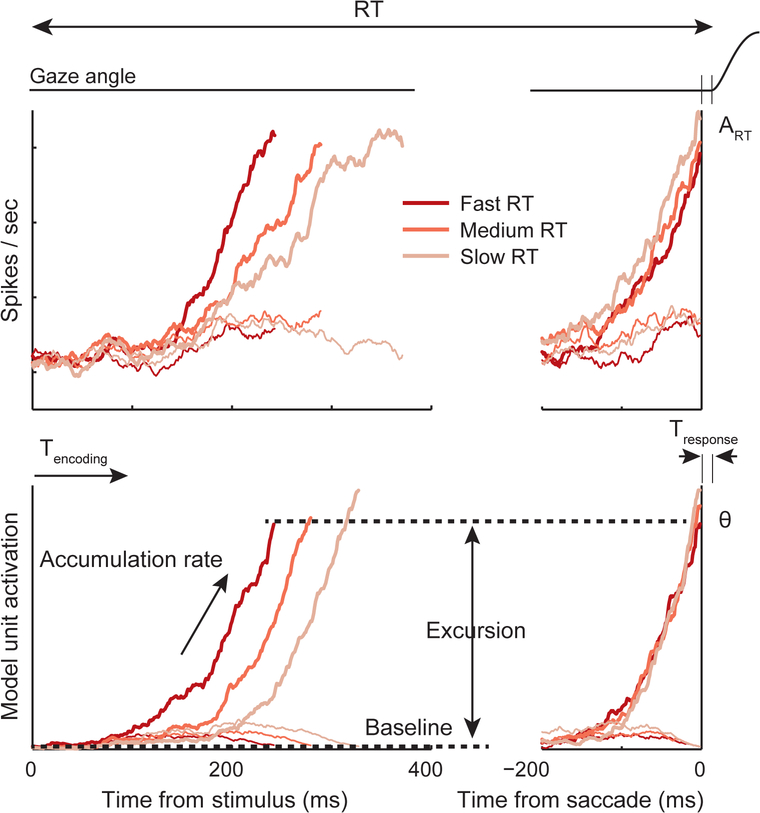
Box 2. Stochastic accumulator models.

A menagerie of stochastic accumulator models has been formulated that offer explanations performance of various tasks under many circumstances. Figure I illustrates some of the key features of the models and how closely model outputs can resemble neural observations.

Accumulator models are characterized by particular parameters. Accumulation begins at a baseline level and terminates when the accumulated value reaches a specified threshold (θ). Neural accumulation is judged to terminate when the overt response is produced (A_RT). The difference between threshold and baseline is referred to as excursion. Larger excursion amounts in longer RT (for a given accumulation rate).

Accumulation does not begin until some interval needed for decoding the stimuli elapses (T_encoding). In addition, some time elapses after θ is reached before the overt response is produced (T_response). The sum T_encoding + T_response is referred to as the residual or non-decision time. For saccade responses T_response is ~10 ms because this is the interval from inhibition of omnipause neurons until saccade initiation. For manual responses T_response can be longer and more variable because limb movements are embedded in posture and may not be ballistic. The interesting “decision” process begins when the evidence accumulates at a particular rate. This accumulation can begin from a baseline level that is above a zero level. For a given threshold and rate, a higher baseline will result in shorter RT because the accumulation requires less excursion.

The rate parameter is supposed to be proportional to the quality or magnitude of evidence, which assumes random values across trials. The residual time is supposed to be invariant. The baseline and threshold (excursion) values are supposed to be under strategic control to enable speed-accuracy tradeoff.

Uncertainties about accumulator <=> neuron linking propositions

The foregoing paints a tidy picture. However, recent empirical observations and theoretical investigations suggest that the mapping of neural processes with stochastic accumulation, whether it is described as evidence accumulation or response preparation, should engender less confidence and encourage more scrutiny. This review is not concerned with whether stochastic accumulator models provide accurate descriptions of performance (they do) nor with the diversity of stochastic accumulator model assumptions, architectures, and tests (there are many) nor with whether neural circuits accomplish perceptual decision-making (they do). It is concerned with how to articulate and understand the relationship between what a stochastic accumulator model requires and what neurons appear to do. Relative to the timeline of identifying the nerve impulse with the action potential, we may be closer to 1850 than to 1950 in establishing linking propositions about neurons and accumulators for RT.

Which neurons instantiate evidence accumulation?

The evidence that particular neurons instantiate evidence accumulation is not unequivocal. In area LIP, which has exemplar status, ambiguity comes from several directions. First, the identification of neural activity in area LIP with the stochastic accumulation process depends on the task used for investigation. When sampled during visual search tasks with multiple objects, several laboratories, have found that neurons in LIP exhibit a pattern of modulation first described in FEF [42] and identified with an evolving salience map representation [43, 44, 45, 46] (Figure 1). Observed in FEF, this pattern of modulation was treated as the evidence that was accumulated by presaccadic movement neurons [40, 41]. How can neurons represent evidence in one task and be the accumulator in another task? Indeed, the presaccadic movement signal that is pronounced in FEF and SC is sparse in LIP [47].

Second, a statistical analysis indicates that the dynamics of LIP activity during the motion discrimination task is better described as discrete steps rather than noisy ramps [48]. This conclusion has been debated [49, 50].

Third, inactivation of LIP does not impair performance of the motion direction discrimination task [51]. This result contrasts with deficits observed in visual search tasks [52], complements the observation that LIP neurons must learn to become accumulators [53], and indicates that the other nodes in the circuit receiving motion signals from area MT, most likely FEF and SC, must be sufficient to perform the motion discrimination task.

Are neural measures and model parameters commensurate?

Localization of stochastic model parameters using functional magnetic resonance imaging

A recent meta-analysis located cortical regions associated with basic parameters like accumulation rate, decision threshold, and non-decision time [29]. Numerous regions in all lobes were identified with accumulation rate. Fewer regions, mainly in the frontal lobe, were identified with decision threshold. Only three, in the temporal lobe, were identified with non-decision time. Several questions arise: Why are different basic parameters not co-localized? If evidence is accumulated in some places, but the threshold is in other places, how are the processes linked? Neurophysiology results all describe stochastic accumulation and threshold in single neurons. Also, the meta-analysis locates decision threshold in cortical areas that have been associated with other functions like performance monitoring in medial frontal lobe, and it does not locate it in areas described by neurophysiology, such as parietal cortex. Finally, why is non-decision time not located in the sensory and motor areas accomplishing the encoding and response production that is supposed to occur during the non-decision time?

Rate of accumulation.

While models with no within-trial variability account for performance measures [17, 18], models with such variability seem more biologically plausible [24]. Certainly, discharge rates of single neurons wax and wane with variable rates; a measure of the variance of spike rates across trials increases over time as expected if the process were like Brownian motion [54]. But, the actual neural variation among the tens of thousands of neurons instantiating the stochastic accumulation trajectory within a single trial has never been measured for two reasons. First, neurophysiological samples within a cortical area are exceedingly heterogeneous [55, 56]. Second, the neural circuit instantiating stochastic accumulation before RT is distributed across cortical areas including parietal, prefrontal, premotor, and motor areas plus subcortical structures basal ganglia, superior colliculus, and thalamus.

If the eye, limb, or digit movement that gives the measure of RT is initiated when the activity of neurons reaches a threshold, but the activity of neurons is variable such that neurons reach their respective threshold at different times, then when is the body movement produced? This question was investigated through simulations of multiple, redundant, idiosyncratic accumulators with different amounts of variability in growth rate and different stopping rules [57]. Distributions of ensemble RT did not vary with ensemble size if the accumulators share at least modestly correlated accumulation rates and RT is not governed by the extremely fast or slow accumulators. Under these parameters the termination times of individual accumulators corresponded to the ensemble RT. A relatively high correlation of the rate of accumulation among redundant neurons has been inferred through experimental analysis [100]. Hence, the within-trial neural variability of the accumulation pooled within the relevant distributed circuit must be less than that observed from single neurons measured on single trials.

Accumulation barrier, boundary, or threshold.

The use of a single term like “threshold” in reference to both models and neurons creates ambiguity. We can distinguish the computational threshold of a model (θ) and the measured neural activation at RT (A_RT). The value of θ is expressed in statistical units of certainty or confidence. Elevation of θ increases accuracy at the cost of speed; reduction of θ reduces accuracy and improves speed. The value of A_RT is in physiological units like spikes per second, or microvolts, or %BOLD. The measurement of A_RT is like any other neural measure, it requires particular assumptions about what to do with “baseline” values, how to scale across neurons, and how much smoothing or averaging is applied (such smoothing or averaging effectively imposes a correlation of growth rates).

To map onto one another, changes of A_RT must parallel changes of θ. The conceptual correspondence but metric difference between A_RT and θ was highlighted in the simulation of multiple redundant accumulators [57]. The θ value was fixed in the simulation. A_RT was measured for representative accumulators under all possible accumulation rate correlations and stopping rules. Under parameters producing realistic distributions of RT, A_RT was invariant across RT, replicating the original neural observation [26]. However, A_RT = θ only when the simulated rate correlation was high, and A_RT systematically underestimated θ when the earliest accumulators dictated RT and overestimated θ when the latest accumulators dictated RT.

In the original formulation of stochastic accumulator models, θ was invariant across RT [but see 13]. Some investigators, based mainly on nonhuman primate findings, have argued that θ can decrease over time under the influence of another factor referred to as urgency [58, 59, 60]. Comprehensive modeling of many data sets from humans and nonhuman primates [61] and further analysis of collapsing bound and diffusion models [62] have raised questions about the generality of this factor across tasks. Hence, the interpretation of model comparisons must encompass the idiosyncrasies of task demands and differences between operantly training nonhuman primates and verbally instructing humans.

Another dramatic difference between A_RT and θ has been revealed in neurophysiological investigations of the speed-accuracy tradeoff (SAT). Canonical stochastic accumulator models achieve SAT through a principled adjustment of θ [63]. SAT offers a powerful test of the linking proposition identifying a neural process with the evidence accumulation process. First, neurons that actually instantiate stochastic accumulation must exhibit higher A_RT in the Accurate relative to the Fast condition. Second, neurons that represent the evidence will not change across conditions. Independently, three laboratories trained monkeys to perform choice tasks with different SAT manipulations and sampled spikes in FEF [64], LIP [65], skeletal motor cortex [66], basal ganglia [67], and SC [68]. None of these studies found robust evidence that neurons identified as accumulators modulated as predicted. All found a pronounced trend for lower discharge rates when accuracy was rewarded. Moreover, the investigations of FEF and SC also found that the neurons representing evidence were strongly modulated in a parallel manner; in other words, the evidence representation also changed across SAT conditions. These neurophysiological findings dovetail with data from human studies showing that SAT adjustments involve changes in noninvasive measures indexing sensory encoding, attention allocation, as well as response preparation [69, 70] and with a more recent modeling study showing how strategic variation of accumulation rate can accomplish SAT [71]. Neuro-compuational modeling of the SAT data from FEF showed that the instantiation of control over speed and accuracy is more complex and idiosyncratic than previously envisioned by psychologists or by the neuroscientists who borrowed their models [72].

The results from the SAT studies seem impossible to interpret without appreciating that multiple operations or stages of processing are involved. Models like the gated accumulator [40, 41] offer a framework in which to clarify relations between different operations or stages, and experimental methods to distinguish and identify such operations are well known [73, 74] but rarely utilized with nonhuman primates [75, 76].

Non-decision or residual time.

Neurons that actually instantiate a stochastic accumulation decision process should begin at the conclusion of the encoding delay and terminate when response initiation begins. For tasks using particular visual stimuli and saccadic eye movement responses, the encoding and production times can be specified with high reliability. For example, in the model of motion discrimination supposing that signals from area MT are integrated in area LIP [100] or in FEF [36], the accumulation begins ~200 ms after the motion stimulus appears (Figure 1). Now, neurons in area MT begin to discriminate the direction of motion ~100 ms after presentation, and visual response latencies in LIP and FEF average <100 ms. Thus, ~100 ms is unaccounted for. In fact, the accumulation in LIP and FEF is measured after a transient reduction of the discharge rate. Most likely a consequence of the motion stimulus falling in the suppressive surround of the receptive field, this reduction artifactually delays measurement of evidence accumulation. Evidence for this inference is the earlier accumulation in the caudate nucleus where the suppression is absent [77]. If different neurons accumulate during different intervals, which is correctly mapped to the model accumulation interval?

The termination of the accumulation in the motion discrimination studies is described as converging on a stereotyped trajectory ~150 ms before the saccade. However, in FEF this convergence time differs across neuron types: neurons with narrow spikes converged 185–259 ms before the saccade while neurons with broad spikes converged 104–157 ms before the saccade [36]. Which of these (non-overlapping) times is correctly mapped to the model accumulation process?

This convergence time has been described as the instant of decision commitment that is followed ~150 ms later by initiation of the response. This assumes that nothing intervenes until the movement is initiated, but the commitment to a given saccade can change within 100 ms of initiation [78, 79]. Nevertheless, to account for the ~150 ms delay between “decision commitment” and response initiation, the model of the motion discrimination task [100] inserts a subsequent accumulation stage, introducing an additional degree of random variation in saccade initiation times (Figure 1). This is sensible, because we know that the final 100 ms before saccade initiation is occupied by build-up of activity of movement neurons in FEF, SC, and related structures. The rate of this build-up can vary even with unambiguous evidence [26]. But, these presaccadic movement neurons have been identified as the evidence accumulation process in other studies [40, 41, 80] (Figure 1). Indeed, the study of FEF during the motion discrimination task reported that most neurons with properties matching stochastic accumulation were characterized as movement related [36].

The juxtaposition of these observations presents a paradox. From one coherent perspective, the movement neurons in FEF and SC are identified with the non-decision time, but from another equally coherent perspective they are identified with the decision-making evidence accumulation process. Do the properties of these neurons vary across tasks? Are they part of the decision process in one condition, and are they not part of the decision process in another? Perhaps the brain switches between tasks by changing the functional properties of neurons. If so, linking propositions about these neurons lose generality. These alternatives can be tested through neural sampling while subjects perform combined tasks such as countermanding with perceptual decision-making [81].

Another issue involves relating the durations derived from neural measures to those derived from a stochastic accumulator model. Much is at stake; an absence of simultaneity violates the identity linking proposition. In the investigation of the motion discrimination task, the non-decision time of the accumulator model fit to the performance approximates the sum of the latency of the neural accumulation measure and the delay from the convergence until the saccade [36, 100]. However, the variability of the model values across testing conditions and the asymmetry for response bias are not paralleled by corresponding differences of neural measures.

Better agreement has been achieved in other investigations. For example, the interactive race model of countermanding constrains model parameters by observed measures of neural accumulation interval and the ballistic period preceding saccade initiation [38]. The best-fit model predicts the timing of a particular neural modulation that corresponded precisely with the measured values. Similarly, with observed spike trains as input, the gated accumulator model of visual search fit to performance measures predicted quantitatively the observed timing and magnitude of activity in presaccadic movement neurons [40, 41]. Therefore, at least under some experimental conditions, simultaneity of model and neural measures can be found.

Do model parameters measure underlying processes?

Another approach to understanding how model parameters relate to underlying mechanisms is to produce RTs from simulated accumulators with different parameters such as non-decision time, rate of accumulation, and threshold [82]. In some cases, model parameters could be successfully inferred from simulated dynamics, but in other cases measures of dynamics alone provided a misleading picture about the underlying sources of RT variability. This is so because noise in the evidence representation and accumulation process complicates the relationship between accumulator dynamics and the mechanisms producing those dynamics. For example, the measured onset of a neural accumulation process does not necessarily correspond to the end of the stimulus encoding time parameter in accumulator models. Noisy variability in the drift rate, starting point, and threshold parameters all manifest as variability in measured onset time. Even in fully characterized systems, the relationships between model parameters and neural dynamics is not transparent. Hence, new approaches to simultaneous modeling of behavior and neural dynamics are being developed [83, 84], and their application to neurophysiological data is anticipated.

Complementarity and converging constraints

The concomitant investigation of mental and neural chronometry has produced many insights through the converging constraints afforded by combining concepts and approaches of neuroscience and psychology. Formal models from psychology specify task conditions in which to obtain neural measurements and offer explanations for patterns of neural modulation in computational rather than biological terms. The utility of the linking proposition formulation is in making explicit the kind and scope of explanation being offered.

For example, the independent race model of stop signal task specifies the quantity stop signal reaction time but does not explain how it is accomplished [20]. Particular neurons have connectivity and modulation dynamics necessary to qualify as instantiating the race [37]. The interactive race model demonstrates the essential characteristics of the circuit that accomplish the computation specified by the abstract model [38]. This seems to support a reasonably secure identity level linking proposition.

By contrast, when we say that SAT is accomplished by changing the accumulation threshold or excursion, we are not describing the neural processes producing the behavior [64]. This and other observations seem to require a similarity or even analogy level linking propositions. Such uncertainty is revealed by the arms-length distinctions that are made between neural events that actually instantiate the stochastic decision process and those that merely “reflect” it, or likewise between neural events corresponding to where decisions are “formed” or “initiated” and neural events that are a “window” onto decision processes. Evidently, the window is veiled.

One might adopt a laissez faire attitude and argue that finding a specific one-to-one identity between sampled neural activity and the abstract stochastic accumulators is too much to expect. The failure of one model just invites development of better models. Certainly so, but “failure” is defined in terms of the goals of the models and the levels of the measurements. Researchers can disagree about such goals. If neuron dynamics in a brain structure do not correspond to accumulator model parameters, shall we decide that the model fails? Or is it just missing particular details? Or do we retain confidence in the model and decide that the neurons actually are not contributing to the process being modeled? For example, if neural measures demonstrate that SAT is not accomplished by varying the excursion of the neural processes producing RT, does it follow that the canonical stochastic accumulator model has failed? The neurophysiologist might say Yes, and the psychologist, No. The different answers arise because they have different goals. The canonical model of SAT remains a convenient characterization of human and monkey performance.

An alternative perspective appreciates the complementarity of the stochastic accumulator descriptions and neural measures. The perspective of complementarity highlights the scientific function (obligation?) of models of different levels of complexity to offer concepts, constraints, and measures for translation between the different levels of description. For example, the abstract race model of the stop signal countermanding task provides the measure stop-signal reaction time. The race model assumes an interaction and specifies when it must happen, but it says nothing about how one process stops another. The interactive race model explains how the racing processes can interact at a time and in a manner necessary to be consistent with the formal race model and sufficient to correspond to the observed modulation of (particular) neurons. The interactive race can have formally different but practically indistinguishable architectures [85]. Also, key features can be instantiated in a network of spiking units [86] or in models of extended brain circuits [87]. Although, with so many free parameters and uncertain assumptions, models at this level are less constrained by the fitting of performance measures like RT distributions. Nevertheless, translation between levels of description can be achieved by incorporating constraints across levels of description, e.g., any model of a countermanding stop signal task must produce proper values of the stop signal reaction time. Similar translations across levels of detail have been developed for perceptual decision-making [88, 89, 90]. Such translations depend, again, on the validity of the linking proposition. Invalid linking propositions support no converging constraints.

Another approach synthesizes particular anatomical, biophysical, and physiological information to construct models of brain circuits that are tested by producing patterns of activation that resemble observed modulation rates and particular aspects of behavior. The utility of this approach is illustrated vividly in our sophisticated understanding of the ocular motor circuits that has proven clinical value [91]. This approach produced models for motion discrimination [92] and visual search [93,94, 95]. Ultimately, we would like to construct models that are constrained by the microcircuitry of the cerebral cortex [96,97]. As more neurobiological constraints are discovered, though, they offer converging insights only with the correct mapping between neural measures and model parameters.

Concluding remarks

The conundrums outlined in the foregoing are not just a theoretical exercise. A failure to map - compellingly and convincingly - computational (mental) constructs onto brain processes has broad consequences. Practically, computational psychiatry is based on the hope that models of normal performance can provide insight into the mechanisms producing abnormal performance [98]. But, can computational psychiatry be useful if model parameters are not reliable indices of specific neural processes? If neurons in a brain structure do not correspond to model parameters or dynamics, should this structure be excluded from further consideration for therapy? Scientifically, if effective mappings between mental and physical cannot be accomplished for a topic with as much apparent scientific traction as perceptual decision-making, what hope have we for topics like language or consciousness? The goal of this review has been to highlight unresolved, important, and tractable questions that can energize further research and understanding.

In 1750, Benjamin Franklin wrote in his Opinions and Conjectures, Concerning the Properties and Effects of the Electrical Matter [99], “These Explanations … when they first occurred to me … appear’d perfectly satisfactory: But now I have wrote them, and considered them more closely in black and white, I must own, I have some Doubts about them. Yet as I have at present Nothing better to offer in their Stead, I do not cross them out: for even a bad Solution read, and it’s Faults discovered, has often given Rise to a good one in the Mind of an ingenious Reader. Nor is it of much Importance to us to know the Manner in which Nature executes her Laws; ‘tis enough, if we know the Laws themselves.” The marriage of cognitive neuroscience and mathematical psychology has enriched both and will never be torn asunder. Still, self-reflection from time to time is healthy for all good marriages.

Box 1, Figure I.

Simplified diagram illustrating major connections between cortical areas MT, LIP, and FEF and with subcortical circuits producing saccades. The nodes and connections are explained in the Box text.

Box 2, Figure I.

Key parameters of stochastic accumulation process. RT of a gaze shift is portrayed. Top panels plot the evolving discharge rate of neurons recorded in a cortical area while monkeys were deciding where to shift gaze. The bottom panels plot the trajectory of stochastic accumulation in a model that was fit to the performance while the neurons were recorded. The left panels plot the values aligned on when the stimulus was presented. The right panels plot the values aligned on when the choice gaze shift was initiated. Progressively less saturated lines plot trajectories for progressively longer RT. The correspondence between observed neural modulation and modeled trajectories is interpreted as support for the model. Implicit in this interpretation is the proposition that the neurons are instantiating the process described by the model. The parameters are explained in the Box text.

Highlights

The collaboration between neuroscience and mathematical psychology has been highly productive. One of the anchors for this collaboration has been the focus on response time during perceptual decision-making, and the investigation of its mechanistic basis in terms of stochastic accumulation of evidence.

This productivity has been powered by the belief that the computational models can explain what neurons or neural circuits do, and that the properties of neurons or neural circuits can guide the selection of more accurate and effective computational models.

The validity of this belief hinges on whether accumulator model parameters and neural measures can be mapped to one another. This mapping is articulated through linking propositions.

This review surveys recent research that raises a variety of questions about the transparency of this mapping. Continued productivity depends on establishing valid and accurate linking propositions.

Outstanding Questions

To what extent are the neurons contributing to RT during perceptual decision-making specific or adaptable? To address this issue, neural measures should be obtained while subjects perform multiple tasks (e.g., perceptual discrimination and visual search) or combined tasks (e.g., perceptual decision making with stop signal trials).

What is the functional architecture and microcircuitry producing RT during decision-making? To address this question, neurophysiological samples should characterize the actual diversity of patterns of neural modulation. Just sampling more neurons is not sufficient, though. Clarity is gained only by sampling the neurons properly mapped to the model process in question. Also needed is information about the cortical layers and modules in which these neurons are located. Finally, simultaneous sampling of neural discharges in multiple structures should be obtained in tasks that can be described by stochastic accumulator models.

How does neural activity in the forebrain reaching some threshold value cause the final release of inhibition that launches the ballistic movement measured as RT? To address this issue, new empirical and theoretical work should investigate this critical gap of knowledge.

What is the relationship between invasive and noninvasive neural measures related to RT during decision-making? To address this issues, simultaneous sampling of neural discharges and EEG or fMRI should be obtained in tasks that can be described by stochastic accumulator models.

What distinct operations and stages of processing produce RT during decision-making? To address this question empirically, more complex tasks with manipulations of multiple factors should be developed. Theoretically, the stochastic properties of multi-stage models should be explored in more detail.

What is the mapping between stochastic accumulator model parameters and neural measures? Further progress can be made with conjoint modeling of neural signals and performance measures.