Influence of background lung characteristics on nodule detection with computed tomography

Abstract.

We sought to characterize local lung complexity in chest computed tomography (CT) and to characterize its impact on the detectability of pulmonary nodules. Forty volumetric chest CT scans were created by embedding between three and five simulated 5-mm lung nodules into one of three volumetric chest CT datasets. Thirteen radiologists evaluated 157 nodules, resulting in 2041 detection opportunities. Analyzing the substrate CT data prior to nodule insertion, 14 image features were measured within a region around each nodule location. A generalized linear mixed-effects statistical model was fit to the data to verify the contribution of each metric on detectability. The model was tuned for simplicity, interpretability, and generalizability using stepwise regression applied to the primary features and their interactions. We found that variables corresponding to each of five categories (local structural distractors, local intensity, global context, local vascularity, and contiguity with structural distractors) were significant ($p<0.01$) factors in a standardized model. Moreover, reader-specific models conveyed significant differences among readers with significant distraction (missed detections) influenced by local intensity- versus local-structural characteristics being mutually exclusive. Readers with significant local intensity distraction ($n=10$) detected substantially fewer lung nodules than those who were significantly distracted by local structure ($n=2$), 46.1% versus 65.3% mean nodules detected, respectively.

1. Introduction

Lung cancer is the leading cause of cancer death in the United States.¹ Each year, more people die of lung cancer than of colon, breast, and prostate cancers combined.² However, when detected early, lung cancer is curable following surgical resection.³ As the most common manifestation of early lung cancer, lung nodule detection is critical to diagnosing cancer at a curable stage.

Lung nodule detection within computed tomography (CT) reconstructions is challenged by complex and distracting lung anatomy. Efforts have been made to determine the relationship of local anatomical complexity and the detectability of lung nodules. Smith et al.⁴ recently demonstrated in a standardized model that nodule detection is influenced by both morphological distractors and local pixel values. However, there are limitations to a standardized model when considering the high degree of interobserver variability among readers seeking to detect lung nodules in CT scans. Specifically, in a study of 13 readers seeking to identify 157 synthetic nodules in 40 CT volumes, detection rate ranged between 29.9% and 72.6%.⁵ Variability in the relative influence of distracting image characteristics on detection rates is supported by the significance of a random effects term in the previously reported generalized linear model that related lung complexity to nodule detectability.⁴ In that prior study, the expected detection rates for a subset of nodule instances was substantially higher than their observed rate of detection by the 13 radiologists.⁵ Many of these outlier instances shared a common characteristic of having nearly equal spacing with neighboring distractors of similar size and shape in the transverse plane. These distractors invariably represented local clusters of pulmonary blood vessels. This observation encouraged the definition of a new variable [archipelago effects (ARC)] for characterizing the impact of local blood vessel clusters with similar size, shape, and spacing with respect to the lung nodule.

This report aims to extend insights into the influence of background lung characteristics on lung nodule detection in three ways. First, based upon a review of the 12 image characteristics modeled by Smith et al.,⁴ two additional characteristics are added, one statistical and one structural. The statistical feature is represented by standard deviation of local voxel values, and the structural feature characterizes a nodule locus as being associated with similarly sized and spaced “dot-like” distractors, termed the “archipelago effect.” Second, fixed linear effects models are developed for each of the 13 readers independently and compared with a generalized mixed effects model to identify interobserver variations and patterns on distractor influence on lung nodule detection. Finally, pairwise interactions between all 14 variables are included in the candidate models with systematic exclusion of primary variables and interactions to balance model fit with variable count.

Motivated by the concerning problem of lung nodule detectability, this study presents a step toward understanding the relationship between reader, local lung complexity, and nodule detection on CT scans, aiming to provide information that might facilitate targeted training for image interpretation.

2. Methods

2.1. Study Framework

For this study, 14 local and global characteristics of lung CT scans enriched with synthetic nodules and their interactions were analyzed and associated with the nodule detection performance of radiologists interpreting the CT scans. Readers were instructed to scroll through the CT sections and identify all pulmonary nodules with a comprehensive search. All examinations had nodules embedded, but this information was hidden from readers. Also, they were encouraged to take as much time and session divisions as needed.

A generalized linear mixed model was fit to the performance of all reads, followed by the creation of generalized linear submodels with fixed effects for each of the 13 readers. These models were iteratively reduced to 11- and 5-variable models to simplify the models and minimize colinearity. Reader-specific models were compared with the standardized model to assess differences and patterns among those differences. Detailed descriptions of these steps follow.

2.2. Source Data

Data collection for this study has been described previously.⁵ In brief, 13 radiologists with varying levels of experience (three first-year residents, three fourth-year residents, two cardiothoracic fellows, and five cardiothoracic attending physicians) identified lung nodules in 40 CT datasets (0.625-mm section thickness). Each dataset was composed of one of three nodule-free lung CT scans into which between three and five synthetic 5-mm nodules were embedded. The readers were instructed to identify all $>4\text{-}\mathrm{mm}$ pulmonary nodules. Their search through the stacks of transverse sections was unconstrained, and they were encouraged to perform a thorough search to assure comprehensive detection. For this study, the loci of all true and false negative detections were recorded and used to analyze characteristics of the background lung CT data without the imbedded nodules. A total of 157 nodules were assessed by each of the 13 readers across the 40 CT datasets.

2.3. Complexity Metrics

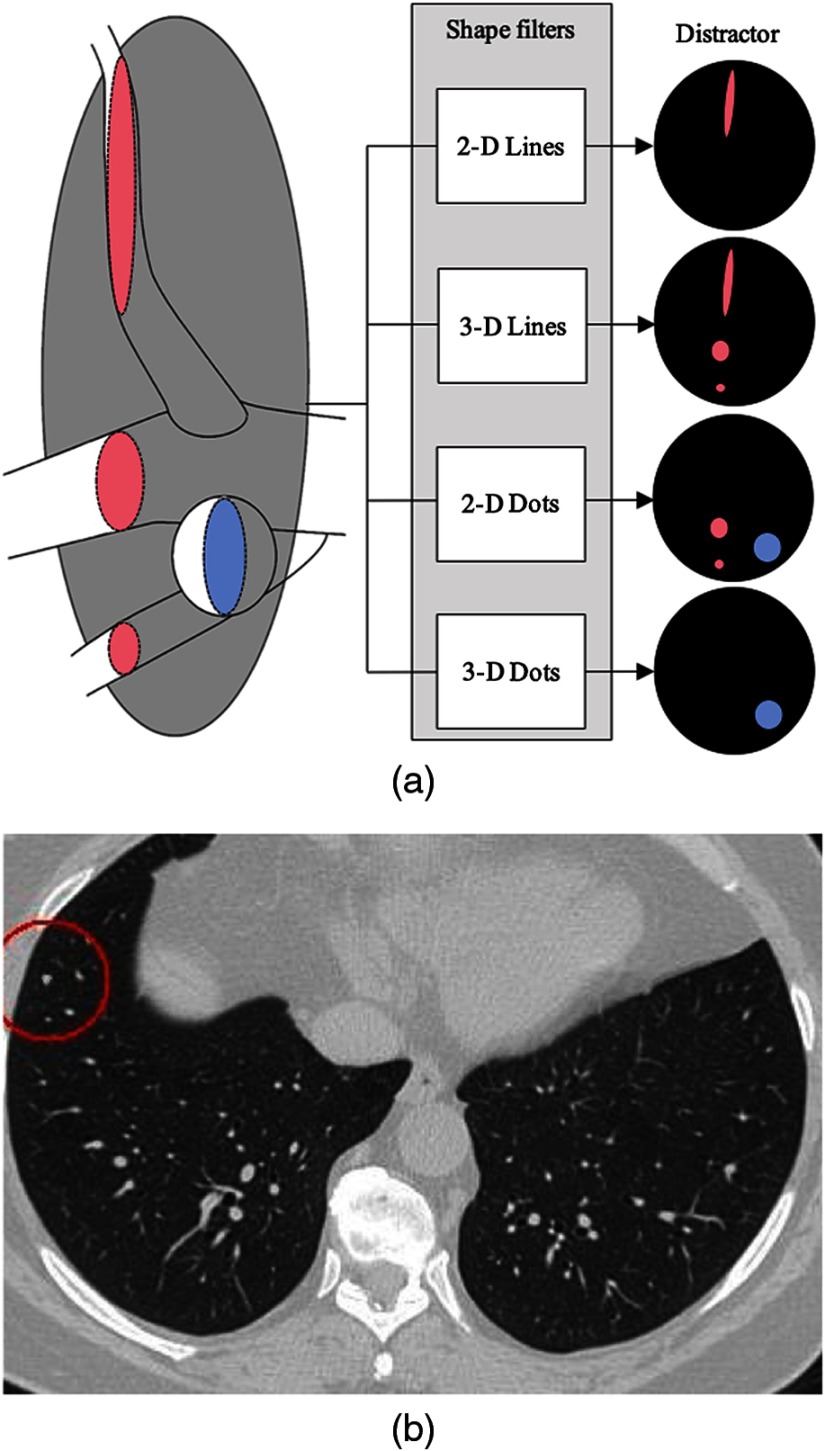
Fourteen characteristics of lung complexity were measured (Table 1). Twelve of these features have been described previously,⁴ and the remaining two features are novel to this study. In brief, previously defined metrics 1 to 4 quantify local structural distractors surrounding a nodule (Fig. 1); metrics 5 and 6 quantify local voxel intensity; and metrics 7 to 10 characterize structural features. Metrics 7 and 8 are global lung characteristics relating to the size of the search field (small at the apices and bases, large in the mid-lung) and central versus peripheral localization based upon proximity to the tracheal carina. Metrics 9 and 10 focus on the quantity and distribution of nearby blood vessels. Finally, contiguity of a nodule with local structural distractors is captured by metrics 11 to 14. Metrics 1 to 8 are continuous variables; metric 9 is ordinal, and metrics 10 to 14 are logical with 1 indicating existence and 0 indicating absence. All variables except the two global context variables were considered within a 25-pixel radius around each nodule locus, and each CT section was reconstructed with a $512\times 512\text{-}\text{pixel}$ matrix.

Table 1.

Lung complexity metrics check table.

Index	Metrics name	Code	Category	Numeric type
1	2-D line-like distractor index	L2D	Locala structural distractors	Continuous
2	2-D dot-like distractor index	D2D
3	3-D line-like distractor index	L3D
4	3-D dot-like distractor index	D3D
5	Log standard deviation in neighborhood of nodule	LSTD	Local intensity
6	Mean gray value in neighborhood of nodule	MPV
7	Fraction of slice containing lung	TR	Global context
8	Distance of nodule from trachea	DTT
9	Number of vascular particles	NP	Local vascularity	Ordinal
10	Archipelago effects	ARC		Logical
11	CL2D	CL2D	Contiguity with structural distractors
12	Contiguity with 2-D dots	CD2D
13	Contiguity with 3-D lines	CL3D
14	Contiguity with 3-D dots	CD3D

^aA local scope (or region of interest) is defined as within an in-plane radius of 25 pixels ($\sim 2\mathrm{cm}$) on five consecutive slices centered at the central slab.⁴ Newly introduced features relative to the features of Smith et al.⁴ are indicated with bold type.

Fig. 1.

(a) Local structural distractors explained. The lung nodule (blue) is spheroid and provides a “dot-like” profile on transverse reconstructions (2-D dots) and volumetrically [three-dimensional (3-D) dots]. Blood vessels (red) may be seen as either dot-like (2-D dots) or line-like (2-D lines) on transverse reconstructions, depending on their local orientation, but they are always line-like volumetrically (3-D lines). (b) Transverse CT section demonstrating numerous dot-like and line-like structures. Only the dot-like structure in the red circle is a lung nodule. All other dot- or line-like structures are pulmonary blood vessels.

Based upon an analysis of outlier cases using our previous detectability modeled, we introduced two new factors to our original 12: a statistical feature represented by the natural logarithm of the standard deviation of local voxel values [log standard deviation in neighborhood of nodule (LSTD), metric 5], and a structural feature characterizing a nodule locus as being associated with similarly sized and spaced two-dimensional (2-D) dot-like distractors, termed “archipelago effect” (ARC, metric 10). The LSTD was added as an additional variable to control for the effects of noise in the CT images. Higher values of LSTD indicate greater variability in pixel values surrounding a nodule. ARC is a logical measure coding the position of a nodule as being within a local cluster of similarly sized particles. Although the previous study accounted for the number of local blood vessels, it did not assess the impact of this specific alignment of similarly sized vessels with respect to the inserted nodule. Here, an ARC value of 1 indicates that the nodule is located within a chain-like cluster of similarly-sized blood vessels, which potentially disguise it as a part of the native vascular system.

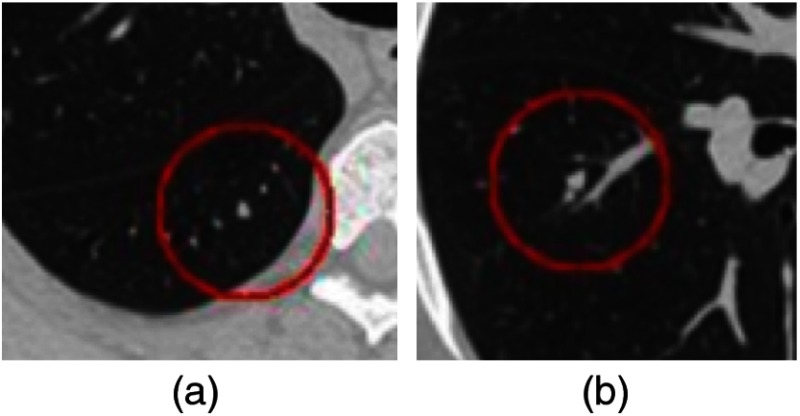
Figure 2 shows synthetic ARC examples where D2D distractors of similar size with respect to inserted nodules cluster in nearly equidistant chain-like spatial distribution. Eight out of 157 nodules were identified with ARC.

Fig. 2.

(a) Examples of ARC presence. (b) Although a nodule is in close proximity to blood vessels, it is not an ARC because the adjacent vessels are either D2L or differently sized D2D distractors. The red circle indicates a radius of 25 pixels within the $512\times 512\text{pixel}$ reconstructions, and the nodules are positioned at the center of the circles.

2.4. Statistical Analysis

The continuous and ordinal features were normalized by minmax scalers. To enhance flexibility and simplicity of the complexity model, feature selection was carried out. A subset of the 14 complexity metrics with selected interactions were related to detection by the 13 radiologists. A total of 2041 binary detection outcomes ($13\text{readers}\times 157\text{nodules}$) were related to complexity features using a generalized linear mixed model with the following equation,^6,7

$$g({\mu }_{ij})={\mathbf{X}}_{ij}\beta +{\mathrm{b}}_i+{ϵ}_{ij},$$ (1)

where $g(·)$ is the probit link function, ${\mu }_i$ is the probability of detection for reader $i$, ${\mathbf{X}}_i$ is a vector of features values for reader $i$ (see Table 1), $\beta$ is a vector of coefficients (fixed effects), and ${\mathrm{b}}_i$ is a reader-specific random effect, assumed to have a zero mean Gaussian distribution independent of the measurement error term ${ϵ}_{ij}$, which is also assumed to have a zero mean Gaussian distribution. The model is fit by the method of restricted maximum likelihood.

One goal of this study was to investigate interobserver variability with an expectation that readers’ detection of nodules is affected by complexity metrics in different ways. To study this, for a selected set of variables, the following two models were established.

• 1.Standardized model: a single generalized linear mixed model fit by all of the 2041 responses.
• 2.Reader-specific model: a set of 13 generalized linear submodels with fixed effects, each fit by 157 observations of an individual reader.

2.4.1. Feature interactions and selection

The feature selection process consists of automatic stepwise regression and manual exclusion of certain highly correlated variables.

To better account for nuances in the effects of lung complexity on nodule detection, in addition to the 14 primary main effects, we considered 55 interactions defined as element-wise products within pairwise combinations of logical and all types of primary variables, leading to a feature space of potentially 69 dimensions. To avoid overfitting the model given the increased feature dimensionality, feature selection was carried out on the basis of the Akaike Information Criterion (AIC) via stepwise regression. The AIC definition is given as⁸

$$\mathrm{AIC}=2k-2\log L,$$ (2)

where $L$ is the likelihood and $k$ is the number of variables in the model.

Feature selection started with the main-effects-only model, followed by iteratively adding items from the interactions set or removing items from the current model at each step. Either a main effect or an interaction could be added or removed, yet the removal of a main effect would cause the removal of all correspondent interactions as well. Actions were driven by minimizing the AIC.

We repeated the stepwise regression for 100 random iterations of 10-fold cross validation to enhance robustness. A random subset of 15 nodules was left out in each fold. Subsequently, the occurrence frequency matrix was binarized at 0.4 threshold. In other words, any variables occurring less frequently than 40% of the time would not appear in the resulting model.

Furthermore, we refined the selected model by removing certain variables that were highly correlated with others. Multicollinearity, investigated by both pairwise correlation and the variance inflation factor (VIF), was avoided to reduce the standard errors of the coefficients. Therefore, we manually removed highly correlated variables that did not substantially contribute to reducing AIC following two baselines: (1) the removal should not increase AIC by a factor $>1\%$ and (2) higher removal priority was given to interactions over main effects. In addition, we computed the adjusted coefficient of determination (adjusted $R^2$) and calculated probability ($p$-value) for resulted models and variables.

2.4.2. Comparison between reader-specific and standardized models

We fit candidate models independently to each reader. Reader-specific models were fit for each of the 13 readers using their binary detection responses for the 157 nodules. The model performance was evaluated and compared on the basis of the receiver operating characteristic accuracy of model-estimated detection rates versus human detection rates.

In addition to these reader-specific models, a standardized model using all 2041 responses was fit to the data. This model accounted for differences in readers by including a random effect term for reader. We examined the difference between standardized and reader-specific models in terms of statistical significance and area under the curve (AUC). Each individual model was compared with the standardized model, as well as with other individual models. We ran statistical tests for the hypothesis that different readers may present different patterns in perceiving anatomy complexity. These comparisons and analyses were conducted to reveal commonly significant complexity metrics that confounded all or groups of readers. For all analyses of feature significance, a conservative threshold of $p<0.01$ was used to guard against false discovery.

3. Results

3.1. Model Selection

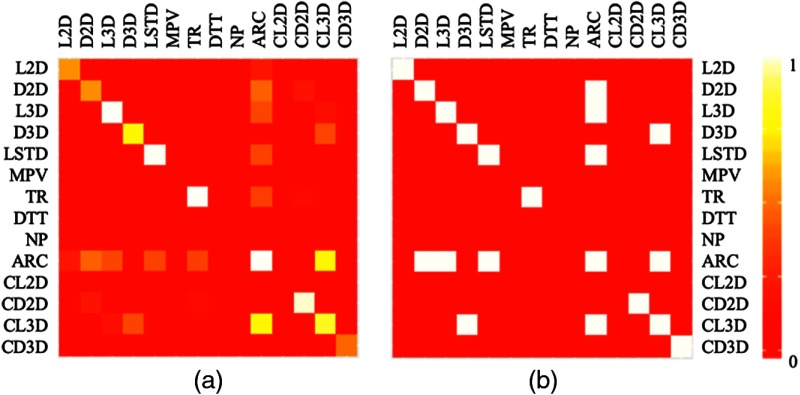
As described in Sec. 2.4.1, the first step of model selection was automatic stepwise regression in a cross-validation manner. Figure 3 shows both raw and binarized (threshold = 0.4) heatmaps of variable occurrence frequencies resulting from this process, with cells on the diagonal being the main effects and cells off the diagonal being interactions between the correspondent rows and columns.

Fig. 3.

Occurrence frequency heatmap. (a) Raw occurrence frequency map. (b) Occurrence frequencies binarized at 0.4.

Based upon their occurrence frequencies, four main effects [distance to trachea (DTT), number of particles (NP), mean pixel value (MPV), and contiguity with 2-D lines (CL2D)] were removed and five interactions (D2D:ARC, ARC:L3D, D3D:CL3D, ARC:LSTD, and ARC:CL3D) were introduced. The AIC of this new model was 2188.3, a reduction compared with the initial main-effects-only model’s 2211.8.

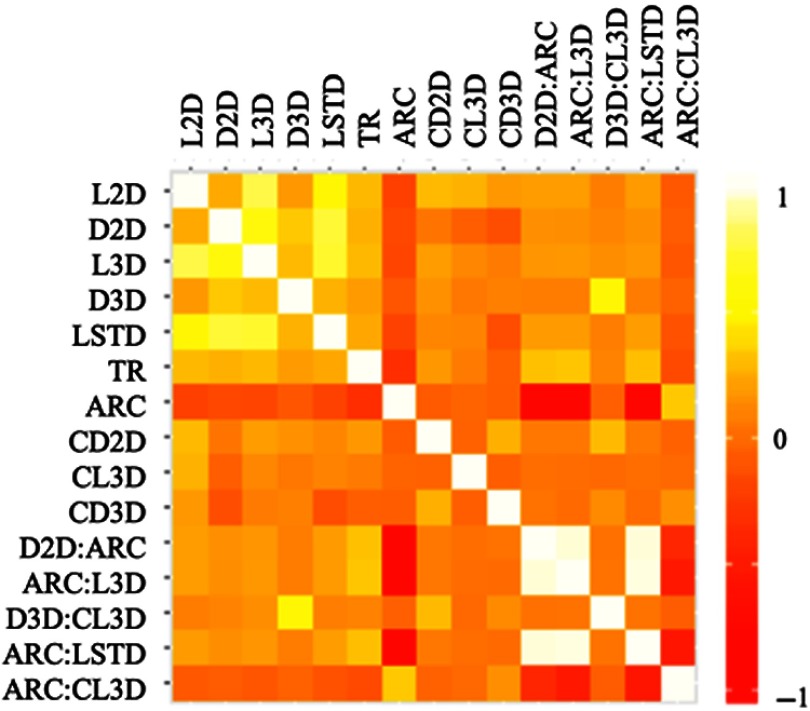
Nevertheless, we observed strong correlations between certain pairs of variables. A strongly correlated pair could indicate feature redundancy. Figure 4 shows pairwise correlations of the new model’s variables, ranging from $-1$ to $+1$. It can be observed that pairs such as ARC-ARC:LSTD have a strong negative correlation and pairs such as ARC:L3D-D2D:ARC have a strong positive correlation.

Fig. 4.

Correlation heatmap of variables considered for stepwise model selection based upon their frequency of occurrence. The final five variables listed are interaction terms between two variables separated by a “:” mark.

Using the manual term removal protocol described in Sec. 2.4.1, we identified two candidate models, one with 11 variables (adjusted $R^2=0.65$, $\mathrm{AIC}=2193.3$, $|p<0.05|=7$) and one with 5 variables (adjusted $R^2=0.62$, $\mathrm{AIC}=2237.0$, $|p<0.05|=5$). To identify multicollinearity, we investigated both pairwise correlation and the VIF. According to Dohoo et al.⁹ and Lin,¹⁰ the critical levels of correlation coefficient and VIF values are 0.9 and 10, respectively. In the 11-variable model, the highest correlation was 0.79 (L2D-L3D) and VIF was 3.69 (L3D). In the 5-variable model, the highest correlation was 0.74 (LSTD-L3D) and VIF was 1.95 (L3D). Hence, we concluded that the multicollinearity of the selected models was acceptable.

3.2. Reader Generalizability Study

In the reader generalizability study, we customized the aforementioned candidate models by fitting them individually to each reader with fixed effects. We looked for any underlying patterns by analyzing weights, $p$ values, and fitness of the reader-specific models.

Tables 2 and 3 show variable coefficients of the 11-variable and 5-variable models, each row being a model fit to the correspondent reader(s). The columns are sorted, descending from left to right, by the number of statistically significant occurrences ($p<0.01$) among all individual models. The bottom three rows of reader-specific models are, respectively, the mean and standard deviation (SD) of a variable coefficient, as well as the total number of its significant occurrences.

Table 2.

The 11-variable models’ coefficients and statistics.

Reader	(Intc.)	LSTD	ARC	L3D	CL3D	L2D	TR	D3D	CD2D	D3D:CL3D	CD3D	CL3D:ARC
(a) Standardized model
All	0.09	−2.22**	−1.01**	−1.99**	−0.30**	1.30*	−0.59*	−0.20	−0.38*	−0.80	0.45	5.39
(b) Reader-specific model
1	0.55	—	−1.05	−4.99**	−0.96*	3.89**	—	—	—	—	—	—
2	0.02	−2.14*	−0.89	−2.27	—	—	—	—	—	4.71	—	—
3	−1.23	—	−1.41*	−2.81	1.12	2.23	—	−24.21	—	19.11	—	—
4	0.08	−2.15*	−1.90**	−2.18	—	2.00	—	—	—	—	—	—
5	0.19	−2.53*	−1.14*	—	—	—	—	—	—	—	—	—
6	−0.22	—	—	−2.70	—	2.13	—	—	—	—	—	—
7	0.81	—	−1.14*	−3.45*	—	—	—	—	—	—	—	—
8	−0.04	−5.01**	—	—	—	—	−1.99*	—	—	—	—	—
9	0.85	−4.30**	−1.08	—	−0.66	—	—	—	−1.11	—	—	—
10	−0.19	−3.22**	−1.09	—	—	—	—	—	—	—	—	—
11	−0.11	−2.98**	−1.07	−2.39	—	—	—	—	—	—	—	—
12	−0.05	−3.66**	—	—	—	—	—	—	—	—	—	—
13	−0.8	−2.39	—	—	—	—	—	—	—	—	—	—
Mean	0.37	−1.66	−0.76	−1.6	−29.31	1.53	−0.51	−2.66	−1.11	−584.7	0.44	5.74
SD	1.45	3.38	1.39	2.71	42.45	0.98	0.69	6.55	2.31	848.90	5.56	1.84
Occ.	5	8	4	2	1	1	1	0	0	0	0	0

The statistical significance of a variable is indicated by (i) no asterisk: $0.01<p\le 0.1$; (ii) single asterisk * $0.001<p\le 0.01$; (iii) double asterisk ** $p\le 0.001$; and (iv) blank cell indicates insignificant $p>0.01$.

Table 3.

The 5-variable model coefficients and statistics.

Reader	(Intc.)	LSTD	L3D	ARC	TR	CD2D
(a) Standardized model
All	0.04	−2.06**	−1.31**	−0.84**	−0.48**	−0.46**
(b) Reader-specific model
1	0.31	—	−2.39**	—	—	—
2	−0.02	−1.93	−1.26	—	—	—
3	−0.25	−2.05*	−1.32	−1.18	—	—
4	0.01	−2.12*	−1.39	−1.54*	—	—
5	0.17	−2.43*	—	−0.98	—	—
6	−0.29	—	−1.78	—	—	—
7	0.76	−	−2.61**	−1.11	—	—
8	−0.14	−4.40**	—	—	−1.65*	—
9	0.69	−3.74**	—	—	—	−1.32*
10	−0.16	−2.99**	—	−0.89	—	—
11	−0.1	−3.07**	−2.01	−1.04	—	—
12	0.05	−3.82**	—	—	—	—
13	−0.65	−2.69*	—	—	—	—
Mean	0.49	−1.5	−1.01	−0.57	−0.42	−1.14
SD	1.64	3.57	1.60	1.33	0.65	2.20
Occ.	6	9	2	1	1	1

The statistical significance of a variable is indicated by (i) no asterisk: $0.01<p\le 0.1$; (ii) single asterisk * $0.001<p\le 0.01$; (iii) double asterisk ** $p\le 0.001$; and (iv) blank cell indicates insignificant $p>0.01$.

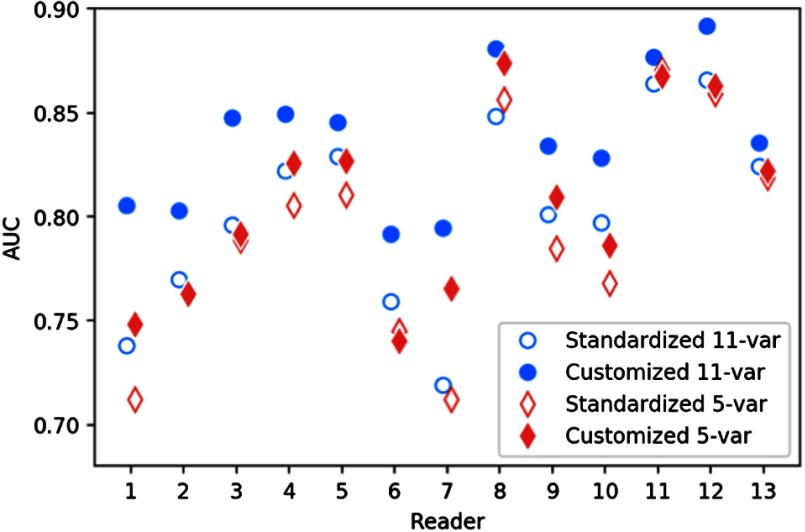
As shown in Fig. 5, we compute the model-determined detectability against the true human detectability and obtain the AUC for each user and each model. The number of variables in the model is also compared within two modeling strategies. For standardized models, we performed a likelihood ratio test (LRT)¹¹ to compare the performance of 11- and 5-variable models. For reader-specify models, we similarly performed an LRT for each user and combined the $p$-values using Fisher’s method.¹² We find that 11-variable models always showed a closer estimate to human detectability than 5-variable models ($p<0.05$). In addition, reader-specific models produce significantly higher estimate accuracy than the standardized models ($p<0.05$). The mean discrepancy ($\pm \mathrm{SD}$) of the two modeling strategies is $0.035\pm 0.02$ and $0.025\pm 0.02$, respectively, for 11-variable and 5-variable models. Thus, while the higher degree of personalization provided by a reader-specific versus a generalized model improves model performance, the improvement was greater for comprehensive (11-variable) compared with compact (5-variable) models.

Fig. 5.

Controlled comparisons of standardized and reader-specific models with different number of variables.

4. Discussion

In this study, two new metrics of lung complexity, the standard deviation of local intensity (LSTD) and the archipelago effect (ARC), are introduced as potential statistical and structural distractors to lung nodule detectability. Following preliminary analysis, the natural logarithm of the standard deviation exhibited greater linear correlation with detectability; thus LSTD was selected to represent the statistical measure of local voxel value variability. Both LSTD and ARC are found to be significant in reducing nodule detectability throughout an iterative stepwise model selection. LSTD was a significant factor in 100% and ARC was significant in 89% of regression models. Their inclusion in the standardized complexity-detectability model resulted in a significant increase in adjusted $R^2$ from 0.57 to 0.64.

The final result of model selection incorporates one variable from each of the five complexity categories, reflecting the role of local structural, local intensity, global context, vascular proximity, and contiguity with other structures in influencing nodule detection. Respectively, the five variables are L3D, LSTD, TR, ARC, and CL2D. While identifying the single most significant feature among each of the distractor categories was not an aim of the analysis, it is an intriguing outcome of our stepwise analysis and supports the importance of each of the identified classes of distractor type for overall nodule detection.

In contrast, MPV, DTT, NP, and CL2D were rarely significant. This observation is generally consistent with our previous work, except that in previous work MPV was found to be significant with a $p$-value of 0.02.⁴ The replacement of MPV with LSTD in the final models suggests that background variability has a greater influence on nodule detectability than average background intensity.

Upon determination of two candidate models with 11 and 5 variables, for each set of variables, 13 personalized submodels were fit as reader-specific models. Given a set of metrics, its generalizability refers to the ability of effectively fitting the detection outcomes across different readers. For metrics with high generalizability, we expect to see less performance degradation when the modeling strategy is switched from customized to generalized. Reader-specific models were compared with the standardized baseline models, and the difference in performance AUC was used to measure the generalizability of the selected metrics. Based upon the principle that generalizability of reader-specific influences increases with smaller differences between the standardized and the reader-specific models, the 5-variable model was more generalizable than the 11-variable model. This is likely because models with more variables provide a basis for greater variations to manifest among readers, expressing greater nuances among readers.

One particularly intriguing result was that statistical significance ($p<0.01$) of L3D and LSTD, the two most commonly occurring variables within reader-specific models, were mutually exclusive. For both 5- and 11-variable configurations, only one model, that derived for reader 6, contained neither L3D nor LSTD as significant variables. For readers 1 and 7, LSTD was significant, while L3D was significant for the remaining 10 readers. No reader-specific models demonstrated significance for both metrics. L3D is classified as a local structural distractor, and LSTD is classified as a local intensity metric. Table 4 identifies the three primary distractor groups with their associated detection rates.

Table 4.

Complexity perception groups.

Group	In-group readers	Detection rate, mean ($\pm \mathrm{SD}$)	Primary distractor ($p<0.01$)
1	1, 7	65.3% ($\pm 7.3\%$)	Local structure
2	2, 3, 4, 5, 8, 9, 10, 11, 12, 13	46.1% ($\pm 8.5\%$)	Local intensity
3	6	38.9% ($\pm \mathrm{NA}$)	None significant

Interestingly, readers 1 and 7, a first-year resident and a cardiothoracic fellow who exhibited two of the three highest detection rates of 58.0% and 72.6%, respectively, were significantly distracted by local structural over intensity-based metrics. The 10 readers with significant intensity-based distraction exhibited an average detection rate of 46.1%. Following validation in a larger sample, this finding may inform strategies for improving detection.

Further study to refine the complexity metrics may also be of interest. In particular, ARC might be defined as a continuous measure instead of the current heuristic binary term. The observation of intensity-inclined and structure-inclined impact patterns could also come from distinct search patterns. In future work, we will assess associations between lung distractors and search characteristics such as gaze duration, search paths, and detection moment.

There are several limitations to the current analysis. We do not address false-positive detections. Our analysis of false-positive detections has revealed that many represent previously undetected native nodules within the substrate datasets. Focusing exclusively on the synthetic nodules for which an absolute reference standard exists limits the speculative nature of an analysis based upon detection of native features where an absolute reference standard does not exist. The dataset size limited the interpretation and verification of interobserver performance differences. In addition to generalized random-effect models and customized individual-independent models, multitask linear models via structural regularization¹³ can be another option for personalizing the detection predictions. Multidimensional analyses could be used to identify clusters of readers who respond to different feature sets. This would be especially interesting considering that readers 1 and 7 had the best performance and the poorest standardized fits. As might be expected, the models are less effective for predicting how distractors affect readers that perform at the extremes. Finally, machine learning approaches offer an opportunity to further understand background lung characteristics that influence nodule detection performance.

5. Conclusion

Using a semiautomatic stepwise optimization strategy for variable selection, the five selected variables for the standardized complexity-detectability model represented one metric within each of the five distractor categories. Both newly assessed distractors, LSTD and ARC, appeared in the refined standardized 5-variable model and many of the reader-specific models as significant distractors for lung nodule detection. The significance of either a local structural (L3D) or intensity-based factor (LSTD) in 12 of 13 reader-specific models, as well as their mutual exclusivity and association with substantially different reader performance, is an intriguing result. The dominant impact of one of two fundamentally different image characteristics might reflect innate or learned perceptual tendencies that may be modifiable. Experiments specifically designed to clarify these tendencies and assess their generalizability across volumetric search tasks would be useful toward establishing their consistency and might inform interventions that assess approaches toward improving feature detection during volumetric search. In addition, this early step toward quantifying reader performance with complexity metrics should inform future refinement of distractor metrics and their application in a larger cohort of readers to assess the hypothesis that reader performance is related to varying sensitivity to distraction by either local structural or intensity factors.

Biographies

Boning Li is a PhD student from the Rice University Scalable Health Labs where she studies how to leverage deep learning to predict mental and physical health using physiological and behavioral wearable sensors. She has also worked on image processing for medical and energy applications. She received her bachelor’s degree in electrical engineering from Harbin Institute of Technology and a master’s degree in electrical and computer engineering from Duke University.

Geoffrey D. Rubin, MD, MBA, FACR, FAHA, FSABI, FNASCI is the George B. Geller Distinguished Professor for Cardiovascular Research and professor of Radiology. He was previously professor of radiology at Stanford University where he also served as chief of cardiovascular imaging. He pioneered the development of CT angiography and a variety of volumetric visualization and analysis techniques including automated detection of lung nodules with CT. His current research focuses on applications of machine learning to medical image analysis and human perception in the interpretation of volumetric medical images.

Biographies of the other authors are not available.

Disclosures

No conflicts of interest relevant to the presented work, financial or otherwise, are declared by the authors.