Optimizing Assessments of Post-Error Slowing: A Neurobehavioral Investigation of a Flanker Task

Abstract

Appropriately adjusting to errors is essential to adaptive behavior. Post-error slowing (PES) refers to the increased reaction times on trials following incorrect relative to correct responses. PES has been used as a metric of cognitive control in basic cognitive neuroscience research as well as in clinical contexts. However, calculation of PES varies widely between studies and has not yet been standardized, despite recent calls to optimize its measurement. Here, using behavioral and electrophysiological data from a modified flanker task, we considered different methods of calculating PES, assessed their internal consistency, examined their convergent correlations with behavioral performance and error-related event-related brain potentials (ERPs), and evaluated their sensitivity to task demands (e.g., presence of trial-to-trial feedback). Results indicated that the so-called “robust” measure of PES, calculated using only error-surrounding trials, provided an estimate of PES that was three times larger in magnitude than the traditional calculation. This robust PES correlated with the amplitude of the error positivity (Pe), an index of attention allocation to errors, just as well as the traditional method. However, all PES estimates had very weak internal consistency. Implications for measurement are discussed.

1. Introduction

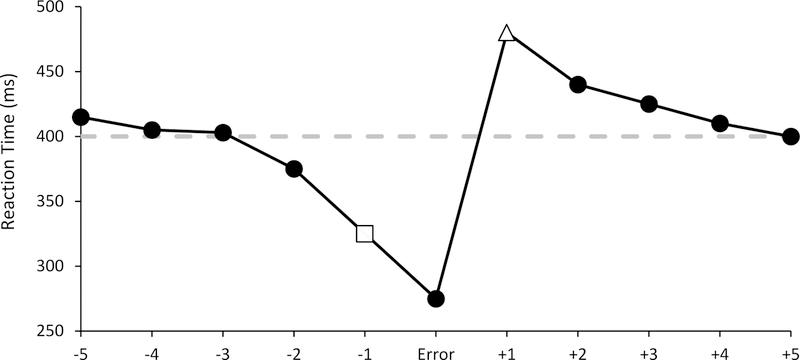
Errors are common in everyday life. The ability to detect, respond, and adjust to mistakes is an important human capacity that has been the subject of decades of cognitive neuroscience research (see Gehring et al., 2012 for a review). One common metric of this capacity is post-error slowing (PES; see Figure 1), which refers to the tendency of respondents to slow their reaction times (RTs) on trials that follow errors, relative to trials that follow correct responses (Rabbitt, 1966). PES has been investigated in basic models of cognitive control (Botvinick et al., 2001; Cavanagh & Shackman, 2015) and in a number of clinical contexts, including ADHD (Balogh & Czobor, 2016), substance abuse disorders (Sullivan, 2018), and Parkinson’s disease (Siegert et al., 2014).

Figure 1.

Typical post-error slowing effect.

There is debate regarding the functional significance of PES (Danielmeier & Ullsperger, 2011; Wessel, 2018). Some contend that PES reflects the output of a cognitive control process aimed at preventing future errors (Botvinick, Braver, Barch, Carter, & Cohen, 2001), while others suggest it reflects a non-adaptive orienting response to uncommon or surprising events (Notebaert et al., 2009). Some of this debate reflects the inconsistent relationship between PES and post-error accuracy (PEA) (Danielmeier & Ullsperger, 2011; Schroder & Moser, 2014). However, emerging evidence using drift-diffusion modeling – which allows specific theoretical accounts to be tested mechanistically with the various parameters this model provides – suggests PES may in some cases reflect an increase in response caution after an error is made (Dutilh et al., 2012b), or is part of an adaptive post-error process in which selective attention is increased and drift rate is reduced (i.e., both control and orienting aspects are present) (Fischer, Nigbur, Klein, Danielmeier, & Ullsperger, 2018). Other evidence indicates that the precise mechanisms underlying PES are nuanced and vary from task to task and across samples (Purcell & Kiani, 2016). Here, we are not so much concerned with the functional significance of PES, but rather how best to measure it. We believe that measuring PES consistently represents a necessary step toward the elucidation of its functional significance and its potential application to clinical populations.

There is currently no consensus on how to best measure PES, an issue poignantly raised by Dutilh and colleagues (Dutilh et al., 2012a). They noted that PES is most typically measured by subtracting the average reaction time (RT) on correct trials following correct trials from the averaged RT on correct trials following errors (PES = M_Post-Error - M_Post-Correct). Dutilh and colleagues referred to this estimate as PES_Traditional. However, based on drift-diffusion modeling and empirical data, these authors showed that this calculation is susceptible to fluctuations over the course of the assessment, including task engagement and fatigue. For some participants, as task engagement declines, most errors occur during the second half of the task. Therefore, the PES_Traditional estimate likely contains post-error RTs from the second half of the task and post-correct RTs from the first half. Depending on the context, this may mask real PES or artificially inflate PES estimates. The PES_Traditional method is also problematic because correct trials and post-correct trials greatly outnumber errors and post-error trials in most speeded-response tasks. To counteract these issues, Dutilh and colleagues recommended measuring PES by limiting the calculation to trials that surround errors (i.e., only consider post-correct trials that also precede errors). They refer to this estimate as PES_Robust. This estimate, as its name implies, is robust to fluctuations in task engagement, and the number of trials included in post-error and post-correct averages are equal (as they come from the same error sequence).

Since the original call to modify the calculation of PES, there have been many studies that have followed this recommendation (e.g., Agam et al., 2014; Navarro-Cebrian, Knight, & Kayser, 2013). However, we are aware of only a few studies that have compared traditional and robust estimates. These studies typically found a larger estimate for the robust method compared to the traditional method and a high correlation between the two metrics (Tabachnick, Simons, Valadez, Dozier, & Palmwood, 2018; van den Brink, Wynn, & Nieuwenhuis, 2014). The larger size for the robust method is due to the faster RTs on trials preceding errors (Brewer & Smith, 1989; Gehring & Fencsik, 2001) that are used in the robust estimate, resulting in larger differences in RT between post-error and pre-error trials. In the current study, we examined electrophysiological and behavioral data from one of the most commonly used tasks in the literature – the Eriksen flanker task (Eriksen & Eriksen, 1974) – to provide a more in-depth exploration of these two estimates.

In particular, we examined how PES estimates relate to two event-related brain potentials (ERPs) elicited after errors – the error-related negativity (ERN) and error positivity (Pe). The ERN is a sharp negative ERP deflection elicited between 50–100ms following error commission and reaches maximal amplitude at frontocentral recording sites (Falkenstein, Hohnsbein, Hoormann, & Blanke, 1991; Gehring, Goss, Coles, Meyer, & Donchin, 1993). The ERN is reliably source-localized to the anterior cingulate cortex (ACC; Herrmann et al., 2004; van Veen & Carter, 2002). The functional significance of the ERN remains debated, although the two most prominent accounts suggest that it either reflects a reinforcement-learning signal mediated by the mesencephalic dopamine system (Holroyd & Coles, 2002) or an automatic response conflict signal (Yeung, Botvinick, & Cohen, 2004). In either case, the ERN is thought to reflect the output of an adaptive error/conflict-signaling process that indicates more control is needed on subsequent trials.

Following the ERN, the Pe is a slower, more broadly distributed ERP that reaches maximal amplitude between 200–500ms over centroparietal recording sites (Falkenstein, Hoormann, Christ, & Hohnsbein, 2000). Whereas the ERN may be more linked to unconscious error/conflict-detection (although see Wessel, 2012), the Pe is consistently linked with the conscious awareness that a mistake has been made (Endrass, Franke, & Kathmann, 2005; Murphy, Robertson, Allen, Hester, & O’Connell, 2012; Shalgi, Barkan, & Deouell, 2009; Steinhauser & Yeung, 2010). Source localization studies indicate the Pe also originates in ACC (Herrmann, Römmler, Ehlis, Heidrich, & Fallgatter, 2004), although other areas including the anterior insula (Ullsperger, Harsay, Wessel, & Ridderinkhof, 2010) have been implicated in its generation. Moreover, the Pe may be related to attentional orienting processes in service of mobilizing resources in response to the error (Tanaka, 2009) and shares topographic and latency properties with the stimulus-locked P300 (Leuthold & Sommer, 1999; Ridderinkhof, Ramautar, & Wijnen, 2009). The ERN and Pe are reliably dissociated from one another in terms of functional significance and sensitivity to task demands (Davies, Segalowitz, Dywan, & Pailing, 2001; Overbeek, Nieuwenhuis, & Ridderinkhof, 2005; Tanaka, 2009).

The relationship between ERN/Pe and post-error behavioral adjustments is complicated and largely inconsistent. A recent meta-analysis attempted to quantify relations between the ERN and PES (Cavanagh & Shackman, 2015). These authors found that correlations were larger for intra-individual relationships (correlations in trial-to-trial variation in ERN and subsequent RT on the next trial) than for inter-individual correlations (averaged ERNs and averaged PES estimates correlated between participants). Yet, closer inspection of these data reveals inconsistent measurement of PES. The five studies that examined intra-individual correlations did not technically examine post-error slowing (which would require a difference to be computed between post-error and post-correct trials)¸ but rather considered only post-error RT (Cavanagh, Cohen, & Allen, 2009b; Debener et al., 2005; Gehring et al., 1993; Weinberg, Riesel, & Hajcak, 2012), or examined the time it took participants to rate the accuracy of their response (Wessel, Danielmeier, & Ullsperger, 2011). These five studies examined ERN on trial N and RT on trial N+1 and produced a significant meta-analytic correlation of r = .52. In contrast, the 20 inter-individual studies almost exclusively used the PES_Traditional estimate (just one used PES_Robust), which, as mentioned above, is subject to contamination. The analysis of these 20 studies revealed a small and non-significant meta-analytic correlation between ERN and PES of r = .19. Thus, because very few studies examined PES optimally, it is difficult to judge the relationship between error-related brain activity and post-error adjustment. A more recent study examined relations between frontal theta, ERN and PES (Valadez & Simons, 2018) and found that post-error RT was negatively correlated with greater frontal theta power, but that PES was unrelated to ERN. We are unaware of any systematic reviews of the relationship between Pe and PES, although some past studies found that individuals with larger Pe amplitudes are characterized by larger PES (Chang, Chen, Li, & Li, 2014; Hajcak, McDonald, & Simons, 2003) and others show relationships between Pe and post-error accuracy, but not slowing (Schroder, Moran, Moser, & Altmann, 2012).

The inconsistent between-subjects correlations involving PES may, in part, be related to low internal reliability of this measure, as between-subjects correlations are always constrained by the internal reliabilities of the measures used (Schmitt, 1996). Although no previous studies have evaluated the internal consistency of PES, recent work has highlighted poor measurement properties within the cognitive neuroscience literature (Hajcak et al., 2017; Hedge, Powell, & Sumner, 2018; Infantolino, Luking, Sauder, Curtin, & Hajcak, 2018). This is particularly true of difference measures – which are calculated by subtracting one measure from another (see Infantolino et al., 2018) – which is the case with PES. Difference scores have long been known to have unfavorable internal consistency, especially if the two constituent scores are highly correlated with one another (Infantolino, Luking, Sauder, Curtin, & Hajcak, 2018; Lord, 1958). Thus, in the current study, we also evaluated the internal reliability of the different PES estimates. It is certainly possible that PES has low internal reliability; in fact, Hedge et al (2017) point out that experimental tasks designed to elicit large within-subjects effects may produce the lowest between-subjects variance (and subsequently low reliability).

Finally, PES and post-error accuracy (PEA) appear to be sensitive to task characteristics. Specifically, when the response-stimulus interval (RSI) is short – i.e., when participants do not have much time between the error trial and the following trial – PES tends to be larger and PEA tends to be lower than trial sequences with longer RSIs (Jentzsch & Dudschig, 2009). Extending these findings, Wessel (2018) outlined an adaptive orienting theory of error processing. This theory distinguishes between orienting-related PES and strategic PES. Specifically, orienting-related PES occurs when the cognitive system in charge of adjusting to errors does not have enough time to complete the adaptation process (short RSI); conversely, strategic PES occurs when the system has enough time to complete the process and is associated with increased PEA (long RSI). PES’s sensitivity to task timing makes it difficult to compare across studies, as many error-monitoring studies use trial-to-trial feedback, which may increase RSI times.

1.1. The Current Study

Owing to the literature summarized above, the overarching goal of the current study was to examine different calculations of PES and compare convergent correlations with task behavior and error-related ERPs (ERN, Pe). We examined traditional and robust estimates of PES, as well as a less commonly used method of calculating PES, which is to subtract the averaged post-error RT by the RT of the error trial (Cavanagh et al., 2009; Smith & Allen, 2019); we called this PES_{Error Trial}. We also evaluated the utility of a single-trial regression approach (Fischer et al., 2018) that estimates PES while simultaneously controlling for other known contributors to RT including previous trial congruency (e.g., Van Der Brought, Braem, & Notebart, 2014). Finally, we examined the internal reliability of each PES calculation, which we believe is the first analysis of its kind for PES. Data were derived from a modified flanker task we developed for a larger project; as such, approximately half of the participants received trial-to-trial feedback and the other half did not. This afforded us the opportunity to also evaluate the above-mentioned effect of increased RSI on PES, PEA, and ERPs.

2. Method

2.1. Participants

A total of 77 psychologically healthy, right-handed adults were recruited from the larger Boston community and participated in the current study. All participants provided written informed consent prior to study procedures, and the Partners Healthcare Institutional Review Board approved the study. Participants were free of any psychiatric history, as determined by a semi-structured clinical interview (SCID-5; First, Williams, Karg, & Spitzer, 2015) administered by a clinical psychologist or clinical psychology doctoral students with extensive SCID-5 training. Participants were compensated at a rate of $20/hour for their time. Participants were recruited as part of a larger cross-species examination of electrophysiology and behavior. As such, participants in this phase were recruited for purposes of task development. We originally proposed to collect 20 participants but continued to collect data until the onset of the next phase of the study, and a total of 77 participants were enrolled.

Prior to statistical analysis, data from 11 participants were excluded due to poor task performance (see below). Data from a further four participants were excluded for excessive EEG and electromyography (EMG) artifacts, and from one participant who was uncooperative and had questionable task engagement. Thus, the final sample for data analysis consisted of 61 participants (37 female, 24 male, M age = 23 years [SD = 5, range 18–42]), who identified as follows: White (N = 36), Asian (N = 20), Black or African American (N = 3), and More than one race (N = 2). Six participants identified as Hispanic or Latino.

2.2. Flanker Task

Participants completed a modified version of the Eriksen flanker task (Eriksen & Eriksen, 1974). Participants were instructed to indicate the color of the center image (target) of a three-image display using one of two buttons on a response pad. Image-button assignments were counterbalanced across participants. Violet flowers and green leaves constituted the images used in the task¹, and flanker images could either match the center image (congruent trials) or could not match it (incongruent trials).

During each trial, the two flanking stimuli were presented 100 ms prior to target onset, and all three images remained on the screen for a subsequent 50 ms (i.e., total trial time: 150 ms). A blank screen followed for up to 1850 ms or until a response was recorded. Another blank screen was presented for a random duration between 750 to 1250 ms, which constituted the intertrial interval. The experimental session included 350 trials grouped into five blocks of 70 trials during which accuracy and speed were equally emphasized. To encourage quick responding, a feedback screen with the message “TOO SLOW!!!” was displayed if responses fell outside of the 1850 ms time window or if RTs were longer than 600 ms in the first block, or outside of the 95^th (or 85^th) percentile of RTs (see footnote 1) in the previous block for blocks 2 through 5. Prior to the experiment, participants completed a short practice block identical to the experiment to become familiar with the task.

Because these data were collected during the task development stage of a larger project, approximately half of the participants received trial-to-trial feedback (N = 31) whereas the remaining 30 participants did not². For the feedback version of the task, an additional 1000–1250 ms (jittered) interstimulus interval (blank screen) followed the response window period before the presentation of the feedback stimulus (1000 ms), which consisted of a dollar sign enclosed in a circle for correct responses and an empty circle for erroneous responses. Thus, for the participants who received feedback, an additional 2000–2250 ms was added at the end of each trial, lengthening the intertrial interval (ITI) and therefore the response stimulus interval. Presence or absence of feedback was used as a factor in the analyses presented below to assess for previously mentioned effects of RSI (Jentzch & Duschig, 2009).

All stimuli were presented on a 22.5-inch (diagonal) VIEWPixx monitor (VPixx Technologies, Saint-Bruno, Canada) using PsychoPy software (Pierce, 2007) to control the presentation and timing of all stimuli, the determination of response accuracy, and the measurement of reaction times. Images were displayed on a black background and subtended 4.16° of visual angle vertically and 17.53° horizontally.

2.3. Behavioral data analysis

The primary analysis concerned the PES calculations. Note that all calculations involved trials that occurred only after incongruent errors to avoid conflating conflict and post-error effects³. Trials following congruent errors were excluded due to low trial counts (few errors occur on congruent trials). The following calculations were used:

$${\text{PES}}_{\text{Traditional}}=M_{\text{Post-Error RT (eC)}}–M_{\text{Post-Correct RT (cC)}}$$

$${\text{PES}}_{\text{Robust}}=M_{\text{Post-Error RT (cceCc)}}–M_{\text{Pre-Error, Post-Correct\hspace{0.17em}RT (cCecc)}}$$

$${\text{PES}}_{\text{Error Trial}}=M_{\text{Post-Error RT (cceCc)}}–M_{\text{Error Trial RT (ccEcc)}}$$

In the above equations, M is numeric mean, c is correct, e is error, and capitalized letters refer to the trial of interest. Five-trial sequences (ccecc) were used for the robust and error-trial estimates to ensure that post-error trials were also pre-correct trials, to avoid the effects of double errors on RTs (Hajcak & Simons, 2008). Pairs of RTs surrounding the same error (pre- and post-error trials) were used to calculate PES_Robust. There was an average of 24.59 (SD = 11.52, range: 5–50) trials for the PES_Traditional estimate, and an average of 14.21 (SD = 5.36, range: 4–26) for the PES_Robust and PES_{Error Trial} estimates as these two were derived from the same trial sequences.

As noted above, 11 participants were removed from analysis due to poor task performance, which was defined as more than 35 trials with outlier reaction times (RTs below 150 ms or ± 3 intra-individual standard deviations from the congruent or incongruent mean), having fewer than 200 congruent and 90 incongruent non-outlier trials, achieving an accuracy below 50% for both congruent and incongruent trials, and having fewer than six non-outlier trials that followed incongruent errors. All behavioral data were processed using Python 3.7 software.

2.4. Internal Reliability of PES

We next examined internal consistency of the different PES calculations using split-half reliability, which is essentially the correlation between odd- and even-numbered trials (see Hajcak, Meyer, & Kotov, 2017). Split-half reliability is particularly useful when trial numbers differ widely across participants, as in cognitive tasks when participants commit different numbers of errors. Here, we used the Spearman-Brown (SB) formula to correct the reliability, as only half of the number of items are being considered for the estimate: (SB = 2r/(1+r)) For all PES estimates, we first computed split-half reliability for post-error and post-correct RTs separately, then the correlation between post-error and post-correct trials, and then the reliability of the difference (the PES estimate). For the PES_Robust and PES_{Error Trial} methods, calculating split-half reliability was straightforward because the number of post-error and post-correct (pre-error and error) trials was completely balanced as these trials came from the same sequences (ccecc). However, for the PES_Traditional estimates, the number of post-error and post-correct trials differed widely, so several different trial-selection techniques were employed to calculate a list of PES values (subtracting post-error RT by post-correct RT), and then odd and even-numbered trials were selected from this list of values. For these different trial-selection techniques, the list of post-error RTs remained the same, but the selection of post-correct RTs differed. The first approach randomly selected post-correct RTs. A second approach selected post-correct RTs that followed error-trial RT-matched correct trials. A computer algorithm began with the first error trial and found the correct trial that was closest in RT, repeating the process for each subsequent error trial with the remaining correct trials (see Hajcak et al., 2005). Then, the post-correct trials were chosen from this list of matched correct trials. As described in previous work, this procedure estimates PES by controlling for slowing caused by regression to the mean after a particularly fast trial (i.e., error trials, Hajcak, McDonald, & Simons, 2003). Finally, we used an even more stringent matching procedure that only accepted post-error and post-correct RTs that were derived from very closely matched error and correct RTs (within 5ms). This final method excluded error and post-error trials if there was not a corresponding correct trial that fell within 5ms of its RT. By design, there were fewer trials included in these averages (M trials = 11.56, SD = 5.24, range: 2–25). For each of these traditional estimates, we first verified whether PES was still observed before estimating the internal reliability.

Several authors warn against simple rules of thumb for interpreting “acceptable” versus “unacceptable” values of internal reliability (Norcini, 1999; Schmitt, 1996), as these values differ widely across different domains of measurement (e.g., self-report measures versus cognitive measures). Nonetheless, in order to provide descriptions for our reliability estimates, we follow the recommendations laid out by Nunnally (1994) in terms of basic and applied sciences: coefficients of .70 are considered acceptable and coefficients of above .90 or .95 are desirable for clinical purposes (see also Rodebaugh et al., 2016).

2.5. Post-Error Accuracy

Like the PES analysis, post-error and post-correct trials were limited to trials that followed incongruent errors and incongruent corrects, respectively. Post-error accuracy (PEA) was computed by summing the number of post-error correct trials and dividing this value by the sum of post-error correct trials and post-error error trials. Post-correct accuracy (PCA) was calculated similarly (number of post-correct correct trials / post-correct correct + post-correct error). Then, the post-error accuracy difference (ΔPEA) was calculated as PEA minus PCA.

2.6. Psychophysiological recording and data reduction

Participants were seated approximately 70 cm in front of a computer monitor inside an acoustically and electrically shielded booth. Continuous electroencephalographic (EEG) activity was recorded from a customized 96-channel actiCAP system using an actiCHamp amplifier (Brain Products GmbH, Gilching, Germany). Impedances were kept below 25 kΩ. The ground (GND) channel was embedded in the cap and was located anterior and to the right of channel 10, which roughly corresponds to electrode Fz. During data acquisition, channel 1 (Cz) served as the online reference channel. All signals were digitized at 500 Hz using BrainVision Recorder software (Brain Products).

Offline analyses were performed using BrainVision Analyzer 2.0 (Brain Products). Gross muscle artifacts and EEG data during the breaks in between blocks were first manually removed by visual inspection. The data were band-pass filtered with cutoffs of 0.1 and 30 Hz, 24dB/oct rolloff. Blinks, horizontal eye movements, and electrocardiogram were removed using independent component analysis (ICA), and corrupted channels were interpolated using spline interpolation. Scalp electrode recordings were re-referenced to the average activity of all electrodes. Response-locked data were segmented into individual epochs beginning 1500 ms prior to response onset and continuing 1500 ms after the response. Epochs were rejected as artifactual if any of the following criteria were met: 1) a voltage step exceeding 50 µV in 200 ms time intervals, 2) a voltage difference of more than 150 µV within a trial, or 3) a maximum voltage difference of less than 0.5 µV within a trial. Similar to the behavioral analysis trial rejection, ERP trials were rejected if responses fell outside of an intra-individually-determined 95% confidence interval of incongruent response times. However, trial number differences between ERP and behavioral trials remained because ERP trials were not required to have happened in specific sequences (e.g., “ec” or “ccecc”) like those imposed in the behavioral data. The average activity between the −800 and −700 ms time window preceding the response was used for the baseline correction.

The ERN and its correct-trial counterpart, the correct response negativity (CRN), were defined as the average activity in the 0–100 ms post-response window at channel 9 (roughly FCz), where these components were maximal. The Pe and its correct-trial counterpart were defined as the average activity in the 200–400 ms window following a response at channel 40 (roughly Pz), where these components reached their maximal amplitude. An average of 28 (SD = 14, range: 7–59) artifact-free ERP trials were retained in the error-trial analysis and an average of 87 (SD = 16, range: 47–112) trials were retained for the correct-trial analysis, consistent with recommendations (Olvet & Hajcak, 2009b). To evaluate internal consistency of the ERPs, we calculated split-half reliability by correlating odd-numbered trials with even-numbered trials and then adjusting with the Spearman-Brown formula (Hajcak, Meyer, & Kotov, 2017). The resulting coefficients for the ERN, CRN at channel 9 were .80 and .92, respectively, and for the Pe and correct-trial Pe at channel 40 were .79 and .90, respectively – these coefficient magnitudes mirror those from prior work (Hajcak et al., 2017).

2.7. Overview of Analyses

First, we computed and compared estimates of PES with paired sample t-tests. Second, we computed reliability estimates of the different PES calculations. Third, we examined how PES relates to other behavioral indices of cognitive control (flanker congruency effects, post-error accuracy) with bivariate Pearson correlations. Fourth, we examined bivariate correlations between PES estimates and error-related ERPs (ERN, Pe). Difference amplitudes were computed by subtracting correct-trial ERPs (CRN, Pe-correct) from error-trial ERPs (ERN/Pe) and were used in these analyses. Repeated-measures analyses of variance (ANOVAs) used Type III Sum of Squares for interactions with the Greenhouse-Geisser correction applied to p values associated with multiple df repeated measures comparisons.

3. Results

3.1. Flanker task behavioral results

As expected, the typical flanker interference effects emerged in our modified task version. Specifically, reaction times were significantly longer on incongruent trials (M = 399, SD = 31) than congruent trials (M = 334, SD = 30, t(60) = 28.14, p < .0001, Cohen’s d = 3.60). Additionally, accuracy rates (%) were significantly lower on incongruent trials (M = 75, SD = 12) than congruent trials (M = 95, SD = 4, t(60) = 14.57, p < .001, Cohen’s d = 1.87). Highlighting the strength of this effect, all participants (61/61) showed longer RTs and lower accuracy rates on incongruent versus congruent trials (binomial tests, p(61/61) < .0001).

To evaluate the impact that trial-to-trial feedback had on congruency effects, a 2 × 2 repeated-measures analysis of variance (ANOVA) with the within-subjects factor congruency (congruent vs. incongruent) and between-subjects factor feedback (absent vs. present) was separately conducted on the RT and accuracy data. For RT, neither the main effect of feedback (F(1, 59) = 0.77, p = .38, η²_p = .013) nor the interaction between congruency and feedback (F(1, 59) = 1.02, p = .32, η²_p = .017) reached statistical significance. Likewise, for accuracy rates, neither the main effect of feedback (F(1, 59) = 2.07, p = .16, η²_p = .034) nor the interaction between congruency and feedback (F(1, 59) = 0.68, p = .42, η²_p = .011) were significant. Thus, feedback had no impact on flanker interference effects on reaction times or accuracy rates.

3.2. Post-Error Slowing

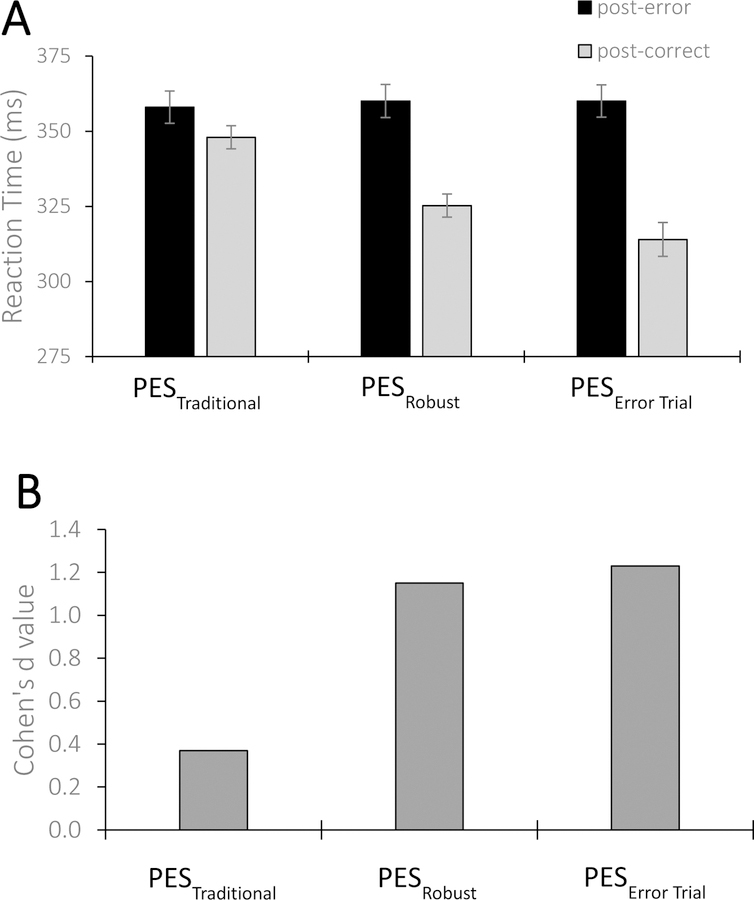
A comparison of post-error and post-correct RTs for each PES estimate, along with the effect size of each estimate, is displayed in Figure 2 and in Table 1. PES was observed when using the traditional method: averaged post-error RT (M = 358, SD = 42) was longer than post-correct RT (M = 348, SD = 30; t(60) = 2.92, p = .005, Cohen’s d = 0.37). That is, PES_Traditional provided a small-to-medium effect size (Cohen, 1988). Notably, the robust calculation also revealed significant PES, with an effect size more than three times larger than the estimate from the traditional method: post-error trials in the cceCc sequence had significantly longer RTs (M = 360, SD = 43) than post-correct, pre-error trials (cCecc; M = 325, SD = 30, t(60) = 8.94, p < .0001, Cohen’s d = 1.15). The robust estimate thus produced a large-to-very large effect size (Cohen, 1988). The PES_Robust estimate (M = 35, SD = 30) was significantly larger than the PES_Traditional estimate (M = 10, SD = 3, t(60) = 8.02, p < .0001, Cohen’s d = 1.03). Finally, the PES_{Error Trial} estimate was also significant, as error trials in the ccEcc sequence (M = 314, SD = 44) were faster than the post-error trials (which was the same post-error value used in the robust calculation, M = 360, SD = 43, t(60) = 9.58, p < .001, Cohen’s d = 1.23). The PES_{Error Trial} provided a very large effect size (Cohen, 1988) and was larger than both the traditional (t(60) = 7.96, p < .001, Cohen’s d = 1.00) and robust (t(60) = 3.01, p = .004, Cohen’s d = 0.38) estimates.

Figure 2.

PES calculations and associated effect sizes.

Table 1.

Split-half reliability coefficients for the different PES estimates

PES Calculation	M (SD)	Cohen’s d	Post-error SB	Post-correct SB	Pearson r between post-error and post-correct	SB of PES
PESTraditional	9.88 (26.44)	0.37	--	--	--	--
Random post-correct trials	10.05 (26.36)	0.40	.84	.83	.78**	.37
RT-matched post-correct trials	17.19 (29.30)	0.59	(.84)	.72	.72**	.28
Restrictive RT-Matched	25.51 (46.34)	0.55	.81	.67	.42	.58
PESRobust	35.11 (30.68)	1.15	.78	.65	.71**	.29
PESError Trial	45.80 (37.32)	1.23	.87	.65	.64**	.63

Note: SB: Spearman-Brown split-half reliability coefficient. Parentheses indicate the same value as the row above because this value was extracted from the same list of post-error RTs.

^**p<.01

Next, we evaluated the different post-correct trial selection schemes for the traditional estimate. When post-correct trials were randomly selected, a significant post-error slowing effect was observed (t(60) = 3.10 p = .003, Cohen’s d = 0.40). In terms of RT matching, the original matching algorithm was partially successful in matching error trials with correspondingly fast correct RTs. The difference in RTs was still significant (t(60) = 9.06, p < .001, Cohen’s d = 1.16), but the effect size was much smaller than the original difference between error and correct RTs (t(60) = 19.85, p < .001, Cohen’s d = 2.54).When post-correct trials were selected on the basis of this RT matching, there was also a significant PES effect (t(60) = 4.59, p < .001, Cohen’s d = 0.58). The more restrictive matching procedure was successful in matching correct and error RTs (t(60) = 1.80, p = .077, Cohen’s d = 0.23). When this most conservative RT-matching approach was used, post-error (M = 365, SD = 48) and post-correct RTs (M = 340, SD = 35) still differed significantly (t(60) = 4.30, p < .001, Cohen’s d = 0.55), indicating a PES effect. These findings replicate previous work in that even after RT-matching, post-error slowing is still observed (Hajcak et al., 2003), suggesting PES does not solely reflect regression to the mean.

Finally, we considered a single-trial regression approach to estimating PES (Fischer et al., 2018). This analysis was conducted using the lmer function in R and considered the full dataset of all non-first and non-outlier trials from all 61 participants (total trials = 20,532). In the model, RT was the dependent variable, and the following factors and all interactions were included: previous accuracy, previous congruency, current accuracy, and current congruency, as well as a random intercept for subject. This model allows the simultaneous prediction of post-error slowing (indicated by main effects and interactions involving the term previous accuracy, which we focus on here) while controlling for other well-known factors that influence RT (including the previous trial’s congruency and post-conflict reduction of interference (see Van der Borght, Braem, & Noteabert, 2014). The model produced a significant main effect of previous accuracy (F(1, 20246.4) = 17.21, p < .0001), a significant interaction term between current and previous accuracy (F(1, 19821.4) = 7.63, p = .006), a significant interaction between previous accuracy and previous congruency (F(1, 20443.5) = 9.24, p = .002) and a significant four-way interaction between current congruency, current accuracy, previous congruency and previous accuracy (F(1, 20454) = 3.93, p = .047). Because the interactions involving previous congruency are less relevant here, we followed up on the Current x Previous Accuracy interaction (averaging over previous and current congruency) with the lsmeans function in R, using Tukey’s post-hoc tests⁴. Notably, the post-hoc tests comparing post-error correct and post-correct correct trials were all significant (all ts > 7.90, ps < .0001). The only post-hoc test that was not significant was the one comparing post-error error and post-correct error trials (t(19879) = 0.77, p = .87); post-error slowing was not observed when the next trials were errors, replicating previous results (Hajcak & Simons, 2008). These results indicate that post-error slowing was observed at a single-trial level, while also controlling for potentially confounding factors.

We next examined how many participants showed post-error slowing, indicated by positive values for the post-error minus post-correct comparison, for each metric separately. A total of 42/61 participants had positive PES values when calculated using the traditional method (binomial test, p(42/61) = .0013), whereas 55/61 participants had positive PES values with the robust estimate (binomial test, p(55/61) < .0001) and 58/61 had positive PES values with the error-trial estimate (binomial test, p(58/61) < .0001). A McNemar Test (McNemar, 1947) was used to evaluate differences in the proportion of individuals categorized as having PES (positive PES values) versus not having PES (negative PES values or PES value of 0 ms) between the estimates of PES. A significant effect emerged for the comparison between traditional and robust estimates (McNemar’s Χ² = 11.08, df = 1, p = .0009). Of note, 13 participants categorized as having post-error speeding (faster RTs on post-error trials than on post-correct trials, indicated by negative PES values) using the traditional method were categorized as having had post-error slowing (positive PES values) when using the robust method. Compared to the traditional method, the error-trial estimate also categorized more participants as having had positive PES values (McNemar’s Χ² = 12.5, df = 1, p = .0002). However, the robust and error-trial estimates did not differ in terms of proportion categorized as having or not having positive PES values (McNemar’s Χ² = 0.80 df = 1, p = .37).

To investigate the impact that feedback had on post-error slowing, a repeated-measures ANOVA with the within-subjects factor trial type (post-error vs. post-correct) and between-subjects factor feedback (absent vs. present) was run on RT data for each PES estimate separately. None of these ANOVAs revealed significant interactions between trial type and feedback: Traditional: F(1, 59) = 0.30, p = .59, η²_p = .0.005; Robust: F(1, 59) = 0.002, p = .97, η²_p < .001; Error-Trial PES: F(1, 59) = 0.44, p = .51, η²_p = .007. Thus, feedback and lengthened ITI had no impact on PES.

3.3. Reliability of PES

Table 1 displays split-half reliability coefficients of the different PES estimates. As can be seen, the post-error and post-correct reliabilities were quite high (all split-half coefficients > .64); this is consistent with previous research on the reliability of reaction times. Moreover, post-error and post-correct RTs were highly correlated (rs > .64). However, the PES reliability estimates were all unacceptably low (range: .29 to .63). The highest coefficients were derived from the PES_{Error Trial} estimate. The robust estimate of PES showed one of the lowest reliability estimates. This is likely due to at least two reasons. First, by the nature of the trial extraction procedure (identified as ccecc sequences), fewer trials were available for the split-half reliability estimates. Reliability is scaled with the number of items. Second, because the post-error and post-correct trials were derived from the same trial sequence, their correlations were quite high. Large correlations between the constituent items in a difference score tend to reduce the reliability of the difference measure (Infantolino et al., 2018).

3.4. Post-Error Accuracy

Data from one participant were excluded from the post-error accuracy (PEA) analysis due to outlier status (Z-score < −3.00). A paired-samples t-test revealed that overall, participants were less accurate after errors (M = 90.67%, SD = 6.81) than after corrects (M = 92.80%, SD = 4.55, t(59) = 3.13, p = .003, Cohen’s d = 0.41). Most participants showed the inverse post-error accuracy improvement effect, as just 25 participants showed increased post-error accuracy vs. post-correct accuracy (binomial test, p(25/60) = .045). A Trial Type x Feedback ANOVA was conducted to evaluate the impact of feedback on post-error accuracy. This analysis revealed a trend-level interaction (F(1, 58) = 3.42, p = .07, η²_p = .06). To evaluate Wessel’s (2018) model, follow-up t-tests were performed in spite of the trending interaction. These tests revealed that post-error accuracy was significantly poorer than post-correct accuracy in the no-feedback condition (t(28) = 3.40, p = .002), but was not significantly different from post-correct accuracy in the feedback condition (t(30) = 1.06, p = .30).

3.5. Event-related brain potentials (ERPs)

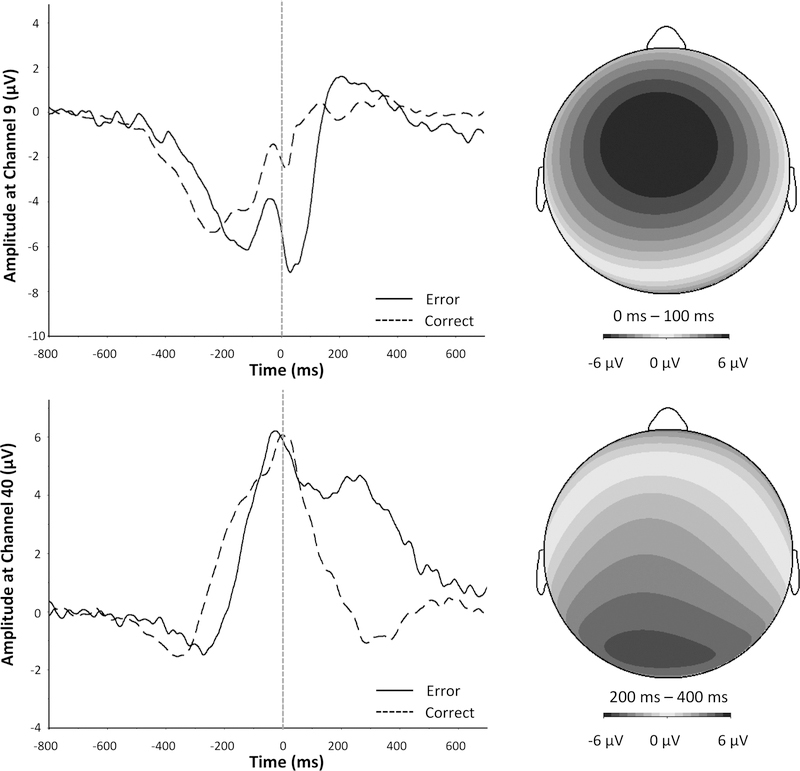
Figure 3 displays response-locked ERPs. As can be seen, a sharp negative deflection was prominent on error trials in the 0–100 ms post-response time window. A Trial Type x Feedback ANOVA was conducted on the ERN and Pe separately. For the ERN, a significant main effect of Trial Type (F(1, 59) = 132.36, p < .001, η²_p = .69) confirmed that error trials elicited a larger negativity than correct trials. Neither the main effect feedback (F(1, 59) = 0.05, p = .82, η²_p = .001) nor the interaction between trial type and feedback (F(1, 59) = 2.34, p = .13, η²_p = .04) reached statistical significance.

Figure 3.

Response-locked event-related potentials.

For the Pe, there was a significant main effect of trial type (F(1, 59) = 88.81, p < .001, η²_p = .60), indicating the positivity in the 200–400 ms post-response window at channel 40 (Pz) was larger for errors than for corrects. Like the ERN, the impact of feedback on the Pe was negligible: neither the main effect of feedback (F(1, 59) = 1.72, p = .20, η²_p = .03) nor the interaction between trial type and feedback (F(1, 59) = 0.44, p = .51, η²_p = .007) was significant.

3.6. Correlations between behavior and ERPs

Table 2 shows bivariate correlations between PES estimates, post-error accuracy difference (ΔPEA), flanker interference effects, and the ERP variables (ERN and Pe). As can be seen, the traditional and robust estimates were correlated with one another (r = .64, p < .001), replicating past research (van den Brink et al., 2014). None of the PES estimates was significantly correlated with ΔPEA. Both the traditional and robust estimates of PES were negatively correlated with the flanker interference effect on accuracy. Because more negative values on this flanker interference effect typically indicate better cognitive control – as participants are disrupted less by the incongruent nature of the stimuli – this finding suggests that participants who slowed down more after errors exhibited better cognitive control on incongruent stimuli. However, when incongruent accuracy rates were controlled for in a partial correlation, these correlations were reduced to non-significance (PES_Traditional partial r = .21, p = .10, PES_Robust partial r = .00007, p = 1.00). As can be seen in Table 2, PES_{Error Trial} was not correlated with any of the behavioral indices.

Table 2.

Descriptive statistics and Pearson correlations between PES estimates, behavior, and ERPs

	PESTraditional (ms)	PESRobust (ms)	PESError Trial (ms)	ΔPEA (%)	Flanker RT (ms)	Flanker Accuracy (%)	ΔERN (µV)	ΔPe (µV)
Mean	9.88	35.11	45.80	−2.46	64.65	19.68	−5.13	4.61
Standard Deviation	26.44	30.68	37.32	5.81	17.95	10.55	3.53	3.80
PESTraditional	--
PESRobust	.64**	--
PESError Trial	.43**	.69**	--
ΔPEA	.10	−.21	−.17	--
Flanker RT	−.03	.02	.11	.15	--
Flanker Accuracy	−.34**	−.28*	.09	−.06	.18	--
ΔERN	.05	.14	.16	.01	.03	−.04	--
ΔPe	.26*	.26*	.04	.05	−.06	−.20	−.20	--

Note. N = 61 except for correlations with ΔPEA, where N = 60. PES: Post-error slowing; ΔPEA: Post-error accuracy minus post-correct accuracy; Flanker RT: RT on incongruent correct trials minus RT on congruent correct trials; Flanker Accuracy: accuracy on congruent trials minus accuracy on incongruent trials; ΔERN: error-related negativity minus correct response negativity; ΔPe: Pe on error minus Pe on correct trials.

^*p < .05

^**p <.01.

None of the PES estimates was correlated with the ERN difference amplitude. However, both traditional (r = .26) and robust (r = .26) estimates of PES were positively correlated with the Pe difference amplitude. These correlation magnitudes did not differ significantly, according to the formula for comparing dependent correlations of Meng, Rosenthal, & Rubin (1992): Z = 0.008, p = 1.00, two-tailed. This suggests that both traditional and robust estimates correlated with electrophysiological index of attention allocation to errors equally. The PES_{Error Trial} estimate did not correlate with the Pe difference amplitude (r = .04).

A final analysis considered relations between PES estimates and number of trials included in the averages. There was a significant negative correlation between number of trials for the traditional estimate and PES_Traditional (r = −.35, p = .001), suggesting smaller PES effects with increasing number of trials available, in line with past studies (Notebaert et al., 2009). However, there was no significant relationship between PES_Robust and the number of five-trial sequences used to calculate this average (r = −.20, p = .12). The PES_{Error Trial} estimate was also not significantly related to the number of five-trial sequences (r = .13, p = .33).

4. Discussion

Post-error slowing has been increasingly used in basic cognitive neuroscience and clinical psychology, yet its precise calculation has not been standardized or optimized. The current study compared different estimates of PES in a modified flanker task, arguably the most common task used to elicit error-related adjustments. Results indicate the robust calculation of PES described by Dutilh et al (2012) provided an estimate of PES that was three times larger than the estimate derived from the traditional method. Moreover, the robust PES correlated with an electrophysiological index of attention allocation (Pe) just as well as the traditional method. The last estimate of PES examined (PES_{Error Trial}) – which compared RTs on error trials with RTs on post-error trials – provided a large estimate of PES but did not correlate with external indicators of error monitoring or cognitive control. However, PES demonstrated very low reliability estimates, regardless of how it was calculated. We consider these results in the context of the error-monitoring literature and discuss implications for consistent measurement.

4.1. Comparing PES metrics

The primary objective of this study was to compare different methods of calculating PES. The few studies that have computed both traditional and robust estimates of PES reported that the robust estimate tends to be larger (Murphy, Moort, & Nieuwenhuis, 2016; van den Brink et al., 2014; Williams, 2016). This pattern was replicated in the current study: PES_Robust provided an effect size three times larger than the PES_Traditional estimate (Cohen’s d: 0.34 vs. 1.15; Figure 2). The two estimates were correlated with one another, further replicating previous research (Tabachnick et al., 2018; van den Brink et al., 2014). As noted in the Introduction, unlike PES_Traditional, the PES_Robust estimate is not sensitive to global fluctuations in task engagement and fatigue, because the trials used in its computation involve the same trial sequence surrounding errors. Thus, participants may be slowing down more after errors than previously thought. Furthermore, significantly more participants showed positive PES values (indicating true post-error slowing) when using the robust method compared to the traditional method (55/61 = 90.16% vs. 40/61 = 65.57%). This analysis, which to the best of our knowledge has not been reported before, indicates that the traditional estimate may underestimate how many participants slow down after their errors. This may have important consequences for studies of clinical populations in which reduced PES_Traditional is a primary outcome (e.g., Yordanova et al., 2011).

Only a few studies have used the error-trial method, in which error-trial RTs are subtracted from post-error RTs (e.g., Smith & Allen, 2019). In our study, this method provided a larger PES estimate than both traditional and robust methods. This is because error trials are almost always faster than surrounding trials in simple two-choice tasks (Brewer & Smith, 1989), and thus when these values are subtracted from post-error RTs, the resulting estimate will be larger. We believe this calculation may overestimate the true magnitude of post-error slowing and has two significant drawbacks. First, from a conceptual standpoint, it does not compare correct RTs with correct RTs, as the other estimates do. This is potentially problematic because it compares the output of a cognitive process that led to a correct decision with a cognitive process that caused an error. Thus, the “slowing” reflected in this estimate is not a true estimate of slowing down the same cognitive process that leads to a correct decision. Second, from a measurement standpoint, the error-trial estimate of PES may be suboptimal because the distributions of error- and correct-trial RTs are known to differ (Rabbitt & Vyas, 1970). Thus, we would recommend researchers not use this method to quantify PES. The robust estimate seems to provide a balanced approximation of post-error slowing both conceptually and methodologically.

One potential issue with the robust estimate of PES is that pre-error trials are associated with unique neural activity compared to pre-correct trials – a phenomenon some have suggested is a waning of attention and performance monitoring activity prior to errors (Allain, Carbonnell, Falkenstein, Burle, & Vidal, 2004; Hajcak, Nieuwenhuis, Ridderinkhof, & Simons, 2005; Ridderinkhof, Nieuwenhuis, & Bashore, 2003; Schroder, Glazer, Bennett, Moran, & Moser, 2017). In this way, the robust estimate compares trials that are associated with differential neural activity. As noted in the Introduction, pre-error trials are also associated with faster RTs than most post-correct trials (Brewer & Smith, 1989); this estimate thus captures the end of a series of increasingly fast response times. It is possible that pre-error speeding and post-error slowing result from different mechanisms. However, we feel this is precisely what a measure of PES should capture – the waning of attention before, and the subsequent reactivity following, an error. Thus, the robust estimate much more definitely captures the essence of a uniquely error-related phenomenon. Appropriately choosing a baseline, however, as we have demonstrated, has an impact on the overall magnitude of the PES estimate, and we encourage further study into choosing the most appropriate baseline comparator (i.e., the post-correct RT).

Finally, future studies will need to further parse competing influences of previous-trial accuracy and congruency effects on response times. Although the single-trial regression approach (e.g., Fischer et al., 2018) implemented here revealed a significant PES effect above and beyond the effects of previous-trial congruency, there were too few trials in the Robust trial sequence (ccecc) to reliably compare various congruency sequences. Future studies using tasks with many more trials will be necessary to more critically evaluate how the robust estimate is sensitive or insensitive to congruency sequence effects.

4.2. Internal Consistency of PES

A novel analysis we examined in this study was the internal reliability of PES. Although previous studies had examined test-retest reliability of PES (Danielmeier & Ullsperger, 2011; Segalowitz et al., 2010), no previous study – to our knowledge – has examined the internal reliability of PES. We find that, despite PES being observed in every comparison between post-error and post-correct RTs, by most standards, the split-half reliability estimates of PES ranged from poor to unacceptable. Analysis of only participants who had sufficiently high numbers of trials did not impact the reliability estimates. These findings are in line with recent studies calling attention to poor psychometric properties of commonly used cognitive neuroscience measures, particularly those based on difference scores (Hajcak et al., 2017; Hedge, Powell, & Sumner, 2018; Infantolino et al., 2018; Meyer, Lerner, Reyes, Laird, & Hajcak, 2017).

There is little doubt that PES is replicable from a within-subjects perspective. Indeed, across all of the calculations we used, a significant PES effect was observed. However, the poor reliability precisely follows as Hedge et al (2017) claimed: “experimental designs aim to minimize between-subject variance, and thus successful tasks in that context should be expected to have low reliability” (pg. 1181). Low reliability of PES may explain the inconsistent correlations reported in the literature between PES and individual differences of psychopathology and of error-related brain activity. This would have serious implications for the use of PES in clinical applications. Indeed, recent calls have urged researchers to routinely report internal consistency of neural measures (Hajcak et al., 2017). We feel that extending this recommendation to behavioral adjustment measures is also warranted, particularly when between-subjects effects are under examination. We did find that reliability estimates were higher for the post-error RTs, and perhaps individual differences research could use this as a metric of post-error adjustment. However, this is not technically slowing, per se, and should be distinguished from PES (and theoretical accounts of slowing adjustments). Our results also invite critical discussion between two divergent lines of research – the basic, experimental work (within-subjects) and the applied sciences aimed at better understanding psychopathology (between-subjects).

One potential reason reliability estimates of PES were so low is that PES may reflect multiple competing mechanisms (Dutilh et al., 2012; Fischer et al., 2018; Purcell & Kiani, 2016). As noted in the Introduction, even researchers using the drift diffusion model have come to varying conclusions regarding the underlying mechanisms giving rise to PES, depending on the particular sample studied as well as the task. Reliability may thus suffer because the internal consistency of a measure is constrained when the measure is multifaceted (Schmitt, 1996). Overall, the results presented here urge future studies to critically evaluate psychometric properties of both behavioral and neural measures, especially if they are to be used in individual-differences research.

4.3. Relations to other indices of behavior

None of the PES estimates correlated with post-error accuracy, which is in line with previous results suggesting these two indices of error monitoring are dissociable (Danielmeier & Ullsperger, 2011). In fact, it is likely that most studies do not find a positive association between PES and PEA (e.g., Tabachnick et al., 2018; see Forster & Cho, 2014, for an exception). Similarly to PES, PEA is also not consistently measured; some studies evaluate it as accuracy after errors, whereas others (including the current study) use the difference between post-error and post-correct accuracy. We believe that in instances where PES is correlated with PEA, a difference PEA score should be used, as PES is also a difference measure. Again, as accumulating evidence indicates that PES may arise for various mechanistic reasons, there are some situations in which a correlation between PES and PEA would not be predicted. It is necessary, then, to take into consideration the precise task parameters, fluctuations across the task, and participant sample when considering correlations between PES and PEA. The relationship between PES and flanker interference effects on accuracy was limited to the traditional and robust estimates of PES. However, both of their correlations were reduced to non-significance after controlling for overall accuracy rates on incongruent trials.

Finally, the number of trials that was used in the average of PES was significantly correlated with PES_Traditional, but not with PES_Robust or PES_{Error Trial}. The direction of this correlation indicates that, as more post-error error trials are included in the average, the effect of PES becomes smaller. In fact, the effect size of the correlation between PES_Traditional and the number of trials (r = −.35, R² = .12) was three times larger than that between PES_Robust and the number of trials (r = .20, R² = .04). Although replications are warranted, these findings indicate that PES_Traditional may be more sensitive to the number of trials included in the average. This is potentially important, as both functional and non-functional (orienting) accounts indicate that one major contributor to the magnitude of PES is the number of errors committed in the task. Again, however, both of these theories have been developed based on traditional estimates of PES. It is necessary to continue evaluating relations between number of post-error trials and PES estimates using both traditional and robust calculations.

4.4. Associations with error-related brain activity

None of the PES estimates correlated with the amplitude of the ΔERN. These results are largely in line with the between-subjects meta-analysis by Cavanagh and Shackman (2015), which found a small and non-significant meta-analytic correlation between ERN and PES. However, in our study, both robust and traditional estimates did correlate with amplitude of the Pe. The Pe is generally considered to be an index of conscious awareness of having made a mistake or attention allocation to the error (Nieuwenhuis, Ridderinkhof, Blom, Band, & Kok, 2001; Overbeek et al., 2005). Notably, there is research suggesting the Pe may also index an orienting response to uncommon events (Ullsperger et al., 2010), as it shares topographic, temporal, and functional similarities to the P3b (Leuthold & Sommer, 1999; Ridderinkhof et al., 2009). Past research found that the Pe correlated with post-error accuracy (Schroder, Moran, Infantolino, & Moser, 2013), but this was not found here; rather, Pe correlated with only PES. Again, the varying correlations reported in the literature may arise for multiple reasons, including low internal reliability of PES and the various parameters, populations, and task contexts that may give rise to PES.

4.5. The impact of trial-to-trial feedback

Finally, we considered the impact of trial-to-trial feedback on post-error adjustments and error-related ERPs. Approximately half of the participants received trial-to-trial feedback, and the presence of feedback significantly lengthened the intertrial interval and also the response-stimulus interval (RSI). Prior literature suggests RSI has a major impact on whether or not PES emerges (Danielmeier & Ullsperger, 2011; Jentzsch & Dudschig, 2009; Wessell, 2018). Specifically, PES tends to be largest when RSIs are very short (<500ms) and tapers off with increasingly large RSI. In the current study, none of the PES estimates was impacted by the effect of feedback and the subsequently increased (+2s) RSI. However, post-error accuracy was marginally improved with the presence of feedback. Specifically, in the no-feedback condition, participants were significantly less accurate after errors compared to after corrects – which is the opposite of the post-error improvement in accuracy described by Laming (1979) and Danielmeier and Ullsperger (2011) – but there was no significant difference between post-error and post-correct accuracy rates in the feedback condition. It is possible that the presence of feedback – and the subsequently lengthened ITI – may have negated the negative impact of errors on subsequent performance (in terms of accuracy).

Collectively, these post-error adjustment data are interesting to consider with respect to Wessel’s (2018) adaptive orienting theory of error processing. This theory specifically predicts that at long ITIs, PES only occurs due to controlled processing (strategic PES). This would suggest that post-error accuracy is enhanced in long ITI trial sequences. In the current study, participants performed equally well after errors compared to correct trials in the feedback condition but performed significantly worse with short ITIs (in the no-feedback condition). This conforms to Wessel’s prediction of ITIs impacting post-error performance. As Wessel (2018) noted, the extant literature is highly inconsistent with regard to finding increased vs. decreased accuracy rates after errors vs. after corrects. Future studies will need to evaluate just how often and under which conditions participants are more accurate after errors than after corrects.

The trial-to-trial feedback had no impact on amplitudes of the ERN and the Pe. This finding replicates a previous study that found identical ERNs between feedback and no-feedback versions of an arrow flanker task (Olvet & Hajcak, 2009a). That study’s feedback version of the task did not have longer ITIs in the feedback version, which is one difference from the current study, in which the feedback trials were substantially (+2s) longer. These data suggest that trial-to-trial feedback may not have a large impact on these ERPs.

4.6. Limitations

There are limitations to the current study that should be addressed in future research. First, the data were collected from healthy, well-adjusted adults and we cannot speak to how clinical or more heterogeneous samples would respond or provide differing estimates of PES. However, the goal of the current study was to evaluate PES in a healthy sample in order to provide some precedent for further evaluation in clinical samples. Second, the examination of the impact of ITI on error monitoring was a convenience analysis as the data were collected while the task was under development. Third, the variation of the flanker task used here was unusual in that it used images, and not arrows or letters, which is more common. However, the task elicited the most common flanker-interference effects as well as ERP and behavioral signatures of error monitoring. Moreover, previous studies have used faces as flanker stimuli and have also elicited similar electrophysiological and behavioral indices of performance monitoring (Moser, Huppert, Duval, & Simons, 2008; Navarro-Cebrian et al., 2013). Thus, our findings are likely generalizable to other flanker tasks. Nonetheless, examining the estimation, reliability, and brain-behavior correlations of different PES calculations in other paradigms (other versions of the flanker task, Stroop task, Simon, Go/No-Go) is certainly warranted.

Conclusions

The precise measurement of PES has significant implications for both cognitive neuroscience research and for applications to clinical populations. Functional and non-functional theories of PES have been developed almost exclusively based on studies using the PES_Traditional estimate, which, as we find here, may underestimate the true magnitude of PES. An important finding here is that, regardless of the precise calculation of PES, this metric produced unacceptably low reliability values, at least based on conventional guidelines (Nunnally, 1994). This adds to the emerging literature on the low reliability of cognitive neuroscience measures (Hedge, Powell, & Sumner, 2018; Infantolino et al., 2018; Rodebaugh et al., 2016) and calls for a careful examination of basic psychometric properties in any individual differences research. Reliably assessing the magnitude of PES is an important endeavor for future studies in the basic and applied sciences. The three calculations of PES in the current work yielded significantly different magnitudes of the slowing effect and differentially correlated with cognitive control-related electrophysiology. We suggest that future studies of error-monitoring continue to evaluate both robust and traditional estimates as well as report their reliabilities. Once we understand how best to measure PES, we can then make finer theories that explain its functional significance and understand its potential variability in clinical populations.