Development and calibration of a dynamic HIV transmission model for 6 US cities

Abstract

Background:

Heterogeneity in HIV microepidemics across US cities necessitates locally-oriented, combination implementation strategies to prioritize resources. We calibrated and validated a dynamic, compartmental HIV transmission model to establish a status quo treatment scenario, holding constant current levels of care for 6 US cities.

Methods:

Built off a comprehensive evidence synthesis, we adapted and extended a previously-published model to replicate the transmission, progression and clinical care for each microepidemics. We identified a common set of 17 calibration targets between 2012 to 2015 and used the Morris method to select the most influential parameters for calibration. We then applied the Nelder-Mead algorithm to iteratively calibrate the model to generate 2,000 best-fitting parameter sets. Finally, model projections were internally validated with a series of robustness checks, externally validated against published estimates of HIV incidence, while the face validity of 25-year projections were assessed by a Scientific Advisory Committee (SAC).

Results:

We documented our process for model development, calibration and validation to maximize its transparency and reproducibility. The projected outcomes demonstrated a good fit to calibration targets, with a mean goodness-of-fit ranging from 0.0174 (New York City (NYC)) to 0.0861 (Atlanta). Most of the incidence predictions were within the uncertainty range for 5/6 cities (ranging from 21% (Miami) to 100% (NYC)), demonstrating good external validity. The face validity of the long-term projections was confirmed by our SAC, showing that incidence would decrease or remain stable in Atlanta, Los Angeles, NYC and Seattle while increasing in Baltimore and Miami.

Discussion:

This exercise provides a basis for assessing the incremental value of further investments in HIV combination implementation strategies tailored to urban HIV microepidemics.

In the United States and most other countries featuring concentrated HIV epidemics, the majority of people living with HIV/AIDS (PLHIV) reside in large urban centers and geographic “hotspot” areas,^1–3 each with distinct underlying epidemiological and socio-structural features.⁴ There are also dramatic disparities among minorities, with black and Hispanic men who have sex with men (MSM) accounting for over half of reported new infections.⁵ Our previous study on six US cities, Atlanta, Baltimore, Los Angeles (LA), Miami, New York City (NYC) and Seattle, home to nearly a quarter of US PLHIV, found fundamental differences in demographic composition, epidemic characteristics and rates of new HIV diagnoses.⁴ Heterogeneity in microepidemics across cities necessitates locally-oriented combination implementation strategies to prioritize resources according to the greatest public health benefit. This approach, however, requires detailed, context-specific information on a range of factors characterizing each HIV microepidemic and the level of available health services.

Mathematical models are simplifications of reality, designed to capture the essence of a problem with a minimally acceptable level of complexity and synthesis of evidence from multiple sources, to extrapolate outcomes that are unavailable, unobservable or unethical to collect. They can provide a unified framework to quantify the public health and economic impact of multiple health interventions, accounting for the synergistic effects between different interventions. Furthermore, setting-specific models can be adapted to capture heterogeneity across settings and are increasingly used to provide objective, localized evidence to prioritize resources according to the greatest public health benefit.

Model complexities and uncertainty surrounding key model inputs can diminish the confidence of decision makers and raise concerns about the credibility of the model-generated results. Assessing the validity and representativeness of a model generally entails explicitly assessing the quality of input data used for its parameters,⁶ calibrating uncertain inputs to observed epidemiological endpoints (calibration targets),⁷ and validating the accuracy of model projections against empirical data on outcomes of interest.⁸ Comprehensive and transparent reporting of these development processes can not only add confidence to the process, but also establish a basis to determine data collection targets to reduce uncertainty in the decisions a model recommends.

Building on an evidence synthesis we have described separately,⁹ our objective was to calibrate and validate a dynamic, compartmental model of HIV transmission for 6 US cities. The 25-year projections of the model are designed to serve as a ‘status quo’ comparator in assessing the incremental value of a range of possible combination implementation strategies to address the unique HIV microepidemics of each city.

Methods

In this section, we first provide a brief description of the construction of the model, followed by a detailed documentation of our calibration and validation process. Model calibration is the process by which uncertain model input values or ranges can be estimated so that model projections match pre-specified calibration targets.^10,11 While there is currently no consensus on what constitutes best practice for calibrating a model,¹⁰ recently-published guidelines offer detailed guidance for model validation, which include the evaluation of a model’s accuracy by comparing its outputs to external empirical data.⁸

Model description

Model construction

We adapted and extended a previously-published HIV dynamic transmission model that was used to estimate the health benefits and costs of HIV prevention and treatment interventions in the United States^12–14, British Columbia, Canada^15–17, and Guangxi province, China¹⁸. We modified the compartmental model both to accommodate the distinctive features in HIV microepidemics across US cities⁴, and to allow for assessment of a range of HIV treatment and prevention interventions to be evaluated jointly in future applications. For each demonstration city, the adult population aged 15 to 64 was partitioned into compartments on the basis of: biological sex; race/ethnicity (black/African American [black], Hispanic/Latino [Hispanic], and non-Hispanic white/others [white]); and HIV risk behavior type (MSM, people who inject drugs [PWID], MSM-PWID, and heterosexual [HET]). To account for within-group heterogeneity, MSM, MSM-PWID and HET were further partitioned into subgroups based on HIV sexual risk behavior intensity (high- vs. low-risk for each of the 3 risk groups), as defined by the proportion of MSM reporting condom-less sex with casual partners¹⁹ (conforming to the CDC recommended indications for PrEP use²⁰) for MSM and MSM-PWID, and by the proportion of individuals who had 5 or more sexual partners in the past 12 months²¹ for HET. PWID and MSM-PWID were also classified based on engagement in opioid agonist treatment (OAT).

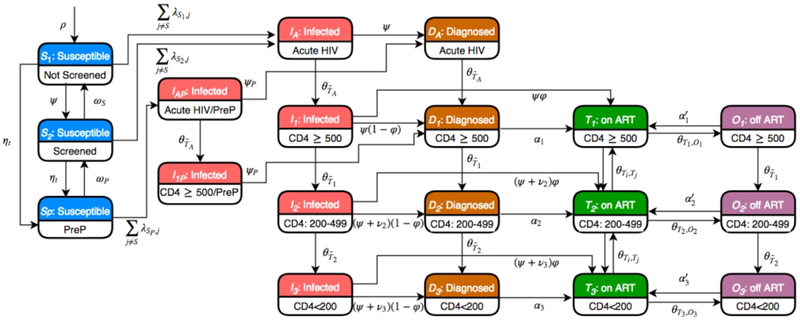
Individuals within each of these 42 groups (MSM: 6, MSM-PWID: 12; PWID: 12; HET: 12) progressed through health states outlined in Figure 1. Susceptible (HIV-uninfected) individuals could be screened for HIV prior to HIV infection, and high-risk MSM (including MSM-PWID) could access pre-exposure prophylaxis (PrEP). Following HIV infection, individuals progressed through acute infection (duration=1.7 months, range: 1-6.8)²² and 3 CD4 cell count strata (CD4≥500, 200-499, and <200 cells/μL), and were classified according to diagnosis and treatment status as those infected but undiagnosed, diagnosed but antiretroviral therapy (ART) naïve, on ART and off ART. Health state transitions occurred at monthly intervals, with mortality a possible transition from each of the health states.

Figure 1.

Model schematic diagram. The schematic shows the 19 compartments that constitute each of the 42 population groups in the model. A key for the symbols denoting transitions within the model is available in the Supplementary Appendix.

HIV transmission

HIV transmission occurred through 3 modes: heterosexual contact, homosexual contact, and needle/syringe sharing. We incorporated a mixture of assortative and proportional mixing by race/ethnicity and sexual risk behavior intensity²³ through Newman’s assortativity coefficient, where a value of 0 indicates random mixing, and a value of 1 indicates complete assortative mixing²⁴ (see Appendix Section 1.2 for details). The rate of transmission through homo- and heterosexual sex was a function of the probability of partnership, the number of sexual partnerships, the probability of condom use, and the probability of transmission per sexual partnership at each CD4 stratum. Similarly, transmission via needle/syringe sharing was a function of injection frequency, the probability of needle/syringe sharing, and transmission per shared needle/syringe at each CD4 stratum. These transmission rates were time-dependent, subject to changes in the distribution of PLHIV at different stages of disease progression, risk behaviours and scale-up of interventions. We assumed ART reduced the risk of sexual transmission by 91% (range: 79%-96%),²⁵,²⁶ and the risk of transmission via needle/syringe sharing by 50% (range: 10%-90%),¹⁷ while PrEP reduced transmissibility of HIV per unprotected sexual partnership and per needle/syringe sharing both by 60% (range: 56.3%-61.9%).²⁷ We note that access to PrEP was only modeled among high-risk MSM and MSM-PWID population in this study. Furthermore, we also allowed for changes to people’s risk behaviours, including following HIV diagnosis (reduction in the number of sexual partners),²⁸ OAT receipt (reduction in the frequency of injection drug use),²⁹ and access to syringe services programs (SSP; reduction in the probability of needle/syringe sharing).¹⁷

Model parameters

All model input parameters were derived by a comprehensive evidence synthesis published separately.⁹ We synthesized evidence from 59 peer-reviewed publications, 24 public health and surveillance reports, and executed primary analyses using 11 data sets to inform the 1,667 parameters needed to populate our model. Parameters ranked as best- to moderate-quality evidence comprised 47% of the 169 common (non-city-specific) parameters. In contrast, 61% to 63% of all city-specific input parameters were populated with at least moderate quality evidence. The parameter grouping, common versus city-specific, is based on whether a common prior value and uncertainty range/distribution can reasonably be used across cities. For parameters with lower quality of evidence, we allowed greater variability, including wider uncertainty ranges or imposing more dispersed distributions (uniform or pert distribution).

Model calibration

A review of calibration methods by Stout et al.³⁰ identified 5 key components, including identifying the calibration target variables, goodness-of-fit (GoF) metric, search algorithm, acceptance criteria and stopping rule.³⁰ An overview of the specifications for the calibration process adopted in this paper is presented in Table 1 and described in more detail below. The calibration routine was applied to each of the 6 cities separately by repeatedly adjusting a set of ‘free’ parameters until model projections matched empirical calibration targets. For each city, the model calibration period was set to 2012 to 2015 to capture at least 2 data points on both the calibration and validation variables.

Table 1.

Specifications for Calibration Process

Key elements10	Calibration specifications
Target	Total number of diagnosed PLHIV (2012-2015)  • MSM: race/ethnicity  • PWID: total  • MSM-PWID: total  • Heterosexual: gender x race/ethnicity Annual number of new HIV diagnoses (2012-2015)  • Total  • Black/African American  • MSM Annual number of all-cause deaths among PLHIV (2012-2015)  • Total  • Black/African American  • MSM
Free parameter	The set of free parameters for calibration is selected by Morris method: randomized one-factor-at-a-time sensitivity analysis to identify parameters leading to the most significant uncertainty in target outcomes
GoF metric	Weighted mean percentage deviation: target weights determined by collecting and analyzing SAC’s preferences using best-worst method
Search algorithm	The Latin hypercube sampling is applied to draw multiple sets of parameter values from their predefined distributions as the simplexes, from which the Nelder-Mead search algorithm was performed to optimize the overall GoF metric
Acceptance criteria	The set of parameter values that minimize the GoF metric with each simplex seeded
Stopping rule	The same calibration routine is repeated 10,000 times with each simplex seeded to derive 2,000 best-fitting parameter subsets

Calibration targets

We selected calibration targets that provided the most concrete indicators of the course of each city-level microepidemic. 3 sets of target data were chosen as our calibration targets for each city during the model calibration period 2012 to 2015: (1) the number of diagnosed PLHIV at each year end, stratified by sex, race/ethnicity, and risk group; (2) the annual number of new HIV diagnoses, separately for the overall estimate, among the Black population, and among MSM (including MSM-PWID), respectively; and (3) the annual number of all-cause deaths among diagnosed PLHIV, separately for the overall estimate, among Black individuals, and among MSM (including MSM-PWID). These 17 calibration targets were available from city-specific annual surveillance reports from each city.

Selection of free parameters

We identified the most influential set of free parameters by applying the Morris method,^31–33 an empirical parameter selection approach that systematically analyzes the impacts of variations of each input on model outputs. This method was chosen due to its efficiency, flexibility (e.g. no requirement for monotonicity), and capability to examine a parameter’s influence at multiple time points.^31–33 All uncertain parameters determining model dynamics (thus excluding parameters used to determine initial population sizes) were assumed to be candidates for free parameters and were explored in this parameter selection process for each city. In the interest of maximizing transparency, we present point estimates, prior ranges, and calibrated ranges for these parameters in the Supplementary Appendix.

Goodness-of-fit metric

A GoF metric serves as the objective function in an optimization procedure, measuring the accuracy of the model’s predictions against the targets. While there is no consensus on the most appropriate GoF metric,¹⁰ we utilized an overall weighted GoF metric (global criterion), that was computed by a weighted sum of the individual calibration target fits, a common practice in addressing multi-objective optimization. The weighting factors allow the modellers to place preferences on the set of targets being evaluated.³⁴

Given the disparate scale and importance of the 17 targets, we used the weighted mean percentage deviation as the overall goodness-of-fit metric (shown in the following equation), with the calibration objective to minimize this metric by fitting with different sets of input parameters.

$$Go{F}_{overall}=\sum _i{w}_i\ast \frac{|pro{j}_i-ob{s}_i|}{ob{s}_i}$$

where w_i is the weight assigned to the i^th target, proj_i is the model-projected result for the i^th target, and obs_i is observed point estimate for the i^th target. Smaller values of the GoF metric indicate a better fit to the observed data.

The weighting factors are usually imposed by assumption on the basis of the relative importance as well as the existence of biases of these targets.¹⁰ We generated the weights using a best-worst method^35,36 to elicit the perceived relative importance of each target from our Scientific Advisory Committee (SAC), for which we developed a brief questionnaire asking them to rank and compare each target in respect of their importance for the model to fit against (see further details and weight vectors in the Supplementary Appendix).

Search algorithm

The search algorithm determines the best-fitting sets of parameter values, drawn from their plausible ranges, which optimize the GoF metric such that the model can reproduce the observed historical trends. We adopted a mixed calibration approach with 2 distinct steps. Latin hypercube sampling was first applied to draw 10,000 parameter sets from predefined distributions as the initial simplexes (starting values), from which the Nelder-Mead search algorithm was performed to minimize the overall GoF metric. Latin hypercube is a multidimensional grid sampling method enabling the whole parameter space to be covered efficiently.³⁷ The Nelder-Mead algorithm is an iterative, directed-search method with high computational efficiency and superior performance over manual and random calibration.³⁸ We used Latin hypercube sampling to generate 10,000 simplexes for the Nelder-Mead algorithm to sufficiently explore the parameter space to overcome its potential drawback of settling on local, rather than global optima, as well as to facilitate uncertainty analysis, as recommended by the ISPOR-SMDM guidelines.⁷

Acceptance criteria

Choosing an acceptance criterion entails defining acceptable sets of input parameter values by defining either the worst acceptable GoF level or the acceptable ranges for the targets or the GoF metric.¹⁰ With each simplex seeded, the Nelder-Mead algorithm seeks to produce one optimal set of input parameter values that locally minimize the overall GoF metric, whereas we deemed only the calibrated parameter sets that best minimize GoF (i.e. below 20^th percentile) as acceptable. The cutoff of 20^th percentile was determined by the actual GoF distributions to warrant the inclusion the densest proportion to the left of the mode providing the best and most similar GoF.

Stopping rule

The stopping rule determines whether the calibration process is complete, usually defined by deriving a sufficient number of acceptable input sets.¹⁰ In this exercise, we seeded the Nelder-Mead optimization algorithm with 10,000 simplexes (that varied only by starting seed), by repeating the same process, to generate 10,000 calibrated parameter sets, from which we selected the 2,000 best-fitting sets with the minimal GoF metric as the acceptable samples for subsequent analysis.

Model validation

Model validation refers to the process of evaluating a model’s accuracy in making relevant projections.⁸ It entails a comprehensive evaluation of how well the model performs, from the problem construct to the credibility of model results, against a variety of internal and external inputs, including expert opinions, clinical knowledge, and empirical evidence. In accordance with ISPOR-SMDM guidelines,⁸ based on the 2,000 calibrated parameter sets, we formally assessed the internal, external and face validity of our model, as follows (Table 2).

Table 2.

Specifications for Validation Process

Key elements8	Validation specifications
Internal	Extensive checks and evaluations  • Cross-check on all codes and equations  • Double-coding force of infection module  • Extreme scenario analysis  • Weekly meeting and updates
External	Validation target – new HIV incidence (range)  • Total  • MSM and MSM/PWID
Face	Continuous consultation with SAC  • Evidence synthesis  • Model development Projection outcomes  • Population dynamics, by race/ethnicity  • Rate of new infections, overall, by race/ethnicity and by risk group  • Rate of new diagnoses, overall, by race/ethnicity and by risk group  • Rate of new infections among MSM, overall and by race/ethnicity  • Rate of new diagnoses among MSM, overall and by race/ethnicity

Internal validity

Internal validation investigates and verifies the accuracy and consistency of all mathematical equations and program coding. To secure a high level of internal validity, we performed a series of checks:

1. Each mathematical equation and program coding script was cross-checked by at least one other analyst other than the developer.

2. Given its complexity, we performed double programming for the force of infection module where two programmers independently coded the functions until the results were identical.

3. An extensive model walk-through was performed internally wherein detailed model structure, underlying assumptions, and corresponding codes were presented by the developers and checked by other team members.

4. We ran extreme value analyses on several scenarios and assessed model predictions against our anticipated outcomes (Supplementary Appendix,).

External validity

External validation entails comparison of city-specific model projections to external estimates of key clinical and epidemiological data not used in the model.^39–41 We selected HIV incidence over 2012 to 2015 as the external validation target, both for the total estimates and among the MSM population (including MSM-PWID). Independent, city-level annual incidence estimates between 2012 and 2015 were only reported in NYC and partially in LA (2012-2013), while estimates for other cities were otherwise triangulated from annual state-level incidence estimated by the CDC³⁹ (triangulation process detailed in the evidence synthesis⁹). We selected these endpoints based on their availability from a common, authoritative source, the availability of confidence intervals for each estimate, and their importance in decision-making.

Establishing the status quo scenario in each city

The status quo scenario for each city was defined by holding treatment and prevention service levels (including the proportion of PLHIV being tested, receiving treatment and accessing OAT and PrEP) in the most recent year for which data was available. In addition, we held constant the proportion of people in high- and low-risk strata. To account for heterogeneity in the rate of aging, we used surveillance data to derive city-level, PLHIV-specific maturation rates (i.e. PLHIV who are 64 turning 65). Finally, we modelled a dynamic cohort allowing model entry and exit (more details in Supplementary Appendix) to match external adult population growth projections throughout the study time horizon for each city, accounting for changes in ethnic compositions.

Assessing the face validity of longitudinal status quo projections

Face validation refers to the subjective review of the model projections by individuals with clinical and epidemiologic expertise in the disease area. Following each of the above steps, we prepared a report for each city detailing 25-year (2016-2040) status quo projections on population growth, stratified by race/ethnicity; longitudinal projections of the number of people in each of the primary HIV stages of the model; rates of incidence and new diagnoses, overall and stratified by race/ethnicity and by risk group; and rates of incidence and new diagnoses among MSM, overall and stratified by race/ethnicity. At least one clinical/epidemiological expert in our SAC from each city was invited to provide qualitative responses on the projections for their city and the modeling team followed-up individually with respondents to resolve any discrepancies.

Results

Model calibration

We identified 381 independent parameters as candidate free parameters in the calibration process, 37 of which were common across cities, 54 capturing sexual risk behaviours, 56 characterizing health service delivery, and 234 dictating movement between ART states (including from/to death and off ART states). Following application of the Morris method, we included 52 unique (176 in total) free parameters in the model calibration across all cities (Table 3). The set of free parameters selected varied across cities, driven in part by variations in race. In cities like Atlanta and NYC, where the HIV epidemic is mainly concentrated in the Black population, the behavioural parameters for this population were more likely to be selected, as compared with cities like LA and Miami, where parameters determining behaviours for the Hispanic population were more often chosen.

Table 3.

Model parameters selected as free-parameters by Morris Method

Common Parameter	ATL	BAL	LA	MIA	NYC	SEA
1.3 Population Dynamics - Mortality Rate
PLHIV (CD4 200-499)	✓	✓	✓	✓	✓	✓
PLHIV (CD4 <200)	✓	✓	✓	✓	✓	✓
PLHIV - PWID multiplier (CD4 200-499)	✓	✓	✓	✓	✓	✓
PLHIV - PWID multiplier (CD4 <200)	✓	✓	✓	✓	✓	✓
2.1 Sexual Risk Behaviors - Number of Sexual Partner Multipliers
PWID relative to HET	✓		✓			✓
Decrease in sexual partners post-diagnosis	✓	✓	✓	✓	✓	✓
2.2 Injection Risk Behaviors
Injection frequency		✓	✓		✓	✓
Decreased probability of injection sharing post-diagnosis		✓	✓		✓	✓
SSP effect on reducing injection sharing						✓
2.4 Probability of Transmission (per partnership)
Sex - Female to Male (CD4 ≥500)	✓		✓	✓	✓	✓
Sex - Female to Male (CD4 200-499)	✓
Sex - Female to Male (CD4 <200)	✓			✓
Sex - Male to Female (CD4 ≥500)	✓	✓	✓	✓	✓	✓
Sex - Male to Female (CD4 200-499)	✓
Sex - Male to Female (CD4 <200)	✓
Sex - Male to Male (CD4 ≥500)	✓	✓	✓	✓	✓	✓
Sex - Male to Male (CD4 200-499)	✓	✓	✓	✓	✓	✓
Sex - Male to Male (CD4 <200)	✓	✓	✓	✓	✓	✓
Shared injection (CD4 ≥500)	✓	✓		✓		✓
Shared injection (CD4 200-499)		✓
Shared injection (CD4 ≥200)		✓
Transmission probability multiplier (Acute HIV)	✓	✓	✓	✓	✓	✓
ART effect on reducing transmission - Sexual		✓	✓	✓	✓	✓
ART effect on reducing transmission - Shared Injection		✓
Condom effect on reducing transmission - Heterosexual Sex	✓		✓			✓
Condom effect on reducing transmission - Homosexual Sex	✓	✓	✓	✓	✓	✓
3.1 HIV Testing - Annual Change in HIV Testing Rate	✓	✓	✓	✓	✓	✓
3.5 HIV Disease Progression Transition Rate from Acute to Chronic HIV	✓	✓	✓	✓	✓	✓
City-Specific Parameter	ATL	BAL	LA	MIA	NYC	SEA
2.1 Sexual Risk Behaviors - Number of Sexual Partners
Heterosexual partners, White, Low-risk MSM	✓
Heterosexual partners, White, High-risk MSM				✓		✓
Heterosexual partners, Black, High-risk MSM	✓
Heterosexual partners, Hispanic, High-risk MSM			✓
Heterosexual partners, Male, White, High-risk HET	✓
Heterosexual partners, Male, Black, High-risk HET	✓		✓
Heterosexual partners, Female, White, High-risk HET	✓				✓
Heterosexual partners, Female, Black, High-risk HET	✓
Heterosexual partners, Female, Hispanic, High-risk HET			✓			✓
Homosexual partners, White, Low-risk MSM		✓				✓
Homosexual partners, Black, Low-risk MSM		✓	✓		✓
Homosexual partners, White, High-risk MSM	✓	✓	✓	✓	✓	✓
Homosexual partners, Black, High-risk MSM	✓	✓	✓	✓	✓	✓
Homosexual partners, Hispanic, High-risk MSM	✓	✓	✓	✓	✓	✓
2.1 Sexual Risk Behaviors - Condom Use Probability
Heterosexual, Male, White, High-risk HET	✓
Homosexual, Male, White, Low-risk MSM						✓
Homosexual, Male, Black, Low-risk MSM		✓	✓	✓	✓
Homosexual, Male, Hispanic, Low-risk MSM			✓	✓	✓
Homosexual, Male, White, High-risk MSM		✓	✓	✓	✓	✓
Homosexual, Male, Black, High-risk MSM		✓		✓	✓	✓
Homosexual, Male, Hispanic, High-risk MSM		✓		✓	✓	✓
2.1 Assortativeness of Heterosexual Partnership Paring, High-risk Black	✓
3.2 ART Initiation
Proportion linked to care post-diagnosis (CD4 ≥500), Male, Black, PWID					✓
Proportion linked to care post-diagnosis (CD4 ≥500), Female, Black, PWID		✓

ATL: Atlanta; BAL: Baltimore; LA: Los Angeles; MIA: Miami; NYC: New York City; SEA: Seattle; Checked cells represent parameters selected for calibration.

Following calibration, we compared the calibrated values (median and 95% credible intervals [CI]) of free parameters against their prior values and ranges (Supplementary Appendix Figure A2). Post-calibration values differed across cities. For example, the probability of MSM transmission (at CD4 ≥ 500) was calibrated to be higher in LA (0.0674, 95% CI: [0.0250-0.1000]) compared to Atlanta (0.0251, 95% CI: [0.0250, 0.0433]).

The resulting epidemiological estimates from the 2,000 best-fitting calibration runs demonstrated a good fit to most targets. Figure 2 shows the model projections for the number of new HIV diagnoses (total and among MSM) against their corresponding targets (2 targets deemed most important by our SAC) for each city. The overall mean GoF, based on the 2,000 best-fitting parameter sets, differed across cities, ranging from 0.0174 in NYC (range: 0.0167-0.0176) to 0.0861 in Atlanta (range: 0.0844-0.0868, Supplementary Appendix Figure A3). The bimodal distribution for GoF values observed in Atlanta and Miami indicate the presence of local optima at poorer levels of GoF. Model calibration results for all 17 targets are presented in Supplementary Appendix Figure A4. While calibration yielded close matches to most targets in most cities, we also observed mismatches for some of the mortality targets. In particular, our model consistently overestimated the number of all-cause deaths in comparison to the 3 death-related targets in Atlanta, even with mortality-related free parameters being calibrated to the lower ends of their respective ranges, likely due to an underreport of the target mortality estimates.

Figure 2.

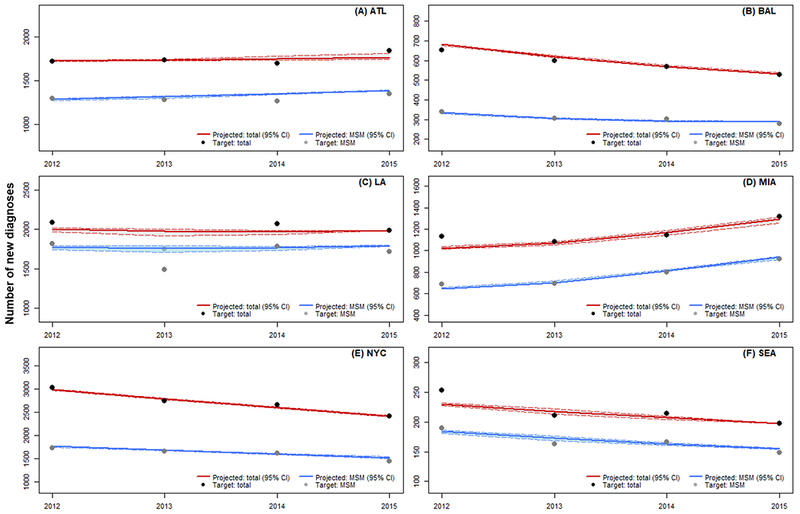
Model fit of new diagnoses for calibration. (A) ATL: Atlanta; (B) BAL: Baltimore; (C) LA: Los Angeles; (D) MIA: Miami; (E) NYC: New York City; (F) SEA: Seattle; 95% CI: 95% credible interval. MSM: men who have sex with men (excluding MSM-PWID)

Model validation

With the 2,000 calibrated parameter sets, most model projections (2012-2015) fell within the confidence interval of the external validity targets. Figure 3 shows the model projections for the rate of total HIV incidence against the external estimates (after transforming the absolute number of infections to rates). The proportion of annual incidence projections, total and for MSM, that fit within the confidence interval varied by cities, from 100% in NYC to 21% in Miami.

Figure 3.

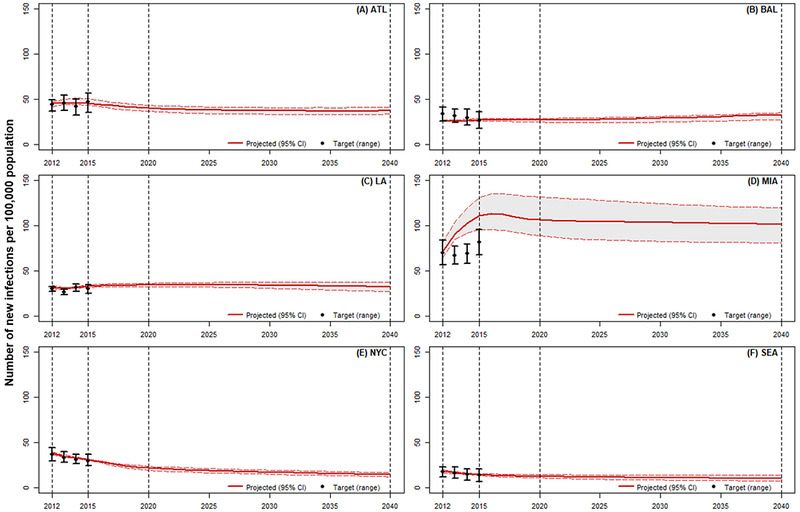
Model external validity and status quo projections for the rate of new incidence. Year 2012-2015: calibration period; Year 2016-2040: projection period; Year 2021-2040: evaluation period. (A) ATL: Atlanta; (B) BAL: Baltimore; (C) LA: Los Angeles; (D) MIA: Miami; (E) NYC: New York City; (F) SEA: Seattle.

We assessed the face validity of our model projections via survey distributed to our SAC. We performed further evidence collection and reanalysis to resolve any discrepancies between model projections and experts’ expectations. Further details regarding this process are available in the Supplementary Appendix.

Over a 25-year time horizon with all HIV services maintained at their 2015 levels (except PrEP, for which we incorporated data up to 2017 to acknowledge its rapid scale-up), our model predicted that the overall rate of new infections would drop in Atlanta (from 45 [95% CI: 43-51] to 37 [3341] cases per 100,000 population), NYC (from 31 [31-32] to 15 [12-17] cases per 100,000 population) and Seattle (from 15 [14-16] to 10 [8-14] cases per 100,000 population, Figure 3A, E and F), while remain relative constant in LA at 33 to 34 [27-38] cases per 100,000 population (Figure 3C). In contrast, the rate of new infections was projected to rise slightly in Baltimore (from 27 [26-28] to 33 [27-35] cases per 100,000 population, Figure 3B). Projections for Miami suggest a slight increase in the rate of new infections in the first few years, ultimately stabilizing at 102 [81-120] cases per 100,000 respectively (Figure 3D). Projections used in the face validation process, displaying overall and stratified estimates and credible ranges of incidence and new diagnoses, are presented the Supplementary Appendix. Model projections suggest the risk for HIV infection will remain highest among MSM and MSM-PWID, and these two risk groups will continue to contribute the majority of all new incident cases across cities: 69.8% [62.3%-76.3%] in Seattle to 90.9% [87.7%-92.0%] in Baltimore in 2040. Further, while our model estimated that black individuals will continue to have the highest rate of HIV incidence across all cities, it also suggests Hispanic MSM will contribute most to the increasing rate of HIV incidence in Miami and LA (Appendix Figure A6).

Discussion

We have detailed our process for calibrating and validating a dynamic HIV transmission model to 6 US cities with disparate HIV microepidemics using a systematic and empirical approach to determining the most influential parameters necessitating calibration. The model provided an excellent fit to the calibration targets across cities, particularly to those determined to be of the greatest importance. On the basis of the 2,000 best-fitting calibrated parameter sets, short-term external validation yielded a majority of incidence projections that were within the uncertainty range for 5 of 6 cities, while the face validity of the long-term status quo epidemiological projections were confirmed with our SAC.

The status quo projections in the selected cities predict the HIV epidemic will stabilize in most urban centers at current service levels, although greater efforts will be required if the US is to achieve its goal of ending the HIV epidemic by 2025.⁴² While we predicted that incidence would decrease or remain stable in Atlanta, LA, NYC and Seattle, we also projected a slight increase in the incidence rate in Baltimore and Miami, driven primarily by projected increases in incidence among black MSM (Baltimore) and Hispanic MSM (Miami).

Disparities in overall incidence correspond to the current features of the distinct city-level microepidemics and the current level of services available for HIV treatment and prevention. Most notably, substantial resources have been devoted to the control of HIV in NYC and Seattle, which have aggressively combatted incidence in the MSM and PWID populations, and have led the nation in the expansion of PrEP, particularly for MSM.⁴

From a methodological standpoint, we found that some parameters were consistently calibrated to the lower/higher end of prior ranges, implying either: (1) the model overestimated/underestimated these parameters; (2) the underlying evidence for the input parameters was biased; or (3) the model simply captured the dynamics in question too coarsely. For example, the number of homosexual partners was consistently calibrated towards the lower bound of the empirical estimates for white high-risk MSM across all cities, while to the upper bound for black high-risk MSM. This difficulty in closely reproducing the racial disparities in HIV incidence among MSM has also been noted in a recent modeling study by Goodreau et al.⁴³. Further, sexual risk behaviour parameters (such as the number of sexual partners and the probability of condom use) and per-partnership transmission probabilities were more likely to be selected for calibration. Collecting additional information on these parameters may help reduce the potential opportunity cost from a suboptimal decision. Value of information analysis^44,45 can estimate a monetary value for additional research to reduce uncertainty in these critical domains, and will serve as an important subsequent step in furthering this argument.

Despite the importance of validating the accuracy of model projections against empirical data on outcomes of interest,⁴⁶ external validation has yet to become a standard component of the model development process.⁴⁷ Best-practice guidelines have noted that it may not be possible to establish absolute criteria to assess the validity of a model, and that one of the key impediments to standardizing the validation process is the availability of target data not previously used to inform the model. In addition, assessing how close a model’s predictions fit the external targets remains mostly subjective,⁴⁷ particularly when there is a need to incorporating uncertainty of the validation targets (as opposed to trying to fit a target to a point estimate). Specifically, determining HIV incidence in city-level microepidemics poses challenges; these estimates are typically generated at the state-level, and even estimates generated at a higher level of aggregation are subject to limitations.⁴⁸ In each of our cities aside from Miami, most of the incidence predictions used for external validation were within the externally estimated uncertainty range. In a growing epidemic such as Miami, and particularly given its relatively low HIV service levels, the discrepancy we found between model projections and short-term incidence validation targets may reflect the long delay between HIV infection and diagnosis. Nonetheless, experts from our SAC confirmed the validity of our model projections for the long-term trend of the epidemic in Miami.

We aimed for comprehensive and transparent reporting of our calibration and validation process to enhance the credibility and reliability of our results, hoping that this effort can help inform the standardization of methods for model calibration and validation and promote better integration of locally-oriented modelling in decision-making. Despite existing guidelines on model calibration and validation, substantial subjectivity remains in the process, particularly in the selection of parameters for calibration^10,32 and determination of the summary measure of model fit when multiple targets are used.^10,11,36 While we adopted the Morris method³¹ to establish an objective criteria for free parameter selection, the technique also substantially improved the efficiency of the calibration. Establishing the weight metric for summary GoF is another common challenge, and we used the best-worst method^35,36 to synthesize information on the preferences of our SAC on each target and solve the weight metric from these preferences. Finally, we also leveraged the expertise of our SAC to assess the face validity of our 25-year status quo scenario projections. The approach proved useful not only in refining the model and its estimates but also in communicating both the functioning and limitations of our model to a multidisciplinary audience. It is possible this approach can be further refined and extended to include a broader range of public health practitioners and policymakers.

Our analysis was not without limitations. First, we imposed a relatively simple proportional mixing assumption among needle/syringe-sharing contacts, rather than a more complex structure that may better approximate PWID networks.⁴⁹ Also, we modeled HIV infectivity indirectly through stages of disease progression based on CD4 cell counts rather than viral load, a limitation we have previously outlined.¹⁵ However, these approximations were consistent with the precision of available evidence and were sufficient in replicating the city-level HIV epidemics with a high degree of precision. Second, drug resistance is not explicitly modeled, but it has been accounted for in disease progression estimates, although resistance levels are stably low and likely to decrease with broader access to new medication regimens.⁵⁰ Third, the model is not age-structured. Given the existing complexity of the model, adding age strata would increase the number of health states substantially, with limited ability to populate these health states with data specific to their description. Instead, we restricted the study population to individuals aged 15 to 64 years to reduce the impact of age on some risk factors. Fourth, we explicitly modeled PrEP only among high-risk MSM. This is in line with current guidelines prioritizing PrEP among individuals at high risk of infection and previous evidence that PrEP may not be cost-effective for other populations.^51–53 Our future work with this model will explore the cost-effectiveness of PrEP for other risk groups. Fifth, one difficulty associated with the choice of a calibration search algorithm such as the Nelder-Mead algorithm is its possibility to converge on local optima. To remedy this potential problem, we randomly drew 10,000 sets of starting values for the algorithm, ensuring the parameter space was adequately covered by the search strategy and substantially improving the likelihood of capturing the global optima. We aim to append the 2,000 best-fitting calibrated parameter sets with samples for all other uncalibrated parameters (aside from parameters defining initial values in each compartment), drawn from their prior distributions to support probabilistic sensitivity analysis of our assessments of combination implementation strategies for each city.³² Lastly, cross-validating this model to assess its structural uncertainty,⁸ remains a topic for future research, as comparable city-level models are developed.

We provided a comprehensive and transparent description for the calibration and validation of a dynamic HIV transmission model to 6 US cities with diverse HIV microepidemics. The resulting model projections will serve as status quo scenarios in each city to identify optimal combination implementation strategies for the HIV treatment and prevention services we have considered in this model, including HIV testing, treatment, SSP, OAT and PrEP. We believe this standardized framework can be applied to diverse settings and disease areas, further underlining the potential value of this approach.