Abstract
The current research work was performed to evaluate the solubilization behavior, solution thermodynamics, and solvation behavior of poorly soluble pyridazinone derivative i.e., 6-phenyl-pyridazin-3(2H)-one (PPD) in various binary solvent systems of dimethyl sulfoxide (DMSO) and water using experimental and various computational approaches. The solubility of PPD in various binary solvent system of DMSO and water was investigated within the temperature range T = 298.2 K to 318.2 K at constant air pressure p = 0.1 MPa, by employing an isothermal technique. The generated solubility data of PPD was computationally represented by five different cosolvency models including van’t Hoff, Apelblat, Yalkowsky–Roseman, Jouyban–Acree, and Jouyban–Acree–van’t Hoff models. The performance of each computational model for correlation studies was illustrated using root mean square deviations (RMSD). The overall RMSD value was obtained <2.0% for each computational model. The maximum solubility of PPD in mole fraction was recorded in neat DMSO (4.67 × 10−1 at T = 318.2 K), whereas the lowest one was obtained in neat water (5.82 × 10−6 at T = 298.2 K). The experimental solubility of PPD in mole fraction in neat DMSO was much higher than its ideal solubility, indicating the potential of DMSO for solubility enhancement of PPD. The computed values of activity coefficients showed maximum molecular interaction in PPD-DMSO compared with PPD-water. Thermodynamic evaluation showed an endothermic and entropy-driven dissolution of PPD in all the mixtures of DMSO and water. Additionally, enthalpy–entropy compensation evaluation indicated an enthalpy-driven mechanism as a driven mechanism for the solvation property of PPD.
Keywords: computational models, pyridazinone derivative, Solution thermodynamics, solubilization
1. Introduction
The investigated molecule 6-phenylpyridazin-3(2H)-one (PPD) [chemical structure: Figure 1; chemical name: 6-phenylpyridazin-3(2H)-one; molecular formula: C10H8N2O; molecular weight: 172.18 g mol−1 and CASRN: 2166-31-6] is a pyridazinone derivative which is being used as cardiotonic agent [1,2].
Figure 1.
Chemical structure of PPD.
Some other biological activities, including insecticidal [3], cardioprotective [4,5], analgesics [6,7], anti-inflammatory [7,8], antinociceptive [1], antiulcer [9], and antimicrobial activity [10], have also been reported for different PPD derivatives. The main problem of PPD and related compounds is high toxicity and week solubilization potential in an aqueous media [1,11]. Hence, the solubilities and other physicochemical information about these molecules in aqueous-cosolvent binary systems are important for their complete physicochemical characterization [12,13]. The potential of dimethyl sulfoxide (DMSO) in enhancing the solubility of various weakly soluble drugs such as 6-methyl-2-thiouracil, sinapic acid, naringin and bergenin have been proved in the literature [12,14,15,16]. The solubility data and other physicochemical properties of PPD have been reported poorly in the literature. The solubility of PPD in neat DMSO and neat water has been reported recently [17]. The solubility and solution thermodynamic properties of PPD in various DMSO + water systems are not reported elsewhere. Hence, in the proposed study, the solubility, solution thermodynamic properties and solvation behavior of PPD in binary DMSO + water systems and neat solvents were studied using experimental and various computational approaches. The solubility of PPD was determined by applying an isothermal technique within temperature range T = 298.2 K to 318.2 K at constant air pressure p = 0.1 MPa. The impact of pressure on the solubility of PPD was not studied in this work and hence these studies were carried out at constant air pressure i.e., p = 0.1 MPa. The temperature range T = 298.2 K to 318.2 K was maintained in this range in such a way that the maximum investigated temperature (i.e., T = 318.2 K) should not exceeds the melting temperature of PPD and boiling points of the studied solvents. The melting temperature of PPD has been found as 476.43 K in our previous work [17]. The boiling points of water and DMSO are 373.2 and 462.2 K, respectively. The maximum investigated temperature (i.e., T = 318.2 K) was found much lower than melting temperature of PPD and boiling points of water and DMSO and hence the proposed temperature range was maintained in this study. Activity coefficients of PPD and various cosolvent mixtures were computed using ideal and experimental solubility data of PPD. Using activity coefficients, solute-solvent interactions at molecular level were evaluated. The physicochemical and solubility data of PPD obtained in this work would motivate the pharmaceutical scientists to obtain similar data for newly synthesized medicinal compounds as well as for already existing compounds [18,19,20]. The solubility data generated in the proposed study would be helpful in purification, recrystallization, drug discovery process, and dosage form design of PPD.
2. Results and Discussion
2.1. Solubility of PPD in Binary DMSO + Water Systems
The experimental mole fraction solubility (xe) values of PPD in binary DMSO + water systems and neat solvents at T = 298.2 K to 318.2 K and p = 0.1 MPa are tabulated in Table 1.
Table 1.
The xe values of PPD against mass fraction value of DMSO (m) in binary DMSO + water mixtures at T = 298.2 K to 318.2 K and p = 0.1 MPa a.
| m | xe | ||||
|---|---|---|---|---|---|
| T = 298.2 K | T = 303.2 K | T = 308.2 K | T = 313.2 K | T = 318.2 K | |
| 0.0 | 5.82 × 10−6 | 6.94 × 10−6 | 8.42 × 10−6 | 1.02 × 10−5 | 1.30 × 10−5 |
| 0.1 | 1.81 × 10−5 | 2.13 × 10−5 | 2.53 × 10−5 | 3.03 × 10−5 | 3.79 × 10−5 |
| 0.2 | 5.47 × 10−5 | 6.31 × 10−5 | 7.54 × 10−5 | 8.78 × 10−5 | 1.08 × 10−4 |
| 0.3 | 1.69 × 10−4 | 1.91 × 10−4 | 2.26 × 10−4 | 2.56 × 10−4 | 3.05 × 10−4 |
| 0.4 | 5.05 × 10−4 | 5.71 × 10−4 | 6.50 × 10−4 | 7.40 × 10−4 | 8.68 × 10−4 |
| 0.5 | 1.54 × 10−3 | 1.73 × 10−3 | 1.93 × 10−3 | 2.17 × 10−3 | 2.49 × 10−3 |
| 0.6 | 4.68 × 10−3 | 5.14 × 10−3 | 5.68 × 10−3 | 6.27 × 10−3 | 7.08 × 10−3 |
| 0.7 | 1.48 × 10−2 | 1.56 × 10−2 | 1.69 × 10−2 | 1.84 × 10−2 | 2.04 × 10−2 |
| 0.8 | 4.34 × 10−2 | 4.62 × 10−2 | 4.96 × 10−2 | 5.33 × 10−2 | 5.76 × 10−2 |
| 0.9 | 1.32 × 10−1 | 1.40 × 10−1 | 1.47 × 10−1 | 1.56 × 10−1 | 1.65 × 10−1 |
| 1.0 | 4.00 × 10−1 | 4.16 × 10−1 | 4.32 × 10−1 | 4.49 × 10−1 | 4.67 × 10−1 |
| xidl | 5.50 × 10−2 | 6.10 × 10−2 | 6.75 × 10−2 | 7.45 × 10−2 | 8.22 × 10−2 |
a The standard uncertainties u are u(T) = 0.12 K, ur(m) = 0.1%, u(p) = 0.003 MPa and ur(xe) = 1.38%.
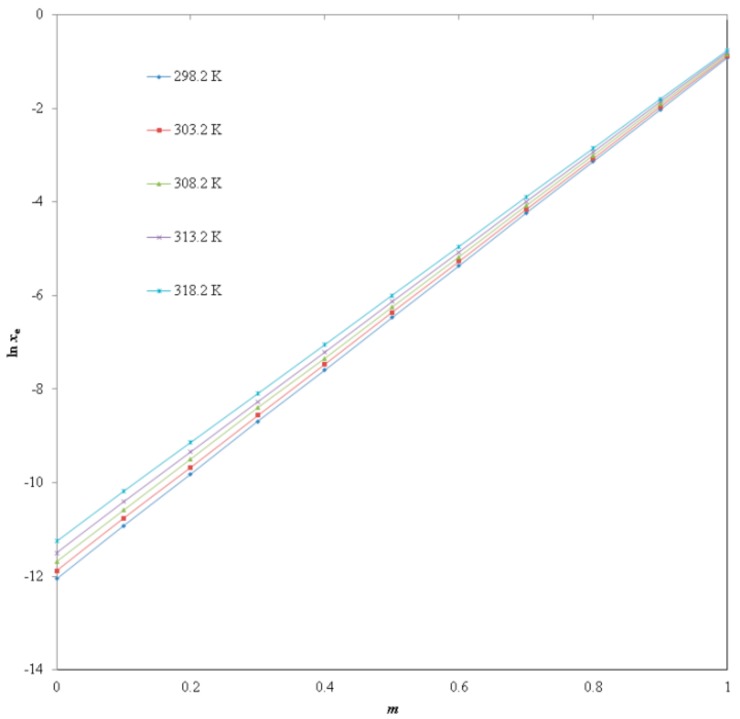
The solubility of PPD in neat DMSO and neat water has been reported at T = 298.2 K to 318.2 K and p = 0.1 MPa [17]. The solubility of PPD in mole fraction in pure DMSO and pure water at T = 298.2 K was estimated as 4.03 × 10−1 (m = 1.0) and 5.75 × 10−6 (m = 0.0), respectively in the literature [17]. The solubility of PPD in mole fraction in pure DMSO and pure water at T = 298.2 K was recorded as 4.00 × 10−1 (m = 1.0) and 5.82 × 10−6 (m = 0.0), respectively in the present work. The solubility of PPD in mole fraction in water (m = 0.0) at other temperatures i.e., T = 303.2, 308.2, 313.2 and 318.2 K was found as 6.91 × 10−6, 8.37 × 10−6, 1.00 × 10−5 and 1.26 × 10−5, respectively in the literature [17]. The solubility of PPD in mole fraction in water (m = 0.0) at T = 303.2, 308.2, 313.2 and 318.2 K was recorded 6.94 × 10−6, 8.42 × 10−6, 1.02 × 10−5 and 1.30 × 10−5, respectively in the present study. The solubility of PPD in mole fraction in DMSO (m = 1.0) at T = 303.2, 308.2, 313.2 and 318.2 K was found as 4.19 × 10−1, 4.38 × 10−1, 4.55 × 10−1 and 4.73 × 10−1, respectively in the literature [17]. The solubility of PPD in mole fraction in DMSO (m = 1.0) at T = 303.2, 308.2, 313.2 and 318.2 K was recorded as 4.16 × 10−1, 4.32 × 10−1, 4.49 × 10−1 and 4.67 × 10−1, respectively in the present study. Overall, the recorded solubilities of PPD in DMSO and water at T = 298.2 K to 318.2 K were very close to the literature values. The solubility of PPD was found to increase linearly with raise in temperature and in all cases the solubility of PPD increases as the proportion of DMSO in binary DMSO + water system increases. The highest solubility of PPD in mole fraction was obtained in neat DMSO (4.67 × 10−1 at T = 318.2 K), whereas, the lowest one was found in neat water (5.82 × 10−6 at T = 298.2 K). The highest solubility of PPD in neat DMSO was possible due to lower polarity of DMSO as compared with water [12,16]. The effect of mass fraction of DMSO (m) on logarithmic solubility of PPD at T = 298.2 K to 318.2 K was also studied and results are presented in Figure 2. The results suggested linear increase in the logarithm solubility of PPD with increase in mass fraction of DMSO in binary DMSO + water systems at each temperature point studied. The solubility of PPD was found to increase significantly from neat water to neat DMSO. Hence, DMSO could be used as a potential cosolvent in solubility enhancement of PPD in an aqueous media such as water.
Figure 2.
Impact of m value of the DMSO on ln xe values of PPD at five different temperatures i.e., T = 29.2 K to 318.2 K.
2.2. Ideal Solubilities and Activity Coefficients for Solute-Solvent Molecular Interactions
The ideal solubility (xidl) values for PPD were calculated using Equation (1) and results are tabulated in Table 1. The ideal solubilities of PPD were recorded in the range of 5.50 × 10−2 to 8.22 × 10−2 within the temperature range of T = 298.2 to 318.2 K. The ideal solubilities of PPD were significantly higher than its mole fraction solubilities in neat water. However, these values were lower than mole fraction solubilities of PPD in neat DMSO at each temperature point studied. Because of significant solubility of PPD in DMSO, it can also be used as an ideal cosolvent for solubility enhancement of PPD.
The values of activity coefficient (γi) for PPD in binary DMSO + water systems at T = 298.2 K to 318.2 K were calculated using Equation (2) and results are tabulated in Table 2. The activity coefficient for PPD was found larger in neat water at each temperature point. However, the activity coefficient for PPD was lowest in neat DMSO at each temperature point. The activity coefficients for PPD were found to be decreasing significantly from neat water to neat DMSO. The larger activity coefficients for PPD in neat water were possible due to the lowest solubility of PPD in water. Overall, these results suggested maximum solute-solvent interactions in PPD-DMSO in comparison with PPD-water.
Table 2.
The estimated values of γi for PPD in binary DMSO + water mixtures (m) at T = 298.2 K to 318.2 K.
| m | γi | ||||
|---|---|---|---|---|---|
| T = 298.2 K | T = 303.2 K | T = 308.2 K | T = 313.2 K | T = 318.2 K | |
| 0.0 | 9460.000 | 8800.000 | 8020.000 | 7340.000 | 6340.000 |
| 0.1 | 3036.053 | 2863.900 | 2671.535 | 2464.940 | 2173.383 |
| 0.2 | 1007.450 | 967.752 | 895.279 | 849.738 | 764.882 |
| 0.3 | 325.566 | 319.655 | 298.478 | 291.063 | 269.649 |
| 0.4 | 109.123 | 106.877 | 103.965 | 100.798 | 94.754 |
| 0.5 | 35.637 | 35.245 | 34.901 | 34.347 | 32.997 |
| 0.6 | 11.761 | 11.865 | 11.885 | 11.884 | 11.617 |
| 0.7 | 3.802 | 3.905 | 3.985 | 4.038 | 4.026 |
| 0.8 | 1.266 | 1.320 | 1.359 | 1.398 | 1.425 |
| 0.9 | 0.417 | 0.435 | 0.457 | 0.477 | 0.496 |
| 1.0 | 0.137 | 0.146 | 0.156 | 0.165 | 0.175 |
2.3. Thermodynamic Behavior of PPD
The values of different thermodynamic parameters for PPD estimated using van’t Hoff and Gibbs equations (Equations (3)–(6)) in binary DMSO + water systems and neat solvents are tabulated in Table 3.
Table 3.
Apparent thermodynamic quantities (ΔsolH0, ΔsolG0 and ΔsolS0) and R2 values for PPD dissolution in binary DMSO + water mixtures b.
| Parameters | m = 0.0 | m = 0.1 | m = 0.2 | m = 0.3 | m = 0.4 | m = 0.5 | m = 0.6 | m = 0.7 | m = 0.8 | m = 0.9 | m = 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔsolH0/kJ mol−1 | 31.35 | 28.75 | 26.59 | 23.28 | 21.22 | 18.68 | 16.21 | 13.51 | 11.20 | 8.90 | 6.10 |
| ΔsolG0/kJ mol−1 | 29.89 | 27.06 | 24.30 | 21.51 | 18.77 | 15.98 | 13.22 | 10.42 | 7.68 | 4.89 | 2.14 |
| ΔsolS0/J mol−1 K−1 | 4.74 | 5.49 | 7.44 | 5.73 | 7.97 | 8.78 | 9.69 | 10.02 | 11.43 | 13.01 | 12.85 |
| R 2 | 0.9941 | 0.9931 | 0.9947 | 0.9949 | 0.9954 | 0.9964 | 0.9958 | 0.9946 | 0.9963 | 0.9990 | 0.9991 |
b The average uncertainties are u(ΔsolH0) = 0.44 kJ mol−1, u(ΔsolG0) = 0.57 kJ mol−1 and u(ΔsolS0) = 0.32 J mol−1 K−1.
The apparent standard enthalpy (ΔsolH0) values for PPD dissolution in binary DMSO + water systems and neat solvents were recorded as positive values (6.10 to 31.35 kJ mol−1), suggesting endothermic dissolution of PPD in all binary solvent systems and neat solvents [21,22].
The ΔsolH0 values for PPD dissolution were found to be decreasing with increase in the mass fraction of DMSO in binary DMSO + water systems and solubility values of PPD. Therefore, the highest ΔsolH0 value was recorded in neat water (31.35 kJ mol−1; m = 0.0), whereas, the lowest value was found in neat DMSO (6.10 kJ mol−1; m = 1.0). The apparent standard Gibbs free energy (ΔsolG0) values for PPD dissolution in binary DMSO + water systems were also found as positive values (2.14 to 29.89 kJ mol−1) as shown in Table 3. The ΔsolG0 values for PPD dissolution were also found to be decreasing with increase in the mass fraction of DMSO in binary DMSO + water systems and solubility values of PPD. The highest and lowest ΔsolG0 values for PPD dissolution were found in neat water (29.89 kJ mol−1; m = 0.0) and neat DMSO (2.14 kJ mol−1; m = 1.0), respectively.
The apparent standard entropy (ΔsolS0) values for PPD dissolution in binary DMSO + water systems were also recorded as positive values (4.74 to 13.01 J mol−1 K−1), suggesting entropy-driven dissolution of PPD in all DMSO + water systems and neat solvents [22]. The average ΔsolH0, ΔsolG0 and ΔsolS0 values for PPD were computed as 18.71 kJ mol−1, 15.99 kJ mol−1 and 8.83 J mol−1 K−1 with relative uncertainties of 0.44, 0.57 and 0.32, respectively. Overall, the dissolution process of PPD was found to be endothermic and entropy-driven in all cosolvent mixtures and neat solvents studied [21,22].
2.4. Enthalpy–Entropy Compensation Analysis for Solvation Property of PPD
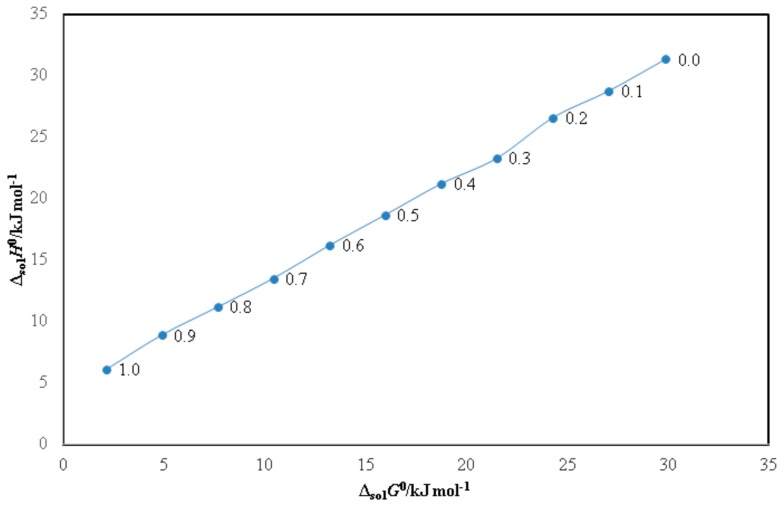
The results of enthalpy–entropy compensation analysis for PPD in binary DMSO + water systems and neat solvents are shown in Figure 3. It was observed that PPD in all binary DMSO + water systems and neat solvents showed linear ΔsolH° vs. ΔsolG° plot with a positive slope value of > 1.0 with R2 value of > 0.99. Based on these results, the driving mechanism for PPD solvation is as an enthalpy-driven in all binary DMSO + water systems and neat solvents. It was possible due to higher solvation of PPD in neat DMSO molecules in comparison with its solvation behavior in neat water molecules [12]. This solvation behavior of PPD in binary DMSO + water systems was in accordance with those reported for solvation properties of various weakly soluble drugs such as 6-methyl-2-thiouracil, sinapic acid, naringin and bergenin in binary DMSO + water mixtures [12,14,15,16].
Figure 3.
ΔsolH0 vs. ΔsolG0 enthalpy–entropy compensation plot for solubility of PPD in binary DMSO + water mixtures at Thm of 308 K.
2.5. Computation Validation
The correlation between experimental and model solubility of PPD was performed using root mean square deviations (RMSD) and correlation coefficient (R2). The results of the van’t Hoff model correlation (Equation (7)) for PPD in binary DMSO + water systems and neat solvents are tabulated in Table 4. The values of RMSD for PPD in binary DMSO + water systems and neat solvents were found as (0.27 to 2.18)%. The overall RMSD for this correlation was obtained as 1.30%. RMSD is deviation between experimental and model/theoretical solubility and it had no correlation with mass fraction of the cosolvent. Its decrease or increase with mass fraction had no significance [12,13]. The average relative uncertainties in model parameters a and b were obtained as 0.33 and 0.44, respectively. In general, the value of model parameter a was found to be increasing slightly with increase in the mass fraction of DMSO in DMSO + water systems. This enhancement was recorded for up to m = 0.9. After m = 0.9, there was little decrease in the value of model parameter a. This change (increase or decrease) in model parameter a was not significant. However, the value of model parameter b was found to be increasing significantly with increase in the mass fraction of DMSO in DMSO + water systems. This enhancement was recorded for up to m = 1.0. The values of R2 for van’t Hoff correlation were computed as 0.9930 to 0.9990. The data of RMSD (lower values) and R2 (higher values) recorded for the van’t Hoff model suggested good correlation of experimental solubility data of PPD with the van’t Hoff model.
Table 4.
The van’t Hoff model parameters (a and b), R2 and RMSD values for PPD in binary DMSO + water mixtures c.
| m | a | b | R2 | RMSD (%) | Overall RMSD (%) |
|---|---|---|---|---|---|
| 0.0 | 0.55 | −3765.70 | 0.9939 | 2.18 | |
| 0.1 | 0.64 | −3454.00 | 0.9930 | 2.17 | |
| 0.2 | 0.87 | −3194.30 | 0.9946 | 1.92 | |
| 0.3 | 0.67 | −2796.20 | 0.9947 | 1.62 | |
| 0.4 | 0.94 | −2549.80 | 0.9953 | 1.42 | |
| 0.5 | 1.04 | −2244.60 | 0.9963 | 1.15 | |
| 0.6 | 1.15 | −1947.30 | 0.9957 | 1.14 | |
| 0.7 | 1.19 | −1623.00 | 0.9944 | 1.20 | |
| 0.8 | 1.36 | −1345.40 | 0.9962 | 1.02 | |
| 0.9 | 1.56 | −1069.60 | 0.9989 | 0.27 | |
| 1.0 | 1.54 | −733.05 | 0.9990 | 0.28 | 1.30 |
c The average relative uncertainties are u(a) = 0.33 and u(b) = 0.44.
The results of the Apelblat model correlation (Equation (8)) for PPD in binary DMSO + water systems are tabulated in Table 5. The values of RMSD for PPD in binary DMSO + water systems and neat solvents were computed as (0.20 to 1.28)%. The overall RMSD for Apelblat correlation was computed as 0.79%. The average relative uncertainties in model parameters A, B, and C were recorded as 0.61, 0.63 and 0.60, respectively. It was observed that the values of model parameter A and C were found to be increasing significantly with increase in the mass fraction of DMSO in DMSO + water systems. This enhancement was recorded for up to m = 1.0. However, the value of model parameter B was found to be decreasing with increase in the mass fraction of DMSO in DMSO + water systems. This enhancement was recorded for up to m = 0.9. The R2 values for this correlation were computed as 0.9984 to 0.9999. The data of RMSD (lower values) and R2 (higher values) recorded for the Apelblat model again suggested good correlation of experimental solubility data of PPD with the Apelblat model.
Table 5.
Apelblat model parameters (A, B, and C), R2 and RMSD for PPD in binary DMSO + water mixtures d.
| m | A | B | C | R2 | RMSD (%) | Overall RMSD (%) |
|---|---|---|---|---|---|---|
| 0.0 | −750.34 | 30686.31 | 111.51 | 0.9996 | 1.17 | |
| 0.1 | −740.88 | 30569.14 | 110.12 | 0.9996 | 1.07 | |
| 0.2 | −587.97 | 23822.39 | 87.45 | 0.9994 | 1.19 | |
| 0.3 | −451.37 | 17943.26 | 67.13 | 0.9984 | 1.28 | |
| 0.4 | −441.66 | 17756.69 | 65.73 | 0.9997 | 0.82 | |
| 0.5 | −331.65 | 13018.47 | 49.41 | 0.9995 | 0.62 | |
| 0.6 | −324.19 | 12979.37 | 48.31 | 0.9997 | 0.67 | |
| 0.7 | −311.35 | 12717.06 | 46.41 | 0.9998 | 0.65 | |
| 0.8 | −214.94 | 8578.56 | 32.12 | 0.9999 | 0.63 | |
| 0.9 | −61.67 | 1829.38 | 9.39 | 0.9995 | 0.20 | |
| 1.0 | −58.21 | 2007.18 | 8.87 | 0.9999 | 0.41 | 0.79 |
d The average relative uncertainties are u(A) = 0.61, u(B) = 0.63 and u(C) = 0.60.
The curve fitting between experimental and Apelblat solubilities of PPD are shown in Figure 4, suggesting good correlation of experimental solubilities of PPD with the Apelblat model.
Figure 4.
Correlation of ln xe values of PPD with the Apelblat model in binary DMSO + water mixtures at T = 298.2 K to 318.2 K (Apelblat solubilities are represented by solid lines and experimental solubilities of PPD are represented by symbols).
The results of the Yalkowsky–Roseman model correlation (Equation (9)) for PPD in binary DMSO + water systems and neat solvents are tabulated in Table 6. The values of RMSD for the Yalkowsky–Roseman model correlation were computed as (0.61 to 2.25)%. The overall RMSD for this correlation was computed as 1.33%. The data of RMSD (lower values) recorded for the Yalkowsky model again suggested good correlation of experimental solubility data of PPD with the Yalkowsky model.
Table 6.
Log xYal values of PPD calculated by Yalkowsky model in binary DMSO + water mixtures at T = 298.2 K to 318.2 K.
| m | Log xYal | RMSD (%) | Overall RMSD (%) | ||||
|---|---|---|---|---|---|---|---|
| 298.15 | 303.15 | 308.15 | 313.15 | 318.15 | |||
| 0.1 | −4.75 | −4.68 | −4.60 | −4.52 | −4.43 | 1.95 | |
| 0.2 | −4.26 | −4.20 | −4.13 | −4.06 | −3.97 | 1.49 | |
| 0.3 | −3.78 | −3.72 | −3.66 | −3.59 | −3.51 | 2.25 | |
| 0.4 | −3.29 | −3.24 | −3.19 | −3.13 | −3.06 | 0.72 | |
| 0.5 | −2.81 | −2.76 | −2.71 | −2.66 | −2.60 | 1.43 | |
| 0.6 | −2.33 | −2.29 | −2.24 | −2.20 | −2.15 | 0.68 | |
| 0.7 | −1.84 | −1.81 | −1.77 | −1.74 | −1.69 | 1.78 | |
| 0.8 | −1.36 | −1.33 | −1.30 | −1.27 | −1.24 | 0.61 | |
| 0.9 | −0.88 | −0.85 | −0.83 | −0.81 | −0.78 | 1.10 | 1.33 |
The results of the Jouyban–Acree (Equation (10)) and the Jouyban–Acree–van’t Hoff model (Equation (11)) correlation for PPD in binary DMSO + water system are listed in Table 7.
Table 7.
The parameters of Jouyban–Acree and Jouyban–Acree–van’t Hoff models for PPD in binary DMSO + water systems.
| System | Jouyban–Acree | Jouyban–Acree–van’t Hoff |
|---|---|---|
|
A1 1.54 B1 −733.05 A2 0.55 B2 −3765.7 Ji 25.32 0.62 |
||
| DMSO + water | Ji 28.19 | |
| RMSD (%) | 0.74 |
The overall RMSD value for the Jouyban–Acree model was computed as 0.74%. However, the overall RMSD value for the Jouyban–Acree–van’t Hoff model was computed as 0.62%. Overall, all five theoretical models performed well as the value of overall RMSD was <2.0% for all models. Nevertheless, the Jouyban–Acree model has been considered to be the best model for this correlation as this model uses the fewest model parameters.
3. Materials and Methods
3.1. Materials
The molecule PPD with mass fraction purity of 0.972 was synthesized, recrystallized, characterized, and identified in the Laboratory of Pharmaceutical Chemistry, Northern Border University, Rafha, Saudi Arabia [17]. DMSO with mass fraction purity of 0.993 was procured from Fluka Chemica (Buchs, Switzerland). Chromatography grades methanol with mass fraction purity of 0.999 and acetic acid with mass fraction purity of 0.997 were procured from Sigma Aldrich (St. Louis, MO, USA). The water was obtained from Milli-Q water purification unit.
3.2. Evaluation of PPD Solubility in Various DMSO + Water Systems
In this work, an isothermal method was applied to achieve solid-liquid equilibrium and solubility determination of PPD in binary solvent system of DMSO + water [23]. The measurements were carried out within the temperature range of T = 298.2 K to 318.2 K at constant air pressure p = 0.1 MPa. The excess amount of PPD was dispersed in glass vial containing 1.0 g of binary solvent system (m = 0.1 to 0.9) or neat solvent (m = 0.0 or 1.0). Each experiment was performed at least for three times. The resultant mixtures were located in the WiseBath® WSB Shaking Water Bath (Model WSB-18/30/-45, Daihan Scientific Co. Ltd., Seoul, Korea) for a definite temperature (uncertainty of 0.12 K) and allowed to equilibrate for 72 h [17,21]. At the end of 72 h i.e., equilibrium time, the samples were taken out from the shaker and allowed to settle PPD particles for 24 h [16,22]. The supernatants from each saturated solution were withdrawn carefully, diluted and analyzed for PPD concentration by reported high performance liquid chromatography (HPLC) technique at the wavelength for maximum absorbance (λmax) of 254 nm [17]. The binary solvent system of methanol and acetic acid (99:1% v/v) was used as mobile phase for HPLC analysis of PPD. The xe values of PPD were obtained using its standard equations reported in the literature [21,22].
3.3. Ideal Solubilities and Activity Coefficients for Solute-Solvent Molecular Interactions
The xidl value of PPD was computed using the following equation [24]:
| (1) |
where T = absolute temperature; Tfus = fusion/melting temperature of PPD; R = universal gas constant; ∆Hfus = molar fusion enthalpy of PPD and ∆Cp = difference in the molar heat capacity of solid form with that of liquid form [24,25]. The values of Tfus, ∆Hfus and ∆Cp for PPD were obtained as 476.43 K, 24.51 kJ mol−1 and 51.44 J mol−1 K−1, respectively from reference [17].
Now using Equation (1), the xidl values for PPD were computed.
The values of γi for PPD in various DMSO + water systems were computed using the following equation [24,26]:
| (2) |
In which xe ≠ 0. Using activity coefficients, the molecular interactions were evaluated.
3.4. Thermodynamic Behavior of PPD
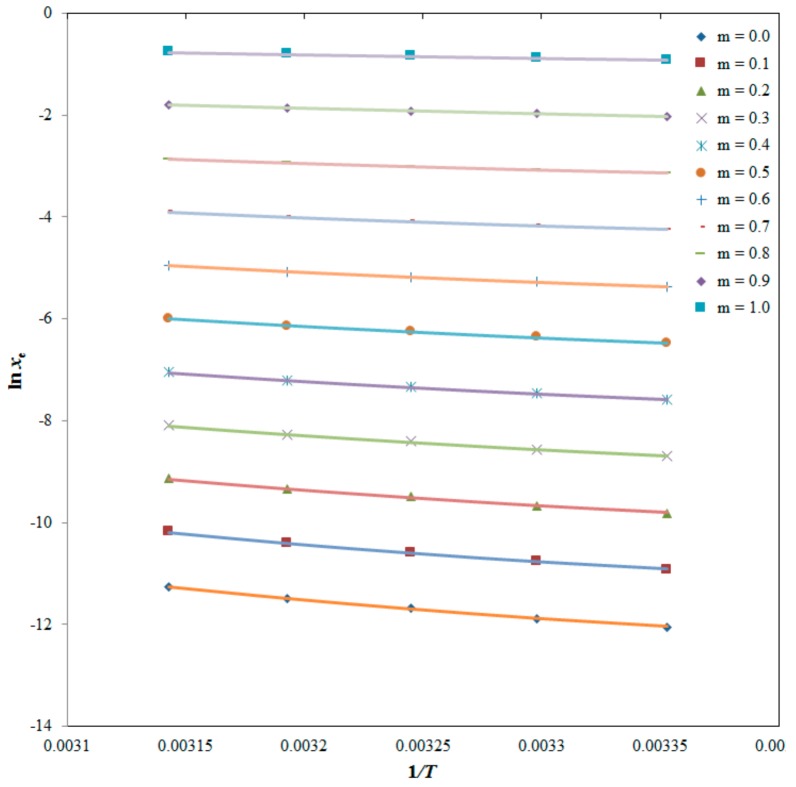
Dissolution thermodynamics of PPD in various solvent mixtures of DMSO + water was studied by estimating apparent thermodynamic analysis based on van’t Hoff and Gibbs equations. The van’t Hoff equation was applied to estimate thermodynamic properties of PPD in investigated binary solvent systems is obtained from the following equation at mean harmonic temperature (Thm) which was computed as 308 K within the temperature range of T = 298.2 to 318.2 K [24,27]:
| (3) |
where xe = mole fraction solubility of PPD in binary solvent system of DMSO + water; T = absolute temperature and R = universal gas constant. Here, T ≠ 0 and Thm ≠ 0. By plotting ln xe versus , the values of ΔsolH0 and ΔsolG0 for dissolution of PPD were calculated from the slope and intercept, respectively by applying the following equations [28]:
| (4) |
| (5) |
The intercept values for PPD in binary DMSO + water systems were obtained from van’t Hoff graphs plotted between ln xe and Finally, the ΔsolS0 values for PPD dissolution in binary DMSO + water systems were computed using Gibbs equation given below [24,27,28]:
| (6) |
3.5. Enthalpy–Entropy Compensation Analysis
The solvation properties of PPD in binary DMSO + water systems were evaluated using an enthalpy–entropy compensation analysis [27,29]. Such analysis was performed by plotting the weighted graphs of ΔsolH° vs. ΔsolG° at Thm value of 308 K [29].
3.6. Computational Validation
The xe values of PPD were fitted using five different computational models including the van’t Hoff, Apelblat, Yalkowsky–Roseman, Jouyban–Acree and Jouyban–Acree–van’t Hoff models [29,30,31,32,33].
The van’t Hoff model solubility (xvan’t) of PPD in binary DMSO + water mixtures and neat solvents was computed using the following equation [29]:
| (7) |
where a and b = model parameters of Equation (7) which were estimated by constructing plots between ln xe values of PPD and of 1/T.
The Apelblat model solubility (xApl) of PPD in binary DMSO + water systems and neat solvents was computed using the following equation [30,31]:
| (8) |
where A, B, and C = model parameters Equation (8) which were estimated by nonlinear multivariate regression analysis of xe values of PPD tabulated in Table 1 [29].
The logarithmic solubility of the Yalkowsky model (log xYal) for PPD in binary DMSO + water systems and neat solvents was computed using the following equation [32]:
| (9) |
where x1 = mole fraction solubility of PPD in neat DMSO; x2 = mole fraction solubility of PPD in neat water; m1 = mass fraction of neat DMSO and m2 = mass fraction of neat water in the absence of solute.
The Jouyban–Acree model solubility (xm,T) of PPD in binary DMSO + water systems was computed by applying the following Equation [33]:
| (10) |
where Ji = model parameter of Equation (10) and it was estimated from no-intercept regression analysis [34].
The Jouyban–Acree–van’t Hoff solubility of PPD in binary DMSO + water systems was computed using the following equation [35]:
| (11) |
where A1, B1, A2, B2 and Ji = model parameters of Equation (11).
4. Conclusions
The solubility, solution thermodynamics and solvation behavior of PPD in binary DMSO + water systems were studied at T = 298.2 K to 318.2 K and p = 0.1 MPa using experimental and various computational approaches. The solubilities of PPD were found to be increasing with raise in temperature and increase in the mass fraction of DMSO in binary DMSO + water systems in all cases. The highest and lowest solubilities of PPD were found in neat DMSO and neat water, respectively. The experimental solubilities of PPD were correlated well by van’t Hoff, Apelblat, Yalkowsky–Roseman, Jouyban–Acree and Jouyban–Acree–van’t Hoff models with overall RMSD of <2.0% in all DMSO + water systems. The results of activity coefficients showed maximum molecular interaction in PPD-DMSO. The dissolution of PPD was observed as endothermic and entropy-driven in all binary DMSO + water systems and neat solvents. Enthalpy–entropy compensation analysis indicated enthalpy-driven mechanism as the driven mechanism for solvation property of PPD.
Acknowledgments
The authors would like to extend their sincere appreciation to the Deanship of Scientific Research at King Saud University for funding this work through the research group project number RGP-1438-013.
Nomenclature
| T | Absolute temperature (K) |
| P | Air pressure (MPa) |
| M | Mass fraction of DMSO in DMSO + water mixtures |
| m 1 | Mass fraction of neat DMSO |
| m 2 | Mass fraction of neat water |
| x e | Experimental mole fraction solubility of PPD |
| x idl | Ideal solubility of PPD in mole fraction |
| x van’t | van’t Hoff model solubility of PPD in mole fraction |
| x Apl | Apelblat model solubility of PPD in mole fraction |
| x Yal | Yalkowsky model solubility of PPD in mole fraction |
| x m,T | Jouyban–Acree model solubility of PPD in mole fraction |
| x 1 | Mole fraction solubility of PPD in neat DMSO |
| x 2 | Mole fraction solubility of PPD in neat water |
| γ i | Activity coefficient of PPD |
| R 2 | Correlation coefficient |
| RMSD | Root mean square deviations (%) |
| a and b | Parameters of van’t Hoff model |
| A, B, and C | Parameters of Apelblat model |
| J i | Parameter of Jouyban–Acree model |
| A1, B1, A2, and B2 | Parameter of Jouyban–Acree–van’t Hoff model |
| ΔsolH0 | Apparent standard dissolution enthalpy (kJ mol−1) |
| ΔsolG0 | Apparent standard Gibbs free energy (kJ mol−1) |
| ΔsolS0 | Apparent standard dissolution entropy (J mol−1 K−1) |
| T hm | Mean harmonic temperature (K) |
| T fus | Fusion temperature (K) |
| λ max | Wavelength for maximum absorbance (nm) |
| R | Universal gas constant (J mol−1 K−1) |
| ΔHfus | Molar fusion enthalpy (kJ mol−1) |
| ΔCp | Difference in molar heat capacity (J mol−1 K−1) |
Author Contributions
Conceptualization, supervision—F.S.; Methodology—M.I., N.H., A.A. and S.A.; Validation—M.K.A. and S.A.; Writing original draft—F.S. and S.A.; Writing-review and editing—N.H., A.A. and M.K.A.; Software—F.S. and S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deanship of Scientific Research at King Saud University via grant number RGP-1438-013 and article processing charge (APC) was also the supported by the Deanship of Scientific Research.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Sample Availability: Samples of the compounds are available from the authors.
References
- 1.Bansal R., Thota S. Pyridazin-3(2H)-ones: The versatile pharmacophore of medicinal significance. Med. Chem. Res. 2013;22:2539–2552. doi: 10.1007/s00044-012-0261-1. [DOI] [Google Scholar]
- 2.Sircar I. Substituted 6-Phenyl-3(2H)-Pyridazinones Useful as Cardiotonic Agents. 4,404,203. U.S. Patent. 1983 Aug 9;
- 3.Wu J., Kang S., Yuan Q., Luo L., Ma J., Shi Q., Yang S. N-Substituted 5-chloro-6-phenylpyridazin-3(2H)-ones: Synthesis, insecticidal activity against Plutella xylostella (L.) and SAR study. Molecules. 2012;17:9413–9420. doi: 10.3390/molecules17089413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang T., Dong Y., Wang L., Xiang B., Chen Z., Qu L. Design, synthesis and structure-activity relationship studies of 6-phenyl-4,5-dihydro-3(2H)-pyridazinone derivatives as cardiotonic agents. Arzneimittelforschung. 2008;58:569–573. doi: 10.1055/s-0031-1296558. [DOI] [PubMed] [Google Scholar]
- 5.Siddiqui A.A., Mishra R., Shaharyar M. Synthesis, characterization and antihypertensive activity of pyridazinone derivatives. Eur. J. Med. Chem. 2010;45:2283–2290. doi: 10.1016/j.ejmech.2010.02.003. [DOI] [PubMed] [Google Scholar]
- 6.Malinka W., Redzicka A., Jastrzebska-Wiesek M., Filipek B., Dybała M., Karczmarzyk Z., Urbanczyk-Lipkowska Z., Kalicki P. Derivatives of pyrrolo[3,4-d]pyridazinone, a new class of analgesic agents. Eur. J. Med. Chem. 2011;46:4992–4999. doi: 10.1016/j.ejmech.2011.08.006. [DOI] [PubMed] [Google Scholar]
- 7.Sukuroglu M., Ergun B.C., Unlu M., Sahin M.F., Kupeli E., Yesilada E., Banoglu E. Synthesis, analgesic, and anti-inflammatory activities of [6-(3,5-dimethyl-4-chloropyrazole-1-yl)-3(2H)-pyridazinon-2-yl]acetamides. Arch. Pharm. Res. 2005;5:509–517. doi: 10.1007/BF02977751. [DOI] [PubMed] [Google Scholar]
- 8.Singh J., Saini V., Kumar A., Bansal R. Synthesis, molecular docking and biological evaluation of some newer 2-substituted-4-(benzo[d][1,3]dioxol-5-yl)-6-phenylpyridazin-3(2H)-ones as potential anti-inflammatory and analgesic agents. Bioorg. Chem. 2017;71:201–210. doi: 10.1016/j.bioorg.2017.02.006. [DOI] [PubMed] [Google Scholar]
- 9.Yamada T., Nobuhara Y., Yamaguchi A., Ohki M. Pyridazinones. 1. Synthesis and antisecretory and antiulcer activities of thioamide derivatives. J. Med. Chem. 1982;25:975–982. doi: 10.1021/jm00350a018. [DOI] [PubMed] [Google Scholar]
- 10.Sonmej M., Berber L., Akbas B. Synthesis, antibacterial and antifungal activity of some new pyridazinone metal complexes. Eur. J. Med. Chem. 2005;41:101–105. doi: 10.1016/j.ejmech.2005.10.003. [DOI] [PubMed] [Google Scholar]
- 11.Imran M., Nayeem N. Synthesis and antihypertensive activity of some novel pyridazinones. Orien. J. Chem. 2016;32:267–274. doi: 10.13005/ojc/320129. [DOI] [Google Scholar]
- 12.Shakeel F., Haq N., Salem-Bekhit M.M., Raish M. Solubility and dissolution thermodynamic analysis of sinapic acid in (DMSO + water) binary solvent mixtures at different temperatures. J. Mol. Liq. 2017;225:833–839. doi: 10.1016/j.molliq.2016.11.009. [DOI] [Google Scholar]
- 13.Shakeel F., Haq N., Salem-Bekhit M.M. Thermodynamics of solubility of isatin in Carbitol + water mixed solvent systems at different temperatures. J. Mol. Liq. 2015;207:274–278. doi: 10.1016/j.molliq.2015.03.038. [DOI] [Google Scholar]
- 14.Zhu Y., Chen G., Cong Y., Xu A., Frajtabar A., Zhao H. Equilibrium solubility, dissolution thermodynamics and preferential solvation of 6-methyl-2-thiouracil in aqueous co-solvent mixtures of methanol, N-methyl-2-pyrrolidone, N,N-dimethyl formamide and dimethylsulfoxide. J. Chem. Thermodyn. 2018;121:55–64. doi: 10.1016/j.jct.2018.02.002. [DOI] [Google Scholar]
- 15.Jabbari M., Khosravi N., Feizabadi M., Ajloo D. Solubility temperature and solvent dependence and preferential solvation of citrus flavonoid naringin in aqueous DMSO mixtures: An experimental and molecular dynamics simulation study. RSC Adv. 2017;7:14776–14789. doi: 10.1039/C7RA00038C. [DOI] [Google Scholar]
- 16.Shakeel F., Mothana R.A., Haq N., Siddiqui N.A., Al-Oqail M.M., Al-Rehaily A.J. Solubility and thermodynamic function of bergenin in different (DMSO + water) mixtures at different temperatures. J. Mol. Liq. 2016;220:823–828. doi: 10.1016/j.molliq.2016.05.015. [DOI] [Google Scholar]
- 17.Shakeel F., Imran M., Haq N., Alshehri S., Anwer M.K. Synthesis, characterization and solubility determination of 6-Phenyl-pyridazin-3(2H)-one in different pharmaceutical solvents. Molecules. 2019;24:3404. doi: 10.3390/molecules24183404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Panigrahi M., Grabda M., Kozak D., Dorai A., Shibata E., Kawamura J., Nakamura T. Liquid–liquid extraction of neodymium ions from aqueous solutions of NdCl3 by phosphonium-based ionic liquids. Sep. Pur. Technol. 2016;171:263–269. doi: 10.1016/j.seppur.2016.07.044. [DOI] [Google Scholar]
- 19.Dorai A., Panigrahi M., Kozak D., Grabda M., Shibata E., Nakamura T., Kawamura J. Effect of paramagnetic metal ions on 1H diffusion in tryhexyltetradecylphosphonium benzoate ionic liquid. ECS Transac. 2016;75:567–573. doi: 10.1149/07515.0567ecst. [DOI] [Google Scholar]
- 20.Grabda M., Panigrahi M., Oleszek S., Kozak D., Eckerte F., Shibata E., Nakamura T. COSMO-RS screening for efficient ionic liquid extraction solvents for NdCl3 and DyCl3. Fluid Phase Equilib. 2014;383:134–143. doi: 10.1016/j.fluid.2014.10.018. [DOI] [Google Scholar]
- 21.Shakeel F., Imran M., Abida Haq N., Alanazi F.K., Alsarra I.A. Solubility and thermodynamic/solvation behavior of 6-phenyl-4,5-dihydropyridazin-3(2H)-one in different (Transcutol + water) mixtures. J. Mol. Liq. 2017;230:511–517. doi: 10.1016/j.molliq.2017.01.077. [DOI] [Google Scholar]
- 22.Imran M., Haq N., Abida Alanazi F.K., Alsarra I.A. Solubility and thermodynamics of 6-phenyl-4,5-dihydropyridazin-3(2H)-one in various neat solvents at different temperatures. J. Mol. Liq. 2017;238:455–461. doi: 10.1016/j.molliq.2017.05.032. [DOI] [Google Scholar]
- 23.Higuchi T., Connors K.A. Phase-solubility techniques. Adv. Anal. Chem. Inst. 1965;4:117–122. [Google Scholar]
- 24.Ruidiaz M.A., Delgado D.R., Martínez F., Marcus Y. Solubility and preferential solvation of indomethacin in 1,4-dioxane + water solvent mixtures. Fluid Phase Equilib. 2010;299:259–265. doi: 10.1016/j.fluid.2010.09.027. [DOI] [Google Scholar]
- 25.Hildebrand J.H., Prausnitz J.M., Scott R.L. Regular and Related Solutions. Van Nostrand Reinhold; New York, NY, USA: 1970. [Google Scholar]
- 26.Manrique Y.J., Pacheco D.P., Martínez F. Thermodynamics of mixing and solvation of ibuprofen and naproxen in propylene glycol + water cosolvent mixtures. J. Sol. Chem. 2008;37:165–181. doi: 10.1007/s10953-007-9228-0. [DOI] [Google Scholar]
- 27.Holguín A.R., Rodríguez G.A., Cristancho D.M., Delgado D.R., Martínez F. Solution thermodynamics of indomethacin in propylene glycol + water mixtures. Fluid Phase Equilib. 2012;314:134–139. doi: 10.1016/j.fluid.2011.11.001. [DOI] [Google Scholar]
- 28.Krug R.R., Hunter W.G., Grieger R.A. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistic effect. J. Phys. Chem. 1976;80:2341–2351. doi: 10.1021/j100562a007. [DOI] [Google Scholar]
- 29.Shakeel F., Haq N., Siddiqui N.A., Alanazi F.K., Alsarra I.A. Solubility and thermodynamics of vanillin in Carbitol-water mixtures at different temperatures. LWT Food Sci. Technol. 2015;64:1278–1282. doi: 10.1016/j.lwt.2015.07.043. [DOI] [PubMed] [Google Scholar]
- 30.Apelblat A., Manzurola E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic and p-toluic acid and magnesium-DL-aspartate in water from T = (278–348) K. J. Chem. Thermodyn. 1999;31:85–91. doi: 10.1006/jcht.1998.0424. [DOI] [Google Scholar]
- 31.Manzurola E., Apelblat A. Solubilities of L-glutamic acid, 3-nitrobenzoic acid, acetylsalicylic, p-toluic acid, calcium-L-lactate, calcium gluconate, magnesium-DL-aspartate, and magnesium-L-lactate in water. J. Chem. Thermodyn. 2002;34:1127–1136. doi: 10.1006/jcht.2002.0975. [DOI] [Google Scholar]
- 32.Yalkowsky S.H., Roseman T.J. Solubilization of drugs by cosolvents. In: Yalkowsky S.H., editor. Techniques of Solubilization of Drugs. Marcel Dekker Inc.; New York, NY, USA: 1981. pp. 91–134. [Google Scholar]
- 33.Jouyban A. Review of the cosolvency models for predicting solubility of drugs in water-cosolvent mixtures. J. Pharm. Pharm. Sci. 2008;11:32–58. doi: 10.18433/J3PP4K. [DOI] [PubMed] [Google Scholar]
- 34.Nozohouri S., Shayanfar A., Cardenas Z.J., Martinez F., Jouyban A. Solubility of celecoxib in N-methyl-2-pyrrolidone + water mixtures at various temperatures: Experimental data and thermodynamic analysis. Korean J. Chem. Eng. 2017;34:1435–1443. doi: 10.1007/s11814-017-0028-y. [DOI] [Google Scholar]
- 35.Shakeel F., Bhat M.A., Haq N., Fatih-Azarbayjani A., Jouyban A. Solubility and thermodynamic parameters of a novel anti-cancer drug (DHP-5) in polyethylene glycol 400 + water mixtures. J. Mol. Liq. 2017;229:241–245. doi: 10.1016/j.molliq.2016.12.067. [DOI] [Google Scholar]