A powerful fine-mapping method for transcriptome-wide association studies

Abstract

Transcriptome-wide association studies (TWAS) have been recently applied to successfully identify many novel genes associated with complex traits. While appealing, TWAS tend to identify multiple significant genes per locus and many of them may not be causal due to confounding through linkage disequilibrium (LD) among SNPs. Here we introduce a powerful fine-mapping method that prioritizes putative causal genes by accounting for local LD. We apply a weighted adaptive test with eQTL-derived weights to maintain high power across various scenarios. Through simulations, we show that our new approach yielded a well-controlled Type I error rate while achieving higher power and AUC than competing methods. We applied our approach to a schizophrenia GWAS summary dataset and successfully prioritized some well-known schizophrenia-related genes, such as C4A. Importantly, our approach identified some putative causal genes (e.g., B3GAT1 and RGS6) that were missed by competing methods and TWAS. Our results suggest that our approach is a useful tool to prioritize putative causal genes, gaining insights into the mechanisms of complex traits.

Introduction

Transcriptome-wide association studies (TWAS) [2, 3, 14, 16, 44, 46] have garnered substantial interest and become increasingly popular within the human genetics community. TWAS integrate one or more external eQTL reference panels (including both genome-wide gene expression and genotype data) with a main GWAS to discover gene-trait associations. Although TWAS [2, 14, 16, 44] have been promising in uncovering many novel genes as possible mediators between a trait and genetic variants, it should be emphasized that the significant genes identified by TWAS are not necessarily causal [24, 39, 41]. As demonstrated by others [24, 39] and here, TWAS frequently identify multiple significant genes per locus (Figure 1b), many of which may not be causal due to confounding through linkage disequilibrium (LD) among SNPs. These phenomena are similar to single variant analysis in GWAS: the association between a gene (or a SNP) and a trait can be indirect, resulting from its expression correlations (or LD) with a nearby and truly causal gene (or SNP) [32]. It can be challenging to determine the underlying causal genes, and this is when fine-mapping helps. Fine-mapping seeks to determine genetic variants (or genes) causal for complex traits, given evidence of an association in a genomic region [32, 35]. Even though many fine-mapping methods have been proposed to deal with a single-variant association, few methods have been proposed to prioritize causal genes, especially for TWAS results.

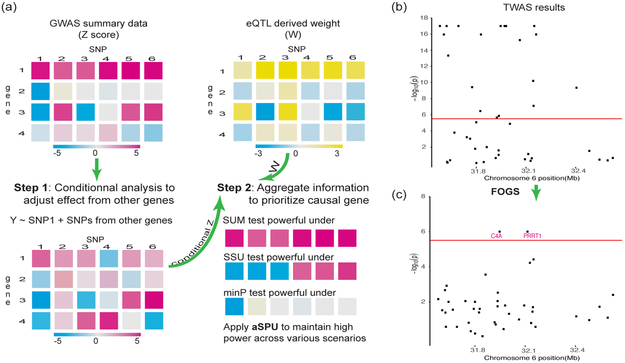
Figure 1: Overview of the fine-mapping method: FOGS.

a. FOGS prioritizes causal genes by two steps: first, FOGS conducts a conditional analysis with ridge regression to account the effects of other SNPs/genes in the locus; second, FOGS integrates eQTL-derived weights and conditional Z scores by an adaptive test to maintain high power. b and c, TWAS and FOGS were performed on summary statistics from a schizophrenia GWAS of 105,318 European individuals [27]. b, TWAS results for a locus on chromosome 6 (31.6–32.7 Mb). c, FOGS results for the same locus on chromosome 6 (31.6–32.7 Mb). 19 out of 42 genes in the locus has been identified to be significant by TWAS, prompting for fine-mapping. FOGS prioritized putative causal genes by successfully identifying the well-known schizophrenia-related gene C4A [33].

Here, we propose a method called FOGS (Fine-mapping Of Gene Sets) to perform statistical fine-mapping over gene sets in a locus by testing whether the conditional effects of SNPs in each gene is null (Figure 1a). The conditional effect is estimated from a joint regression model including all the SNPs in a locus. First, we estimate the conditional effects for the SNPs via ridge regression. Since high LD (or correlations) among the SNPs can make standard regression estimation unstable, we add a small ridge penalty to regularize the estimation. Next, we apply an adaptive test, called aSPU [26], to combine the conditional effects and eQTL-derived weights effectively. The idea is that since we do not know how many SNPs are causal, we construct a class of sum of powered score (SPU) tests such that hopefully at least one of them would be powerful for a given situation. Then aSPU selects the most significant testing result data-adaptively with a proper adjustment for multiple testing.

By extensive simulations, we show that FOGS adequately controls Type I error rates under various null scenarios, and outperforms other competing methods. Specifically, compared to FOCUS (a Bayesian fine-mapping method [24]) and p-value ranking of TWAS results, FOGS achieves a higher AUC, identifies more causal genes at the same false positive rate, and yields a smaller number of false positives at the same true positive rate. Finally, we applied FOGS to a large schizophrenia GWAS summary dataset of 105,318 European individuals [27]. We found that FOGS prioritizes some causal genes with established roles in schizophrenia (e.g., C4A [33]). In addition, FOGS identifies some putative causal genes with literature support, which however would be missed by FOCUS and TWAS (e.g., B3GAT1 [15, 43] and RGS6 [9, 15, 22, 31]). Overall, our results showcase the power of FOGS to prioritize putative causal genes and to better understand the genetic basis of complex diseases.

Results

Overview of FOGS method

To prioritize causal genes at a TWAS significant region, we test on the conditional effect of each SNP in a gene after adjusting for other genes in the same locus (Figure 1a). Specifically, we model the phenotype y as

$$\mathbf{y}=\mathbf{V}\alpha +\mathbf{X}\beta +ϵ,$$

where X and V are genotype matrices for gene A (of interest) and other genes in the same region, respectively (see Methods). We are interested in testing if gene A is putatively causal with a null hypothesis H₀ : β = 0. Although we refer to genes with non-zero effects (β ≠ 0) as putatively causal, it is important to realize that statistical fine-mapping alone is unable to completely determine causality.

First, we construct the conditional Z score for X via a newly proposed summary statistics-based ridge regression (see Methods). Here, we apply ridge regression with a small penalty to avoid collinearity induced by high LD among SNPs. To account for genes without eQTL-derived weights in the relevant tissue, we include eQTL-derived weights from proxy tissues for such genes. This approximation is supported by the fact that eQTLs are largely shared across tissues [10] as also adopted in FOCUS [24]. Next, different tests will be powerful under different scenarios. For example, the SUM test will be most powerful when the conditional effect sizes of all the SNPs are the same and in the same directions. Since we do not know how many SNPs are causal and the true pattern of their effect sizes and directions, we apply an adaptive test, called weighted aSPU [26], to combine the conditional effects and eQTL-derived weights efficiently. Specifically, we first construct a class of sum of powered score (SPU) tests such that hopefully at least one of them would be powerful for a given situation. Then aSPU selects the most significant testing result data-adaptively with a proper adjustment for multiple testing. In the end, we use one layer of Monte Carlo simulations to estimate the p-values for both SPU and aSPU tests simultaneously and efficiently [26].

FOGS prioritizes and improves resolution for fine-mapping causal genes

We simulated GWAS summary data from the real genotype data drawn from the Lung Health Study (dbGAP: phs000335.v2.p2), and used the corresponding gene definitions. To mimic real GWAS summary data, we generated the phenotype and then ran a simple regression for each SNP to obtain its estimated effect size and variance. To obtain robust and unbiased results, we varied the number of causal SNPs, causal effect sizes, and relationship between causal SNPs and eQTL-derived weights (See Methods).

First, we confirmed that some non-causal genes were highly significant and yielded inflated Type I error rates under various scenarios, and fine-mapping was needed to prioritize causal genes (Supplementary Figure S1). This phenomenon was previously reported by others [24, 39].

Next, we simulated GWAS summary data with two causal SNPs in one causal gene (see Methods) and assessed the performance of FOGS. For comparison, we considered a Bayesian fine-mapping method (FOCUS, as described in Mancuso et al. [24]) and the p-value ranking of TWAS results (denoted as TWAS ranking for simplicity, see Methods). Figure 2 shows the performance of different methods under different criteria. First, an AUC measures the whole area under a ROC curve and has been widely used for performance comparison, while the partial AUC (pAUC) is most useful when only certain regions of the ROC (e.g., high specificity) are of particular interest [12]. We calculated pAUC with specificity in the ranges of (0.95, 1) and of (0.9, 1), denoted pAUC1 and pAUC2 respectively. We further applied the Delong test [11] to compare AUCs, and the bootstrap with 10⁴ bootstrap replications to compare pAUCs. Compared to TWAS and FOCUS FOGS achieved a significantly higher AUC (85.8%), pAUC1 (60.4%) and pAUC2 (65.9%) (Supplementary Table S1).

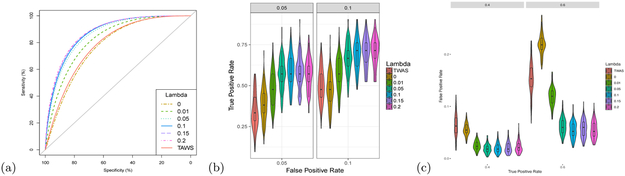
Figure 2: Performance assessment of different methods with simulated data.

We randomly selected two SNPs in one gene to be causal, and the effect size was c = 0.1. The estimated hertibability was about 2.5%. a, AUC comparison between different methods. b, True positive rate (Power) comparison under some specified false positive rates. c, False positive rate comparison under some specified true positive rates. The violin plot and box plot inside display the false/true positive rates of different methods under specified true/false positive rates.

Second, both FOGS and FOCUS significantly reduced the number of false positives (FOGS: 0.33; FOCUS: 0.27; TWAS: 1.97) per locus compared to TWAS, and yielded lower numbers of true positives (FOGS: 0.39; FOCUS: 0.36; TWAS: 0.53), making it hard to compare different methods directly (Supplementary Table S1). To facilitate a fair comparison, we compared different methods under either the same false positive rates or the same true positive rate (Figures 2b and 2c). For example, at a false positive rate of 10%, the true positive rate of FOGS, FOCUS and TWAS were 69.8%, 51.5%, and 61.2%, respectively. Under various true positive rates, FOGS significantly reduced the number of false positives compared to both FOCUS and TWAS. For example, at a true positive rate of 60%, the false positive rates of FOGS, FOCUS and TWAS were 5.1%, 9.3%, and 15.1% respectively.

We considered several additional settings, including varying the number of causal SNPs (Supplementary Figures S2-S3), and the relationship between causal SNPs and eQTL constructed weights (Supplementary Figure S4). Importantly, we further considered some settings where all eSNPs in the causal gene were causal SNPs (Supplementary Figures S5-S6). Across all the above simulation settings, FOGS had consistent advantages over TWAS and FOCUS, yielding higher AUC and partial AUC, higher true positive rates and lower false positive rates under a given false/true positive rate. Interestingly, under the challenging settings such as when one casual SNP regulated at least two genes in the locus, FOGS performed either similalry to or slightly better than FOCUS (Supplementary Figure S7). Overall, FOGS performed well in prioritizing causal genes across all the settings considered; more studies are needed for other challenging settings.

FOGS is robust to the choice of penalty parameter λ

Figure 3 compares the performance of FOGS with various values of the ridge penalty parameter λ (see Methods) on the simulated data (two causal SNPs in one causal gene per locus). λ = 0 stands for the standard conditional model without penalization, which yielded similar or even slightly worse performance when compared to TWAS, and much worse performance compared to FOGS with a small penalty (λ = 0.1). For example, under a false positive rate of 5%, the power of FOGS with λ = 0 was 38.7%, much lower than the power of FOGS with λ = 0.1 (58.3%). At the true positive rate of 40%, FOGS with λ = 0 identified 179.1% more false positive genes than FOGS with λ = 0.1. These results confirmed the importance of adding a small ridge penalty to stabilize the estimation in the presence of collinearity induced by LD among SNPs.

Figure 3: Sensitive analysis of ridge penalty parameter λ of FOGS with simulated data.

We randomly selected two SNPs in one gene to be causal and the effect size was c = 0.1. a, AUC comparison between different methods. b, True positive rate (Power) comparison under some specified false positive rates. c, False positive rate comparison under some specified true positive rates. The violin plot and box plot inside display the false/true positive rates of different methods under specified true/false positive rates.

Importantly, FOGS was robust to the choice of λ as long as a reasonable λ value was used. The AUCs of FOGS with λ = 0.1, λ = 0.15, and λ = 0.2 were 85.2%, 85.6%, and 85.8%, respectively (Figure 3b). Under false positive rate at 5%, the power of FOGS with λ = 0.1, λ = 0.15, and λ = 0.2 were 58.3%, 57.1%, and 57.4%, respectively (Figure 3b). FOGS with λ = 0.1, λ = 0.15, and λ = 0.2 had similar false positive rates at various true positive rates (Figure 2c). Furthermore, we compared the results of FOGS with different λ values under different sample sizes of the reference panel (Supplementary Figures S8-S9). We showed that FOGS was robust to the choice of λ with different reference panels, though FOGS with a slightly larger λ (i.e., λ = 0.2) performed slightly better than that with the default setting λ = 0.1 when the sample size was small. In summary, we recommend using the default λ = 0.1 for FOGS in real data applications, partly because it has been widely used by others [16, 28].

Robustness analysis of FOGS

First, under the null (no SNP-trait association for all SNPs in the locus), the type I error rates of FOGS were satisfactorily controlled (Figure 4a) under different α levels. Perhaps due to the small bias induced by the ridge penalty, FOGS yielded a slightly conservative Type I error rate, even though the 95% confidence interval covered the truth most time under various nominal levels α.

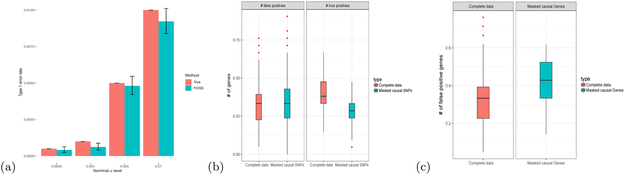
Figure 4: FOGS performance under situations with causal SNPs missing.

We considered the following three cases: a, no SNP-trait association for all SNPs in the locus; b, the two causal SNPs were missing; c, the causal gene (with all its SNPs) was missing (see main text for details). a, Histogram of Type I error rates under different α levels. Vertical line segments mark 95% confidence intervals for the estimated Type I error rates. b, Numbers of false positives and true positives per locus for FOGS with either complete data or data with causal SNPs missing. c, Number of false positives per locus for FOGS with either complete data or data with the causal gene missing.

Next, we simulated data as in the previous sections, randomly selecting two SNPs in one gene to be causal with effect size c = 0.1. We pruned out the causal SNPs to evaluate the robustness of FOGS. Note that FOGS estimated a conditional effect for each SNP by conditioning on all the SNPs from any of other genes in the locus to prioritize putative causal genes accordingly. Since some SNPs might be highly correlated with causal SNPs, the effect from causal SNPs can be indirectly adjusted. This property of FOGS explained why applying FOGS to the masked causal SNP data yielded a similar number of false positives as that of applying FOGS to the complete data (0.34 vs. 0.33; Figure 4b). FOCUS yielded similar numbers of false positives for both masked causal SNP data and complete data (0.27 vs. 0.26; Supplementary Figure S10). As expected, because the causal SNPs was pruned out before the analysis, the number of true positives for masked causal SNP data was smaller than that with complete data (0.28 vs. 0.39; Figure 4b). Interestingly, FOCUS was robust, though yielding a smaller number of true positives when analyzing masked causal SNP data (0.29 vs. 0.36 (for complete data); Supplementary Figure S10).

We further considered the situation where all the SNPs in the causal gene were pruned out before analysis. Since the whole causal gene had been removed, fewer SNPs remained highly associated with the causal SNPs and the effects of the causal SNPs might not be fully captured, leading to a much higher number of false positives. It is observed that applying FOGS to the masked causal gene data increased the false positives per locus from 0.33 to 0.41 (by 124%, Figure 4c). In comparison, FOCUS increased the false positives per locus from 0.27 to 0.46 (by 170%, Supplementary Figure S10). Importantly, a simple ranking of the TWAS results yielded much higher false positives per locus (Supplementary Figure S11).

In summary, we found that FOGS incurred some performance loss in the challenging settings when some causal SNPs were missing in the data. Importantly, the competing methods such as FOCUS suffered similarly, and we leave this interesting topic for future study.

Application to a schizophrenia GWAS summary dataset

Schizophrenia is a psychiatric disorder affecting about 0.7% of adults worldwide [25]. Although more than 100 risk loci have been identified [27, 31], schizophrenia, is truly complex; many risk regions contained more than one significantly associated gene, and it is hard to determine which gene is causal. This is when fine-mapping helps. Having validated our new fine-mapping method FOGS in simulations, we re-analyzed a large schizophrenia GWAS summary dataset [27] to provide insights into the genetic architecture of schizophrenia. As others [24], we defined the loci as in LDetect [6]. We conducted genome-wide analysis and then focused on the 57 loci containing at least one genome-wide significant SNP and at least one TWAS significant gene (see Methods). Specifically, we applied TWAS first and then applied fine-mapping methods to prioritize putative causal genes. For TWAS and later fine-mapping, we used the CMC eQTL weights when available; otherwise, we included the eQTL weights with the best accuracy across all other tissues, leading to 15,460 genes with eQTL weights (see Methods).

First, TWAS identified 203 significant genes at 71 independent loci after stringent Bonferroni correction (0.05/16,000 ≈ 3.1 × 10⁻⁶; Figure 5a and Supplementary Table S2). Of these, 23 gene-schizophrenia associations did not overlap a genome-wide significant SNP, residing in 14 independent loci. However, many identified TWAS significant genes were located in the same locus (Supplementary Figure S12). 29 out of 71 loci contained more than one gene, and 11 loci contained more than five significant genes. For example, for one locus on chromosome 6 (31.6–32.7 Mb), it contained 42 genes, 19 of which have been identified as significant by TWAS (1b). Importantly, seven genes were highly significant (p-value < 1 × 10⁻¹⁷), and simply ranking the TWAS results was unlikely to work for this locus; more sophisticated fine-mapping methods were needed.

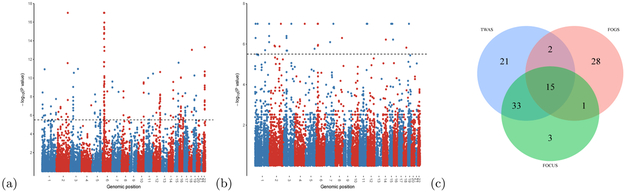
Figure 5: Applications to a GWAS schizophrenia summary data [27].

a, Manhattan plot of all TWAS associations. b, Manhattan plot of FOGS results (see Methods). For a and b, each point represents a single gene tested, with physical position (P0) plotted on the x axis and −log(p) values plotted on the y axis. Dashed lines indicate genome-wide significant threshold (0.05/16,000 ≈ 3.1 × 10⁻⁶). c, Venn diagram of the putative causal genes prioritized by different methods for the risk regions that contained at least two genes. TWAS stands for the results of selecting the most significant gene in each region plus the genes with p-value < 1e − 17 (unable to distinguish) as putative causal genes. FOGS and FOCUS represent the results of FOGS with a stringent cutoff (0.05/16,000 ≈ 3.1 × 10⁻⁶) and FOCUS with 90% credible gene-sets, respectively (see Methods).

We applied both FOGS and FOCUS to all the loci with more than two genes. For FOGS, we used the same Bonferroni cutoff (0.05/16,000 ≈ 3.1 × 10⁻⁶) as used in TWAS. For FOCUS, we used the default 90%-credible gene-sets to prioritize causal genes (see Methods). First, FOGS is quite computationally efficient: it took about 4.1 seconds on average to compute the p-value for a gene by using one core in a Minnesota Supercomputing Institute (MSI) server, and for the most time-consuming gene, it took about 12.0 minutes. Second, Figure 5c compares the different methods for prioritizing putative causal genes. Since in some loci TWAS identified more than two genes with highly significant results (unable to distinguish which one was more significant), we selected the most significant gene in each locus plus 19 genes with p-value < 1 × 10⁻¹⁷ as the results of the p-value ranking of TWAS statistics, denoted as TWAS ranking. FOCUS identified 52 putative causal genes (Supplementary Table S3), 48 (92.3%) of which have been identified by TWAS ranking. In other words, for the GWAS schizophrenia summary data analyzed here, there was not much difference between TWAS ranking and FOCUS. In contrast, FOGS identified 46 putative causal genes (Figure 5b, Supplementary Table S4), 29 (63.0%) of which would be missed by the TWAS ranking. Compared to FOCUS, FOGS narrowed down the candidates of causal genes to a shorter list, which was very different from the results of TWAS ranking.

Since the majority of the significant genes (180 out of 203; 89%) were located in the 57 GWAS risk loci that contained at least one genome-wide significant SNPs, we discussed these loci in detail. Table 1 shows the putative causal genes identified by FOGS in these 57 loci. Interestingly, FOGS identified some putative causal genes (e.g., RGS6, p-value < 1.0 × 10⁻⁷) that were missed by both TWAS and FOCUS. Several GWAS have indicated that some genome-wide schizophrenia significantly associated SNPs in RGS6 (rs35607894, p-value = 5 × 10⁻¹¹ [22]; rs2332700, p-value = 1 × 10⁻⁹ [15]; p-value = 5 × 10⁻⁹ [31]). The possible role of RGS6 in schizophrenia is further supported by the fact that RGS6 is required for rapid deactivation of GABA-B receptor in the cerebellum and thus may play a role in schizophrenia pathogenesis [9]. Another example is B3GAT1 (FOGS p-value < 1 × 10⁻⁷). Several studies have indicated that B3GAT1 contained a significant SNP (rs893949, p-value = 5 × 10⁻⁷ [15]) associated with schizophrenia and rare de novo copy number mutations in B3GAT1 contribute to the genetic component of schizophrenia [43]. As a positive control, we examined one locus on Chromosome 6 (Figures 1b and 1c), as this locus exhibited the strongest genetic signal while containing a well known putative causal gene, C4A [33]. Both FOCUS and FOGS identified the gene C4A (FOCUS p-value < 1 × 10⁻⁷ and FOCUS posterior probability > 0.99), partially validating the usefulness of both methods. One caveat is that C4A resides in the MHC/HLA region with complicated and pervasive LD structures, and one should pay special attention when applying FOGS to this region. Finally, FOGS identified some putative causal genes (e.g., FAM114A2 and PPP1R18) without much literature support. These new findings suggest that further study of these putative causal genes is needed and may help us gain new insights into the genetic basis of schizophrenia.

Table 1: Putative causal genes identified by our new method FOGS in the GWAS risk loci that contained at least one genome-wide significant SNP.

FOGS identified 22 putative causal genes with their chromosomes (CHR), transcription start sites (TSS) and relevant previous studies (Reported) in the GWAS Catalog [23]. For comparison, we also list the p-values of TWAS [14, 16] and the posterior probabilities of FOCUS [24]

Gene	CHR	Position	FOGS	TWAS	FOCUS	Reported
PTPRF	1	43990858	< 1.0 × 10−7	2.2 × 10−2	0.00	[15, 22, 31, 37]
MED8	1	43849578	9.0 × 10−7	1.1 × 10−11	1.00	[15, 31, 37]
THOC7	3	63819545	1.7 × 10−6	2.7 × 10−11	1.00	[15, 31, 37]
FAM114A2	5	153371268	5.0 × 10−7	5.3 × 10−6	0.78
BTN2A1	6	26458152	< 1.0 × 10−7	2.8 × 10−4	0.00	[37]
HIST1H2BJ	6	27093676	< 1.0 × 10−7	5.5 × 10−1	0.00
HIST1H4L	6	27840926	< 1.0 × 10−7	< 1.0 × 10−17	1.00
TRIM27	6	28870779	< 1.0 × 10−7	< 1.0 × 10−17	0.00
HLA-F-AS1	6	29696142	5.0 × 10−7	8.1 × 10−1	0.00
MICE	6	29709508	< 1.0 × 10−7	1.9 × 10−1	0.00
ZFP57	6	29640168	< 1.0 × 10−7	< 1.0 × 10−17	1.00	[15, 37]
PPP1R18	6	30644166	< 1.0 × 10−7	< 1.0 × 10−17	1.00
FLOT1	6	30695486	< 1.0 × 10−7	1.3 × 10−8	0.00
IER3	6	30710979	< 1.0 × 10−7	< 1.0 × 10−17	0.54
C4A	6	31949801	< 1.0 × 10−7	< 1.0 × 10−17	1.00
PRRT1	6	32116136	2.0 × 10−7	7.4 × 10−2	0.00	[37]
OPCML	11	132284874	< 1.0 × 10−7	1.2 × 10−6	0.94
IGSF9B	11	133778459	< 1.0 × 10−7	3.4 × 10−11	1.00	[15]
B3GAT1	11	134248397	< 1.0 × 10−7	3.3 × 10−3	0.01	[15]
RGS6	14	72398816	< 1.0 × 10−7	2.8 × 10−2	0.00	[15, 31, 37]
HYKK	15	78799906	< 1.0 × 10−7	6.0 × 10−2	0.27
FURIN	15	91411884	4.0 × 10−7	2.3 × 10−12	1.00	[15, 31]

In the end, we emphasized the importance of using an adaptive test like aSPU to aggregate information across conditional Z-scores of multiple SNPs. Because there is no uniformly most powerful test, any non-adaptive test may not be powerful for a given situation and thus fail to identify putative causal genes. For example, if we applied the popular weighted SUM test for FOGS, we identified eight putative causal genes, all of which have been identified by FOGS with aSPU. FOGS with the weighted SSU test identified 19 putative causal genes, 18 of which have been identified by FOGS with aSPU. In summary, by applying aSPU to select the most significant testing result data-adaptively, FOGS maintained high power to detect putative causal genes.

Taken together, these results strongly support the potential usefulness of FOGS to identify putative causal genes that could be missed by other competing fine-mapping methods like FOCUS and TWAS. The schizophrenia-related genes identified by FOGS may improve our understanding of the genetic mechanisms of schizophrenia.

Discussion

In this work, we have presented a new fine-mapping method called FOGS to prioritize putative causal genes for TWAS. As demonstrated before [24, 39] and further here, TWAS frequently identify multiple significant genes per locus, many of which may not be causal due to confounding through LD among SNPs; in these situations, fine-mapping using FOGS would help. We have demonstrated that FOGS has several potential advantages through extensive simulations and real data analyses. First, by adjusting for the effects of other genes in the same locus, FOGS adequately controls Type I error rates under various null scenarios. Second, by data-adaptively aggregating information among multiple SNPs and eQTL-derived weights, FOGS outperforms the p-value ranking of TWAS results and FOCUS [24], a Bayesian fine-mapping method, in identifying causal genes with reduced numbers of false positives. Third, FOGS is robust to the choice of the ridge penalty parameter λ, and we recommend using the default value λ = 0.1 in real applications.

To better understand the genetic component of schizophrenia, we reanalyzed a large-scale schizophrenia GWAS summary dataset [27]. FOGS correctly identified a positive control gene C4A. Interestingly, FOGS identified some putative causal genes such as RGS6 and B3GAT1 that were missed by both TWAS and FOCUS, but might be related to schizophrenia as shown by other studies [9, 43].

Our proposed method FOGS has conceptual similarities with conditional and joint multiple SNP analysis [47] that aims to identify secondary associated SNPs in a locus. Our method extends the standard regression model to ridge regression to account for possibly strong LD among SNPs, then aggregates conditional effect sizes of multiple SNPs (in the same gene) efficiently. Using ridge regression is important for FOGS as applying standard regression model leads to the results similar to or even slightly worse than the p-value ranking of TWAS results as shown in our simulations. Our work was motivated by FOCUS [24] that prioritizes causal genes by adjusting the effects of the imputed gene expression levels of other genes in the same locus. In contrast, our approach adjusts the effects at the SNP level since a causal SNP might mediate its effect on the trait through pathways other than cis-transcriptional regulation.

We list some limitations of FOGS. First, to account for LD among SNPs from other genes in the locus, we adopt ridge regression. However, the ridge penalty introduces some small bias, leading to slightly conservative inference with potential power loss. It might be interesting to apply some non-convex penalties, such as MCP [48] and truncated Lasso penalty [34], to reduce the bias. Importantly, ridge regression can be viewed as a Bayesian method with independent normal priors on the components of ${\tilde{\beta }}_j$. Zhu et al. [51] introduced a “Regression with Summary Statistics” likelihood with promising performance with a spike-and-slab type prior [51]. Adopting the Bayesian framework may yield even better performance. Second, like other GWAS summary data based methods, FOGS is dependent on the use of a reference panel. Using a small reference panel such as the 1000 Genomes Project Phase 3, or a panel from a different population, might introduce some biases [5, 47]. In real data analysis, we used the Lung Health Study data with about 4,100 individuals as the reference panel. We might achieve more robust results and identify more putative causal genes if a larger reference panel (e.g., UK Biobank data) is applied. Third, we only focus on the European ancestry here. While we expect that FOGS can be directly applied to non-European GWAS summary data (with a corresponding reference), one caveat is that applying FOGS with an European reference panel to non-Europeans GWAS summary data may lead to suspicious results. Several fine-mapping methods [17, 20, 32] have been developed by taking advantage of the variability in the genetic backgrounds across populations; we expect FOGS may provide more robust results if trans-ancestry information can be incorporated. Fourth, like FOCUS, our proposed method is based on a reference eQTL dataset from a single tissue; as shown by others in the context of TWAS (but not TWAS-fine mapping), using multiple eQTL datasets drawn from multiple tissues to construct weights may gain power for TWAS by taking advantage of shared eQTL across multiple tissues [19]; our method can be similarly extended. Fifth, there has been continuing interest in TWAS with many new methods being developed, such as CoMM [46] and MultiXcan [3]. Incorporating into FOGS these new ideas and/or more informative eQTL-derived weights may further improve the power. We leave these interesting topics to future work.

Conclusions

In this study, we have developed a new fine-mapping method, FOGS, to prioritize putative causal genes by accounting for local linkage disequilibrium (LD). We have shown that this approach maintains correct Type I error rates and achieves higher power than the competing methods through extensive simulations. We have applied our method to a schizophrenia GWAS summary datasets of 105,318 European individuals and identified 46 putative causal genes, some of which were missed by the competing methods but might be related to schizophrenia as shown by other studies.

Methods

New fine-mapping method: FOGS

Fine-mapping Of Gene Sets (FOGS) prioritizes causal genes by testing for the conditional association of each gene in a locus. Here, we focus on one gene, say gene A, and repeat the same procedure for every gene in the locus. The conditional effect is estimated from a joint regression model, in which all the SNPs in the locus are analyzed jointly. Specifically, we model a quantitative phenotype for n unrelated individuals, y, as

$$\mathbf{y}=\mathbf{V}\alpha +\mathbf{X}\beta +ϵ,$$ (1)

where y = {y_i} is a centered n × 1 vector of phenotypes, X = {x_ij} is a centered (with mean 0) n × p genotype matrix at p SNPs with non-zero eQTL-derived weights for gene A (of interest) and V = {v_ij} is a centered n × q genotype matrix at q SNPs with non-zero eQTL weights for any of other genes in the same locus, and β and α are the joint effects for gene A (of interest) and other genes, respectively. To account for genes without eQTL-derived weights in the relevant tissue, we include eQTL weights from a proxy tissue with the best prediction accuracy (i.e., out of sample R²). This approximation is supported by the fact that eQTLs are largely shared across tissues [10] as also adopted in FOCUS [24].

We test the causal effect between the phenotype y and gene A with the null hypothesis H₀ : β = 0. Testing H₀ : β = 0 is similar to fine-mapping of single variants [47]: instead of prioritizing a secondary SNP, here we focus on prioritizing a causal gene with multiple SNPs in the locus. To test H₀, we need to address two technical questions: 1. how to estimate the conditional Z score $({\beta }_j∕\sqrt{\text{var}({\beta }_j)})$ for each SNP in gene A? 2. how to construct an adaptive and powerful test to aggregate conditional Z scores and eQTL-derived weights efficiently? In the following, we will discuss our solutions for these two questions accordingly.

Estimating the conditional Z score via ridge regression.

For simplicity, we denote the conditional Z score for gene A as Z = (Z₁, Z₂ , . . . , Z_p)′. To have a better estimation of conditional Z score, we estimate Z_j (j = 1 , . . . , p) for each SNP j in gene A separately. Under H₀ : β = 0, the effect of SNPs in gene A is zero and thus no need to adjust for them while estimating the conditional score Z_j for SNP j. For SNP j, our updated model is y = Vα + X_jβ_j + ϵ. For simplicity, we denote $\tilde{\mathbf{X}}=(X_j,\mathbf{V})$ and $\tilde{\beta }=({\beta }_j,\alpha )$ and rewrite our model as $\mathbf{y}=\tilde{\mathbf{X}}\tilde{\beta }+ϵ$. Due to LD, some SNPs in $\tilde{\mathbf{X}}$ are highly correlated. To alleviate the multicollinearity problem and get a stable estimate, we add a small ridge penalty to the objective function as

$$\text{minimize}(\mathbf{y}-\tilde{\mathbf{X}}\tilde{\beta }{)}^{\prime }(\mathbf{y}-\tilde{\mathbf{X}}\tilde{\beta })+\lambda \Vert \tilde{\beta }{\Vert }_2^2.$$ (2)

By ridge regression, we can estimate the joint effects of multiple SNPs as

$$\widehat{\beta }=({\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}+\lambda {\mathbf{I}}_{p\ast }{)}^{-1}\tilde{\mathbf{X}}\mathbf{y}\text{and}\text{var}(\widehat{\beta })={\sigma }_J^2({\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}+\lambda {\mathbf{I}}_{p\ast }{)}^{-1}{\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}({\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}+\lambda {\mathbf{I}}_{p\ast }{)}^{-1},$$ (3)

where ${\sigma }_J^2$ is the residual variance in the joint analysis, λ is the penalty parameter controlling the extent of ridge regularization, and ${\mathbf{I}}_{p\ast }$ is the (q + 1) × (q + 1) identify matrix. When GWAS individual-level data is available, we can use the above formulas to estimate conditional Z score for SNP j as $Z_j={\widehat{\beta }}_1∕\sqrt{\text{var}({\widehat{\beta }}_1)};$ however, we often have only GWAS summary statistics resulting from single-SNP models as follows

$$\mathbf{y}={\tilde{X}}_j{b}_j+ϵ,$$ (4)

where ${\tilde{X}}_j$ is the jth column of $\tilde{\mathbf{X}}$ for j = 1, 2, . . . , (q + 1). Inspired by Yang et al. [47], we estimate the conditional Z score by converting marginal effects (4) to joint effects (2) without using individual-level phenotype data.

The marginal effects of multiple SNPs $\tilde{\mathbf{X}}$ estimated from single-SNP models can be written in matrix form as [47]

$$\widehat{\mathbf{b}}={\mathbf{D}}^{-1}{\tilde{\mathbf{X}}}^{\prime }\mathbf{y}\text{and}\text{var}(\widehat{\mathbf{b}})={\sigma }_M^2{\mathbf{D}}^{-1},$$

where b = {b_j} is a (q +1) × 1 vector of marginal SNP effects, D = {D_j} is a diagonal matrix with $D_j={\sum }_{i=1}^n{\tilde{x}}_{ij}^2$, and ${\sigma }_M^2$ is a (q + 1) × 1 vector of residual variances in the single-SNP analyses. By ${\tilde{\mathbf{X}}}^{\prime }\mathbf{y}=\mathbf{D}\widehat{\mathbf{b}}$, we can rewrite equation (3) as

$$\widehat{\beta }=({\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}+\lambda {\mathbf{I}}_{p\ast }{)}^{-1}\mathbf{D}\widehat{\mathbf{b}}\text{and}\text{var}(\widehat{\beta })={\sigma }_J^2({\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}+\lambda {\mathbf{I}}_{p\ast }{)}^{-1}{\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}({\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}+\lambda {\mathbf{I}}_{p\ast }{)}^{-1}.$$ (5)

We estimate the residual variance as

$${\widehat{\sigma }}_J^2=\frac{\text{SSE}}{n-df}=\frac{{\mathbf{y}}^{\prime }\mathbf{y}-{\widehat{\beta }}^{\prime }\mathbf{D}\widehat{\mathbf{b}}}{n-df}.$$

SSE is the Sum of Squared Errors and df is the degrees of freedom, which can be estimated as $df={\sum }_{j=1}^{q+1}{d}_j∕(d_j+\lambda )$, where d_j are the eigenvalues of ${\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}$. By Yang et al. [47], ${\mathbf{y}}^{\prime }\mathbf{y}=(n-1)D_j{S}_j^2+D_j{\widehat{b}}_j^2$, where $S_j^2={\widehat{\sigma }}_{M(j)}^2∕D_j$ is the squared standard error of ${\widehat{b}}_j$. Then we take the median of $(n-1)D_j{S}_j^2+D_j{\widehat{b}}_j^2$ across all the SNPs [47] to estimate y′y. In the end, we use equation (5) to estimate the conditional Z score $Z_j={\widehat{\beta }}_1∕\sqrt{\text{var}({\widehat{\beta }}_1)}$ for SNP j. We repeat the procedure for all the SNPs in gene A and get the conditional Z score vector Z = (Z₁, Z₂, . . . , Z_p)′.

For GWAS summary statistics, we are usually unable to obtain pooled individual-level genotype data and thus ${\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}$ is unavailable. Following [16, 47], we use a reference sample, such as the Lung Health Study data (dbGAP: phs000335.v2.p2), to approximate ${\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}$.

Note that the scale of measurement of a quantitative trait Y has no impact on the method derived above and thus some constant can be dropped from the equations. As in the standard practice, we rescaled $\tilde{\mathbf{X}}$ to make ${\tilde{\mathbf{X}}}^{\prime }\tilde{\mathbf{X}}$ the sample covariance matrix of $\tilde{\mathbf{X}}$. Inspired by Pasaniuc et al. [28], we set the penalty parameter λ = 0.1 as the default, only adding a small ridge penalty to alleviate the collinearity problem. Of note, rescaling $\tilde{\mathbf{X}}$ is important; otherwise the choice of penalty parameter λ will depend on the sample size of the reference panel.

Ideally, we may want to center and standardize/scale the genotype matrix $\tilde{\mathbf{X}}$. However, because the GWAS summary statistics are often provided for unstandardized genotype data, we derived the model under the assumption that genotype matrices are only centered but not standardized. If we make the standardization assumption, we have to recalculate the corresponding marginal effect size for each SNP j as ${\widehat{b}}_j=s_j(z_j∕\sqrt{N_j})$, where s_j is the sign, z_j is the Z score, and N_j is the sample size for SNP j [38]. Since the sample sizes for the SNPs often vary and are unavailable, the approximation will not be accurate if the maximum or average sample size is used. Importantly, the main reason of adding a small ridge penalty is to stabilize the model and alleviate the collinearity problem. Thus, we prefer to work on the current setting and leave the study of whether to standardize genotype matrices to future work.

Furthermore, the same method described above for a quantitative trait can be applied to a binary trait, as long as the effect size b and its corresponding standard errors are measured on the log odds ratio (log(OR)) scale [47]. As shown by others [45, 49], a linear regression model can be used to well approximate a logistic regression model for a binary trait due to small effect sizes of SNPs (and genes). Also, the log odds ratio scale effect size can be viewed as being an effect estimate for an underlying quantitative (continuous) liability [29, 47].

Aggregating conditional Z scores to prioritize causal gene

Once we get the conditional score Z for each SNP j in gene A, the next question is how to aggregate information from multiple SNPs to test H₀ : β = 0 efficiently. Because there is no uniformly most powerful test, any non-adaptive test may not be powerful for a given situation. Since we do not know the underlying truth, we construct a class of sum of powered score (SPU) tests such that hopefully at least one of them would be powerful for a given situation. Then we apply an adaptive test called aSPU [21, 26] to select the most significant testing result data-adaptively with a proper adjustment for multiple testing. To further improve statistical power, we apply the weighted aSPU with eQTL-derived weights.

First, we denote the weighted conditional score vector for β in (1) as

$$\mathbf{U}=(U_1,\dots ,U_p{)}^{\prime }=\mathbf{W}\mathbf{Z},$$

where $\mathbf{W}=\text{Diag}({\widehat{w}}_1,\dots ,{\widehat{w}}_p)$ are the eQTL-derived weights and Z is the conditional Z score estimated from the previous subsection.

Second, we construct a class of SPU tests as follows:

$$T_{\text{SPU}(\gamma )}=\sum _{j=1}^p{U}_j^{\gamma },$$

where γ is a positive integer and we further define T_SPU(∞) = max_j |U_j| since $T_{\text{SPU}(\gamma )}\propto ({\sum }_{j=1}^p\mid U_j{\mid }^{\gamma }{)}^{1∕\gamma }\to {\max }_j\mid U_j\mid$ as an even integer γ → ∞. The SPU tests cover many popular tests as special cases. For example, SPU(1) equals to the SUM or burden test, which yields high power if all SNPs are causal with similar effect sizes and causal direction. Meanwhile, SPU(2) equals to the SSU, which would be powerful if the causal direction of SNPs are different. As γ increases, SPU(γ) will be more powerful for sparser signals.

Third, since the optimal value of γ is data-dependent and unknown, we propose using aSPU to combine the results from a class of SPU tests: the aSPU test statistic is defined as

$$T_{\text{aSPU}}=\underset{\gamma \in \Gamma }{\text{min}}{P}_{\mathbf{SPU}(\gamma )},$$

where P_SPU(γ) is the p-value of the SPU(γ) test. The default setting of Γ is Γ = {1, 2, . . . , 6, ∞}, which usually performs well in real applications [42, 44]. We have demonstrated that the result of aSPU is relatively robust to the choice of Γ set from both empirical and theoretical sides [18, 42].

In the end, we apply one layer of Monte Carlo simulations to estimate the p-values for both SPU and aSPU tests simultaneously [26]. Specially, first, we simulate B copies of the null score vectors independently, U^(b) ~ N(0, Σ) for b = 1, . . . , B, from its asymptotic null distribution and then calculate the null statistics T_SPU(γ) based on each null score vector U^(b) accordingly. Next, the p-value of SPU(γ) is $P_{\text{SPU}(\gamma )}=[1+{\sum }_{b=1}^{B}I(\mid \text{SPU}(\gamma {)}^{(b)}\mid \ge \mid \text{SPU}(\gamma )\mid )]∕(B+1)$, and the p-value for aSPU is $P_{\text{aSPU}}=[1+{\sum }_{b=1}^{B}I(T_{\text{aSPU}}^{(b)}\le T_{\text{aSPU}})]∕(B+1)$, with $T_{\text{aSPU}}^{(b)}={\text{min}}_{\gamma \in \Gamma }{p}_{\gamma }^{(b)}$ and $p_{\gamma }^{(b_1)}=[{\sum }_{b\ne b_1}I(\mid T_{\text{SPU}(\gamma )}^{(b)}\mid \ge \mid T_{\text{SPU}(\gamma )}^{b_1}\mid )]∕B$. To save computational time, we wrote highly efficient code in C and start with a small B, say B = 10, 000, to scan a genome, then gradually increase B for the more significant genes that pass a significance criterion (p-value < 5/B) [26].

While both FOGS and TWAS share some similarities such as using the information from external transcriptome data (e.g., GTEx) to construct the test statistics, they differ in two aspects. First, TWAS and its related methods estimate the relationship between cis-SNPs and gene expression based on an external transcriptome dataset, then test the association between the predicted gene expression and phenotype. Under the stringent assumptions that all cis-eSNPs are valid instrumental variables, the standard TWAS, as a special case of instrumental variables regression, like Mendelian randomization (MR) [4], would conclude the causal relationship between the gene and the phenotype. In contrast, our proposed method FOGS conducts a weighted association test on the cis-SNPs and the phenotype. Second, TWAS fails to consider the effects of other SNPs or genes in the same locus, e.g. LD between a true causal SNP and a nearby eSNP, which may lead to the violation of the modeling assumptions for valid instrumental variables regression, and thus lead to invalid causal conclusions. In contrast, FOGS, like FOCUS, is more likely to identify a true causal relationship between the gene and the phenotype after adjusting for the effects of other SNPs and genes in the same locus, similar to multivariable MR [7]. Generally speaking, due to the likely violation of the modeling assumptions required by instrumental variables regression, we regard both TWAS and FOGS as methods to prioritize putative causal genes.

Simulations

We conducted extensive simulations to compare the performance of the proposed method with other two methods: FOCUS [24] and the p-value ranking of TWAS results, which, to our knowledge, are the only two existing fine-mapping methods for TWAS. FOCUS is a Bayesian fine-mapping method, and the p-value ranking of TWAS results simply chooses the most significant gene in the locus as the putative causal gene.

We focused on Chromosome 22 for all simulations and partitioned genotype data into 24 independent LD blocks by LDetect [6]. We used the CMC eQTL weights (from dorsolateral prefrontal cortex) when available; otherwise, we included the eQTL weights with the best accuracy across all other tissues. 21 out of 24 independent LD blocks contained more than two genes, and we focused on these 21 LD blocks in the following. For each LD block, we considered all the genes whose transcription start sites are inside the block. Then we applied the fine-mapping methods to each LD block separately.

We first generated GWAS summary statistics from the real genotype data of the Lung Health Study (dbGAP: phs000335.v2.p2) with 4,145 subjects after quality control. Next, we generated the phenotype Y by Y = Xβ + ϵ, where ϵ follows a normal distribution with mean 0 and standard deviation 0.5, representing a random environmental noise; X is a centered n × p genotype matrix at p SNPs in the LD block and β = (β₁, . . . , β_p)′ is the corresponding effect size vector.

Under the null, we set β = 0. Under the alternative, we considered several simulation settings with randomly choosing one gene to be causal gene. Setting 1: For each causal gene, we randomly selected one or two eSNPs (with non-zero eQTL weights) to be causal SNPs and assigned the corresponding β_j = c, where c is some constant. We also considered the situations where the effect size of causal SNP is proportional to the non-zero eQTL weights. Specifically, we set ${\beta }_j=c({\widehat{w}}_j∕{\sum }_j\mid {\widehat{w}}_j\mid )$, where ${\widehat{w}}_j$ is the corresponding eQTL weights. Setting 2: We selected all eSNPs in the causal gene to be causal SNPs, assigning ${\beta }_j=c({\widehat{w}}_j∕{\sum }_j\mid {\widehat{w}}_j\mid )$. Of note, eSNPs for the causal genes are often shared by nearby genes, making setting 2 more challenging in general. In the end, we ran a univariate regression analysis of each SNP and the phenotype, then computed SNP-trait summary results (i.e. the estimated effect sizes and their standard errors, minor allele frequencies, major alleles and minor alleles). For each simulation setting, the heritability was estimated by the R-squared of a linear regression model with the phenotype as the outcome and all causal SNPs as covariates. We repeated this process 120 times for each LD block, resulting in 2,520 LD blocks in total. We then compared and evaluated different methods based on these 2,520 LD blocks.

Analysis of schizophrenia GWAS summary data

We reanalyzed a schizophrenia GWAS summary data of European ancestry with 105,318 individuals (40,675 cases and 64,643 controls) [27]. To our knowledge, this is to date the largest publicly available schizophrenia GWAS summary data.

Data pre-processing.

We removed variants that were either non-biallelic or strand ambiguous (SNPs with A/T, C/G alleles). We further filtered out the variants without rs IDs or not in the 1000 Genomes Project Phase 3 reference panel. We kept the variants on autosomal chromosomes with a minor allele frequency greater than 0.01. 1,146,939 variants passed these filters.

Next, we used the LD loci definition in LDetect [6]. We further obtained publicly available 51 sets of eQTL-derived weights from the FUSION website. Forty-seven sets of the eQTL weights were based on GTEx [10], and the other four were based on NTR [40], YFS [30], METSIM [36], and CMC [13] consortiums, respectively. We assumed the relevant tissue for driving schizophrenia is dorsolateral prefrontal cortex (CMC eQTL weights) because it controls complex, higher-level executive and cognitive functions, many of which are abnormal in schizophrenia patients [13], and because years of studies have pointed out its well-characterized role in schizophrenia [8, 50]. Similar to Mancuso et al. [24], we used the CMC eQTL weights when available; otherwise, we included the eQTL weights with the best accuracy across all other tissues, leading to 15,460 genes with eQTL weights, 5,420 of which were taken from CMC eQTL weights directly.

Statistical analysis.

We first applied TWAS to all the loci with at least two genes and then applied both FOGS and FOCUS to prioritize putative causal genes.

First, we applied TWAS [16] to identify significantly associated genes. TWAS uses a weighted sum of the Z-scores with eQTL weights to construct its test statistic. Reference LD was estimated by the Lung Health Study (dbGAP: phs000335.v2.p2) data with 4,145 individuals. Because the size of the reference data should scale with the GWAS sample size [5, 47] to reduce the bias, we used the Lung Health Study data as the reference panel instead of the 1000 Genomes Project Phase 3 [1] with about 500 European individuals. We applied TWAS on the loci with more than two genes (14,770 genes in total) and used a stringent Bonferroni cutoff (0.05/16, 000 ≈ 3.1 × 10⁻⁶) to consider the genes and loci we ignored.

Next, we applied two fine-mapping methods, FOGS and FOCUS [24], to prioritize causal genes. We focused on the risk loci that contained at least one genome-wide significant SNP. As before, we used the Lung Health Study (dbGAP: phs000335.v2.p2) data to estimate LD reference panel and ran up to B = 10⁷ permutations for each gene. For FOGS, we used the same Bonferroni cutoff (0.05/16, 000 ≈ 3.1 × 10⁻⁶) as used in TWAS. For FOCUS, we used the default 90%-credible gene-sets to prioritize causal genes. We also reported the results of the p-value ranking of TWAS results, which chose the most significant gene in the locus as the putative causal gene. In the end, we discussed the results in the loci that contained at least one genome-wide significant SNP in the pre-processed GWAS summary data (p-value < 5 × 10⁻⁸) in detail.