Internal fluid pressure influences muscle contractile force

Significance

Skeletal muscles are hierarchical structures with important functional components spread across molecular, cellular, and tissue levels of organization. Studying interactions across these levels is crucial, as multiscale mechanics can yield emergent properties not exhibited by isolated tissue components. Here, through physical modeling of muscle morphology and experiments on bullfrog muscle, we show that fluid pressure within muscle acts as an important but largely unacknowledged intermediary between contractile proteins operating at molecular scales and extracellular matrix elements present throughout the tissue. We show that forces transmitted through pressurized fluid to the extracellular matrix significantly influence the mechanics of both actively contracting and passively deformed muscle, a finding with implications for our understanding of both normal and pathological muscle physiology.

Abstract

Fluid fills intracellular, extracellular, and capillary spaces within muscle. During normal physiological activity, intramuscular fluid pressures develop as muscle exerts a portion of its developed force internally. These pressures, typically ranging between 10 and 250 mmHg, are rarely considered in mechanical models of muscle but have the potential to affect performance by influencing force and work produced during contraction. Here, we test a model of muscle structure in which intramuscular pressure directly influences contractile force. Using a pneumatic cuff, we pressurize muscle midcontraction at 260 mmHg and report the effect on isometric force. Pressurization reduced isometric force at short muscle lengths (e.g., −11.87% of P₀ at 0.9 L₀), increased force at long lengths (e.g., +3.08% of P₀ at 1.25 L₀), but had no effect at intermediate muscle lengths ∼1.1–1.15 L₀. This variable response to pressurization was qualitatively mimicked by simple physical models of muscle morphology that displayed negative, positive, or neutral responses to pressurization depending on the orientation of reinforcing fibers representing extracellular matrix collagen. These findings show that pressurization can have immediate, significant effects on muscle contractile force and suggest that forces transmitted to the extracellular matrix via pressurized fluid may be important, but largely unacknowledged, determinants of muscle performance in vivo.

Like most biological structures, muscles are primarily made up of water. Water is present in intracellular, interstitial, and capillary fluid spaces within muscle, and due to its near incompressibility, has the potential to transmit or oppose forces generated within the tissue. During both active contraction and passive deformation of muscle, intramuscular fluid pressures develop that can be measured empirically (e.g., ref. 1) and predicted computationally (2, 3). These pressures typically fall within a range of 15 to 250 mmHg (4–6); however, much larger pressures of over 500 mmHg (7) and over 1,000 mmHg (8) have been reported. Intramuscular pressures result from the action of curved muscle fibers, which necessarily exert a portion of their developed tension inward (4, 9), and from the distension of circumferential elastic elements, such as the sarcolemma, which resist radial changes in muscle shape (10).

Multiple theoretical models of muscle predict that intramuscular pressure should influence muscle performance by directly opposing sarcomere shortening forces (10–12). Consistent with predictions from these models, experimentally applied radial constraints that likely increase intramuscular fluid pressure have been shown to reduce force (13–16) and limit muscle shortening (17) during active contraction. Computational and physical models of muscle morphology have also identified intramuscular pressure as an important determinant of the passive forces generated by relaxed muscles subjected to stretch (18–20). This latter phenomenon relies on the interaction of intramuscular fluid with fibrous collagen in the muscle extracellular matrix (ECM).

To investigate the relationship between intramuscular pressure and contractile muscle force, we used a small pneumatic pressure cuff to squeeze isolated bullfrog semimembranosus muscle midcontraction at a series of isometric lengths. This perturbation allowed measurement of the immediate effects of increased intramuscular fluid pressure on contractile force. Based on previous models of fluid pressure in passively stretched muscle (18, 19), we hypothesized that interactions between pressurized intramuscular fluid and ECM collagen might influence force developed during active contraction. To explore this hypothesis, we built simple physical models of muscle and ECM morphology and compared their responses to squeezing to that of muscle. Physical models were made of fluid-filled silicone tubes, representing muscle fibers or fascicles, wrapped by helically oriented thread, representing ECM collagen fibrils or fibers. Collagen in the muscle ECM reorients spatially as a function of muscle length (21, 22), and multiple physical models were built with a range of helical wrapping angles to mimic the morphology of the extracellular matrix in muscle held at various lengths. The effect of squeezing on passive force generated by relaxed muscle was also investigated and is compared to the effect of squeezing on active muscle and the physical models.

Methods

Isolated Muscle Preparation.

All experimental protocols were approved by the Brown University Institutional Animal Care and Use Committee. Semimembranosus muscles (n = 7; 3.5 g ± 0.2 g [mean weight ± SD]) were isolated from the legs of bullfrogs (Rana catesbeiana), bathed in oxygenated amphibian Ringer’s solution (115 mmol·L⁻¹ NaCl, 2.5 mmol·L⁻¹ KCl, 1.0 mmol·L⁻¹ MgSO₄, 20 mmol·L⁻¹ imidazole, 1.8 mmol·L⁻¹ CaCl₂, 11 mmol·L⁻¹ glucose, pH 7.9, 20 °C), and stimulated to contract via a bipolar stimulating electrode attached to a branch of the sciatic nerve. Muscle force and length were monitored via a 5-kg load cell (LCM703-5, OMEGA Engineering, Inc.) mounted on a height gauge (192-606, Mitutoyo Corporation) equipped with a linear displacement transducer (LD621, OMEGA Engineering, Inc.). Muscles were connected to the load cell at their distal ends via a length of Kevlar thread knotted about the knee capsule and held stationary at their proximal ends via a sliver of hip bone secured in a custom clamp. A length-tension curve was constructed by contracting muscle isometrically at a series of lengths, allowing determination of L₀, the length at which muscles produced maximum contractile force (P₀). To prevent fatigue, muscles were rested in oxygenated Ringer’s solution for at least 5 min after all contractions.

Pneumatic Cuff Perturbations.

At a series of lengths above and below L₀ (0.9 L₀ to 1.25 L₀ in 0.05 L₀ increments), muscles were squeezed midcontraction via a modified neonatal blood pressure monitoring cuff fit about the muscle belly (Soft cloth single tube neonatal blood pressure cuff size 1, Medline Industries, Inc.; Fig. 1; see also Movie S1). Cuffs covered approximately the middle third of the muscle belly and were inflated to an internal pressure of 260 mmHg. Muscles were allowed to reach an isometric force plateau over a period of 150 ms prior to cuff inflation, allowing measurement of isometric force immediately before and immediately after squeezing (Fig. 2). The magnitude and timing of cuff pressurization were controlled via an electrically triggered solenoid valve (MHJ10-S-2,5-QS-1/4-HF-U, FESTO Co.) connected to a compressed air cylinder and low-pressure regulator. Cuff internal pressure was monitored via an in-series pressure probe (Mikrotip SPC-340, Millar Instruments). Note that cuff pressure is reflective of pneumatic pressure developed within the cuff only and may differ quantitatively from intramuscular pressure, which was not measured. The effect of 260 mmHg squeezes on passive force developed by relaxed, uncontracting muscle was also measured at each length.

Fig. 1.

An isolated bullfrog semimembranosus muscle fit with a small pneumatic pressure cuff. The cuff covers approximately the middle third of the muscle belly. The distal (knee) end of the muscle is connected to a force transducer (above the frame) via Kevlar thread. The proximal (hip) end remains attached to a bony sliver secured in a custom clamp. Small black suture knots allowed tracking of muscle fiber length in high-speed video recordings (SI Appendix, Fig. S1). The muscle pictured is ∼7 cm in length.

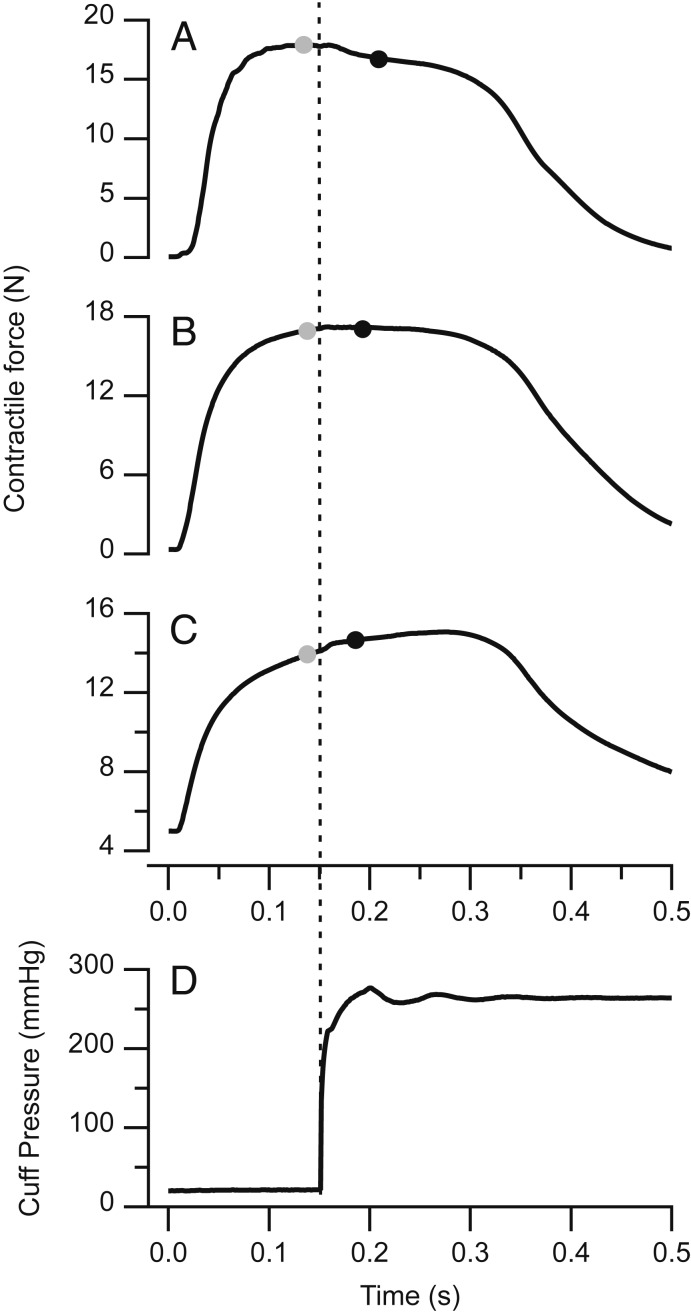
Fig. 2.

Representative traces (n = 1) showing the effects of a 260 mmHg squeeze applied midcontraction via a pneumatic pressure cuff. Squeezing can have a negative (A), neutral (B), or positive (C) effect on isometric contractile force. Contractions were performed at 0.90, 1.10, and 1.25 L₀ in A–C, respectively. Force was measured immediately before (gray circles) and immediately after (black circles) squeezing. Changes in isometric force correspond with the rise of pneumatic pressure inside the cuff (D, dotted line).

Cuffs hung loosely about muscles prior to inflation and were connected to the compressed air system via thin, flexible tubing (Tygon R-3603 1/8 inch outer diameter, Saint-Gobain Performance Plastics). This arrangement minimized physical connections between the pressure cuff and surrounding experimental apparatus, reducing the chance the cuff could transmit muscle forces to structures other than the load cell. To prevent buoyant forces acting on inflated cuffs, muscles were temporarily removed from Ringer’s solution for a period of ∼15 s during cuff inflation and measurement of force. To ensure pressurization of the cuff and Tygon tubing did not exert a direct pushing or pulling force on muscle that would be transmitted to the load cell, a muscle was frozen solid overnight, connected to the load cell under tension, and squeezed at 260 mmHg. Squeezing had no effect on longitudinal tension measured from frozen muscle, indicating that pressurization of the cuff squeezed muscle radially but did not exert a direct pushing or pulling force along its long axis.

In a subset of experiments, a highspeed video camera (FASTCAM-X 1280PCI, Photron Ltd.) was used to monitor changes in muscle fiber length during cuff inflation. Changes in muscle fiber length were indicated by movement of pairs of suture markers knotted about superficial muscle fibers in proximal and distal portions of the muscle belly (Markers visible in Fig. 1 and Movie S1. Marker tracking data presented in SI Appendix, Fig. S1).

Data Analysis and Statistics.

Force and pressure data from individual contractions were recorded at 1,000 Hz using a DAQ (PCI-MIO-16, National Instruments) and Igor Pro software (IGOR Pro v. 7.05, Wavemetrics). Changes in active and passive isometric muscle force during squeezing (postsqueeze force minus presqueeze force) were normalized to P₀ (determined from initial length-tension curves collected prior to squeezing perturbations), and statistically significant changes in force were identified via paired, 2-tailed t tests comparing presqueeze and postsqueeze forces at each muscle length. The position of suture markers in high-speed video data were digitized using marker tracking software (23) and used to calculate distal and proximal muscle fiber strains during the period of cuff inflation (SI Appendix, Fig. S1).

Data Availability Statement.

Tabulated presqueeze and postsqueeze muscle force data are available as Dataset S1.

Physical Models of Muscle Morphology.

In separate experiments, simple physical models of muscle and extracellular matrix morphology were also subjected to 260 mmHg squeezes. Models comprised water-filled silicone tubes (Dragon Skin FX-Pro, Smooth-On, Inc.) representing fluid-filled muscle fibers or fascicles, reinforced by Kevlar sewing thread representing fibrous extracellular matrix collagen. A length of latex tubing spanned the interior of each model and could be pretensioned to simulate production of isometric contractile force by myofibrils. Six models were built, each with a roughly uniform fiber reinforcement angle of ∼75°, 65°, 55°, 45°, 35°, or 25° relative to the model long axis. Reinforcing fibers wrapped the length of each model in both left- and right-hand helixes. Fibrous collagen in the ECM reorients spatially as a function of muscle length, becoming more parallel to the long axis of muscle fibers as muscle length is increased (21). Models with different fiber angles represented muscle stretched to various lengths, and the range of fiber angles studied was chosen based on empirical measurements of endomysial and perimysial collagen angles in the ECM of stretched and shortened muscle (21, 22).

Models were connected to a load cell (LCM703-5, OMEGA Engineering, Inc.) at one end via Kevlar thread and held in a stationary ring stand clamp at the other. Active isometric force production was simulated by pretensioning the latex tube running through the core of each model to an initial static tension of 10 N. Pretensioned models were squeezed at 260 mmHg via blood pressure cuff, and the effect of squeezing on tension was recorded and analyzed in Igor Pro (version 7.05; Wavemetrics). In a subset of experiments, models hung vertically with a 200-g mass suspended from their free end were squeezed to illustrate the effect of pressurization on model length.

Results

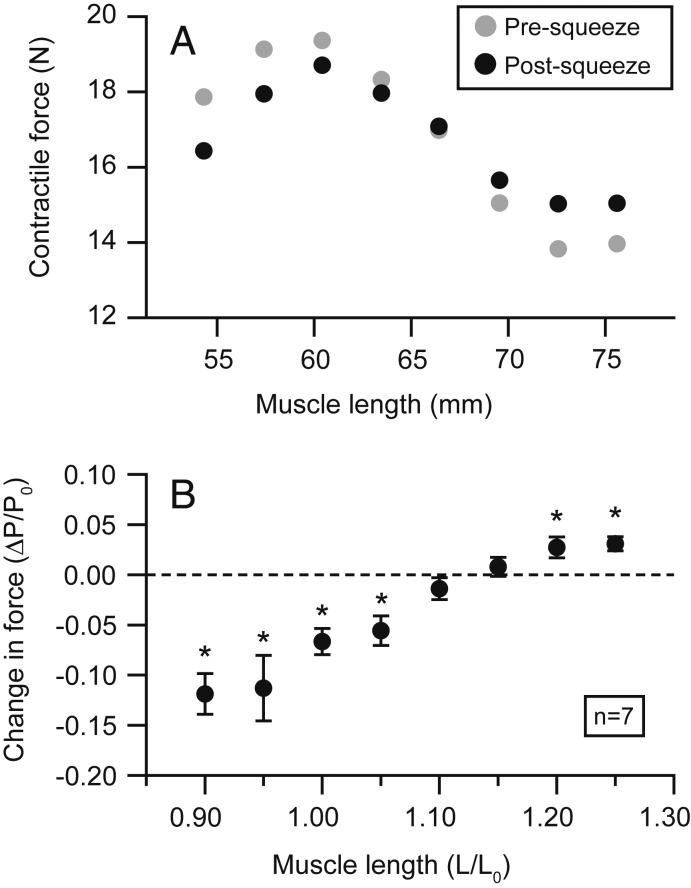
The effect of the pressure cuff on muscle force varied depending on the length at which an isometric contraction was performed (Figs. 2 and 3). At short and intermediate muscle lengths corresponding to the ascending limb and plateau of the active length-tension curve, squeezing significantly reduced active contractile force (P = 0.002, 0.014, 0.002, 0.009 at 0.90, 0.95, 1.00, and 1.05 L₀, respectively). At long muscle lengths corresponding to the descending limb of the curve, squeezing significantly increased active force (P = 0.039, 0.007 at 1.20 and 1.25 L₀). The effect of the cuff was not significant at lengths intermediate to these extremes (P = 0.246, 0.435 at 1.10 and 1.15 L₀). The largest reduction in contractile force was −11.87% ± 2.03% of P₀ (mean ± SEM) and occurred at the shortest muscle length studied (0.90 L₀). The largest increase in active force was +3.08% ± 0.69% of P₀ (mean ± SEM) and occurred at the longest length studied (1.25 L₀).

Fig. 3.

The effect of squeezing on contractile force varies with muscle length. A representative length-tension curve (n = 1) shows isometric force produced at a series of lengths immediately before (gray circles) and after (black circles) squeezing (A). The effect of squeezing on isometric force is consistent across multiple semimembranosus muscles (n = 7) (B). The average change in isometric force (postsqueeze force minus presqueeze force) is negative at short lengths and positive at long lengths. Squeezing has little to no effect on isometric force at intermediate lengths ∼1.1–1.15 L₀. Asterisks denote statistically significant differences in presqueeze and postsqueeze forces. Error bars represent SEs of means. Total muscle forces are reported, representing the sum of both active and passive contributions to force.

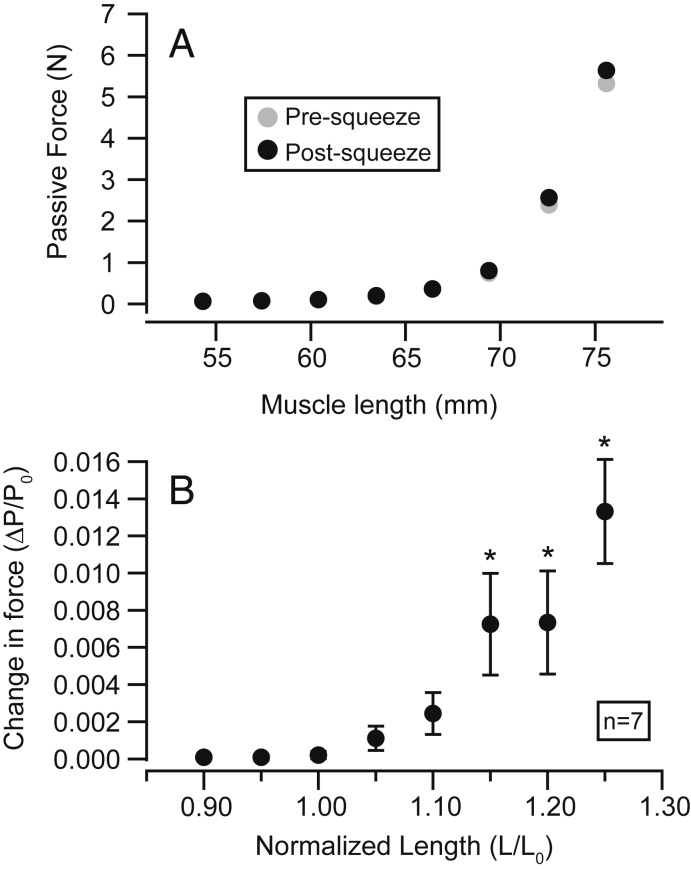
Relaxed, uncontracted muscle displayed significant increases in passive force when squeezed at relatively long muscle lengths (P = 0.028, 0.009, and 0.005 at 1.15, 1.20, and 1.25 L₀) but not at shorter lengths (P = 0.231, 0.565, 0.349, 0.141, 0.075 at 0.90, 0.95, 1.00, 1.05, and 1.10 L₀) (Fig. 4). The largest increase in passive force following squeezing was 1.33% ± 0.28 of P₀ (mean ± SEM) and occurred at 1.25 L₀. In both active and passive conditions, changes in tensile force corresponded temporally with the rise of pneumatic pressure measured within the cuff (Fig. 2D).

Fig. 4.

The effect of squeezing on passive force varies with muscle length. A representative passive length-tension curve (n = 1) shows force produced at a series of lengths in relaxed, uncontracted muscle immediately before (gray circles) and after (black circles) squeezing (A). The effect of squeezing on passive force is consistent across multiple semimembranosus muscles (n = 7) (B). Markers in B represent the average change in passive force (postsqueeze force minus presqueeze force) at each length. Error bars represent SEs of means. Statistically significant increases in passive force were observed at lengths 1.15 L₀ and higher, indicated by asterisks.

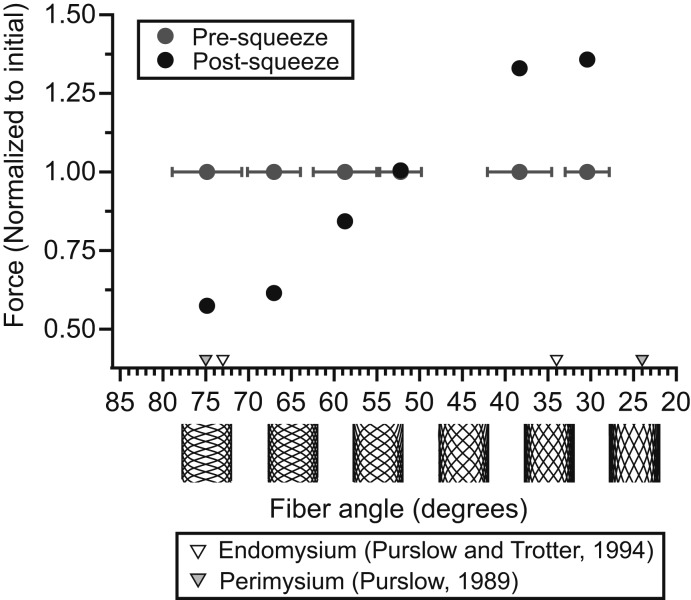
The mechanical behavior of the physical models demonstrated the importance of helical fibers reinforcing a constant-volume cylindrical container. Squeezing models hung with a 200-g mass suspended from their free end caused either an increase or decrease in length depending on the orientation of their reinforcing fibers (Fig. 5 and Movie S2). When squeezed at fixed length with their latex cores pretensioned, models with relatively high fiber angles displayed decreased longitudinal tensile force, while models with relatively low fiber angles displayed increased force (Fig. 6). Squeezing had little to no effect on a model with reinforcing fibers oriented at 52.2° ± 2.4 (mean ± SD). Across all 6 physical models the effect of squeezing on force transitioned gradually from negative to neutral to positive at successively lower fiber angles. This pattern was qualitatively similar to the gradual transition from negative to positive effects on contractile force observed in muscle held at successively longer lengths (Fig. 3).

Fig. 5.

Physical models of muscle morphology demonstrate the influence of fiber angle on the mechanical response to pressurization. Physical models comprise a fluid-filled silicone tube, representing fluid-filled muscle fibers or fascicles, reinforced by helically wrapped thread, representing ECM collagen (A). A core of latex tubing (shown by cutting away a strip of the reinforced silicone wall) spans the model interior and can be manually pretensioned to simulate isometric force production (B). The orientation of reinforcing fibers determines the effect of pressurization on model length (C and D). Squeezing via pressure cuffs elicits shortening of a model with reinforcing fibers oriented at ∼25° relative to the model long axis (C). In contrast, squeezing elicits lengthening of a model with more perpendicular reinforcements oriented at ∼75° (D). The latex core is left slack in both (C and D) to prevent it interfering with length changes.

Fig. 6.

The effect of squeezing on force generated by 6 physical models with various reinforcing fiber angles. Models were connected to a force transducer at constant length, pretensioned to an initial “active” force of 10 N via stretching of the internal latex core, and squeezed at 260 mmHg with a pneumatic pressure cuff. Mean fiber angles (measured from photographs of models taken immediately prior to squeezing) and SDs (gray horizontal error bars) are displayed for each model. Forces immediately before squeezing (gray circles) and after squeezing (black circles) are reported. Squeezing decreased tensile force in models with relatively high fiber angles oriented more perpendicular to the long axes of models. Squeezing increased tensile force in models with relatively low angles more parallel to the long axes of models. Triangular markers indicate minimum and maximum mean collagen fiber angles observed in the ECM endomysium (white triangles; ref. 22) and perimysium (gray triangles; ref. 21) of skeletal muscle fixed at either very short or very long lengths.

Discussion

We find that pressurizing muscle via squeezing can cause immediate, significant changes in passive and active isometric force. The most surprising result was that the application of squeezing force resulted in a decrease in contractile force at short muscle lengths but an increase in force at long muscle lengths. A simple model of muscle fiber and extracellular matrix (ECM) morphology replicates this behavior, suggesting that it can be explained by the interaction of intramuscular fluid pressures with fibrous collagen surrounding muscle fibers and fascicles. Recent evidence from computational models and empirical studies suggest that forces are transmitted between the ECM and intramuscular fluids during passive deformation of muscle, resulting in the development of intramuscular fluid pressures that affect passive muscle mechanics (18–20). The current work suggests that forces transmitted from pressurized intramuscular fluid to the ECM can also affect force produced during active contraction. The collagenous extracellular matrix has been recognized as a pathway for force transmission from sarcomeres to tendon, with costamere protein complexes serving as a mechanical link between myofibrils and the ECM (24). Our observations on pressurized muscle and models suggest that pressurized fluid may serve as an additional medium through which myofibril force is transmitted to the extracellular matrix and eventually the skeletal system. Additionally, the ECM may provide an avenue by which off-axis forces and fluid pressures within muscle are transformed and redirected into longitudinal forces oriented along the long axes of muscle fibers. These results highlight the complexity and 3-dimensionality of pathways for force transmission within muscle and suggest that intramuscular pressure should be considered in physiological models that attempt to predict or simulate muscle force production in vivo.

Collagen Fiber Angle Mediates the Influence of Pressure on Force.

The physical models demonstrate the potential for helically arranged fibers to redirect and transform hydrostatic forces within a cylindrical container. The models presented here are mechanically similar to McKibben actuators, a class of engineered pneumatic actuator developed for use in robotics and artificial limb research (25). McKibben actuators are cylindrical tubes that either forcibly shorten or lengthen when inflated with compressed air. Helical fibers surrounding a McKibben actuator translate the radial forces developed by internal air pressure into longitudinal forces oriented along the long axis of the actuator. Whether this results in forceful shortening or lengthening of the actuator depends on the helical pitch at which reinforcing fibers are oriented. Geometric analysis shows that a pitch of 54° 44′ relative to the long axis maximizes the volume of space bounded by a sleeve of helically wound fibers (26). Thus, pressurization can always be expected to elicit a change in the length of a McKibben actuator that brings its reinforcing fibers closer to this ideal pitch. Our physical models behave in a manner consistent with this theory. Pressurization of models with helical fibers pitched below 54° 44′ results in tension and shortening, while pitches greater than 54° 44′ yield forceful elongation.

The skeletal muscle ECM is heavily reinforced by fibrous collagen that ensheathes individual muscle fibers (endomysial collagen) and groups of muscle fibers (perimysial collagen) (27, 28). Empirical measurements reveal that the orientation of collagen relative to the axis of muscle fibers varies as a function of muscle length (21, 22, 29–31). The relationship between ECM collagen angle and muscle length has been systematically quantified in cow muscle (21, 22), but changes in collagen orientation with muscle length have also been observed in frog (30), sheep (29), and chicken (31) muscle, suggesting that variation in ECM orientation with muscle length is a general feature of vertebrate skeletal muscle. ECM collagen is primarily oriented at high angles greater than 54° 44′ (relative to the axis of muscle fibers) at short muscle lengths and low angles less than 54° 44′ at long muscle lengths (refs. 21 and 22; see triangular markers in Fig. 6). Variation in collagen orientation facilitates low-force deformation of the ECM and is predominantly considered a mechanism that accommodates stretching and shortening of muscle over its functional length range (21).

In addition to influencing muscle’s mechanical response to stretch, our findings indicate that ECM collagen orientation mediates muscle’s mechanical response to pressurization. We observed reductions in active contractile force following squeezing at short muscle lengths (which correspond with high collagen angles) and increases in active contractile force at long lengths (which correspond with low collagen angles) (Fig. 3). Pressurization did not have a significant influence on tensile force at intermediate muscle lengths 1.1 and 1.15 L₀, suggesting that collagen may be oriented close to 54° 44′ at these lengths. Empirical measurements of collagen orientation suggest than an angle of 54° 44′ should occur at sarcomere lengths ∼2–2.5 μm (21, 22), which correspond roughly with the plateau of the vertebrate active length-tension curve (32) and the length range of 1.1–1.15 L₀ in which we did not observe a significant effect of squeezing on contractile force.

One potentially relevant feature of skeletal muscle not reflected in the design of our physical models is the crimped morphology of ECM collagen. Regular crimps present along the length of ECM collagen fibers increase the elasticity of the ECM and provide an additional strain mode that accommodates deformation of the ECM over the functional length range of muscle (21, 29). Crimps in ECM collagen are most apparent at intermediate muscle lengths when collagen is oriented close to 54° 44′, and decrease in size at longer and shorter muscle lengths as collagen is drawn taught against the bulk of incompressible muscle fibers it surrounds (21). In all physical models, Kevlar sewing thread of uniform stiffness was used to represent ECM collagen regardless of the helical orientation of fibers. This design represents a simplification of the mechanical properties of the muscle ECM, in which the stiffness of individual collagen fibers varies with the degree of crimping and is thus correlated with muscle length and collagen fiber angle. We do not think that this simplification significantly alters the mechanical behavior of the physical models. If variable fiber stiffness had been incorporated into models with different reinforcing fiber angles, we would still expect squeezing to increase force in models with more parallel (lower than 54° 44′) fiber angles and decrease force in models with more perpendicular (greater than 54° 44′) fiber angles. Introducing crimping or slack into reinforcing fibers in models with intermediate pitches would only reduce the effect of squeezing on these models, exaggerating the angle-dependent effects of pressure on force already displayed. The models presented here focus primarily on the influence of fiber pitch on the mechanical response to pressurization, but it is important to note that the increased presence of crimps and decreased stiffness of the ECM is likely an additional factor that contributes to the reduced effects of pressurization on force observed in muscle at intermediate lengths.

Sources and Effects of Pressure in Muscle.

Intramuscular fluid pressures develop during normal physiological activities, such as walking and running (33), in both actively contracting and passively deformed muscle (1). Intramuscular pressures likely arise as complex functions of muscle fiber geometry, tension, and the material properties of the sarcolemma and extracellular matrix. In single isolated muscle fibers, the development of intracellular fluid pressure coincides with fiber shortening and circumferential distension of the sarcolemma but is not influenced by the development of active isometric force in the absence of shortening (10). In whole muscles with more complex spindle-shaped or pennate architectures, pressure is inevitably influenced by muscle force as muscle fibers are often curved in these muscles and necessarily exert a portion of their developed tension inwards along their concave sides, effectively squeezing neighboring muscle fibers within the muscle belly (4, 9, 34). Intramuscular pressure has been shown to correlate with both passive and active tensile force in some muscles (1, 35), making intramuscular pressure of clinical interest as a potential indicator of force produced by individual muscles in vivo. The current work suggests that in addition to serving as an indicator of force, intramuscular pressure likely acts as a determinant of force, altering the mechanical behavior of both passively stretched and actively contracting muscle during normal physiological activity.

A growing body of evidence indicates that radial constraints that hinder muscle bulging during contraction can have significant impacts on muscle force and work production. Transverse loads applied to a muscle belly reduce isometric force developed during contraction (13) and the magnitude of these effects is correlated with the magnitude of the transverse load applied (14, 15). Similarly, inhibiting radial expansion of muscle during shortening contraction reduces mechanical work produced along the shortening axis of muscle (17). Such effects are physiologically relevant as many muscles are surrounded in vivo by fascial constraints and other muscles that have been shown to influence force via mechanisms that are not fully understood (36–38). It has been suggested that increased mechanical work done in the radial direction underlies decreases in muscle performance in the presence of radial constraints and transverse loads (13). A notable feature of the current work is that rather than muscle exerting force or doing work on a radial constraint, here the radial constraint is loaded with mechanical energy (in the form of pressurized air) and, thus, does work and exerts force on the muscle. That force is altered by this perturbation suggests radial constraints and their associated forces can influence muscle mechanics even when muscles do no mechanical work on them. Variations in internal pressure may ultimately underlie the effects of transverse loads on muscle force and work production, and anatomical structures that surround or constrain muscles in vivo may influence performance via their effects on intramuscular pressure.

Previous studies have used isolated muscles and muscle fibers mounted in sealed pressure chambers to explore the influence of increased hydrostatic pressure on contractile force (e.g., refs. 39–41). These studies show hydrostatic pressure having relatively small effects on contractile force, even when pressures applied are orders of magnitude larger than those used in the present study. Using a sealed pressure chamber, Vawda et al. (41) report reductions in contractile force of less than 1% per 7,500 mmHg (1 MPa) of applied pressure. In contrast, we found that squeezing muscle with a pneumatic cuff at an inflation pressure of only 260 mmHg could elicit force reductions in excess of 10%. A crucial difference between pressure chamber studies and the current work is the method of pressure application. Pressurization of muscle via an enclosed pressure chamber results in equalization of intramuscular and external pressure, such that pressures in all parts of the muscle are increased significantly but balanced by external forces. Although the precise mechanism remains undetermined, it has been proposed that that such global changes in muscle pressure influence force via an effect on cross-bridge kinetics during tetanic contraction, altering the rate of cross-bridge cycling or the force generated per crossbridge (41). Squeezing via a pneumatic cuff represents a distinct perturbation as it affects only a portion of the muscle belly, causing an increase in intramuscular pressure that is not balanced by external pressures over much of the muscle belly. Intramuscular pressures vary in magnitude with anatomical position within the muscle belly (2, 7), and the inhomogeneous forces generated by the pressure cuff are likely representative of pressures experienced by muscles in vivo. Being unbalanced by external forces, these pressures must be balanced internally by either sarcomere-generated forces or by material deformation of tissue components, such as the sarcolemma or ECM, processes that we propose alter the amount of force ultimately delivered to the muscle insertion. Pressure-induced movements of intramuscular fluid from high to low pressure spaces within muscle are likely an important consequence of squeezing; however, whether these occur in intracellular, extracellular, capillary, or a combination of these fluid spaces is not obvious. The ECM ensheathes muscle fibers, fascicles, intramuscular blood vessels, and the muscle perimeter (27) and, thus, it is conceivable that interactions between intramuscular fluid and the ECM could influence muscle mechanics at multiple spatial scales.

Differential Effects of Pressure on Active and Passive Muscle.

The effect of squeezing on muscle force was lower in passive, relaxed muscle than in actively contracting muscle. At relatively short muscle lengths 1.0 L₀ and below, squeezing had no effect on passive muscle force (Fig. 4 A and B). Presqueeze passive force was effectively 0 at these lengths, and we hypothesize that the presence of slack in muscles prevented pressurization from having a detectable effect on force measured at the load cell. At long muscle lengths 1.15, 1.20, and 1.25 L₀, squeezing caused significant increases in passive muscle force; however, these increases were smaller in magnitude than increases in active force observed at the same lengths. For example, at muscle length 1.25 L₀, squeezing elicited a 3.08% of P₀ increase in active force but only a 1.33% of P₀ increase in passive force, more than a 2-fold difference (Figs. 3B and 4B). The distribution and magnitude of intramuscular pressure varies considerably between active and passive muscles (1, 2), and this variation could underlie the differing responses of active and passive muscle to squeeze. Intramuscular pressures have the potential to mechanically load the ECM, drawing ECM collagen into tension and increasing its ability to transmit force within muscle. Such a mechanism could allow the ECM to influence active state mechanics at muscle lengths where collagen would be partially or fully slack in the passive condition.

Alternative Mechanisms.

Regarding the perturbation used in this study, it is possible that squeezing muscle could influence contractile force via additional or alternative mechanisms that do not involve the extracellular matrix. Multiple mathematical models of muscle suggest that increased intracellular fluid pressure alone could influence contractile force (10–12). These models do not incorporate the effects of ECM collagen, but instead suggest that intracellular fluid pressure should reduce contractile force by exerting a force over the cross-sectional area of muscle fibers. Such forces would directly oppose shortening forces generated by myofibrils, resulting in a net reduction in force delivered to the muscle insertion. This mechanism has the potential to account for reductions in isometric contractile forces during pressurization, as occurred on the ascending limb and plateau of the length-tension curve in the current study (Fig. 3). However, such mechanisms cannot account for increases in contractile force observed at long muscle lengths and would not predict the length-dependent relationship between squeezing and contractile force observed here.

Changes in muscle fiber dimensions resulting from squeezing also have the potential to influence force. Since muscles maintain a nearly constant volume over short time scales, radial squeezing could conceivably alter the length of individual muscle fibers and influence force via length-tension effects (32). Lattice spacing, the radial distance between actin and myosin filaments within muscle sarcomeres, also influences contractile force (42) and could conceivably be altered by radial squeezing. We do not expect that changes in either muscle fiber length or lattice spacing are likely explanations for the effects of localized pressure seen in the present study. High-speed video tracking of suture markers during muscle contraction and cuff inflation allowed quantification of muscle fascicle strain during squeezing (SI Appendix, Fig. S1). Changes in marker distance during cuff inflation were small, on the order of 0.1–0.5 mm (∼1–4% fascicle strain) and could not account for observed changes in active contractile force based on length-tension properties alone. Additionally, both length-tension and lattice spacing effects are unlikely to explain our result as squeeze-induced shifts in either muscle fiber length or lattice spacing would be expected to alter the length (L₀) at which muscles produce maximum force (P₀) but would not be expected to reduce the magnitude of P₀. Comparison of presqueeze and postsqueeze active length-tension curves from one representative muscle shows that P₀, the maximum isometric contractile force produced by the muscle, is reduced in magnitude in a postsqueeze length-tension curve relative to a presqueeze length-tension curve (Fig. 3A). Similar reductions were observed across all experimental muscles (n = 7).

Skeletal Muscle in Relation to Other Biological Hydrostatic Skeletons.

Interactions between pressurized fluid spaces and tensile reinforcing fibers are common in biological systems. Among animals, hydrostatic skeletons bound by fibrous connective tissues are crucial to the mechanical development of the vertebrate notochord (43) and provide rigid support to such diverse structures as the body cavities of worms, the tube feet of echinoderms, and the reproductive organs of mammals and turtles (44). Among plants and fungi, interactions between intracellular turgor pressure and the fibrous cell wall give rise to hydrostatic skeletons that control many aspects of cell morphogenesis and organismal growth (45). Classic Hill-type models of skeletal muscle mechanics do not incorporate fluid mechanics into their designs, and instead replicate the mechanical behaviors of muscle through interactions of force producing elements with in-series and in-parallel elastic springs (46). Models of muscle that incorporate the interaction of intramuscular fluid with ECM collagen can explain peculiarities of muscle behavior that are not accounted for by classic muscle models, such as tension-compression asymmetry in passively deformed muscle (18) and the effect of fluid volume changes on passive muscle force (19, 20). The current results suggest that intramuscular pressure, via a hydrostat-like interaction with extracellular matrix collagen, may act as an important but largely unacknowledged determinant of muscle force. Continued study of the hydrostat-like nature of muscle has great potential to advance our understanding of the tissue and may reveal new parallels between muscle physiology and seemingly disparate areas of biomechanical research.