A compartment size-dependent selective threshold limits mutation accumulation in hierarchical tissues

Significance

Renewed tissues of multicellular organism accumulate mutations that lead to aging and cancer. To mitigate these effects, self-renewing tissues produce cells along differentiation hierarchies, which have been shown to suppress somatic evolution both by limiting the number of cell divisions, and thus reducing mutational load, and by differentiation “washing out” mutations. Our analytical results reveal the existence of a third mechanism: a compartment size-dependent threshold in proliferative advantage, below which mutations cannot persist, but are rapidly expelled from the tissue by differentiation. In sufficiently small compartments, the resulting selective barrier can greatly slow down somatic evolution and reduce the risk of cancer by preventing the accumulation of mutations even if even they confer substantial proliferative advantage.

Abstract

Cancer is a genetic disease fueled by somatic evolution. Hierarchical tissue organization can slow somatic evolution by two qualitatively different mechanisms: by cell differentiation along the hierarchy “washing out” harmful mutations and by limiting the number of cell divisions required to maintain a tissue. Here we explore the effects of compartment size on somatic evolution in hierarchical tissues by considering cell number regulation that acts on cell division rates such that the number of cells in the tissue has the tendency to return to its desired homeostatic value. Introducing mutants with a proliferative advantage, we demonstrate the existence of a third fundamental mechanism by which hierarchically organized tissues are able to slow down somatic evolution. We show that tissue size regulation leads to the emergence of a threshold proliferative advantage, below which mutants cannot persist. We find that the most significant determinant of the threshold selective advantage is compartment size, with the threshold being higher the smaller the compartment. Our results demonstrate that, in sufficiently small compartments, even mutations that confer substantial proliferative advantage cannot persist, but are expelled from the tissue by differentiation along the hierarchy. The resulting selective barrier can significantly slow down somatic evolution and reduce the risk of cancer by limiting the accumulation of mutations that increase the proliferation of cells.

Tumors develop as genetic and epigenetic alterations spread through a population of premalignant cells, and some cells accumulate changes over time that enable them and their descendants to persist within tissues (1, 2). From an evolutionary perspective, each tumor is an independent realization of a common reproducible evolutionary process involving “adaptive” mutations that are preferentially selected by the tumor environment. This process is clonal, which means that a subset of mutations termed “drivers” confer clonal growth advantage, and they are causally implicated in cancer development.

A large body of work (2–5) has focused on understanding clonal evolution of an initially homogeneous population of identical cells, a subset of which progress toward cancer as they accrue driver mutations. Beerenwinkel et al. (6), for instance, considered the Wright–Fisher process (a homogeneous population of initially identical cells) to explore the basic parameters of this evolutionary process and derive an analytical approximation for the expected waiting time to the cancer phenotype and highlighted the relative importance of selection over both the size of the cell population at risk and the mutation rate.

Self-renewing tissues, which must generate a large number of cells during an individual’s lifetime and in which tumors typically arise, comprise a hierarchy of progressively differentiated cells and, as a result, are not homogeneous populations of identical cells. There is empirical evidence (7–9) and theoretical rationale (10–12) that such hierarchical tissue architecture has a profound effect on neoplastic progression. Theoretical work has demonstrated that hierarchically organized tissues suppress tumor evolution by limiting the accumulation of somatic mutations in two fundamentally different ways, as follows.

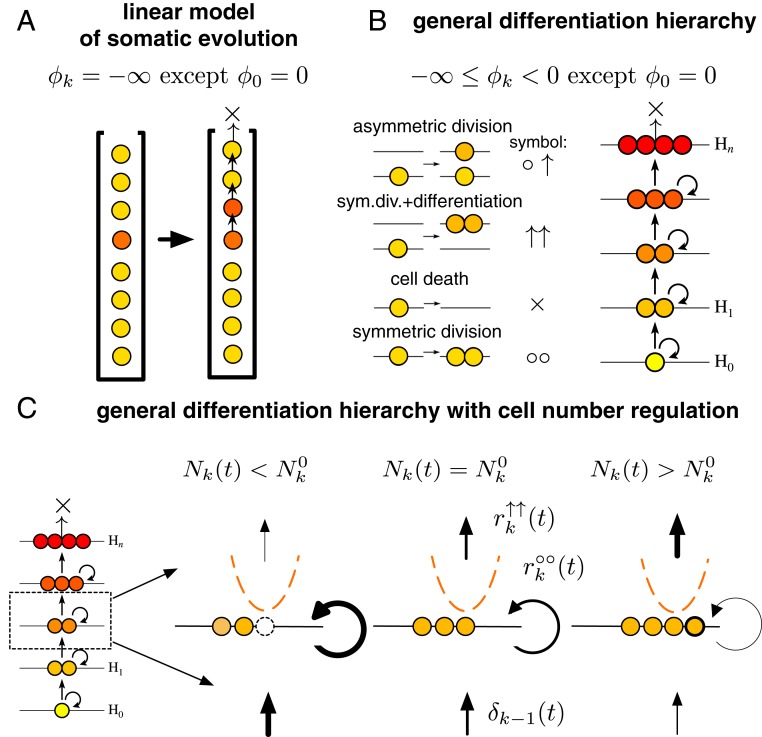
As described in a seminal paper by Nowak et al. (11), the linear flow from stem cells to differentiated cells to apoptosis in a spatially explicit, strictly linear organization has the property of canceling out selective differences. Nowak et al. considered a system where only asymmetric cell divisions are allowed, that is, after each cell division, one of the daughter cells differentiates to the next level of the hierarchy, pushing all cells at higher levels farther along the hierarchy (Fig. 1A). In this idealized construction, mutations, irrespective of how much they increase division rate, are invariably “washed out” unless they occur in the stem cell at the root of the hierarchy. In a more general setting, where symmetric divisions are allowed, the strength of this washing out effect can be quantified by introducing the self-renewal potential of cells. The self-renewal potential is defined as the logarithm of the ratio between the rate of cell divisions that increase the number of cells at a given level of the hierarchy (division producing two cells at the same level) and the rate of events that result in the reduction at that level (division producing two differentiated cells that move higher up in the hierarchy or cell death). In healthy homeostatic tissues, the self-renewal potential of stem cells is zero (corresponding to equal rates of differentiation and self-renewal), while, for differentiated cells, it is always negative, as these cells have an inherent proliferative disadvantage as a result of which they are eventually washed out of the tissue from cells differentiating from lower levels of the hierarchy. In the following, lower (higher) refers to levels closer to (farther away from) the stem cell compartment.

Fig. 1.

Self-renewing tissue comprising a hierarchy of progressively differentiated cells can suppress somatic evolution. (A) The linear process of somatic evolution considers a strict linear organization, where, after each cell division, one of the daughter cells differentiates to the next level, pushing all cells above farther along, and the top-most cell is lost from the system. Such an idealized construction, where self-renewal at individual levels of the hierarchy is not allowed, has a minimal self-renewal potential ${\varphi }_k=-\infty$, with the exception of the stem cell level at the root of the hierarchy with ${\varphi }_0=0$. This has the effect of canceling out selective differences between cells; that is, any non-stem cell, regardless of how large its division rate is, will be washed out of the tissue by cell differentiating from below. (B) General differentiation hierarchies are characterized by intermediate values of the self-renewal potential, with the exception of the stem cell. In such systems, in the absence of cell number regulation, any mutant with a proliferative advantage, that is, a positive self-renewal potential, will spread exponentially if it does not go extinct stochastically. (C) We introduce cell number regulation that changes the rate of different events such that the strength and direction of the regulation depends on the difference between the number of cells present at a given time $N_k\left(t\right)$ and the homeostatic number $N_k^0$ in a manner equivalent to being in a quadratic potential (Eq. 3). As described in the text, this leads to the emergence of a positive threshold proliferative advantage below which mutants cannot persist.

More recently, Derényi and Szöllősi (12) showed that, in self-renewing tissues, hierarchical organization provides a robust and nearly ideal mechanism to limit the divisional load (the number of divisions along cell lineages) of tissues and, as a result, minimize the accumulation of somatic mutations. The theoretical minimum number of cell divisions can be very closely approached: As long as a sufficient number of progressively slower dividing cell types toward the root of the hierarchy are present, optimal self-sustaining differentiation hierarchies can produce $N$ terminally differentiated cells during the course of an organism’s lifetime from a single precursor with no more than ${\log }_2\left(N\right)+2$ cell divisions along any lineage.

Here, we examine the effect of compartment size by introducing interaction among cells in the form of cell number regulation, which acts on the cell division rates such that the number of cells at each hierarchical level of the tissue has the tendency to return to its desired homeostatic value. We consider a single (non-stem cell) level of the hierarchy that is renewed from below by cell differentiation. We introduce mutants with a proliferative advantage, that is, mutants with a positive self-renewal potential. As detailed below, using both simulations and an approximation adopted from nonequilibrium statistical physics, we find that, under a wide range of parameters, a third fundamental mechanism exists by which hierarchically organized tissues can slow down somatic evolution and delay the onset of cancer.

Results

We consider level $k>0$ of a general differentiation hierarchy that is renewed by cell differentiation from level $k-1$ below. The tissue dynamics is described by the rates of asymmetric differentiation ($○\hspace{0.17em}\uparrow$), symmetric division with differentiation ($\uparrow \uparrow$), symmetric division ($○○$), and cell death ($\times$) (Fig. 1 B and C).

At homeostasis (i.e., when the number of cells, $N_k$, at each level coincides with its homeostatic value, $N_k^0$), the evolutionary dynamics of level $k$ is determined by the per cell rate $r_k^{+}=r_k^{○○}$ of cell number increase through symmetric cell division ($○○$), the per cell rate $r_k^{-}=r_k^{\uparrow \uparrow }+r_k^{\times }$ of cell number decrease through either symmetric division with differentiation ($\uparrow \uparrow$) or cell death ($\times$), and the per level rate ${\delta }_k^{+}={\delta }_{k-1}=\left(2r_{k-1}^{\uparrow \uparrow }+r_{k-1}^{○\uparrow }\right)N_{k-1}$ of cell number increase through differentiation from below. In the following, we focus on a single (non-stem cell) level, and drop index $k$ for brevity. Homeostasis implies that the rates satisfy the stationarity condition

$$\left(r^{-}-r^{+}\right)N^0={\delta }^{+}.$$ [1]

To model tissue size regulation, we consider a generic cell number-dependent regulation scheme that acts to return the number of cells in the compartment to its homeostatic value. Biologically, such a regulation scheme corresponds to, for example, the local concentration of a regulatory signal that conveys information on the density of cells in a compartment. To formalize cell number regulation, we introduce cell number-dependent multiplicative rate modifiers ${\rho }^{+}\left(N\right)$ and ${\rho }^{-}\left(N\right)$ for, respectively, events that increase and decrease cell number. Maintaining homeostasis requires that ${\rho }^{+}\left(N\right)>1$ and ${\rho }^{-}\left(N\right)<1$ if $N<N^0$, and ${\rho }^{+}\left(N\right)<1$ and ${\rho }^{-}\left(N\right)>1$ if $N>N^0$. These rate modifiers define an abstract confining potential $U\left(N\right)$ up to an additive constant,

$$U\left(N+1\right)-U\left(N\right)=-\log \frac{{\rho }^{+}\left(N\right)}{{\rho }^{-}\left(N+1\right)},$$ [2]

with a minimum at $N=N^0$. For mathematical convenience, we approximate the confining potential with a parabolic (harmonic) form,

$$U\left(N\right)=\frac{1}{2}\beta \frac{{\left(N-N^0\right)}^2}{N^0},$$ [3]

characterized by a single parameter (potential strength) $\beta$. The role of the confining potential is to limit the variance of the number of cells to $N^0/\beta$. It is this confining potential that plays the most significant role in slowing down somatic evolution, as shown below.

The particular choice of how the confining potential is distributed between the cell number increasing and decreasing rate modifiers (to satisfy Eq. 2) has only marginal effect on the dynamics. Here, for simplicity, we make the symmetric choice,

$${\rho }^{+}\left(N\right)={\mathrm{e}}^{-\frac{1}{2}\beta \frac{N-N^0}{N^0}}\hspace{1em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{1em}{\rho }^{-}\left(N\right)={\mathrm{e}}^{\frac{1}{2}\beta \frac{N-N^0}{N^0}}.$$ [4]

We measure time in units of $1/\left(2r^{-}{N}^0\right)$. Thus, the lifetime of the tissue $T$ is identical to the expected number of differentiated cells that would be produced by this level under homeostatic conditions during the individual’s lifetime, if all of the cell number decreasing events were symmetric cell differentiations. As the asymmetric differentiations ($○\hspace{0.17em}\uparrow$) do not have any influence on the number of cells of this level, we set its rate ($r^{○\uparrow }$) to zero for convenience.

The self-renewal potential of the cells in a healthy homeostatic tissue is defined as

$$\varphi =\ln \frac{r^{+}}{r^{-}}\le 0,$$ [5]

which converges to $-\infty$ as the rate of the ($○○$) events approaches zero.

We introduce mutants with an elevated rate of divisions that increase cell number, $r_{\mathrm{m}}^{+}$, such that it exceeds the rate of cell number decrease: $r_{\mathrm{m}}^{+}>r^{-}$. This corresponds to a positive self-renewal potential for mutant cells,

$${\varphi }_{\mathrm{m}}=\ln \frac{r_{\mathrm{m}}^{+}}{r^{-}}>0.$$ [6]

In the absence of cell number regulation (i.e., $\beta =0$), a single such mutant either goes extinct stochastically or spreads exponentially with probability (13)

$$S_{\mathrm{m}}=1-\frac{r^{-}}{r_{\mathrm{m}}^{+}}=1-{\mathrm{e}}^{-{\varphi }_{\mathrm{m}}}.$$ [7]

In the following, we use $S_{\mathrm{m}}$ to parametrize the selective advantage of mutants. We note that, in the absence of differentiation from below (i.e., ${\delta }^{+}=0$), for fixed population size (i.e., $\beta \to \infty$), for all but extremely small populations or nearly neutral mutations, $S_{\mathrm{m}}$ also corresponds to the probability of fixation of the mutant (14–16).

Denoting the number of mutant cells by $N_{\mathrm{m}}$ and denoting wild-type cells by $N_{\mathrm{w}}$, the dynamics is described by the transition rates

$$\begin{array}{ll}\hfill k_{\mathrm{m}}^{+}\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)& =\hspace{1em}{N}_{\mathrm{m}}{r}_{\mathrm{m}}^{+}\hspace{0.17em}{\rho }^{+}\left(N_{\mathrm{m}}+N_{\mathrm{w}}\right),\hfill \\ \hfill k_{\mathrm{m}}^{-}\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)& =\hspace{1em}{N}_{\mathrm{m}}{r}^{-}\hspace{0.17em}{\rho }^{-}\left(N_{\mathrm{m}}+N_{\mathrm{w}}\right),\hfill \\ \hfill k_{\mathrm{w}}^{+}\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)& =\hspace{0.17em}\left(N_{\mathrm{w}}{r}^{+}+{\delta }^{+}\right)\hspace{0.17em}{\rho }^{+}\left(N_{\mathrm{m}}+N_{\mathrm{w}}\right),\hfill \\ \hfill k_{\mathrm{w}}^{-}\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)& =\hspace{1em}{N}_{\mathrm{w}}{r}^{-}\hspace{0.17em}{\rho }^{-}\left(N_{\mathrm{m}}+N_{\mathrm{w}}\right),\hfill \end{array}$$ [8]

where the lower index (m or w) denotes the type of the cell (mutant or wild, respectively), and the upper index indicates whether the number of cells of the given type is increased ($+$) or decreased ($-$). The transition rates can be shown to correspond to a reversible Markov process in the effective potential

$$\begin{array}{ll}\hfill \mathrm{\Psi }\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)=& -N_{\mathrm{m}}{\varphi }_{\mathrm{m}}+\ln N_{\mathrm{m}}-N_{\mathrm{w}}\varphi \hfill \\ \hfill & +\ln \frac{\mathrm{\Gamma }\left(N_{\mathrm{w}}+1\right)}{\mathrm{\Gamma }\left(N^0\left({\mathrm{e}}^{-\varphi }-1\right)+N_{\mathrm{w}}\right)}\hfill \\ \hfill & +U\left(N_{\mathrm{m}}+N_{\mathrm{w}}\right),\hfill \end{array}$$ [9]

where $\mathrm{\Gamma }$ represents the gamma function.

The continuous interpolation of this potential is shown in Fig. 2, Bottom for different parameters. An effective potential, such as Eq. 9, can always be defined if the mutant and wild-type transition rates depend only on the number of cells of the given type, and if cell number regulation—which acts as a multiplicative modifier of these rates—depends only on the total number of cells (SI Appendix).

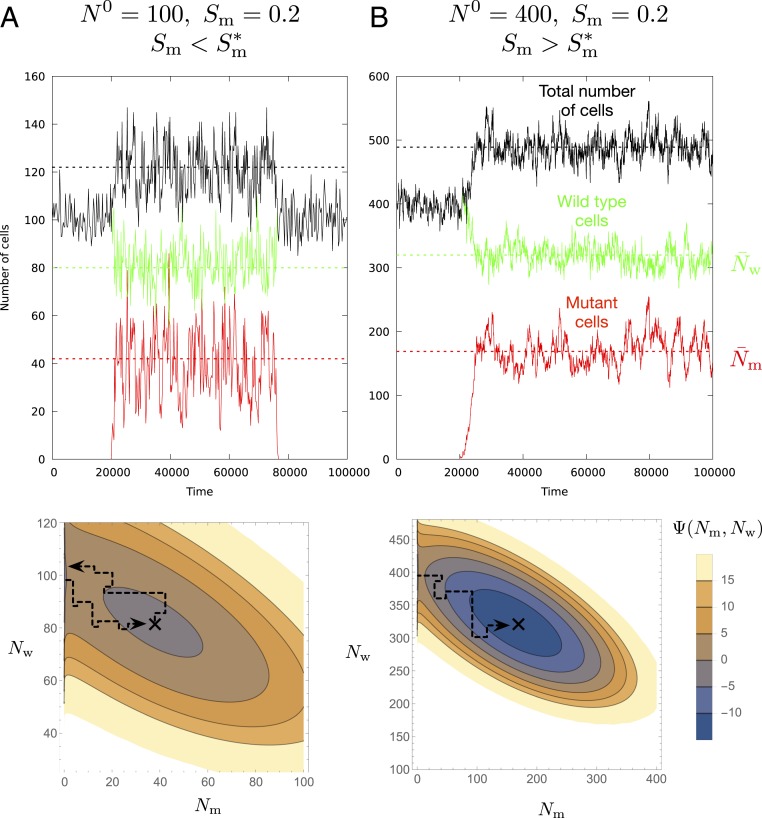
Fig. 2.

Mutants go extinct under a threshold proliferation advantage. The continuous lines show the size of the mutant (red) and wild-type (green) populations and their combined number (black) during the simulation. The dashed lines correspond to the theoretical mean population sizes in the quasi-stationary state. (A, Top) If the proliferation advantage of the mutant is below the threshold, the mutant will rapidly escape from the shallow quasi-stationary state and go extinct. (A, Bottom) The black $\times$ on the continuous approximation of the potential marks the quasi-stationary state. Parameters are $N^0=100$, $\beta =1$, and $r^{+}=0$, and $S_{\mathrm{m}}=0.2$ is below the threshold $S_{\mathrm{m}}^{*}=0.34$. (B, Top and Bottom) Increasing the compartment size to $N^0=400$, the potential well becomes deeper and the threshold proliferation advantage becomes correspondingly smaller $S_{\mathrm{m}}^{*}=0.17$, allowing a mutant with the same advantage of $S_{\mathrm{m}}=0.2$ to persist in the tissue during the individual’s lifetime.

Here we are concerned with cell number regulation that can be described by a confining potential with a single minimum, for which Eq. 3 is the parabolic approximation. In this case, the presence of size regulation (i.e., $\beta >0$) leads to a quasi-stationary state in which the mean number of mutant ${\overline{N}}_{\mathrm{m}}$ and wild-type ${\overline{N}}_{\mathrm{w}}$ cells can be determined to good approximation by solving

$$\frac{k_{\mathrm{m}}^{+}\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)}{k_{\mathrm{m}}^{-}\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)}=\frac{k_{\mathrm{w}}^{+}\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)}{k_{\mathrm{w}}^{-}\left(N_{\mathrm{m}},N_{\mathrm{w}}\right)}=1,$$ [10]

which gives

$$\begin{array}{ll}\hfill {\overline{N}}_{\mathrm{m}}& \approx N^0\left(\frac{S_{\mathrm{m}}}{1-r^{+}/r_{\mathrm{m}}^{+}}+\frac{{\varphi }_{\mathrm{m}}}{\beta }\right)=N^0\left(\frac{{\mathrm{e}}^{{\varphi }_{\mathrm{m}}}-1}{{\mathrm{e}}^{{\varphi }_{\mathrm{m}}}-{\mathrm{e}}^{\varphi }}+\frac{{\varphi }_{\mathrm{m}}}{\beta }\right),\hfill \\ \hfill {\overline{N}}_{\mathrm{w}}& \approx N^0\left(\frac{1-S_{\mathrm{m}}}{1-r^{+}/r_{\mathrm{m}}^{+}}\hspace{0.17em}\frac{{\delta }^{+}}{N^0{r}^{-}}\right)=N^0\left(\frac{1-{\mathrm{e}}^{\varphi }}{{\mathrm{e}}^{{\varphi }_{\mathrm{m}}}-{\mathrm{e}}^{\varphi }}\right).\hfill \end{array}$$ [11]

As illustrated in Fig. 2, the behavior of this quasi-stationary state can be divided into two regimes based on the value of the proliferative advantage $S_{\mathrm{m}}$ of the mutant. Below a threshold proliferative advantage, $S_{\mathrm{m}}^{*}$ mutants, even if they initially spread (i.e., avoid early stochastic extinction with probability $S_{\mathrm{m}}$), will nonetheless rapidly go extinct and, as a result, have vanishing probability to persist in the tissue throughout its lifetime. Above this threshold, however, if a single mutant avoids early stochastic extinction, with probability $S_{\mathrm{m}}$, a population of its descendants will persist with near certainty in the tissue throughout its lifetime.

The characteristic residence time of a population of mutants that have initially spread corresponds to the mean exit time $\tau$ of escape from the quasi-stationary state described above. Following the approach described by Gardiner (17) and Derényi et al. (18), an analytical approximation can be derived for $\tau$ of the general form (for details, see SI Appendix)

$$\tau ={\tau }_0{\mathrm{e}}^{\mathrm{\Delta }\mathrm{\Psi }},$$ [12]

where ${\tau }_0$ is the reciprocal of the attempt frequency and $\mathrm{\Delta }\mathrm{\Psi }=\mathrm{\Psi }\left(1,N^0\right)-\mathrm{\Psi }\left({\overline{N}}_{\mathrm{m}},{\overline{N}}_{\mathrm{w}}\right)$ is the height of the potential barrier for the escape from the quasi-stationary state (Fig. 2). $\mathrm{\Delta }\mathrm{\Psi }$ scales linearly with $N^0$ (for large $N^0$), corresponding to an exponential increase in $\tau$. In contrast, ${\tau }_0$, which depends only on the local geometries of the potential well and barrier, is proportional to ${\left(N^0\right)}^{3/2}$.

Using the mean exit time for escape from the quasi-stationary state, the probability $P$ that a single mutant persists (i.e., first spreads, and then avoids escape) for the lifetime of the individual can be expressed as

$$P=S_{\mathrm{m}}\hspace{0.17em}{\mathrm{e}}^{-T/\tau }.$$ [13]

As shown in Fig. 3A Top, the above approximation for the escape time $\tau$ is highly accurate, and it depends very sharply on the selective advantage of mutants. This results in a well-defined threshold selective advantage (Fig. 3A, Bottom) below which mutants, even if they avoid early stochastic extinction, will rapidly go extinct, that is, will be washed out by cells differentiating from below. Furthermore, the threshold value depends only weakly on the value of $\beta$ for reasonably strong cell number regulation, that is, for $\beta >1$ corresponding to the variance (in time) of the cell number being smaller than $N^0$.

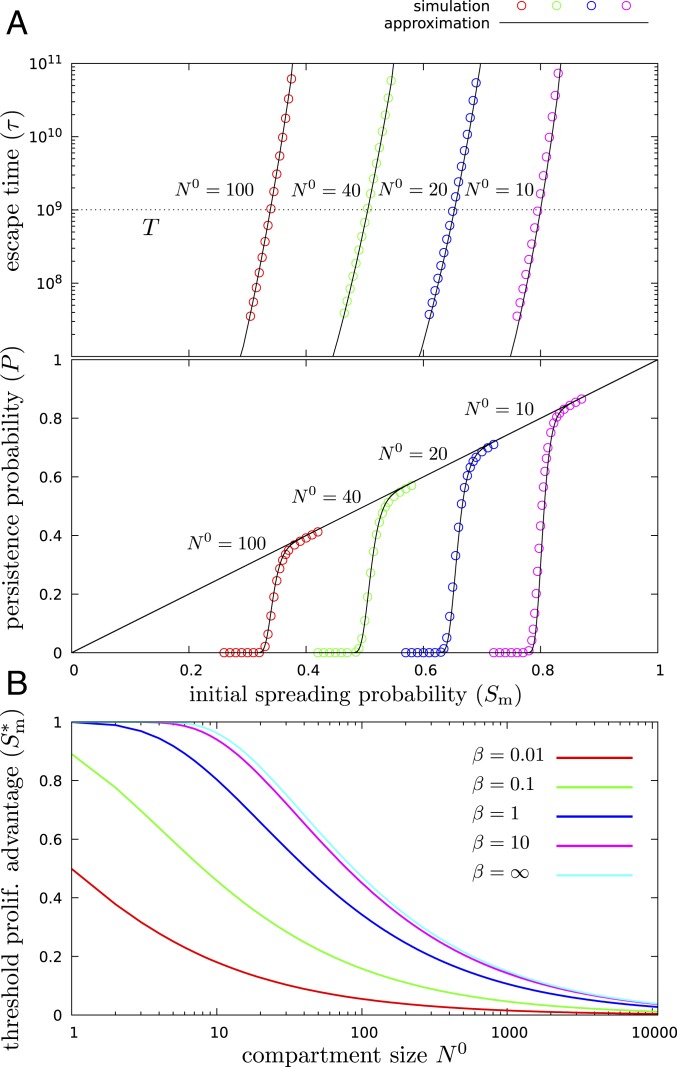
Fig. 3.

There is no somatic evolution under the threshold spreading factor. (A) In the presence of tissue size regulation ($\beta >0$), below a threshold proliferation advantage, $S_{\mathrm{m}}^{*}$, mutants rapidly go extinct and, as a result, have vanishing probability to persist in the tissue through its lifetime, while, above this threshold, if a single mutant avoids early stochastic extinction, which occurs with probability $S_{\mathrm{m}}$, it will persist with near certainty. Top shows the escape time of mutants, while Bottom displays their persistence probability. The diagonal line corresponds to the initial spreading probability, the colored circles show the results of the simulation, and the black continuous curves show the theoretical approximation, for different compartment sizes ($N^0$). $\beta =1$, $r^{+}=0$, and $T=10^9$ throughout. (B) The threshold separates the plot into two distinct regimes: Below the curve, the persistence probability is zero, and mutations cannot accumulate; above the curve, the mutants that avoid early stochastic extinction, which occurs with probability $S_{\mathrm{m}}$, will persist in the tissue during the lifetime of the individual, and mutations can accumulate, leading to neoplastic progression.

Realistic values for the rates $r^{-}$, $r^{+}$, and ${\delta }^{+}$ can vary greatly depending on tissue type and differentiation state [e.g., in humans, long-term stem cells of the hematopoietic system divide a few times a year, while, in the top layers of epithelial tissues, cell divisions occur daily (8, 12)]. Under homeostatic conditions, the three rates, however, cannot be chosen independently but must satisfy the stationary condition in Eq. 1. Furthermore, in the context of our model, as is apparent on inspection of $\mathrm{\Psi }$, the dynamics does not depend on the absolute rates but only on the ratio $r^{+}/r^{-}$, the logarithm of which defines the self-renewal potential $\varphi$ (Eq. 5).

Fixing $r^{-}$ specifies the absolute time scale, while changing the value of, for example, $r^{+}$ changes the values of the self-renewal potential $\varphi =\ln \left(r^{+}/r^{-}\right)$ and the strength of washing out, defined as the fraction of cells being produced by differentiation from below instead of self-renewal: ${\delta }^{+}/\left(N^0{r}^{-}\right)=1-r^{+}/r^{-}=1-\exp \left(\varphi \right)$. In particular, $r^{+}=0$, the default value used in several examples above, corresponds to minimal self-renewal potential ($\varphi =-\infty$) and maximal washing out (${\delta }^{+}/\left(N^0{r}^{-}\right)=1$). Increasing values of $r^{+}/r^{-}>0$ correspond to increasing self-renewal potential and weakening washing out. As shown in SI Appendix, Fig. S4, even for strong self-renewal and correspondingly weak washing out, the threshold spreading factor can be large in small compartments.

Discussion

In classical population genetics models of finite populations, a mutation is either fixed in the population or lost from it within a finite length of time. A fundamental result of population genetics theory is that, in constant populations, mutations with a given selective advantage will avoid early stochastic extinction and fix with a probability independent of population size and proportional to the selective advantage (14–16). As a corollary, in the context of somatic evolution, Michor et al. (19) demonstrated that the accumulation of oncogene-activating mutations (i.e., mutations that provide a proliferative advantage) that occur at a constant rate per cell division is faster in large than in small compartments. Consequently, as pointed out by Michor et al., the classical theory of finite populations of constant size implies that the organization of self-renewing tissues into many small compartments, such as the stem cell pools in colonic crypts, from which the tissue is derived, protects against cancer initiation (5). Further work by Beerenwinkel et al. (6), using qualitatively similar models with a single compartment without differentiation from below, found that the average waiting time for the appearance of the tumor is strongly affected by the selective advantage, with the average waiting time decreasing roughly inversely proportional to the selective advantage. The mutation rate and the size of the population at risk, in contrast, were found to contribute only logarithmically to the waiting time and hence have a weaker impact.

In hierarchically organized tissues with finite compartment size, the situation is more complicated. A mutant that avoids early stochastic extinction and achieves a sizable seemingly stable population can go extinct as a result of differentiation from below. This results in a qualitatively different and more profound ability of smaller compartment size to limit the accumulation of mutations. Similarly to classical population genetics models, the initial spreading probability of a mutation in a compartment of a hierarchical tissue is proportional to the proliferative advantage $S_{\mathrm{m}}$ and independent of the compartment size. However, as can be seen in Fig. 3A, the probability of the mutation to persist in the tissue exhibits a threshold that is strongly dependent on compartment size. For small compartments, even mutants with a very large selective advantage will only persist for a very short time; for example, a mutant with a selective advantage of $10\%$, that is, $S_{\mathrm{m}}\approx 0.1$, the largest value considered by Beerenwinkel et al. (6), will rapidly go extinct in compartments with up to several hundred cells.

An important exception is constituted by tissue-specific stem cell compartments residing at the bottom of the hierarchy, such as the stem cells at the bottom of colonic crypts. As these compartments do not receive an influx of cells from lower levels, their dynamics can be described by the classical population genetics models discussed above, that is, mutations can accumulate more easily.

The derivation of the results presented above relies on the existence of the potential defined in Eq. 9. In our model, this is ensured by the assumptions that 1) the transition rates for cells of each type depend only on the number of cells of that type and 2) cell number regulation acts as a multiplicative rate modifier and depends only on the total number of cells. There are several biologically relevant violations that must be considered. In real tissues, the first assumption, the independence in the absence regulation, is, in general, violated by mutation of wild-type cells into mutant cells (and vice versa), as this increases the number of mutant cells at a rate dependent on the number of wild-type cells (and vice versa). In the context of most, if not all, somatic tissues, the rate of mutations that confer significant selective advantage is sufficiently low that the waiting time between successive mutations is much longer than the relevant time scale of the dynamics considered here; thus, it has a negligible effect on the persistence time, and, as a result, it does not affect our conclusions. This is even more the case for back-mutations from mutants to the wild type. The second assumption, the postulation of a simple form of cell number regulation that acts as a multiplicative modifier and depends only on the total number of cells, is clearly a simplification. It neglects, for instance, explicit spatial organization and any potential long-term memory, such as hysteresis of the homeostatic compartment size dependent on either intrinsic or extrinsic parameters. Such a simplified form of regulation, however, is consistent with more detailed models of homeostatic tissue size regulation, such as recent work on the stability of regulation (20–22) and its optimality in terms of reducing mutation accumulation (23).

In order to quantitatively discuss the biological relevance of our results, we must consider relevant values of two parameters: compartment size ($N^0$) and the strength of the homeostatic cell number regulation ($\beta$). Consider, for instance, the intestinal crypts. Our knowledge of intestinal crypt organization is most extensive for murine tissues, where crypts are believed to consist of approximately 250 cells in total, out of which 160 to 180 are proliferative progenitor cells and 4 to 8 are stem cells residing near the bottom of the crypt (24–27). Methods using bromodeoxyuridine labeling (28), Ki-67 antibody staining (20), and analysis of methylation patterns (29) conclude that the crypts in humans contain around 2,000 cells, with the number of progenitor cells being between 500 and 700. In the context of our model, assuming that proliferative cells can be regarded as belonging to between 1 and 10 discrete levels of progressively faster dividing cells corresponds to values of $N^0\approx 170\text{to}17$ cells in mice and $N^0\approx 600\text{to}60$ in humans. Experimental evidence on the strength of cell number regulation is much more limited. Bravo and Axelrod (20), however, have measured the variation in cell numbers across biopsies in 49 crypts from human individuals and found a mean of 624 proliferative cells with an SD of 234. Assuming that 1) all of the proliferative cells belong to a single compartment and 2) all of the observed variation across crypts can be attributed to cell number fluctuations around a common homeostatic value, that is, ignoring completely variation in homeostatic size across crypts and neglecting measurement error, provides a lower bound on the strength of regulation of $\beta \gg 624/234^2\approx 0.01$. The generally well-defined cylindrically symmetric morphology of crypts, however, suggests that an SD corresponding to, at most, $10\%$ of the mean cell number is more realistic. Assuming between 1 and 10 levels, this corresponds to $1/\left(62.4\times 0.1^2\right)\approx 1.6>\beta >1/\left(624\times 0.1^2\right)\approx 0.16$ in human and $1/\left(17\times 0.1^2\right)\approx 6>\beta >1/\left(170\times 0.1^2\right)\approx 0.6$ in mouse. This, together with the above values for $N^0$, places the threshold selective advantage at between 0.1 and 0.5 in the human colon and between 0.15 and 0.7 in mouse (Fig. 3B).

At present, systematic data on the selection advantage of mutations in somatic tissues is not available. Vermeulen et al. (7), however, measured the fixation probability of several known drivers of colorectal cancer in the mouse intestine, finding values between 0.4 (Kras $+/-$) and 0.75 (Kras G12D), which are consistent with the above estimates. In the context of a different epithelial tissue, the human esophagus, a survey by Martincorena et al. (30) of clones persisting in normal tissue showed genomic evidence of strong selective advantage of mutations, again consistent with our predictions. Future data on tissue organization and the selection advantage of mutations that persist in normal tissue will offer exciting opportunities to confront them with our results.

Methods

Detailed derivation of the results presented above are provided in SI Appendix. All data are contained in the manuscript text and SI Appendix.