Distributed Deep Learning Across Multi-site Datasets for Generalized CT Hemorrhage Segmentation

Abstract

Purpose

As deep neural networks achieve more success in the wide field of computer vision, greater emphasis is being placed on the generalizations of these models for production deployment. With sufficiently large training datasets, models can typically avoid overfitting their data; however, for medical imaging it is often difficult to obtain enough data from a single site. Sharing data between institutions is also frequently nonviable or prohibited due to security measures and research compliance constraints, enforced to guard protected health information (PHI) and patient anonymity.

Methods

In this paper, we implement cyclic weight transfer with independent datasets from multiple geographically disparate sites without compromising PHI. We compare results between single-site learning (SSL) and multi-site learning models (MSL) on testing data drawn from each of the training sites as well as two other institutions.

Results

The MSL model attains an average Dice Similarity Coefficient (DSC) of 0.690 on the holdout institution datasets with a volume correlation of 0.914, respectively corresponding to a 7% and 5% statistically significant improvement over the average of both SSL models, which attained an average DSC of 0.646 and average correlation of 0.871.

Conclusions

We show that a neural network can be efficiently trained on data from two physically remote sites without consolidating patient data to a single location. The resulting network improves model generalization and achieves higher average DSCs on external datasets than neural networks trained on data from a single source.

I. Introduction

Automated quantitative analysis of radiological images is becoming increasingly important in the pursuit of imaging-based biomarkers. While many successes in medical image processing have involved approaches such as atlas-guided techniques^1,2, statistical methods^3,4,5,⁶,⁷,⁸ and classical filter-based techniques ⁹, deep learning has become a central focus of image analysis ¹⁰. Neural networks are now being applied to a multitude of problems in imaging fields, e.g., to segment body and head scans^11,12,13, detect lesions¹⁴ and other abnormalities¹⁵, as well as classify and diagnose pathologies¹⁶.

Deep learning-based segmentation specifically has seen a recent history of rapid advancement. Inception-based¹⁷, U-Net¹⁸, and ResNet¹⁹ neural network architectures have all seen success in the segmentation of anatomical brain structures as well as pathologies. Additionally, the Mask R-CNN approach has achieved very promising results for parsing scenes taken from traffic as well as detection of hemorrhages in head computed tomography (CT) scans²⁰ and a related R-CNN has seen success with the detection of extremely small objects ²¹.

The identification and segmentation of intracranial hemorrhages is an important consideration for diagnosis, prediction of patient recovery, and for examining correlations with long-term neurologic disabilities²² such as cognitive impairment²³. Improving the efficacy of hemorrhage segmentation will therefore assist developments in understanding and treating neurological disorders such as traumatic brain injury (TBI) and stroke.

However, the deployment of these neural networks is not trivial. Neural networks are function approximators²⁴, and to properly design, train, and tune them requires sufficient data²⁵ with appropriate preprocessing and annotation. Even under ideal conditions, deep learning may not perform as expected if the observed dataset is not representative of the original data distribution^26,27. For example, if new data points deviate far from the distribution of the training set used to deploy and train the model, we might expect the model to produce sub-par results.

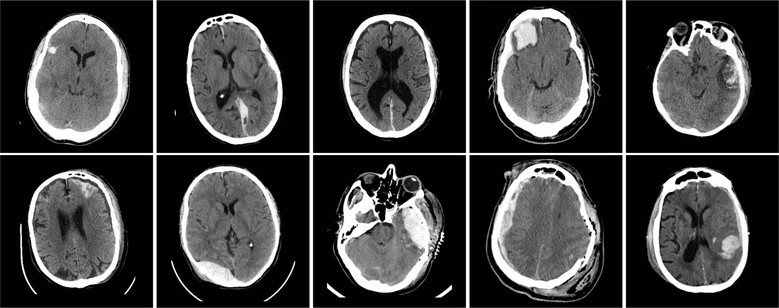
One method to address this problem is to acquire a large enough dataset that will sufficiently span the target space. This is extremely challenging with regards to medical imaging, as there are many scanner manufacturers, models, protocols, and contrasts^28,29 in addition to the inherent biological variations. Single institutions are unlikely to have access to or use the same scanner hardware and software as another institution. Furthermore, even with respect to a specific class of images, such as head CT scans, anatomical morphology and pathologies are highly heterogeneous; see Figure 1.

Figure 1:

Representative 5.0 mm thick transverse CT sections through the head in 10 subjects with TBI. In-plane resolution is approximately 0.5 × 0.5 mm. In each case, the hemorrhagic lesions appear intermediate density between normal brain tissue and bone. Note the heterogeneity of size, location, density and configuration.

The Health Insurance Portability and Accountability Act (HIPAA) was established to guard protected health information (PHI) as technological advances increased the chances of private information leaks³⁰. Part of this protective act includes restrictions on electronic data transfers and requirements for de-identification. Data transfer between medical institutions is often prohibited to respect patient privacy and anonymity³¹. Requirements for de-identification, according to HIPAA, include either the assurance of a qualified expert that de-identification has been done or the removal of all personally identifiable information from the data³⁰.

While it is possible to obtain HIPAA-compliant health data transfer permits, this is a rightfully tedious process and often infeasible when considering medical institutions located in differing legal jurisdictions^32,33,34. Thus, with the restricted ability to accrue large, diverse datasets, we propose to train a neural network using multi-site data without medical data transfer. Instead of centralizing the data at a single institution, we transfer the model which in turn learns in an iterative fashion from data at each site.

The distributive training of neural networks has previously been explored with a few different means of implementation. Federated learning aims to update a central neural model with distributed datasets by sending copies of the model to each institution, calculating gradients from that institution’s data, and sending the gradients back to a centralized location to update the model once more³⁵. The motivation for its use came from the need to learn from user data on many independent mobile devices. Work has also been done to evaluate different techniques to perform distributed learning³⁶. Somewhat related is the process of asynchronous stochastic gradient descent, which splits the training data set and calculates gradients independently on separate GPUs³⁷ before aggregating them to a central model. It aims to speed up learning for deep neural networks and does not necessarily try to improve generalizability of the model nor is its use intended for inherently multi-site data.

Continual learning is a set of training techniques for neural networks which allows a model to train on new datasets without sacrificing the ability to accurately predict on old datasets^38,39,40. Recently, distributed weight consolidation⁴¹ was proposed, considering the multi-site problem as a continual learning problem. The authors constructed neural networks which, instead of single values for parameters, used distributions of values for each parameter. This allowed for weight averaging of multiple neural networks and the use of a common network as a Bayesian prior.

Transfer learning is the process by which some neural model is trained on a different, but related task before being trained for the target task^42,27. The goal of transfer learning is to better initialize the weights of a neural network using somewhat related data. An example of transfer learning could be training a model to segment 40 anatomical regions of the brain by first training a model on the coarser task of segmenting 3 classes: white matter, grey matter, and cerebrospinal fluid.

Cyclic weight transfer builds upon transfer learning. Instead of a uni-directional transfer of weights from one dataset to another, cyclic weight transfer continues to pass a trained model between locations⁴³. Chang et al. simulated a multi-site scenario for classification of retinal fundus and mammography images by separating an open-source dataset and applying noise and other transformations to make the data appear multi-institutional⁴³. The authors investigated different training techniques and showed that cyclic weight transfer provided the best accuracy and generalizability.

Previously, we described preliminary work applying cyclic weight transfer to multi-site data⁴⁴, utilizing data from the Center for Neuroscience and Regenerative Medicine (CNRM) and Vanderbilt University Medical Center (VUMC). It was shown that cyclic weight transfer allowed for learning between sites on a CT hemorrhage segmentation task, which was not necessarily guaranteed due to differences in scanners, acquisitions, and delineation protocols.

Here, we investigate the generalization, defined as the average performance over withheld, external datasets, of a multi-site U-Net model trained to segment hemorrhages in patients with TBI, improving on our recent results with Inception architectures⁴⁴. Using head CT data from the CNRM and VUMC, a multi-site learning (MSL) neural network is trained to convergence and compared against two separate single-site learning (SSL) models. Performance is evaluated not only on holdout sets from the training institutions, but also on two outside datasets. The distribution of CT image volumes is shown in Table 1.

Table 1:

Distribution of CT image volumes and hemorrhage volume statistics between training and test sets for each data set. Data from UMD and VCU were not used to train any model. Note the disparity in hemorrhage size for each data set, particularly between VUMC data and the rest.

Location	# Training Images	# Testing Images	Median Hemorrhage Volume	Mean Hemorrhage Volume
VUMC	33	29	25.3 mm3	38.4 mm3
CNRM	34	34	11.2 mm3	18.6 mm3
UMD	Holdout	11	9.9 mm3	18.3 mm3
VCU	Holdout	20	9.2 mm3	12.7 mm3

To the best of our knowledge, beyond our preliminary work,⁴⁴ this is the first application and validation of cyclic weight transfer on geographically separated, multi-institutional head CT data with traumatic brain injury. As such, and since cyclic weight transfer is model-agnostic, we herein do not compare to existing head CT hemorrhage segmentation methods, such as those by Muschelli et. al⁴⁵ and Chang et al.²⁰ We provide code for performing our implementation of multi-site learning and expect these other segmentation methods to also benefit from the proposed framework.⁴⁶

II. Materials and Methods

II.A. Data

Data were obtained from five institutions: VUMC, Suburban Hospital, Washington Hospital Center, University of Maryland (UMD), and Virginia Commonwealth University (VCU). Data from Suburban Hospital and Washington Hospital Center were coalesced and referred to here as CNRM data for the purposes of this experiment, in order to provide the model with sufficient training data. Data from UMD and VCU are used as holdout datasets.

Every data sample was a de-identified 3D CT scan of a patient presenting with head injury. For the CNRM, VCU, and UMD data, images were acquired under the same IRB-approved protocol, and participants provided consent for their data to be used for research purposes⁴⁷. For VUMC, imaging data were retrieved retrospectively in de-identified form under IRB supervision. Because sharing was not permitted between sites, the CNRM, VCU, and UMD data were housed at one site, and the VUMC data were housed at a separate site. Each CT scan was acquired as DICOM and converted to NIFTI by means of dcm2niix⁴⁸ with all intensities in Hounsfield units. Scan resolution was approximately 0.5 × 0.5 × 5 mm³, except data from VCU, which was approximately 0.45 × 0.45 × 2.5 mm³ and subsequently resampled to 0.5 × 0.5 × 5 mm³ via 3dresample, a part of the AFNI software package⁴⁹.

All data underwent the same preprocessing steps:

1. Skull-stripping by CT_BET⁵⁰

2. Rigid transformation to the “RAI” orientation

3. Collect 1, 000 positive and 1,000 negative 255 × 255 2D axial patches from each CT volume

A positive patch is one which contains at least one hemorrhage pixel, and a negative patch is one which contains zero hemorrhage pixels. Only patches collected from the axial plane were considered due to the low through-plane resolution. We did not impose a non-overlapping constraint on the patches; although no collected patches are identical, redundant information in patches are supplemented by additional spatial context where patches are not equal. Additionally, as our model is a convolutional neural network, patches are shuffled each epoch during training. Patches that could have redundant information are therefore mixed with others in the batch, and the calculated gradient will still allow for learning of the recognition of hemorrhages.

Two independent raters performed manual segmentations for all data, which were subsequently reviewed independently by a neuroradiologist. One rater segmented data from VUMC, and the other rater segmented data from the CNRM, UMD, and VCU. The data distributions and hemorrhage volume statistics for each site are presented in Table 1.

Data from the CNRM was acquired using GE MEDICAL SYSTEMS LightSpeed VCT and Philips Brilliance 64 scanners, while data from VUMC was acquired using the following scanner models: Philips Brilliance 64, Philips Mx8000 IDT 16, GE MEDICAL SYSTEMS LightSpeed Ultra, GE MEDICAL SYSTEMS BrightSpeed, and MX8000IDT Philips Brilliance 64. At UMD, the Philips Brilliance 64 and Philips Brilliance 40 scanners were used and at VCU, the SIEMENS SOMATOM Definition Flash, AS, and AS+ scanner models were used. Note also that in addition to scanner differences, VUMC patients generally presented with much larger lesions (Table 1).

II.B. Model Architecture and Hyperparameters

Previously, an Inception-based architecture was shown to perform well on TBI lesion segmentation from magnetic resonance images⁵¹ as well as for CT hemorrhage segmentation⁴⁴. Here, we implemented a variation of the U-Net¹⁸ architecture using large 2-D patches, finding that it yielded fewer false positives compared to the Inception network. The U-Net architecture is also very commonly used in medical image segmentation. Our demonstration of multi-site learning is therefore likely to benefit other approaches using similar networks.

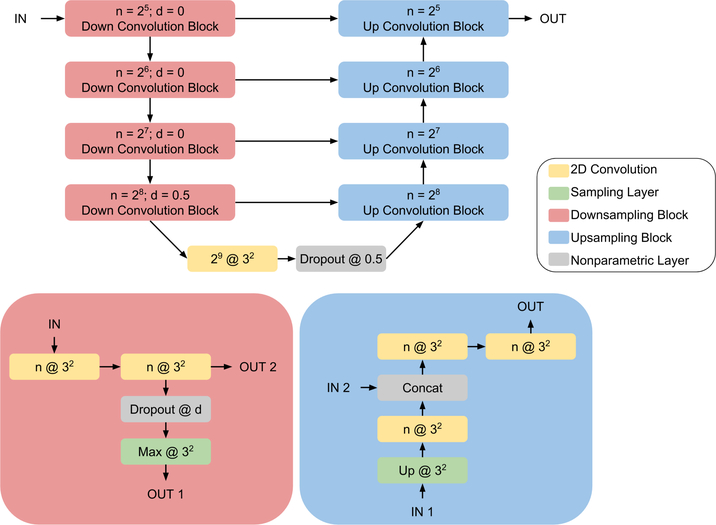
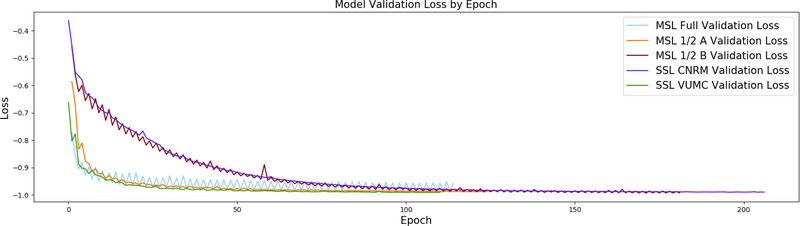
Our implementation of the U-Net is illustrated in Figure 2. Training occurred on 2D patches extracted from the training datasets and continued to convergence, defined as improvement of model loss by less than 1 × 10⁻⁴ in 10 epochs on the validation patch set. This is visualized for all models in Figure 3. Continuous Dice coefficient ⁵²(cDC) was used as the loss function due to its improved efficacy over binary crossentropy⁵², and the learning rate was set at 1 × 10⁻⁴ with the Adam⁵³ optimizer. Due to the final sigmoidal activation function, the final output is a probability of hemorrhage at each voxel on [0, 1]. Therefore, to obtain a binary mask and measure volumes, the output was thresholded at 0.5 to form a mask of hemorrhage vs non-hemorrhage. Our primary focus in this work, however, is not the neural network architecture, but the implementation in training across multiple sites, as described next.

Figure 2:

The U-Net¹⁸ architecture is illustrated above. Downsampling convolution and upsampling convolution blocks are indicated in red and blue with their constituent parts outlined below the model architecture diagram. Convolution layers are indicated in yellow, with notation n @ k² representing n 2D kernels of size k × k. The activation for all convolution layers is ReLU, except for the final 1 @ 1² convolution which uses a sigmoid activation. Up @ k² and Max @ k² respectively correspond to upsampling and max pooling with kernels of size 3 × 3 and strides k × k. Feature concatenation occurs at each up convolution block where indicated.

Figure 3:

Comparison of training curves for multi-site learning (MSL) vs single site learning (SSL) for each of the five models. Since convergence is defined as improvement of model loss by less than 1 × 10⁻⁴ in 10 epochs on the validation patch set, the curves between models above terminate at different epochs. Note how MSL and MSL 1/2 B exhibit oscillating loss values, yet still see convergence for both sites. Convergence still occurs between oscillations because the criteria only considers loss values at sites independently. It is interesting that MSL 1/2 A does not observe the same jumps in loss between institutions; this may be due to similarities in the randomly chosen datasets between sites.

II.C. Training

To ensure patient privacy, data at each institution was never accessible to investigators outside that site. As such, our implementation of MSL established a tertiary secure server which could be accessed by the CNRM and VUMC on which only the neural network weights were kept. This model was loaded, trained, and saved via secure shell access by means of identical Python scripts installed at both institutions, permitting cyclic weight transfer without opening public channels to either site’s data⁴⁶.

Regarding training strategies, five models were trained. First, traditional SSL was performed over CNRM and VUMC datasets. Next, MSL was implemented by iteratively training the neural network on both the CNRM and VUMC training datasets. The model would view one institution’s data for one epoch, and the other institution’s data on the next. Alternations between sites for every batch were not considered, as the additional real time overhead of sending weights through an SSH tunnel becomes infeasible. Finally, to further investigate properties of MSL, we trained two additional MSL models, labeled MSL 1/2 A and MSL 1/2 B, using random halves of the training datasets at the CNRM and VUMC, thus restricting the number of training data points for the MSL model to be equivalent to that of the SSL models. In other words, MSL 1/2 A trained on 16 randomly selected images from the CNRM and 16 randomly selected images from VUMC, and MSL 1/2 B trained on the remaining 16 images from the CNRM and the remaining 17 images from VUMC.

III. Results

Five distinct sets of weights were present after training: CNRM SSL, VUMC SSL, MSL, MSL 1/2 A and MSL 1/2 B. All models converged at different epochs due to our convergence criteria, illustrated in Figure 3. Each of these was evaluated over the four holdout testing datasets, two of which were external institutions. We validated all weight sets with two quantitative metrics: DSC and hemorrhage volume correlation between the automatic and manual segmentations. Further explanation of these measurements follows.

III.A. Qualitative Evaluation

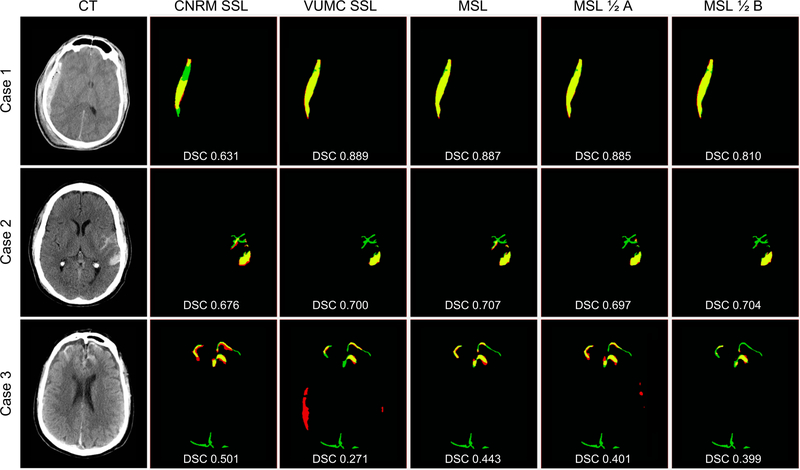
Three CT axial slices from different patients are shown in Fig. 4 alongside comparisons between the manual gold standard segmentation and the five network predictions. All models accurately segment the larger, more apparent lesions while more false positives and false negatives occur on smaller lesions, particularly subarachnoid hemorrhages.

Figure 4:

Results of automatic segmentations compared with manual gold standard for each training method for 3 cases representing a range of DSCs (top quartile - Case 1 (VUMC dataset), median - Case 2 (CNRM dataset), and bottom quartile - Case 3(VCU dataset)). For each case, manual segmentation only (FN) is green, automatic segmentation only (FP) is red, and the overlap of manual and automatic segmentations (TP) is yellow. Black is TN. Corresponding DSC are overlaid. As we aim to show that MSL generalizes across different institutions on average, we encourage consideration of DSCs as a whole rather than the individual cases.

III.B. Quantitative Evaluation

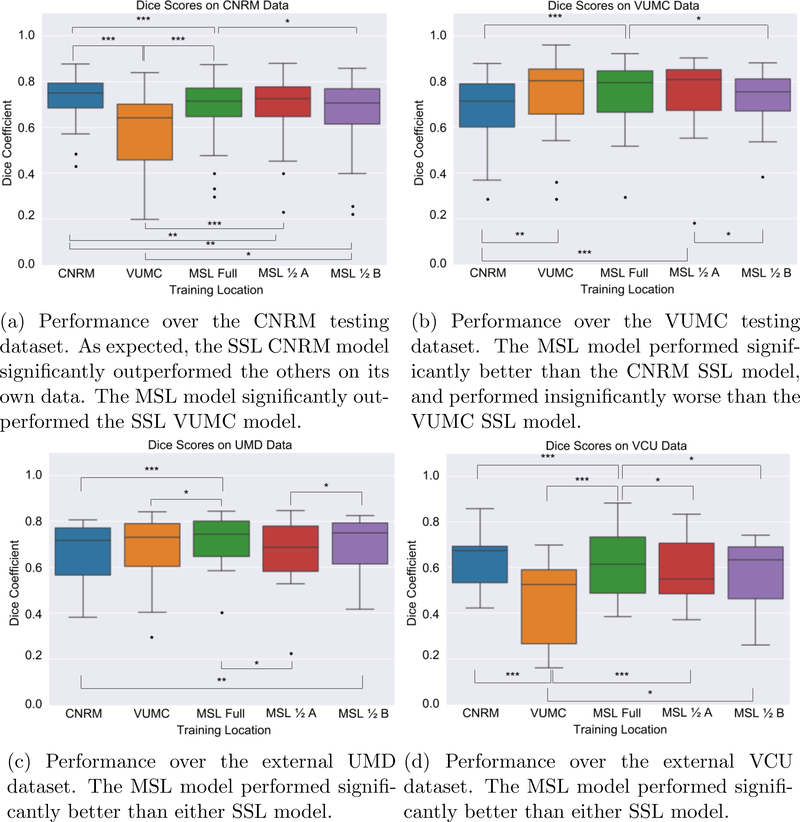
The DSC was utilized to evaluate the accuracy of each network’s automatic segmentations, not to be confused with the cDC loss function. As an additional metric, we also computed the Pearson correlation coefficient between the total volume in mm³ of each model’s predicted segmentations and the raters’ manual segmentations. These values are reflected in Table 2. Overall, the MSL model performs best across all data on average, and individually outperforms the two SSL models significantly on the external UMD and VCU datasets, visible in Figures 5c and 5d

Table 2:

Average DSCs and Pearson correlation coefficients for the five trained models. Inter-rater metrics are calculated from 10 images segmented by two independent raters. Excluding inter-rater metrics, an asterisk indicates significant improvements in DSC (p < 0.05) between the MSL and each of the CNRM SSL and VUMC SSL models as evaluated by the Wilcoxon signed-rank test, and bold text indicates the highest Pearson correlation coefficient between automatic and manual segmented hemorrhage volumes.

	CNRM Data		VUMC Data		UMD Data		VCU Data		Mean of all data
	DSC	Correlation	DSC	Correlation	DSC	Correlation	DSC	Correlation	DSC	Correlation
Inter-Rater	0.687	0.996	n/a	n/a	n/a	n/a	n/a	n/a	n/a	n/a
CNRM SSL	0.734*	0.955	0.684	0.863	0.670	0.927	0.631*	0.814	0.680	0.890
VUMC SSL	0.582	0.952	0.737	0.888	0.666	0.989	0.458	0.575	0.612	0.851
MSL	0.684	0.953	0.748*	0.889	0.705*	0.988	0.621	0.826	0.690*	0.914
MSL 1/2 A	0.670	0.887	0.746	0.870	0.655	0.979	0.586	0.898	0.664	0.909
MSL 1/2 B	0.660	0.912	0.719	0.804	0.701	0.969	0.571	0.760	0.663	0.861

Figure 5:

Model DSCs over each dataset. Regarding significance tests, * corresponds to p < 0.05, ** corresponds to p < 0.01, and * * * corresponds to p < 0.001, according to the Wilcoxon signed-rank test. For p >= 0.05, no comparison brackets are drawn.

The distributions of DSCs for each model at each site are illustrated in Figure 5. Significance was computed via the Wilcoxon signed-rank test. For the CNRM and VUMC testing datasets, best performance was achieved with the corresponding SSL model. Sensibly, for the CNRM data the MSL model outperforms the VUMC model and for the VUMC data the MSL outperforms the CNRM model. Regarding the two external datasets, the MSL model significantly outperforms both SSL models. Note the poor performance of the SSL VUMC model on the CNRM and VCU datasets; this could be because VUMC data is clinical data, and CNRM, UMD, and VCU data are all on the same research protocol, which presents a specific patient selection bias. Also of note is the performance of the two MSL 1/2 models, in which we can see comparable performance to the MSL full model, though the 1/2 models appear to lack some salient features necessary for better segmentation in some testing datasets. This is possibly an explanation for the disparity in DSCs between MSL 1/2 A and MSL 1/2 B on the UMD and VCU datasets.

IV. Discussion

As expected, both SSL models perform best on their respective testing datasets, but do not generalize as well to the outside sources. It is worth noting that the CNRM SSL model performs comparably to the MSL model on the two external datasets, potentially related to the sizes of hemorrhage as described in Table 1, as the volumes of objects being compared are known to bias the DSC.

Considering both MSL 1/2 models, we find similar performance between the MSL 1/2 models and either SSL model, but less variability. Notably, as apparent in Table 2, the MSL 1/2 models achieve similar results to the MSL model, with disparity occurring likely due to the random split of data at each institution during the training phase.

Note that MSL does not outperform SSL models over each task individually. On average, though, when considering all datasets MSL performs the best significantly. Table 2 demonstrates that training with MSL allows for inclusion of datasets while preserving patient privacy, and thus models trained in this fashion are not susceptible to overfitting a single institutions dataset, seen by VUMC SSL’s performance on the VCU dataset and CNRM SSL’s performance on VUMC and UMD datasets. We summarize this with the mean performance of all data in Table 2.

However, the evaluation of multi-site testing data is not straightforward. We take the mean of each model’s performance at every site and interpret models as better or worse on average over these sites, but there are more factors involved. For example, Table 2 shows that regarding the VCU data, the CNRM SSL model significantly outperforms the MSL model, but regarding the VUMC and UMD data, the MSL model significantly outperforms the CNRM SSL model, and by a much larger DSC. This suggests a couple of possibilities. First, it is possible that the scans in the CNRM dataset had more in common with the VCU data than the VUMC data (such as class, location, and size of hemorrhage, scan acquisition parameters, CT dosage). This could explain how the CNRM SSL model achieved a higher DSC on the VCU data compared to the MSL model, but significantly lower DSC on the VUMC and UMD data sets. Second, the epoch of convergence for the MSL model occurred at the VUMC site, leading to a potential shift towards increased performance for VUMC data and decreased performance for CNRM data. Our findings suggest that for a controlled, homogeneous data set, it is not necessary, and in fact may be preferable, to train a model only using that data. However, for deployment of the model across diverse data sets, improved generalization afforded by larger scale, multi-site training will yield superior performance on average.

Inter-rater variability was also calculated for 10 images in the CNRM dataset, also visible in Table 2. Although the manual segmentations were reviewed by a neuroradiologist, a discrepancy still exists due to the challenge of applying binary labels to a boundary that is not perfectly defined. This discrepancy between human raters may explain some of the variability in scores across the two SSL models. Regarding the CNRM dataset specifically, the DSC calculated between the CNRM SSL and all MSL models and the ground truth are comparable or more performant than the DSC calculated between the two human raters. Note the inter-rater correlation, however. With higher volume correlation but lower DSCs, the two human segmentations may have very similar masks in general, but disagree with regards to the edges of hemorrhages.

Despite our quantitative analysis of segmentation results, our goal is not to prove that more data leads to better generalization, which is well known, but rather that cyclic weight transfer can be applied to traditional convolutional neural networks between institutions in different locations. Specifically, our implementation of cyclic weight transfer does not detract from model performance and is a step towards multi-site data collaborations which cannot share patient data between sites.

Practical considerations restrict alternative multi-site training methods. Federated learning³⁶ is theoretically sound but has a high programming overhead, requiring manipulation of gradients and proper handling of asynchronous updates. Distributed weight consolidation ⁴¹ (requires a Bayesian neural network and thus prevents use of non-Bayesian pre-trained networks, and also has a high programming overhead, requiring that all weights in the network represent probability distributions that must be sampled appropriately. Overall, both these methods require application-specific implementations, and therefore cannot be easily adapted across different types of CNN models.

In contrast, the main advantage of using cyclic weight transfer is its lower programming overhead and model agnostic approach. However, it suffers two main drawbacks: potential instability due to alternation of training location (converging at one institute and not the others) and higher real-time cost (all institutes must wait their turn). Our results for TBI lesion segmentation show that the potential instability did not significantly limit performance when applied to a real, multi-site dataset. Regarding real-time cost, our training alternated between sites every epoch instead of every batch, resulting in a training time of approximately 200 hours. With the added overhead of network data transfer, an alternating batch approach would have required an estimated four to six months to achieve convergence.

V. Conclusions

From this work, we conclude that multi-site training of a neural network model is feasible and exhibits improved generalization to external datasets. With our implementation of cyclic weight transfer, CNN models can be constructed with traditional means and can learn from patient image data that is never transferred, preserving PHI confidentiality. Recently, there have been efforts towards ensuring neural network models are differentially private⁵⁴, such that examining the model weights after training reveals no information regarding the training dataset. Our MSL models are trained with 2D patches extracted from axial slices, alleviating some concerns. However, future work will consider implementations that guarantee differential privacy as well as explore comparisons to federated learning and other asynchronous gradient averaging methods for distributed learning.