Abstract
Recent advances in parallel imaging and simultaneous multi-slice techniques have permitted whole-brain fMRI acquisitions at sub-second sampling intervals, without significantly sacrificing the spatial coverage and resolution. Apart from probing brain function at finer temporal scales, faster sampling rates may potentially lead to enhanced functional sensitivity, owing possibly to both cleaner neural representations (due to less aliased physiological noise) and additional statistical benefits (due to more degrees of freedom for a fixed scan duration). Accompanying these intriguing aspects of fast acquisitions, however, confusion has also arisen regarding (1) how to preprocess/analyze these fast fMRI data, and (2) what exactly is the extent of benefits with fast acquisitions, i.e., how fast is fast enough for a specific research aim? The first question is motivated by the altered spectral distribution and noise characteristics at short sampling intervals, while the second question seeks to reconcile the complicated trade-offs between the functional contrast-to-noise ratio and the effective degrees of freedom. Although there have been recent efforts to empirically approach different aspects of these two questions, in this work we discuss, from a theoretical perspective accompanied by some illustrative, proof-of-concept experimental in vivo human fMRI data, a few considerations that are rarely mentioned, yet are important for both preprocessing and optimizing statistical inferences for studies that employ acquisitions with sub-second sampling intervals. Several summary recommendations include concerns regarding advisability of relying on low-pass filtering to de-noise physiological contributions, employment of statistical models with sufficient complexity to account for the substantially increased serial correlation, and cautions regarding using rapid sampling to enhance functional sensitivity given that different analysis models may associate with distinct trade-offs between contrast-to-noise ratios and the effective degrees of freedom. As an example, we demonstrate that as TR shortens, the intrinsic differences in how noise is accommodated in general linear models and Pearson correlation analyses (assuming Gaussian distributed stochastic signals and noise) can result in quite different outcomes, either gaining or losing statistical power.
Keywords: fMRI, simultaneous multi-slice (SMS), multi-band, rapid sampling, statistical analysis, physiological noise, serial correlations, autocorrelations, GLM, resting-state, pre-whitening, task frequency
1. Introduction
The ever-growing availability of simultaneous multi-slice (SMS) pulse sequences has offered the fMRI community an option to examine brain activities at much faster temporal scales than conventional 2~3 s temporal sampling intervals (Barth et al., 2016; Feinberg et al., 2010; Feinberg and Setsompop, 2013; Feinberg and Yacoub, 2012; Hennig et al., 2007; Larkman et al., 2001; Lin et al., 2006; Moeller et al., 2010; Narsude et al., 2016; Setsompop et al., 2016; Setsompop et al., 2012; Zahneisen et al., 2011). With fast fMRI, researchers have been able to probe neural oscillations at frequencies well above the limits of conventional acquisitions (e.g., (Lee et al., 2013; Lewis et al., 2016)) and characterize brain temporal dynamics at much finer temporal resolutions (e.g., (Lewis et al., 2018; Lin et al., 2018; Smith et al., 2012)). Furthermore, additional temporal samples are achieved without increasing the scan duration, which is commonly thought to be advantageous for enhanced sensitivity to neural fluctuations (e.g., (Feinberg et al., 2010; Posse et al., 2012; Smith et al., 2013)).
However, faster sampling rates come at the penalty of reduced signal-to-noise ratio (SNR) per time frame due to reduced longitudinal magnetization recovery (Barth et al., 2016; Edelstein et al., 1986; Feinberg and Setsompop, 2013), which will result in altered contributions from various sources of fMRI noise by virtue of their distinct dependencies on signal amplitudes (Liu, 2016; Wald and Polimeni, 2017). For instance, the level of noise resulting from slow physiological processes (e.g., end-tidal CO2 levels and cardiac-related pulsation) scales with signal levels while thermal noise remains constant across different TR values. Such alterations in noise characteristics, including having broadened spectral distributions, pose the concern that conventional analysis pipelines that are optimized for longer-TR acquisitions may not be well suited for data collected at subsecond TRs. Indeed, a few recent studies have demonstrated that certain steps in conventional acquisitions may introduce spurious high-frequency network patterns in the observed fMRI data (Chen et al., 2017), and that conventional parametric models that characterize the noise fluctuations may fail to summarize the temporal characteristics of short-TR data and lead to invalid statistical inferences regarding brain activation (Bollmann et al., 2018; Corbin et al., 2018; Eklund et al., 2012; Olszowy et al., 2018; Sahib et al., 2016).
Because the reduced SNR per time frame may offset the enhanced statistical power yielded by additional sampling points (Constable and Spencer, 2001), it is not obvious at first glance whether fast acquisitions indeed contribute to increased functional sensitivity and if so, under what conditions. To examine whether sub-second TRs are superior to conventional long-TR acquisitions, several studies have empirically evaluated the performance of fast acquisitions in specific cases and analysis strategies, which led to somewhat conflicting observations. For instance, a few task-based studies showed that sub-second TRs could lead to enhanced sensitivity to neural activation, evidenced by higher statistical scores in general linear model (GLM)-based sensory task activation analyses (Chen et al., 2015; McDowell and Carmichael, 2018; Posse et al., 2012), detection of additional task clusters when combined with multi-echo acquisition (Boyacioglu et al., 2015), enhanced classification accuracy of complex cognitive states (Chen et al., 2015; Demetriou et al., 2018), and better correspondence with epileptic spikes identified by concurrent EEG recordings (Jacobs et al., 2014). However, a recent study assessed brain activation under a broad range of task types and showed that the benefits of fast acquisitions analyzed with GLM-based approaches were very modest (Demetriou et al., 2018). The benefits of rapid sampling for resting-state functional connectivity are also controversial. A few studies reported that shorter TRs significantly enhanced both the number of detected resting-state networks identified with independent component analysis (ICA) (Akin et al., 2017; Olafsson et al., 2015) as well as the peak Z-scores of these networks if they were resolved by multi-component dual-regression analyses (Demetriou et al., 2018; Feinberg et al., 2010; Preibisch et al., 2015). However, such statistical gains became minor if the networks were derived separately from a single-component/network or seed-based regression (Demetriou et al., 2018; Feinberg et al., 2010). Thus, existing studies of both task activation and resting-state sub-second fMRI have resulted in discordant findings regarding the value of rapid sampling.
The aim of this work is hence twofold: (1) to highlight a few novel considerations for both data preprocessing and modeling for fast fMRI; and (2) to provide some basic theory, along with measured and simulated data, to clarify certain aspects of previous conflicting observations on statistical characteristics of rapid sampling. This manuscript is organized as follows: Section 2 will define signal and noise within the scope of this work; Section 3 will review a few caveats in preprocessing rapid fMRI data, involving nuisance regression and removal of physiological noise in short-TR fMRI data; Section 4 will discuss appropriate models that can characterize the temporal autocorrelation of short-TR fMRI time series, supported by both theory and real data results; Section 5 will employ elaborate simulations to illustrate how different factors in study design, statistical models (with primarily GLM and linear Pearson correlation as examples) and signal characteristics can affect the potential benefits of fast acquisitions; and finally in Section 6, we will present our recommendations for the fast fMRI field, which hopefully can contribute to more effective and consistent usage of rapid sampling protocols in future applications.
2. Signal and Noise
To unify discussion in the following sections, we first define signal and noise within the scope of this manuscript:
Signal: fluctuations in image intensity causally linked with the neural activity of interest.
Physiological noise: any remaining T2/T2* related fluctuations that scale linearly with the signal (Kruger and Glover, 2001), including, for instance, neural activity-related fluctuations that are not of interest, residual effects from end-tidal CO2 fluctuations (Birn et al., 2006; Wise et al., 2004), or basic maintenance of hemodynamic stasis that is controlled by the autonomic system. Of note, such a definition of physiological noise deviates from that in conventional literature—which typically refers to quasi-periodical fluctuations induced by respiratory and cardiac cycles. Here, we assume that such quasi-periodical fluctuations have already been effectively removed by either temporal filtering or model-based approaches (e.g., (Glover et al., 2000)), unless mentioned otherwise.
White (thermal) noise: broadband signal fluctuations arising from the thermal agitation of charge carriers in both the subject and the MRI system electronics. This noise is spatially and temporally white and is independent of signal level.
Other noise types: signal fluctuations arising from brain motion, system drift, system instability (see (Liu, 2016) for a review), image errors from reconstructing data that are undersampled in the in-plane or slice directions (e.g., g-factor penalty (Pruessmann et al., 1999)). This noise is in general structured in space and/or time.
The discussion in this work will focus primarily on the relative contributions of physiological and white noise, assuming that other types of system and pulse sequence-related noise have been effectively removed or have minimal contributions. As we shall see, the relative levels of additive (white) and multiplicative (physiological) noise can have a profound effect on the benefits of sub-second sampling.
3. Preprocessing
3.1. Spectra misspecification in nuisance regression
Nuisance regression, which projects out of each voxel’s time series noisy components (e.g., motion and fluctuations triggered by physiological processes) under a linear regression framework, has been routinely employed in data preprocessing. Here, we review a few caveats that warrant particular attention when removing nuisance factors from data collected with short TRs.
First, respiratory artifacts, which are less noticeable at conventional 2~3 s TRs due to aliasing effects, become pronounced in head motion estimates as TR shortens (Fair et al., 2018; Siegel et al., 2017), as illustrated in Fig. 1 (a) and supplementary material SM2). Such artifacts stem both from true mechanical movements of the head (e.g. linked to chest expansion and contraction) and from quasi-periodical perturbations of main magnetic field caused by respiration processes (Van de Moortele et al., 2002). The former is the result of head displacements in multiple directions and rotation, typically predominant about the left-right axis (Fig. 1 (a), more pronounced in HCP subject 01); whereas the latter induces apparent (but artifactual) head displacements along the phase-encoding direction of an echo planar imaging (EPI) acquisition, which can manifest in all directions of the rigid-body motion estimates due to cross-talk effects (Fair et al., 2018) (Fig. 1 (a), observable in HCP subject 02). It is noteworthy that, unlike actual head displacements, respiration-induced field perturbation does not cause intensity fluctuations through spin history effects, however nuisance regression is only intended to remove motion-induced intensity changes. Therefore in this case, deleterious respiratory fluctuations may be introduced into fMRI datasets after regression against the estimated motion traces. To avoid this deleterious effect, one can either notch-filter the quasi-periodic respiration waveforms from motion estimates prior to nuisance regression (Fair et al., 2018), or include co-varying physiological parameters (e.g., RETROICOR covariates (Glover et al., 2000)) together with the estimated motion traces in the nuisance regression.
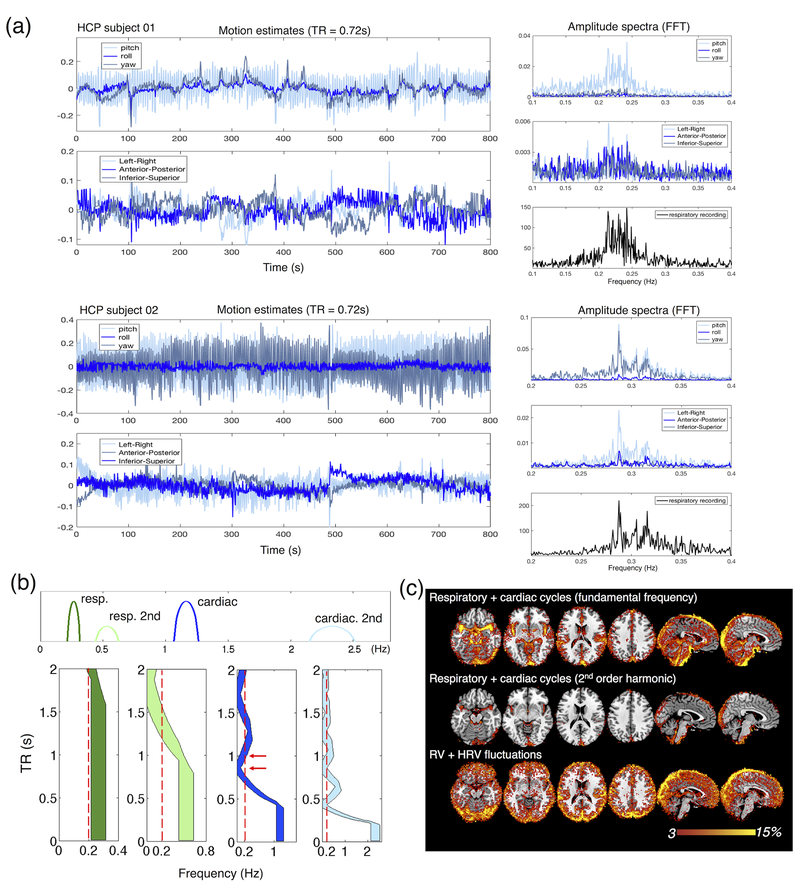
Figure 1.
(a) Illustration of respiratory artifacts in rigid-body-based head motion estimates (three rotational + three translational directions) in two example subjects from the WU-UMinn Human Connectome Project (HCP) resting-state cohort (Van Essen et al., 2013) (3T, TR = 0.72 s, 2 mm isotropic resolution). The mechanical-movement-based effect dominates in subject 01 (evidenced by the most prominent quasi-periodical fluctuation along the ‘pitch’ direction), and the field-perturbation-based artifact is observable in subject 02 (evidenced by the occurrence of quasi-periodical fluctuations along all rotational directions due to potential cross-talk effects and stronger effects along the phase encoding direction (‘left-right’) than other translational directions). Left: raw motion estimates after 2nd-order temporal detrending. Right: amplitude spectra of motion estimates aligned with respiratory fluctuations directly recorded with a respiratory belt. There is a strong correspondence between the amplitude spectra of certain components of head motion and the respiration, indicating that respiration may be driving the head motion. (b) Top: simulated spectral components of cardiac and respiratory noise; Bottom: Aliased physiological frequencies as a function of TR for respiratory components (‘resp.’), cardiac components (‘cardiac’), and their second-order harmonics (‘resp. 2nd’ + ‘cardiac. 2nd’). Although aliasing is always resolved at high-enough sampling rates, aliasing into frequency bands of interest can also be absent in lower sampling rates as well. (c) Percent signal variance explained by sinusoids representing the fundamental frequencies and second-order harmonics of respiratory/cardiac cycles (Glover et al., 2000), and covariates related to slow physiological processes—respiratory variation (RV) and heart rate variability (HRV) (Chang et al., 2009). The characterization is single-voxel based, after minimal preprocessing, and averaged across 190 subjects from the WU-UMinn HCP resting-state cohort (Glasser et al., 2013).
Second, as we have discussed in earlier work (Chen et al., 2017), linear nuisance regression results are dominated by the strongest frequency components (typically < 0.2 Hz) present both in the fMRI signal and in common nuisance components, implying that higher-frequency oscillations resolved by fast acquisitions may not be de-noised as effectively if these high-frequency bands are preprocessed together with the low-frequency bands containing the strongest fluctuations. Therefore, we recommend (and reinforce in section 6 (2)) that future studies perform matched-band nuisance regression (i.e., filtering both the fMRI time series and nuisance regressors into identical frequency bands (Carp, 2013; Chen et al., 2017; Hallquist et al., 2013)) if the frequencies of interest do not dominate, i.e., if the frequencies of interest are > 0.2 Hz; otherwise, filtering the fMRI time series after regression is preferable for resting-state data, because filtering can diminish the effective degrees of freedom in statistical inferences (Bright et al., 2017; Davey et al., 2013).
3.2. Correcting for respiratory and cardiac confounds
An intriguing aspect of fast acquisitions is that respiratory/cardiac peaks can be clearly resolved at their fundamental frequencies (for sufficiently short TRs) and will not alias into lower frequencies where most neural activity resides. As such, it is commonly assumed that one can simply de-noise rapidly-acquired fMRI time series via temporal filtering, without needing to collect additional physiological data required by most model-based approaches.
Appealing as it may seem to employ low-pass temporal filtering for physiological noise elimination, one should be aware that cardiac and respiratory noise waveforms are far from sinusoidal and thus include higher-order harmonics not unambiguously resolved at the sampling rate employed. Thus, only very short TRs (much smaller than 0.5 s) can guarantee no aliasing of physiological peaks (as simulated in Fig. 1 (b)). It is also noteworthy that, if aliasing occurs, faster acquisitions may paradoxically not necessarily lead to cleaner neural representations. For instance, if we assume neural fluctuations are confined to < 0.2 Hz (Fig. 1 (b), red dashed lines), then a 1.2 s TR can result in less contamination from the 1st-order cardiac spectrum (for the assumed range) than a 1 s TR (Fig. 1 (b), highlighted by red arrows).
Aside from the fundamental fluctuations that are time-locked to cardiac/respiratory cycles, it is noteworthy that (1) the 2nd-order harmonics in physiological processes also account for considerable variance of fMRI time series (Glover et al., 2000); and that (2) certain slow changes in regular physiological process (e.g., fluctuations in end-tidal CO2 levels (Golestani et al., 2015; Wise et al., 2004), respiration volume per unit time (RVT) (Birn et al., 2006), and heart rate variability (HRV) (Chang et al., 2009; Shmueli et al., 2007)) can also induce significant low-frequency nuisance fluctuations (as illustrated with HCP datasets in Fig. 1 (c)). Because the spectra of these slow physiological processes overlap with the spectra of true neuronal components, they cannot be effectively removed by filtering.
Collectively, despite the fact that filtering can address the fundamental frequencies of physiological processes when TR is sufficiently short, model-based (e.g., (Birn et al., 2008; Chang et al., 2009; Glover et al., 2000)) or recently proposed data-driven alternatives (e.g., (Glasser et al., 2018; Griffanti et al., 2014; Salimi-Khorshidi et al., 2014)) should still be employed to account for the effects of these physiological processes both in frequency bands above the fundamental frequency (i.e., the higher harmonics) and below the fundamental (i.e., the slow changes in the physiological processes occurring over several cycles).
4. Modeling signal and noise autocorrelations at sub-second TRs
Because fMRI time series comprise various colored noise components that render the neighboring temporal samples non-independent, it is important to account for such serial correlations (i.e., the dependencies among distinct samples) in order to yield valid statistical inferences on functional activity. Although it is impossible to find a unified model that optimally characterizes every brain voxel’s autocorrelation pattern given the expected dependence of the autocorrelation structure on local vasculature (Gonzalez-Castillo et al., 2012; Handwerker et al., 2012), on the spatially-varying mixture of noise components (Liu, 2016), and on the specific data manipulation and processing steps performed (Friston et al., 2000), we may still seek a simple yet flexible model that effectively summarizes the temporal structure of fMRI time series across a vast set of brain areas and experimental conditions. Indeed, various parametric models (e.g., autoregressive models (AR), 1/f noise) and nonparametric models (see (Monti, 2011) for a review) have been proposed since the seminal treatment of fMRI time series analysis (Friston et al., 1995). While the parametric model conventionally employed with long-TR acquisitions (the 1st-order AR or AR1 model) appear to be adequate, adding a small amount of complexity to the model (e.g., 2nd-order AR, or regularization) has been shown to further improve the fitting performance in conventional-TR analyses (Lenoski et al., 2008).
As TR gradually shortens to the sub-second regime, one may naturally wonder whether certain parametric long-TR models still apply, because the temporal dependencies of fMRI time series change in several ways. First, diminished SNR per time frame leads to increased fractional contribution from white noise, which manifests as a sharp peak of the autocorrelation function at 0 s lag, and a flatter amplitude spectrum at higher frequencies (Fig. 2(a), highlighted by green arrows in the exemplar real data time series). Second, because time series of fMRI data are discretely sampled, reduced temporal intervals between adjacent samples will result in longer-range dependencies in the autocorrelation function and faster amplitude decays in the normalized frequency domain (Fig. 2(a), highlighted by light blue arrows). As a result, the performance of certain conventional long-TR models degrades as TR shortens, as shown by the fitting of exemplar real data in Fig. 2(b).
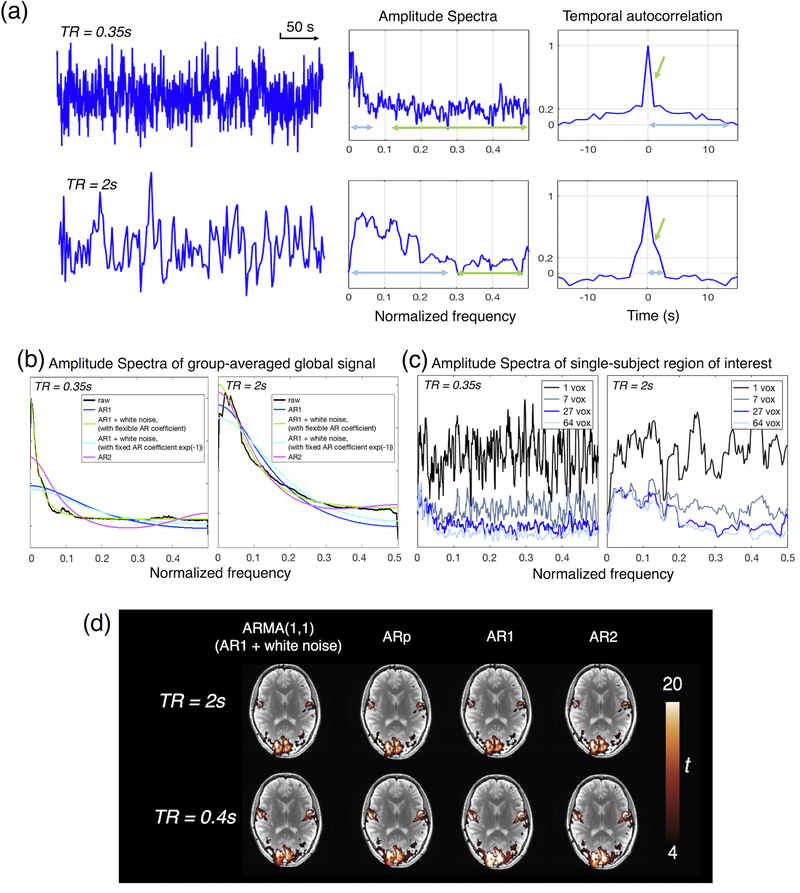
Figure 2.
(a) Illustration of altered autocorrelation structure at short TR values. Time series were extracted from a region of interest (ROI) located in the posterior cingulate cortex (averaged across 27 voxels, voxel size 1.72×1.72×3 mm3) in two different scans (TR = 0.35 and 2 s). See supplementary material S1A for descriptions of data acquisition and analysis. The temporal autocorrelation function is clearly broader in the white noise dominated data, as expected. Light blue and green arrows highlight the distinct features of temporal autocorrelation structures at long- and short-TR values (see main text Section 4 for discussion). (b) Amplitude spectra and model fitting of the global signal, averaged across two cohorts of datasets collected with different TR values. See supplementary material S1B for descriptions of data acquisition and analysis. Common serial correlation models describe conventional long-TR data well, however they can be inappropriate when applied to short-TR data. (c) Amplitude spectra as a function of ROI size, same ROI and datasets as shown in panel (a) for illustration. The power spectrum of a gray matter region can sometimes be very noisy at a single- or very few-voxel level, and multiple voxels may need to be averaged to obtain a valid model fit. (d) Dependence of task activation t-statistics on serial correlation models. The optimal AR order (ARp) was chosen according to the Bayesian information criterion (BIC). See supplementary material S1C for descriptions of data acquisition and analysis. Inappropriate models for short-TR data can lead to inflated t-statistic values.
Implications of such discrepancies between the serial structure of short-TR data and parametric models implemented in common toolkits have been cautioned by several studies (Bollmann et al., 2018; Eklund et al., 2012; McDowell and Carmichael, 2018; Olszowy et al., 2018; Sahib et al., 2016), and the proposed solutions include invoking nonparametric alternatives (e.g., (Woolrich et al., 2001)) or a slightly more complicated parametric model (essentially with more free parameters for model fittings), such as higher-order AR models (Bollmann et al., 2018; Jacobs et al., 2014; Sahib et al., 2016; Worsley et al., 2002), and the new FAST option of SPM (https://www.fil.ion.ucl.ac.uk/spm/), which fits the serial correlation structure with more versatile dictionary components based on exponential covariance functions (Corbin et al., 2018; Todd et al., 2016). These more complicated models flexibly adapt to data collected at different TRs and have been demonstrated to be effective. Yet, increasing model complexity always raises concerns of potential overfitting, particularly in scenarios when the data suffer from low SNR (accompanying high spatiotemporal resolution) or when considering analyses with short durations (i.e., studies investigating a diseased population or time-varying patterns of dynamic brain functional connectivity). For instance, as shown by the real data example in Fig. 2(c), the power spectrum of a gray matter region can sometimes be very noisy at the single- or very few-voxel level, and good model fitting is only obtained when multiple voxels are averaged. In such cases, models with simple a priori constraints may be preferred. Inspecting Fig. 2(b) closely, one observes that the conventional models fail to varying extents at short TRs: AR1 + white noise (Purdon and Weisskoff, 1998) (TR = 0.35 s, green waveform) still fits the global signal well if the AR coefficient is allowed to vary freely, which agrees with a recent comparison that suggests the ARMA(1,1) (a.k.a., AR1 + white noise) model in AFNI (https://afni.nimh.nih.gov) outperforms other conventional models as TR shortens (Olszowy et al., 2018). This is possibly because increased fractional contribution of white noise can be addressed by the additional white noise component in the serial correlation model; and the remaining colored noise present in data acquired with different TR values can still be captured by very low-order AR models if we allow the AR coefficients to vary flexibly (essentially, longer range correlations between time points do not necessarily require a higher-order AR model). It is also noteworthy that, in the discussion above, we assume that fluctuations time-locked to respiratory and cardiac cycles have been accurately eliminated, such that a very-low-order AR model alone is adequate to fit the slow physiological noise components (Bollmann et al., 2018). Apart from conventional approaches that address the DOFs on an individual voxel or region basis as discussed above, an alternative solution is spatial-wise mixture-modeling, see section 5.7 for more detailed discussion.
Finally, why is it so important to model the serial correlation structure correctly? An empirical illustration is offered in Fig. 2 (d): compared to models applicable to different TR values (ARMA(1,1) or higher-order AR models), AR1 and AR2 models perform well at TR = 2 s and lead to almost identical statistical results, but fail to capture the serial correlations of fMRI time series at TR = 0.4 s, resulting in inflated t-statistics and thus overestimated statistical gains compared to TR = 2 s. This effect can induce false positives and exaggerate statistical benefit of short TRs (Purdon and Weisskoff, 1998; Sahib et al., 2016).
5. How fast is fast enough? Factors in task design and analyses that affect the statistical outcomes
As briefly reviewed in the Introduction, existing empirical comparisons of fast and conventional long-TR acquisitions do not conclusively demonstrate whether the functional sensitivity of fMRI studies can be significantly improved by faster sampling. The statistical outcomes have been shown to depend heavily on a broad range of factors, e.g., study designs and the statistical analyses employed (e.g., (Demetriou et al., 2018)). In this section, we employ simulations (with fMRI signal and noise models outlined in Appendices A–C) and some exemplar human scan results (with acquisition and analysis details listed in supplementary material S1D) to demonstrate certain theoretical considerations regarding how study designs, data analyses, and temporal characteristics of fMRI time series can affect the benefits of fast acquisitions. These results may contribute to better understanding of the conflicting observations of empirical comparisons, and guide usage of fast fMRI protocols in future applications.
5.1. Estimating signal or noise in the presence of serial temporal correlations
As we have discussed in the previous section, correctly modeling the serial correlation structures of fMRI time series is critical for yielding valid statistical inferences regarding brain activation or connectivity metrics. Yet, depending on the statistical models we employ, fluctuations in an fMRI time series may be considered partly or completely stochastic, leading to different estimates of serial correlations. For instance, the GLM views the fMRI time series as a linearly additive mixture of deterministic signals and stochastic noise, hence only characterizes the serial correlations of the residual noise in statistical inferences; whereas in the linear Pearson correlation analysis (often used in seed-based or region-of-interest-based functional connectivity estimation), the serial correlation summarizes the temporal dependencies of the entire time series, because both the signal and noise are considered stochastic. Fig. 3 (a) gives an illustrative example in which the estimates of serial correlations in an fMRI time series can vary depending on whether the entire time series is viewed as stochastic, and therefore possessing temporal autocorrelation that requires modeling, or whether only the noise is stochastic (blue vs. green curve). Because fMRI signals are generally sluggish due to hemodynamic delays, models that evaluate the serial correlations only of the residual noise (e.g., in GLM analyses) benefit more from fast sampling via increased degrees of freedom (DOFs) (provided that the data are not pre-whitened) arising from lower temporal dependencies among adjacent samples.
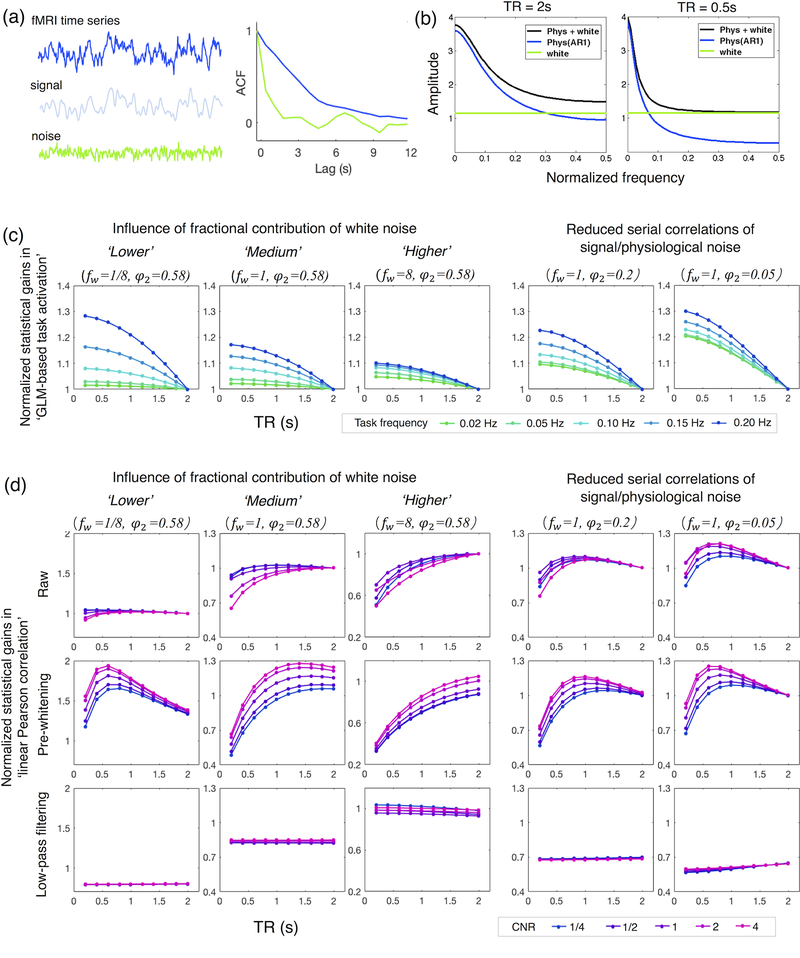
Figure 3.
(a) Distinct estimates of autocorrelation functions (ACFs) if the entire time series (blue) or only residual noise (green) are considered as stochastic as in Pearson correlation or GLM analyses, respectively. (b) Examples of simulated fMRI noise at two different TR values (based on the models presented in Appendix A, 0.5 is Nyquist frequency). Noise (black) was modeled as a linearly additive mixture of physiological noise (blue color, an AR1 process) and white noise (green). (c) Simulated statistical gains of fast sampling in GLM-based task activation analysis, normalized by the t-scores at TR = 2 s. The amplitudes of fMRI signals were computed from the Ernst angles at different TR values (e.g., ATR of eqn. (A.6) in Appendix A), noise at different TR values were simulated according to Appendix A, and the statistical scores were simulated based on eqn. (B.5) in Appendix B. Task frequencies are highlighted by distinct color lines. Influences of fractional contributions from white noise (first three columns) were simulated by scaling the power of white noise by different factors fw (‘lower’:1/8, ‘medium’:1, ‘higher’:8). Influences of lower serial correlations of signal/physiological noise (last two columns) were simulated by reducing the AR1 coefficient at TR = 2 s (φ2) from the estimated value 0.58 (see Appendix A) to 0.2 or 0.05. (d) Simulated statistical gains of fast sampling in linear Pearson correlation-based functional connectivity analyses; results of different preprocessing options were all normalized by the t-scores at TR = 2 s of the ‘Raw’ data for comparison. Simulations were performed based on the model assumptions outlined in Appendix C. Influences of distinct preprocessing steps are displayed across rows (‘Raw’: no additional preprocessing; ‘Pre-whitening’: pre-whitening, i.e., removal of serial correlations; ‘Low-pass filtering’: < 0.1 Hz low-pass filtering). Dependence of CNR levels are highlighted by distinct color lines (values in the legend quantify the CNR level at TR = 2 s, ‘Raw’).
5.2. Contrast to noise ratio (CNR) penalty and effective DOFs as functions of summary statistics: GLM vs. linear Pearson correlation
The performance of an fMRI protocol and final statistical outcomes are commonly approximated by the metric , where tSNR refers to voxel-wise temporal SNR, defined as the voxel’s temporal mean divided by its temporal standard deviation, and N is the total number of time points collected in the protocol (e.g., (Smith et al., 2013)). However, existing fMRI research has employed a broad range of summary statistics (e.g., GLM-based task activation, linear Pearson correlation-based functional connectivity, complex network behavior, etc.), each of which are affected by distinct CNR (the ratio of neural fluctuations of interest to nuisance fluctuations) penalties and DOFs gains that occur as the TR value shortens. For instance, at the single-subject level, the t-score of a task covariate derived from a GLM scales roughly linearly with the CNR, and the effective DOFs approximate the total number of time points for modest number of covariates (as pre-whitening is routinely implemented in most toolboxes to address noise serial correlations (Bullmore et al., 1996; Woolrich et al., 2001)); whereas the t-statistics of linear Pearson correlation values (typically employed to quantify the temporal synchrony between two remote brain regions) scale nonlinearly with CNR, and the effective DOFs increase more modestly at short TRs due to serial correlations ((Davey et al., 2013), please refer to Appendices B and C). As such, even under identical CNR levels and acquisition protocols/environments, the ‘optimal’ TR value (that yields the highest expectation of t-statistics) may vary according to the types of summary statistics employed. For example, when comparing GLM-based task activation analysis to linear Pearson correlation-based functional connectivity analysis, the latter favors slightly longer TRs by virtue of both stronger penalty on CNR loss and limited benefits in DOFs at short TRs. This is demonstrated by the trend of normalized t-score gains vs. TR simulated in Fig. 3 (comparing panels (c) GLM and (d) Correlation, ‘Raw’), as well as with real data in Fig. 4 (comparing the ‘Raw’ data in panels (b) and (d), given that of the estimated region exhibited similar TR dependence).
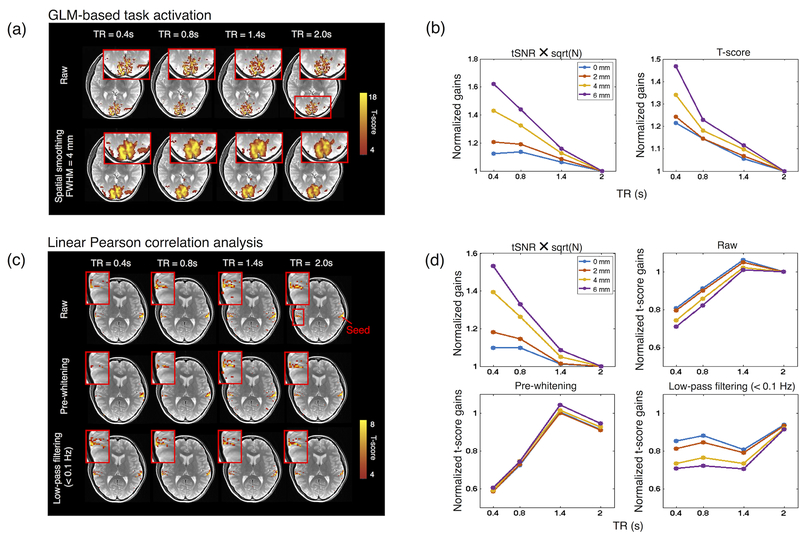
Figure 4.
(a) GLM-based single-subject visual task activation at different TR values without (‘Raw’, 1.72×1.72×3 mm3) and with spatial smoothing. (b) (Left) Predicted (, N is the number of temporal frames) and (Right) estimated (real data) t-score gains (i.e., divided by the t-score values at TR = 2 s) for the data shown in panel (a). Data were smoothed by different spatial extents with isotropic Gaussian kernels at different FWHMs (highlighted with distinct colors) to manipulate the fractional contribution of physiological and white noise in the real data. (c) Linear Pearson correlation based auditory network patterns at different TRs and preprocessing. (d) Predicted and estimated (real data) t-score gains in (c). Note that only the contralateral side of the seed (highlighted by a red rectangle in (c)) was included for comparison. The statistical gains of different preprocessing steps were normalized by the t-scores at TR = 2 s of the ‘Raw’ data. See supplementary material S1D for descriptions of task design, data acquisition and analysis.
5.3. Influence of increased contribution of physiological noise in GLM: CNR reduction at short TRs
Akin to signal, the strength of physiological noise also diminishes as TR shortens (Kruger and Glover, 2001; Liu, 2016; Wald and Polimeni, 2017). In an extreme scenario where physiological noise overwhelmingly dominates, the reduction in CNR caused by rapid sampling is very minor. Hence, the relative ratio between white and physiological noise can also strongly influence the observed benefits of faster sampling. As simulated in Fig. 3 (c left, different levels of white noise) and demonstrated by real data in Fig. 4 (a and b, different extents of spatial smoothing), with reduced fractional contribution from white noise (through increasing levels of spatial smoothing, which reduces white noise due to noise averaging and cancellation) normalized gains of statistical scores at short TR values become more pronounced.
5.4. Influence of the task paradigm in GLM
The timing of the imposed task is another factor that can influence the benefit achieved from faster acquisitions. Because physiological noise extends beyond the sampling Nyquist frequency despite decaying monotonically, reduced aliasing of physiological noise due to short TR values will lead to more significant noise reduction at relatively higher frequencies (e.g., close to 0.25 Hz, the Nyquist frequency at TR = 2 s) compared to lower frequencies. In Fig. 3 (c), we simulated the fractional contributions from white noise by scaling the power of white noise by different factors fw. Although the employed noise model (shown in Fig. 3 (b) and detailed in Appendix A) may not well characterize fluctuations at very low frequencies that can be distorted by system drifts or other un-modeled phenomena (as illustrated in Fig. 2 (b, TR = 2 s)), the simulations will still offer some qualitative insights on the impacts of task paradigm on statistical outcomes. The simulations show that the influence of task timing is very minor if white noise is substantial (Fig. 3 (c, ‘Influence of fractional contribution of white noise’), fw = 8); however, as the fractional contribution from physiological noise increases, tasks operating at faster temporal scales will elicit large gains in expected t-scores (Fig. 3 (c, ‘Influence of fractional contribution of white noise’), fw = 1/8). As expected, such an effect of task paradigm depends on the autocorrelation structure of signal or physiological noise: if we reduce the temporal dependencies of signal or physiological noise, such a dependence becomes less prominent (Fig. 3 (c, ‘Reduced serial correlations of signal/physiological noise’). In these simulations lower serial correlation was achieved by reducing the AR coefficient at TR = 2 s (φ2) from the estimated value 0.58 to 0.2 and to 0.05).
5.5. Influence of preprocessing in linear Pearson correlation
As fast fMRI data become more widely available, questions arise regarding whether to pre-whiten or not to pre-whiten the time series, as described above, or whether to smooth or not to smooth. The influence of preprocessing has been intensively evaluated in the context of GLM-based task activation analysis (Friston et al., 2000; Monti, 2011). These preprocessing steps can significantly alter the statistical outcomes by indirectly influencing the CNR penalty and DOF gains, however the impact of preprocessing on linear Pearson correlation analysis has received less attention. Here, we discuss the effects of temporal filtering and pre-whitening on linear Pearson correlation metrics and show that the trend of statistical gains on TR value may vary depending on the specific preprocessing steps taken.
Low-pass temporal filtering (< ~0.1 Hz) has been routinely applied to improve the overall CNR of resting-state fMRI time series (as noise is considered to dominate signal at frequencies > 0.1 Hz). However, filtering can also reduce DOFs available in the datasets (leading to almost constant DOFs across TR values) (Davey et al., 2013). It is hence not obvious whether temporal filtering is advantageous for improved efficiency of statistical testing. In particular, we may benefit less from temporal filtering when performing linear Pearson correlation analysis in cases where one attains very modest improvements in CNR and the penalty caused by reduced DOFs dominates, such as in physiological noise-dominated regimes (see Fig. 3 (d, ‘Influence of fractional contribution of white noise’), ‘Low-pass filtering’ vs. ‘Raw’, fw = 1/8, and at long TR values). In time series with relatively lower temporal correlations of the signal/physiological noise, such reduction in DOFs caused by temporal filtering is more prominent and one observes more severe reduction in statistical power (Fig. 3 (d, ‘Reduced serial correlations of signal/physiological noise’), ‘Low-pass filtering’ vs. ‘Raw’, fw = 1, comparing φ2 = 0.05 or 0.2 vs. φ2 = 0.58).
Contrary to temporal filtering, pre-whitening can recover the lost DOFs due to autocorrelation. If physiological noise dominates, pre-whitening will incur very minor CNR reduction and significantly improve the statistical power (Fig. 3 (d, ‘Influence of fractional contribution of white noise’), ‘pre-whitening’ vs. ‘raw’, fw = 1/8). Further, if the noise consists only of physiological components (which has similar serial correlation structure as the signal), pre-whitening can also reduce the bias of estimated linear Pearson correlation values (induced by potentially inconsistent autocorrelation structures of two time series) (Arbabshirani et al., 2014; Christova et al., 2011; Lewis et al., 2012). However, as the fractional contribution from white noise increases, a huge penalty on CNR and reduced statistical scores will be incurred (Fig. 3 (d, ‘Influence of fractional contribution of white noise’), ‘pre-whitening’ vs. ‘raw’, fw = 1, 8, at short TR values). Because of autocorrelation, the signal contribution to the total variance will thus decrease more dramatically compared to the contribution of white noise after pre-whitening. As expected, if we reduce the temporal dependencies in the physiological noise, making it more similar to white noise, pre-whitening will lead to more moderate reduction in the fractional contributions from signal/physiological noise to the total variance of fMRI time series, and thus more modest reduction in final statistical power at short TRs (Fig. 3 (d, ‘Reduced serial correlations of signal/physiological noise’), ‘pre-whitening’ vs. ‘raw’, fw = 1, comparing φ2 = 0.05/0.2 vs. φ2 = 0.58).
According to the discussion above, it is not trivial to determine the influence exerted by either temporal filtering or pre-whitening on the TR-dependence of linear Pearson correlation results and make generic recommendations. The exerted changes in CNRs and DOFs vary according to the original temporal characteristics of collected time series; and the impacts on associated statistics can be further complicated by the nonlinear relationship between CNR and statistical outcomes (t-scores scale supra-linearly with CNR at low CNR values, while more linear with CNR at high CNR values, see eqn. (C.6) in Appendix C). However, it is clear that preprocessing decisions (e.g., temporal filtering and pre-whitening discussed here) may incur distinct trade-offs between CNRs and DOFs and hence lead to incongruent dependence of statistical outcomes on TRs (simulation in Fig. 3 (d), comparing across columns, and real data results in Fig. 4 (c, d)). Therefore, temporal filtering and pre-whitening ought to be considered when piloting protocols for specific studies.
5.6. GLM-based functional connectivity analysis
Apart from linear Pearson correlation, resting-state functional connectivity has also been assessed within the framework of the GLM, by viewing the seed time series as a known model factor in the design matrix.
Such analyses differ from typical task-based analyses in two respects, which make the statistical benefits at short TRs less evident. First, the seed time series may also carry neural fluctuations that are unrelated to the target signal, which can reduce the quality of the model fitting and introduce additional sources of unmodeled noise that reduce CNR (resembling inaccurate modelling of task effects). For instance, if we assume that the time series of the medial prefrontal cortex (MPFC) contains fluctuations that covary independently with both the posterior cingulate cortex (PCC) and the insula, then using the time series of the MPFC as a regressor to assess its association with the PCC, insula-related variance in the MPFC regressors will be introduced into the residuals and increase the variance of unmodeled noise. Second, unlike modeled task effects, seed time series extracted from real data are inevitably contaminated by non-neural sources of noise (e.g., thermal and motion noise), which can further degrade model fits at short TRs due to the reduced SNR. As such, benefits of fast sampling are more ambiguous in seed-based regression than task activation results where the model is noise-free. Nonetheless, if the seed time series has minimal level of noise, and only comprises fluctuations that uniquely model variance of the target voxel, the statistical outcomes will resemble those derived from task activation and benefit more from short TRs (e.g., using temporal courses derived from ICA (Beckmann et al., 2005; Calhoun et al., 2001; McKeown et al., 1998)).
As is the case with task-driven short-TR fMRI, the statistical inferences in resting-state analyses made from the GLM and from linear Pearson correlation may not agree, arising from distinct model assumptions and associated conventions in data preprocessing. Briefly, GLM-based analysis tests against the null hypothesis whether a known seed signal could account for significant variance in a target random signal, whereas Pearson correlation analysis views both signals as samples randomly drawn from two distributions, and tests against the null hypothesis that the two distributions are independent. When accounting for serial correlations, the GLM estimates the correlations from the fitted residuals and pre-whitens the data, while linear Pearson correlation considers the serial correlations of both time series and includes the estimated serial correlations into final statistical inferences.
5.7. Adjusting for temporal autocorrelations using mixture-modeling
In the notable report by Feinberg et al., the authors observed significant increases in the peak Z-scores of common resting-state networks by sampling 6-fold faster than conventional acquisitions, and these detected networks appeared to be much more evident if different resting-state networks were resolved jointly through a multiple-regression analysis (100 regressors) than through several separate single-regression steps (Feinberg et al., 2010). There are multiple potential causes that could lead to these observations. As carefully pointed out by the authors, such observations could be a synergistic effect of more complete reduction of residual noise with multiple regressors, better modeling of noisy components (including quasi-periodical physiological sources), and the benefits of the additional DOFs in these data when a large number of regressors are applied. As such, the authors also pointed out that such advantages may not be observed by single-regression-like analyses, e.g., conventional seed-based or task-based GLM analyses.
Another factor that may possibly contribute to such superiority of multiple-regression over single-regression could relate to the manner in which serial autocorrelation was accounted for in this study (Feinberg et al., 2010). In lieu of conventional approaches that address the DOFs on an individual voxel or region basis, the authors employed a mixture-modeling approach (Everitt and Bullmore, 1999; Hartvig and Jensen, 2000)—they modeled the distribution of Z-score values (derived from ordinary least-squares fitting) as a mixture of a central Gaussian distribution (‘un-activated’ voxels) combined with separate Gamma distributions for positive/negative ends of the Z-score histogram (‘activated’ voxels). All the Z-scores were shifted and rescaled such that the null central Gaussian distribution had zero mean and unit variance, and altered DOFs due to serial correlations were thus corrected. This is a sophisticated procedure and is beyond the scope of this work to assess the relative superiority of this approach compared to conventional single-voxel-based approaches that adjust for serial autocorrelations. However, we would like to advise caution in using mixture-modeling to adjust for Z-scores after single-regression, either when multiple brain networks are inter-correlated or when this regressor carries information relating to a broad range of brain areas. In such cases, the fitted central Gaussian distribution may also comprise voxels with true effects (because the ‘activation’ class may not be well isolated from the ‘nulls’ or may not be characterized by a single Gamma model), which will over-adjust the Z-scores and limit the potential benefits of fast sampling.
Additionally, if rapid sampling is accompanied by reduced spatial resolution, partial volume contamination may also impact the results of mixture-modeling, thus mitigating the potential benefits of rapid sampling, since relevant signal properties (e.g., temporal autocorrelation) likely differ amongst gray matter, white matter and CSF.
5.8. Other considerations
5.8.1. Influence of image reconstruction parameters and hardware configuration on noise
As stated above, shortening the sampling interval in fMRI acquisitions causes changes in the temporal structure of the time-series data. While faster sampling can be achieved through conventional approaches, such as reducing the number of slices with the penalty of reducing spatial coverage, simultaneous multi-slice methods are increasingly becoming the method of choice for whole-brain fast fMRI. Modern simultaneous multi-slice methods utilize accelerated parallel imaging techniques, and like any parallel imaging technology, performance will depend on the image reconstruction parameters and hardware configuration. Although simultaneous multi-slice accelerates the acquisition by acquiring groups of multiple 2D slices simultaneously, it does not undersample the in-plane image data, and in the case of perfect reconstruction and slice separation there is no associated intrinsic SNR loss. However, with higher slice acceleration factors, artifact and noise levels will increase due to poor numerical conditioning of the image reconstruction. Structured artifacts such as unresolved spatial aliasing stemming from incomplete separation of collapsed slices (sometimes referred to as “leakage” (Cauley et al., 2014; Todd et al., 2016; Xu et al., 2013)) can occur when the acceleration factor is higher than what the receive coil array can support, resulting in spurious spatial correlations that can be mistaken for long-range functional connectivity. Similarly, high acceleration can also exacerbate noise amplification, or statistical errors in parallel imaging, manifested as spatially varying noise patterns (referred to as “g-factor” effects (Pruessmann et al., 1999; Setsompop et al., 2012; Todd et al., 2017; Zhu K et al., 2016). This is because high acceleration will result in shorter distances between aliased pixels, which can place a high demand on the spatial variations in coil sensitivity. The maximal achievable acceleration factor for a particular scanner setup, above which these two forms of error become unacceptable, is often difficult to estimate because it depends not only on the number of coil channels but also on their geometric layout in the array. The latter will influence the total number of distinct coil elements that intersect a given prescribed slice group, which means slice orientation and slice position within the coil array is also a factor.
All of these considerations complicate any prediction of the artifact and noise levels expected for a given simultaneous multi-slice acquisition, and their impact on the temporal structure of the fMRI time series. Therefore caution must be employed when designing protocols and comparing data collected with different acquisition or image reconstruction parameters.
5.8.2. Influence of field strength
An increase in field strength results, for a given voxel volume, in an increase in signal amplitude (Edelstein et al., 1986; Macovski, 1996). Consequently, the fractional contribution of white noise is reduced, and the relative influence of physiological, signal-dependent noise sources increases (Bianciardi et al., 2009; Kruger and Glover, 2001; Triantafyllou et al., 2005). Overall, the temporal SNR increases with field strength (Triantafyllou et al., 2005), and is often traded for higher resolution in either space or time.
Most ultra-high field applications currently focus on high spatial (sub-millimeter) resolution (Polimeni et al., 2018), and are characterized by high fractional contributions of white noise and reduced serial correlations. However, sub-second TR acquisitions at ultra-high field might also be attractive for tasks operating at higher temporal scales (Fig. 3 (c)), if the reduction in white noise outweighs the increase in serial correlations. Similarly, correlation-based analyses in combination with pre-whitening (Fig. 3 (d)) might significantly benefit from the simultaneous increase in tSNR (Triantafyllou et al., 2005) and CNR (Gati et al., 1997; Okada et al., 2005) provided at higher fields.
Apart from varying noise contributions, also the relaxation times change with increasing field strength. Pertinent to this discussion is the increase in the longitudinal relaxation time T1 (Pohmann et al., 2016), which leads to smaller Ernst angles and, thereby, a reduction in signal amplitude at a greater rate at short TRs.
5.8.3. Influence on cluster-wise inference
As recently noted (Wald and Polimeni, 2017), another potential benefit of short-TR acquisitions lies in the impact of the associated reduced signal levels on spatial autocorrelation observed in fMRI time series. Because lower signal levels at short TRs will lead to enhanced fractional contribution of white noise, the long range spatial correlations will be mitigated, making the assumptions of many cluster-wise inference methods more fully met and thereby reducing the inflated false-positive rates examined in the recent Eklund et al. study (Eklund et al., 2016).
5.8.4. Influence of inter-subject variability on the group-level inference
Changes in the effect size or variability of summary statistics at the first-level analysis (discussed in this work) may be obscured by large inter-subject variability and will not manifest in the group-level statistical outcomes (Kirilina et al., 2016). Therefore, the extents of inter-subject variability may be another factor that limits the observation of increased/reduced efficacy of fast sampling at the group-level.
5.9. Limitations of our simulation results
Signal, physiological and thermal noise fluctuations are assumed Gaussian in the present simulations (see appendix A–C for details). Such assumptions, however, may not hold for acquisitions with low SNR or multiple-channel coil arrays (Constantinides et al., 1997; Gudbjartsson and Patz, 1995; Henkelman, 1985; Kellman and McVeigh, 2005; Triantafyllou et al., 2011), in which detection bias of image magnitudes (and therefore tSNR) can be substantial (see supplementary material SM4 for simulations). With the ever-growing interest in high spatiotemporal acquisitions (which are commonly accompanied by lower levels of SNR) and the necessity for employment of multiple-channel coil arrays, one future avenue is to consider non-central chi distributed image magnitudes in existing statistical models for multiple-channel coil arrays.
Surprisingly, unlike GLM analysis, the influence of serial correlations on linear Pearson correlation analysis has not yet been thoroughly characterized and is only briefly discussed here. The statistical model simulated in this study (Appendix C) was adapted from an earlier model that evaluates the influence of temporal filtering on fMRI serial correlations (Davey et al., 2013), with additional assumptions of identical serial correlations and CNRs in the signal pair for simplicity. Further work will be necessary to establish more sophisticated statistical models that address distinct CNRs and serial correlations (given that the time series of a seed region is commonly derived by averaging across multiple voxels, and should have higher CNR and less white noise than the time series of a single brain voxel), for both valid significance testing and more accurate characterization (i.e., recovering the true cross-correlation values biased by inconsistent CNR and by serial autocorrelations within the pair of cross-correlated time series).
To compare the t-statistics across different TR values, we assume implicitly that the associated DOFs are sufficiently large (e.g., > 30) such that the null distributions converge to a standard normal distribution and are consistent across TR values. Such assumptions may not hold for studies that evaluate brain activity across extremely short temporal windows (e.g., 30 s), in which altered null distributions (associated with having too few DOFs) should be considered when designing the acquisition protocols.
Finally, it is noteworthy that the simulations performed in this study aimed at offering a qualitative illustration on how different factors in experiment design, statistical analyses, and the temporal characteristics of fMRI time series can affect the actual statistical gains of fast sampling. Other considerations, such as the influence of image reconstruction parameters and hardware configuration, were not incorporated in the simulation results due to their complexity. Parameters used in signal/noise models, although adapted from real data, should be generalized with caution for specific applications.
6. Recommendations
Based on the discussions presented here, we make the following recommendations for studies employing short-TR acquisitions.
If apparent head movements due to quasi-periodical magnetic field perturbations are present in fMRI data, motion parameters should be temporally notch-filtered or modeled along with respiratory covariates in nuisance regression to prevent introduction of fallacious respiratory effects into fMRI time series. See Section 3.1.
Nuisance regressors should be filtered to match the frequency bands of interest, in order to avoid potential spectra misspecifications such as introducing spurious components. See Section 3.1.
While it is commonly thought that sub-second sampling allows the complete removal of physiological noise effects because the fundamental frequencies can be low-pass-filtered out, it remains beneficial to record subjects’ physiological information (e.g., heart rates, respiratory waveforms) to account for substantial higher-order harmonics in quasi-periodical physiological components not resolved by fast sampling, as well as to mitigate additional noise caused by slow physiological effects (e.g., changes in RVT, HRV). See Section 3.2.
Serial correlation becomes substantially more important to accurately account for in acquisitions with fast sampling rates, as does the influence of white noise. Parametric models with more free parameters (e.g., higher-order AR or ARMA models, or the FAST method of the SPM toolbox), or nonparametric alternatives should be considered when modeling serial correlations of short-TR time series. Additionally, the AR1 + white noise (a.k.a. ARMA(1,1)) model may be a reasonable option for data vulnerable to model over-fitting (e.g., data with low SNR) if the AR coefficient is allowed to vary flexibly. See Section 4.
- Because reduced SNR due to shorter T1 magnetization recovery time can offset the increased DOFs at short TRs, and the noise structure can change dramatically at short TRs, determining the efficacy of fast sampling is not straightforward. Existing studies and simulations performed in this note have suggested some cases in which the benefits of rapid sampling are more evident:
- for summary statistics with more lenient CNR penalty (e.g., GLM-based task activation compared to linear Pearson correlation-based functional connectivity);
- in task paradigms that utilize faster oscillating frequencies;
- in data that reside in the physiological noise-dominated regime; and
- in data with reduced serial correlations in the signal and/or in the physiological noise (note, this is different from higher fractional contribution of white noise).
Despite these generic trends, whether it is beneficial to sample faster for a study depends upon the specific experimental design, statistical analyses, and temporal characteristics of collected time courses. Considerations include hardware configuration as well as decisions in acquisition, reconstruction and preprocessing, and how they interact with the employed experimental design and statistical analyses. For example, simply changing the voxel size can result in complex effects on statistical inferences in Pearson correlation vs. GLM analyses at short TRs as variously shown in Figs. 2–4 because of variation in the fractional contribution of white noise relative to physiological noise. As such, results of published empirical comparisons may provide limited insight for more generic studies; thus one should pilot acquisitions along with experimental design and the analysis pipeline to determine the optimal protocol for a specific study aim. See Section 5 for considerations.
Supplementary Material
Acknowledgements
The authors acknowledge Hesam Jahanian, Patricia Lan, Seul Lee, Ned Ohringer, Nina Fultz and Christine Law for assistance with data acquisition, and are grateful to Thomas Nichols, Soroosh Afyouni, Weidong Cai, Catie Chang, Laura Lewis, Kawin Setsompop, Isik Karahanoglu for valuable discussions regarding the present results. Study funding was supported by NIH (P41-EB015891, P41-EB015896, R21-NS106706, R01-MH111438 and R01-EB019437), the Lucas Foundation, and by the MGH/HST Athinoula A. Martinos Center for Biomedical Imaging. The authors also want to thank three anonymous reviewers, whose comments have substantially improved the quality of this manuscript.
Appendix A: Modelling physiological and white noise at different TR values
Noise at each TR value was modeled using an ARMA(1,1) model, i.e., physiological noise Np,TR (AR1 process) + white noise Nw,TR:
| eqn. (A.1) |
| eqn. (A.2) |
Where φTR is the autoregressive coefficient of the AR1 process, εp,TR[n] and εw,TR[n] refer to two white Gaussian noise processes with zero mean and constant variance and . Parameters for TR = 0.35 s (φ0.35 = 0.9089, , and ) were estimated from the normalized spectra shown in Fig. 2 (b) (TR = 0.35 s, ‘green’). The level of white noise was kept constant across TR values:
| eqn. (A.3) |
whereas φTR and were adapted from φ0.35 and using:
| eqn. (A.4) |
| eqn. (A.5) |
Please refer to the supplementary material SM5 for the mathematical derivation. The scaling factor ATR was computed from the Ernst angles at different TR values, assuming the tissue T1 = 1350 ms at 3T:
| eqn. (A.6) |
Appendix B: Simulating the statistical outcomes of GLM as a function of TRs
In GLM, the fMRI time series y is modeled as: y = Xβ + ε, where X refers to the model factors, β quantifies the associated fitting parameters, and denotes the residual noise with Vj being the serial correlation term. After pre-whitening (Bullmore et al., 1996; Woolrich et al., 2001), we obtain the unbiased, yet most efficient, estimation:
| eqn. (B.1) |
| eqn. (B.2) |
For simplicity, we assume that the imposed task is periodic, and X only comprises the task-evoked response oscillating at the task fundamental frequency f (the responses evoked at higher harmonics are minor and are thus ignored). When the number of time frames N is very large, we then have:
| eqn. (B.3) |
| eqn. (B.4) |
| eqn. (B.5) |
where βf quantifies the amplitude of BOLD responses evoked by the task, λf is the eigenvalue of Vi associated with the periodically varying eigenvector at f (Worsley and Friston, 1995), and CNRf represents the CNR at task frequency f. Intuitively, reflects the noise level at the normalized task frequency (amplitude in Fig. 3(b), adapted with discrete sampling).
Appendix C: Simulating the statistical outcomes of the linear Pearson correlation as a function of TR values
Linear Pearson correlation quantifies the instantaneous temporal synchrony between a pair of time courses {x[n], y[n]} as:
| eqn. (C.1) |
where N is the total number of samples, and are the sample means. If we model the fMRI observation y as an additive mixture of a stochastic signal ys, physiological noise εp, and white noise εw as follows:
| eqn. (C.2) |
where , , and , we have:
| eqn. (C.3) |
To simplify the simulation, we make a few additional assumptions: (1) x and y have identical CNR (CNRx = CNRy = CNR), signal and noise serial correlation structure; (2) signal xs and ys are both AR1 processes, and can be characterized by the same autoregression coefficient as εp, i.e., Vs = kVp, k is a scaling constant determined by CNR; and (3) (uncorrelated portion could always be considered as physiological noise). As such, we have ρx,y (the expectation of rx,y) as:
| eqn. (C.4) |
When testing the significance of sample correlation against the null hypothesis:
| eqn. (C.5) |
where (assuming ys, εp, and εw are independent of each other) (Davey et al., 2013; Kumar, 2009), the expected t-score (approximated by 1st-order Taylor expansion) is:
| eqn. (C.6) |
References
- Akin B, Lee HL, Hennig J, LeVan P, 2017. Enhanced subject-specific resting-state network detection and extraction with fast fMRI. Hum Brain Mapp 38, 817–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arbabshirani MR, Damaraju E, Phlypo R, Plis S, Allen E, Ma S, Mathalon D, Preda A, Vaidya JG, Adali T, Calhoun VD, 2014. Impact of autocorrelation on functional connectivity. Neuroimage 102 Pt 2, 294–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth M, Breuer F, Koopmans PJ, Norris DG, Poser BA, 2016. Simultaneous multislice (SMS) imaging techniques. Magn Reson Med 75, 63–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM, 2005. Investigations into resting-state connectivity using independent component analysis. Philos Trans R Soc Lond B Biol Sci 360, 1001–1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianciardi M, Fukunaga M, van Gelderen P, Horovitz SG, de Zwart JA, Shmueli K, Duyn JH, 2009. Sources of functional magnetic resonance imaging signal fluctuations in the human brain at rest: a 7 T study. Magn Reson Imaging 27, 1019–1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn RM, Diamond JB, Smith MA, Bandettini PA, 2006. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. Neuroimage 31, 1536–1548. [DOI] [PubMed] [Google Scholar]
- Birn RM, Smith MA, Jones TB, Bandettini PA, 2008. The respiration response function: the temporal dynamics of fMRI signal fluctuations related to changes in respiration. Neuroimage 40, 644–654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollmann S, Puckett AM, Cunnington R, Barth M, 2018. Serial correlations in single-subject fMRI with sub-second TR. Neuroimage 166, 152–166. [DOI] [PubMed] [Google Scholar]
- Boyacioglu R, Schulz J, Koopmans PJ, Barth M, Norris DG, 2015. Improved sensitivity and specificity for resting state and task fMRI with multiband multi-echo EPI compared to multi-echo EPI at 7 T. Neuroimage 119, 352–361. [DOI] [PubMed] [Google Scholar]
- Bright MG, Tench CR, Murphy K, 2017. Potential pitfalls when denoising resting state fMRI data using nuisance regression. Neuroimage 154, 159–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Brammer M, Williams SC, Rabe-Hesketh S, Janot N, David A, Mellers J, Howard R, Sham P, 1996. Statistical methods of estimation and inference for functional MR image analysis. Magn Reson Med 35, 261–277. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ, 2001. A method for making group inferences from functional MRI data using independent component analysis. Hum Brain Mapp 14, 140–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carp J, 2013. Optimizing the order of operations for movement scrubbing: Comment on Power et al. Neuroimage 76, 436–438. [DOI] [PubMed] [Google Scholar]
- Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K, 2014. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn Reson Med 72, 93–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Cunningham JP, Glover GH, 2009. Influence of heart rate on the BOLD signal: the cardiac response function. Neuroimage 44, 857–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JE, Jahanian H, Glover GH, 2017. Nuisance Regression of High-Frequency Functional Magnetic Resonance Imaging Data: Denoising Can Be Noisy. Brain Connect 7, 13–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L, A TV, Xu J, Moeller S, Ugurbil K, Yacoub E, Feinberg DA, 2015. Evaluation of highly accelerated simultaneous multi-slice EPI for fMRI. Neuroimage 104, 452–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christova P, Lewis SM, Jerde TA, Lynch JK, Georgopoulos AP, 2011. True associations between resting fMRI time series based on innovations. J Neural Eng 8, 046025. [DOI] [PubMed] [Google Scholar]
- Constable RT, Spencer DD, 2001. Repetition time in echo planar functional MRI. Magn Reson Med 46, 748–755. [DOI] [PubMed] [Google Scholar]
- Constantinides CD, Atalar E, McVeigh ER, 1997. Signal-to-noise measurements in magnitude images from NMR phased arrays. Magn Reson Med 38, 852–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbin N, Todd N, Friston KJ, Callaghan MF, 2018. Accurate modeling of temporal correlations in rapidly sampled fMRI time series. Hum Brain Mapp. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davey CE, Grayden DB, Egan GF, Johnston LA, 2013. Filtering induces correlation in fMRI resting state data. Neuroimage 64, 728–740. [DOI] [PubMed] [Google Scholar]
- Demetriou L, Kowalczyk OS, Tyson G, Bello T, Newbould RD, Wall MB, 2018. A comprehensive evaluation of increasing temporal resolution with multiband-accelerated protocols and effects on statistical outcome measures in fMRI. Neuroimage 176, 404–416. [DOI] [PubMed] [Google Scholar]
- Edelstein WA, Glover GH, Hardy CJ, Redington RW, 1986. The intrinsic signal-to-noise ratio in NMR imaging. Magn Reson Med 3, 604–618. [DOI] [PubMed] [Google Scholar]
- Eklund A, Andersson M, Josephson C, Johannesson M, Knutsson H, 2012. Does parametric fMRI analysis with SPM yield valid results? An empirical study of 1484 rest datasets. Neuroimage 61, 565–578. [DOI] [PubMed] [Google Scholar]
- Eklund A, Nichols TE, Knutsson H, 2016. Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. Proc Natl Acad Sci U S A 113, 7900–7905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everitt BS, Bullmore ET, 1999. Mixture model mapping of the brain activation in functional magnetic resonance images. Hum Brain Mapp 7, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair DA, Miranda-Dominguez O, Snyder AZ, Perrone AA, Earl EA, Van AN, Koller JM, Feczko E, Klein RL, Mirro AE, Hampton JM, Adeyemo B, Laumann TO, Gratton C, Greene DJ, Schlaggar B, Hagler D, Watts R, Garavan H, Barch DM, Nigg JT, Petersen SE, Dale A, Feldstein-Ewing SW, Nagel BJ, Dosenbach NUF, 2018. Correction of respiratory artifacts in MRI head motion estimates. bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Uğurbil K, Yacoub E, 2010. Multiplexed Echo Planar Imaging for sub-second whole brain fMRI and fast diffusion imaging. PLoS One. 5(12):e15710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg DA, Setsompop K, 2013. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. J Magn Reson 229, 90–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg DA, Yacoub E, 2012. The rapid development of high speed, resolution and precision in fMRI. Neuroimage 62, 720–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Holmes AP, Worsley KJ, Poline JP, Frith CD, Frackowiak RS, 1995. Statistical parametric maps in functional imaging: a general linear approach. Human brain mapping 2, 22. [Google Scholar]
- Friston KJ, Josephs O, Zarahn E, Holmes AP, Rouquette S, Poline J, 2000. To smooth or not to smooth? Bias and efficiency in fMRI time-series analysis. Neuroimage 12, 196–208. [DOI] [PubMed] [Google Scholar]
- Gati JS, Menon RS, Ugurbil K, Rutt BK, 1997. Experimental determination of the BOLD field strength dependence in vessels and tissue. Magn Reson Med 38, 296–302. [DOI] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Bijsterbosch JD, Harrison SJ, Harms MP, Anticevic A, Van Essen DC, Smith SM, 2018. Using temporal ICA to selectively remove global noise while preserving global signal in functional MRI data. Neuroimage 181, 692–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, Consortium WU-MH, 2013. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover GH, Li TQ, Ress D, 2000. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn Reson Med 44, 162–167. [DOI] [PubMed] [Google Scholar]
- Golestani AM, Chang C, Kwinta JB, Khatamian YB, Jean Chen J, 2015. Mapping the end-tidal CO2 response function in the resting-state BOLD fMRI signal: spatial specificity, test-retest reliability and effect of fMRI sampling rate. Neuroimage 104, 266–277. [DOI] [PubMed] [Google Scholar]
- Gonzalez-Castillo J, Saad ZS, Handwerker DA, Inati SJ, Brenowitz N, Bandettini PA, 2012. Whole-brain, time-locked activation with simple tasks revealed using massive averaging and model-free analysis. Proc Natl Acad Sci U S A 109, 5487–5492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffanti L, Salimi-Khorshidi G, Beckmann CF, Auerbach EJ, Douaud G, Sexton CE, Zsoldos E, Ebmeier KP, Filippini N, Mackay CE, Moeller S, Xu J, Yacoub E, Baselli G, Ugurbil K, Miller KL, Smith SM, 2014. ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. Neuroimage 95, 232–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gudbjartsson H, Patz S, 1995. The Rician distribution of noisy MRI data. Magn Reson Med 34, 910–914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallquist MN, Hwang K, Luna B, 2013. The nuisance of nuisance regression: Spectral misspecification in a common approach to resting-state fMRI preprocessing reintroduces noise and obscures functional connectivity. Neuroimage 82, 208–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handwerker DA, Gonzalez-Castillo J, D’Esposito M, Bandettini PA, 2012. The continuing challenge of understanding and modeling hemodynamic variation in fMRI. Neuroimage 62, 1017–1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartvig NV, Jensen JL, 2000. Spatial mixture modeling of fMRI data. Hum Brain Mapp 11, 233–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henkelman RM, 1985. Measurement of signal intensities in the presence of noise in MR images. Med Phys 12, 232–233. [DOI] [PubMed] [Google Scholar]
- Hennig J, Zhong K, Speck O, 2007. MR-Encephalography: Fast multi-channel monitoring of brain physiology with magnetic resonance. Neuroimage 34, 212–219. [DOI] [PubMed] [Google Scholar]
- Jacobs J, Stich J, Zahneisen B, Asslander J, Ramantani G, Schulze-Bonhage A, Korinthenberg R, Hennig J, LeVan P, 2014. Fast fMRI provides high statistical power in the analysis of epileptic networks. Neuroimage 88, 282–294. [DOI] [PubMed] [Google Scholar]
- Kellman P, McVeigh ER, 2005. Image reconstruction in SNR units: a general method for SNR measurement. Magn Reson Med 54, 1439–1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirilina E, Lutti A, Poser BA, Blankenburg F, Weiskopf N, 2016. The quest for the best: The impact of different EPI sequences on the sensitivity of random effect fMRI group analyses. Neuroimage 126, 49–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruger G, Glover GH, 2001. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Magn Reson Med 46, 631–637. [DOI] [PubMed] [Google Scholar]
- Kumar R, 2009. Signals and systems. PHI Learning Pvt. Ltd. [Google Scholar]
- Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G, 2001. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging 13, 313–317. [DOI] [PubMed] [Google Scholar]
- Lee HL, Zahneisen B, Hugger T, Levan P, Hennig J, 2013. Tracking dynamic resting-state networks at higher frequencies using MR-encephalography. Neuroimage 65, 216–222. [DOI] [PubMed] [Google Scholar]
- Lenoski B, Baxter LC, Karam LJ, Maisog J, Debbins J, 2008. On the Performance of Autocorrelation Estimation Algorithms for fMRI Analysis. IEEE Journal of Selected Topics in Signal Processing 2, 828–838. [Google Scholar]
- Lewis LD, Setsompop K, Rosen BR, Polimeni JR, 2016. Fast fMRI can detect oscillatory neural activity in humans. Proc Natl Acad Sci U S A 113, E6679–E6685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis LD, Setsompop K, Rosen BR, Polimeni JR, 2018. Stimulus-dependent hemodynamic response timing across the human subcortical-cortical visual pathway identified through high spatiotemporal resolution 7T fMRI. Neuroimage 181, 279–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis SM, Christova P, Jerde TA, Georgopoulos AP, 2012. A compact and realistic cerebral cortical layout derived from prewhitened resting-state fMRI time series: Cherniak’s adjacency rule, size law, and metamodule grouping upheld. Front Neuroanat 6, 36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin FH, Polimeni JR, Lin JL, Tsai KW, Chu YH, Wu PY, Li YT, Hsu YC, Tsai SY, Kuo WJ, 2018. Relative latency and temporal variability of hemodynamic responses at the human primary visual cortex. Neuroimage 164, 194–201. [DOI] [PubMed] [Google Scholar]
- Lin FH, Wald LL, Ahlfors SP, Hamalainen MS, Kwong KK, Belliveau JW, 2006. Dynamic magnetic resonance inverse imaging of human brain function. Magn Reson Med 56, 787–802. [DOI] [PubMed] [Google Scholar]
- Liu TT, 2016. Noise contributions to the fMRI signal: An overview. Neuroimage 143, 141–151. [DOI] [PubMed] [Google Scholar]
- Macovski A, 1996. Noise in MRI. Magn Reson Med 36, 494–497. [DOI] [PubMed] [Google Scholar]
- McDowell AR, Carmichael DW, 2018. Optimal repetition time reduction for single subject event-related functional magnetic resonance imaging. Magn Reson Med. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeown MJ, Makeig S, Brown GG, Jung TP, Kindermann SS, Bell AJ, Sejnowski TJ, 1998. Analysis of fMRI data by blind separation into independent spatial components. Hum Brain Mapp 6, 160–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K, 2010. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med 63, 1144–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monti MM, 2011. Statistical Analysis of fMRI Time-Series: A Critical Review of the GLM Approach. Front Hum Neurosci 5, 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narsude M, Gallichan D, van der Zwaag W, Gruetter R, Marques JP, 2016. Three-dimensional echo planar imaging with controlled aliasing: A sequence for high temporal resolution functional MRI. Magn Reson Med 75, 2350–2361. [DOI] [PubMed] [Google Scholar]
- Okada T, Yamada H, Ito H, Yonekura Y, Sadato N, 2005. Magnetic field strength increase yields significantly greater contrast-to-noise ratio increase: Measured using BOLD contrast in the primary visual area. Acad Radiol 12, 142–147. [DOI] [PubMed] [Google Scholar]
- Olafsson V, Kundu P, Wong EC, Bandettini PA, Liu TT, 2015. Enhanced identification of BOLD-like components with multi-echo simultaneous multi-slice (MESMS) fMRI and multi-echo ICA. Neuroimage 112, 43–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olszowy W, Aston J, Rua C, Williams GB, 2018. Accurate autocorrelation modeling substantially improves fMRI reliability. bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohmann R, Speck O, Scheffler K, 2016. Signal-to-noise ratio and MR tissue parameters in human brain imaging at 3, 7, and 9.4 tesla using current receive coil arrays. Magn Reson Med 75, 801–809. [DOI] [PubMed] [Google Scholar]
- Polimeni JR, Renvall V, Zaretskaya N, Fischl B, 2018. Analysis strategies for high-resolution UHF-fMRI data. Neuroimage 168, 296–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posse S, Ackley E, Mutihac R, Rick J, Shane M, Murray-Krezan C, Zaitsev M, Speck O, 2012. Enhancement of temporal resolution and BOLD sensitivity in real-time fMRI using multi-slab echo-volumar imaging. Neuroimage 61, 115–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preibisch C, Castrillon GJ, Buhrer M, Riedl V, 2015. Evaluation of Multiband EPI Acquisitions for Resting State fMRI. PLoS One 10, e0136961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P, 1999. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 42, 952–962. [PubMed] [Google Scholar]
- Purdon PL, Weisskoff RM, 1998. Effect of temporal autocorrelation due to physiological noise and stimulus paradigm on voxel-level false-positive rates in fMRI. Hum Brain Mapp 6, 239–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahib AK, Mathiak K, Erb M, Elshahabi A, Klamer S, Scheffler K, Focke NK, Ethofer T, 2016. Effect of temporal resolution and serial autocorrelations in event-related functional MRI. Magn Reson Med 76, 1805–1813. [DOI] [PubMed] [Google Scholar]
- Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM, 2014. Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. Neuroimage 90, 449–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Feinberg DA, Polimeni JR, 2016. Rapid brain MRI acquisition techniques at ultra-high fields. NMR Biomed 29, 1198–1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL, 2012. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 67, 1210–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmueli K, van Gelderen P, de Zwart JA, Horovitz SG, Fukunaga M, Jansma JM, Duyn JH, 2007. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal. Neuroimage 38, 306–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel JS, Mitra A, Laumann TO, Seitzman BA, Raichle M, Corbetta M, Snyder AZ, 2017. Data Quality Influences Observed Links Between Functional Connectivity and Behavior. Cereb Cortex 27, 4492–4502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Beckmann CF, Andersson J, Auerbach EJ, Bijsterbosch J, Douaud G, Duff E, Feinberg DA, Griffanti L, Harms MP, Kelly M, Laumann T, Miller KL, Moeller S, Petersen S, Power J, Salimi-Khorshidi G, Snyder AZ, Vu AT, Woolrich MW, Xu J, Yacoub E, Ugurbil K, Van Essen DC, Glasser MF, Consortium WU-MH, 2013. Resting-state fMRI in the Human Connectome Project. Neuroimage 80, 144–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF, Van Essen DC, Feinberg DA, Yacoub ES, Ugurbil K, 2012. Temporally-independent functional modes of spontaneous brain activity. Proc Natl Acad Sci U S A 109, 3131–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd N, Josephs O, Zeidman P, Flandin G, Moeller S, Weiskopf N, 2017. Functional Sensitivity of 2D Simultaneous Multi-Slice Echo-Planar Imaging: Effects of Acceleration on g-factor and Physiological Noise. Front Neurosci 11, 158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd N, Moeller S, Auerbach EJ, Yacoub E, Flandin G, Weiskopf N, 2016. Evaluation of 2D multiband EPI imaging for high-resolution, whole-brain, task-based fMRI studies at 3T: Sensitivity and slice leakage artifacts. Neuroimage 124, 32–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Triantafyllou C, Hoge RD, Krueger G, Wiggins CJ, Potthast A, Wiggins GC, Wald LL, 2005. Comparison of physiological noise at 1.5 T, 3 T and 7 T and optimization of fMRI acquisition parameters. Neuroimage 26, 243–250. [DOI] [PubMed] [Google Scholar]
- Triantafyllou C, Polimeni JR, Wald LL, 2011. Physiological noise and signal-to-noise ratio in fMRI with multi-channel array coils. Neuroimage 55, 597–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van de Moortele PF, Pfeuffer J, Glover GH, Ugurbil K, Hu X, 2002. Respiration-induced B0 fluctuations and their spatial distribution in the human brain at 7 Tesla. Magn Reson Med 47, 888–895. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium WUMH, 2013. The WU-Minn Human Connectome Project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wald LL, Polimeni JR, 2017. Impacting the effect of fMRI noise through hardware and acquisition choices - Implications for controlling false positive rates. Neuroimage 154, 15–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wise RG, Ide K, Poulin MJ, Tracey I, 2004. Resting fluctuations in arterial carbon dioxide induce significant low frequency variations in BOLD signal. Neuroimage 21, 1652–1664. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Ripley BD, Brady M, Smith SM, 2001. Temporal autocorrelation in univariate linear modeling of FMRI data. Neuroimage 14, 1370–1386. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Friston KJ, 1995. Analysis of fMRI time-series revisited--again. Neuroimage 2, 173181. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Liao CH, Aston J, Petre V, Duncan GH, Morales F, Evans AC, 2002. A general statistical analysis for fMRI data. Neuroimage 15, 1–15. [DOI] [PubMed] [Google Scholar]
- Xu J, Moeller S, Auerbach EJ, Strupp J, Smith SM, Feinberg DA, Yacoub E, Ugurbil K, 2013. Evaluation of slice accelerations using multiband echo planar imaging at 3 T. Neuroimage 83, 991–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahneisen B, Grotz T, Lee KJ, Ohlendorf S, Reisert M, Zaitsev M, Hennig J, 2011. Threedimensional MR-encephalography: fast volumetric brain imaging using rosette trajectories. Magn Reson Med 65, 1260–1268. [DOI] [PubMed] [Google Scholar]
- Zhu K, Wu H, Dougherty RF, Middione MJ, Pauly JM, AB K, 2016. Analytical G-factor for Cartesian Simultaneous Multi-Slice Imaging. Proc Intl Soc Mag Reson Med. 0609. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.