Nanoscale stacking fault–assisted room temperature plasticity in flash-sintered TiO2

Jin Li; Jaehun Cho; Jie Ding; Harry Charalambous; Sichuang Xue; Han Wang; Xin Li Phuah; Jie Jian; Xuejing Wang; Colin Ophus; Thomas Tsakalakos; R Edwin García; Amiya K Mukherjee; Noam Bernstein; C Stephen Hellberg; Haiyan Wang; Xinghang Zhang

doi:10.1126/sciadv.aaw5519

. 2019 Sep 20;5(9):eaaw5519. doi: 10.1126/sciadv.aaw5519

Nanoscale stacking fault–assisted room temperature plasticity in flash-sintered TiO₂

Jin Li ¹, Jaehun Cho ¹, Jie Ding ¹, Harry Charalambous ², Sichuang Xue ¹, Han Wang ¹, Xin Li Phuah ¹, Jie Jian ¹, Xuejing Wang ¹, Colin Ophus ³, Thomas Tsakalakos ², R Edwin García ¹, Amiya K Mukherjee ⁴, Noam Bernstein ⁵, C Stephen Hellberg ⁵, Haiyan Wang ^1,^6,^*, Xinghang Zhang ^1,^*

PMCID: PMC6984969 PMID: 32047855

Flash-sintered ceramics exhibit unexpected room temperature plasticity due to the high density preexisting defects.

Abstract

Ceramic materials have been widely used for structural applications. However, most ceramics have rather limited plasticity at low temperatures and fracture well before the onset of plastic yielding. The brittle nature of ceramics arises from the lack of dislocation activity and the need for high stress to nucleate dislocations. Here, we have investigated the deformability of TiO₂ prepared by a flash-sintering technique. Our in situ studies show that the flash-sintered TiO₂ can be compressed to ~10% strain under room temperature without noticeable crack formation. The room temperature plasticity in flash-sintered TiO₂ is attributed to the formation of nanoscale stacking faults and nanotwins, which may be assisted by the high-density preexisting defects and oxygen vacancies introduced by the flash-sintering process. Distinct deformation behaviors have been observed in flash-sintered TiO₂ deformed at different testing temperatures, ranging from room temperature to 600°C. Potential mechanisms that may render ductile ceramic materials are discussed.

INTRODUCTION

Ceramics often provide numerous advantages over metallic materials, such as wear and corrosion resistance, high hardness, high-temperature strength, electrical insulation, and light weight, and thus have been widely used as structural materials for various environments (1–3). However, the applications of ceramics have frequently been limited by their brittle nature, especially at low-to-moderate operation temperatures. In general, the plastic deformation of crystalline metallic materials proceeds through the activity of dislocations at room temperature (RT) and/or diffusion creep at elevated temperatures (1, 3). In contrast, ceramics with ionic or covalent bonding are strong but mostly brittle at low temperatures due to the lack of dislocations to accommodate plasticity. Thus, the fracture toughness of ceramics is much lower than that of deformable metallic materials. The plastic deformation of ceramic materials has been intensively investigated at high temperatures, where diffusional creep or grain boundary sliding becomes prominent (3).

RT plasticity remains largely absent in most ceramic materials. It has been shown that fracture can be suppressed to some extent in a few ceramics at low temperatures, such as single-crystal SrTiO₃ (4) and MgO (5), and polycrystalline ZrO₂ (6) and yttria-stabilized zirconia (YSZ) (6–8). For example, YSZ, which experiences martensitic phase transformations (6, 8), may exhibit superelasticity at RT depending on the doping concentration and its grain size (6, 8). Another approach to improve plasticity of ceramics is significant grain refinement: It has been demonstrated that plastic deformation of ceramics at low temperature is sometimes possible if their grain sizes are in the range of a few nanometers (2). However, the sintering of ceramics while maintaining such small grain sizes is challenging.

To produce advanced ceramic materials with low porosity and small grains, various sintering techniques have been extensively investigated. In general, conventional sintering techniques typically require high temperatures and long sintering times and thus often lead to substantial grain coarsening (9). With the assistance of electrical field and pressure, spark plasma sintering has been used to sinter ceramics to nearly full density over several minutes (10–12). A recently discovered technique, flash sintering, however, can be used to sinter ceramics to full density within an even shorter time, a few seconds, without pressure, and at a furnace temperature much lower than the conventional sintering temperature (13–15). During flash sintering, a ramp heating process and moderate electrical fields are applied. Once reaching the onset of the flash temperature, a densification process occurs nearly instantaneously, accompanied by a sudden increase in electrical conductivity (13, 14, 16). Despite the broad interest in flash sintering of ceramics, investigations on the deformability of flash-sintered ceramics remain scarce.

Titanium dioxide (TiO₂) has diverse and broad applications for solar cells, semiconductors, and water purification, and has been intensively investigated in the past decades (17). The mechanical properties of TiO₂ prepared by different techniques have been widely investigated (18–20). For instance, rutile TiO₂ single crystals of various stoichiometries have been tested at temperatures varying from RT to 1300°C by compression (18, 19, 21). Previous studies showed that TiO₂ was brittle when tested below 600°C and most specimens fractured before yielding. Plastic deformation becomes feasible in TiO₂ only when test temperatures exceed 600°C (18, 19, 21).

In this study, we report that, by using in situ micropillar compression tests inside a scanning electron microscope (SEM), prominent RT plasticity has been observed in flash-sintered TiO₂ with an average grain size of ~10 μm. In contrast to the conventionally sintered TiO₂, flash-sintered TiO₂ inherits a high density of stacking faults and dislocations introduced during the nonequilibrium sintering process. Different from the previously reported low-temperature plastic deformation in flash-sintered 3YSZ (7), where phase transformation–induced plastic deformation and dislocation-assisted plastic deformation beyond 400°C were observed, flash-sintered TiO₂ in this work presents no phase transformation and the prominent plastic deformations in the testing temperatures ranging from RT to 600°C are correlated with abundant preexisting defects, and deformation induced high-density stacking faults, nanotwins, and dislocations. This study suggests that flash sintering may be an effective approach to significantly improve the low-temperature plasticity of ceramic materials in general.

RESULTS

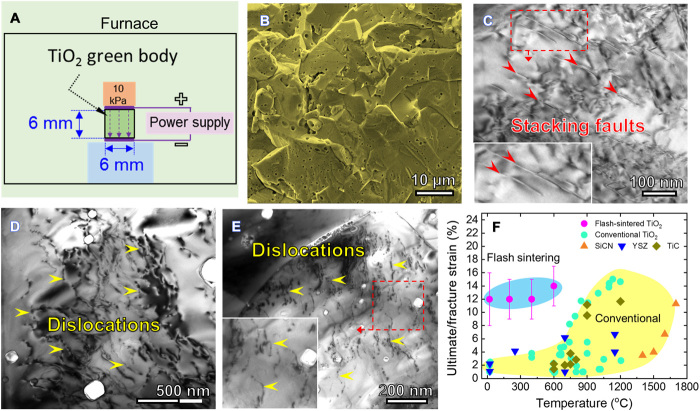
The schematics of flash sintering and the microstructure of flash-sintered TiO₂ are shown in Fig. 1. The density of flash-sintered TiO₂ (900°C for 1 min) was measured to be ~98%. Conventional sintered (1350°C/5 hours) TiO₂ (~95% density) and zero-field sintered TiO₂ (1100°C without an applied electric field, ~95% density) were also prepared for comparison studies. Micropillars were fabricated using focused ion beam (FIB) lithography on the polished surface of the sintered TiO₂ cylinder for in situ SEM compression studies. Bright-field transmission electron microscopy (TEM) micrographs in Fig. 1 (C to E) show the existence of stacking faults and a high density of dislocations in the flash-sintered TiO₂. For both conventional and zero-field sintered TiO₂, the grain interiors are relatively clean, with few preexisting defects. More details on sintering conditions and microstructures of conventional and zero-field sintered TiO₂ are shown in fig. S1.

Figure 1F compares ultimate/fracture strain (%) as a function of testing temperatures for flash-sintered TiO₂, conventional TiO₂ (19, 21), and several other conventional ceramic systems (22–24). All data were obtained from compression studies. Among all the data points, the flash-sintered TiO₂ exhibits significantly enhanced deformability even at RT.

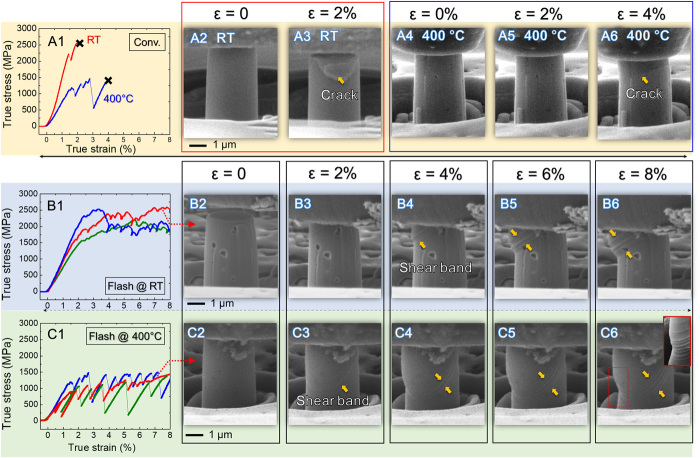
Stress-strain behaviors of conventional and flash-sintered TiO₂ obtained from in situ microcompression studies from RT to 600°C at a constant strain rate of 5 × 10⁻³ s⁻¹ are shown in Fig. 2 and fig. S2. For conventional sintered TiO₂ tested at both RT and 400°C (Fig. 2, A1 to A6), all pillars experienced brittle catastrophic fractures at an average true strain of 2% for RT tests and 3% for 400°C tests (see movies S1 and S2 for more details). Similarly, micropillar compression tests on the zero-field sintered TiO₂ performed at RT and 400°C at a constant strain rate of 5 × 10⁻³ s⁻¹ (fig. S3) showed brittle catastrophic fractures at an average strain of ~2% at RT and ~3.5% at 400°C (see movies S3 and S4 for more details).

In contrast, the flash-sintered TiO₂ tested at RT (Fig. 2, B1 to B6) shows work hardening to a maximum flow stress of 2 to 2.5 GPa, and the stress-strain curves have small serrations. The in situ SEM movie snapshots of a pillar (red data in Fig. 2B1) compressed to different strain levels show the formation of successive slip bands (indicated by arrows). No fracture was observed up to a strain of ~12%. For pillars tested at 400°C (Fig. 2, C1 to C6), prominent load-drops dominate the stress-strain curves. Each load-drop corresponds to the formation of one major shear band as indicated by arrows. The inset of Fig. 2C6 shows a magnified view of multiple shear bands generated during deformation. No crack was observed in the deformed pillar. See movies S5 and S6 for more details.

When the test temperature is 200°C (fig. S2), a mixture of small serrations and large load-drops were observed in the stress-strain curves. The maximum flow stress is ~1.5 GPa. At a strain of ~4%, a shear band emerged. The shear band broadened or propagated as indicated by yellow arrows. For the pillars tested at 600°C (fig. S2), the maximum flow stress decreased further to ~1 GPa, after a few percent of strain. In addition, as compared to RT and 400°C, no obvious stress serrations were observed. SEM snapshots show a relatively smooth surface without noticeable slip bands in the deformed pillars. These pillars deformed in a ductile manner without indication of fracture. See movies S7 and S8 for more details.

To investigate the influence of deformation on the evolution of microstructure, we performed post-deformation TEM analyses on the flash-sintered TiO₂ pillars tested to a strain of 8 to 10%. As shown in Fig. 3A1 for the pillar compressed at RT, the deformed portion of the pillar contains high-density parallel slip bands. The slip bands intersected with the left surface of the pillar and led to prominent shear offsets, as shown in Fig. 2B6. The pillar also contained several nanopores, but no cracks were observed to initiate from any of these nanopores. Several locations (indicated by red boxes) were selected to examine the microstructure in detail. Figure 3A2 shows that most of these parallel slip bands are composed of a high density of stacking faults, as confirmed by the streaking lines in the inserted selected-area diffraction (SAD) pattern. The average spacing between stacking faults is ~10 nm. Although most stacking faults are parallel along one direction, Fig. 3A3 captures another set of high-density stacking faults on {101} planes forming an intersection angle of 66° relative to the stacking faults in the other direction. Twin boundaries also formed, but their density is low. High-resolution TEM (HRTEM) micrograph in Fig. 3A4 shows an example of a twin boundary decorated with stacking faults.

The pillars compressed at 400°C have microstructures drastically different from those tested at RT. Although Fig. 3B1 shows that the deformed pillar also contains high-density slip bands, a careful examination shows that these slip bands are primarily twin boundaries, as confirmed by the inserted SAD pattern in Fig. 3B2. The average twin spacing is ~150 nm. The complex contrast in grain interiors may arise from the intersection of dislocations with twin boundaries. HRTEM micrograph in Fig. 3B3 shows two typical types of twin boundaries, relatively sharp coherent twin boundaries and stacking fault decorated twin boundaries. Although twin boundaries are the predominant defects in the deformed pillar, stacking faults were also observed, as shown in Fig. 3B4. These stacking faults, parallel to the direction of predominant twin boundaries, are mostly fragmented, appearing as discontinuous segments.

For pillars compressed at 600°C, no shear bands were observed (Fig. 3C1), in agreement with the SEM observations in fig. S2. A high density of dislocations and stacking fault segments formed near the pillar top surface, as shown in Fig. 3 (C2 and C3). Figure 3C4 shows an example of stacking fault segments that intersect on two sets of {101} planes with an angle of 66°.

DISCUSSION

Preexisting defects in flash-sintered TiO₂

Ceramic materials often have a low dislocation density due to the nature of their ionic and covalent bonds. Dislocations appear in ceramics during high-temperature deformations (1–3). However, a high density of dislocations and stacking faults was observed in flash-sintered TiO₂ before any deformation (Fig. 1 and fig. S4). The as-received nanocrystalline TiO₂ powders have no preexisting dislocations (as shown in fig. S1). These dislocations may be generated during flash sintering wherein the rapid sintering introduces drastic plastic deformation at high temperatures within a short time, and the consequent rapid cooling process may be able to “freeze” a large number of dislocations in the flash-sintered TiO₂. Furthermore, it has been reported that defect catastrophes frequently occur during flash sintering (16). The colossal generation of electrons, holes, and point defects can enhance electrical conductivity, promote phase transformations, and accelerate sintering simultaneously (14, 16). Both Joule heating and the applied electric field are important for defect catastrophes (16). An in situ biasing study of rutile TiO₂ inside TEM has shown that under the presence of electric field (±1.5 V), oxygen (O) vacancies were created at low temperatures and then migrated under the electric field (25). Eventually, O vacancies coalesced into stacking faults. These stacking faults have the form of vacancy discs on {110} and {121} planes and are bounded by partial dislocation loops. It is reasonable to speculate that a similar but more aggressive process took place during flash sintering of the TiO₂ under the influence of the electric field. Massive formation and migration of O vacancies occur simultaneously at the onset of flash sintering and lead to the creation of high-density defects after flash sintering. The x-ray photoelectron spectroscopy results shown in fig. S5 have confirmed the deficiency of oxygen in the flash-sintered TiO₂ samples in this study.

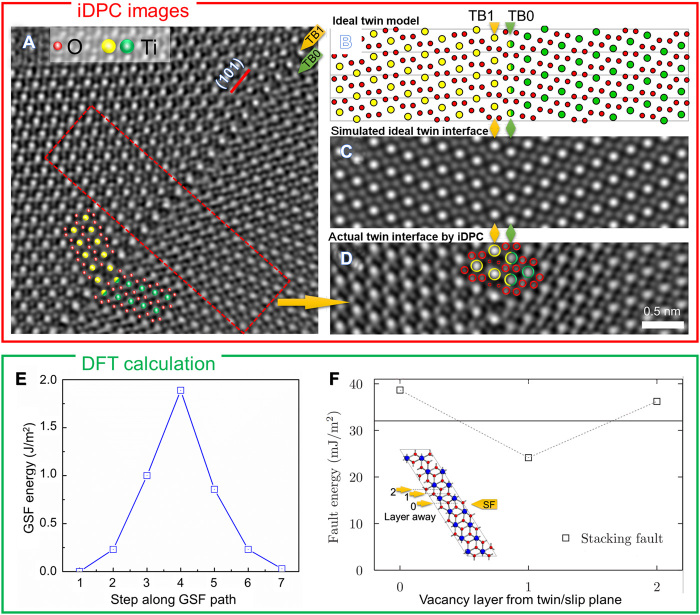
To examine point defects in flash-sintered specimens, atomic-resolution TEM experiments were conducted to investigate the flash-sintered TiO₂. Figure 4A shows an integrated differential phase contrast (iDPC) scanning TEM (STEM) image of a twin boundary (projected from [101] zone) in a flash-sintered TiO₂ pillar after deformation at 400°C. The iDPC image was reconstructed to best correct aberrations. Both Ti and O columns can now be resolved. The Ti columns above and below the twin boundary are intentionally shown in yellow and green, and the O columns are shown in red. It is noted that some aberration may exist in the image, and therefore, further analyses of the image and simulation have been conducted, and the results are shown in Fig. 4 (B to D). Figure 4 (B and C) shows the estimated atomic structure and the simulated image, respectively, of the magnified area of the red box in Fig. 4A. For the simulation, the atomic coordinates were estimated from the measured DPC images, and the ideal image was simulated by computing a complex phase image, assuming a roughly 10-nm-thick sample, and then applying the contrast transfer function (26, 27) for DPC to the phase images, using the same microscope parameters as the DPC experiments. As shown in Fig. 4D, a few Ti and O columns adjacent to the twin boundary are shown by open circles for clarity. It is noted that the actual twin interface is more complicated than the ideal twin interface simulated (Fig. 4C). The observed dimmer oxygen sites locate on the TB1 plane, one atomic layer next to the actual twin interface TB0, as shown by small open red circles. The dimmer oxygen sites next to the boundary can be explained by removing oxygen along those columns, but cannot be explained by aberrations, indicating the O deficiency close to the twin boundary. Such observation is consistent with the density functional theory (DFT) modeling results in Fig. 4 (E and F), which show a lower stacking fault energy when O vacancies are located one atomic layer away from the twin interface. However, due to the minor sample mistilt in one side of the twin structure, further imaging or spectroscopy studies are required to conclusively determine the chemistry at the twin boundary.

Fig. 4 — (A) iDPC image of a twin boundary showing the atomic arrangement of both Ti and O columns. For clarity, Ti columns above and below the twin boundary are shown in yellow and green, respectively. Further analyses of a magnified area as shown by red dashed lines are shown in (B) to (D). (B) Estimated atomic structure. (C) Simulated DPC image without aberrations. (D) Experimental observation. Selected Ti and O columns close to the twin boundary are shown by open circles. O columns surrounding Ti on the plane TB1 (next to the real twin interface TB0) have relatively dimmer contrast as shown by small open red circles, indicating the O deficiency close to the twin boundary. (E) Variation of generalized stacking fault (GSF) energies with displacement. The unstable stacking fault energy is high, ~1.9 J/m², while the stable stacking fault energy is much lower, 30 to 40 mJ/m². (F) Stacking fault and twin fault formation energy versus O vacancy position. The embedded figures show (left) a basic stacking fault (unit cell vector shift) and (right) a basic twin fault (supercell). The solid line indicates the fault energy without a vacancy.

It is worth mentioning that there are twice as many Ti columns along the twin boundary and stacking faults as compared to the perfect crystal lattices in flash-sintered TiO₂, as shown in fig. S6. Such a phenomenon could be an indication that the lack of O may lead to severe lattice distortion after twinning or faulting. Moreover, the geometric phase analysis results of a typical stacking fault inside the flash-sintered TiO₂ after pillar compression are shown in fig. S6. Strain and lattice distortion near the stacking faults, which may arise from O vacancies, have been observed. Future investigations on the role of the O partial pressure on the formation of defects during flash sintering as well as the influence of O stoichiometry on the mechanical behavior of flash-sintered TiO₂ are necessary to further understand the mechanisms of defect formation and mechanical response of flash-sintered TiO₂.

Defect-assisted RT plasticity in flash-sintered TiO₂

Most ceramics, including TiO₂, are brittle, especially when tested at low temperatures. Few ceramics have shown limited deformability at ambient temperatures, such as single-crystal SrTiO₃ (4) and MgO (5), and polycrystalline ZrO₂ (6) and YSZ (6–8). MgO can be plastically deformed at RT, as dislocations in MgO are mobile at relatively low stresses (28). ZrO₂ exhibits superelasticity because of the martensitic phase transformation (6). Previous studies show that bulk TiO₂ has no plasticity unless deformed above 600°C (18, 19, 21).

Our micropillar compression studies show that the zero-field and conventional sintered TiO₂ fractured at an average strain of ~2% at RT, and at ~3% strain when tested at 400°C (Fig. 2 and fig. S3). The poor deformability of these TiO₂ is in line with previous studies on the brittle nature of conventional sintered TiO₂. In contrast, it is unexpected to observe substantial plasticity in the flash-sintered TiO₂ deformed at RT. No catastrophic failure was observed in the flash-sintered TiO₂ after a strain level of 8%, as shown in Fig. 2B6. Numerous stress-strain plots compiled in fig. S7 show good reproducibility. Figure 1F compares ultimate/fracture strain (%) as a function of testing temperatures for flash-sintered TiO₂, conventional TiO₂ (19, 21), and several other conventional ceramic systems (22–24). All data were obtained from compression studies. As shown in Fig. 1F, fracture strain, in general, is very limited at low temperatures (~2% or less) and increases with testing temperatures for most conventional ceramics, such as TiO₂ (19, 21), SiCN (22), YSZ (23), and TiC (24). In contrast, the flash-sintered TiO₂ in the current study exhibits significantly improved deformability well below 600°C, and the large plastic strain at RT (exceeding 10%) has not been reported in any TiO₂ tested previously.

In ductile metallic materials, plasticity is accommodated by the nucleation and migration of dislocations. As the lattice friction stress is low in metallic materials, dislocations can be highly mobile and improve the plasticity of metallic materials. However, the corresponding friction stress in ceramic materials is typically high due to the strong directional interatomic bonding (1, 3). What makes the situation even worse is that the resolved shear stress required for dislocation nucleation in ceramics is exceptionally high, on the order of the theoretical shear strength for perfect crystals under athermal conditions (1, 3). Hence, the high friction stress and resistance to dislocation nucleation lead to the brittle behavior in most ceramics at low to intermediate temperatures. Nanotwinned metals have shown high strength and plasticity, as twin boundaries can significantly increase the work-hardening ability of metals (29–33). However, twin boundaries are generally absent in ceramic materials, and twin boundary– or stacking fault–dominated plasticity is scarce in ceramics (34, 35). In comparison, the flash-sintered TiO₂ already contains abundant preexisting defects, such as dislocations and short segments of stacking faults, which may foster plastic deformation at RT. Moreover, O vacancies and the preexisting defects could also facilitate the nucleation and propagation of defects, such as the high-density stacking faults and nanotwins formed during deformation at RT.

Grain size and porosity also affect the deformability of TiO₂. The grain size of flash-sintered and conventional sintered TiO₂ is ~10 and ~50 μm, respectively, and ~1 μm for zero-field sintered TiO₂. It is likely that the micropillars (diameter, ~3 μm) fabricated from the flash-sintered and conventional sintered TiO₂ specimens contain one or few grains, while the pillars from zero-field sintered TiO₂ contain multiple grains. Although smaller grain size often improves the plasticity of ceramics (2), the flash-sintered TiO₂ with large grains has substantial plasticity at RT compared to the brittle fracture of zero-field sintered TiO₂. It is worth mentioning that the existence of nano-/micropores inside the materials may also affect the mechanical behavior under compression. The pores inside conventional sintered and zero-field sintered TiO₂ are dominated by intergranular pores, and the shape of these pores is usually triangular or irregular, as shown in fig. S1. In comparison, the pores in the flash-sintered TiO₂ are usually intragranular pores, and their shape is either circular or faceted, as shown in Fig. 1 and fig. S4. Our studies suggest that the intergranular pores can act as the sources for crack formation, as indicated in fig. S3. In comparison, the intragranular pores in flash-sintered TiO₂ have little or no deleterious effect on the plasticity or fracture behavior, as shown in Fig. 3 (A1, B1, and C1).

DFT calculations show that the stacking fault energy of TiO₂ is low (comparable to some metals like Ag and Cu), 30 to 40 mJ/m², but the unstable stacking fault energy, which gives an approximation of the barrier to dislocation nucleation and motion (36), is high, ~1.9 J/m², as shown in Fig. 4C. Furthermore, the existence of an O vacancy in planes next to stacking faults does not significantly increase the stacking fault energy of TiO₂, as shown in Fig. 4D. The density of deformation-induced stacking faults is low in conventional TiO₂ deformed at RT due to the high unstable stacking fault energy. However, in the flash-sintered TiO₂, there are abundant O vacancies and preexisting short stacking fault segments, which may foster the formation of high-density long stacking faults during deformation. These stacking faults once formed after deformation are stable due to the low stacking fault energy.

Temperature-dependent deformation behavior in flash-sintered TiO₂

In general, conventional sintered TiO₂ fractures before yielding at RT, and hence, no yield strength values were reported for TiO₂ at RT. The yield stress of TiO₂ tested at 500°C maybe ~800 MPa based on a previous high-temperature test of TiO₂ single-crystal specimen (18). It has also been reported that the flow stress of TiO₂ is sensitive to test temperature (18, 19, 21). At high temperatures (>600°C), the primary slip systems in TiO₂ are { $10 \bar{1}$ }/<101> and/or {110}/<001>, and the former slip system is often more active (18, 19). Low-temperature (<600°C) plasticity in TiO₂, however, has not been reported to date. Unexpectedly, substantial plasticity was observed in the flash-sintered TiO₂ tested at RT in the present study.

The difference between the continuously serrated stress flows at RT (Fig. 2B1) versus the consecutive sudden load-drops at 400°C (Fig. 2C1) is remarkable. The formation of abundant stacking faults is the predominant deformation mechanism during compression at RT (Fig. 3, A1 to A4), while deformation-induced twin bands become more pronounced at 400°C (Fig. 3, B1 to B3). The habit planes of the stacking faults and twin bands are both { $10 \bar{1}$ } and it has been shown that twinning occurs more readily at higher temperatures in Al₂O₃ (37) and CaCO₃ (38). Previous studies showed that the propagation of stacking faults (dislocations) in certain systems is sluggish compared with twin boundaries (39), and the velocity of twin propagation normally increases with increasing test temperature (40). Also, the twinning stress is inversely proportional to temperature, i.e., lower temperatures lead to higher twinning stress (37). Consequently, the deformation behavior of the flash-sintered TiO₂ at RT is dominated by the stress-induced nanoscale stacking faults that propagate slowly, and thus, the corresponding stress-strain curves are continuous with few and small serrations, while the sharp load-drops at 400°C are caused by the formation and rapid propagation of deformation twins. When the test temperature is 200°C (fig. S2), the deformability is controlled by a mixture of stacking faults and deformation twins, and thus, the stress-strain curve has a mixture of large stress-drops and small serrations.

At 600°C, no slip bands were observed in flash-sintered TiO₂, and the stress-strain curves appear smooth with minor serrations (fig. S2). Post-compression TEM studies show that high-density dislocations and stacking fault segments formed after compression at 600°C (Fig. 3, C1 to C3). No shear bands were detected. Diffusion creep may not be pronounced as the test temperature is still well below the melting point of TiO₂ (~1800°C), ~0.33 T_m.

It has been shown that conventional TiO₂ can sustain certain plastic strain when deformed above 600°C (18, 19, 21). Post-compression TEM studies of conventional TiO₂ show that there are few scattered stacking faults and twin boundaries accompanied by numerous intragranular cracks, as shown in fig. S8.

It is worth mentioning that although the flash-sintered TiO₂ contains a small number of preexisting stacking faults, deformation at RT induces a prominent increase of stacking fault density. Most of these stacking faults may arise from the migration of partials from preexisting dislocations. As the density of deformation-induced stacking faults is high, the stress-strain curve appears relatively smooth with small serrations. In addition, the effect of crystal orientation on the mechanical behavior of flash-sintered TiO₂ in this study shall be briefly discussed. In general, the mechanical behavior of ceramics is largely determined by the crystal orientation (1, 3). In this study, as the average grain size of the flash-sintered TiO₂ is ~5 μm, most flash-sintered pillars have single-crystal– or bicrystal-like nature, and these pillars may have different crystal orientation depending on the position at which the pillars were made. One may expect that the reproducibility of stress-strain curves should be poor in this study if the crystal orientation plays an important role in the plasticity of pillars. However, the reproducibility is generally good at all test temperatures. Such a phenomenon suggests that crystal orientation plays a relatively insignificant role in determining the mechanical behavior of the flash-sintered TiO₂. The preexisting defects may have a major impact on the mechanical behavior of the flash-sintered TiO₂. In addition, residual stress due to orientation-dependent coefficient of thermal expansion mismatch or defect annihilation if occurred during the pillar fabrication may add some uncertainty on the reproducibility of micropillar compression studies. However, given the comparable large grain size in both conventional and flash-sintered TiO₂, the difference of residual stress between the two types of specimens may be insignificant. Also, the reasonable reproducibility of stress-strain curves for TiO₂ pillars tested at various temperatures suggests that the microstructures developed in flash-sintered TiO₂ may be similar in these pillars, containing high-density defects. For instance, preexisting defects can be readily identified in the lower (largely undeformed) portion of the pillar in Fig. 3 (A1 and B1). Therefore, preexisting defects that were introduced during the flash-sintering process survived after the pillar fabrication.

It is also worth mentioning that nonuniform grain and pore size distributions exist in the current flash-sintered samples, preventing reliable macroscopic mechanical testing. Continuous efforts have been devoted to explore the flash-sintering mechanisms and to achieve better control on the sample uniformity and quality. Promising results have been demonstrated by AC field sintering (41), controlled current ramping (42), SPS (spark plasma sintering)-flash combined process (43), and others. Given the potentials in microstructure and defect density control offered by the flash–sintering process, flash-sintered ceramics hold great potential in demonstrating improved ductility in macroscopic specimens under moderate temperatures or RT compared to conventional sintered samples.

Summary

In conclusion, in situ micropillar compression tests show that flash-sintered TiO₂ exhibits unexpected substantial plasticity at RT, sustaining 10% strain without noticeable cracks. The high-density preexisting defects and O vacancies introduced during the nonequilibrium flash-sintering process facilitates the nucleation of dislocations. RT deformation is dominated by the formation of nanoscale stacking faults, followed by the creation of nanotwins when tested at 200° to 400°C. Dislocation glide takes over the deformation mechanism at 600°C. This study strongly suggests that the flash-sintering method presents great potential in promoting plasticity in a broad range of ceramic materials.

MATERIALS AND METHODS

Flash sintering

Rutile TiO₂ powder (product no. 22N-0814R, 50 ± 20 nm particle size, Inframat Advanced Materials) was pressed uniaxially to make cylindrical green bodies. The dimensions of the green bodies were 6 mm diameter by 6 ± 0.5 mm height with 40 to 45% density. A pressure of 10 kPa was used to maintain consistent electrical contact between the green body and electrodes. Specimens were heated at a rate of 10°C/min to the preflash temperature of 900°C. An electric field of 60 V/cm was applied across the sample faces, which resulted in a small current passing through the specimen, which rose gradually with time. Once the preflash temperature was reached, the electric field was applied across the samples. The rise in conductivity of the sample led to a nonlinear rise in the current until it has reached the limit of 1.5 A/cm² in the feedback loop. The power supply was switched from voltage control to current control and held constant for 1 min. The samples were then cooled down to RT at a rate of 25°C/min without any applied electric field.

Microstructure characterization by TEM

Plan-view TEM samples of flash-sintered TiO₂ were prepared through the conventional approach, including manual grinding, polishing, dimpling, and final polishing in an Ar ion milling system (PIPS II, Gatan). Low-energy Ar ion polishing (2 kV) was used to minimize ion milling–induced damage. An FEI Talos 200X TEM/STEM with ChemiSTEM Technology [X-FEG and SuperX energy-dispersive x-ray spectroscopy (EDS) with four silicon drift detectors] operated at 200 kV was used in this study for microstructure characterization and EDS chemical mapping. In addition, the high-resolution STEM images were obtained using the modified FEI Titan STEM TEAM 0.5 with a convergence semi-angle of 17 mrad operated at 300 kV at the National Center for Electron Microscopy at the Lawrence Berkeley National Laboratory. The iDPC images were obtained using FEI Themis Z with a Schottky electron emitter, an electron energy monochromator, and a fifth-order probe spherical aberration corrector operated at 300 kV at the Materials Research Laboratory at the University of Illinois, Urbana-Champaign. The DPC reconstruction was carried out by first estimating the STEM probe shift by measuring the difference between opposite detectors, giving images I_x and I_y for the horizontal and vertical shifts respectively. Next, the phase of the exit wave of the sample was reconstructed by a regularized inverse gradient operator method, where the phase image φ was given by

φ = iFFT ((i \cdot 0.25) \cdot (G_{x} \cdot q_{x} + G_{y} \cdot q_{y}) / (q_{x}^{2} + q_{y}^{2} + λ))

with G_x = FFT(I_x) and G_y = FFT(I_y), where G_x and G_y are the Fourier transforms of the image gradients, (q_x,q_y) are the Fourier space coordinates, λ is the regularization parameter, i is the imaginary constant, and iFFT() represents the inverse Fourier transform. The reconstruction space was padded by a factor of 2, and φ was updated iteratively by reconstructing the difference in φ as a function of the differences in I_x and I_y between the measurement and the reconstruction. This iterative procedure minimizes the error at the reconstruction boundaries.

Microcompression test

Micropillars of flash-sintered TiO₂ with ~3 μm in diameter and a diameter-to-height aspect ratio of ~1:2 were prepared using FIB (FEI quanta 3D FEG), and a series of concentric annular milling and polishing with progressively de-escalated currents were adopted to reduce the tapering angle.

Micropillar compression experiments were performed using the Hysitron PI 88 × R PicoIndenter equipped with a piezoelectric actuator on the capacitive transducer, which enables the collection of force-displacement data inside an FEI Quanta 3D FEG SEM. Moreover, a 20-μm diamond flat punch tip designed for high-temperature compression experiments was used to conduct in situ compression experiments, and the geometric variation of micropillars was synchronized to evolving force-displacement curve. For high-temperature in situ compression setups, the flat punch was attached to a probe heater, and the specimens were clamped by a V-shaped molybdenum clamp to a ceramic heating stage. The temperature on two heating terminals was simultaneously ramped up at a rate of 10°C/min and isothermally preserved for 30 min before implementing every single compression experiment to eliminate the thermal-driven drifts on both probe and stage sides. An average drift rate of <0.5 nm/s was estimated in the preloading process for 45 s, and the estimated force noise level was less than 8 μN before compression. The specimen displacement during the compression test was systematically measured and corrected during in situ SEM studies.

Atomistic simulations

Atomistic simulations used DFT with the Perdew-Burke-Enzerhoff exchange correlation functional (44), as implemented in the VASP software version 5.4.4 (45) with a projector-augmented wave (PAW) basis (46). The plane wave cutoff was set to 450 eV, and we used PAWs with six and four electrons in valence for O and Ti, respectively. Simulations of stacking faults without point defects used a 1 × 1 × 8 supercell of a [100] × [011] × $[01 \bar{1}]$ interface cell and a 3 × 3 × 1 k-point mesh. The stacking fault was introduced by adding slip to the out-of-plane lattice vector, creating one stacking fault per supercell. Simulations with point defects used a 3 × 3 × 6 supercell of the primitive interface cell, one vacancy per supercell (i.e., one vacancy per nine interface plane sites), and only the Γ-point. Unstable stacking fault calculations determined a low-energy path between stable configurations using the variable-cell nudged elastic band method as implemented in the TSASE python software (47). Twin boundary calculations used a 3 × 3 × 6 supercell, with half of the layers reflected on the (100) plane, creating two twin boundaries per supercell.

Supplementary Material

http://advances.sciencemag.org/cgi/content/full/5/9/eaaw5519/DC1

supp_5_9_eaaw5519__index.html^{(4.2KB, html)}

Download PDF

aaw5519_SM.pdf^{(1.5MB, pdf)}

Movie S1

Download video file^{(1.4MB, mp4)}

Movie S2

Download video file^{(3.9MB, mov)}

Movie S3

Download video file^{(7.3MB, mov)}

Movie S4

Download video file^{(3.8MB, mov)}

Movie S5

Download video file^{(2.1MB, mov)}

Movie S6

Download video file^{(2.2MB, mov)}

Movie S7

Download video file^{(5.5MB, mov)}

Movie S8

Download video file^{(2.7MB, mov)}

Nanoscale stacking fault–asisted room temperature plasticity in flash-sintered TiO2

supp_5_9_eaaw5519__index.html^{(4.2KB, html)}

Acknowledgments

Funding: We are thankful for the primary financial support by the U.S. Office of Naval Research N00014-17-1-2087 for flash sintering of specimens and N00014-16-1-2778 for in situ microscopy work. J.L. is also partly supported by NSF-CMMI (grant no. 1728419). We also acknowledge access to NCEM funded by Molecular Foundry supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under contract no. DE-AC02-05CH11231, Life Science Microscopy Facility, and the microscopy center of School of Materials Engineering at Purdue University. The work of N.B. and C.S.H. was supported by the U.S. Office of Naval Research. The access to microscopy center at Materials Research Laboratory at University of Illinois, Urbana-Champaign is also acknowledged. Author contributions: J.L. and J.C. fabricated the TiO₂ micropillars and performed the temperature-dependent compression experiments. J.D. prepared the TEM samples from the deformed pillars by FIB. Han Wang prepared plan-view TEM specimens. J.L. and J.J. collected the TEM and SEM images. H.C. and T.T. provided both flash-sintered and no-field TiO₂ samples. J.L. and J.C. prepared the conventional sintered TiO₂ sample. J.L., Haiyan Wang, and X.Z. designed the project and conducted data analyses and manuscript preparations. S.X., X.L.P., R.E.G., and A.K.M. prepared the sintered specimens and were involved in the discussion. N.B. and C.S.H. performed the DFT calculations and were involved in the discussion and manuscript preparation. J.J., X.W., and C.O. performed further DPC image analysis, and C.O. performed DCP reconstruction. Competing interests: Han Wang, J.L., J.C., X.Z., Haiyan Wang, and X.L.P. are inventors on a patent application related to this work filed by the USPTO (USPTO no. 62843406, filed on 4 May 2019). The authors declare no other competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/9/eaaw5519/DC1

Fig. S1. Parameters for sintering of TiO₂ and the microstructures of TiO₂ prepared by various sintering techniques.

Fig. S2. True stress-strain curves and in situ movie snapshots of flash-sintered TiO₂ specimens tested at 200° and 600°C.

Fig. S3. True stress-strain curves and corresponding in situ movie snapshots of zero-field sintered TiO₂ tested at RT and 400°C.

Fig. S4. Examples of abundant preexisting dislocations and stacking faults in the flash-sintered TiO₂.

Fig. S5. XPS profiles of the flash sintered TiO₂.

Fig. S6. High-resolution STEM micrographs of twin boundaries and stacking faults in flash-sintered TiO₂ after compression at 400°C.

Fig. S7. Stress-strain curves of flash-sintered TiO₂ obtained from in situ micropillar compression tests at different temperatures.

Fig. S8. Bright-field TEM micrographs of a compressed conventional sintered TiO₂ pillar tested at RT.

Supplementary Methods

Movie S1. Micropillar compression of conventional sintered TiO₂ tested at RT.

Movie S2. Micropillar compression of conventional sintered TiO₂ tested at 400°C.

Movie S3. Micropillar compression of zero-field sintered TiO₂ tested at RT.

Movie S4. Micropillar compression of zero-field sintered TiO₂ tested at 400°C.

Movie S5. Micropillar compression of flash-sintered TiO₂ tested at RT.

Movie S6. Micropillar compression of flash-sintered TiO₂ tested at 400°C.

Movie S7. Micropillar compression of flash-sintered TiO₂ tested at 200°C.

Movie S8. Micropillar compression of flash-sintered TiO₂ tested at 600°C.

REFERENCES AND NOTES

1.J. B. Wachtman, Mechanical Properties of Ceramics, W. R. Cannon, M. J. Matthewson, Eds. (Wiley, ed. 2, 2009). [Google Scholar]
2.Karch J., Birringer R., Gleiter H., Ceramics ductile at low temperature. Nature 330, 556–558 (1987). [Google Scholar]
3.J. Pelleg, Mechanical Properties of Ceramics (Cham Springer International Publishing, Imprint, Springer, 2014). [Google Scholar]
4.Brunner D., Taeri-Baghbadrani S., Sigle W., Rühle M., Surprising results of a study on the plasticity in strontium titanate. J. Am. Ceram. Soc. 84, 1161–1163 (2001). [Google Scholar]
5.Gorum A. E., Parker E. R., Pask J. A., Effect of surface conditions on room-temperature ductility of ionic crystals. J. Am. Ceram. Soc. 41, 161–164 (1958). [Google Scholar]
6.Lai A., Du Z., Gan C. L., Schuh C. A., Shape memory and superelastic ceramics at small scales. Science 341, 1505–1508 (2013). [DOI] [PubMed] [Google Scholar]
7.Cho J., Li Q., Wang H., Fan Z., Li J., Xue S., Vikrant K. S. N., Wang H., Holland T. B., Mukherjee A. K., García R. E., Zhang X., High temperature deformability of ductile flash-sintered ceramics via in-situ compression. Nat. Commun. 9, 2063 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Swain M. V., Shape memory behaviour in partially stabilized zirconia ceramics. Nature 322, 234–236 (1986). [Google Scholar]
9.R. Castro, Sintering Mechanisms of Convention Nanodensification and Field Assisted Processes, R. Castro, K. v. Benthem, Eds. (Springer, 2013). [Google Scholar]
10.Munir Z. A., Anselmi-Tamburini U., Ohyanagi M., The effect of electric field and pressure on the synthesis and consolidation of materials: A review of the spark plasma sintering method. J. Mater. Sci. 41, 763–777 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Guillon O., Gonzalez-Julian J., Dargatz B., Kessel T., Schierning G., Räthel J., Herrmann M., Field-assisted sintering technology/spark plasma sintering: Mechanisms, materials, and technology developments. Adv. Eng. Mater. 16, 830–849 (2014). [Google Scholar]
12.Chen S., Wu Y., Influence of temperature on the spark plasma sintering of calcium fluoride ceramics. J. Mater. Res. 29, 2297–2302 (2014). [Google Scholar]
13.Luo J., The scientific questions and technological opportunities of flash sintering: From a case study of ZnO to other ceramics. Scr. Mater. 146, 260–266 (2018). [Google Scholar]
14.Todd R. I., Zapata-Solvas E., Bonilla R. S., Sneddon T., Wilshaw P. R., Electrical characteristics of flash sintering: Thermal runaway of Joule heating. J. Eur. Ceram. Soc. 35, 1865–1877 (2015). [Google Scholar]
15.Narayan J., A new mechanism for field-assisted processing and flash sintering of materials. Scr. Mater. 69, 107–111 (2013). [Google Scholar]
16.Jha S. K., Terauds K., Lebrun J.-M., Raj R., Beyond flash sintering in 3 mol % yttria stabilized zirconia. J. Ceram. Soc. Jpn. 124, 283–288 (2016). [Google Scholar]
17.Chen X., Selloni A., Introduction: Titanium dioxide (TiO2) nanomaterials. Chem. Rev. 114, 9281–9282 (2014). [DOI] [PubMed] [Google Scholar]
18.Takeuchi S., Hashimoto T., Deformation mechanisms in titanium dioxide single crystals. J. Mater. Sci. 25, 417–423 (1990). [Google Scholar]
19.Ashbee K. H. G., Smallman R. E., Stress-strain behavior of titanium dioxide (rutile) single crystals. J. Am. Ceram. Soc. 46, 211–214 (1963). [Google Scholar]
20.Perry A. J., Pulker H. K., Hardness, adhesion and abrasion resistance of TiO₂ films on glass. Thin Solid Films 124, 323–333 (1985). [Google Scholar]
21.Ashbee K. H. G., Smallman R. E., The fracture of titanium dioxide single crystals with particular reference to non-stoichiometry. Phys. Status Solidi B 4, 289–298 (1964). [Google Scholar]
22.Ishihara S., Bill J., Aldinger F., Wakai F., Compressive deformation of precursor-derived Si-C-N ceramics at elevated temperatures. Mater. Trans. 44, 794–797 (2003). [Google Scholar]
23.Lankford J., Deformation and fracture of yttria-stabilized zirconia single crystals. J. Mater. Sci. 21, 1981–1989 (1986). [Google Scholar]
24.Miracle D. B., Lipsitt H. A., Mechanical properties of fine-grained substoichiomebic titanium carbide. J. Am. Ceram. Soc. 66, 592–597 (1983). [Google Scholar]
25.Kwon J., Sharma A. A., Bain J. A., Picard Y. N., Skowronski M., Oxygen vacancy creation, drift, and aggregation in TiO₂-based resistive switches at low temperature and voltage. Adv. Funct. Mater. 25, 2876–2883 (2015). [Google Scholar]
26.Pennycook T. J., Lupini A. R., Yang H., Murfitt M. F., Jones L., Nellist P. D., Efficient phase contrast imaging in STEM using a pixelated detector. Part 1: Experimental demonstration at atomic resolution. Ultramicroscopy 151, 160–167 (2015). [DOI] [PubMed] [Google Scholar]
27.Yang H., Pennycook T. J., Nellist P. D., Efficient phase contrast imaging in STEM using a pixelated detector. Part II: Optimisation of imaging conditions. Ultramicroscopy 151, 232–239 (2015). [DOI] [PubMed] [Google Scholar]
28.Stokes R. J., Li C. H., Dislocations and the tensile strength of magnesium oxide. J. Am. Ceram. Soc. 46, 423–434 (1963). [Google Scholar]
29.Wang Y. M., Sansoz F., LaGrange T., Ott R. T., Marian J., Barbee T. W., Hamza A. V., Defective twin boundaries in nanotwinned metals. Nat. Mater. 12, 697–702 (2013). [DOI] [PubMed] [Google Scholar]
30.Yu Q., Qi L., Chen K., Mishra R. K., Li J., Minor A. M., The nanostructured origin of deformation twinning. Nano Lett. 12, 887–892 (2012). [DOI] [PubMed] [Google Scholar]
31.Lu L., Shen Y., Chen X., Qian L., Lu K., Ultrahigh strength and high electrical conductivity in copper. Science 304, 422–426 (2004). [DOI] [PubMed] [Google Scholar]
32.Wang J., Zhang X., Twinning effects on strength and plasticity of metallic materials. MRS Bull. 41, 274–281 (2016). [Google Scholar]
33.Li X., Wei Y., Lu L., Lu K., Gao H., Dislocation nucleation governed softening and maximum strength in nano-twinned metals. Nature 464, 877–880 (2010). [DOI] [PubMed] [Google Scholar]
34.Tian Y., Xu B., Yu D., Ma Y., Wang Y., Jiang Y., Hu W., Tang C., Gao Y., Luo K., Zhao Z., Wang L.-M., Wen B., He J., Liu Z., Ultrahard nanotwinned cubic boron nitride. Nature 493, 385–388 (2013). [DOI] [PubMed] [Google Scholar]
35.Huang Q., Yu D., Xu B., Hu W., Ma Y., Wang Y., Zhao Z., Wen B., He J., Liu Z., Tian Y., Nanotwinned diamond with unprecedented hardness and stability. Nature 510, 250–253 (2014). [DOI] [PubMed] [Google Scholar]
36.Rice J. R., Dislocation nucleation from a crack tip: An analysis based on the Peierls concept. J. Mech. Phys. Solids 40, 239–271 (1992). [Google Scholar]
37.Scott W. D., Orr K. K., Rhombohedral twinning in Alumina. J. Am. Ceram. Soc. 66, 27–32 (1983). [Google Scholar]
38.Turner F., Griggs D., Heard H., Experimental deformation of calcite crystals. Bull. Geol. Soc. Am. 65, 883–934 (1954). [Google Scholar]
39.Zhao F., Wang L., Fan D., Bie B. X., Zhou X. M., Suo T., Li Y. L., Chen M. W., Liu C. L., Qi M. L., Zhu M. H., Luo S. N., Macrodeformation twins in single-crystal aluminum. Phys. Rev. Lett. 116, 075501 (2016). [DOI] [PubMed] [Google Scholar]
40.Yasutake K., Shimizu S., Umeno M., Kawabe H., Velocity of twinning partial dislocations in silicon. J. Appl. Phys. 61, 940–946 (1987). [Google Scholar]
41.Steil M. C., Marinha D., Aman Y., Gomes J. R. C., Kleitz M., From conventional ac flash-sintering of YSZ to hyper-flash and double flash. J. Eur. Ceram. Soc. 33, 2093–2101 (2013). [Google Scholar]
42.Charalambous H., Jha S. K., Christian K. H., Lay R. T., Tsakalakos T., Flash sintering using controlled current ramp. J. Eur. Ceram. Soc. 38, 3689–3693 (2018). [Google Scholar]
43.Grasso S., Saunders T., Porwal H., Milsom B., Tudball A., Reece M., Flash spark plasma sintering (FSPS) of α and β SiC. J. Am. Ceram. Soc. 99, 1534–1543 (2016). [Google Scholar]
44.Perdew J. P., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
45.Kresse G., Furthmüller J., Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
46.Blöchl P. E., Projector augmented-wave method. Phys. Rev.B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
47.Sheppard D., Xiao P., Chemelewski W., Johnson D. D., Henkelman G., A generalized solid-state nudged elastic band method. J. Chem. Phys. 136, 074103 (2012). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials