Diffuse reflectance spectroscopy, a potential optical sensing technology for the detection of cortical breaches during spinal screw placement

Abstract.

Safe and accurate placement of screws remains a critical issue in open and minimally invasive spine surgery. We propose to use diffuse reflectance (DR) spectroscopy as a sensing technology at the tip of a surgical instrument to ensure a safe path of the instrument through the cancellous bone of the vertebrae. This approach could potentially reduce the rate of cortical bone breaches, thereby resulting in fewer neural and vascular injuries during spinal fusion surgery. In our study, DR spectra in the wavelength ranges of 400 to 1600 nm were acquired from cancellous and cortical bone from three human cadavers. First, it was investigated whether these spectra can be used to distinguish between the two bone types based on fat, water, and blood content along with photon scattering. Subsequently, the penetration of the bone by an optical probe was simulated using the Monte-Carlo (MC) method, to study if the changes in fat content along the probe path would still enable distinction between the bone types. Finally, the simulation findings were validated via an experimental insertion of an optical screw probe into the vertebra aided by x-ray image guidance. The DR spectra indicate that the amount of fat, blood, and photon scattering is significantly higher in cancellous bone than in cortical bone ($p<0.01$), which allows distinction between the bone types. The MC simulations showed a change in fat content more than 1 mm before the optical probe came in contact with the cortical bone. The experimental insertion of the optical screw probe gave similar results. This study shows that spectral tissue sensing, based on DR spectroscopy at the instrument tip, is a promising technology to identify the transition zone from cancellous to cortical vertebral bone. The technology therefore has the potential to improve the safety and accuracy of spinal screw placement procedures.

1. Introduction

Spinal fusion surgeries have been increasing all over the world due to a rise in aging population and recent advances in surgical techniques and anesthesia.^1–3 In these surgeries, screws are commonly placed through the bony pedicles into the vertebral bodies of the spinal vertebra. These serve as anchoring points for rigid constructs in order to fuse parts of the spine to regain and maintain spinal stability. Spinal instability might be caused by congenital, degenerative, or traumatic conditions.⁴ The inaccurate placement of such screws in the spine can cause severe vascular and neurological injuries in patients.^5–7 The increase in aging population and pressure on healthcare systems has led to a trend toward minimally invasive spine (MIS) procedures. The benefits of these procedures are, among others, shorter hospital stays and faster recovery times. MIS aims to minimize the disruption of soft tissue, induce muscle splitting rather than stripping and to reduce blood loss. Surgery is performed through several small incisions, which emphasizes the need for techniques to guide the surgeon in order to compensate for the limited exposure of the surgical site. Moreover, the close proximity of vital neural and vascular structures and the variability in anatomy within and between patients contribute to the difficulty in accurate placement of spinal screws. There are several techniques practiced by surgeons to accurately and safely place spinal screws. Techniques used in clinical practice for spinal screw placement include the free-hand technique and the image-guided technique. The image-guided technique involves the preplanning and intraoperative guidance of screws with the help of either 2-D fluoroscopy images or a 3-D navigation planning system.^8–10 In the conventional free-hand technique described by Kim et al.,¹¹ the surgeons need to perform several additional steps before the final insertion of each of the screws into the vertebrae. These additional steps are usually performed to prepare a pilot hole in vertebral bone and to ensure a safe trajectory for the screw. The surgeons usually use anatomical landmarks, tactile feedback, and experience-based judgment, in order to plan the spinal screw path. The 2-D x-ray images are also commonly acquired intraoperatively to confirm safe trajectory of the screws.⁹ Given that several spinal screws are usually placed per patient, these additional screw trajectory verification steps can contribute significantly to surgery time and radiation exposure, especially for the surgeon. Reoperation rates due to mislocated instrumentation are also a major concern for patients as well as the hospitals.^7,12,13 Some of the other screw guidance techniques have been described extensively by Manbachi et al.⁸

The complex nature of the procedure coupled with a heavy reliance on the surgeon’s experience contributes to the high variability in accuracy rates reported in literature. Accuracy rates of screw placement are reported to be as low as 27.6% and as high as 96.5% based on a meta-analysis by Kosmopoulos and Schizas.¹⁴ A more recent meta-analysis paper published by Mason et al.¹⁵ found the accuracy rates to lie in the range of 50% to 92%. Therefore, there is a need for a reliable yet cost-effective solution for increasing accuracy and safety in the placement of spinal screws during spinal fusion surgery.

Spectral tissue sensing by diffuse reflectance (DR) spectroscopy may offer the possibility for real-time tissue discrimination during surgery and thereby provide an early warning of an impending breach of the cortical bone boundary. Such a technique might help optimize the screw trajectory verification workflow thereby contributing to less radiation, shorter surgery time, and fewer revision surgeries, thus, contributing toward increased safety and surgeon confidence during spinal screw placement procedures. In this optical spectroscopy-based technique, tissue is probed by sending white light from a broadband light source through an optical fiber. After the light has interacted with the tissue, a similar optical fiber is used to collect the diffusely reflected light from the tissue. The light is then analyzed further to identify spectral changes. These spectral changes originate from the highly specific nature of the absorption and scattering characteristics of individual tissue types.¹⁶ Therefore, by analyzing the differences in reflected spectrum of light, different tissue types can be distinguished. DR spectroscopy has already been shown to be able to estimate the concentration of blood, fat, and other optical properties in various clinical applications, such as tumor and nerve detection.^17–22

Although DR spectroscopy has been extensively studied for applications in oncology, its usefulness in accurate guidance of spinal screws has received little attention in the scientific community. The group of Li et al.^23–25 has recently investigated the possibility of monitoring the reduced scattering coefficient extracted after sending near-infrared light into the vertebral bone for tissue boundary detection. Their approach involves the use of a wavelength window of 200 to 1100 nm. A single parameter, namely a reduced scattering coefficient, was used to detect cortical breaches.

In our study, we use a broader wavelength window (400 to 1600 nm) and a spectrum analysis algorithm. This enables the quantification of various optical properties, such as blood content, fat content, water content, and photon scattering in various tissue types, each of them contributing to the possibility of breach detection. Therefore, the goal of this study is to investigate fundamental differences between the two tissue types namely cancellous and cortical vertebral bone. In the context of a clinical screw placement, we explore the possibility of cortical bone detection using DR spectroscopy. To this end, we extract optical properties from the DR spectra acquired from the two bone types making up the vertebra, in order to analyze the differences between them. We investigate the variability of optical property distribution across cancellous bone by spatially mapping the vertebral body using a stencil system. We attempt to measure the distribution of thickness of cortical bone surrounding the cancellous bone and spinal canal at various regions within the vertebra.

We also perform three-layered Monte-Carlo (MC) simulations in order to visualize and analyze the spectral changes that might occur as the modeled optical probe within cancellous bone, approaches a cortical bone boundary and subsequently other surrounding tissues. The MC model was used as it is the gold standard method to model light transport in tissues.²⁶ Finally, the results of the simulation are validated by a cadaver experiment involving the image-guided insertion of an in-house developed optical screw probe into a human vertebra.

2. Methods

2.1. Spinal Tissues

Two cadaver experiments were conducted at the Radboud University Medical Center Nijmegen, The Netherlands, and Cincinnati Children’s medical hospital, Ohio, United States, respectively. All ethical guidelines for human cadaver studies were followed. The donors allowed their bodies and body parts to be used for research and educational purposes. One female (63 years; 90 kg; 180 cm) (cadaver1) and one male (78 years; 50 kg; 186 cm) (cadaver2) were used for the first cadaver experiment. One female (76 years; 63.5 kg; 145 cm) (cadaver3) was used for the second cadaver experiment. No embalming process was used, in order to preserve the optical properties of the cadaver specimens.

2.2. Experimental Set Up

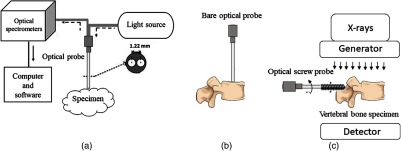
The experimental set up for DR spectra acquisition consists of a tungsten halogen broadband light source (360 to 2500 nm) with two optical spectrometers, as shown in the schematic diagram of Fig. 1(a). The two spectrometers collectively cover the visible, near-infrared, and shortwave infrared wavelength range; the first spectrometer resolves light in the visible and near-infrared wavelength range of 400 to 1100 nm (Andor Technology, DU420ABRDD), and the second resolves light in the shortwave infrared wavelength range of 900 to 1700 nm (Andor Technology, DU492A-1.7). LabVIEW software (National Instruments, Austin, Texas) developed in-house was used to control the spectrometers and acquire the data. The DR spectroscopy system used in this study has been extensively described previously, together with the calibration method.^27–29

Fig. 1.

(a) Schematic of the general experimental setup used to perform DR spectra measurements. (b) Bare optical probe used for cross-section experiment. (c) Optical screw probe used for image-guided insertion.

In the first cadaver experiment, a bare optical probe was used to obtain DR spectra, whereas in the second cadaver experiment [Fig. 1(b)], an optical screw probe was used, as shown in Fig. 1(c).

In both the cadaver experiments, the bare optical probe and optical screw probe had the same internal construction. Both optical probes consisted of two optical fibers with core diameter of $200\mu \mathrm{m}$. One of the fibers was used to transport the light from the source to the tissue, and the other fiber was used to transport the light from the tissue to both spectrometers. The distance between the collecting fiber and the delivering fiber was set at 1.22 mm, as shown in Fig. 1(a). In earlier work, we found that a good trade-off between signal-to-noise ratio and probing depth can be achieved by choosing a fiber-to-fiber distance around 1.2 mm. The diameter of the optical screw probe and manufacturing constraints, in order to house the fibers in the screw, also influenced the fiber distance selection.

2.3. Preclinical Cadaver Experiment 1: Cross-Section Experiment

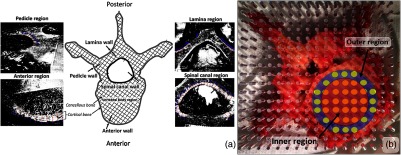
In the first cadaver experiment, resection of two cervical vertebrae, four thoracic vertebrae, and one lumbar vertebra were carried out collectively from cadaver1 and cadaver2 and sliced in the axial direction using a bone saw to visualize the view, as shown in Fig. 2(a). This axial view provided visual confirmation of cancellous and cortical bone. This allowed DR spectra acquisition of bone types at various locations. The axial cross-section of the vertebrae also helped the determination of cortical bone thickness. A senior medical doctor performed all surgical procedures.

Fig. 2.

(a) Axial view of vertebra with grey scale images indicating cortical bone walls at various regions and (b) glass stencil with holes placed on top of a vertebra for spatial optical mapping.

2.3.1. Determination of optical properties of vertebral bone

Subsequently, the bony surface of a total of seven vertebrae was probed from cervical, thoracic, and lumbar regions. DR spectra were acquired from both cadavers (cadaver1 and cadaver2) using a bare optical probe, as shown in Fig. 1(b). In order to extract the optical properties of vertebral bone, which consists of cancellous and cortical bone, the two bone tissue types were first identified visually under the supervision of a trained medical doctor. DR spectra were acquired across 147 random locations from cancellous bone and across 119 locations from cortical bone. Each location was probed five times. Adequate fiber-tissue coupling was achieved by applying gentle pressure. No coupling fluid was used.

2.3.2. Determination of distribution of optical properties based on vertebral body region

Figure 2(a) shows the vertebral body region, which consists of cancellous bone. In order to measure how the optical properties spatially vary across the entire region, DR spectra were acquired at various locations within the vertebral body. In order to perform the experiment in a systematic way, a transparent acrylic glass stencil was placed on top of the axial slice of a vertebra, as shown in Fig. 2(b). The stencil was a $120\times 120\times 10\mathrm{mm}$ plate with 289 patterned holes of diameter 1.9 mm spaced 5 mm apart from each other. DR spectra were acquired by inserting the bare optical probe into the stencil holes and ensuring that the probe is perpendicular to the tissue surface. DR spectra were acquired from all the stencil holes, which roughly cover the vertebral body region of the vertebra. The vertebral body was then divided into an inner and outer region, as shown in Fig. 2(b). The yellow dots indicate the locations, where DR spectra were extracted for analysis. The inner red region consisted of all the measurements within the inner ring and the outer blue region consisted of all the measurements within the outer annulus ring.

From the two cadavers, out of the seven vertebrae resected, DR spectra were acquired from three vertebrae belonging to cervical, thoracic, and lumbar regions. Spectra from a total of 80 unique locations were obtained, divided equally between the inner and outer vertebral body regions for further analysis.

2.3.3. Cortical thickness measurements using a microscope

First, a portable microscope camera (5 megapixel, DigiMicro Profi, dnt^®) was used for acquisition of magnified ($6\times$) images of the sliced vertebrae. Images were then processed via image processing software (ImageJ).³⁰ The red–green–blue images were converted into grayscale, and a suitable thresholding window (based on trial-and-error) was applied in order to better visualize the cortical bone boundary, as shown in Fig. 2(a). Four regions were identified during the measurement of the cortical boundary: spinal canal region, anterior wall region, pedicle wall region, and the lamina wall region. The spinal canal region is the region that houses the spinal cord. The anterior wall region surrounds the cancellous bone in the vertebral body. The pedicle wall region refers to mainly the pedicle wall separating the bony pedicle from the surrounding tissues. Measurements of cortical thickness surrounding the lamina region were also performed. This region makes up the bony structure surrounding the spinal cord posteriorly. During image acquisition, a reference scale of known lengths was placed in the camera view in order to set a measurement standard before any measurements were performed. The distance between each cortical thickness measurement was kept approximately constant.

2.4. Monte-Carlo Simulations

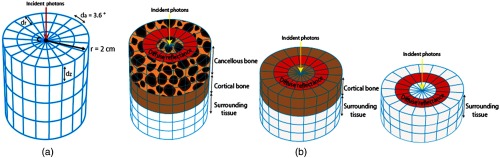
MC simulations were performed by adopting the model developed by Wang et al.³¹ known as the MC model of light transport in multilayered tissues. This model was applied because of its ability to simulate photon propagation through multiple tissue layers. A three-layered model was thus developed consisting of cancellous, cortical, and surrounding tissue, simulating the order of tissue types encountered by a spinal screw tip during a typical clinical insertion. The surrounding tissue in the thoracolumbar region could be subcutaneous fat, muscle, or ligament. The wavelength-dependent absorption and scattering coefficients for all three tissues were used as input for the model. These were derived after fitting the pure tissue spectra using a modified version of the model²⁷ developed by Farrell et al.³² Based on our experiments, pure tissue spectra refer to the spectra that contain information only about one type of tissue. The tissue type was confirmed using x-ray imaging by a trained medical doctor.

Before performing a three-layered optical probe simulation, the MC simulations were first validated by using a single layer model for each of the three tissue types. The optical properties retrieved from the three experimental pure spectra were used as input for the MC model. Three MC simulation spectra were then calculated for the respective tissue types and compared to the experimental pure spectra.

In order to simulate the optical probe penetrating through different layers of tissue, the thickness of the layer equal to dz was reduced in steps, as shown in Fig. 3(b). At several depths, DR spectrum was recorded and subsequently fitted to obtain simulated estimates of fat content. Five simulations per step were performed.

Fig. 3.

(a) Cylindrical grid system used to model a tissue layer in MC simulations. (b) Modeling insertion of optical probe by recording the reflectance spectra of top tissue layer (in red) followed by tissue layer removal in steps.

Wavelengths were simulated at a sample rate of 2 nm over the near-infrared range of 1000 to 1600 nm. The fiber distance was chosen to be equal to 0.122 cm. A refractive index of 1.44 and an anisotropy factor of 0.9 were chosen for all the three tissue types as input for the MC model.³³ Each simulation was performed with 1 million photons, which led to one reflectance data point per wavelength. Simulations were processed using a Linux cluster made available at Philips Research, Eindhoven.

The cylindrical grid system adopted to model the geometry of a tissue layer is shown in Fig. 3(a). The geometry is a function of total depth $z$, total radius $r$, and a total sweep angle equal to $\alpha$. The geometry is subdivided into grid elements using distances $dr$, $d\alpha$, and $dz$. In this study, the radius grid width $dr$ and the angular sweep width $d\alpha$ were chosen to be equal to 0.002 cm and 3.6 deg, respectively. A pencil beam of light enters the tissue layer at the center of the grid system C as denoted by the red arrow perpendicular to the top surface. The top layer with $dz=0$ contains information about the amount of DR. Tissue layer depth is chosen as an integer multiple of $dz$ so that information within each grid element only pertains to one tissue type.

2.5. Preclinical Cadaver Experiment 2: Image-Guided Insertion

A second cadaver experiment was performed to benchmark the MC simulation results. A custom-made optical screw probe (diameter: 55 mm) with integrated fiber-optics was used to perform an insertion in a vertebra of cadaver3. The bony vertebra was first exposed by stripping off the subcutaneous fat, muscles, and ligaments using scalpels. A pilot hole was subsequently made in the vertebral bone using an awl in order to provide a gripping surface for the optical screw probe. The optical screw probe was then inserted turn by turn into the vertebral body, with DR spectra recorded at each turn [Fig. 1(c)]. X-ray images were also acquired in order to correlate the DR spectra to the optical screw probe tip position within the tissue. Five DR spectra were acquired per turn, and the corresponding fat content was averaged per turn.

2.6. Data Analysis

Data processing was performed by in-house developed software using MATLAB version 9.3 (MathWorks Inc.) and its statistics toolbox.

2.6.1. Determination of tissue optical properties

Tissue optical properties were extracted from the measured spectra by adopting a modified version of the model developed by Farrell et al.³² The absorption coefficient ${\mu }_a(\lambda )$ and reduced scattering coefficients ${\mu }_{\mathrm{s}}^{\prime }(\lambda )$ can be extracted from the model expressed in ${\mathrm{cm}}^{-1}$. From the known fiber distance between the emitting and collecting fibers as well as the wavelength-dependent absorption coefficients, the amount of fat (%), water (%), and total hemoglobin in blood (%) present in the tissue was determined following a procedure, as previously described by our group.^28,29 The scattering parameter ($S_{800}$) was derived from the empirical model based on Rayleigh and Mie scattering described by

$${\mu }_{s^{\prime }}(\lambda )=S_{800}[F_{\mathrm{MR}}{\left(\frac{\lambda }{{\lambda }_0}\right)}^{-b}+(1-F_{\mathrm{MR}}){\left(\frac{\lambda }{{\lambda }_0}\right)}^{-4}],$$

where ${\lambda }_0$ is set to 800 nm, which corresponds to a wavelength normalization value, $S_{800}$ is the reduced scattering amplitude at ${\lambda }_0$, $b$ is the Mie scattering slope, the Mie-to-Rayleigh scattering fraction is denoted by $F_{\mathrm{MR}}$.²⁸

2.6.2. Statistics

A Kolmogorov–Smirnov test was used to test the DR spectral data for normality. As the data were found not to be normally distributed, a nonparametric Wilcoxon rank-sum test was used to perform the necessary inferential statistics in order to analyze the differences between cancellous and cortical bone. The significance level was set to 0.01.

3. Results

3.1. Optical Properties Distribution Among Vertebral Bone Types

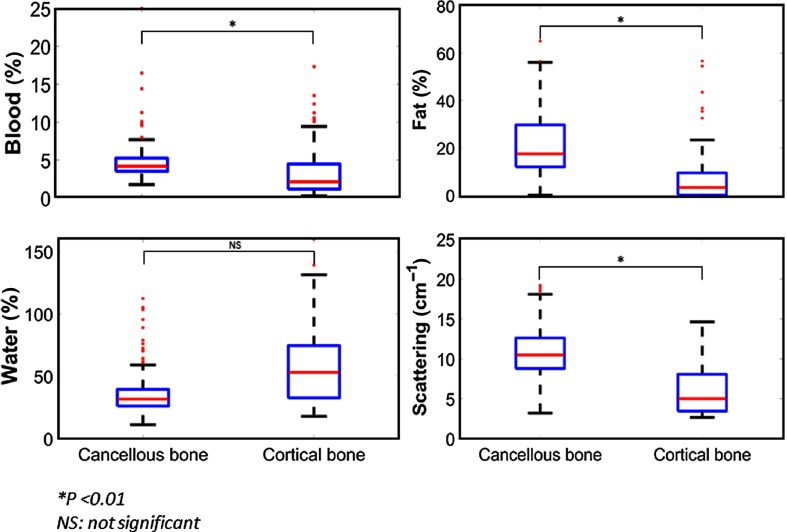
The amount of blood [Median (Mdn) = 4.2%], fat (Mdn = 17.4 %), and light scattering ($\mathrm{Mdn}=10.5{\mathrm{cm}}^{-1}$) in cancellous bone is found to differ from amount of blood ($\mathrm{Mdn}=2.2\%$), fat ($\mathrm{Mdn}=3.2\%$), and light scattering ($\mathrm{Mdn}=5.0{\mathrm{cm}}^{-1}$) in cortical bone, as illustrated in Fig. 4. This result is found to be statistically significant ($p<0.01$), as also indicated in Table 1.

Fig. 4.

Distribution of optical properties across cancellous and cortical vertebral bone types.

Table 1.

Optical properties summary data across vertebral bone type.

	Vertebral bone type
Optical properties	Cancellous bone ($N=147$)	Cortical bone ($N=119$)
	Median	Median	$P$ value
Blood (%)	4.2	2.1	$<{10}^{-5}$
Fat (%)	17.4	3.2	$<{10}^{-5}$
Water (%)	31.7	53.1	0.0115
Scattering (${\mathrm{cm}}^{-1}$)	10.5	5.0	$<{10}^{-5}$

However, the amount of water found in cancellous bone ($\mathrm{Mdn}=31.7\%$) did not significantly differ from the water content in cortical bone ($\mathrm{Mdn}=53.1\%$), $p>0.01$. Overall, all parameters except water concentration exhibit a drop from cancellous to cortical bone type.

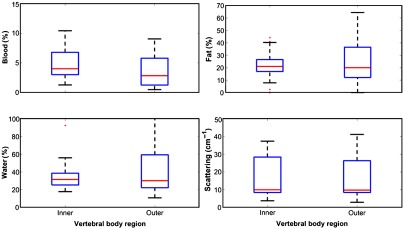
3.2. Optical Properties Distribution Among Vertebral Body Regions

The inner and outer regions of the vertebral body do not seem to differ in terms of the optical properties, as shown via the nonsignificant results of Table 2.

Table 2.

Optical properties summary data across vertebral body regions.

Optical properties	Vertebral body regions
	Inner ($N=40$)	Outer ($N=40$)
	Median	Median	$P$ value
Blood (%)	4.0	2.8	0.04
Fat (%)	21.0	20.0	0.79
Water (%)	31.4	30.1	0.85
Scattering (${\mathrm{cm}}^{-1}$)	9.9	9.7	0.95

However, the high range indicates variability in the properties across the vertebral body, as illustrated via the box plots of Fig. 5.

Fig. 5.

Distribution of optical properties across vertebral body regions.

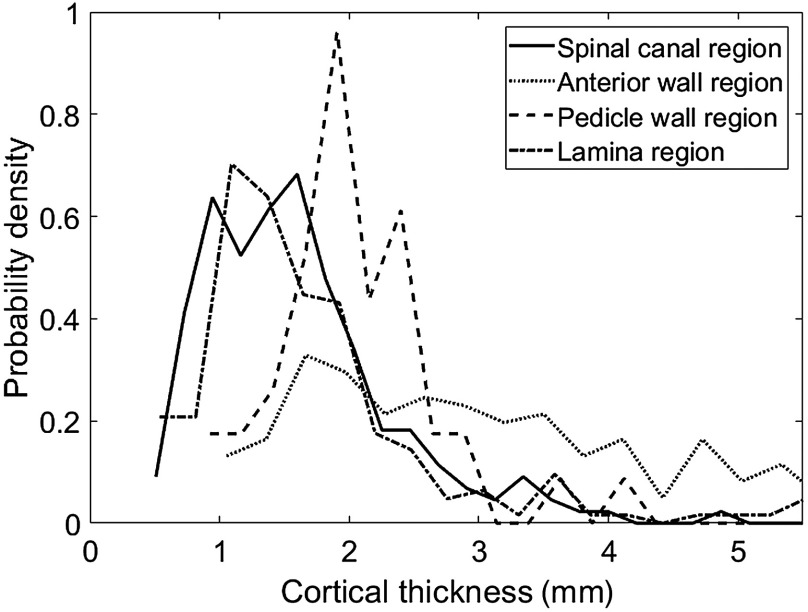
3.3. Cortical Wall Thickness Distribution Analysis

Figure 6 describes the distribution of cortical thickness across different regions of the vertebra. The probability density curve indicates that a thickness range of $\sim 1$ to 2 mm can be found for the cortical wall thickness surrounding the spinal canal. The median thickness in this region is found to be 1.5 mm, as shown in Table 3.

Fig. 6.

Distribution of cortical thickness across various vertebral regions.

Table 3.

Cortical thickness central tendencies across various vertebral regions.

Vertebral region	Number of data points ($N$)	Median (mm)
Spinal canal region	201	1.5
Anterior region	171	2.8
Pedicle region	42	2.0
Lamina region	213	1.5

The lamina wall, pedicle wall, and the anterior wall collectively have the highest probability distribution of cortical thickness in the range of 1 to 3 mm.

3.4. Monte-Carlo Model Validation

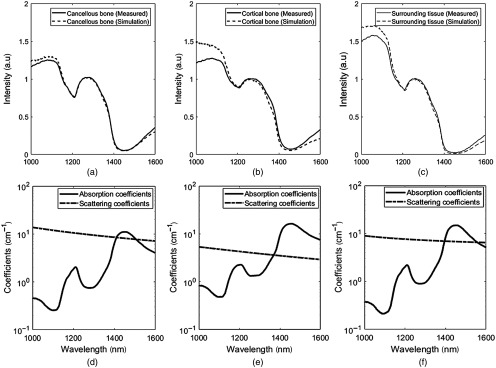
Figures 7(a)–7(c) show three typical spectra of the three tissue types probed. Qualitatively, from $\sim 1150\text{-}\mathrm{nm}$ wavelength onward, the simulated spectra and measured spectra exhibit an overlap. Figures 7(d)–7(f) display the wavelength-dependent absorption and scattering coefficients of the three tissue types.

Fig. 7.

(a–c) Typical experimentally measured and MC simulated spectra of cancellous, cortical and surrounding tissue. (d–f) Wavelength-dependent absorption and scattering coefficients of the three tissue types.

The quantitative comparison between measured and simulated fat content (Table 4) shows that these values are similar for the three investigated tissue types.

Table 4.

Quantitative comparison of measured and simulated spectra based on fat content.

Tissue type	Measured fat (%)	Simulation fat (%)
Cancellous bone	34	35
Cortical bone	0	0
Surrounding tissue	26	29

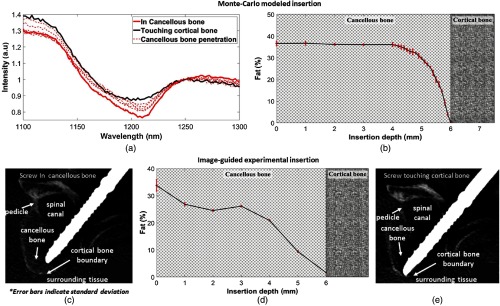
3.5. Comparison of Monte-Carlo Modeled Insertion with Image-Guided Experimental Insertion

In Fig. 8, the simulated changes in DR spectra [Fig. 8(a)] and corresponding fat content [Fig. 8(b)], as the modeled optical probe approaches the cortical boundary, are compared to an image-guided experimental insertion [Fig. 8(d)]. Note that during the modeled insertion, fat content is observed to decrease more than 1 mm before the optical probe comes in contact with the cortical bone boundary. The decrease in measured fat content [Fig. 8(d)] also seems to begin more than 1 mm before reaching the cortical bone.

Fig. 8.

Comparison between simulated and measured probe insertion. (a) Simulated changes in DR spectra during the transition of the modeled optical probe from cancellous bone to cortical bone. (b) Corresponding drop in simulated fat content. (c) X-ray image showing optical screw probe in cancellous bone. (d) Drop in measured fat content as the optical screw probe approaches cortical bone. (e) X-ray image showing the tip of optical screw probe in contact with cortical bone.

4. Discussion

Accurate and safe placement of spinal screws remains a critical issue in spine surgery. In this study, we explored the potential of adopting a DR sensor at the tip of a spinal screw in order to detect cortical bone boundaries, thereby preventing screw misplacement. In the first cadaver experiment, vertebral bones were resected from the spine. DR measurements were performed on the surface of the axial slice of these vertebrae to investigate the differences between cancellous and cortical bone. A range of cortical bone thickness was determined from thickness distributions. These were calculated for various regions within the vertebrae using images from a microscope. MC simulations were performed to simulate a modeled optical probe as it approaches a cortical bone boundary. Finally, a second cadaver experiment involving the turn by turn insertion of an optical screw probe with integrated fiber optics was carried out under image guidance, in order to validate the simulation findings.

Based on DR measurements of seven vertebrae across all spinal levels of two cadaver specimens, the blood content, fat content, and photon scattering were found to be higher in cancellous bone than in cortical bone. The higher amount of blood in the cancellous bone can potentially be attributed to the fact that cancellous bone houses red bone marrow, which is an important site for red blood cell formation.³⁴ However, this finding must be interpreted with caution as this study was performed in an ex vivo setting. Blood content and blood oxygen saturation are known to be different between ex vivo and in vivo settings. This is because the lack of blood circulation and uptake of oxygen from the air is bound to effect the local blood oxygenation concentration. The local blood content will also be influenced by the settling of blood (livor mortis) in the ex vivo setting.³⁵ The effect of blood derived from DR spectra in an in-vivo setting needs to be investigated, before any solid conclusions can be drawn.

The higher fat content found in cancellous bone is also an intuitive finding as it is well known that cancellous bone houses triglyceride (fat) storage sites within its cavities.³⁴ The higher photon scattering can be linked to this diverse mix of organic materials found within the same tissue type of cancellous bone. These mixtures of materials have different refractive indices, which could thereby increase the number of photon scattering events. As such in an in vivo setting, the tissues would be ideally at 37°C. The ex vivo human cadaver tissue used in this study was refrigerated at $\sim 2°\mathrm{C}$ to 4°C immediately after death and then allowed to rest at room temperature for several hours during the experiment. However, based on literature, lipids are known to be relatively less sensitive to temperature changes. Nachabé et al.²⁷ found no changes in the absorption values of lipids upon increasing the temperature of a sample tissue from 30°C to 45°C. Therefore, a large influence on fat values derived from bone due to the ex vivo nature of the tissues probed is less likely.

Several researchers have attempted to quantify fat or fat fraction in vertebral bones for characterizations of cancerous tumors and as a diagnosis parameter for various diseases, such as osteoporosis, diabetes, HIV, and obesity.^36–39 Nachabé et al.⁴⁰ quantified fat fraction in liver specimens of mice using near-infrared spectroscopy, which is a specific type of DR spectroscopy, and magnetic resonance spectroscopy. In this study, the fat fraction derived from cancellous bone via DR spectroscopy was found to be 35.4%, which falls within the wide range of proton density fat fraction (15% to 60%) found in published MRI literature.^41,42 The effect of vertebral level, age, gender, and diseases on the fat content or fat fraction within vertebral bones shall be part of future investigations.

We showed that although cancellous bone is heterogeneous in nature, its optical properties spread across the vertebral body are very similar, as indicated by the nonsignificant results of Table 2.

In this study, we confirmed pervious findings of cortical thickness found in literature that are based on CT-imaging.^43,44 However, Ritzel et al.⁴⁵ measured the cortical bone thickness using a bone staining approach and found the cortical thickness range to be lower than the range found in this study. The specimen preparation, staining, and subsequent evaluation of cortical thickness measurements by a semiautomatic image processing software could have all cumulatively caused the discrepancy in thickness measurements.

In this study, an attempt was made to substantially reduce the subjectivity in discerning the boundary between cortical and cancellous bone with the help of image analysis techniques, but it could not fully be eliminated. A reliable estimate of the cortical thickness in vertebral bone is mainly required to ascertain the optimal fiber distance of the optical probe and the effect of the thickness range on spectral changes. Ritzel et al.⁴⁵ found a significant loss of cortical thickness in the lower thoracic and lumbar spine in patients with osteoporosis. Effect of various bone related diseases on the thickness of cortical boundary needs to be further investigated.

We found a strong correlation between simulated and experimentally measured DR spectra (see Fig. 7). The initial deviation of the spectra between 1000 and 1100 nm can be attributed to the discrepancies in the wavelength-dependent scattering coefficients derived from the Farrell model,³² which is used as input for the MC model. The fact that the fat content found in the two spectra showed close agreement (Table 4), further strengthens this claim.

A three-layered MC model was developed and an insertion of an optical probe penetrating through cancellous bone and touching cortical bone was simulated. This simulated insertion was then compared to an image-guided experimental insertion (see Fig. 8) of an in-house developed optical screw probe.

During the modeled insertion, the fat content [Fig. 8(b)] was observed to drop more than 1 mm before the cortical bone boundary. The image-guided experimental insertion also showed a drop in fat more than 1 mm before cortical contact. However, the decrease in measured fat content was found to be more gradual [Fig. 8(d)]. In both types of insertions, the drop in fat content or the fat transition was seen before the modeled optical probe or optical screw probe reached the cortical boundary, thereby indicating the potential of breach detection. Although widely used, the MC model used in this study has limitations, which stem from the assumptions inherent in the model development. The model assumes each tissue layer to be homogenous in nature, which implies that optical properties are uniformly distributed throughout each tissue layer. Cancellous bone consists of organic compounds, such as blood and fat, within its inorganic porous structure. Therefore, treating cancellous bone as a homogenous tissue is not fully true, which might influence the fat transition or the breach transition profile as the optical screw penetrates from cancellous to cortical bone. The higher variation in the fat content within cancellous bone, observed in the experimental insertion [Fig. 8(d)] as compared to the simulation [Fig. 8(b)] insertion, seems to support this observation. To overcome this limitation and model the heterogeneities of cancellous bone, one possible solution could be to randomly burry well-defined geometric shapes containing blood and fat optical properties within cancellous bone. Early work by Smithies and Butler,⁴⁶ Lucassen et al.,⁴⁷ and Wang et al.⁴⁸ and more recent work by Zhu⁴⁹ could be a good starting point for such a model development. Margallo-Balbás and French⁵⁰ propose another interesting approach by modeling the complex trabecular bone structure using the geometry recovered from microCT data. All of these different approaches to model the bone tissue types as close to reality as possible could enhance the understanding of breach transition profiles. Assumptions made in the Farrell model used to calculate fat content from spectra might also influence the model validity.²⁷

It must be noted that these breach transition profiles are a function of several factors including fiber-to-fiber distance of the probe, incident light geometry, optical properties of the tissue layers, thickness of the cortical boundary, and probe angulation with respect to the cortical boundary. The influence and interaction of these parameters on the breach transition profile needs to be explored further.

Successful clinical adoption of DR spectroscopy as a guidance system holds several different kinds of challenges. Real-time guidance of instrument or screw provided by DR spectroscopy would have to be integrated seamlessly into the existing clinical workflow. In order to achieve this, several outcome measures, such as surgery time, radiation exposure, sensitivity, and specificity of breaches detection, would have to be tested in a clinical setting. We hypothesize that surgery time to either shorten or remain constant due to the added feedback at the tip of the instrument. This could potentially boost the surgeon’s confidence for safe screw placement. This could also lead to fewer safety measures, such as repeated tactile probing events and image acquisitions during surgery, thereby contributing toward reduction in infection rates and revision surgeries.^12,13 However, the additional set-up time for the DR spectroscopy system to run optimally needs to be considered as well. Investigating the value of DR spectroscopy in the clinical environment shall be part of future studies.

5. Conclusion

This study shows that spectral tissue sensing, based on DR spectroscopy at the needle tip, is a promising technique to detect cortical boundary perforations or breaches during spinal screw placement. In this ex vivo study, fat content, blood content, and photon scattering were found to be statistically different in cancellous bone as compared to cortical bone. Fat content was found to be significantly higher in cancellous bone compared to cortical bone. This finding was consistent with a drop in fat content observed before a simulated probe reached the cortical bone. An image-guided experimental insertion gave similar results, thus pointing to the potential of DR spectroscopy as a sensing tool at the instrument tip in aiding the detection of cortical boundary breaches. The optical sensing technology therefore shows promise to improve the safety and accuracy of spinal screw placement procedures.

Biography

Biographies of the authors are not available.

Disclosures

This study was supported by Philips Research, Eindhoven, Netherlands. The authors who are affiliated with Philips Research (B.H.W.H., J.W.S., D.B., C.R., and J.G.) only have financial interests in the subject matter, materials, and equipment, in the sense that they are an employee of Philips. None of the other authors have any financial relationship with Philips Research or conflict of interests.