Vibration analysis of healthy skin: toward a noninvasive skin diagnosis methodology

Abstract.

Several noninvasive imaging techniques have been developed to monitor the health of skin and enhance the diagnosis of skin diseases. Among them, skin elastography is a popular technique used to measure the elasticity of the skin. A change in the elasticity of the skin can influence its natural frequencies and mode shapes. We propose a technique to use the resonant frequencies and mode shapes of the skin to monitor its health. Our study demonstrates how the resonant frequencies and mode shapes of skin can be obtained using numerical and experimental analysis. In our study, natural frequencies and mode shapes are obtained via two methods: (1) finite element analysis: an eigensolution is performed on a finite element model of normal skin, including stratum corneum, epidermis, dermis, and subcutaneous layers and (2) digital image correlation (DIC): several in-vivo measurements have been performed using DIC. The experimental results show a correlation between the DIC and FE results suggesting a noninvasive method to obtain vibration properties of the skin. This method can be further examined to be eventually used as a method to differentiate healthy skin from diseased skin. Prevention, early diagnosis, and treatment are critical in helping to reduce the incidence, morbidity, and mortality associated with skin cancer; thus, making the current study significant and important in the field of skin biomechanics.

1. Introduction

The early detection of skin cancer has great potential to make an impact on the morbidity and mortality of this disease. Moreover, the savings in treatment costs are considerable when skin cancer is caught early. Recently, several new approaches have been developed to detect skin cancer, among them dermoscopy (epiluminescent microscopy and dermatoscopy), high-resolution MRI, and ultrasound aid in determining the extent and depth of skin cancers in vivo.¹ In addition, research is underway in the field of imaging technology that will allow in-vivo detection and analysis of skin cancers which may yield a higher degree of diagnostic certainty than the current methodologies.² To that end, we have previously explored imaging skin with promising results using optical coherence tomography (OCT) and photoacoustic imaging.^3–9 Certainly, additional research on skin cancer screening and detection is needed to compare the benefits of these modalities and to recognize the most effective methods. The mechanical properties of the skin are important tissue parameters useful for understanding skin pathophysiology, which can aid in diagnosis and treatment.¹⁰

Several attempts have been made to simulate and monitor the behavior of the skin using numerical and experimental models; however, modeling skin properties is still challenging due to its complex biological structure. To better understand the skin, Flynn developed a multilayer finite element model of the skin using ABAQUS. The model, consisting of the stratum corneum, dermis, and hypodermis, simulated skin deformations that cause wrinkles and was used to explore the wrinkle formation around contracting healing scars.¹¹ Finite element models have also been developed to determine the hyperelastic parameters of the skin.¹² Talarico et al.¹³ developed a multilayered structural three-dimensional (3-D) FE fingertip model to analyze the deformation distribution characteristics within fingertip soft tissues. Evans and Holt¹⁴ studied the mechanical properties of human skin using finite element modeling. Most of these efforts focus on static techniques to measure the elasticity of skin to monitor its health. However, the elasticity can also affect the dynamic behavior of the human body. The idea of using frequency to cure diseases was first put into practice in the early 1900s. By determining the vibrational frequency rate of a cancer cell, scientists can use frequency generators to generate a specific frequency capable of cancer cell destruction.¹⁵ Various organs of the human body vibrate at different natural frequencies¹⁶; studies show that the stiffness of an afflicted tissue varies from that of a healthy one,¹⁷ thus leading to the differences in natural frequencies between healthy and diseased skin tissue.¹⁸

Traditionally, worrisome skin lesions are removed with a skin biopsy, stained histochemically, and then evaluated under a microscope.¹⁹ In the next few years, however, developments in imaging technology can aid in the detection and diagnosis of skin cancer without the need for a skin biopsy. With the advances in optical techniques, researchers have started to use digital image correlation (DIC) and photogrammetry for structural health monitoring²⁰ and nonintrusive vibration measurements²¹ for mechanical components.^22–34 The optical techniques have also been used for full-field deformations in the biomechanical field.^35,36 Evans and Holt¹⁴ used an optical technique to study mechanical properties of human skin and validate finite element results. DIC has been shown to improve the detection of basal cell carcinoma.³⁷ However, the potential of using optical sensing technique in conjunction with vibration analysis technique to monitor skin health has not previously been explored.

In this work, numerical and experimental techniques are suggested that can be used to identify the vibrational behavior of the skin. By monitoring the dynamic characteristics of skin tissues using noninvasive measurement techniques in conjunction with vibration analysis methods, healthy and diseased skin tissues can be distinguished. To improve the diagnostic accuracy of noninvasive skin cancer detection, the proposed methodology has the potential to facilitate the early diagnosis and treatment of various skin diseases. This paper proposes the use of DIC which is an imaging technology that will allow in-vivo detection and analysis of skin cancers to obtain resonant frequencies and mode shapes of the skin to monitor its health. The experimental results are calculated by adopting the finite element analysis (FEA) approach for developing a numerical model of the skin.

2. Methodology

To obtain the natural frequencies and mode shapes of human skin, a numerical analysis and an experimental study were conducted. This paper describes these methodologies in two sections.

2.1. Numerical Analysis using a Finite Element Model of Skin

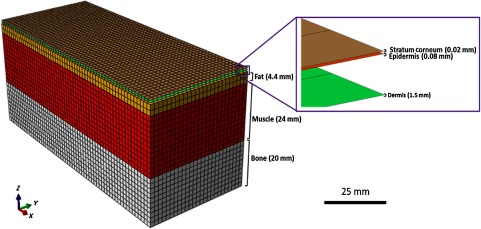
A finite element model of the skin was developed using ABAQUS CAE 2017 engineering software for vibration analysis. For this analysis, a small area of the forearm measuring $120\times 50{\mathrm{mm}}^2$ was modeled (see Fig. 1). Because the human skin extends over the entire body, symmetrical boundary conditions were assumed on the sides of this model. This ensures that the edge effects of the section are not shown in the results. This 3-D FE model of the human skin, which consists of the stratum corneum, epidermis, dermis, subcutaneous, and fat, was developed with muscle and bone layers included beneath the skin. The forearm was assumed to be perfectly flat. For this study, the natural frequencies and mode shapes of the skin were calculated using the numerical eigensolution results from the model. Although we started with a 3-D FE model of flat skin, this model can also represent the wrinkling deformations of the skin.

Fig. 1.

The FE model of the human forearm with different layers of skin connected to muscle and bone. The thickness of each layer is obtained from Ref. 38.

2.1.1. Finite element mesh and boundary conditions

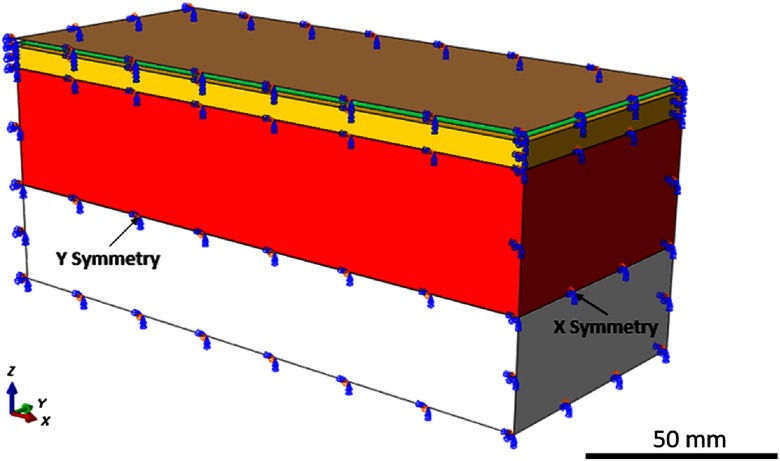
The stratum corneum, epidermis, and dermis were modeled using conventional shell elements because they are very thin layers of the skin. Eight-nodded reduced integration shell elements (S8R) with enhanced hourglass control were used to mesh these layers. These elements have been used by a previous researcher to model human skin.^11,39 Because shear movement of the fat layer plays an important role in the deformations of the skin, this layer was modeled using continuum shell elements (SC8R) in ABAQUS. Continuum shell elements can replicate the sheer deformations of the layers while conventional shell elements can only show bending deformations. The muscle and bone layers were designed as solid structures and were meshed using eight-nodded reduced integration linear brick elements (C3D8R) with enhanced hourglass control and distortion control enabled. These elements and setting are suggested for vibration analysis.⁴⁰ Each layer was connected to the underlying layer using tie constraints. Symmetric boundary conditions were applied to the model, the nodes along the width were given $X$ symmetry ($UX=URY=URZ=0$) while the nodes along the length had $Y$ symmetry ($UY=URX=URZ=0$) as shown in Fig. 2.

Fig. 2.

Symmetric boundary conditions applied on the FE model.

2.1.2. Choice of material

Although skin can behave visco-elastically, nonlinearly hyperelastically, and anisotropically,⁴¹ the skin can be assumed linear isotropic in a specific range of vibration analysis. For this research, the material properties for isotropic skin model were obtained from McBride et al.³⁸ and are shown in Table 1.

Table 1.

Mechanical properties of different layers of skin tissue, muscle, and bone.³⁸

Mechanical properties	Symbol	Unit	Stratum corneum	Epidermis	Dermis	Subcutaneous fat	Muscle	Bone
Young’s modulus	$E$	$\mathrm{N}/{\mathrm{m}}^2$	$1.998\times {10}^9$	$1.02\times {10}^8$	$1.02\times {10}^7$	10,200	$8.88\times {10}^8$	$1.7\times {10}^{10}$
Poisson’s ratio	$N$	m/m	0.48	0.48	0.48	0.48	0.3	0.3
Density	$P$	$\mathrm{Kg}/{\mathrm{m}}^3$	1500	1119	1116	971	1200	2000

The mechanical properties of the skin are not constant parameters, and the properties vary according to the skin type, age, gender, location, and other environmental factors.⁴² For example, the skin of a young person is stiffer when compared to that of an older person.⁴³ This changes the Young’s modulus for their skin types. Nevertheless, the results shown in Table 1 are for an average skin layer in the forearm.

2.1.3. Results from finite element analysis

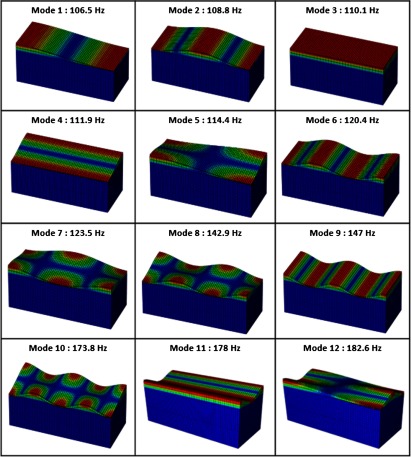
An eigensolution was performed on the model to obtain the first 20 resonant frequencies and their corresponding mode shapes for the specified boundary conditions. The first 20 natural frequency ranges are located between 106 and 240 Hz. Figure 3 shows the first 12 mode shapes of the model. The wrinkling pattern of the skin is more dominant in mode shapes 9, 10, 11, and 12 with the frequency ranging from 147 to 182 Hz.

Fig. 3.

The first 12 prominent mode shapes and their corresponding frequencies.

2.2. Experimental Analysis using Digital Image Correlation

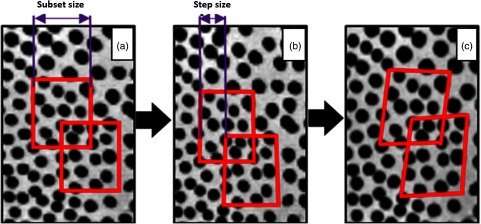
The experimental analysis of the skin was performed using DIC. DIC is a 3-D, full-field, noncontact optical technique to measure contour, deformation, vibration, and strain on almost any material. The technique analyzes two images taken before and after the object has been deformed due to external mechanical forces and yields a vector field corresponding to the deformation. The deformation in the images is calculated by tracking the speckles on the object. A point and its signature are recorded in the undeformed image; the deformed image is searched for the point containing a signature that maximizes a given similarity function (see Fig. 4).

Fig. 4.

(a) The reference subset in the undeformed image, (b) step size to determine the number of data points being tracked, and (c) target subset in deformed image.

DIC can be used to identify the natural frequencies of the skin when the skin vibrates. For this study, DIC was used on 11 healthy volunteers aged 21 to 27. The tests were performed on the ventral forearm, the dorsal forearm, the dorsal palm, and the calf. The in-vivo testing conducted on the skin at the ventral forearm of a healthy volunteer is shown in Fig. 5. The results from four of the DIC experiments are presented in this paper. Prior to performing the DIC, informed consent was obtained from all the volunteers with approval from the Kettering University Institutional Review Board.

Fig. 5.

The experimental setup of DIC with the cameras focused on the speckle pattern located on the volunteer’s forearm.

To calculate the measurement, a pair of high-speed cameras was used. These photon high-speed cameras can capture images up to 80,000 frames per second (fps). The cameras are equipped with 35-mm lenses and have a stereo angle of $\sim 30\mathrm{deg}$ [Fig. 5(b)]. A speckle pattern was created on a patch of skin using skin-friendly eyeliner liquid [see Fig. 5(a)]. The lenses were focused on the speckled part of the skin. An aperture adjusts how much light falls on the sensor and aperture size is indicated by the $f$-number. For this experiment, an $f$-number of 5.6 and an exposure time of 0.9 to 2 ms were used. The cameras were then calibrated using calibration plates as shown in Fig. 5 (a gridded plate). To induce vibrations in the skin, small impacts (taps) were made on the region close to the speckled area. The response of the skin to the tapping of the forearm with fingers was recorded by the cameras and was accurately captured by setting an appropriate frame rate. FEA results suggest that the first few wrinkling resonant frequencies of the skin are $<200\mathrm{Hz}$. Thus, the experiments in this study were conducted using frame rates of 1080 and 500 fps. Due to memory limitations, the high-speed cameras can only record 2724 images. Therefore, the data were sampled at a frequency of 1080 and 500 Hz to record the vibrations for 2.52407 and 5.452 s, respectively. The high-speed cameras are coupled to VIC-3D software from Correlated Solutions, which is a complete, turn-key system for measuring the shape, displacement, and strain of surfaces in three dimensions. The recorded images were processed in VIC-3D software to extract the strain, displacement, operating deflection shapes (ODSs), and the resonant frequency values.

2.2.1. Results from digital image correlation

The high-speed camera images were processed using DIC technique in VIC-3D to extract full-field displacement and strain on the speckled area. DIC can calculate the displacement for all points on the skin during the measurement. Thus, the displacement data in the time domain for several points on the speckled area were exported from VIC-3D into a spreadsheet. A MATLAB code was developed using MATLAB version R2016b to read the time-domain data from VIC-3D and transfer it into the frequency domain using a fast Fourier transformation (FFT) algorithm. In the frequency domain, the frequency content of the response can be obtained. After retrieving the frequency components, response plots were acquired by implementing a Nyquist theorem in the code, which states that to adequately reproduce a signal, it should be periodically sampled at a rate that is $2\times$ the frequency one wishes to record. The response plots of the skin were plotted on a semi-log scale thereby providing a better understanding of the event and an idea about the range of resonant frequencies of healthy human skin tissue.

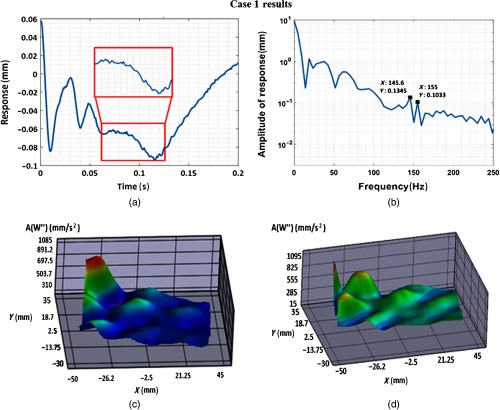
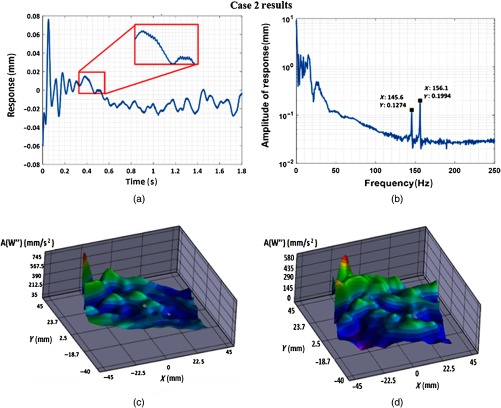
The results for 11 test cases were analyzed, among which the best 2 cases are shown in this section. The frequency and phase response plots for these two test cases were much more prominent when compared to the rest, thereby facilitating better results. To check for the influence of sampling rates on the conclusive results, case 1 and case 2 experiments were performed with different frame rates: 1080 fps for case 1 and 500 fps for case 2.

Figures 6(a) and 7(a) show the response in the time domain for the two test cases for a short sample period. There are large displacements occurring due to hand movements (or pulse), while there are also some low-frequency fluctuations. To obtain the frequency content of the signal, the time-domain data are transferred into the frequency domain. The peaks in the FFT plots show the resonant frequencies. The large displacements at low frequencies are due to hand movements (rigid body modes). For case 1, the plot represented in Fig. 6(b) shows two peaks at 145.6 and 155 Hz. For test case 2, Fig. 7(b) shows two peaks, one at 145 Hz and the other at 156 Hz. As shown, better results were obtained for the test with a frame rate of 500 fps (case 2) when compared to 1080 Hz (case 1). This occurs because the higher acquisition time allows us to average the noise and obtain better FFT plots.

Fig. 6.

(a) Response of the skin in the time domain extracted from MATLAB, (b) response of the skin at 145.6 Hz in the frequency domain extracted from MATLAB, (c) ODSs at 145.6 Hz extracted from DIC measurement, and (d) ODSs at 155 Hz extracted from DIC measurement for test case 1.

Fig. 7.

(a) Response of the skin in the time domain extracted from MATLAB, (b) response of the skin at 145.6 and 156.1 Hz in the frequency domain extracted from MATLAB, (c) ODSs at 145.6 Hz extracted from DIC measurement, and (d) ODSs at 156.1 Hz extracted from DIC measurement for test case 2.

The displacement of the skin at each frequency shows the operating mode shapes of the skin corresponding to that resonant frequency. The imaginary parts of the FFT results for the entire surface are used to obtain the ODSs of the skin. ODSs are in fact unscaled mode shapes of the skin (because they are not scaled using the imparted forces). Parts c and d of Figs. 6 and 7 show the operating shapes corresponding to the resonant frequencies. These shapes show wrinkling operating shapes of the skin at different frequencies.

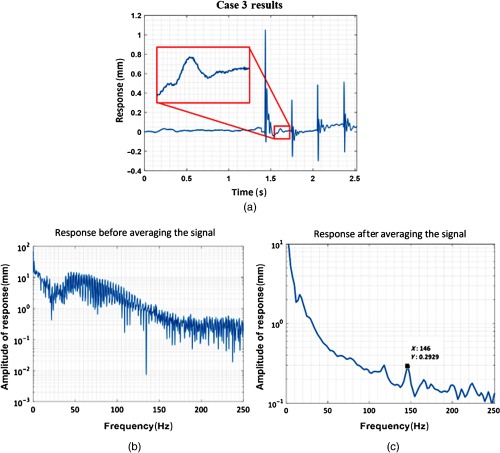
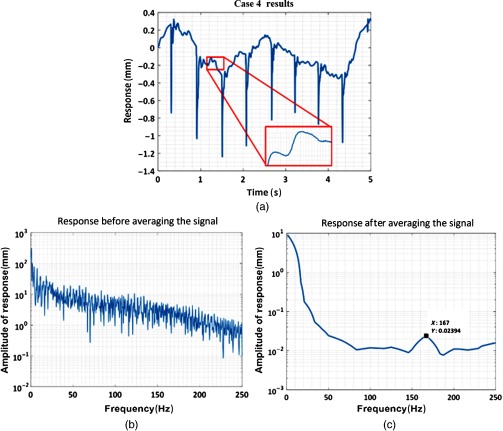
Not all the experiments conducted on volunteers using DIC yielded results that could be easily interpreted. For some measurements, the mode shapes could be readily obtained (e.g., case 1 and 2) while for some measurements, we need to perform an averaging on the data to obtain better signal-to-noise ratio (e.g., case 3 and 4). The data for two such test cases are shown in Figs. 8 and 9, respectively. For these cases, the data need to be further processed to obtain appropriate results. For test case 3, the experiment was conducted on the ventral forearm, whereas, the calf region was tested for case 4. Figures 8(a) and 9(a) present the time-domain amplitude of the response obtained by processing the displacement data for 2724 images captured over a total time span of 2.52407 s (1080 fps) for case 3 and a total time span of 5.452 s (500 fps) for case 4. As can be seen, the original FFTs using the entire signal did not show very clear peaks [see Fig. 8(b) and 9(b)]. This could be due to the noise from external sources or disturbances caused internally due to the effects of blood flow and pulse. The objectives of the current research are not only to extract the natural frequencies of skin but also to prove the efficacy of DIC in evaluating the properties of a nonlinear structure, such as skin. Thus, the original data were examined and re-evaluated in MATLAB.

Fig. 8.

(a) Response of the skin in the time domain, (b) response of the skin in the frequency domain extracted using original data case 3, and (c) response of skin in frequency domain extracted after averaging the signal in the frequency domain for test case 3.

Fig. 9.

(a) Response of the skin in the time domain, (b) response of the skin in the frequency domain extracted using original data case 4, and (c) response of skin in frequency domain extracted after averaging the signal in the frequency domain for test case 4.

To reduce the noise, a signal averaging technique was implemented on the data for both test cases. In this process, three epochs of displacement data from the time trace for each test case were selected; an FFT was performed on each signal epoch. The FFTs for all three epochs were then averaged to increase the signal-to-noise ratio. After averaging the sampled signal, the prominent peaks representing a frequency of 146 Hz in case 3 and 167 Hz in case 4 were obtained as shown in Figs. 8(c) and 9(c), respectively. This indicates that although some original results from DIC may not manifest a clear peak for the resonant frequencies, the resonant frequencies can still be obtained by further processing the signal and averaging the data. Furthermore, signal averaging can be performed by capturing several trial measurements for a single volunteer in the future measurements (in the conventional model analysis, 3 to 5 trials are performed and averaged to obtain resonant frequencies and mode shapes). Performing several trials and averaging them ensure that the noise can be reduced and FFTs with clear peaks can be obtained.

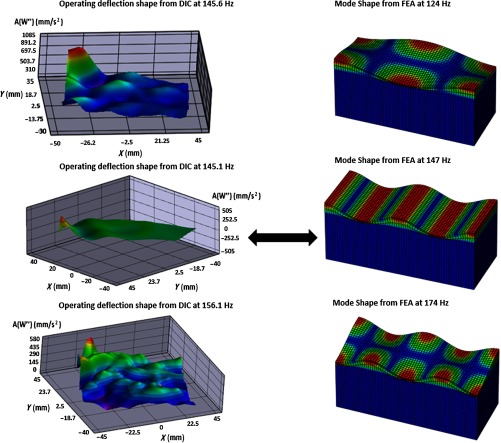
The finite element model provided a good approximation to the experimental data. The wrinkling mode shapes obtained at 124, 147, and 174 Hz from the finite element model can be correlated with the DIC results that show ODSs at 145.6, 145.1, and 156.1 Hz, respectively, as shown in Fig. 10. The DIC results reveal several deflections shapes, yet, not all the modes extracted using the FE method can be obtained using DIC, as tapping the skin might not excite all the modes. Furthermore, the location/orientation of the excitation can affect the modes that are excited. Figure 10 shows the three DIC shapes that qualitatively show the highest similarities to the mode shapes from FEA.

Fig. 10.

A comparison between wrinkling mode shapes obtained from DIC and FE model.

3. Discussion

DIC is a robust noninvasive technique that can be used to evaluate the mechanical properties of the skin. Furthermore, the combination of DIC and finite element modeling is a very powerful methodology, with a great deal of potential for measuring the mechanical properties of biological tissues. In this study, we have derived the resonant frequencies of the skin from the response of the skin in the patterned area using DIC and signal processing. Figures 6 and 7 represent the wrinkling modes from DIC and response plots from MATLAB at 145.6 and 155 Hz for case 1, 145.6 and 156.1 Hz for case 2, respectively, thereby supporting the result that the natural frequency of the skin could be in the range of 140 to 156 Hz. The slight variation in the results calculated from the test cases could be due to several factors that influence the behavior and mechanical properties of the skin. For example, the elasticity of the skin varies by location along with the amount of fat beneath it, the moisture content, and the age of the subject.^44,45 Accordingly, the stiffer the tissue, the greater the natural frequency. Since this study is focused on determining the resonant frequencies of the skin, the elasticity of the skin tissue is an essential factor affecting the results. One phenomenon of skin aging is the loss of cutaneous elasticity. Additionally, good moisture content in the skin tissue (usually present in younger people) gives better elasticity to the skin. As such, dry and inelastic skin could result in a reduction in natural frequency. In future experiments, we plan to include older volunteers to catalog the difference in the mechanical properties of skin tissue. The tests in this study were conducted on individuals with different body weights, skin types, and genders, to show their effect on the natural frequency of the skin. The relationship between sensitivity/specificity of this technique and natural frequency and body weights, skin types, and gender and their role in differentiating between healthy and diseased skin is the topic of our future study.

As the test results demonstrate, it is evident that the constitutive model could represent the mode shapes of the skin very well, as seen by the difference between the measured and predicted frequencies. A significant cause for uncertainty in the results is the material properties that are used in the FE model. The FE model uses isotropic and linearly elastic materials. However, DIC was performed on real skin tissue and the material properties might be different and may show anisotropic, nonlinear, and hyperelastic behavior. Additionally, possible modeling and experimental errors could hinder a data match, as the calculated percentage difference between the FEA and experimental data is $\sim 11.6\%$. For this study, the skin thickness and material properties were estimated from literature data; however, skin with a different thickness is likely to behave differently. Certainly, interesting areas for further investigation would be to use ultrasound or OCT to determine the thickness of the skin, and work to calculate results with greater accuracy by improving the FE models by determining and inserting the actual behavioral properties of skin.

The main objective of this work was to study the feasibility of using vibration behavior of the skin to monitor its health. Resonant frequencies and operating shapes are two main indicators of the vibrational behavior of the skin. These two components change when the material properties of the structure change. This study demonstrates that the resonant frequencies and operating shapes of the skin can be obtained using DIC. This technique can be a robust, noncontact, and nonintrusive approach to monitor the health of the skin. In a future investigation, the finite element model developed in this paper will be used in a sensitivity study to see how the resonant frequencies and mode shapes of healthy skin differ from unhealthy skin. These results can then be verified with experimental tests using DIC.

4. Conclusions

The objective to determine the natural frequencies and mode shapes of human skin using a noninvasive imaging technique, such as DIC and FE modeling, has been achieved successfully. Based on the results, the natural frequencies of the skin when considered attached to muscle and bone elements of the body can be estimated to range from 140 to 185 Hz. The DIC experiment exhibits ODSs at a frequency range of 145 to 156 Hz, whereas wrinkling modes obtained from the FE model are in the range of 143 to 183 Hz. However, a literature study reveals the natural frequencies of the skin vary as the elasticity of the skin is distinct at various locations on the body.^44,46 Age also plays a significant role as the skin loses its elasticity with age thereby influencing the natural frequencies.⁴⁷

There are many areas for further study, including the opportunity to develop various FE models incorporating nonlinearity, hyperelasticity, and anisotropy in the material stiffness. Additionally, by limiting rigid body motions and disturbances caused by internal and external factors, experimental errors could be reduced. Notably, the technique presented here measures the natural frequencies and mode shapes of healthy skin by a quick, noninvasive diagnostic method. This has enormous potential for a more systematic study to evaluate the variations in natural frequency in different individuals, different body sites, and different environmental conditions. Vibration analysis offers the opportunity to analyze the variations in dynamic characteristics (e.g., resonant frequencies, mode shapes, and strain mode shapes) of healthy skin and diseased skin, which can further form a base to support the diagnosis of skin diseases.

Measurement of resonant frequencies for skin could be another valuable noninvasive approach to evaluate cutaneous function. As mentioned earlier stiffness is one of the factors that influence natural frequency, the cancerous skin tissues are certainly stiffer than a healthy one. Using a finer grid size when performing the experiment, faster computation, a more compact instrumentation will help in transability of the device to the clinic. We plan to test the methodology on more common types of skin cancers, such as basal cell carcinoma and squamous carcinoma, before moving to melanoma lesions. Some of the technical obstacles could be to gauge the resonant frequencies of only the skin tissue by removing the effects of muscles, blood flow, and various layers that lie below the skin tissue.

Biographies

Rakshita Panchal is pursuing her master’s in automotive engineering at Kettering University and works as a graduate research assistant in the Noise, Vibration, Harshness, and Experimental Mechanics Laboratory (NVHEM Lab). She works on FEA- and NVH-related studies.

Luke Horton received his bachelor of arts degree from Claremont McKenna College in 2017, graduating cum laude with honors in the science and management major. Currently, he is a second-year medical student at Wayne State University School of Medicine and is a medical research assistant in the Opira Lab of Dr. Mohammad R.N. Avanaki.

Peyman Poozesh works as a postdoctoral research associate at Noise, Vibration, Harshness, and Experimental Mechanics Laboratory. He received his PhD in mechanical engineering from the University of Massachusetts Lowell in 2017. His research is focused on NVH and acoustics.

Javad Baqersad is the director of Noise, Vibration, Harshness, and Experimental Mechanics Laboratory at Kettering University. His research interests are related to vibration and acoustics, finite element analysis, digital image correlation, and signal processing. He works on federally-funded and industry-funded projects and has published more than 70 journal articles and conference papers. He organizes optical sessions for the Society for Experimental Mechanics and is an associate technical editor for Experimental Techniques.

Mohammadreza Nasiriavanaki received his PhD with outstanding achievement in medical optical imaging and computing from the University of Kent in the United Kingdom, in 2012. His bachelor’s and master’s degrees with honors are in electronics engineering. Currently, he is an assistant professor in the Biomedical Engineering Department of Wayne State University. His area of expertise is designing medical devices for skin and brain diseases diagnosis using photoacoustic imaging and optical coherence tomography technologies.

Disclosures

The authors have no relevant financial interests in this article and no potential conflicts of interest to disclose.