A model of mitochondrial O₂ consumption and ATP generation in rat proximal tubule cells

Abstract

Oxygen tension in the kidney is mostly determined by O₂ consumption (Qo₂), which is, in turn, closely linked to tubular Na⁺ reabsorption. The objective of the present study was to develop a model of mitochondrial function in the proximal tubule (PT) cells of the rat renal cortex to gain more insight into the coupling between Qo₂, ATP formation (G_ATP), ATP hydrolysis (Q_ATP), and Na⁺ transport in the PT. The present model correctly predicts in vitro and in vivo measurements of Qo₂, G_ATP, and ATP and P_i concentrations in PT cells. Our simulations suggest that O₂ levels are not rate limiting in the proximal convoluted tubule, absent large metabolic perturbations. The model predicts that the rate of ATP hydrolysis and cytoplasmic pH each substantially regulate the G_ATP-to-Qo₂ ratio, a key determinant of the number of Na⁺ moles actively reabsorbed per mole of O₂ consumed. An isolated increase in Q_ATP or in cytoplasmic pH raises the G_ATP-to-Qo₂ ratio. Thus, variations in Na⁺ reabsorption and pH along the PT may, per se, generate axial heterogeneities in the efficiency of mitochondrial metabolism and Na⁺ transport. Our results also indicate that the G_ATP-to-Qo₂ ratio is strongly impacted not only by H⁺ leak permeability, which reflects mitochondrial uncoupling, but also by K⁺ leak pathways. Simulations suggest that the negative impact of increased uncoupling in the diabetic kidney on mitochondrial metabolic efficiency is partly counterbalanced by increased rates of Na⁺ transport and ATP consumption. This model provides a framework to investigate the role of mitochondrial dysfunction in acute and chronic renal diseases.

INTRODUCTION

The renal tubules reabsorb >99% of the glomerular filtrate, in part via active transport processes that necessitate energy. The transcellular concentration gradients that drive tubular transport are primarily established by Na⁺-K⁺-ATPase pumps that use ATP hydrolysis as a source of energy, which, in turn, requires a sustained rate of ATP generation, mostly by aerobic processes. The kidneys thus have the second highest O₂ consumption rate (Qo₂) after the heart (14, 68). The greatest density of mitochondria is found in the proximal tubule (PT) and thick ascending limb (8, 44).

In contrast to most other organs, metabolic control of blood flow is poor in the kidney. To stabilize glomerular filtration, renal blood flow and, therefore, the O₂ supply are kept within tight limits and do not increase in proportion with Qo₂ (70). The inability of the kidney to regulate perfusion independently, coupled to its high metabolic demand, contributes to the kidney’s particular susceptibility to hypoxia. It also implies that intrarenal Po₂ is predominantly determined by Qo₂ (70). Since chronic hypoxia is now firmly recognized as a unifying pathway that drives the progression of kidney disease (13, 30, 38, 65, 66), understanding the factors that govern renal Qo₂ is essential.

Understanding the determinants of Qo₂ in the kidney requires, in turn, linking explicitly tubular Na⁺ transport and Qo₂. We have previously built detailed cell-based models of water and solute transport along the nephron, accounting for the specific apical, basolateral, and paracellular transport pathways in each segment, and applied these models to predict segmental Qo₂ (55–59). We have also developed organ-scale models that describe the interactions among renal tubules and the vasculature and predict medullary oxygenation (18, 36, 37). However, none of these models included O₂ metabolism and instead postulated a fixed Na⁺ transport-to-Qo₂ ratio. We developed the present model of mitochondrial function to couple Na⁺-driven ATP hydrolysis to Qo₂ in the PT.

The PT oxidizes mostly fatty acids and some intermediates of the tricarboxylic acid (TCA) cycle that are reabsorbed from the lumen (3). Under normal conditions, the PT reabsorbs the full load of glucose but only metabolizes <1% of that load (63). The PT also has a significant capacity for gluconeogenesis and may account for 45% of glucose production during prolonged starvation (69, 86). In the model described below, the concentration of pyruvate is specified without explicitly considering the substrates that generated it.

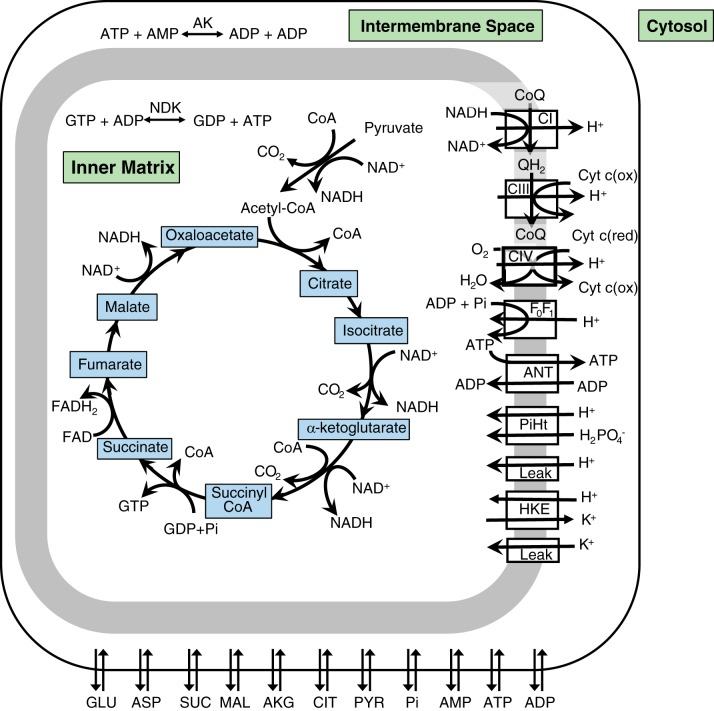
As shown in Fig. 1, pyruvate enters the mitochondria, where it is converted to acetyl CoA, which then enters the TCA cycle. The cycle is formed by a series of eight redox, dehydration, hydration, and decarboxylation reactions that transfer electrons stripped from metabolic substrates to NADH and FADH₂. During the process of oxidative phosphorylation, these electrons are sequentially transferred to electron carriers in the respiratory chain, the last step of which consists of the reduction of O₂ to H₂O. The energy released during electron transfer is used by respiratory complexes I, III, and IV to pump protons from the inner matrix into the intermembrane space, thereby creating an electrochemical potential gradient known as the proton motive force (pmf). The reentry of protons into the matrix across F₀F₁-ATP synthase drives ADP phosphorylation, i.e., the formation of ATP, which dissipates the pmf. However, some protons reenter the matrix across H⁺ leak pathways: this shunt also dissipates the pmf and reduces the coupling between oxidative phosphorylation and ATP formation, a phenomenon hence referred to as mitochondrial uncoupling. The newly formed ATP is exchanged for ADP across the inner mitochondrial membrane via adenine nucleotide translocase (ANT).

Fig. 1.

Schematic representation of the transport and metabolic processes included in the model: the tricarboxylic acid cycle, oxidative phosphorylation, chemical reactions, and metabolite transport between the cytoplasm and mitochondria. AK, adenylate kinase; ANT, adenine nucleotide translocase; CI, complex I; CIII, complex III; CIV, complex IV; CoQ, coenzyme Q; Cyt c(ox), cytochrome c (Cyt c) oxidase; Cyt c(red), cytochrome c reductase; HKE, H⁺/K⁺ exchange; NDK, nucleoside diphosphokinase; PiHt, P_i-H⁺ transporter.

In the present study, we examined the impact of ATP hydrolysis, Po₂, pH, and electrolyte concentration on the mitochondrial processes described above to better understand the coupling between Qo₂, ATP formation, ATP hydrolysis, and Na⁺ transport in the PT.

MODEL DESCRIPTION

We adapted to the proximal convoluted tubule the model of mitochondria metabolism and electrophysiology developed by Wu and colleagues for cardiac and skeletal muscle (96). The model represents the TCA cycle, oxidative phosphorylation, and metabolite transport between the cytosol and mitochondria and is based on mass and charge conservation equations that consider detailed reaction kinetics and transmembrane fluxes. We adjusted the model’s parameter values to represent mitochondria in the cortical PT of the rat kidney.

Differential Equations

The full set of model equations can be found in Wu et al. (96). Given our focus on the production and consumption of ATP in the PT, the equations that govern the concentration of ATP in the inner mitochondrial matrix (subscript x), intermembrane space (subscript i), and cytoplasm (subscript c) are recapitulated below:

$$\text{Mitochondrial}\text{inner}\text{matrix:}\frac{{\text{d[ATP]}}_{\text{x}}}{\text{d}t}=\left(+{\text{G}}_{\text{ATP}}+{\text{Q}}_{\text{ndk}}-J_{\text{ANT}}\right)/{\text{W}}_{\text{x}}$$ (1)

$$\text{Mitochondrial}\text{intermembrane}\text{space:}\frac{{\text{d[ATP]}}_{\text{i}}}{\text{d}t}=\left(+J_{\text{ANT}}+J_{\text{ATPt}}+{\text{Q}}_{\text{AKi}}\right)/{\text{W}}_{\text{i}}$$ (2)

$$\text{Cytoplasm:}\frac{{\text{d[ATP]}}_{\text{c}}}{\text{d}t}=\left[-J_{\text{ATPt}}\left({\text{V}}_{\text{mito}}/{\text{V}}_{\text{cyto}}\right)+{\text{Q}}_{\text{AKc}}+{\text{Q}}_{\text{CK}}-{\text{Q}}_{\text{ATP}}\right]/{\text{W}}_{\text{c}}$$ (3)

where W_x, W_i, and W_c are the fractional volume occupied by water in the inner matrix, intermembrane space, and cytoplasm, respectively; V_mito and V_cyto are the proportion of cell volume occupied by the mitochondria and cytoplasm, respectively; G_ATP is the rate of ATP formation by F₀F₁-ATP synthase; Q_ndk is the nucleoside diphosphokinase reaction rate; J_ANT is the flux of ATP across ANT; J_ATPt is the flux of ATP across the outer mitochondrial membrane; Q_AKi and Q_AKc are the mitochondrial and cytoplasmic adenylate kinase reaction rates, respectively; Q_CK is the creatine kinase reaction rate; and Q_ATP is the ATP consumption rate in the cytosol.

ATP formation is driven by the pmf, which is a function of the electric potential (Ψ) and proton concentration gradients across the inner membrane:

$$\text{pmf}=\left({\Psi }_{\text{i}}-{\Psi }_{\text{x}}\right)-\frac{R\text{T}\ln (10)}{F}\left({\text{pH}}_{\text{i}}-{\text{pH}}_{\text{x}}\right)=\Delta \Psi +\frac{R\text{T}\ln (10)}{F}\Delta \text{pH}$$ (4)

where R is the ideal gas constant, F is the Faraday constant, and T is the absolute temperature. We adopt here the bioenergetics convention (11), such that ΔΨ, ΔpH, and pmf all have positive signs under typical conditions. Given the permeability properties of the outer mitochondrial membrane, pH_i is assumed to equal pH_c (96). The model equation for pH_x is based on conservation of mass and takes into account the generation and consumption of H⁺ via chemical reactions as well as H⁺ binding and unbinding. Note that the model considers the binding of H⁺, K⁺, and Mg²⁺ to multiple reactants, including ATP, GTP, GDP, and isocitrate (96). As an example, four ionic forms of ATP are considered: ATP⁴⁻, HATP³⁻, KATP³⁻, and MgATP²⁻.

In the original model of Wu et al. (96), hereafter referred to as the Wu et al. model, the flux of protons via leak pathways (J_H,leak) was computed based on the Goldman equation. To account for the observed non-Ohmic, quasi-exponential dependence of proton leak on ΔΨ (76), the corresponding flux in the present study is calculated as in later models (5, 47):

$$J_{\text{H,leak}}=P_{\text{H,leak}}\left[{[{\text{H}}^{+}]}_{\text{i}}\exp \left(\frac{F\Delta \Psi }{2R\text{T}}\right)-{[{\text{H}}^{+}]}_{\text{x}}\exp \left(-\frac{F\Delta \Psi }{2R\text{T}}\right)\right]$$ (5)

where P_H,leak is H⁺ leak permeability. We also include herein a K⁺ leak pathway (not considered in the Wu et al. model) to represent the diffusion of K⁺ from the intermembrane space into the inner matrix (40). K⁺ leak flux (J_K,leak) is computed as follows:

$$J_{\text{K,leak}}=P_{\text{K,leak}}\left[{[{\text{K}}^{+}]}_{\text{i}}\exp \left(\frac{F\Delta \Psi }{2R\text{T}}\right)-{[{\text{K}}^{+}]}_{\text{x}}\exp \left(-\frac{F\Delta \Psi }{2R\text{T}}\right)\right]$$ (6)

K⁺ leak permeability (P_K,leak) is taken as P_H,leak × 10⁻⁶ in the base case. Note that K⁺ entry is counterbalanced by K⁺ exit via H⁺/K⁺ exchangers (Fig. 1).

Model Parameters

Structural/volume parameters for renal cortex mitochondria are shown in Table 1. The model assumes fixed cytoplasmic K⁺, H⁺, and Mg²⁺ concentrations. These are, respectively, taken as 110 mM (26), 0.40 mM (49), and 10^−7.2 M (71, 97), as measured in PT cells. The concentration of O₂ in the matrix is also fixed and set to 67 μM (i.e., Po₂ = 50.0 mmHg) under basal conditions. The initial values of the cytoplasmic concentrations of P_i ([P_i]_c), citrate, α-ketoglutarate, fumarate, malate, aspartate, pyruvate, glutamate, glucose, and glucose-6-phosphate are taken from Lemieux et al. (61), assuming a wet weight fraction of 0.80 (6). The initial values of the cytoplasmic concentration of succinate and phosphate creatine are taken from Horn et al. (48) and Toma et al. (90). The total concentration of adenosine phosphate species (ATP + ADP + AMP) is set to 2.75 mM (23, 61). Other initial values are those of the original model (96).

Table 1.

Model parameters for proximal convoluted tubule mitochondria

Parameter	Value	Reference(s)
Fractional mitochondrial volume, L mitochondria/L cell	0.25	15, 27, 46, 53
Fractional cytoplasmic volume, L cytoplasm/L cell	0.72	Based on Ref. 72
Cytoplasm water fraction, L water/L cytoplasm	0.77	41, 60
Mitochondria water fraction, L water/L mitochondria	0.659	60
Protein density of mitochondria, mg protein/L mitochondria	3.274 × 105	Based on Refs. 83, 94
Total matrix concentration of NADH, mol/L matrix water	0.824 × 10−3	19
Total matrix concentration of coenzyme Q, mol/L matrix water	2.15 × 10−3	7
Total intermembrane concentration of cytochrome c, mol/L intermembrane water	1.96 × 10−3	7
Kidney-to-heart complex I activity ratio	0.75	20, 98
Kidney-to-heart complex III activity ratio	0.50	7
Kidney-to-heart complex IV activity ratio	0.25	7

The model assumes that the total concentrations of NADH, coenzyme Q (CoQ), and cytochrome c (Cyt c) remain fixed. The total concentration of CoQ and Cyt c in renal cortex mitochondria is estimated based on kidney-to-heart content ratios (7), taking into account differences in mitochondrial protein density. Similarly, the activity of complexes I, III, and IV in PT mitochondria is estimated based on kidney-to-heart activity ratios (7, 20, 98). The hexokinase reaction rate is set to zero, given the very low hexokinase activity in the PT (82, 93). Other parameter values (including the adenylate kinase and creatine kinase reaction rate constants) are those of the original model. Kidney-specific parameter values are shown in Table 1.

ATP Consumption Rate

The baseline rate of ATP consumption in the proximal convoluted tubule is estimated as 9.57 pmol ATP·s⁻¹·tubule⁻¹ based on our published model of transport along the PT (58). The length and inner radius of the proximal convoluted tubule are taken as 0.97 and 12.5 × 10⁻⁴ cm, respectively; assuming that the cytoplasmic water volume equals 10⁻³ cm³/cm² epithelium (95), the volume of water in the cytoplasm is 7.62 × 10⁻⁶ cm³/tubule, and the ATP consumption rate is equivalent to 1.26 × 10⁻³ mol ATP·s⁻¹·L cytoplasm⁻¹.

RESULTS

Isolated Mitochondria

The model was validated by comparing its predictions with our laboratory’s recent measurements of mitochondrial function in the renal cortex of Sprague-Dawley rats: the simulations mimicked the experimental protocol and bath conditions previously described in Schiffer et al. (79). In addition to the parameter choices described above (which were based on experimental data), P_H,leak (Eq. 5) was set to 345 mol·s⁻¹·M⁻¹·L mitochondrial volume⁻¹ to match measured leak respiration rates.

State 2 respiration, which is determined in the presence of glutamate and malate without ADP, characterizes Qo₂ in the absence of ATP formation; under these “idle conditions,” the protons pumped into the intermembrane space reenter the matrix via H⁺ leak pathways that consume the pmf. On the subsequent addition of ADP, during state 3 respiration, F₀F₁-ATP synthase becomes the dominant pathway for proton reentry. Thus, the state 3-to-state 2 Qo₂ ratio (Jo_2,s3/Jo_2,s2), also known as the respiratory control ratio (RCR), is a common measure of mitochondrial coupling. P/O is defined as the amount of ATP produced by F₀F₁-ATP synthase per oxygen atom reduced by the respiratory chain. The leak respiration is usually measured in the presence of oligomycin, which inhibits the F₀ unit of ATP synthase and prevents ATP formation (51). As shown in Table 2, model predictions agree well with measured values of the state 3 respiration rate, RCR, leak respiration, and P/O (79).

Table 2.

Model predictions for isolated mitochondria

	Experimental Values (79)	Model Predictions
State 3 respiration, nmol O2·mg−1·s−1	4.08 ± 0.60	4.09
Respiratory control ratio	8.5 ± 0.9	9.6
Leak respiration, nmol O2·mg−1·s−1	0.37 ± 0.06	0.46
P/O at half-maximum respiration	1.8 ± 0.1	1.92

Respiration fluxes are per milligram of mitochondrial protein. P/O, amount of ATP produced by F₀F₁-ATP synthase per oxygen atom reduced by the respiratory chain.

The most uncertain parameters in this study are the leak permeabilities. To assess the sensitivity of model predictions to P_H,leak, we varied its value by a factor ranging from 0.1 to 10 and computed the corresponding respiration rates under the experimental conditions of Schiffer et al. (79). As shown in Fig. 2, increasing P_H,leak raises Jo_2,s2 more than Jo_2,s3, thereby lowering RCR. Indeed, as more protons reenter the matrix via H⁺ leak pathways, they dissipate a greater fraction of the pmf generated by substrate oxidation and reduce the driving force for ATP formation (i.e., the difference between Jo_2,s3 and Jo_2,s3). A twofold increase in P_H,leak from its baseline value is predicted to reduce RCR from 9.6 to 6.9, if P_K,leak is set to its baseline value.

Fig. 2.

Predicted effect of proton leak permeability (P_H,leak) on state 2 and state 3 O₂ consumption (A) and the respiratory control ratio (RCR; B) in isolated mitochondria. Results are shown for three different values of K⁺ leak permeability: 0, baseline ($P_{\text{K,leak}}^{\text{0}}$), and baseline × 10.

We also examined the impact of P_K,leak. By itself, increasing P_K,leak stimulates the cycling of K⁺ across the inner mitochondrial membrane; the resulting increase in H⁺/K⁺ exchange, in turn, stimulates the cycling of H⁺ and raises the respiration rate in both states 2 and 3 (Fig. 2A). Conversely, decreasing P_K,leak reduces H⁺/K⁺ exchange, thereby diminishing H⁺ reentry via pathways other than F₀F₁-ATP synthase, lowering Jo_2,s2 more than Jo_2,s3, and elevating RCR (Fig. 2B).

Mitochondria In Vivo

Base case.

We then performed simulations of renal mitochondria function in vivo; the cytosolic concentration of pyruvate was set to 0.15 mM. Mitochondrial O₂ concentration, which is also fixed in the model, was set to 67 μM (50 mmHg) in the base case and pH_c to 7.20. Based on our previously published model of rat PT function (58), the baseline rate of ATP consumption in the cytoplasm (Q_ATP) was set to 1.26 mmol·s⁻¹·(L·cytoplasm)⁻¹ [or 0.904 mmol·s⁻¹·(L·cell)⁻¹], as described above. Base-case results at steady state are shown in Table 3.

Table 3.

Model predictions for mitochondria in vivo

	Qo2*, nmol O2·mg−1·s−1	GATP*, nmol ATP·mg−1·s−1	P/O	pmf, mV	[ATP]c, mM	[ATP]c/[ADP]c
Base case
Po2 = 50 mmHg, pHc = 7.20	2.49	10.05	2.02	172.76	2.51	10.94
Variations in Po2
Po2 = 60 mmHg	2.49	10.05	2.02	173.12	2.51	11.10
Po2 = 20 mmHg	2.48	10.06	2.03	169.75	2.47	9.47
Po2 = 10 mmHg	2.46	10.07	2.05	164.93	2.35	6.44
Variations in QATP
QATP × 0.75	1.93	7.52	1.95	173.52	2.54	12.84
QATP × 1.25	3.05	12.59	2.06	172.02	2.43	8.24
QATP × 1.50	3.61	15.12	2.09	171.14	2.18	4.43
Variations in pHc
pHc = 7.40	2.47	10.06	2.04	175.54	2.40	7.48
pHc = 7.00	2.52	10.04	1.99	169.06	2.57	14.49
pHc = 6.80	2.57	10.02	1.95	164.55	2.58	16.06
Variations in [K+]c
[K+]c = 60 mM	2.42	10.08	2.08	172.84	2.52	11.92
[K+]c = 140 mM	2.53	10.04	1.99	172.70	2.50	10.48
Variations in [Mg2+]c
[Mg2+]c = 0.2 mM	2.49	10.05	2.02	172.71	2.45	8.66
[Mg2+]c = 0.8 mM	2.49	10.05	2.02	172.89	2.57	14.74
Variations in H+ and K+ leak permeability
PH,leak = 0, PK,leak = 0	2.25	10.15	2.25	173.82	2.52	11.39
PH,leak = 0, PK,leak × 1	2.40	10.09	2.10	173.17	2.51	11.12
PH,leak = 0, PK,leak × 10	3.52	9.64	1.37	168.69	2.45	8.78
PH,leak × 10, PK,leak = 0	3.08	9.82	1.59	169.96	2.47	9.58
PH,leak × 10, PK,leak × 1	3.21	9.77	1.52	169.50	2.47	9.33
PH,leak × 10, PK,leak × 10	4.17	9.38	1.13	165.87	2.38	7.05

[ADP]_c, cytoplasmic ADP concentration; [ATP]_c, cytoplasmic ATP concentration; [ATP]_c/[ADP]_c, ratio of [ATP]_c to [ADP]_c; G_ATP, ATP generation; [K⁺]_c, cytoplasmic K⁺ concentration; [Mg²⁺]_c, cytoplasmic Mg²⁺ concentration; pH_c, cytoplasmic pH; P_H,leak, H⁺ leak permeability; P_K,leak, K⁺ leak permeability; pmf, proton motive force; P/O, amount of ATP produced by F₀F₁-ATP synthase per oxygen atom reduced by the respiratory chain; Q_ATP, rate of ATP hydrolysis in the cytoplasm; Qo₂, O₂ consumption.

^*Results are given per milligram mitochondrial protein.

The predicted rate of ATP generation by F₀F₁-ATP synthase, 10.05 nmol·s⁻¹·mg protein⁻¹, is equivalent to 0.823 mmol·s⁻¹·(L·cell)⁻¹, which means that ATP synthase provides 91.0% of the ATP that is hydrolyzed in the cytoplasm. Some ATP is also generated by the conversion of phosphocreatine to creatine (catalyzed by creatine kinase) and by the conversion of ADP into AMP and ATP (catalyzed by adenylate kinase).

The cytoplasmic concentration of ATP ([ATP]_c) at steady state is computed as 2.5 mM, in good agreement with measured values (1.5–2.8 mM) in rat renal tissue (23, 61). The predicted [P_i]_c (1.7 mM) also falls within the published range of values (1–10 mM) (1, 23, 32, 61), and the predicted ATP-to-ADP cytoplasmic concentration ratio ([ATP]_c/[ADP]_c), 10.9, is comparable to that measured (~9) in mouse PTs (99). Freeman and colleagues (31) reported a P/O of 1.7–2.0 for the whole kidney in vivo (32) and 2.5 in the perfused kidney, and the model value (2.0) lies within these measured values. The predicted pmf (173 mV) is also within the typical 170- to 200-mV range (25).

Renal cortical Po₂ is not limiting at the basal ATP consumption rate.

Renal tissue Po₂ varies between 50 and 60 mmHg (67–80 μM) in the renal cortex and drops to 10–20 mmHg (13–27 μM) in the renal medulla (13, 62, 88). To determine whether O₂ may be rate limiting in this range, we computed [ATP]_c/[ADP]_c as a function of mitochondrial Po₂ for different values of Q_ATP. The dependence of [ATP]_c/[ADP]_c on Po₂ and Q_ATP, as shown in Fig. 3, is qualitatively similar to that observed by Balaban et al. (4) in suspensions of rabbit cortical tubules: a decrease in Q_ATP raises [ATP]_c/[ADP]_c, whereas low Po₂ reduces [ATP]_c/[ADP]_c.

Fig. 3.

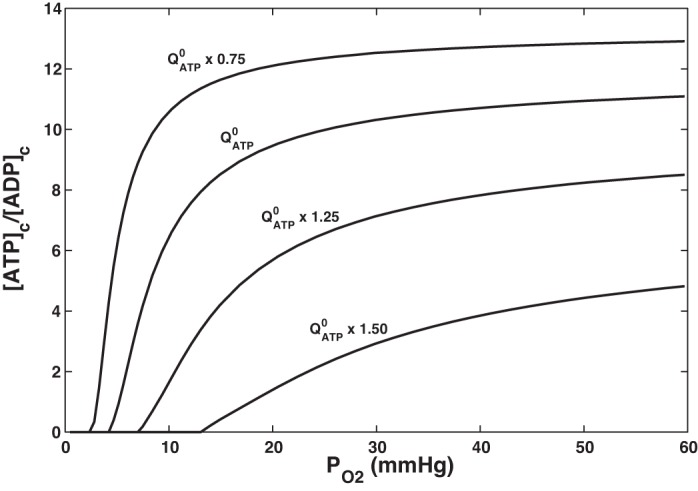
Predicted effect of Po₂ on the ATP-to-ADP cytoplasmic concentration ratio ([ATP]_c/[ADP]_c) for different rates of ATP hydrolysis (Q_ATP). ${\text{Q}}_{\text{ATP}}^{\text{0}}$ denotes the baseline value of Q_ATP. Cytoplasmic pH is set to 7.20.

At high Po₂ and low Q_ATP values, [ATP]_c/[ADP]_c exhibits a weak dependence on Po₂. At baseline Q_ATP, the predicted [ATP]_c/[ADP]_c remains > 10 if Po₂ remains >25 mmHg. Below that threshold, the concentration ratio begins to fall rapidly with decreasing Po₂ and is close to zero at Po₂ ~5 mmHg. Furthermore, at baseline Q_ATP, the predicted Qo₂ and G_ATP change very little over the physiological Po₂ range (10–60 mmHg). Toward the lower end of that interval, Qo₂ and G_ATP are maintained to the detriment of [ATP]_c, but the latter is predicted to remain >2 mM (Table 3).

We should note that Q_ATP may not be independent of [ATP]_c at lower ATP levels. The affinity of Na⁺-K⁺-ATPase for ATP is between 0.3 and 0.8 mM in most cells, and a value of 0.4 mM was measured in the rabbit PT (87). Hence, fixing the rate of ATP hydrolysis independently of [ATP]_c is a reasonable assumption, unless the latter falls below millimolar levels.

Altogether, these results suggest that renal cortex O₂ levels are not rate limiting when Q_ATP remains close to its base-case value in the proximal convoluted tubule.

Raising Q_ATP increases P/O.

The rate of Na⁺ reabsorption, which governs the rate of ATP hydrolysis, may vary substantially in the PT, depending on many hemodynamic, hormonal, and neurogenic factors. We then examined the impact of ATP consumption on Qo₂ and G_ATP at a fixed Po₂ (50 mmHg). Raising Q_ATP reduces [ATP]_c/[ADP]_c, which increases the driving force across ANT, in turn stimulating the production of ATP by F₀F₁-ATP synthase and Qo₂ (Fig. 4A). When Q_ATP was raised from 75% to 150% of its base-case value (at pH_c = 7.20), the computed Qo₂ and G_ATP doubled, and P/O increased from 1.95 to 2.09 (Table 3).

Fig. 4.

Predicted effect of ATP hydrolysis (Q_ATP) on ATP formation by F₀F₁-ATP synthase and O₂ consumption (A), P/O (amount of ATP produced by F₀F₁-ATP synthase per oxygen atom reduced by the respiratory chain; B), and the proton motive force (pmf; C) for different values of cytosolic pH (pH_c): 7.4, 7.2, 7.0 and 6.8. Po₂ is fixed at 50 mmHg.

These results can also be analyzed based on the proton circuit. Increasing Q_ATP is predicted to lower the pmf (Fig. 4C), because it stimulates ATP formation and enhances proton reentry through F₀F₁-ATP synthase; the relative contribution of proton leak pathways to H⁺ reentry then diminishes. The drop in pmf, in turn, stimulates the electron transport chain and Qo₂, since it lowers the energy required to pump protons across the inner mitochondrial membrane (11). As H⁺ leak pathways consume a smaller fraction of the pmf, G_ATP rises proportionally more than Qo₂ and their ratio (i.e., P/O) increases.

P/O decreases with decreasing cytoplasmic pH.

Cytoplasmic pH (pH_c) decreases along the PT. In rat tubules, pH_c decreased from 7.14 in early proximal convolutions to 6.87 in late proximal convolutions under free-flow conditions and from 7.26 to 7.15 when tubules were perfused with 15 mM luminal ${\text{HCO}}_3^{-}$ (71). In the next set of simulations, we varied pH_c between 7.4 and 6.8.

Lowering pH_c (at a given Q_ATP) is predicted to decrease the mitochondrial membrane potential and pmf (Fig. 4C), in accordance with the results of Wu et al. (96). This reduces the driving force across F₀F₁-ATP synthase, stimulates H⁺ pumping along the electron transport chain, and raises Qo₂ (Fig. 4A). As a result, P/O is predicted to decrease with decreasing pH_c (Fig. 4B). At baseline Q_ATP, the computed P/O is 2.04 at pH_c = 7.4 and 1.95 at pH_c = 6.8.

Effects of cytosolic potassium, magnesium, and phosphate.

In all simulations, the cytosolic and intermembrane concentrations of K⁺ are taken to be equal and fixed, and so are those of Mg²⁺. As noted above, the model accounts for the binding of K⁺, Mg⁺, and H⁺ to pertinent reactants, including ATP. Thus, varying [K⁺]_c (between 60 and 140 mM) and [Mg²⁺]_c (between 0.2 and 0.8 mM) is predicted to affect the kinetic (time-dependent) behavior of the system, but has a small impact on the steady-state values of Qo₂ and G_ATP (Table 3), as further described below.

Note first that the intracellular concentration and activity of K⁺ are significantly lower in PT cells than in myocytes (21, 26, 52, 73), and our baseline [K⁺]_c value (110 mM) may be in the upper range (16, 26, 50). Decreasing [K⁺]_c from 110 to 60 mM reduces H⁺/K⁺ exchange across the inner mitochondrial membrane (i.e., H⁺ reentry into the matrix) and raises the pmf. While this stimulates the activity of F₀F₁-ATP synthase, it also increases the electrochemical gradient against which the respiratory complexes have to pump H⁺, which acts to reduce Qo₂ and raise P/O (Table 3).

A twofold increase or decrease in [Mg²⁺]_c has a negligible effect on G_ATP, Qo₂, and P/O; it has a more noticeable effect on [ATP]_c/[ADP]_c (Table 3) since the largest fraction of the Mg²⁺ pool in the cytoplasm and mitochondria is bound to ATP (77). Similarly, if the rate of ATP hydrolysis is fixed, reducing [P_i]_c has a small impact on ATP production and Qo₂, but it shifts the [ATP]_c/[ADP]_c toward lower values, in both the cytoplasm and mitochondria (results not shown).

Impact of H⁺ and K⁺ leak pathways.

The main determinant of P/O is the conductance of H⁺ leak pathways, which shunt protons across the inner mitochondrial membrane, bypassing F₀F₁-ATP synthase. As discussed below, mitochondrial uncoupling is thought to help maintain homeostasis and reduce oxidative damage, but it may be harmful in the kidney as it elevates Qo₂ and promotes hypoxia (80).

In the absence of H⁺ leak pathways, P/O is computed as 2.10. As expected, augmenting the leak of protons into the inner matrix decreases ΔpH and the pmf, thereby raising Qo₂ while reducing ATP formation and P/O (Fig. 5). If P_H,leak is increased 10-fold relative to the base case, Qo₂ is predicted to rise by 29%, and ATP formation to decrease by 3%, yielding a P/O of 1.52. Note that if the rate of ATP hydrolysis is augmented at a given P_H,leak value, ATP formation increases more than Qo₂ (see above), and P/O is higher (Fig. 5).

Fig. 5.

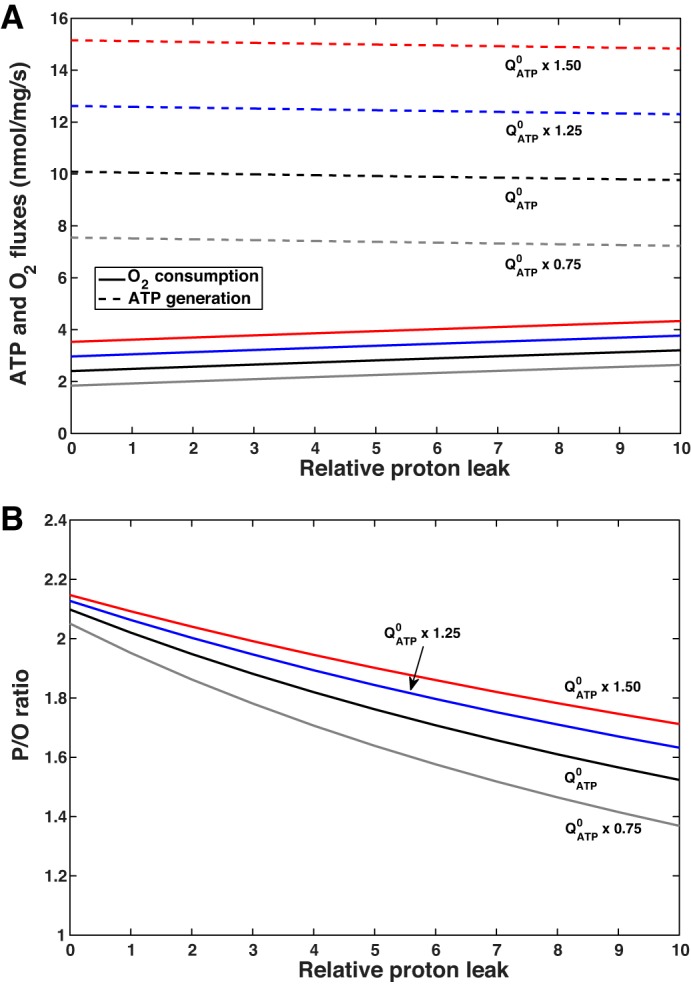
Predicted effect of proton leak permeability on ATP formation by F₀F₁-ATP synthase and O₂ consumption (A) and P/O (amount of ATP produced by F₀F₁-ATP synthase per oxygen atom reduced by the respiratory chain; B) for different values of ATP hydrolysis (Q_ATP). K⁺ leak permeability is kept constant. ${\text{Q}}_{\text{ATP}}^{\text{0}}$ denotes the baseline value of Q_ATP.

Similarly, if K⁺ leak permeability is augmented at a given P_H,leak value, K⁺ cycling across the inner membrane is enhanced, and more protons enter the inner matrix via H⁺/K⁺ exchangers, which lowers the pmf and reduces ATP formation. Conversely, Qo₂ increases slightly, since less energy is then required to pump protons across the electron transport chain complexes (Fig. 6A). Thus, P/O decreases with increasing P_K,leak, all else being constant (Fig. 6B).

Fig. 6.

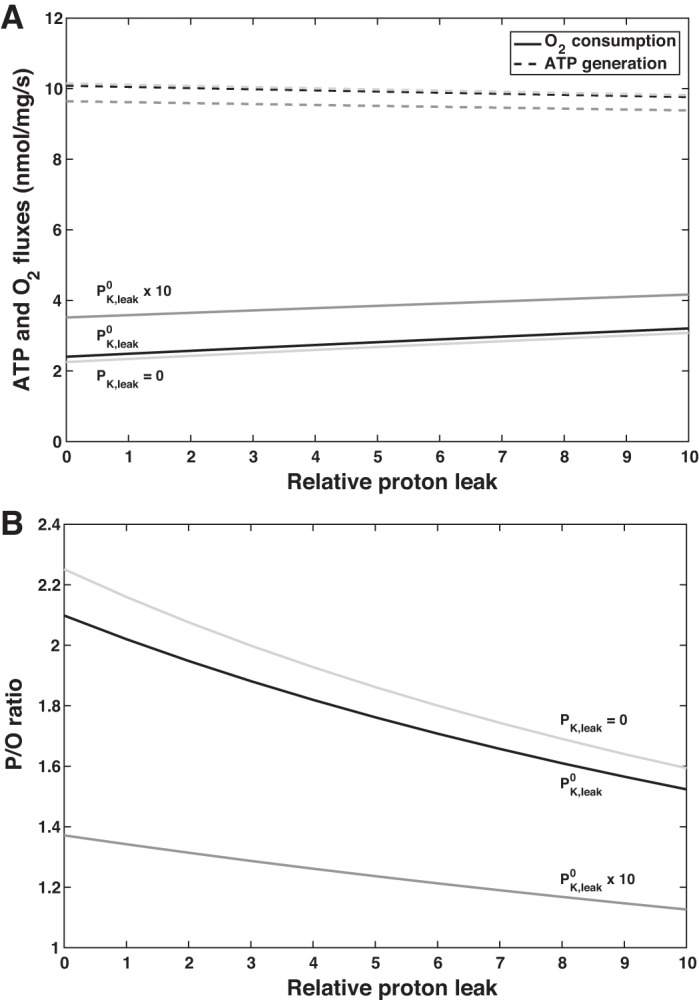
Predicted effect of proton leak permeability on ATP formation by F₀F₁-ATP synthase and O₂ consumption (A) and P/O (amount of ATP produced by F₀F₁-ATP synthase per oxygen atom reduced by the respiratory chain; B) for different values of K⁺ leak permeability (P_K,leak). ATP hydrolysis (Q_ATP) is maintained equal to the baseline value of Q_ATP (${\text{Q}}_{\text{ATP}}^{\text{0}}$). $P_{\text{K,leak}}^{\text{0}}$ denotes the baseline value of P_K,leak.

Uncoupling in diabetic PTs.

The expression of uncoupling protein (UCP)2 is enhanced in the diabetic kidney, and leak respiration is augmented (34, 67). A 50% increase in leak respiration in isolated mitochondria, as measured in diabetic rats (67), can be simulated by multiplying P_H,leak by a factor of 2.5. Per se, a 2.5-fold increase in P_H,leak is predicted to lower P/O by 5% (from 2.02 to 1.91) in mitochondria in vivo. However, other diabetes-related changes may conversely elevate P/O. Uncoupling contributes to increased Qo₂ and intrarenal hypoxia in the diabetic kidney. A 15-mmHg decrease in cortical Po₂, as previously reported in Friederich-Persson et al. (34), is predicted to very slightly raise P/O (see Table 3). In addition, increased Na⁺ reabsorption in the diabetic PT raises the rate of ATP hydrolysis, which by itself also elevates P/O (see above). Specifically, a 15% increase in Q_ATP, reflecting the measured 15% increase in ⁸⁶Rb uptake by PTs in diabetic rats (2), is predicted to raise P/O from 1.91 to 1.95. As discussed below, the present model can serve to elucidate the contribution of individual factors to altered mitochondrial metabolism in diabetes.

DISCUSSION

The goal of the present study was to develop a model of mitochondrial function in proximal convoluted tubule cells to gain more insight into the coupling between Qo₂, ATP formation, ATP hydrolysis, and Na⁺ transport in that segment. We considered the proximal convoluted tubule in isolation herein, without taking into account cross-talk with other segments and possible compensating mechanisms. For this purpose, we extended the model developed by Wu et al. (96) for cardiac tissue and skeletal muscle mitochondria. The structural parameters and concentration values of the present model were adjusted based on PT-specific measurements (Table 1). We also modified the equation that characterizes the proton leak flux (Eq. 5) and added K⁺ leak conductance (Eq. 6). With these changes, the model correctly predicted both in vitro and in vivo measurements of Qo₂, RCR, and P/O as well as ATP and P_i levels in PT cells (Table 2).

RCR is often used to assess mitochondrial function in vitro, because it encompasses three key metabolic processes, namely substrate oxidation, ATP formation, and proton leak (11). However, many factors affect RCR, including the nature of the exogenous substrate, and the concentrations of mitochondria and ATP (89). In isolated mitochondria from the rat renal cortex, RCR varies from ~4 to 9 (28, 64, 75, 78). We compared our theoretical results with the recently published in vitro measurements of Schiffer et al. (79) because experimental conditions in other studies were not fully characterized, and/or measurements related to succinate-based respiration, whereas the Wu et al. model does not account for succinate dehydrogenase (complex II).

The model predicts pmf values on the lower end of the typical 170–200 mV range (25), owing to a small contribution of the pH gradient (Eq. 4). Whereas the predicted ΔΨ is comparable to typical values (150–180 mV; see Ref. 11), the predicted ΔpH (~0.1 pH units, or 6 mV) is lower than most reported values (~0.5 pH units, or 30 mV), including indirect measurements in renal cortical tubules (1, 84). There are several possible explanations for these discrepancies. First, the mitochondrial model is based in part on the study of Bose et al. (9), who suggested that the low ΔpH values (~0.05 mV) they measured reflect the complex incubation ionic medium and higher temperature (37°C) they used. Second, accurate ΔpH measurements are difficult, owing to substantial heterogeneity within both the cytosol and mitochondria. Rieger et al. (74a) observed significant lateral ΔpH variations in HeLa cells, where the local pH at F₀F₁ dimers was 0.3 units less acidic than that at complex IV. Aw and Jones (1) ascribed inconsistencies in their data to a transcellular pH gradient within the cytosol of PT cells. Finally, theoretical analysis by Dzbek and Korzeniewski (25) suggests that the magnitude of ΔpH is strongly determined by K⁺ leak conductance. This conductance, which represents the K⁺ diffusion pathway that contributes to the cycling of K⁺ across the inner membrane (40), was not considered in the original Wu et al. model. In the present study, we assumed a small K⁺ leak conductance in PT mitochondria, as this pathway remains to be properly characterized. Moreover, the inner mitochondrial membrane expresses a variety of K⁺ channels, such as the ATP-regulated (mitoK_ATP) and Ca²⁺-activated (mitoBK_Ca) K⁺ channels that also regulate mitochondrial respiration (54). Experimental investigations of K⁺ transport pathways in renal mitochondria could shed more light on the specific impact of K⁺ on respiration in the kidney.

We should also note that Po₂ is fixed in our computations. This assumption is appropriate for the proximal convoluted tubule, which is surrounded by a dense network of peritubular capillaries that maintain Po₂ in the renal cortex at 50–60 mmHg. The simulations shown in Table 3 indicate that Qo₂ and ATP generation vary imperceptibly when Po₂ varies within the 50- to 60-mmHg range, if Q_ATP is kept constant. Taken together, our results suggest that O₂ levels are not rate limiting in the proximal convoluted tubule absent large metabolic (or pathological) perturbations.

Po₂ may drop to 10–20 mmHg in the renal medulla (88), and our recent investigation suggests that the mitochondria of medullary cells are able to adapt to their hypoxic environment because of their higher efficiency: their RCR, P/O, and O₂ affinity are higher than those of cortical mitochondria (81). Whether these adjustments result from greater abundance of TCA cycle components and/or electron transport chain complexes, as suggested by findings in porcine renal cells (91), remains to be ascertained.

The metabolic efficiency of a nephron segment is usually assessed by measuring the number of Na⁺ moles reabsorbed (T_Na) per O₂ mole consumed, often designated as the T_Na-to-Qo₂ ratio (T_Na/Qo₂). Three key factors determine T_Na/Qo₂: 1) the relative contributions of transcellular and paracellular Na⁺ transport, 2) the basal energy requirements of the cells, and 3) mitochondrial P/O. First, transcellular Na⁺ reabsorption is driven by basolateral Na⁺-K⁺-ATPase, which couples the hydrolysis of 1 ATP to the transport of 3 Na⁺ and 2 K⁺, but a significant fraction of luminal Na⁺ is passively reabsorbed across the paracellular route: ~30–50% of total T_Na in the PT (42, 43, 58, 74). Hence, the ratio of T_Na to the rate of ATP hydrolysis by Na⁺-K⁺-ATPase may differ substantially from 3. Second, not all of the ATP that is generated by oxidative phosphorylation is subsequently hydrolyzed by Na⁺-K⁺-ATPase. ATP serves to fuel other biochemical processes (including gluconeogenesis and H⁺-ATPase-mediated H⁺ secretion in the PT), and it is also generated or consumed in reactions such as the interconversion of ADP into ATP and AMP in the mitochondria and cytosol and the exchange of terminal phosphate between GTP and ATP in the mitochondria, both of which are considered in this study. Finally, some ATP is generated in the cytosol, and ATP generation in the mitochondria is not perfectly coupled to Qo₂, owing to H⁺ leak pathways. The reentry of H⁺ into the inner matrix by pathways other than F₀F₁-ATP synthase dissipates part of the pmf generated by substrate oxidation and diminishes the driving force for ATP synthesis.

The coupling between Qo₂ and ATP generation is encapsulated by P/O: the larger the H⁺ leak conductance, the smaller the P/O. In the base case, P/O is computed as 2.02. Assuming that all ATP generated by F₀F₁-ATP synthase is hydrolyzed by the Na⁺-K⁺ pump to actively transport Na⁺ and that Na⁺ transport is 40% passive and 60% active in the PT (see above), extrapolation of this P/O value yields a T_Na/Qo₂ of (1 + 0.40/0.60)(3)(2.02)(2) = 20.2, which is consistent with the reported range of 15–26 in the rat kidney (29).

Our simulations of mitochondrial function in vivo suggest that, if the levels of TCA cycle substrates and enzymes are maintained constant, P/O is strongly determined by Q_ATP (Fig. 4B). An isolated increase in Q_ATP raises P/O because it stimulates mitochondrial formation and export of ATP, thereby augmenting the fraction of the pmf that is consumed by ATP synthesis, relative to that consumed by H⁺ leak pathways. These results suggest that stimulating the activity of Na⁺-K⁺-ATPase may by itself increase the number of Na⁺ moles actively reabsorbed per O₂ mole consumed (${\text{T}}_{\text{Na}}^{\text{active}}$/Qo₂), provided that Po₂ levels are not limiting. ${\text{T}}_{\text{Na}}^{\text{active}}$/Qo₂ ratio has been assumed until now to be independent of the Na⁺ transport rate (58, 59). Overall Na⁺ transport efficiency (T_Na/Qo₂) depends not only on basolateral Na⁺-K⁺-ATPase activity but also on Na⁺ fluxes across apical transporters as well as transepithelial concentration and electric potential gradients. These driving forces vary substantially along the PT, thereby modulating local T_Na/Qo₂. Our results suggest that ${\text{T}}_{\text{Na}}^{\text{active}}$-induced variations in mitochondrial metabolism efficiency also contribute to axial heterogeneities in Na⁺ transport efficiency.

Our results also suggest that pH has a significant impact on Na⁺ transport efficiency in the PT. Pastoriza-Munoz et al. (71) reported a decrease in pH_c from the early to the late PT. Our simulations indicate that, at a fixed Q_ATP, lowering pH_c reduces the pmf; this, in turn, decreases ATP formation and P/O (Fig. 4B). In PT cells, pH_c is linked to the activity of the apical Na⁺/H⁺ exchanger (NHE3), which is itself coupled to the activity of basolateral Na⁺-K⁺-ATPase and thus to Q_ATP; in other words, the different factors (e.g., Q_ATP and pH_c) that regulate P/O and T_Na/Qo₂ in vivo are interwoven.

Since proton leak pathways partially uncouple Qo₂ and ATP synthesis, they substantially increase metabolic expenditures; yet they must serve broadly beneficial purposes given their ubiquity (22). The electron transport chain generates reactive oxygen species (ROS), such as superoxide and hydrogen peroxide, as a byproduct of oxidative metabolism. According to the “uncoupling to survive” hypothesis, H⁺ leaks act to minimize the formation of ROS by lowering the pmf (10). The present model does not include the formation of ROS, but it does predict a significant impact of H⁺ leak fluxes on the pmf (Table 3).

Mitochondrial H⁺ leaks occur via basal and inducible pathways. Basal H⁺ conductance is mostly catalyzed by ANT, independently of its ATP/ADP exchange activity (12). The inducible H⁺ conductance is catalyzed by UCPs; UCP2 is the only isoform detected in the rat kidney, where its expression is confined to the PT and medullary thick ascending limb (35). Diabetes stimulates UCP2-mediated uncoupling in the rat kidney; interestingly, blockade of diabetes-induced UCP2 regulation activates mitochondrial uncoupling via ANT (33). However, the H⁺ transport properties of these pathways remain poorly understood, and the present model does not distinguish between constitutive and inducible proton leak conductances.

Mitochondrial uncoupling is thought to help maintain homeostasis and reduce oxidative damage, but, in pathological conditions where uncoupling is enhanced in the kidney, it may be harmful since it elevates Qo₂ and promotes hypoxia (80). Our laboratory recently demonstrated that leak respiration and Qo₂ are significantly elevated, and Po₂ conversely decreased, in diabetic mice and that deletion of UCP2 lowers Qo₂ and restores intrarenal O₂ to normal levels (34). Baines and Ho (2) reported that ${\text{T}}_{\text{Na}}^{\text{active}}$/Qo₂ decreases from 10.8 in nondiabetic PTs to 8.8 in diabetic tubules, an 18% reduction that they postulated stems from increased fatty acid metabolism. Simulations using the present model indicate that, by itself, a diabetes-induced 50% increase in leak respiration, as measured in diabetic rats (67), would lower P/O (a proxy for ${\text{T}}_{\text{Na}}^{\text{active}}$/Qo₂) by 5%, but enhanced ATP consumption would attenuate this decrease. Diabetes is accompanied by hyperfiltration, hypertrophy (particularly of the PT) (92), increased flux of carbohydrate substrates into the mitochondria, and altered levels of TCA cycle enzymes (85); a decrease in mitochondrial protein content has also been observed in the diabetic mouse kidney (24). The present model may serve to assess the impact of each of these changes, in isolation and together, on mitochondrial function, when quantification of diabetes-induced changes in enzymatic and substrate content in PT cells becomes available.

In conclusion, our model of mitochondrial function in proximal convoluted tubule cells predicts that the rate of ATP hydrolysis and pH_c are essential determinants of mitochondria metabolic efficiency, as assessed by P/O. Since Na⁺ reabsorption and pH vary along the PT, these results suggest that axial heterogeneities in Na⁺ transport efficiency stem in part from axial variations in mitochondrial metabolism. Our results also suggest that P/O may be significantly modulated by mitochondria K⁺ leak pathways, which remain to be characterized in the PT. Incorporating this model into cellular models of water and solute transport along the nephron and accounting for ROS formation will allow us to gain more insight into the role of mitochondrial dysfunction in acute and chronic renal diseases (17, 39, 45).

GRANTS

This work was supported by the Canada 150 Research Chair program and by National Institute of Diabetes and Digestive and Kidney Diseases Grant R01-DK-106102 (to A. T. Layton).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.E. and A.T.L. conceived and designed research; A.E. performed experiments; A.E. analyzed data; A.E., F.P., and A.T.L. interpreted results of experiments; A.E. prepared figures; A.E. drafted manuscript; A.E., F.P., and A.T.L. edited and revised manuscript; A.E., F.P., and A.T.L. approved final version of manuscript.