Binocular 3D otolith-ocular reflexes: responses of normal chinchillas to tilt and translation

Abstract

Head rotation, translation, and tilt with respect to a gravitational field elicit reflexive eye movements that partially stabilize images of Earth-fixed objects on the retinas of humans and other vertebrates. Compared with the angular vestibulo-ocular reflex, responses to translation and tilt, collectively called the otolith-ocular reflex (OOR), are less completely characterized, typically smaller, generally disconjugate (different for the 2 eyes) and more complicated in their relationship to the natural stimuli that elicit them. We measured binocular 3-dimensional OOR responses of 6 alert normal chinchillas in darkness during whole body tilts around 16 Earth-horizontal axes and translations along 21 axes in horizontal, coronal, and sagittal planes. Ocular countertilt responses to 40-s whole body tilts about Earth-horizontal axes grew linearly with head tilt amplitude, but responses were disconjugate, with each eye’s response greatest for whole body tilts about axes near the other eye’s resting line of sight. OOR response magnitude during 1-Hz sinusoidal whole body translations along Earth-horizontal axes also grew with stimulus amplitude. Translational OOR responses were similarly disconjugate, with each eye’s response greatest for whole body translations along its resting line of sight. Responses to Earth-horizontal translation were similar to those that would be expected for tilts that would cause a similar peak deviation of the gravitoinertial acceleration (GIA) vector with respect to the head, consistent with the “perceived tilt” model of the OOR. However, that model poorly fit responses to translations along non-Earth-horizontal axes and was insufficient to explain why responses are larger for the eye toward which the GIA vector deviates.

NEW & NOTEWORTHY As the first in a pair of papers on Binocular 3D Otolith-Ocular Reflexes, this paper characterizes binocular 3D eye movements in normal chinchillas during tilts and translations. The eye movement responses were used to create a data set to fully define the normal otolith-ocular reflexes in chinchillas. This data set provides the foundation to use otolith-ocular reflexes to back-project direction and magnitude of eye movement to predict tilt axis as discussed in the companion paper.

INTRODUCTION

Sensory input from the vestibular labyrinths drives ocular, postural, and autonomic reflexes that help maintain stable vision, posture, spatial perception and cerebral perfusion during head rotations, translations, and tilt orientations encountered during every day activities (Carey and Della Santina 2005; Leigh and Zee 2006; Priesol et al. 2014; Valko et al. 2012; Yates and Miller 1994; Zhu et al. 2007). In mammals, the anterior, posterior, and horizontal semicircular canals sense head rotation, while the utricle and saccule (collectively called the otoconial or otolith end organs) sense gravitoinertial acceleration (GIA), which is the vector sum of gravitational and translational accelerations acting on the head. Canal signals encoding head rotational acceleration and velocity provide input to the three-dimensional angular vestibulo-ocular reflex (3D aVOR), which normally drives eye rotation responses that are approximately conjugate (i.e., the same for both eyes) and act to keep the images of Earth-fixed objects stable on the retinas (Carey and Della Santina 2005; Ewald 1892; Goldberg et al. 2012a). Relative to the canal-mediated 3D aVOR, the situation for otolith-ocular reflexes (OOR) is more complex and consequently less well understood. Utricle and saccule activity driven by changes in GIA drive compensatory eye movement responses analogous to the 3D aVOR, but changes in GIA can result from static tilts (reorientations with respect to Earth-vertical, which elicit an ocular countertilt response), translational accelerations [which elicit a translational VOR (tVOR)], or combinations of the two, and the eye movement response appropriate to stabilize gaze for a given peak GIA depends on which of type of head motion or reorientation occurred (Carey and Della Santina 2005; Leigh and Zee 2006).

Prior studies of ocular countertilt responses to static tilts (typically whole body reorientations about an Earth-horizontal axis that are held long enough for decay of the 3D aVOR response to the head rotation required to reorient) have been studied in many species, including lateral-eyed vertebrates (e.g., fish, frogs, mice, rabbits, chinchillas, pigeons; Cohen et al. 2001; Dickman and Angelaki 1999; Maruta et al. 2001; Migliaccio et al. 2010; Oommen and Stahl 2008; Rohregger et al. 2002), nonhuman primates (e.g., Angelaki 1998; Haslwanter et al. 1992; Paige and Tomko 1991), and humans (Collewijn et al. 1985). Most published studies report monocular and 1- or 2D countertilt responses to head tilts about a small subset of possible head tilt axes (typically the Earth-horizontal naso-occipital and/or interaural axes). Results of those studies [reviewed in Cohen et al. (2001)] indicate that the change in GIA during a static tilt about an Earth-horizontal axis elicits a compensatory ocular countertilt in both lateral- and frontal-eyed animals.

Prior studies of tVOR responses to whole body translation in lateral-eyed animals, including rabbits (Baarsma and Collewijn 1975), pigeons (Dickman and Angelaki 1999), and rats (Hess and Dieringer 1991), also focused on a limited range of head movements and primarily on monocular recordings. Those studies reported that changes in rotational eye position due to tVOR were typically <2° during peak head accelerations ranging from 0.2 to 3 m/s² (Baarsma and Collewijn 1975; Hess and Dieringer 1991) and vertical and torsional eye movements, which account for most of the response to translations along Earth-horizontal axes, compensate not for the translational shift of the visual scene but instead for the head tilt that would have yielded a similarly oriented GIA (Baarsma and Collewijn 1975; Dickman and Angelaki 1999; Hess and Dieringer 1991). This observation led to a perceived tilt model for interpretation of the tVOR in lateral-eyed animals, whereby the tVOR response to head translation is interpreted as if it were an ocular countertilt OOR to a static head tilt that would yield the same GIA as the sum of translational acceleration and gravitational acceleration. In this report, we will use the term equivalent tilt to reflect the fact that reflex responses do not require conscious perception.

Despite differing from humans in being a lateral-eyed animal with optic axes ~55° from the midsagittal plane and having no retinal foveae, the chinchilla is an attractive species for vestibular research due to its relatively large and accessible labyrinth, the large body of literature on chinchilla vestibular anatomy and physiology, and our group’s experience with prosthetic stimulation targeting the semicircular canals for aVOR restoration in this species. However, OORs have yet to be described in detail for this species, and the available data on 3D OOR of other lateral-eyed animals are insufficient to specify the relationship between observed OOR eye movements and the natural stimuli that elicit them. We sought a more comprehensive characterization that quantitatively relates six-dimensional stimuli (3D head tilt orientation and 3D translational velocity) to a six-dimensional response (i.e., the 3D angular positions or velocities of both eyes) using binocular recording along/about a higher resolution of axes. Our key motivations for this study of normal function were 1) to provide context for understanding and optimizing responses to prosthetic electrical stimulation targeting the otolith end organs, and 2) to gain insight into how the central nervous system processes vestibular input encoding changes in GIA in the setting of the two eyes having nearly perpendicular resting directions, absence of retinal foveal regions, and lack of volitional saccades.

METHODS

Scleral coil design.

Scleral coils of 3- to 4-mm diameter were custom made using 20 turns of 42-awg copper magnet wire, resulting in a torus with inner diameter of ~2 mm, outer diameter of ~4 mm, and height of ~1 mm. Two pieces of multistranded stainless steel wire (A-M Systems 793200) were soldered to each end of the magnet wire coil. The stainless steel leads were wrapped once around the perimeter of the copper coil so the point of flexion as the coil moves is purely stainless-steel wire to mitigate chances of magnet wire breaking due to repeated flexing during eye movements. The two stainless steel wires were then tightly twisted to minimize artifacts due to magnetic field flux passing between the leads anywhere other than at the copper coil. After the assembly was implanted, connectors were soldered to the stainless steel wire leads to connect to the scleral coil system for eye movements recording.

Surgical methods.

All experiments were performed using six normal adult chinchillas (Chinchilla lanigera animals Ch125, Ch128, Ch129, Ch131, Ch132, and Ch133). Surgical procedures were conducted in accordance with a protocol approved by the Johns Hopkins Animal Care and Use Committee, which is accredited by the Association for the Assessment and Accreditation of Laboratory Animal Care International and consistent with European Community Directive 86/609/EEC. Under general anesthesia (isoflurane, 1.5–5%), an adult chinchilla was fit with a head post to stabilize the head during experiments and a head cap using dental acrylic. Two scleral eye coils were implanted in each eye for 3D binocular tracking of eye movements. In each eye, two pockets were created under the conjunctiva at approximately orthogonal locations (superotemporal and anterosuperior/nasal side of the eye). Coil location was chosen to avoid injury to or restriction of extraocular muscles. Each coil was sutured to the sclera using polypropylene suture. The tightly twisted stainless steel leads of each coil were routed out of the orbit and subcutaneously to the head cap, and then, the conjunctiva was sutured closed with a fast gut suture. Each animal recovered for 10–14 days before onset of experiments.

Eye movement recording.

We recorded 3D binocular eye movements with a magnetic scleral coil system adapted from the design first described by Robinson (1963). The system uses alternating magnetic fields generated by three coil pairs, with each pair comprising two opposite faces of a cubic frame, operating at one of three different frequencies (X: 245 kHz; Y: 498 kHz; and Z: 763 kHz) and inducing one frequency component of a time-varying voltage in each of four implanted scleral coils (2 per eye). The system’s analog gain stage amplifies the induced voltage by ~100 and then filters with a passband of 24 kHz to 1.5 MHz. The resulting voltage signals from each of the four implanted coils are sampled at 25 MHz, demodulated in the digital domain using a field programmable gate array to determine the 3D axis of each scleral coil with respect to the coil frame and then averaged over every 50 ksamples to yield a net sample rate of 1 kHz per channel and peak-to-peak noise floor ≤0.024°. Before each data acquisition session, the system was calibrated using nonimplanted reference coils identical in construction and lead length to the implanted coils.

During experiments, the animal was head fixed in a plastic cylindrical enclosure with the head centered in the middle of the coil frame. All experiments were completed in total darkness to avoid visual suppression of the VOR. Eye position data were acquired with the head tilted nose-down ~50° to align the horizontal canals with Earth-horizontal (Hullar and Williams 2006) and are reported in right-hand-rule canal coordinates, where +X is anterior, +Y is out the left ear along the interaural axis, and +Z is superior along a dorsoventral axis perpendicular to Earth-horizontal and to the mean plane of the horizontal semicircular canals. To confirm proper calibration of the coil system and to ensure that scleral coil implantation did not result in limitation or distortion of eye movements, each animal’s 3D aVOR responses in darkness to 1 Hz, 20°/s peak sinusoidal rotations about the left-horizontal/right horizontal, left-anterior/right-posterior (LARP), and right-anterior/left-posterior (RALP) axes were measured and found to have gains and phases consistent with data we have published previously (Migliaccio et al. 2010) for the 3D angular VOR of normal chinchillas (data not shown).

Motion paradigm.

We employed a six degree of freedom (DOF) motion platform (6DOF2000E; Moog) to deliver linear accelerations and static whole body tilts along/~21 different axes in 3D canal coordinates (Figs. 1 and 2). Before we began collection of data for normal tVOR and ocular counter tilt, the motion platform was programmed to deliver 0.5-, 1-, and 2-Hz sinusoidal rotations about the Yaw, Pitch, Roll, LARP, and RALP axes at peak 20 and 30°/s. For comparison to an existing database of aVOR responses previously recorded from normal chinchillas (Della Santina et al. 2007; Migliaccio et al. 2005), we used this measurement as a baseline to ensure the eyes were not tethered from the scleral eye coil surgery. After we ensured normal aVOR responses, data collection proceeded with translations and static tilts.

Fig. 1.

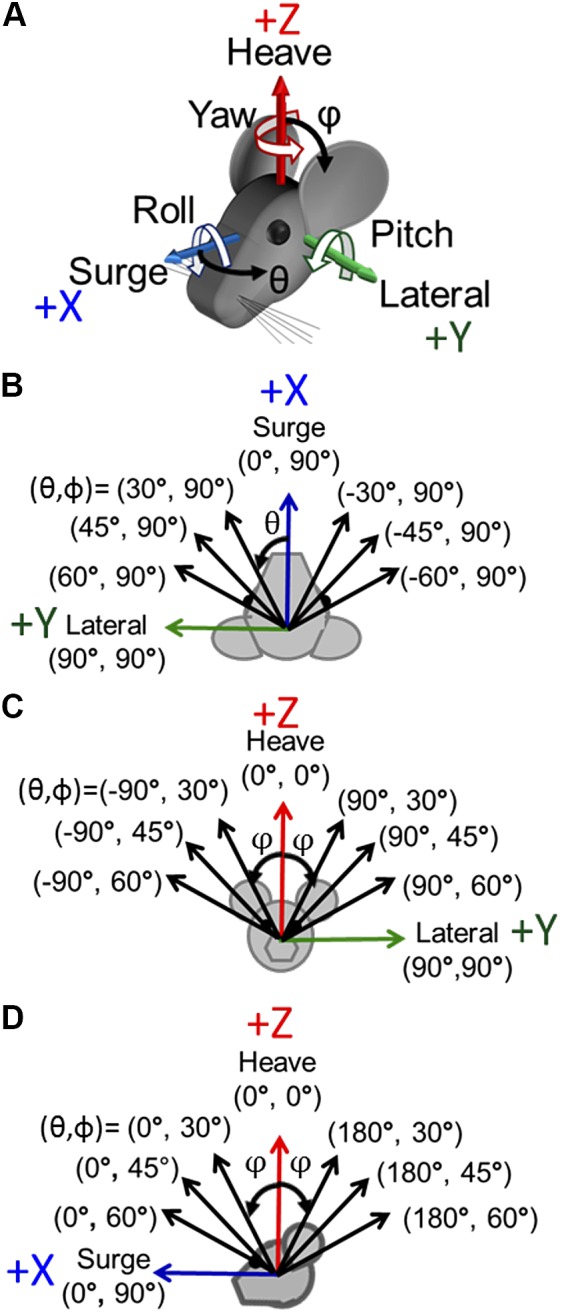
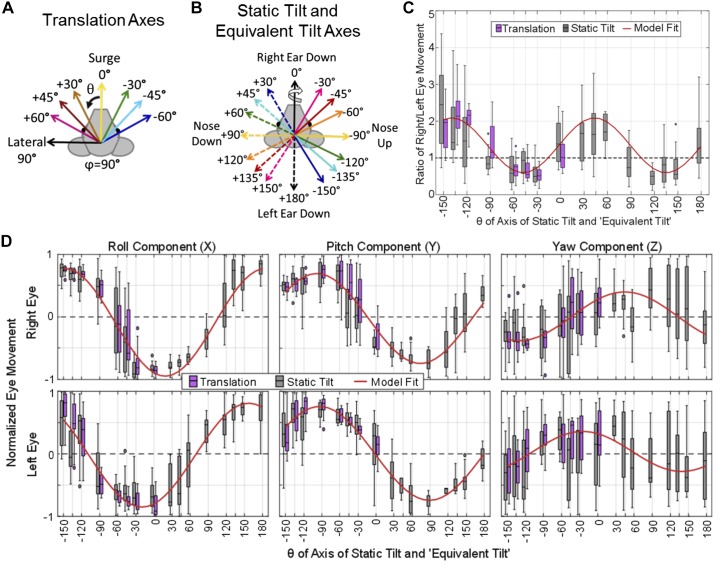
Axes of sinusoidal translations for characterization of the 3-dimensional translational vestibulo-ocular reflex. A: the chinchilla was oriented ~50° nose-down to put the horizontal canals approximately in the Earth-horizontal plane (Hullar and Williams 2006). The +X, +Y, and +Z axes of the coordinate system shown correspond, respectively, to (θ, φ) = (0°, 90°), (90°, 90°), and (0°, 0°). For translation along an axis, those 3 cardinal axes represent surge (fore-aft, positive anterior), lateral (interaural, positive leftward), and heave (up-down, positive up). For rotations about an axis, the same 3 axes represent roll, pitch, and yaw, respectively, with positive rotations defined by a right-hand rule (curved white arrows). B–D: sinusoidal translation stimuli at 1 Hz were delivered along each of 8 axes in the Earth-horizontal plane (B), 8 axes in the coronal plane (C), and 8 axes in the sagittal plane (D). Note that in spherical coordinates, θ is the azimuth referenced to +X, φ is the always-positive polar angle referenced to +Z, and (90 – φ) is the elevation from the XY plane.

Fig. 2.

Axes of whole body static tilts, viewed from above. Whole body static tilt reorientations were completed about these 16 Earth-horizontal axes (via right-hand-rule rotations). All tilts were 20° from horizontal held for 40 s before a return to the starting orientation. The rotation to get to and return from the tilt orientation was 4°/s for a 5-s duration.

The motion platform’s peak acceleration, velocity, and position limits constrained our choice of translation and tilt stimuli. To collect tVOR during translations in the full 3D space, we programmed the motion platform to deliver 1-Hz sinusoidal translations along all of the axes illustrated in Fig. 1. Each direction is shown in spherical coordinates, where azimuth θ ranges over [−180, +180] and polar angle φ, which ranges over [0, +180], is the polar angle as measured from the +Z (i.e., dorsal and superior) axis. In this coordinate system, (θ, φ) = (0, +90) points anteriorly/nasal along +X; (+90, +90) points left along +Y; and (0, 0) points superiorly along +Z. Note that as implied in Fig. 1, the chinchilla’s head was pitched relative to the coil system so that the horizontal semicircular canal plane was approximately Earth-horizontal at the outset of each trial (i.e., the horizontal canals’ axes were approximately Earth-vertical and parallel to the +Z axis [(θ, φ) = (0, 0)]). Sinusoidal translation peak acceleration was 1, 2, and 3 m/s² for translations in the Earth-horizontal plane (i.e., for φ = 90) and 2 m/s² for sagittal, coronal, and oblique plane translations.

A frequency sweep of whole body translations was conducted along the surge: front/back initially along the +x-axis (θ, φ) = (0, +90) and lateral: left/right initially along the +y-axis (θ, φ) = (+90, 0). The motion platform’s peak acceleration varied for different frequencies as shown in Table 1.

Table 1.

Peak sinusoidal translational acceleration varied as a function of motion axis and frequency due to motion platform limitations

Frequency, Hz	Peak Acceleration, m/s2	Peak Velocity, m/s	Peak Displacement, m	Peak GIA Tilt Angle,* °
0.1	0.07	0.11	0.35	0.41
0.2	0.1, 0.2, 0.3	0.08, 0.16, 0.24	0.13, 0.25, 0.38	0.58, 1.17, 1.75
0.4	0.5, 1	0.20, 0.40	0.16, 0.32	2.9, 5.8
0.5	1	0.32	0.20	5.8
0.6	1, 1.5	0.27, 0.40	0.14, 0.21	5.8, 8.7
0.8	1, 2	0.20, 0.40	0.08, 0.16	5.8, 11.5
1	1, 2, 3	0.16, 0.32, 0.48	0.05, 0.10, 0.15	5.8, 11.5, 17.0
2	1, 2, 3	0.08, 0.16, 0.24	0.01, 0.03, 0.04	5.8, 11.5, 17.0
3	1, 2, 3	0.05, 0.11, 0.16	0.01, 0.01, 0.02	5.8, 11.5, 17.0

^*Gravitoinertial acceleration (GIA) tilt angle values listed are for translations along Earth-horizontal axes (polar angle φ = 90°); translations along other directions at the same frequency and peak translational acceleration along non-Earth-horizontal axes with 0 ≤ φ ≤ 90° are smaller that equal to tan⁻¹[Asin(φ)/(g + Acos(φ)], where A is peak translational acceleration in m/s² and g = 9.8 m/s².

Whole body static tilts were executed for 40-s duration about the 16 axes shown in Fig. 2. The axis of tilt is depicted using the right-hand rule, as the example arrow on the black “Right Ear Down” vector illustrates. Due to angular position limitations of the motion platform, the maximum angle achievable for static tilt was 20° from Earth horizontal.

The hexapod motion platform’s six linear actuators are inaudible (to the authors) above the platform’s cooling fan noise when stationary but acoustically noisy during any platform motion. We did not attempt to deafen the animals, plug their ears, play masking sounds, or otherwise prevent animals from detecting sound generated by the motion platform, which could therefore provide a nonvestibular cue informing the animal that the platform is moving. However, the arrangement of the six actuators below the platform, the fact that all move during every platform motion, and the reverberant acoustics of the metal-walled chamber in which experiments occurred combined to make the platform’s sounds similar enough for all translations and rotations about all axes.

Eye movement analysis.

We developed a custom data analysis software package in MATLAB (MathWorks, Natick, MA) that employs methods of rotational kinematics previously described by Haslwanter (1995) and Migliaccio and Todd (1999). In brief, for each of the four scleral coils, the coil system demodulated the coil voltage into its three dominant frequency components, which represented the X, Y, and Z components of the coil’s axis with respect to the field col frame. Data from the two scleral coils per eye were first mathematically orthogonalized to account for variability in placement on the scleral surface (Migliaccio et al. 2004). For static tilt eye responses, the average eye rotation vector for the final 5 s of the tilt was calculated and used to represent the final ocular countertilt position. For translations, the orthogonalized data were converted to rotation vectors and then to angular eye velocity vectors. Each binocular component of angular eye velocity (R_X, R_Y, R_Z, L_X, L_Y, L_Z) was fit with a single frequency discrete Fourier transform at the frequency of translation. The axis of eye velocity was determined based on the value of the eye velocity at peak positive acceleration defined by the right-hand rule. Example data analysis steps are shown in Fig. 3 and discussed below in results. Additionally, each component of eye movement was fit with a nonlinear mixed-effect model, incorporating fixed effects and random effects (Bolker et al. 2009).

Fig. 3.

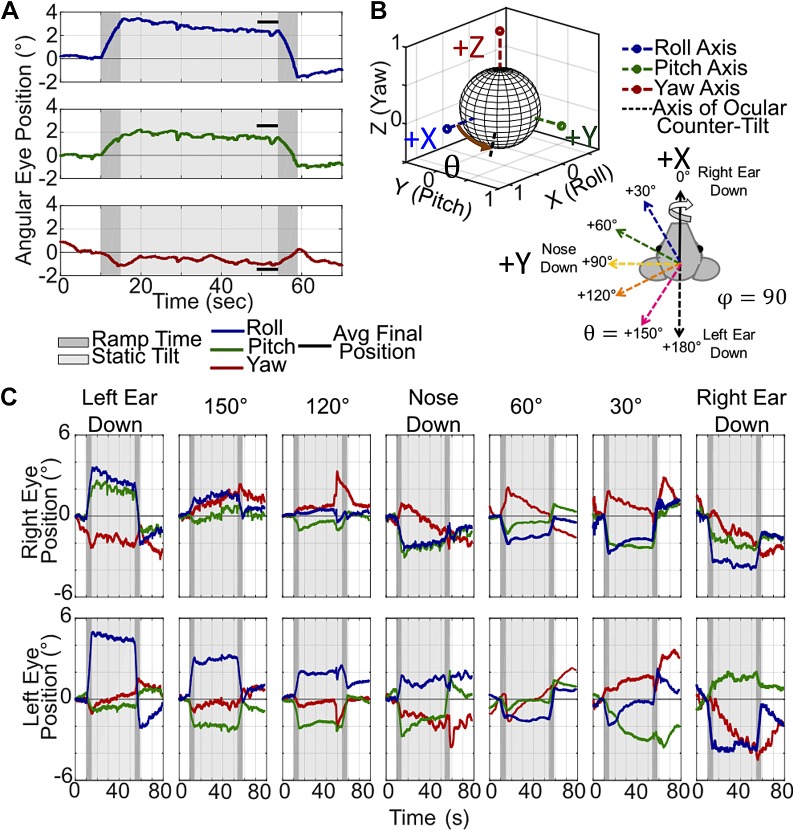
Example ocular countertilt responses recorded during 20° from horizontal tilts. A: example left eye position during a left ear down tilt. The time during the ~4°/s rotation to reach the static orientation is shaded in dark gray, and the time during the static tilt in light gray. The final ocular countertilt position is calculated by averaging each component over the last 5 s in the tilted orientation, indicated by solid black lines near the eye movement traces. B: the final ocular countertilt position can be plotted in 3 dimensions, shown with the black dashed line. C: example ocular countertilt responses during static tilts about 7 of the 16 different axes. The magnitude of each component of the ocular countertilt data changes as the tilted orientation of the animal changes from left ear down to right ear down.

To test for systematic variation between animals, a nonparametric Kruskal-Wallis test was run for each combination of factors eye (left or right), stimulus type (tilt or translation), stimulation axis (X, Y, and Z values for that axis), and eye movement response component (roll, pitch, or yaw). If a Kruskal-Wallis test result was significant (P < 0.05), we performed a set of post hoc nonparametric, pairwise rank sum tests. A pairwise significant difference (P < 0.05) between animals occurred in 147 out of 3,330 (4.4%) pairwise comparisons. This is approximately the 5% fraction we would expect purely by chance if there is, in truth, no systematic variation between animals for this data set. We therefore pooled data across animals for study of other factors.

RESULTS

The 3D binocular eye movements during angular rotations, whole body static tilts, and 1-Hz translations along all axes shown in Fig. 1 in the horizontal, sagittal, and coronal planes were collected from six normal chinchillas. The frequency sweep data were collected from five normal chinchillas.

3D binocular ocular countertilt.

Examples of the ocular countertilt to 20° tilts about Earth-horizontal axes, each starting from Earth horizontal and held for 40 s duration, are shown in Fig. 3. Figure 3A shows an example from the left eye during a left-ear-down static tilt (a tilt about the 180° axis). To plot this eye movement in 3D, as shown in Fig. 3B, the average over the final 5 s of the ocular countertilt (indicated in Fig. 3A) for each component of eye movement was used to create a 3D vector to represent the final ocular countertilt position. By the end of the 40-s tilt, it can safely be assumed that there are no influences of the angular rotation to achieve the static reorientation with position traces from semicircular canal movement returning to starting position within 2–3 s of the end of the angular rotation. Figure 3C shows right and left eye position recorded during static tilts about seven Earth-horizontal axes. As the axis of the static tilt changes from left-ear-down to right-ear-down, the progression of the magnitude and direction of each component of eye movement changes to account for the change in GIA. Overall, the roll-component flips polarity moving from left to right ear down, as expected. Additionally, the pitch component moves from disconjugate at left ear down, to conjugate at nose down, and finally disconjugate again at right ear down. The yaw component shows greater variability throughout the trials, making it difficult to determine a meaningful interpretation of the yaw data from these examples.

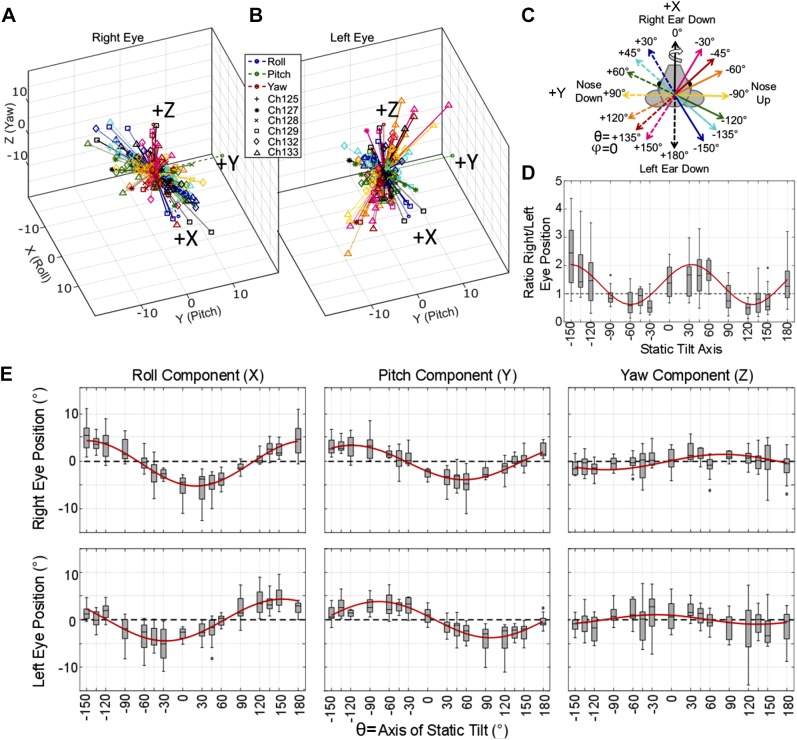
Figure 4, A and B, shows a summary of all ocular countertilt responses measured from six chinchillas during 20° static tilts about the 16 axes indicated in Fig. 4C. The direction of static tilt is determined using the right-hand rule, as shown with the arrow on the solid black “Right Ear Down, 0°” vector. Figure 4, A and B, shows the 3D vector of ocular counter tilt for the right and left eye, respectively, with vector magnitude signifying eye tilt rotation about that axis, in degrees. The same data are shown individually for every animal in Supplemental Fig. S1 (see https://doi.org/10.6084/m9.figshare.10275386). An asymmetry is apparent between the magnitude of the change in angular eye position of the right and left eye during tilts about axes aligned with the contralateral eye. For example, the right eye responses are larger in magnitude than the left for tilts about axes aligned with the left eye. Similarly, the left eye responses are larger in magnitude than the right eye responses for tilts about axes aligned with the right eye. This is further illustrated in Fig. 4D, where the ratio of right/left eye ocular countertilt position is plotted based on the tilt axis. These data show a ratio >1 (right eye is larger) for tilt axes through the left eye. A ratio <1 (left eye is larger) for the tilt axes aligned with the right eye. Tilts about the antero-posterior and interaural axes elicit right and left eye responses with similar magnitudes.

Fig. 4.

Ocular countertilt responses recorded from 6 chinchillas during static tilts. A–C: summary (A and B) of all ocular countertilt responses during the last 5 s of a 40-s whole body tilt, measured for all 6 chinchillas during 20° static whole body tilts about the 16 axes indicated in C. A and B: right eye and left eye responses, respectively, for all 6 animals, with vector direction describing the axis of eye tilt response rotation and vector length describing the angle, in degrees, of that tilt rotation response. Each animal is denoted uniquely by a marker defined in B. Each response vector is color coded to represent the stimulus tilt axis as shown in the legend in B. The direction of eye movement response is described using the right-hand rule, as shown by the curved arrow around the solid black “Right Ear Down 0°” vector in C. The data summarized across all 6 animals in A and B are shown individually for each animal in Supplemental Fig. S1 (https://doi.org/10.6084/m9.figshare.10275386). An asymmetry is seen between the magnitude of the change in angular eye position of the right and left eye during tilts with a larger change in angular eye position during tilts about axes aligned with the contralateral eye. Tilts about the naso-occipital and interaural axes elicit ocular countertilts in the left and right eye of similar magnitude. D: to further illustrate this asymmetry, a boxplot of the ratio of right/left eye ocular countertilt position is shown. E: component-wise results from all static tilts in the 6 animals is shown. Outliers larger than 3 times the interquartile range were removed for both D and E (<11 of 184 samples were removed for each plot). Nonlinear mixed-effect models were created to predict each component of eye movement and the ratio of right eye/left eye magnitude based on the tilt axis, with a fixed effect of tilt axis and a random effect of chinchilla ID number, meaning that the fit is conditional on individual animals, (Bolker et al. 2009). The fits are shown in red, with root mean square error ≤2.53 for all fits. All fit parameters are detailed in Table 2. Each axis of static tilt has sample number n ≥ 11.

Each component of eye movement from the data in Fig. 4, A and B, is plotted in Fig. 4E. During tilts that reorient the head via a negative roll from its starting orientation (i.e., bring the left ear down), the ocular countertilt shows a positive roll component for both eyes. In contrast, responses to tilts that bring the right ear down have a negative roll component. The polarity of the pitch component depends on whether the tilt axis moves the nose up or down. For pitch tilts that reorient the head in a negative pitch-tilt direction (nose up), the ocular pitch component (in head coordinate frame) for both eyes is positive. Tilts that bring the nose down elicit a negative pitch eye movement.

A nonlinear mixed-effect statistical model of the static tilt data from five of the chinchillas (1 animal was eliminated from the model due to an incomplete data set) predicted the ratio of the magnitude of right eye angular position over the magnitude of left eye angular position, and six models were fitted to predict each component of eye movement based on the tilt axis. All models used the fixed effect (independent variable) of the tilt axis and a random effect of chinchilla ID number due to the small sample size [see Bolker et al. (2009) for review on random effects in mixed-effect models]. Each nonlinear model was fit using the equation y = a × cos(b × tiltAxis + c) + d function. Parameters a, b, c, and d are estimated by the nonlinear fit, y is the predicted value (component of eye movement or the ratio of eye position magnitudes), and tiltAxis is the angle of the axis about which the tilt occurred. Values for the root mean square error (RMSE) for each fit were all ≤2.53. The results of the model are listed in Table 2 and plotted atop the data in red in Fig. 4, D and E.

Table 2.

Model parameters to predict eye movements from tilt or translation axis

Predicted Value (y)	a	B	c	d	RMSE
Static tilt model equation: y = a × cos(b × tiltAxis + c) + d
Magnitude ratio	−0.71	1.94	114.5	1.33	0.81
Right eye X-component	4.77	1.05	158.3	−0.30	2.06
Right eye Y-component	3.61	1.03	121.5	−0.12	1.81
Right eye Z-component	−1.62	0.99	100.1	0.01	2.20
Left eye X-component	−4.39	0.99	26.5	−0.06	1.98
Left eye Y-component	3.82	1.03	78.5	−0.04	2.22
Left eye Z-component	1.00	1.14	26.7	0.03	2.53

Horizontal plane translation model equation: y = a × TranslationAmplitude × cos(b × tiltAxis + c) + d
Magnituderatio	0.36	2.03	77.5	1.41	0.55
Right eye X-component	0.79	1.01	64.3	0.005	0.66
Right eye Y-component	0.57	1.0	15.9	0.0003	0.50
Right eye Z-component	−0.41	0.99	54.6	0.001	0.61
Left eye X-component	0.68	1.03	110.4	−0.03	0.58
Left eye Y-component	0.46	1.0	−12.1	0.0	0.45
Left eye Z-component	0.39	1.01	−69.5	0.008	0.74

Model output for 2 different nonlinear mixed effect models created to predict a component of eye movement based on the fixed effect (input) of tilt or translation axis. Equations for each model are listed. Static tilt results are shown in Fig. 4. Horizontal plan translation results are shown in Fig. 8. RMSE, root mean square error.

3D binocular translational VOR.

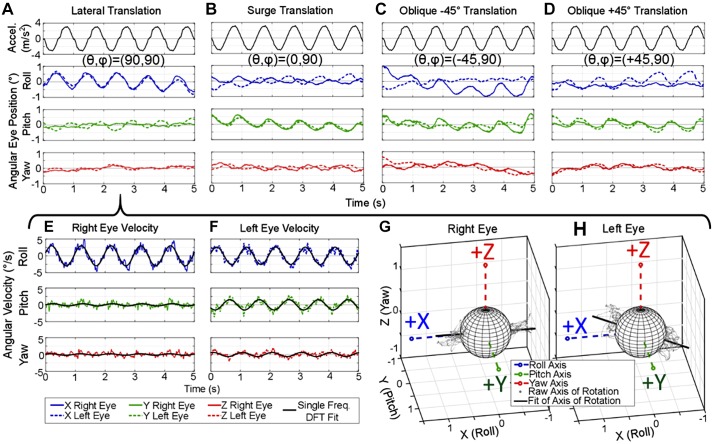
Example data traces of recorded tVOR eye movement responses to whole body translations are shown in Fig. 5. These representative right and left eye position traces recorded from one chinchilla were collected during translation along the following axes: lateral (Earth-horizontal interaural), surge (Earth-horizontal fore-aft), oblique approximately along the left eye’s resting line of sight (+45°), and oblique approximately along the right eye’s resting line of sight (−45°). Motion platform acceleration and each component of eye 3D angular position, X (Roll), Y (Pitch), and Z (Yaw) are shown in Fig. 5, A–D, respectively. Aside from analog filtering of the scleral coil signal before demodulation, these data represent the unfiltered rotation vector of eye position showing the ability of the low-noise scleral coil system to capture the small eye movements elicited during translations. The angular eye velocity for the Lateral example is shown in Fig. 5, E and F, with the single frequency discrete Fourier transform (DFT), used to fit each component of the angular eye velocity for both eyes at the frequency of the sinusoidal translation. A 3D vector of this fit represents the axis of angular eye velocity during the lateral translation and closely models the cloud of points (angular velocity at each time point during the trial) shown in Fig. 5, G and H. The lateral translation in Fig. 5A elicits a primarily conjugate roll eye movement, whereas surge translation in Fig. 5B elicits conjugate pitch and disconjugate roll. During oblique translations shown in Fig. 5, C and D, the eye along which the animal is translating has a larger magnitude than the opposite eye.

Fig. 5.

Example binocular translational vestibulo-ocular reflex (tVOR) position and velocity traces during translations along Earth-horizontal axes. A–D: eye position traces from 1 chinchilla recorded during translations alonglateral/interaural axis (θ, φ) = (90°, 90°) (A); surge/fore-aft (0°, 90°) (B); anterior-right (−45°, 90°), which is approximately along the right eye’s resting line of sight (C); and anterior-left (+45°, 90°) (D), which is approximately along the left eye’s resting line of sight. Right and left eye responses (solid and dashed lines, respectively) are shown with no postprocessing filtering, illustrating the capability of the system to record the small tVOR eye movements. E and F: the eye position for the lateral translation in A can be converted to angular velocity, as shown: each component of angular velocity is fit with a single frequency discrete Fourier transform (DFT) at the frequency of the sinusoidal translation, 1 Hz in this case. G and H: the X (roll), Y (pitch), and Z (yaw) components of the eye velocity plotted in 3 dimensions over time are shown as a cloud of gray points. These points represent the axis of angular eye velocity at each point in time throughout the trial. This cloud of points can be summarized to show the axis of angular eye velocity with the DFT fit, shown as the black line in G and H.

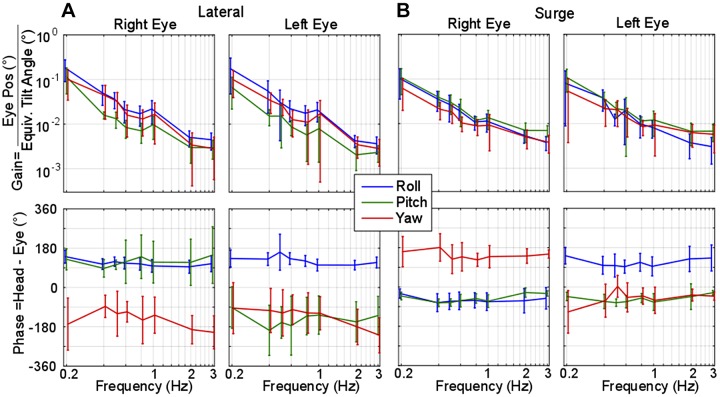
Binocular, 3D tVOR results were recorded during sinusoidal translations at frequencies ranging from 0.2 to 3 Hz with the corresponding peak accelerations listed in Table 1 and shown in Fig. 6. Gain was defined as angular eye position (in degrees) divided by the equivalent tilt angle [defined by Baarsma and Collewijn (1975) as equivalent tilt = arctan(acceleration/gravity), in degrees]. Phase was calculated as the difference between peak head acceleration and peak eye movement of the single frequency DFT, where a negative phase indicates eye movement lags head movement. Resultant tVOR during lateral translations (Fig. 6A) shows overall low-pass filter dynamics for all three components of eye position with a steep drop in gain as frequency extends beyond 1 Hz. Phase comparison between the two eyes reveals conjugate roll and yaw responses for all frequencies. Roll and pitch directions are compensatory for the change in gravity that would be sensed about the equivalent tilt axis associated with the translation direction. The pitch component was disconjugate (i.e., 180° out of phase for the 2 eyes) at all frequencies, supporting equivalent tilt theory where a lateral translation follows right-ear-down equivalent tilt. With a right-ear-down tilt, the right eye is brought closer to the ground, and thus should pitch up, while the opposite is true for the left eye.

Fig. 6.

Gain and phase of the chinchilla translational vestibulo-ocular reflex (tVOR) during lateral and surge translations. A and B: frequency sweep results during lateral (A) and surge translations (B) at 0.2–3 Hz recorded from 5 normal chinchillas. Gain is reported as the position of angular eye position in degrees divided by the equivalent tilt of the gravitation vector due to the linear acceleration [equivalent tilt = arctan(acceleration/gravity)] and plotted on a log-log scale. Steady state sinusoidal phase was calculated as the difference between peak head position and peak eye position. Negative phase indicates eye position lags head acceleration. Error bars depict one standard deviation from the mean values of either gain or phase. Lateral translations elicit a primary roll component of tVOR with a gain around 0.2; all gains decrease as frequency increases. The roll component leads head acceleration by 90° while yaw lags the head by −90 to −180°. The pitch components between both eyes are disconjugate, as expected from the equivalent head tilt theory of interpretation for tVOR. Surge translations elicit approximately equal roll and pitch gain at low frequencies, showing a decline of all gains as frequency increased. Phase values indicate disconjugate yaw and roll components while pitch was conjugate throughout all frequencies.

Figure 6B summarizes tVOR responses to surge (fore-aft) translations at frequencies from 0.2 to 3 Hz. During the forward acceleration, the apparent nose-up tilt elicits conjugate positive pitch, where the phase between both eyes remain conjugate and approximately in phase with the head acceleration. The two eyes have disconjugate yaw and roll for frequencies above 0.2 Hz, consistent with the vergence eye movement one might envision a bull makes as it pitches its head down in preparation for a charge and directs its gaze forward. The roll component is compensatory in direction for an apparent nose-up tilt (showing a positive roll in the right eye and negative in the left during forward translations, i.e., both eyes roll away from the nose).

Although gain for lateral-eyed animals tVOR has been historically defined as shown in Fig. 6, the low-pass filter nature is simply due to the choice of numerator and quotient to define a gain. Comparing (eye rotational velocity/head translational velocity), as shown in Fig. 7, illustrates how the physiologic system appears to have high-pass dynamics when the stimulus of interest is chosen to be head translational velocity (Fig. 7, bottom), suggesting that lateral tVOR eye velocity grows relative to head velocity as stimulus frequency increases. Data from rhesus monkeys, reported by Fig. 5 in Angelaki (1998), are shown atop the chinchilla responses in Fig. 7 for comparison. The gain responses for monkey torsional and chinchilla roll show similar dynamics for all three plots, while comparison of monkey and chinchilla yaw responses reveals a much larger difference, with monkey gains (or sensitivities) exceeding those of chinchillas for eye velocity re-head acceleration and velocity. This difference is likely attributable to the greater adaptive drive for monkeys (and other frontal-eyed animal species with retinal foveae) to stabilize the image of a near target on the retina despite the relative motion of the head and target during left-right head translation.

Fig. 7.

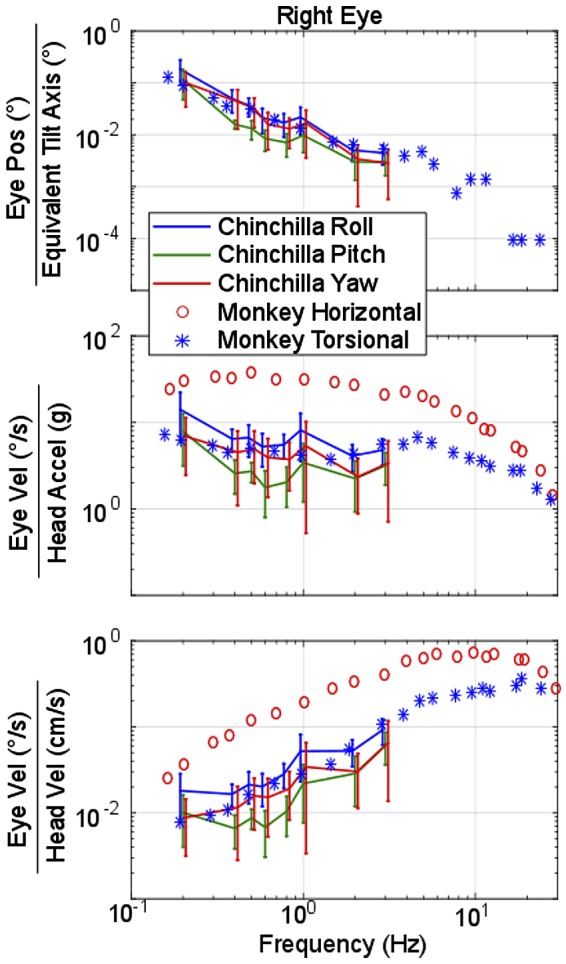
Comparison of monkey and chinchilla translational vestibulo-ocular reflex (tVOR) frequency response during lateral translation. Gain or sensitivity calculated in 3 different ways for right eye lateral translations. Top: angular eye position (°) divided by equivalent tilt angle [arctan(head acceleration/gravity)]. Middle: eye velocity (°/s) divided by head acceleration (g = 981 cm/s²). Bottom: eye velocity (°/s) divided by head velocity (cm/s). Data collected from Fig. 5 in Angelaki (1998) show the equivalent data recorded in monkeys, where the monkey horizontal (red circles) is equivalent to our chinchilla yaw (red lines) and monkey torsional (blue *) is equivalent to our chinchilla roll (blue lines). Note the similarity the roll/torsional components between species. However, the monkey horizontal response is much more robust than the chinchilla, a common difference seen between frontal and lateral-eyed animals. Error bars depict 1 SD from the mean values of either gain or phase.

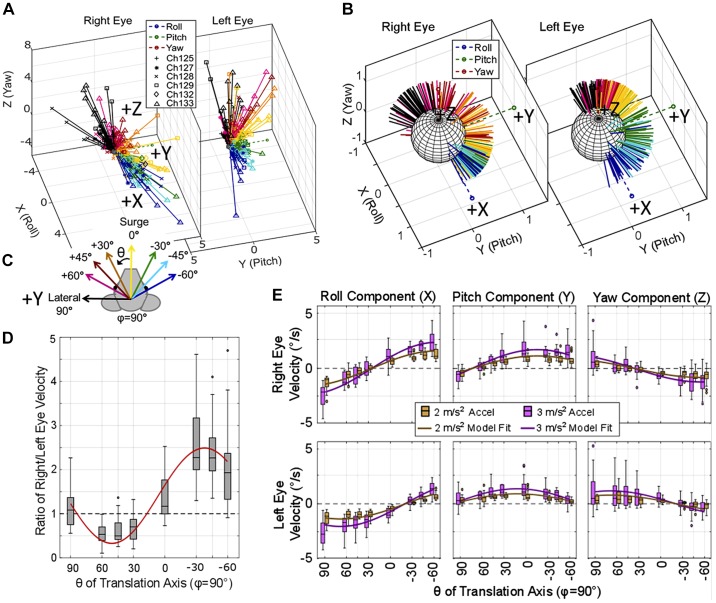
Figure 8 shows tVOR data elicited during 1-Hz sinusoidal whole body translations along eight axes in the Earth-horizontal plane from six chinchillas. Each translation was completed with peak 2 or 3 m/s² acceleration. The 3D vector of eye velocity at the instant of the peak positive acceleration (in the direction of the arrows in Fig. 8C) is represented by a 3D vector in Fig. 8A for the right and left eyes. The corresponding vectors at the peak negative head acceleration are simply the inverse of the plotted DFT fit for eye velocity during positive peak acceleration and are not pictured. Translations along axes approximately aligned with the left eye show an apparent asymmetry in the magnitude of left versus right eye velocities, with larger magnitudes in the left eye. Similarly, during translations along axes approximately aligned with the right eye, the magnitude of eye velocity in the right eye is larger than that elicited in the left (Fig. 8A). Figure 8D shows the ratio of right eye velocity magnitude/left eye velocity magnitude to further illustrate this asymmetry between the velocity magnitudes of each eye.

Fig. 8.

Translational vestibulo-ocular reflex (VOR) elicited during translations along axes in the horizontal plane. A and B: 3-dimensional axis of right and left eye velocity recorded from 6 chinchillas during translations along eight axes in the horizontal plane is illustrated (A), with the normalized vectors (B). Each vector represents the single frequency discrete Fourier transform fit of the eye velocities elicited during the positive peak of acceleration of a 1-Hz sinusoidal translation in the horizontal plane (φ = 90°) with peak 2 or 3 m/s². C: the color of the vector indicates the theta of the translation axis and the peak positive acceleration is in the direction of the arrows, as illustrated. Data for each animal are represented with the markers described in the legend in B. Translations along axes approximately aligned with the right eye’s resting line of sight (θ = −30°, −45°, −60°) produce a larger magnitude eye movement in the right eye than the left. Conversely, translations along axes approximately aligned with the left eye (θ = +60, +45, +30) elicit larger eye velocities from the left eye. D: this is further emphasized where the ratio of right/left eye velocity is shown. E: boxplots show component-wise responses grouped by θ for the eye movements elicited by both 2 m/s² (brown) and 3 m/s² (purple). Outliers greater than three times the interquartile range were removed for D and E (fewer than 16 of 257 samples were removed for each plot). Nonlinear mixed-effect models were created to predict each component of eye movement and the ratio of right eye/left eye magnitude based on the magnitude of translation and the theta of the translation axis with a random effect of chinchilla ID number. The fits for each component of eye movement during 2 and 3 m/s² translations are shown in brown and purple in E and the fit for the ratio of right/left eye velocity is shown in red in E. All model results had root means square error ≤0.74. All fit parameters are detailed in Table 2. Each axis of translation for each amplitude (i.e., each individual box and whisker plot has n ≥ 11).

Normalized data are shown in Fig. 8B to illustrate the spread of direction of eye movements from translations in the horizontal plane. Additionally, the plots in Fig. 8E show eye velocity components for each angle of translation. As the direction of translation changes, the axis of eye velocity response changes systematically in a way that best fits the expected response to an equivalent tilt rather than the response one might expect if an animal were trying to minimize retinal slip during motion of an Earth-stationary visible target near the eye and along the eye’s line of sight. The two eyes maintain a conjugate roll response during translations along the lateral (interaural) axis and when moving about the left and right eyes (+60, +45, +30 and −30, −45, −60, respectively), as might be expected if the stimulus is interpreted as an apparent head tilt. However, during surge (0°), disconjugacy is evident, with a positive roll in the right eye and negative roll in the left eye. The yaw component of eye movement does not offer compensatory direction of eye movement to the direction of head movement (where compensatory would provide an eye movement to counteract the head movement and stabilize vision). Instead, the yaw component of eye movement tends to move in the direction of the translation (i.e., a leftward translation elicits a binocular leftward yaw eye velocity).

A nonlinear mixed-effect statistical model was created to fit each component of eye movement, with fixed effects including translation amplitude and translation direction and a random effect of chinchilla ID number. The model was based on the nonlinear equation y = a × TranslationAmp × cos(b × tiltAxis + c) + d, where a, b, c, and d are model variables for the fit, TranslationAmp is the amplitude of the translation in m/s², and tiltAxis is the angle of the axis about which the static tilt occurred in degrees. An additional model was created to predict the ratio of right eye velocity magnitude/left eye velocity magnitude based on this same equation, fixed effects, and random effect. Model results are plotted atop the boxplots in Fig. 8, D and E, for each component of eye movement and the ratio of right/left eye velocities, respectively. All models created for the horizontal plane translations had a RMSE ≤0.74. The fit parameters can be found in Table 2.

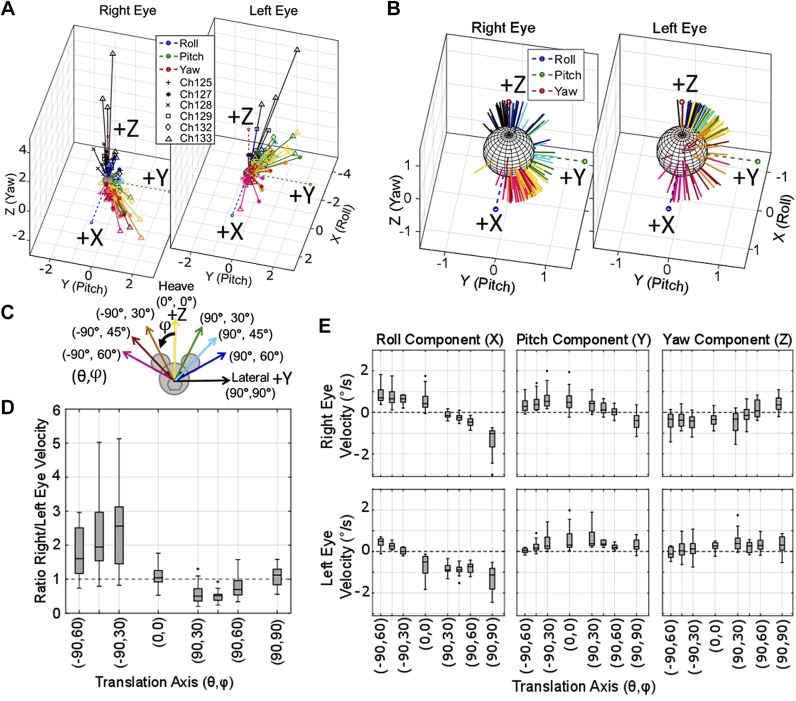
Similar data were collected for translations along axes in the coronal (Fig. 9) and sagittal (Fig. 10) planes. Figure 9 shows the tVOR during 1-Hz sinusoidal translations at peak 2 m/s² along eight axes in the coronal plane. The coronal plane tVOR, Fig. 9A shows an inequality between left and right eye velocities, similar to that seen in Fig. 8A. Translations along axes approximately aligned with the right eye elicit binocular responses with larger eye velocity magnitudes in the right eye. Comparatively, translations along axes approximately aligned with the left eye elicit responses with larger magnitudes in the left eye. This is further illustrated by the boxplot in Fig. 9D, showing the ratio of right eye/left eye velocity magnitudes. Figure 9B shows the normalized data to better visualize direction-specific characteristics related to each translation direction. The boxplot in Fig. 9E shows conjugate roll responses when the translation component along the y-axis is largest. Additionally, when translation in the z-axis dominates, i.e., (−90°, 30°), (0°, 0°), and (90°, 30°), the roll component becomes disconjugate. The pitch component of both eyes maintains conjugacy for all head translational movements except for lateral. The yaw component is more variable and smaller in amplitude than the roll and pitch.

Fig. 9.

Translational vestibulo-ocular reflex (VOR) elicited during translations along axes in the coronal plane. Binocular 3-dimensional eye velocities recorded from 6 chinchillas, elicited during 1-Hz sinusoidal translations in the coronal plane with a 2 m/s² peak acceleration. A: the binocular axes of eye velocity; normalized vectors shown in B to better visualize the spatial spread for each translation direction. B: each animal’s data are represented with the markers described in the legend. C: color of each vector indicates the translation direction as illustrated. In A, an asymmetry between the right and left eye velocity magnitude is seen, similar to that seen in Fig. 8A, where each eye’s velocity is greatest during translations along axes approximately aligned with the ipsilateral eye. D: boxplot further emphasizes the point from A, showing the ratio of right eye/left eye velocity. Translations oriented along the quadrant of the right eye (pink, red, and orange in A and B) elicit a larger right eye velocity than left (ratio>1 in D). Translations oriented along the quadrant of the left eye (green, light blue, and dark blue in A and B) elicit a larger left eye velocity than right (ratio <1 in D). E: boxplot shows component-wise eye velocities. During coronal plane translations, the eyes generally show conjugacy in all 3 components, except during heave (0°, 0°) and lateral (90°, 90°) movements. All outliers larger than three times the interquartile range for D and E were removed (fewer than 13 of 131 samples were removed for each plot). Each box for each axis has samples n ≥ 14.

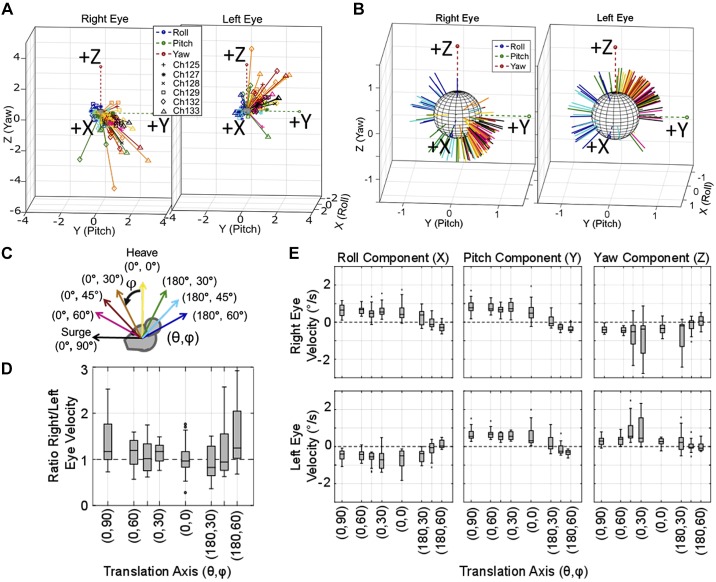
Fig. 10.

Translational vestibulo-ocular reflex (tVOR) elicited during translations along axes in the sagittal plane. A: axes of the right and left eyes, which have larger magnitudes for translations toward the front of the animals (black, pink, red, and orange) than toward the back of the animal (green, light blue, dark blue). B: normalized data are shown to visualize the spatial spread of the sagittal plane tVOR; each animal’s data are represented with the markers described in the legend. C: axis of eye velocity recorded from 6 chinchillas during 1-Hz sinusoidal translations along 8 axes in the sagittal plane with peak 2 m/s² acceleration is shown. D: a boxplot of the ratio of right eye/left eye velocity illustrates that the 2 eyes rotate at approximately the same velocity for translations in all the directions. F: the boxplot shows component-wise eye velocity for each axis of translation, illustrating that the 2 eye remain primarily disconjugate in roll and yaw, and conjugate in pitch. All outliers larger than 3 times the interquartile range for D and E were removed (fewer than 6 of 131 samples were removed for each plot). Each box plot for each axis has samples n ≥ 13.

Figure 10 illustrates the tVOR elicited by 1-Hz sinusoidal whole body translations at peak 2 m/s² along eight axes in the sagittal plane. The data in Fig. 10A show the right and left eye tVOR eye velocities elicited by the corresponding translations shown in Fig. 10C. Translations along these axes elicit binocular eye velocity magnitudes that are approximately equal between the two eyes. Figure 10B shows the normalized eye velocity vectors to visualize the directional differences between the left and right eye tVOR, which is further illustrated by the component-wise plots shown in Fig. 10E. Translations in the sagittal plane elicit disconjugate roll and yaw components and conjugate pitch. Roll and pitch components are compensatory for the equivalent tilt axis instead of the direction to maintain visual acuity during the translational acceleration. The data from both coronal and sagittal plane translations support the previously mentioned equivalent tilt theory (Baarsma and Collewijn 1975; Dickman and Angelaki 1999; Hess and Dieringer 1991).

Tilt-translation comparison.

To compare ocular responses elicited by reorientations due to static tilts and those driven by translation, the tVOR data can be interpreted according to the equivalent tilt axis (Fig. 11B) instead of the translation axis (Fig. 11A). For example, a leftward acceleration along the lateral (interaural) axis causes a deflection of the otoconial mass to the right, which is similar to the otoconial deflection during a right-ear-down tilt in the Earth’s gravitational field. Even though these two conditions differ (because the action of tilting necessarily involves a head rotation and because the net GIA’s magnitude is larger during a pure interaural translation than when the head is stationary in some tilted orientation), the concept of equivalent tilt is both an intuitive heuristic and explains tVOR responses of lateral-eyed animals reasonably well (Baarsma and Collewijn 1975; Dickman and Angelaki 1999; Hess and Dieringer 1991). Baarsma and Collewijn (1975) called this perceived tilt, but we use equivalent tilt to avoid implying that the measured responses require conscious perception. In fact, tilt perception and tilt-driven ocular responses are not identical; Merfeld et al. (2005) showed tilt perception is largely driven by canal sensation during a tilt reorientation.

Fig. 11.

Comparison of tilt versus translation eye movement data. A and B: to compare the changes in eye position elicited during static tilts to the axis of eye velocity during translations, the axes of translation (A) can be converted to equivalent tilt axes (B). The color and style of each line in A corresponds to the equivalent tilt axis of the same color and style in B. For example, a surge acceleration toward the front (solid yellow line at 0° in A) is equivalent to a tilt axis about the solid yellow at −90°, nose up in B. C and D: after adjusting the translation axes, we accounted for difference in the magnitude of eye movements between the 2 groups by taking the ratio of right eye/left eye magnitude (C) and by normalizing the data (D). C: similar pattern for tilts and translations with larger magnitude of eye movement elicited in the eye that is contralateral to the axis of the tilt (i.e., tilts about the left eye elicit larger right eye magnitudes of ocular countertilt and vice versa). D: to compare the direction of eye movements elicited from translations versus tilts, the normalized components for each case are shown, where the direction of eye movement is similar for each component between tilts and translations. Outliers larger than 1.5 times the interquartile ranger were removed (fewer than 14 of 441 samples were removed for each plot). A nonlinear mixed-effect model was created to predict each of these components (D) and the ratio of right/left eye movement (C), with fixed effects of tilt direction and type of movement (tilt or translation) and a random effect of chinchilla ID number. Model output is shown in red in C and D; model parameters are detailed in Table 3. An ANOVA of the results of this nonlinear mixed-effect models and a similar one after eliminating type of movement showed no detectable difference when a fixed effect of “type of movement” is included (P values for each model all >0.86), indicating that whether the eye movement was recorded during a tilt or translation did not play a significant role in creation of the model.

The magnitude of change in eye position during the static tilts described was larger than the magnitude of eye velocity during translation because the temporal dynamics and amplitude of the 1-Hz sinusoidal translation were quite different from a 40-s whole body static tilt. Equipment limitations prevented a linear translation of duration similar to the duration of the static tilt, so direct comparison between tilt and translation is difficult. Therefore, to eliminate the big difference between eye movement magnitudes elicited from tilts versus translations, the ratio of the right eye/left eye magnitude was used. This ratio captures and illustrates any common patterns in magnitude relationships between the right and left eyes. Figure 11C shows the ratio of right/left eye movements in response to tilts (right eye position/left eye position) and translations (right eye velocity/left eye velocity, with the translation axis adjusted to indicate axis of equivalent tilt) from all six chinchillas, illustrating a larger magnitude of eye movement in one eye during tilts (or equivalent tilts from a translation) about axes approximately aligned with the contralateral eye. The direction of ocular countertilt and tVOR were compared after normalization and after reparameterizing translation axes as equivalent tilt axes. Figure 11D shows each normalized component of binocular eye movements (angular eye position during static tilts, angular eye velocity for tVOR), illustrating obvious similarities between the direction of eye movements elicited by a static tilt and the corresponding linear translation.

A nonlinear mixed-effect model was created to forward-predict each component of eye movement (all RMSE ≤0.37°) and the ratio of right/left eye movement (RMSE = 0.64°) using fixed effects of tilt axis and type of stimulus (static tilt or translation), where axis for the translation files is the equivalent tilt axis for the translation. A random effect of chinchilla ID number is also used. The nonlinear model was fit to the following formula: y = [a × cos(b × TiltAxis + c) + d] + (e × TypeOfStimulus), where a, b, c, d, and e are all fit parameters for the model, TiltAxis is the theta of the axis about which each tilt (or equivalent tilt), and TypeOfStimulus was a binary value indicating whether the data were collected during a tilt or translation paradigm. The parameters for the fit for each normalized component of eye movement are listed in Table 3. All fits are shown in red in Fig. 11, C and D. A two-way ANOVA between the predicted data from this model using type of stimulus as a fixed effect and a similar model without the type of stimulus as a fixed effect was completed to determine the significance of the type of stimulus. The ANOVA for all components of eye movements and ratio of right/left eye movement magnitudes returned F ≤ 0.03 with all P ≥ 0.86, suggesting no detectable difference with fixed effect of type of stimulus (tilt or translation) for each normalized component of eye movement. This implies that type of stimulus (tilt or translation) did not play a significant role in fitting the models.

Table 3.

Model parameters to predict axis of tilt/translation based on grouped OORs

Predicted value (y)	a	b	c	d	e	RMSE	F Statistic	P Value
Combined tilt-translation model equation: y = [a × cos(b × TiltAxis + c) + d] + (e × TypeOfStimulus)
Magnitude ratio	−0.75	1.96	93.0	1.35	−4e-4	0.64	0.01	0.92
Right eye X-component	−0.86	1.08	−20.36	−0.06	−4.2e-5	0.28	8.87e-5	0.99
Eye Y-component	−0.72	1.04	−77.34	−0.012	0.0003	0.25	0.01	0.94
Right eye Z-component	0.39	1.02	−46.7	0.005	0.0003	0.34	0.03	0.87
Left eye X-component	−0.83	1.01	19.8	−0.01	−3.6e-5	0.28	7.18e-5	0.99
Left eye Y-Component	0.75	0.98	92.1	0.003	−2.9e-5	0.23	5.46e-5	0.99
Left eye Z-component	0.32	1.09	27.37	0.02	−3e-4	0.37	0.03	0.86

Model output for a nonlinear mixed effect model created to predict a component of eye movement based on the fixed effect (input) of translation and tilt axis and type of stimulus. The equation for the model is listed. An ANOVA of the results of this nonlinear mixed-effect model and a similar one after eliminating “TypeOfStimulus” showed no detectable difference between the 2 models (all P > 0.86), indicating that whether the eye movement was recorded during a tilt or translation did not play a significant role in creation of the model. Model results are shown in Fig. 11. OOR, otolith-ocular reflex; RMSE, root mean square error.

DISCUSSION

The data presented here corroborate trends previously reported in the literature for other lateral-eyed species while also extending the range of stimuli tested. This work makes apparent that 3D, binocular oculography is needed to fully characterize and understand responses to a given tilt or translation.

Ocular countertilt responses due to static tilts have been shown to maintain spatial orientation due to reorientation of the head with respect to gravity in both lateral- and frontal-eyed animals and humans (Cohen et al. 2001; Collewijn et al. 1985; Maruta et al. 2001; Oommen and Stahl 2008). While the direction of ocular countertilt provides compensatory response to the head reorientation, the magnitude of the ocular countertilt is smaller than ideal for chinchillas (these results and those previously collected by Migliaccio et al. (2010) and in rabbits during static tilts Maruta et al. (2001) and further supported by the gains at very low frequencies of sinusoidal translation by Baarsma and Collewijn (1975). Each component of the ocular response showed cosine dependence on the axis of the tilt angle (i.e., the azimuth angle from +X) with larger eye movements seen during tilts about axes aligned with the line of sight of the contralateral eye.

As discussed by Goldberg et al. (2012b), tVOR of humans and other primates seems to have been optimized to maintain visual acuity for targets on the retinal foveae during linear translations, especially at high frequencies. Research by Paige and Tomko (1991), Schwarz et al. (1989) and Schwarz and Miles (1991), and Angelaki (1998) and Hess and Angelaki (1999) support these observations, emphasizing the importance of fixating a visual target for generation of a robust tVOR response in monkeys. Compared with chinchillas, monkeys show larger horizontal eye velocities during lateral translations; a difference readily apparent in Fig. 7. The tVOR evidently plays a lesser role in afoveate, lateral-eyed animals such as rabbits, rats, and chinchillas, probably because they have little or no need to precisely stabilize a near target’s image on a small retinal fovea (Migliaccio et al. 2010; Walls 1942).

Our chinchilla tVOR data corroborate trends seen in previously published data in other lateral-eyed species (Baarsma and Collewijn 1975; Dickman and Angelaki 1999; Hess and Dieringer 1991) where the tVOR responses support compensation for an equivalent tilt angle based on the vector sum of acceleration and gravity instead of the translation direction. Similar to results discussed by Baarsma and Collewijn (1975) in rabbits and Hess and Dieringer (1991) in rats, the positional changes in eye movement during translation in chinchillas were very small, ~1 to 2° peak-to-peak during 1-Hz sinusoidal accelerations (Fig. 6, A–D). The chinchilla’s tVOR roll and pitch components of eye position were compensatory for apparent head tilt.

Like Baarsma and Collewijn (1975), Hess and Dieringer (1991), and Dickman and Angelaki (1999), we found that tVOR velocity results were generally well approximated by an equivalent tilt model. To refine that model, we created quantitative, eye-specific models to relate ocular countertilt eye position during tilts and tVOR eye velocity during horizontal plane translations. Simple observation of the variation in eye movement revealed a quasisinusoidal relationship between the input of tilt or translation axis and each model’s predicted output of component of eye position or velocity.

Additionally, we explored responses to translations along axes outside the Earth-horizontal plane. The ocular responses and the disconjugacy between the left and right eye observed for those stimuli maintain the trends of the apparent tilt model. However, when translating along the +Z axis, there is no longer an apparent tilt equivalent to this type of signal. The ocular responses to these types of translations, which functionally represent movements a chinchilla may make while falling or jumping, can lead to a better understanding of how the central nervous system uses input from the utricle and saccule to respond differently to translational and tilt movements. These data also provide a basis for generation of predictive models describing how the labyrinths encode changes in GIA along all three dimensions. It is not yet clear whether GIA deviations over time are decomposed into a set of mutually orthogonal components like the 3D angular VOR, for which the three canals sense three independent spatial components of head angular velocity, effectively driving three independent components of eye angular velocity that sum in a vector sense to achieve the final 3D aVOR response (Cohen et al. 1964; Cohen and Suzuki 1963; Suzuki et al. 1964; Suzuki and Cohen 1964). If the 3D OOR enacts a similar decomposition into three independent components, which then drive eye movement response components that combine downstream to yield a final response, then the algebra underlying that process is not readily apparent in the our data.

Understanding and emulating that process will be a necessary precursor to development of vestibular prostheses that encode tilt and translational stimuli via artificial stimulation of the utricle and saccule, analogous to canal-stimulating prostheses that have shown promise for restoration of the 3D aVOR in the setting of bilateral vestibular hypofunction [reviewed in the companion paper by Hageman et al. (2020) and Boutros et al. (2019)].

Until now, vestibular prosthesis development has focused on stimulation of the three canals with the goal of restoring the aVOR, while ignoring the utricle, saccule, and OOR. In part, this reflected the aVOR’s dominant role in stabilizing vision during head rotation, and the fact that the canals are easier targets to stimulate selectively than are the utricle and saccule. However, the initial focus on canals also reflects the existence of an extensive literature on normal aVOR eye movements elicited during head rotation and the ability to back-project the axis of electrically evoked 3D aVOR responses to infer the relative degree of activity on the three canal’s ampullary nerves in an ear receiving prosthetic stimulation (Cohen and Suzuki 1963; Fridman et al. 2010; Suzuki et al. 1964; Suzuki and Cohen 1964). Better understanding how natural eye movement responses relate to head orientation, translation, and rotation stimuli in 3D therefore will not only provide insight on how the central nervous system encodes these stimuli but will also support progress toward effective vestibular implants able to provide useful input not only to the semicircular canals but also to the utricle and saccule.

In conclusion, we characterized binocular 3D otolith-ocular responses of chinchillas. Ocular countertilt responses showed a compensatory roll and pitch eye movement for changes in whole body static reorientation. The translational VOR elicited changes in eye position that were small compared with countertilt responses, and the relationship between tVOR eye rotational velocity and head linear acceleration exhibited low-pass dynamics. To a first approximation, roll and pitch tVOR velocities were compensatory in direction for the change in GIA that would result from a head tilt toward the axis of translation. However, the magnitude of eye movements differed for the two eyes, particularly when the axis along which the head translated was nearly parallel to the resting line of site for one eye.

GRANTS

This work was supported by National Institute of Deafness and Other Communications Disorders Grants (NIDCD) Grants R01-DC-009255 and T32-DC-000023. The efforts of K. N. Hageman and M. R. Chow to develop equipment for use in this work were supported in part by NIDCD Grant R01-DC-014503.

DISCLOSURES

C. C. Della Santina holds an equity interest in Labyrinth Devices, LLC, which is working to develop a vestibular implant for clinical use through a collaboration with Johns Hopkins School of Medicine and Med-El, GmbH. The terms of that arrangement are managed in accordance with John Hopkins University policies on conflicts of interest and interaction with industry.

AUTHOR CONTRIBUTIONS

K.N.H. and C.C.D.S. conceived and designed research; K.N.H. and M.R.C. performed experiments; K.N.H., M.R.C., and D.R. analyzed data; K.N.H., M.R.C., and C.C.D.S. interpreted results of experiments; K.N.H. and M.R.C. prepared figures; K.N.H. drafted manuscript; K.N.H., M.R.C., and C.C.D.S. edited and revised manuscript; K.N.H. and C.C.D.S. approved final version of manuscript.