Trans-ethnic Meta-analysis of Metabolic Syndrome in a Multi-ethnic Study

Abstract

Genome-wide association studies (GWAS) have been used to establish thousands of genetic associations across numerous phenotypes. To improve the power of GWAS and generalize associations across ethnic groups, trans-ethnic meta-analysis methods are used to combine the results of several GWAS from diverse ancestries. The goal of this study is to identify genetic associations for eight quantitative metabolic syndrome (MetS) traits through a meta-analysis across four ethnic groups. Traits were measured in the GENetics of Non-Insulin dependent Diabetes mellitus (GENNID) Study which consists of African-American (families=73, individuals=288), European-American (families=79, individuals=519), Japanese-American (families=17, individuals=132), and Mexican-American (families=113, individuals=610) samples. Genome-wide association results from these four ethnic groups were combined using four meta-analysis methods: fixed effects, random effects, TransMeta, and MR-MEGA. We provide an empirical comparison of the four meta-analysis methods from the GENNID results, discuss which types of loci (characterized by allelic heterogeneity) appear to be better detected by each of the four meta-analysis methods in the GENNID Study, and validate our results using previous genetic discoveries. We specifically compare the two trans-ethnic methods, TransMeta and MR-MEGA, and discuss how each trans-ethnic method’s framework relates to the types of loci best detected by each method.

Introduction

Meta-analysis methods are commonly used to combine the results of multiple genome-wide association studies (GWAS) and can boost power by increasing overall sample size. Performing a meta-analysis on studies from diverse populations can begin to address the issue of whether associations present within one population are consistent over other populations. These trans-ethnic meta-analysis methods have been used to understand the role of allelic heterogeneity across diverse ethnic groups. This knowledge will be necessary for applications such as precision medicine, where correct diagnoses are tailored to the patient’s genetics and ancestry. A major benefit of meta-analysis methods is that they only require summary statistics from each GWAS rather than raw genotype data, which gives preference to meta-analysis when using publicly available resources or when privacy concerns arise.

Trans-ethnic meta-analysis methods are recent extensions of traditional meta-analysis methods designed to allow heterogeneity between studies, while also leveraging information between studies of similar ethnicity or ancestry. When performing a meta-analysis on studies from diverse backgrounds, we expect studies from similar ethnic backgrounds to have more homogeneous allelic effects, while we expect studies from diverse ethnic backgrounds to more likely have heterogeneous allelic effects. Thus, trans-ethnic methods model the between-study correlation of each variant’s effect through some metric of genetic distance.

The GENNID Study (Raffel, Robbins, Norris, Boerwinkle, et al., 1996) will be used to empirically compare four meta-analysis methods. This data set is representative of trans-ethnic effects because it consists of samples from four diverse backgrounds: African-American, European-American, Japanese-American, and Mexican-American. We compare the results of four existing meta-analysis methods when applied to the GENNID data set (Raffel et al., 1996). We compare the two standard methods, fixed effects (FE) (Stram, 2014) and random effects (RE2) (Han & Eskin, 2011) meta-analysis, along with two trans-ethnic methods, TransMeta (Shi & Lee, 2016) and MR-MEGA (Magi et al., 2017). The two trans-ethnic methods, TransMeta and MR-MEGA, are both relatively new and have not been compared to each other, either through real data application or simulation. Thus, our overarching goal is to gain a better understanding of each method’s empirical performance when applied to the GENNID data set. In particular, we will consider the validity of each test, evaluate the types of loci best found by each method in the GENNID data set, and discuss validation of each method’s observed findings from previous genetic studies.

Methods

-. Study subjects and data

The GENNID data set (Raffel et al., 1996) contains samples from Type 2 Diabetes multiplex families across four diverse ethnic groups: African-American (AA, families = 73, individuals = 288), European-American (EA, families = 79, individuals = 519), Japanese-American (JA, families = 17, individuals = 132), and Mexican-American (MA, families = 113, individuals = 610). Phenotypic information for the following metabolic traits were collected for all GENNID samples: body weight (kg), waist circumference (cm), systolic and diastolic blood pressure (mmHg), triglyceride (mg/dl), hdl cholesterol (mg/dl), fasting glucose (mg/dl), and fasting insulin (mg/dl). Genotypic data was obtained for all samples using the Infinium Multi-Ethnic Global BeadChip (v1.0) with the following number of single nucleotide polymorphisms (SNPs) passing post-genotyping quality control (QC) and a minor allele frequency (MAF) threshold of 0.01 in each ethnic group: 864,805 SNPs in AA, 704,357 SNPs in EA, 583,902 SNPs in JA, and 761,432 SNPs in MA (see Appendix A for full QC information).

Samples were phased using EAGLE2 by the Sanger Imputation Service (Loh et al., 2016). The Haplotype Reference Consortium (HRC) panel (McCarthy et al., 2016) was used to phase the EA sample, and the 1000 Genomes Phase 3 (1000G) panel (Gibbs et al., 2015) was used to phase the AA, MA, and JA samples, respectively. The choice for reference panels during phasing was based on Supplementary Table 5 of Loh et al. (2016). Since EAGLE2 cannot account for familial relatedness, the software DuoHMM was used to correct phasing switch errors based on pedigree structures (O’Connell et al., 2014). The samples were then imputed separately using Minimac3 by the Michigan Imputation Server using the HRC panel (Das et al., 2016; McCarthy et al., 2016). Since the HRC panel contains 1000 Genomes, the HRC panel was chosen to align with recommendations to use a cosmopolitan approach when imputing admixed multi-ethic populations (Howie, Marchini, & Stephens, 2011; Medina-Gomez et al., 2015). After imputation, imputed data from detected chromosomal anomalies was removed (see Appendix A). SNPs with an imputed R-squared ≥ 0.7 and MAF ≥ 0.01 were used in association analyses. Genotypes for all Mendelian errors (MEs) were blanked using PLINK1.9, and SNPs with > 2 MEs in each ethnic group were removed. Hardy-Weinberg equilibrium (HWE) checks were performed for all remaining SNPs, and variants with HWE p-value < 1e-6 were removed (Chang et al., 2015). Final SNP counts used in each ethnic group for association analyses were 13,042,663 in AA, 7,681,619 in EA, 5,495,615 in JA, and 7,907,815 in MA. Only SNPs that passed QC and had MAF ≥ 0.05 in all four ethnic groups were included in the meta-analyses (3,153,931 SNPs).

-. Association Analyses

A linear mixed-effects model (LMM) was performed separately for the EA, AA, and MA samples using GCTA (Yang, Lee, Goddard, & Visscher, 2011). The phenotypes hdl, triglycerides, waist, and insulin average were log transformed, and a rank-based inverse normal transformation was applied to the phenotypes weight, diastolic average, systolic average, and glucose average. The same transformations were applied across ethnic groups, so the effect size estimates are on the same scale. A genetic relationship matrix (GRM) was created separately for each of the three samples in LDAK using all SNPs with MAF ≥ 0.01 that were either genotyped SNPs or had Imputed R-squared ≥ 0.99 (Speed, Hemani, Johnson, & Balding, 2012). The covariates age, sex, and self-reported diabetes status (yes/no) were modeled as fixed effects in the LMM, and the effect of the GRM, K, was modeled as a random effect, g. An association p-value for each SNP was generated by testing the coefficient β_SNP = 0 for each LMM described below. The vector SNP in the equation below is the additively coded genotype for each subject at the tested SNP. The vector ϵ is additive noise due to statistical variability (modeled by ${\sigma }_e^2$), while g models the variability between individuals due to genetic relatedness (modeled by ${\sigma }_g^2$ and K). In the equation below, all underlined variables represent m × 1 vectors, where m is the number of subjects included in the LMM.

$$\underset{\_}{\mathit{\text{Phenotype}}}={\beta }_0+{\beta }_{Age}*\underset{\_}{Age}+{\beta }_{Sex}*\underset{\_}{Sex}+{\beta }_D*\underset{\_}{\mathit{\text{DiabetesStatus}}}+{\beta }_{SNP}*\underset{\_}{SNP}+\underset{\_}{g}+\underset{\_}{ϵ}$$

$\underset{\_}{g}~N\left(0,{\sigma }_g^2\cdot K\right), \underset{\_}{ϵ}~N\left(0,{\sigma }_e^2\cdot I\right)$, where ${\sigma }_g^2$ and ${\sigma }_e^2$ are estimated by GCTA

Since the validity of an LMM depends on asymptotics due to large sample size, association analysis using unconditional gene-dropping (GD) was performed in the JA sample (families = 15, individuals = 125). Unconditional GD data sets were generated using Merlin (100,000–20,000,000 simulations per SNP, Appendix B), and additive association effect sizes were found for each GD data set using phenotypes pre-adjusted for age, sex and diabetes status (Abecasis, Cherny, Cookson, & Cardon, 2001). The effect sizes from the 100,000–20,000,000 data sets per SNP were used to generate the empirical distributions of the effect size estimates and produce empirical p-values for each SNP (Appendix B).

-. Meta-analysis Methods

The summary statistics from the association analyses in each sample were combined in meta-analyses separately by phenotype using Fixed Effects (FE) (Stram, 2014), Random Effects (RE2) (Han & Eskin, 2011), TransMeta (Shi & Lee, 2016), and MR-MEGA (Magi et al., 2017). FE and RE2 were implemented using METASOFT (Han & Eskin, 2011).

The FE implementation performed by METASOFT produces an FE p-value using the typical inverse-variance weighted estimator (Stram, 2014):

$${\widehat{\beta }}_{FE,\mathcal{l}}=\frac{{\sum }_{i=1}^n\frac{{\widehat{\beta }}_{i\mathcal{l}}}{{\widehat{\sigma }}_{i\mathcal{l}}^2}}{{\sum }_{i=1}^n\frac{1}{{\widehat{\sigma }}_{i\mathcal{l}}^2}}$$

where n is the number of studies combined in the meta-analysis (n = 4 in our case), ${\widehat{\beta }}_{i\mathcal{l}}$ is the effect size estimate for SNP ℓ in study i, and ${\widehat{\sigma }}_{i\mathcal{l}}^2$ is the estimated variance of ${\widehat{\beta }}_{i\mathcal{l}}$ (found using the LMM or GD distributions). The test statistic:

$$T_{FE,\mathcal{l}}=\left({\widehat{\beta }}_{FE,\mathcal{l}}\cdot \sqrt{\sum _{i=1}^n\frac{1}{{\widehat{\sigma }}_{i\mathcal{l}}^2}}\right)$$

is distributed N(0,1) under the null hypothesis of no association and can be used to produce a p-value for testing for association at SNP ℓ (Han & Eskin, 2011). Note that FE assumes homogeneous effects between all studies and is thus ideal when all studies come from the same ethnic background.

The RE2 implementation in METASOFT produces a p-value using Han & Eskin’s corrected random effects meta-analysis method (2011). The method performs a likelihood ratio test where the likelihoods assume that the estimators, ${\widehat{\beta }}_{i\mathcal{l}}$, are normally distributed with mean β_ℓ and variance differing between the two hypotheses. The parameter β_ℓ is the expected effect size across all populations at SNP ℓ. The variance of ${\widehat{\beta }}_{i\mathcal{l}}$ is equal to ${\widehat{\sigma }}_{i\mathcal{l}}$ under H₀ and equal to ${\widehat{\sigma }}_{i\mathcal{l}}+{\tau }_{\mathcal{l}}^2$ under H₁, where ${\widehat{\sigma }}_{i\mathcal{l}}$ is the variability attributed to estimation error and ${\tau }_{\mathcal{l}}^2$ is the between study variability. This method tests the hypotheses: H₀: β_ℓ = 0, τ_ℓ = 0 vs. H₁: β_ℓ ≠ 0, τ_ℓ ≠ 0 by finding the maximum likelihood estimates, ${\widehat{\beta }}_{\mathcal{l},MLE}$ and ${\widehat{\tau }}_{\mathcal{l},MLE}^2$, and performing a likelihood ratio test of the following likelihoods (Han & Eskin, 2011).

$${\mathcal{L}}_0: {\prod }_{i=1}^n\frac{1}{\sqrt{2\pi {\widehat{\sigma }}_{i\mathcal{l}}^2}}{e}^{-\frac{{\widehat{\beta }}_{i\mathcal{l}}^2}{2{\widehat{\sigma }}_{i\mathcal{l}}^2}},{\mathcal{L}}_1:{\prod }_{i=1}^n\frac{1}{\sqrt{2\pi \left({\widehat{\sigma }}_{i\mathcal{l}}^2+{\tau }_{\mathcal{l}}^2\right)}}{e}^{-\frac{{\left({\widehat{\beta }}_{i\mathcal{l}}-{\beta }_{\mathcal{l}}\right)}^2}{2({\widehat{\sigma }}_{i\mathcal{l}}^2+{\tau }_{\mathcal{l}}^2)}}$$

Therefore, the two hypotheses can be interpreted as: H₀: no effect (β_ℓ = 0) and no heterogeneity present (τ_ℓ = 0) vs. H₁: Test for non-zero effect (β_ℓ ≠ 0) or heterogeneity between studies (τ_ℓ ≠ 0). Since RE2 models additional heterogeneity between studies through the parameter ${\tau }_{\mathcal{l}}^2$, RE2 is ideal when studies come from very diverse backgrounds or there is a strong environmental effect.

The trans-ethnic method, TransMeta, follows a hierarchical framework that incorporates a kernel matrix K into the covariance structure of the effect size estimates (Shi & Lee, 2016). The hierarchy described below is in multivariate form where every underlined element is an n × 1 vector and MVN(·, ·) is the n-dimensional multivariate normal distribution.

$${\widehat{\underset{\_}{\beta }}}_{\mathcal{l}}|\underset{\_}{{\beta }_{\mathcal{l}}}~MVN\left({\underset{\_}{\beta }}_{\mathcal{l}},{\text{Σ}}_{\mathcal{l}}\right)$$

$${\underset{\_}{\beta }}_{\mathcal{l}}|\tau ~MVN\left(\underset{\_}{0}, \tau \cdot V_{\rho }\right)$$

$$V_{\rho }=\left(1-\rho \right)K+\rho \underset{\_}{11}\text{'}$$

The vector ${\underset{\_}{\widehat{\beta }}}_{\mathcal{l}}$ contains the estimated effect sizes ${\widehat{\beta }}_{i\mathcal{l}}$, β_ℓ is the vector of true effect sizes in each study, and ${\text{Σ}}_{\mathcal{l}}=\mathit{\text{diag}}\left({\widehat{\sigma }}_{1\mathcal{l}}^2, \dots , {\widehat{\sigma }}_{n\mathcal{l}}^2\right)$. The term 1 1′ is an n × n matrix of ones, while the n × n matrix, K, describes the pairwise correlation between studies using the genetic distance metric F_st (matrix form described by the Transmeta.Fst method (Shi & Lee, 2016)). For this matrix, F_st was calculated using a pruned set of 54,431 SNPs (using PLINK1.9’s --indep-pairwise flag with 10 Mb sliding windows and LD r² = 0.2) and the R package BEDASSLE (Bradburd, Ralph, & Coop, 2013; Purcell et al., 2007). TransMeta tests the hypotheses, H₀: τ = 0 vs. H₁: τ ≠ 0, by computing Wald test p-values for the values ρ ∈ {0, 0.09, 0.25, 1}. The minimum of the four Wald test p-values is used as the final p-value for this method which is corrected for multiple testing over ρ.

The final trans-ethnic method, MR-MEGA (Magi et al., 2017), follows a meta-regression framework that includes Multi-Dimensional Scaling (MDS) axes as covariates to adjust for trans-ethnic effects between studies. The MDS axes are found from an n × n pairwise genetic distance matrix whose ijth entry is $\frac{{\sum }_{\mathcal{l}}{I}_{\mathcal{l}}{\left(p_{i\mathcal{l}}-p_{j\mathcal{l}}\right)}^2}{{\sum }_{\mathcal{l}}{I}_{\mathcal{l}}}$, where I_ℓ is the indicator function for inclusion of the ℓth variant and p_iℓ and p_jℓ are the allele frequency estimates of the ℓth variant in the ith and jth population. MR-MEGA fits a weighted least squares regression with the estimated study specific effect sizes, ${\widehat{\beta }}_{i\mathcal{l}}$, as the response variable and the inverse of the estimated variance for each ${\widehat{\beta }}_{i\mathcal{l}}$, $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\widehat{\sigma }}_{i\mathcal{l}}^2$}\right.$, as the weight for each study. Mathematically, for the ℓth variant, where I ∈ {1,2, …, n}, indexes the ith GWAS study, we model (Magi et al., 2017):

$$E\left({\widehat{\beta }}_{i\mathcal{l}}\right)={\alpha }_{\mathcal{l}}+\sum _{t=1}^T{\gamma }_{t\mathcal{l}} x_{it}$$

where x_it is the tth MDS axis. The MDS axes utilized in MR-MEGA are automatically calculated by the MR-MEGA software, and no alterations were specified for this calculation (Magi et al., 2017). One MDS axis was included in the MR-MEGA model during analyses (T = 1) given the constraint of T < n − 2 discussed in (Magi et al., 2017). The test of overall association at the ℓth variant compares the unconstrained model (equation above) to the model with α_ℓ = γ_1ℓ = ⋯ = γ_Tℓ = 0 using a likelihood ratio test. This results in a test statistic asymptotically distributed ${\chi }_{T+1}^2$ under the null hypothesis that can be used to calculate the association p-value for each variant.

Results

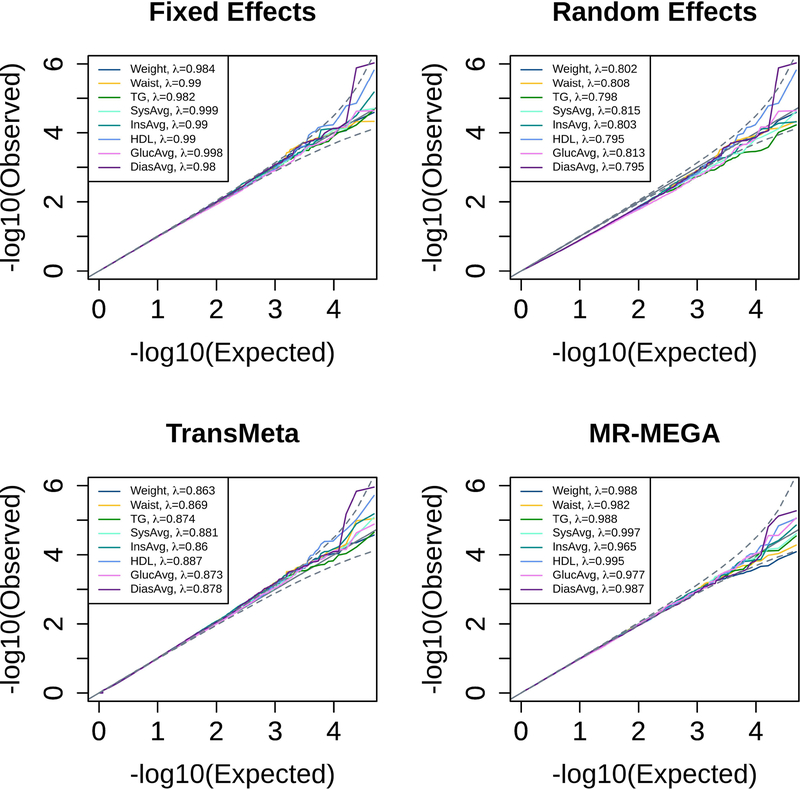
We assessed the validity of the four methods by constructing QQplots of the −log10 pvalues from a LD-pruned set of 48,624 SNPs, where these SNPs were the intersection of the list of LD-pruned SNPs used to calculate F_st and the list of SNPs included for meta-analysis (see Methods). Figure 1 shows the QQplots and inflation factors (λ) for all four methods and eight phenotypes. The expected line is shown in black with dashed black lines for the 95% confidence interval around this expectation. Figure 1 shows that the results of FE appear to be well controlled (both through the plot and λ values), while the results of RE2 appear to be deflated (maximum RE2 λ = 0.815). The λ values for TransMeta show deflation as well (maximum TransMeta λ = 0.887), and the QQplot depicts an excess of p-values equal to 1 (bottom left of TransMeta QQplot), which skews the rest of the distribution from expectation. MR-MEGA appears to be a better controlled test with slight deflation (minimum MR-MEGA λ = 0.965). Inflation factors calculated at the 10^th percentile, 1^st percentile, and 0.1^th percentile (instead of the median) for each method’s results are shown in Appendix C. These results show that FE is well-controlled using all metrics, and that the deflation observed for RE2 improves for the 1^st and 0.1^th percentile results, where we only observe slight deflation in the tail for RE2. The TransMeta results in Supplemental Table C.3 show that while the method is slightly deflated at the median, we observe slight inflation in the tail (1^st and 0.1^th percentile results). With Supplemental Table C.4, we observe slight deflation across all four metrics for MR-MEGA, illustrating this test to be slightly conservative.

Figure 1:

QQplots of −log10(p − value) for FE, RE, TransMeta, and MR-MEGA meta-analysis methods. The expected line is shown in black and confidence bands are shown in dashed black lines. All 8 phenotypes used are shown using different colored lines (legend). QQplots were generated using a genome-wide LD pruned set of 48,624 SNPs.

Table 1 summarizes the results of the four methods using a suggestive threshold of 1e − 6 and a genome-wide significant threshold of 5e − 8. The table provides the number of the 3,153,931 SNPs at least one meta-analysis method found to be suggestively significant (p − value < 1e − 6). There were 78 such SNPs in total (further information for the 78 SNPs found in Appendix D). TransMeta found the most SNPs (62 SNPs) to be suggestive (p − value ≤ 1e − 6), while MR-MEGA found the least to be suggestive (31 SNPs). Although TransMeta found more SNPs to be suggestive than FE and RE2, results among FE, RE2, and TransMeta are comparable at the genome-wide significance level (p − value ≤ 5e − 8). All methods besides MR-MEGA found at least one SNP to be genome-wide significant. Two of the three SNPs found to be genome-wide significant by TransMeta were found to be genome-wide significant by RE2, and all three genome-wide significant SNPs found by TransMeta were found to be genome-wide significant by FE. The additional SNPs found to be genome-wide significant by FE and RE2 did not overlap between the methods. TransMeta had the smallest p-value of the four methods most frequently (48 times). We notice that although MR-MEGA does not find as many SNPs to be suggestive or genome-wide significant as FE or RE2, MR-MEGA has the lowest p-value of the four methods more frequently than FE or RE2. This result appears to be driven by the fact that there was a locus detected only by MR-MEGA.

Table 1:

Summary of Meta-analyses Results

Method	Type of Effects Best Detected	# SNPs w/P≤ 1e − 6 (suggestive significance)	# SNPs w/P≤ 5e − 8 (genome-wide significant)	# of times method had the lowest P
Fixed Effects	Homogeneous Effects	47	4	11
Random Effects	Independent Effects	45	3	6
TransMeta	Trans-ethnic effects	62	3	48
MR-MEGA	Trans-ethnic effects	31	0	13

^*Table counts are found by counting how many of the 3,153,931 SNPs reached suggestive or genome-wide significance by each method. Of the 3,153,931 SNPs, 78 SNPs were found to be suggestive by at least one method. Column 5 counts the number of times each method had the lowest p-value for the 78 SNPs.

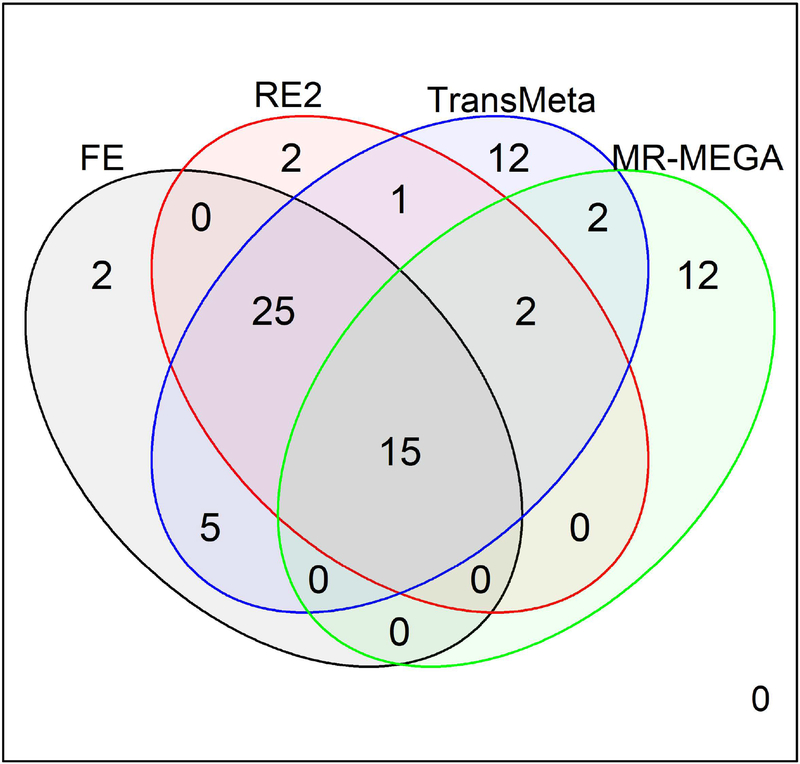
A Venn Diagram of the 78 SNPs detected by the four methods is displayed in Figure 2. We see that there is a large amount of overlap between the SNPs detected by each of the methods. FE and RE2 only found 2 SNPs each that were undetected by the other methods, while MR-MEGA and TransMeta both found 12 SNPs each that were undetected by any other method (Figure 2). Ten of the 12 SNPs detected by only MR-MEGA make up the locus that was only detected by MR-MEGA, while the additional 12 SNPs detected by only TransMeta were scattered across multiple loci.

Figure 2:

Venn Diagram of the 78 suggestively significant (p – value ≤ 1e − 6) SNPs found by the four meta-analysis methods: FE (black), RE2 (red), TransMeta (blue), and MR-MEGA (green).

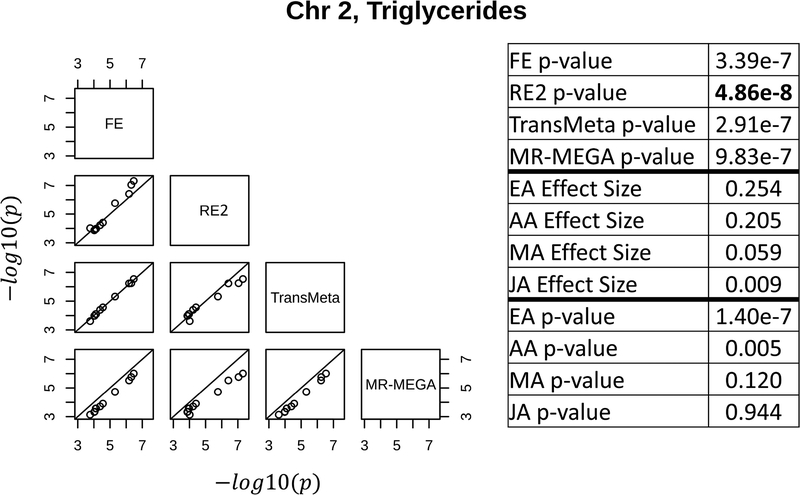
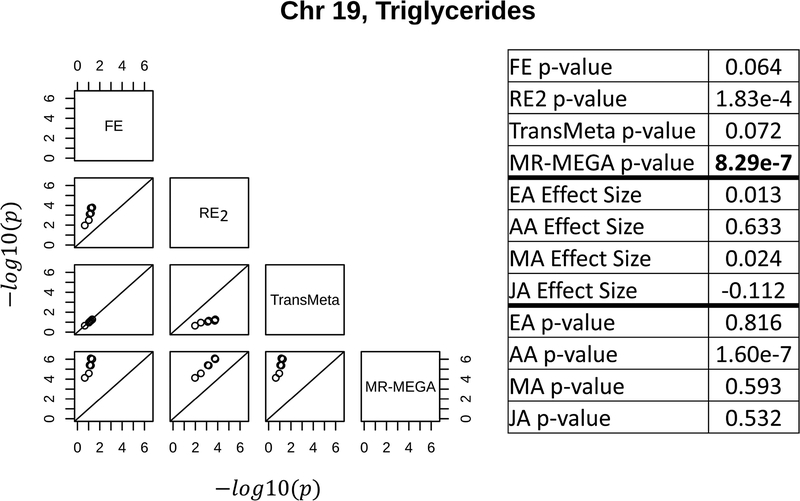
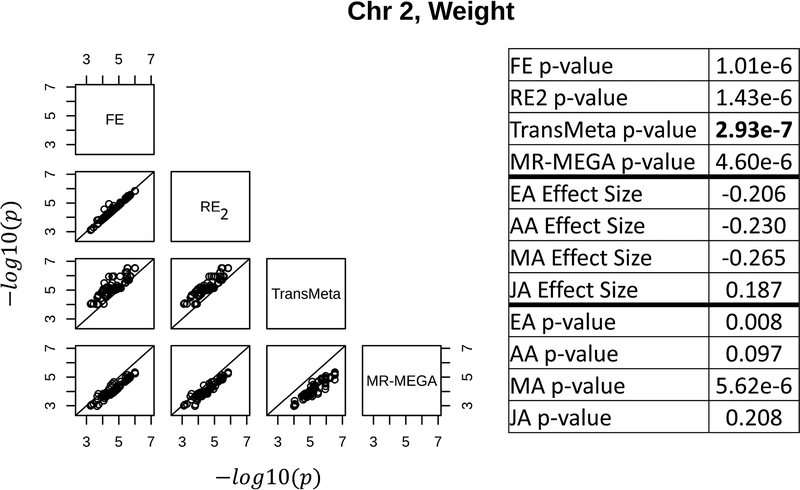
The results of the four meta-analysis methods suggest that each method may be better able to detect loci with specific types of effects (either as suggestive or genome-wide significant) than the other methods (column 2 of Table 1). The three loci shown in Figures 3, 4, and 5 depict the types of loci best captured by RE2, MR-MEGA, and TransMeta, respectively, in the GENNID data set. Figure 3 shows a locus (for triglycerides) only found to be genome-wide significant by RE2 on chromosome 2. The table in Figure 3 shows that this locus is primarily driven by the EA sample, with some moderate influence from the AA sample. We note that the effect size estimates in the EA and AA samples (0.254 & 0.205, respectively) are very different than the effect size estimates in the MA and JA samples (0.059 & 0.009, respectively) at the lead SNP in this locus. Figure 4 shows the locus (for triglycerides) detected only by MR-MEGA (p − value ≤ 1e − 6) on chromosome 19. The individual sample p-values in the table of Figure 4 show that this locus is solely driven by the association observed in the AA sample. Figure 5 shows a locus where TransMeta had the lowest p-value of the four methods (chromosome 2, weight association). The table in Figure 5 demonstrates that this suggestive locus is driven by moderate effects in the EA, AA, and MA samples. The effect size estimates in the three samples vary slightly (−0.206, −0.230, and −0.265, respectively), while the JA effects size estimate is quite different at this locus (0.187). We characterize and discuss the types of loci that appear to be best captured by each method in the Discussion.

Figure 3:

The left figure shows pairwise scatterplots of the −log10(p − value) for all SNPs with p – value ≤ 1e − 4 by at least one meta-analysis method for a locus at 27,598,097 – 28,774,081 bp on chromosome 2 associated with triglycerides (11 SNPs total). RE2 is better able to detect this locus at the genome-wide significance threshold of 5e-8 than the trans-ethnic methods (TransMeta, MR-MEGA). The right table shows the summary statistics (effect sizes and p-values) from each ethnic group for the SNP with the lowest p-value by any of the four meta-analysis methods. The meta-analysis p-values for each method are also shown for the leading SNP, with the lowest meta-analysis p-value (by RE2) in bold. Base pair coordinates are in Build 37. See Supplemental Figure S1 and Supplemental Table D.1 for more information about this locus.

Figure 4:

The left figure shows pairwise scatterplots of the −log10(p − value) for all SNPs with p – value ≤ 1e − 4 by at least one meta-analysis method for a locus at 38,030,933 – 38,097,313 bp on chromosome 19 associated with triglycerides (14 SNPs total). MR-MEGA is better able to detect the locus at the suggestive threshold of 1e-6 than TransMeta. The right table shows the summary statistics (effect sizes and p-values) from each ethnic group for the SNP with the lowest p-value by any of the four meta-analysis methods. The meta-analysis p-values for each method are also shown for this leading SNP, with the lowest meta-analysis p-value (by MR-MEGA) in bold. Base pair coordinates are in Build 37. See Supplemental Figure S2 and Supplemental Table D.1 for more information about this locus.

Figure 5:

The left figure shows pairwise scatterplots of the −log10(p − value) for all SNPs with p – value ≤ 1e − 4 by at least one meta-analysis method for a locus at 161,435,255 – 161,916,409 bp on chromosome 2 associated with weight (107 SNPs total). TransMeta is better able to detect the locus at the suggestive threshold of 1e-6 than MR-MEGA. The right table shows the summary statistics (effect sizes and p-values) from each ethnic group for the SNP with the lowest p-value by any of the four meta-analysis methods. The meta-analysis p-values for each method are also shown for this leading SNP, with the lowest meta-analysis p-value (by TransMeta) in bold. Base pair coordinates are in Build 37. See Supplemental Figure S3 and Supplemental Table D.1 for more information about this locus.

Discussion

The QQplots of the results from the four methods show that the FE meta-analysis appears to be the only method with a well-controlled Type 1 error rate when applied to the multi-ethnic GENNID data set (Figure 1). The slight deflation observed in the tail of the RE2 results (Appendix C) can likely be attributed to the small number of samples used for the meta-analysis. Han & Eskin stress in the methodological paper for RE2 that when a meta-analysis is comprised of a small number of studies, their table of pre-tabulated p-values should be used (2011). However, these pre-tabulated p-values were created based on the assumption of equal sample sizes between studies and deviations from this assumption (like in the GENNID data set) will lead to slightly conservative results (Han & Eskin, 2011). An excess of p-values equal to 1 in the TransMeta QQplot leads to deviations from the expected distribution and deflated λ values at the median (Figure 1). The authors of TransMeta have communicated that the excess of p-values equal to 1 is due to the algorithm’s use of numerical integration when generating final p-values for the method (personal correspondence). However, since we observe slight inflation in the tail of the results (Appendix C) it is unclear whether some of the significant or suggestive results found by TransMeta are spurious. Slight deflation is observed in MR-MEGA’s QQplot and by all four metrics explored in Appendix C, and this deflation can likely be attributed to the small number of samples combined in the GENNID meta-analysis (n = 4). MR-MEGA follows a weighted least squares regression framework, and it may be that four studies are insufficient to meet the assumptions of the model. Simulations and applications on MR-MEGA in Magi et al. (2017) use at least 9 studies, so we are unsure from the existing literature of MR-MEGA as to how many studies are required to produce valid results. In order to compare the results found by each method, we will assume that the suggestive and genome-wide significant results produced by each method are unlikely to be spurious for the rest of the Discussion.

As expected, we observed FE to better detect loci characterized by homogeneous effects across studies and observed RE2 to better detect loci characterized by completely heterogeneous/independent effects across studies. The locus described in Figure 3 is best described by heterogeneous effects since the effect size estimates for the MA and JA samples (MA = 0.059, JA = 0.009) are quite different from the effect size estimates in the EA and AA samples (EA = 0.254, AA = 0.205). RE2 was the only method able to declare this locus to be genome-wide significant since the other three meta-analysis methods cannot adequately accommodate completely heterogeneous effects. Even though the two trans-ethnic methods modeled as much heterogeneity between the samples as possible at the locus described in Figure 3 (ρ = 0 in TransMeta, 1 MDS axis included in MR-MEGA), the trans-ethnic methods could not capture the same effects as RE2 at this locus. This locus is located in the intronic and exonic regions of the gene GCKR, and SNPs in this region have been previously reported in multiple ethnicities for association with metabolic traits (Coram et al., 2013; Jason et al., 2017; Kamatani et al., 2010; Scott et al., 2012). The lead SNP at this locus was also found to be associated with triglycerides in the Global Lipids Genetics Consortium (GLGC) with a p-value = 2.29e-239 (Willer et al., 2013). Figure 3 shows that this locus is driven primarily by the EA samples, and this matches with the locus identified by GLGC since the consortium is made up of primarily European samples. This prior evidence supports the validity of the locus shown in Figure 3 and gives us a better understanding of how the trans-ethnic methods behave with loci characterized by heterogeneity.

While TransMeta found more SNPs to be suggestive than the other methods, the additional SNPs detected by TransMeta were typically not independent from the SNPs detected by other methods. TransMeta found more SNPs to be suggestive because it detected additional SNPs at loci not captured by the other methods. This is because TransMeta would produce slightly lower p-values than the other methods at a SNP, leading to a suggestive result by TransMeta while the other method’s p-values were only on the order of 10⁻⁶ or 10⁻⁵. However, it should again be noted that slight inflation was observed in the tail of the TransMeta distribution (Appendix C), so it is unclear whether some of the additional suggestive results found by TransMeta are spurious. Since TransMeta contains FE in its hierarchical framework, TransMeta detected most of the loci detected by FE; there was also a large overlap between the loci detected by RE2 and TransMeta (Figure 2). In addition to being able to adequately capture homogeneous and heterogeneous effects, the trans-ethnic approach of TransMeta allows it to more easily detect loci characterized by moderate trans-ethnic effects, such as the locus described in Figure 5. We define the locus described in Figure 5 as having moderate trans-ethnic effects because neither homogeneity nor complete heterogeneity is observed since the effect size estimates of the EA, AA, and MA samples are similar (EA = −0.206, AA = −0.230, MA = −0.265) and the effect size estimate of JA is quite different (JA=0.187). While the other three methods had p-values on the order of 10⁻⁶ at this locus, TransMeta was able to declare this locus as suggestively significant because it was better able to capture the moderate trans-ethnic effects seen at this locus than the other methods. While this locus was primarily driven by the MA sample in the GENNID sample, this locus showed evidence of replication in the UK BioBank (UKBB) (Mahajan et al., 2018), with the lead SNP at this locus being associated with weight in the UKBB with a p-value =1.88e-4. This passes a replication threshold of $\frac{0.05}{17}=2.94e-3$, where 17 is the number of independent loci in our results with meta-analysis p-value ≤1e − 6. Thus, there is evidence for replication at this locus in UKBB, providing support for the validity of the locus described in Figure 5.

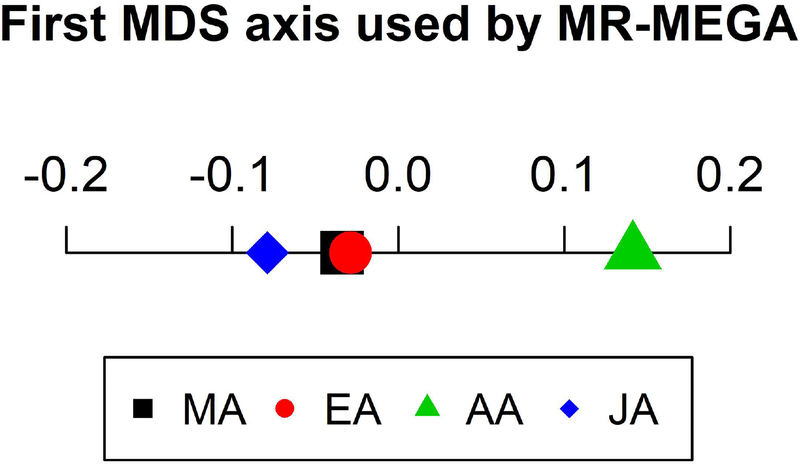
MR-MEGA appears to be slightly more conservative than the other methods and detected half as many SNPs to be suggestive compared to TransMeta and did not detect any SNPs to be genome-wide significant (Table 1). However, MR-MEGA may be better able to detect loci driven by a single ethnic group compared to the other methods. This observation is also supported by (Magi et al., 2017) where simulations found that MR-MEGA had the greatest increases in power over FE and RE2 in a simulation scenario characterized by a single ethnic group driven locus. Figure 6 shows that the MDS axis used by MR-MEGA when analyzing the GENNID data set separates the African-American group from the other three ethnic groups. This explains why MR-MEGA best detects loci driven by African-American effects (Figure 4), where all other methods had p – value >1e − 4 at this locus. Although replication through an independent data set is needed, this locus may represent a novel finding that resulted from increased power from using the trans-ethnic method MR-MEGA.

Figure 6:

First MDS axis of the genetic distance matrix calculated by MR-MEGA. The axis separates the African-American group from the other three groups, allowing MR-MEGA to better detect loci driven by African-American effects.

Generally, the same set of variants were detected by the four meta-analysis methods; however, there were some differences. While it is unclear why the two trans-ethnic methods seem to detect different types of loci, it is possible that the use of slightly different genetic distance metrics to model trans-ethnic effects (see Methods) or how each method integrates trans-ethnic effects into its model structure contributes to these differences. Simulations could help to answer these questions and provide additional information on which to judge performance. Since TransMeta can adaptively choose the appropriate amount of heterogeneity to model and is able to collapse to an FE model, TransMeta may have more power to detect loci across a wider range of effects than MR-MEGA (homogeneous to moderate trans-ethnic effects). However, TransMeta does not seem able to capture the same heterogeneity as MR-MEGA in the GENNID data. This is likely because MR-MEGA always models heterogeneity by permanently including the MDS axes as covariates, where the MDS axes explain the directions of most variation between studies. Thus, MR-MEGA is better able to capture scenarios of heterogeneity characterized by the MDS axes than TransMeta (as seen in the GENNID data set with African-American driven signals). However, since the framework of MR-MEGA is not as flexible as TransMeta, the types of trans-ethnic signals MR-MEGA can detect is limited to the MDS axes included. This can be an issue for meta-analyses with a small number of samples (like the GENNID data set), since the maximum number of MDS axes that can be included is n − 3.

Additionally, since MR-MEGA always models heterogeneity between studies, it is poorly powered to capture homogeneous effects, and the authors recommend implementing FE in conjunction to MR-MEGA to help address this shortcoming of the method (Magi et al., 2017). Since the process of applying MR-MEGA and FE would call for a multiple testing correction, more study is needed to discern if this dual approach is advantageous to TransMeta in practice. Note that we did not compare the trans-ethnic meta-analysis method MANTRA (Morris, 2011) because TransMeta and MR-MEGA have been shown to be more powerful or comparable to MANTRA across all simulation comparisons (Magi et al., 2017; Shi & Lee, 2016).

In conclusion, we empirically evaluated four trans-ethnic methods and found apparent differences between the methods when applied to the GENNID data set. Simulations are needed to adequately compare the efficiency of the methods under a wider range of ethnic group combinations not captured by the GENNID data. Simulations could better address differences between TransMeta and MR-MEGA by allowing better characterization as to when each method is optimal, which could lead to a better understanding of when each trans-ethnic method appears to be better powered in different scenarios.